Optimal Scheduling of Power Systems with High Proportions of Renewable Energy Accounting for Operational Flexibility
Abstract
1. Introduction
2. Flexibility Resources and Demand on Multiple Time Scales
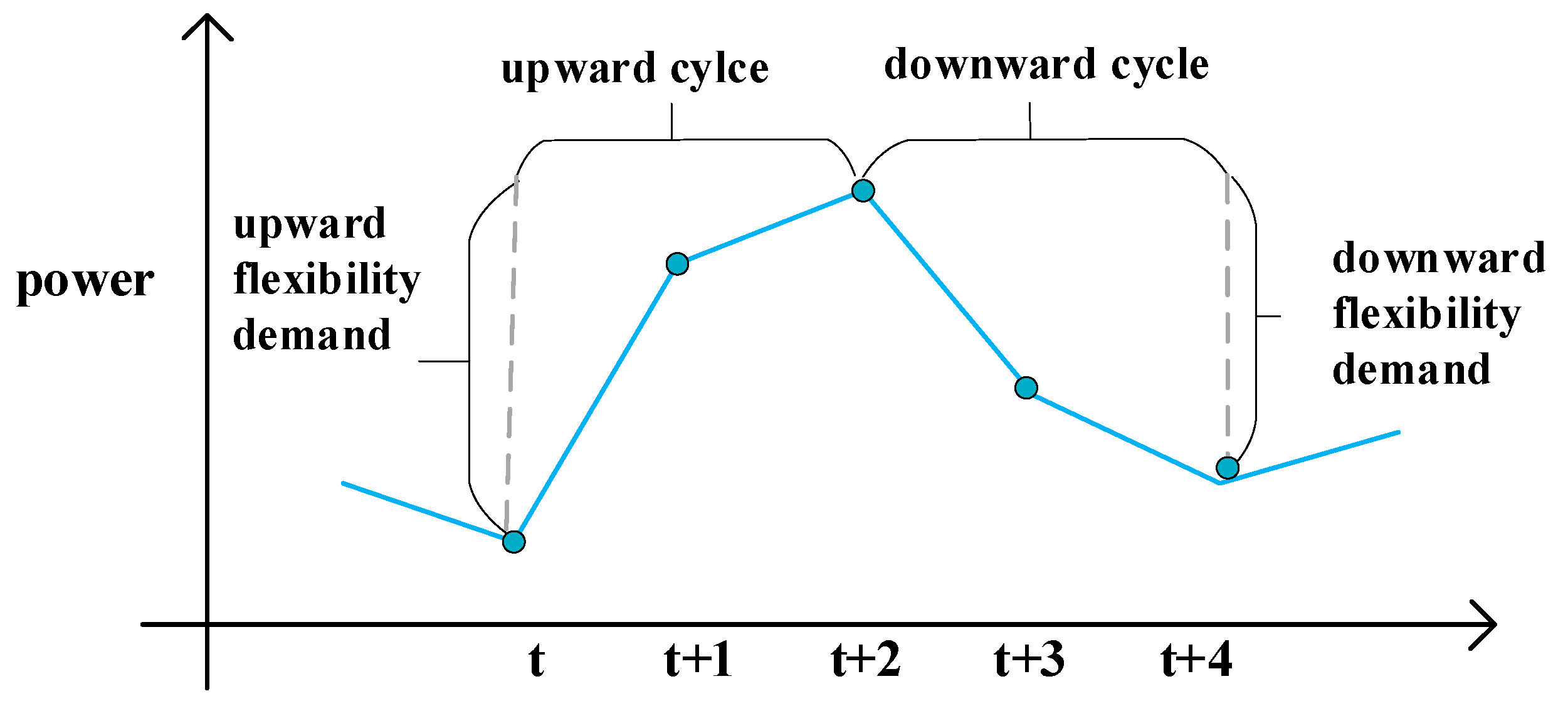
2.1. Flexibility Demand
2.2. Flexibility Resources
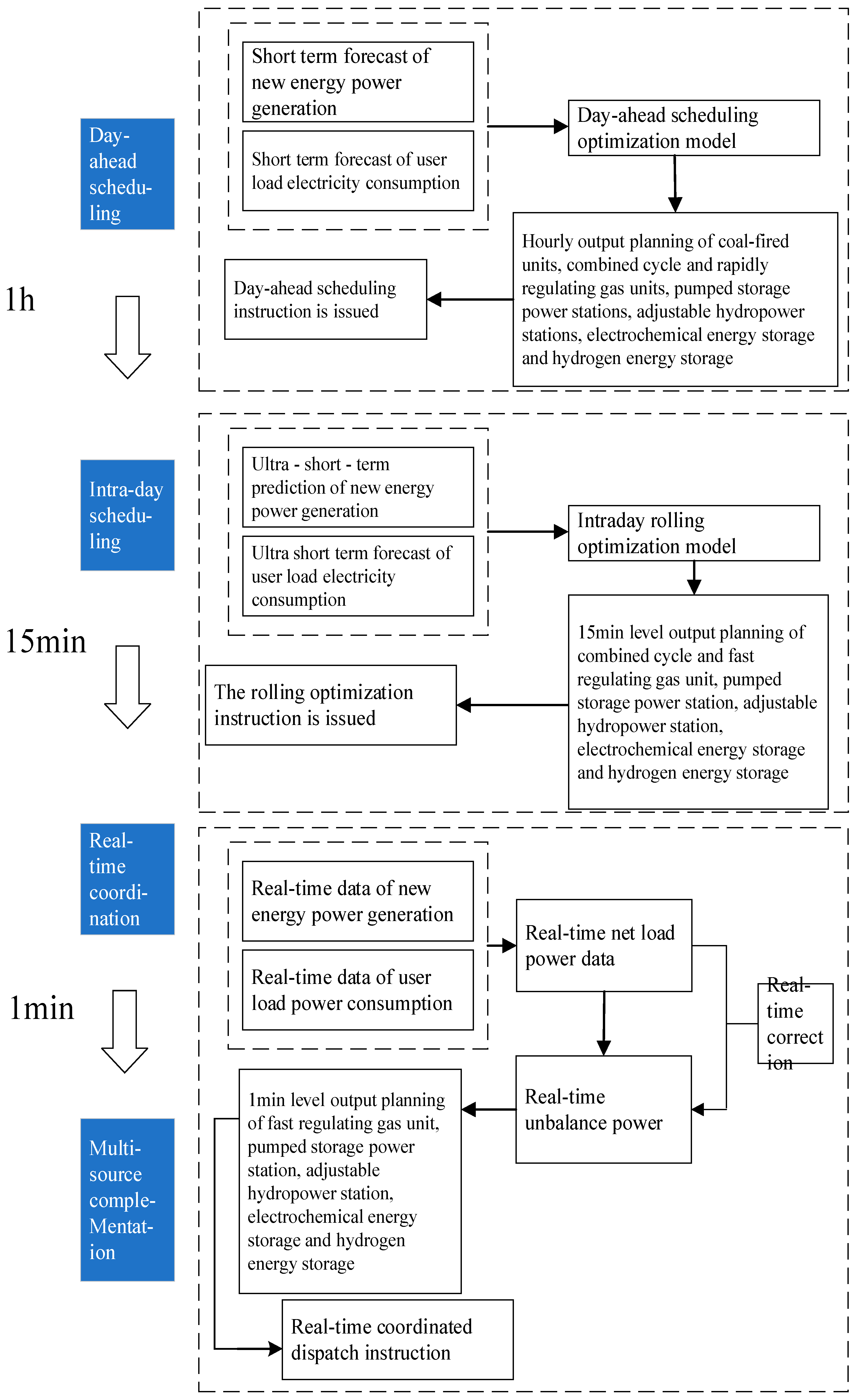
3. Flexibility Resource Scheduling Based on Multi-Time Scale
3.1. Day-Ahead Unit Commitment Based on the Flexibility Index
3.2. Multi-Time Scale Optimal Scheduling for Flexibility Resources
3.3. Intra-Day Rolling Scheduling Model
3.3.1. Objective Function
3.3.2. Constraints
3.4. Intra-Day Real-Time Scheduling Model
3.4.1. Objective Function
3.4.2. Constraints
4. Case Studies
4.1. System Parameters
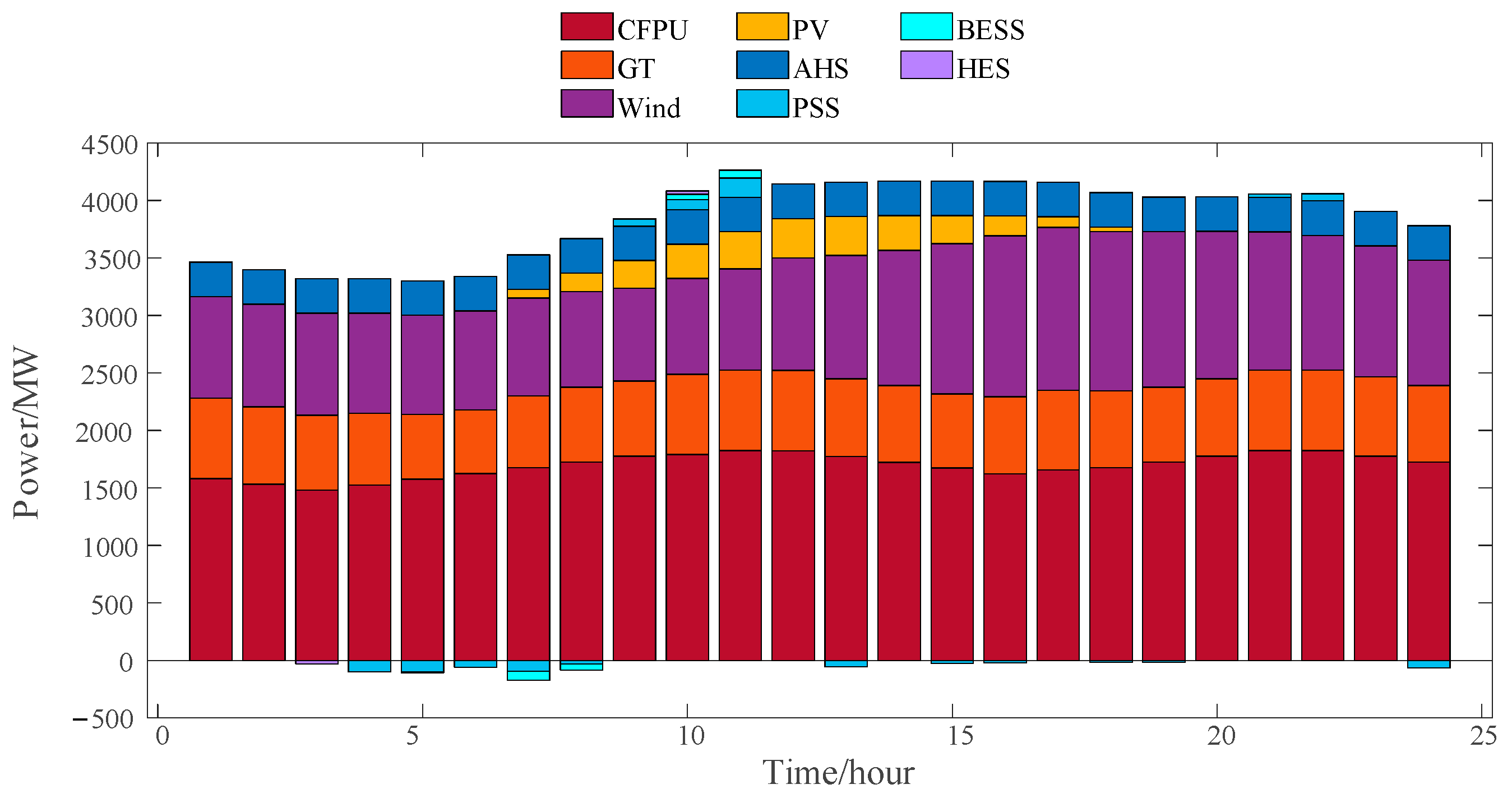
4.2. Analysis of Typical Summer Day Scheduling
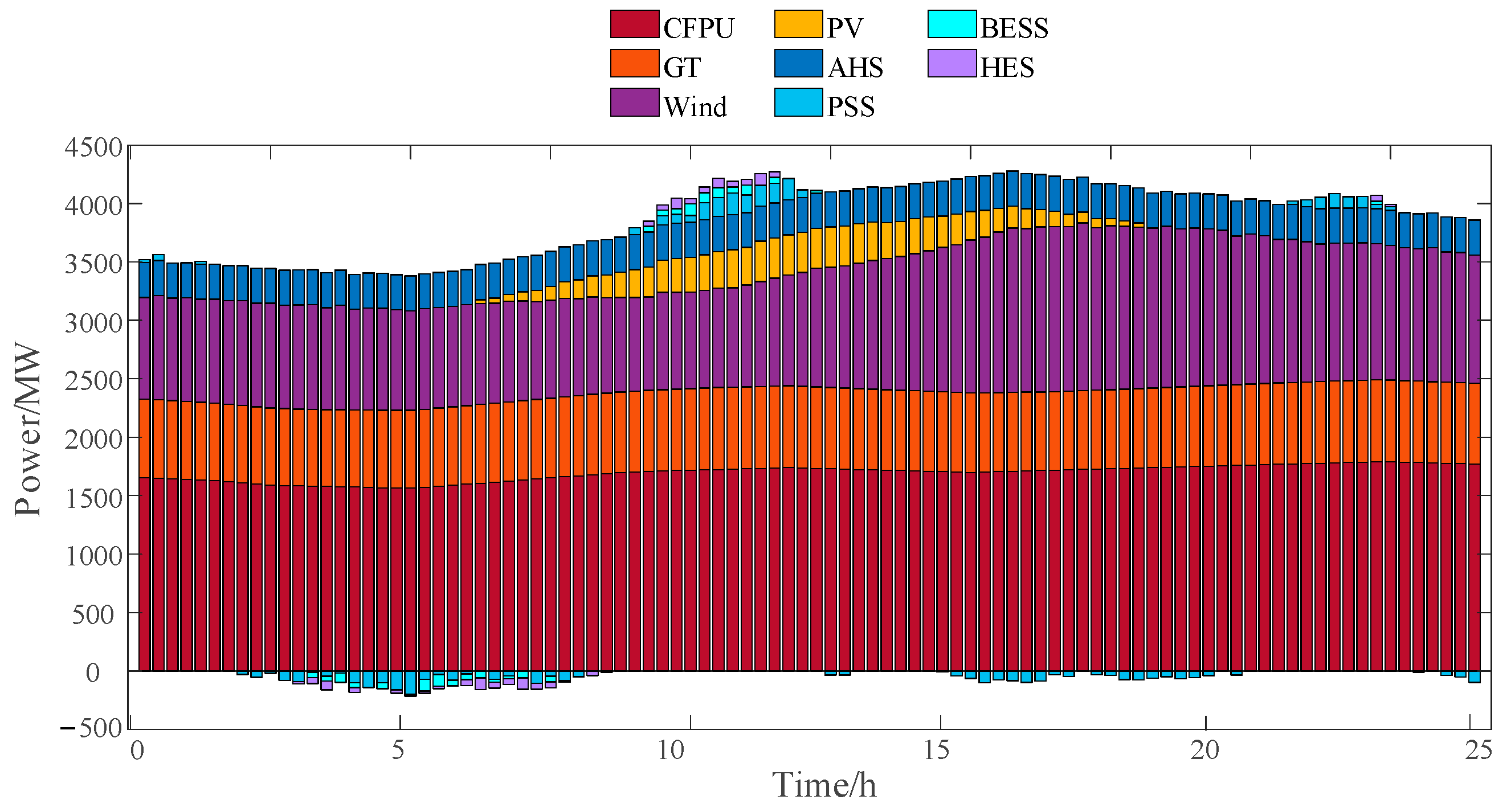
4.2.1. Day-Ahead Scheduling Analysis
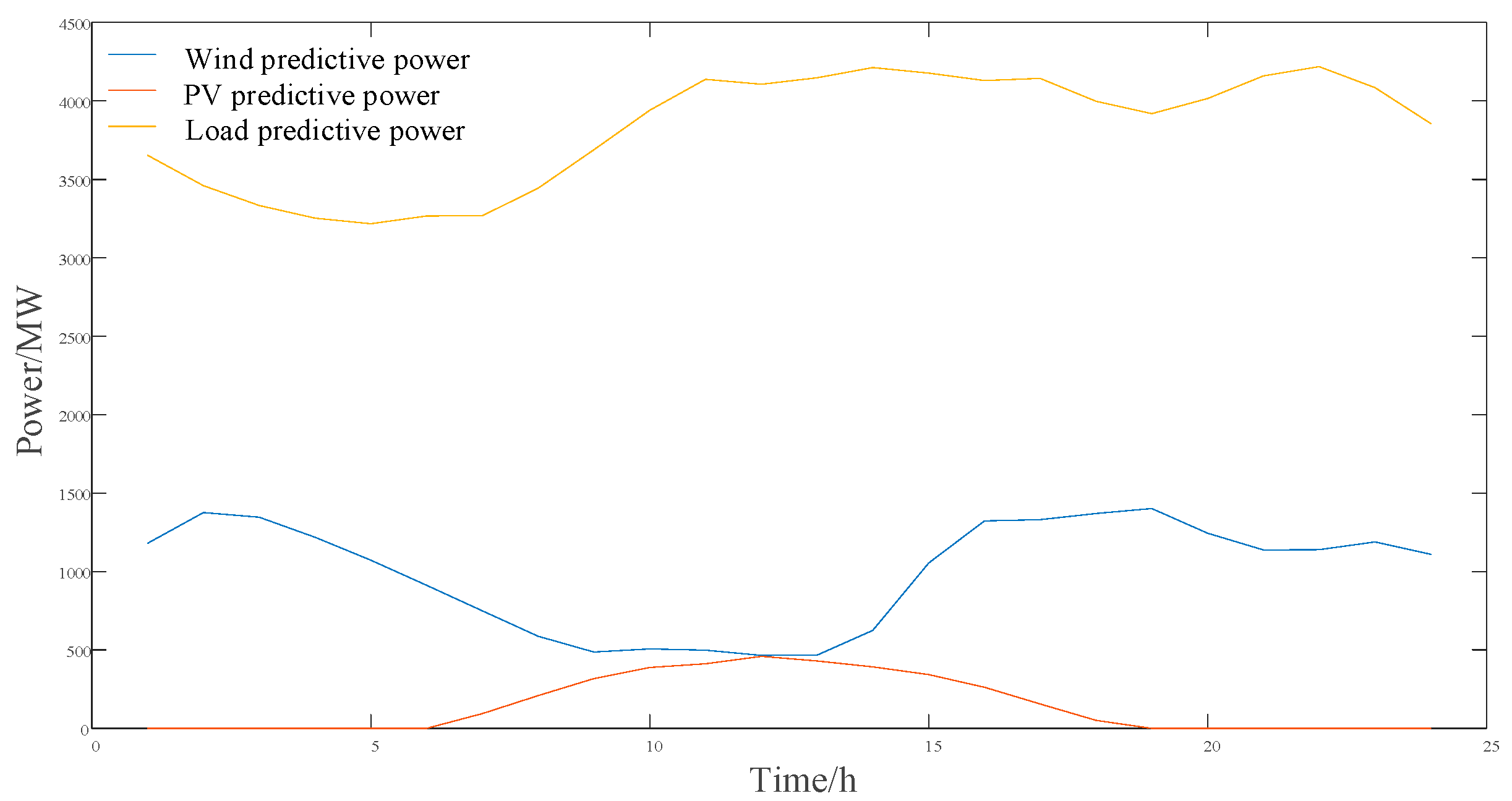
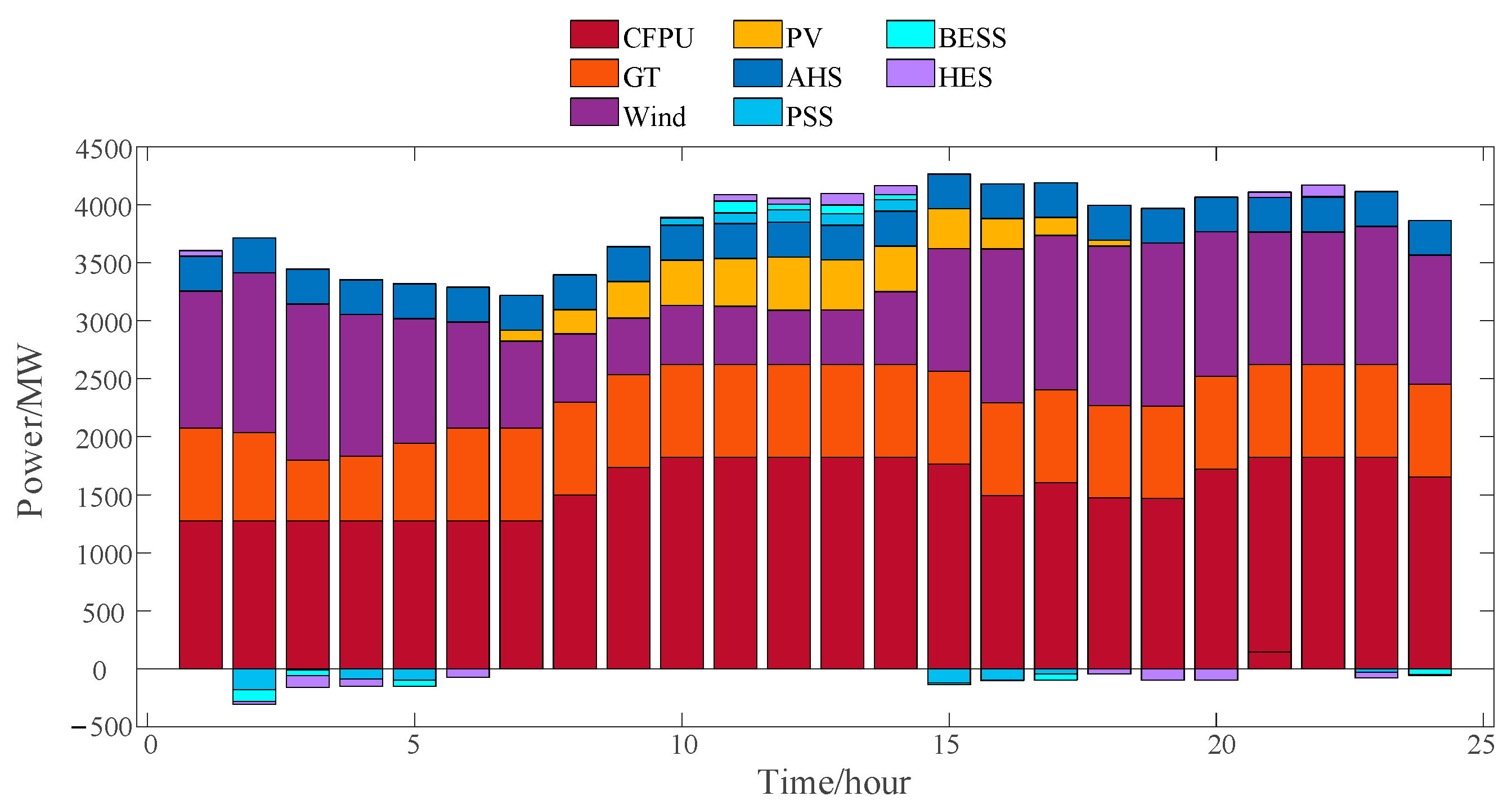
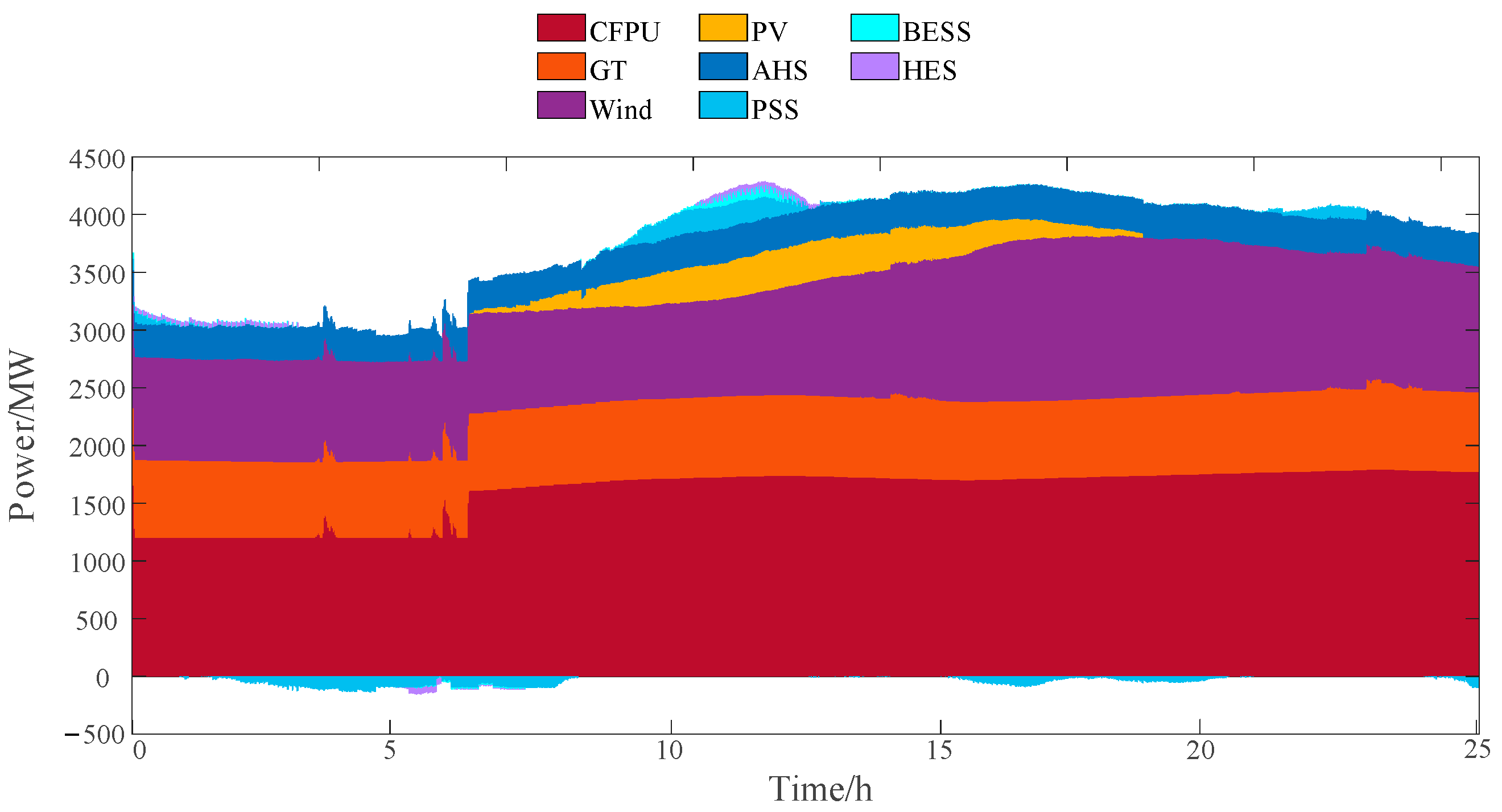
4.2.2. Intra-Day Scheduling Analysis
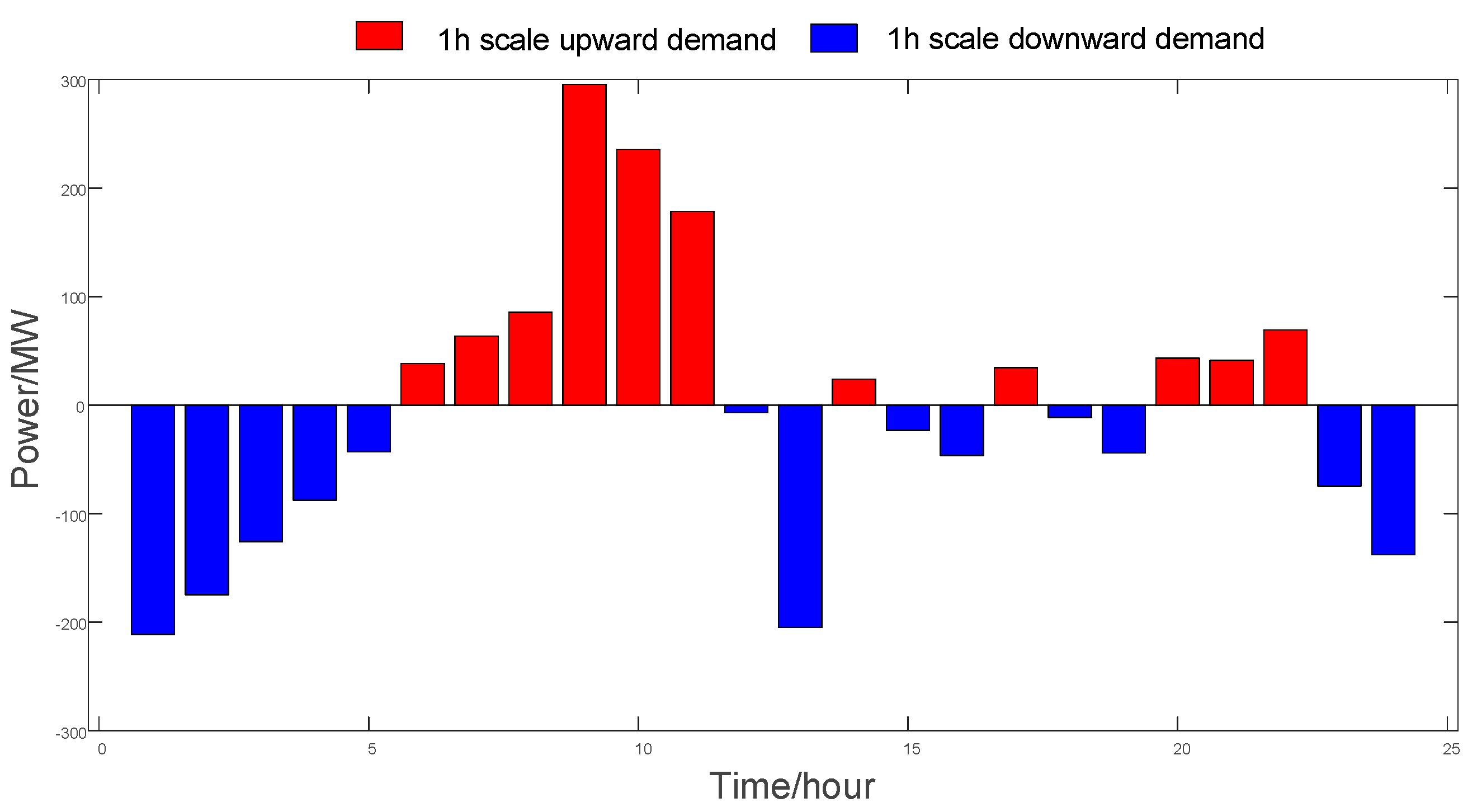
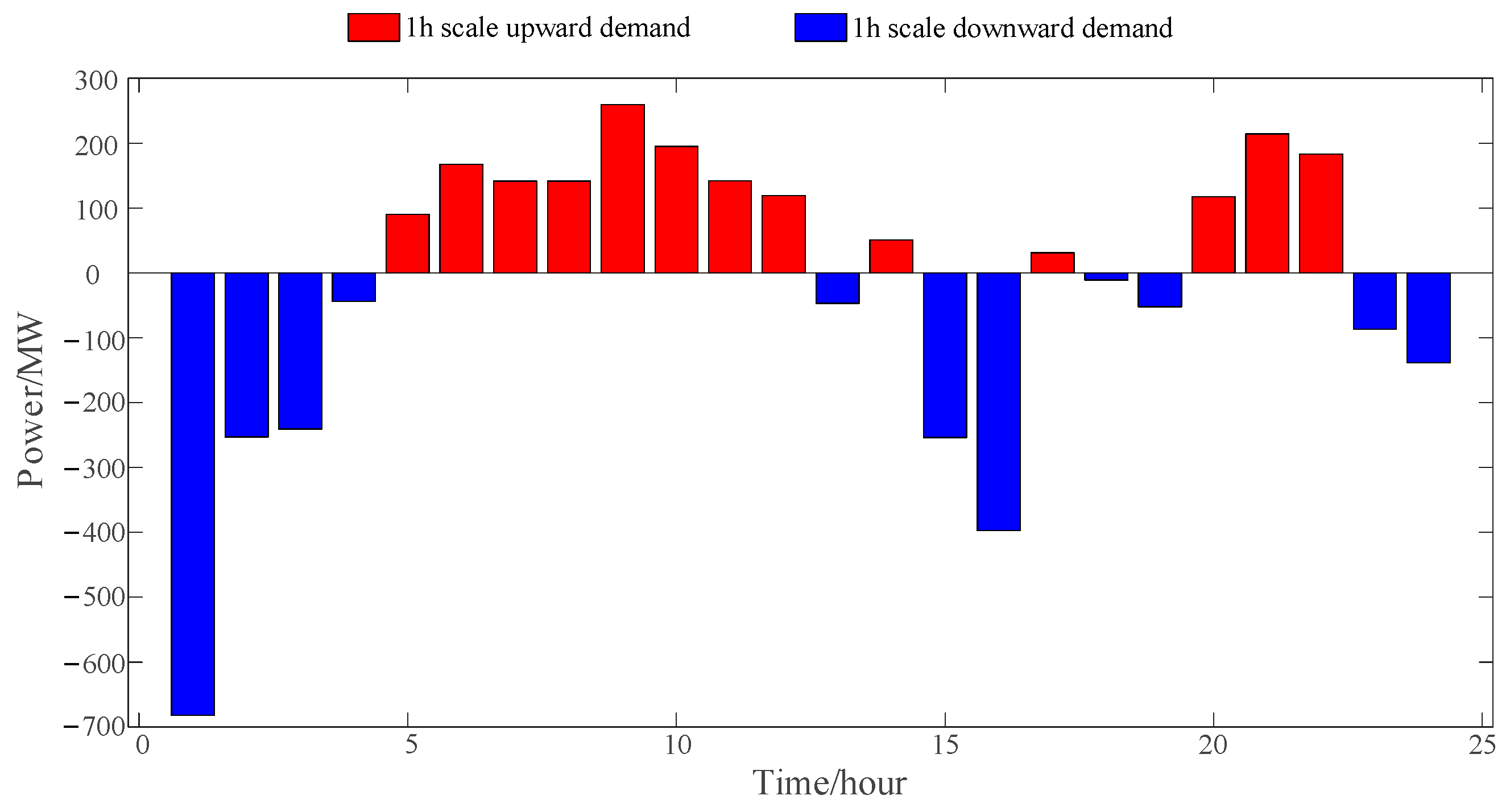
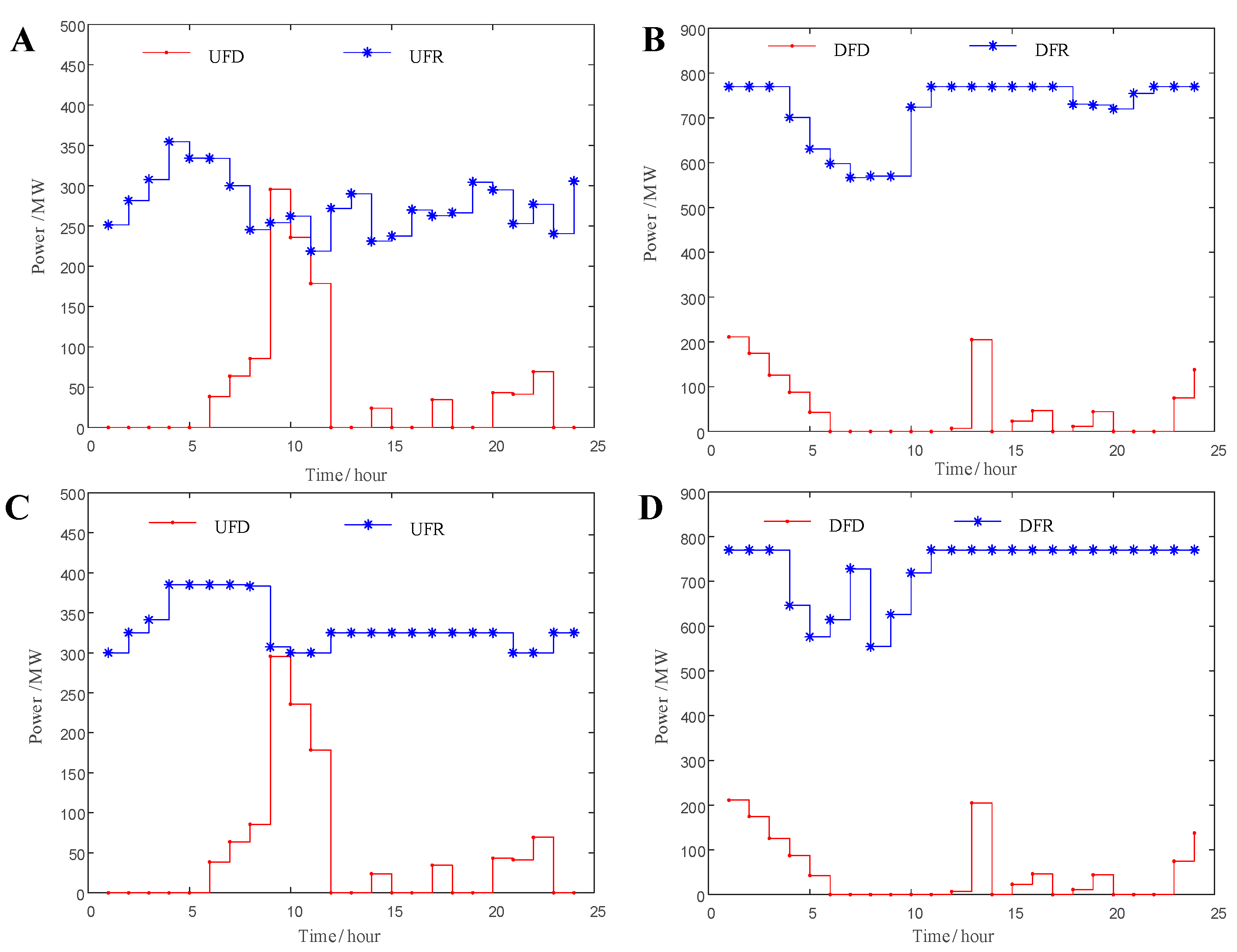
4.2.3. System Flexibility Constraint Analysis
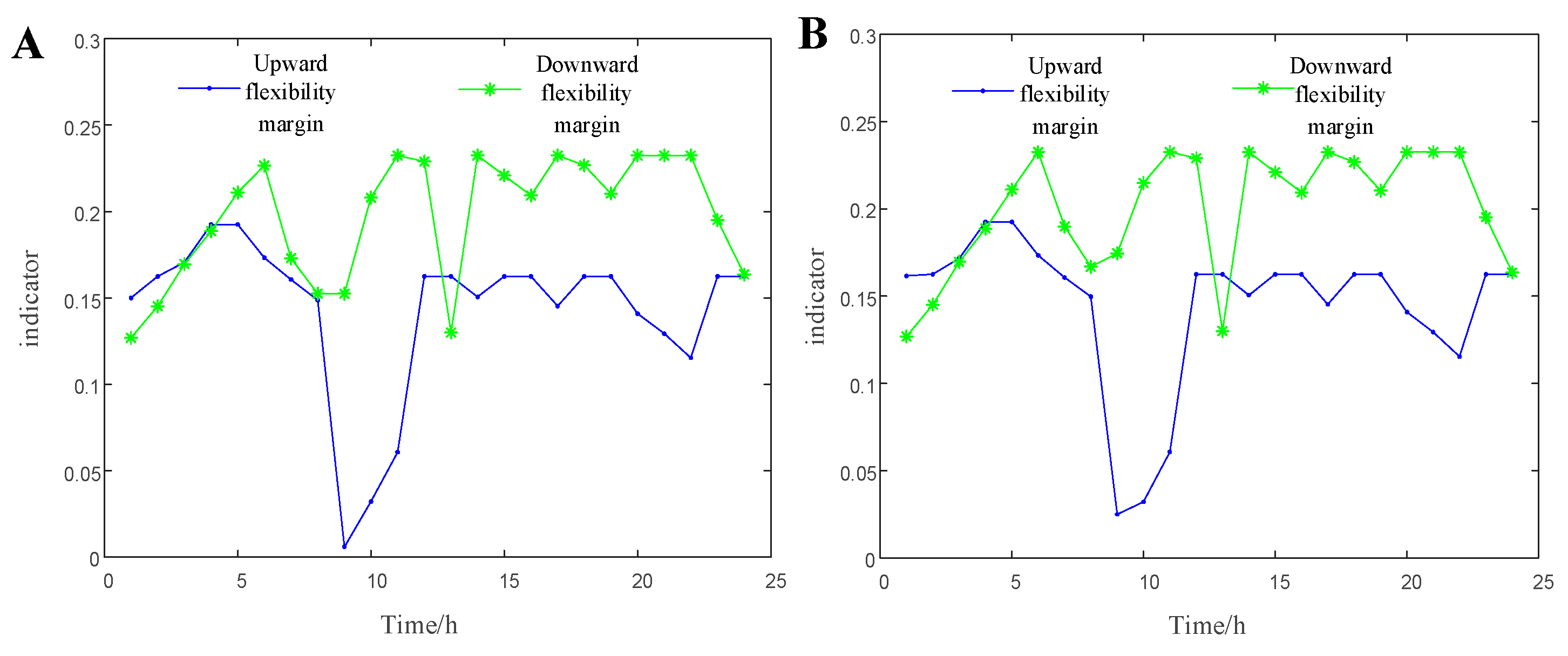
4.2.4. System Flexibility Margin
4.3. Scheduling Scheme with Hydrogen Energy Storage
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
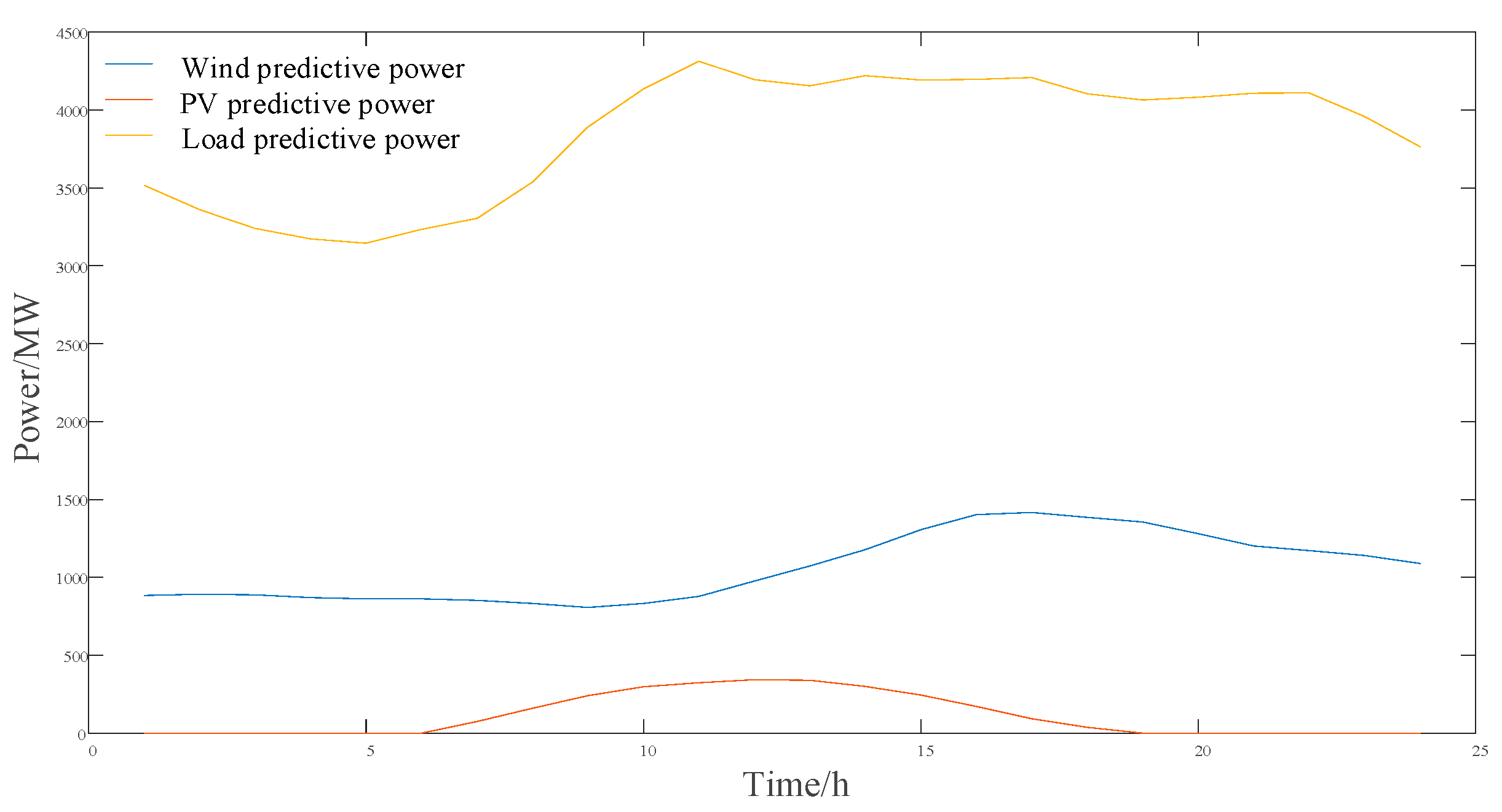
| Unit Number | Node | Pmax/MW | Pmin/MW | a/b/c/($/(MWh)2)/($/(MWh))/$ | Ramp Rate/(MW/h) | Startup Cost/$ | Minimum Startup Time/h |
|---|---|---|---|---|---|---|---|
| 1 | 30 | 550 | 50 | 0.00024/25.53/615.40 | 50 | 84.79 | 5 |
| 2 | 31 | 400 | 50 | 0.00031/22.31/610.74 | 200 | 70.65 | 5 |
| 3 | 32 | 325 | 50 | 0.00101/14.88/339.85 | 55 | 79.13 | 5 |
| 4 | 33 | 350 | 50 | 0.00056/18.16/321.48 | 40 | 70.65 | 5 |
| 5 | 38 | 300 | 50 | 0.00028/20.48/367.40 | 150 | 36.74 | 5 |
| 6 | 39 | 600 | 50 | 0.00069/27.78/918.51 | 80 | 127.18 | 5 |
References
- Taibi, E.; Nikolakakis, T.; Gutierrez, L.; Fernandez, C.; Kiviluoma, J.; Rissanen, S.; Lindroos, T. Power System Flexibility for the Energy Transition: Part 1, Overview for Policy Makers. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2018/Nov/IRENA_Power_system_flexibility_1_2018.pdf (accessed on 15 November 2022).
- Project Team on the Strategy and Pathway for Peaking Carbon Emissions and Carbon Neutrality. Analysis of a Peaked Carbon Emission Pathway in China Toward Carbon Neutrality. Engineering 2021, 7, 1673–1677. [Google Scholar] [CrossRef]
- IEA. European Union 2020 Energy Policy Review. 2020. Available online: https://www.iea.org/reports/european-union-2020 (accessed on 1 December 2022).
- Lu, X.; McElroy, M.B.; Peng, W.; Liu, S.; Nielsen, C.P.; Wang, H. Challenges faced by China compared with the US in developing wind power. Nat. Energy 2016, 1, 16061. [Google Scholar] [CrossRef]
- IEA. Empowering Variable Renewables: Options for Flexible Electricity Systems; IEA: Paris, France, 2008. [Google Scholar]
- Orvis, R.; Aggarwal, R. A Roadmap for Finding Flexibility in Wholesale Markets; Energy Innovation: Policy and Technology LLC.: San Francisco, CA, USA, 2017. [Google Scholar]
- Khorramdel, B.; Chung, C.Y.; Safari, N.; Price, G.C.D. A Fuzzy Adaptive Probabilistic Wind Power Prediction Framework Using Diffusion Kernel Density Estimators. IEEE Trans. Power Syst. 2018, 33, 7109–7121. [Google Scholar] [CrossRef]
- Du, P.; Mago, N.V.; Li, W.; Sharma, S.; Hu, Q.; Ding, T. New Ancillary Service Market for ERCOT. IEEE Access 2020, 8, 178391–178401. [Google Scholar] [CrossRef]
- Chen, F.; Huang, C.; Wang, L.; Zhu, C.; Wang, C.; Xie, N. Flexibility evaluation of distribution network with high penetration of variable generations. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017. [Google Scholar]
- Tang, X.; Hu, Y.; Chen, Z.; You, G. Flexibility Evaluation Method of Power Systems with High Proportion Renewable Energy Based on Typical Operation Scenarios. Electronics 2020, 9, 627. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Y.; Wang, X.; Chang, J.; Chen, Y.; Zhou, Y.; Guo, A. Flexibility evaluation of wind-PV-hydro multi-energy complementary base considering the compensation ability of cascade hydropower stations. Appl. Energy 2022, 315, 119024. [Google Scholar] [CrossRef]
- Xu, H.; Chang, Y.; Zhao, Y.; Wang, F. A new multi-timescale optimal scheduling model considering wind power uncertainty and demand response. Int. J. Electr. Power Energy Syst. 2023, 147, 108832. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Y.; Ning, J.; Zhao, J. Multi-Time Scale Coordinated Scheduling Strategy with Distributed Power Flow Controllers for Minimizing Wind Power Spillage. Energies 2017, 10, 1804. [Google Scholar] [CrossRef]
- Jiang, X.M.; Li, Q.F.; Yang, Y.W.; Zhang, L.T.; Liu, X.J.; Ning, N. Optimization of the operation plan taking into account the flexible resource scheduling of the integrated energy system. Energy Rep. 2022, 8, 1752–1762. [Google Scholar] [CrossRef]
- Castillo, A.; Gayme, D.F. Grid-scale energy storage applications in renewable energy integration: A survey. Energy Convers. Manag. 2014, 87, 885–894. [Google Scholar] [CrossRef]
- El-Taweel, N.A.; Khani, H.; Farag, H.E.Z. Hydrogen Storage Optimal Scheduling for Fuel Supply and Capacity-Based Demand Response Program Under Dynamic Hydrogen Pricing. IEEE Trans. Smart Grid 2019, 10, 4531–4542. [Google Scholar] [CrossRef]
- Yang, Y.; Chao, M.; Chong, L.; Yusheng, Z.; Xiulan, P. Optimal power reallocation of large-scale grid-connected photovoltaic power station integrated with hydrogen production. J. Clean. Prod. 2021, 298, 126830. [Google Scholar] [CrossRef]
- Marchenko, O.V.; Solomin, S.V. Modeling of hydrogen and electrical energy storages in wind/PV energy system on the Lake Baikal coast. Int. J. Hydrogen Energy 2017, 42, 9361–9370. [Google Scholar] [CrossRef]
- Wang, H.; Hu, J.; Dong, D.; Wang, C.; Tang, F.; Wang, Y.; Feng, C. Research on Evaluation of Multi-Timescale Flexibility and Energy Storage Deployment for the High-Penetration Renewable Energy of Power Systems. Comput. Model. Eng. Sci. 2022, 134, 1137–1158. [Google Scholar] [CrossRef]
- Su, S.; Tan, D.; Li, X.; Li, X.; Chen, Z.; Lian, R.; Lenz Soronga, B.K. Multi-time Scale Coordinated Optimization of New Energy High Permeability Power System Considering Flexibility Requirements. J. Electr. Eng. Technol. 2022, 18, 815–828. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Y.; Li, K.; Li, Z. Unit commitment of power system with large-scale wind power considering multi time scale flexibility contribution of demand response. Energy Rep. 2021, 7, 342–352. [Google Scholar] [CrossRef]
- Zenebe, D.M.; Bakken, S.I.; Hanne, S. Comprehensive classifications and characterizations of power system flexibility resources. Electr. Power Syst. Res. 2021, 194, 107022. [Google Scholar]
- Bødal, E.F.; Lakshmanan, V.; Sperstad, I.B.; Degefa, M.Z.; Hanot, M.; Ergun, H.; Rossi, M. Demand flexibility modelling for long term optimal distribution grid planning. IET Gener. Transm. Distrib. 2022, 16, 5002–5014. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Wang, Z.; Yang, J.; Lou, S. Multi-Flexibility Resources Planning for Power System Considering Carbon Trading. Sustainability 2022, 14, 13296. [Google Scholar] [CrossRef]
| 0 min | 15 min | 1 h | ||
|---|---|---|---|---|
| Thermal power unit | RRGT |  | ||
| CCGT |  | |||
| CFPU |  | |||
| Hydroelectric power unit | AHS |  | ||
| PSS |  | |||
| BESS |  | |||
| HES |  | |||
| Scheduling Scheme | Total Operating Cost/$ | Wind Power Curtailment Rate/% |
|---|---|---|
| 1 | 1.1544 × 106 | 5.63 |
| 2 | 1.1333 × 106 | 3.41 |
| 3 | 1.1178 × 106 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Lin, W.; Wu, W.; Zhu, Z. Optimal Scheduling of Power Systems with High Proportions of Renewable Energy Accounting for Operational Flexibility. Energies 2023, 16, 5537. https://doi.org/10.3390/en16145537
Lin Y, Lin W, Wu W, Zhu Z. Optimal Scheduling of Power Systems with High Proportions of Renewable Energy Accounting for Operational Flexibility. Energies. 2023; 16(14):5537. https://doi.org/10.3390/en16145537
Chicago/Turabian StyleLin, Yi, Wei Lin, Wei Wu, and Zhenshan Zhu. 2023. "Optimal Scheduling of Power Systems with High Proportions of Renewable Energy Accounting for Operational Flexibility" Energies 16, no. 14: 5537. https://doi.org/10.3390/en16145537
APA StyleLin, Y., Lin, W., Wu, W., & Zhu, Z. (2023). Optimal Scheduling of Power Systems with High Proportions of Renewable Energy Accounting for Operational Flexibility. Energies, 16(14), 5537. https://doi.org/10.3390/en16145537






