Abstract
Machine learning-based time-series forecasting has recently been intensively studied. Deep learning (DL), specifically deep neural networks (DNN) and long short-term memory (LSTM), are the popular approaches for this purpose. However, these methods have several problems. First, DNN needs a lot of data to avoid over-fitting. Without sufficient data, the model cannot be generalized so it may not be good for unseen data. Second, impaired data affect forecasting accuracy. In general, one trains a model assuming that normal data enters the input. However, when anomalous data enters the input, the forecasting accuracy of the model may decrease substantially, which emphasizes the importance of data integrity. This paper focuses on these two problems. In time-series forecasting, especially for photovoltaic (PV) forecasting, data from solar power plants are not sufficient. As solar panels are newly installed, a sufficiently long period of data cannot be obtained. We also find that many solar power plants may contain a substantial amount of anomalous data, e.g., 30%. In this regard, we propose a data preprocessing technique leveraging convolutional autoencoder and principal component analysis (PCA) to use insufficient data with a high rate of anomaly. We compare the performance of the PV forecasting model after applying the proposed anomaly detection in constructing a virtual power plant (VPP). Extensive experiments with 2517 PV sites in the Republic of Korea, which are used for VPP construction, confirm that the proposed technique can filter out anomaly PV sites with very high accuracy, e.g., 99%, which in turn contributes to reducing the forecasting error by 23%.
1. Introduction
Recently, carbon neutrality has become crucial to prevent climate change. Carbon neutrality is a concept that reduces greenhouse gas (GHG) emissions from human activities with the goal of net emission zero. To realize carbon neutrality, renewable generation should increase up to 71% by 2050 to reform the energy system [1,2]. The transition to a sustainable energy system is a pressing challenge, and renewable energy sources such as solar power are critical to achieving this goal. In this regard, the Republic of Korea’s government has also announced a commitment to carbon neutrality by 2050, given that the Republic of Korea’s greenhouse gas emissions are the seventh highest in the world [3].
Solar energy has the potential to provide a reliable, sustainable, and cost-effective source of electricity, particularly in regions with high levels of solar radiation. However, the integration of large amounts of solar energy into the grid presents technical challenges, including the need for accurate forecasting of solar power generation. Many papers have recently discussed the challenges and opportunities associated with its implementation. For example, In [4], the authors discussed the importance of solar energy technology in promoting sustainable development, arguing that it has the potential to reduce greenhouse gas emissions and increase access to energy in developing countries. In [5], the authors provided a comprehensive review of the literature on renewable energy and its role in promoting sustainable development. Specifically, the authors examined various aspects of renewable energy (including solar power generation) such as technology, policy, and finance.
The main factors that affect solar power forecasts are daily weather conditions and seasonal insolation [6]. In an early study, a physical model that considers the relationship between insolation and solar power generation among the above factors was studied first [7], which approximates the insolation with a model that calculates power generation through the rotation of the earth and the equivalent circuit of the PV cell. Since then, statistical prediction models using traditional forecasting techniques such as autoregressive moving average (ARMA) [8] and multiple linear regression (MLR) [9], have been proposed [10]. However, traditional solar forecasting through such modeling lacks adaptability to weather changes, and it is difficult to accurately predict how much solar power will be generated under different weather conditions.
Since then, there has been a need for an artificial intelligence (AI)-based PV forecasting model that can handle data uncertainty. Recently, machine learning and artificial intelligence techniques have shown great promise in improving the accuracy of PV forecasting. In one paper, ref. [11] proposed a method for estimating global solar radiation using meteorological variables, including sunshine duration. This method is popular as a benchmark for solar radiation estimation. In [12], the authors reviewed the state-of-the-art in solar radiation modeling, including physical models and empirical models. In [13], the authors investigated the impact of feature selection methods on solar power forecasting performance.
In early studies applying deep learning, multi-layer perceptron (MLP)-based models were the most commonly used for solar power generation forecasting. For example, in [14], an MLP was used to forecast solar power generation in Zimbabwe. Similarly, in [15], an MLP was used to forecast solar power generation in Malaysia, using historical weather data and solar radiation measurements as inputs to the artificial neural network (ANN) model. Later studies started to explore the use of more advanced models, such as recurrent neural network (RNN) [16] and LSTM [17]. In [18], an RNN was used to forecast solar power generation. The space–time convolutional neural network (STCNN), which exploits the location information of multiple PV sites and historical PV generation data, is used in [19]. In [20], a PV forecasting model was based on wavelet transform and LSTM-dropout network. Very recently, studies have focused on more advanced models such as attention-based models, graph neural network (GNN) [21], and transformer-based models [22]. By leveraging a transformer encoder and gated recurrent unit (GRU), a framework based on Delaunay triangulation and TransGRU model forecasts PV with robustness against weather forecast error [23]. In [24], leveraging deep reinforcement learning using proximal policy optimization [25], error compensable forecasting is adopted, which switches the objective of forecasting from reducing errors to making compensable errors.
Although the above studies show improved solar power forecasting performance, they assume data without abnormal points. However, the reliability of collected solar power generation data directly affects the performance and reliability of the learning model. That is, when anomalous data enters the input, the accuracy of deep learning-based forecasting models can substantially deteriorate. Therefore, it is necessary to include anomaly detection as a preprocessing stage in PV power forecasting. Note that anomaly detection studies in solar power forecasting mainly focused on cyberattacks or false detection. They detected the data points with false data injection to prevent the power systems from malicious attackers. However, even without false data injection, anomalous data points can exist. In [26], the authors designed a fault classifier based on thermal image processing using a support vector machine (SVM) by performing anomaly detection at the physical level. In [27], the authors proposed an unsupervised monitoring system at the physical level by inspecting the DC part of the PV system through momentary shading based on SVM. In [28], the authors learned by replacing anomalies with predicted values. At each time step, the authors performed simple anomaly detection and then replaced it with DL-based predicted values to compare the prediction performance. By analyzing the performance of the machine learning models, in [6], the authors identified the best model that can accurately detect anomalies in PV systems. The correlation coefficient between the internal and external characteristic parameters of the power plant is obtained to analyze the anomaly detection efficiency of the machine learning models.
In the real world, solar data potentially have anomalous values due to errors in sensor measurements. In addition, many solar power plants in the Republic of Korea are classified as behind-the-meters (BTMs), which are small-scale generators of 1 MW or less and do not have real-time generation metering. This is one of the factors that greatly increases the uncertainty of power generation forecasts and hinder the forecasting model’s ability to learn in a supervised manner.
In the case of a virtual power plant (VPP), the next day’s power generation is forecasted through collective resources, and a forecasting incentive is given depending on accuracy. However, when anomalous data are included and the power generation pattern is erratic, forecasting performance may be significantly degraded. In fact, we observe that the collected solar power plant data from private owners differ from general power generation patterns, possibly due to the combination of energy storage systems (ESS), which may not be known in advance from the VPP operator’s perspective.
To this end, we propose an integrated anomaly detection framework leveraging a convolutional autoencoder that proactively identifies and removes anomalous data. Then, we configure VPP after filtering out anomaly and forecast power generation using deep learning. We summarize our key contributions as follows.
- We propose a preprocessing method along with a forecasting model for various PV sites that exhibit anomalous power generation. Unlike general PV forecasting, which assumes normal power generation or knowledge of the anomaly in the BTM situation, we proactively detect anomalous sites.
- For interpretable anomaly detection, we develop a model that combines convolutional autoencoder (CAE) and principal component analysis (PCA) to extract and analyze the features of solar power data with scree plot analysis. As a result, we can extract and utilize features that contain important information from solar power data as low-dimensional vectors.
- Our methodology is designed to be robust to real-world data. Leveraging the proposed anomaly detection above, we compare two types of VPPs: the VPP with only normal sites and the VPP with a random mixture of anomaly and normal sites. Based on this, we show that simple and efficient unsupervised learning to construct a VPP with only normal PV sites leads to better forecasting performance than the other case. We observe that the forecasting error of the normal VPP is 6% or less, which satisfies the condition for receiving full incentives in the renewable energy wholesale market run by Korea Power Exchange (KPX).
The rest of this paper is organized as follows. Section 2 analyzes the actual PV site data and proposes an anomaly detection model and the structure of the PV forecasting model. Section 3 presents the forecasting results before and after anomaly detection for VPPs of two experimental groups, followed by the conclusion in Section 4.
2. Proposed Methodologies
2.1. Dataset
The power generation data consists of 2517 PV sites. The data collection period is 616 days of an hour per unit. To motivate our study, we first show the forecasting performance using a multi-perceptron neural network in Table 1. As can be seen in Table 1 and Figure 1, the individual forecasting performance of three sites, “site S6”, “site S7” and “site S8”, shows a big difference even though these sites are closely located; the performance difference mainly comes from the presence of anomalous data.

Table 1.
PV forecasting with MLP based single site model.
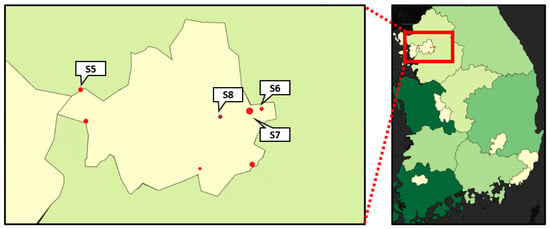
Figure 1.
Visualization of PV sites (S5 to S8).
To investigate the anomalous data pattern, we show the normal pattern of the daily PV generation profiles in Figure 2. As can be seen in Figure 2, a typical daily PV generation has a bell shape. Since using only a daily PV profile is not good for PV site anomaly detection, we use overlapped PV profiles for the whole period of data. Similarly, anomalous PV profiles are shown in Figure 3. As can be seen, anomalous daily PV profiles have distinctive patterns, which do not seem to be solely PV generation. This could be the combination of PV generation and battery charging/discharging and/or data collection errors. Surprisingly, 33% of PV sites turn out to have these anomalous patterns, which leads us to develop an anomaly detection technique.

Figure 2.
Overlapped PV daily curves of normal sites.

Figure 3.
Overlapped PV daily curves of anomalous sites.
2.2. Anomaly Detection
Prior to anomaly detection, 1-dimensional time-series data are normalized first. The normalized data of overlapped PV profiles are represented as a stacked daily solar profile (SDSP) as shown in Figure 4, which is a 2-dimensional image. CAE is trained using this image, and a latent vector is obtained from the last layer of the encoder. The obtained latent vector has compressed information, and we use this feature in anomaly detection. Specifically, we use PCA to reduce the dimension of the latent vector and also to project the vector into new feature axes which have lower dimensions. Based on the covariance matrix of PCA-projected vectors and its eigenvalue, the scree plot analysis is used to determine the valid feature dimension. Finally, K-means clustering is used to separate the normal PV sites and the anomalous PV sites. The overall process of the proposed anomaly detection is summarized in Figure 5, and we here present each part one by one.

Figure 4.
Heatmap visualization of normal and anomaly data.
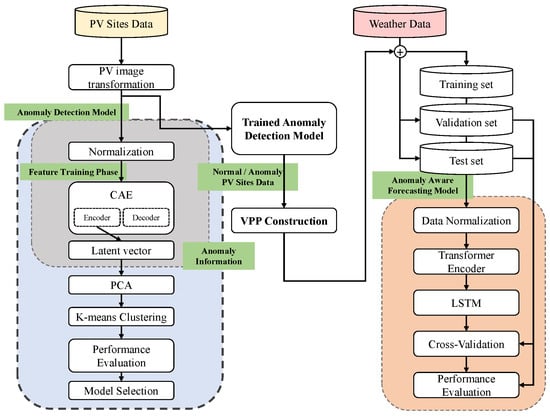
Figure 5.
Anomaly-aware Forecasting Architecture.
2.2.1. Convolutional Autoencoder
The autoencoder is a well-known unsupervised learning algorithm that has the target output the same as its input, which can be used in various applications. The most representative applications include data compression and feature extraction, and convolutional autoencoder (CAE) [29] shows great performance with image input data. This technique also has an advantage in denoizing input image data. CAE removes noise from input data, thereby improving the quality of the data and improving the performance of forecasting models or classification models. We use this model to learn and capture the time-series feature in SDSP. Normal SDSP and anomalous SDSP are converted into latent vectors using CAE, of which the structure is shown in Figure 6. The CAE has three convolutional layers using batch normalization, ReLU activation function, and max pooling. The fully connected network is used at the fourth layer, whose output, i.e., the latent vector, is an input of the next step of PCA.

Figure 6.
Convolutional autoencoder (CAE) architecture.
2.2.2. Principal Component Analysis
Since CAE-converted SDSP’s latent vectors are in high-dimension, it is not good to directly apply clustering techniques. For example, it is well-known that K-means clustering is not effective in high-dimensional space [30]. To overcome this, we use PCA [31], which is one of the most widely used dimensional reduction techniques. PCA converts data from high-dimensional space into low-dimensional space while preserving the distribution of original data as much as possible. PCA combines existing variables to create new variables that are not related to each other. This technique attempts to explain the variance-covariance structure in a linear combination by using multivariate data composed of several features. Each vector’s variables are mapped to a low-dimensional graph, and the covariance matrix of latent vectors can form new coordinate axes. The new axes maximize the variation in the data and make it easier to interpret the covariance structure.
2.2.3. K-Means Clustering
As we mentioned above, PCA-projected latent vectors have lower dimensions than the original latent vectors so the K-means algorithm can be used for clustering the PV sites into the normal group and the abnormal group. When K-means clustering is applied, we need to determine which cluster corresponds to anomaly data. For this, we check a few PV sites we already know as an anomaly site and see where they belong to. Since this is unsupervised learning it does not require a threshold to separate two groups. Nevertheless, in Figure 12, one can imagine an implicit threshold that can separate two groups. K-means clustering is one of the clustering methods to bundle of data with similar characteristics [32]. In this algorithm, a similar characteristic means a location close to it. Euclidian distance is used to calculate each location of data. In K-means clustering, the number of clusters K should be determined using clustering indices such as the Dunn index, silhouette index, etc. In our case, it is obvious that two clusters are enough for normal and anomaly PV sites. Nevertheless, we check the clustering index in the experiment section where K = 2 is found to be the most appropriate: one for the normal group and the other for the anomalous group. The training process including model selection is given in the next section, where we explain how to select the model while avoiding overfitting or underfitting. The test result of forecasting is given in Section 3.2.
2.3. Model Selection
In this section, we show the structure of each model determined by model selection.
2.3.1. Model Selection of CAE
First, the CAE for anomaly detection is trained. The latent vector is said to be well extracted when the input of the CAE is well reconstructed. Figure 7 visualizes the reconstructed PV profiles of the randomly selected normal and anomalous sites. Comparing the input SDSP with the reconstructed one confirms that normal and anomalous patterns are clearly preserved during reconstruction. In addition, the reconstructed SDSP is not visually distinguishable from the original SDSP.

Figure 7.
Visualization of CAE reconstruction with heatmap (left: original, right: reconstructed).
The latent vector dimension of CAE is chosen as 64 by the model selection process shown in Table 2. We test CAE with different a, b, and c layer configurations, where a and b indicate the kernel size and output channel size of the convolutional layer, and c indicates the latent vector size of the CAE. Then we compare the model complexity, which is the number of parameters of the CAE. As can be seen in Table 2, the layer configuration with 3, 2, 64 shows the highest silhouette score while others show similar anomaly detection scores such as accuracy, precision, recall, and F1 score. With our proposed model, we can minimize the model complexity and also maximize the silhouette score.

Table 2.
Anomaly detection model structures in the model selection process.
2.3.2. Model Selection of PCA
Then, the latent vector of each PV site is projected into a 10 dimension space using PCA. The first two principal components (PCs) are plotted in Figure 8 for visualization. As can be seen in Figure 8, the latent vectors are not well separated when PCA is not applied (see Figure 8a). However, after PCA is applied, two groups are separated distinctively as shown in Figure 8b. This can again be verified by a scree plot [33] in Figure 9.

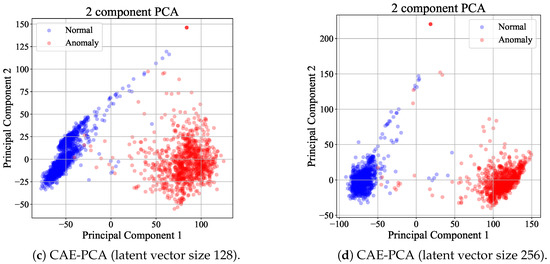
Figure 8.
Scatter plot of latent vectors. Our selection is (b).

Figure 9.
Scree plot analysis.
The scree plot is a graph that shows the variances of the main principal components in decreasing order. The proper number of PCs is determined when the cumulative percentage reaches 80 to 90% and when an abrupt change is observed. Following this rule, it is sufficient to use only one principal component when the latent vector dimension is 64, for example.
Figure 8 and Figure 9 visualize the data distribution of the results with the PCA-excluded model and the CAE-PCA model with different parameters. It can be seen that the CAE-PCA model with the latent vector size of 64 outperforms other models and the scree plot of the selected parameter has 88% of the cumulative eigenvalues, while other models have lower cumulative eigenvalues in the first PC. To confirm this further, we plot the distributions of the most dominant PC (PC1) and the second dominant PC (PC2) in Figure 10a,b, respectively. In this, blue is applied to the normal PV sites and red to the anomalous PV sites. Figure 10a shows that the anomalous distribution is clearly separated from the normal one. In contrast, the distributions of PC2 are largely overlapped, and thus separating the anomaly is not possible at all. This result is also confirmed by the violin plot in Figure 11 where two distributions of normal and anomaly locations are separated [34].

Figure 10.
Histogram of PC1 and PC2.

Figure 11.
Violin plot of PC1 and PC2.
2.3.3. Model Selection of K-Means Clustering
Finally, the vectors to which CAE-PCA is applied are separated into two clusters by K-means clustering for anomaly detection. To demonstrate the effectiveness of CAE-PCA, we consider three cases of K-means clustering depending on the input: (a) the raw SDSP, (b) applying CAE to SDSP, and (c) applying CAE-PCA to SDSP. We use five evaluation indexes of accuracy, precision, recall, F1 score, and silhouette score [35]. The silhouette score is obtained by calculating the distance between each data point and the surrounding data points. In general, it is a measure of whether the data in each cluster is well collected and whether the clusters are well distinguished from each other. The larger the score value, the better the clustering. The results are shown in Table 3, which confirms the effectiveness of the proposed method; for example, the silhouette score is 0.97 and the recall of the proposed model is 99.61%, which shows higher performance than the other two models. We also compare the proposed model with a different number of clusters K. We vary K from 2 to 5 and compare the silhouette score. The results in Table 4 and Figure 12 show that clustering with only two clusters is the most appropriate to cluster the anomalous and normal PV sites.

Table 3.
Anomaly detection performance comparison.

Table 4.
Anomaly detection performance comparison.

Figure 12.
K-means clustering experiment with different K = 2, 3, 4, 5.
2.4. Forecasting Model
After anomaly detection, we construct VPP and forecast the PV power generation of VPP. TransLSTM model, given in Figure 13, is a simple modification of our previous model TransGRU in [23]; we replace GRU with LSTM for better forecasting with more parameters. For the operational description of the transformer encoder along with its mathematical representation, please refer to [23]. The structure of the forecasting model is shown in Figure 13 and Table 5.

Figure 13.
TransLSTM Architecture.

Table 5.
Structure of the forecasting model.
2.4.1. Transformer Encoder
We only adopt the encoder structure of the transformer model to put more weight on important weather and PV generation factors as we did in our previous work [23]. For PV forecasting, we use one of the most popular time-series forecasting models called transformer. The transformer model has shown great performance in machine translation [36], which is also associated with a time series. The transformer model follows the encoder-decoder, the structure of the existing seq2seq but only implements attention as the name of the paper. The model does not use RNNs, and even though it designs an encoder-decoder structure, it also outperforms RNNs in translation performance.
2.4.2. LSTM
The performance of GRU and LSTM is similar. GRU has fewer parameters than LSTM since it has only two gates and GRU has fast convergence compared to LSTM. It is common that LSTM is efficient if sufficient data are given. We choose LSTM as a forecasting block which differs from TransGRU. We feed the transformer’s encoded output into the LSTM-based time-series forecasting block. LSTM overcomes the shortcomings of RNN and is good at holding long-term memories. Forecasting a sequence of long-term samples can be influenced by an input sequence given many time steps before. We use seven days of past data as an input sequence. So we choose LSTM as a forecasting block to solve the long-term dependencies in the network by LSTM’s gating mechanisms.
3. An Application of Anomaly Detection for VPP Power Forecasting
3.1. Data Preprocessing
In this section, we provide the experimental results of anomaly detection as well as VPP forecasting.
3.1.1. PV Data
We use SDSP as an input of the anomaly detection model. Daily load profile consists of 24-h PV data. PV data are normalized with the min-max method. Then, they are converted into a 2-dimensional matrix by stacking all daily PV profiles. Using SDSP, it is easy to visualize the reconstruction performance of CAE, and we use a heatmap of SDSP for visualization. With the heatmap images in Figure 7, one can compare the original image with the reconstructed one.
3.1.2. Weather Data
In general, solar power generation is greatly affected by the weather conditions such as the number of clouds, temperature, humidity, wind speed whether it rains or not, etc. We use public weather data provided by the weather stations of the Korean Meteorological Administration at over 100 different locations. We also use the information on the latitude and longitude of weather stations in each region and the accumulated weather observation data provided by the stations. When training the forecasting model, we add Gaussian noise to the observation data so that the observation value has weather forecasting errors, just like the actual weather forecast data.
The overall configuration of the dataset is shown in Figure 14. Using the latitude and longitude of the solar power plant, the Euclidean distance of each weather station is calculated. Then, the data from the closest PV site and the observatory are combined to form a dataset. For day-ahead PV forecasting of the target day denoted by D, we use the past seven days of PV generation D-7, D-6, ..., D-1. In addition, we use weather forecast data for the past six days and the target day D-6, D-5, ..., D. In using the weather forecast data, we add Gaussian noise with 15% error to the measured weather data to mimic the weather forecast error. All models are trained using the hyperparameters in Table 6.

Figure 14.
PV and Weather merged dataset.

Table 6.
Hyperparameters of model optimization.
3.2. Forecasting Result
For the experiment, PV sites are divided into two groups consisting of only the normal site’s dataset and the mixed site’s dataset where normal and anomaly data exist. As shown in Figure 15, we consider four regions, in each of which a VPP is composed of randomly selected 20 PV sites. Random VPP construction is repeatedly performed in each region. As a result, a total of 68 VPPs are constructed across four reasons, as summarized in Table 7. On average, the total facility capacity of each VPP is 20 MW. About 600 days of power generation and weather data for each VPP are divided into 70%, 15%, and 15% train, validation, and test set, and the results for each VPP are shown in Table 7, Table 8, Table 9 and Table 10. The TransLSTM models that combine MLP, Transformer, and LSTM are used as forecasting models. The forecasting performance measured in NMAE for regions A, B, C, and D shows an improvement of 20–23% compared to the mixed data set. We also observe a similar improvement when other forecasting models such as MLP or LSTM are used, which shows the effectiveness of the proposed anomaly detection.

Figure 15.
PV site visualization of each region (A–D).

Table 7.
VPP forecasting before and after anomaly detection in region A.

Table 8.
VPP forecasting before and after anomaly detection in region B.

Table 9.
VPP forecasting before and after anomaly detection in region C.

Table 10.
VPP forecasting before and after anomaly detection in region D.
Forecasting performance is visualized in Figure 16 and Figure 17, in which the forecasting results for the same site with anomaly-unaware and anomaly-aware situations, respectively. We see that the anomaly-aware forecasting model shows a more accurate result than the anomaly-unaware case.

Figure 16.
Normal site forecasting before anomaly detection (Site Num: 38627).

Figure 17.
Normal Site’s forecasting after anomaly detection (Site Num: 38627).
4. Conclusions
In this paper, we propose a methodology for training a forecasting model by configuring a VPP using weather data and PV sites with normal power generation patterns, which involves detecting anomalies in PV site data. The anomaly detection model is constructed using CAE, PCA, and K-means clustering. After extracting the latent vectors by applying CAE, power generation with normal patterns can be determined by PCA and K-means clustering. By validating and testing PV site data as an input to the model trained by training data, normal and anomalous sites are separated. These normal and anomalous data sets are then merged with weather data corresponding to each PV site. The results show that forecasting performance improves when a forecasting model is trained using normal data only. In the case of a VPP composed of normal data, the aggregated forecast performance improve more than 23%, on average compared to the mixed VPP. This substantial improvement can be possible because the proposed anomaly detection is highly accurate, e.g., 99% of accuracy.
There still remain some challenges. It is hard to detect a mixed anomaly site that has both normal and anomalous generation patterns in different time periods. This could be due to changes in the way an ESS is installed or operated. As a future work, the impact of site changes on anomaly detection can be investigated, in addition to the methodologies to ensure that anomaly detection is robust for newly added sites with little historical data. Anomaly detection per daily power generation pattern, rather than over the entire data of each site, could probabilistically represent anomalies in power generation; for example, it is possible to extend the proposed preprocessing method to forecast power generation for newly installed sites with limited data.
Author Contributions
Conceptualization, T.P., K.S., J.J. and H.K.; methodology, T.P. and H.K.; software, T.P., K.S. and J.J.; validation, T.P., K.S., J.J. and H.K.; writing—original draft preparation, T.P.; writing—review and editing, T.P., J.J. and H.K.; visualization, T.P.; supervision, H.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT under Grant NRF-2021R1A2C1095435, in part by the Korea Institute of Energy Technology Evaluation and Planning (KETEP), and in part by the Ministry of Trade, Industry and Energy (MOTIE), Republic of Korea, under Grant 20192010107290.
Data Availability Statement
The weather data used in this study are openly available in Open MET Data Portal (https://data.kma.go.kr/cmmn/main.do (accessed on 23 December 2022)) operated by KMA (Korea Meteorological Administration).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DL | Deep learning |
| DNN | Deep neural network |
| LSTM | Long short-term memory |
| PV | Photovoltaic |
| PCA | Principal component analysis |
| VPP | Virtual power plant |
| GHG | Greenhouse gas |
| AI | Artificil intelligence |
| MLP | Multi-layer perceptron |
| ANN | Artificial neural network |
| RNN | Recurrent neural network |
| STCNN | Space–time convolutional neural network |
| GNN | Graph neural network |
| GRU | Gated recurrent unit |
| ESS | Energy storage system |
| CAE | Convolutional autoencoder |
| KPX | Korea Power Exchange |
| SDSP | Stacked daily solar profile |
| PCs | Principal components |
| ARMA | Autoregressive moving average |
| MLR | Multiple linear regression |
| SVM | Support vector machine |
References
- Bouckaert, S.; Pales, A.F.; McGlade, C.; Remme, U.; Wanner, B.; Varro, L.; D’Ambrosio, D.; Spencer, T. Net Zero by 2050: A Roadmap for the Global Energy Sector; International Energy Agency: Paris, France, 2021. [Google Scholar]
- Höhne, N.; Gidden, M.J.; den Elzen, M.; Hans, F.; Fyson, C.; Geiges, A.; Jeffery, M.L.; Gonzales-Zuñiga, S.; Mooldijk, S.; Hare, W.; et al. Wave of net zero emission targets opens window to meeting the Paris Agreement. Nat. Clim. Chang. 2021, 11, 820–822. [Google Scholar] [CrossRef]
- Government of the Republic of Korea. 2050 Carbon Neutral Strategy of the Republic of Korea: Towards a Sustainable and Green Society; Government of the Republic of Korea: Seoul, Republic of Korea, 2020; pp. 1–131. [Google Scholar]
- Maka, A.O.; Alabid, J.M. Solar energy technology and its roles in sustainable development. Clean Energy 2022, 6, 476–483. [Google Scholar] [CrossRef]
- Dincer, I. Renewable energy and sustainable development: A crucial review. Renew. Sustain. Energy Rev. 2000, 4, 157–175. [Google Scholar] [CrossRef]
- Ibrahim, M.; Alsheikh, A.; Awaysheh, F.M.; Alshehri, M.D. Machine learning schemes for anomaly detection in solar power plants. Energies 2022, 15, 1082. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, J.; Liu, C.; Xu, X.; Wang, W.; Zhou, X. Comparative study of power forecasting methods for PV stations. In Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Benjamin, M.A.; Rigby, R.A.; Stasinopoulos, D.M. Generalized autoregressive moving average models. J. Am. Stat. Assoc. 2003, 98, 214–223. [Google Scholar] [CrossRef]
- Aiken, L.S.; West, S.G.; Pitts, S.C. Multiple linear regression. In Handbook of Psychology; Wiley: Hoboken, NJ, USA, 2003; pp. 481–507. [Google Scholar]
- Alam, A.M.; Razee, I.A.; Zunaed, M.; Al-Masood, N. Solar PV power forecasting using traditional methods and machine learning techniques. In Proceedings of the 2021 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 19–20 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- El-Sebaii, A.; Al-Ghamdi, A.; Al-Hazmi, F.; Faidah, A.S. Estimation of global solar radiation on horizontal surfaces in Jeddah, Saudi Arabia. Energy Policy 2009, 37, 3645–3649. [Google Scholar] [CrossRef]
- Viorel, B. Modeling Solar Radiation at the Earth’s Surface: Recent Advances; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hossain, M.R.; Oo, A.M.T.; Ali, A. The effectiveness of feature selection method in solar power prediction. J. Renew. Energy 2013, 2013, 952613. [Google Scholar] [CrossRef]
- Chiteka, K.; Enweremadu, C. Prediction of global horizontal solar irradiance in Zimbabwe using artificial neural networks. J. Clean. Prod. 2016, 135, 701–711. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K.; Mahmoud, M. Solar energy prediction for Malaysia using artificial neural networks. Int. J. Photoenergy 2012, 2012, 419504. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Wang, H.; Zhang, S.; Xin, J.; Liu, H. Recurrent neural networks based photovoltaic power forecasting approach. Energies 2019, 12, 2538. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, H. Multi-site photovoltaic forecasting exploiting space-time convolutional neural network. Energies 2019, 12, 4490. [Google Scholar] [CrossRef]
- Mishra, M.; Dash, P.B.; Nayak, J.; Naik, B.; Swain, S.K. Deep learning and wavelet transform integrated approach for short-term solar PV power prediction. Measurement 2020, 166, 108250. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- López Santos, M.; García-Santiago, X.; Echevarría Camarero, F.; Blázquez Gil, G.; Carrasco Ortega, P. Application of Temporal Fusion Transformer for Day-Ahead PV Power Forecasting. Energies 2022, 15, 5232. [Google Scholar] [CrossRef]
- Song, K.; Jeong, J.; Moon, J.H.; Kwon, S.C.; Kim, H. DTTrans: PV Power Forecasting Using Delaunay Triangulation and TransGRU. Sensors 2022, 23, 144. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, H. DeepComp: Deep reinforcement learning based renewable energy error compensable forecasting. Appl. Energy 2021, 294, 116970. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Natarajan, K.; Bala, P.K.; Sampath, V. Fault detection of solar PV system using SVM and thermal image processing. Int. J. Renew. Energy Res. 2020, 10, 967–977. [Google Scholar]
- Harrou, F.; Dairi, A.; Taghezouit, B.; Sun, Y. An unsupervised monitoring procedure for detecting anomalies in photovoltaic systems using a one-class support vector machine. Sol. Energy 2019, 179, 48–58. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, L.; Gu, C.; Li, D. Lstm-based short-term electrical load forecasting and anomaly correction. In Proceedings of the E3S Web of Conferences, Tokyo, Japan, 19–21 June 2020; EDP Sciences: Les Ulis, France, 2020; Volume 182, p. 01004. [Google Scholar]
- Zhang, Y. A Better Autoencoder for Image: Convolutional Autoencoder. In Proceedings of the ICONIP17-DCEC, Guangzhou, China, 14–18 October 2017; Available online: http://users.cecs.anu.edu.au/Tom.Gedeon/conf/ABCs2018/paper/ABCs2018_paper_58.pdf (accessed on 23 March 2017).
- Ding, C.; He, X.; Zha, H.; Simon, H. Adaptive dimension reduction for clustering high dimensional data. In Proceedings of the 2002 IEEE International Conference on Data Mining, Maebashi, Japan, 9–12 December 2002; pp. 147–154. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Cattell, R.B. The scree test for the number of factors. Multivar. Behav. Res. 1966, 1, 245–276. [Google Scholar] [CrossRef]
- Hintze, J.L.; Nelson, R.D. Violin plots: A box plot-density trace synergism. Am. Stat. 1998, 52, 181–184. [Google Scholar]
- Shahapure, K.R.; Nicholas, C. Cluster quality analysis using silhouette score. In Proceedings of the 2020 IEEE 7th International Conference on Data Science and Advanced Analytics (DSAA), Sydney, NSW, Australia, 6–9 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 747–748. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).