Analytical Calculation of Air Gap Magnetic Field of SPMSM with Eccentrically Cut Poles Based on Magnetic Pole Division
Abstract
1. Introduction
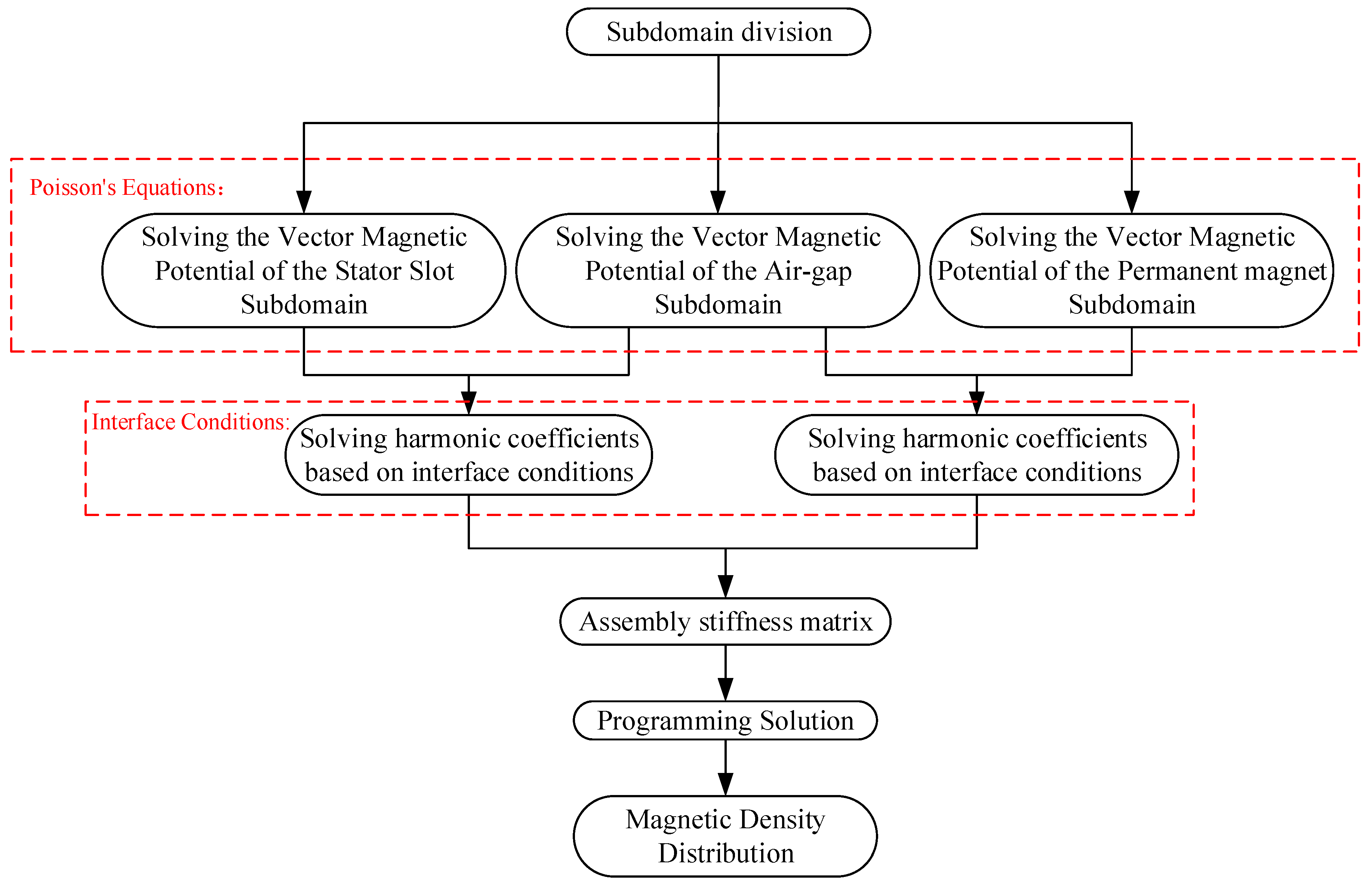
2. Analytical Solution Process of Air Gap Magnetic Field
- (1)
- The magnetic permeability of the ferromagnetic material is set to infinity.
- (2)
- The magnetic permeability of the air gap between the magnetic poles is the same as that of the permanent magnet.
- (3)
- The stator slot type is a radial fan-shaped open slot with a regular shape.
- (4)
- Neglecting the end effect, the model is solved in the two-dimensional region.
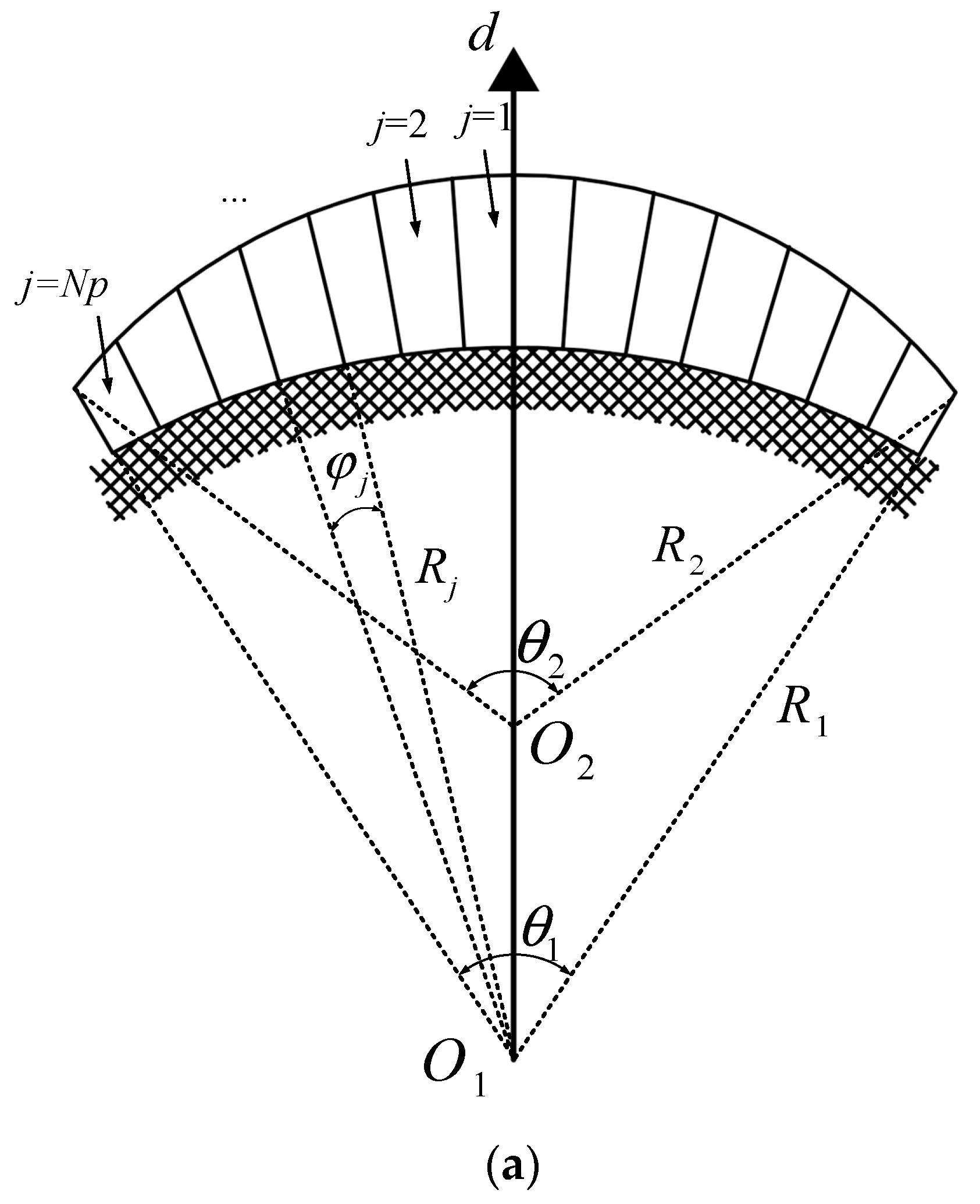
2.1. The Model of the Eccentrically Cut Permanent Magnet and Its Equal-Area Integral Block
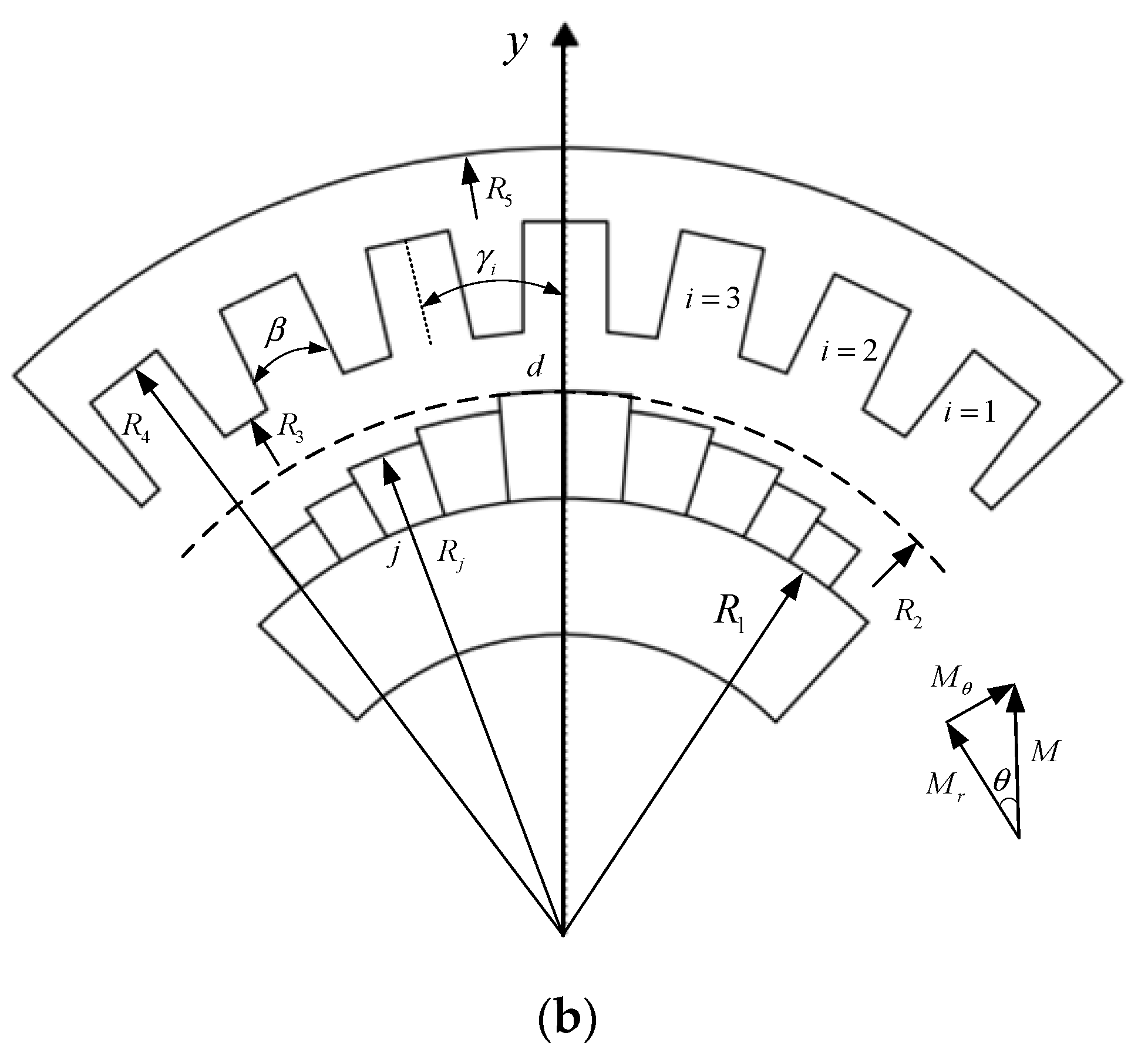
2.2. General Solution of Each Subdomain
2.2.1. Subdomain 1—Slot
2.2.2. Subdomain 2—Air Gap
2.2.3. Subdomain 3—Permanent Magnet
2.3. Harmonic Coefficient Solution
2.3.1. The Interface between Air Gap and Permanent Magnet
2.3.2. The Interface between Air Gap and Stator Slot
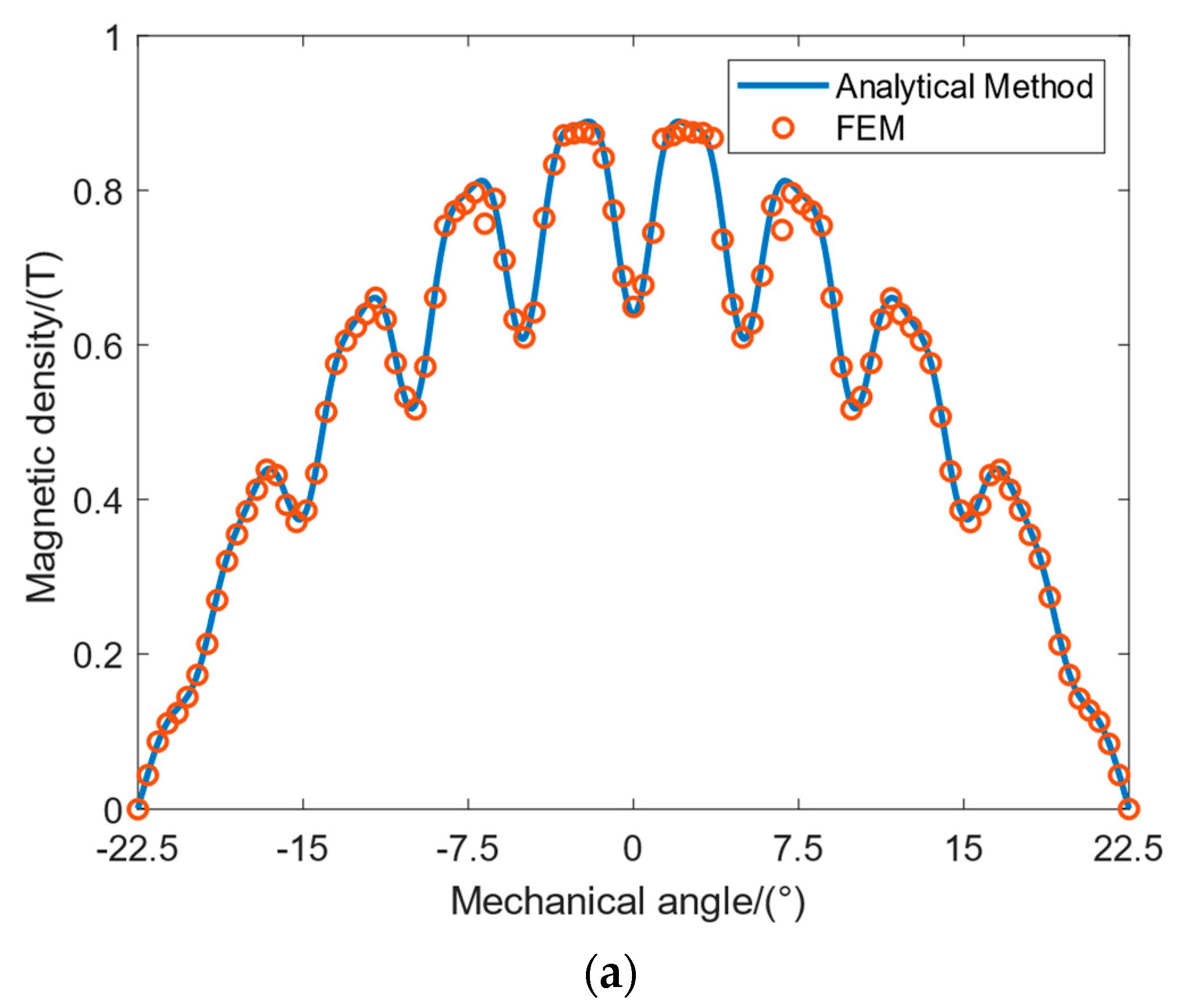
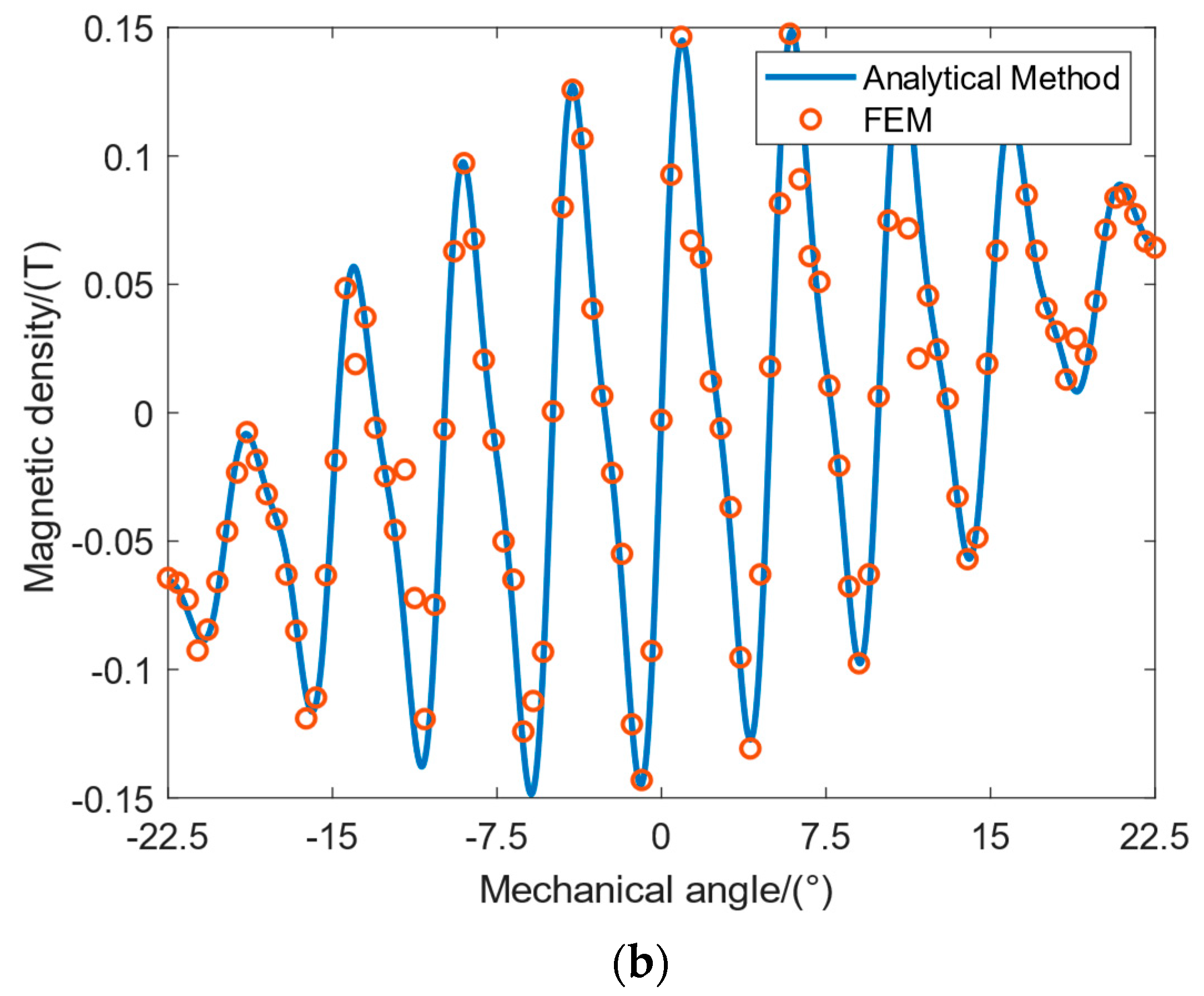
2.4. Air Gap Magnetic Density Distribution
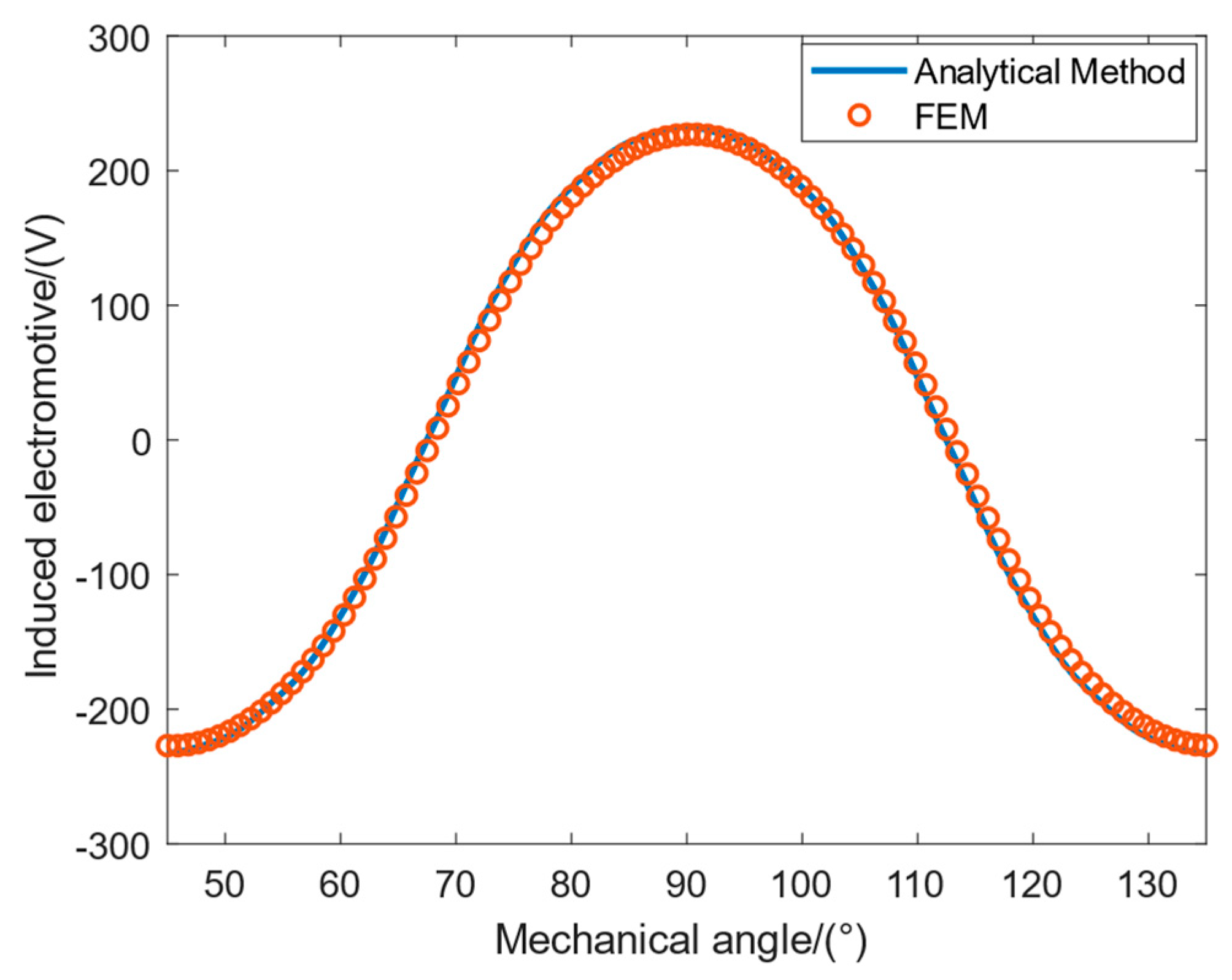
2.5. Calculation of No-Load back Electromotive Force
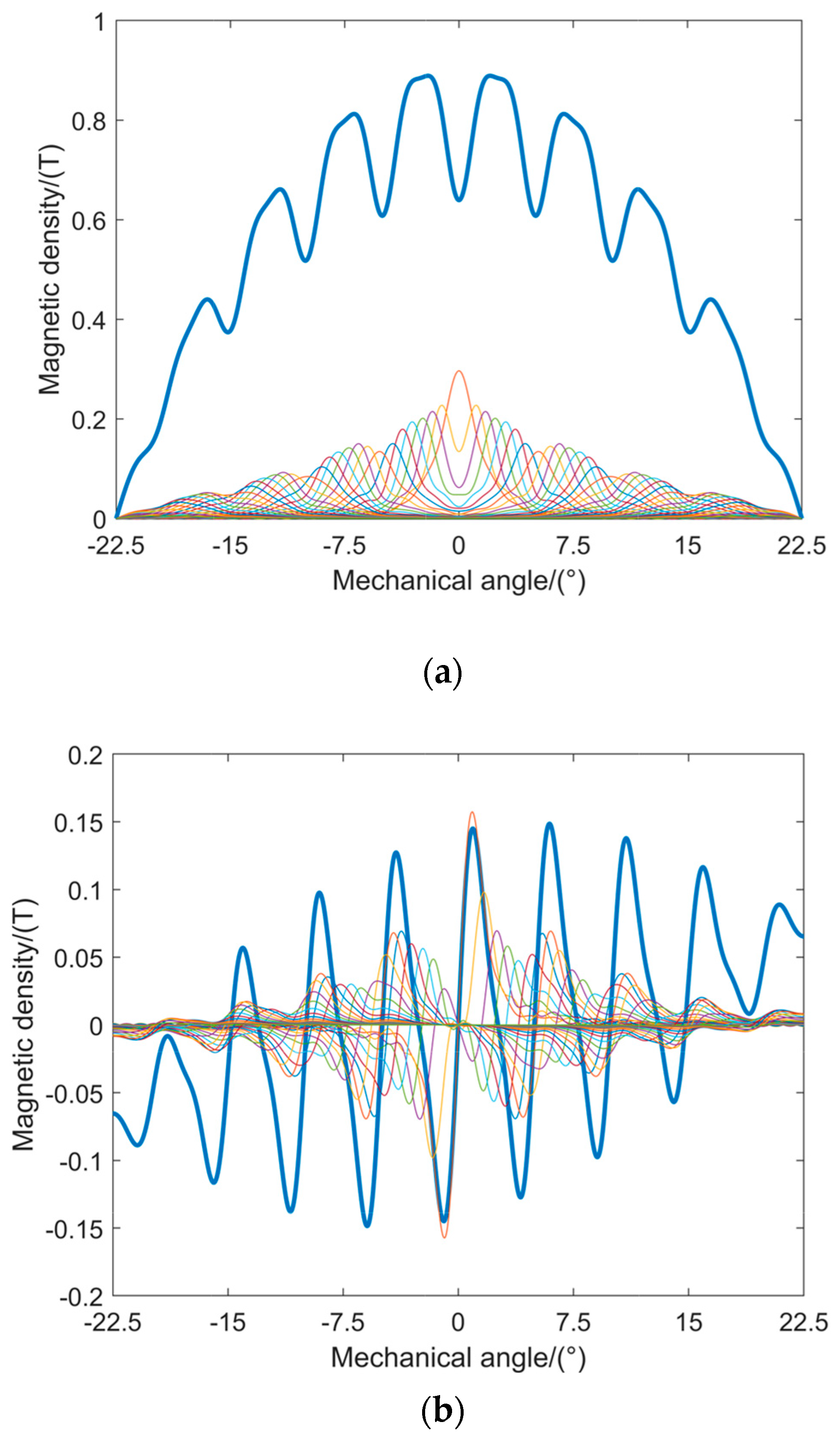
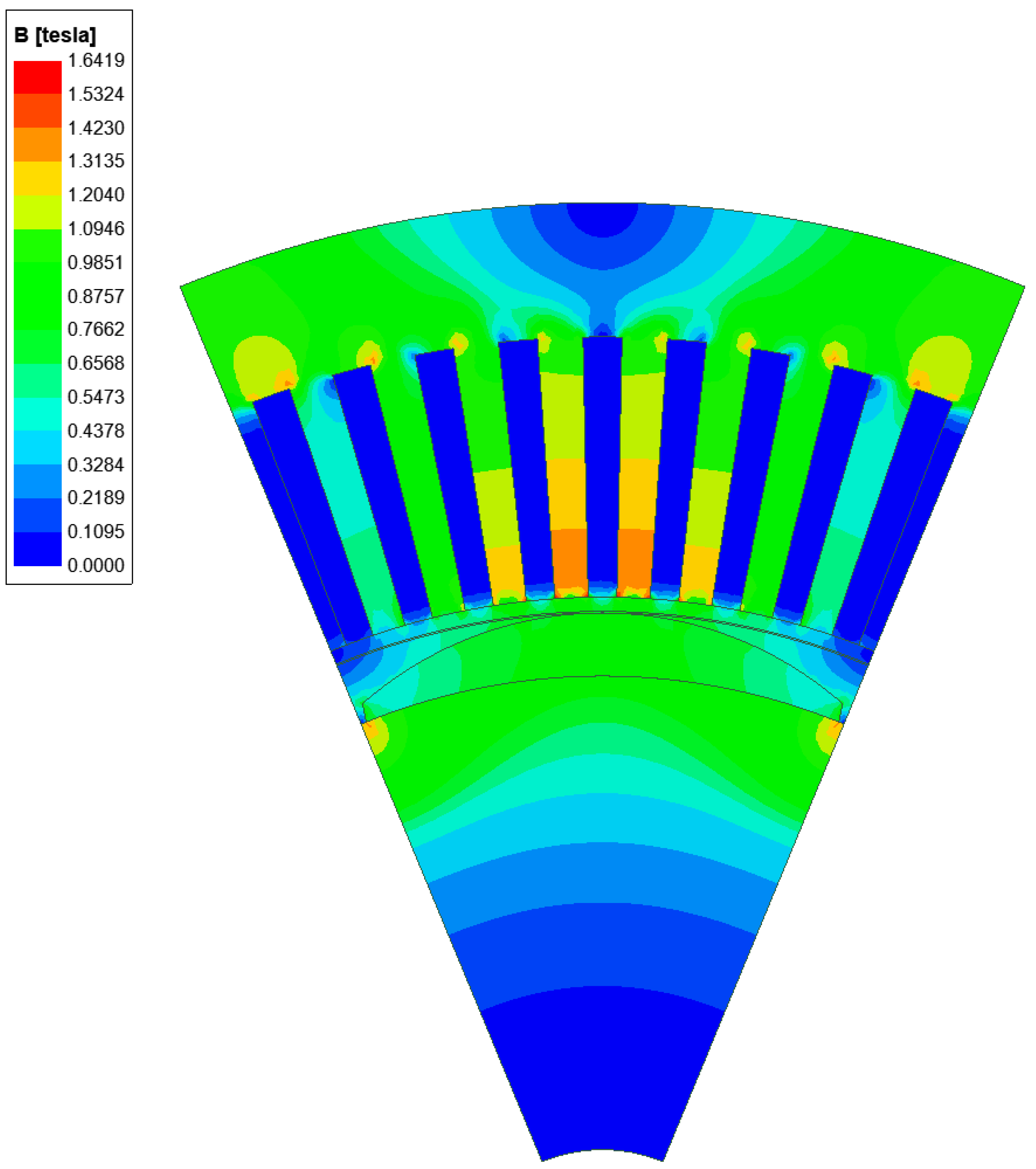
3. Model Calculation and FEM Verification
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Center of the inner arc of the magnetic pole | |
| Center of the outer arc of the magnetic pole | |
| Radius of the inner arc of the magnetic pole | |
| Radius of the outer arc of the magnetic pole | |
| Radius at the top of the slot | |
| Radius at the bottom of the slot | |
| Radius of the magnetic block | |
| Central angle of the magnetic pole of block | |
| Central angle of the inner arc of the magnetic pole | |
| Central angle of the outer arc of the magnetic pole | |
| Pole block number | |
| Pairs of poles | |
| Total number of blocks for half a magnetic pole | |
| Number of stator slots | |
| Slot number | |
| Harmonic order in slot | |
| Harmonic orders in permanent magnet and air gap | |
| Relative permeability of permanent magnet | |
| Vacuum permeability | |
| Central angle corresponding to the slot | |
| Position angle of the center of the slot | |
| Starting position of the slot | |
| Pole distance | |
| Core axial length(mm) | |
| Pole arc coefficient | |
| Fundamental frequency | |
| Total number of turns in series for each phase | |
| Winding coefficient of the harmonic |
References
- Wang, K.; Sun, H.; Zhang, L.; Liu, C.; Zhu, Z. An overview of rotor pole optimization techniques for permanent magnet synchronous machines. Proc. CSEE 2017, 37, 7304–7318. [Google Scholar]
- Yang, Y.; Wang, X.; Ding, T. Analysis of the optimization of pole arc combination to reduce the cogging torque in PM machines. Proc. CSEE 2007, 27, 7–11. [Google Scholar]
- Hu, P.; Wang, D.; Jin, Q. Sinusoidal optimization model for air gap magnetic field of eccentric magnetic pole permanent magnet machine. Trans. China Electrotech. Soc. 2019, 34, 3759–3768. [Google Scholar]
- Hu, P.; Wang, D.; Jing, S. Research on the optimization of harmonic pole shaping technology for arcuate pole permanent magnet motor. Proc. CSEE 2020, 40, 5987–5997. [Google Scholar]
- Ho, S. An optimal method for the minimization of cogging torques of a permanent magnet motor using FEM and genetic algorithm. IEEE Trans. Appl. Supercond. 2010, 20, 861–864. [Google Scholar] [CrossRef]
- Chen, N.; Ho, S.L.; Fu, W. Optimization of permanent magnet surface shapes of electric motors for minimization of cogging torque Using FEM. IEEE Trans. Magn. 2010, 46, 2478–2481. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, Z.; Staton, D. Analytical model of eddy current loss in windings of permanent magnet machines accounting for load. IEEE Trans. Magn. 2012, 48, 2138–2151. [Google Scholar] [CrossRef]
- Golovanov, D.; Gerada, C. An analytical subdomain model for dual-rotor permanent magnet motor with halbach array. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Q.; Gong Xiao. Network-varying equivalent magnetic circuit modeling of novel disk transverse-flux permanent magnet brushless machine. Trans. China Electrotech. Soc. 2016, 31, 147–153. [Google Scholar]
- Yang, D.; Deng, Z.; Zhang, H. Exact analytical solution of magnetic field in permanent magnet in-wheel motor. Trans. China Electrotech. Soc. 2019, 34, 1423–1433. [Google Scholar]
- Zhu, Z.; Wu, L.; Xia, Z. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines. IEEE Trans. Magn. 2010, 46, 1100–1115. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, Z.; Staton, D. An improved subdomain model for predicting magnetic field of surface-mounted permanent magnet machines accounting for tooth-tips. IEEE Trans. Magn. 2011, 47, 1693–1704. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Meng, G. Analytical calculation of magnetic field and cogging torque in surface-mounted permanent-magnet machines accounting for any eccentric rotor shape. IEEE Trans. Ind. Electron. 2015, 62, 3438–3447. [Google Scholar] [CrossRef]
- Guo, Y.; Jin, P.; Hou, S. Analytical method for predicting air-gap magnetic field distribution of surface mounted permanent magnet machine with non-concentric magnetic poles. In Proceedings of the 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11 August 2017. [Google Scholar]
- Yang, S.; Xia, C.; Wang, H. Modeling and analyzing for surface mounted permanent magnet machine with segmented pole. Trans. China Electrotech. Soc. 2015, 30, 49–55. [Google Scholar]
- Lubin, T.; Mezani, S.; Rezzoug, A. Exact analytical method for magnetic field computation in the air gap of cylindrical electrical machines considering slotting effects. IEEE Trans. Magn. 2010, 46, 1092–1099. [Google Scholar] [CrossRef]
- Lubin, T.; Mezani, S.; Rezzoug, A. 2-D exact analytical model for surface-mounted permanent-magnet machines with semi-closed slots. IEEE Trans. Magn. 2011, 47, 479–492. [Google Scholar] [CrossRef]
- Jing, L.; Zhang, Y. An exact analytical method for magnetic field computation and electromagnetic torque in a concentric magnetic gear. Proc. CSEE 2012, 32, 139–146. [Google Scholar]
- Guo, S.; Zhou, L.; Qi, G. Analytical calculation of electromagnetic performance of dual three-phase permanent magnet synchronous machine. Trans. China Electrotech. Soc. 2014, 29, 17–28. [Google Scholar]
- Li, J.; Jing, L.; Zhou, X. Exact analytical method for surface-mounted permanent-magnet brushless machines. Trans. China Electrotech. Soc. 2012, 27, 83–88. [Google Scholar]
- Hu, H. Electromagnetic Analysis and Optimal Design of the Permanent Magnet Synchronous Machine Based on the Exact Subdomain Method. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2017. [Google Scholar]
- Ma, Z.; Qi, Z.; Wang, S.; Jing, Y.; He, B.; Cao, H. Multi-Objective Optimization of Outer Rotor Hub Permanent Magnet Synchronous Motor Based on Global Analytical Method. Electr. Mach. Control. Appl. 2023, 50, 44–54. [Google Scholar]
- Zhang, S.; Guo, S. Analytical Magnetic Field Method of Permanent Magnet Synchronous Machine Considering Step-Skewed Magnets and Magnetic Slot Wedge. Trans. China Electrotech. Soc. 2019, 34, 11–22. [Google Scholar]
- Yang, Y.; Liu, G.; Chen, P.; Yang, X. Electromagnetic performance investigation of vernier hybrid machine. Electr. Mach. Control 2019, 23, 9–17. [Google Scholar]
- Yu, Z.; Li, Y.; Jing, Y.; Du, J.; Wang, Z. No-Load Characteristic Analysis of Surface-Mounted Permanent Magnet Synchronous Motor with Non-Concentric Pole Based on Hybrid Magnetic Field Analysis Method. Trans. China Electrotech. Soc. 2020, 35, 3811–3820. [Google Scholar]
- Liang, P.; Chai, F. Analytical Prediction of Magnetic Field Distribution in Spoke-Type Permanent-Magnet Synchronous Machines Accounting for Bridge Saturation and Magnet Shape. IEEE Trans. Ind. Electron. 2017, 64, 3479–3488. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, J.; Zhang, C.; Li, Z.; Meng, Y. Analytical Calculation of Magnetic Field of Permanent Magnet Synchronous Motor with Uneven Air Gap Structure. Trans. China Electrotech. Soc. 2022, 37, 3502–3513. [Google Scholar]
- Li, J.; Wu, X.; Chen, C. Analytical Calculation of Air Gap Magnetic Field for Permanent Magnet Machines Based on Pole Partition Processing. Proc. CSEE 2021, 41, 6390–6399. [Google Scholar]
- Pourahmadi-Nakhli, M.; Rahideh, A.; Mardaneh, M. Analytical 2-D Model of Slotted Brushless Machines With Cubic Spoke-Type Permanent Magnets. IEEE Trans. Energy Convers. 2018, 33, 373–382. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, M.; Wang, D.; Fang, Y. A Subdomain Model for Open-Circuit Field Prediction in Dual-Stator Consequent-Pole Permanent Magnet Machines. IEEE Trans. Magn. 2019, 55, 1–12. [Google Scholar] [CrossRef]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Phase m | 3 | Stator outer diameter D1/mm | 290 |
| Rated voltage UN/V | 234 | Stator inner diameter Di1/mm | 180 |
| Pairs of poles P | 4 | Rotor outer diameter D2/mm | 176 |
| Rated speed n1/rpm | 750 | Rotor inner diameter Di2/mm | 80 |
| Permanent magnet material | SmCo30 | Core Axial Length l/mm | 88 |
| Pole arc coefficient αp | 0.978 | Number of stator slots Ns | 72 |
| Items | Analytical Method | FEM |
|---|---|---|
| CPU | Intel(R) Core(TM) i7-10750 H CPU @ 2.60 GHz | |
| Number of equations/matrixes | 1792 | 36,118 |
| Mesh accuracy | - | 1 mm |
| Number of subdomains/triangles | 3 | 18,124 |
| Elapsed time | 8.7 s | 249 s |
| Harmonic Order | Analytical Method | FEA |
|---|---|---|
| 1 | 0.8391 T | 0.8338 T |
| 3 | 0.0516 T | 0.0591 T |
| 5 | 0.0118 T | 0.0125 T |
| 7 | 0.0078 T | 0.0077 T |
| 9 | 0.0032 T | 0.0026 T |
| 11 | 0.0002 T | 0.0002 T |
| 17 | 0.0666 T | 0.0646 T |
| 19 | 0.0635 T | 0.0612 T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Hu, J.; Gu, G.; Du, F. Analytical Calculation of Air Gap Magnetic Field of SPMSM with Eccentrically Cut Poles Based on Magnetic Pole Division. Energies 2023, 16, 4450. https://doi.org/10.3390/en16114450
Zhang J, Hu J, Gu G, Du F. Analytical Calculation of Air Gap Magnetic Field of SPMSM with Eccentrically Cut Poles Based on Magnetic Pole Division. Energies. 2023; 16(11):4450. https://doi.org/10.3390/en16114450
Chicago/Turabian StyleZhang, Jiahe, Jiapei Hu, Guobiao Gu, and Fangmian Du. 2023. "Analytical Calculation of Air Gap Magnetic Field of SPMSM with Eccentrically Cut Poles Based on Magnetic Pole Division" Energies 16, no. 11: 4450. https://doi.org/10.3390/en16114450
APA StyleZhang, J., Hu, J., Gu, G., & Du, F. (2023). Analytical Calculation of Air Gap Magnetic Field of SPMSM with Eccentrically Cut Poles Based on Magnetic Pole Division. Energies, 16(11), 4450. https://doi.org/10.3390/en16114450






