A Novel AI-Based Thermal Conductivity Predictor in the Insulation Performance Analysis of Signal-Transmissive Wall
Abstract
1. Introduction
2. Laboratory Samples
3. Conventional Thermal Conductivity Measurement Approaches
3.1. Steady-State Methods
3.2. Transient State Methods
4. Novel Thermal Conductivity Estimation Method
4.1. Laboratory Measurement Setup
4.2. AI-Based Conductivity Predictor
4.3. Harmony Search Algorithm
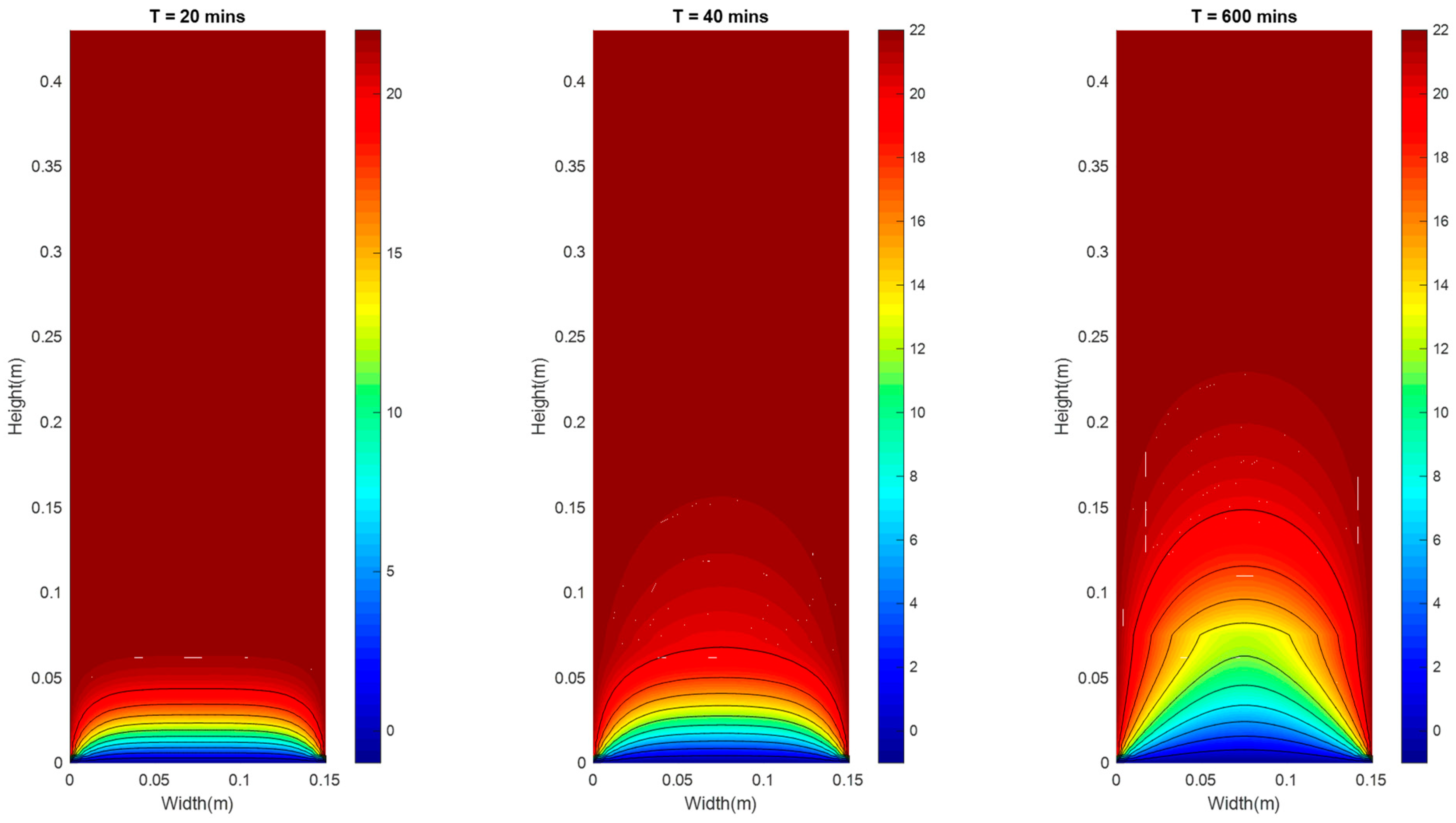
5. Results and Analysis
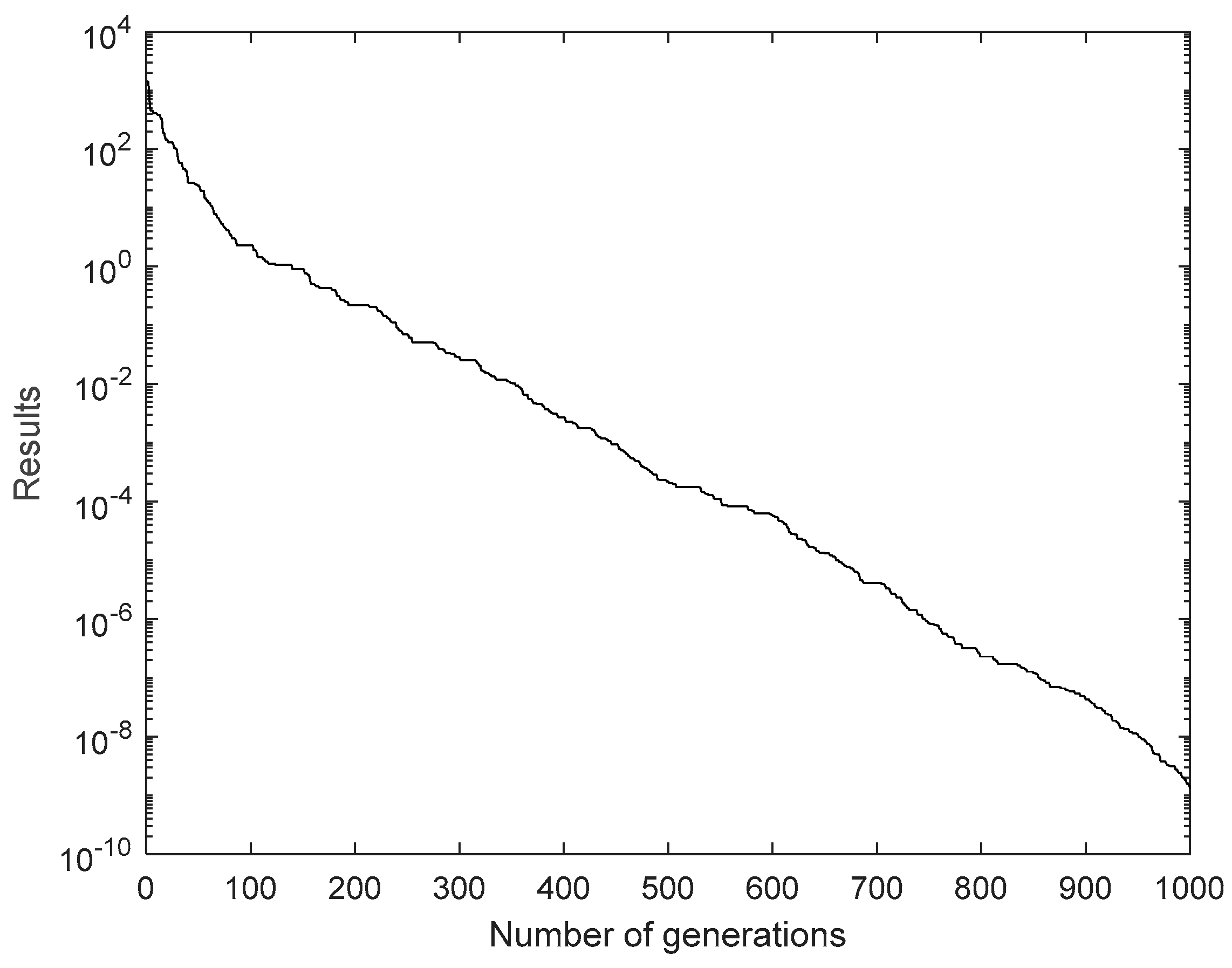
5.1. Results Based on Proposed HS Algorithms
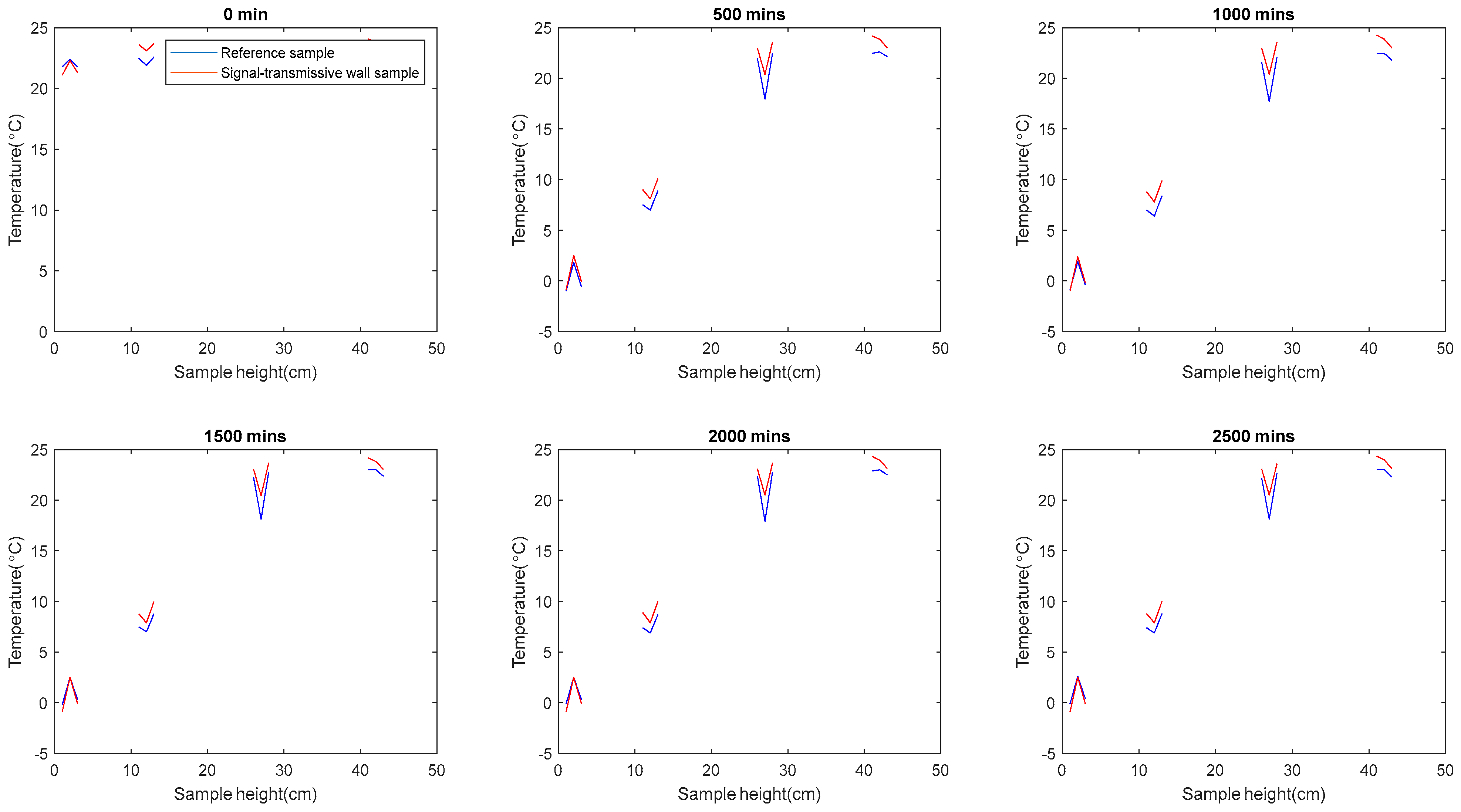
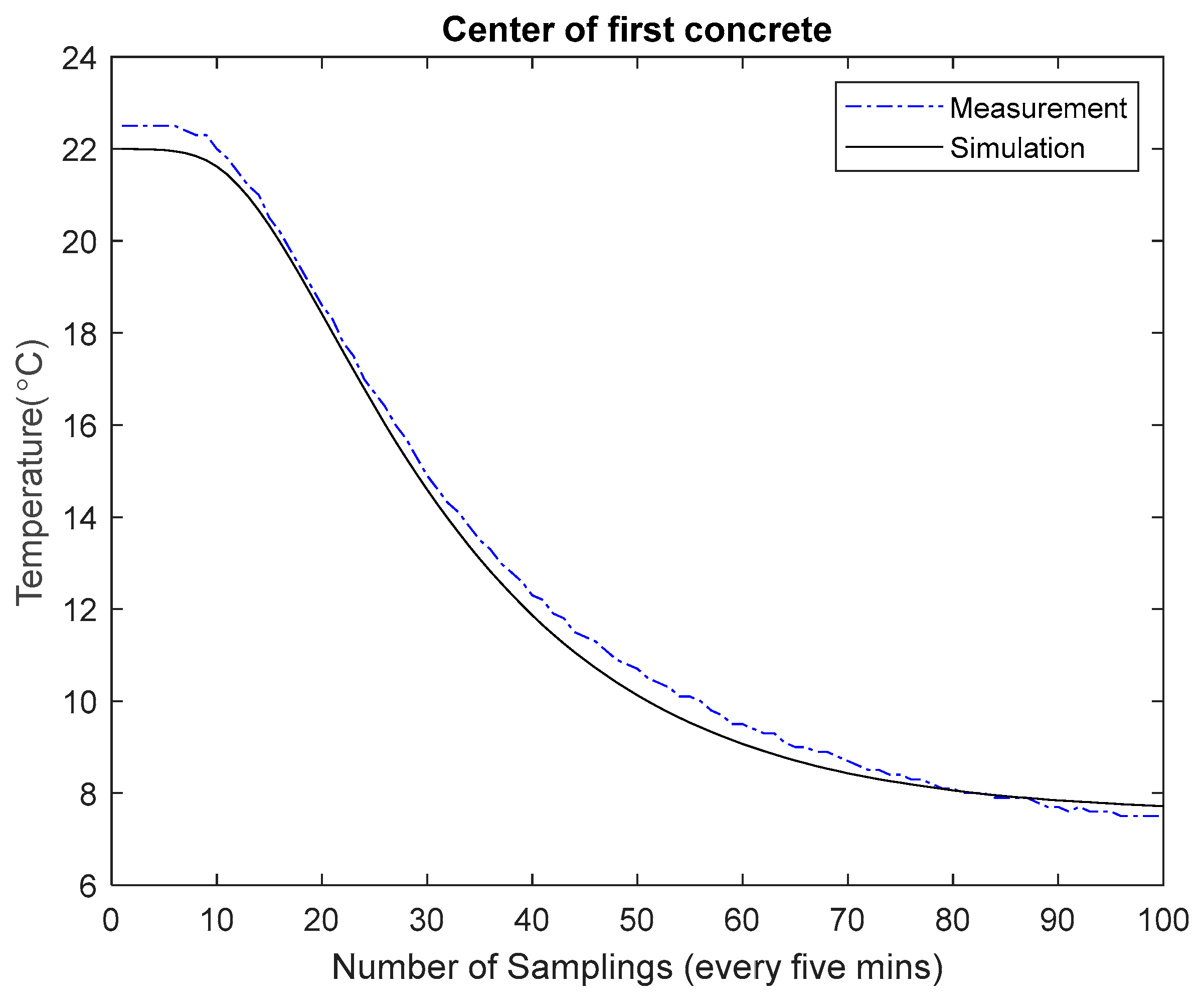
5.2. Analysis and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Telecommunication Union. Available online: https://www.itu.int (accessed on 1 March 2023).
- Vähä-Savo, L.; Atienza, A.G.; Cziezerski, C.; Heino, M.; Haneda, K.; Icheln, C.; Lü, X.; Viljanen, K. Passive antenna systems embedded into a load bearing wall for improved radio transparency. In Proceedings of the 50th European Microwave Conference (EuMC), Utrecht, The Netherlands, 12–14 January 2021. [Google Scholar]
- Ntontin, K.; Verikoukis, C. Relay-aided outdoor-to-indoor communication in millimeter-wave cellular networks. IEEE Syst. J. 2020, 14, 2473–2484. [Google Scholar] [CrossRef]
- Er-reguig, Z.; Ammor, H. Towards designing a microcell base station using a software-defined radio platform. In Proceedings of the 2019 7th Mediterranean Congress of Telecommunications, Fes, Morocco, 24–25 October 2019. [Google Scholar]
- Vähä-Savo, L.; Koivumäki, P.; Haneda, K.; Icheln, C.; Chen, J. 3-D Modeling of Human Hands for Characterizing Antenna Radiation from a 5G Mobile Phone. In Proceedings of the 2022 16th European Conference on Antennas and Propagation, Madrid, Spain, 27 March–1 April 2022. [Google Scholar]
- Salmon, D. Thermal conductivity of insulations using guarded hot plates including recent developments and sources of ref-erence materials. Meas. Sci. Technol. 2001, 12, R89. [Google Scholar] [CrossRef]
- Flaata, T.; Michna, G.J.; Letcher, T. Thermal conductivity testing apparatus for 3D printed materials. In Proceedings of the Heat Transfer Summer Conference, Washington, DC, USA, 9–12 July 2017. [Google Scholar]
- Elkholy, A.; Sadek, H.; Kempers, R. An improved transient plane source technique and methodology for measuring the thermal properties of anisotropic materials. Int. J. Therm. Sci. 2019, 135, 362–374. [Google Scholar] [CrossRef]
- Asadi, I.; Shafigh, P.; Hassan, Z.F.; Mahyuddin, N.B. Thermal conductivity of concrete—A review. J. Build. Eng. 2018, 20, 81–93. [Google Scholar] [CrossRef]
- Llavona, M.A.; Zapico, R.; Blanco, F.; Verdeja, L.F.; Sancho, J.P. Methods for measuring thermal conductivity. Rev. Minas. 1991, 6, 89–98. [Google Scholar]
- Palacios, A.; Cong, L.; Navarro, M.E.; Ding, Y.; Barreneche, C. Thermal conductivity measurement techniques for characterizing thermal energy storage materials—A review. Renew. Sustain. Energy Rev. 2019, 108, 32–52. [Google Scholar] [CrossRef]
- Meshgin, P.; Xi, Y. Multi-scale composite models for the effective thermal conductivity of PCM-concrete. Constr. Build. Mater. 2013, 48, 371–378. [Google Scholar] [CrossRef]
- Zhao, D.; Qian, X.; Gu, X.; Jajja, S.A.; Yang, R. Measurement techniques for thermal conductivity and interfacial thermal conductance of bulk and thin film materials. J. Electron. Packag. 2016, 138, 040802. [Google Scholar] [CrossRef]
- Elkholy, A.; Kempers, R. An accurate steady-state approach for characterizing the thermal conductivity of additively manufactured polymer composites. Case Stud. Therm. Eng. 2022, 31, 101829. [Google Scholar] [CrossRef]
- Cahill, D.G. Thermal conductivity measurement from 30 to 750 K: The 3ω method. Rev. Sci. Instrum. 1990, 61, 802–808. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comput. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
- Wang, X.; Gao, X.Z.; Zenger, K. An Introduction to Harmony Search Optimization Method; Springer International Publishing: New York, NY, USA, 2015. [Google Scholar]
- Vähä-Savo, L.; Haneda, K.; Icheln, C.; Lü, X. Electromagnetic-Thermal Analyses of Distributed Antennas Embedded into a Load Bearing Wall. arXiv 2022, arXiv:2207.06185. [Google Scholar]
- Lu, T.; Vähä-Savo, L.; Lü, X.; Haneda, K. Thermal Impact of 5G Antenna Systems in Sandwich Walls. Energies 2023, 16, 2657. [Google Scholar] [CrossRef]
- Aksöz, S.; Öztürk, E.; Maraşlı, N. The measurement of thermal conductivity variation with temperature for solid materials. Measurement 2013, 46, 161–170. [Google Scholar] [CrossRef]
- Assael, M.J.; Chen, C.F.; Metaxa, I.; Wakeham, W.A. Thermal conductivity of suspensions of carbon nanotubes in water. Int. J. Thermophys. 2004, 25, 971–985. [Google Scholar] [CrossRef]
- Guo, R.; Ren, Z.; Bi, H.; Xu, M.; Cai, L. Electrical and thermal conductivity of polylactic acid (PLA)-based biocomposites by incorporation of nano-graphite fabricated with fused deposition modeling. Polymers 2019, 11, 549. [Google Scholar] [CrossRef]
- Shemelya, C.; De La Rosa, A.; Torrado, A.R.; Yu, K.; Domanowski, J.; Bonacuse, P.J.; Martin, R.E.; Juhasz, M.; Hurwitz, F.; Wicker, R.B.; et al. Anisotropy of thermal conductivity in 3D printed polymer matrix composites for space based cube satellites. Addit. Manuf. 2017, 16, 186–196. [Google Scholar] [CrossRef]
- Rich, E. Artificial Intelligence; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Spector, L. Evolution of artificial intelligence. Artif. Intell. 2006, 170, 1251–1253. [Google Scholar] [CrossRef]
- Bastani, F.; Chen, I. The Reliability of Embedded AI Systems. IEEE Intell. Syst. Appl. 2018, 8, 72–78. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Sharma, N.; Gupta, R.D.; Khanna, R.; Sharma, R.C.; Sharma, Y.K. Machining of Ti-6Al-4V biomedical alloy by WEDM: Investigation and optimization of MRR and Rz using grey-harmony search. World J. Eng. 2023, 20, 221–234. [Google Scholar] [CrossRef]
- Abdulkhaleq, M.T.; Rashid, T.A.; Alsadoon, A.; Hassan, B.A.; Mohammadi, M.; Abdullah, J.M.; Chhabra, A.; Ali, S.L.; Othman, R.N.; Hasan, H.A.; et al. Harmony search: Current studies and uses on healthcare systems. Artif. Intell. Med. 2022, 131, 102348. [Google Scholar] [CrossRef] [PubMed]
- Güven, A.F.; Yörükeren, N.; Samy, M.M. Design optimization of a stand-alone green energy system of university campus based on Jaya-Harmony Search and Ant Colony Optimization algorithms approaches. Energy 2022, 253, 124089. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–80. [Google Scholar] [CrossRef]
- Geem, Z.W. Music-Inspired Optimization Algorithm: Harmony Search. Available online: http://www.hydroteq.com/ (accessed on 1 March 2023).
- Poli, R.; Langdon, W.B. Foundations of Genetic Programming; Springer: Berlin, Germany, 2002. [Google Scholar]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. Harmony search optimization: Application to pipe network design. Int. J. Simul. Model. 2002, 22, 125–133. [Google Scholar] [CrossRef]
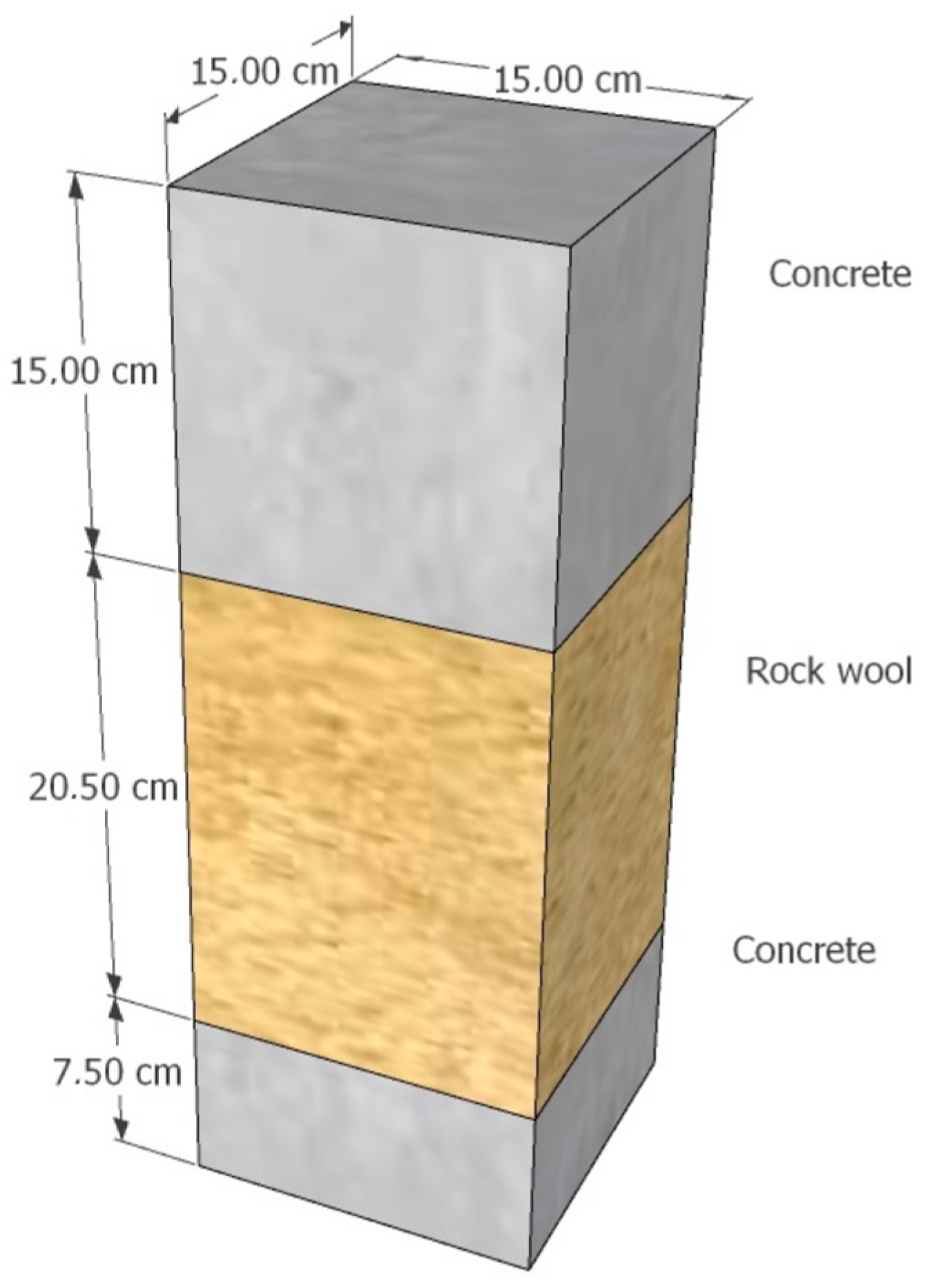
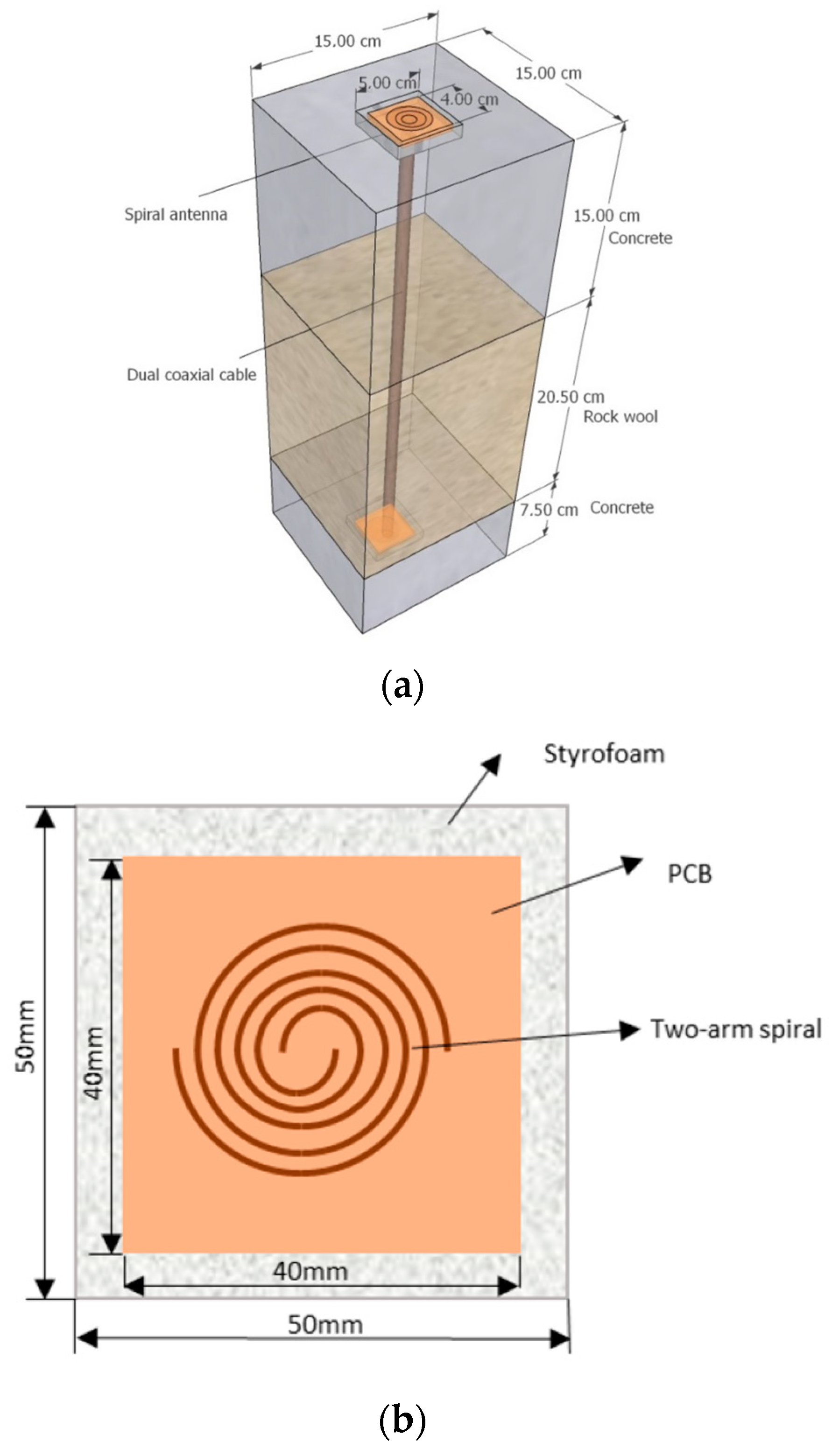


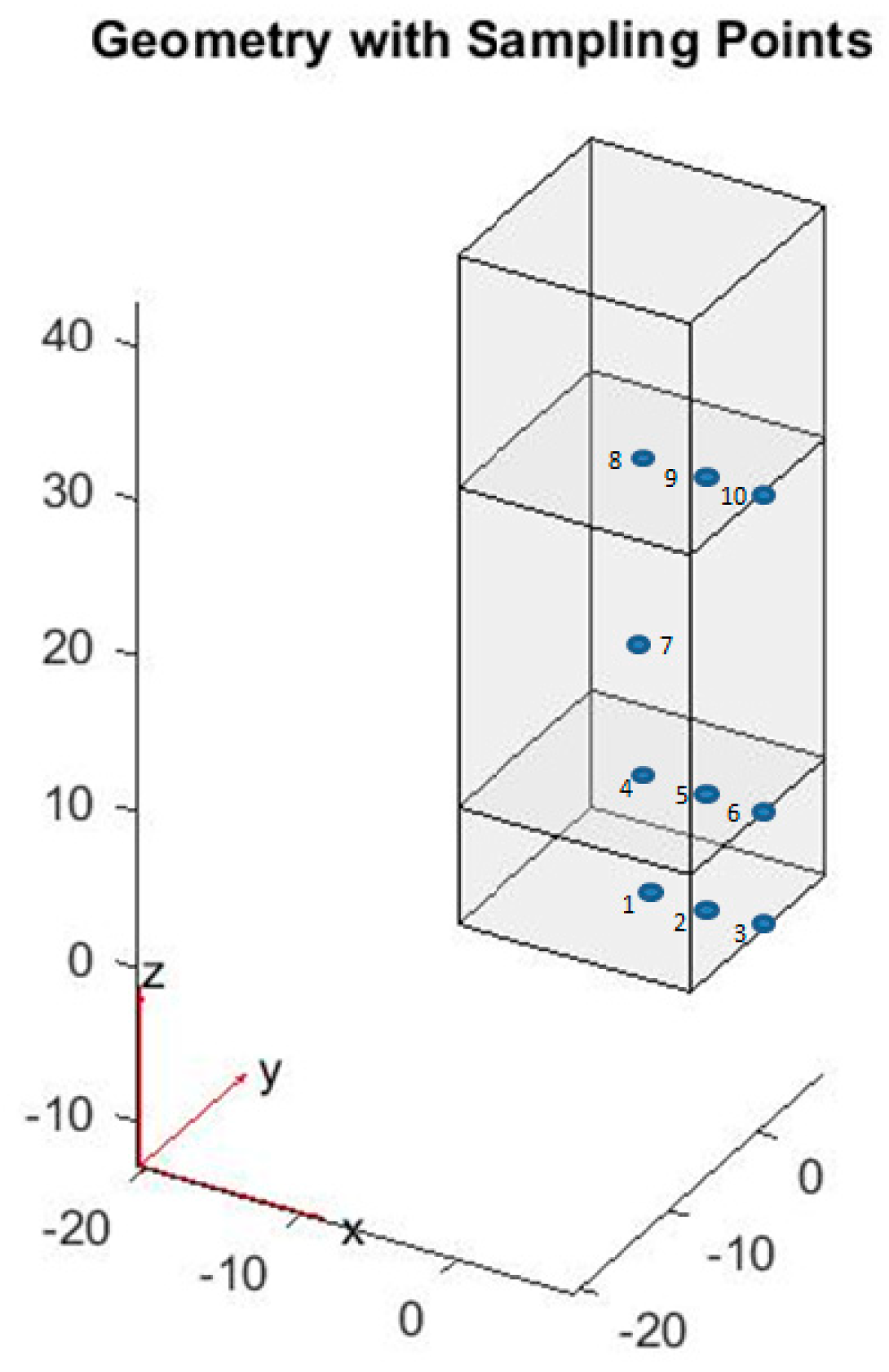
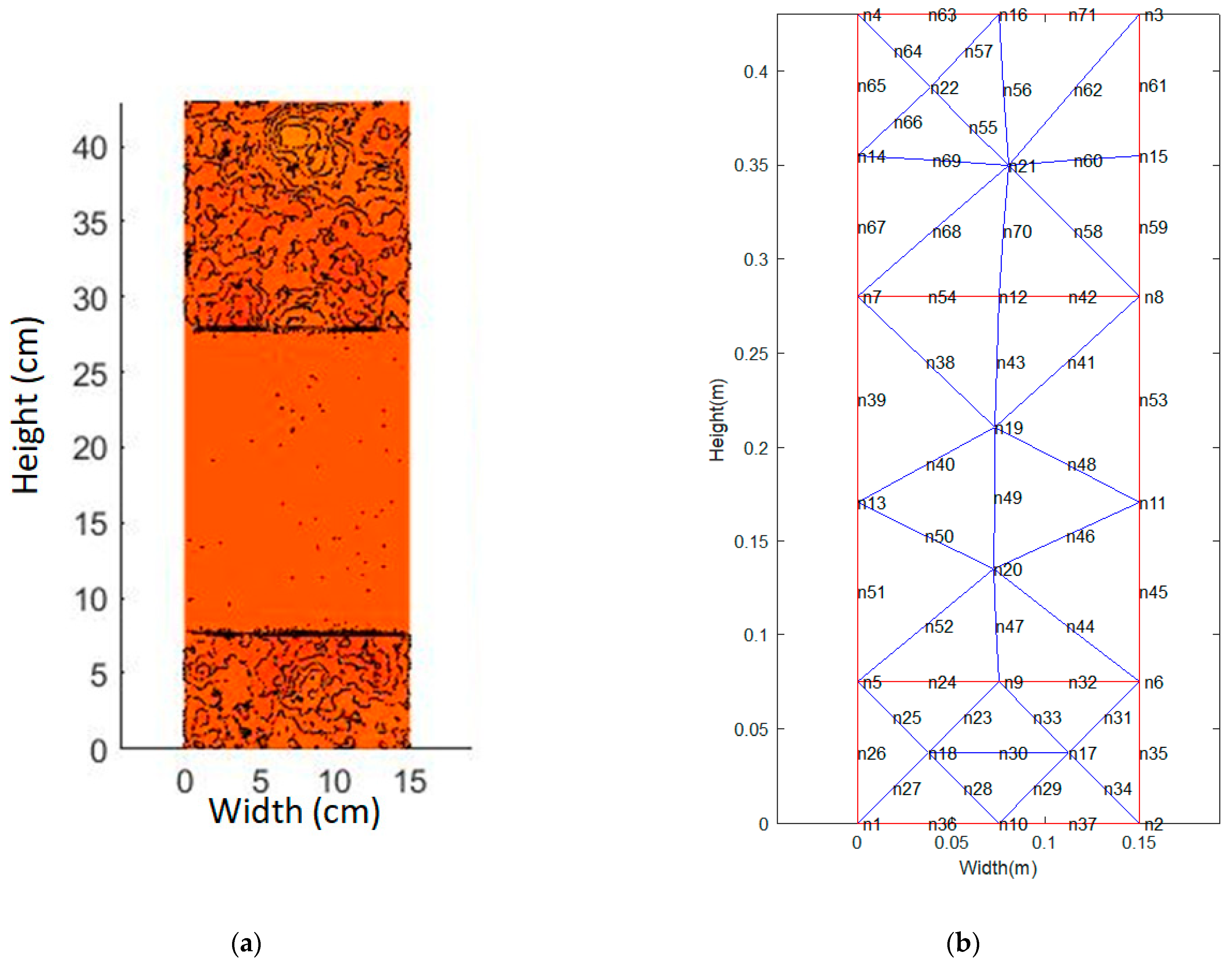


| Layer | Material | Length (cm) | Width (cm) | Height (cm) | Density (kg/m3) |
|---|---|---|---|---|---|
| Layer 1 (top) | Concrete | 15 | 15 | 15 | 2197.9 |
| Layer 2 (middle) | Rock wool | 15 | 15 | 20.5 | 56.15 |
| Layer 3 (bottom) | Concrete | 15 | 15 | 7.5 | 2197.9 |
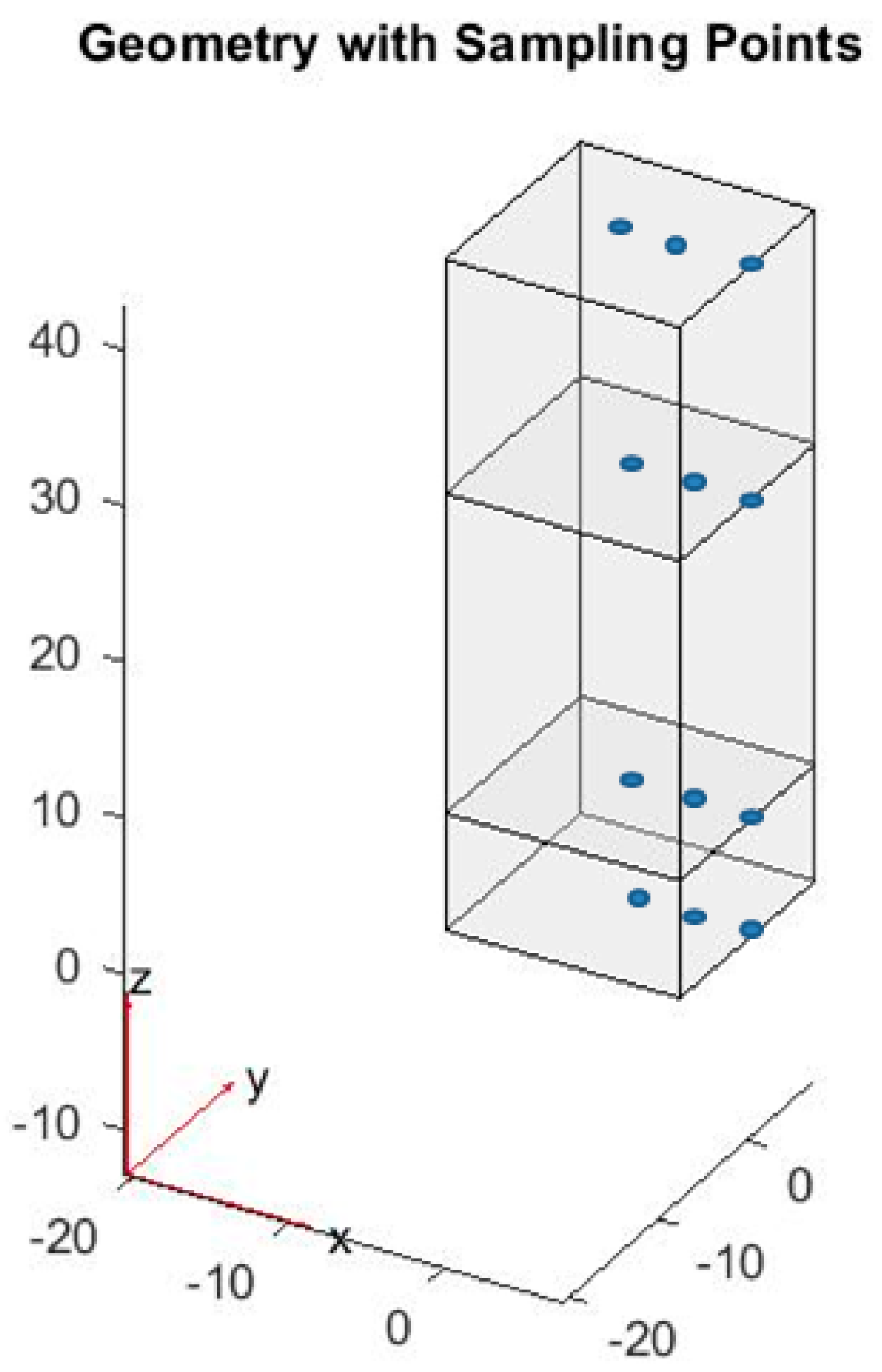
| Number of Sampling Points in Measurement | Node on Mesh in Simulation | Number of Sampling Points in Measurement | Node on Mesh in Simulation |
|---|---|---|---|
| 1 | n10 | 6 | n5 (n6) |
| 2 | n36 (n37) | 7 | n49 |
| 3 | n1 (n2) | 8 | n12 |
| 4 | n9 | 9 | n54 (n42) |
| 5 | n24 (n32) | 10 | n7 (n8) |
| Comparison Issues | Harmony Improvisation | Optimization Task |
|---|---|---|
| Objects | Aesthetic standard | Fitness function |
| Best results | Wonderful melody | Global optimum |
| Elements | Pitches | Values of parameters |
| Process units | Every practice | Every generation |
| Parameters | Values |
|---|---|
| Initial pool size | 4 |
| HMCR | 0.8 |
| PAR | 0.8 |
| Max variation step | 10% |
| Dimension | Parameters in Sample | Searching Ranges | Optimal Values |
|---|---|---|---|
| 1 | Concrete thermal conductivity | 0~20 (W/mK) | 0.8961 (W/mK) |
| 2 | Concrete specific heat | 800~1200 (J/kgK) | 1165 (J/kgK) |
| 3 | Rock wool thermal conductivity | 0~2 (W/mK) | 0.104 (W/mK) |
| 4 | Rock wool specific heat | 400~1000 (J/kgK) | 709 (J/kgK) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lü, X.; Vähä-Savo, L.; Haneda, K. A Novel AI-Based Thermal Conductivity Predictor in the Insulation Performance Analysis of Signal-Transmissive Wall. Energies 2023, 16, 4211. https://doi.org/10.3390/en16104211
Wang X, Lü X, Vähä-Savo L, Haneda K. A Novel AI-Based Thermal Conductivity Predictor in the Insulation Performance Analysis of Signal-Transmissive Wall. Energies. 2023; 16(10):4211. https://doi.org/10.3390/en16104211
Chicago/Turabian StyleWang, Xiaolei, Xiaoshu Lü, Lauri Vähä-Savo, and Katsuyuki Haneda. 2023. "A Novel AI-Based Thermal Conductivity Predictor in the Insulation Performance Analysis of Signal-Transmissive Wall" Energies 16, no. 10: 4211. https://doi.org/10.3390/en16104211
APA StyleWang, X., Lü, X., Vähä-Savo, L., & Haneda, K. (2023). A Novel AI-Based Thermal Conductivity Predictor in the Insulation Performance Analysis of Signal-Transmissive Wall. Energies, 16(10), 4211. https://doi.org/10.3390/en16104211








