Investment Risk and Energy Security Assessment of European Union Countries Using Multicriteria Analysis

Abstract

Investment opportunities are analyzed from the perspective of the variables that influence risk. The present study analyzes some energy characteristics using data from the Eurostat Data Browser. First, we identified a gap in energy research. Second, we proposed a multicriteria analysis using the analytic hierarchy process (AHP). An algorithm was developed to simulate how experts think to determine pairwise comparisons. A procedure identified the levels of importance of each criterion and alternative based on extracted data from the Eurostat website. The method was used to rate countries according to data regarding their energy policy results. The present study shows that applying the AHP method is possible without expert support and using data regarding the theme studied. The results show that Malta and Estonia are the most suitable countries to receive investments since they are presently at the top of the energy security ranking. The selected set of criteria seems to properly correspond with the assessment of the sector security as far as risk investment is concerned. The results of the current study may represent a base to support investment decision-making in the energy sector of EU countries.

1. Introduction

The energy production, consumption and condition of the energy sector have become urgent and frequently raised topics nowadays. Considering the socio-political, technological and environmental aspects, the energy sector is a significant issue for every country. The sector’s condition often determines the condition of other sectors, such as industry or services. Decision-making problems concerning the energy sector have recently been widely discussed in the scientific literature [1,2]. As these problems are usually complex and require many aspects to be considered, multicriteria analysis methods are frequently applied to support such decision-making tasks [3,4,5,6,7,8,9,10,11,12].

The energy sector nowadays deals with many different issues as rising carbon dioxide emissions, problems with conventional sources or probable energy crises. Many authors have raised the subject of renewable energy sources, bioenergy parks and sustainable energy production and planning [13,14,15]. Studies published since 2010 about the life cycle assessment (LCA) of hydropower projects show that depending on the characteristics of the hydro project, it could be a significant source of GHG emissions. Although, statistics show that electric power contributes to around 16% of global electricity and more than 72% of renewable electricity. A systematic literature review has shown that emissions associated with the engineering work are well addressed; however, efforts to estimate and model reservoir GHG emissions accurately are constrained by limited availability of data [16]. Another issue is the long-term solution to the climate and air pollution crises with the electrification of various modes of transport and the transition of non-renewable energy sources to clean, renewable sources. This transition will not be so simple when considering the transport models since there are no solutions yet for electric alternatives for long-distance, heavy-passenger aircraft, freight locomotives or ships. A literature review has shown that armored tanks, freight trains, boats, oceangoing vessels, helicopters, prop planes, and jumbo jets have the potential to transition using identified technological advancements and solutions [17].

Monitoring and control systems are critical issues in the energy sector. These are structures of specialized information that are not managed by the same information technology standards as the rest of the world’s information systems. Different forms make up the control system of the industrial equipment of connectivity, such as the Internet, wireless or cable, and several types of structures, such as smart grids, oil and gas facilities, nuclear power plants and water management systems, can be handled by the industrial control system. A previous study used a fuzzy-based analytic hierarchy process (AHP) method and the technique for order of preference by similarity to ideal solution (TOPSIS) to assess the industrial control system cyber security. The results showed that cybersecurity projects for the industrial control system may be achieved using multicriteria analysis [18].

The condition and development of the energy sector highly depend on the country or global energy policy, and the European Union policy and regulations influence other countries’ energy strategies [19]. To avoid negative change, the European Union has implemented energy guidelines that determine specific changes to the priorities that will be presented until 2050, as in Poland and Germany [20]. Another objective of the European Union is to become a global climate power according to climate neutrality principles. Then, to bring to reality this objective, a system of external policies is being developed concerning finance, trade and investment mechanisms, carbon border adjustment, emission trading, regulations and standards, and cooperation between international institutions [21]. The European Green Deal strategy includes supplying clean, affordable and secure energy [22]. The European Union energy sector has been the subject of recent trends in Chinese investments that have increased in size, targeted a wider number of countries and focused on multiple energy sectors, such as fossil fuels, renewable energies, and energy infrastructure [23].

Among the countless investment opportunities faced daily, some seem more promising than others. However, it is not always adequately judged at first sight. According to management theory, advanced information technology would likely come closer to guaranteeing a sound investment choice. Investment experts bring risk and return together. No enterprise is immune to the dangers that constitute risk [24]. Risk identification and analysis facilitates countermeasures, management and avoiding them [25]. Energy power has had its development severely hindered because of the inherent high risks. A previous study considered four types of risks (political, economic, social and technical) of distributed wind power investments to assess the risks in the life cycle of the distributed wind farm. Results showed that the risk of changes in the electricity price policy is the most critical impact on the distributed wind power system to obtain sustainable development and make profits [26]. This study used the analytic hierarchy process (AHP) method to assess a project’s risks. Intending to mitigate the inherent risks of investing in and developing renewable energy projects (REPs) in Turkey, the research applied the assessment and analysis of the risk factors of renewable energy investments (REIs) for a practical and profound policy guideline. The study provided a multicriteria decision methodology (MCDM) based on a three-stage decision framework on assessing and examining the risk factors of REIs. First was the identification of risk factors using the Delphi method. The second was assessing identified risk factors using the analytical hierarchy process (AHP), and the third was evaluating and prioritizing strategies to overcome risk factors using fuzzy weighted aggregated sum product assessment (FWASPAS). The results presented the AHP analysis, which has unfolded economic and business risk as a significant risk factor [27].

A project of an energy system composed of renewable and non-renewable equipment, comprising a gas boiler, solar collector, photovoltaic panels, wind turbines, and absorption and compression chillers, was also previously proposed [28]. Their study used a combination of two methods (parametric studies and investment risk analysis) to provide additional information about the system. The method considered the environmental and financial combined gains, and the results presented a significant gain in environmental value versus a slight decrease in financial value. The risk analysis indicated that this system’s high adaptability led to low investment risk [28].

A literature review and bibliometric analysis conducted within this study revealed that there are risk analysis studies investigating the problems connected with the energy sector; however, they focus on particular energy technologies. We identified a lack of studies on risk investment analysis of the energy sector as a whole. Both private and institutional investors would benefit from an analysis of the energy sector security of a country that could be a premise for investing in the energy sector of a specific country. The authors propose an analysis that may be considered an energy security assessment in the present study. AHP was applied to build up a country’s ranking in terms of energy security. The analysis was based on publicly available data so that it can be easily repeated for different criteria (energy sector data) or alternatives (countries). The authors also propose an objective way to assign weights so that no energy sector experts need to be involved in the process.

2. Literature Review

The AHP establishes hierarchical levels for the problem and seeks to identify the best alternatives for decision-making. The decision alternatives are assigned from the highest to the lowest level to solve the problem based on the factors that influence it [29]. Saaty’s proposal to perform this comparison was based on a scale from 1 to 9. The criteria were pairwise compared and determined how important the first was concerning the second [30]. The scale from 1 to 9 defined values for odd numbers and intermediate ones. Values from 2 to 8 are described in Table 1. Table 1 shows the AHP weights in five levels, in which only odd numbers represent the main weights, and the pair numbers represent the intermediate levels.

Table 1. Relative scale to pairwise comparison.

Intensity of Importance	Weight	Description
Equal importance	1	Equal contribution of both activities to the objective.
Moderate importance	3	Weak importance of one activity over the other activity.
Strong importance	5	Stronger importance of one activity over the other activity.
Very strong importance	7	Very strong importance of one activity over the other.
Extreme importance	9	Extreme importance (maximum) of one activity over the other.

Adapted from [29].

Many researchers have applied the AHP methodology to different kinds of problems within the areas of engineering management, environmental problems or sustainability development. They often involve technology selection or assessment and therefore build rankings of technologies in the energy sector [31]. Below are a few works that address the different applications of the analytical hierarchy process for energy-related problems.

Improving the business’s profitability is one of the challenges of a globalized market. The analytic hierarchy process (AHP) and a deep learning (DL) algorithm were applied to the bidding strategy problem as a data-driven method. The application aimed to improve an electricity retailer’s profitability by investigating the interaction between a retailer and a set of residential customers by the reaction data of price-responsive customers to the announced prices [32]. Another application of the AHP method (combined with the fuzzy set theory) was connected to the risk avoidance for electricity retailers in China. The main problem triggered by the Chinese power system reform concerned the market power of electricity retailers and retailer risk. New energy market conditions encouraged mixed ownership and private capital. Thus, the authors determined the business categories of electricity retailers, analyzed the impact of welfare on stakeholders in the distribution and retail markets, and finally analyzed each retailer’s risk with the fuzzy analytical hierarchy process. The study results disclosed that the highest risk concerns private enterprises, and the lowest is assigned to power grid ventures [33].

In a specific problem of transitioning from fossil fuels to cleaner energy sources, affordable prices are one of the benefits. A challenge like this was faced in Vietnam, in which solar energy was an attractive option chosen by the local government. Various policy measures were implemented to make this project viable, as substantial investment plans to accelerate the national spread of solar energy. A strategic decision was implemented to optimize the location for solar power installation to maximize the results. Some criteria were evaluated based on a numerical database, numerous qualitative criteria under expert judgments in linguistic terms, and represented through grey numbers. Due to the coexistence of multiple factors, a proposition of combination techniques was presented in this case. This technique combination contained the data envelopment analysis (DEA) method, grey analytic hierarchy process (G-AHP), and grey technique for order preference by Similarity to ideal solution (G-TOPSIS). The results provided parameters to save costs and resources towards determining hot spots for solar power plant installation [34].

Previous studies applied the AHP methodology in Iran. One study entailed rice farmers’ choice of suitable weeding machines for paddy fields. This choice was supported by evaluating and identifying the criteria using a fuzzy-decision-making system to develop criteria for selecting suitable weeder machines. The best engine choice was found using the analytical hierarchy process (AHP) method and prioritizing the selected criteria (agronomic, technical, economic and environmental) [35]. Another study using the AHP method revealed that solar energy was known to be the best renewable energy source for private individual investment due to the geographic location. This source would be attractive to investors due to the wide variety of uses of solar energy in cleaner productions [3]. The AHP methodology is used for various complex decision-making problems, as evidenced from the given examples. Additionally, most frequently, experts are engaged to give their opinions when assigning weights to criteria. The bibliometric analysis focused on the energy sector problems and risk investment analysis is presented next.

First, the authors search the online academic database Scopus to check the existence of similar published work. The criteria and results of this search are shown in Table 2.

Table 2. Search results for similar papers in the Scopus online database.

Sequence	Theme	Criteria	Results
1	AHP Method	TITLE-ABS-KEY (“AHP” AND “ANALYTIC HIERARCHY PROCESS”) AND (LIMIT-TO (SUBJAREA, “ENER”))	18,699
2	Investment Risk Analysis	TITLE-ABS-KEY (“INVESTMENT” AND “RISK ANALYSIS”) AND (LIMIT-TO (SUBJAREA, “ENER”))	2535
3	Characteristics of the Energy Sector	TITLE-ABS-KEY (“CHARACTERISTICS” AND “ENERGY SECTOR”) AND (LIMIT-TO (SUBJAREA, “ENER”))	772
4	Present Article Theme	TITLE-ABS-KEY ((“AHP” AND “ANALYTIC HIERARCHY PROCESS”) AND (“INVESTMENT” AND “RISK ANALYSIS”) AND (“ENERGY SECTOR”))	0

Table 2 presents the search results for similar articles in the Scopus online database. The three main subtopics of this research were searched separately to know the frequency of works and the level of interest in those subtopics. Finally, a search with all subtopics was performed to verify if some similar work was conducted in the past. The evolution of paper production has been almost constant over the years.

The evolution in the number of publications since 1981 is shown in Figure 1, and it is possible to note that all three curves have exponential growth. The curves’ behavior shows a positive increase in these subjects of research.

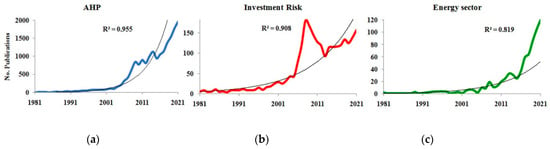
Figure 1. Evolution of scientific publications in AHP (blue line, chart (a)), investment risk (red line, chart (b)), and energy sector (green line, chart (c)) research.

Studies that have applied AHP in the energy sector are essential to identify how many studies with the two searched topics are published, and Figure 2 shows this information. Most studies applied AHP in the engineering sector, with 8157 publications, while in energy there were 1767 works published.

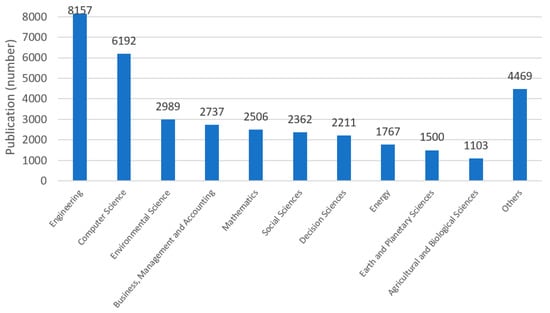
Figure 2. Studies using AHP in various research areas, including the energy sector.

To the best of the authors’ knowledge, no research concerning assessing risk investment based on the condition of the whole energy sector of a country was identified. Therefore, the present study might fill this gap. Some studies have raised the question of investment in general or in risk investment analysis. However, it usually concerned a particular energy technology or subsector, e.g., risk investment in distributed wind energy [26], investment in solar photovoltaic power generation [36] or the investment risk factors of renewable technologies [27]. Furthermore, some studies have applied the AHP approach in the energy sector. However, they have focused mainly on selection issues (e.g., selection of places for construction activities [37], selection of technology transfer strategy for wind turbines [6]) or evaluation problems [8,35,36,38]. The present research combines all of these questions in one analysis. Table 3 presents a comparison between the present work and related articles.

Table 3. The main features of the present study and the topics of related articles are marked (X).

Author (Year) [Source]	AHP	Energy Security	Decision Making	Investment	Energy Sector	Risk Analysis
Azmi et al. (2022) [39]	X			X
Gaur et al. (2022) [40]			X
Van Thanh and Lan (2022) [41]	X				X
Ilbahar et al. (2022) [42]	X			X
Hosseini and Hosseini (2022) [7]			X		X
Chou et al. (2021) [43]						X
Min et al. (2021) [37]	X				X
Ayağ and Samanlioglu (2020) [38]	X				X
Del Giudice et al. (2019) [44]				X
Kwast-Kotlarek and Heådak (2019) [45]	X			X
Kim et al. (2018) [46]				X
Lyu et al. (2018) [47]	X					X
Dinmohammadi and Shafiee (2017) [6]	X				X
Adamus and Florkowski (2016) [48]	X	X
Garbuzova-Schlifter and Madlener (2016) [49]	X					X
Apostolopoulos and Liargovas (2016) [50]	X				X
Ren and Sovacool (2015) [51]	X	X
Han and Park (2012) [52]	X					X
Bao et al. (2011) [53]	X					X
Present study	X	X	X	X	X	X

In the current research, an AHP was proposed to rate the countries of the European Union regarding energy security. The results may suggest which country is the most promising to receive possible investments in this area. Usually, the opinion of experts is needed to assign weights for the phase of pairwise comparison between criteria. The innovation proposed here relies on the fact that weights were obtained based on an algorithm applied to the dataset retrieved from Eurostat Data Browser.

3. Materials and Methods

This research used a quantitative approach of multicriteria analysis through the analytic hierarchy process (AHP) methodology [26,27] in which the influence of indicator data on the energy sector of countries from the European Union was analyzed. Based on the obtained results, it is possible to determine the condition of the energy sector, the indicator of which will be each EU country’s energy security level. A ranking of countries can be used in investment projects in the productive sector since energy availability is a prerequisite for this activity, considering energy security. The data used for this research was extracted from the Eurostat Data Browser [54]. The research was developed according to a sequence of tasks described as a flowchart (Figure 3).

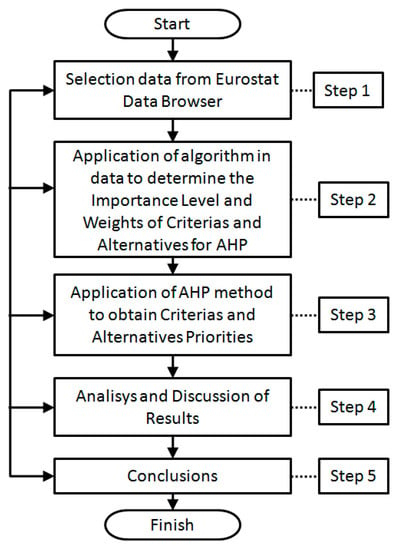
Figure 3. Steps of the research flowchart.

Algorithm Description

Step 1 of the research focused on the choice of factors that will compose the criteria of the AHP decision tree and the search and selection of data that have similarities with these factors.

The opinion of experts in the current area was generally used to determine the importance level of criteria (ILC) and alternatives (ILA) of the AHP. However, in this study, we proposed to determine these levels of importance by the data described in step 2.

In step 2, an algorithm was used to simulate how experts think to determine these levels. The levels of importance of each criterion and alternative were identified by a procedure described below from extracted data from the Eurostat website (a) to the value that represents the importance level (IL) (c).

• Download the data files available on the Eurostat Data Browser website. The database is available in several file formats. In the case of this research, it was decided to download the files in the Microsoft Excel^® spreadsheet format;
• Selection and collection of energy data from European Union countries. In this step, data from the 27 countries that make up the bloc were extracted from the database. Nine data tables were also selected, one for each AHP criterion. In these tables, the data were organized and separated. Finally, regarding the selection period of data generation, those in the range from 2012 to 2020 were considered;
• As the data obtained may have different measurement units, the concept of frequency distribution was used to determine the importance level (IL) for the alternatives based on data regarding the energy of countries in the Eurostat Data Browser. The values for importance level considering their frequency distribution were obtained according to the algorithm described in Table 4. The resulting data of the algorithm was assumed as the importance level of alternatives (ILA) because each country stands for an alternative of the AHP decision tree.
  Table 4. Algorithm to determine the importance level of alternatives.

  Steps	Action
  1	MAX = maximum value of the country data in the criterion
  2	MIN = minimum value of the country data in the criterion
  3	AVE = average value of the country data in the criterion
  4	RANGE = MAX–MIN
  5	Divide RANGE into ten parts
  6	Number the parts sequentially from 1 to 10
  7	Assign the value of the Alternative’s importance level (ILA), according to the part in which the AVERAGE fits

The importance level of a criteria (ILC) was obtained by the average importance level of countries (that are the alternatives) (ILA). The equation that calculates their value of importance level of criteria (ILC) is described in Equation (1).

$$ILC=\frac{{\sum }_{n=1}^{9}IL{A}_n}{9}$$

(1)

Equation (2) was used to determine the weight values for criteria (WOC).

$$Criteria weight{\left(WOC\right)}_n=\frac{IL{C}_{1,n}}{IL{C}_{n,1}}$$

(2)

where n is the index of the criterion (1 ≤ n ≤ 9), ILC_1,n is the value of ILC located in line “1” and column “n” in Table A1 (Appendix A), and ILC_n,1 is the value of ILC located in line “n” and column “1” in Table A1 (Appendix A). The final results of the calculated weights for each criterion after pairwise comparison is shown in Appendix A.

Equation (3) determined the weight values for alternatives (WOA).

$$Alternative weight{\left(WOA\right)}_{c,n}=WO{C}_C\left(\frac{IL{C}_{c,1,n}}{IL{C}_{c,n,1}}\right)$$

(3)

where c is the index of ILC (1 ≤ c ≤ 9), n is the index of alternatives (1 ≤ n ≤ 27), ILA_c,1,n is the value of ILA located in table Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9 and Table A10 in Appendix B (“c” takes values from 1 to 9 and corresponds with the number of a criterion, e.g., for c = 1 we have ILA_1,1,n what means first table in Appendix B and also first criterion), line “1” and column “n”, and ILA_c,n,1 is the value of ILA located in Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9 and Table A10 in Appendix B line “n” and column “1”. The result of calculated weights for each alternative after pairwise comparison is shown in the tables in Appendix B.

In step 3, the weights of the criteria and alternatives obtained in step 2 were used to calculate their priorities according to the AHP methodology. In the case of this, Microsoft Excel^® was used to complete this task.

In step 4, the results obtained by the AHP methods were collected, organized, and analyzed.

Step 5 of this study included formulating and reporting conclusions that may be drawn from conducted analysis and calculations.

4. Results and Discussion

4.1. Results of the Analytical Hierarchy Process

A tree representing the structure of the hierarchy of criteria and alternatives (Figure 4) to identify the ranking of European Union countries’ energy security is presented in Figure 4.

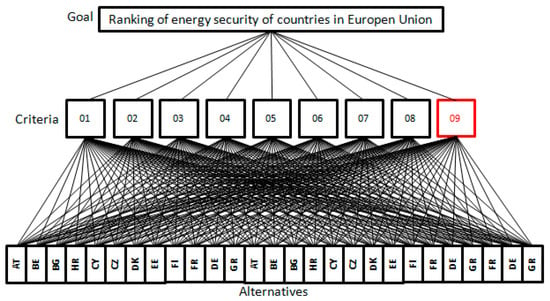
Figure 4. The hierarchy tree represents the question of this research.

In the tree (Figure 4), it is possible to see the three layers that represent the questions to be answered by the AHP method. There are 9 criteria (numbered from 01 to 09 on the hierarchy tree) and 27 alternatives (countries denoted by abbreviated names) in our AHP model. Since the Criterion 09 (Energy imports dependency, %) is the focus of this study we used the red font to highlight it. Table 5 presents the legends which describe the energy indicators that compound the criteria. The initials of the countries’ names that compound the alternatives are shown in Appendix C.

Table 5. Legend of the AHP criteria and their description.

Criterion	Description
1	Electricity available for final consumption
2	Gross electricity production
3	Primary energy consumption (efficiency)
4	Energy productivity—Euro per kilogram of oil equivalent (KGOE)
5	Electricity production capacities for renewables and wastes (Megawatt)
6	Stock levels for oil products
7	Stock levels for gaseous and liquefied natural gas (Million cubic meters)
8	Electricity available to the internal market (Gigawatt-hour)
9	Energy imports dependency (%)

Table 5 presents a description of the selected data as the criteria of the AHP. These criteria originated from data on energy indicators obtained by the Eurostat Data Browser. The variables for the criteria were chosen with the following prerequisite: a higher level of variable influences a better condition of the country’s energy sector. Only one of them, criterion 9 (in red font), had the opposite effect on the energy sector. Therefore, it also had an inverse impact on the criteria and alternative assessment priority. Considering this, the importance level of criteria (ILC) and importance level of alternatives (ILA) final values were calculated by Equations (4) and (5).

$$IL{C}_{Final}=\left(1-ILC\right)$$

(4)

$$IL{A}_{Final}=\left(1-ILA\right)$$

(5)

After compiling the data, a table of importance level (IL) data was prepared (Table 6). The IL is the data that represents the opinion of the experts. Then, it becomes possible to substitute the expert opinion into the weighting phase in the AHP pairwise comparison phase of criteria and alternatives. The importance level (IL) data (Table 6) replaced the experts’ opinions in the AHP pairwise comparison phase. A characteristic of this pairwise comparison is that the decision for the weights attribution in the pairwise comparison is based on the data. This attribution weight does not have the subjectivity of the specialist opinion. The necessary calculations were made to obtain the values of the AHP criteria and alternatives priorities.

Table 6. Importance level (IL) data used in the AHP pairwise comparison phase.

Seq.	European Union Country	Abbreviations	Importance Level of Countries in Each Criterion									IL Country
			Crit_1	Crit_2	Crit_3	Crit_4	Crit_5	Crit_6	Crit_7	Crit_8	Crit_9
1	Austria	AT	5	5	6	5	5	6	5	3	6	5.111111
2	Belgium	BE	7	5	6	5	4	3	3	4	6	4.777778
3	Bulgaria	BG	5	6	6	5	5	5	4	6	5	5.222222
4	Croatia	HR	5	6	6	5	8	6	5	5	5	5.666667
5	Cyprus	CY	5	5	5	3	10	4	10	10	5	6.333333
6	Czech Rep.	CZ	5	6	7	5	8	7	3	3	5	5.444444
7	Denmark	DK	5	4	7	4	5	5	4	5	5	4.888889
8	Estonia	EE	4	7	6	4	6	5	10	10	6	6.444444
9	Finland	FI	5	5	7	4	6	6	6	3	5	5.222222
10	France	FR	6	7	7	4	4	5	4	4	4	5.000000
11	Germany	DE	7	7	6	5	6	5	5	7	6	6.000000
12	Greece	GR	5	4	5	5	7	5	5	4	5	5.000000
13	Hungary	HU	5	5	6	5	6	4	6	3	6	5.111111
14	Ireland	IE	5	5	5	4	10	5	4	4	6	5.333333
15	Italy	IT	6	5	6	6	5	4	5	4	4	5.000000
16	Latvia	LV	4	5	4	5	6	8	10	3	5	5.555556
17	Lithuania	LT	5	5	5	6	8	4	4	6	5	5.333333
18	Luxembourg	LU	5	4	6	5	7	4	10	10	4	6.111111
19	Malta	MT	5	7	5	5	10	7	10	3	6	6.444444
20	Netherlands	NL	5	5	6	5	10	5	5	6	5	5.777778
21	Poland	PL	5	5	4	5	6	4	5	4	5	4.777778
22	Portugal	PT	5	6	6	4	6	6	4	6	4	5.222222
23	Romania	RO	5	6	4	6	6	7	5	4	6	5.444444
24	Slovakia	SK	5	5	5	6	4	3	5	3	6	4.666667
25	Slovenia	SI	5	5	6	5	6	5	4	10	4	5.555556
26	Spain	ES	6	4	6	6	7	4	5	4	4	5.111111
27	Sweden	SE	6	5	7	5	7	5	4	10	4	5.888889
IL Criteria			5.22222	5.33333	5.74074	4.88889	6.59259	5.07407	5.55556	5.33333	5.07407

As noted, a few countries gained the highest scores of 10 as an effect of the pairwise comparisons. This means that these alternatives (countries) were assessed higher in the paired comparison with every other country within a particular criterion (criterion 5, 7, or 8). This fact does not prejudge the final effect of the overall evaluation of all alternatives, as this result depends on the importance of the criterion in question. However, a few countries (alternatives) gained an importance level (IL) greater than six (last column of Table 6), which shows the advantage of these countries over others in this analysis.

In Figure 5, the AHP hierarchy tree is shown with the results of the priorities of the criteria and alternatives obtained. Criterion 9, which represents the data on energy import dependency (%), is shown in red because it has an opposite effect on the priority of the criteria. That is, the higher the importance level, the lower the criterion’s weight must be. Noteworthy is that of criterion 5 (electricity production capacities for renewables and wastes in megawatts) was the most important from the whole set of criteria (IL = 13.5%). Another two, primary energy consumption (efficiency) and stock levels for gaseous and liquefied natural gas (million cubic meters), also obtained a higher importance level (IL over 11%) than the remaining criteria, of which their importance was on the level of 10%.

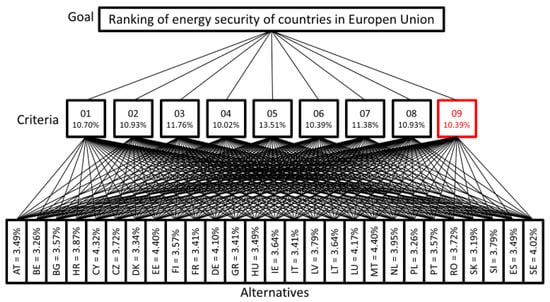
Figure 5. The hierarchy tree with results of the proposed AHP methodology.

The results of the calculations and the position of the countries in the security rankings are shown in Table 7. It is important to mention that the level of decimal precision is seven digits. It was necessary to compare Table 7, presenting the Security ranking obtained after the final AHP calculation process and Table 8, the security ranking obtained by sensitivity analysis ran to simulate a possible scenario in which the weights of the criteria change.

Table 7. Ranking of the countries in terms of energy security.

Country	Ranking Position	Final Priorities of Alternatives
Estonia	1	4.3996683%
Malta	1	4.3996683%
Cyprus	3	4.3238989%
Luxembourg	4	4.1723506%
Germany	5	4.0965718%
Sweden	6	4.0207898%
Netherlands	7	3.9450047%
Croatia	8	3.8692164%
Latvia	9	3.7934250%
Slovenia	9	3.7934250%
Czech Republic	11	3.7176305%
Romania	11	3.7176305%
Ireland	13	3.6418329%
Lithuania	13	3.6418329%
Bulgaria	15	3.5660322%
Finland	15	3.5660322%
Portugal	17	3.5660322%
Austria	18	3.4902283%
Hungary	18	3.4902283%
Spain	18	3.4902283%
France	21	3.4144214%
Greece	21	3.4144214%
Italy	21	3.4144214%
Denmark	24	3.3386114%
Belgium	25	3.2627983%
Poland	25	3.2627983%
Slovakia	27	3.1908008%

Table 8. Ranking of the countries in terms of energy security after priority equalization.

Country	Ranking Position	Final Priorities of Alternatives
Estonia	1	4.3996697%
Malta	1	4.3996697%
Cyprus	3	4.3239000%
Luxembourg	4	4.1723511%
Germany	5	4.0965720%
Sweden	6	4.0207897%
Netherlands	7	3.9450043%
Croatia	8	3.8692158%
Latvia	9	3.7934242%
Slovenia	9	3.7934242%
Romania	11	3.7176294%
Czech Republic	12	3.7176294%
Ireland	13	3.6418316%
Lithuania	13	3.6418316%
Bulgaria	15	3.5660307%
Finland	15	3.5660307%
Portugal	15	3.5660307%
Hungary	18	3.4902266%
Austria	19	3.4902266%
Spain	19	3.4902266%
France	21	3.4144195%
Greece	21	3.4144195%
Italy	21	3.4144195%
Denmark	24	3.3386093%
Belgium	25	3.2627961%
Poland	25	3.2627961%
Slovakia	27	3.1908251%

At the end of the analytical hierarchy process, the list of the priorities of alternatives was presented. The AHP method results allowed for building the ranking of European Union countries regarding energy security. In other words, according to the importance (weight) of each security energy criterion, it was possible to identify the rank of European countries with less probability of investment risk. The data are presented in descending order. The criteria here concerned, among other things, gross electricity production, energy productivity, electricity production capacities for renewables and wastes, and electricity available to the internal market. The countries with the highest-ranking position may be considered the most stable and safe regarding energy security. Thus, the risk of power outages seems lower in these countries. Therefore, according to the results, Malta and Estonia were characterized as the lowest investment risk in the energy sector. While countries situated at the end of the ranking list (i.e., Belgium, Poland and Slovakia) seemed to be more risky investment alternatives in the energy field, taking into account the selected criteria.

The final probabilities of the AHP are influenced by the criteria weights. It would be helpful to examine the stability of the ranking results, namely, to analyze: What would happen with the results if criteria weights changes? The answer to such a question may be obtained by sensitivity analysis. Sensitivity analysis allows an understanding of how robust a decision can be if it is based on the results obtained by the AHP. This part of the decision process is important, and no decision should be taken without a previous sensitivity analysis. The sensitivity analysis requires modifying the weights of the criteria, recalculating the AHP, and verifying if and how far these changes influence the ranking list order, i.e., the priorities of the alternatives [29,30]. In this case, the weight values were equalized, so the changes in their values varied from 1.7% to 17.8% compared to the starting weights.

According to data presented in Table 8, which was generated after the equalization of the criteria weights in the sensitivity analysis process and compared to the data presented in Table 7, it is possible to note that minor changes occurred in the positions of four countries: Romania, Czech Republic, Hungary, and Austria. A very small difference in results triggered this. However, the top and bottom of the list did not change. This proves that the criterion weight evaluator algorithm proposed and used in this analysis tends to give reliable and stable outcomes. New weights are available in Appendix D.

4.2. Discussion

According to Jałowiec et al. [20], the EU adopting the critical assumptions of the integrated energy and climate program precedes the energy policy model until 2050. Future energy investments need a risk analysis before project financing [21,23]. Furthermore, from the perspective of harsher divisions within the EU, member states need to coordinate their tactics to maximize the effectiveness of the policy responses. The decision-making process is a very complex problem due to the complexities involved. A previous study [27] pointed out various investment risks that might threaten green energy project development. Since each risk differs, the decision is complicated, making the investors’ decision difficult. Therefore, steps toward reducing the investment risks for sustainable energy projects may help future decision-making [23,24,25,26].

In this study, we proposed a popular AHP method to build a ranking of countries in terms of their energy sector security. Here, we understand security as the stability of an energy sector, in particular energy industry and market. Estonia and Malta gained the top two positions and opened the ranking list, followed by Cyprus and Luxembourg. According to Enerdata reports, Estonia aims to develop wind power energy and LNG (liquefied natural gas) terminals. Luxembourg intends to increase electricity and gas interconnections between Belgium, Germany and France. While in Cyprus, the main priorities of the energy policies are the liberalization of the market and the promotion of natural gas and renewables [55]. These areas may therefore be the most promising energy investment targets in these countries. Malta as an island is highly dependent on imported energy sources, of which over 90% are fossil fuels. However, the demand for energy there tends to increase steadily, and the island has the potential for renewable energy infrastructure (mainly solar energy) [56]. As the country has also developed a low-carbon development strategy, there is potential for investment in clean energy in Malta. The ranking list closed with Slovakia with the lowest rate of the final priority value. The country has struggled with a severe energy crisis in recent years and is officially described as a country experiencing energy poverty [57]. This could influence the value of the criteria and, as a result, the final ranking position in investment security.

Previous studies, which analyzed risk factors in investments in the energy sector or energy technologies, revealed that the most critical risk factors were economic- or financial-oriented (e.g., electricity price policy [26], economic and business risk [27] or political risk, environmental factors, and financial risk [43]). In this study, the most critical factor appeared to be the electricity production capacity of the energy sector in each country that considers different types of renewables and waste. This criterion gained the highest weight value and may reflect European policy goals to increase the share of renewable energy production [22]. Two other criteria that obtained quite a high level of importance were primary energy consumption (efficiency) and stock levels for gaseous and liquefied natural gas. The first one measures the total demand for energy in each country. Although the EU’s goal is to reduce energy consumption in some countries (e.g., Malta), it has recently increased [58]. The second one reflects the energy policy to reduce coal emissions in favor of using more “clean” energy, such as liquefied natural gas. Therefore, each country aims to increase stock levels for gas. These tendencies influenced the importance of the above-mentioned criteria.

It should be mentioned, however, that the proposed ranking, as a result of multicriteria analysis, is susceptible and depends on criteria selection. With slightly different criteria, the ranking list with a high probability would not stay the same. Nevertheless, the chosen set of criteria seems to correspond correctly with the assessment of the sector security as far as risk investment is concerned. The results of this study may represent a base to support investment decision-making in the energy sector of EU countries.

4.3. Managerial Implications

This study’s managerial implications concern improving the quality of information supporting managers involved in investment projects in the energy area. It is based on the proposed algorithm’s innovativeness for the weight assignment process. The process is based on empirical data on the analyzed area available in reliable databases, such as EUROSTAT. The main advantage of this algorithm’s weighting criteria procedure is eliminating bias that may affect an expert’s opinion. Consequently, the results of the analytical hierarchy seem to be more reliable. It should also be emphasized that the involvement of a group of experts in the analyzed field to provide opinions and assign weights to the criteria is usually costly and time-consuming. The proposed methodology can therefore generate savings in time and money at the investment management level. The proposed algorithm could be a huge advantage in favor of using the AHP method as a decision support tool.

5. Conclusions

This article presents the application of the analytical hierarchy process to support the decision-making process concerning investments in the energy sector. The main goal of the conducted analysis was to evaluate the performance level of countries in the European Union regarding energy policies. The innovation presented was that no expert opinion was needed to make the pairwise comparison between criteria and alternatives of the AHP decision tree, eliminating any opinion bias. Two things were necessary to substitute the work of experts. First, we accessed the data about the performance of European Union countries in energy policies. This information was responsible for giving an importance level of each criterion and alternative at the moment of pairwise comparison and, second, the development of an algorithm that uses these data for pairwise comparison. Using an algorithm and data to determine the weights of criteria and alternatives is the more important point to be highlighted in this paper. This innovation removes the aspect of intuition derived from the opinion of a human being and pragmatically provides support for decision-making through data. The authors believe that the algorithm proved to be feasible and could be easily replicated by any decision-maker or analyst, as well as in other multicriteria problems. It should be considered as a contribution of this study in applying multicriteria analysis in complex decision-making problems.

The results (Table 7) show a ranking of European Union countries regarding energy sector security. This ranking shows the level of countries’ performance in their policy in the energy sector, which means that the higher the priority of the alternative, the better its performance. Consequently, the highest score suggests the inverse level of risk in energy sector investments of that country. In the case of the present research, results showed that Malta and Estonia are the best countries to receive investments because they are at the top of the ranking for energy security. This report can help investors in their decisions about which country while deciding on investments in the energy sector.

The authors are fully aware of some limitations of the study. First, only one multicriteria analysis method was applied to create the ranking of countries in terms of energy security to support risk assessment in investment in the energy sector. It would be valuable to compare the results of the AHP method with other multicriteria analysis methods. Additionally, it should be noted that the choice of database was determined by its accessibility to researchers. Moreover, the type of data available in the Eurostat Data Browser impacted the final list of criteria. Nevertheless, in the authors’ opinion, the chosen variables describe well the condition of the energy sector of each country. Consequently, the results may be considered a strong base for investment decision-making.

This study raises at least a few exciting challenges for future research. One direction is building a ranking using other criteria sets. Another noteworthy issue could be comparing the ranking built by AHP methodology with other multicriteria method results (e.g., TOPSIS) or other methods that enable building rankings using many variables (e.g., data envelopment analysis—DEA). What also seems to be a promising direction for future studies is the application of the presented in this study algorithm to determine the weights of criteria in other methods of multicriteria analysis.