An Improved Technique of Hybridization of PSO for the Optimal Coordination of Directional Overcurrent Protection Relays of IEEE Bus System

Abstract

The use of a directional overcurrent protection relay (DOPR) to protect an electrical power system is a crucial instrument for keeping the system dynamic and avoiding undue interruption. The coordination of a DOPR’s primary and backup relays is modelled as a highly constrained optimization problem. The goal is to determine an ideal value that will reduce the overall working time of all primary relays. The coordination is accomplished by the use of particle swarm optimization hybridization (HPSO). Comprehensive simulation experiments are carried out to evaluate the efficacy of the proposed HPSO by employing the time multiplier setting (TMS) and plug setting (PS) as an optimization variable and constant, respectively. The HPSO has been examined satisfactorily utilizing certain IEEE benchmark test systems (9-bus and 14-bus). The outcomes are contrasted with earlier heuristics and evolutionary approaches. Based on the acquired findings, it is clear that the obtained results exceed the other conventional and state of the art procedures in terms of total DOPR operation and the computing time necessary to achieve the global optimal solution.

1. Introduction

Over the decades, numerous improvements have been made to solve the problem of the coordination of relays for power system protection. The purpose of relay coordination for power system protection is to quickly find the faulty section and resume the services throughout the remaining sections. A directional overcurrent protection relay (DOPR) is an economical method for the primary and secondary/backup protection of power systems [1]. In general, a DOPR is dependent upon many factors such as the plug setting (PS), time multiplier setting (TMS), coordination time interval (CTI), current transformer ratio (CTR) primary fault current, and secondary fault current, etc. To improve reliability in electrical systems, other relays are integrated, which serve as a second line of protection in the event of a failure of the first protection, and to ensure the stability of the power system, an alternate protection circuit must be placed in case the first one does not work properly [2,3]. The reliability of the operating time of a DOPR depends on two parameters that are the plug setting (PS) and time multiplier setting (TMS). In this manuscript, linear programming is formulated because the plug setting is constant and the time multiplier setting is variable for the DOPR problem.

Some evolutionary techniques have been used for the coordination of DOPR either in multiple networks or in ring networks. Metaheuristics evolutionary techniques include the genetic algorithm (GA) [4], particle swarm optimization (PSO) algorithm [5], firefly algorithm (FA) [6,7], whale optimization [8], Jaya algorithm (JA) [9], electromagnetic field optimization (EFO) [10], teaching learning based optimization (TLBO) algorithm [11], root tree algorithm [12], differential evolution (DE) algorithm [13,14], gray wolf optimization [15], and seeker algorithm [16]. Some computer-generated MATLAB simulated techniques include IDE (integrated development environment) [17], and NLP (Nonlinear Programming) [18], IPOPT (Interior Point Optimization) [19,20], SNOPT (Sparse Nonlinear Optimizer) [21], OPTI Tool [21], and IPM (Interior Point Method) [21], etc. The particle swarm optimization (PSO) algorithm was presented with different IEEE benchmark test systems for the optimal coordination of DOPRs [22]. For simulations of the grounding grids and to achieve optimal DOPR coordination, the genetic algorithm was used [23]. For the improvement in the coordination of DOPR, some hybrid techniques have also been used, such as a combination of the firefly algorithm with the artificial neural network (ANN), proposed for the IEEE 9-bus system; in this work, more DGs are used in the IEEE-9 bus system [24]. An algorithm, OJAYA (oppositional Jaya), is proposed for the DOPR’s coordination problem by using the distance adaptive coefficient (DAC) method. The Oppositional Learning (OL) firstly formulates in the Jaya algorithm to stretch the searching space and to fortify the population, and secondly, DAC is used to escape from the worst position and to gain the best position [25]. A Mathematical Programming Language (AMPL)-based Interior Point Optimization (IPOPT) solver is deployed on an IEEE 14-bus system by using DGs and without DGs. In [26], a hybrid BBO–LP (BBO with LP) is proposed for the coordination of DOPRs. In [27], a hybrid GA with nonlinear programming (NLP) method is deployed to solve the DOPR problem and find the TMS. In [28], a hybrid PSO with LP method is proposed; in this case, both the PS and TMS are optimization variables. In summary, all these optimization techniques perform well for simple problems; however, for complex problems, they take more computational time and converge with a greater number of iterations. The main advantage of this research with the other mentioned metaheuristics techniques is that hybridization is performed by introducing simulated annealing (SA) in the original PSO to avoid being trapped in local optima and to successfully search for a global optimum solution. The suggested HPSO has extraordinary exploration competency and speed as compared to other metaheuristic techniques; this characteristic makes the population members of the HPSO more discriminative when searching for the optimal solution compared to other metaheuristic algorithms. Therefore, this shows the clear novelty and contribution of this method, while most other studies just utilized or applied the existing or emerging optimization methodologies from the literature rather than developing a new methodology themselves. In this context, this paper also aims to explore ways of improving and finding the optimal coordination of the overcurrent relay through a newly developed hybrid swarm-based optimization approach named as “HPSO”.

In this case, linear programming is deployed, in which only TMS is variable, while other settings are constant such as pickup current and PS, etc. Normally in these cases, there is a risk of catching in the local optima and found nonlinearity in the coordination problem. For the solutions of these issues, a hybrid PSO–SA (particle swarm optimization algorithm–simulated annealing) technique and adaptive protection setting has been proposed [29] to avoid being trapped in local optima. By using this technique, premature convergence and the nonlinearity problem of DOPR is solved efficiently and the optimal global solution is achieved. The idea of using PSO with SA occurred because PSO has the ability to converge earlier and SA has the capability to remove from the local optima [30].

Two standard benchmarks of IEEE case studies (i.e., IEEE 9- and 14-bus systems) are formulated by using the PSO and HPSO techniques. The objective is to find the minimum total operating time taken by primary relays to trace the fault. Organization of this paper is as follows: In Section 2, the coordination of a DOPR is described. In Section 3, a detailed explanation of PSO and SA is presented. Simulation results and the comparison of this technique with other techniques are evaluated in Section 4, and, lastly, the conclusion is presented in Section 5.

2. Problem Formulation

The optimization coordination problem of the DOPR is to minimize the total operating time of all the relays [31]. To minimize the total operating time, coordination between the DOPRs should be synchronized. The plug setting (PS) and time multiplier setting (TMS), should be maintained for the coordination of the DOPR. This research is about the linear programming function; therefore, the value of the PS is kept constant, while the TMS is a variable [32,33].

The objective function (F) is to find the sum of the total operating time of the relays given in Equation (1). The problem of coordinating optimal DOPR protection is to minimize the sum of the operating times of all relays corresponding to the maximum fault current. The number of relays are denoted by $\mathrm{N}$, and ${\mathrm{T}}_{\mathrm{i}}$ is the total operating time of the $i$-th relay [5].

$$\mathrm{Objective} \mathrm{Function} \left(\mathrm{F}\right)=\left|{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{i}}\right|$$

(1)

This objective function is subjected to the LCT (least coordination time), PS, TMS, and minimum time of the relays, and in this proposed technique, absolute value is used.

$$\left|{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{j}}\right|-\left|{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{i}}\right|\ge \left|\mathrm{LCT}\right|$$

(2)

$${\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{TMS}}_{\mathrm{i},\min }\le {\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{TMS}}_{\mathrm{i}}\le {\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{TMS}}_{\mathrm{i},\max }$$

(3)

$${\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{i},\min }\le {\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{i}}\le {\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{i},\max }$$

(4)

In Equation (2), ${\mathrm{T}}_{\mathrm{i}}$ is the operating time of the primary relay, ${\mathrm{T}}_{\mathrm{j}}$ is the operating time of the backup relay, and LCT is the least coordination time required for the proper coordination. LCT is the absolute value of the primary and backup. In Equation (3), ${\mathrm{TMS}}_{\mathrm{i},\min }$ is the minimum limit on TMS and ${\mathrm{TMS}}_{\mathrm{i},\max }$ is the maximum limit on the TMS. The PS in this case is constant, which is why it does not have boundaries of a maximum and minimum limit. In Equation (4), ${\mathrm{T}}_{\mathrm{i},\min }$ and ${\mathrm{T}}_{\mathrm{i},\max }$ are the minimum and maximum time required for the operation of the relays, respectively. Here, the point to note is that the objective function given in Equation (1) is to minimize the total operating time of the primary relays without the requirement of the operating time of the backup relays while satisfying LCT requirements. Equations (3) and (4) are about the boundary limits of the required time to trace the fault.

Equation (5) defines the operating time of the relay according to the IEC (International Electrotechnical Commission) standard, in which α and$\sigma$ are constant parameters and their values are α = 0.02 and $\sigma$= 0.14 respectively [19]. The pickup current and fault current flowing through the relays are${ \mathrm{I}}_{\mathrm{p} }$,${ \mathrm{I}}_{\mathrm{f}}$ respectively. In this proposed technique, the absolute value of the operating time is used, which is either the primary time or the backup time.

$${\mathrm{T}}_{\mathrm{i}}=\left|\frac{{\mathrm{TMS}}_{\mathrm{i}}\times \mathsf{\sigma }}{{\left({\mathrm{I}}_{\mathrm{fi}}{\mathrm{I}}_{\mathrm{pi}}\right)}^{\mathsf{\alpha }}-1}\right|$$

(5)

Generally, ${\mathrm{I}}_{\mathrm{p}}$ is a product of the plug setting (PS) and current transformer ratio (CTR), which is given in Equation (6).

$${\mathrm{I}}_{\mathrm{pi}}={\mathrm{PS}}_{\mathrm{i}}\times {\mathrm{CTR}}_{\mathrm{i}}$$

(6)

The coordination time interval (CTI) between the operating time of the primary ${\mathrm{T}}_{\mathrm{i}}$ and backup ${\mathrm{T}}_{\mathrm{j}}$ relay and their relationship is given in Equation (7). The most important coordination constraint is the operating delay between a primary relay and its backup relay. This delay is known as the coordination time interval (CTI) and it depends on many factors, such as the operating time of the CBs and the other safety factors. Their relation is given in Equation (7). The value of the primary and backup time is taken as absolute in this proposed technique; also, the achieved results of the CTI are taken as absolute to avoid any operating time error.

$${\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{j}}-{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{i}}=\left|\mathrm{CTI}\right|$$

(7)

The relationship between the primary and backup relay is said to integrate well when the CTI between the operating time of the primary and backup relay is more than the defined LCT. In this case, the LCT value is set to 0.2 s [25].

$${\mathrm{T}}_{\mathrm{i}}=\left|\frac{{\mathrm{TMS}}_{\mathrm{p}}\times \mathsf{\sigma }}{{\left({\mathrm{I}}_{\mathrm{fp}}({\mathrm{PS}}_{\mathrm{p}}\times {\mathrm{CTR}}_{\mathrm{p}})\right)}^{\mathsf{\alpha }}-1}\right|$$

(8)

$${\mathrm{T}}_{\mathrm{j}}=\left|\frac{{\mathrm{TMS}}_{\mathrm{b}}\times \mathsf{\sigma }}{{\left({\mathrm{I}}_{\mathrm{fb}}({\mathrm{PS}}_{\mathrm{b}}\times {\mathrm{CTR}}_{\mathrm{b}})\right)}^{\mathsf{\alpha }}-1}\right|$$

(9)

Equations (8) and (9) are derived from Equations (5) and (6). These equations are for the operating times of the primary and backup relays. Where, p and b denote the primary and backup relay, respectively. Equation (8) is used to calculate the operating time of the primary relay, whereas Equation (9) is used to calculate the backup relay. In general, from these equations, the relationship between the DOPR operating time of $\mathrm{T}$ and the TMS relay is found. Thus, this problem is considered as a linear problem because all the parameters of the objective function are known except for the TMS. Therefore, the optimal value of this parameter will be determined simultaneously by solving this linear optimization problem.

3. Optimization Algorithm for the Protection of Coordination Problems

PSO and SA are robust, productive, and dependable optimization techniques. These optimization techniques can be applied easily to the DOPR problems. In this research, the implementation and the mathematical modelling of the PSO and SA will be explained.

The PSO algorithm belongs to the navigation of flocks of birds or schools of fishes. In the problem of the coordination of a DOPR, PSO is used to find the fault in the DOPR in the minimum total operating time. As one of the abilities of PSO is to converge as earlier stated, that is why it is very helpful in the case of the coordination of a DOPR [34,35]. After the convergence, PSO gives two solutions, one is the personal best and the other is the global best. The personal best is the overall solution achieved after the simulation of the desired function and is denoted by “$pbest$”. The global best is the minimum value or objective function that is achieved from the personal best solution and is denoted by “$gbest$”. The stepwise process of PSO is as follows

$$x_i^k=x_{i,min}+\left(x_{i,max}-x_{i,min}\right)r_i$$

(10)

$$F_i^k=f\left(x_i^k\right)$$

(11)

$$pbest=F_i^k$$

(12)

$$gbest=minimum \left(pbest\right)$$

(13)

$$v_{i,j}^{k+1}=\omega .v_{i,j}^k+c_1.r_1.\left(pbes{t}_{i,j}^k-x_{i,j}^k\right)+c_2.r_2.\left(gbes{t}_{i,j}^k-x_{i,j}^k\right)$$

(14)

$$x_{i,j}^{k+1}=x_{i,j}^k+v_{i,j}^{k+1}$$

(15)

Pseudocode of HPSO

The pseudocode of the proposed HPSO algorithm is reported in Algorithm 1.

Algorithm 1 Pseudocode of Hybrid Particle Swarm Optimization (HPSO)

Step 1: Initialize wmin,wmax (Inertia), c1,c2 (Acceleration Factor), r1,r2 (Random value), T0 (Initial Temperature) and α (Cooling Factor) for the Hybrid PSO (PSO–SA).

Step 1.1: Initialize the generation system within the parameter’s boundary conditions.

Step 1.2: The initial results are obtained after evaluating the objective function by using Equation (12). From the function, pbest is achieved; the minimum value of this function is gbest.

Step 2: This step belongs to the cycle of iteration until the desired results are achieved.

Step 2.1: Particle velocity and position is updated within a certain boundary limit by using the Equations (14) and (15).

Step 2.2: Result of pbest and gbest are achieved according to Equations (12) and (13).

Step 2.3: SA is started here after obtaining the gbest as the initial solution.

Step 2.4: Function for the new solution defined with respect to the old solution.

Step 2.5: The new solution is generated after evaluating the old solution.

Step 2.6: If the difference between the old and new solution is less than 0, the solution is accepted as a good solution by using Equation (18).

Step 2.7: Otherwise use Equation (19) until it satisfies step 2.6

Step 2.8: From the objective function, the new solution is achieved.

Step 2.9: Update temperature according to Equation (21).

Step 2.10: Repeat Step 2 until the stopping criterion is met.

Step 3: Show estimated parameters, objective values, and gbest solution.

Equation (10) is a modified position of the particle also called the initial position. From this initial position, initial velocity is generated. The initial position that is achieved goes through the objective function given in Equation (11). Equation (12) shows the objective value achieved is called the personal best of the solution. The minimum of this personal best is called the global best given in Equation (13). At this point, if the results are acceptable then the best minimum total operating time is achieved. If not, then it will move forward to Equation (14), where the velocity and the position of the particle are updated as given in Equations (14) and (15). After updating the velocity and position of the particle, the solution will go through Equations (11)–(13) until the best solution is achieved. The abbreviations $x_{i,max}$ and $x_{i,min}$ from Equations (10)–(15) are the maximum and minimum boundary limits of the variables, respectively, and $r_i$ denotes the random number of the $i$-th variable whose value varies from 0 to 1. The objective function at a certain position is denoted by$F_i^k$. The inertia, ω, value varies from 0.1 to 0.9, ($c_1, c_2$) are the acceleration factors and their values vary around 2, and$(r_1$, $r_2)$ are the random values from 0 to 1.

To hybridize the PSO, SA is used as a partner to further improve the total operating time of the DOPR in the minimum convergence time. Simulated annealing (SA) works on the principle of annealing in metallurgy [36]. Annealing is the process of the slow cooling of the metal after heating. Slow cooling is carried out because metal deforms to the desired shape at a low energy state where it cannot be broken easily. In the case of optimization, it works on the principle of a good move and a bad move, where a good move is acknowledged, and the bad move will go through certain functions to make it a good move. The stepwise process of the HPSO is as follows

$$O.solution=gbest$$

(16)

$$N.solution=createneighbour \left(O.solution\right)$$

(17)

$$D \left(Delta\right)=N.solution-O.solution$$

(18)

$$P=exp\left(-D/T\right)$$

(19)

$$r\le exp\left(-D/T\right)$$

(20)

$$T_k=\alpha *T_{k-1}$$

(21)

The PSO results are further improved by using the SA algorithm, such as the global best from PSO being taken as the old solution given in Equation (16). The new solution is achieved by putting the old result in the new function given in Equation (17). Equation (18) tells us about the difference between the new and the old solution; when the delta is less than 0, the new solution becomes equal to the old solution and it is called a good move. The good solution is passed through the cooling function given in Equation (21) and the required results are achieved. If the delta is greater than 0, then the solution will pass through the probability equation given in Equation (19) and it will continually move through that equation until it satisfies Equation (20). By following these steps, the local optima is removed and the global best solution is achieved. The abbreviations (P, D, and T) used in the Equations (16)–(21) are the probability, the difference between the two variables and the temperature, respectively, whereas $r$ is a random number from 0 to 1. The initial temperature is T₀ and α is the cooling factor. $T_k$ is the new temperature, α is the cooling factor, and $T_{k-1}$ is the previous temperature. The value of the initial temperature ($T_0$) is 1 and the cooling factor (α) is 0.99.

The flow chart and the pseudocode of the desired algorithm are shown in Figure 1 and Algorithm 1, respectively. Firstly, all the parameters of the PSO are defined according to the objective function of the DOPR. By using the Equations (11)–(13), the total operating time and the minimum value from that operating time are calculated, also known as the initial personal best and the global best. Equations (14) and (15) are used to update the velocity and position of the DOPR to enhance the speed to trace the fault as quickly as possible. If the results are acceptable, then the iteration stops and the desired results are achieved; if not, then it keeps on iterating until the desired results are achieved. After obtaining the PSO results, then the SA is initialized and uses the global best value as the old solution given in Equation (16). The new solution is achieved from the neighborhood of the old solution given in Equation (17). The desired value is updated by using the Equations (19)–(21) until a more improved minimum operating time of the DOPR is achieved. It is worth noticing that the results can be achieved at any section when desired, needing either the PSO or HPSO. The two IEEE test cases, undertaken through this proposed algorithm, and their results are given in Section 4.

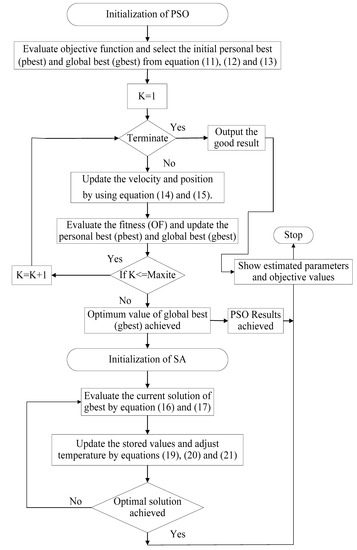
Figure 1. Flow chart of the Proposed Technique.

In summary, after using the HPSO for the coordination of the DOPR problem, improved results are obtained compared to other metaheuristic techniques. This is because PSO has the ability to update the speed after every iteration and yields a lower operating time, and SA has a high search capability and removes the local optima. Therefore, using these two algorithms together gives a competitive operating time compared to other state of the art techniques.

4. Simulation Results and Discussion of IEEE Bus Systems

The PSO and HPSO algorithms described in the previous section have been applied to solve the two IEEE bus systems for the protection of coordination problem. As the objective function is a linear programming function, therefore, for these two cases, the limit of the TMS varies from a 0.1 minimum limit to a 1.2 maximum limit, respectively, whereas the PS and CTI are kept constant at 0.5 and 0.2 s, respectively. The obtained results and the comparison with other algorithms are discussed in the following subsection.

4.1. Case 1: IEEE 9-Bus System

A single line diagram with single source of power distribution system is shown in Figure 2. This 9-bus system has a single source that is supplied at Bus 1. In this system, there are 12 fault points (L1, L2, L3, …, L12), nine buses (Bus 1, Bus 2, …, Bus 9), 24 relays (R1, R2, R3, …, R24), and the number of combinations between the primary and backup of these 24 relays is 32. The current transformer ratio (CTR) for this bus system is set to 500:1 for all the relays. The relationship between the primary and backup relays at different fault points for all 32 combinations are executed in Table 1. The fault current passing through the primary relay and the backup relay are shown in Table 2. As this DOPR problem is solved by a linear programming function, the PS is kept constant at 0.5 and the optimized TMS of the proposed results of the PSO and HPSO are achieved in Table 3, by taking the CTI value at 0.2 s. The analysis of other techniques with the proposed technique are shown in Table 4.

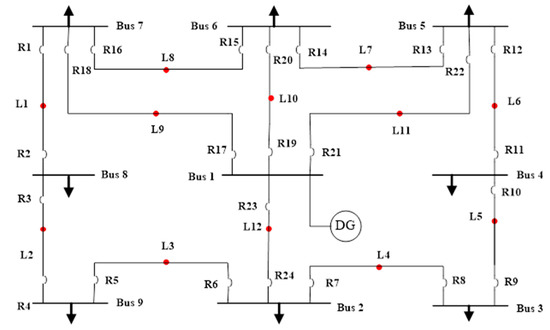
Figure 2. Single line diagram of IEEE 9-bus system.

Table 1. Relationships between primary and backup relays at different fault points.

Faulty Point	Primary Relay	Backup Relay	Faulty Point	Primary Relay	Backup Relay
L1	1	15, 17	L7	13	11, 21
	2	4		14	16, 19
L2	3	1	L8	15	13, 19
	4	6		16	2, 17
L3	5	3	L9	17	NB
	6	8, 23		18	2, 15
L4	7	5, 23	L10	19	NB
	8	10		20	13, 16
L5	9	7	L11	21	NB
	10	12		22	11, 14
L6	11	9	L12	23	NB
	12	14, 21		24	5, 8

NB means no backup relay.

Table 2. Primary and backup relays fault currents of IEEE 9-bus system.

Relays	$\mathbf{Primary} \mathbf{Relay} \left({\mathit{I}}_{\mathit{f}\mathit{p}}\right)$	$\mathbf{Backup} \mathbf{Relay} \left({\mathit{I}}_{\mathit{f}\mathit{b}}\right)$	Relays	$\mathbf{Primary} \mathbf{Relay} \left({\mathit{I}}_{\mathit{f}\mathit{p}}\right)$	$\mathbf{Backup} \mathbf{Relay} \left({\mathit{I}}_{\mathit{f}\mathit{b}}\right)$
R1	4863.6	1361.6	R13	3684.5	1031.7
R2	1634.4	653.6	R14	4172.5	1168.3
R3	2811.4	1124.4	R15	4172.5	1168.3
R4	2610.5	1044.2	R16	3684.5	1031.7
R5	1778.0	711.2	R17	7611.2	1293.9
R6	4378.5	1226.0	R18	2271.7	1953.7
R7	4378.5	1226.0	R19	7435.8	1264.1
R8	1778.0	711.2	R20	2624.2	2256.8
R9	2610.5	1044.2	R21	7611.2	1293.9
R10	2811.4	1124.4	R22	2271.7	1953.7
R11	1634.4	653.6	R23	7914.7	1345.5
R12	2811.4	787.2	R24	1665.5	1432.3

Table 3. Optimized TMS of PSO and HPSO of IEEE 9-Bus system.

TMS	PSO	HPSO	TMS	PSO	HPSO
Relay 1	0.3142	0.1000	Relay 13	0.1000	0.1000
Relay 2	0.1000	0.1000	Relay 14	0.1000	0.1000
Relay 3	0.1000	0.2168	Relay 15	0.1000	0.1000
Relay 4	0.1000	0.1000	Relay 16	0.1000	0.1000
Relay 5	0.1066	0.1000	Relay 17	0.3648	0.1000
Relay 6	0.4362	0.1081	Relay 18	0.1000	0.1000
Relay 7	0.2423	0.3137	Relay 19	0.1000	0.1041
Relay 8	0.2900	0.1000	Relay 20	0.1000	0.1000
Relay 9	0.1000	0.1000	Relay 21	0.1616	0.1526
Relay 10	0.1000	0.1000	Relay 22	0.1000	0.2499
Relay 11	0.1000	0.2419	Relay 23	0.1000	0.1000
Relay 12	0.1000	0.1000	Relay 24	0.2054	0.1000
Objective Function (F)	9.8894	8.5732

Table 4. Comparison of PSO and HPSO with other techniques.

Optimization Techniques	Objective Function (F)
GA [27]	32.6058
MEFO [10]	25.884
IDE [17]	59.6471
MATLBO [17]	41.9041
TLBO [17]	82.9012
BBO [16]	28.8348
NLP [18]	19.4041
PSO	9.8894
HPSO	8.5732

It is noted that the proposed PSO and HPSO algorithm performs better than the GA, MEFO, BBO, NLP, MATLBO, TLBO, and IDE algorithms. This is because PSO has an exceptional quickness and exploration capability to trace the fault, and the addition of SA in the algorithm helps to improve the optimal solution. The operating times of individual relays by using the optimized values of the TMS are given in Table 5. The analysis of the net gain of the HPSO with the other defined techniques is displayed in Figure 3, which justifies that this technique is better than the other optimization techniques. The convergence graph of the PSO and HPSO are given in Figure 4 after the simulation with the help of MATLAB.

Table 5. Operating time of individual relays for the optimized values of the TMS.

No. of Relays	Operating Time of Each Relay (s)		No. of Relays	Operating Time of Each Relay (s)
	PSO	HPSO		PSO	HPSO
Relay 1	0.7192	0.2289	Relay 13	0.2532	0.2532
Relay 2	0.3659	0.3659	Relay 14	0.2418	0.2418
Relay 3	0.2823	0.6121	Relay 15	0.2418	0.2418
Relay 4	0.2915	0.2915	Relay 16	0.2532	0.2532
Relay 5	0.3730	0.3499	Relay 17	0.7223	0.1980
Relay 6	1.0363	0.2568	Relay 18	0.3102	0.3102
Relay 7	0.5756	0.7452	Relay 19	0.1994	0.2076
Relay 8	0.9411	0.3499	Relay 20	0.2908	0.2908
Relay 9	0.2915	0.2915	Relay 21	0.3200	0.3022
Relay 10	0.2823	0.2823	Relay 22	0.3102	0.7753
Relay 11	0.3659	0.8850	Relay 23	0.1957	0.1957
Relay 12	0.2823	0.2823	Relay 24	0.7439	0.3622

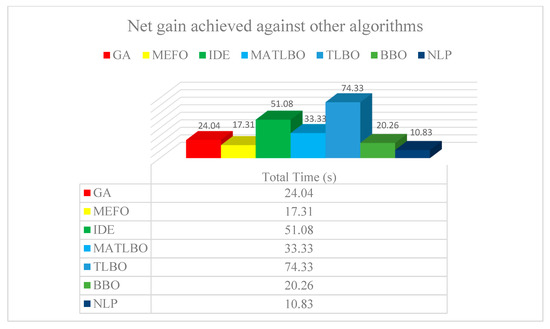
Figure 3. Analysis of net gain for the IEEE 9-Bus system.

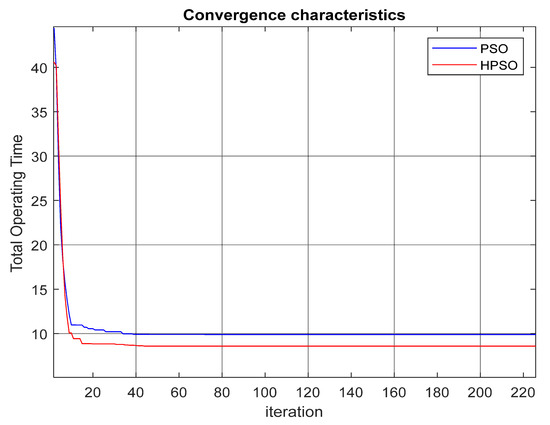
Figure 4. PSO and HPSO convergence characteristics of IEEE 9-Bus system.

4.2. Case 2: IEEE 14-Bus System

The IEEE 14-bus system is shown in Figure 5, which consists of one DG, 3 generators, 20 fault points (L1, L2, L3, …, L20), 14 buses (Bus 1, Bus 2, …, Bus 14), and 40 relays (R1, R2, R3, …, R24). There are 92 combinations among these 40 primary–backup relays. One DG is connected at bus 14 and three generators are connected at buses 1, 2, and 6, respectively. The current transformer ratios (CTR) for all the relays for this bus system are given in Table 6. The relationships between the primary and backup relays at different fault points for all the 92 combinations of relays are given in Table 7. The fault currents for all the 40 relays either passing through the primary relay or from the backup relay are given in Table 8.

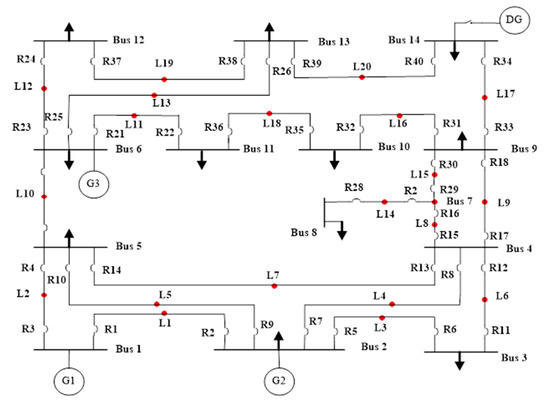
Figure 5. Single line diagram of IEEE 14-bus system.

Table 6. CT ratio between the relays for the IEEE 14-bus system.

Relay	CT Ratio	Relay	CT Ratio
1	8000:5	7	2500:5
2, 4, 8, 10, 13, 24	400:5	12, 36, 39	2000:5
3, 14	3500:5	20, 35, 38	1000:5
5, 25	4000:5	16, 18	800:5
9, 19, 23, 27, 31	1600:5	17, 26, 34	500:5
15, 30, 33	1200:5	22, 32, 37, 40	600:5
6	200:5	11	250:5
21	3000:5	28	50:5
29	5000:5

Table 7. Relationships between primary and backup relays at different fault points of IEEE 14-bus system.

Faulty Point	Primary Relay	Backup Relay	Faulty Point	Primary Relay	Backup Relay
L1	1	4	L11	21	19, 24, 26
	2	6, 8, 10		22	35
L2	3	2	L12	23	19, 22, 26
	4	9, 13, 20		24	38
L3	5	1, 8, 10	L13	25	19, 22, 24
	6	12		26	37, 40
L4	7	1, 6, 10	L14	27	15, 30
	8	11, 14, 16, 18		28	-
L5	9	1, 6, 8	L15	29	15, 28
	10	3, 13, 20		30	17, 32, 34
L6	11	5	L16	31	17, 29, 34
	12	7, 14, 16, 18		32	36
L7	13	7, 11, 16, 18	L17	33	17, 29, 32
	14	3, 9, 20		34	39
L8	15	7, 11, 14, 18	L18	35	31
	16	28, 30		36	21
L9	17	7, 11, 14, 16	L19	37	23
	18	29, 32, 34		38	25, 40
L10	19	3, 9, 13	L20	39	25, 37
	20	22, 24, 26		40	33

Table 8. Primary and backup relays fault currents of IEEE 14-bus system.

Relays	$\mathbf{Primary} \mathbf{Relay} \left({\mathit{I}}_{\mathit{f}\mathit{p}}\right)$	$\mathbf{Backup} \mathbf{Relay} \left({\mathit{I}}_{\mathit{f}\mathit{b}}\right)$	Relays	$\mathbf{Primary} \mathbf{Relay} \left({\mathit{I}}_{\mathit{f}\mathit{p}}\right)$	$\mathbf{Backup} \mathbf{Relay} \left({\mathit{I}}_{\mathit{f}\mathit{b}}\right)$
R1	11,650	3920	R21	564	434
R2	4260	1980	R22	1930	1310
R3	7310	1280	R23	1200	806
R4	3920	750	R24	1870	1130
R5	12,400	1370	R25	1430	449
R6	3830	654	R26	4640	1230
R7	7330	1270	R27	2030	638
R8	3880	723	R28	633	634
R9	3260	2080	R29	4720	499
R10	3110	1990	R30	1810	179
R11	7180	1380	R31	2060	783
R12	3130	845	R32	547	280
R13	3280	1120	R33	783	368
R14	4030	1250	R34	1390	547
R15	4610	1110	R35	1480	572
R16	1490	560	R36	781	284
R17	2210	955	R37	572	51
R18	725	388	R38	2530	781
R19	955	564	R39	2400	1110
R20	1310	725	R40	654	191

The optimized TMS results of the proposed PSO and HPSO are shown in Table 9 when the CTI value is 0.2 s and the PS is kept constant at 0.5. The operating times of individual relays by using the optimized values of the TMS are given in Table 10. The optimized results are then compared with the other state of the art techniques. Table 11 shows the proposed PSO and HPSO algorithm is better than the metaheuristic techniques such as GA and DE. Furthermore, the proposed technique is better than the MATLAB-implemented techniques such as IPOPT, SNOPT (Sparse Nonlinear Optimizer), OPTI Tool, and IPM (Interior Point Method). Net gain analysis also justifies the superiority of the proposed technique given in Figure 6. In summary, the proposed HPSO and PSO perform better because of their faster convergence speed and finding capability. After the MATLAB simulation, the convergence graph between the PSO and HPSO is given in Figure 7.

Table 9. Optimized TMS of PSO and HPSO of IEEE 14-Bus system.

TMS	PSO	HPSO	TMS	PSO	HPSO
Relay 1	0.2492	0.1000	Relay 21	0.1000	0.1000
Relay 2	0.1000	0.1000	Relay 22	0.1000	0.1578
Relay 3	0.5250	0.1000	Relay 23	0.1000	0.1000
Relay 4	0.1000	0.1000	Relay 24	0.2958	0.1000
Relay 5	0.1000	0.1000	Relay 25	0.1000	0.2603
Relay 6	0.2204	0.1000	Relay 26	0.9851	0.1000
Relay 7	0.3004	0.1000	Relay 27	0.1000	0.1530
Relay 8	0.3894	0.1000	Relay 28	0.1000	0.1000
Relay 9	0.1000	0.1000	Relay 29	0.5677	0.1000
Relay 10	0.2561	0.1000	Relay 30	0.1000	0.2420
Relay 11	0.4437	0.1000	Relay 31	0.1000	0.1500
Relay 12	0.2635	0.1000	Relay 32	0.1000	0.1000
Relay 13	0.1000	0.1000	Relay 33	0.1000	0.1591
Relay 14	0.3072	0.1002	Relay 34	0.1000	0.1000
Relay 15	0.1000	0.1000	Relay 35	0.1000	0.1000
Relay 16	0.1000	0.1000	Relay 36	0.1000	0.1000
Relay 17	0.1000	0.1000	Relay 37	0.1000	0.2000
Relay 18	0.1000	0.1000	Relay 38	0.1000	0.1000
Relay 19	0.1000	0.1000	Relay 39	0.1000	0.1000
Relay 20	0.1000	0.1000	Relay 40	0.1000	0.2868
Objective Function (F)	17.2757	13.2817

Table 10. Operating time of individual relays for the optimized values of the TMS.

No. of Relays	Operating Time of Each Relay (s)		No. of Relays	Operating Time of Each Relay (s)
	PSO	HPSO		PSO	HPSO
Relay 1	0.6340	0.2544	Relay 21	1.1019	1.1019
Relay 2	0.1431	0.1431	Relay 22	0.1948	0.3073
Relay 3	1.1729	0.2234	Relay 23	0.3405	0.3405
Relay 4	0.1458	0.1458	Relay 24	0.1752	0.1752
Relay 5	0.1969	0.1969	Relay 25	0.5425	1.4121
Relay 6	0.2784	0.1263	Relay 26	1.4542	0.1476
Relay 7	0.6017	0.2003	Relay 27	0.2686	0.4109
Relay 8	0.5690	0.1461	Relay 28	0.1377	0.1377
Relay 9	0.2253	0.2253	Relay 29	1.7307	0.3049
Relay 10	0.3941	0.1539	Relay 30	0.2510	0.6075
Relay 11	0.5183	0.1168	Relay 31	0.2670	0.4005
Relay 12	0.6523	0.2476	Relay 32	0.3098	0.3098
Relay 13	0.1520	0.1520	Relay 33	0.3662	0.5827
Relay 14	0.8587	0.2801	Relay 34	0.2036	0.2036
Relay 15	0.1849	0.1849	Relay 35	0.2528	0.2528
Relay 16	0.2324	0.2324	Relay 36	0.5069	0.5069
Relay 17	0.1778	0.1778	Relay 37	0.3035	0.6070
Relay 18	0.3106	0.3106	Relay 38	0.2097	0.2097
Relay 19	0.3849	0.3849	Relay 39	0.2748	0.2748
Relay 20	0.2652	0.2652	Relay 40	0.2861	0.8205

Table 11. Comparison of PSO and HPSO with other techniques.

Technique	Objective Function (F)
GA [37]	19.7349
DE [37]	14.5620
IPM [21]	14.4341
OPTI Tool [21]	14.4341
SNOPT [21]	14.4341
IPOPT [19]	14.4341
PSO	17.2757
HPSO	13.2817

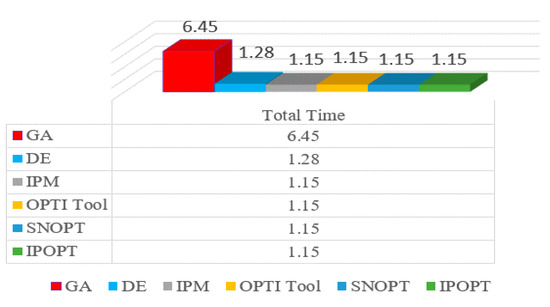
Figure 6. Analysis of net gain for the IEEE 14-Bus system.

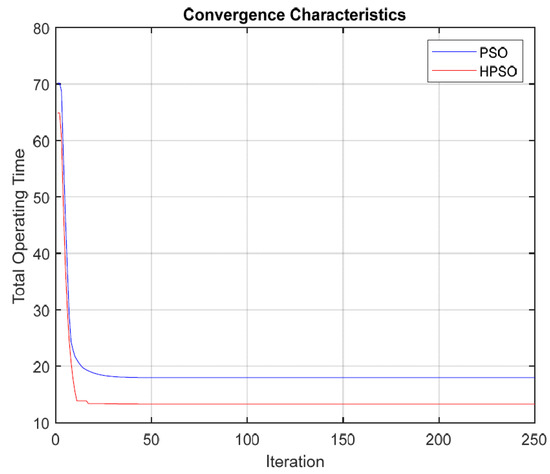
Figure 7. PSO and HPSO convergence characteristics of IEEE 14-Bus system.

4.3. Results Discussion

The DOPR problem is solved on the IEEE 9-bus and 14-bus test system by using the PSO and HPSO algorithms. The proposed technique’s results are then compared with the evolutionary optimization techniques such as GA [27], MEFO [10], IDE [17], MTALBO [17], TLBO [17], BBO [16], NLP [18], DE [37], IPM [21], OPTI Tool [21], SNOPT [21], and IPOPT [19]. The IEEE 9-bus test system is compared with the metaheuristic techniques such as GA, TLBO, BBO, MATLBO (modified adaptive teaching learning based optimization), MEFO (modified electromagnetic field optimization), and some computer-generated MATLAB simulated techniques such as IDE (integrated development environment), and NLP (Nonlinear Programming). The obtained results confirm that the HPSO has a high detection rate and a degree of convergence when compared to other solutions. The defined algorithm was the best solution for eliminating the problem in the leading overcurrent protection relay in a short operating time. The obtained compared results are shown in Table 4 and the net gain analysis is given in Figure 3. The analysis in terms of the net gain shows that values of 24.04 s, 17.31 s, 51.08 s, 33.33 s, 74.33 s, 20.26 s, and 10.83 s are seen against GA, MEFO, IDE, MATLBO, TLBO, BBO, and NLP, respectively. In terms of percentage, there was a 60.94% improvement against the GA, 50.8% against the MEFO, 78.65% against IDE, 72.12% against MATLBO, 86.14% against TLBO, 57.93% against BBO, and 36.34% against NLP observed. For case 2, the IEEE-14 bus system shows less computational time in Figure 6 and Table 9 tells the comparison results of the objective functions of the different techniques. It is observed that the optimum setting obtained by IPM, OPTI Tool, SNOPT, and IPOPT in MATLAB shows the same result, whereas the metaheuristics GA and DE shows different results. IPM, OPTI Tool, SNOPT, and IPOPT are much faster than GA and DE in solving the protection coordination problem of DOPR but are not faster than the HPSO. The HPSO yields a high net gain over GA, DE, IPM, OPTI Tool, SNOPT, and IPOPT which is 6.45 s, 1.4 s, 1.15 s, 1.15 s, 1.15 s, and 1.15 s, respectively. In this case, a good improvement in performance of 39.80% against GA, 9.89% against DE, 8.98% against IPM, OPTI Tool, SNOPT, and IPOPT was achieved. The IEEE convergence characteristics graphs for the PSO and HPSO for the 9-bus and 14-bus systems are shown in Figure 4 and Figure 7. These characteristics graphs show that convergence is quick and, in a few repetitions, a good solution is achieved.

5. Conclusions

Metaheuristic algorithms such as PSO and the hybridization of PSO algorithms are proposed in this article. To identify the global solution, PSO hybridization is used in conjunction with simulated annealing (SA). After each PSO iteration, SA was employed as a local search operator around selected search agents in the proposed algorithm to discover the best solution in the neighborhood. The optimal coordination issue for a DOPR has been stated as a linear programming problem. For various test systems, DOPR issues are handled using the PSO and HPSO algorithms. The HPSO algorithm’s performance has been determined and tested in a range of IEEE single line power distribution systems, with an analysis of its superiority over published approaches such as GA, TLBO, BBO, MATLBO, IDE, and NLP, whereas the IEEE 14-bus system is compared with the GA, DE, IPM, OPTI Tool, SNOPT, and IPOPT algorithms. The obtained results justify that the proposed technique is better than the other optimization techniques.