An Improved Approach to Calculate Eddy Current Loss in Soft Magnetic Materials Based on Measured Hysteresis Loops
Abstract
:1. Introduction
2. Methodology
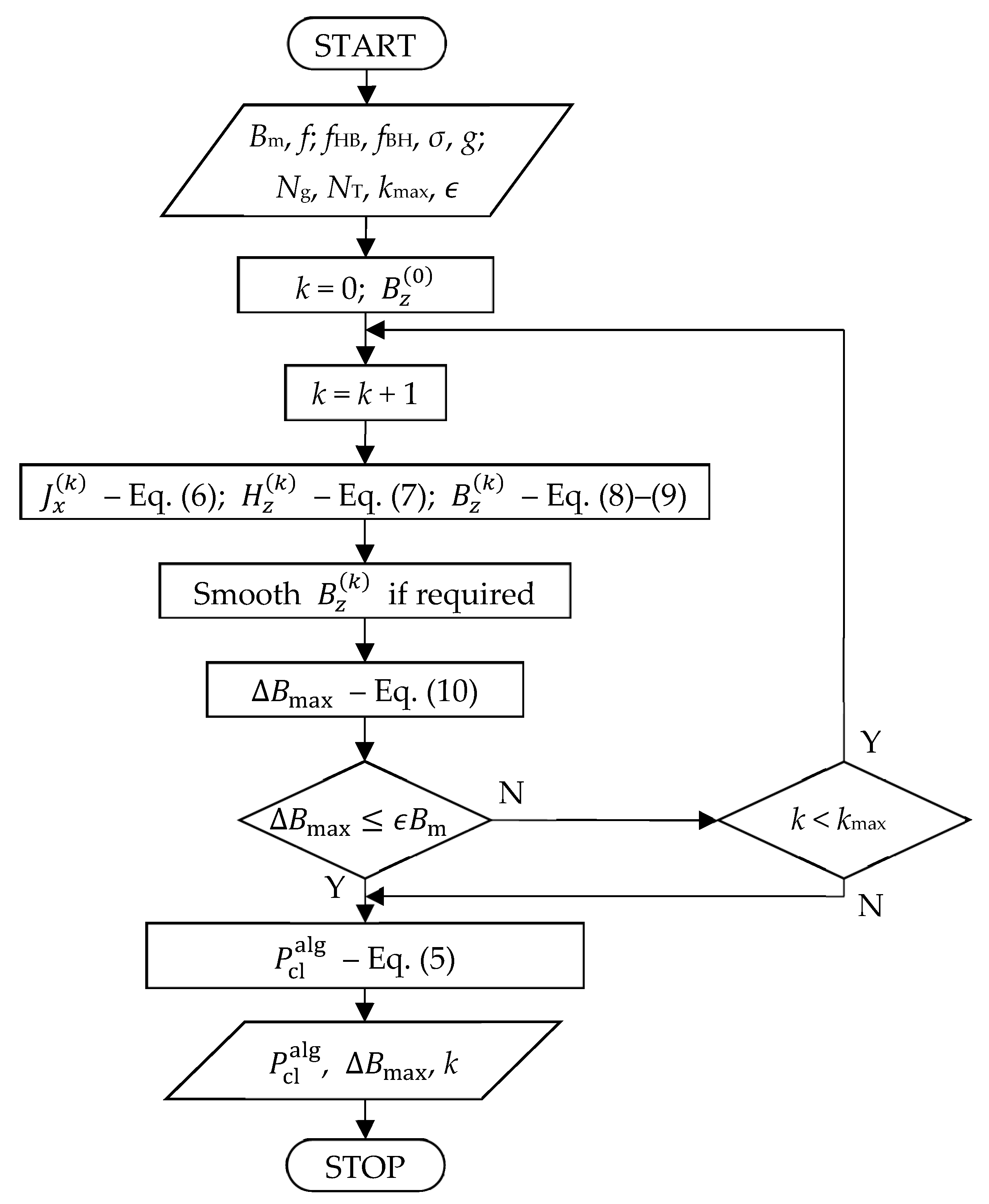
2.1. Theoretical Background: Governing Equations and Their Solving
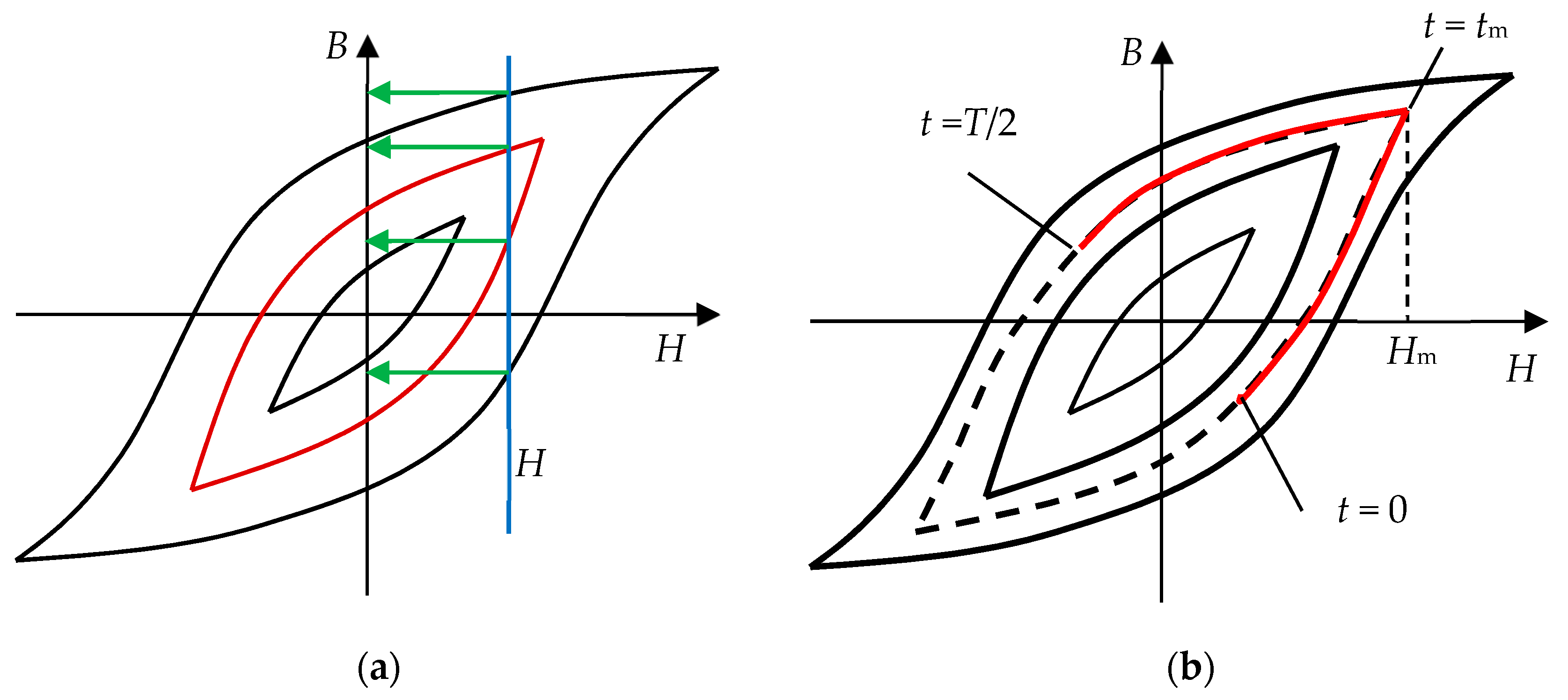
2.2. Conversion between H and B Fields
- Given: H(t), {Hl(t)}, {Bl(t)};
- Construct linear interpolation between Hl(t) and Hl+1(t) in the following form:and detect l, θ, a and b to satisfy h(t) = H(t) at some characteristic times or cases (the origin of Equation (13) is explained below);
- Use detected values of l, θ, a, b to calculate:
- 2a.
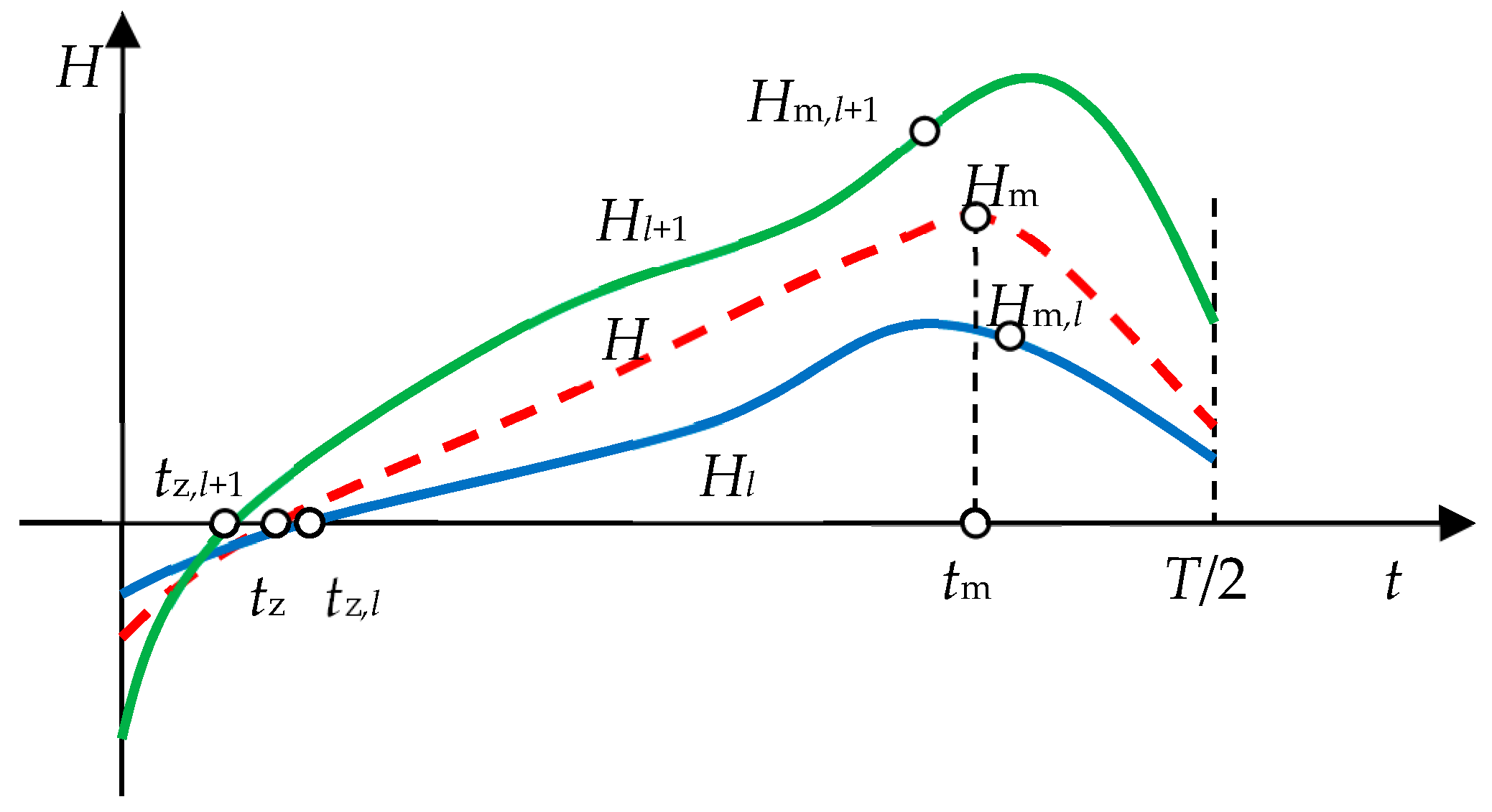
- Find the maximum value of H(t): Hm = maxH(t);
- 2b.
- Find time tm such that H(tm) = Hm;
- 2c.
- Find the ascending zero of H(t), i.e., time tz < tm such that H(tz) = 0;
- 2d.
- Construct a list of values Hm,l using Equation (20);
- 2e.
- Find waveforms between which to interpolate, i.e., find such l that Hm,l ≤ Hm < Hm,l+1; if this is not possible, use the last two waveforms;
- 2f.
- Calculate the interpolation factor using Equation (19);
- 2g.
- Calculate a, b and the time displacement using Equation (17).
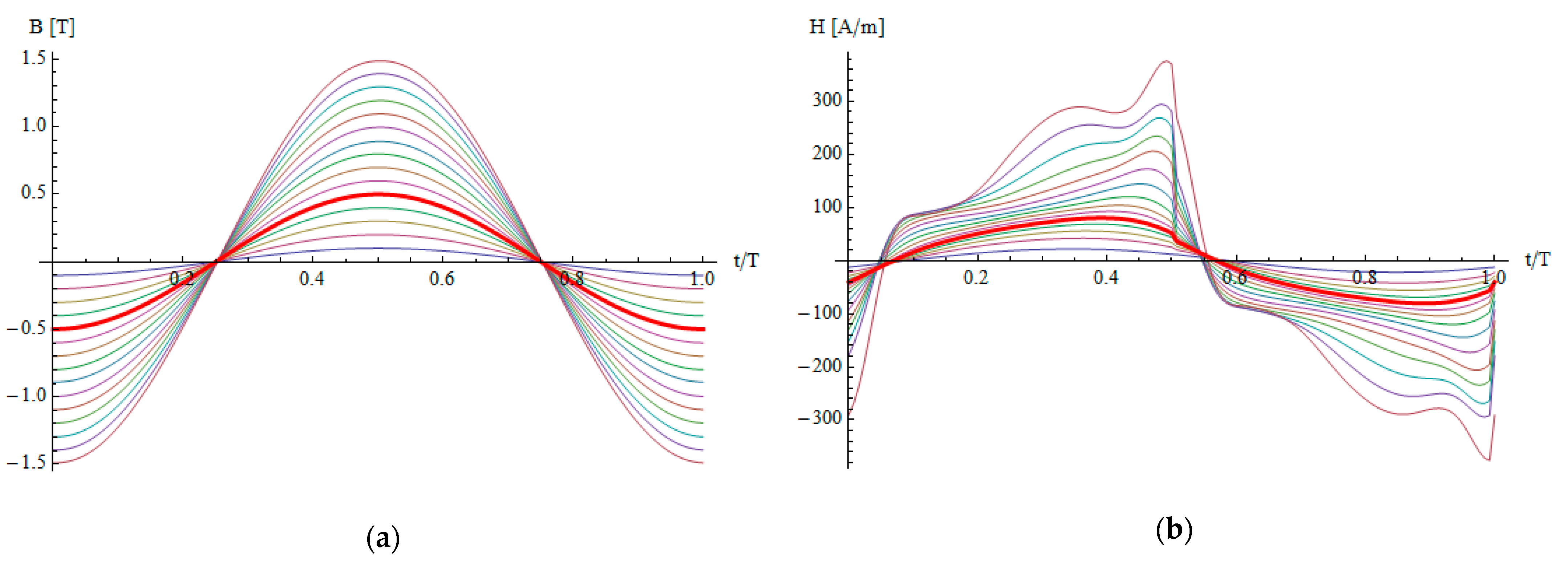
3. Results and Discussion
- Maximum relative error: ϵ = 0.001;
- Maximum number of iterations: kmax = 40;
- Number of time intervals per half the period: NT = 32;
- Number of spatial segments per half the thickness: Ng = 20.
- M1: −2.6% for f = 20 Hz and Bm = 0.6 T;
- M2: −28% for f = 200 Hz and Bm = 0.4 T;
- M3: −24% for f = 1500 Hz and Bm = 0.4 T.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barranger, J. Hysteresis and Eddy-Current Losses of Transformer Lamination Viewed as an Application of the Pointing Theorem; NASA Technical Note; National Aeronautics and Space Administration: Washington, DC, USA, 1965; p. D-3114. [Google Scholar]
- Bertotti, G. Hysteresis in Magnetism; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Pieper, W.; Gerster, J. Total power loss density in a soft magnetic 49% Co-49% Fe-2% V-alloy. J. Appl. Phys. 2011, 109, 07A312. [Google Scholar] [CrossRef]
- Bertotti, G. A general statistical approach to the problem of eddy current losses. J. Magn. Magn. Mater. 1984, 41, 253–260. [Google Scholar] [CrossRef]
- Bertotti, G. General properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Bertotti, G. Some considerations on the physical interpretation of eddy current losses in ferromagnetic materials. J. Magn. Magn. Mater. 1986, 54, 1556–1560. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.; Moses, A.J. Loss separation in nonoriented electrical steels. IEEE Trans. Magn. 2010, 46, 286–289. [Google Scholar] [CrossRef]
- Kollár, P.; Birčákováa, Z.; Füzera, J.; Bureš, R.; Fáberováb, M. Power loss separation in Fe-based composite materials. J. Magn. Magn. Mater. 2013, 327, 146–150. [Google Scholar] [CrossRef]
- Kollár, P.; Olekšáková, D.; Vojtek, V.; Füzer, J.; Fáberová, M.; Bureš, R. Steinmetz law for ac magnetized iron-phenolformaldehyde resin soft magnetic composites. J. Magn. Magn. Mater. 2017, 424, 245–250. [Google Scholar] [CrossRef]
- Sun, H.; Li, Y.; Lin, Z.; Zhang, C.; Yue, S. Core loss separation model under square voltage considering DC bias excitation. AIP Adv. 2020, 10, 015229. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wang, L.; Li, J.; Zhang, J. An improved loss-separation method for transformer core loss calculation and its experimental verification. IEEE Access 2020, 8, 204847–204854. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, X. Modified loss separation in FeSi laminations under arbitrary distorted flux. AIP Adv. 2020, 10, 085222. [Google Scholar] [CrossRef]
- Olekšáková, D.; Kollár, P.; Jakubčin, M.; Füzer, J.; Tkáč, M.; Slovenský, P.; Bureš, R.; Fáberová, M. Energy loss separation in NiFeMo compacts with smoothed powders according to Landgraf’s and Bertotti’s theories. J. Mater. Sci. 2021, 56, 12835–12844. [Google Scholar] [CrossRef]
- Chwastek, K.; Szczygłowski, J.; Wilczyński, W. Modeling magnetic properties of high silicon steel. J. Magn. Magn. Mater. 2010, 322, 799–803. [Google Scholar] [CrossRef]
- Pluta, W. Some properties of factors of specific total loss components in electrical steel. IEEE Trans. Magn. 2010, 46, 322–325. [Google Scholar] [CrossRef]
- De Campos, F.M. Loss Separation Model: A Tool for Improvement of Soft Magnetic Materials. Mater. Sci. Forum 2016, 869, 569–601. [Google Scholar] [CrossRef]
- De Campos, F.M. Interpretation of loss separation with the Haller-Kramer model. Acta Phys. Pol. A 2019, 136, 705–708. [Google Scholar] [CrossRef]
- Bereźnicki, M. The influence of skin effect on the accuracy of eddy current energy loss calculation in the electrical sheets. In Proceedings of the 2015 Selected Problems of Electrical Engineering and Electronics (WZEE), Kielce, Poland, 17–19 September 2015; IEEE: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Butler, O.I.; Sarma, M.R. Relaxation methods applied to the problem of a.c. magnetization of ferromagnetic laminae. Proc. IEE Part II Electr. Eng. 1951, 98, 389–397. [Google Scholar] [CrossRef]
- Zakrzewski, K.; Pietras, F. Method of calculating the electromagnetic field and power losses in ferromagnetic materials, taking into account magnetic hysteresis. Proc. Inst. Electr. Eng. 1971, 118, 1679–1685. [Google Scholar] [CrossRef]
- Petrun, M.; Steentjes, S.; Hameyer, K.; Ritonja, J.; Dolinar, D. Effects of saturation and hysteresis on magnetisation dynamics. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2015, 34, 710–723. [Google Scholar] [CrossRef]
- Takahashi, N.; Sakura, T.; Cheng, Z. Nonlinear analysis of eddy current and hysteresis losses of 3-D stray field loss model (Problem 21). IEEE Trans. Magn. 2001, 37, 3672–3675. [Google Scholar] [CrossRef]
- Górecki, J.; Nowak, L.; Poltz, J. Numerical calculation of eddy current losses in conductive ferromagnetic plate. Electr. Hear. 1976, 22, 677–685. [Google Scholar]
- Bereźnicki, M.; Jabłoński, P. Calculating macroscopic eddy current losses in ferromagnetic materials considering hysteresis loop. Pozn. Univ. Technol. Acad. J. Electr. Eng. 2018, 93, 205–214. [Google Scholar] [CrossRef]
- Bereźnicki, M.; Jabłoński, P.; Najgebauer, M. Using measured hysteresis loop family in calculating the eddy current losses. In Proceedings of the 2018 Progress in Applied Electrical Engineering (PAEE), Koscielisko, Poland, 18–22 June 2018; IEEE: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Operating Instruction, REMACOMP® C-200; Magnet-Physik, Dr. Steingroever GmbH: Köln, Germany, 2017.
- Pry, R.H.; Bean, C.P. Calculation of the energy loss in magnetic sheet materials using a domain model. J. Appl. Phys. 1958, 29, 532–533. [Google Scholar] [CrossRef]
- Zakrzewski, K. The influence of magnetic hysteresis on the separation and distribution of power losses in ferromagnetic sheets. Rozpr. Elektrotechniczne 1971, 17, 431–446. (In Polish) [Google Scholar]


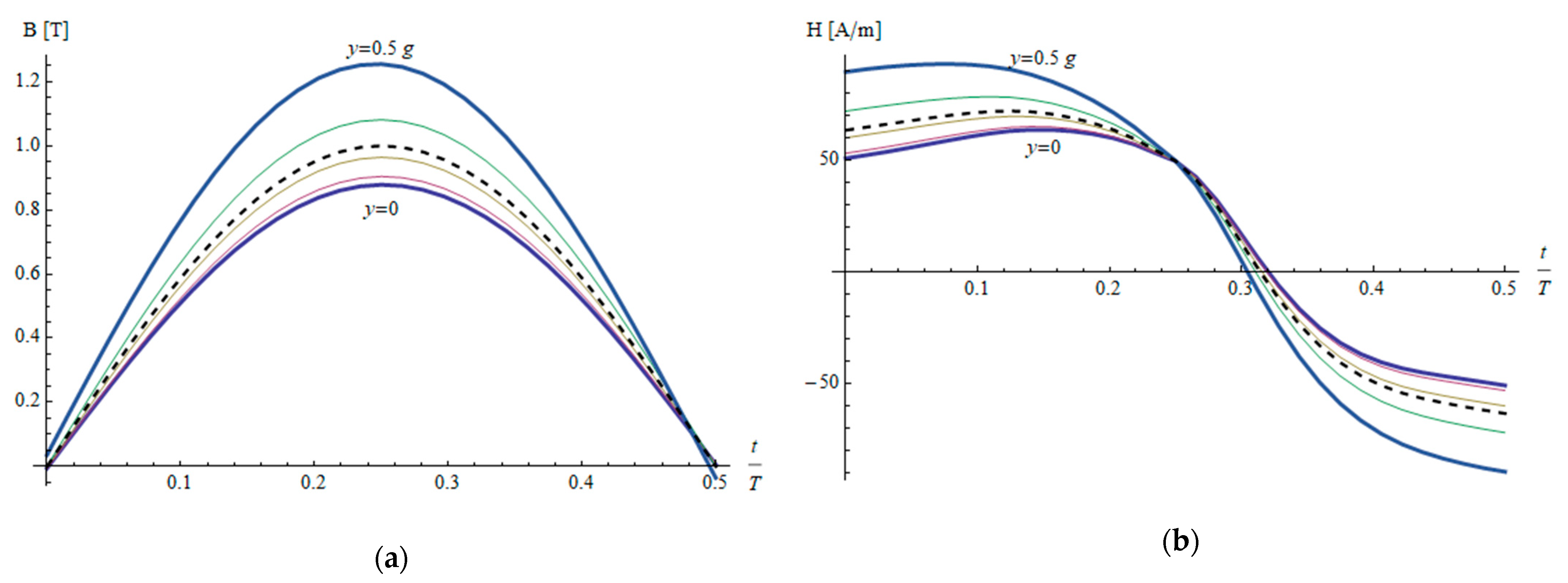

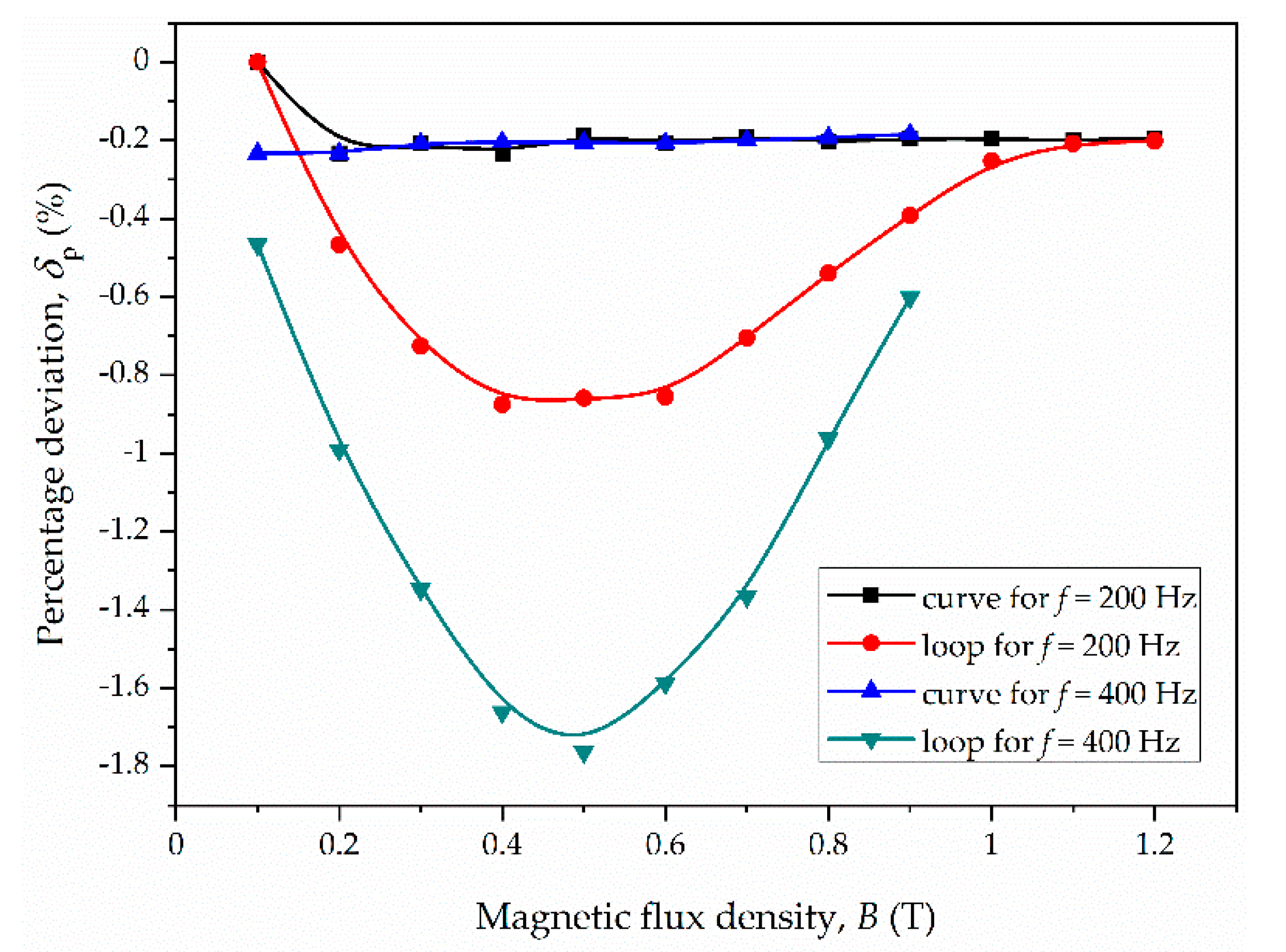


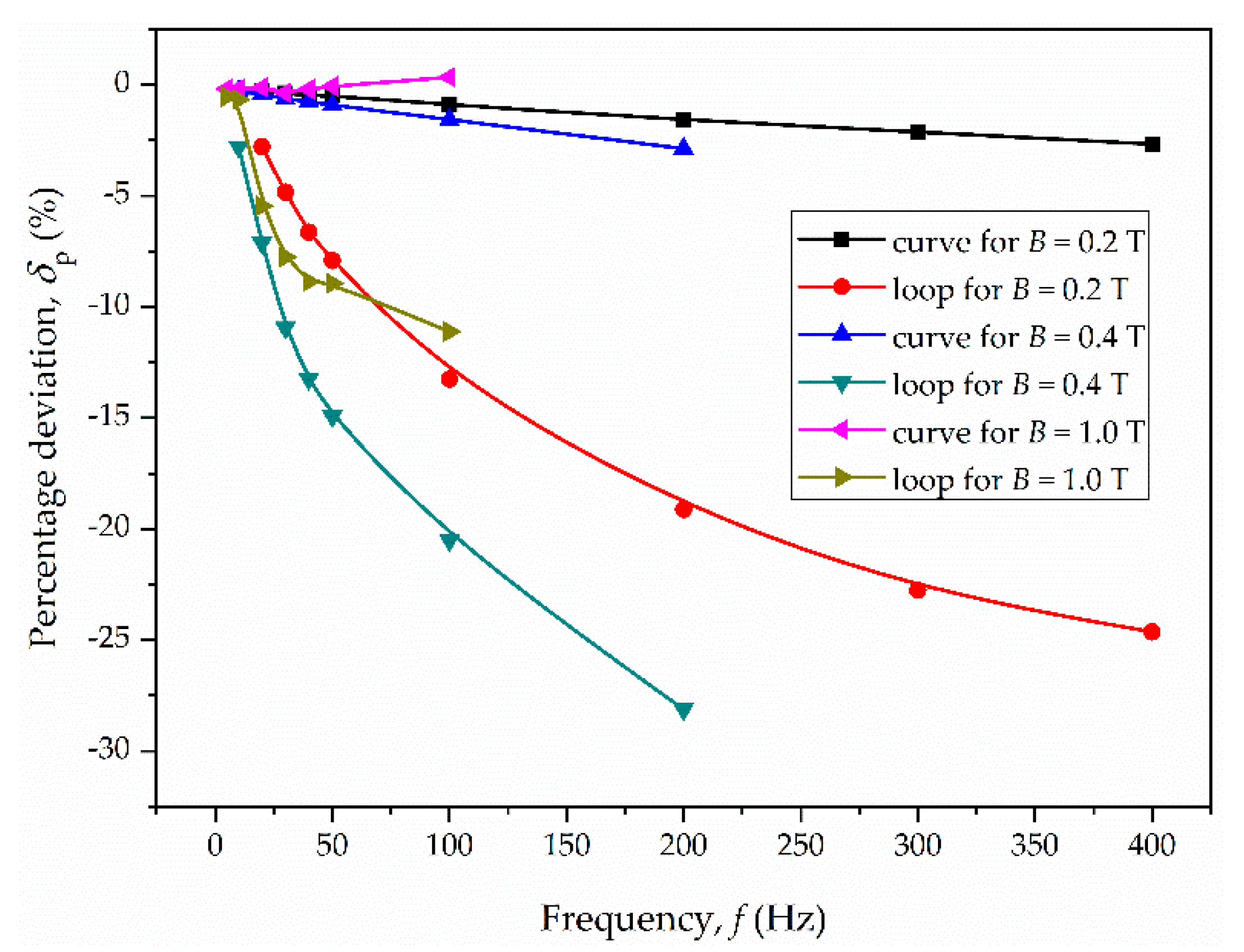
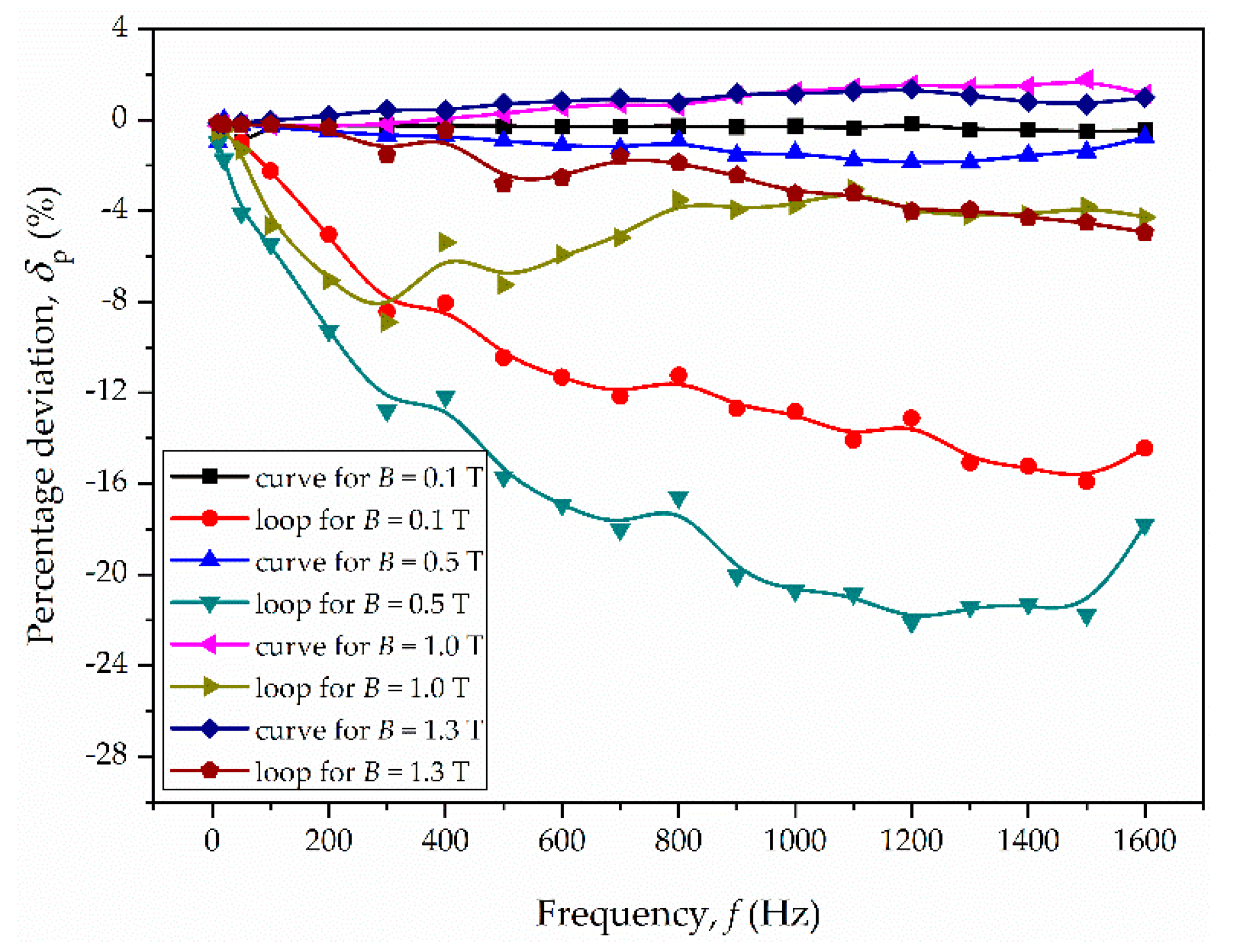
| Parameter | Material M1 | Material M2 | Material M3 |
|---|---|---|---|
| Type | Non-oriented steel JNEX (6.5% Si-Fe) | Non-oriented steel M530-65A (3.2%Si-Fe) | Grain-oriented steel ET122-30 (3% Si-Fe) |
| Thickness (g) | 0.1 mm | 0.65 mm | 0.3 mm |
| Conductivity (σ) | 1.22 MS/m | 2.56 MS/m | 2.08 MS/m |
| Frequency (f) | 10–400 Hz | 5–400 Hz | 10–1600 Hz |
| Magnetic flux density range (B) | 0.1–1.2 T | 0.1–1.6 T | 0.1–1.5 T |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabłoński, P.; Najgebauer, M.; Bereźnicki, M. An Improved Approach to Calculate Eddy Current Loss in Soft Magnetic Materials Based on Measured Hysteresis Loops. Energies 2022, 15, 2869. https://doi.org/10.3390/en15082869
Jabłoński P, Najgebauer M, Bereźnicki M. An Improved Approach to Calculate Eddy Current Loss in Soft Magnetic Materials Based on Measured Hysteresis Loops. Energies. 2022; 15(8):2869. https://doi.org/10.3390/en15082869
Chicago/Turabian StyleJabłoński, Paweł, Mariusz Najgebauer, and Michał Bereźnicki. 2022. "An Improved Approach to Calculate Eddy Current Loss in Soft Magnetic Materials Based on Measured Hysteresis Loops" Energies 15, no. 8: 2869. https://doi.org/10.3390/en15082869
APA StyleJabłoński, P., Najgebauer, M., & Bereźnicki, M. (2022). An Improved Approach to Calculate Eddy Current Loss in Soft Magnetic Materials Based on Measured Hysteresis Loops. Energies, 15(8), 2869. https://doi.org/10.3390/en15082869







