A Descriptive Review to Access the Most Suitable Rib’s Configuration of Roughness for the Maximum Performance of Solar Air Heater
Abstract
:1. Introduction
2. Performance of SAH
2.1. Heat Transfer Performance
2.2. Hydraulic Performance
3. Historical Background of Conceptualization of Artificial Roughness in SAH
- a = −0.4 when e+ < 35 and a = 0 when e+ ≥ 35
- b = −0.13 when p/e < 10 and when p/e ≥ 10
- i = 0 when e+ < 35 and i = 0.28 when e+ ≥ 35
- j = 0.5 when α < 45° and j = −0.45 when α ≥ 45°
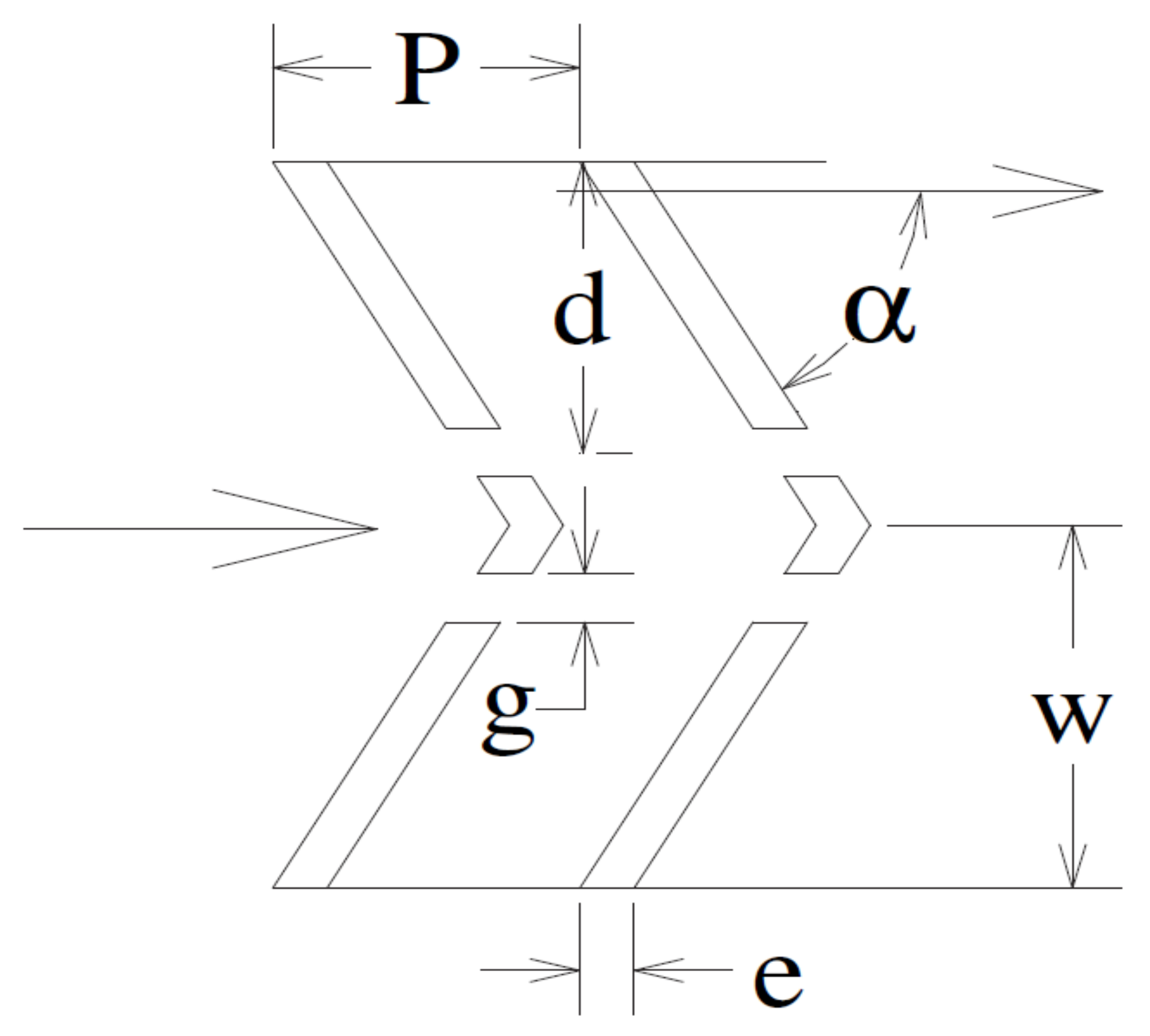
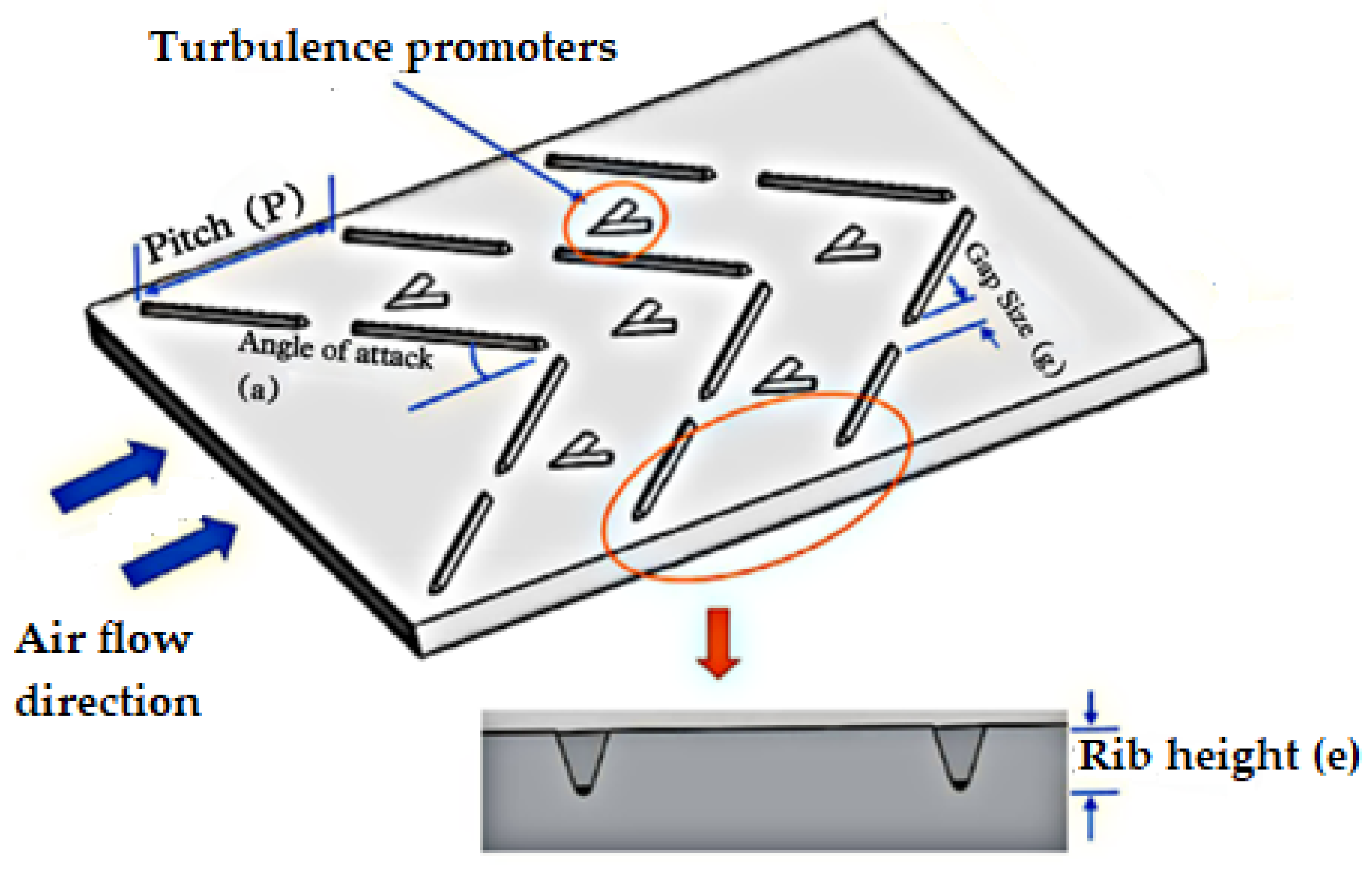
4. Effect of Distinct Roughness Parameters
4.1. Effect of Relative Rib Height
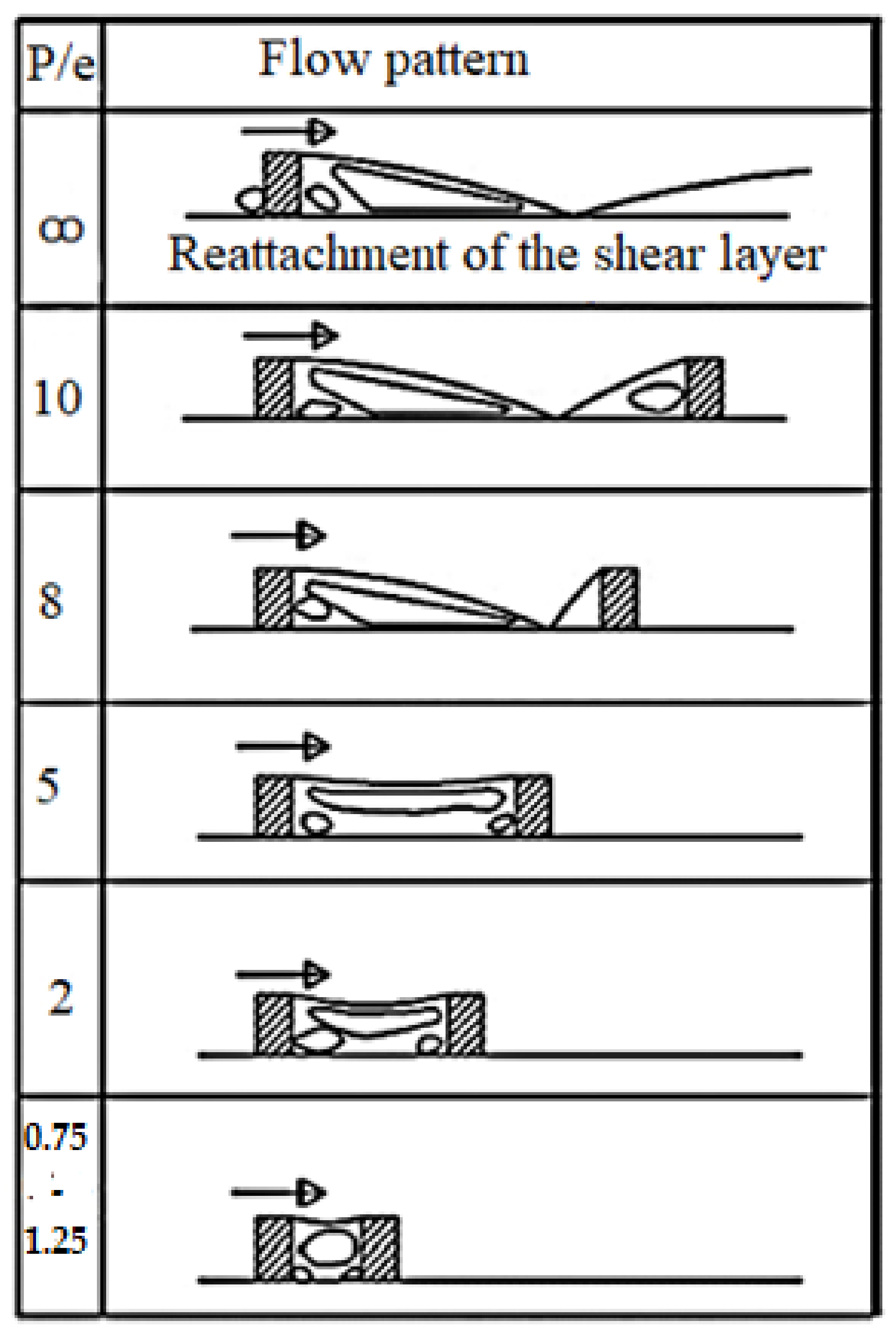
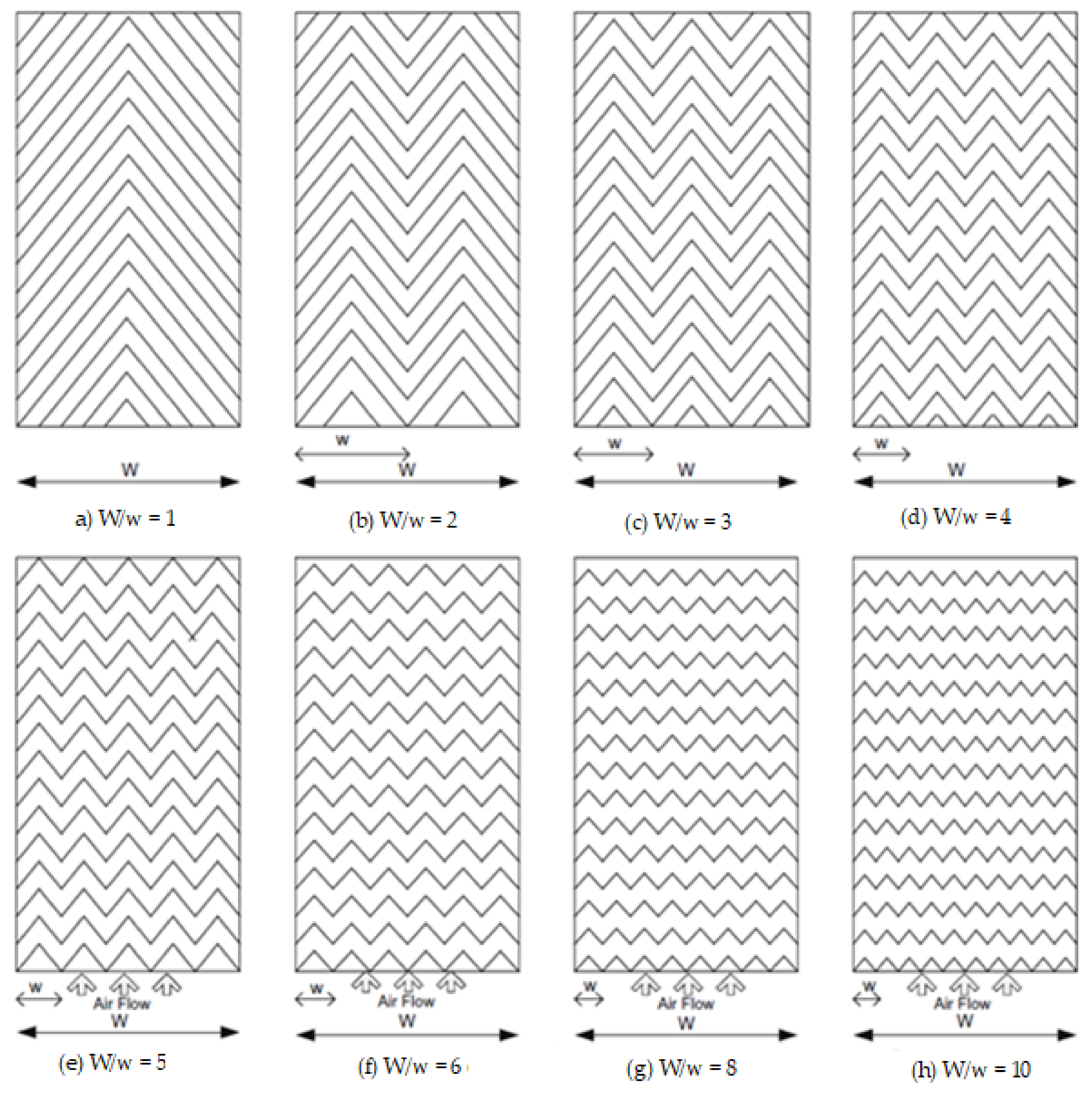
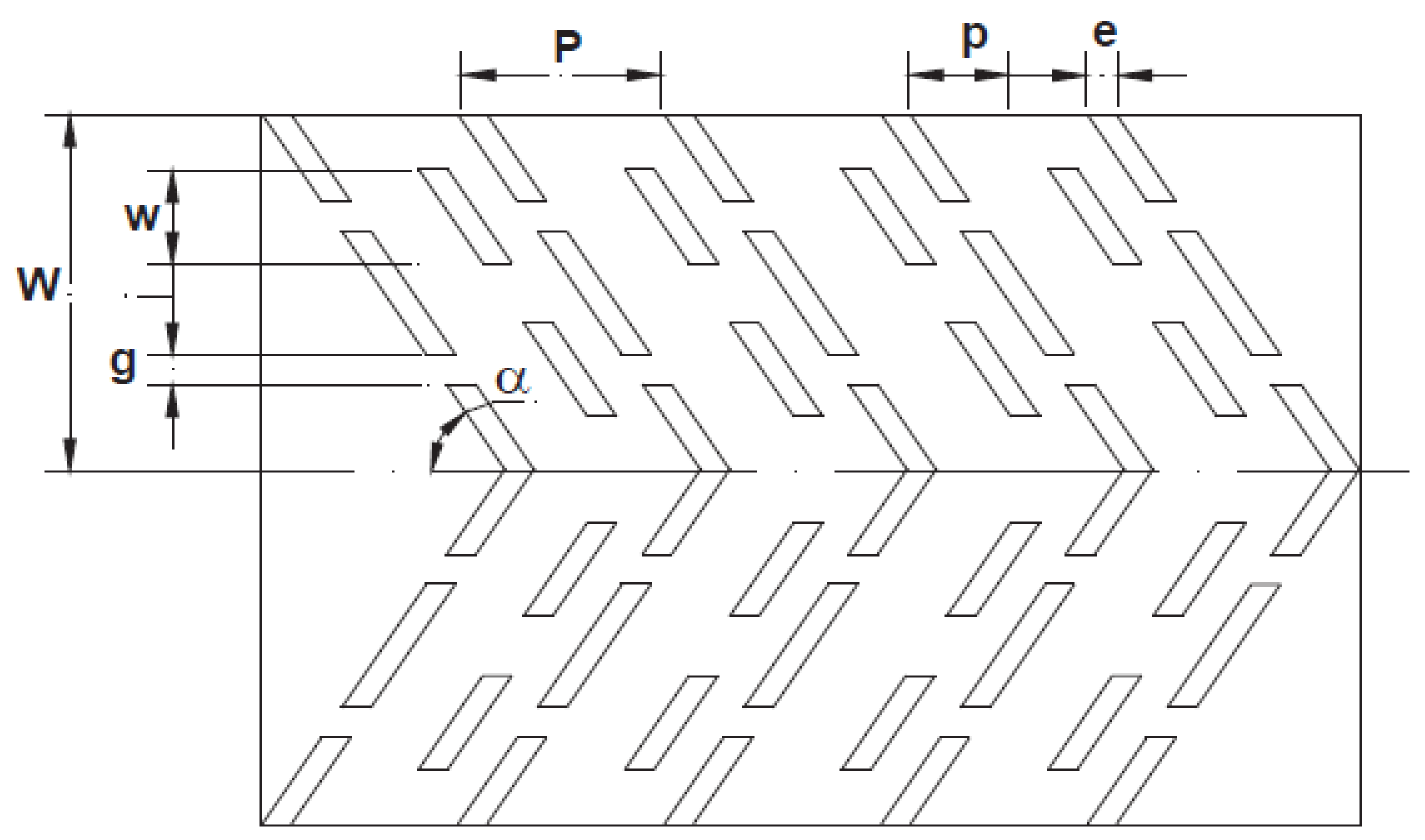
4.2. Effect of Relative Rib Pitch
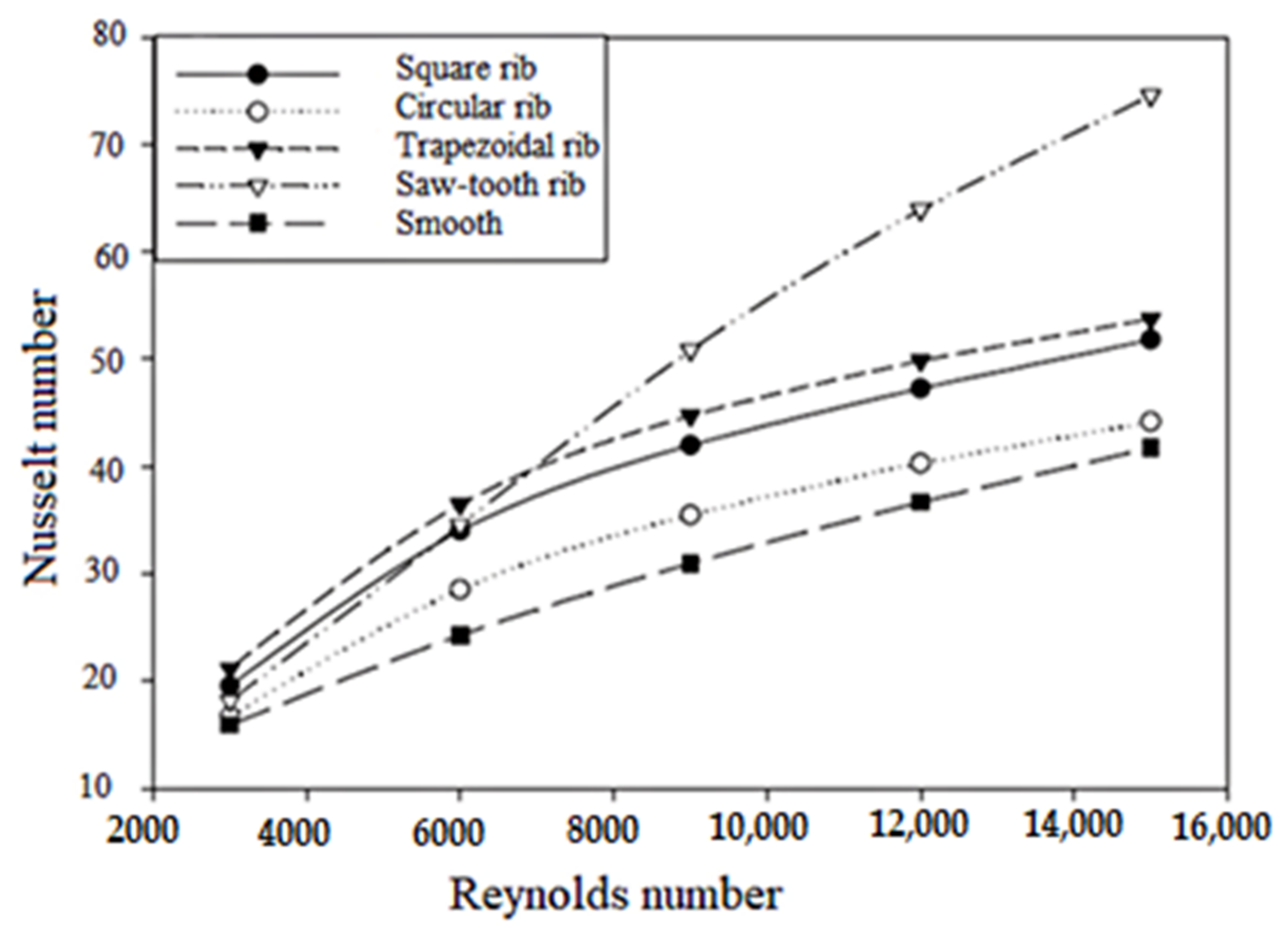
4.3. Effect of the Cross Section of Rib
4.4. Effect of Angle of Attack
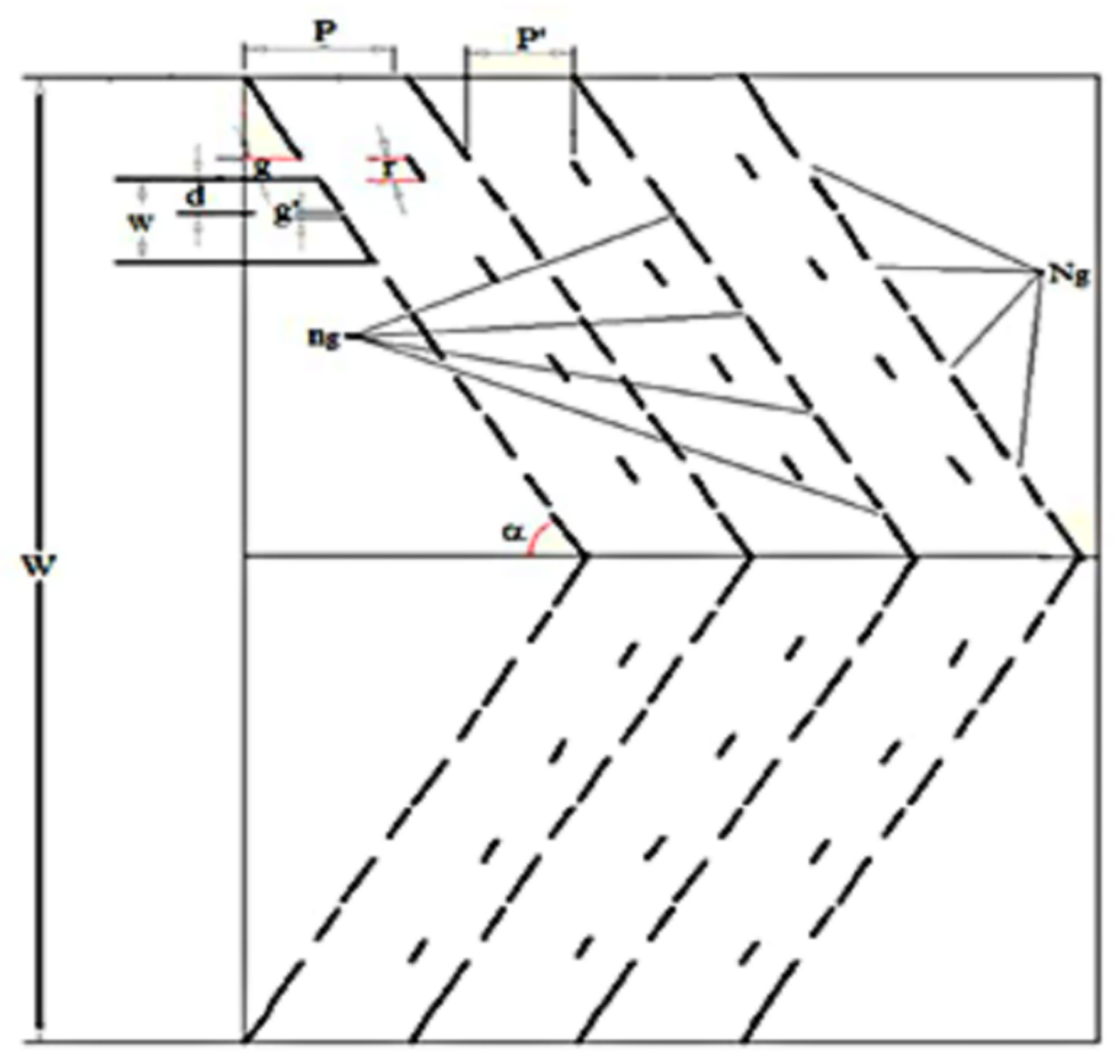
4.5. Effect of Relative Gaps in Continuous Rib
4.6. Effect of Reynolds Number
5. Artificial Roughness/Turbulators
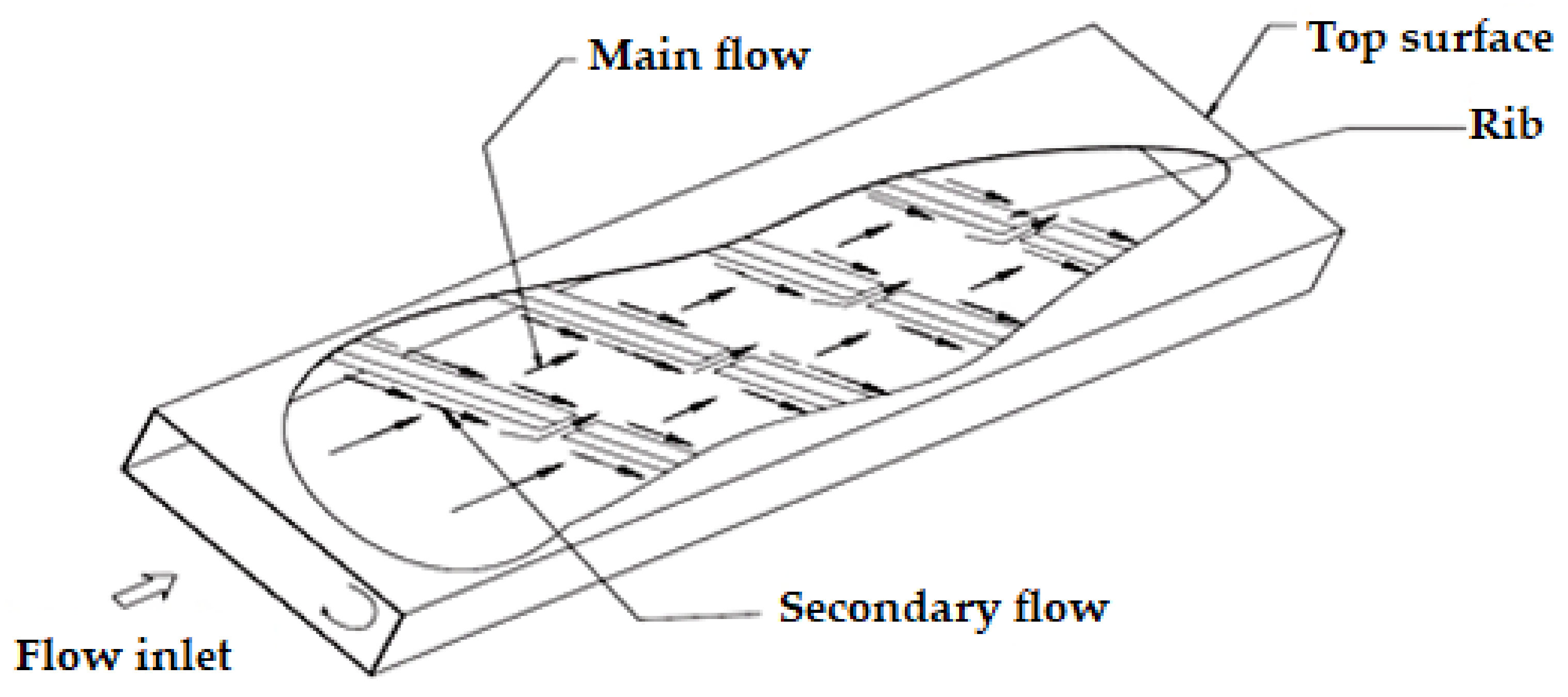
5.1. Transverse Ribs
5.2. Inclined Ribs
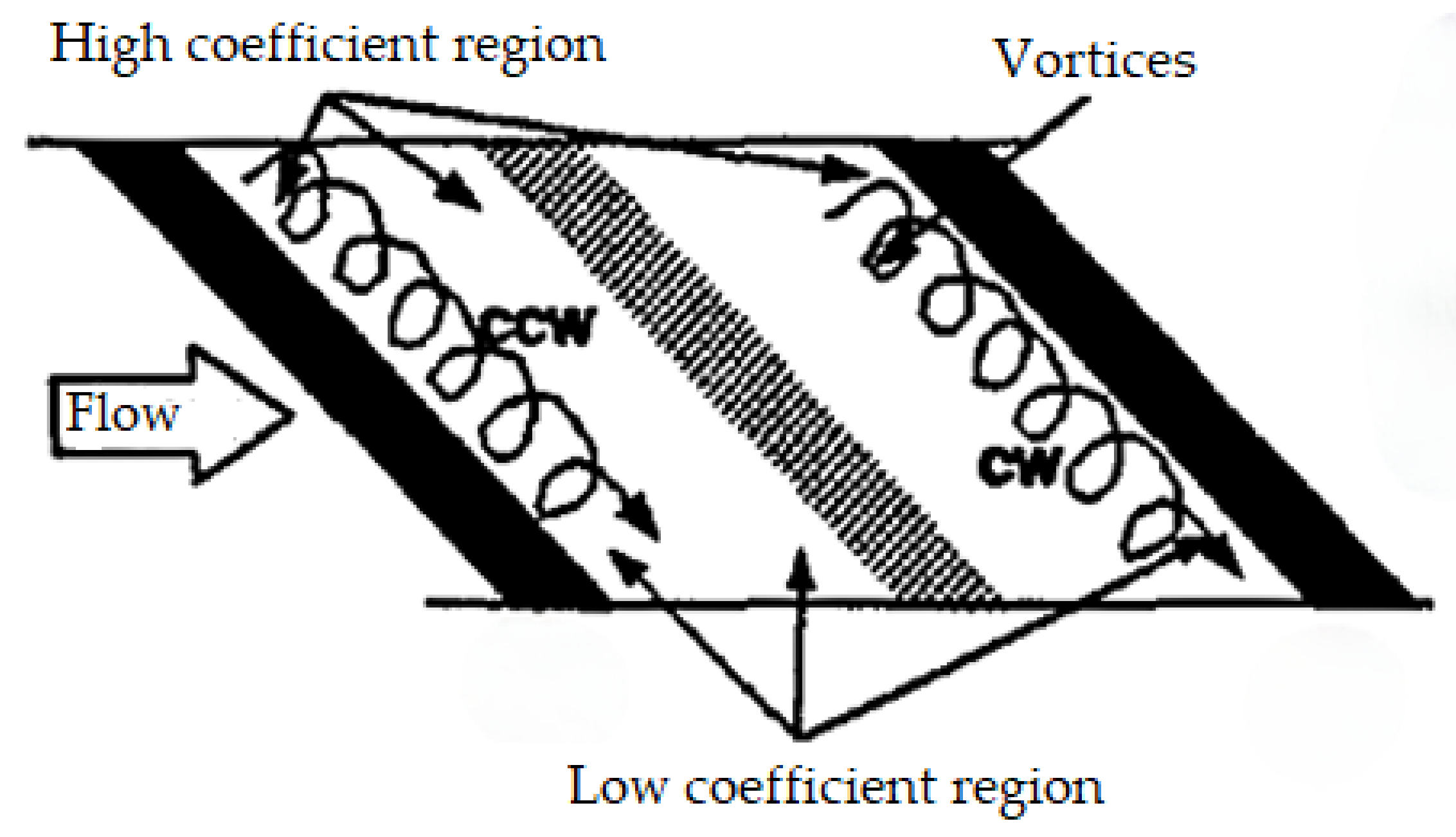
5.3. V-Shaped Ribs
5.4. Multi-V-Shaped Ribs
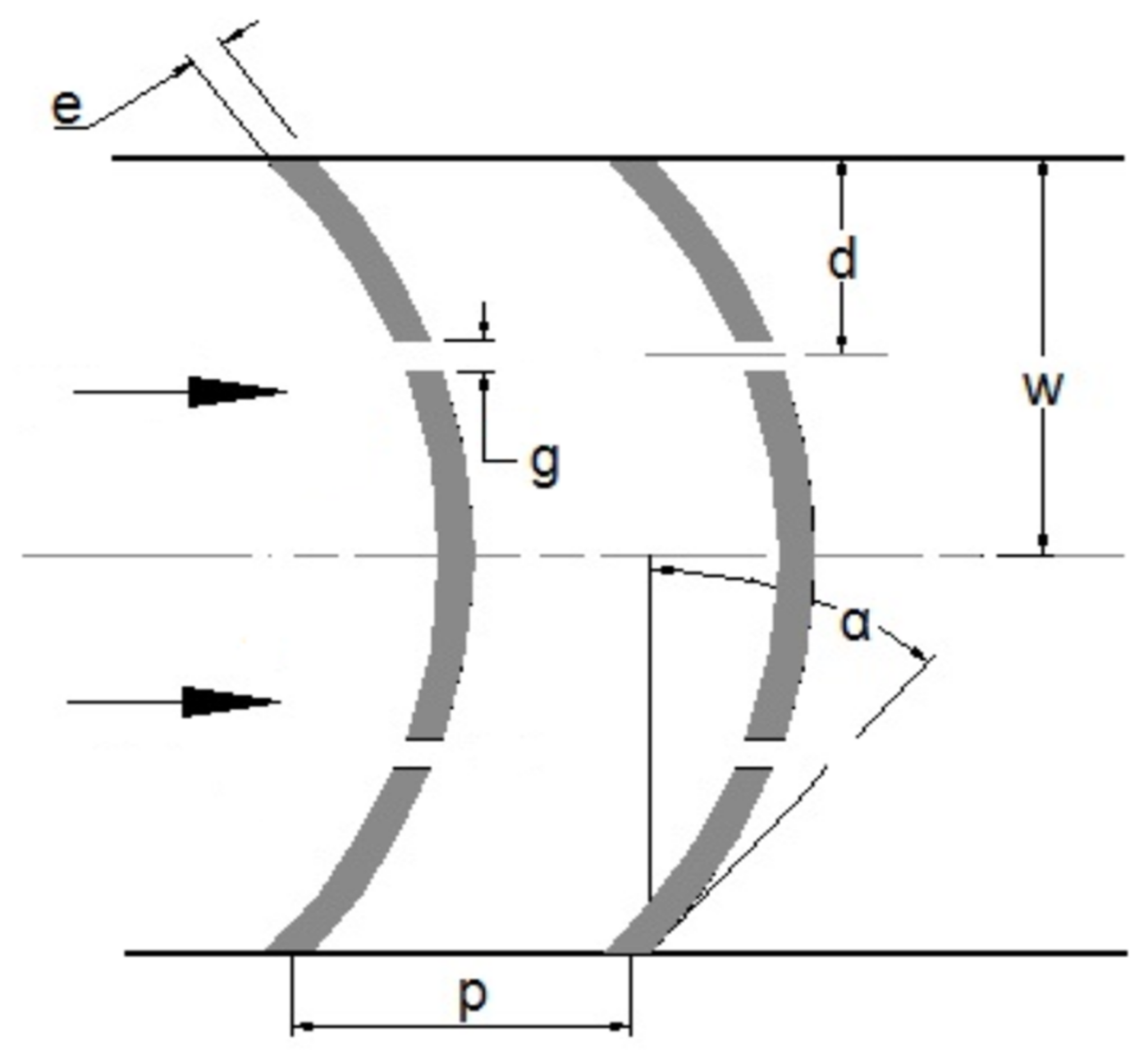
5.5. Arc-Shaped Ribs
5.6. Multi-Arc-Shaped Ribs
5.7. W-Shaped Ribs
5.8. L-Shaped Ribs
5.9. S-Shaped Ribs
5.10. Delta Winglet-Shaped Ribs
5.11. Quarter Circular-Shaped Ribs
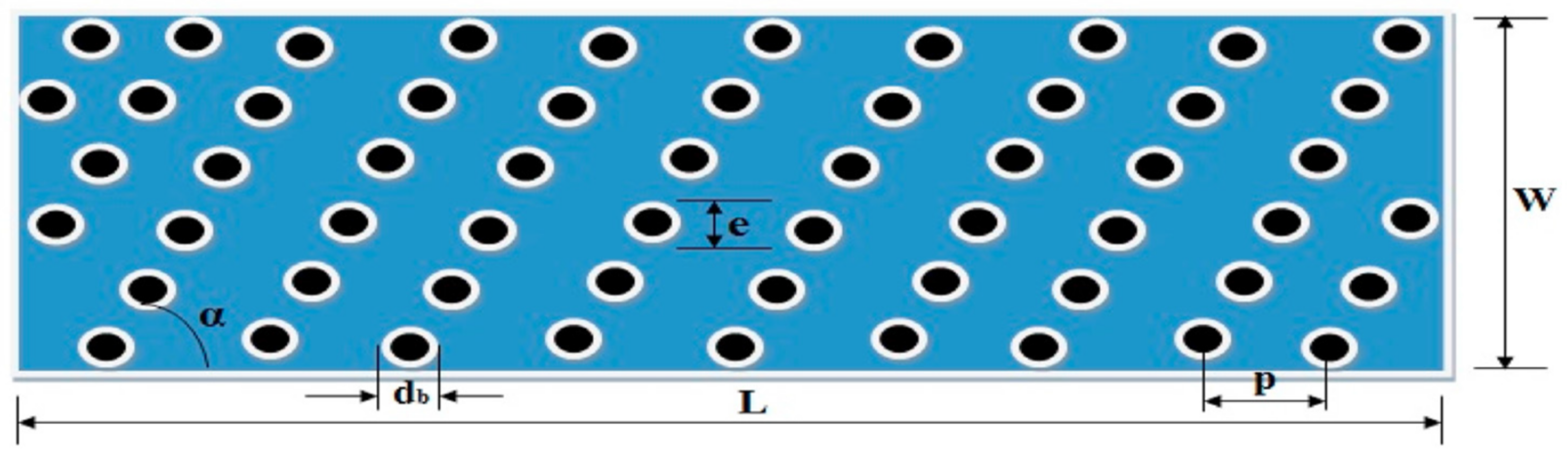
5.12. Dimple/Protrusion-Shaped Roughness
5.13. Pentagonal Shape Ribs
5.14. Stepped Cylinder Ribs
5.15. NACA Profile Ribs
5.16. C-Type Rib Roughness
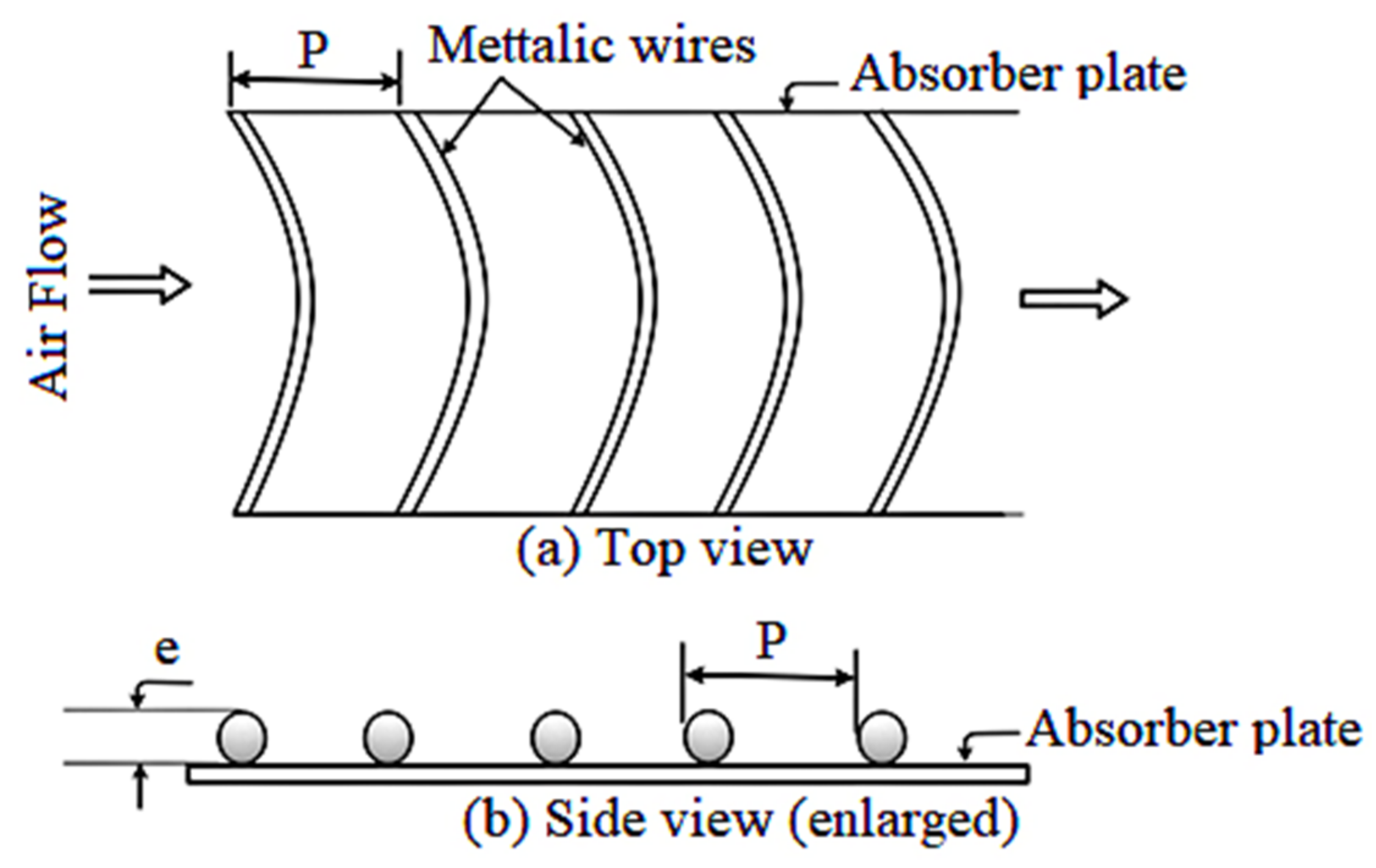
5.17. Twisted Tapes
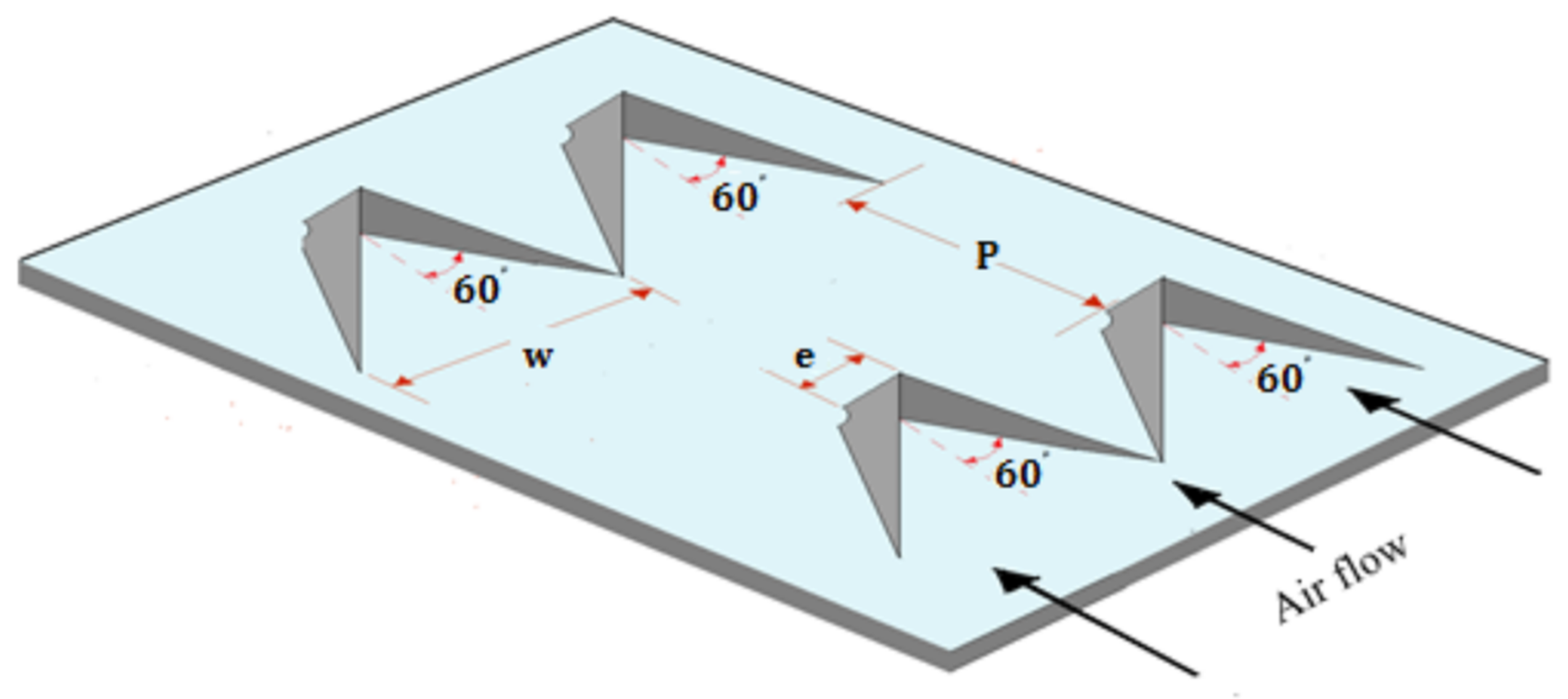
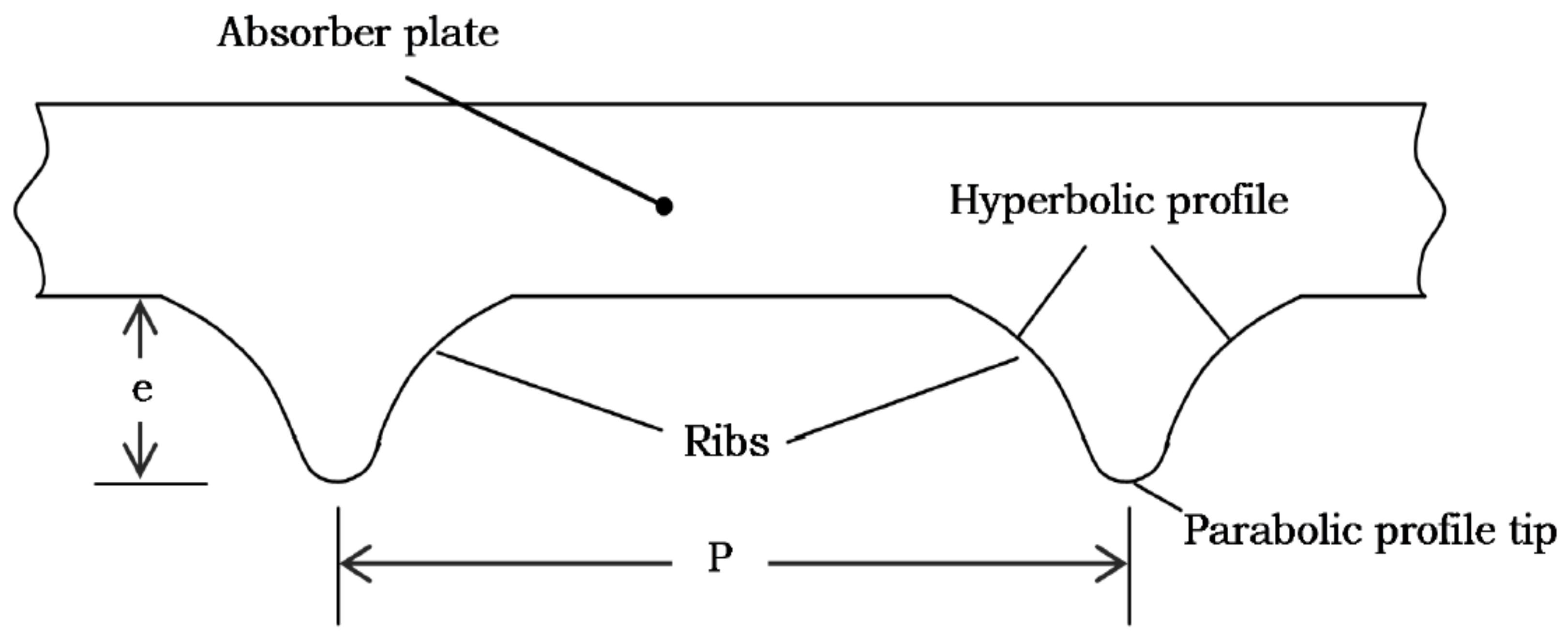
5.18. Hyperbolic-Shaped Ribs
5.19. Wedge-Shaped Rib
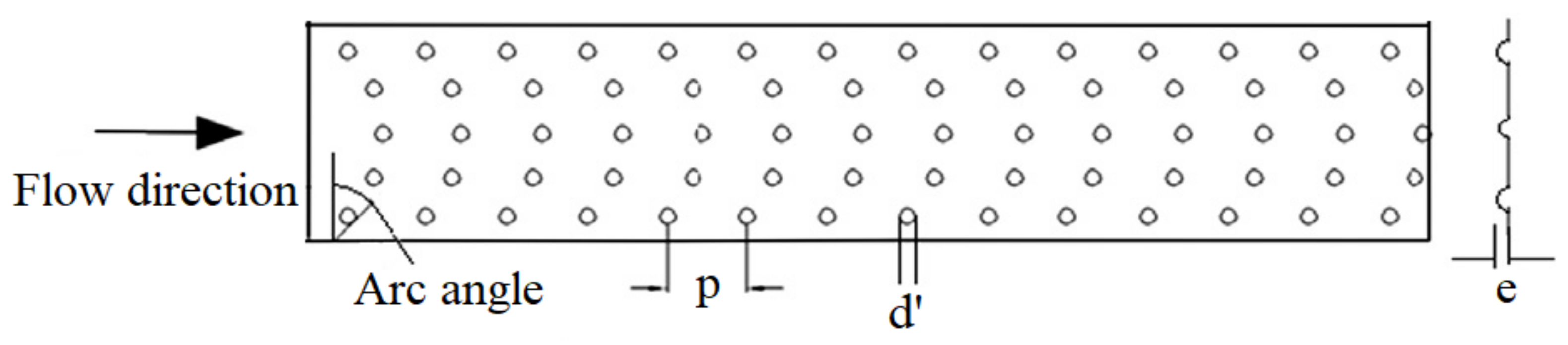
5.20. Spherical-Ball-Type Roughness
5.21. Combination of Different Types of Ribs
5.22. Other Roughnesses
6. Performance Evaluation Parameters
7. Methodology and Formation of MATLAB Code for Calculating Thermal Efficiency
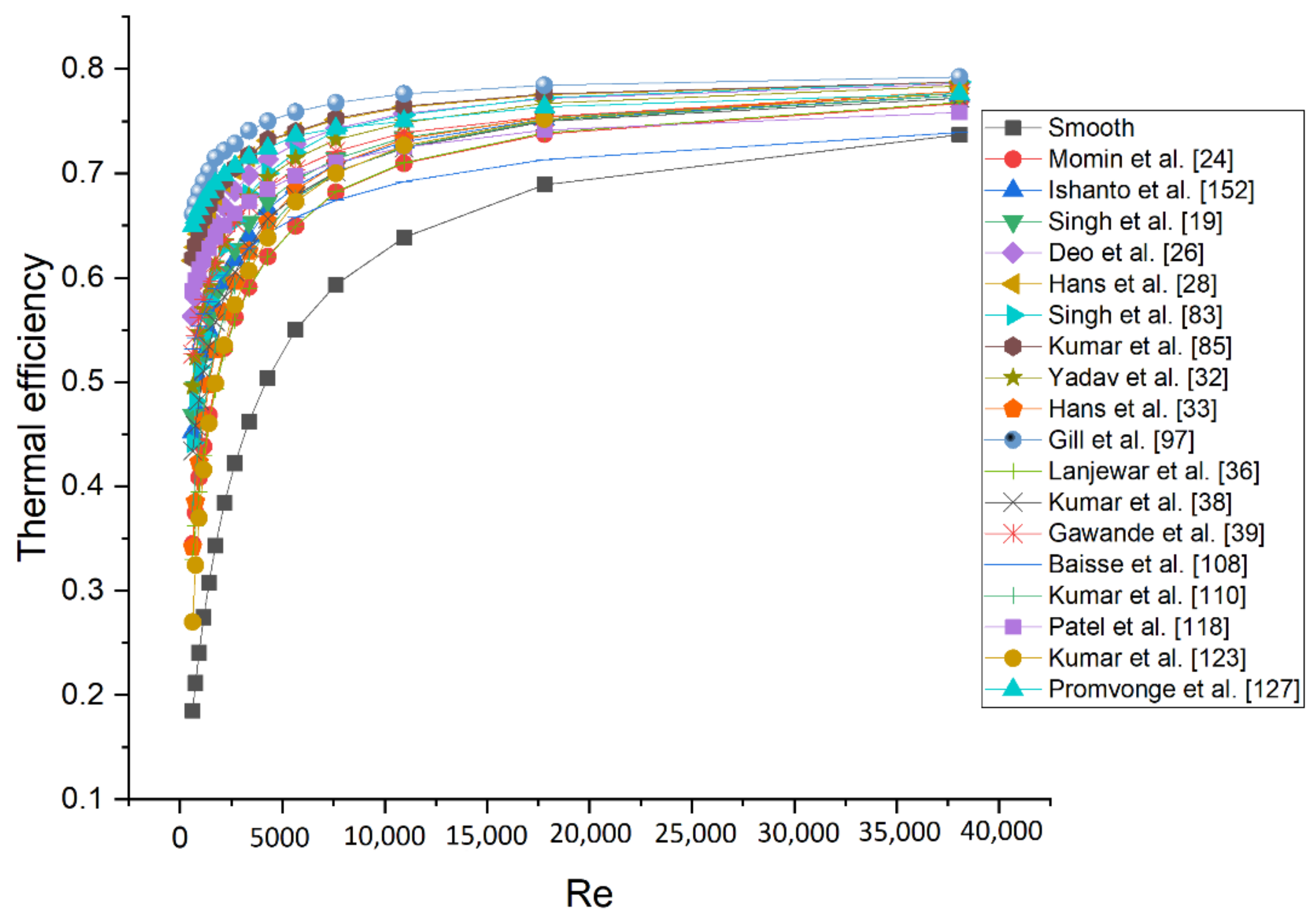
8. Thermal Performance of Roughened SAH
9. Conclusions
- The shape and size of artificial roughness and their pattern of arrangements on the duct surface are the most important factors for the performance optimization of the SAH.
- The thermohydraulic characteristics of a large number of rib geometries have been investigated by many researchers. For most of the rib roughness geometries, the optimum performance has been achieved at the following parameters: p/e = 10, W/w = 6, α = 60°, and e/Dh = 0.043.
- THPP and thermal efficiency show the highest values in the case of staggered broken-arc type of hybrid rib and least values in the case of metal grit, twisted tape, and delta-shaped vortex generator type of roughness.
- The multi-V and multiarc-shaped roughnesses show higher thermohydraulic performance over other roughness geometries. The introducing gaps in the limb of multi-V-ribs enhance the level of turbulence significantly.
- The multi-V-shaped ribs show a higher value of the friction factor, and arc-shaped circular dimples show a lower value of the friction factor.
- The broken-arc-shaped rib combined with a staggered-arc rib piece has better performance than broken-arc-shaped and arc-shaped rib roughness.
- The creation of gaps in the continuous ribs has shown remarkable improvement in thermohydraulic performance over the continuous ribs. The improvement in Nu due to the creation of gaps in the continuous ribs ranges from 1.1 to 1.3 times, and corresponding increase in pumping power requirement ranges from 1.0 to 1.4 times.
- THPP shows higher values in the case of an S-shape rib, multi-V ribs, and arc-shaped roughnesses with gaps. However, the performance of an S-shaped rib is not considerable at low Re, but the performance increases remarkably with the increase in Re.
- The arc arrangement of rib roughness shows lower value pressure losses over the V-shaped arrangement due to the curved nature of the induced secondary flow along with the roughness.
- In general, higher roughnesses’ height has a higher Nusselt number; however, higher roughnesses’ height contributes to higher pressure drop. Therefore, the thermohydraulic performance of roughnesses needs to be optimized. In this regard, net effective efficiency is the best tool to analyze roughnesses. On the basis of net effective efficiency, a multiarc rib with gaps is found to be best around 79% in comparison with other rib configurations, which is recommended for overall better performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Title | Unit |
| b | Roughness width | m |
| c | Characteristic separation length | m |
| d’ | Diameter of dimples | m |
| d/x | Relative gap position | - |
| dR | Relative punched hole size | - |
| D | Pipe inside diameter (to base of ribs) | m |
| De | Equivalent diameter of annulus (d1 − d2) | m |
| Dh | Hydraulic diameter of duct | m |
| e | Height of roughness element | m |
| e+ | Roughness Reynolds number | - |
| e/Dh | Relative roughness height | - |
| e/H | Blockage ratio | - |
| fs | Smooth surface friction factor | - |
| f | Friction factor of roughened surface | - |
| FR | Heat removal factor | - |
| g | Roughness function of heat transfer | - |
| g/e | Relative gap width | - |
| H | Duct height | m |
| I | Insolation | W/m2 |
| L | Length of test section | m |
| Nu | Nusselt number | - |
| Ng | Number of gaps on half arc | - |
| p/g | Relative pitch-to-gap ratio | - |
| p’/p | Relative staggered rib pitch | - |
| p/H | Rib-pitch-to-channel-height ratio | - |
| Pt/b | Relative longitudinal length of obstacles | - |
| Pt/e | Relative transversal length of obstacles | - |
| PR | Relative winglet pitch | - |
| Qu | Heat gain | W |
| Qe+ | Heat transfer function | - |
| r/e | Relative staggered rib size | - |
| R | Momentum transfer roughness function | - |
| Ra | Rayleigh number | - |
| Re | Reynolds number | - |
| S | Short way length between dimples | m |
| s’/s | Relative gap position | - |
| St | Stanton number | - |
| Ta | Ambient temperature | K |
| Ti | Air inlet temperature | K |
| Tf | Mean air temperature | K |
| Tp | Plate temperature | K |
| Tw | Wall temperature | K |
| ΔP | Pressure drops | N/m2 |
| UO | Overall heat loss coefficient | W/m2·K |
| V | Velocity of air in the SAH duct | m/s |
| w/e | Staggered rib length to rib height | - |
| W/e | Width-to-height ratio | - |
| W/H | Width-to-duct-height ratio | - |
| W/w | Relative roughness width | - |
| W1/w | Relative gap position | - |
| x | Distance from starting | m |
| η | Thermohydraulic performance parameter | - |
| ηth | Thermal efficiency of solar collectors | - |
| Ρ | Density | kg/m3 |
| Temperature factor Tw/Tf | - | |
| α | Angle of attack | degree |
| α’ | Arc angle | degree |
| α/90 | Relative arc angle | - |
| Chamfering angle of rib | degree | |
| β | Slope | degree |
| β’ | Thermal expansion coefficient of air | 1/K |
| εg | Glass cover emissivity | |
| εp | Absorber plate emissivity | |
| υ | Kinematic viscosity | m2/s |
| τ | Transmissivity | |
| σ | Stefan–Boltzmann constant | W/m2·K4 |
References
- Gupta, N.K.; Karmveer; Alam, T. A Review on Augmentation in Thermal Performance of Solar Air Heater. IOP Conf. Series Mater. Sci. Eng. 2021, 1116, 012064. [Google Scholar] [CrossRef]
- Bliss, R.W. The derivations of several “Plate-efficiency factors” useful in the design of flat-plate solar heat collectors. Sol. Energy 1959, 3, 55–64. [Google Scholar] [CrossRef]
- Lewis, M.J. Optimizing the thermo-hydraulic performance of rough surfaces. Int. J. Heat Mass Transf. 1975, 18, 1243–1248. [Google Scholar] [CrossRef]
- Okamoto, S.; Seo, S.; Nakaso, K.; Kawai, I. Turbulent shear flow and heat transfer over the repeated two-dimensional square ribs on ground plane. J. Fluids Eng. Trans ASME 1993, 115, 631–637. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Kang, S.S.; Chuck, W. Relation between the points of flow reattachment and maximum heat transfer for regions of flow separation. Int. J. Heat Mass Transf. 1987, 30, 1237–1246. [Google Scholar] [CrossRef]
- Cortés, A.; Piacentini, R. Improvement of the efficiency of a bare solar collector by means of turbulence promoters. Appl. Energy 1990, 36, 253–261. [Google Scholar] [CrossRef]
- Nikuradse, J. Laws of Flow in Rough Pipes. J. Appl. Phys. 1950, 3, 399. [Google Scholar]
- Dipprey, D.F.; Sabersky, R.H. Heat and momentum transfer in smooth and rough tubes at various prandtl numbers. Int. J. Heat Mass Transf. 1963, 6, 329–353. [Google Scholar] [CrossRef]
- Webb, R.L.; Eckert, E.R.G.; Goldstein, R.J. Heat transfer and friction in tubes with repeated-rib roughness. Int. J. Heat Mass Transf. 1971, 14, 601–617. [Google Scholar] [CrossRef]
- Webb, R.L.; Eckert, E.R.G.; Goldstein, R.J. Generalized heat transfer and friction correlations for tubes with repeated-rib roughness. Int. J. Heat Mass Transf. 1972, 15, 180–184. [Google Scholar] [CrossRef]
- Vilemas, J.V.; Šimonis, V.M. Heat transfer and friction of rough ducts carrying gas flow with variable physical properties. Int. J. Heat Mass Transf. 1985, 28, 59–68. [Google Scholar] [CrossRef]
- Han, J.C.; Glicksman, L.R.; Rohsenow, W.M. An investigation of heat transfer and friction for rib-roughened surfaces. Int. J. Heat Mass Transf. 1978, 21, 1143–1156. [Google Scholar] [CrossRef]
- Prasad, B.N.; Saini, J.S. Effect of artificial roughness on heat transfer and friction factor in a solar air heater. Sol. Energy 1988, 41, 555–560. [Google Scholar] [CrossRef]
- Gupta, D.; Solanki, C.; Saini, J.S. Heat and fluid flow in rectangular solar air heater ducts having transverse rib roughness on absorber plates. Sol. Energy 1993, 51, 31–37. [Google Scholar] [CrossRef]
- Boulemtafes-Boukadoum, A.; Absi, R.; El Abbassi, I.; Darcherif, M.; Benzaoui, A. Numerical investigation of absorber’s roughness effect on heat transfer in upward solar air heaters. Energy Procedia 2019, 157, 1089–1100. [Google Scholar] [CrossRef]
- Singh, S.; Singh, B.; Hans, V.S.; Gill, R.S. CFD (computational fluid dynamics) investigation on Nusselt number and friction factor of solar air heater duct roughened with non-uniform cross-section transverse rib. Energy 2015, 84, 509–517. [Google Scholar] [CrossRef]
- Aharwal, K.R.; Gandhi, B.K.; Saini, J.S. Heat transfer and friction characteristics of solar air heater ducts having integral inclined discrete ribs on absorber plate. Int. J. Heat Mass Transf. 2009, 52, 5970–5977. [Google Scholar] [CrossRef]
- Singh, S.; Chander, S.; Saini, J.S. Investigations on thermo-hydraulic performance due to flow-attack-angle in V-down rib with gap in a rectangular duct of solar air heater. Appl. Energy 2012, 97, 907–912. [Google Scholar] [CrossRef]
- Singh, S.; Chander, S.; Saini, J.S. Heat transfer and friction factor correlations of solar air heater ducts artificially roughened with discrete V-down ribs. Energy 2011, 36, 5053–5064. [Google Scholar] [CrossRef]
- Sahu, M.M.; Bhagoria, J.L. Augmentation of heat transfer coefficient by using 90° broken transverse ribs on absorber plate of solar air heater. Renew. Energy 2005, 30, 2057–2073. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J.L. A CFD based thermo-hydraulic performance analysis of an artificially roughened solar air heater having equilateral triangular sectioned rib roughness on the absorber plate. Int. J. Heat Mass Transf. 2014, 70, 1016–1039. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J.L. A numerical investigation of square sectioned transverse rib roughened solar air heater. Int. J. Therm. Sci. 2014, 79, 111–131. [Google Scholar] [CrossRef]
- Gupta, D.; Solanki, S.C.; Saini, J.S. Thermohydraulic performance of solar air heaters with roughened absorber plates. Sol. Energy 1997, 61, 33–42. [Google Scholar] [CrossRef]
- Ebrahim-Momin, A.M.; Saini, J.S.; Solanki, S.C. Heat transfer and friction in solar air heater duct with V-shaped rib roughness on absorber plate. Int. J. Heat Mass Transf. 2002, 45, 3383–3396. [Google Scholar] [CrossRef]
- Maithani, R.; Saini, J.S. Heat transfer and friction factor correlations for a solar air heater duct roughened artificially with V-ribs with symmetrical gaps. Exp. Therm. Fluid Sci. 2016, 70, 220–227. [Google Scholar] [CrossRef]
- Deo, N.S.; Chander, S.; Saini, J.S. Performance analysis of solar air heater duct roughened with multigap V-down ribs combined with staggered ribs. Renew. Energy 2016, 91, 484–500. [Google Scholar] [CrossRef]
- Patil, A.K.; Saini, J.S.; Kumar, K. Heat transfer and friction characteristics of solar air heater duct roughened by broken V-shape ribs combined with staggered rib piece. J. Renew. Sustain. Energy 2012, 4, 013115. [Google Scholar] [CrossRef]
- Hans, V.S.; Saini, R.P.; Saini, J.S. Heat transfer and friction factor correlations for a solar air heater duct roughened artificially with multiple v-ribs. Sol. Energy 2010, 84, 898–911. [Google Scholar] [CrossRef]
- Kumar, A.; Saini, R.P.; Saini, J.S. Experimental investigation on heat transfer and fluid flow characteristics of air flow in a rectangular duct with Multi V-shaped rib with gap roughness on the heated plate. Sol. Energy 2012, 86, 1733–1749. [Google Scholar] [CrossRef]
- Saini, S.K.; Saini, R.P. Development of correlations for Nusselt number and friction factor for solar air heater with roughened duct having arc-shaped wire as artificial roughness. Sol. Energy 2008, 82, 1118–1130. [Google Scholar] [CrossRef]
- Sethi, M.; Thakur, N.S. Correlations for solar air heater duct with dimpled shape roughness elements on absorber plate. Sol. Energy 2012, 86, 2852–2861. [Google Scholar] [CrossRef]
- Yadav, S.; Kaushal, M.; Varun; Siddhartha. Nusselt number and friction factor correlations for solar air heater duct having protrusions as roughness elements on absorber plate. Exp. Therm. Fluid Sci. 2013, 44, 34–41. [Google Scholar] [CrossRef]
- Hans, V.S.; Gill, R.S.; Singh, S. Heat transfer and friction factor correlations for a solar air heater duct roughened artificially with broken arc ribs. Exp. Therm. Fluid Sci. 2016, 80, 77–89. [Google Scholar] [CrossRef]
- Pandey, N.K.; Bajpai, V.K. Experimental investigation of heat transfer augmentation using multiple arcs with gap on absorber plate of solar air heater. Sol. Energy 2016, 134, 314–326. [Google Scholar] [CrossRef]
- Singh, A.P.; Varun; Siddhartha. Effect of artificial roughness on heat transfer and friction characteristics having multiple arc shaped roughness element on the absorber plate. Sol. Energy 2014, 105, 479–493. [Google Scholar] [CrossRef]
- Lanjewar, A.M.; Bhagoria, J.L.; Sarviya, R.M.; Lanjewar, A.M.; Bhagoria, L. Performance analysis of W-shaped rib roughened solar air heater. J. Renew. Sustain. Energy 2011, 3, 043110. [Google Scholar] [CrossRef]
- Lanjewar, A.; Bhagoria, J.L.; Sarviya, R.M. Experimental study of augmented heat transfer and friction in solar air heater with different orientations of W-Rib roughness. Exp. Therm. Fluid Sci. 2011, 35, 986–995. [Google Scholar] [CrossRef]
- Kumar, A.; Bhagoria, J.L.; Sarviya, R.M. Heat transfer and friction correlations for artificially roughened solar air heater duct with discrete W-shaped ribs. Energy Convers. Manag. 2009, 50, 2106–2117. [Google Scholar] [CrossRef]
- Gawande, V.B.; Dhoble, A.S.; Zodpe, D.B.; Chamoli, S. Experimental and CFD investigation of convection heat transfer in solar air heater with reverse L-shaped ribs. Sol. Energy 2016, 131, 275–295. [Google Scholar] [CrossRef]
- Kumar, K.; Prajapati, D.R.; Samir, S. Heat Transfer and Friction Factor Correlations Development for Solar Air artificially roughened with ‘S’shape ribs. Heater Duct. Exp. Therm. Fluid Sci. 2016, 82, 249–261. [Google Scholar] [CrossRef]
- Bhushan, B.; Singh, R. Nusselt number and friction factor correlations for solar air heater duct having artificially roughened absorber plate. Sol. Energy 2011, 85, 1109–1118. [Google Scholar] [CrossRef]
- Singh, I.; Singh, S. CFD analysis of solar air heater duct having square wave profiled transverse ribs as roughness elements. Sol. Energy 2018, 162, 442–453. [Google Scholar] [CrossRef]
- Saini, R.P.; Saini, J.S. Heat transfer and friction factor correlations for artificially roughened ducts with expanded metal mesh as roughness element. Int. J. Heat Mass Transf. 1997, 40, 973–986. [Google Scholar] [CrossRef]
- Karmare, S.V.; Tikekar, A.N. Heat transfer and friction factor correlation for artificially roughened duct with metal grit ribs. Int. J. Heat Mass Transf. 2007, 50, 4342–4351. [Google Scholar] [CrossRef]
- Karwa, R. Experimental studies of augmented heat transfer and friction in asymmetrically heated rectangular ducts with ribs on the heated wall in transverse, inclined, v-continuous and v-discrete pattern. Int. Commun. Heat Mass Transf. 2003, 30, 241–250. [Google Scholar] [CrossRef]
- Saini, R.P.; Verma, J. Heat transfer and friction factor correlations for a duct having dimple-shape artificial roughness for solar air heaters. Energy 2008, 33, 1277–1287. [Google Scholar] [CrossRef]
- Bhagoria, J.L.; Saini, J.S.; Solanki, S.C. Heat transfer coefficient and friction factor correlations for rectangular solar air heater duct having transverse wedge shaped rib roughness on the absorber plate. Renew. Energy 2002, 25, 341–369. [Google Scholar] [CrossRef]
- Layek, A.; Saini, J.S.; Solanki, S.C. Heat transfer and friction characteristics for artificially roughened ducts with compound turbulators. Int. J. Heat Mass Transf. 2007, 50, 4845–4854. [Google Scholar] [CrossRef]
- Ahn, S.W. The effects of roughness types on friction factors and heat transfer in roughened rectangular duct. Int. Commun. Heat Mass Transf. 2001, 28, 933–942. [Google Scholar] [CrossRef]
- Taslim, M.E.; Li, T.; Kercher, D.M. Experimental heat transfer and friction in channels roughened with angled, V-shaped and discrete ribs on two opposite walls. ASME J. Turbomach. 1996, 118, 20–28. [Google Scholar] [CrossRef]
- Alam, T.; Saini, R.P.; Saini, J.S. Use of turbulators for heat transfer augmentation in an air duct-A review. Renew. Energy 2014, 62, 689–715. [Google Scholar] [CrossRef]
- Sahu, R.K.; Gandhi, B.K. Numerical Simulation of Heat Transfer Enhancement due to a Gap in an Inclined Continuous Rib Arrangement in a Solar Air Heater Duct. Int. J. Adv. Mech. Eng. 2014, 4, 687–693. [Google Scholar]
- Aharwal, K.R.; Gandhi, B.K.; Saini, J.S. An experimental investigation of heat transfer and fluid flow in a rectangular duct with inclined discrete ribs. Int. J. Energy Environ. 2010, 1, 987–998. [Google Scholar]
- Xi, L.; Xu, L.; Gao, J.; Zhao, Z.; Li, Y. Study on heat transfer performance of steam-cooled ribbed channel using neural networks and genetic algorithms. Int. J. Heat Mass Transf. 2018, 127, 1110–1123. [Google Scholar] [CrossRef]
- Sherry, M.; Lo Jacono, D.; Sheridan, J. An experimental investigation of the recirculation zone formed downstream of a forward-facing step. J. Wind Eng. Ind. Aerodyn. 2010, 98, 888–894. [Google Scholar] [CrossRef] [Green Version]
- Essel, E.E.; Nematollahi, A.; Thacher, E.W.; Tachie, M.F. Effects of upstream roughness and Reynolds number on separated and reattached turbulent flow. J. Turbul. 2015, 16, 872–899. [Google Scholar] [CrossRef]
- Singh, I.; Vardhan, S.; Singh, S.; Singh, A. Experimental and CFD analysis of solar air heater duct roughened with multiple broken transverse ribs: A comparative study. Sol. Energy 2019, 188, 519–532. [Google Scholar] [CrossRef]
- Prasad, K.; Mullick, S.C. Heat transfer characteristics of a solar air heater used for drying purposes. Appl. Energy 1983, 13, 83–93. [Google Scholar] [CrossRef]
- Karwa, R.; Solanki, S.C.; Saini, J.S. Thermo-hydraulic performance of solar air heaters having integral chamfered rib roughness on absorber plates. Energy 2001, 26, 161–176. [Google Scholar] [CrossRef]
- Verma, S.K.; Prasad, B.N. Investigation for the optimal thermo-hydraulic performance of artificially roughened solar air heaters. Renew. Energy 2000, 20, 19–36. [Google Scholar] [CrossRef]
- Xi, L.; Xu, L.; Gao, J.; Zhao, Z.; Li, Y. Numerical analysis and optimization on flow and heat transfer performance of a steam-cooled ribbed channel. Case Stud. Therm. Eng. 2021, 28, 101442. [Google Scholar] [CrossRef]
- Behura, A.K.; Rout, S.K.; Pandya, H.; Kumar, A. Thermal Analysis of Three Sides Artificially Roughened Solar Air Heaters. Energy Procedia 2017, 109, 279–285. [Google Scholar] [CrossRef]
- Aharwal, K.R.; Gandhi, B.K.; Saini, J.S. Experimental investigation on heat-transfer enhancement due to a gap in an inclined continuous rib arrangement in a rectangular duct of solar air heater. Renew. Energy 2008, 33, 585–596. [Google Scholar] [CrossRef]
- Lu, B.; Jiang, P.X. Experimental and numerical investigation of convection heat transfer in a rectangular channel with angled ribs. Exp. Therm. Fluid Sci. 2006, 30, 513–521. [Google Scholar] [CrossRef]
- Alam, T.; Kim, M.-H. A critical review on artificial roughness provided in rectangular solar air heater duct. Renew. Sustain. Energy Rev. 2017, 69, 387–400. [Google Scholar] [CrossRef]
- Patil, A.K. Heat transfer mechanism and energy efficiency of artificially roughened solar air heaters—A review. Renew. Sustain. Energy Rev. 2015, 42, 681–689. [Google Scholar] [CrossRef]
- Singh, S.; Chander, S.; Saini, J.S. Thermal and effective efficiency-based analysis of discrete V-down rib-roughened solar air heaters. J. Renew. Sustain. Energy 2011, 3, 023107. [Google Scholar] [CrossRef]
- Singh, S.; Chander, S.; Saini, J.S. Thermo-hydraulic performance due to relative roughness pitch in V-down rib with gap in solar air heater duct—Comparison with similar rib roughness geometries. Renew. Sustain. Energy Rev. 2015, 43, 1159–1166. [Google Scholar] [CrossRef]
- Karwa, R.; Bairwa, R.D.; Jain, B.P.; Karwa, N. Experimental study of the effects of rib angle and discretization on heat transfer and friction in an asymmetrically heated rectangular duct. J. Enhanc. Heat Transf. 2005, 12, 343–355. [Google Scholar] [CrossRef]
- Jain, P.K.; Lanjewar, A. Overview of V-RIB geometries in solar air heater and performance evaluation of a new V-RIB geometry. Renew. Energy 2019, 133, 77–90. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, M.H. Heat transfer and fluid flow characteristics in air duct with various V-pattern rib roughness on the heated plate: A comparative study. Energy 2016, 103, 75–85. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, M.H. Thermo-hydraulic performance of rectangular ducts with different multiple V-rib roughness shapes: A comprehensive review and comparative study. Renew. Sustain. Energy Rev. 2016, 54, 635–652. [Google Scholar] [CrossRef]
- Nidhul, K.; Kumar, S.; Yadav, A.K.; Anish, S. Enhanced thermo-hydraulic performance in a V-ribbed triangular duct solar air heater: CFD and exergy analysis. Energy 2020, 200, 117448. [Google Scholar] [CrossRef]
- Misra, R.; Singh, J.; Jain, S.K.; Faujdar, S.; Agrawal, M.; Mishra, A. Prediction of behavior of triangular solar air heater duct using V-down rib with multiple gaps and turbulence promoters as artificial roughness: A CFD analysis. Int. J. Heat Mass Transf. 2020, 162, 120376. [Google Scholar] [CrossRef]
- Patel, S.S.; Lanjewar, A. Experimental and numerical investigation of solar air heater with novel V-rib geometry. J. Energy Storage 2019, 21, 750–764. [Google Scholar] [CrossRef]
- Patel, S.S.; Lanjewar, A. Heat transfer enhancement using additional gap in symmetrical element of V-geometry roughened solar air heater. J. Energy Storage 2021, 38, 102545. [Google Scholar] [CrossRef]
- Alam, T.; Saini, R.P.; Saini, J.S. Experimental investigation on heat transfer enhancement due to V-shaped perforated blocks in a rectangular duct of solar air heater. Energy Convers. Manag. 2014, 81, 374–383. [Google Scholar] [CrossRef]
- Alam, T.; Saini, R.P.; Saini, J.S. Experimental investigation of thermo hydraulic performance due to angle of attack in solar air heater duct equipped with V-shaped perforated blockages. Int. J. Renew. Energy Technol. 2015, 6, 164–180. [Google Scholar] [CrossRef]
- Alam, T.; Saini, R.P.; Saini, J.S. Experimental investigation of thermo-hydraulic performance of a rectangular solar air heater duct equipped with V-shaped perforated blocks. Adv. Mech. Eng. 2014, 6, 948313. [Google Scholar] [CrossRef]
- Alam, T.; Saini, R.P.; Saini, J.S. Heat transfer enhancement due to V-shaped perforated blocks in a solar air heater duct. Appl. Mech. Mater. 2014, 619, 125–129. [Google Scholar] [CrossRef]
- Alam, T.; Saini, R.P.; Saini, J.S. Effect of circularity of perforation holes in V-shaped blockages on heat transfer and friction characteristics of rectangular solar air heater duct. Energy Convers. Manag. 2014, 86, 952–963. [Google Scholar] [CrossRef]
- Singh Bisht, V.; Kumar Patil, A.; Gupta, A. Review and performance evaluation of roughened solar air heaters. Renew. Sustain. Energy Rev. 2018, 81, 954–977. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, R.; Singh, P.; Goel, V. Solar air heater having multiple V-ribs with Multiple-Symmetric gaps as roughness elements on Absorber-Plate: A parametric study. Sustain. Energy Technol. Assess. 2021, 48, 101559. [Google Scholar] [CrossRef]
- Kumar, A.; Saini, R.P.; Saini, J.S. Experimental Investigations on Thermo-hydraulic Performance due to Flow- Attack- Angle in Multiple V-ribs with Gap in a Rectangular Duct of Solar Air Heaters. J. Sustain. Energy Environ. 2013, 4, 1–7. [Google Scholar]
- Kumar, A.; Saini, R.P.; Saini, J.S. Development of correlations for Nusselt number and friction factor for solar air heater with roughened duct having multi-V-shaped with gap rib as arti fi cial roughness. Renew. Energy 2013, 58, 151–163. [Google Scholar] [CrossRef]
- Jin, D.; Zhang, M.; Wang, P.; Xu, S. Numerical investigation of heat transfer and fluid flow in a solar air heater duct with multi-V-shaped ribs on the absorber plate. Energy 2015, 89, 178–190. [Google Scholar] [CrossRef]
- Jin, D.; Zuo, J.; Quan, S.; Xu, S.; Gao, H. Thermo-hydraulic performance of solar air heater with staggered multiple V-shaped ribs on the absorber plate. Energy 2017, 127, 68–77. [Google Scholar] [CrossRef]
- Jin, D.; Quan, S.; Zuo, J.; Xu, S. Numerical investigation of heat transfer enhancement in a solar air heater roughened by multiple V-shaped ribs. Renew. Energy 2018, 134, 78–88. [Google Scholar] [CrossRef]
- Promvonge, P.; Skullong, S. Thermal characteristics in solar air duct with V-shaped flapped-baffles and chamfered-grooves. Int. J. Heat Mass Transf. 2021, 172, 121220. [Google Scholar] [CrossRef]
- Sahu, M.K.; Prasad, R.K. Exergy based performance evaluation of solar air heater with arc- shaped wire roughened absorber plate. Renew. Energy 2016, 96, 233–243. [Google Scholar] [CrossRef]
- Gill, R.S.; Hans, V.S.; Saini, J.S.; Singh, S. Investigation on performance enhancement due to staggered piece in a broken arc rib roughened solar air heater duct. Renew. Energy 2016, 104, 148–162. [Google Scholar] [CrossRef]
- Gill, R.S.; Hans, V.S.; Singh, S. Investigations on thermo-hydraulic performance of broken arc rib in a rectangular duct of solar air heater. Int. Commun. Heat Mass Transf. 2017, 88, 20–27. [Google Scholar] [CrossRef]
- Ghritlahre, H.K.; Sahu, P.K.; Chand, S. Thermal performance and heat transfer analysis of arc shaped roughened solar air heater—An experimental study. Sol. Energy 2020, 199, 173–182. [Google Scholar] [CrossRef]
- Yadav, K.D.; Prasad, R.K. Performance analysis of parallel flow flat plate solar air heater having arc shaped wire roughened absorber plate. Renew. Energy Focus 2020, 32, 23–44. [Google Scholar] [CrossRef]
- Ambade, J.; Lanjewar, A. Experimental investigation of solar air heater with new symmetrical GAP ARC GEOMETRY and staggered element. Int. J. Therm. Sci. 2019, 146, 106093. [Google Scholar] [CrossRef]
- Azad, R.; Bhuvad, S.; Lanjewar, A. Study of solar air heater with discrete arc ribs geometry: Experimental and numerical approach. Int. J. Therm. Sci. 2021, 167, 107013. [Google Scholar] [CrossRef]
- Gill, R.S.; Hans, V.S.; Singh, R.P. Optimization of artificial roughness parameters in a solar air heater duct roughened with hybrid ribs. Appl. Therm. Eng. 2021, 191, 116871. [Google Scholar] [CrossRef]
- Sureandhar, G.; Srinivasan, G.; Muthukumar, P.; Senthilmurugan, S. Performance analysis of arc rib fin embedded in a solar air heater. Therm. Sci. Eng. Prog. 2021, 23, 100891. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, V.; Singh, P.; Saxena, A.; Singh, A. Performance evaluation and optimization of solar assisted air heater with discrete multiple arc shaped ribs. J. Energy Storage 2019, 26, 100978. [Google Scholar] [CrossRef]
- Saravanakumar, P.T.; Somasundaram, D.; Matheswaran, M.M. Thermal and thermo-hydraulic analysis of arc shaped rib roughened solar air heater integrated with fins and baffles. Sol. Energy 2019, 180, 360–371. [Google Scholar] [CrossRef]
- Saravanakumar, P.T.; Somasundaram, D.; Matheswaran, M.M. Exergetic investigation and optimization of arc shaped rib roughened solar air heater integrated with fins and baffles. Appl. Therm. Eng. 2020, 175, 115316. [Google Scholar] [CrossRef]
- Agrawal, Y.; Bhagoria, J.L. Proceedings Experimental investigation for pitch and angle of arc effect of discrete artificial roughness on Nusselt number and fluid flow characteristics of a solar air heater. Mater. Today Proc. 2020, 46, 5506–5511. [Google Scholar] [CrossRef]
- Hassan, A.K.; Hasan, M.M.; Khan, M.E. Parametric investigation and correlation development for heat transfer and friction factor in multiple arc dimple roughened solar air duct. Renew. Energy 2021, 174, 403–425. [Google Scholar] [CrossRef]
- Agrawal, Y.; Bhagoria, J.L.; Pagey, V.S. Materials Today: Proceedings Enhancement of thermo-hydraulic performance using double arc reverse ribs in a solar collector: Experimental approach. Mater. Today Proc. 2021, 47, 5749–6336. [Google Scholar] [CrossRef]
- Kumar, A.; Behura, A.K.; Saboor, S.; Gupta, H.K. Comparative study on W-shaped roughened solar air heaters by using booster mirror. Mater. Today Proc. 2020, 46, 5675–5680. [Google Scholar] [CrossRef]
- Singh, I.; Singh, S. A review of artificial roughness geometries employed in solar air heaters. Renew. Sustain. Energy Rev. 2018, 92, 405–425. [Google Scholar] [CrossRef]
- Wang, D.; Liu, J.; Liu, Y.; Wang, Y.; Li, B.; Liu, J. Evaluation of the performance of an improved solar air heater with “S” shaped ribs with gap. Sol. Energy 2020, 195, 89–101. [Google Scholar] [CrossRef]
- Baissi, M.T.; Brima, A.; Aoues, K.; Khanniche, R.; Moummi, N. Thermal behavior in a solar air heater channel roughened with delta-shaped vortex generators. Appl. Therm. Eng. 2019, 165, 113563. [Google Scholar] [CrossRef]
- Kumar, A.; Layek, A. Nusselt number and friction characteristics of a solar air heater that has a winglet type vortex generator in the absorber surface. Exp. Therm. Fluid Sci. 2020, 119, 110204. [Google Scholar] [CrossRef]
- Kumar, A.; Layek, A. Nusselt number and friction factor correlation of solar air heater having winglet type vortex generator over absorber plate. Sol. Energy 2020, 205, 334–348. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, S.; Thapa, S.; Sethi, M.; Fekete, G.; Singh, T. Impact of artificial roughness variation on heat transfer and friction characteristics of solar air heating system. Alex. Eng. J. 2021, 61, 481–491. [Google Scholar] [CrossRef]
- Promvonge, P.; Promthaisong, P.; Skullong, S. Numerical heat transfer in a solar air heater duct with punched delta-winglet vortex generators. Case Stud. Therm. Eng. 2021, 26, 101088. [Google Scholar] [CrossRef]
- Mahanand, Y.; Senapati, J.R. Thermo-hydraulic performance analysis of a solar air heater (SAH) with quarter-circular ribs on the absorber plate: A comparative study. Int. J. Therm. Sci. 2021, 161, 106747. [Google Scholar] [CrossRef]
- Gilani, S.E.; Al-kayiem, H.H.; Woldemicheal, D.E.; Gilani, S.I. Performance enhancement of free convective solar air heater by pin protrusions on the absorber. Sol. Energy 2017, 151, 173–185. [Google Scholar] [CrossRef]
- Perwez, A.; Kumar, R. Thermal performance investigation of the fl at and spherical dimple absorber plate solar air heaters. Sol. Energy 2019, 193, 309–323. [Google Scholar] [CrossRef]
- Debnat, S.; Das, B.; Randive, P. Influences of pentagonal ribs on the performance of rectangular solar air heater. Energy Procedia 2019, 158, 1168–1173. [Google Scholar] [CrossRef]
- Antony, A.L.; Shetty, S.P.; Madhwesh, N.; Sharma, N.Y.; Karanth, K.V. Influence of stepped cylindrical turbulence generators on the thermal enhancement factor of a flat plate solar air heater. Sol. Energy 2020, 198, 295–310. [Google Scholar] [CrossRef]
- Patel, Y.M.; Jain, S.V.; Lakhera, V.J. Thermo-hydraulic performance analysis of a solar air heater roughened with reverse NACA profile ribs. Appl. Therm. Eng. 2020, 170, 114940. [Google Scholar] [CrossRef]
- Gabhane, M.G.; Kanase-Patil, A.B. Experimental analysis of double flow solar air heater with multiple C shape roughness. Sol. Energy 2017, 155, 1411–1416. [Google Scholar] [CrossRef]
- Saravanan, A.; Murugan, M.; Reddy, M.S.; Ranjit, P.S.; Elumalai, P.V.; Kumar, P.; Sree, S.R. Thermo-hydraulic performance of a solar air heater with staggered C-shape finned absorber plate. Int. J. Therm. Sci. 2021, 168, 107068. [Google Scholar] [CrossRef]
- Kumar, A.; Layek, A. Thermo-hydraulic performance of solar air heater having twisted rib overthe absorber plate. Int. J. Therm. Sci. 2018, 133, 181–195. [Google Scholar] [CrossRef]
- Kumar, A.; Layek, A. Nusselt number and friction factor correlation of solar air heater having twisted-rib roughness on absorber plate. Renew. Energy 2019, 130, 687–699. [Google Scholar] [CrossRef]
- Kumar, A.; Layek, A. Energetic and exergetic performance evaluation of solar air heater with twisted rib roughness on absorber plate. J. Clean. Prod. 2019, 232, 617–628. [Google Scholar] [CrossRef]
- Thakur, D.S.; Khan, M.K.; Pathak, M. Performance Evaluation of Solar Air Heater with Novel Hyperbolic Rib Geometry. Renew. Energy 2016, 105, 786–797. [Google Scholar] [CrossRef]
- Manjunath, M.S.; Karanth, K.V.; Sharma, N.Y. Numerical analysis of the influence of spherical turbulence generators on heat transfer enhancement of flat plate solar air heater. Energy 2017, 121, 616–630. [Google Scholar] [CrossRef]
- Kumar, V.; Murmu, R. Experimental investigation for thermal performance of inclined spherical ball roughened solar air duct. Renew. Energy 2021, 172, 1365–1392. [Google Scholar] [CrossRef]
- Promvonge, P.; Khanoknaiyakarn, C.; Sripattanapipat, S.; Skullong, S. Heat transfer in solar air duct with multi-V-ribbed absorber and grooved back-plate. Chem. Eng. Res. Des. 2021, 168, 84–95. [Google Scholar] [CrossRef]
- Sharma, S.K.; Kalamkar, V.R. Experimental and numerical investigation of forced convective heat transfer in solar air heater with thin ribs. Sol. Energy 2017, 147, 277–291. [Google Scholar] [CrossRef]
- Prakash, C.; Saini, R.P. Heat transfer and friction in rectangular solar air heater duct having spherical and inclined rib protrusions as roughness on absorber plate. Exp. Heat Transf. 2018, 32, 469–487. [Google Scholar] [CrossRef]
- Luo, L.; Wen, F.; Wang, L.; Sundén, B.; Wang, S. On the solar receiver thermal enhancement by using the dimple combined with delta winglet vortex generator. Appl. Therm. Eng. 2016, 111, 586–598. [Google Scholar] [CrossRef]
- Skullong, S.; Kwankaomeng, S.; Thianpong, C.; Promvonge, P. Thermal performance of turbulent flow in a solar air heater channel with rib-grove turbulators. Int. Commun. Heat Mass Transf. 2014, 50, 34–43. [Google Scholar] [CrossRef]
- Kumar, B.V.; Manikandan, G.; Kanna, P.R. Enhancement of heat transfer in SAH with polygonal and trapezoidal shape of the rib using CFD. Energy 2021, 234, 121154. [Google Scholar] [CrossRef]
- Tanda, G.; Satta, F. Heat transfer and friction in a high aspect ratio rectangular channel with angled and intersecting ribs. Int. J. Heat Mass Transf. 2021, 169, 120906. [Google Scholar] [CrossRef]
- Farhan, A.A.; Issam, A.; Ali, M.; Ahmed, H.E. Energetic and exergetic efficiency analysis of a v-corrugated solar air heater integrated with twisted tape inserts. Renew. Energy 2021, 169, 1373–1385. [Google Scholar] [CrossRef]
- Alam, T.; Kim, M.-H. A comprehensive review on single phase heat transfer enhancement techniques in heat exchanger applications. Renew Sustain. Energy Rev. 2018, 81, 813–839. [Google Scholar] [CrossRef]
- Ansari, M.; Bazargan, M. Optimization of Flat Plate Solar Air Heaters with Ribbed Surfaces. Appl. Therm. Eng. 2018, 136, 356–363. [Google Scholar] [CrossRef]
- Alfarawi, S.; Abdel-moneim, S.A.; Bodalal, A. Experimental investigations of heat transfer enhancement from rectangular duct roughened by hybrid ribs. Int. J. Therm. Sci. 2017, 118, 123–138. [Google Scholar] [CrossRef]
- Alam, T.; Kim, M.-H. Numerical study on thermal hydraulic performance improvement in solar air heater duct with semi ellipse shaped obstacles. Energy 2016, 112, 588–598. [Google Scholar] [CrossRef]
- Xiao, H.; Dong, Z.; Liu, Z.; Liu, W. Heat transfer performance and flow characteristics of solar air heaters with inclined trapezoidal vortex generators. Appl. Therm. Eng. 2020, 179, 115484. [Google Scholar] [CrossRef]
- Manjunath, M.S.; Karanth, K.V.; Sharma, N.Y. Numerical Investigation on Heat Transfer Enhancement of Solar Air Heater using Sinusoidal Corrugations on Absorber Plate. Int. J. Mech. Sci. 2018, 138–139, 219–228. [Google Scholar] [CrossRef]
- Bezbaruah, P.J.; Das, R.S.; Sarkar, B.K. Experimentally validated 3D simulation and performance optimization of a solar air duct with modified conical vortex generators. Sol. Energy 2021, 224, 1040–1062. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, P.; Xiao, H.; Liu, Z.; Liu, W. A study on heat transfer enhancement for solar air heaters with ripple surface. Renew. Energy 2021, 172, 477–487. [Google Scholar] [CrossRef]
- Alam, T.; Meena, C.S.; Balam, N.B.; Kumar, A.; Cozzolino, R. Thermo-Hydraulic Performance Characteristics and Optimization of Protrusion Rib Roughness in Solar Air Heater. Energies 2021, 14, 3159. [Google Scholar] [CrossRef]
- Alam, T.; Kumar, A.; Balam, N.B. Thermo-Hydraulic Performance of Solar Air Heater Duct Provided with Conical Protrusion Rib Roughnesses. Adv. Energy Res. 2020, 2, 159–168. [Google Scholar]
- Kumar, R.; Kumar, A.; Goel, V. Performance improvement and development of correlation for friction factor and heat transfer using computational fluid dynamics for ribbed triangular duct solar air heater. Renew. Energy 2018, 131, 788–799. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, V. Unconventional solar air heater with triangular flow-passage: A CFD based comparative performance assessment of different cross- sectional rib-roughnesses. Renew. Energy 2021, 172, 1267–1278. [Google Scholar] [CrossRef]
- Goel, V.; Kumar, R.; Bhattacharyya, S.; Tyagi, V.V.; Abusorrah, A.M. A comprehensive parametric investigation of hemispherical cavities on thermal performance and flow-dynamics in the triangular-duct solar-assisted air-heater. Renew. Energy 2021, 173, 896–912. [Google Scholar] [CrossRef]
- Xi, L.; Xu, L.; Gao, J.; Zhao, Z. Study on Conjugate Thermal Performance of a Steam-Cooled Ribbed Channel with Thick Metallic Walls. In Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, Online, 7–11 June 2021. [Google Scholar] [CrossRef]
- Alam, T.; Kim, M.-H. Performance improvement of double-pass solar air heater—A state of art of review. Renew Sustain. Energy Rev. 2017, 79, 779–793. [Google Scholar] [CrossRef]
- Patil, A.K.; Saini, J.S.; Kumar, K. A comprehensive review on roughness geometries and investigation techniques used in artificially roughened solar air heaters. Int. J. Renew Energy Res. 2012, 2, 1–15. [Google Scholar] [CrossRef]
- Alam, T.; Balam, N.B.; Kulkarni, K.S.; Siddiqui, M.I.H.; Kapoor, N.R.; Meena, C.S.; Kumar, A.; Cozzolino, R. Performance Augmentation of the Flat Plate Solar Thermal Collector: A Review. Energies 2021, 14, 6203. [Google Scholar] [CrossRef]
- Istanto, T.; Danardono, D.; Yaningsih, I.; Wijayanta, A.T. Experimental study of heat transfer enhancement in solar air heater with different angle of attack of V-down continuous ribs. AIP Conf. Proc. 2016, 1737, 060002. [Google Scholar] [CrossRef]
- Singh, A.P.; Varun; Siddhartha. Heat transfer and friction factor correlations for multiple arc shape roughness elements on the absorber plate used in solar air heaters. Exp. Therm. Fluid Sci. 2014, 54, 117–126. [Google Scholar] [CrossRef]
- Karim, M.A.; Perez, E.; Amin, Z.M. Mathematical modelling of counter flow v-grove solar air collector. Renew. Energy 2014, 67, 192–201. [Google Scholar] [CrossRef] [Green Version]
- Bondi, P.; Cicala, L.; Farina, G. Performance analysis of solar air heaters of conventional design. Sol. Energy 1988, 41, 101–107. [Google Scholar] [CrossRef]
- Pandey, N.K.; Bajpai, V.K. Thermo-hydraulic performance enhancement of solar air heater (SAH) having multiple arcs with gap shaped roughness element on absorber plate. Int. J. Eng. Sci. Technol. 2016, 8, 34–42. [Google Scholar] [CrossRef] [Green Version]



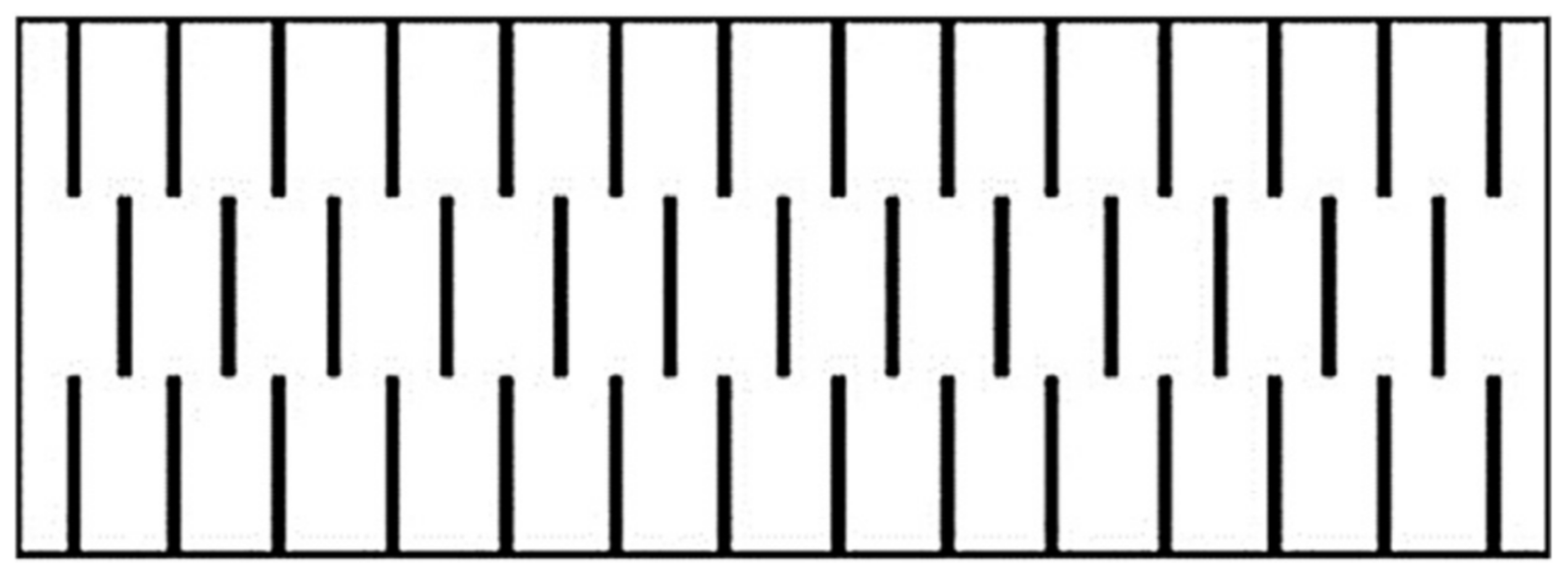
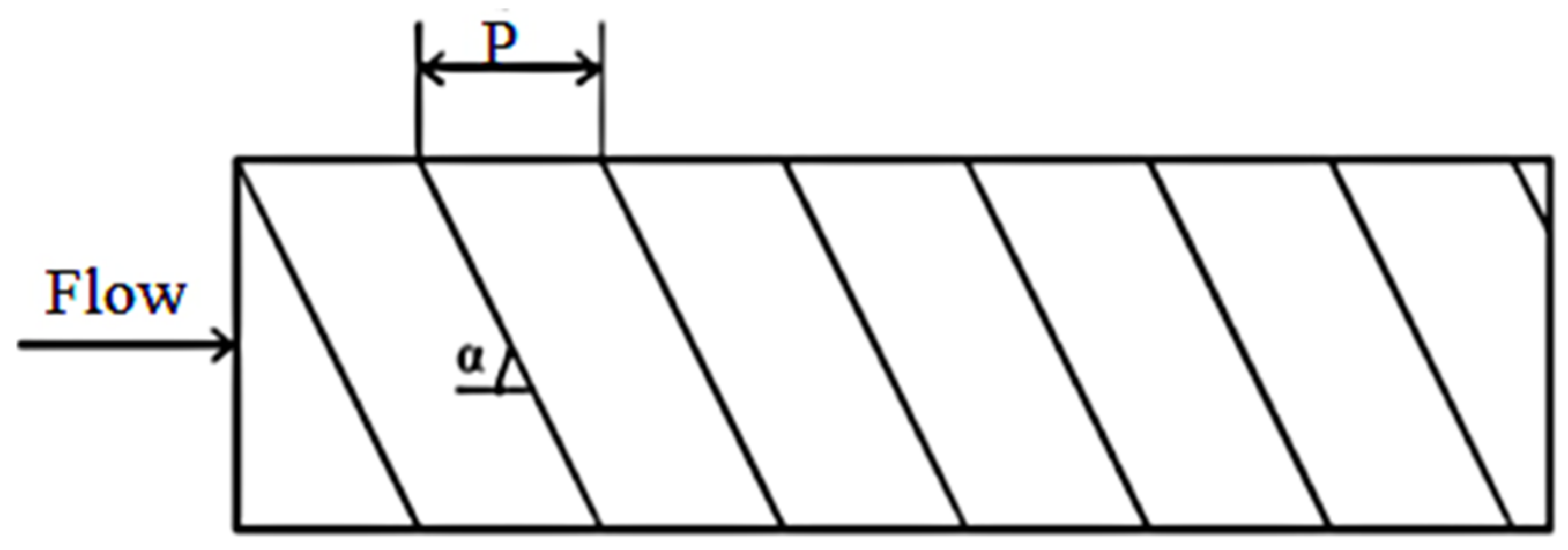

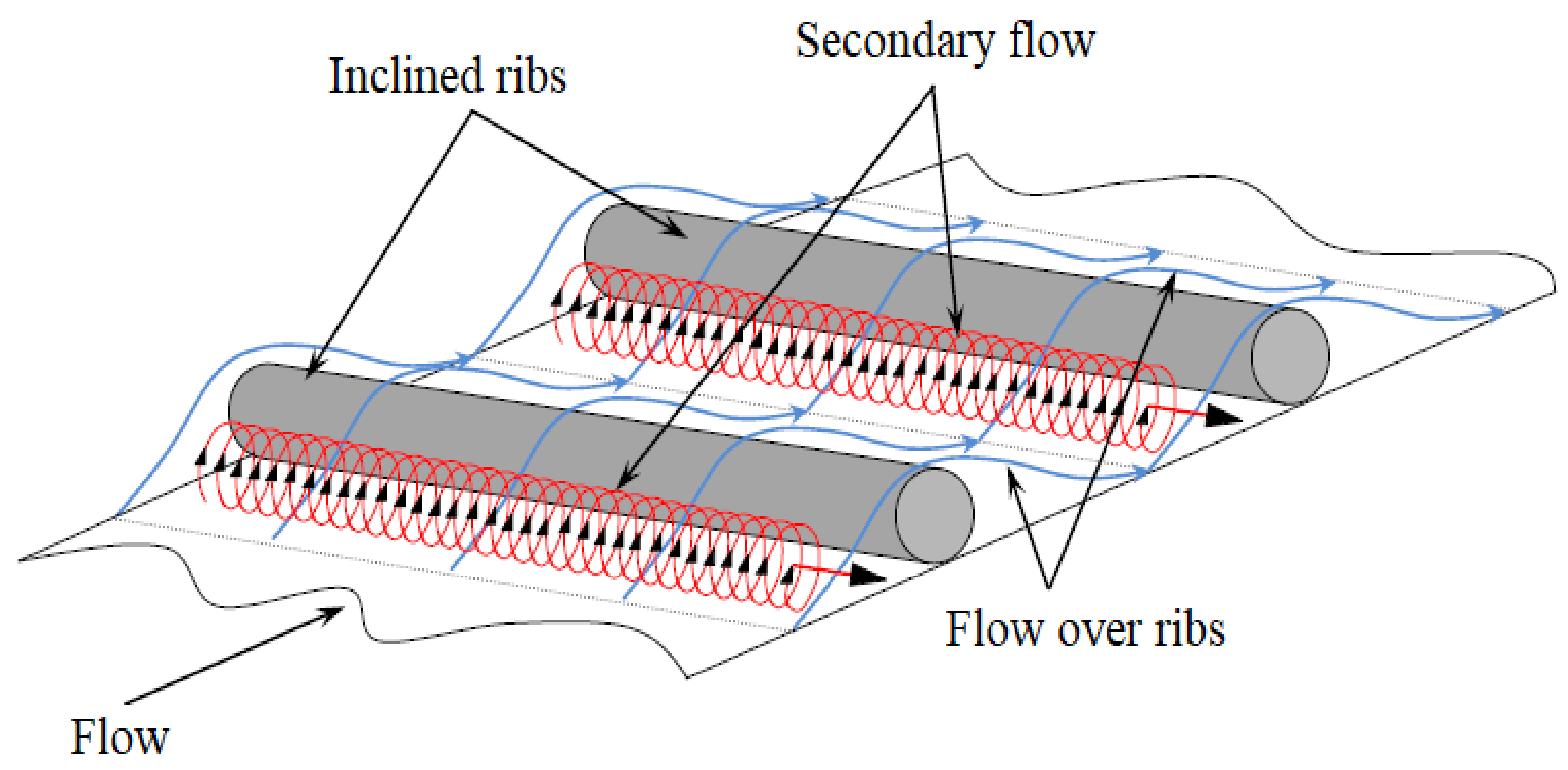
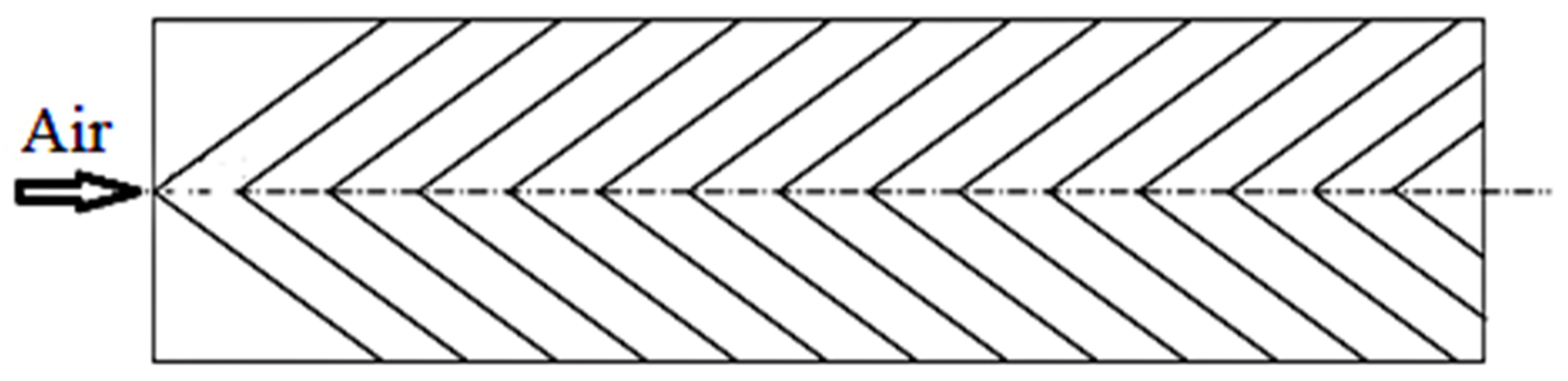





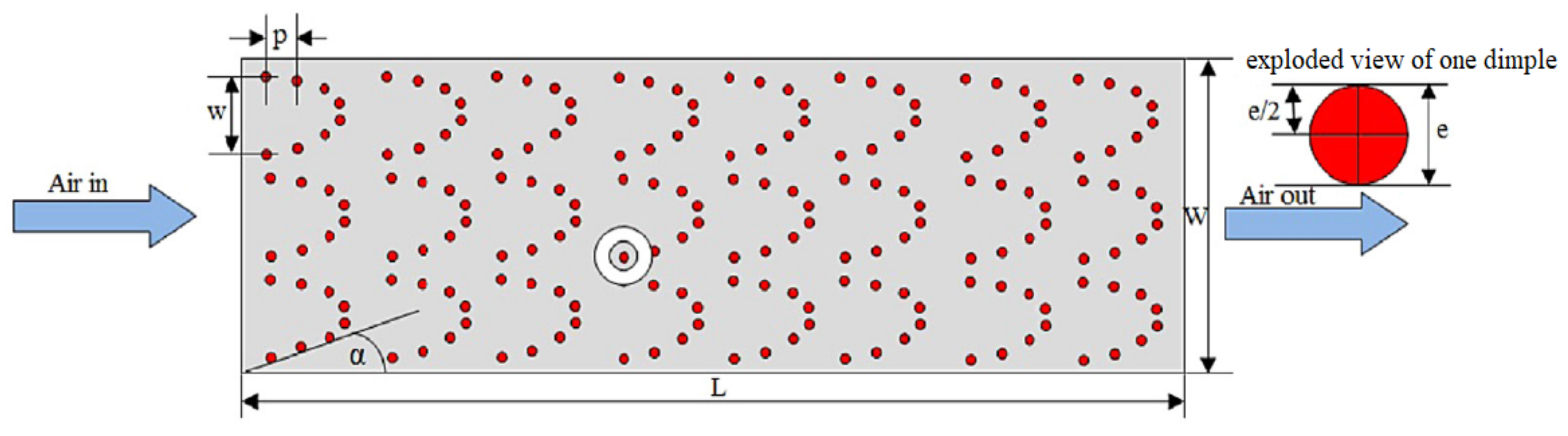
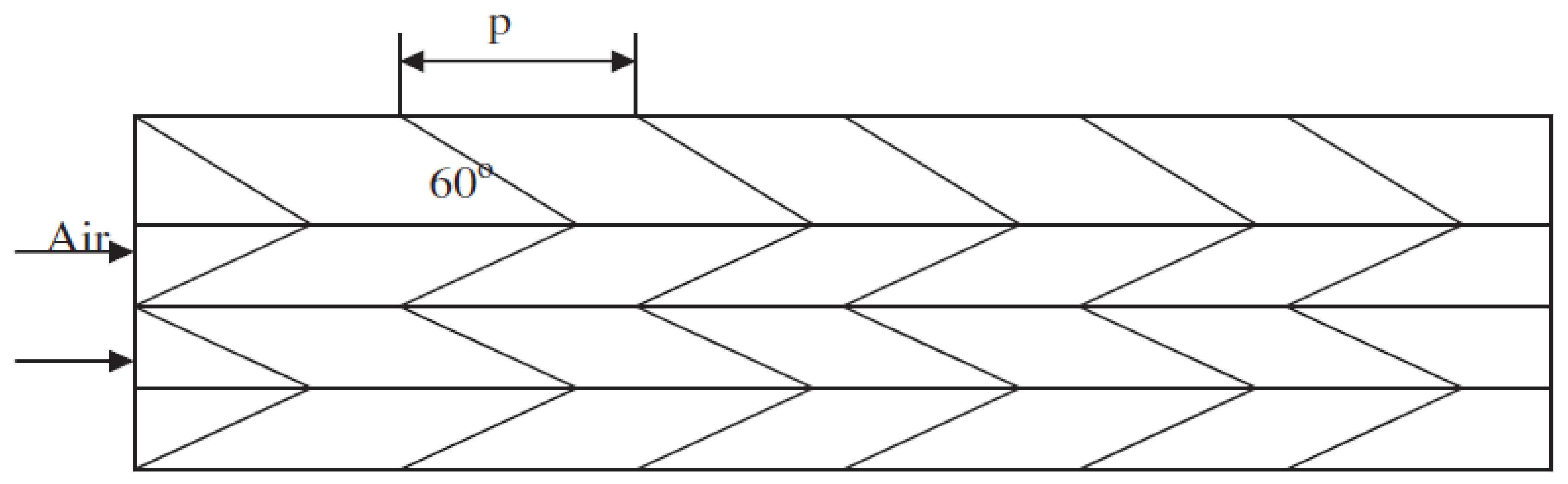
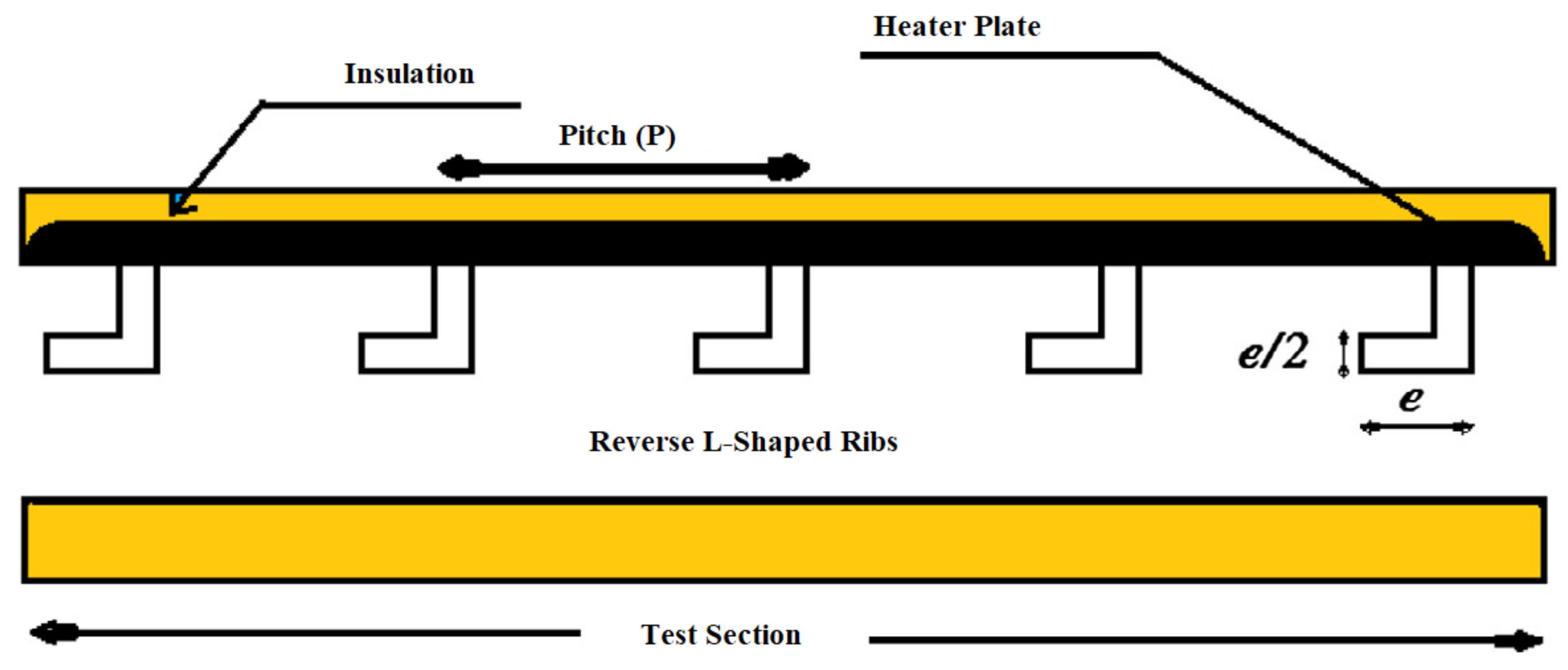
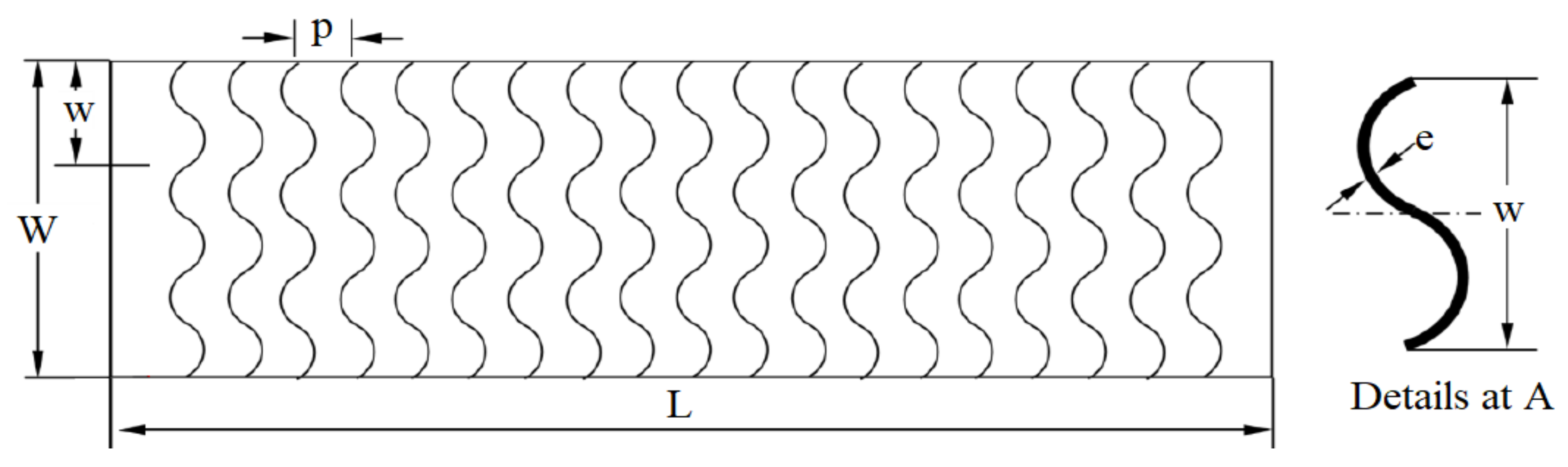






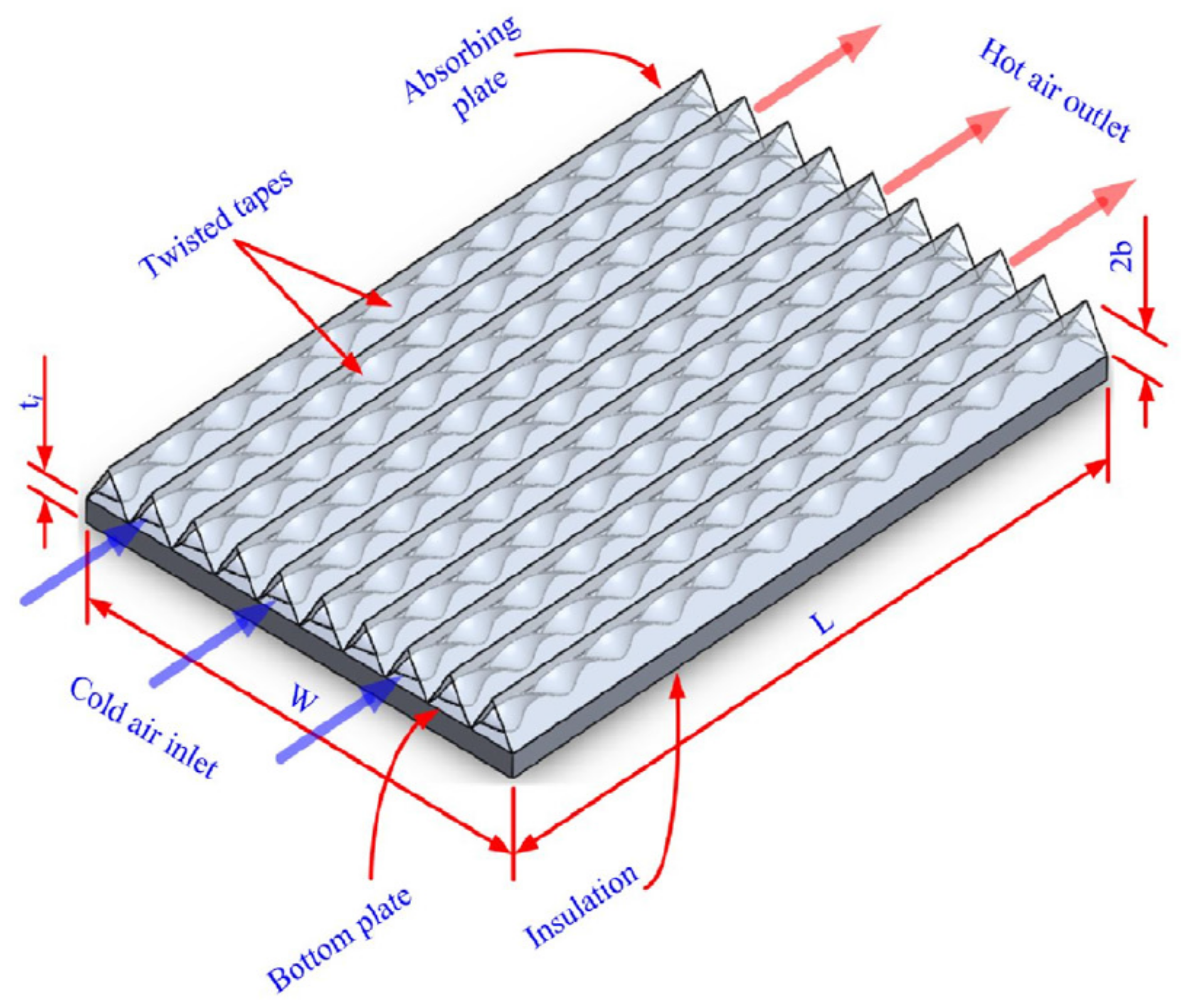
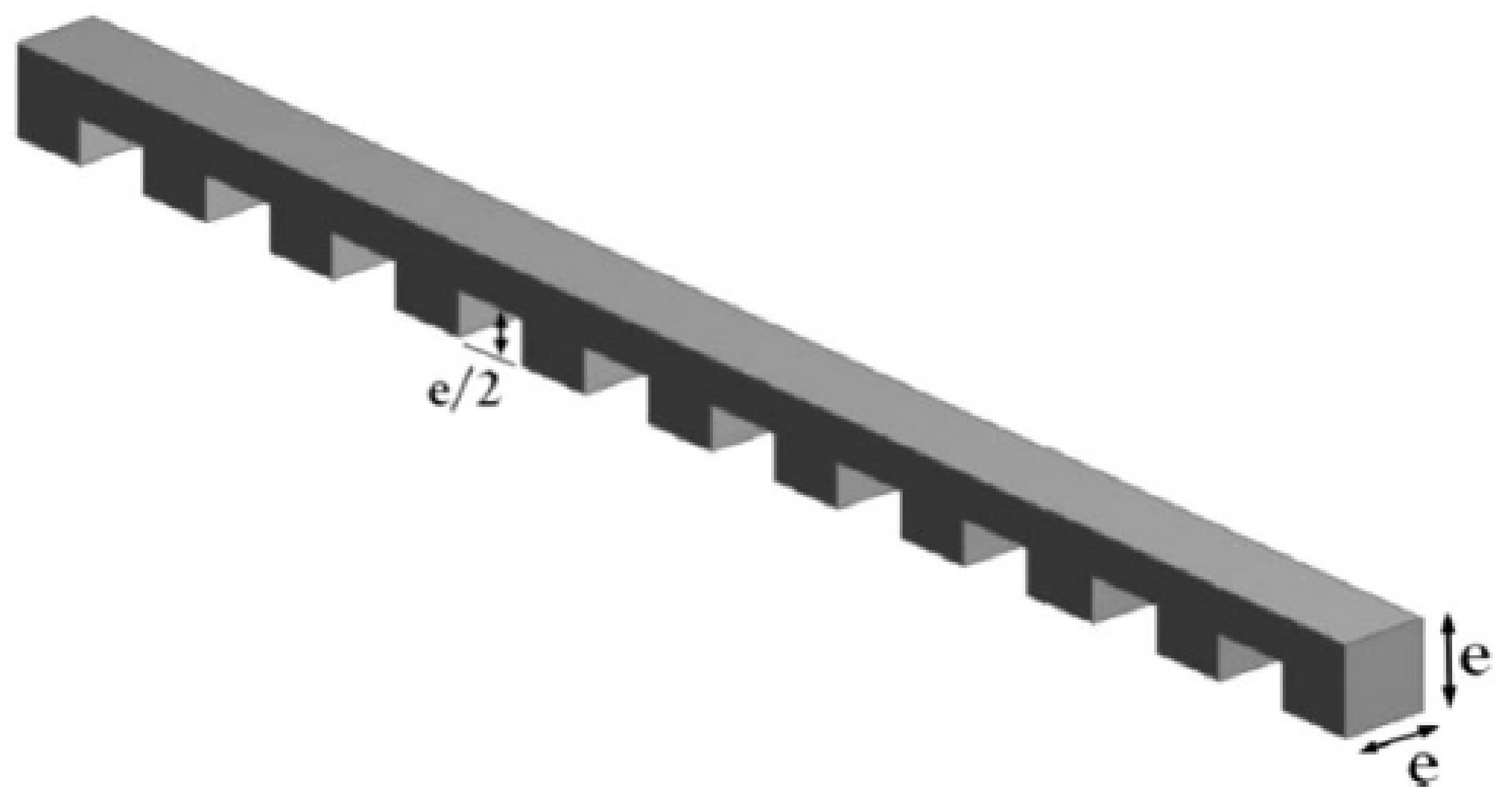




| S. No. | Researchers | Geometry of Artificial Roughness | Value of e/Dh |
|---|---|---|---|
| 1 | Prasad and Saini [13] | Continuous transverse rib | 0.0333 |
| 2 | Singh et al. [16] | Nonuniform saw-tooth-shaped rib | 0.043 |
| 3 | Aharwal et al. [17] | Inclined rib with gap | 0.0377 |
| 4 | Singh et al. [18,19] | V-shaped with gap | 0.043 |
| 5 | Sahu and Bhagoria [20] | Broken transverse rib | 0.0338 |
| 6 | Yadav and Bhagoria [21] | Triangular-shaped rib | 0.042 |
| 7 | Yadav and Bhagoria [22] | Square-shaped rib | 0.042 |
| 8 | Gupta et al. [23] | Continuous inclined rib | 0.033 |
| 9 | Momin et al. [24] | V-shaped continuous rib | 0.034 |
| 10 | Maithani and Saini [25] | V-shaped rib with symmetrical gap | 0.043 |
| 11 | Deo et al. [26] | Multi-V-shaped rib with gap combined with staggered rib | 0.044 |
| 12 | Patil et al. [27] | V-rib with gaps combined with staggered rib | 0.0433 |
| 13 | Hans et al. [28] | Continuous multi-V-rib | 0.043 |
| 14 | Kumar et al. [29] | Multi-V-rib with gap | 0.043 |
| 15 | Saini and Saini [30] | Arc rib | 0.0422 |
| 16 | Sethi et al. [31] | Dimple rib in arc pattern | 0.036 |
| 17 | Yadav et al. [32] | Dimple rib in arc pattern | 0.030 |
| 18 | Hans et al. [33] | Brocken arc rib | 0.043 |
| 19 | Pandey et al. [34] | Multiarc rib with gaps | 0.044 |
| 20 | Singh et al. [35] | Multiarc rib | 0.045 |
| 21 | Lanjewar et al. [36,37] | Continuous W-rib | 0.03375 |
| 22 | Kumar et al. [38] | Discrete W-rib | 0.03375 |
| 23 | Gawande et al. [39] | L-shaped rib | 0.042 |
| 24 | Kumar et al. [40] | S-shaped rib | 0.043 |
| 25 | Bhushan and Singh [41] | Protrusion roughness | 0.030 |
| 26 | Singh I and Singh S [42] | Transverse rib with square wave profile | 0.043 |
| 27 | Saini and Saini [43] | Expanded metal mesh | 0.039 |
| 28 | Karmare and Tikekar [44] | Metal grit | 0.044 |
| S. No. | Investigators | Type of Roughness | p/e |
|---|---|---|---|
| 1 | Prasad and Saini [13] | Continuous transverse rib | 10 |
| 2 | Singh et al. [16] | Nonuniform saw-tooth-shaped rib | 8 |
| 3 | Aharwal et al. [17] | Inclined rib with gap | 10 |
| 4 | Singh et al. [18,19] | V-shaped with gap | 8 |
| 6 | Yadav and Bhagoria [21] | Triangular-shaped rib | 7.14 |
| 7 | Yadav and Bhagoria [22] | Square-shaped rib | 7.14 |
| 8 | Gupta et al. [23] | Continuous inclined rib | 10 |
| 9 | Momin et al. [24] | V-shaped continuous rib | 10 |
| 10 | Karwa [45] | Transverse rib | 10 |
| 11 | Maithani and Saini [25] | V-shaped rib with symmetrical gap | 10 |
| 12 | Deo et al. [26] | Multi-V-shaped rib with gap combined with staggered rib | 12 |
| 13 | Patil et al. [27] | V-shaped rib with gap combined with staggered rib | 10 |
| 14 | Saini and Verma [46] | Dimple-shaped | 10 |
| 15 | Hans et al. [28] | Continuous multi-V-rib | 8 |
| 16 | Kumar et al. [29] | Multi-V-ribs with gap | 10 |
| 17 | Saini and Saini [30] | Arc ribs | 10 |
| 18 | Sethi et al. [31] | Dimple rib in arc pattern | 10 |
| 19 | Yadav et al. [32] | Dimple rib in arc pattern | 12 |
| 20 | Hans et al. [33] | Brocken arc rib | 8 |
| 21 | Pandey et al. [34] | Multiarc rib with gaps | 8 |
| 22 | Singh et al. [35] | Multiarc rib | 8 |
| 23 | Lanjewar et al. [36,37] | Continuous W-rib | 10 |
| 24 | Kumar et al. [38] | Discrete W-rib | 10 |
| 25 | Gawande et al. [39] | L-shaped rib | 7.14 |
| 26 | Kumar et al. [40] | S-shaped rib | 8 |
| 27 | Bhagoria et al. [47] | Wedge-shaped rib | 7.57 |
| 28 | Karmare and Tikekar [44] | Metal grit | 17.5 |
| 29 | Layek et al. [48] | Chamfered rib combined with groove | 6 |
| S. No. | Investigators | Type of Roughness | Value of α |
|---|---|---|---|
| 1 | Aharwal et al. [17] | Inclined rib with gaps | 60 |
| 2 | Gupta et al. [23] | Continuous inclined rib | 60 |
| 3 | Momin et al. [24] | V-shaped continuous rib | 60 |
| 4 | Maithani and Saini [25] | V-shaped rib with symmetrical gaps | 60 |
| 5 | Deo et al. [26] | Multi-V-shaped rib with gaps combined with staggered rib | 60 |
| 6 | Patil et al. [27] | V-shaped rib with gaps combined with staggered rib | 60 |
| 7 | Hans et al. [28] | Continuous multi-V-rib | 60 |
| 8 | Kumar et al. [29] | Multi-V-shaped rib with gap | 60 |
| 9 | Sethi et al. [31] | Dimple rib in arc pattern | 60 |
| 10 | Yadav et al. [32] | Dimple rib in arc pattern | 60 |
| 11 | Pandey et al. [34] | Multiarc rib with gap | 60 |
| 12 | Singh et al. [35] | Multiarc rib | 60 |
| 13 | Lanjewar et al. [36,37] | Continuous W-rib | 60 |
| 14 | Kumar et al. [38] | Discrete W-rib | 60 |
| 15 | Kumar et al. [40] | S-shaped rib | 60 |
| 16 | Saini and Saini [43] | Expanded metal mesh | 61.9 |
| Investigators | Type of Roughness | Parameter Used | Augmentation |
|---|---|---|---|
| Prasad and Saini [13] | Continuous transverse rib | e/D = 0.02–0.033 p/e = 10–20 | Nu/Nus = 2.35 f/fs = 4.25 |
| Singh et al. [16] | Nonuniform saw-tooth-shaped rib | e/Dh = 0.043, p/e = 8 Re = 3000–15,000 | Nu/Nus = 1.78 f/fs = 2.49 |
| Aharwal et al. [17] | Inclined rib with gaps | g/e = 0.5–2 e/Dh = 0.018–0.0377 α = 30°–90° d/W = 0.16–0.67 p/e = 4–10 | Nu/Nus = 2.83 f/fs = 3.60 |
| Singh et al. [18,19] | V-shape with gap | e/Dh = 0.015–0.043 d/w = 0.2–0.8 g/e = 0.5–2.0 p/e = 4–12 α = 30°–75° | Nu/Nus = 3.04 f/fs = 3.11 |
| Sahu and Bhagoria [20] | Broken transvers ribs | p = 10–30 mm e/D = 0.0338 | h/hs = 1.25–1.4 |
| Yadav and Bhagoria [21] | Triangular-shaped ribs | Re = 800–18,000 p/e = 7.14–35.71 | Nu/Nus = 3.07 f/fs = 3.35 |
| Yadav and Bhagoria [22] | Square shape ribs | e/Dh = 0.021–0.042, Re = 000–18,000, p/e = 7.14–35.71 | Nu/Nus = 2.86 f/fs = 3.84 |
| Gupta et al. [23] | Continuous inclined ribs | W/H = 6.8–11.5 e/D = 0.023–0.050 α = 60° | η/ηs = 1.16–1.25 |
| Momin et al. [24] | V-shaped continuous rib | p/e = 4–10 e/Dh = 0.02–0.034 α = 30°–90° | Nu/Nus = 2.30 f/fs = 2.89 |
| Maithani and Saini [25] | V-rib with symmetrical gaps | α = 30°–75° Ng = 1–5 g/e = 1–5 p/e = 6–12 | Nu/Nus = 3.6 f/fs = 3.67 |
| Deo et al. [26] | Multiple V-rib with gaps combined with staggered rib | n = 2 e/Dh = 0.026–0.057 w/e = 4.5 p/e = 4–14 p/P = 4.5 g/e = 1 α = 60° | Nu/Nus = 3.34 f/fs = 2.45 |
| Patil et al. [27] | V-ribs with gap combined with staggered rib | e/D = 0.0433 p’/p = 0.2–0.8 s’/s = 0.2–0.8 p/e = 10 r/e = 1–2.5 α = 60° | Nu/Nus = 3.18 |
| Hans et al. [28] | Continuous multiple V-rib | W/w = 1–10, e/D = 0.019–0.043 α = 30°–75°, p/e = 6–12 | Nu/Nus ~ 6 f/fs ~ 4.3 |
| Kumar et al. [29] | Multi-V-ribs with gaps | g/e = 0.5–1.5 Gd/Lv = 0.24–0.80 e/D = 0.019–0.043 W/w = 1–10, p/e = 6–12 α = 30°–75° | Nu/Nus = 6.74 f/fs = 6.37 |
| Jin et al. [86] | Multiple V-shaped ribs | p/e = 3–20, e/Dh = 0.03–0.11 α = 30°–75°, Re = 8000–20,000 | THPPmax = 1.93 |
| Saini and Saini [30] | Arc rib | e/D = 0.0213–0.0422 α/90 = 0.333–0.666 p/e = 10 | Nu/Nus = 3.8 f/fs = 1.75 |
| Sethi et al. [31] | Dimple rib in arc fashion | e/d = 0.5 e/Dh = 0.021–0.036 α = 45°–75° p/e = 10–20 | η = 1.10–1.887 |
| Yadav et al. [32] | Dimple rib in arc pattern | α = 45°–75° e/Dh = 0.015–0.030 p/e = 12–24 | Nu/Nus = 2.89, f/fs = 2.93 |
| Hans et al. [33] | Brocken arc rib | e/Dh = 0.022–0.043 d/w = 0.2–0.8 g/e = 0.5–2.5 p/e = 4–12 Re = 2000–16,000 | Nu/Nus = 2.63 f/fs = 2.44 |
| Pandey et al. [34] | Multiple-arc rib with gaps | W/w = 1–7 e/D = 0.016–0.044 d/x = 0.25–0.85 g/e = 0.5–2 p/e = 4–16 α = 30°–75° | Nu/Nus = 5.85 f/fs = 4.96 |
| Singh et al. [35] | Multiple-arc rib | e/D = 0.018–0.045 p/e = 4–16 W/w = 1–7 α = 30°–75° | Nu/Nus = 5.07 f/fs = 3.71 |
| Lanjewar et al. [36,37] | Continuous W-rib | e/Dh = 0.018–0.03375 α = 30°–75° p/e = 10 | Nu/Nus = 2.36 f/fs = 2.01 |
| Kumar et al. [38] | Discrete W-rib | e/Dh = 0.018–0.03375 α = 30°–75°, p/e = 10 | Nu/Nus = 2.16 f/fs = 2.75 |
| Gawande et al. [39] | L-shaped rib | e/D = 0.042 p/e = 7.14–17.86 | Nu/Nus = 2.827 f/fs = 2.434 |
| Kumar et al. [40] | S-shaped rib | e/Dh = 0.022–0.054 α = 30°–75° W/w = 1–4 p/e = 4–16 Re = 2400–20,000 | Nu/Nus = 4.64 f/fs = 2.71 |
| Bhushan and Singh [41] | Protrusion roughness | e/D = 0.03 L/e = 25–37.5 S/e = 18.75–37.5 d/D = 0.0147–0.0367 | Nu/Nus = 3.8 f/fs = 2.2 |
| Bhagoria et al. [47] | Wedge-shaped ribs | e/Dh = 0.015–0.033 ϕ = 8°–15°, p/e = 4.7–12.12 | Nu/Nus = 2.4 f/fs = 5.3 |
| Singh I and Singh S [42] | Transverse rib with square wave profile | p/e = 4–30, e/Dh = 0.043, Re = 3000–15,000 | Nu/Nus = 2.14 f/fs = 3.55 |
| Alam and Kim [137] | Semiellipse-shaped obstacle | p/e = 3.5, α = 30°–90°, Re = 6000–18,000 | Nu/Nus = 2.05 f/fs = 5.3 |
| Karmare and Tikekar [44] | Metal grit | e/Dh = 0.035–0.044 l/s = 1–1.72, p/e = 12.5–36 | Nu/Nus =1.87 f/fs = 6.93 |
| Layek et al. [48] | Chamfered rib combined with groove | g/p = 0.3–0.6 e/Dh = 0.022–0.04 ϕ = 5°–30° p/e = 4.5–10 | Nu/Nus = 3.24 f/fs = 3.74 |
| Investigators | Roughness | Correlations |
|---|---|---|
| Aharwal et al. [17] (2009) | Inclined rib with gap | |
| Verma and Prasad [60] (2000) | Wire roughness | |
| Ebrahim-Momin et al. [24] (2002) | V-shaped continuous ribs | |
| Istanto et al. [152] (2016) | V-shaped rib | |
| Singh et al. [19] (2011) | V-shape with gap | |
| Maithani and Saini [25] (2016) | V-ribs with symmetrical gap | |
| Deo et al. [26] (2016) | Multi-gap-V-down rib | |
| Saini and Verma [46] (2008) | Dimple shape | |
| Hans et al. [28] (2010) | Continuous multi-V-ribs | |
| Singh et al. [83] (2021) | Multi-V-ribs with uniform gap | |
| Kumar et al. [85] (2013) | Multi-V-ribs with gap | |
| Saini and Saini [30] (2008) | Arc ribs | |
| Sethi et al. [31] (2012) | Dimple shape | |
| Yadav et al. [32] (2013) | Dimple ribs in arc arrangement | |
| Hans et al. [33] (2017) | Broken-arc rib | |
| Ambade et al. [95] (2019) | L-shaped rib | |
| Gill et al. [97] (2021) | Hybrid rib | |
| Pandey et al. [34] (2016) | Multiarc ribs with gap | |
| Singh et al. [153] (2014) | Multiarc ribs | |
| Hasan et al. [103] (2021) | Multiarc dimple shape | |
| Lanjewar et al. [36] (2011) | Continuous W-ribs | |
| Kumar et al. [38] (2009) | Discrete W-ribs | |
| Gawande et al. [39] (2016) | S-shaped rib | |
| Kumar et al. [98] (2016) | S-shaped rib | |
| Baissi et al. [108] (2019) | Delta-shaped tubulators | |
| Kumar and Layek [110] (2020) | Winglet turbulators | |
| Bhushan and Singh [41] (2011) | Protrusions | |
| Patel et al. [118] (2020) | NACA 0040 profile rib | |
| Gabhane and Patil [119] (2017) | Multi-C-shape rib | |
| Kumar and Layek [123] (2019) | Twisted tape | |
| Bhagoria et al. [47] (2002) | Wedge-shaped rib | |
| Promvonge et al. [127] (2021) | Combination of V-shaped rib and delta groove | |
| Alfarawi et al. [137] (2017) | Hybrid rib | |
| Saini and Saini [43] (1997) | Expanded metal mesh | |
| Karmare and Tikekar [44] (2007) | Metal grit | |
| Layek et al. [48] (2007) | Chamfered rib combined with groove |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karmveer; Gupta, N.K.; Alam, T.; Cozzolino, R.; Bella, G. A Descriptive Review to Access the Most Suitable Rib’s Configuration of Roughness for the Maximum Performance of Solar Air Heater. Energies 2022, 15, 2800. https://doi.org/10.3390/en15082800
Karmveer, Gupta NK, Alam T, Cozzolino R, Bella G. A Descriptive Review to Access the Most Suitable Rib’s Configuration of Roughness for the Maximum Performance of Solar Air Heater. Energies. 2022; 15(8):2800. https://doi.org/10.3390/en15082800
Chicago/Turabian StyleKarmveer, Naveen Kumar Gupta, Tabish Alam, Raffaello Cozzolino, and Gino Bella. 2022. "A Descriptive Review to Access the Most Suitable Rib’s Configuration of Roughness for the Maximum Performance of Solar Air Heater" Energies 15, no. 8: 2800. https://doi.org/10.3390/en15082800
APA StyleKarmveer, Gupta, N. K., Alam, T., Cozzolino, R., & Bella, G. (2022). A Descriptive Review to Access the Most Suitable Rib’s Configuration of Roughness for the Maximum Performance of Solar Air Heater. Energies, 15(8), 2800. https://doi.org/10.3390/en15082800










