Energy Evolution and Damage Mechanism of Fractured Sandstone with Different Angles
Abstract
:1. Introduction
2. Test Scheme and Equipment
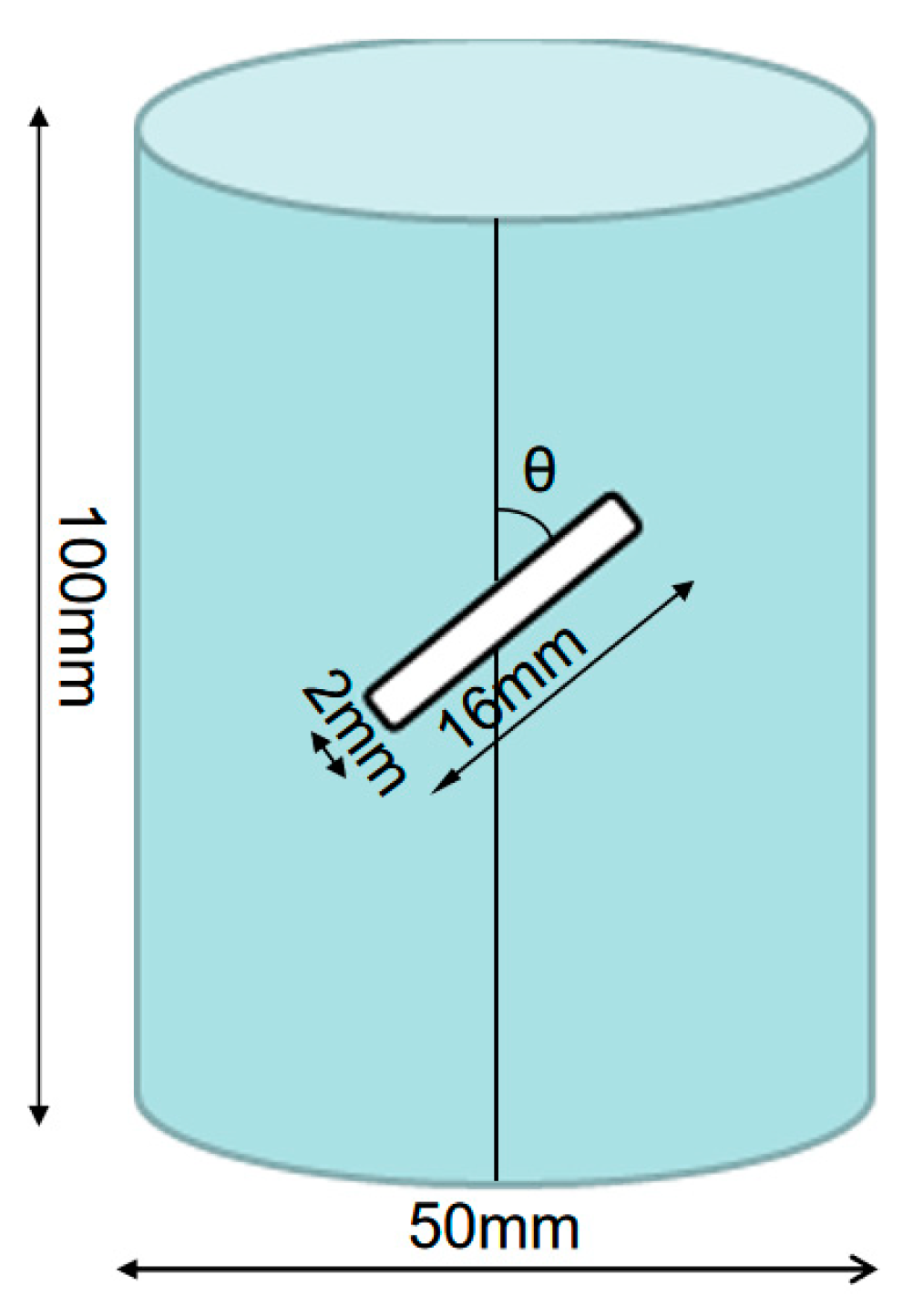
2.1. Test Preparation
2.2. Test Scheme and Results
3. Analysis of Mechanical Properties
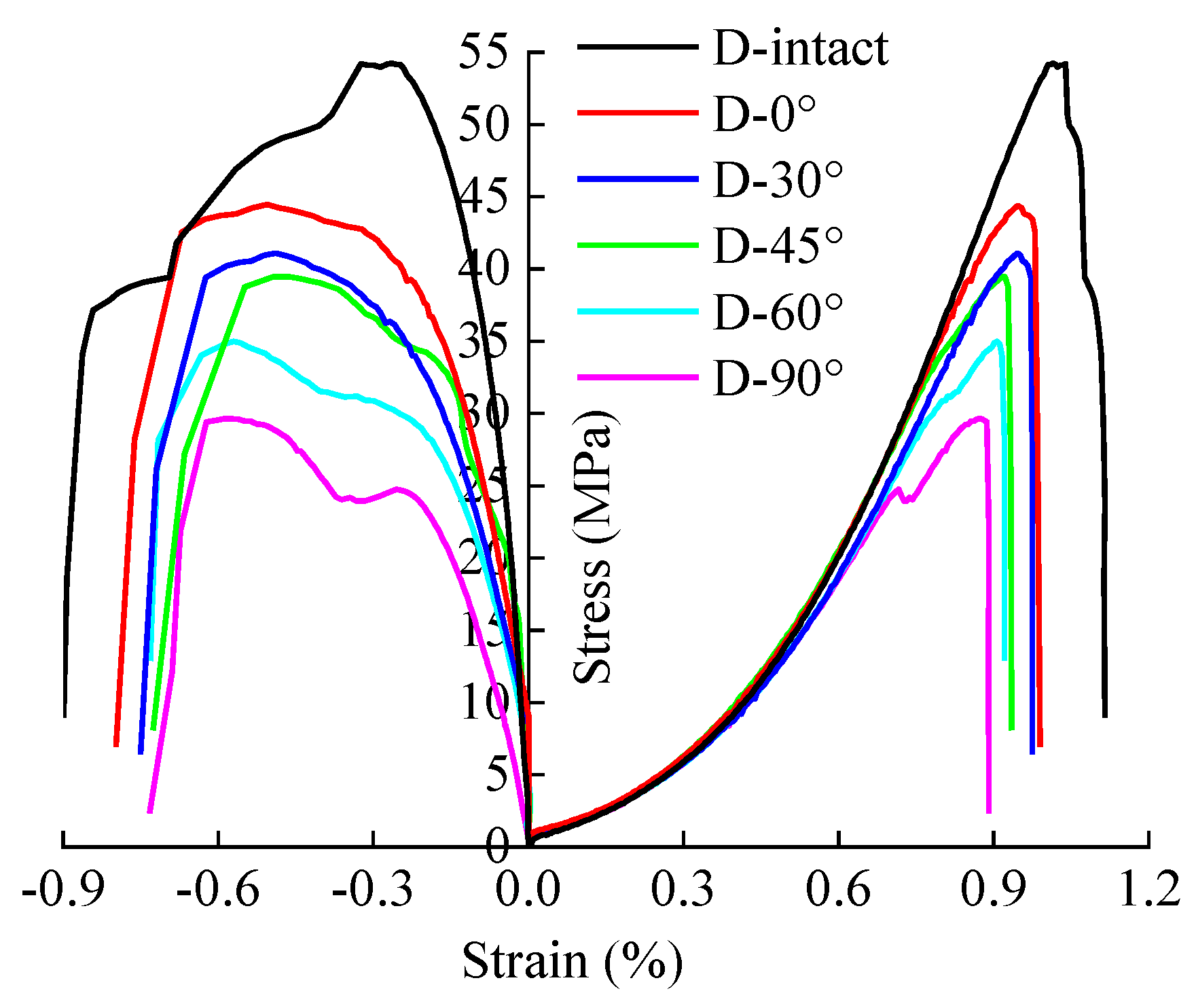
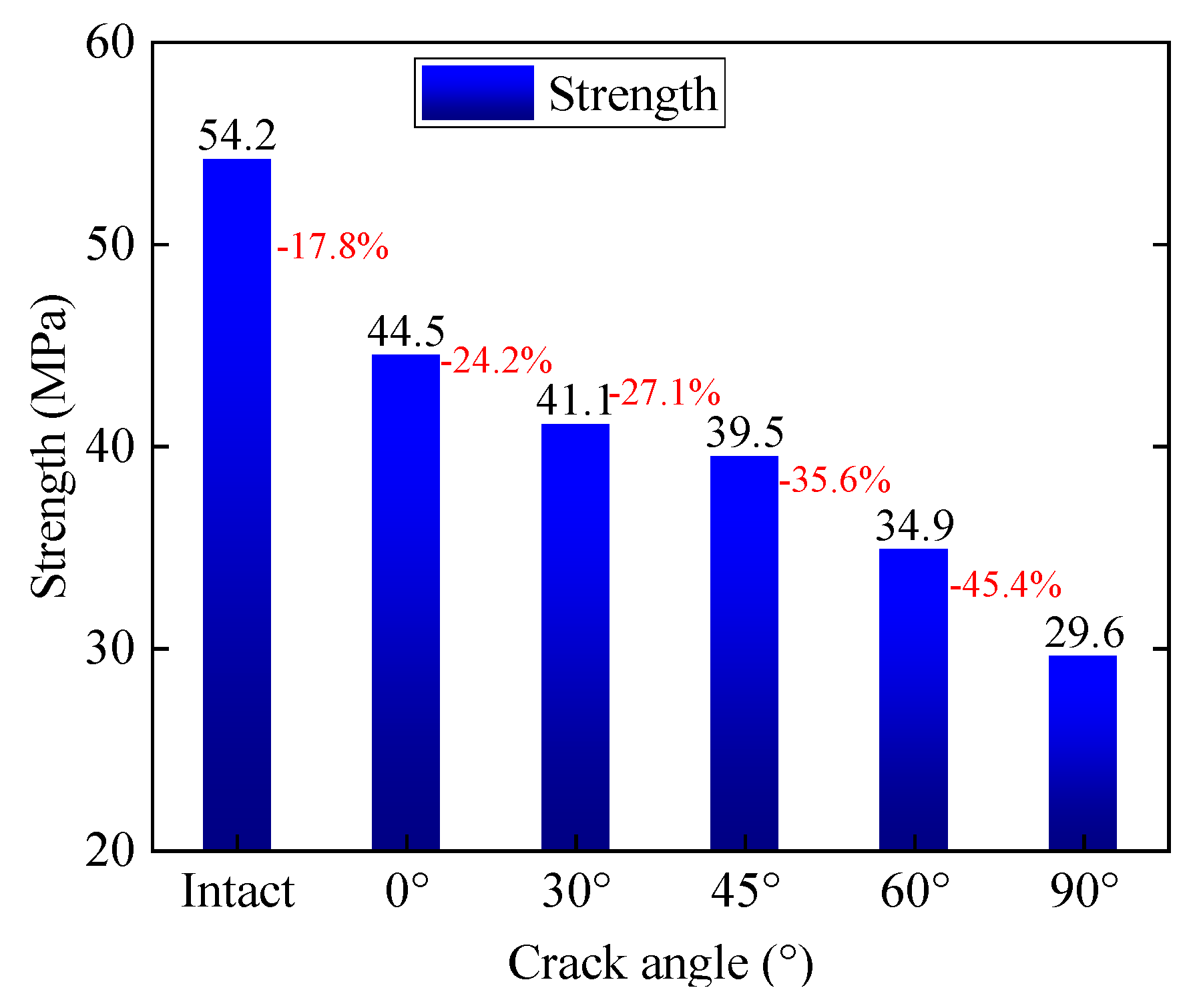
3.1. Influence of Crack Angle on Strength and Deformation Characteristics
3.2. Failure Mode
4. Analysis of Energy Evolution of Fractured Sandstone
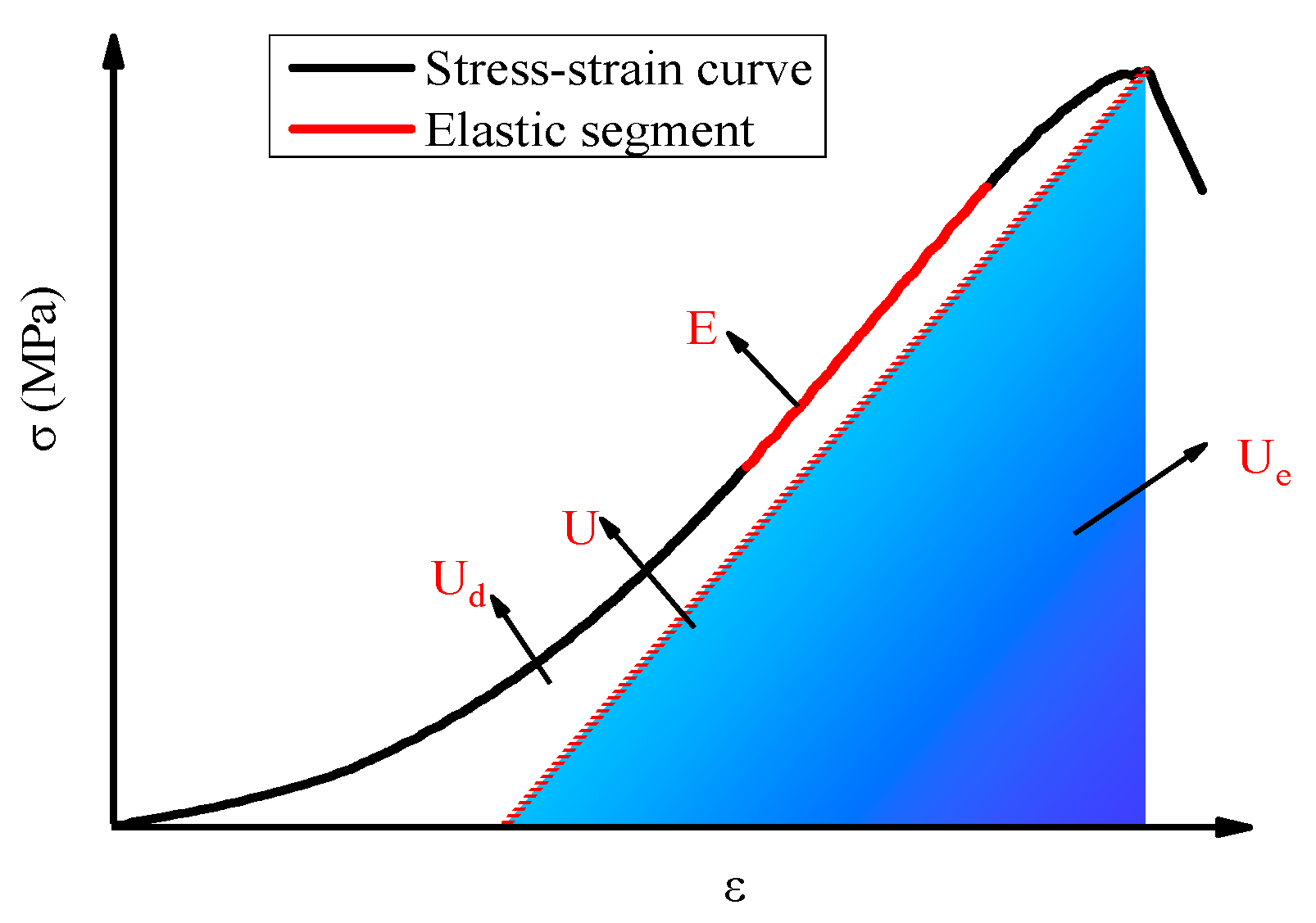
4.1. Energy Conversion Theory under Cyclic Loading
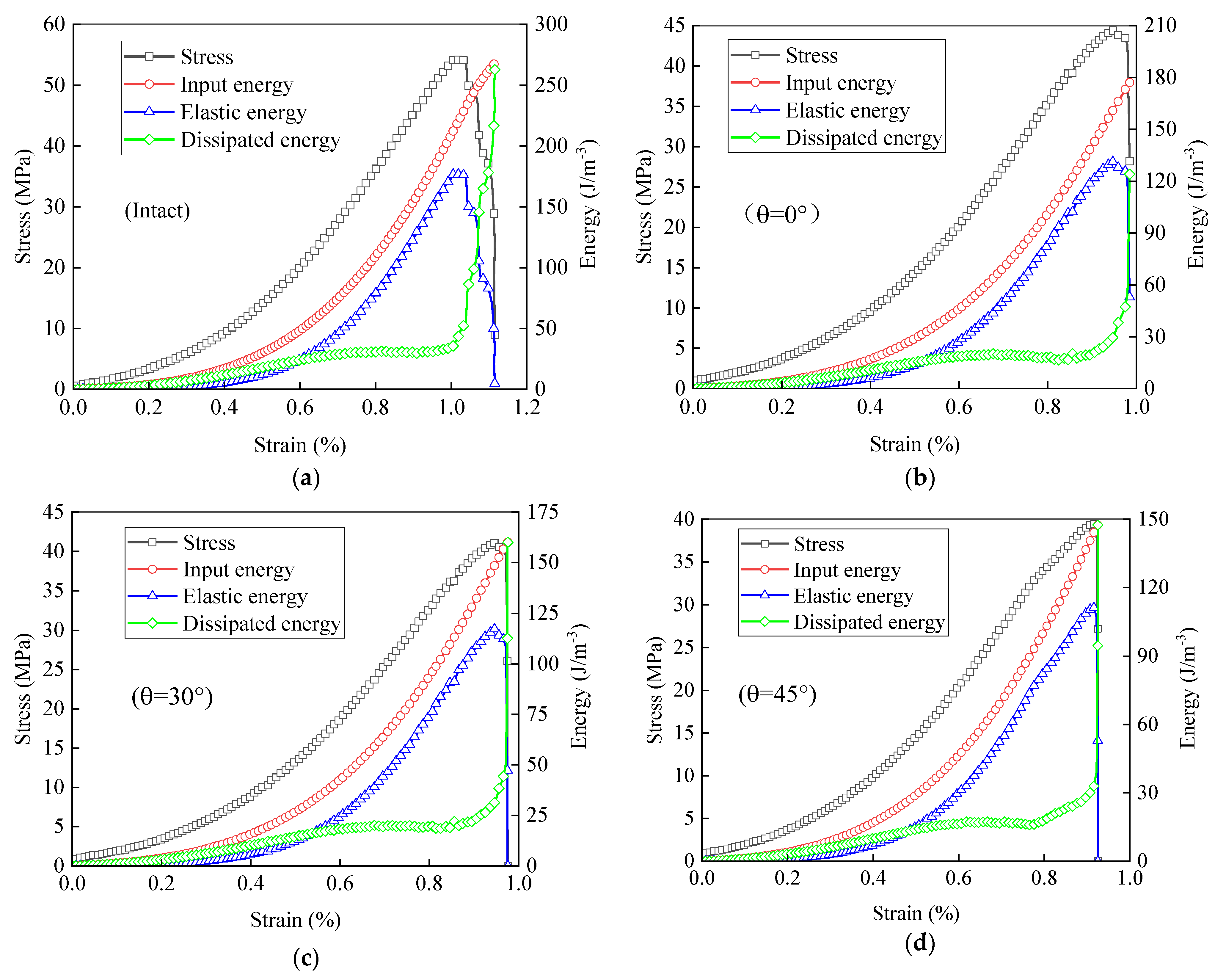
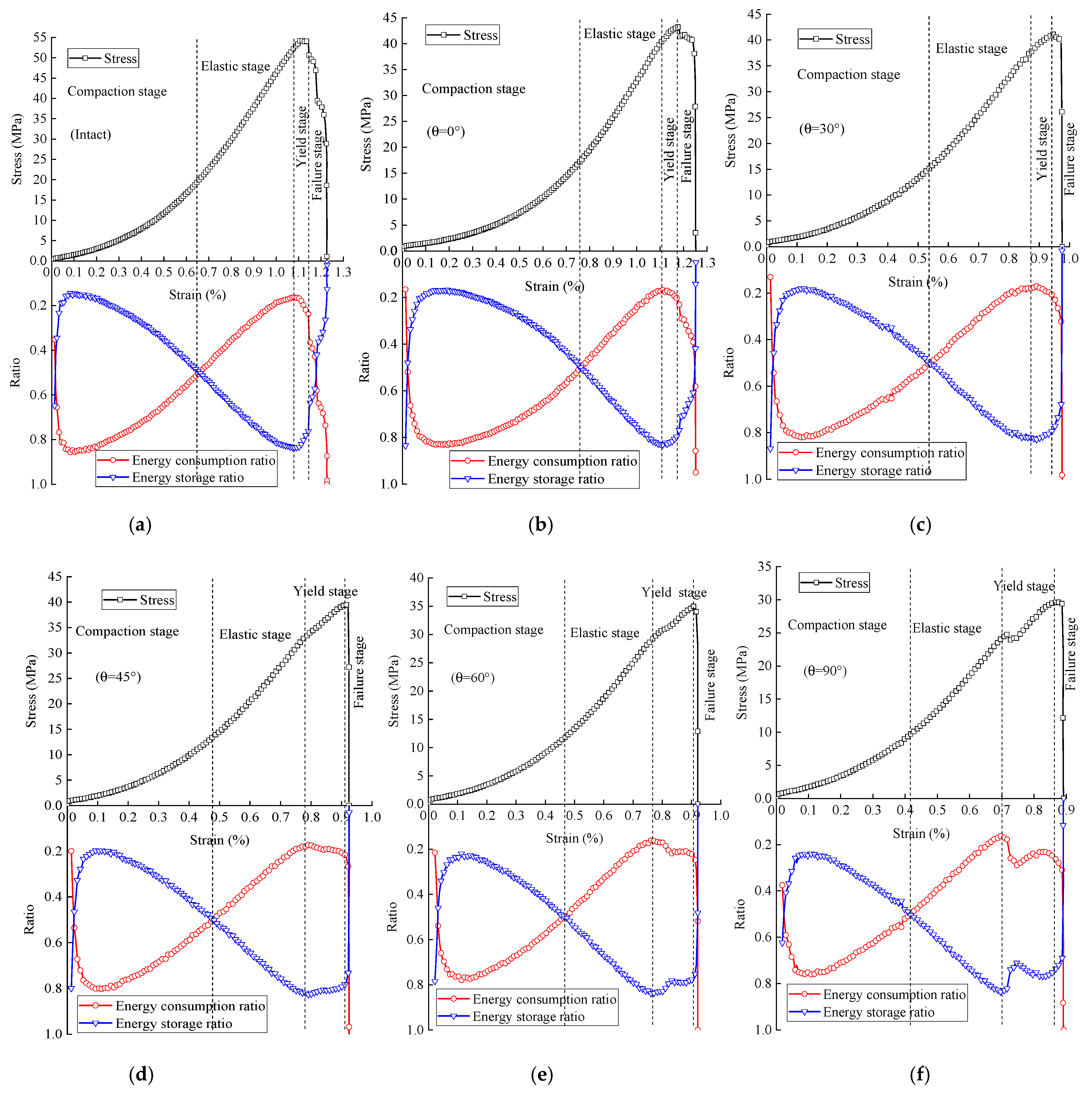
4.2. Energy Evolution Laws and Stage Divisions of Fractured Sandstone
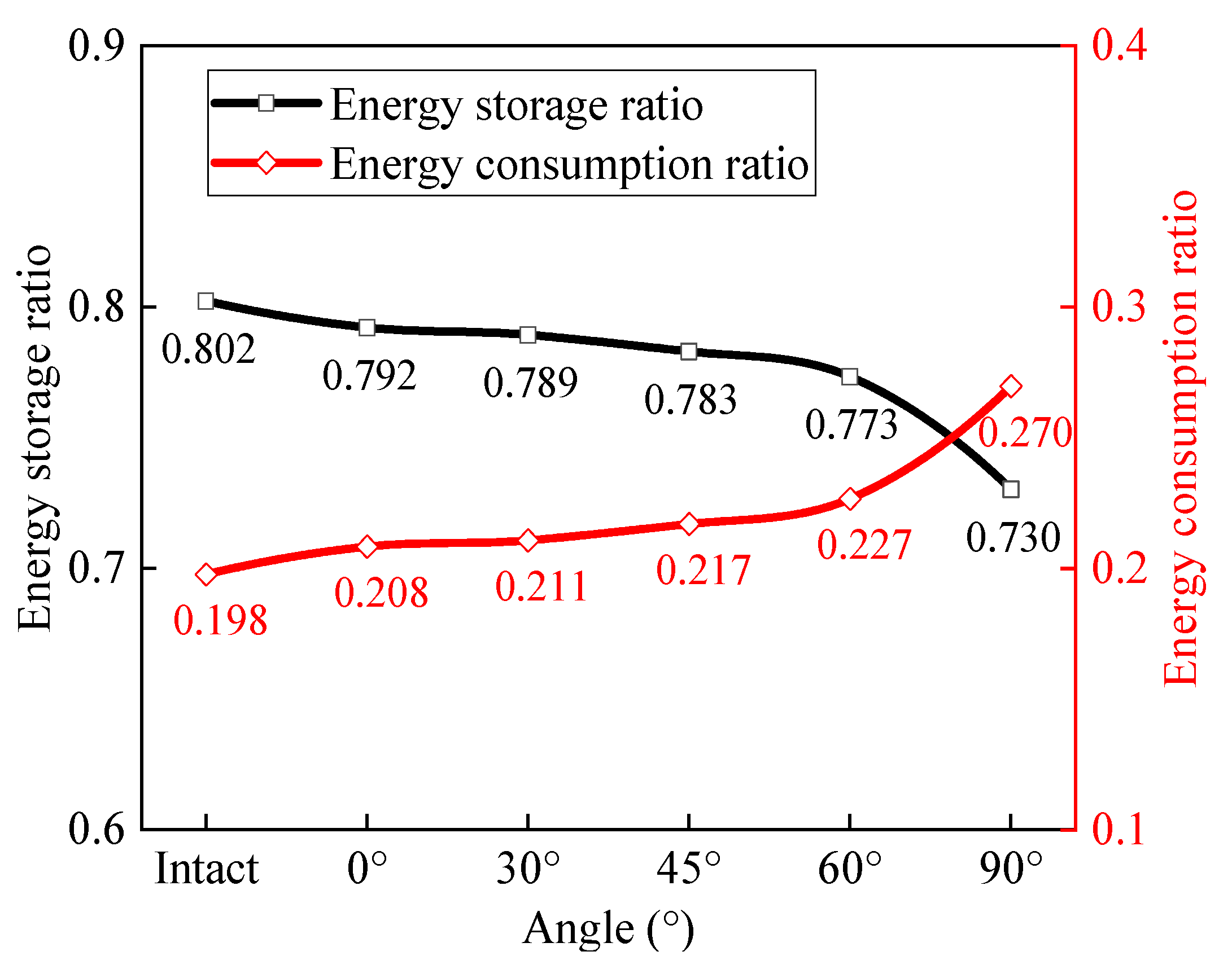
4.3. Influence of Crack Angle on Energy at Peak Point
5. Damage Mechanism Based on Energy Dissipation
5.1. Damage Model Based on Energy Dissipation Theory and Initial Damage
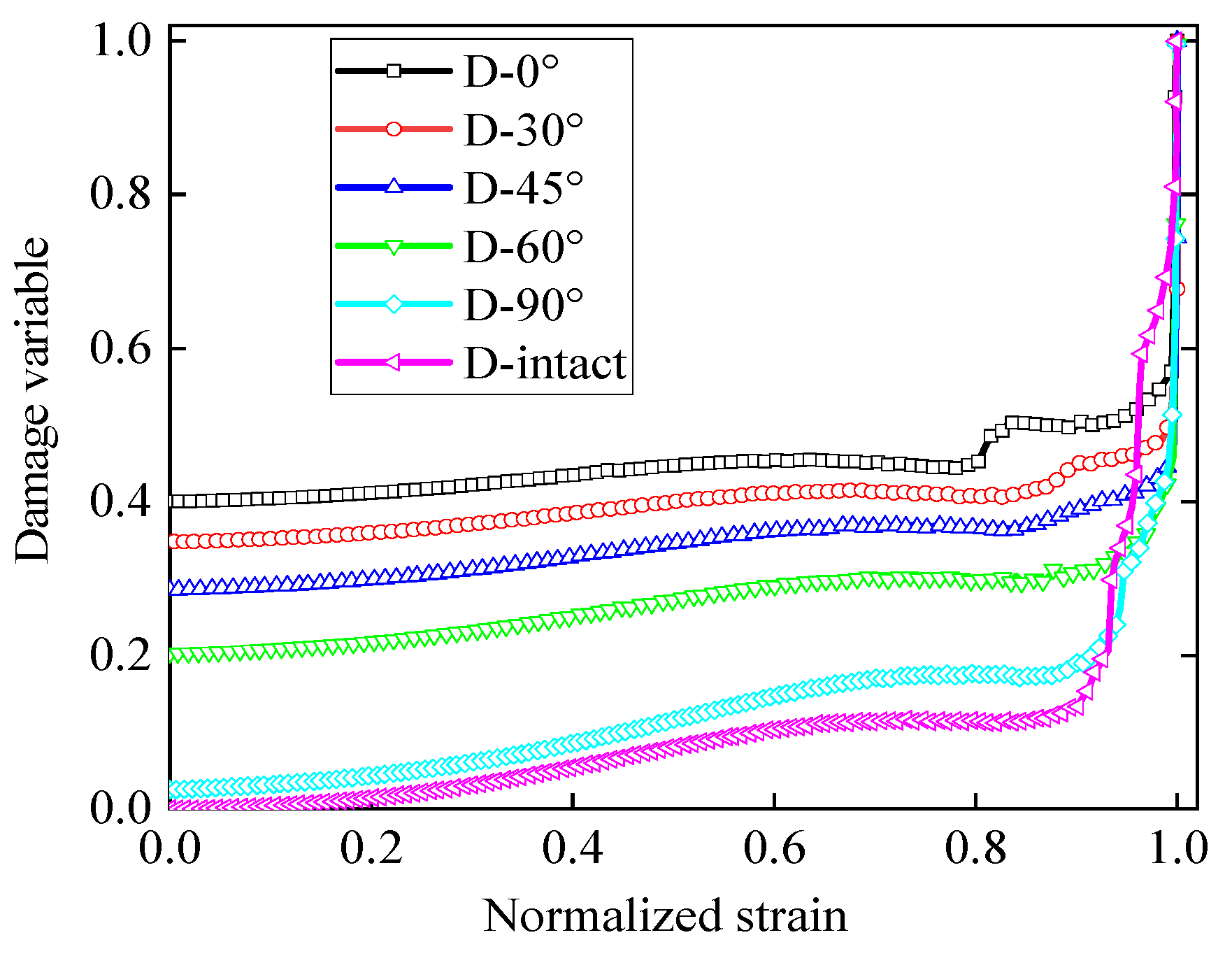
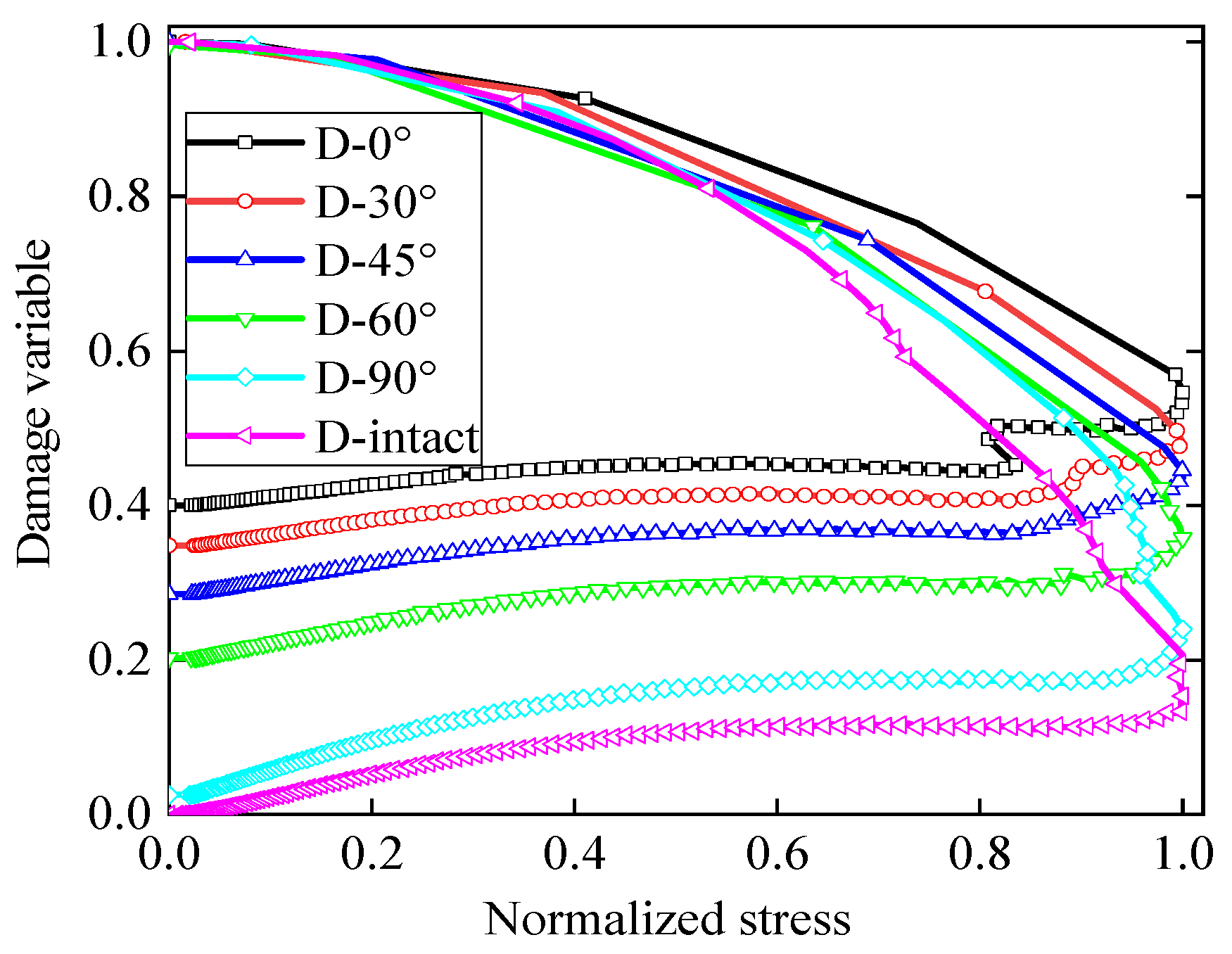
5.2. Damage Evolution and Energy Damage Mechanism
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, Y.H.; Feng, X.T. Study on damage evolution of intact and jointed marble subjected to cyclic true triaxial loading. Eng. Fract. Mech. 2019, 215, 224–234. [Google Scholar] [CrossRef]
- Akdag, S.; Karakus, M.; Nguyen, G.D.; Taheri, A. Strain burst vulnerability criterion based on energy-release rate. Eng. Fract. Mech. 2020, 237, 107232. [Google Scholar] [CrossRef]
- Bi, X.F.; Wang, W.C.; Zhu, G.F.; Liu, X.L. Study of mechanical behavior of salt rock with prefabricated fissures under different confining pressures. Arab. J. Geosci. 2021, 14, 785. [Google Scholar] [CrossRef]
- Wang, Y.; Han, J.Q.; Li, C.H. Acoustic emission and CT investigation on fracture evolution of granite containing two flaws subjected to freeze–thaw and cyclic uniaxial increasing-amplitude loading conditions. Constr. Build. Mater. 2020, 260, 119769. [Google Scholar] [CrossRef]
- Huang, X.W.; Yao, Z.S.; Cai, H.B.; Li, X.W.; Chen, H.Q. Performance evaluation of coaxial borehole heat exchangers considering ground non-uniformity based on analytical solutions. Int. J. Therm. Sci. 2021, 170, 107162. [Google Scholar] [CrossRef]
- Yin, L.; Li, M.; Sun, W.B.; Chen, J.T.; Liu, B.; Wang, Z.Q. Mechanical mechanism and propagation law of fissure-tip cracks of large-size rock specimens with two precut fissure. Shock Vib. 2021, 2021, 8812902. [Google Scholar] [CrossRef]
- Gratchev, L.; Kim, D.H.; Yeung, C.K. Strength of rock-like specimens with pre-existing cracks of different length and width. Rock Mech. Rock Eng. 2016, 49, 4491–4496. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Gong, F.Q.; Luo, S. Effects of pre-existing single crack angle on mechanical behaviors and energy storage characteristics of red sandstone under uniaxial compression. Theor. Appl. Fract. Mec. 2021, 113, 102933. [Google Scholar] [CrossRef]
- Zhong, Z.B.; Deng, R.G.; Zhang, J.; Hu, X.Z. Fracture properties of jointed rock infilled with mortar under uniaxial compression. Eng. Fract. Mech. 2020, 228, 106822. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, M.; Jin, Y.; Zou, D.W. Theoretical analysis and experimental research on the energy dissipation of rock crushing based on fractal theory. J. Nat. Gas Sci. Eng. 2016, 33, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.C.; Yang, T.H.; Xu, T.; Zhang, P.H.; Shi, W.H. Mechanical and energy release characteristics of different water-bearing sandstones under uniaxial compression. Int. J. Damage Mech. 2018, 27, 640–656. [Google Scholar] [CrossRef]
- Gao, D.Y.; Sang, S.X.; Liu, S.Q.; Geng, J.S.; Wang, T.; Sun, T.M. Investigation of the Energy Evolution of Tectonic Coal under Triaxial Cyclic Loading with Different Loading Rates and the Underlying Mechanism. Energies 2021, 14, 8124. [Google Scholar] [CrossRef]
- Li, K.Q.; Li, D.Q.; Liu, Y. Meso-scale investigations on the effective thermal conductivity of multi-phase materials using the finite element method. Int. J. Heat Mass Tran. 2020, 151, 119383. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, G.L.; Lei, R.D.; Wen, X.X.; Liu, B.L.; Sun, F. Study on the energy damage evolution mechanism of single jointed rock mass with different length under uniaxial compression. China J. Highw. Transt. 2021, 34, 24–34. (In Chinese) [Google Scholar]
- Han, Z.Y.; LI, D.Y.; Zhu, Q.Q.; Liu, M.; Li, X.B. Uniaxial compression failure and energy dissipation of marble specimens with flaws at the end surface. Adv. Eng. Sci. 2020, 42, 1588–1596. (In Chinese) [Google Scholar]
- Jiang, J.D.; Xu, J. Investigation of energy mechanism and acoustic emission characteristics of mudstone with different moisture contents. Shock Vib. 2018, 2018, 2129639. [Google Scholar] [CrossRef]
- Meng, Q.B.; Zhang, M.W.; Han, L.J.; Pu, H.; Nie, T.Y. Effects of acoustic emission and energy evolution of rock specimens under the uniaxial cyclic loading and unloading compression. Rock Mech. Rock Eng. 2016, 49, 3873–3886. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, F.Y.; Ahmed, Z.K.; Wang, K.Y.; Wang, Z.H. Mechanical characteristics and damage evolution law of sandstone with prefabricated cracks under cyclic loading. Arab. J. Sci. Eng. 2021, 46, 10641–10653. [Google Scholar] [CrossRef]
- Yin, Z.M.; Liu, X.R.; Yang, Z.P.; Wang, Y.L. Shear behavior of marlstone containing parallel fissure under normal unloading. KSCE J. Civ. Eng. 2021, 25, 1283–1294. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, X.H.; Chen, Y.L.; Cheng, H.M. Quantitative description of infrared radiation characteristics of preflawed sandstone during fracturing process. J. Rock Mech. Geotech. 2021, 13, 131–142. [Google Scholar] [CrossRef]
- Peng, R.; Ju, Y.; Wang, J.G.; Xie, H.; Gao, F.; Mao, L. Energy dissipation and release during coal failure under conventional triaxial compression. Rock Mech. Rock Eng. 2015, 48, 509–526. [Google Scholar] [CrossRef]
- Jiang, C.; Duan, M.; Yin, G.; Wang, J.G.; Lu, T.; Xu, J.; Zhang, D.; Huang, G. Experimental study on seepage properties, AE characteristics and energy dissipation of coal under tiered cyclic loading. Eng. Geol. 2017, 221, 114–123. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, C.J.; Zhao, M.H.; Li, X.B. Statistical damage constitutive model for rocks considering residual strength. Int. J. Geomech. 2017, 17, 04016033. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, N.; Feng, X.W.; Kan, J.G.; Pan, D.J.; Qian, D.Y.; Reccia, E. Experimental investigation of sandstone under cyclic loading: Damage assessment using ultrasonic wave velocities and changes in elastic modulus. Shock Vib. 2018, 2018, 7845143. [Google Scholar] [CrossRef]
- Zhao, G.J.; Chen, C.; Yan, H.; Hao, Y.L. Study on the damage characteristics and damage model of organic rock oil shale under the temperature effect. Arab. J. Geosci. 2021, 14, 722. [Google Scholar] [CrossRef]
- Wang, C.L.; He, B.B.; Hou, X.L.; Li, J.Y.; Liu, L. Stress–energy mechanism for rock failure evolution based on damage mechanics in hard rock. Rock Mech. Rock Eng. 2020, 53, 1021–1037. [Google Scholar] [CrossRef]
- Gong, F.Q.; Zhang, P.L.; Luo, S.; Li, J.C.; Huang, D. Theoretical damage characterisation and damage evolution process of intact rocks based on linear energy dissipation law under uniaxial compression. Int. J. Rock Mech. Min. 2021, 146, 104858. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F.; Dong, L.; Xu, N.W.; Feng, P. Experimental investigation on the fatigue mechanical properties of intermittently jointed rock models under cyclic uniaxial compression with different loading parameters. Rock Mech. Rock Eng. 2018, 51, 47–68. [Google Scholar] [CrossRef]
- Cheng, C.; Li, X. Cyclic experimental studies on damage evolution behaviors of shale dependent on structural orientations and confining pressures. Energies 2018, 11, 160. [Google Scholar] [CrossRef] [Green Version]
- Peng, K.; Wang, Y.Q.; Zou, Q.L.; Liu, Z.P.; Mou, J.H. Effect of crack angles on energy characteristics of sandstones under a complex stress path. Eng. Fract. Mech. 2019, 218, 106577. [Google Scholar] [CrossRef]
- Yin, Q.; Jing, H.W.; Su, H.J. Investigation on mechanical behavior and crack coalescence of sandstone specimens containing fissure-hole combined flaws under uniaxial compression. Geosci. J. 2010, 22, 825–842. [Google Scholar] [CrossRef]
- Tian, J.J.; Xu, D.J.; Liu, T.H. An experimental investigation of the fracturing behaviour of rock-like materials containing two V-shaped parallelogram flaws. Int. J. Min. Sci. Technol. 2020, 30, 777–783. [Google Scholar] [CrossRef]
- Gong, F.Q.; Yan, J.Y.; Luo, S.; Li, X.B. Investigation on the linear energy storage and dissipation laws of rock materials under uniaxial compression. Rock Mech. Rock Eng. 2019, 52, 4237–4255. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Xie, H.P.; Zhang, R.; Zhang, Z.T.; Gao, M.Z.; Jia, Z.Q.; Xie, J. Deformation damage and energy evolution characteristics of coal at different depths. Rock Mech. Rock Eng. 2019, 52, 1491–1503. [Google Scholar] [CrossRef]
- Yang, S.; Wang, J.; Ning, J.G.; Qiu, P.Q. Experimental study on mechanical properties, failure behavior and energy evolution of different coal-rock combined specimens. Appl. Sci. 2019, 9, 4427. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.Q.; He, C.; Wu, D.; Xu, G.W.; Yang, W.B. Fracture evolution and energy mechanism of deep-buried carbonaceous slate. Acta Geotech. 2017, 12, 1243–1260. [Google Scholar] [CrossRef]
- Zhu, Z.N.; Tian, H.; Wang, R.; Jiang, G.S.; Dou, B.; Mei, G. Statistical thermal damage constitutive model of rocks based on Weibull distribution. Arab. J. Geosci. 2021, 14, 495. [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.Y.; Fang, X.Y.; Wang, P.X. Energy dissipation and damage evolution analyses for the dynamic compression failure process of red-sandstone after freeze-thaw cycles. Eng. Geol. 2017, 221, 104–113. [Google Scholar] [CrossRef]
- Zhou, C.T.; Zhang, K.; Wang, H.B.; Xu, Y.X. A plastic strain based statistical damage model for brittle to ductile behaviour of rocks. Geomech. Eng. 2020, 21, 349–356. [Google Scholar]






| Samples | Crack Angle/ ° | Crack Length/ mm | Horizontal Projection Area/ mm2 | Peak Stress/ MPa | Peak Strain | Elastic Modulus/ GPa | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|
| D–0° | 0° | 16 | 786.2 | 24.7 | 0.00875 | 5400 | 0.56 |
| D–30° | 30° | 16 | 683.8 | 28.8 | 0.0088 | 6300 | 0.443 |
| D–45° | 45° | 16 | 560.9 | 35.6 | 0.00803 | 7000 | 0.39 |
| D–60° | 60° | 16 | 398.3 | 36. 9 | 0.00857 | 7200 | 0.33 |
| D–90° | 90° | 16 | 100.0 | 44.3 | 0.01041 | 7300 | 0.252 |
| D–intact | / | 16 | 0 | 47.3 | 0.0097 | 8300 | 0.229 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yao, Z.; Liu, X.; Huang, X. Energy Evolution and Damage Mechanism of Fractured Sandstone with Different Angles. Energies 2022, 15, 1518. https://doi.org/10.3390/en15041518
Li X, Yao Z, Liu X, Huang X. Energy Evolution and Damage Mechanism of Fractured Sandstone with Different Angles. Energies. 2022; 15(4):1518. https://doi.org/10.3390/en15041518
Chicago/Turabian StyleLi, Xinwei, Zhishu Yao, Xiaohu Liu, and Xianwen Huang. 2022. "Energy Evolution and Damage Mechanism of Fractured Sandstone with Different Angles" Energies 15, no. 4: 1518. https://doi.org/10.3390/en15041518
APA StyleLi, X., Yao, Z., Liu, X., & Huang, X. (2022). Energy Evolution and Damage Mechanism of Fractured Sandstone with Different Angles. Energies, 15(4), 1518. https://doi.org/10.3390/en15041518







