Structural Architecture and Permeability Patterns of Crystalline Reservoir Rocks in the Northern Upper Rhine Graben: Insights from Surface Analogues of the Odenwald
Abstract
1. Introduction
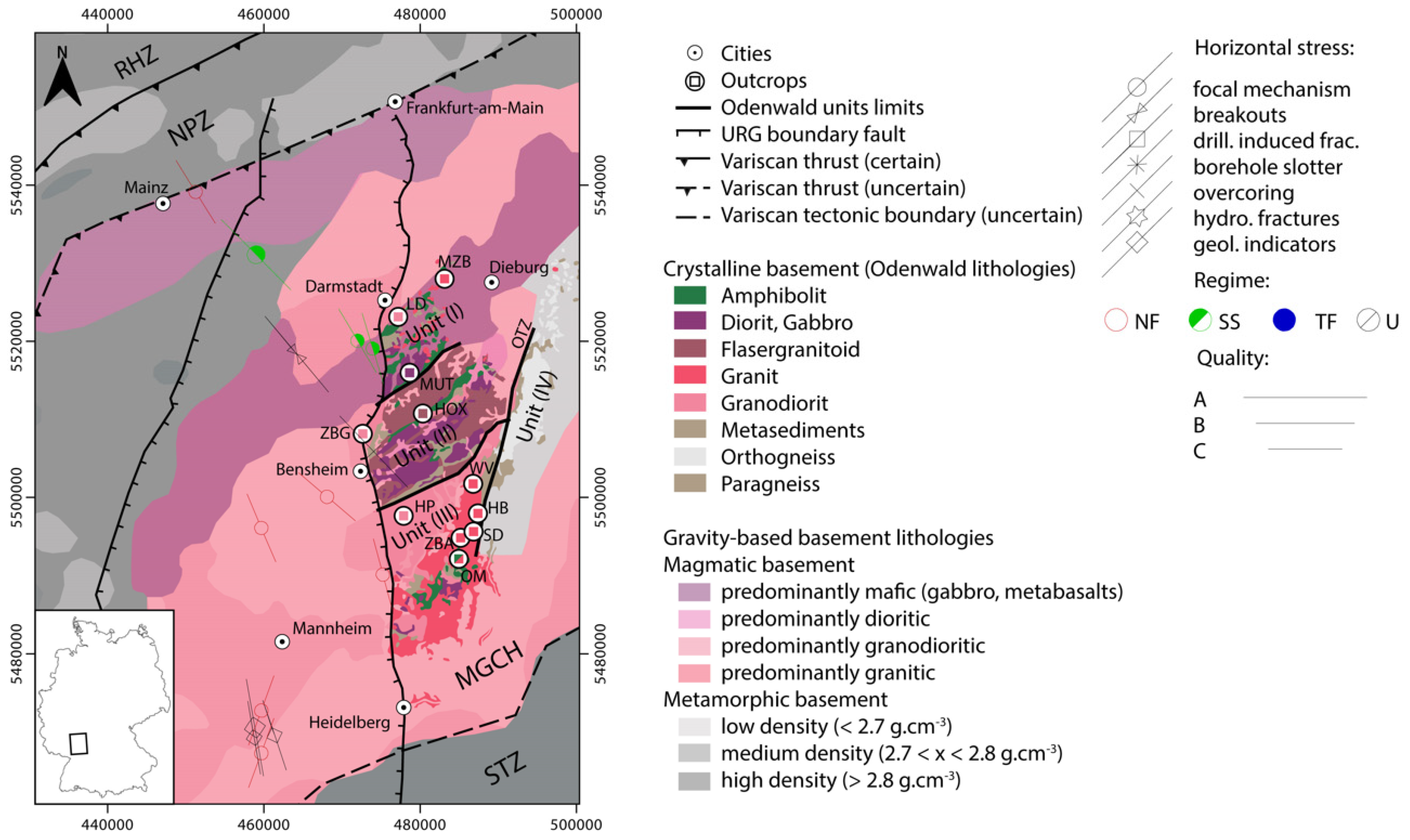
2. Geological Context
3. Materials and Methods
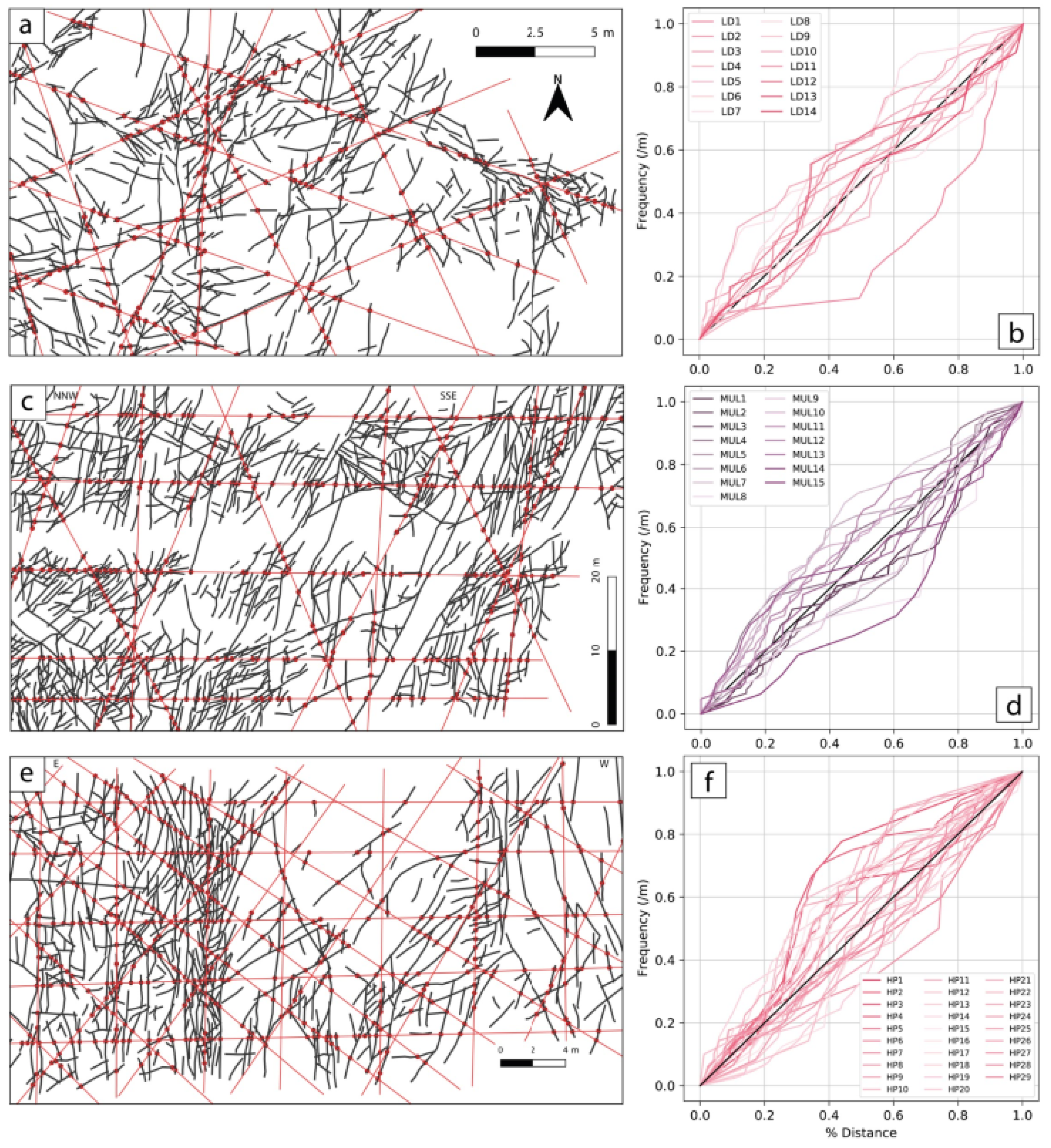
3.1. Structural Data Acquisition and Treatment

3.2. DFN Properties Modelling from the Near-Surface Dataset
4. Results
4.1. Structural Pattern of the Northern URG
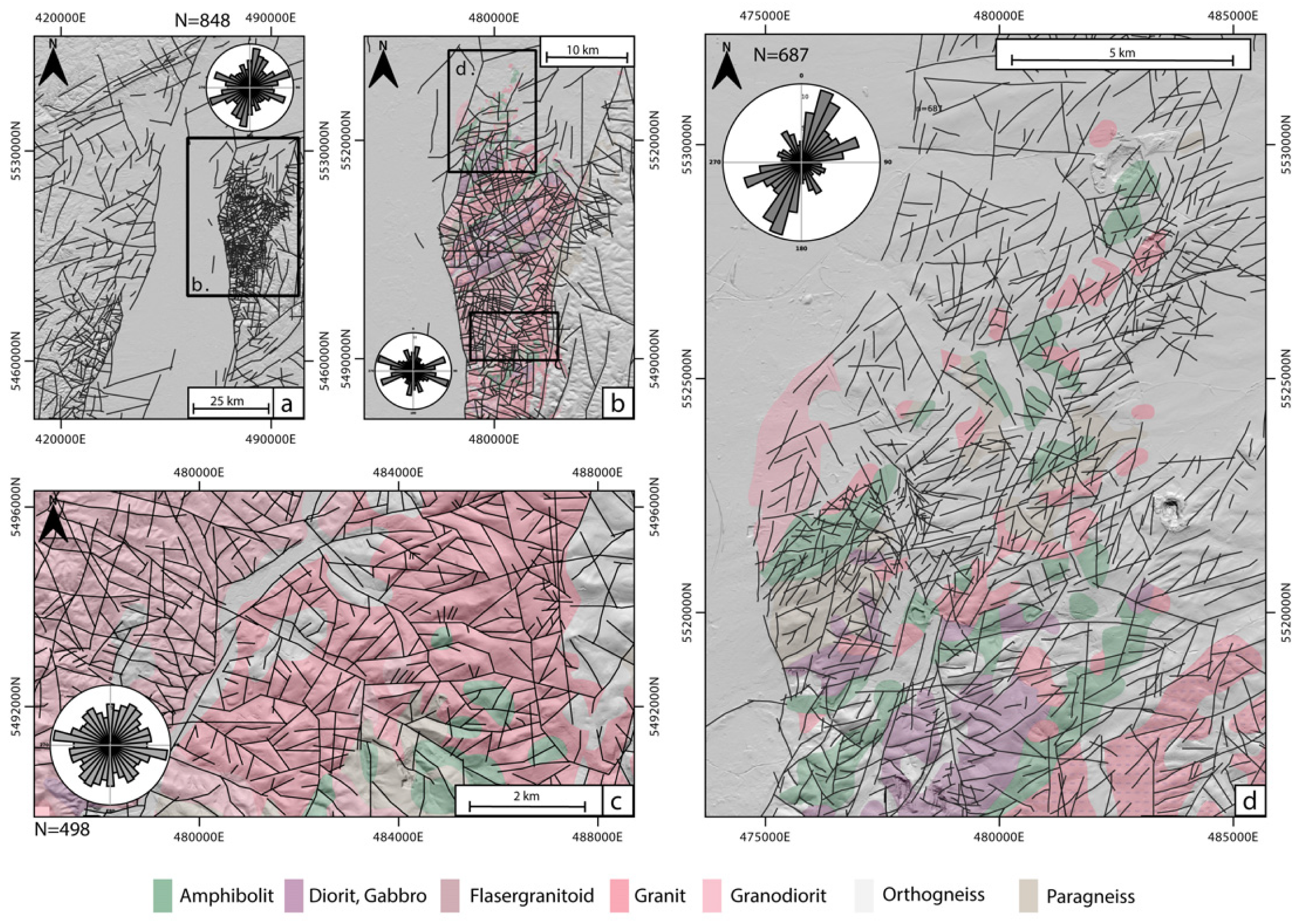
4.2. Fracture Network Patterns and Their Structural Context
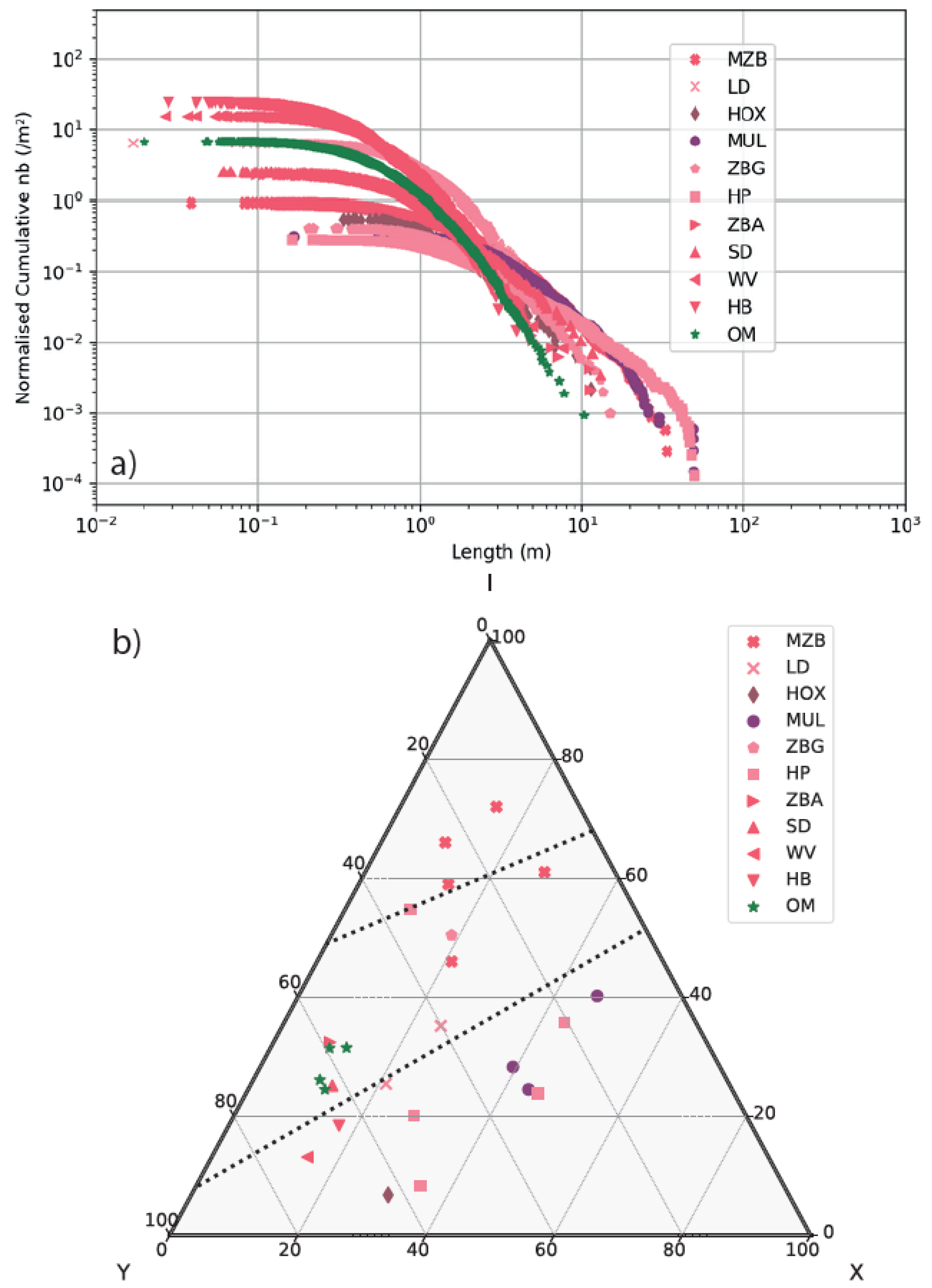
4.3. Geometrical Features of the Fracture Network
4.4. Semi-Artificial Discrete Fracture Network Models
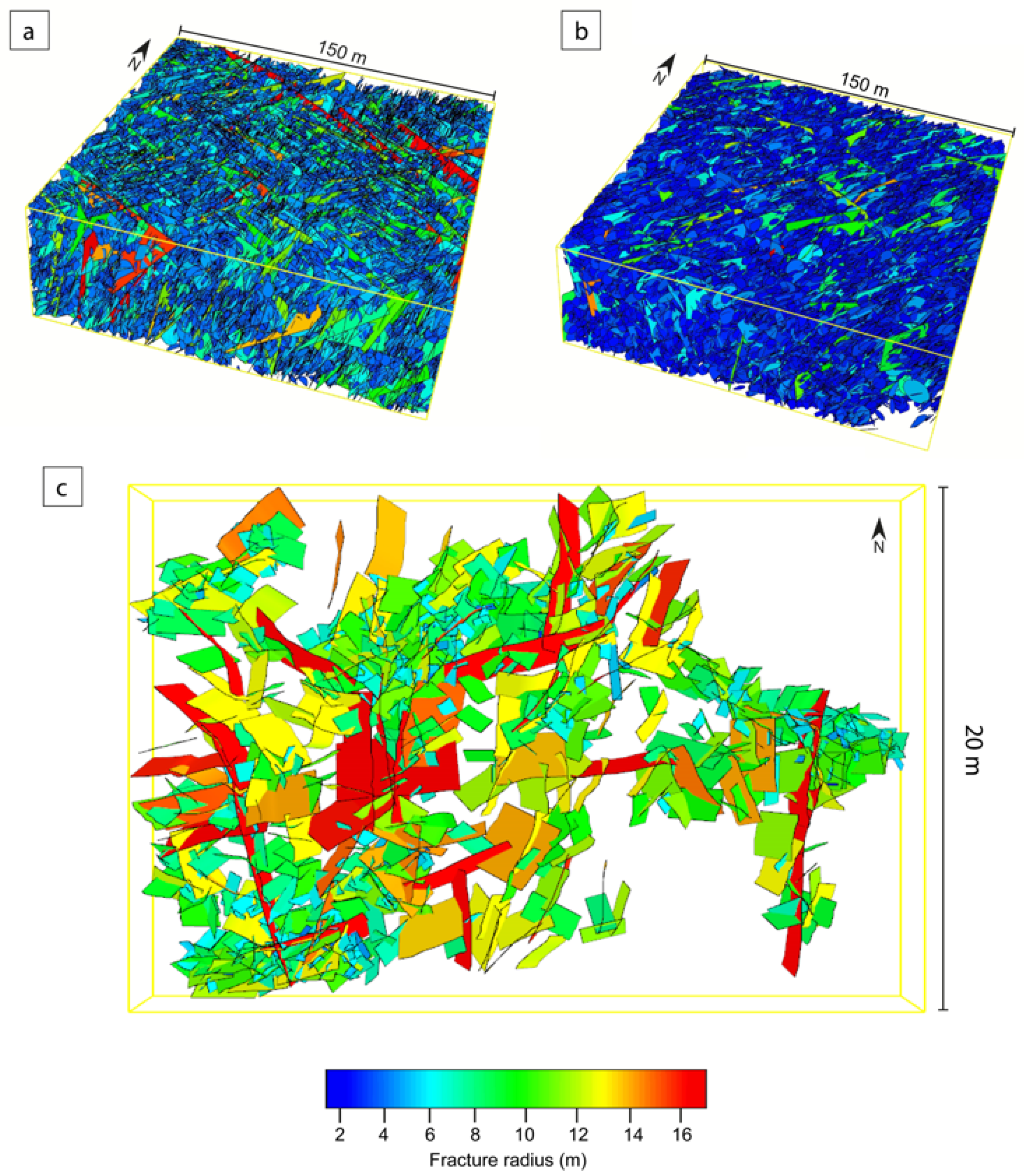
4.4.1. Aperture Distributions
4.4.2. Permeability Field
5. Discussion
5.1. Near-Surface Architecture of Crystalline Reservoirs
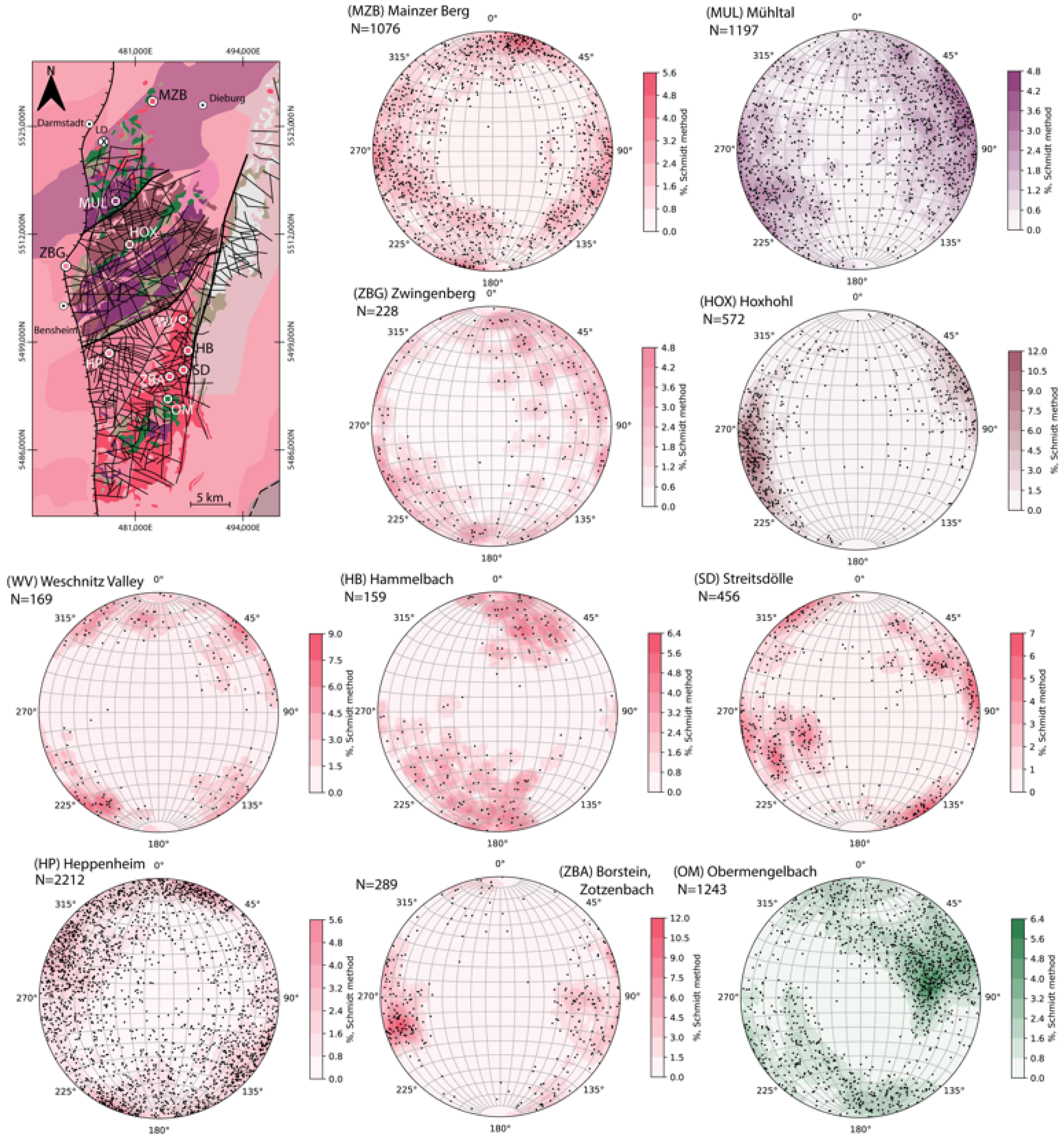
5.1.1. Fracture Network Topology and Clustering
5.1.2. Multi-Scale Behaviour from Regional Scale to Outcrop Scale
5.2. Estimation of Flow Properties in Deep-Seated Reservoirs
5.3. Structural Uncertainties Related to Sub-Surface Transfer
5.4. Applicability of the Conceptual Model of Crystalline Faulted Rocks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baujard, C.; Genter, A.; Dalmais, E.; Maurer, V.; Hehn, R.; Rosillette, R.; Vidal, J.; Schmittbuhl, J. Hydrothermal Characterization of Wells GRT-1 and GRT-2 in Rittershoffen, France: Implications on the Understanding of Natural Flow Systems in the Rhine Graben. Geothermics 2017, 65, 255–268. [Google Scholar] [CrossRef]
- Bertrand, L.; Géraud, Y.; Diraison, M. Petrophysical Properties in Faulted Basement Rocks: Insights from Outcropping Analogues on the West European Rift Shoulders. Geothermics 2021, 95, 102144. [Google Scholar] [CrossRef]
- Frey, M.; Weinert, S.; Bär, K.; van der Vaart, J.; Dezayes, C.; Calcagno, P.; Sass, I. Integrated 3D Geological Modelling of the Northern Upper Rhine Graben by Joint Inversion of Gravimetry and Magnetic Data. Tectonophysics 2021, 813, 228927. [Google Scholar] [CrossRef]
- Freymark, J.; Sippel, J.; Scheck-Wenderoth, M.; Bär, K.; Stiller, M.; Kracht, M.; Fritsche, J.-G. Heterogeneous Crystalline Crust Controls the Shallow Thermal Field—A Case Study of Hessen (Germany). Energy Procedia 2015, 76, 331–340. [Google Scholar] [CrossRef]
- Freymark, J.; Sippel, J.; Scheck-Wenderoth, M.; Bär, K.; Stiller, M.; Fritsche, J.-G.; Kracht, M. The Deep Thermal Field of the Upper Rhine Graben. Tectonophysics 2017, 694, 114–129. [Google Scholar] [CrossRef]
- Baillieux, P.; Schill, E.; Edel, J.-B.; Mauri, G. Localization of Temperature Anomalies in the Upper Rhine Graben: Insights from Geophysics and Neotectonic Activity. Int. Geol. Rev. 2013, 55, 1744–1762. [Google Scholar] [CrossRef]
- Baillieux, P.; Schill, E.; Abdelfettah, Y.; Dezayes, C. Possible Natural Fluid Pathways from Gravity Pseudo-Tomography in the Geothermal Fields of Northern Alsace (Upper Rhine Graben). Geotherm. Energy 2014, 2, 16. [Google Scholar] [CrossRef]
- Bossennec, C.; Géraud, Y.; Moretti, I.; Mattioni, L.; Stemmelen, D. Pore Network Properties of Sandstones in a Fault Damage Zone. J. Struct. Geol. 2018, 110, 24–44. [Google Scholar] [CrossRef]
- Glaas, C.; Vidal, J.; Genter, A. Structural Characterization of Naturally Fractured Geothermal Reservoirs in the Central Upper Rhine Graben. J. Struct. Geol. 2021, 148, 104370. [Google Scholar] [CrossRef]
- Vidal, J.; Genter, A. Overview of Naturally Permeable Fractured Reservoirs in the Central and Southern Upper Rhine Graben: Insights from Geothermal Wells. Geothermics 2018, 74, 57–73. [Google Scholar] [CrossRef]
- Walter, B.F.; Burisch, M.; Fusswinkel, T.; Marks, M.A.W.; Steele-MacInnis, M.; Wälle, M.; Apukhtina, O.B.; Markl, G. Multi-Reservoir Fluid Mixing Processes in Rift-Related Hydrothermal Veins, Schwarzwald, SW-Germany. J. Geochem. Explor. 2018, 186, 158–186. [Google Scholar] [CrossRef]
- Bertrand, L.; Géraud, Y.; Le Garzic, E.; Place, J.; Diraison, M.; Walter, B.; Haffen, S. A Multiscale Analysis of a Fracture Pattern in Granite: A Case Study of the Tamariu Granite, Catalunya, Spain. J. Struct. Geol. 2015, 78, 52–66. [Google Scholar] [CrossRef]
- Bertrand, L.; Jusseaume, J.; Géraud, Y.; Diraison, M.; Damy, P.-C.; Navelot, V.; Haffen, S. Structural Heritage, Reactivation and Distribution of Fault and Fracture Network in a Rifting Context: Case Study of the Western Shoulder of the Upper Rhine Graben. J. Struct. Geol. 2018, 108, 243–255. [Google Scholar] [CrossRef]
- Place, J.; Géraud, Y.; Diraison, M.; Herquel, G.; Edel, J.-B.; Bano, M.; Le Garzic, E.; Walter, B. Structural Control of Weathering Processes within Exhumed Granitoids: Compartmentalisation of Geophysical Properties by Faults and Fractures. J. Struct. Geol. 2016, 84, 102–119. [Google Scholar] [CrossRef]
- Bossennec, C.; Frey, M.; Seib, L.; Bär, K.; Sass, I. Multiscale Characterisation of Fracture Patterns of a Crystalline Reservoir Analogue. Geosciences 2021, 11, 371. [Google Scholar] [CrossRef]
- Ceccato, A.; Viola, G.; Antonellini, M.; Tartaglia, G.; Ryan, E.J. Constraints upon Fault Zone Properties by Combined Structural Analysis of Virtual Outcrop Models and Discrete Fracture Network Modelling. J. Struct. Geol. 2021, 152, 104444. [Google Scholar] [CrossRef]
- Weinert, S.; Bär, K.; Sass, I. Database of Petrophysical Properties of the Mid-German Crystalline Rise. Earth Syst. Sci. Data 2021, 13, 1441–1459. [Google Scholar] [CrossRef]
- Bär, K.; Reinsch, T.; Bott, J. The PetroPhysical Property Database (P3)—A Global Compilation of Lab-Measured Rock Properties. Earth Syst. Sci. Data 2020, 12, 2485–2515. [Google Scholar] [CrossRef]
- Edel, J.-B.; Schulmann, K. Geophysical Constraints and Model of the “Saxothuringian and Rhenohercynian Subductions—Magmatic Arc System” in NE France and SW Germany. Bull. Soc. Géol. Fr. 2009, 180, 545–558. [Google Scholar] [CrossRef]
- Edel, J.-B.; Schulmann, K.; Rotstein, Y. The Variscan Tectonic Inheritance of the Upper Rhine Graben: Evidence of Reactivations in the Lias, Late Eocene–Oligocene up to the Recent. Int. J. Earth Sci. (Geol. Rundsch.) 2007, 96, 305–325. [Google Scholar] [CrossRef]
- McCaffrey, K.J.W.; Holdsworth, R.E.; Pless, J.; Franklin, B.S.G.; Hardman, K. Basement Reservoir Plumbing: Fracture Aperture, Length and Topology Analysis of the Lewisian Complex, NW Scotland. J. Geol. Soc. 2020, 177, 1281–1293. [Google Scholar] [CrossRef]
- Trice, R. Basement Exploration, West of Shetlands: Progress in Opening a New Play on the UKCS. Geol. Soc. Lond. Spec. Publ. 2014, 397, 81–105. [Google Scholar] [CrossRef]
- Bonter, D.A.; Trice, R. An Integrated Approach for Fractured Basement Characterization: The Lancaster Field, a Case Study in the UK. Pet. Geosci. 2019, 25, 400–414. [Google Scholar] [CrossRef]
- Frey, M.; Bossennec, C.; Seib, L.; Bär, K.; Sass, I. Interdisciplinary Fracture Network Characterization in the Crystalline Basement: A Case Study from the Southern Odenwald, SW Germany. Solid Earth Discuss. 2021, 1–35. [Google Scholar] [CrossRef]
- Li, X.; Li, D.; Xu, Y.; Feng, X. A DFN Based 3D Numerical Approach for Modeling Coupled Groundwater Flow and Solute Transport in Fractured Rock Mass. Int. J. Heat Mass Transf. 2020, 149, 119179. [Google Scholar] [CrossRef]
- Lei, Q.; Latham, J.-P.; Tsang, C.-F. The Use of Discrete Fracture Networks for Modelling Coupled Geomechanical and Hydrological Behaviour of Fractured Rocks. Comput. Geotech. 2017, 85, 151–176. [Google Scholar] [CrossRef]
- Le Goc, R.; Darcel, C.; Davy, P. Advanced DFN Models from Multi-Support Data for Underground Facilities. Procedia Eng. 2017, 191, 1015–1022. [Google Scholar] [CrossRef]
- Bardossy, G.; Fodor, J. Evaluation of Uncertainties and Risks. In Geology: New Mathematical Approaches for Their Handling; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-540-20622-4. [Google Scholar]
- Mann, C.J. Uncertainty in Geology. In Computers in Geology—25 Years of Progress; Oxford University Press, Inc.: New York, NY, USA, 1993; pp. 241–254. ISBN 978-0-19-508593-8. [Google Scholar]
- Wilson, C.E.; Aydin, A.; Karimi-Fard, M.; Durlofsky, L.J.; Amir, S.; Brodsky, E.E.; Kreylos, O.; Kellogg, L.H. From Outcrop to Flow Simulation: Constructing Discrete Fracture Models from a LIDAR Survey. AAPG Bull. 2011, 95, 1883–1905. [Google Scholar] [CrossRef]
- Voeckler, H.; Allen, D.M. Estimating Regional-Scale Fractured Bedrock Hydraulic Conductivity Using Discrete Fracture Network (DFN) Modeling. Hydrogeol. J. 2012, 20, 1081–1100. [Google Scholar] [CrossRef]
- Bisdom, K.; Nick, H.M.; Bertotti, G. An Integrated Workflow for Stress and Flow Modelling Using Outcrop-Derived Discrete Fracture Networks. Comput. Geosci. 2017, 103, 21–35. [Google Scholar] [CrossRef]
- Bisdom, K.; Gauthier, B.D.M.; Bertotti, G.; Hardebol, N.J. Calibrating Discrete Fracture-Network Models with a Carbonate Three-Dimensional Outcrop Fracture Network: Implications for Naturally Fractured Reservoir Modeling. Bulletin 2014, 98, 1351–1376. [Google Scholar] [CrossRef]
- Min, K.-B.; Rutqvist, J.; Tsang, C.-F.; Jing, L. Stress-Dependent Permeability of Fractured Rock Masses: A Numerical Study. Int. J. Rock Mech. Min. Sci. 2004, 41, 1191–1210. [Google Scholar] [CrossRef]
- French, M.E.; Chester, F.M.; Chester, J.S.; Wilson, J.E. Stress-Dependent Transport Properties of Fractured Arkosic Sandstone. Geofluids 2016, 16, 533–551. [Google Scholar] [CrossRef]
- Lepillier, B.; Bruna, P.-O.; Bruhn, D.; Bastesen, E.; Daniilidis, A.; Garcia, Ó.; Torabi, A.; Wheeler, W. From Outcrop Scanlines to Discrete Fracture Networks, an Integrative Workflow. J. Struct. Geol. 2020, 133, 103992. [Google Scholar] [CrossRef]
- Welsch, B.; Rühaak, W.; Schulte, D.O.; Bär, K.; Sass, I. Characteristics of Medium Deep Borehole Thermal Energy Storage. Int. J. Energy Res. 2016, 40, 1855–1868. [Google Scholar] [CrossRef]
- Schulte, D.O.; Welsch, B.; Boockmeyer, A.; Rühaak, W.; Bär, K.; Bauer, S.; Sass, I. Modeling Insulated Borehole Heat Exchangers. Environ. Earth Sci. 2016, 75, 910. [Google Scholar] [CrossRef]
- Formhals, J.; Hemmatabady, H.; Welsch, B.; Schulte, D.; Sass, I. A Modelica Toolbox for the Simulation of Borehole Thermal Energy Storage Systems. Energies 2020, 13, 2327. [Google Scholar] [CrossRef]
- Dèzes, P.; Schmid, S.M.; Ziegler, P.A. Evolution of the European Cenozoic Rift System: Interaction of the Alpine and Pyrenean Orogens with Their Foreland Lithosphere. Tectonophysics 2004, 389, 1–33. [Google Scholar] [CrossRef]
- Bourgeois, O.; Ford, M.; Diraison, M.; de Veslud, C.L.C.; Gerbault, M.; Pik, R.; Ruby, N.; Bonnet, S. Separation of Rifting and Lithospheric Folding Signatures in the NW-Alpine Foreland. Int. J. Earth Sci. (Geol. Rundsch.) 2007, 96, 1003–1031. [Google Scholar] [CrossRef]
- Michon, L.; Merle, O. Mode of Lithospheric Extension: Conceptual Models from Analogue Modeling. Tectonics 2003, 22, 1028. [Google Scholar] [CrossRef]
- Michon, L.; Merle, O. Discussion on “Evolution of the European Cenozoic Rift System: Interaction of the Alpine and Pyrenean Orogens with Their Foreland Lithosphere” by P. Dèzes, S.M. Schmid and P.A. Ziegler, Tectonophysics 389 (2004) 1–33. Tectonophysics 2005, 401, 251–256. [Google Scholar] [CrossRef]
- Ziegler, P.A.; Schumacher, M.E.; Dèzes, P.; Van Wees, J.-D.; Cloetingh, S. Post-Variscan Evolution of the Lithosphere in the Rhine Graben Area: Constraints from Subsidence Modelling. Geol. Soc. Lond. Spec. Publ. 2004, 223, 289–317. [Google Scholar] [CrossRef]
- Schumacher, M.E. Upper Rhine Graben: Role of Preexisting Structures during Rift Evolution. Tectonics 2002, 21, 6-1–6-17. [Google Scholar] [CrossRef]
- Ustaszewski, K.; Schumacher, M.E.; Schmid, S.M. Simultaneous Normal Faulting and Extensional Flexuring during Rifting: An Example from the Southernmost Upper Rhine Graben. Int. J. Earth Sci. (Geol. Rundsch.) 2005, 94, 680–696. [Google Scholar] [CrossRef]
- Korsch, R.J.; Schäfer, A. Geological Interpretation of DEKORP Deep Seismic Reflection Profiles 1C and 9N across the Variscan Saar-Nahe Basin Southwest Germany. Tectonophysics 1991, 191, 127–146. [Google Scholar] [CrossRef]
- Krohe, A. Structural Evolution of Intermediate-Crustal Rocks in a Strike-Slip and Extensional Setting (Variscan Odenwald, SW Germany): Differential Upward Transport of Metamorphic Complexes and Changing Deformation Mechanisms. Tectonophysics 1992, 205, 357–386. [Google Scholar] [CrossRef]
- Murawski, H.; Albers, H.J.; Bender, P.; Berners, H.-P.; Dürr, S.; Huckriede, R.; Kauffmann, G.; Kowalczyk, G.; Meiburg, P.; Müller, R.; et al. Regional Tectonic Setting and Geological Structure of the Rhenish Massif. In Plateau Uplift; Fuchs, K., von Gehlen, K., Mälzer, H., Murawski, H., Semmel, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1983; pp. 9–38. ISBN 978-3-642-69221-5. [Google Scholar]
- Hirschmann, G. Some Remarks on the Position of the Rhenish Massif Between the Variscides and the Caledonides. In The Rhenish Massif; Vogel, A., Miller, H., Greiling, R., Eds.; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1987; pp. 104–112. ISBN 978-3-663-01888-9. [Google Scholar]
- Hirschmann, G. Lithological Characteristics. In Pre-Permian Geology of Central and Eastern Europe; Dallmeyer, R.D., Franke, W., Weber, K., Eds.; IGCP-Project 233; Springer: Berlin/Heidelberg, Germany, 1995; pp. 155–163. ISBN 978-3-642-77518-5. [Google Scholar]
- Dörr, W.; Stein, E. Precambrian Basement in the Rheic Suture Zone of the Central European Variscides (Odenwald). Int. J. Earth Sci. (Geol. Rundsch.) 2019, 108, 1937–1957. [Google Scholar] [CrossRef]
- Will, T.M.; Schulz, B.; Schmädicke, E. The Timing of Metamorphism in the Odenwald–Spessart Basement, Mid-German Crystalline Zone. Int. J. Earth Sci. (Geol. Rundsch.) 2017, 106, 1631–1649. [Google Scholar] [CrossRef]
- Stein, E. The Geology of the Odenwald Crystalline Complex. Mineral. Petrol. 2001, 72, 7–28. [Google Scholar] [CrossRef]
- Rotstein, Y.; Edel, J.-B.; Gabriel, G.; Boulanger, D.; Schaming, M.; Munschy, M. Insight into the Structure of the Upper Rhine Graben and Its Basement from a New Compilation of Bouguer Gravity. Tectonophysics 2006, 425, 55–70. [Google Scholar] [CrossRef]
- Kirsch, H.; Kober, B.; Lippolt, H.J. Age of Intrusion and Rapid Cooling of the Frankenstein Gabbro (Odenwald, SW-Germany) Evidenced By40Ar/39Ar and Single-Zircon207Pb/206Pb Measurements. Geol. Rundsch. 1988, 77, 693–711. [Google Scholar] [CrossRef]
- Krohe, A.; Willner, A.P. The Odenwald Crystalline Complex. In Pre-Permian Geology of Central and Eastern Europe; Dallmeyer, R.D., Franke, W., Weber, K., Eds.; IGCP-Project 233; Springer: Berlin, Heidelberg, 1995; pp. 174–181. ISBN 978-3-642-77518-5. [Google Scholar]
- Altherr, R.; Henes-Klaiber, U.; Hegner, E.; Satir, M.; Langer, C. Plutonism in the Variscan Odenwald (Germany): From Subduction to Collision. Int. J. Earth Sci. 1999, 88, 422–443. [Google Scholar] [CrossRef]
- McCann, T. The Geology of Central Europe: Volume 1: Precambrian and Palaeozoic; Geological Society of London: London, UK, 2008. [Google Scholar] [CrossRef]
- Mezger, J.E.; Felder, M.; Harms, F.-J. Crystalline Rocks in the Maar Deposits of Messel: Key to Understand the Geometries of the Messel Fault Zone and Diatreme and the Post-Eruptional Development of the Basin Fill. zdgg 2013, 164, 639–662. [Google Scholar] [CrossRef] [PubMed]
- Anderle, H.J. The Evolution of the South Hunsrück and Taunus Borderzone. Tectonophysics 1987, 137, 101–114. [Google Scholar] [CrossRef]
- Izart, A.; Barbarand, J.; Michels, R.; Privalov, V.A. Modelling of the Thermal History of the Carboniferous Lorraine Coal Basin: Consequences for Coal Bed Methane. Int. J. Coal Geol. 2016, 168, 253–274. [Google Scholar] [CrossRef]
- Duringer, P.; Aichholzer, C.; Orciani, S.; Genter, A. The Complete Lithostratigraphic Section of the Geothermal Wells in Rittershoffen (Upper Rhine Graben, Eastern France): A Key for Future Geothermal Wells. BSGF-Earth Sci. Bull. 2019, 190, 13. [Google Scholar] [CrossRef]
- Liang, F.; Niu, J.; Linsel, A.; Hinderer, M.; Scheuvens, D.; Petschick, R. Rock Alteration at the Post-Variscan Nonconformity: Implications for Carboniferous–Permian Surface Weathering versus Burial Diagenesis and Paleoclimate Evaluation. Solid Earth 2021, 12, 1165–1184. [Google Scholar] [CrossRef]
- Edel, J.B.; Schneider, J.L. The Late Carboniferous to Early Triassic Geodynamic Evolution of Variscan Europe in the Light of Magnetic Overprints in Early Permian Rhyolites from the Northern Vosges (France) and Central Black Forest (Germany). Geophys. J. Int. 1995, 122, 858–876. [Google Scholar] [CrossRef]
- McCann, T.; Pascal, C.; Timmerman, M.J.; Krzywiec, P.; López-Gómez, J.; Wetzel, L.; Krawczyk, C.M.; Rieke, H.; Lamarche, J. Post-Variscan (End Carboniferous-Early Permian) Basin Evolution in Western and Central Europe. Geol. Soc. Lond. Mem. 2006, 32, 355–388. [Google Scholar] [CrossRef]
- Böcker, J.; Littke, R. Thermal Maturity and Petroleum Kitchen Areas of Liassic Black Shales (Lower Jurassic) in the Central Upper Rhine Graben, Germany. Int. J. Earth Sci. (Geol. Rundsch.) 2016, 105, 611–636. [Google Scholar] [CrossRef]
- Böcker, J.; Littke, R.; Forster, A. An Overview on Source Rocks and the Petroleum System of the Central Upper Rhine Graben. Int. J. Earth Sci. (Geol. Rundsch.) 2017, 106, 707–742. [Google Scholar] [CrossRef]
- Meulenkamp, J.E.; Sissingh, W. Tertiary Palaeogeography and Tectonostratigraphic Evolution of the Northern and Southern Peri-Tethys Platforms and the Intermediate Domains of the African–Eurasian Convergent Plate Boundary Zone. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2003, 196, 209–228. [Google Scholar] [CrossRef]
- Sissingh, W. Tectonostratigraphy of the North Alpine Foreland Basin: Correlation of Tertiary Depositional Cycles and Orogenic Phases. Tectonophysics 1997, 282, 223–256. [Google Scholar] [CrossRef]
- Ford, M.; Le Carlier de Veslud, C.; Bourgeois, O. Kinematic and Geometric Analysis of Fault-Related Folds in a Rift Setting: The Dannemarie Basin, Upper Rhine Graben, France. J. Struct. Geol. 2007, 29, 1811–1830. [Google Scholar] [CrossRef]
- Ziegler, P.A.; Dèzes, P. Cenozoic Uplift of Variscan Massifs in the Alpine Foreland: Timing and Controlling Mechanisms. Glob. Planet. Chang. 2007, 58, 237–269. [Google Scholar] [CrossRef]
- Derer, C.E.; Schumacher, M.E.; Schäfer, A. The Northern Upper Rhine Graben: Basin Geometry and Early Syn-Rift Tectono-Sedimentary Evolution. Int. J. Earth Sci. (Geol. Rundsch.) 2005, 94, 640–656. [Google Scholar] [CrossRef]
- Meixner, J.; Schill, E.; Grimmer, J.C.; Gaucher, E.; Kohl, T.; Klingler, P. Structural Control of Geothermal Reservoirs in Extensional Tectonic Settings: An Example from the Upper Rhine Graben. J. Struct. Geol. 2016, 82, 1–15. [Google Scholar] [CrossRef]
- Rotstein, Y.; Schaming, M.; Rousse, S. Tertiary Tectonics of the Dannemarie Basin, Upper Rhine Graben, and Regional Implications. Int. J. Earth Sci. (Geol. Rundsch.) 2005, 94, 669–679. [Google Scholar] [CrossRef]
- Lutz, H.; Kaulfuss, U.; Wappler, T.; Löhnertz, W.; Wilde, V.; Mertz, D.F.; Mingram, J.; Franzen, J.L.; Frankenhäuser, H.; Koziol, M. Eckfeld Maar: Window into an Eocene Terrestrial Habitat in Central Europe. Acta Geol. Sin.—Engl. Ed. 2010, 84, 984–1009. [Google Scholar] [CrossRef]
- Lutz, H.; Lorenz, V.; Engel, T.; Häfner, F.; Haneke, J. Paleogene Phreatomagmatic Volcanism on the Western Main Fault of the Northern Upper Rhine Graben (Kisselwörth Diatreme and Nierstein–Astheim Volcanic System, Germany). Bull. Volcanol. 2013, 75, 741. [Google Scholar] [CrossRef]
- Krohe, A. Emplacement of Synkinematic Plutons in the Variscan Odenwald (Germany) Controlled by Transtensional Tectonics. Geol. Rundsch. 1991, 80, 391–409. [Google Scholar] [CrossRef]
- Thews, J.-D. Erläuterungen Zur Geologischen Übersichtskarte von Hessen 1:300000 (GÜK300 Hessen) Teil I: Kristallin, Ordoviz, Silur, Devon, Karbon.-Geologische Abhandlungen von Hessen, Bd. 96, 1996; Hessisches Landesamt Für Umwelt Und Geologie: Wiesbaden, Germany, 1996. [Google Scholar]
- Heidbach, O.; Rajabi, M.; Cui, X.; Fuchs, K.; Müller, B.; Reinecker, J.; Reiter, K.; Tingay, M.; Wenzel, F.; Xie, F.; et al. The World Stress Map Database Release 2016: Crustal Stress Pattern across Scales. Tectonophysics 2018, 744, 484–498. [Google Scholar] [CrossRef]
- Bossennec, C.; Frey, M.; Seib, L.; Bär, K.; Sass, I. Multi-Scale Structural Dataset of a Crystalline Reservoir Analogue (Northern Odenwald); TUdatalib: Darmstadt, Germany, 2021. [Google Scholar]
- Frey, M.; Bossennec, C.; Seib, L.; Bär, K.; Sass, I. Interdisciplinary Dataset on the Fracture Network of the Tromm Granite, Southern Odenwald, SW Germany; TUdatalib: Darmstadt, Germany, 2021. [Google Scholar]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for Point-Cloud Shape Detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- SAGA Tool Library Documentation. Available online: http://www.saga-gis.org/saga_tool_doc/ (accessed on 27 September 2021).
- Ghosh, K.; Mitra, S. Structural Controls of Fracture Orientations, Intensity, and Connectivity, Teton Anticline, Sawtooth Range, Montana. Bulletin 2009, 93, 995–1014. [Google Scholar] [CrossRef]
- Ortega, O.J.; Marrett, R.A.; Laubach, S.E. A Scale-Independent Approach to Fracture Intensity and Average Spacing Measurement. Bulletin 2006, 90, 193–208. [Google Scholar] [CrossRef]
- Primaleon, L.P.; McCaffrey, K.J.W.; Holdsworth, R.E. Fracture Attribute and Topology Characteristics of a Geothermal Reservoir: Southern Negros, Philippines. J. Geol. Soc. 2020, 177, 1092–1106. [Google Scholar] [CrossRef]
- Sanderson, D.J.; Nixon, C.W. The Use of Topology in Fracture Network Characterization. J. Struct. Geol. 2015, 72, 55–66. [Google Scholar] [CrossRef]
- Outters, N. A Generic Study of Discrete Fracture Network Transport Properties Using FracMan/MAFIC; Swedish Nuclear Fuel and Waste Management Co.: Stockholm, Sweden, 2003. [Google Scholar]
- Lee, C.-C.; Lee, C.-H.; Yeh, H.-F.; Lin, H.-I. Modeling Spatial Fracture Intensity as a Control on Flow in Fractured Rock. Environ. Earth Sci. 2011, 63, 1199–1211. [Google Scholar] [CrossRef]
- Kemeny, J.; Post, R. Estimating Three-Dimensional Rock Discontinuity Orientation from Digital Images of Fracture Traces. Comput. Geosci. 2003, 29, 65–77. [Google Scholar] [CrossRef]
- Ahlers, S.; Henk, A.; Hergert, T.; Reiter, K.; Müller, B.; Röckel, L.; Heidbach, O.; Morawietz, S.; Scheck-Wenderoth, M.; Anikiev, D. 3D Crustal Stress State of Germany According to a Data-Calibrated Geomechanical Model. Solid Earth 2021, 12, 1777–1799. [Google Scholar] [CrossRef]
- Lanaro, F.; Fredriksson, A. Rock Mechanics Model—Summary of the Primary Data—Preliminary Site Description—Forsmark Area—Version 1.2. 41; Swedish Nuclear Fuel and Waste Management Co.: Stockholm, Sweden, 2005. [Google Scholar]
- Andrianov, N.; Nick, H.M. Modeling of Waterflood Efficiency Using Outcrop-Based Fractured Models. J. Pet. Sci. Eng. 2019, 183, 106350. [Google Scholar] [CrossRef]
- Lawn, B. Fracture of Brittle Solids; Cambridge Solid State Science Series; Cambridge University Press: London, UK, 1993. [Google Scholar]
- Klimczak, C.; Schultz, R.A.; Parashar, R.; Reeves, D.M. Cubic Law with Aperture-Length Correlation: Implications for Network Scale Fluid Flow. Hydrogeol. J. 2010, 18, 851–862. [Google Scholar] [CrossRef]
- Oda, M. Permeability Tensor for Discontinuous Rock Masses. Géotechnique 1985, 35, 483–495. [Google Scholar] [CrossRef]
- Chiles, J.-P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Abrahamsen, P.; Hauge, R.; Kolbjørnsen, O. Geostatistics Oslo 2012; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 978-94-007-4153-9. [Google Scholar]
- Wellmann, J.F.; Horowitz, F.G.; Schill, E.; Regenauer-Lieb, K. Towards Incorporating Uncertainty of Structural Data in 3D Geological Inversion. Tectonophysics 2010, 490, 141–151. [Google Scholar] [CrossRef]
- Chabani, A.; Trullenque, G.; Ledésert, B.A.; Klee, J. Multiscale Characterization of Fracture Patterns: A Case Study of the Noble Hills Range (Death Valley, CA, USA), Application to Geothermal Reservoirs. Geosciences 2021, 11, 280. [Google Scholar] [CrossRef]
- Greiling, R.O.; Verma, P.K. Strike-Slip and Tectonics Granitoid Emplacement: An AMS Fabric Study from the Odenwald Crystalline Complex, SW Germany. Mineral. Petrol. 2001, 72, 165–184. [Google Scholar] [CrossRef]
- Meixner, J.; Grimmer, J.C.; Becker, A.; Schill, E.; Kohl, T. Comparison of Different Digital Elevation Models and Satellite Imagery for Lineament Analysis: Implications for Identification and Spatial Arrangement of Fault Zones in Crystalline Basement Rocks of the Southern Black Forest (Germany). J. Struct. Geol. 2018, 108, 256–268. [Google Scholar] [CrossRef]
- Egert, R.; Korzani, M.G.; Held, S.; Kohl, T. Implications on Large-Scale Flow of the Fractured EGS Reservoir Soultz Inferred from Hydraulic Data and Tracer Experiments. Geothermics 2020, 84, 101749. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Turan, A.; Bär, K.; Sass, I. Hydro-Thermal Modeling for Geothermal Energy Extraction from Soultz-Sous-Forêts, France. Geosciences 2021, 11, 464. [Google Scholar] [CrossRef]
- Sausse, J. Hydromechanical Properties and Alteration of Natural Fracture Surfaces in the Soultz Granite (Bas-Rhin, France). Tectonophysics 2002, 348, 169–185. [Google Scholar] [CrossRef]
- Bonneau, F.; Henrion, V.; Caumon, G.; Renard, P.; Sausse, J. A Methodology for Pseudo-Genetic Stochastic Modeling of Discrete Fracture Networks. Comput. Geosci. 2013, 56, 12–22. [Google Scholar] [CrossRef]
- Lepillier, B.; Daniilidis, A.; Doonechaly Gholizadeh, N.; Bruna, P.-O.; Kummerow, J.; Bruhn, D. A Fracture Flow Permeability and Stress Dependency Simulation Applied to Multi-Reservoirs, Multi-Production Scenarios Analysis. Geotherm. Energy 2019, 7, 24. [Google Scholar] [CrossRef]
- Bruna, P.-O.; Straubhaar, J.; Prabhakaran, R.; Bertotti, G.; Bisdom, K.; Mariethoz, G.; Meda, M. A New Methodology to Train Fracture Network Simulation Using Multiple-Point Statistics. Solid Earth 2019, 10, 537–559. [Google Scholar] [CrossRef]
- Sahu, A.; Roy, A. Evaluating Flow in Fractal-Fracture Networks: Effect of Variable Aperture. Adv. Geosci. 2021, 56, 117–128. [Google Scholar] [CrossRef]
- Sanderson, D.J.; Peacock, D.C.P. Line Sampling of Fracture Swarms and Corridors. J. Struct. Geol. 2019, 122, 27–37. [Google Scholar] [CrossRef]
- Peacock, D.C.; Sanderson, D.J.; Bastesen, E.; Rotevatn, A.; Storstein, T.H. Causes of Bias and Uncertainty in Fracture Network Analysis. Nor. J. Geol. 2019, 99, 113–128. [Google Scholar] [CrossRef]
- Ngoc, N.H.; Aziz, S.B.; Duc, N.A. The Application of Seismic Attributes for Reservoir Characterization in Pre-Tertiary Fractured Basement, Vietnam-Malaysia Offshore. Interpretation 2014, 2, SA57–SA66. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Bär, K.; Sass, I. Impact of Well Placement in the Fractured Geothermal Reservoirs Based on Available Discrete Fractured System. Geosciences 2022, 12, 19. [Google Scholar] [CrossRef]
- Calò, M.; Dorbath, C.; Frogneux, M. Injection Tests at the EGS Reservoir of Soultz-Sous-Forêts. Seismic Response of the GPK4 Stimulations. Geothermics 2014, 52, 50–58. [Google Scholar] [CrossRef]
- Schmittbuhl, J.; Lengliné, O.; Cornet, F.; Cuenot, N.; Genter, A. Induced Seismicity in EGS Reservoir: The Creep Route. Geothermal Energy 2014, 2, 14. [Google Scholar] [CrossRef][Green Version]
- Zang, A.; Oye, V.; Jousset, P.; Deichmann, N.; Gritto, R.; McGarr, A.; Majer, E.; Bruhn, D. Analysis of Induced Seismicity in Geothermal Reservoirs—An Overview. Geothermics 2014, 52, 6–21. [Google Scholar] [CrossRef]

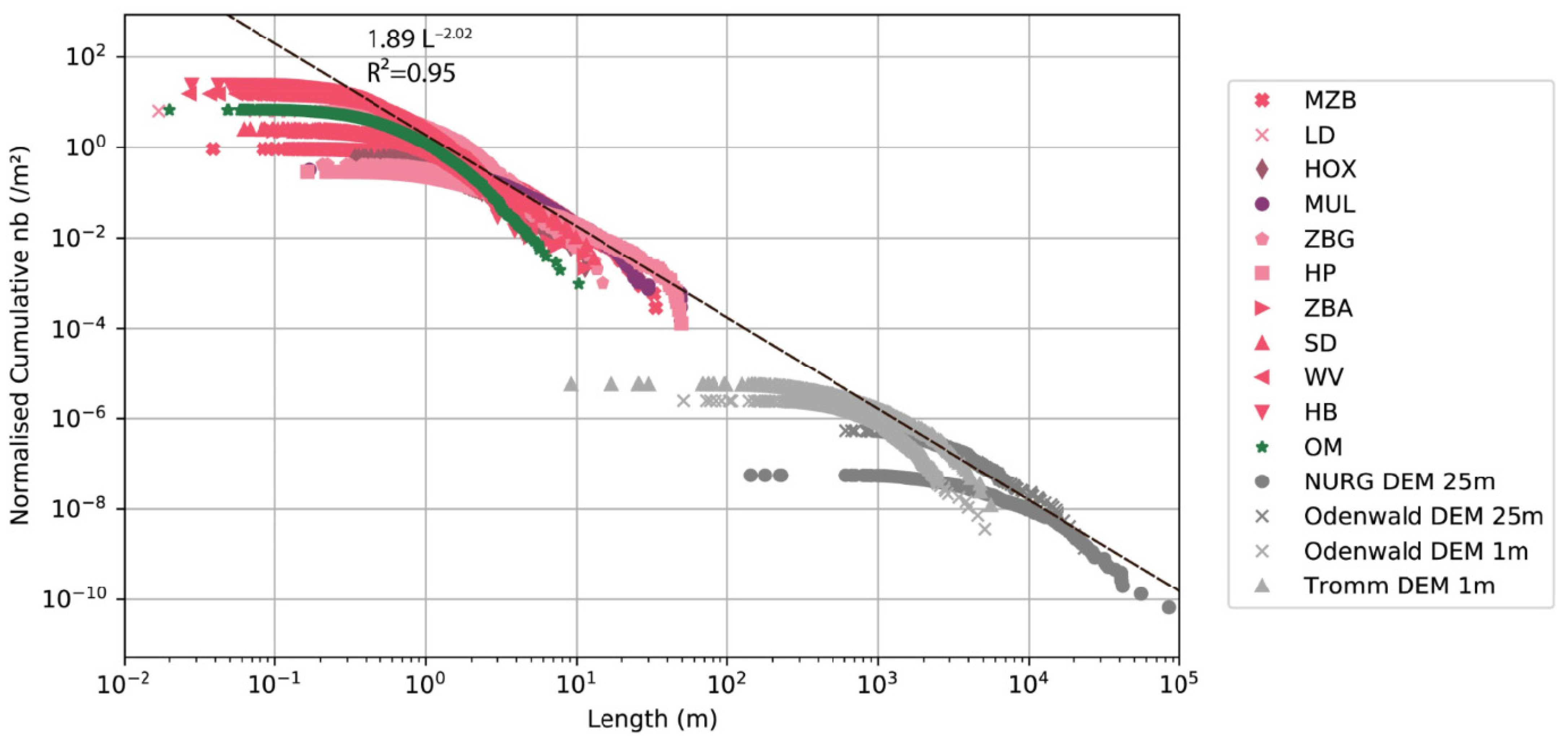
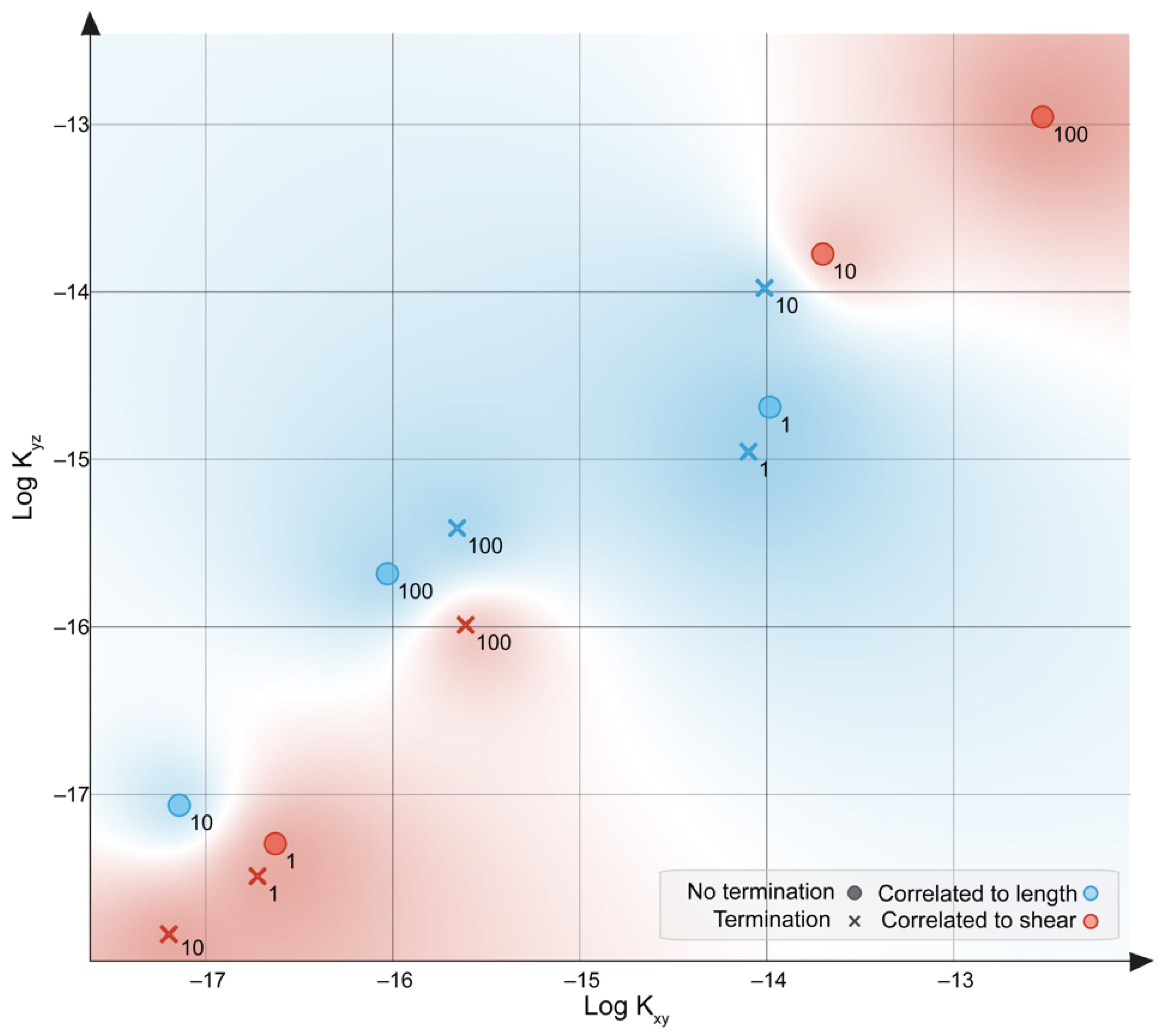
| Location | UTM 32 Coordinates X | UTM 32 Coordinates Y | Main Lithology | Nb LiDAR Identified Planes | Profile ID | Profile Main Orientation | Nb GIS Digitised Items | Reference |
|---|---|---|---|---|---|---|---|---|
| Mainzer Berg | 483,094 | 5,528,012 | Granite | 1076 | 1 | N010 | 542 | [15] |
| (MZB) | 2 | N120 | 414 | |||||
| 3 | N120 | 1377 | ||||||
| 4 | N170 | 380 | ||||||
| 5 | N095 | 516 | ||||||
| Lichtwiese, Darmstadt | 477,176 | 5,523,147 | Granodiorite | - | 1 | N175 | 141 | This study |
| (LD) | - | 2 | Horizontal plane | 629 | ||||
| Mühltal | 478,635 | 5,515,978 | Gabbro | 1197 | 1 | N010 | 309 | This study |
| (MUL) | 2 | N150 | 492 | |||||
| 3 | N075 | 841 | ||||||
| Hoxhohl (HOX) | 480,333 | 5,510,764 | Flasergranitoid | 572 | 1 | N100 | 257 | This study |
| Zwingenberg (ZBG) | 472,627 | 5,508,186 | Granodiorite | 228 | 1 | N090 | 413 | This study |
| Heppenheim | 477,885 | 5,497,621 | Granodiorite | 2212 | 1 | N170 | 785 | This study |
| (HP) | 2 | N080 | 470 | |||||
| 3 | N020 | 510 | ||||||
| 4 | N080 | 310 | ||||||
| 5 | N015 | 150 | ||||||
| Weschnitz (WV) | 486,775 | 5,501,752 | Granite | 169 | 1 | N090 | 1842 | [24] |
| Hammelbach (HB) | 487,401 | 5,497,948 | Granite | 159 | 1 | N080 | 1351 | [24] |
| Streitsdölle (SD) | 486,817 | 5,495,632 | Granite | 456 | 1 | N100 | 521 | [24] |
| Zotzenbach (ZBA) | 485,183 | 5,494,821 | Granite | 289 | 1 | N130 | 1111 | [24] |
| Obermengelbach | 484,957 | 5,492,114 | Amphibolite, Granite | 1243 | 1 | N150 | 767 | [24] |
| (OM) | 2 | N095 | 1647 | |||||
| 3 | N150 | 2383 | ||||||
| 4 | N045 | 981 |
| Layer | Min Length (m) | Max Length (m) | Mean Length (m) | a | b | r2 | P20 (lin·m−2) | P21 (m·m−2) |
|---|---|---|---|---|---|---|---|---|
| DEM 25 m regional (Figure 3a) | 143 | 84,253 | 6247 | 4.09 × 10−3 | −1.41 | 0.98 | 5.74 × 10−8 | 3.58 × 10−4 |
| DEM 25 m Odenwald (Figure 3b) | 611 | 23,405 | 3419 | 1.07 | −1.91 | 0.99 | 5.43 × 10−7 | 1.86 × 10−3 |
| DEM 5 m Northern Odenwald (Figure 3c) | 9 | 5606 | 845 | 2.06 × 10−1 | −1.69 | 0.99 | 5.77 × 10−6 | 4.87 × 10−3 |
| DEM 5 m Southern Odenwald (Figure 3d) | 50 | 5112 | 872 | 3.26 | −2.2132 | 0.98 | 2.47 × 10−6 | 2.16 × 10−3 |
| Locality | Profile n° | Area (m2) | Nb Frac | Min Length (m) | Max Length (m) | Mean Length (m) | P10 (frac·m−1) | P20 (frac·m−2) | P21 (m·m−2) | CL | a | b | r2 | N scanline | Mean Nf | Mean Cv | Min Cv | Max Cv |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MZB | 1 | 610 | 414 | 0.48 | 13.90 | 1.97 | 1.32 | 0.68 | 1.34 | 2.06 | 1.13 | −1.95 | 0.99 | 36 | 19.36 | 0.94 | 0.54 | 1.55 |
| 2 | 129 | 542 | 0.17 | 4.73 | 1.01 | 3.03 | 4.20 | 4.24 | 1.53 | 1.06 | −1.71 | 0.99 | 36 | 4.00 | 0.92 | 0.59 | 1.41 | |
| 3 | 400 | 1377 | 0.04 | 11.68 | 1.01 | 3.05 | 3.44 | 3.48 | 2.82 | 1.12 | −1.55 | 0.99 | 7 | 56.71 | 0.93 | 0.67 | 1.41 | |
| 4 | 3870 | 380 | 1.02 | 32.58 | 5.23 | 0.44 | 0.10 | 0.51 | 2.55 | 0.71 | −1.87 | 1.00 | 12 | 28.67 | 1.10 | 0.74 | 1.89 | |
| 5 | 2525 | 516 | 0.50 | 33.47 | 4.22 | 0.76 | 0.20 | 0.86 | 2.78 | 0.27 | −1.95 | 0.99 | 17 | 30.41 | 1.00 | 0.54 | 1.29 | |
| LD | 1 | 44 | 141 | 0.11 | 5.12 | 0.94 | 2.05 | 3.20 | 3.02 | 3.78 | 1.04 | −1.51 | 0.97 | 14 | 27.36 | 1.02 | 0.65 | 1.91 |
| 2 | 375 | 629 | 0.01 | 8.46 | 1.18 | 3.06 | 1.68 | 1.98 | 3.45 | 0.72 | −1.43 | 0.99 | 10 | 13.20 | 0.94 | 0.61 | 1.26 | |
| MUL | 1 | 745 | 309 | 0.62 | 16.86 | 3.00 | 1.29 | 0.41 | 1.24 | 5.37 | 0.61 | −1.37 | 0.99 | 12 | 23.92 | 0.94 | 0.72 | 1.22 |
| 2 | 2926 | 492 | 0.17 | 23.81 | 5.26 | 0.77 | 0.17 | 0.88 | 4.48 | 0.38 | −1.13 | 0.97 | 13 | 44.62 | 0.98 | 0.51 | 1.39 | |
| 3 | 3278 | 841 | 0.55 | 48.92 | 3.96 | 0.76 | 0.26 | 1.01 | 4.74 | 0.52 | −1.40 | 0.99 | 16 | 39.25 | 0.94 | 0.77 | 1.20 | |
| HOX | 1 | 238 | 257 | 0.34 | 11.30 | 1.72 | 1.77 | 1.08 | 1.86 | 5.39 | 0.63 | −1.02 | 0.97 | 14 | 21.64 | 1.00 | 0.68 | 1.49 |
| ZBG | 1 | 920 | 413 | 0.21 | 14.89 | 2.33 | 0.85 | 0.45 | 1.05 | 2.44 | 0.40 | −1.17 | 0.97 | 17 | 23.00 | 1.13 | 0.66 | 1.67 |
| HP | 1 | 885 | 785 | 0.16 | 13.34 | 2.26 | 1.41 | 0.89 | 2.01 | 2.01 | 1.23 | −1.69 | 0.99 | 14 | 42.07 | 1.00 | 0.74 | 1.43 |
| 2 | 1233 | 470 | 0.75 | 36.23 | 4.15 | 0.80 | 0.38 | 1.58 | 5.64 | 1.36 | −2.00 | 0.99 | 17 | 37.29 | 0.89 | 0.68 | 1.14 | |
| 3 | 3289 | 510 | 0.40 | 13.19 | 2.30 | 0.80 | 0.16 | 0.36 | 5.59 | 0.43 | −2.30 | 0.99 | 23 | 23.26 | 0.93 | 0.64 | 1.22 | |
| 4 | 454 | 310 | 0.24 | 13.25 | 1.85 | 1.53 | 0.68 | 1.26 | 4.56 | 0.92 | −1.69 | 1.00 | 29 | 25.90 | 0.91 | 0.58 | 1.41 | |
| 5 | 14,798 | 150 | 4.60 | 49.26 | 16.82 | 0.15 | 0.01 | 0.17 | 4.45 | 0.29 | −1.57 | 0.99 | 19 | 15.26 | 0.79 | 0.55 | 1.19 | |
| WV | 1 | 119 | 1842 | 0.03 | 7.57 | 0.81 | 6.02 | 15.48 | 12.54 | 4.09 | 2.02 | −2.11 | 1.00 | 28 | 46.25 | 1.09 | 0.69 | 2.40 |
| HB | 1 | 67 | 1351 | 0.03 | 3.91 | 0.54 | 7.74 | 20.16 | 10.89 | 3.94 | 1.62 | −2.34 | 1.00 | 30 | 42.53 | 0.88 | 0.64 | 1.55 |
| SD | 1 | 288 | 521 | 0.06 | 12.96 | 1.57 | 2.23 | 1.81 | 2.84 | 3.44 | 0.92 | −1.48 | 0.99 | 28 | 24.11 | 0.98 | 0.57 | 2.21 |
| ZBA | 1 | 475 | 1111 | 0.10 | 11.22 | 1.28 | 1.98 | 2.34 | 2.99 | 2.96 | 1.28 | −2.54 | 1.00 | 29 | 31.14 | 1.04 | 0.77 | 1.61 |
| OM | 1 | 200 | 973 | 0.05 | 7.27 | 0.98 | 2.65 | 4.87 | 4.77 | 3.02 | 1.08 | −1.80 | 0.99 | 20 | 31.20 | 0.91 | 0.67 | 1.17 |
| 2 | 300 | 1981 | 0.06 | 6.24 | 0.89 | 3.26 | 6.60 | 5.88 | 3.11 | 1.38 | −1.91 | 0.99 | 33 | 48.27 | 0.93 | 0.53 | 1.40 | |
| 3 | 250 | 2895 | 0.02 | 7.74 | 0.62 | 4.00 | 11.58 | 7.18 | 3.30 | 1.07 | −2.20 | 1.00 | 31 | 52.13 | 0.98 | 0.65 | 1.54 | |
| 4 | 300 | 1280 | 0.06 | 10.28 | 1.10 | 2.50 | 4.27 | 4.69 | 3.43 | 1.12 | −1.75 | 0.99 | 36 | 30.61 | 1.05 | 0.70 | 1.79 |
| Model | Cluster name | Global P10 (frac·m−1) | Trend | Plunge | a95 | a99 | kappa | P10 |
|---|---|---|---|---|---|---|---|---|
| LD (Case 1) | 1 | 3.06 | 33.9 | 16 | 2.2 | 2.7 | 30.4 | 1.03 |
| 2 | 3.06 | 99.4 | 14.3 | 2 | 2.4 | 52.7 | 0.71 | |
| 3 | 3.06 | 132.6 | 15.4 | 2 | 2.5 | 64.7 | 0.54 | |
| 4 | 3.06 | 345.1 | 16.3 | 2.1 | 2.6 | 44.1 | 0.77 | |
| HP (Case 2) | 1 | 1.53 | 199.4 | 13.8 | 14.5 | 18.2 | 4.4 | 0.48 |
| 2 | 1.53 | 130.4 | 18.5 | 4.6 | 5.8 | 25.2 | 0.66 | |
| 3 | 1.53 | 307.6 | 8.8 | 6.1 | 7.6 | 26 | 0.38 |
| Model | Model nb. | Fracture Law | Fracture Clusters | Termination | % Open Fractures | Shear Dependent Aperture |
|---|---|---|---|---|---|---|
| LD (case 1) | 9 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | o | 100 | x |
| 12 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | o | 100 | o | |
| 3 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | x | 100 | o | |
| 8 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | o | 100 | x | |
| 10 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | x | 10 | x | |
| 4 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | o | 10 | o | |
| 5 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | o | 10 | x | |
| 2 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | x | 10 | o | |
| 7 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | x | 1 | x | |
| 6 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | o | 1 | o | |
| 11 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | o | 1 | x | |
| 1 | powerlaw (2,2) | LD1, LD2, LD3, LD4 | x | 1 | o | |
| 13 | deterministic | - | - | 100 | o | |
| 14 | deterministic | - | - | 100 | x | |
| HP (case 2) | 1 | powerlaw (2,2) | HP1, HP2, HP3 | o | 100 | x |
| 2 | powerlaw (2,2) | HP1, HP2, HP3 | o | 100 | o | |
| 3 | powerlaw (2,2) | HP1, HP2, HP3 | x | 100 | o | |
| 4 | powerlaw (2,2) | HP1, HP2, HP3 | x | 100 | x | |
| 5 | powerlaw (2,2) | HP1, HP2, HP3 | o | 10 | x | |
| 6 | powerlaw (2,2) | HP1, HP2, HP3 | o | 10 | o | |
| 7 | powerlaw (2,2) | HP1, HP2, HP3 | x | 10 | x | |
| 8 | powerlaw (2,2) | HP1, HP2, HP3 | x | 10 | o | |
| 9 | powerlaw (2,2) | HP1, HP2, HP3 | o | 1 | o | |
| 10 | powerlaw (2,2) | HP1, HP2, HP3 | x | 1 | o | |
| 11 | powerlaw (2,2) | HP1, HP2, HP3 | o | 1 | x | |
| 12 | powerlaw (2,2) | HP1, HP2, HP3 | x | 1 | x | |
| 13 | deterministic | - | - | 100 | o | |
| 14 | deterministic | - | - | 100 | x |
| Model | Number | Termination(1/0) | % Open | Shear (x/o) | Aperture Mean (m) | std | log(Kxx) | log(Kyy) | log(Kzz) | log(K1) | log(K2) | log(K3) | KTS (N°E) | KTD (°) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LD | 1 | 1 | 1 | o | 2.66 × 10−6 | 1.33 × 10−6 | −16.32 | −16.62 | −16.20 | −16.28 | −16.38 | −16.73 | 179 | 64 |
| LD | 2 | 1 | 10 | o | 2.92 × 10−6 | 1.42 × 10−6 | −15.78 | −15.81 | −15.58 | −15.57 | −15.67 | −15.98 | 127 | 34 |
| LD | 3 | 1 | 100 | o | 2.91 × 10−6 | 1.41 × 10−6 | −14.66 | −14.70 | −14.47 | −14.47 | −14.60 | −14.78 | 163 | 16 |
| LD | 4 | 0 | 10 | o | 2.91 × 10−6 | 1.40 × 10−6 | −16.06 | −15.99 | −15.81 | −15.03 | −15.12 | −15.49 | 128 | 36 |
| LD | 5 | 0 | 10 | x | 1.48 × 10−5 | 8.56 × 10−6 | −13.29 | −13.33 | −13.16 | −15.12 | −15.23 | −15.48 | 141 | 56 |
| LD | 6 | 0 | 1 | o | 2.92 × 10−5 | 1.48 × 10−5 | −13.47 | −13.66 | −13.31 | −13.32 | −13.45 | −13.73 | 177 | 63 |
| LD | 7 | 1 | 1 | x | 2.41 × 10−6 | 1.93 × 10−6 | −16.38 | −16.71 | −16.28 | −16.28 | −16.38 | −16.73 | 179 | 64 |
| LD | 8 | 1 | 100 | x | 1.52 × 10−5 | 1.99 × 10−5 | −15.01 | −15.51 | −14.98 | −14.97 | −15.02 | −15.51 | 179 | 38 |
| LD | 9 | 0 | 100 | x | 1.52 × 10−5 | 1.99 × 10−5 | −11.89 | −12.21 | −11.82 | −11.81 | −11.90 | −12.22 | 179 | 31 |
| LD | 10 | 1 | 10 | x | 1.48 × 10−5 | 8.56 × 10−6 | −16.82 | −17.02 | −16.67 | −16.66 | −16.80 | −17.05 | 168 | 30 |
| LD | 11 | 0 | 1 | x | 2.57 × 10−6 | 1.94 × 10−6 | −16.32 | −16.62 | −16.20 | −16.20 | −16.31 | −16.63 | 179 | 63 |
| LD | 12 | 0 | 100 | o | 2.91 × 10−6 | 1.41 × 10−6 | −14.77 | −14.77 | −14.56 | −14.56 | −14.69 | −14.87 | 110 | 16 |
| LD | 13 | 0 | 100 | o | 8.67 × 10−4 | 3.22 × 10−4 | −16.84 | −16.70 | −16.55 | −16.55 | −16.63 | −17.10 | 172 | 68 |
| LD | 14 | 0 | 100 | x | 3.10 × 10−6 | 4.67 × 10−6 | −17.08 | −17.61 | −17.03 | −17.02 | −17.08 | −17.63 | 179 | 72 |
| Model | Number | Termination (1/0) | % Open | Shear (x/o) | Aperture Mean (m) | std | log(Kxx) | log(Kyy) | log(Kzz) | log(K1) | log(K2) | log(K3) | KTS (N°E) | KTD (°) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HP | 1 | 0 | 100 | x | 1.98 × 10−6 | 1.39 × 10−6 | −16.19 | −16.34 | −16.10 | −16.08 | −16.19 | −16.38 | 172 | 35 |
| HP | 2 | 0 | 100 | o | 2.66 × 10−6 | 9.63E−07 | −16.17 | −16.08 | −15.93 | −15.92 | −16.03 | −16.26 | 141 | 25 |
| HP | 3 | 1 | 100 | o | 2.31 × 10−6 | 1.12 × 10−6 | −16.20 | −16.10 | −15.95 | −15.94 | −16.05 | −16.29 | 135 | 25 |
| HP | 4 | 1 | 100 | x | 1.72 × 10−6 | 1.37 × 10−6 | −16.22 | −16.37 | −16.13 | −16.11 | −16.22 | −16.41 | 171 | 34 |
| HP | 5 | 0 | 10 | x | 1.60 × 10−6 | 1.61 × 10−6 | −17.28 | −17.26 | −17.09 | −17.07 | −17.18 | −17.42 | 167 | 51 |
| HP | 6 | 0 | 10 | o | 2.66 × 10−6 | 9.71 × 10−7 | −17.07 | −17.04 | −16.87 | −16.85 | −16.96 | −17.22 | 166 | 47 |
| HP | 7 | 1 | 10 | x | 1.51 × 10−6 | 1.63 × 10−6 | −17.80 | −18.04 | −17.82 | −17.08 | −17.18 | −17.42 | 168 | 51 |
| HP | 8 | 1 | 10 | o | 2.48 × 10−6 | 1.06 × 10−6 | −17.09 | −17.05 | −16.89 | −16.87 | −16.98 | −17.24 | 166 | 47 |
| HP | 9 | 0 | 1 | o | 2.65 × 10−6 | 9.45 × 10−7 | −15.77 | −15.84 | −15.57 | −16.17 | −16.32 | −16.57 | 178 | 70 |
| HP | 10 | 1 | 1 | o | 2.49 × 10−5 | 1.02 × 10−5 | −14.65 | −14.64 | −14.41 | −14.40 | −14.54 | −14.80 | 178 | 70 |
| HP | 11 | 0 | 1 | x | 1.04 × 10−5 | 3.94 × 10−6 | −17.64 | −17.62 | −17.39 | −15.56 | −15.71 | −15.96 | 178 | 70 |
| HP | 12 | 1 | 1 | x | 1.79 × 10−6 | 1.40 × 10−6 | −17.59 | −17.82 | −17.47 | −17.46 | −17.59 | −17.86 | 178 | 71 |
| HP | 13 | 0 | 100 | o | 3.12 × 10−6 | 1.17 × 10−6 | −17.60 | −17.08 | −17.00 | −16.99 | −17.05 | −17.75 | 174 | 77 |
| HP | 14 | 0 | 100 | x | 3.75× 10−7 | 2.16× 10−6 | −17.62 | −18.01 | −17.51 | −17.51 | −17.60 | −18.06 | 179 | 82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bossennec, C.; Seib, L.; Frey, M.; van der Vaart, J.; Sass, I. Structural Architecture and Permeability Patterns of Crystalline Reservoir Rocks in the Northern Upper Rhine Graben: Insights from Surface Analogues of the Odenwald. Energies 2022, 15, 1310. https://doi.org/10.3390/en15041310
Bossennec C, Seib L, Frey M, van der Vaart J, Sass I. Structural Architecture and Permeability Patterns of Crystalline Reservoir Rocks in the Northern Upper Rhine Graben: Insights from Surface Analogues of the Odenwald. Energies. 2022; 15(4):1310. https://doi.org/10.3390/en15041310
Chicago/Turabian StyleBossennec, Claire, Lukas Seib, Matthis Frey, Jeroen van der Vaart, and Ingo Sass. 2022. "Structural Architecture and Permeability Patterns of Crystalline Reservoir Rocks in the Northern Upper Rhine Graben: Insights from Surface Analogues of the Odenwald" Energies 15, no. 4: 1310. https://doi.org/10.3390/en15041310
APA StyleBossennec, C., Seib, L., Frey, M., van der Vaart, J., & Sass, I. (2022). Structural Architecture and Permeability Patterns of Crystalline Reservoir Rocks in the Northern Upper Rhine Graben: Insights from Surface Analogues of the Odenwald. Energies, 15(4), 1310. https://doi.org/10.3390/en15041310






