Contribution of the 2010 Maule Megathrust Earthquake to the Heat Flow at the Peru-Chile Trench
Abstract
1. Introduction
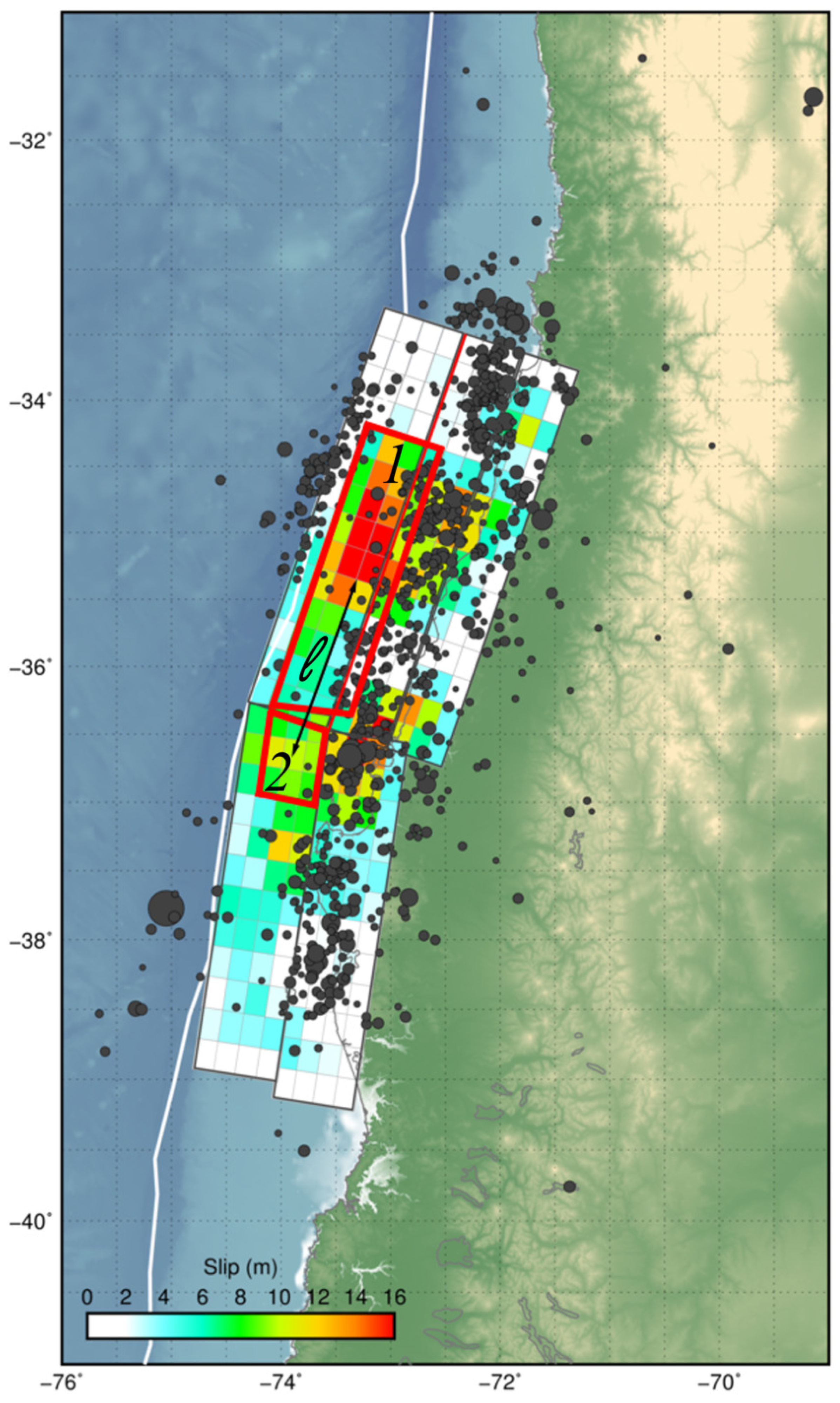
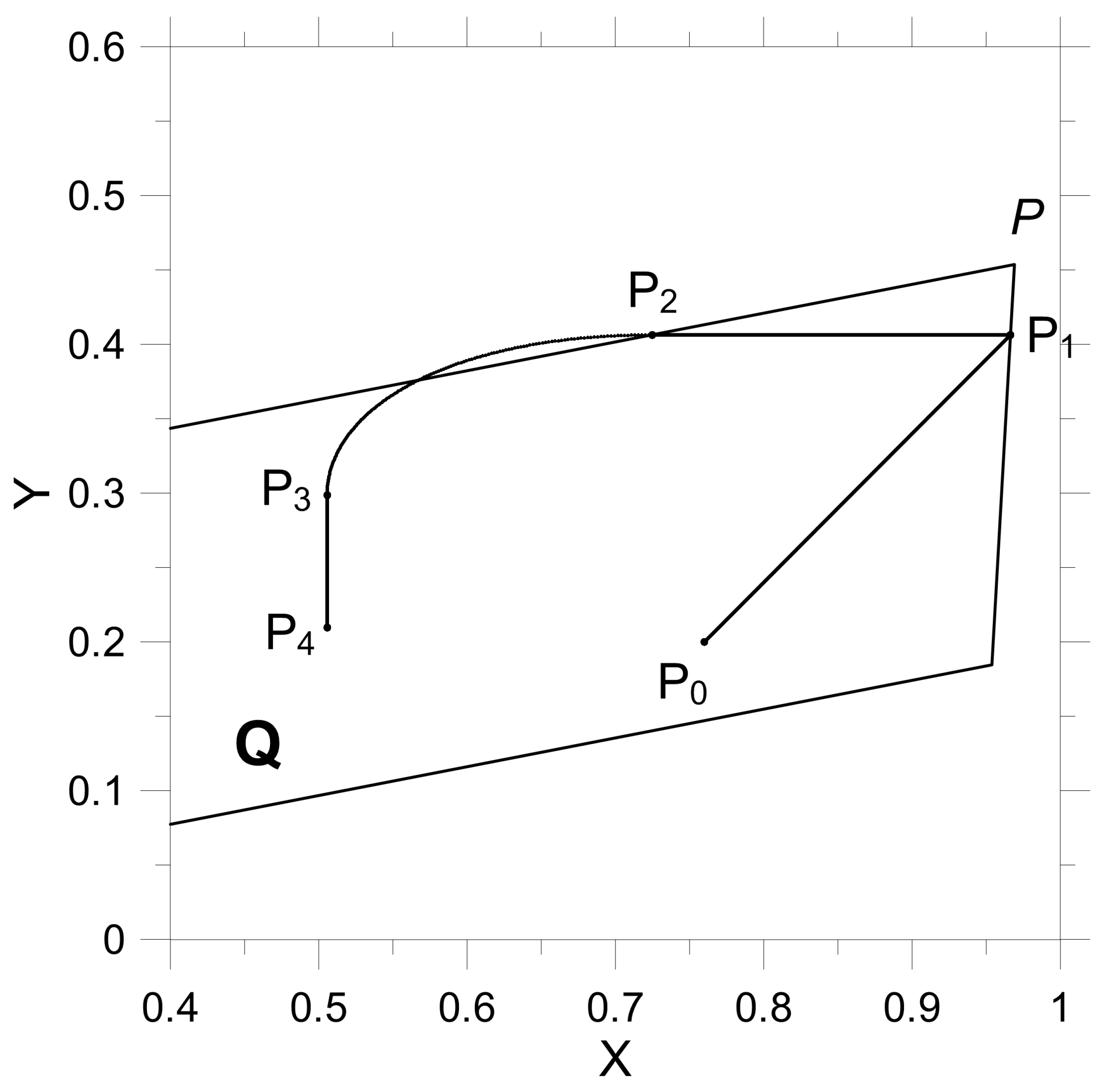
2. Fault Model
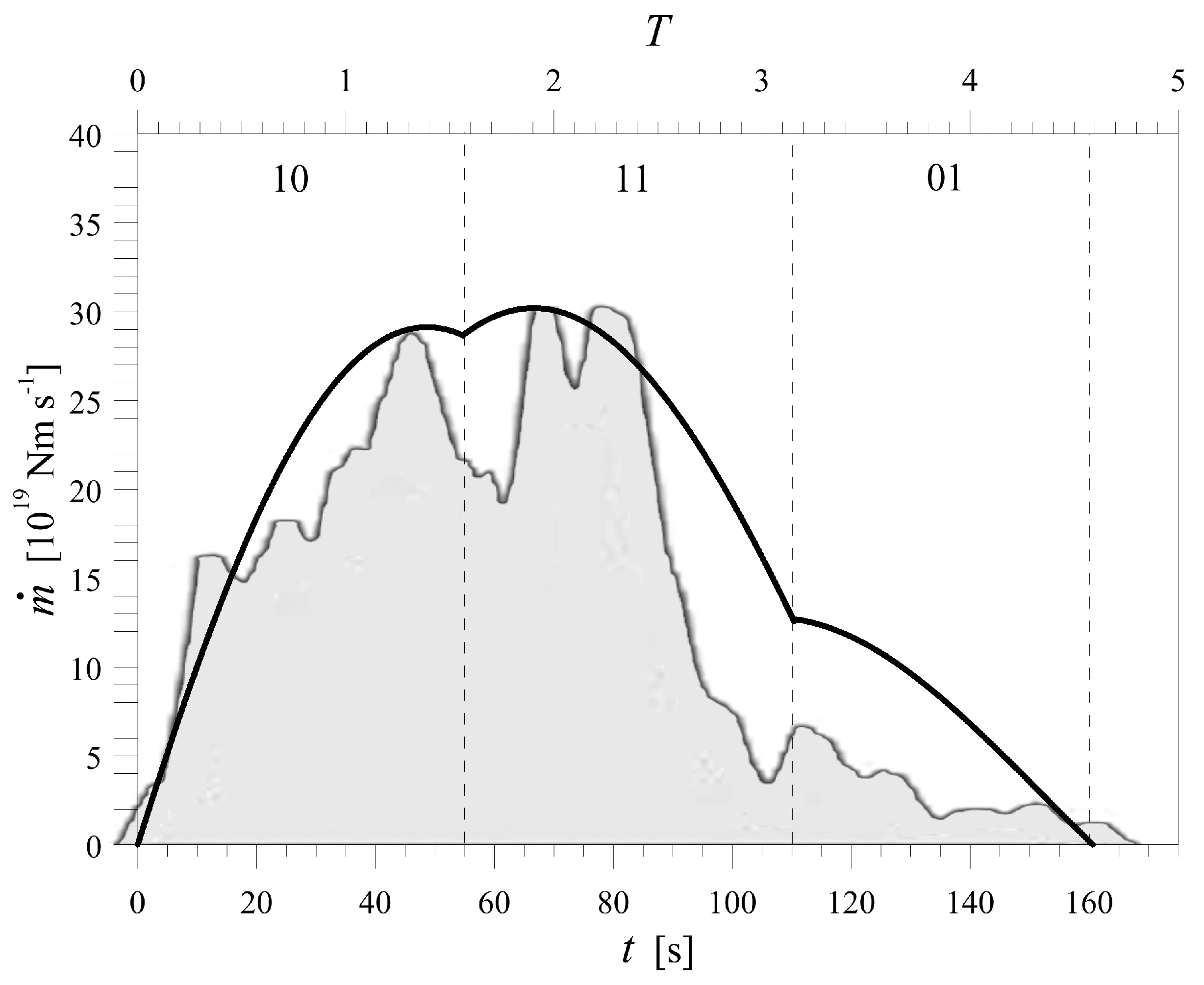
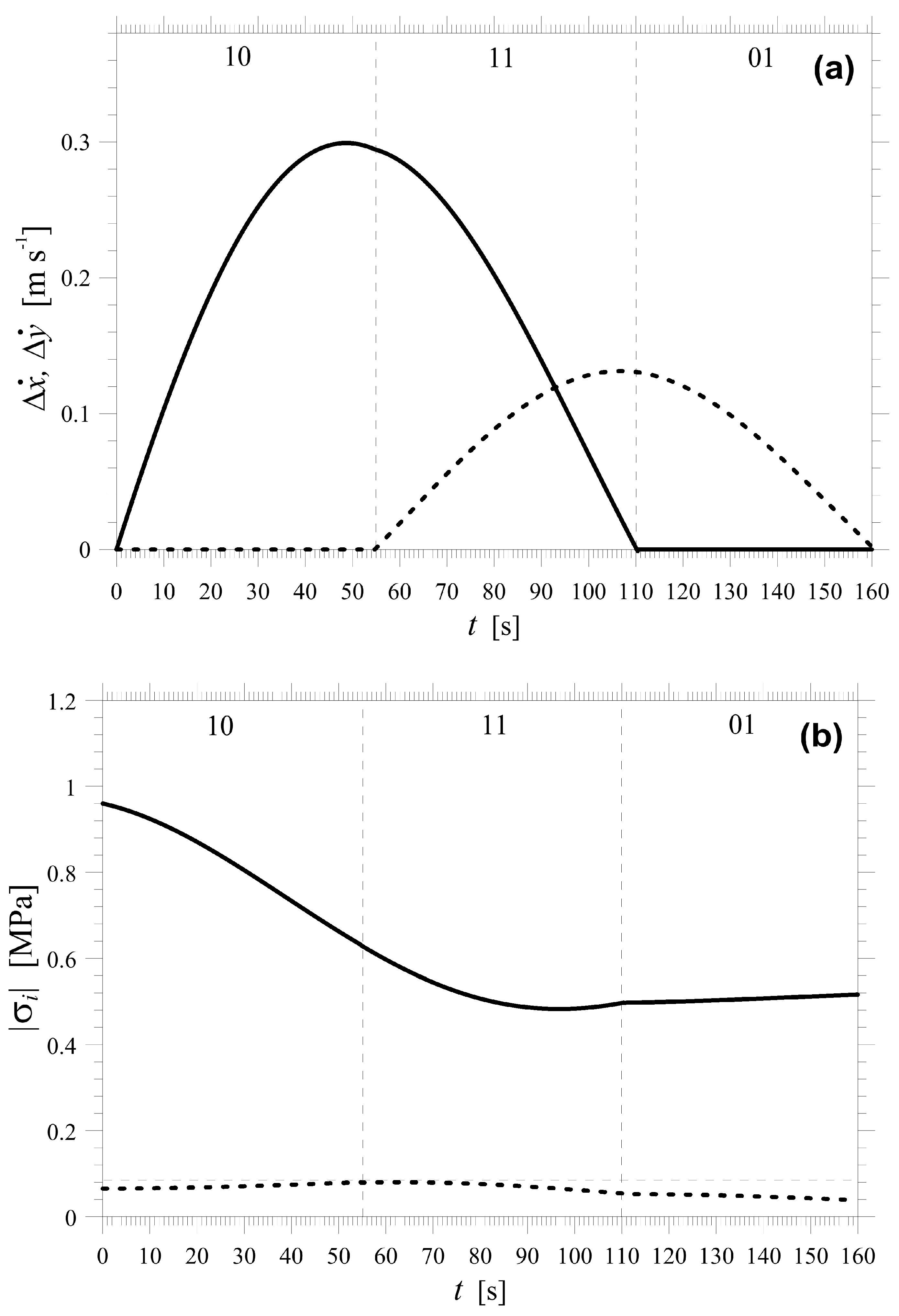
3. The Moment Rate
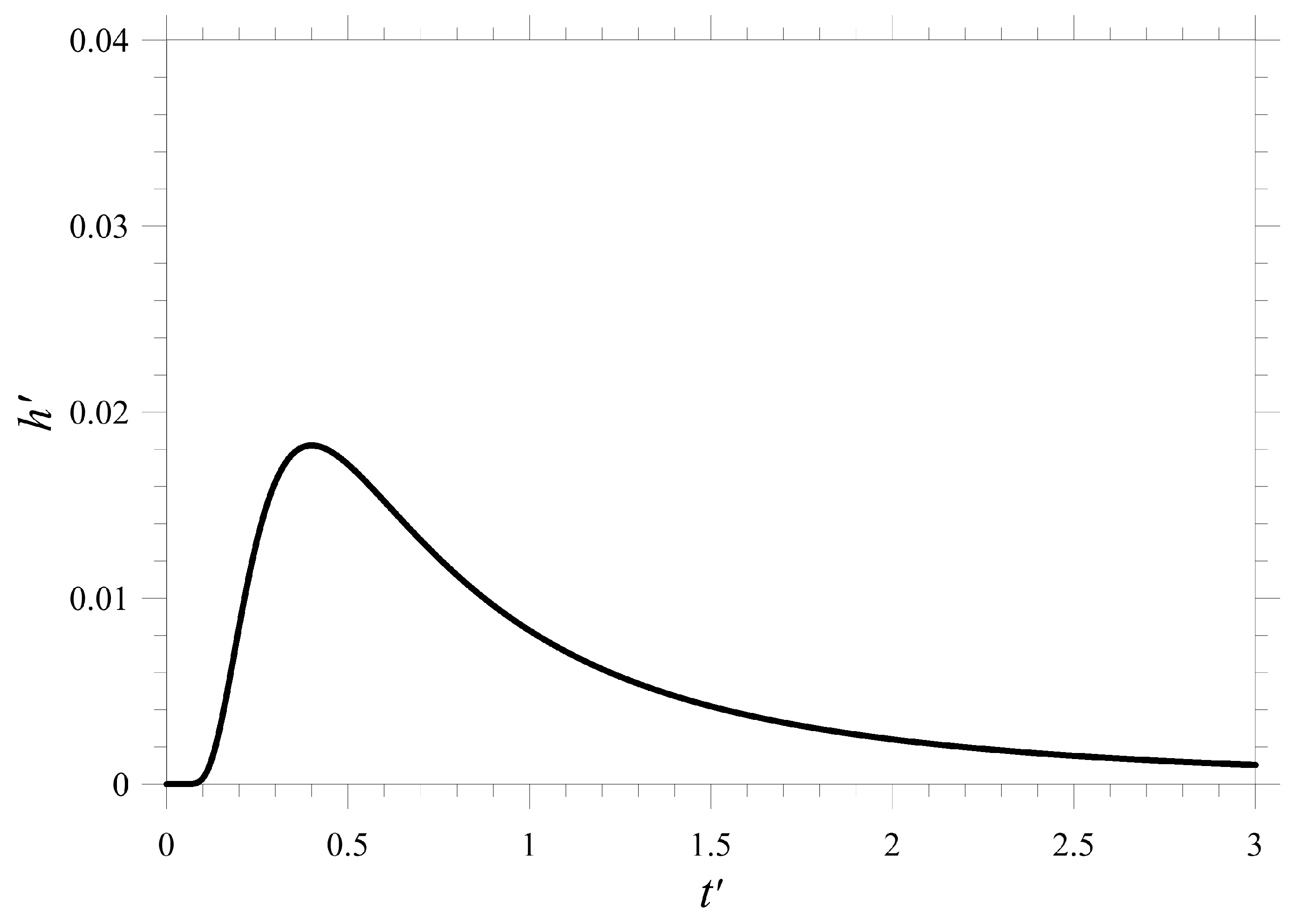
4. Surface Heat Flow
5. Heat Pulse
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Delouis, B.; Nocquet, J.M.; Vallée, M. Slip distribution of the February 27, 2010 Mw = 8.8 Maule earthquake, central Chile, from static and high-rate GPS, InSAR, and broadband teleseismic data. Geophys. Res. Lett. 2010, 37, L17305. [Google Scholar] [CrossRef]
- Lay, T.; Ammon, C.J.; Kanamori, H.; Koper, K.D.; Sufri, O.; Hutko, A.R. Teleseismic inversion for rupture process of the 27 February 2010 Chile (Mw 8.8) earthquake. Geophys. Res. Lett. 2010, 37, L13301. [Google Scholar] [CrossRef]
- Vigny, C.; Socquet, A.; Peyrat, S.; Ruegg, J.C.; Métois, M.; Madariaga, R.; Morvan, S.; Lancieri, M.; Lacassin, R.; Campos, J.; et al. The 2010 Mw 8.8 Maule Megathrust Earthquake of Central Chile, Monitored by GPS. Science 2011, 332, 1417–1421. [Google Scholar] [CrossRef] [PubMed]
- Lay, T.; Kanamori, H.; Ruff, L. The asperity model and the nature of large subduction zone earthquakes. Earthq. Pred. Res. 1982, 1, 3–71. [Google Scholar]
- Scholz, C.H. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019; p. 512. [Google Scholar]
- Ruff, L.J. Asperity distributions and large earthquake occurrence in subduction zones. Tectonophysics 1992, 211, 61–83. [Google Scholar] [CrossRef][Green Version]
- Somerville, P.; Irikura, K.; Graves, R.; Sawada, S.; Wald, D.; Abrahamson, N.; Kagawa, T.; Iwasaki, Y.; Smith, N.; Kowada, A. Characterizing crustal earthquake slip models for the prediction of strong ground motion. Seismol. Res. Lett. 1999, 70, 59–80. [Google Scholar] [CrossRef]
- Rice, J.R. Spatio-temporal complexity of slip on a fault. J. Geophys. Res. 1993, 98, 9885–9907. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997; p. 398. [Google Scholar]
- Nussbaum, J.; Ruina, A. A two degree-of-freedom earthquake model with static/dynamic friction. Pure Appl. Geophys. 1987, 125, 629–656. [Google Scholar] [CrossRef]
- Huang, J.; Turcotte, D.L. Are earthquakes an example of deterministic chaos? Geophys. Res. Lett. 1990, 17, 223–226. [Google Scholar] [CrossRef]
- Huang, J.; Turcotte, D.L. Chaotic seismic faulting with mass-spring model and velocity-weakening friction. Pure Appl. Geophys. 1992, 138, 569–589. [Google Scholar] [CrossRef]
- McCloskey, J.; Bean, C.J. Time and magnitude predictions in shocks due to chaotic fault interactions. Geophys. Res. Lett. 1992, 19, 119–122. [Google Scholar] [CrossRef]
- Dragoni, M.; Santini, S. Simulation of the long-term behaviour of a fault with two asperities. Nonlin. Proc. Geophys. 2010, 17, 777–784. [Google Scholar] [CrossRef][Green Version]
- Dragoni, M.; Santini, S. Conditions for large earthquakes in a two-asperity fault model. Nonlin. Proc. Geophys. 2011, 18, 709–717. [Google Scholar] [CrossRef]
- Dragoni, M.; Santini, S. Long-term dynamics of a fault with two asperities of different strengths. Geophys. J. Int. 2012, 191, 1457–1467. [Google Scholar]
- Dragoni, M.; Santini, S. Source functions of a two-asperity fault model. Geophys. Res. Lett. 2014, 196, 1803–1812. [Google Scholar] [CrossRef]
- Dragoni, M.; Piombo, A. Effect of stress perturbations on the dynamics of a complex fault. Pure Appl. Geophys. 2015, 172, 2571–2583. [Google Scholar] [CrossRef]
- Dragoni, M.; Santini, S. A two-asperity fault model with wave radiation. Phys. Earth Planet. Int. 2015, 248, 83–93. [Google Scholar] [CrossRef]
- Dragoni, M.; Santini, S. Effects of fault heterogeneity on seismic energy and spectrum. Phys. Earth Planet. Int. 2017, 273, 11–22. [Google Scholar] [CrossRef]
- Dragoni, M.; Tallarico, A. Complex events in a fault model with interacting asperities. Phys. Earth Planet. Int. 2016, 257, 115–127. [Google Scholar] [CrossRef]
- Lorenzano, E.; Dragoni, M. A fault model with two asperities of different areas and strengths. Math. Geosci. 2018, 50, 697–724. [Google Scholar] [CrossRef]
- Shearer, P.M. Introduction to Seismology, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009; p. 412. [Google Scholar]
- McGarr, A. On relating apparent stress to the stress causing earthquake fault slip. J. Geophys. Res. 1999, 104, 3003–3011. [Google Scholar] [CrossRef]
- Lachenbruch, A.H.; Sass, J.H. Heat flow and energetics of the San Andreas fault zone. J. Geophys. Res. 1980, 85, 6185–6222. [Google Scholar] [CrossRef]
- Stacey, F.D.; Davis, P.M. Physics of the Earth, 4th ed.; Cambridge University Press: Cambridge, UK, 2008; p. 532. [Google Scholar]
- Santini, S.; Dragoni, M. Moment rate of the 2018 Gulf of Alaska earthquake. Phys. Earth Planet. Int. 2020, 298, 106336. [Google Scholar] [CrossRef]
- Clouard, V.; Campos, J.; Lemoine, A.; Perez, A.; Kausel, E. Outer rise stress changes related to the subduction of the Juan Fernandez Ridge, central Chile. J. Geophys. Res. 2007, 112, B05305. [Google Scholar] [CrossRef]
- Maksymowicz, A.; Trehu, A.M.; Contreras-Reyes, E.; Ruiz, S. Density-depth model of the continental wedge at the maximum slip segment of the Maule Mw8.8 megathrust earthquake. Earth Planet. Sci. Lett. 2015, 409, 265–277. [Google Scholar] [CrossRef]
- United States Geological Survey, Finite Fault of the M 8.8–36 km WNW of Quirihue, Chile, Earthquake. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/official20100227063411530_30/moment-tensor?source=us&code=pde20100227063411530_22_C_WCMT (accessed on 27 July 2021).
- Seno, T. Stress drop as a criterion to differentiate subduction zones where Mw 9 earthquakes can occur. Tectonophysics 2014, 621, 198–210. [Google Scholar] [CrossRef]
- Valdenegro, P.; Munoz, M.; Yanez, G.; Parada, M.A.; Morata, D. A model for thermal gradient and heat flow in central Chile: The role of thermal properties. J. S. Am. Earth Sci. 2019, 91, 88–101. [Google Scholar] [CrossRef]
- Molnar, P.; England, P. Temperatures, Heat Flux, and Frictional Stress Near Major Thrust Faults. J. Geophys. Res. 1990, 95, 4833–4856. [Google Scholar] [CrossRef]
- Sibson, R.H. Frictional constraints on thrust, wrench and normal faults. Nature 1974, 249, 542–544. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Schubert, G. Geodynamics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2014; p. 626. [Google Scholar]
- Seno, T. Determination of the pore fluid pressure ratio at seismogenic megathrusts in subduction zones: Implications for strength of asperities and Andean-type mountain building. J. Geophys. Res. 2009, 114, B05405. [Google Scholar] [CrossRef]
- Vllar-Munoz, L.; Behrmann, J.H.; Diaz-Naveas, J.; Klaeschen, D.; Karstens, J. Heat flow in the southern Chile forearc controlled by large-scale tectonic processes. Geo-Mar. Lett. 2014, 34, 185–198. [Google Scholar] [CrossRef]
- Luikov, A.V. Analytical Heat Diffusion Theory; Academic Press: New York, NY, USA, 1968; p. 685. [Google Scholar]

| , | Area of asperity 1 |
| , | Area of asperity 2 |
| s, | Tectonic strain rate |
| m s, | Acceleration of gravity |
| , | Heat productivity of the lower crust |
| , | Heat productivity of the upper crust |
| km, | Thickness of the lower crust |
| km, | Thickness of the upper crust |
| km, | Distance between asperity centroids |
| mW m, | Heat flow density from the mantle |
| m, | Average slip of asperity 1 |
| m, | Average slip of asperity 2 |
| cm a, | Relative plate velocity |
| km, | Distance between epicenter and trench |
| km, | Depth of the hypocenter |
| s, | Duration of the event |
| , | Coefficient of static friction |
| , | Pore fluid factor |
| GPa, | Rigidity of the lithosphere |
| kg m, | Density of the lithosphere |
| m s, | Thermal diffusivity |
| , | Coupling parameter between asperities |
| , | Ratio between frictions of asperity 2 and 1 |
| , | Impedance parameter |
| , | Ratio between dynamic and static frictions |
| , | Ratio between asperity areas |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dragoni, M.; Santini, S. Contribution of the 2010 Maule Megathrust Earthquake to the Heat Flow at the Peru-Chile Trench. Energies 2022, 15, 2253. https://doi.org/10.3390/en15062253
Dragoni M, Santini S. Contribution of the 2010 Maule Megathrust Earthquake to the Heat Flow at the Peru-Chile Trench. Energies. 2022; 15(6):2253. https://doi.org/10.3390/en15062253
Chicago/Turabian StyleDragoni, Michele, and Stefano Santini. 2022. "Contribution of the 2010 Maule Megathrust Earthquake to the Heat Flow at the Peru-Chile Trench" Energies 15, no. 6: 2253. https://doi.org/10.3390/en15062253
APA StyleDragoni, M., & Santini, S. (2022). Contribution of the 2010 Maule Megathrust Earthquake to the Heat Flow at the Peru-Chile Trench. Energies, 15(6), 2253. https://doi.org/10.3390/en15062253






