An Improved Finite Control Set Model Predictive Current Control for a Two-Phase Hybrid Stepper Motor Fed by a Three-Phase VSI
Abstract
:1. Introduction
- (1)
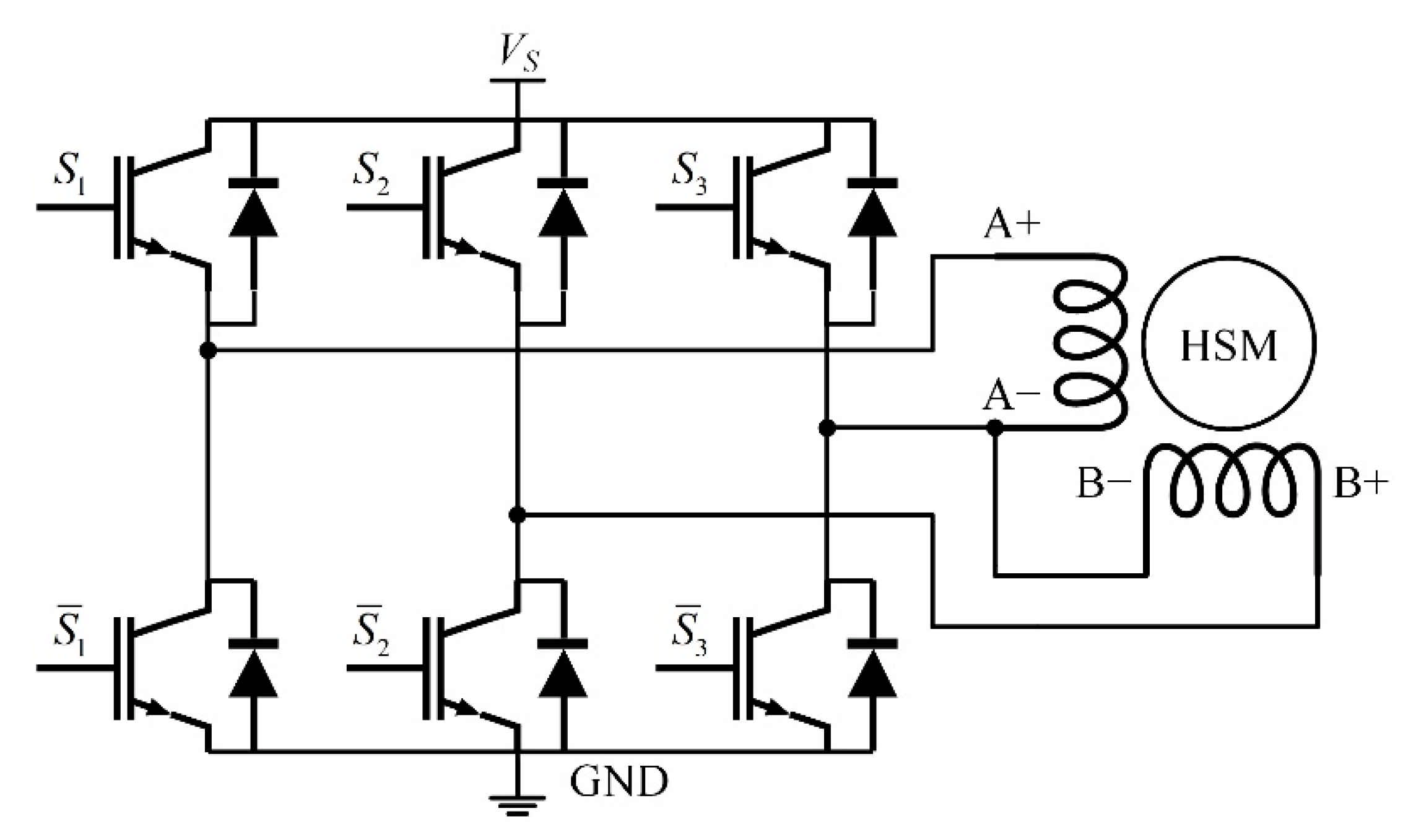
- The two-phase HSM is fed by a low-cost, high-compatibility three-phase two-level VSI, and two-phase currents are regulated simultaneously by an improved FCS-MPCC.
- (2)
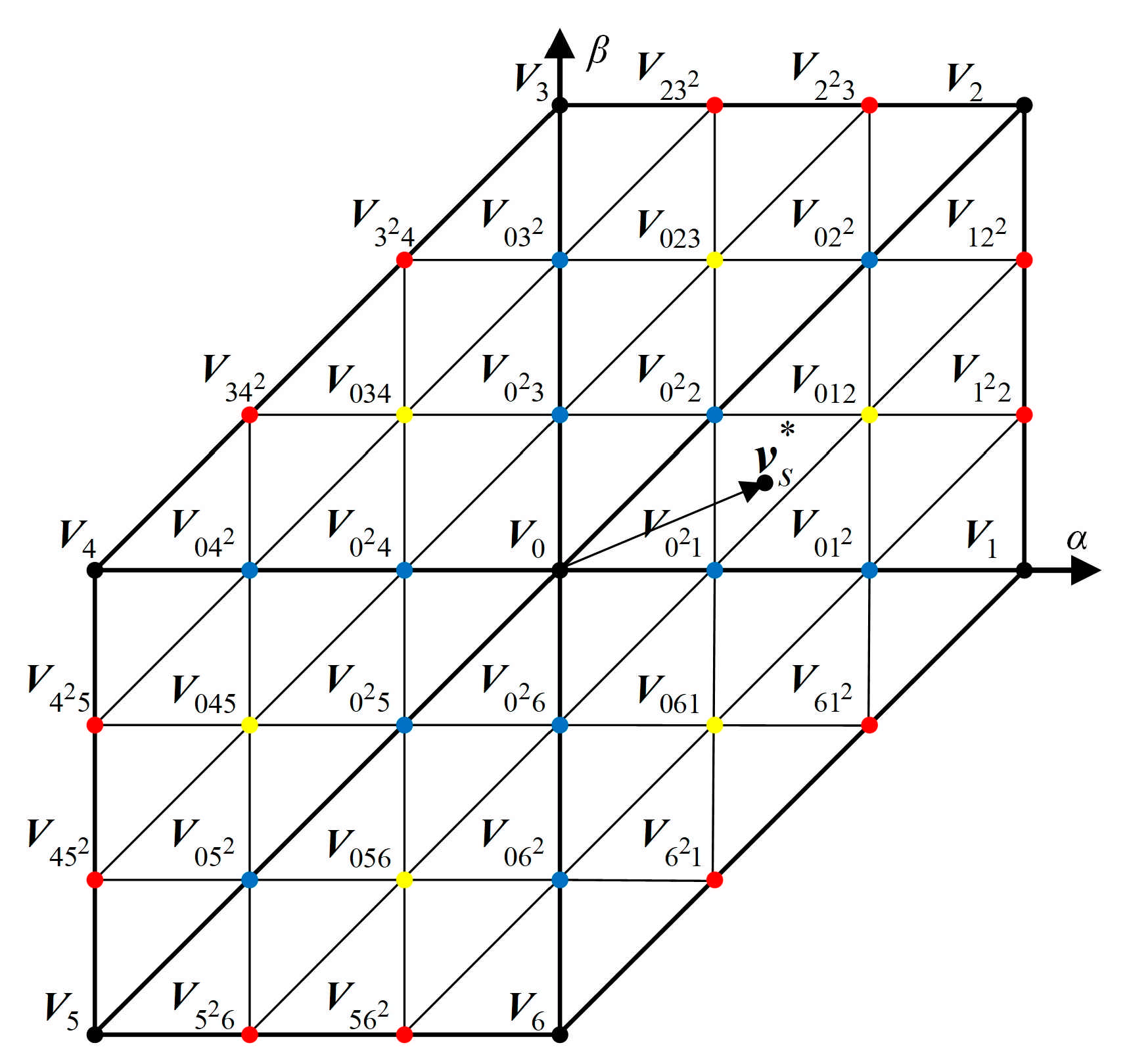
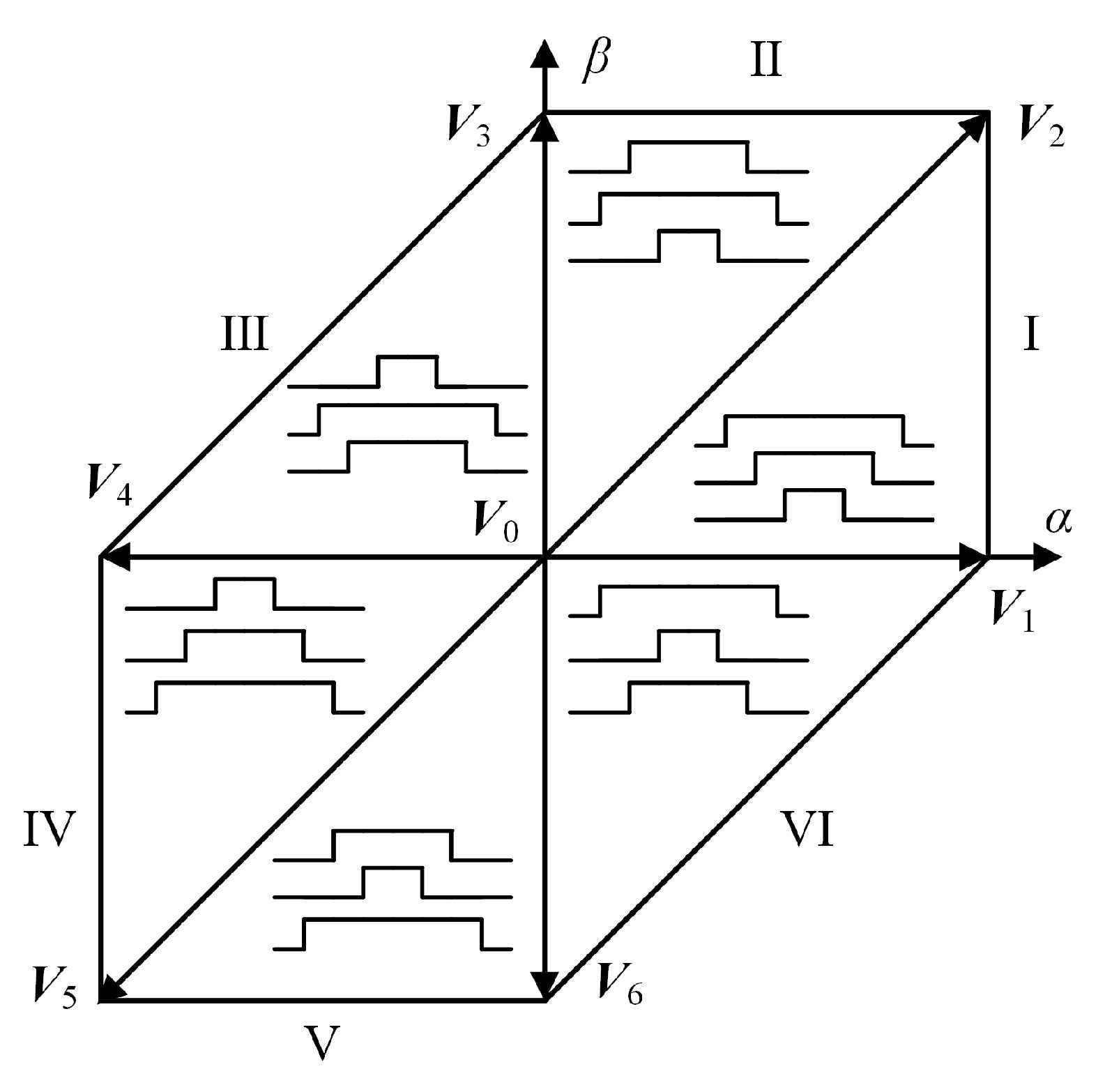
- An extended control set having 37 VVs is built to replace the conventional control set with only six active VVs and one null VVs. The increased VVs improve current quality in rejecting of current ripple and decreasing total harmonic distortion (THD).
- (3)
- Compared with the conventional FCS-MPCC, although the number of admissible VVs in the control set is greatly increased, the workload of determining an optimal VV is significantly reduced. This is because only three VVs adjacent to the reference VV are evaluated in each control period; where the reference VV is obtained using deadbeat control, correspondingly, seven VVs need to be processed in the conventional method.
- (4)
- Build general waveform patterns for each sector, and then instantiate each generalized waveform using corresponding action time to obtain 37 specific waveforms for all VVs. Discrete space vector modulation (DSVM) modulates an optimal VV using the specific waveform related to the VV.
2. Dynamic Model of Two-Phase HSM
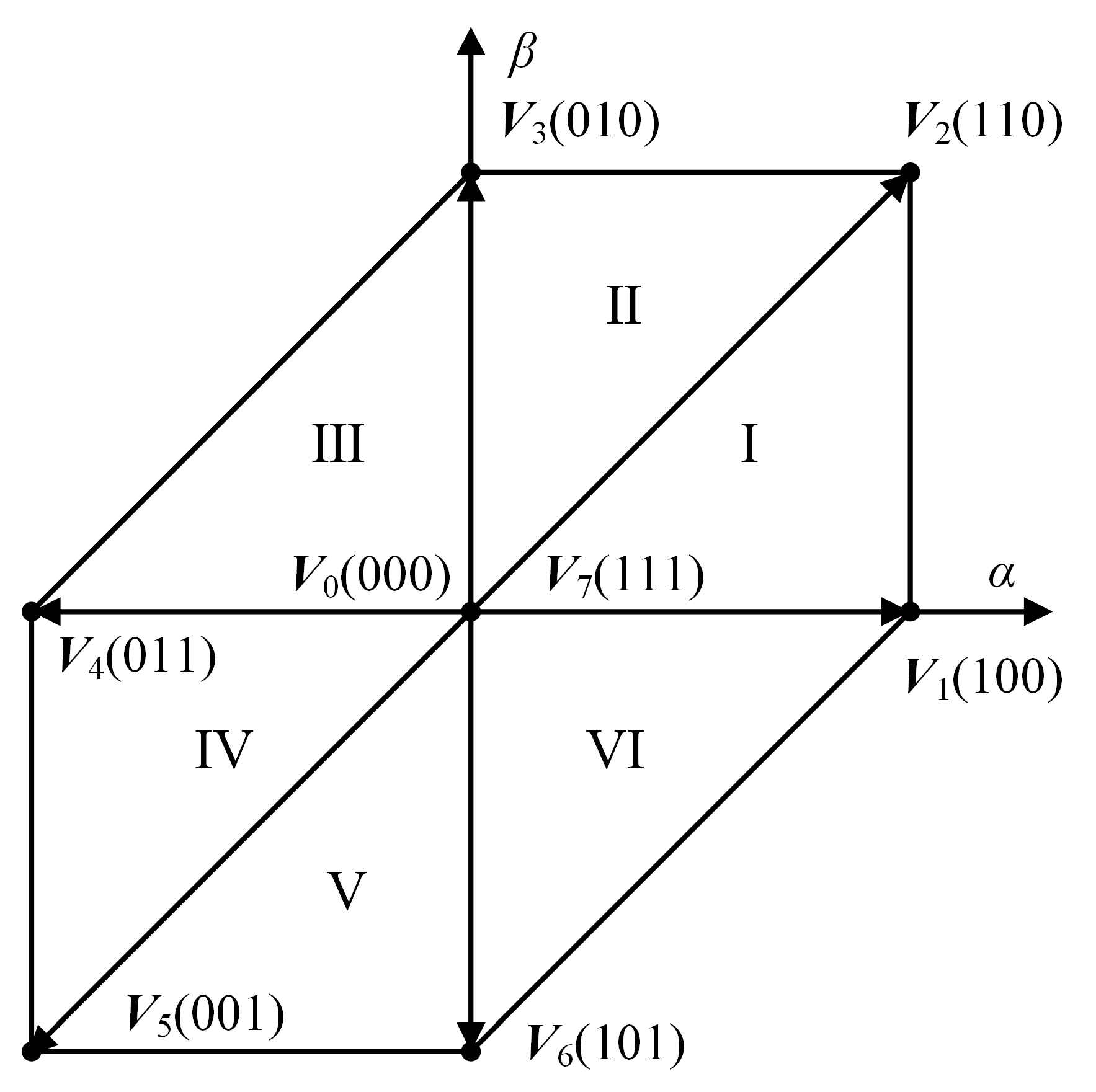
3. The Conventional FCS-MPCC
3.1. Predictive Model of Current
3.2. Cost Function
3.3. Compensation for Computation Delay
4. The Improved FCS-MPCC
4.1. Virtual VV Syntheses by DSVM
4.2. Computational Cost Reduction by Deadbeat Control
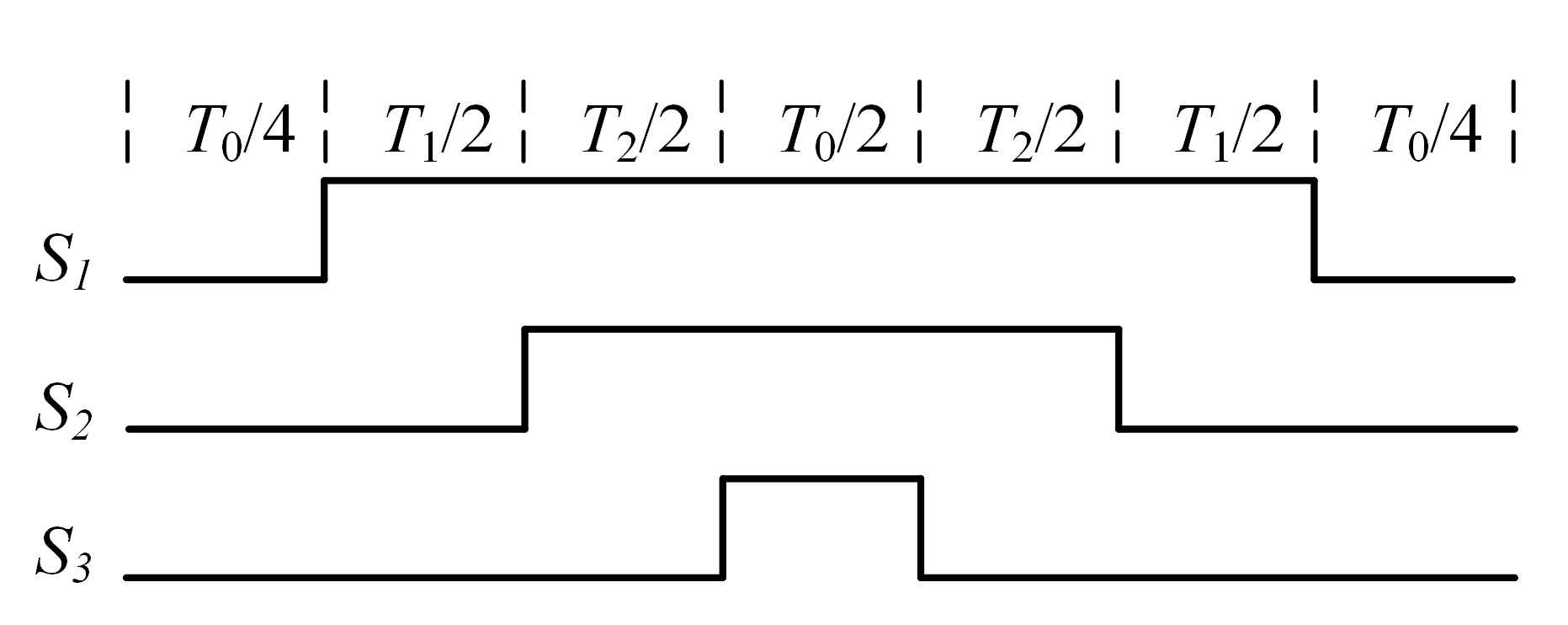
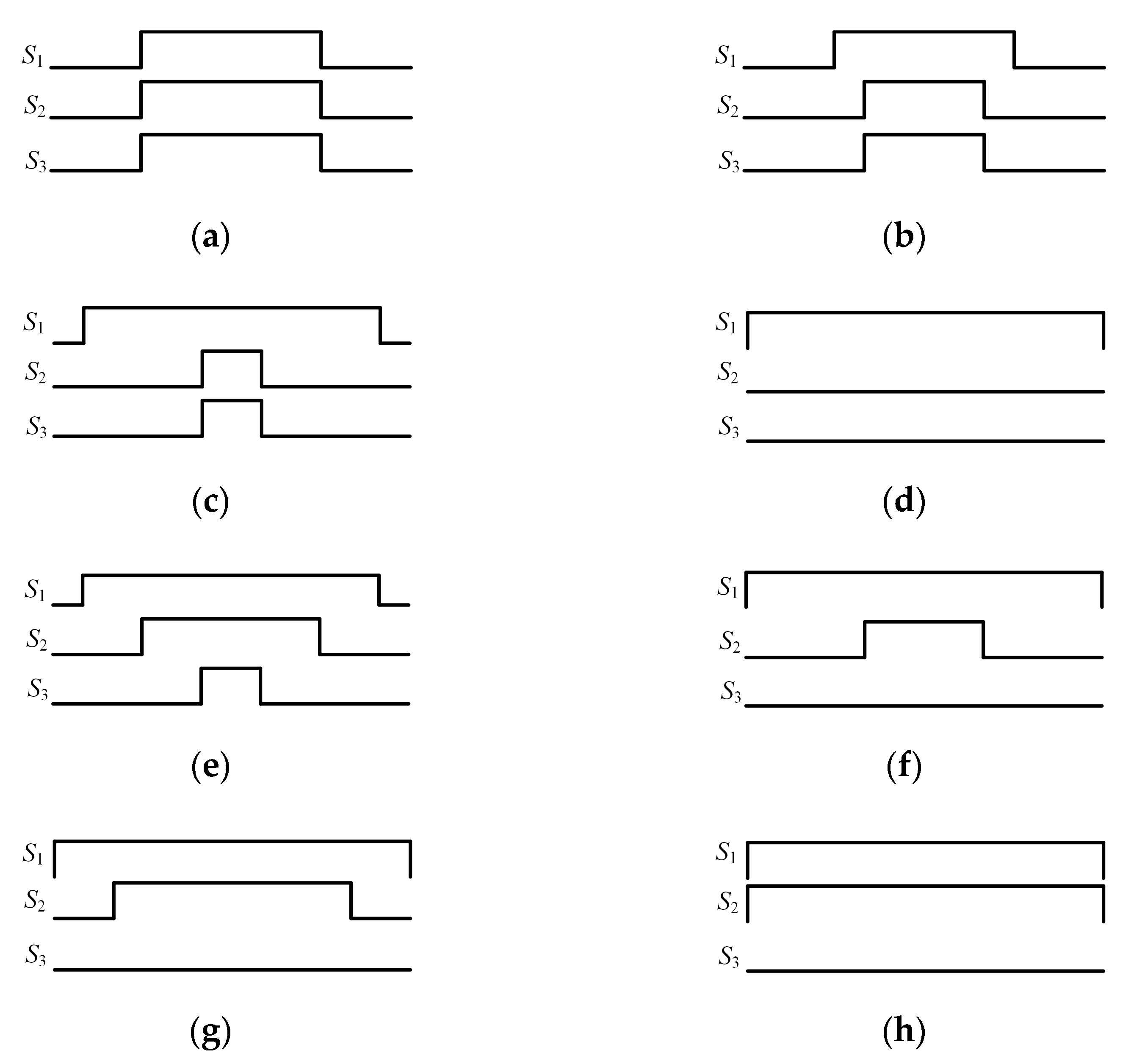
4.3. Switching State Generation
- (1)
- The noninverted control signals for , , and are symmetrical to the middle of the PWM period. This is because the symmetrical waveforms are easy to be realized in DSP; furthermore, additional harmonics exist around the switching frequency when the asymmetry waveforms are used.
- (2)
- The switching orders are S000-S100-S110-S111-S110-S100-S000, where numeral subscripts represent the switching states of the noninverted control signal S1, S2, and S3. Correspondingly, VSI generates V0-V1-V2-V7-V2-V1-V0 sequentially, which is identical to the general SVPWM.
- (3)
- Each control period starts and ends with S000, and S111 is inserted into the control period. Therefore, each noninverted control signal switches twice per PWM period except when the duty cycle is 0% or 100%, which can assure the control signal switching at constant frequency except for the cases in which the duty cycle is 0% or 100%.
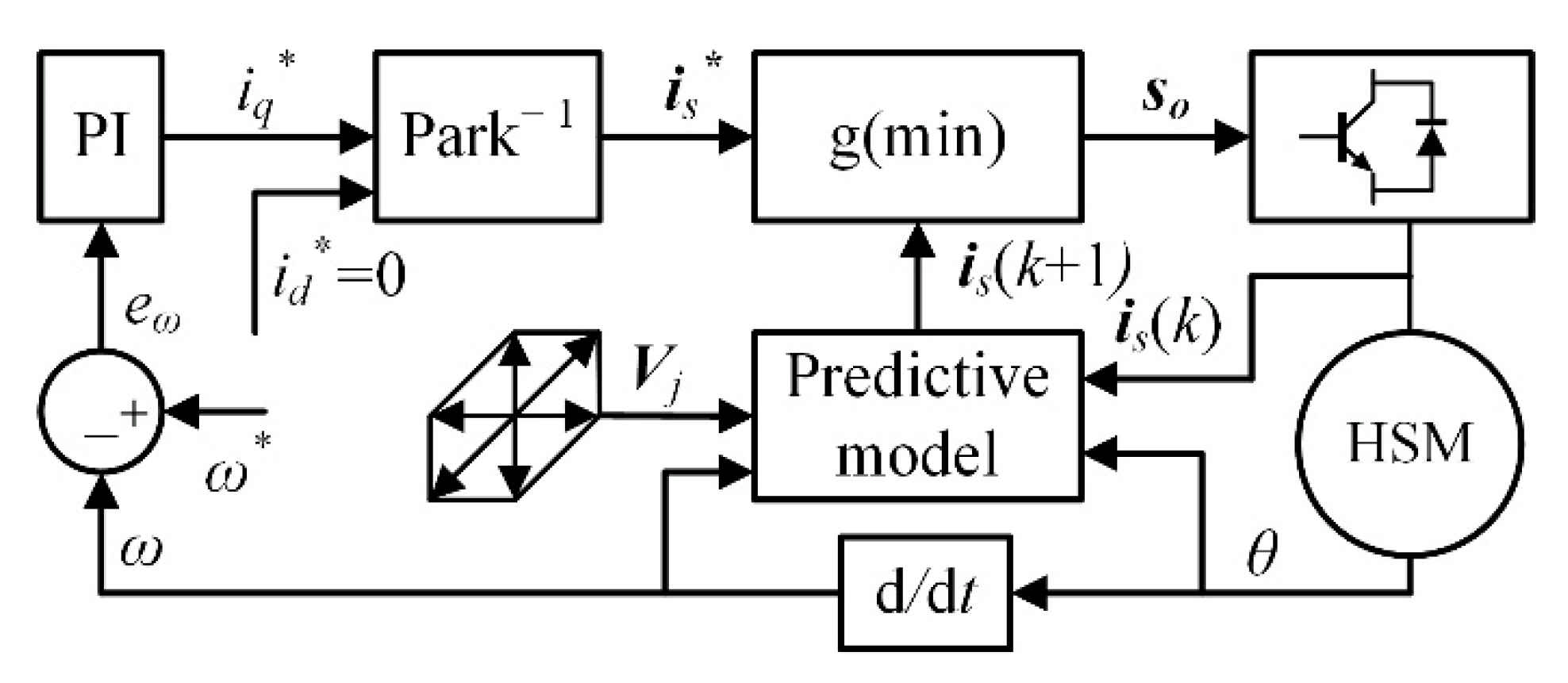
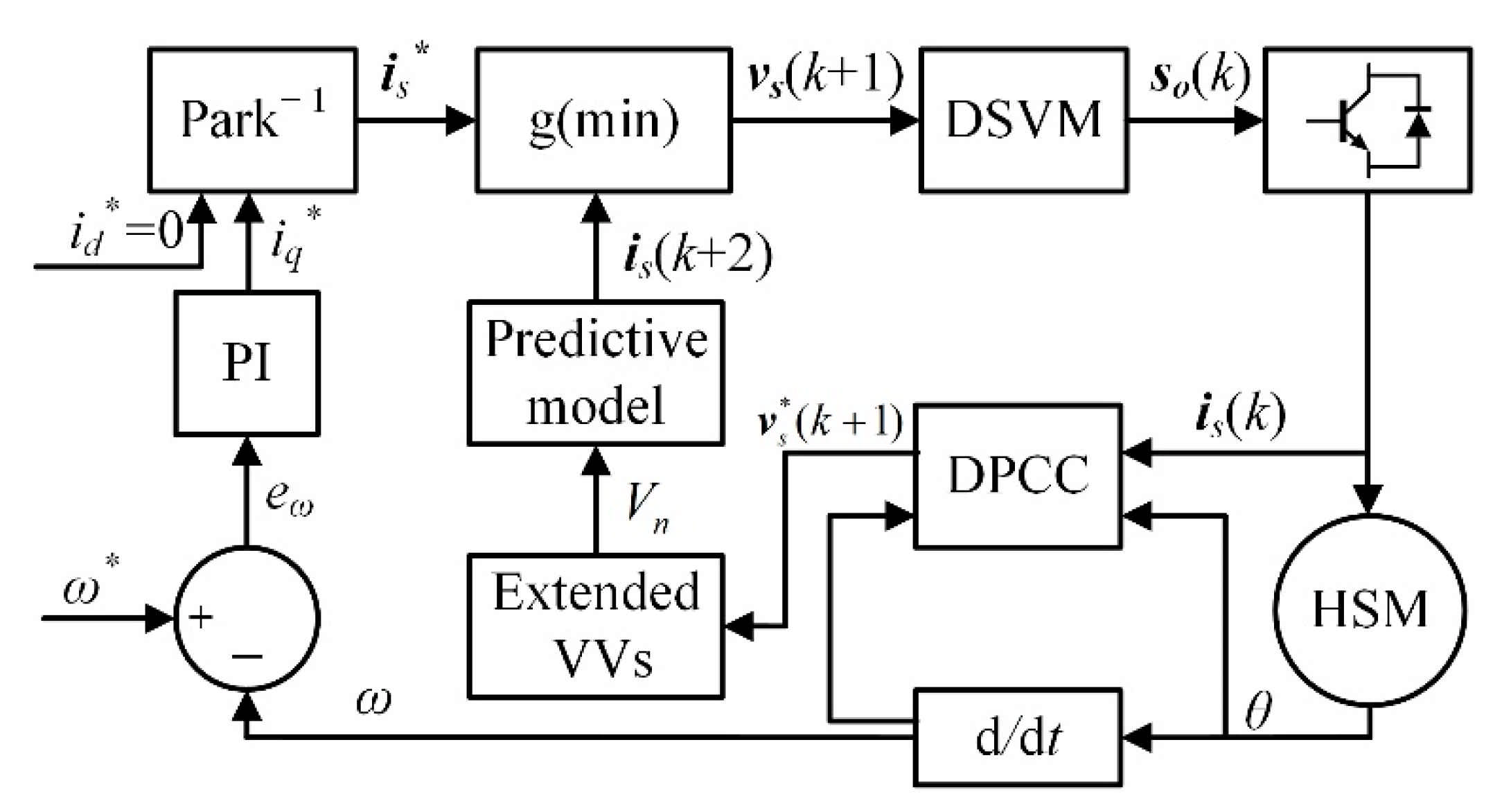
4.4. Overall Improved FCS-MPCC Scheme
- (1)
- Measure current , rotor mechanical position , and speed at the th instant.
- (2)
- Modulate the optimal VV using DSVM, where was obtained at the (k − 1)th sampling period.
- (3)
- Estimate current , taking advantage of , , and , etc.
- (4)
- Predict a reference VV using DPCC, and then build a new control set , consisting of only three VVs adjacent to .
- (5)
- Predict current for each VV in , and then evaluate them using a cost function; finally, determine the optimal VV based on the minimum value principle.
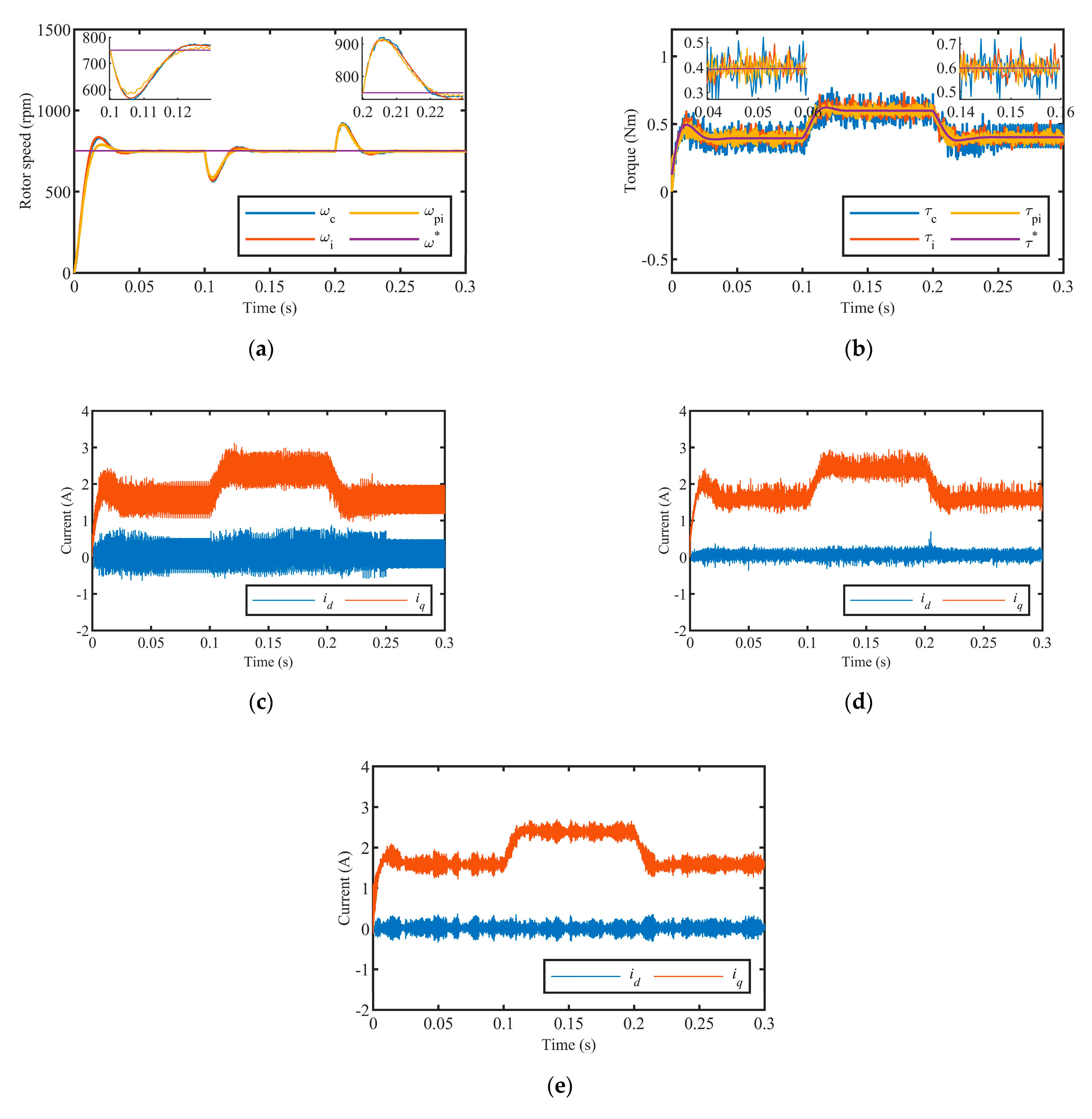
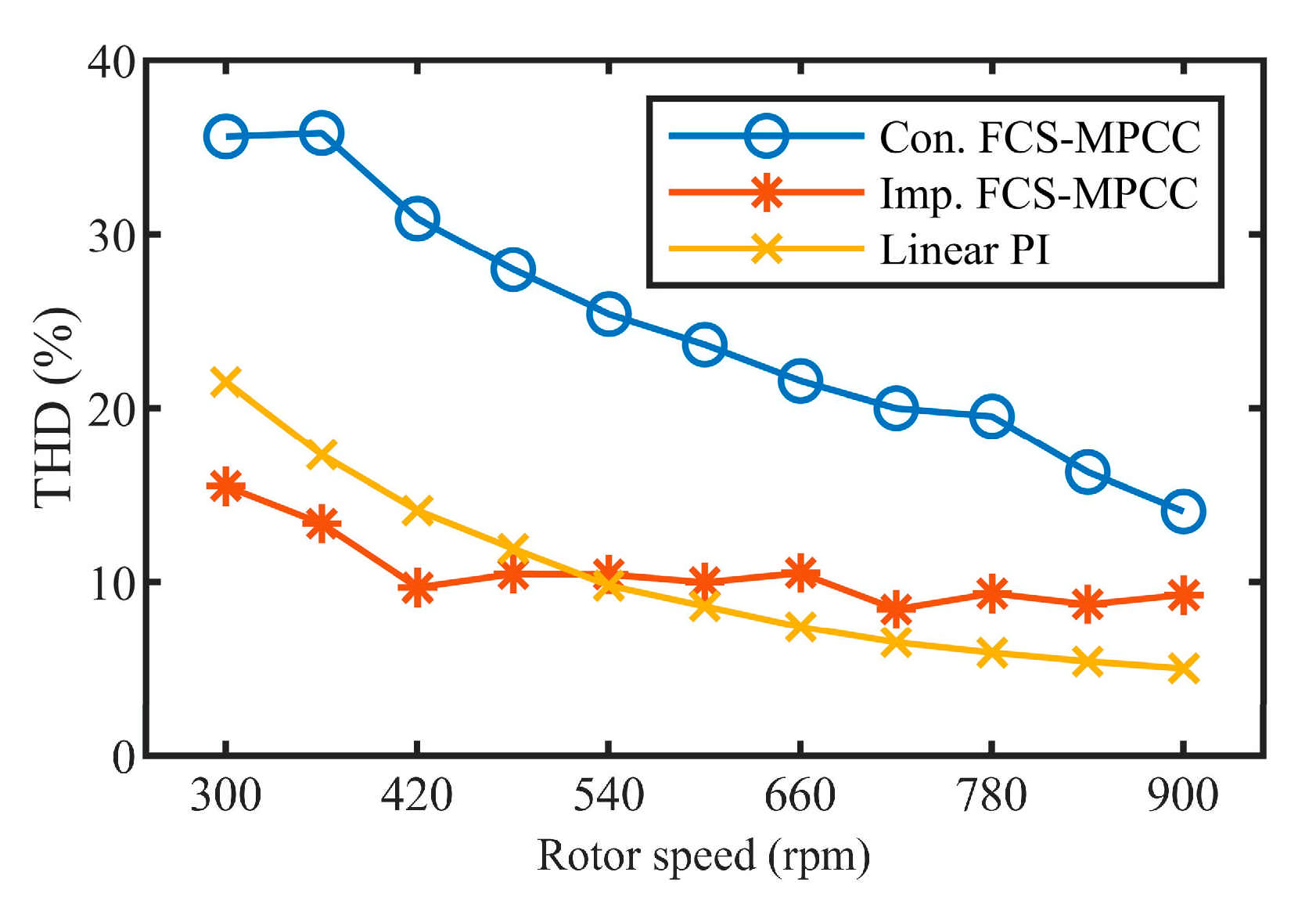
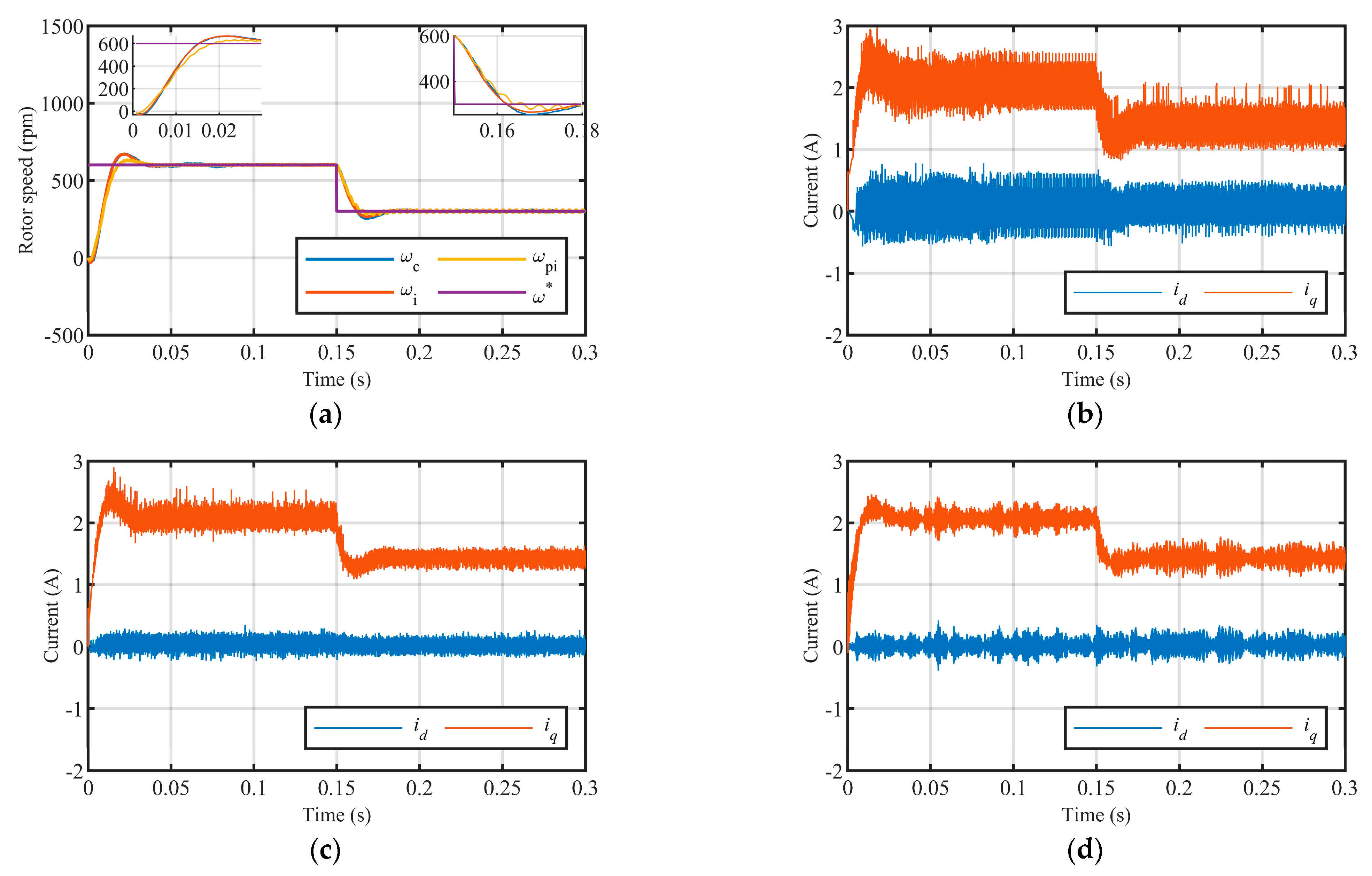
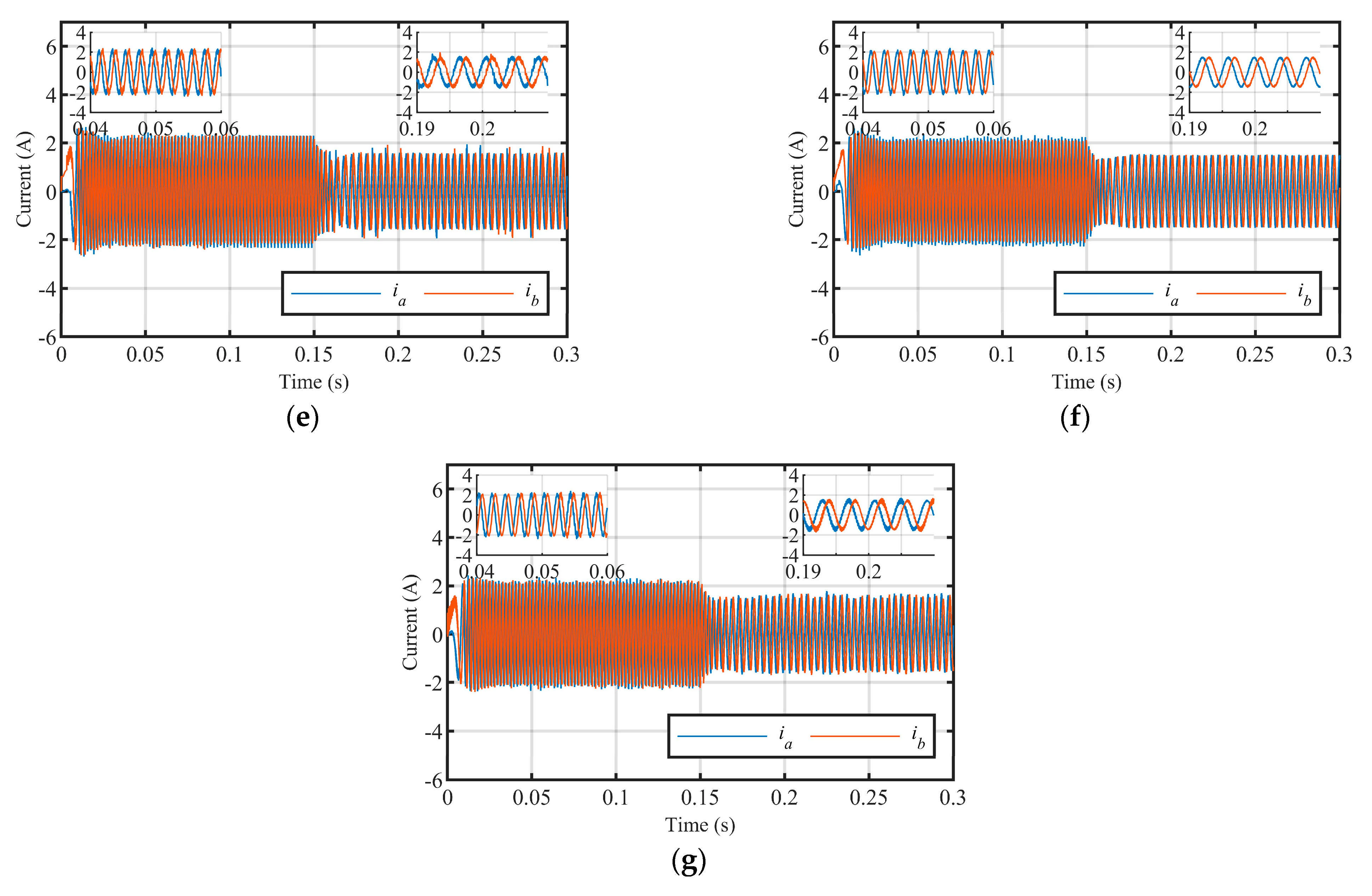
5. Simulation and Experimental Verification
5.1. Simulation Verification
5.2. Experimental Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zaky, M.S. A self-tuning PI controller for the speed control of electrical motor drives. Electr. Power Syst. Res. 2015, 119, 293–303. [Google Scholar] [CrossRef]
- Derammelaere, S.; Vervisch, B.; De Viaene, J.; Stockman, K. Sensorless load angle control for two-phase hybrid stepper motors. Mechatronics 2017, 43, 6–17. [Google Scholar] [CrossRef]
- Derammelaere, S.; Vervisch, B.; Belie, F.D.; Vanwalleghem, B.; Cottyn, J.; Cox, P.; Abeele, G.V.d.; Stockman, K.; Vandevelde, L. The Efficiency of Hybrid Stepping Motors: Analyzing the Impact of Control Algorithms. IEEE Ind. Appl. Mag. 2014, 20, 50–60. [Google Scholar] [CrossRef]
- Kim, W.; Shin, D.; Lee, Y.; Chung, C.C. Simplified torque modulated microstepping for position control of permanent magnet stepper motors. Mechatronics 2016, 35, 162–172. [Google Scholar] [CrossRef]
- Gaan, D.R.; Kumar, M.; Sudhakar, S. Real-Time Precise Position Tracking with Stepper Motor Using Frequency Modulation Based Microstepping. IEEE Trans. Ind. Appl. 2018, 54, 693–701. [Google Scholar] [CrossRef]
- Le, K.M.; Hoang, H.V.; Jeon, J.W. An Advanced Closed-Loop Control to Improve the Performance of Hybrid Stepper Motors. IEEE Trans. Power Electron. 2017, 32, 7244–7255. [Google Scholar] [CrossRef]
- Tran, H.N.; Le, K.M.; Jeon, J.W. Adaptive Current Controller Based on Neural Network and Double Phase Compensator for a Stepper Motor. IEEE Trans. Power Electron. 2019, 34, 8092–8103. [Google Scholar] [CrossRef]
- Betin, F.; Pinchon, D.; Capolino, G.A. Fuzzy logic applied to speed control of a stepping motor drive. IEEE Trans. Ind. Electron. 2000, 47, 610–622. [Google Scholar] [CrossRef]
- Rubaai, A.; Castro-Sitiriche, M.J.; Garuba, M.; Burge, L. Implementation of Artificial Neural Network-Based Tracking Controller for High-Performance Stepper Motor Drives. IEEE Trans. Ind. Electron. 2007, 54, 218–227. [Google Scholar] [CrossRef]
- Ghanooni, P.; Yazdani, A.M.; Mahmoudi, A.; MahmoudZadeh, S.; AhmadiMovahed, M.; Fathi, M. Robust precise trajectory tracking of hybrid stepper motor using adaptive critic-based neuro-fuzzy controller. Comput. Electr. Eng. 2020, 81, 106535. [Google Scholar] [CrossRef]
- Zaky, M.S. Robust chatter-free continuous VSC for the speed control of electrical motor drives using adaptive feedback gain. Electr. Power Syst. Res. 2016, 140, 786–796. [Google Scholar] [CrossRef]
- Daouda, M.; Lin, C.-L.; Lee, C.-S.; Yang, C.-C.; Chen, C.-A. Model predictive control of sensorless hybrid stepper motors in auxiliary adjuster for stereotactic frame fixation. Mechatronics 2017, 47, 160–167. [Google Scholar] [CrossRef]
- Wang, C.; Cao, D. New Sensorless Speed Control of a Hybrid Stepper Motor Based on Fuzzy Sliding Mode Observer. Energies 2020, 13, 4939. [Google Scholar] [CrossRef]
- Harnefors, L.; Saarakkala, S.E.; Hinkkanen, M. Speed Control of Electrical Drives Using Classical Control Methods. IEEE Trans. Ind. Appl. 2013, 49, 889–898. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, W.; Du, Y.; Cheng, Y.; Zhu, J. Simplified Fault-Tolerant Model Predictive Control for a Five-Phase Permanent-Magnet Motor with Reduced Computation Burden. IEEE Trans. Power Electron. 2020, 35, 3850–3858. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, Y. Model Predictive Current Control for PMSM Drives with Parameter Robustness Improvement. IEEE Trans. Power Electron. 2019, 34, 1645–1657. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y. Direct Voltage-Selection Based Model Predictive Direct Speed Control for PMSM Drives Without Weighting Factor. IEEE Trans. Power Electron. 2019, 34, 7838–7851. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef] [Green Version]
- Bolognani, S.; Bolognani, S.; Peretti, L.; Zigliotto, M. Design and Implementation of Model Predictive Control for Electrical Motor Drives. IEEE Trans. Ind. Electron. 2009, 56, 1925–1936. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zanchetta, P.; Abu-Rub, H.; Young, H.A.; Rojas, C.A. State of the Art of Finite Control Set Model Predictive Control in Power Electronics. IEEE Trans. Ind. Inform. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model Predictive Control—A Simple and Powerful Method to Control Power Converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Sheng-Ming, Y.; Feng-Chieh, L.; Ming-Tsung, C. Micro-stepping control of a two-phase linear stepping motor with three-phase VSI inverter for high-speed applications. IEEE Trans. Ind. Appl. 2004, 40, 1257–1264. [Google Scholar] [CrossRef]
- Bodson, M.; Chiasson, J.N.; Novotnak, R.T.; Rekowski, R.B. High-performance nonlinear feedback control of a permanent magnet stepper motor. IEEE Trans. Control Syst. Technol. 1993, 1, 5–14. [Google Scholar] [CrossRef]
- Wang, F.; Zuo, K.; Tao, P.; Rodríguez, J. High Performance Model Predictive Control for PMSM by Using Stator Current Mathematical Model Self-Regulation Technique. IEEE Trans. Power Electron. 2020, 35, 13652–13662. [Google Scholar] [CrossRef]
- Hang, J.; Wu, H.; Zhang, J.; Ding, S.; Huang, Y.; Hua, W. Cost Function-Based Open-Phase Fault Diagnosis for PMSM Drive System with Model Predictive Current Control. IEEE Trans. Power Electron. 2021, 36, 2574–2583. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Niu, S.; Luo, Y.; Fu, W.; Zhang, X. An Indirect Reference Vector-Based Model Predictive Control for a Three-Phase PMSM Motor. IEEE Access 2020, 8, 29435–29445. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Liang, J.; Xia, B.; Walker, P.D.; Zhang, N. Deadbeat control based on a multipurpose disturbance observer for permanent magnet synchronous motors. IET Electr. Power Appl. 2018, 12, 708–716. [Google Scholar] [CrossRef] [Green Version]
- Bellini, A.; Concari, C.; Franceschini, G.; Toscani, A. Mixed-Mode PWM for High-Performance Stepping Motors. IEEE Trans. Ind. Electron. 2007, 54, 3167–3177. [Google Scholar] [CrossRef]


| VVs | T0 | T1 | T2 |
|---|---|---|---|
| 0 |
| Parameter | Value |
|---|---|
| Phase resistance (R) | |
| Phase inductance (L) | 1.38 mH |
| Torque constant (Km) | 0.25 Nm/A |
| Rotor inertia (J) | 280 × 10−7 Nm s2/rad |
| Viscous friction coefficient (B) | 5 × 10−3 Nm·s/rad |
| Number of teeth on the rotor (Nr) | 50 |
| Supply voltage (Vs) | 36 V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Cao, D.; Qu, X.; Fan, C. An Improved Finite Control Set Model Predictive Current Control for a Two-Phase Hybrid Stepper Motor Fed by a Three-Phase VSI. Energies 2022, 15, 1222. https://doi.org/10.3390/en15031222
Wang C, Cao D, Qu X, Fan C. An Improved Finite Control Set Model Predictive Current Control for a Two-Phase Hybrid Stepper Motor Fed by a Three-Phase VSI. Energies. 2022; 15(3):1222. https://doi.org/10.3390/en15031222
Chicago/Turabian StyleWang, Chunlei, Dongxing Cao, Xiangxu Qu, and Chen Fan. 2022. "An Improved Finite Control Set Model Predictive Current Control for a Two-Phase Hybrid Stepper Motor Fed by a Three-Phase VSI" Energies 15, no. 3: 1222. https://doi.org/10.3390/en15031222
APA StyleWang, C., Cao, D., Qu, X., & Fan, C. (2022). An Improved Finite Control Set Model Predictive Current Control for a Two-Phase Hybrid Stepper Motor Fed by a Three-Phase VSI. Energies, 15(3), 1222. https://doi.org/10.3390/en15031222






