Abstract
A novel Artificial Neural Network (ANN) Based Optimal Feedforward Torque Control (OFTC) strategy is proposed which, after proper ANN design, training and validation, allows to analytically compute the optimal reference currents (minimizing copper and iron losses) for Interior Permanent Magnet Synchronous Machines (IPMSMs) with highly operating point dependent nonlinear electric and magnetic characteristics. In contrast to conventional OFTC, which either utilizes large look-up tables (LUTs; with more than three input parameters) or computes the optimal reference currents numerically or analytically but iteratively (due to the necessary online linearization), the proposed ANN-based OFTC strategy does not require iterations nor a decision tree to find the optimal operation strategy such as e.g., Maximum Torque per Losses (MTPL), Maximum Current (MC) or Field Weakening (FW). Therefore, it is (much) faster and easier to implement while (i) still machine nonlinearities and nonidealities such as e.g., magnetic cross-coupling and saturation and speed-dependent iron losses can be considered and (ii) very accurate optimal reference currents are obtained. Comprehensive simulation results for a real and highly nonlinear IPMSM clearly show these benefits of the proposed ANN-based OFTC approach compared to conventional OFTC strategies using LUT-based, numerical or analytical computation of the reference currents.
Notation
: natural, real numbers; : column vector, where “” and “” mean “transposed” and “is defined as”, resp.; : scalar product of vectors & ; : Euclidean norm of ; : matrix (n rows & columns); , : inverse, inverse transpose of (if exist), resp.; : identity matrix; : zero vector; : rotation matrix (by ).
Remark: All physical quantities are introduced and explained in the text to ease reading.
1. Introduction
1.1. Motivation
Electric machines are widely used in plenty of applications for manufacturing, grinding, pumping or in robots, electric vehicles, wind turbines or conventional power plants. For all applications, reliability and efficiency play key roles. Though electric motors still consume over 50% of the world’s generated electric energy [1] from which 84.3% is generated from fossil fuels [2]. In particular for the mobility sector, for the consumer, besides the lacking charging opportunities, the range of electric vehicles is considered the major obstacle for quick penetration of the future mobility market [3]. Nevertheless, hybrid electric vehicles (HEV) and battery electric vehicles (BEV) will become standard vehicles in the mobility sector. Therefore, engineers worldwide are striving to optimize the electrical drive system in order to reduce energy consumption and increase efficiency.
In this regard, the optimal feedforward torque control (OFTC) problem must be solved to compute optimal reference currents which minimize iron and copper losses by invoking optimal operation strategies for all operating conditions [4,5]. The different operation strategies are usually Maximum Torque per Ampere/Current (MTPA/MTPC), Maximum Torque per Losses (MTPL; considering also iron losses), Field Weakening (FW), Maximum Current (MC) and Maximum Torque per Voltage (MTPV). As alternative, Maximum Torque per Flux (MTPF) has been proposed as it is easier to compute, but it should be avoided as it represents an oversimplification with suboptimal operation and MTPV should be used instead [6]. All of those optimal operation strategies exploit the non-uniqueness of the current pairs which produce the same torque [4]. In order to minimize conduction and switching losses additionally, optimal pulse patterns (OPPs) must be implemented [7] which have to be computed separately for nonlinear machines with significant anisotropy [8,9].
In this paper, a novel ANN-based OFTC is proposed. The OFTC problem has been discussed in numerous publications (see e.g., [10,11,12,13,14,15,16,17,18,19] for MTPC/MTPA, [12,14,18,20,21,22,23,24] for FW, [4,5,12,25] for MC, [4,5,13,26,27,28,29] for MTPL, and [6,14,20,21,22,23] for MTPV). The goal of OFTC is to compute or look up optimal reference currents for each of the aforementioned operation strategies. This is mostly done numerically or in few cases analytically imposing simplifying assumptions such as the neglection of the nonidealities: (a) varying stator resistance, (b) nonlinear magnetic cross-coupling and saturation, (c) physical current and voltage constraints, (d) iron losses and (e) temperature dependencies.
Analytical approaches are in particular of interest due to their rather simple, equation-based implementation, high accuracy and fast computation. However, if all nonidealities (see (a)–(e) above) shall be considered, the analytical solution must be computed iteratively due to the online linearization of the highly nonlinear OFTC problem. Numerical approaches usually rely on look-up tables (LUTs). To account for all nonidealities (see (a)–(e) above), the LUTs become rather huge and often depend on more than three inputs. In conclusion, both approaches come with drawbacks either due to limited computational power or limited memory storage.
In this paper, these drawbacks shall be overcome by using a rather simple ANN to solve the OFTC problem still analytically but not iteratively. To not hit computational and memory constraints, the ANN must be tailored to the capability of the utilized real-time platforms (e.g., digital signal processor (DSP) or field-programmable gate array (FPGA)).
As artificial neural networks are a promising technology, machine learning-based approaches in electrical drives have already been reported in numerous publications (see the recent overview preprint [30] with 259 references). Exemplary applications of ANNs in the field of electrical drive systems are: ANN-based speed, current or speed and current controllers [31,32,33,34,35,36,37,38], ANN-based parameter/system identification [39,40,41], ANN-based temperature or resistance estimation [42,43], ANN-based direct/predictive torque or model predictive control [44,45,46], ANN-based torque observers [47], ANN-based current waveform prediction [48], ANN-based encoderless control [49,50,51,52], ANN-based torque ripple reduction [53,54], ANN-based condition monitoring or fault detection [55,56,57,58], ANN-based optimal pulse patterns [59], and ANN-based multi-objective optimization for machine design [60].
However, to the best knowledge of the authors, ANNs have not been used this far to solve the OFTC problem as proposed in this paper. Therefore, this paper is the very first considering ANN-based OFTC.
The remainder of the paper is structured as follows: In the following three subsections, a detailed literature review is presented, the problem is formally stated and the proposed solution is briefly introduced (see Section 1.2, Section 1.3 and Section 1.4, respectively.). In Section 2, the novel idea of ANN-based OFTC is discussed in detail; starting with the ANN design in Section 2.1, followed by the ANN training (including a thorough explanation of the required data set creation) in Section 2.2, completed by the ANN validation in Section 2.3. In Section 3, the ANN-based OFTC strategy is implemented in the closed-loop control system of an electrical drive with highly nonlinear magnetic characteristics and iron losses and its performance is compared to conventional state-of-the-art OFTC with analytical optimal reference current computation (ORCC). Finally, Section 4 concludes the paper by (a) summarizing the proposed idea and obtained results and (b) by giving a short outlook on future research directions.
1.2. Detailed Literature Review
In this subsection, the references listed above concerning OFTC and ANN in electrical drives are discussed in more detail.
1.2.1. Optimal Feedforward Torque Control (OFTC)
The most common OFTC strategy is MTPC (often also called MTPA) which minimizes copper (Joule) losses only. A comprehensive literature review on MTPC was recently published in [19]. The early contribution [10] computes optimal stator current angles considering current and voltage limits in PMSM electrical drives to minimize copper losses. Iron losses, magnetic cross-coupling and saturation effects are neglected. The MTPC algorithm in [11] is based on [10] but in addition, considers cross-coupling effects. The optimal current angles are obtained by online perturbation of the current magnitude. In [14], an analytical computation of the optimal MTPC currents is presented based on Lagrangian multipliers and Ferrari’s method. However, iron losses and magnetic cross-coupling and saturation effects are not considered.
Iron losses complicate efficiency enhancement but have also been considered in several publications. Loss Minimization Control (LMC) was proposed in [26] by formulating and solving a convex optimization problem numerically and iteratively to minimize copper and iron losses. In [27], a novel calculation method for the iron loss resistance is introduced which is based on a slope evaluation of the linear approximation of the relation between semi-input power and squared speed-dependent electromotive force. The loss minimization algorithm (LMA) proposed in [28] conducts an iterative search to minimize copper and iron losses online. Magnetic cross-coupling and saturation effects are not considered. In [13], it proposes an optimal current feed-forward angle to minimze copper and iron losses in nonlinear traction drives. In [29], Maximum Efficiency per Ampere (MEPA; i.e., MTPL) control is proposed and performs an online search to find optimal stator current angles minimizing copper and iron losses for PMSMs with significant magnetic cross-coupling and saturation effects.
In [20], an MTPV strategy for reluctance synchronous machines is proposed which allows to analytically compute the optimal MTPV reference currents. Stator resistance and magnetic saturation are considered while iron losses and magnetic cross-coupling effects are not considered. In [21], the effect of neglecting the stator resistance on the MTPV operation is discussed and an analytical computation of the optimal MTPV currents is proposed. Iron losses, magnetic saturation and cross-coupling effects are neglected. [6] computes the MTPV hyperbola analytically while considering the stator resistance. Magnetic saturation and iron losses are neglected. Magnetic cross-coupling effects were not explicitly addressed but the presented approach allows to incorporate those as well. [23] combines FW and MTPV with sensorless control. Iron losses are considered and the position estimation error due to iron losses is compensated for by a modified disturbance observer.
Only a few publications deal with the overall operation management for OFTC including MTPC, MC, FW and MTPV. LUT-based OFTC strategies for MC, MTPC and MTPV are proposed in [12] while magnetic cross-coupling effects and iron losses are neglected. OFTC for PMSMs including MTPC, MC, FW and MTPV is proposed in [15]. The optimal stator currents are obtained by an analytical computation but iron losses, magnetic cross-coupling and saturation effects are not considered. In [16], a complete operation management for nonlinear PMSMs including MTPC, MC, FW and MTPV is presented. An iterative algorithm finds the optimal stator currents by evaluating machine maps (e.g., flux linkages) online. Iron losses are neglected. The algorithm presented in [17] achieves MTPC, MC and FW by “incremental current setpoint shaping” (online linearization of torque, voltage and current limit). However, current-dependent inductances, magnetic cross-coupling effects or iron losses are not considered. In [18], an MTPC and FW based speed controller is derived using Lyapunov’s direct method. The controller is combined with online parameter estimation of inductance, torque and viscous friction but iron losses, magnetic cross-coupling and saturation effects are not covered. In [24], optimal saliency ratio and power factor are considered during machine design to minimize copper and iron losses for high efficiency operation of nonlinear IPMSMs. Magnetic cross-coupling is not considered. In [22], MTPC, MC, FW and MTPV are discussed in combination with model predictive direct torque control. Iron losses, magnetic cross-coupling and saturation effects are neglected. In [25], a unified theory for OFTC is presented which allows to analytically compute the optimal reference currents for MTPC, MC, FW, MTPV and Maximum Torque per Flux (MPTF) while magnetic cross-coupling and saturation effects are considered. Iron losses are neglected. The approach has been extended in [4] by MTPL to account for iron losses as well. In [5], MTPL, FW, MC and MTPV are introduced for current and speed-dependent iron losses and the optimal reference currents are obtained analytically but iteratively due to the necessary online linearization of the nonlinear optimization problem.
1.2.2. Artificial Neural Networks in Electrical Drives
As already mentioned in the motivation, there exists a huge variety of ANN-based approaches in electrical drive systems (recall the overview preprint [30] with more than 250 references). Although [30] is very comprehensive, in the following, several additional and exemplary applications of ANNs in electrical drives are (re-)discussed in more detail to highlight that ANN-based OFTC has neither been considered nor published this far.
ANN-based speed and/or current controllers are the most common applications of ANNs in electrical drives. [31] proposes an ANN-based speed control method for PMSMs. The ANN has two inputs (actual and previous machine speed) and one output (the predicted machine speed) and is trained to identify the nonlinear machine dynamics to improve control performance. [32] presents an ANN-based model reference adaptive controller (MRAC) whose controller parameters are adjusted with the help of an ANN-based state observer performing online model identification. The closed-loop system performance shows negligible overshooting and fast rise times under various loading conditions and speed reversals. In [33], an ANN-based speed controller for a PMSM has been implemented, where the ANN is used to predict the actual machine torque which is then fed to a classical field-oriented current control system with flux observer. In [34], the PI speed controller for a PMSM is also replaced by an ANN-based speed controller, whereas an ANN-based PID speed controller is proposed in [35]. In [36], both, PI speed controller and PI current controllers, are replaced by ANN-based controllers. In general, overshoot as well as settling time were improved by the proposed ANN-based controllers. [37] proposes a real-time capable ANN-based controller for a linear tubular permanent magnet direct current motor (LTPMDCM) prototype. The used multilayer perceptron (MLP) recurrent neural network (RNN) is trained with conventional backpropagation. [38] presents an ANN-based speed controller for induction motor drives using an ANN with adaptive linear neurons (ADALINE) trained with the Widrow-Hoff learning rule. The closed-loop system shows a significantly improved tracking performance compared to the standard PI speed controller.
In [44], it proposes an ANN-based direct torque control method for synchronous motors. The proposed ANN controller outputs optimal voltages to increase the motor’s efficiency. However, losses or OFTC with ORCC are neither considered nor discussed. In [45], an ANN is utilized to enable long-horizon finite control set model predictive control (FCS-MPC) for IPMSM drive systems. The ANN can identify the optimal switching states with high accuracy (85–90%) which allows for a real-time capable implementation of the long-horizon FCS-MPC algorithm. In [46], the weighting factors of the cost functions of a predictive torque controller (PTC) were calculated by ANNs which not only improved the control function but also the calculation time and the computational effort.
Besides ANN-based controllers, ANN-based parameter and/or system identification is very popular. In [39], a feedforward ANN with sigmoid activation functions is used to identify the electro-magnetic dynamics for stator current and rotor speed control of induction machines. The ANN is trained by arbitrarily injected noise signals during closed-loop operation. In [40], an ANN with two hidden layers and sigmoid activation functions is used to identify the nonlinear DC motor drive dynamics to implement a nonlinear speed controller for the electrical drive system. The ANN is trained online by backpropagation with adjustable learning rate. [41] proposes an ANN with radial basis functions (RBF) for the identification of the rotor resistance and the estimation of the rotor speed of induction machines. The ANN is trained online during closed-loop operation.
In [42], recurrent and convolutional neural networks (RNNs & CNNs) are utilized and compared for temperature estimation in the stator (resistance) and rotor (permanent magnet) of PMSMs. The ANN’s optimal architecture (number of layers and neurons) is found by Bayesian optimization. Nevertheless, only local minima are reached. The ANNs are implemented on a Raspberry Pi allowing for real-time execution. In [43], an ANN is trained to predict the wire insulation resistance with resprect to its aging time and temperature. Compared to conventional thermal qualification methods used in electrical machines, the ANN-based approach saves about 57% of the time needed for a conventional accelerated aging test campaign.
An ANN-based torque observer has been implemented in [47] achieving very high accuracies (up to 98%) in the observed torque using a relatively small ANN with only one hidden layer. The observed torque is fed to a PI controller which outputs the q-current reference for the underlying current PI controllers. The d-current reference is computed based on the q-current reference with a conventional MTPC method (ANN is not involved).
In [48], an artificial recurrent neural network (RNN) with long short-term memory (LSTM) is proposed to predict three-phase current waveforms to account for parameter uncertainties in PMSM modeling. The prediction error reduces with the number of learning epochs and is minimized to deviations below after 7000 iterations.
Another important application of ANNs is in the field of encoderless (or sensorless) control of electrical drives. In [49], it proposes a feedforward neural network (FNN) with one hidden layer capable of achieving sensorless speed control of an induction machine. The rotor angle estimation errors during speed transients are lower than . In [50], structured ANNs are used for saliency-tracking-based sensorless control of AC drives. The ANN designs are based on physical system knowledge leading to a fixed number of layers and neurons with physically motivated interconnections. Due to their structured nature, the trained ANNs provide physical insights as activation functions and weights have physical meaning. In [51], the rotor position of a switched reluctance machine is obtained with the help of an ANN used to estimate the unsaturated stator inductances. The proposed ANN has a very simple structure and reduces the computational effort significantly compared to conventional encoderless methods. In [52], it describes advantages and limitations of ANN-based encoderless control. In particular, at zero speed, the ANN-based encoderless control approach must be extended by conventional high-frequency signal injection methods. The additional consideration of the DC-link voltage improves control performance during field weakening. The used ANN has one hidden layer and is trained by supervised learning.
In many electrical drive systems, torque ripples induced by cogging torques or non-sinusoidal back-electromotive forces (back-EMFs) must be suppressed to their minimum to improve system performance. In [53], it proposes the utilization of ANNs for torque ripple reduction in PMSM based electrical drive systems with significant cogging torque and non-sinusoidal back-EMF. The structured ANN takes geometry (presence of harmonics in back-EMF and cogging torque) into account and are implemented as ADALINE-ANN-based speed or torque controllers. Alternatively, in [54], an unstructured ANN with one hidden layer in combination with a voltage matching circuit (VMC) is used to compute optimal state-feedback controller parameters online in order to minimize the torque ripple factor of a PMSM. To realize the VMC, an additional buck converter with state-feedback dc-link controller must be installed in the electrical drive system. The approach is simulatively tested for a two-level and three-level voltage source inverter.
To increase live time and reduce maintenance costs, condition monitoring and fault detection in electrical drive systems became very popular in the research community recently. In [55], an MLP-based ANN is used for fault detection. The approach is capable of proper fault/non-fault identification by different fault index evaluations. Detectable faults are e.g., significant changes in the stator windings or open-phase faults. For ANN training, data from simulations, machine design and closed-loop experiments was used. In [56], it shows that probabilistic neural networks (PNNs) or radial basis function networks (RBFNs), both with more than 100 hidden layers, are capable of detecting rotor failures such as broken rotor bars, bearing damage or air gap eccentricity. In contrast to the commonly used motor current signature analysis (MCSA), axial flux monitoring and vibration monitoring, the two proposed ANN-based methods allow to detect broken rotor bar faults online with very high accuracy even under different voltage supplies. In [57], a convolutional neural network (CNN) based condition monitoring system for permanent magnet synchronous motors with interturn and demagnetization faults is proposed. The CNN-based condition monitoring system is able to detect those motor faults in the deteriorated current response with extremely high accuracy (errors less than ). In [58], it presents a deep neural network (DNN) based condition monitoring and data evaluation system for highly automated laboratory test benches. The proposed approach aims at a fully automated implementation of predictive maintenance, test process automation, fault detection and downtime reduction of motor test stands. In the paper, a first study shows that fault detection and failure type classification can be achieved by the proposed DNN-based condition monitoring system.
Another important aspect in drive control are loss minimization in the power electronic devices. In [59], an ANN is trained by supervised learning and used to reduce voltage harmonics induced by low switching frequency modulation. The obtained ANN-based optimal pulse patterns (OPPs) are then implemented and compared to conventional patterns obtained by pulse width modulation. The ANN-based OPPs reduces harmonic losses in the induction machine-based electrical drive system in V/f operation and its efficiency can be improved by roughly .
Finally, ANN-based multi-objective optimization during machine design has been proposed in [60]. The ANN is used to reduce the need for excessive finite element (FE) simulations in order to minimize computational effort and, hence, to find pareto optimal machine designs in a simpler and faster manner. To do so, the ANN is trained by extensive FE simulation data.
1.2.3. Summary of Detailed Literature Review
In conclusion, the detailed literature review above underpins the absolute novelty of the proposed ANN-based OFTC approach. This far, ANNs have not yet been proposed, implemented or tested for OFTC or ORCC in particular. Hence, to the best knowledge of the authors, this publication is the very first in this regard and of its kind. Therfore, the goal of this publication is an initial but comprehensive description of the idea and a feasibility study and performance comparison of ANN-based OFTC with state-of-the-art OFTC approaches.
1.3. Problem Statement
The main goal of OFTC is to analytically (or numerically) compute (or to look up) the optimal and feasible reference currents
which are functions of the reference torque , the voltage limit , the current limit , the electrical angular velocity and possibly also of the electrical angle , the stator temperature and the rotor temperature to account for e.g., slotting effects and temperature dependency of stator (winding) resistance(s) and permanent magnet, respectively.
OFTC consists of two steps: Optimal reference current computation (ORCC) and optimal operation strategy selection (OOSS) which, depending on the actual operating conditions, allows to select the optimal operation strategy such as MTPC, MTPL, FW, MC or MTPV as illustrated in Figure 1.
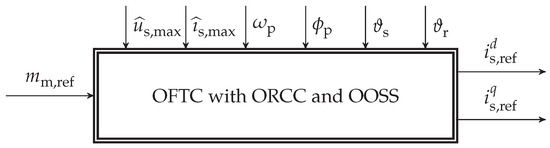
Figure 1.
Optimal feedforward torque control (OFTC) with optimal reference current computation (ORCC) and optimal operation strategy selection (OOSS): The reference currents depend on desired (reference) torque, machine constraints, actual operating conditions and selected operation strategy (such as MTPL, FW, MC or MTPV).
The overall block diagram of a typical control system with OFTC and current controllers of an electrical drive consisting of IPMSM and inverter is shown in Figure 2.
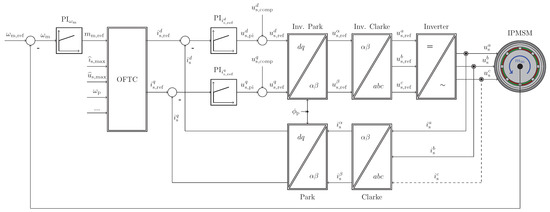
Figure 2.
Block diagram of the control system with OFTC and underlying current controllers of a typical electrical drive system consisting of IPMSM and inverter.
The reference currents , obtained from OFTC, are then fed to the underlying current control system with feedforward disturbance compensation eliminating cross-coupling terms in the current dynamics (see e.g., [61,62]). The reference voltages are the sum of the outputs of the PI controllers and the compensation voltages . The references are then transformed back to the three-phase reference voltages which are fed to the modulator of the inverter to obtain duty cycles or switching (gate) signals for the power semiconductors. Speed and angle are assumed to be measured and are available for feedback.
To solve the OFTC problem and to compute the optimal reference currents as in (1), a precise machine model must be available. A generic, dynamic transformer-like model for synchronous machines (SMs; considering magnetic cross-coupling and saturation and iron losses) can be used [4,5]. The electrical equivalent circuit of the stator windings and the iron core is shown in Figure 3: Similar to a transformer, the stator windings are magnetically coupled with the stator iron core by the stator flux linkages .

Figure 3.
Electrical equivalent circuit of the stator windings and the magnetically coupled iron core in the -reference frame.
The governing stator and stator iron voltage equations are, respectively, given by
with stator voltages , stator currents , iron currents , and electrical speed (i.e., pole pair number times mechanical angular velocity ; see (3)). Furthermore, and (both ; all entries may be non-zero) denote the resistance matrices of stator windings and iron core, respectively. Often, if the windings are symmetric (i.e., the resistances are identical in all phases), the matrices simplify to diagonal matrices and with scalar stator and stator iron resistances. The dynamics of the mechanical subsystem can be described as follows
with mechanical angular velocity , mechanical angle , inertia constant , load torque and (nonlinear) machine torque (derivation details omitted, see [4])
The constant is used to choose between amplitude or power invariant Clarke transformation, respectively. The right-hand side of (4) is obtained by solving (2) for and inserting the result into the middle part of (4). The sum of the stator and iron currents can be interpreted as magnetizing current. The machine torque of IPMSMs is highly nonlinear; an exemplary torque map is illustrated in Figure 4a. It shows the nonlinear torque of a IPMSM (used later for implementation) over the current locus overlaid by an exemplary reference torque (gray shaded plane) and the intersection torque hyperbola (black line) with the admissible currents pairs which can produce this desired torque. Moreover, several torque hyperbolas for several reference torques are projected to the current locus (colored lines). Figure 4b depicts the speed-dependent iron losses of the IPMSM. The current-dependent flux linkages and of this machine are shown in Figure 4c,d, respectively.

Figure 4.
Illustration of machine torque, iron loss and flux linkage nonlinearities of a IPMSM (losses are shown for different speeds). (a) Nonlinear machine torque. (b) Nonlinear iron losses. (c) Nonlinear d-flux linkage. (d) Nonlinear q-flux linkage.
Remark 1
(Machine nonlinearities). In the most general case, stator flux linkages are nonlinear functions of currents, speed, angle and temperatures, i.e., . Similarly, the stator and stator iron resistance matrices may depend on currents (proximity and skin effect), speed, angle (asymmetric case) and stator temperature, i.e., and , respectively. To simplify notation, those dependencies (arguments) are dropped in the remainder of this paper but should be kept in mind as they highlight the complexity and nonlinearity of the OFTC problem.
With the electrical and mechanical model, i.e., (2) and (3) above, the ORCC iteratively solves the nonlinear optimization problem (NLP) with two inequality constraints and one equality constraint, given by
where stator copper losses and stator iron losses (see Figure 4b)
are minimized while the machine constraints, i.e., the current limit in (5b) and the voltage limit in (5c) and, must not be violated and the saturated (feasible) reference torque must be produced. The reference torque must be saturated to the sign-correct maximally available (feasible) machine torque
as not all reference torques are feasible and, hence, can not be produced due to the current and/or voltage constraints in (5b) and (5c). The per-unit machine constraints and the reference torque are illustrated in Figure 5 in the current locus as (a) current circles for multiples of the rated current magnitude , (b) voltage ellipses for multiples of rated electrical angular velocity and (c) (reference) torque hyperbolas for multiples of rated machine torque .
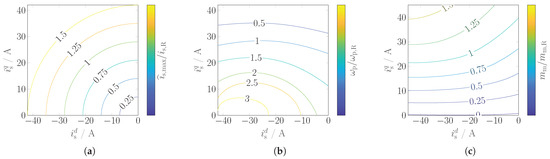
Figure 5.
Illustration of machine constraints and reference torque in current locus for multiples of rated current , angular velocity and machine torque . (a) Current circles. (b) Voltage ellipses. (c) Torque hyperbolas.
Remark 2
(Nonideal voltage ellipses and reference torque hyperbolas). Voltage ellipses and reference torque hyperbolas in the current locus can (locally) be represented as quadrics of the form with constant matrix , vector and scalar [4]. However, for nonlinear machines with highly current dependent magnet cross-coupling and saturation, these global “ellipses” and “hyperbolas” are actually distorted (see Figure 5) and holds where matrix, vector and scalar depend on the currents as well. That is why an online linearization must be performed which eventually only allows solving the NLP iteratively.
1.4. Proposed Solution
In this paper, in contrast to the conventional (LUT-based or numerically or analytically computed) OFTC approaches, an ANN-based OFTC for IPMSMs is proposed. Basically, the OFTC block in Figure 2 is replaced by a properly designed, trained and validated ANN as illustrated in Figure 6. Therefore, the modularity of the control system is preserved and the implementation effort is minimized. In addition, for the implementation of the ANN, (data) preprocessing is required in order to accelerate and improve training and validation and to assure the real-time capability of the ANN. The ANN will compute analytically but recursively the desired optimal reference currents which then are fed to the inner current control loop. The ANN-based OFTC is performed based on (a) its inputs (such as voltage and current constraints, reference torque, electrical angular velocity, etc.) and (b) its input, hidden and output ANN layers with simple but trained activation functions. The aimed at advantages of the ANN-based OFTC strategy are (i) a simple implementation, (ii) a faster computation of the reference currents than with classical ORCC (as no iterations are required) and (iii) no OOSS is necessary as the trained ANN directly outputs the optimal reference currents without following a decision tree (as required for conventional OFTC; see e.g., [4,25]).
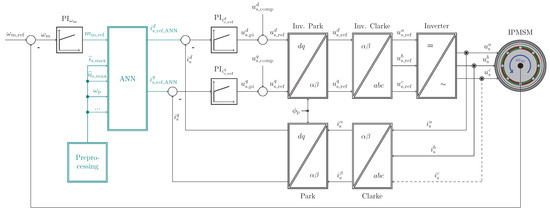
Figure 6.
Block diagram of the newly proposed control system with ANN-based OFTC and underlying current controllers of a typical electrical drive system consisting of IPMSM and inverter.
2. Artificial Neural Network based Optimal Feedforward Torque Control
To replace ORCC by an Artificial Neural Network (ANN; ANNs are often also called Multi-Layer Perceptron (MLP) networks, see Section 3.10 in [63]), the ANN must be properly designed such that input, hidden and output layers have adequate size and the used activation functions are simple but powerful enough to be capable of reduplicating the nonlinear machine behavior. After ANN design, it must be trained and validated by properly selected training and validation data sets. The data sets must be created and preprocessed with care such that ANN training and ANN validation are feasible.
For the present application, the following specifications are imposed on ANN design, training and validation:
- The approximation accuracy of the ANN for OFTC must be (very) high, i.e., approximation errors should be smaller than ;
- Assuming the required data is available, there are no stringent restrictions on training and validation as it is performed offline, i.e., there are (almost) no computational or memory storage constraints during training and validation; and
- The trained ANN should be simple to implement and run in real-time, i.e., a rather small feedforward network architecture (i.e., without dynamics; no recurrent network) with a low number of neurons and one or (at most) two hidden layers should be used.
In the following, ANN design, training and validation are explained in more detail.
2.1. Artificial Neural Network Design
The goal of the ANN used for OFTC is to approximate the nonlinear behavior
between reference torque, physical constraints and operating conditions (the inputs collected in the vector ; recall Figure 1) and the optimal reference currents (the outputs collected in the vector ). As the nonlinear function is not known, the ANN must be trained properly to obtain approximated output and approximating function (approximated quantities are indicated by hat) such that the following holds
The ANN output is (i) for binary classification tasks typically one or zero and (ii) for non-binary classification or regression tasks a numerical value. Every input with of the input vector has a different impact, also called weight, on the outcome of the neural network.
2.1.1. Preliminaries: Neurons, Layers and Recursive Output Computation
In general, an ANN consists of several layers and each layer of several neurons. Each neuron of the j-th layer is fed by the -dimensional input vector The i-th neuron of the j-th layer is equipped with its respective activation function [see Section 2.1.2], which processes the input vector —weighted by the weight vector and biased by the bias in order to compute the neuron’s output
Therefore, the j-th layer with neurons generates the output vector
where
collect the weights and biases in compact form in the overall weighting matrix and bias vector of the j-th layer, respectively. The overall output vector of the ANN then is recursively defined by the outputs of the activation functions in the different layers; i.e., for an ANN with L layers and input vector , it is given by
where the first layer is the input layer, the second to the -th layers are hidden layers and the L-th layer is the output layer. From (13), the recursive nature of the output computation becomes clear. The output vector of the preceding -th layer becomes the input to the j-th layer. The output vector of the L-th layer represents the overall output of the neural network. For further details, the interested reader is referred to e.g., [64] or [63].
2.1.2. Activation Functions
The core of each ANN are its neurons with their respective activation function ; recall (10), (11) and (13). Depending on the location of the neuron in the input, hidden or output layer, different activation functions have proven to be useful. Most common activation functions [64], such as sigmoid, tangens hyperbolicus, signum (sign), identity, rectified linear unit (ReLU) and saturation are illustrated in Figure 7. Their mathematical definitions with respective derivatives are collected in Table 1.
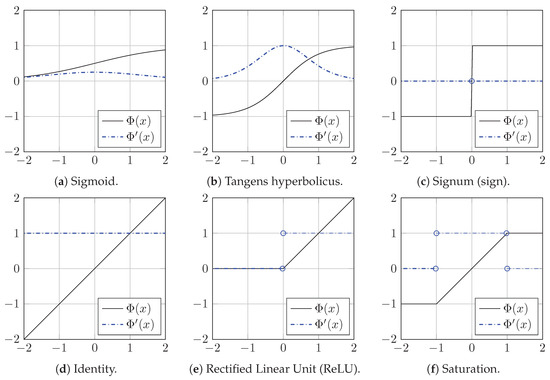
Figure 7.
Illustration of different activation functions and their derivatives, i.e., (a) , (b) , (c) , (d) , (e) and (f) (for mathematical definitions, see Table 1).

Table 1.
Mathematical definitions of different activation functions and their derivatives.
For input and output layer, simple activation functions such as the identity are most common whereas for the hidden layers typically sigmoid or tangens hyperbolicus functions are used [64].
2.1.3. Implemented Artificial Neural Network Architectures
For the considered application in electrical drive systems with small cycle times (<10 ) sophisticated networks with hundreds of neurons, more than two hidden layers and complicated activation functions are (still) too complex for real-time implementation. In particular, implementation and evaluation of the sigmoid and tangens hyperbolicus activation functions and their derivatives (recall Table 1) are computationally demanding.
Therefore, in this paper, due to its low computational requirements, simple ReLU activation functions with their super simple derivative are utilized for the hidden layers. Input and output layer are equipped with the identity activation function as the approximation problem can be considered as a regression problem.
Regarding the layers, it is stated in [65] that a single hidden layer is sufficient to train the ANN to match “any non-linearity”. Following this statement, a network with one hidden layer is chosen as the minimum requirement and, for comparison, a network with two layers is implemented as well (the maximum depth of the hidden layers considered here).
For OFTC of IPMSMs, the ANN must output two reference currents and process at least four input variables. The number of input and output layer neurons should match the input and output dimensions. For this paper, four input variables, the reference torque, the (possibly varying) current and voltages limits and the electrical angular velocity, i.e.,
are considered. Clearly, more inputs such as angular position or rotor and stator temperature are feasible and might be of interest but are considered as future work. The output vector comprises the two optimal reference currents, i.e.,
and, therefore, the output layer consists of two neurons.
Lastly, the number of neurons must be defined. A sufficient amount of neurons in the hidden layer(s) to approximate one single (scalar) output varies between three (see [34,36]) and up to 100 (see [47,66]). To specify the number of neurons per hidden layer, the guidelines presented in [47] were adapted to obtain an initial number as starting point or initial guess. The formula
is proposed to calculate the approximate number of neurons of the j-th hidden layer (for ANN-based OFTC, one (i.e., ) or two hidden layers (i.e., ) were chosen). and represents the numbers of the input and output neurons of the j-th hidden layer, whereas specifies the number of ANN outputs and is an integer. In [47], the formula was presented for a single output neuron (i.e., ). Evaluating (16) for the considered case and all yields
- for one hidden layer (i.e., ) and
- for two hidden layers (i.e., ).
Based on these initial guesses, several ANN designs with one and two hidden layers and different number of neurons per hidden layer have been implemented, trained and validated. The best compromise between accuracy and complexity were obtained for twenty neurons per hidden layer as illustrated in Figure 8 which shows exemplarily estimation accuracy (norm of estimation error) and floating point operations (FLOPs; i.e., the number of required computations incorporating summations and multiplications) over the number of neurons in the hidden layers of Architecture (A). Obviously, the estimation accuracy increases quickly (norm of estimation error reduces) until, for 20 hidden neurons, one of the lowest values of the error norm (i.e., ) is reached. For 23 neurons, a similar value is obtained with and, finally, for 28 neurons, the best accuracy is achieved with . In contrast to that, the FLOPs increase quadratically with the increasing number of hidden neurons.

Figure 8.
Illustration of estimation accuracy (norm of estimation error) and floating point operations of ANN Architecture (A) for different numbers of hidden layer neurons.
Based on the discussion above, two ANN architectures were implemented: Architecture (A) with three layers including one hidden layer and Architecture (A) with four layers including two hidden layers. Both are illustrated in Figure 9. The key data of both ANN designs is collected in Table 2.
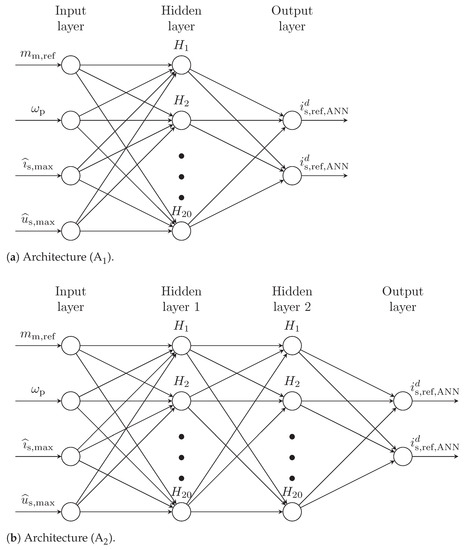
Figure 9.
Illustration of the two implemented ANN architectures: Each architecture has four input layer neurons and two output layer neurons; Architecture (A) has one hidden layer, whereas Architecture (A) has two hidden layers with 20 hidden layer neurons each.

Table 2.
Key data of implemented ANN architectures (centered entries hold for both architectures).
2.2. Artificial Neural Network Training
Neural networks can be trained by using one of three training or learning methods which are supervised, unsupervised and reinforced learning (for details see e.g., [64] or [63]). Supervised learning requires (comprehensive) data, including both input and corresponding output data. Unsupervised learning mainly is used to cluster input data, therefore no output data is required. Reinforced learning needs the interaction of a machine or person that rewards the neural network if it is working as expected. In this paper, supervised learning is utilized, in order to train both ANN Architectures (A) and (A), as input and corresponding output data are available.
2.2.1. Preliminaries: Data Sets, Performance Measures and Training Algorithms
The available data must be collected and preprocessed. To do so, all individual (e.g., for each sampling instant n) input-output data sets
are collected, for all , in the overall input-output data set
which is then preprocessed, split into training data set
of size and validation data set
of size and finally used for ANN training and validation.
With these two data sets and at hand, training and validation of the ANN can be conducted. To analyze the learning and validation performance of the ANN, performances measures are required, which quantify the approximation error
of the ANN for each data subset k (or each sampling instant k) chosen from the training set or validation set (i.e., or ). The performance measures for a regression neural network, such as the used ANNs, differ considerably from the accuracy measures for a classification network. Usually, the following performance measures (see e.g., [64,66] or [63]):
- Mean Error (ME)
- Standard Error Deviation (SED)
- Quadratic Euclidean Distance (or Mean Squared Error (MSE))
are used (i) to quantify the approximation error and its probability and (ii) to finally train and validate the regression network. Note that mean error and standard error deviation are computed (“averaged”) over all entries of the chosen data set, whereas the quadratic Euclidean distance is evaluated for each individual entry k (as it is used for data training and adaption of the weights of the ANN).
Based on mean error and standard error deviation, usually three probability distribution regions are of interest:
- (Region I);
- (Region II); and
- (Region III);
as those cover pre-defined regions of the normal distribution [67] and are used later for performance analyses.
Finally, to train (or optimize) the ANN in order to update the weights and to minimize the approximation error (17) (more, precisely, its error norm, the Euclidean distance (20)), a training algorithm must be chosen [68]. Very often, the Gradient descent method is applied to update the weights by using the negative and by some scaled gradient of the error norm [63], Section 10.4.4, i.e.,
where all weights of all L layers (recall (12)) are collected in the overall weighting vector
However, the main problem of the gradient descent method is its slow to moderate convergence speed. As alternative, the Levenberg-Marquardt algorithm has become popular to update the weights as follows [63], Section 4.1
with Jacobian matrix
identity matrix (of appropriate dimensions) and scaled & approximated Hessian matrix scaled by some . The Levenberg-Marquardt algorithm represents a mixture between gradient descent and the Gauss-Newton method in order to combine both of their strengths. It uses the Gradient descent method to converge when the current error is far from its minimum and the Gauss-Newton method to converge quickly when near a local minimum. The downsides of this algorithm are the relatively high computational demand during training since the inverse of the (approximated) Hessian matrix must be computed for each sub-data set or sampling time k to update the weights. The Levenberg-Marquardt algorithm works very effectively for small(er) networks but loses against the gradient descent methods in terms of convergence speed for large (deep) networks.
In this paper, as rather small networks are considered and there are no restrictions on computational power, the Levenberg-Marquardt algorithm is used for ANN training. The ANN training (and validation) procedure is illustrated in Figure 10 for the two chosen ANN architectures.
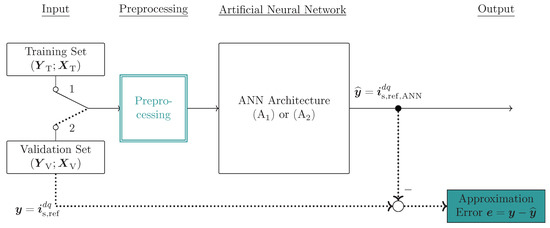
Figure 10.
Illustration of ANN training and validation procedure, training set and validation set, respectively: Approximation error is the difference between the numerically computed optimal reference currents and the ANN outputs.
2.2.2. Data Set(s) Creation for Training (and Validation)
Before the ANNs can be trained and validated, in this subsection, it will be shown how, based on available measurement data or available data from Finite Element Analysis (FEA) of the IPMSM, the required data sets and for training and validation can be created, respectively. Starting points are
- the available rated machine parameters (see Table 3) such as e.g., pole pair number , resistance at rated temperature, moment of inertia , rated torque and rated current magnitude ;
- the available LUTs for iron losses, flux linkages and machine torque parametrized by the angular velocity (or ; see Figure 4) and the -currents within the current circle
- the admissible ranges of the current and voltage limits, given bywith lower (, ) and upper (, ) bounds on these limits.
Based on this data, either measurements or simulations can be performed for a prespecified range of different electrical angular velocities (or speeds), i.e.,
and a prespecified range of different reference torques, i.e.,
The implemented automated software framework for data set creation is illustrated as workflow diagram in Figure 11.
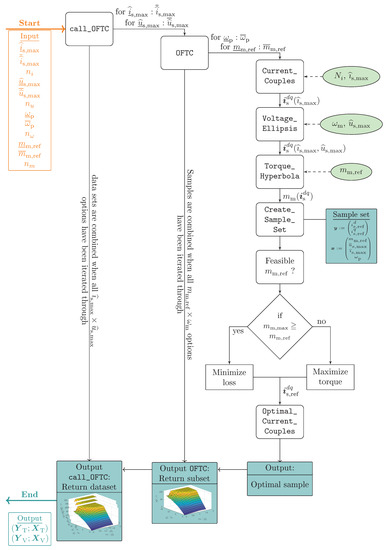
Figure 11.
Software framework and workflow for data set creation: Outputs are the Training Set(s) and Validation Set(s) .
The user has to provide the upper and lower bounds on current and voltage constraints, angular electrical velocity and reference torque (i.e., , , , , , , , ) as inputs to the software framework. In addition, the user must specify the desired resolution (number of data points) of the intervals (24), (25) and (26) by , , and , respectively. With this input data, the software framework starts the routine call_OFTC which will iteratively compute the optimal reference currents numerically based on the available measurement and/or FEA data and finally outputs training sets and validation sets for ANN training and validation, respectively.
The iteration over the current and voltage limit intervals (24) starts by calling the subroutine OFTC which then iterates over the speed (25) and torque (26) intervals by subsequently calling the subroutines Current_Couples, Voltage_Ellipsis, Torque_Hyperbola and Create_Sample_Set. If the actual reference torque is feasible (i.e., no current or voltage constraint is violated), the losses are minimized numerically or, if it is not feasible, the feasible torque is maximized by the subroutine Optimal_Current_Couples to finally obtain the optimal reference currents as comparative output for later training and validation. For each iteration, the software framework returns and stores a data subset. These individual data subsets are then combined to the overall data set which can be split in training set(s) and validation set(s) .

Table 3.
Rated machine parameters of the considered 4 IPMSM.
Table 3.
Rated machine parameters of the considered 4 IPMSM.
| Description | Symbol & Value | Unit |
|---|---|---|
| Rated power (mechanical) | ||
| Rated torque (mechanical) | = | |
| Rated speed (mechanical) | = 5500 ( = ) | () |
| Rated current (magnitude) | = 35 | |
| Maximal stator current (magnitude) | = 35 | |
| Maximal stator voltage (magnitude) | = 110 | |
| Stator resistance (at nominal temperature) | = | |
| Inertia | = | |
| Pole pair number | - |
In the following, the subroutines introduced above are explained in more detail. At first, Current_Couples returns a prespecified and large number of current couples within the admissible current circle, satisfying the current constraint (5b), as data basis for the later computation. The current couples are randomly chosen by Monte Carlo sampling [69] over a square and equidistant current grid and then truncated in view of the limitations imposed by the circular current constraint . The remaining admissible current couples within the current circle are shown in teal color in Figure 12a.
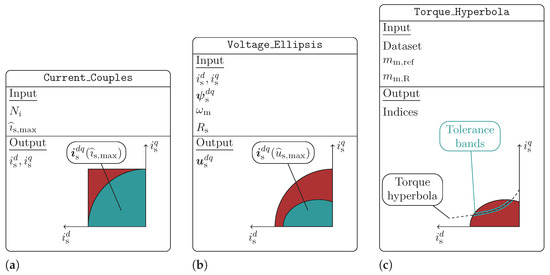
Figure 12.
Illustration of subroutines Current_Couples, Voltage_Ellipsis and Torque_Hyperbola. (a) Current constraint. (b) Voltage constraint. (c) Reference torque.
In the next step, the subroutine Voltage_Ellipsis extracts from the current couples obtained by Current_Couples those current couples which satisfy the voltage constraint (5c) and, hence, lie within the voltage ellipse (see teal elliptic area in Figure 12b).
The subroutine Torque_Hyperbola determines those remaining current couples within the voltage ellipse which satisfy the equality constraint for the given reference torque . Therefore, Torque_Hyperbola returns those current couples on the torque hyperbola which satisfy current and voltage constraint (see teal line in Figure 12c). The thickness of the teal line can be set by a tolerance band around the torque hyperbola depending on the actual reference torque and the rated torque . As the current couples lying on this teal line are not necessarily equidistantly located on a square grid, the returned current couples are interpolated. If the reference torque is not feasible as current and/or voltage constraint would be violated, the subroutine returns an empty set of current couples.
The subroutine Create_Sample_Set merges the obtained data in a sample set of the desired form .
Finally, after a feasibility check for the reference torque is performed (see Figure 11), the subroutine Optimal_Current_Couples selects the optimal reference current couple which either is feasible and produces the desired torque while minimizing copper and iron losses or which maximizes the torque if voltage and/or current constraints are violated. This selection is illustrated in Figure 13.
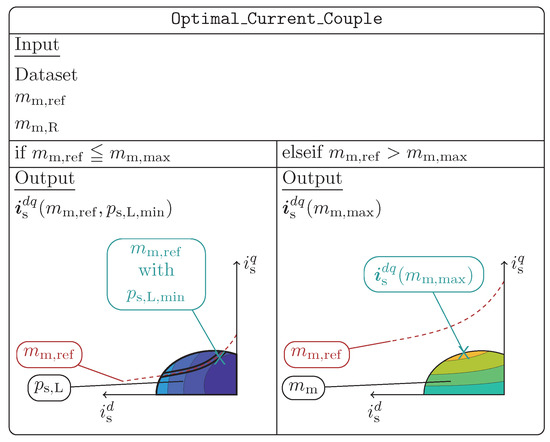
Figure 13.
Illustration of subroutines Optimal_Current_Couples with input (dashed line) and output : If is feasible, the current couple is returned which minimizes losses (see left X); if is not feasible the current couple is returned which maximizes the torque (see right X).
In conclusion, based on the inputs to the software framework, it automatically creates the three small, medium and large training data sets , and and the two small and large validation data sets and . The key data of these created data sets is collected in Table 4. Amount and size of training and validation sets can be adjusted if required.

Table 4.
Inputs for data set creation by the software framework illustrated in Figure 11: The created data set(s) are then split into three training and two validation data sets used for ANN training and validation, respectively.
2.2.3. Data Set Preprocessing for Training (and Validation)
In general, before the training of the ANN, it is beneficial to preprocess the training set(s). This data set preprocessing workflow is illustrated in Figure 14. It consists of data correction, flattening and normalization.
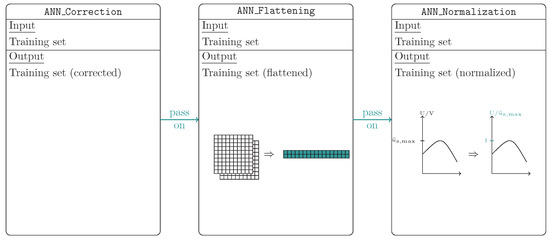
Figure 14.
Illustration of the workflow of the data preprocessing.
The subroutine ANN_Correction removes and corrects erroneous data entries. After that the subroutine ANN_Flattening adjusts the data dimensions to the input dimensions of the neural network (recall in (14) and in (15) for the considered case). This is required as the data set creation provides data with the dimensions
which must be reduced to
resulting in data sets of the form with which can be represented as single column vectors of dimension . In the last subroutine ANN_Normalization, the corrected and flattened data vectors are normalized for all to accelerate the training time as shown in Table 5 for three different training scenarios. An average decrease in the training time of at least 26% can be achieved, as by reducing the absolute values of the inputs, the weight values will decrease as well resulting in less computational effort.

Table 5.
Comparison of training duration and achievable time reduction of the training process by data set normalization for ANN Architecture (A) trained with small, medium and large training data set , or .
The normalization is realized by dividing all input and output data entries by their respective absolute maximal value in order to return a normalized data set with values within the intervals . This division also motivates for the initial data correction step to assure that the interval is fully exploited.
2.2.4. Network Training
During the training, the Levenberg-Marquardt algorithm minimizes the squared Euclidean distance (20) by adapting the ANN weights according to (22). Such an ANN training can easily be implemented in MATLAB R2019b using the feedforwardnet-function of MATLAB’s Deep Learning Toolbox. The training should happen in several epochs (during which the whole training data set is used once), to improve the generalization capability of the ANN. Before the training, multiple training terminators must be specified to provide stopping criteria for the training process. The most important termination parameters are collected in Table 6.

Table 6.
Training termination parameters to end training after requirements have been met.
In Figure 15, the training results are shown for ANN Architectures (A) and (A) and three different training sets [small set], [medium set] and [large set]. It can be seen that, independently of the training data sets in use, Architecture (A) with two hidden layers, reaches smaller error norms after a smaller number of epochs. Moreover, note that only for Architecture (A) with the large training set all 400 epochs are required for training. All other trainings terminate earlier due to the fact that no further training improvements are achieved.
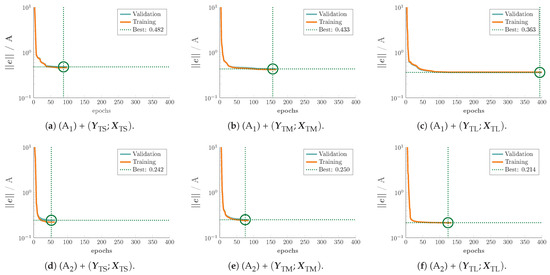
Figure 15.
Evolution of approximation error norm (learning error) over epochs during the training of the ANN Architectures (A) & (A) with the small, medium and large training data sets and , respectively.
2.2.5. Avoidance of Overfitting
Overfitting must be avoided to circumvent deteriorated performance of the trained ANN outside (and within) the used training data set. To do so, two main aspects must be considered:
- proper training (and validation) sets must be chosen in order to cover all relevant regions (operating points) for ANN-based OFTC; in particular, a proper size of the training set (number of operating points) must be found. Therefore, three different sizes (small, medium and large) of training sets for training and two validation sets for validation were used and their respective results were compared. The sets have been generated by Monte Carlo simulation while an optimal coverage of the desired operating points was assured. Those sets leading to the best approximation performance of the ANN were finally used; and
- proper termination criteria for the training process must be formulated (see Table 6 and, for more details, see Chapter 11.5.2 in [66]), in particular, during training a quick parallel validation is performed and if here the validation approximation error increases for a certain number of epochs in a row (see solid green lines in Figure 15), the training is stopped and the trained weights before the increase of the approximation error are used as final weights for the trained ANN.
2.3. Artificial Neural Network Validation
After the training of both ANN Architectures (A) and (A) with the created small, medium and large training sets , and , both are validated with the help of the created small and large validation sets and .
2.3.1. Validation Procedure
The validation procedure is similar to the training procedure as illustrated in Figure 10. However, instead of using as input the training sets, the validation sets are fed to the preprocessing block while weight adaption is turned off. Finally, the trained ANNs will output the optimal reference currents according to the validation input data.
The validation scenarios as well as the closed-loop simulations are performed on a conventional personal computer (see specification in Table 7).

Table 7.
Computer specification of the utilized MacBook Pro (16-inch, 2019).
Two validation scenarios are considered. The first scenario aims at evaluating the execution time of the ANN to compute the optimal reference currents based on the provided input validation data and (with ) of the validation sets and , respectively. The second scenario aims at validating the approximation accuracy of the trained ANNs by computing and evaluating the approximation error
between numerically obtained optimal reference currents and those computed by the ANN. The results of both validation scenarios are discussed in the following two subsections.
2.3.2. Validation Scenario I: Execution Time
The execution times of one executation call (i.e., computing an individual sample ) of the ANN Architectures (A) and (A) trained each with the training sets , and are validated using the small validation set . The results are shown in Figure 16 over the 10,000 samples of the small validation set. All six validation test results show that almost the same average execution time of 3.45 μs per ANN execution are obtained. The size of the training set (small, medium or large) does not significantly have impact on the executation time. Only the size of the ANN architecture affects the execution time. The execution time of Architecture (A) increases by 16–35% to 3.85 μs on average compared to that of Architecture (A).
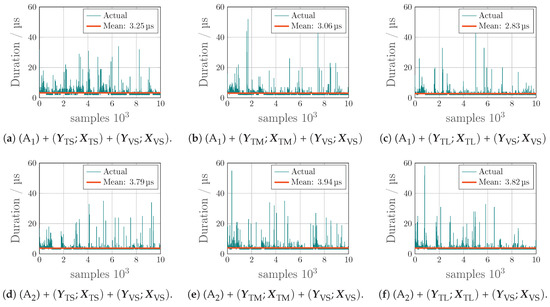
Figure 16.
Illustration of execution times over 10.000 samples during the validation of the ANN Architectures (A) [top row] & (A) [bottom row] with the small validation data set (trained each with the small, medium and large , and ).
2.3.3. Validation Scenario II: Approximation Accuracy
In contrast to the execution time, both, the size of the training sets as well as the size of the ANN architecture, have a strong impact on the achievable approximation accuracy (i.e., the norm of the approximation error). The results of the second validation scenario are shown in Figure 17. For each architecture, the individual approximation errors
of d- and q-reference currents are computed for all samples of the considered validation set and, then, associated to and collected in error bars with a width of 0.1 A. Finally, mean error as in (18), standard error deviation as in (19) and error distribution probability
of each error bar are computed, where represents the number of samples bundled in one error bar.

Figure 17.
Illustration of individual error distributions [left subplots] and [right subplots] obtained during the validation of the ANN Architectures (A) [left column, i.e., (a,c,e)] & (A) [right column, i.e., (b,d,f)] with the small, medium and large validation data sets and , respectively.
Figure 17 shows six subplots [see Figure 17a–f] with two error distributions for d- and q-current approximation error each. The left column shows the results for ANN Architecture (A) [see Figure 17a,c,e]; whereas the right column contains the results for ANN Architecture (A) [see Figure 17b,d,f]. The vertical red and yellow lines in each subplot indicate the error regions which cover 95% (i.e., similar to Region II above) and (i.e., similar to Region III above) of all error bars, i.e., and of all errors lie between the red and yellow lines, respectively. It becomes clear that the larger Architecture (A) has a better approximation accuracy than Architecture (A). Moreover, it becomes even better for larger training sets (i.e., red and yellow line move closer to zero). Note that no approximation errors larger than ±2 A occur. For example, in the right subplot of Figure 17f, more than 90% of the q-current error bars yield approximation errors smaller than , which is conform to the specified approximation accuracy. For the d-current error bars [see left subplot of Figure 17f] about satisfy the specified approximation accuracy, which is still acceptable. This significant difference is due to the used distribution of the current couples shown in Figure 18, where clearly more q-currents were in the exemplary training set due to the voltage and current constraints. Nevertheless, as the following closed-loop implementation results will show, the approximation accuracy of the ANN Architecture (A) trained with the large training set definitely achieves a very acceptable overall performance for ANN-based OFTC.
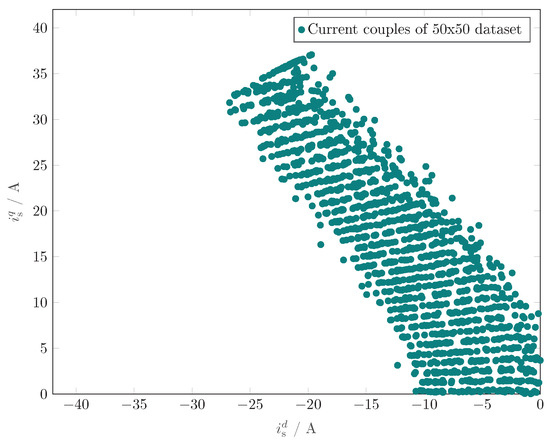
Figure 18.
Distribution of the current couples of an exemplary dataset with constant current and voltage constraints and but variable and .
3. Closed-Loop Implementation and Comparison
Finally, five OFTC approaches are implemented in closed-loop operation of the electrical drive system and compared concerning approximation accuracy and execution time:
- OFTC: OFTC with ORCC using the MATLAB-function fmincon (solving the nonlinear problem (NLP) directly);
- OFTC: OFTC with ORCC using pre-generated LUTs;
- OFTC: OFTC with numerical ORCC;
- OFTC: OFTC with analytical ORCC; and
- OFTC: OFTC with ORCC utilizing the proposed ANN.
The trained and validated ANN with two hidden layers and 20 neurons per layer (as described in Section 2) is implemented to achieve ANN-based OFTC (OFTC) as illustrated in Figure 6. OFTC is considered as the benchmark for all other approaches concerning the accuracy of the obtained reference currents as the nonlinear optimization problem with all constraints is solved directly with the powerful fmincon MATLAB-function. However, concerning the execution time, OFTC is by far the slowest with and, hence, it is clearly not applicable in real-time. For OFTC and OFTC, the respective ORCC and decision tree are implemented as discussed in e.g., [4,25] with numerical and analytical solution of the quadric intersection problem (i.e., finding roots of fourth-order polynomials). Both, OFTC and OFTC, require an iterative computation due to the necessary online linearization of the nonlinear optimization problem. OFTC is based on pre-generated LUTs from which the optimal reference currents are extracted online with inverse interpolation (as mostly used in industry). More details about implementation, results and comparison are provided in the following subsections.
3.1. Description of Closed-Loop Implementation
The presented machine model of Section 1.3 is implemented in MATLAB & Simulink R2019b. The simulated machine is a real, nonlinear IPMSM with rated parameters as introduced in Table 3 and nonlinearities like flux linkages and iron losses as shown in Figure 4. An inverter with pulse-width modulation (PWM) and a switching frequency of applies the stator voltages to the machine. The idealized inverter model is taken from [70], Chapter 14 and neglects switching and conduction losses but allows for switching and varying dc-link voltages (not considered here). For all five OFTC approaches, a field-oriented control (FOC) system as shown in Figure 6 is used.
For the ANN-based OFTC approach, the utilized ANN Architecture (A) was trained with the large Training Set , validated by the large Validation Set and implemented in Simulink using the feedforwardnet-function which allows to specify the to be used activation functions, number of layers and training terminators (recall Table 2 and Table 6). Architecture (A) was chosen as it is more accurate than Architecture (A) [recall Figure 17] and its execution time is not significantly longer [recall Figure 16].
All five OFTC approaches (i.e., OFTC, OFTC, OFTC, OFTC and OFTC) are implemented in Simulink R2019b in combination with FOC, modulator and voltage source inverter and nonlinear machine model as a closed-loop electrical drive system. An identical simulation scenario is run for all five OFTC approaches to allow for a fair and direct comparison of their individual performances (accuracies) and execution times.
The chosen simulation scenario represents a typical start-up operation of an electrical drive system: The IPMSM is accelerated from stand-still to 150% of its rated speed while a constant load torque of about 64% of the rated torque is applied to illustrate the optimal operation management over a wide range of different operating conditions and for several optimal operation strategies (such as MTPL, MC and FW). For all operation strategies, optimal and feasible reference currents are computed and tracked to stay within the imposed current and voltage constraints.
3.2. Implementation Results and Discussion
In Figure 19, Figure 20 and Figure 21, the implementation results are shown. To ease readability of the presented results, not all OFTC approaches are depicted. Figure 19 presents the time series plots of OFTC (as best conventional OFTC approach) and OFTC (as newly proposed OFTC approach) and Figure 21 shows the comparison of these two time series plots against those of OFTC (as benchmark concerning accuracy); whereas in Figure 20, the current loci of OFTC and OFTC are depicted. The results of all five approaches are actually very similar (as will be discussed later; see also Table 8) and, hence, no more insight would be obtained by showing all implementation results.

Figure 19.
Implementation results: (a) OFTC with analytical ORCC (OFTC) with smooth transition between all operation strategies (i.e., MTPL [  ], MC [
], MC [  ], MC [
], MC [  ] and FW [
] and FW [  ]) and (b) ANN-based OFTC (OFTC).
]) and (b) ANN-based OFTC (OFTC).
 ], MC [
], MC [  ], MC [
], MC [  ] and FW [
] and FW [  ]) and (b) ANN-based OFTC (OFTC).
]) and (b) ANN-based OFTC (OFTC).

Figure 20.
Implementation results: Illustration of optimal operation management considering copper and iron losses minimization and voltage and current constraints—Left column: OFTC with analytical ORCC (OFTC) with (a) speed-torque map and (c) current locus; Right column: ANN-based OFTC OFTC with (b) speed-torque map and (d) current locus.

Figure 21.
Implementation results: Direct comparison between OFTC with analytical ORCC= ORCC [  ], ANN-based OFTC [
], ANN-based OFTC [  ] and OFTC solved directly by fmincon (NLP) [
] and OFTC solved directly by fmincon (NLP) [  ].
].
 ], ANN-based OFTC [
], ANN-based OFTC [  ] and OFTC solved directly by fmincon (NLP) [
] and OFTC solved directly by fmincon (NLP) [  ].
].

Table 8.
Comparison of the time series of the implementation results of OFTC (LUT-based OFTC), OFTC (OFTC with numerical ORCC), OFTC (OFTC with analytical ORCC) and proposed OFTC (ANN-based OFTC) against OFTC (OFTC with fmincon-based ORCC) evaluating the Integral Absolute Error (IAE) performance measure and the executation time.
The time series of actual [  ] and reference or maximum values [
] and reference or maximum values [  ] of stator currents and , current magnitude , voltage magnitude , machine speed (in ) and torque are shown in Figure 19, where the left column [see Figure 19a] presents the simulation results for OFTC with analytical ORCC (OFTC) and the right column [see Figure 19b] for ANN-based OFTC (OFTC).
] of stator currents and , current magnitude , voltage magnitude , machine speed (in ) and torque are shown in Figure 19, where the left column [see Figure 19a] presents the simulation results for OFTC with analytical ORCC (OFTC) and the right column [see Figure 19b] for ANN-based OFTC (OFTC).
 ] and reference or maximum values [
] and reference or maximum values [  ] of stator currents and , current magnitude , voltage magnitude , machine speed (in ) and torque are shown in Figure 19, where the left column [see Figure 19a] presents the simulation results for OFTC with analytical ORCC (OFTC) and the right column [see Figure 19b] for ANN-based OFTC (OFTC).
] of stator currents and , current magnitude , voltage magnitude , machine speed (in ) and torque are shown in Figure 19, where the left column [see Figure 19a] presents the simulation results for OFTC with analytical ORCC (OFTC) and the right column [see Figure 19b] for ANN-based OFTC (OFTC).The background colors in Figure 19a,b indicate the active optimal operation strategy such as MTPL [  ], MC [
], MC [  ], MC [
], MC [  ] and FW [
] and FW [  ] (for details see [4,5,25]). Despite the fact, that the ANN-based OFTC does not distinguish between different operation strategies, the background colors from Figure 19a are used in Figure 19b as well to allow for an easier comparison.
] (for details see [4,5,25]). Despite the fact, that the ANN-based OFTC does not distinguish between different operation strategies, the background colors from Figure 19a are used in Figure 19b as well to allow for an easier comparison.
 ], MC [
], MC [  ], MC [
], MC [  ] and FW [
] and FW [  ] (for details see [4,5,25]). Despite the fact, that the ANN-based OFTC does not distinguish between different operation strategies, the background colors from Figure 19a are used in Figure 19b as well to allow for an easier comparison.
] (for details see [4,5,25]). Despite the fact, that the ANN-based OFTC does not distinguish between different operation strategies, the background colors from Figure 19a are used in Figure 19b as well to allow for an easier comparison.Besides the time series plots, the speed-torque maps with efficiency contour lines [top row] and the current evolution in the current locus (plane) [bottom row] are depicted in Figure 20 for the same closed-loop implementation scenario: Again, the left column shows the results for OFTC with analytical ORCC [i.e., OFTC, see Figure 20a,c], whereas the right column contains the results for ANN-based OFTC [i.e., OFTC, see Figure 20b,d]. The actual speed-torque pairs or actual current pairs are marked by [■]. The final (optimal) operating point is marked by [★].
Initially (), the machine is slowly ramped up to 20% of [cf. Figure 19a,c]. Neither current nor voltage constraints are violated. Therefore, the OFTC goal is to maximize efficiency by minimizing copper and iron losses during MTPL operation. The requested reference torques are feasible and nicely tracked.
At time , the reference speed jumps to 150% of and subsequently, the reference torque reaches its maximum at . Consequently, the feasible reference currents are limited to the current circle and the optimale operation strategy MC [  ] is active until .
] is active until .
 ] is active until .
] is active until .Due to the increasing speed, the voltage constraint is reached at and, therefore, the operation strategy MC [  ] becomes active. The valid current couples move on the current circle to more negative reference currents [i.e., , see also current loci in Figure 20b,d, respectively]. Consequently, the produced machine torque is smaller than the reference torque, since it is not feasible anymore due to the active current and voltage constraints.
] becomes active. The valid current couples move on the current circle to more negative reference currents [i.e., , see also current loci in Figure 20b,d, respectively]. Consequently, the produced machine torque is smaller than the reference torque, since it is not feasible anymore due to the active current and voltage constraints.
 ] becomes active. The valid current couples move on the current circle to more negative reference currents [i.e., , see also current loci in Figure 20b,d, respectively]. Consequently, the produced machine torque is smaller than the reference torque, since it is not feasible anymore due to the active current and voltage constraints.
] becomes active. The valid current couples move on the current circle to more negative reference currents [i.e., , see also current loci in Figure 20b,d, respectively]. Consequently, the produced machine torque is smaller than the reference torque, since it is not feasible anymore due to the active current and voltage constraints.The reference speed is reached at for OFTC with ORCC and at for ANN-based OFTC, respectively. As no accelerating torque is required, the reference torque drops to the load torque. The current constraint does not limit operation anymore, but the voltage constraint is still active as the IPMSM operates at high speeds. Hence, the optimal operation strategy now is FW [  ]. After some transients due to the current control system, the final operating point [★] is reached at and the machine speed remains constant until the simulation ends at . The efficiency for both strategies is at its maximum for all operating conditions [cf. Figure 20a,b for OFTC with analytical ORCC and for ANN-based OFTC, respectively].
]. After some transients due to the current control system, the final operating point [★] is reached at and the machine speed remains constant until the simulation ends at . The efficiency for both strategies is at its maximum for all operating conditions [cf. Figure 20a,b for OFTC with analytical ORCC and for ANN-based OFTC, respectively].
 ]. After some transients due to the current control system, the final operating point [★] is reached at and the machine speed remains constant until the simulation ends at . The efficiency for both strategies is at its maximum for all operating conditions [cf. Figure 20a,b for OFTC with analytical ORCC and for ANN-based OFTC, respectively].
]. After some transients due to the current control system, the final operating point [★] is reached at and the machine speed remains constant until the simulation ends at . The efficiency for both strategies is at its maximum for all operating conditions [cf. Figure 20a,b for OFTC with analytical ORCC and for ANN-based OFTC, respectively].Finally, in Figure 21, the simulation results of OFTC with analytical ORCC [  ], ANN-based OFTC [
], ANN-based OFTC [  ] are compared with the optimal reference currents and obtained by directly solving the Nonlinear Optimization Problem (NLP) problem (5) with the MATLAB function fmincon [
] are compared with the optimal reference currents and obtained by directly solving the Nonlinear Optimization Problem (NLP) problem (5) with the MATLAB function fmincon [  ]. The NLP values are considered the benchmark values for the other two OFTC approaches. The plotted signals in Figure 21 are the actual reference currents, utilized reference current magnitude , utilized voltage magnitude , actual machine speed (in ) and actual machine torque . The results show that, in particular, all reference current pairs of OFTC with ORCC and ANN-based OFTC are very similar and close to those obtained by the OFTC solved directly by fmincon (NLP). Only very small deviations can be observed: From to , the current magnitude of ANN-based OFTC is slightly below the current limit. Therefore, the torque potential is not completely utilized to its full extent. That is why the target speed is reached about later by the ANN-based OFTC than by the other OFTC approaches.
]. The NLP values are considered the benchmark values for the other two OFTC approaches. The plotted signals in Figure 21 are the actual reference currents, utilized reference current magnitude , utilized voltage magnitude , actual machine speed (in ) and actual machine torque . The results show that, in particular, all reference current pairs of OFTC with ORCC and ANN-based OFTC are very similar and close to those obtained by the OFTC solved directly by fmincon (NLP). Only very small deviations can be observed: From to , the current magnitude of ANN-based OFTC is slightly below the current limit. Therefore, the torque potential is not completely utilized to its full extent. That is why the target speed is reached about later by the ANN-based OFTC than by the other OFTC approaches.
 ], ANN-based OFTC [
], ANN-based OFTC [  ] are compared with the optimal reference currents and obtained by directly solving the Nonlinear Optimization Problem (NLP) problem (5) with the MATLAB function fmincon [
] are compared with the optimal reference currents and obtained by directly solving the Nonlinear Optimization Problem (NLP) problem (5) with the MATLAB function fmincon [  ]. The NLP values are considered the benchmark values for the other two OFTC approaches. The plotted signals in Figure 21 are the actual reference currents, utilized reference current magnitude , utilized voltage magnitude , actual machine speed (in ) and actual machine torque . The results show that, in particular, all reference current pairs of OFTC with ORCC and ANN-based OFTC are very similar and close to those obtained by the OFTC solved directly by fmincon (NLP). Only very small deviations can be observed: From to , the current magnitude of ANN-based OFTC is slightly below the current limit. Therefore, the torque potential is not completely utilized to its full extent. That is why the target speed is reached about later by the ANN-based OFTC than by the other OFTC approaches.
]. The NLP values are considered the benchmark values for the other two OFTC approaches. The plotted signals in Figure 21 are the actual reference currents, utilized reference current magnitude , utilized voltage magnitude , actual machine speed (in ) and actual machine torque . The results show that, in particular, all reference current pairs of OFTC with ORCC and ANN-based OFTC are very similar and close to those obtained by the OFTC solved directly by fmincon (NLP). Only very small deviations can be observed: From to , the current magnitude of ANN-based OFTC is slightly below the current limit. Therefore, the torque potential is not completely utilized to its full extent. That is why the target speed is reached about later by the ANN-based OFTC than by the other OFTC approaches.Table 8 summarizes the results of the comparison by computing the Integral Absolute Errors (IAE)
of reference current differences, reference torque differences (during MTPL, MC and FW operation), voltage utilization difference (during MC & FW operation), current utilization difference (during MC & MC operation) and mechanical speed difference. Moreover, the mean execution times of the OFTC with analytial ORCC and ANN-based OFTC are listed. The mean execution time is averaged over 10 simulation runs which results in 81,000 OFTC calls for each of the five OFTC approaches.
The first observation is that all differences between the IEA values of all five OFTC approaches with ORCC and ANN-based OFTC are negligibly small. Only the IAE value of the current utilization of the ANN-based OFTC is slightly larger than the IAE of the worst of all other OFTC algorithms (here: OFTC). As already mentioned that is because the utilized current magnitude is slightly below the current limit during the time interval .
Most important, the ANN-based approach requires only for one OFTC execution, i.e., almost less than a hundredth of the execution time of the implemented OFTC with analytical or numerical ORCC and nearly less than a five hundredth of the execution time of the LUT-based approach. This is a rather impressive result as as the executation time without OFTC approach takes about . In this case, “without OFTC” means that the q-reference current is computed by whereas the d-reference current is simply set to zero, i.e., .
In conclusion, the execution time of ANN-based OFTC is significantly shorter than those of the state-of-the-art OFTC approaches and, hence, it seems definitely more promising and suitable for real-time implementation.
4. Summary and Outlook
A novel artificial neural network (ANN) based optimal feedforward torque control (OFTC) strategy has been proposed where the ANN replaces the computationally expensive numerical, analytical or LUT-based optimal reference current computation (ORCC) to minimize copper and iron losses in an electrical drive system with highly nonlinear interior permanent magnet synchronous machine (IPMSM). ANN design, training and validation have been explained in detail. Special focus has been put on the data set(s) creation to obtain training and validation sets for the implemented ANNs.
Finally, the ANN-based OFTC strategy has been implemented in Matlab/Simulink in combination with field-oriented control of a real, nonlinear IPMSM electrical drive system and it has been compared to state-of-the-art OFTC approaches with e.g., analytical, numerical and LUT-based ORCC. The validation tests have shown that the ANN is capable of (a) approximating the nonlinear OFTC behavior accurately with approximation errors of less than and (b) computing the optimal reference currents within less than compared to at least of the fastest state-of-the-art OFTC approach. Drive performance and achieved efficiency for all OFTC strategies are almost identical, which proves not only that the novel ANN-based OFTC is capable of controlling an electrical drive system requiring less computational time but also doing so with very high accuracy.
Future research will aim at (i) optimizing ANN design (architecture) for typically used microcontrollers in electrical drive systems (e.g., exploiting DSP resources and/or FPGA parallelization capabilities as much as possible), (ii) selecting other reasonable and suitable input parameters (features) for ANN training to achieve even higher approximation accuracies, (iii) considering additional operating conditions (such as angular position and stator and/or rotor temperature) during ANN training, validation and closed-loop implementation to improve OFTC performance and efficiency at their maxima, (iv) implementing recursive or structured neural networks to be able to possibly even cover dynamical effects (such as e.g., current and/or dc-link dynamics) or optimal pulse patterns (OPP) and (v) implementing optimized ANN-based OFTC on different real-time platforms to validate its performance and real-time capability via measurements in the laboratory.
Author Contributions
Conceptualization, C.M.H. and N.M.; methodology, M.A.B. and N.M.; software, M.A.B.; validation, M.A.B. and N.M.; formal analysis, M.A.B., N.M. and C.M.H.; investigation, M.A.B. and N.M.; resources, M.A.B., N.M. and C.M.H.; data curation, M.A.B. and N.M.; writing—original draft preparation, M.A.B., N.M. and C.M.H.; writing—review and editing, C.M.H.; visualization, M.A.B., N.M. and C.M.H.; supervision, N.M. and C.M.H.; project administration, C.M.H.; funding acquisition, C.M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADALINE | Adaptive Linear Neuron |
| ANN | Artificial Neural Network |
| back-EMF | back-Electromotive Force |
| BEV | Battery Electric Vehicle |
| CNN | Convolutional Neural Network |
| DNN | Deep Neural Network |
| DSP | Digital Signal Processor |
| FE | Finite Element |
| FEA | Finite Element Analysis |
| FNN | Feedforward Neural Network |
| FLOPS | Floating Point Operations |
| FOC | Field-Oriented Control |
| FPGA | Field-Programmable Gate Array |
| FW | Field Weakening |
| HEV | Hybrid Electric Vehicle |
| IPMSM | Interior Permanent Magnet Synchronous Machine |
| IAE | Integral Absolute Error |
| LMA | Loss Minimization Algorithm |
| LMC | Loss Minimization Control |
| LSTM | Long Short-Term Memory |
| LUT | Look-Up Table |
| MC | Maximum Current |
| MCSA | Motor Current Signature Analysis |
| MLP | Multilayer Perceptron |
| MDPI | Multidisciplinary Digital Publishing Institute |
| ME | Mean Error |
| MEPA | Maximum Efficiency per Ampere |
| MPC | Model Predictive Control |
| MRAC | Model Reference Adaptive Controller |
| MSE | Mean Squared Error |
| MTPA | Maximum Torque per Ampere |
| MTPC | Maximum Torque per Current |
| MTPF | Maximum Torque per Flux |
| MTPL | Maximum Torque per Losses |
| MTPV | Maximum Torque per Voltage |
| NAN | Not A Number |
| NLP | Nonlinear Optimization Problem |
| OFTC | Optimal Feedforward Torque Control |
| OOSS | Optimal Operation Strategy Selection |
| OPP | Optimal Pulse Pattern |
| ORCC | Optimal Reference Current Computation |
| PHEV | Hybrid Electric Vehicles |
| PMSM | Permanent Magnet Synchronous Machine |
| PNN | Probabilistic Neural Network |
| PTC | Predictive Torque Controller |
| RBF | Radial Basis Function |
| ReLU | Rectified Linear Unit |
| RNG | Random Number Generator |
| RNN | Recurrent Neural Network |
| SED | Standard Error Deviation |
| SM | Synchronous Machine |
| VMC | Voltage Matching Circuit |
References
- De Almeida, A.; Ferreira, F.; Fong, J. Standards for Efficiency of Electric Motors. IEEE Ind. Appl. Mag. 2011, 17, 12–19. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M. Energy Mix. 2021. Available online: https://ourworldindata.org/energy-mix (accessed on 28 June 2021).
- Eroglu, I.; Horlbeck, L.; Lienkamp, M.; Hackl, C. Increasing the Overall Efficiency of Induction Motors for BEV by using the Overload Potential through Downsizing. In Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC 2017), Miami, FL, USA, 21–24 May 2017. [Google Scholar]
- Hackl, C.; Kullick, J.; Monzen, N. Optimale Betriebsführung für nichtlineare Synchronmaschinen. In Elektrische Antriebe–Regelung von Antriebssystemen; Böcker, J., Griepentrog, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Hackl, C.M.; Kullick, J.; Monzen, N. Generic loss minimization for nonlinear synchronous machines by analytical computation of optimal reference currents considering copper and iron losses. In Proceedings of the 2021 IEEE International Conference on Industrial Technology (ICIT), Valencia, Spain, 10–12 March 2021. [Google Scholar] [CrossRef]
- Horlbeck, L.; Hackl, C.M. Analytical solution for the MTPV hyperbola including the stator resistance. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT 2016), Taipei, Taiwan, 14–17 March 2016; pp. 1060–1067. [Google Scholar] [CrossRef]
- Holtz, J.; Qi, X. Optimal Control of Medium-Voltage Drives—An Overview. IEEE Trans. Ind. Electron. 2012, 60, 5472–5481. [Google Scholar] [CrossRef]
- Birda, A.; Reuss, J.; Hackl, C.M. Synchronous Optimal Pulsewidth Modulation for Synchronous Machines With Highly Operating Point Dependent Magnetic Anisotropy. IEEE Trans. Ind. Electron. 2021, 68, 3760–3769. [Google Scholar] [CrossRef]
- Birda, A.; Grabher, C.; Reuss, J.; Hackl, C.M. Dc-link capacitor and inverter current ripples in anisotropic synchronous motor drives produced by synchronous optimal PWM. IEEE Trans. Ind. Electron. 2021, 69, 4484–4494. [Google Scholar] [CrossRef]
- Morimoto, S.; Takeda, Y.; Hirasa, T.; Taniguchi, K. Expansion of operating limits for permanent magnet motor by current vector control considering inverter capacity. IEEE Trans. Ind. Appl. 1990, 26, 866–871. [Google Scholar] [CrossRef]
- Niazi, P.; Toliyat, H.A.; Goodarzi, A. Robust Maximum Torque per Ampere (MTPA) Control of PM-Assisted SynRM for Traction Applications. IEEE Trans. Veh. Technol. 2007, 56, 1538–1545. [Google Scholar] [CrossRef]
- Cheng, B.; Tesch, T. Torque Feedforward Control Technique for Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2010, 57, 969–974. [Google Scholar] [CrossRef]
- Finken, T. Fahrzyklusgerechte Auslegung von Permanenterregten Synchronmaschinen für Hybrid- und Elektrofahrzeuge. Ph.D. Thesis, Insitut für elektrische Maschinen, RWTH Aachen, Aachen, Germany, 2012. [Google Scholar]
- Jung, S.Y.; Hong, J.; Nam, K. Current Minimizing Torque Control of the IPMSM using Ferrari’s Method. IEEE Trans. Power Electron. 2013, 28, 5603–5617. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Optimal State Reference Computation with Constrained MTPA Criterion for PM Motor Drives. IEEE Trans. Power Electron. 2015, 30, 4524–4535. [Google Scholar] [CrossRef]
- Gemaßmer, T. Effiziente und Dynamische Drehmomenteinprägung in hoch Ausgenutzten Synchronmaschinen mit Eingebetteten Magneten. Ph.D. Thesis, Fakultät für Elektrotechnik und Informationstechnik, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2015. [Google Scholar]
- Lemmens, J.; Vanassche, P.; Driesen, J. PMSM Drive Current and Voltage Limiting as a Constraint Optimal Control Problem. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 326–338. [Google Scholar] [CrossRef]
- Schoonhoven, G.; Uddin, M.N. MTPA- and FW-Based Robust Nonlinear Speed Control of IPMSM Drive Using Lyapunov Stability Criterion. IEEE Trans. Ind. Appl. 2016, 52, 4365–4374. [Google Scholar] [CrossRef]
- Dianov, A.; Tinazzi, F.; Calligaro, S.; Bolognani, S. Review and classification of MTPA control algorithms for synchronous motors. IEEE Trans. Power Electron. 2021, 37, 3990–4007. [Google Scholar] [CrossRef]
- Ahn, J.; Lim, S.B.; Kim, K.C.; Lee, J.; Choi, J.H.; Kim, S.; Hong, J.P. Field weakening control of synchronous reluctance motor for electric power steering. IET Electr. Power Appl. 2007, 1, 565–570. [Google Scholar] [CrossRef]
- Tursini, M.; Chiricozzi, E.; Petrella, R. Feedforward Flux-Weakening Control of Surface-Mounted Permanent-Magnet Synchronous Motors Accounting for Resistive Voltage Drop. IEEE Trans. Ind. Electron. 2010, 57, 440–448. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Model Predictive Direct Torque Control with Finite Control Set for PMSM Drive Systems, Part 2: Field Weakening Operation. IEEE Trans. Ind. Inform. 2013, 9, 648–657. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, I.; Nam, K.; Yang, J.; Hwang, T. Sensorless Control of PMSM in a High-Speed Region Considering Iron Loss. IEEE Trans. Ind. Electron. 2015, 62, 6151–6159. [Google Scholar] [CrossRef]
- Zhang, P.; Ionel, D.M.; Demerdash, N.A.O. Saliency Ratio and Power Factor of IPM Motors With Distributed Windings Optimally Designed for High Efficiency and Low-Cost Applications. IEEE Trans. Ind. Appl. 2016, 52, 4730–4739. [Google Scholar] [CrossRef]
- Eldeeb, H.; Hackl, C.M.; Horlbeck, L.; Kullick, J. A unified theory for optimal feedforward torque control of anisotropic synchronous machines. Int. J. Control. 2018, 91, 2273–2302. [Google Scholar] [CrossRef]
- Panaitescu, R.C.; Topa, I. Optimal Control Method For PMSM By Minimization Of Electrical Losses. In Proceedings of the IEEE International Conference on Optimization of Electrical and Electronic Equipments (OPTIM), Brasov, Romania, 14–15 May 1998; Volume 2, pp. 451–456. [Google Scholar]
- Urasaki, N.; Senjyu, T.; Uezato, K. A novel calculation method for iron loss resistance suitable in modeling permanent-magnet synchronous motors. IEEE Trans. Energy Convers. 2003, 18, 41–47. [Google Scholar] [CrossRef]
- Cavallaro, C.; Tommaso, A.O.D.; Miceli, R.; Raciti, A.; Galluzzo, G.R.; Trapanese, M. Efficiency Enhancement of Permanent-Magnet Synchronous Motor Drives by Online Loss Minimization Approaches. IEEE Trans. Ind. Electron. 2005, 52, 1153–1160. [Google Scholar] [CrossRef] [Green Version]
- Ni, R.; Xu, D.; Wang, G.; Ding, L.; Zhang, G.; Qu, L. Maximum Efficiency Per Ampere Control of Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2015, 62, 2135–2143. [Google Scholar] [CrossRef]
- Zhang, S. Artificial Intelligence in Electric Machine Drives: Advances and Trends. arXiv 2021, arXiv:2110.05403. [Google Scholar]
- Kumar, R.; Gupta, R.A.; Bansal, A.K. Identification and Control of PMSM Using Artificial Neural Network. In Proceedings of the 2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 30–35. [Google Scholar] [CrossRef]
- Gaur, P.; Singh, B.; Mittal, A. Artificial Neural Network based Controller and Speed Estimation of Permanent Magnet Synchronous Motor. In Proceedings of the 2008 Joint International Conference on Power System Technology and IEEE Power India Conference, New Delhi, India, 12–15 October 2008. [Google Scholar] [CrossRef]
- Zare, J. Vector control of permanent magnet synchronous motor with surface magnet using artificial neural networks. In Proceedings of the 2008 43rd International Universities Power Engineering Conference, Padua, Italy, 1–4 September 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Nagarajan, V.; Balaji, M.; Kamaraj, V.; Seetha, B. Comparative analysis of neural and P-I controller for PMSM Drive. In Proceedings of the 2014 IEEE 2nd International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 January 2014; pp. 126–131. [Google Scholar] [CrossRef]
- Leena, N.; Shanmugasundaram, R. Artificial neural network controller for improved performance of brushless DC motor. In Proceedings of the 2014 International Conference on Power Signals Control and Computations (EPSCICON), Kerala, India, 6–11 January 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Suman, S.K.; Gautam, M.K.; Srivastava, R.; Giri, V.K. Novel approach of speed control of PMSM drive using neural network controller. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 2780–2783. [Google Scholar] [CrossRef]
- Guney, E.; Dursun, M.; Demir, M. Artificial neural network based real time speed control of a linear tubular permanent magnet direct current motor. In Proceedings of the 2017 International Conference on Control, Automation and Diagnosis (ICCAD), Hammamet, Tunisia, 19–21 January 2017. [Google Scholar] [CrossRef]
- Ghlib, I.; Messlem, Y.; Chedjara, Z. ADALINE-Based Speed Control For Induction Motor Drive. In Proceedings of the 2019 International Conference on Advanced Electrical Engineering (ICAEE), Algiers, Algeria, 19–21 November 2019. [Google Scholar] [CrossRef]
- Wishart, M.; Harley, R. Identification and control of induction machines using artificial neural networks. IEEE Trans. Ind. Appl. 1995, 31, 612–619. [Google Scholar] [CrossRef] [Green Version]
- Rubaai, A.; Kotaru, R. Online identification and control of a DC motor using learning adaptation of neural networks. IEEE Trans. Ind. Appl. 2000, 36, 935–942. [Google Scholar] [CrossRef]
- Kenne, G.; Ahmed-Ali, T.; Lamnabhi-Lagarrigue, F.; Nkwawo, H. Identification of electrical parameters and rotor speed of induction motor using radial basis neural network. In Proceedings of the 2004 IEEE International Symposium on Industrial Electronics, Ajaccio, France, 4–7 May 2004. [Google Scholar] [CrossRef]
- Kirchgassner, W.; Wallscheid, O.; Böcker, J. Deep Residual Convolutional and Recurrent Neural Networks for Temperature Estimation in Permanent Magnet Synchronous Motors. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019. [Google Scholar] [CrossRef]
- Turabee, G.; Khowja, M.R.; Giangrande, P.; Madonna, V.; Cosma, G.; Vakil, G.; Gerada, C.; Galea, M. The Role of Neural Networks in Predicting the Thermal Life of Electrical Machines. IEEE Access 2020, 8, 40283–40297. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Banakher, F.A. Direct Torque Control of Synchronous Motors Using Artificial Neural Network. In Proceedings of the 2019 IEEE International Conference on Electro Information Technology (EIT), Brookings, SD, USA, 20–22 May 2019. [Google Scholar] [CrossRef]
- Hammoud, I.; Hentzelt, S.; Oehlschlaegel, T.; Kennel, R. Long-Horizon Direct Model Predictive Control Based on Neural Networks for Electrical Drives. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 19–21 October 2020. [Google Scholar] [CrossRef]
- Novak, M.; Xie, H.; Dragicevic, T.; Wang, F.; Rodriguez, J.; Blaabjerg, F. Optimal Cost Function Parameter Design in Predictive Torque Control (PTC) Using Artificial Neural Networks (ANN). IEEE Trans. Ind. Electron. 2021, 68, 7309–7319. [Google Scholar] [CrossRef]
- Yan, Y.B.; Liang, J.N.; Sun, T.F.; Geng, J.P.; Xie, G.; Pan, D.J. Torque Estimation and Control of PMSM Based on Deep Learning. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Matsuura, K.; Akatsu, K. A motor control method by using Machine learning. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; pp. 652–655. [Google Scholar] [CrossRef]
- Wlas, M.; Krzeminski, Z.; Guzinski, J.; Abu-Rub, H.; Toliyat, H. Artificial-Neural-Network-Based Sensorless Nonlinear Control of Induction Motors. IEEE Trans. Energy Convers. 2005, 20, 520–528. [Google Scholar] [CrossRef]
- Garcia, P.; Briz, F.; Raca, D.; Lorenz, R.D. Saliency-Tracking-Based Sensorless Control of AC Machines Using Structured Neural Networks. IEEE Trans. Ind. Appl. 2007, 43, 77–86. [Google Scholar] [CrossRef]
- Echenique, E.; Dixon, J.; Cardenas, R.; Pena, R. Sensorless Control for a Switched Reluctance Wind Generator, Based on Current Slopes and Neural Networks. IEEE Trans. Ind. Electron. 2009, 56, 817–825. [Google Scholar] [CrossRef]
- Zine, W.; Makni, Z.; Monmasson, E.; Idkhajine, L.; Condamin, B. Interests and Limits of Machine Learning-Based Neural Networks for Rotor Position Estimation in EV Traction Drives. IEEE Trans. Ind. Inform. 2017, 14, 1942–1951. [Google Scholar] [CrossRef]
- Flieller, D.; Nguyen, N.K.; Wira, P.; Sturtzer, G.; Abdeslam, D.O.; Merckle, J. A Self-Learning Solution for Torque Ripple Reduction for Nonsinusoidal Permanent-Magnet Motor Drives Based on Artificial Neural Networks. IEEE Trans. Ind. Electron. 2014, 61, 655–666. [Google Scholar] [CrossRef] [Green Version]
- Tarczewski, T.; Niewiara, L.; Grzesiak, L.M. Torque ripple minimization for PMSM using voltage matching circuit and neural network based adaptive state feedback control. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014. [Google Scholar] [CrossRef]
- Azzini, A.; Cristaldi, L.; Lazzaroni, M.; Monti, A.; Ponci, F.; Tettamanzi, A. Incipient Fault Diagnosis in Electrical Drives by Tuned Neural Networks. In Proceedings of the 2006 IEEE Instrumentation and Measurement Technology Conference Proceedings, Sorrento, Italy, 24–27 April 2006. [Google Scholar] [CrossRef]
- Marmouch, S.; Aroui, T.; Koubaa, Y. Application of statistical neuronal networks for diagnostics of induction machine rotor faults. In Proceedings of the 2016 17th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2017. [Google Scholar] [CrossRef]
- Pasqualotto, D.; Zigliotto, M. A comprehensive approach to convolutional neural networks-based condition monitoring of permanent magnet synchronous motor drives. IET Electr. Power Appl. 2021, 15, 947–962. [Google Scholar] [CrossRef]
- Botache, D.; Bethke, F.; Hardieck, M.; Bieshaar, M.; Brabetz, L.; Ayeb, M.; Zipf, P.; Sick, B. Towards Highly Automated Machine-Learning-Empowered Monitoring of Motor Test Stands. In Proceedings of the 2021 IEEE International Conference on Autonomic Computing and Self-Organizing Systems (ACSOS), Washington, DC, USA, 27 September–1 October 2021. [Google Scholar] [CrossRef]
- Puron, L.D.R.; Neto, J.E.; Fernandez, I.A. Neural networks based estimator for efficiency in VSI to PWM of induction motors drives. In Proceedings of the 2016 IEEE International Conference on Automatica (ICA-ACCA), Curico, Chile, 19–21 October 2016. [Google Scholar] [CrossRef]
- Zăvoianu, A.C.; Bramerdorfer, G.; Lughofer, E.; Silber, S.; Amrhein, W.; Klement, E.P. Hybridization of multi-objective evolutionary algorithms and artificial neural networks for optimizing the performance of electrical drives. Eng. Appl. Artif. Intell. 2013, 26, 1781–1794. [Google Scholar] [CrossRef]
- Hackl, C.M.; Kamper, M.J.; Kullick, J.; Mitchell, J. Current control of reluctance synchronous machines with online adjustment of the controller parameters. In Proceedings of the 2016 IEEE International Symposium on Industrial Electronics (ISIE 2016), Santa Clara, CA, USA, 8–10 June 2016; pp. 153–160. [Google Scholar] [CrossRef]
- Hackl, C.; Kullick, J.; Landsmann, P. Nichtlineare Stromregelverfahren für Reluktanz-Synchronmaschinen. In Elektrische Antriebe—Regelung von Antriebssystemen; Böcker, J., Griepentrog, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Schröder, D.; Buss, M. Intelligente Verfahren: Identifikation und Regelung Nichtlinearer Systeme; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Stursa, D.; Dolezel, P. Comparison of ReLU and linear saturated activation functions in neural network for universal approximation. In Proceedings of the 2019 22nd International Conference on Process Control (PC19), Strbske Pleso, Slovakia, 11–14 June 2019; pp. 146–151. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Lee, D.K.; In, J.; Lee, S. Standard deviation and standard error of the mean. Korean J. Anesthesiol. 2015, 68, 220. [Google Scholar] [CrossRef]
- Jaiswal, P.; Gupta, N.K.; Ambikapathy, A. Comparative study of various training algorithms of artificial neural network. In Proceedings of the 2018 International Conference on Advances in Computing, Communication Control and Networking (ICACCCN), Greater Noida, Uttar Pradesh, India, 12–13 October 2018; pp. 1097–1101. [Google Scholar] [CrossRef]
- Ruszczyński, A.P.; Shapiro, A. (Eds.) Stochastic Programming; Number v. 10 in Handbooks in Operations Research and Management Science; Elsevier: Amsterdam, The Netherlands; Boston, MA, USA, 2003. [Google Scholar]
- Hackl, C.M. Non-Identifier Based Adaptive Control in Mechatronics: Theory and Application; Number 466 in Lecture Notes in Control and Information Sciences; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).