Thermal Investigations of Hemispherical Shell Vapor Chamber Heat Sink

Abstract

In the current study, a hemispherical shell vapor chamber (HSVC) was proposed and manufactured. A unique system of the HSVC consists of a very short evaporator space and a large condenser area with an inner and outer surface. The HSVC has a bottom surface that can be easily attached to the heat source and its radius varies from 0.045 m (near the bottom surface) to 0.078 m at the top with a curved side. An entirely new design of the integrated section of the large condenser with the evaporator section was verified using a new but simple concept. The current hemispherical shell vapor chamber (HSVC) was made from stainless steel. The current HSVC was specified with an outer/inner diameter of 78/70 mm at the top, a depth of 47 mm in the inner surface area, a total height of 60 mm, 30 mm at the bottom of the inner center, and a diameter of 45 mm on the surface of the outer bottom area. Three different models were manufactured and tested to verify which HSVC reached a high thermal performance. The effects of various operation parameters such as the filled volume ratio, heat load, coolant flow velocity, orientation, and so forth, were investigated experimentally. The experimental results showed that the optimum charge amount in terms of temperature difference is 20–30% of the charging ratio, and the condenser area has a direct effect on the thermal performance. Moreover, a one-dimensional thermal resistance model was tested to predict and simulate the thermal performance of the current system associated with various empirical correlations. Furthermore, the CFD (Computational Fluid Dynamics) model can simulate a lot of detailed flow behavior inside the HSVC. Both simulation methods can predict the thermal performance of the HSVC, and they can help to design the system with a focus on the optimum configuration of the design target for any application.

1. Introduction

Heat pipes come in a variety of shapes and sizes, including single heat pipes, thermosyphons, loop heat pipes, micro heat pipes, flat heat pipes, plate heat pipes, variable conductance heat pipes, pulsating heat pipes, vapor chambers, and more. Miniature and micro heat pipes are suitable for electronics cooling [1,2,3,4,5,6,7,8,9]. Each heat pipe has a conventional shape for its given applications. It is obvious from the literature that vapor chambers in previous studies are typically flat-plate types, as shown in Figure 1. As shown in Figure 2a,b, the novel concept design of the HSVC to cool electronic components is a new idea and has been patented [6]. The current study is to verify the thermal flow behavior related to the thermal performance as a possible cooling or thermal management device for future electronics [10,11,12,13,14]. In particular, recent electronics require a high-performance chip and, hence, large heat generation in a small surface area is compulsory. Therefore, a new heat sink idea with a large heat transfer area is needed to satisfy electronics cooling in the future [7,8,9,10,11,12,13]. This can motivate the novel concept of the present HSVC. As illustrated in Figure 2, an appropriate amount of working fluid is contained in the hemispherical shell vapor chamber, and the internal working fluid is formed to transfer heat from the bottom to the internal working fluid to induce evaporation, and the evaporated vapor moves upward through a three-dimensional shell space of 360°. As can be seen from the conceptual diagram of Figure 2b, the HSVC is a flexible structure that can be designed by adjusting the size according to the amount of heat generated. In addition, there is an advantage in that the maximum heat transfer area can be designed and attached to the outer surface area of the vapor chamber itself.

Egbo et al. [10] reviewed recent vapor chamber research in terms of various design and performance parameters. They presented various vapor chambers studied in recent literature, but they mentioned that the typical shapes of vapor chambers are flat types with various wick structures, similar to the previous review papers of Mochizuki et al. [11], Egbo et al. [10], and Bulut et al. [12]. In particular, Mochizuki et al., Egbo et al., Bulut et al., and Elnaggar et al. [13] reviewed vapor chambers in electronics cooling applications such as thermal ground planes and heat spreaders in terms of thin structures and removing non-condensable gas, material compatibility, and lifetime reliability. Recent developments of vapor chambers are focused on ultra-thin structures that are less than 0.4 mm thick due to the recent development of high-performance smart devices. As described in reviews on vapor chambers, the current hemispherical vapor chamber is a novel concept design and structure which has not been researched and reported in previous literature. In particular, the HSVC can make large condensing areas, in contrast to conventional heat pipes or vapor chambers. The hemispherical structure can make the inner and outer surface area the condensing surfaces and this can be a unique design, in contrast to previous vapor chambers [1,2,3,4,5,6,11,12,13].

As mentioned briefly above, vapor chambers, which are one type of heat pipes, may passively convey heat with a modest temperature gradient from a limited heat source to a wide range of heat removal surfaces. There are a lot of studies being conducted on vapor chambers for electronic temperature control [14,15,16,17]. Vapor chambers are used to dissipate heat away from hot regions, lowering the temperature of sensitive components. A working fluid is contained in the enclosed vapor chamber, and vapor is produced in the evaporator section above the heated zone. The vapor is forced upward, spread out from the heating part, and condenses on the inner surface of a near wall. Gravity aids the passive transmission of the condensed liquid back to the evaporator through a porous wick or wall (Figure 1). Active air-cooling technology or heat sink surfaces with a significantly increased area are not practical due to space constraints for power consumption and heat dissipation. In such cases, the vapor chamber may be a viable option. The present work describes a method for determining the performance of uneven, three-dimensionally formed vapor chambers which can be used in electronic devices [15,16,17]. As shown in Figure 1 and Figure 2, vapor chambers are vacuum containers that have been saturated with hydraulic fluid and have a core structure along the inner wall. When this space is heated, the liquid rapidly evaporates, and vapor swiftly travels to fill the empty vacuum space. The vapor condenses and comes back to the evaporated surface when it comes into contact with another cooled surface. Previous research has used a common test technique to evaluate the performance of heat pipes and vapor chambers, which involves transmitting heat from a heating section to a cold section to determine the thermal resistance to the environment. [17,18,19].

Wang et al. [20] studied the evaporative resistances in the sintered powder wick evaporators in running flat-plate-type heat pipes and tried to carry out a visualization study using a glass plate on the top side to view the evaporation process. A heat load of 16~170 W/cm² was applied to the 1.1 cm² plate as the heating zone at one end. They reported an approximate thermal resistance of 0.08–0.09 K-cm²/W for sintered wicks with tiny particles.

A flat-plate heat pipe with two layers of sintered screen mesh wire was investigated by [21]. Three different kinds of working fluids such as water, methanol, and acetone were tested to find their effects on the evaporation process and evaporator resistance. They also reported the visualization study in which the liquid layer’s up and down motion was observed with acetone. They also reported that the minimum evaporator resistance was achieved with water.

Hwang et al. [22] built an elementary network model for the multiple artery wick heat pipe heat spreader to enhance the 3D heat and liquid flow. Although a high number of columns are necessary to produce maximal capillary pressure to eliminate as much heat as possible, the columns also restrict the available space for evaporation. They claimed that the ideal column number was found at about 37 for a vapor chamber with a diameter of 5 cm (a heater with a diameter of 1 cm).

Berhe [23] reported 41 °C for the surface temperature limit of the aluminum surface and 43 °C for the plastic surface of the portable device. This study shows that their measuring methodology emphasizes the characteristics of the thermal resistance in the vapor chamber. Additionally, they highlighted that the detailed modeling of the distribution of the surface temperature is important to quantify the thermal performance for portable devices using a vapor chamber.

Go [24] investigated the heat transfer characteristics of a vapor chamber accompanied by heat ink with a unique micro-wick structure that uses acetone as the working fluid. The operating temperature, thermal resistance, and three tilt angles for various heat inputs were tested to study its cooling effectiveness. Their vapor chamber system had a cooling capacity of 80 W/cm² at a source temperature of 85 °C and a surrounding temperature of 24 °C, with a thermal resistance of 0.76 °C/W.

Koito et al. [25] numerically analyzed the flat-type vapor chamber. The authors provided a mathematical model based on the system created as a closed disk-type vapor chamber located at the small heating section with a large cooling heat sink. To induce liquid circulation, a wick sheet and column were supplied within the vapor chamber. Experiments were also carried out, and the experimental results closely corresponded to the numerical simulation results.

Ming et al. [26] created a vapor chamber with a grooved wick in the evaporator. The wick structure may increase the heat transfer rate to the axial and radial directions while also providing a capillary-driven liquid circulation between the inner surfaces of condensation and evaporation. They examined how heat flow, charge, and gravity affect the thermal characteristics of this vapor chamber. Their simulation results showed non-uniform liquid layer thickness in the groove. The numerical model’s validity may be assessed by comparing experiments with a numerical simulation. A parametric study that included the effects of the thickness and height of the partition was used.

Liu et al. [27] created a vapor chamber with drilled micro flow channels using copper foam-coated support columns (95% porosity). The largest percentage of porosity had the lowest spreading resistance (approximately 0.05 K/W) and the orientation effect was minor. Increases of 50 percent in foam porosity boosted the spreading resistance to 0.11 K/W.

Chen et al. [28] built a basic linear model to approximate a vapor chamber. In their proposed design, the vapor is regarded as a single interface between the evaporator and the condenser wick, enabling the vapor chamber to be separated and irradiated into minimal control volumes. Compared with previously known results, the calculated transient response was well matched. It was confirmed that the thermal capacitance of the heating block affects the transient variation of the vapor chamber. The calculated unsteady behavior is similar to experimental data; however, there is a little divergence when the heat capacity of the insulating section and the cold plate are not included. The expected thermal resistance is 8.6% lower than the average of the test measurements.

Wiriyasart and Naphon [29] examined a vapor chamber with a sintered and grooved structure. They investigated two types of vapor chambers such as a groove structure wick type and a groove type wick accompanied with sintering powder. They were all made of copper and ran with water as a working fluid. The total thermal resistance of their system with a sintered structure was approximately 0.20 K/W, whereas that of the vapor chamber without a sintered structure was 0.25 K/W.

Yao et al. [30] developed a vapor chamber characterized by a tree-shaped groove wick and a screen mesh wick that fills the vapor area. Their vapor chamber showed better performance in the top heating mode with mesh wicks, and with very small increases in thermal resistances. When the mesh wick was removed, it showed poor thermal performance and considerable temperature fluctuations. The thermal resistance rose by around 10% when the grooved wick was replaced with a flat surface.

Chang et al. [31] developed a semi-empirical conduction-based model for predicting the thermal resistance of a vapor chamber with a total thickness of less than 0.5 mm. Based on the assumptions of symmetry, isotropic effective thermal conductivity, and no temperature change with rises in thickness, it might estimate thermal resistance. The determined value, according to the author, was only applicable to specific vapor chamber designs.

Patankar et al. [32] developed a simulation model to assess the transient thermal response of a thin vapor chamber. Their model of the vapor chamber is just 0.1 mm thick, and the simulation model solely included the vapor and wick structure. The transient performance of such a thin device is determined by three processes: the device’s overall thermal capacity, the effective in-plane diffusivity, and the conductivity of the vapor core.

Wang et al. [33] used a numerical simulation model to evaluate the effect of various parameters such as wick porosity and particle size on the thermal performance of a vapor chamber. The phase change processes inside the vapor chamber were only predicted to occur at the interface between the wicks and the vapor area in their model. The temperature of the vapor zone was also assumed to remain continuous, and laminar flow was present throughout the model. The best results were achieved when the pressure losses in the vapor chamber were near the capillary pressure of the wick.

Zhang et al. [34] examined the thermal efficiency of a flip-chip package including a vapor chamber shape heat spreader. The effect of the varied heater sizes was also studied. A numerical simulation showed that replacing the TIM from Al gel filler to a copper vapor chamber boosts the thermal performance considerably at a heat dissipation of 160 W. Furthermore, when the size of the heat source is reduced, the performance of a vapor chamber progressively improves, then worsens.

Hsieh et al. [35,36] provide a three-dimensional simulation model based on the variable separation for spreading thermal resistances with the heat sources in the center of a vapor chamber heat sink. Using parametric analysis, various parameters such as partition thickness and height on the thermal performance related to the base spreading resistance were investigated.

Ghanbarpour et al. [37] used phase change materials (PCM) and a vapor chamber at the bottom as a thermal ground plane for the heat source to conduct a numerical study on the thermal performance of a heat sink. Their numerical results in terms of natural and forced convection were reported and were dependent on fin shapes.

Kim et al. [38] investigated the thermal performance of a 138 × 90 mm² flat-plate aluminum vapor chamber used for battery thermal control. Two metal plates with respective thicknesses of 2.5 and 1.5 mm were used to create the vapor chamber, as well as a 500 μm porous layer within the vapor chamber, with a grooved channel on the opposite side (depths of 1.0 and 1.5 mm). When the filling ratio was 25%, the vapor chamber performed well.

Koukoravas et al. [39] studied metal wicks in a hermetically enclosed vapor chamber. On the condenser side, the wettability patterns of the metal wick were investigated and compared to the unpatterned mirror-finish copper. At an 87 W heat load (heat flux of 97 W/cm²), the lowest thermal resistance achieved with a horizontally placed vapor chamber with a 0.5 mm thick evaporator wick was 0.24 K/W.

Liu et al. [40] examined the use of a small silicon vapor chamber to redistribute heat at the die level. The model considers the effects of the wick’s microstructure and is compared to experimental data from a prototype device to ensure that they are within 5% of each other. The vapor chamber’s thermal performance is compared to simulation results for solid silicon spreaders of equivalent diameters, and it was discovered that for heat fluxes greater than 60 W/cm², the uniformity of the hotspot temperature improves.

Huang et al. [41] studied ultra-thin vapor chambers with a thickness of 0.5 mm and 0.3 mm. Their vapor chambers were created for the purpose of cooling electronics. They wanted to see how the filling ratio and interior space affected the results. Chen et al. [42] investigated the circular plate type vapor chamber for LED cooling and found that the 3 mm thick vapor chamber cooling system can lower thermal resistance by 19–48 percent. Li et al. [43] also attempted a numerical analysis of the disk type vapor chamber with grooved wick construction. They used the ‘area to line’ method to solve the heat transfer issue in the vapor chamber.

Luo et al. [44] combined fractal network microchannels with copper foam to produce a vapor chamber with a bionic wick that emulated the macroscopic leaf vein network and microscopic mesophyll tissue. The bionic vapor chamber’s total thermal resistance is just 0.094 K/W.

Several heat pipes [45,46,47,48,49,50,51,52] were subjected to numerical analysis. The volume of fluid (VOF) methodology, which is one of the most well-known methods, was used in their computational fluid dynamics to simulate the two-phase flow of liquid–vapor phases. For mass transfer, previous research investigations used the VOF model in conjunction with the Lee model. By solving the governing momentum equation and analyzing each fluid’s volume fraction across the domain, the VOF model may emulate two or more immiscible fluids. In the VOF model, the variables and attributes in each cell are either purely representational of one of the phases. The computational fluid dynamics (CFD) modeling of heat pipes using a VOF model was used to address these issues by identifying the motion of all phases and indirectly characterizing the motion of the interfaces. Previous CFD simulation studies from the literature are two-dimensional simulation works [45,46,47,48,49,50,51]. This is induced by a long calculation time. Song et al. [52] tried to simulate annular heat pipes numerically using the VOF model. Song et al. showed that 3D simulation agrees well with the experimental results compared with 2D simulation. However, they reported that the difference between 2D and 3D simulation can be compared in terms of time cost.

As shown in Figure 2a,b, the current HSVC has a unique two-phase flow structure in the inside area and on the large condensing surfaces. In addition, the two-phase flow in the HSVC cannot be clearly predicted. Therefore, the working principle based on the two-phase flow in the vacuumed hemispherical shell vapor chamber, in terms of thermal performance, should be investigated parametrically. Moreover, as illustrated in the conceptional design of Figure 2b, the current HSVC can be very versatile in terms of sizing depending on the heat generation rate. In the present study, various examinations were performed by experimental works, one-dimensional resistance model simulation, and CFD (computational fluid dynamics) simulation to examine the heat transfer performance of the HSVC which is shaped with a height of 60 mm and a 30 to 74 mm tapered inner condenser surface using distilled water and methanol at different fill charge ratios, heat fluxes, coolant velocities, types, and so on. The evaporator of HSVC in the experimental apparatus was connected to a hot spot. In addition, the condenser of HSVC is manufactured in a structure in which heat is released by natural convection or forced convection on the surface of the condenser.

2. Experiment

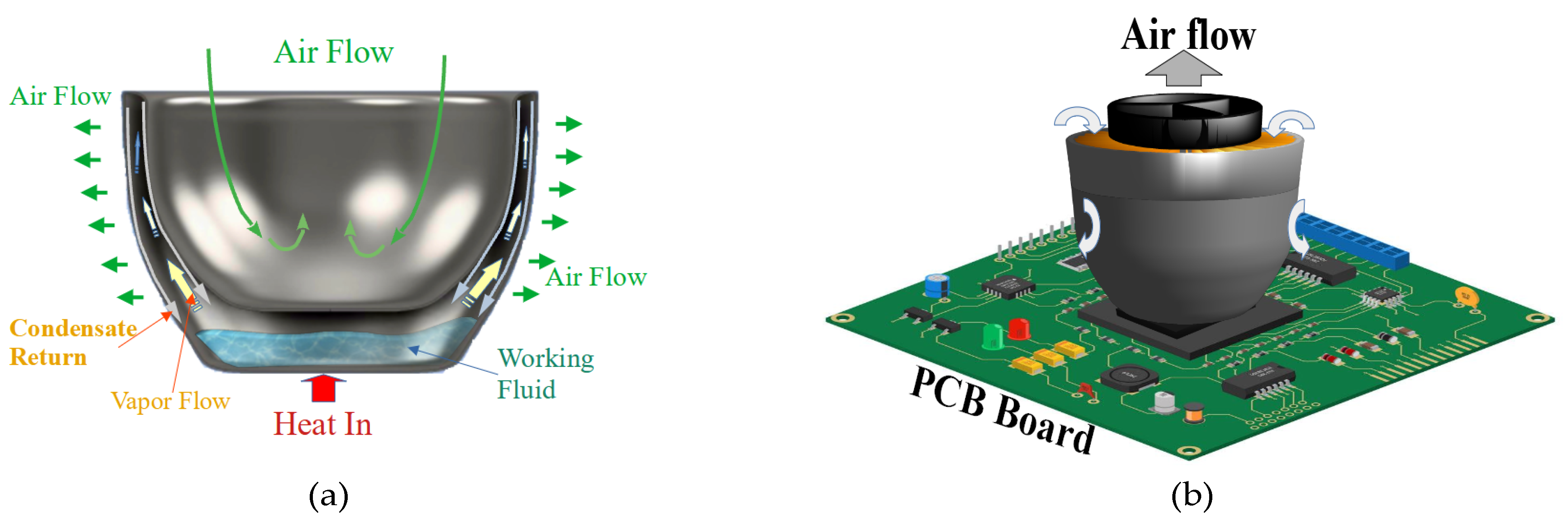
2.1. Main Assembly of the Hemispherical Shell-Shaped Vapor Chamber

The present cooling system using the HSVC has potential applications for real industry. To evaluate the heat transfer performance of the proposed cooling system utilizing the HSVC, and to replicate the heat sink under controlled laboratory settings, the experimental setup shown in Figure 3 and Figure 4 was built.

The current HSVC pre-models in Figure 3 were first sized to produce the experimental HSVCs using the thermal resistance estimation approach which will be described in a later section. Moreover, in the preliminary concept design, various shapes and sizes of the HSVC were also tested in order to estimate and anticipate thermal performance. After a few trial errors, the current experimental system was designed and built. As illustrated in Figure 3 and Figure 4, the main HSVC system comprises the cooling system in the condenser part, the heating part, and the working fluid charging system.

For the suggested cooling system, the HSVC’s heat transfer investigations were performed experimentally and were simulated under controlled laboratory circumstances. From the design of the system to the experimentation, all steps were carried out considering the heat sink and its operating conditions. The components of the current HSVC assembly are separated into two sections, including the small evaporation section, and the finned/bared condensers. The adiabatic transporting section cannot be verified. The HSVC has a flat bottom which can be easily attached to the heat source and its radius varies from 0.045 m (near the bottom surface) to 0.078 m at the top. The thickness of the HSVC, which is denoted by shell thickness in Figure 3, varies from 0.3 mm (just below the top) to 0.7 mm (at the bottom surface of the HSVC). From the measurement at different points of the HSVC’s points along the circumference, the minimum, mean, and maximum values of the thickness are 0.33 mm, 0.5 mm, and 0.83 mm, respectively. Based on a new simple concept, a totally new structure of the integrated large condenser area with the evaporator section was confirmed. The current hemispherical shell vapor chamber (HSVC) was made from stainless steel. As shown in Figure 3, the current HSVC was specified with 78/70 mm in the outer/inner diameter of the top, 47 mm deep in the inner surface area, 60 mm in height, 30 mm in the bottom of the inner center, and 45 mm in diameter on the outer bottom surface. The three currently manufactured models are dependent on whether wick and fins are installed or not. In the current, uneven-shaped vapor chamber, it is not easy to precisely recognize the condenser section, because the condenser section can be the whole surface except the heated evaporator area. The current HSVC has radial forms, as illustrated in Figure 3a,b. The HSVC has a height of 60 mm. The top has an outward diameter of 78 mm and an interior diameter of 70 mm. The outside and inner diameters of the bottom are 45 mm and 30 mm, respectively. The internal volume of the vapor chamber is 80 mL, and it is made of stainless steel.

As shown in

Table 1. Experimental Conditions.

Models	Wick	Fin	Working Fluid	Charged Ratio (%)	Orientation (Degree)	Air Flow Velocity (m/s)
1	No	No	Water, Methanol	5, 10, 15, 20, 30, 40, 50	10, 20, 30, 40, 50, 60. 70, 80, 90	0, 1, 2, 3
2	No	Inner space, Trapezoid-Shaped Finned, 30 mm top, 47 mm bottom, 0.35 mm thickness, 32 Fins	Water, Methanol	10, 20, 30, 40, 50	10, 20, 30, 40, 50, 60. 70, 80, 90	0, 1, 2, 3
3	Cooper 100 Mesh, 1 layer	No	Water, Methanol	5, 10, 15, 20, 30, 40, 50	10, 20, 30, 40, 50, 60. 70, 80, 90	0, 1, 2, 3

, three models are described in terms of structure and experimental conditions. ‘Model 1′ is a thermosyphon type vapor chamber, ‘Model 2′ is a finned Model 1, and the micro wick-installed vapor chamber is defined as Model 3. Model 2 consists of the same components as Model 1, with 32 fins on the inner surface of the HSVC. The fins are trapezoid-shaped, with 30 mm on the top and 47 mm on the bottom. The experimental variables were set in consideration of factors affecting the shape of the vapor chamber and the performance of the heat pipe. As presented in Figure 4, the experimental devices were composed of a vapor chamber, heater, cooling fan, power supply, injector, and dater logger. The ceramic heater with a cross-sectional area of 20 × 20 mm and a thickness of 2 mm can operate in the range of 50 V and 65 W or less. Moreover, the heater was attached to the bottom of the vapor chamber through a thermal pad. The dimension of the thermal pad was 40$\times 40\times 1.5$ mm, and the thermal resistance and thermal conductivity were 0.25 $℃/\mathrm{W}$ and 5$\mathrm{W}/\mathrm{mk},$ respectively. The model of the power supply connected to the heater was Toyotech’s TDP-1005B model, and the indication accuracy was ±(0.1% rdg +5 digit). The cooling fan with an outer diameter of 45 mm and inner diameter of 25mm was used, and it operates within the range of DC 12 V and 0.1 A. The power supply connected to the cooling fan was adjusted in 12 steps at a maximum of 48 W. The velocity of a cooling fan was measured using a thermal anemometer (Testo 405i), and the accuracy of the velocity measurement was ±(5% rdg + 0.1 m/s). The pipe, having an outer diameter of 3 mm, was joined to the chamber to enable the filling of the working fluid and to establish a vacuum state. The vacuum pump used was Value’s FY-4C-N model, and it is possible to vacuum with a flow rate of 14.4 ${\mathrm{m}}^3/\mathrm{h}$ and a maximum partial pressure of 2$\mathrm{Pa}$. Additionally, the minimum scale of the injector was 1 mL. The data logger is Yokogawa’s MX100 model, and the measurement error rate for the K-type thermocouple was ±(0.05% rdg + 0.7). The operating fluids were water and methanol, with a set of charged amounts.

As described in Figure 5, a total of 17 thermocouples were attached to the vapor chamber for temperature measuring. The thermocouple used is the K-type, and it is possible to measure −200 °C and 1250 °C through the Seebeck effect. The measurement error rate of the thermocouple was ±0.75%. Thermocouples were attached to the heater, and the outside and inside wall of the vapor chamber. For watching the temperature change on the radial wall, a total of fifteen thermocouples (five thermocouples per line along with A, B, and C measuring lines) were attached at intervals of 120 degrees at the specific heights. The positions of the thermocouples are shown in Figure 5.

2.2. Uncertainty Analysis

The steady-state temperatures of the evaporator and heater, as well as the provided heat load, were estimated to evaluate the present cooling system’s thermal performance. The provided heat, Q, is the electric power input, as calculated by

$$Q=VI$$

(1)

During the present experimental investigation, several measurement sets of voltage, temperature, and current were obtained. These measurements are then utilized to compute the desired thermal performance outcome of the experiment. The uncertainty of the current experimental works with the independent experimental variables can be characterized as U. Then, let U_Q be the result’s uncertainty, with the variables of the voltage (V) and current (I) of the input power mentioned in Equation (1). These variables denote the independent variables’ uncertainties.

$$U_Q={\left[{{\displaystyle \sum }}_{i=1}^n{\left(\left(\frac{\partial Q}{\partial V_I}\right)U_{VI}\right)}^2\right]}^{1/2}$$

(2)

When this connection was applied to the electric-power relationship, the system’s uncertainty, as described by Equation (2) [53], was synthesized by the experimental uncertainties of measurement variables such as T, V, and I. U_VI is the partial uncertainty errors and U_Q is the total uncertainty errors in Equation (2). From the methodology of Ref [53], the calculated uncertainty of the current power was less than 1%.

2.3. Experimental Procedure

Before beginning the experimental tests, the HSVC was thoroughly cleaned, first with methanol and then with distilled water. After that, the HSVC was then vacuumed and dried, vacuum checked, and leaks were verified. Next, the removal procedure for the internal, non-condensable gases such as the air was proceeded by connecting the vacuum pump. The vacuum state generally reached $8\times {10}^{-3}$ torr in a dry environment. Following the evacuation of the HSVC, a predetermined amount of the working fluid was injected into the system. In the current investigation, the quantity of charged working fluid was typically about 5% of the total volume of the HSVC. The charging system was thoroughly cleaned to eliminate any air and other non-condensable gases. Special efforts were also taken to eliminate non-condensable gases from the working fluids. Non-condensable gases will be pushed out of moving vapor into the upper end of the HSVC during the operation and the system can be deteriorated. Therefore, after the verification of the system without non-condensable gas, all data were recorded step by step until the system had reached a stable state. The HSVC was carefully cleaned by repeated washing, vacuum drying, and leak testing after each test series for a specific working fluid.

2.4. Data Reduction

The heat load of the current HSVC is defined as Equation (3), which is associated with the overall temperature difference of the HSVC, ∆T_e, and the input power induced from the voltage and current for the cooling system.

$$Q=VI=\frac{∆T_e}{\sum R}=\frac{T_1-T_{air}}{\sum R}$$

(3)

Temperatures in the heating and condensing parts were recorded using calibrated thermocouples connected to the data logger. It was not possible to get the working fluid’s saturation temperature since it is a function of the heat transfer rates inside the systems. As a result, the surface temperatures of the HSVC’s whole outside area were measured. Additionally, the average temperature in the same position of the circular measuring lines A, B, and C (as shown in Figure 5) was estimated as (T_i,A+T_i,B+T_i,C)/3. T_i,A is the temperature of each measuring position on line ‘A’. T_i,B and T_i,C have a similar definition, but for lines ‘B’ and ‘C’, respectively.

3. One-Dimensional Simulation Model Based on the Resistance Network

3.1. Thermal Resistance Network

Figure 6 shows the HSVC’s thermal resistance network. The evaporator temperature would be higher than the surface temperature of the top condenser. Heat is transferred from the heat source and diffused to the surrounding environment. As the fluid saturation temperature, the evaporator and condenser temperatures, or the temperatures of the fin surfaces, would be re-estimated.

Empirical correlations of several heat transfer coefficients such as boiling, condensing, forced convection, and natural convection were collected and used as variable factors for thermal resistances used in the simulation. Thermal resistance connected from the hot source to the sink may be described in the following manner:

$$R_{TOT}=R_{Pad}+R_{ev\_wall}+R_{ev\_wick}+R_{Vapor}+R_{Cond}$$

(4)

where R_TOT is the total resistances between the hot section and the cold section.

Each of these thermal resistances is presented below. As shown below, the thermal resistance method needs many empirical correlations involved in the thermal resistances of the current models. Several empirical correlations (for boiling, condensation, forced convection, and natural convection) were collected and used in calculations as variable factors for each thermal resistance. [14,15,16,53,54,55,56,57].

$$R_{Cond\_i}=R_{c\_i\_wick}+R_{c\_i\_wall}+R_{c\_i\_Air}$$

(5)

$$R_{Cond\_o}=R_{c\_o\_wick}+R_{c\_o\_wall}+R_{c\_o\_Air}$$

(6)

$$\frac{1}{R_{Cond}}=\frac{1}{R_{Cond\_i}}+\frac{1}{R_{Cond}\_o}=\frac{1}{R_{c\_i\_wick}+R_{c\_i\_wall}+R_{i\_Air}}+\frac{1}{R_{c\_o\_wick}+R_{c\_o\_wall}+R_{o\_Air}}$$

(7)

$$\frac{1}{R_{cond}}=\frac{(R_{cond\_i})+\left(R_{cond}{}_o\right)}{(R_{cond\_i})\times \left(R_{cond}{}_o\right)}$$

(8)

Then, the thermal resistance of the condenser can be defined as Equation (9):

$$R_{cond}=\frac{(R_{Cond\_i})\times \left(R_{Cond}{}_o\right)}{(R_{Cond\_i})+\left(R_{Cond}{}_o\right)}$$

(9)

$$R_{tot}=R_{pad}+R_{ev\_wall}+R_{ev\_wick}+R_{Vapor}+\frac{(R_{con{d}_i})\times \left(R_{cond}{}_o\right)}{(R_{con{d}_i})+\left(R_{cond}{}_o\right)}$$

(10)

where the involved thermal resistances in the current HSVC system can be defined as

- The thermal resistance of the filler between the evaporator and heat surface:

$$R_{Pad}=\frac{t_{pad}}{k_{pad}{A}_{pad}}$$

(11)

- The thermal resistance in the evaporator wall:

$$R_{ev\_wall}=\frac{t_{wall}}{k_{wall}{A}_{ev}}$$

(12)

- The thermal resistance in the evaporator wick:

$$R_{Ev\_wick}=\frac{t_{ev\_wick}}{k_{ev\_w\_e}{A}_{ev}}$$

(13)

where $k_{ev\_w\_e}$ is related to the effective thermal conductivity which should be estimated by the relationship between the wick material and the working fluid.

- The thermal resistance of the vapor flow in the vapor core region [14,15,16]:

$$R_{vapor}=\frac{128L_e{\mu }_v{T}_v}{\pi d_v^4{\rho }_v^{2}r}$$

(14)

- The thermal resistance through the condenser wick into the inner area:

$$R_{C\_i\_wick}=\frac{t_{c\_i\_wick}}{k_{c\_i\_w\_e}{A}_{c\_i\_wick}}$$

(15)

$$R_{C\_i\_wall}=\frac{t_{c\_i\_wall}}{k_{c\_i\_wall}{A}_{c\_i\_wall}}$$

(16)

$$R_{C\_i\_air}=\frac{1}{h_{c\_i\_air}{A}_{c\_i\_surf}}$$

(17)

- The thermal resistance through the condenser wick through the outer area:

$$R_{c\_o\_wick}=\frac{t_{c\_o\_wick}}{k_{c\_o\_w\_e}{A}_{c\_o\_wick}}$$

(18)

In Model 1 and 3, there is nucleate pool boiling inside the two-phase flow in the evaporator; therefore, the heat transfer coefficient of nucleate pool boiling was calculated by a known empirical correlation, as shown in Equations (19)–(21) of Bier et al. [54].

$$\mathrm{F}\left(\mathrm{P}\right)=0.7+2P_r\left(4+\frac{1}{1-P_r}\right)$$

(19)

A* = 3.596 × 10⁻⁵ P_cr^0.69

(20)

$$h_e=A^{\ast }{q}^{0.7}F\left(P\right)$$

(21)

where P_r is saturated pressure and P_cr is the critical pressure of the working fluid.

- The thermal resistance of the condenser outer wall:

$$R_{C\_o\_wall}=\frac{t_{c\_o\_wall}}{k_{c\_o\_wall}{A}_{c\_o\_wall}}$$

(22)

$$R_{C\_o\_air}=\frac{1}{h_{c\_o\_air}{A}_{c\_o\_surf}}$$

(23)

The heat transfer coefficient of film condensation inside the HSVC was estimated from the Nusselt correlation [55,56]

$$\overline{h}=0.943\left[\frac{{\rho }_f\left({\rho }_f-{\rho }_v\right)g{h}_{fg}{k}_f^3}{L_{vc}{\mu }_f\left(T_g-T_{wall}\right)}\right]$$

(24)

If fins are installed in the inner surface in Model 2, efficiency was applied to the convection resistance.

$$R_{c\_i\_air}=\frac{1}{{\eta }_{tot}{h}_{c\_i\_air}{A}_{c\_i_{Tot}}}$$

(25)

If the flow is forced convection, Fand’s correlation (Equation (26)) of the Nusselt number for the forced convective heat transfer coefficient was applied [55,56]:

$$N{u}_f=0.37\times \left(R{e}_f^{0.6}\right) \mathrm{for} 17 < {\mathrm{Re}}_{\mathrm{d}} < \mathrm{70,000}$$

(26)

If the flow is a free convection case, Lefevere and Edge’s following correlation was applied [55,56]:

$$\overline{Nu}=\frac{4}{3}{\left[\frac{7RaPr}{5(20+21Pr)}\right]}^{\frac{1}{4}}+\frac{4\left(272+315\mathrm{Pr}\right)H_{VC}}{35\left(64+63\mathrm{Pr}\right)D}$$

(27)

By attaching fins to a primary surface, heat transmission can be improved. In actuality, a fin of the current HSVC is extremely difficult to build, hence trapezoidal proportions are not commonly used. The fin efficiency of trapezoid fins attached to the HSVC was estimated by the usual estimation method with the assumption of the fin tip insulated. The fin’s surface area ($A_{fin})$ and base area ($A_{base})$ were estimated as follows with the fin dimensions given in Figure 3:

$$A_{fin}=2\times \frac{\left(a+b\right)\times \pi \times H_{fin}}{2}+t_{fin}\left(a+H_{fin}\right)$$

(28)

$$A_{base}=\frac{\left(r_1+r_2\right)\times \pi \times L_1}{2}-A_{fin}+\frac{\left(r_3+r_4\right)\times \pi \times L_2}{2}$$

(29)

Then, the total forced convection area of the finned condenser section was estimated:

$$A_{tot}=A_{fin}+A_{base}$$

(30)

Moreover, the efficiency of one fin was estimated by Equation (31) with the definition of m as (hP/kA)^1/2, (where h is the heat transfer coefficient, P is defined as the perimeter of the fin, and A is defined as the cross-sectional area of the fin). Then, the total fin efficiency with 32 fins can be estimated using Equation (32). The fin efficiency in Model 2 was calculated as 0.95 [55,56]:

$${\eta }_{ fin}=\frac{\tan \mathrm{h}\left(m{L}_{ fin}\right)}{m{L}_{ fin}}$$

(31)

$${\eta }_{ tot}=1-\frac{A_{fin}}{A_{tot}}\left(1-{\eta }_{ fin}\right)$$

(32)

The optimum working fluid amount is a very important parameter in the study of heat pipes. Imura et al. [57] developed the following formula for V_H,I⁺ based on the average temperature measured in the parts of the heat pipe:

$$q_{cr}=\frac{0.64{({\rho }_l/{\rho }_g)}^{0.13}}{\left(\frac{4l_e}{d}\right)/h_{fg}{\left[\sigma g{\rho }_g^2\left({\rho }_l-{\rho }_g\right)\right]}^{1/4}}$$

(33)

$$\begin{array}{c}{V}_{H,I}^{+}=\frac{V_{LP}}{V_{ev}}=\left(1/5~1/3\right)+\frac{0.8l_{cond}+l_a}{l_{e}v}{\left(\frac{3{\mu }_l{l}_{ev}{q}_{cr}}{{\rho }_l^{2}g{h}_{fg}}\right)}^{1/3}\\ +\frac{{\rho }_g}{{\rho }_l}\left[\frac{l_{cond}+l_a}{l_{ev}}-\frac{0.8l_{cond}+l_a}{l_{ev}}{\left(\frac{3{\mu }_l{l}_{ev}{q}_{cr}}{{\rho }_l^{2}g{h}_{fg}}\right)}^{1/3}\right]\end{array}$$

(34)

They decided that 1/5~1/3 of the first term is insufficient in the case when l_e is substantially smaller than (l_c+l_a) and that additional research is required. However, Equations (33) and (34) may be used to calculate the minimum charged quantity of a working fluid. Moreover, the calculation may be conducted with an estimate and with an equivalent evaporator area. The determined quantity for the existing system to pour the right amount of working fluid into the HPHC was roughly V_H.I⁺ ≈ 0.2 for water. However, in the current experimental results proposed with a very short evaporator, the optimum charging ratio should be enough to pool the evaporating space; it was approximately 20~30% for the current HSVC. Calculations were performed with equivalent l_e as 0.01 m, the same heating surface area as the current HSVC, and no adiabatic section. Using Imura’s approximation approach, the system was charged incrementally from VF = 5 to 50%. With this information, a series of experiments was carried out to obtain the optimal charge ratio. The HSVC employed in this investigation was built without a transporting adiabatic section. Furthermore, previous research by Attia [58] on vapor chambers on the optimum charge ratio, reported around 10%; therefore, the current charge ratio can be in a reasonable range.

3.2. Operating Limit

The vapor produced in the heating part of an HSVC transports heat vertically to the top. As it travels through the chamber, the vapor rises and condenses in the cooling condenser. Following that, gravity or capillary force (in the event of a wicked structure) is utilized to return the condensed liquid to the heating part. The current HSVC is an excellent heat transfer device, but if the heat transfer rate increases significantly, the maximum limit can be reached. In addition, the wall temperature may rise sharply, or the heat transfer coefficient of the heating section may decrease. Many researchers have investigated this performance constraint and concluded that it may be divided into three categories. [14,15,16,17,18,19] One type of performance limitation emerges when liquid fill charges are exceedingly low. The HSVC requires a minimum amount of working fluid to sustain a continuous circulation of vapor and condensed liquid. If the charged amount of the working fluid is less than the required minimum amount, the falling condensate liquid film cannot reach the bottom of the evaporator, which eventually dries or increases the wall temperature. As a result, this kind of operating limit is commonly referred to as the dry-out limit. This can lead to the heat transfer limit such as the boiling or entrainment limit. Vapor bubbles occur in the liquid pool of the evaporator section, and nucleate pool boiling accelerates as the heat flux increases. After that, individual vapor bubbles rapidly combine and grow to create a vapor film along the wall. The vapor sheet shields the surface of the evaporator from the evaporating liquid. Due to the low thermal conductivity of vapor, only a portion of the heat input to the wall produces a fast rise in the evaporator’s surface temperature. This boiling temperature is also the burn-out point. High charging ratio, high supply heat, but low evaporator heat flux has a flooding limit. Due to the high heat flow, the speed of the counter-current flow between the vaper and the liquid is quite high, resulting in an increase in shear stress at the vapor/liquid interface, while a large surface wave is formed. As a consequence of this, the liquid flow became unstable, resulting in liquid entrainment. The entrained liquid is carried by the vapor flow to the condenser and collected there. High shear stresses have the potential to entirely block the flow of the returning condensate. At the flooding point, the condensate flow separates. In either instance, excessive entrainment or flooding results in a lack of liquid supply to the evaporator. This causes a local dry-out, followed by an evaporator-wide dry-out. The existing research does not offer a precise solution to the flooding limit. Furthermore, the current study made use of a hemispherical shell vapor chamber with a very small evaporator and a very large condensing area. The proposed HSVC system’s flooding limit is also incorporated in the 1D resistance simulation to determine if a given operating situation is possible or not. As demonstrated in Equation (35), Wallis’ flooding correlation in vertical tubes [54,59] was employed as a correlation of the flooding limit to roughly predict the correct operation of the current system.

$$j_g^{\ast }{}^{1/2}+m{j}_f^{\ast }{}^{1/2}=\mathrm{C}$$

(35)

where $j_g^{\ast }$ is the dimensionless superficial velocity of the gas and $j_f^{\ast }$ is the case of the liquid, and these are defined as:

$$j_g^{\ast }=j_g{\rho }_g^{1/2}{\left[gD\left({\rho }_f-{\rho }_g\right)\right]}^{-1/2}$$

(36)

$$j_f^{\ast }=j_f{\rho }_f^{1/2}{\left[gD\left({\rho }_f-{\rho }_g\right)\right]}^{-1/2}$$

(37)

In the calculation, the HSVC was assumed to have a multi-thermosyphon array with 41 thermosyphons with a diameter of 5 mm that were connected each other. Additionally, the mass flow rate and heat flow rates were estimated based on the experimental result. In general, m is one, and the simulation showed that $j_g^{\ast }$ = 0.0016 is much higher than $j_f^{\ast }$ = 0.00028. This means that the HSVC does not meet the criteria of the flooding limit which prevents the correct operation of the HSVC. Additionally, the flooding limit as the heat transfer limitation was estimated as 245 W [59].

4. Results and Discussion

4.1. Experimental Results

Figure 7 shows the effect of the temperature difference on the charged volume ratio obtained from the experiment and simulation. As shown in Figure 7, three types of HSVC were tested and investigated to find various effects of parameters influencing the current vapor chamber. The current uneven structure of the vapor chamber was not previously studied. Usually, the vapor chamber had a flat-type shape. Therefore, the current shape of the vapor chamber cannot be expected as the usual case. In the current HSVC, the large condenser area seriously influenced the thermal performance of the vapor chamber.

The HSVC cooling system will first be evaluated in terms of the temperature coefficient (∆T_e). The current experimental results allow for the assessment of the various characteristics of the HSVC’s temperature difference. As shown in Figure 7, the temperature differential of the HSVC is affected by several variables, including the air speed in the condenser section, the heat flux (q), and the charged ratio of the working fluid. This section will go through the effect of each of these factors. The clear goal of this study is to attain the highest heat transfer rate while simultaneously meeting future heat sink requirements. Although water has a high latent heat, the results showed a high heat transfer capacity relative to the ∆T_e of other working fluids, as shown in Figure 7.

• Effect of the Quantity of the Working Fluid, VF

The amount of working fluid inside the HSVC was defined in this research as the ratio of the volume of working fluid within the HSVC to the total volume of the chamber inside:

$$\mathrm{Volume} \mathrm{Fraction} \left(\mathrm{VF}\right)=\frac{\mathrm{Charged} \mathrm{Liquid} \mathrm{Volume} }{\mathrm{Total} \mathrm{Inside} \mathrm{Volume}}$$

(38)

Finding the optimal quantity of a working fluid in HSVC is crucial information to design the HSVC system as any kind of heat pipes. The charged volume fraction of the working fluid has a considerable effect on the operations of an HSVC. The amount of working fluid was discovered to change immediately with an increase or decrease in the system’s heat transfer capabilities, as seen in Figure 7. Imura et al. [28] proposed a helpful formula for the optimum charge rate as explained above. However, it could not predict the optimum charge rate for the current HSVC. They proposed that the optimum charge rate by their formula is quite underestimated.

With this knowledge, one can estimate the ideal quantity of a specific working fluid, and a series of tests were conducted to discover the best charge amount. The HSVC employed in this study was developed without an adiabatic section and with a relatively high condenser surface area encompassing inner and outer surfaces, compared to the evaporator area of 20 mm × 20 mm. The influence of the volume fraction (VF) on the HSVC temperature differential at different heat fluxes with varying charged ratios is seen in Figure 7. The working fluid volume should be sufficient to convey heat from the evaporator to the condenser. As a result, as shown in Figure 7, the VF is substantially influenced not only by the heat transfer rate (heat flux) and air velocity on the condenser section but also by the working fluids.

The HSVC temperature difference when water is utilized as the working fluid is lower than when methanol is used. As shown in Figure 3, test results using water and methanol as working fluids followed a similar pattern, with the results varying depending on factors such as the VF, v_air, and Q. In the case of water, the findings of Model 1 and Model 2 indicated an optimal VF in the range of a 15~25 percent charge ratio with a low temperature difference, indicating a low thermal resistance. However, the Model 2 data did not reveal any potential optimal charge ratio; however, 10% of VF demonstrated the smallest temperature differential. The results using methanol did not predict the best charge ratio. However, the tested results of 10% indicated the smallest temperature difference. ∆T_e, on the other hand, did not differ much between Models 1 and 3. However, in the instance of Model 2, ∆T_e grew with the increasing VF and then reduced over 40 percent. This pattern was seen in the water results as well. The prior flat vapor chamber study agreed on the low charge ratio. According to Attia et al., the optimal charge ratio was 10–30%, and at 50 percent VF, the thermal resistance was reduced once more [58].

This is because as the thickness of the liquid film grows, so does the charge ratio, and since heat is first transmitted through the liquid film layer through conduction, the thermal resistance increases as the charging ratio increases. For Model 3, the optimal VF for water was observed to be 20–30%. At the same temperature as water, methanol has a lower latent heat of vaporization, as well as a lower density and viscosity. According to Figure 7, the higher the charge ratio, the lower the temperature difference. This is owing to the fact that for specified heat load values, the amount of working fluid is inadequate, producing dry-out in specific sections of the chamber, which vanishes with an increase in charge ratio. This is because the amount of working fluid is inappropriate for the specified heat load value, resulting in dry-out in a specific section of the chamber and disappearing as the charge ratio increases. If the charge rate rises, the effect of the thickness of liquid film is manifested, and in each case of Figure 7, ∆T_e of Model 2 and Model 1 decreases again from a charge rate of 40%. This trend was comparable to the case of water. It was supposed that Model 2 had a large condensing area.

• Effect of Air Flow Velocity, v_air

The velocity of the air is a factor that determines the system’s heat transfer capacity. The effect of the coolant air’s flow speed in the condenser section on the performance of the HSVC is presented in Figure 7. The temperature difference decreases as a consequence of forced convection. However, as shown in Figure 7, an increase in air flow velocity higher than 2–3 m/s would not considerably boost the assembly’s total heat transfer capability. This tendency is evident in all models. The observed influence of increasing heat transfer capacity with air velocity was detected in all working fluids, as shown in Fig 7. Because the cooling air flow velocity of the condenser section affects the activity of the two-phase flow in the HSVC, the air flow velocity is a vital component in boosting the system’s heat transfer capacity. When the vapor is cooled by a low flow velocity, the comparably large volume of rising vapor from the evaporator obstructs the return flow of the condensed liquid. A greater air flow velocity, on the other hand, may reduce the vapor flow against the growing counterflow of condensed liquid. A high flow velocity does not always imply a greater heat transfer ability. In the absence of HSVC deterioration, the most probable failure mechanism of the system would be the case when the fan used for removing heat from the condenser section fails. Therefore, in the event of fan failure, the heat transfer capacity of the system must be known. As shown in Figure 7a–f), the temperature difference for natural convection (0 m/s) represents the heat transfer capability of the proposed system without a fan. Figure 7 shows that the current cooling system can achieve up to 20 W of cooling performance when using water and methanol as working fluids.

• Effect of the Heat Load

Figure 7a–f shows the influence of heat flux on the vapor chamber’s overall temperature difference of the HSVC for varying charge ratios, flow velocities, and working fluids during different experiments. Moreover, Figure 7 shows the effect of the heat loads on different air flow velocities with three models. Variations in charge ratio have little influence on v_air when the heat load is low. Water outperforms methanol across all charge ratio ranges and heat loads. The increasing heat load and temperature difference, ∆T_e, was increased with the same manner of varying charge ratios. This is because the latent heat of water is substantially bigger than that of methanol. The increasing heat load, ∆T_e, with high VF shows a different trend between water and methanol. In all cases, it was observed that increasing the supplied heat and VF leads to a decrease in ∆T_e. This may be a phenomenon caused by an increase in heat capacity accompanied by an increase in the quantity of the working fluid inside. However, in the case of water in Model 1, it was observed that ∆T_e increased when the supplied heat and the VF were increased. In general, as the internal working fluid amount is increased, the cooling capacity is improved as the heat capacity increases and, thus, the temperature generally drops. This phenomenon also occurred in Model 2 when Q = 20 W. Model 1 and Model 2 have a structure in which there is no wick inside, and it can be predicted that the internal vapor flow space rapidly decreases as the internal working fluid amount increases. As shown in Figure 7, in all cases, the ∆T_e of Model 3 with wicks was observed to be high. However, in the case of water, Model 2 was observed to have a generally higher ∆T_e than Model 1, and in the case of methanol, Model 1 was observed to have a higher temperature. This showed a higher temperature than when there was no wick structure, and in the case of water, there was a lower temperature with fins; in the case of methanol, there was a lower temperature without fins. It can be seen that the thermal behavior of the HSVC is affected by the relationship between the physical properties of the working fluid and the wick.

• Temperature profiles along the vapor flow

As shown in Figure 8, the temperature profile has been shown by the average temperature in the same position of the A, B, and C lines. As you can see in Figure 8, from #1 to #7 of thermocouple number, the temperature decreased due to reaching the top condenser area. After that, the temperature is increased again due to being close to the evaporator. This temperature profile is similar to all models with variable air flow speeds. Thermocouple #5 shows the lowest temperature, #6 and #7 also show a slightly lower temperature in the inner surfaces than #3. It means that vapor flows upwards inside the core space, after which it condenses on both wall surfaces. The condensed liquid returns, flowing through both inner wall surfaces. Therefore, the current HSVC with the inner and outer cooling surface is operated more actively to cool. As can be seen in Figure 8a–c, the overall temperature distribution in Model 2 was observed to be the lowest. It is judged that this is because the finned surface area increases the heat transfer area in the condensing region, thereby increasing the cooling effect. In natural convection conditions, it was observed that the temperature distribution of all models was similar regardless of the difference in supplied heat loads. In Figure 8, it was observed that the temperature distribution was lowest in the order of Model 2, Model 1, and Model 3. As explained in the previous section, this would be due to the relationship between the working fluid and the wick. In the case of Model 2, it was observed that the difference between temperature profiles according to the flow rate of the cooling air was large. It can be determined that this was caused by the heat transfer enhancement of fins attached to the condensing section.

• Temperature profiles in different angular positions (A, B, and C lines)

Figure 9 shows the temperature profile measured in different angular measuring lines such as A, B, and C lines placed in 120° angular positions. These temperature profiles indicate that the working fluid motion is flowing in three-dimensional directions with active vapor formation and fluid motion. As shown in Figure 9, the temperature profile of Q = 10 W is very close to the temperature of other positions with different air speeds. It means that in the low heat load, fluid is moving around in the evaporator space and is not very active. However, in Q = 20 W, the temperature gap was high between temperatures in the same angular position. This implies that the inside working motion of liquid is very active to vaporize and the degree of freedom of the fluid’s moving directions is high enough for the top condensing space. The temperature profile for Q = 20 W of Model 1 shows a higher temperature difference than Model 3. This means that the wick structure of Model 3 helps to make a stable motion of vapor through capillary-driven liquid circulation.

• Effect of the Orientation

Figure 10a–c represent the temperature difference (ΔTe) measured on the HSVC with various orientations from the vertical base (0°) to the horizontal position (90°) in three models. As can be seen from the figure, Model 1 and Model 2 have no wicks inside, so the temperature rises sharply at an inclination angle of 20° or more. However, it was observed that ΔTe is somewhat stable or maintains a constant temperature range at more than VF = 40% because the working fluid always wets the evaporation surface at more than 40% of the internal working fluid. As shown in Figure 10, the thermal performance depends on the charging ratio of the working fluid. In Model 1, it was observed that, as there is no wick inside, a working fluid cannot return by capillary force, so the heat transfer performance is maintained generally until the inner surface of evaporator is maintained wet due to sufficient working fluid capacity. When VF = 10%, ΔTe suddenly increases after 20° in Model 2. This point can be implied about the operating limitations of the HSVC. These points differ from 50° for VF = 20% and 60° for VF = 30% and 40%. As a result of the experiment with VF = 50%, it was confirmed that it was a stable operation without deterioration due to directionality. This is due to a large pool of liquid that can wet the evaporative surface. In the case of Model 3, it is observed that the heat transfer performance is uniformly maintained up to 50° regardless of the amount of the working fluid, particularly in the case of VF = 40%; as the inclination angle increases, it can be predicted that liquid circulation due to internal capillary force becomes more active.

• Transient Temperature Variation

Figure 11 shows transient temperature variations of three models with VF = 10%. As shown in Figure 11, three models show different temperature variations and fluctuations. The temperature difference between thermocouples #1 and #2 of Model 1 and Model 3 is higher than Model 2. This means that the finned cooling area helps liquid circulation inside the working fluid. However, it leads to large temperature fluctuations with a decreasing temperature difference between positions. In the case of Model 2, compared with other models, the temperature of thermocouple #2 is not increased very much. This must be because the finned area can help improve heat transfer performance. In addition, in the case of Model 2, a temperature fluctuation phenomenon at thermocouple #2 was observed at the heat loads of 10 W and 20 W. It was observed that the amplitude of the temperature fluctuation was large in Model 2 and Q = 10 W; additionally, in Q = 20 W, the vibration frequency was short, which can be observed in the density oscillation. Moreover, this phenomenon was observed in Model 3 in the case of Q = 20 W. This phenomenon may occur when the evaporation activity is actively performed in the internal evaporation region. As a result, it was proven in this investigation that connected fins play a key role in the HSVC’s thermal performance.

• Effect of Non-Condensable Gas

The presence of non-condensable gases, such as dissolved gases in the working fluid and absorbed gas in the thermosyphon structure, has been recognized as degrading the performance of a thermosyphon. When non-condensable gases are present in the system, they are swept along with the vapor flow and accumulate at the condenser end. This will generate a gas plug, which will act as a barrier to the flowing vapor, and a small amount of gas could cause a HSVC to shut down. To eliminate non-condensable gas sources, the working fluid must be carefully purged of dissolved gases. In the present study, the HSVC was correctly operated without deterioration due to the non-condensable gas.

• Comparison with previous works in the literature

The present HSVC has a very unique shape and structure. It is not easy to compare with other vapor chambers, but the concept of heat transfer in the heat pipe system is similar. Therefore, the thermal resistance between the average bottom surface temperature and the average top surface temperatures can be roughly compared. Moreover, the thermal performance of the present HSVC can be judged. The average bottom–top thermal resistance can be defined with average temperatures in A, B, and C position lines, as in Equation (39).

$$R_{BT}=\frac{\frac{1}{3}\left(T_2+T_3+T_4\right)}{\frac{1}{4}\left(T_1+T_5+T_6+T_7\right)}$$

(39)

As shown in Figure 12, thermal resistance, R_BT, with Model 2 showed the lowest values of 0.15 (v_air = 1 m/s) and 0.3 (v_air = 0.29). The thermal resistance increased by adding heat flux from 10 W to 20 W. This trend is similar for all models and the results from the literature. Bottom–top thermal resistance for the flat, thin vapor chamber is very important, because this can imply a high heat spreading performance. The present HSVC of Model 2 showed the lowest bottom–top thermal resistance. This can be explained by the fact that the thermal spreading performance is high enough compared with the others. In the case of Model 2, it was accompanied by fins. It can be explained that Model 2, with the extended finned surface area, can enhance heat transfer between bottom and top surfaces.

4.2. Model Validation of the Thermal Resistance Model

As shown in Figure 13, the one-dimensional resistance model was validated with experimental results in terms of flow velocities and heat loads. From the figures, the resistance model with modified correlations of the forced convective heat transfer coefficient agreed with the experimental results of the 20 W heat load with a varied air coolant speed. The modification was validated with the experimental results of VF = 20% (h = 0.0833h_fand³ − 1.05 h_fand ² + 5.8667h_fand + 21.5 for Model 1 and 3, h = 0.0185h_fand³ − 0.233h_fand ² + 1.303h_fand + 1.78 for Model 2). After the validation test, the HSVC-based heat sink was predicted and compared with experiments. As shown in Figure 13a,b, the resistance-based simulation method can predict the current system, but can simulate the HSVC system with slight differences within a reasonable range. Based on the simulation of the one-dimensional resistance model, it was judged that the fin design of the current Model 2 was overestimated. It was demonstrated that the performance of the 1D simulation based on analytical thermal resistance network techniques is dependent on the selection of a few empirical correlations for different thermal resistances. Because the solution relied on the thermal resistance network model, this demonstrates that the algorithm’s validity necessitates comparing the temperature distribution or temperature difference inside the HSVC’s assembly produced through the simulation with that achieved through experimentation, as seen in Figure 13a,b. Depending on the empirical correlations employed for boiling and condensation, the simulated interior temperature difference could deviate significantly from the experimental data. In the present simulation, Bier et al.’s correlation for boiling [54] and Nusselt’s correlation for condensation [55,56] were used.

4.3. Numerical Method by CFD Analysis

A thermal flow analysis was used to assess the parameters impacting heat transfer performance using a CFD analysis in comparison with experimental data acquired in the experimental study [59]. The simulation system includes a method for decomposing the Navier–Stokes equation into numerous equations and solving the dominant equation using numerical analytical techniques. We ran numerical analyses under a variety of situations using the ANSYS FLUENT 2020 R2 program. To compare the simulated and experimentally derived temperatures, the analysis focused on the following circumstances and assumptions [52,59].

-

Incompressible flow was assumed for all phases.

-

The vapor flowed in a turbulent manner.

-

The pressure in the inner space was about 25,000 Pa as a result of measuring using a vacuum gauge. Based on the measured pressure value and the experimental temperature data, the saturation temperature and operating pressure values were set to 338.15 K and 25041.6 Pa, respectively.

-

Components other than the heating and cooling section were insulated.

-

The heat transfer coefficient was obtained by calculating the dimensionless number related to natural convection heat transfer based on the experimental values [54,55,56].

4.3.1. Governing Equations and the Simulation Model

The governing equations in the simulation involved continuity, mass conservation, and momentum equations based on the Navier–Stokes principle, as follows [52,60]:

- The continuity equation:

$$\frac{\partial \mathsf{\rho }}{\partial \mathrm{t}}+\nabla \cdot \left(\mathsf{\rho }\overrightarrow{v}\right)=S_m$$

(40)

where the mass transferred to the continuous phase from the scattered second phase is denoted by the source $S_m$.

- The momentum equation:

$$\frac{\partial }{\partial \mathrm{t}}\left(\mathsf{\rho }\overrightarrow{v}\right)+\nabla \cdot \left(\mathsf{\rho }\overrightarrow{v}\overrightarrow{v}\right)=-\nabla \mathrm{p}+\nabla \cdot \left(\stackrel{=}{\tau }\right)+\mathsf{\rho }\overrightarrow{g}+\overrightarrow{F}$$

(41)

where ρ is the static pressure, $\mathsf{\rho }\overrightarrow{g}$ represents the gravitational body force, $\overrightarrow{F}$ is the external body force. $\stackrel{=}{\tau }$ is the stress tensor and the equation was described below.

$$\stackrel{=}{\tau }=\mu \left[\right(\nabla \overrightarrow{v}+\nabla {\overrightarrow{v}}^T)-\frac{2}{3}\nabla \cdot \overrightarrow{v}I$$

(42)

where $\mu$ is the molecular viscosity and I is the unit tensor.

- The energy equation:

$$\frac{\partial }{\partial t}\left(\rho E\right)+\nabla \cdot \left(\overrightarrow{v}\left(\rho E+p\right)\right)=\nabla \cdot \left(k_{eff}\nabla T-{\displaystyle {\sum }_i}{h}_j\overrightarrow{J_j}+\left({\stackrel{=}{\tau }}_{eff}\cdot \overrightarrow{v}\right)\right)+S_h$$

(43)

where $k_{eff}$ is the effective thermal conductivity, $\overrightarrow{J_j}$ is a diffusion flux of the species $j$. $S_h$ includes the source of volumetric heat and the heat generation rate from chemical reactions. In Equation (43), E is defined as

$$E=h-\frac{p}{\rho }+\frac{v^2}{2}$$

(44)

where sensible enthalpy, h, is defined for incompressible flows as

$$h={\displaystyle {\sum }_j}{Y}_j{h}_j+\frac{p}{\rho }$$

(45)

In Equation (45), $Y_j$ is the mass fraction of species $j$.

$$h_j=\underset{T_{ref}}{\overset{T}{{\displaystyle \int }}}{c}_{p,j}dT$$

(46)

$\mathrm{where} T_{ref}$ is the reference temperature as 298.15 K for the pressure-based solver.

A numerical simulation based on the VOF model in ANSYS FLUENT has been performed to investigate the condensation process and flow characteristics in the HSVC. Among the multiphase flow approaches in ANSYS FLUENT, the Euler–Euler approach is used in the HSVC. This approach solves by assuming that each phase is a permeable continuum. The VOF (volume of fluid) method is a model for analyzing two or more immiscible fluids and can be employed to simulate the evaporation and bubble condensation in two-phase flows [59,60,61,62]. The VOF algorithm for the current simulation is well described in Ref [52,60]. In addition, the expression of the phase change used the Lee model in the evaporation–condensation model [52,60,61,62,63,64,65]. The surface tension between the liquid and vapor is used in the equation proposed Fadhl et al. [66]

$$\sigma =0.09805856-1.845\ast {10}^{-5}\ast T-2.3\ast {10}^{-7}\ast T^2$$

(47)

For the analysis of the HSVC, energy, viscous (SST k-omega) and multiphase (VOF, implicit, Lee model) were applied, and it proceeded for 100 s with a time step of 0.002 s under a pressure-based transient solver and SIMPLE scheme [52,60]. The analysis consisted of 10%–10 W, 30%–10 W, 30%–20 W and 50%–10 W, and the boundary conditions for each are shown below in

Table 2. Boundary Conditions of the CFD Simulation.

Boundary Condition
Initial Temperature of the Liquid	337.15 K
Initial Saturation Temperature	338.15 K
Operating Pressure	25041.6 Pa
Free stream Temperature	298.15 K

. The temperature value obtained in the experiment was applied to the heating of the HSVC. For the natural convection coefficient, a dimensionless number was calculated based on the experimental data and then the value substituted into the natural convection heat transfer equation was used [27]. Convective heat transfer coefficients of the inner and outer cooling surface used in the simulation were estimated by known empirical correlations from Ref. [56]. The heat transfer coefficients of natural convection were 6.17 to 8.51 W/m²∙°C for simulation cases.

4.3.2. Mesh Sensitivity Analysis

The mesh for the CFD analysis of the HSVC was created using the sweep method. The working fluid area was divided by measuring the volume according to the amount of working fluid (10%, 30% or 50%). In general, as the number of elements increases, the accuracy of the analysis increases, but there are disadvantages in that the time required for the analysis becomes longer, and it may require excessive calculations compared to the performance of the computer. Therefore, it is important to select a suitable mesh. Four sweep mesh models were analyzed to determine the appropriate mesh size for the CFD analysis. In particular, the current CFD simulation is a three-dimensional structure that is different from the two-dimensional modeling of previous research in the literature [45,46,47,48,49,50,51]. Moreover, Song et al. [52] reported the importance of 3D simulation to reach accuracy and to see multidimensional flow behavior. The information about the quality for each case is shown in

Table 3. Sensitivity Analysis of Grid Quality: Model 1.

	Element Size (m)	Number of Elements	Skewness			Orthogonal Quality			$\mathbf{∆}\mathit{T}$ $\left({\mathit{T}}_1-{\mathit{T}}_4\right)$
			Min	Average	Max	Min	Average	Max
Case 1	0.005	1184	1.31 × 10−10	0.377	0.677	0.323	0.85	0.999	26.907
Case 2	0.003	5012		0.286	0.647	0.353	0.895	1	27.232
Case 3	0.001	118,809		0.189	0.566	0.696	0.951	1	26.921
Case 4	0.00098	124,080		0.17	0.568	0.705	0.957	1	26.767

. Therefore, to save time for 3D simulation, mesh quality and size were considered with the accuracy and time cost. Among the methods for judging cell quality, in the case of skewness, the maximum value should be less than 0.95, and the lower the average value, the better. If the value is less than 0.25, it can be determined that the quality of the grid is excellent. Furthermore, for orthogonal quality, the minimum value should be 0.01 or higher, and the closer the value is to 1, the better the cell quality [66]. Table 3 lists the number of elements in each case and information on cell quality, with Case 4 having the best cell quality. As a result of the analysis with the same boundary conditions in 50%–10 W, there was no significant difference in temperature. However, since the number of the elements was small, there is a problem that the internal flow is not clearly expressed. In addition, as a result of considering the performance of the computer and the time required for the analysis, Case 3 was selected. Figure 14 shows the mesh of Case 3.

4.3.3. CFD Simulation Results

As a result of the CFD analysis, as predicted when designing the HSVC, the condensation of the fluid in the inner wall space occurred. Figure 15 shows a liquid volume fraction between 16.5 s and 16.8 s in the HSVC’s inner space under the condition in the case of VF = 30% and Q = 20 W. The evaporated fluid loses heat on the wall and condenses back to the bottom of the HSVC. This process is repeated, and the working fluid is circulated.

Figure 16a–d show the difference in the vapor volume fraction at the inner wall in cases of varying charge ratios and heat loads (VF = 10, 30, 50% and Q = 10, 20 W). As shown in Figure 16a, Figure 16 shows only the vaper fraction, so the vaper volume fraction is shown as a hotspot. The rest of the area marked in blue shown in the figure does not display liquid as a whole, but is also an area where vapors are insufficient. In other words, it may be liquid or air because areas other than the initial liquid are set as air. Therefore, the vapor volume fraction on Figure 16 focused on the vapor phase in the space. As a result of the comparison by setting the range of the vapor volume fraction to 0 to 1, in the case of 10%–10 W and 30%–10 W, a region where vaporized fluid exists on the inner wall was observed. In the case of 30%–20 W, vapor fractions are high in the evaporator. However, in the case of 50%–10 W, almost no vapor was observed. As the volume capacity of water increases, the heat capacity of water also increases, and the area where heat exchange occurs in contact with the atmosphere becomes wider. These are considered to be the cause of the phenomenon in which vapor is not generated well in the 50%–10 W condition, and the tendency of $∆T_e$ to decrease again after a 30% volume fraction in Figure 7a can also be explained. However, since heat exchange does not occur while repeating evaporation and condensation, it cannot be regarded as the correct operation of the vapor chamber.

Figure 17a–d shows the temperature contour and velocity vector distribution inside HSVC-Model 1. It is difficult to express the path-line of the fluid-specific particles with the VOF model, as it represents the ratio that each fluid contains per cell, rather than representing each particle. Therefore, the current simulation could check the flow direction through the streamline. As shown in Figure 17, the heated fluid passes through the center and rises to the inner wall, and on the outer wall, the cooled fluid flows downward and returns to the bottom of the device. In addition, it can be confirmed that the swirl occurs at the fluid interface in the inner space of the wall. As shown in Figure 17a–d, the vapor from the surface of the water is evaporated. On both sides, flow resistance occurs due to evaporation; however, at the center of the bottom, the flow shows that the vapor is condensed upwards without resistance. Therefore, the evaporated vapor was rapidly condensed. Additionally, as shown in Figure 17a–d, due to the large outer cooling surface, some of the vapor rising to the top end was unable to reach the end, resulting in a condensing phenomenon, which was guessed to be the local recirculation flow. As a result, the internal fluid oscillated from side to side, showing a phenomenon that circulated intermittently. In addition, the flow behavior in the irregular direction was also observed in the evaporator section, and which temperatures were varied in the A, B, and C lines was confirmed in the experiment, as shown in Figure 9.

Figure 18 shows the velocity vector and streamline of the fluid according to the circulation of the internal working fluid under various environmental conditions. The streamlines in Figure 18a–d represent vertical flow streams. It also shows the horizontal flow along with the wall space. Therefore, it is possible to observe how the 3D flow occurs inside the HSVC. Figure 19a,b in which the field of view of Figure 18b,c is enlarged, show that the streamline has a wave-shaped circular motion that passes through both walls. As shown in Figure 19, steam evaporated from the surface appears to move from the inner surface to the central space of the evaporator along HSVC. Figure 19a,b show an active streamlined flow of wall space as the heat rod increases at 30% capacity. As a result of a reasonable comparison of the same wall area, the fluid flow direction is the same. However, as the amount of heat increases, the liquid present in the wall space increases. It can be seen that the rise of the vapor due to the phase change inside and the liquid flow due to condensation on the wall have a complex effect. Due to the structure of HSVC, the cooling area of the upper end decreases from the lower end to the upper end according to the thin structure of the upper end. In a small condensation space, the vapor flows horizontally along with some condensation spaces at the same time as condensation. It can be seen that continuous liquid circulation, which is the flow characteristic of the typical vaper chamber, is taking place according to the active vaper flow activity and condensation inside.

As shown in Figure 13, the simulation results should be compared and validated with the experimental results. In the current study, the CFD simulation was validated by comparing the experimental temperature profile under the given conditions. Figure 20a–d show the results of comparing the temperatures at each temperature measurement position under some experimental conditions (VF = 10%, 30%, and 50%, Q = 10 W, 20 W). As shown in Figure 20, both CFD results and experimental results show similar temperature distribution trends. Figure 20a shows results that are close to the experimental results of VF = 10% and Q = 10 W. However, in the case of Figure 20b–d, it was confirmed that there was a slight temperature difference from the experimental results. As shown in Figure 20b,c, the CFD results were calculated to be approximately close to the temperature of thermocouple #2 at 10%–10 W, the upper part of the evaporation unit and, accordingly, the temperature of the rest seems to be close to the experimental results. However, in Figure 20b–d, as the temperature of thermocouple #2 showed a large deviation from the experimental results, the temperature of the rest also showed a somewhat large difference. As shown in Figure 20, the 3-D simulation showed partially inconsistent results with the experimental results. This is because the boundary conditions of the condensation area were slightly underestimated compared to the experiment. In addition, the two-phase flow inside HSVC was underestimated in terms of the vaper flow motion, and it was not easy to fully simulate the vapor flow characteristics. In particular, it is not possible to effectively analyze the active circulation behavior occurring inside the HSVC system with a very large condensation area and irregular condensation structure of Model 1. In addition, as shown in Figure 20, the experimental results showed a higher temperature profile. However, the 3-D simulation of HSVC has the advantage of being able to predict detailed flow that cannot be simulated in the one-dimensional modeling based on the previous thermal resistance network.

5. Conclusions

In electronics cooling, a vapor chamber is one of the most effective thermally dispersed approaches. The thermal performance of a HSVC containing water and methanol at varying charge volume fractions, heat fluxes, and cooling air velocities is evaluated. The experimental results with water show better thermal performance than methanol. The optimum working fluid was within the range of 20~30% of the total inside volume. The large condenser area leads to an improved thermal performance due to the decrease in thermal resistance. It was verified by comparison with other research results from the literature. The temperature profile of the HSVC shows condensation on both sides of the inner and outer surfaces. To maintain the temperature profile, the optimal charge ratio was 20–30 percent.

In addition, the 1D resistance model and 3D CFD simulations were studied and validated by comparing them with the experimental results.

Through the 3D CFD analysis, it was possible to see the flow of the working fluid occurring inside the HSVC. The simulation can observe the main two-phase process of evaporation and condensation areas. Moreover, the flow of working fluid was consistent with what was expected in the HSVC design. The 3D streamline of the inside fluid circulation showed the correct evaporation and condensation behavior induced by the pressure difference.

It was concluded that thermal characteristics of the present HSVC are affected by various performance parameters such as a conventional heat pipe. Therefore, more research and comprehensive investigations are necessary for industrial application requirements.

Future work should be carried out with a parametric consideration of the HSVC. Based on the present study, the thermal flow behavior with performance parameters such as the shell thickness, shell’s curve angle, evaporator space, condenser structure, various working fluids, and wick structure will be studied in depth. Moreover, the HSVC should be designed and manufactured to meet industry standards for its real application in future cooling devices.