Optimal Power Sharing in Microgrids Using the Artificial Bee Colony Algorithm
Abstract
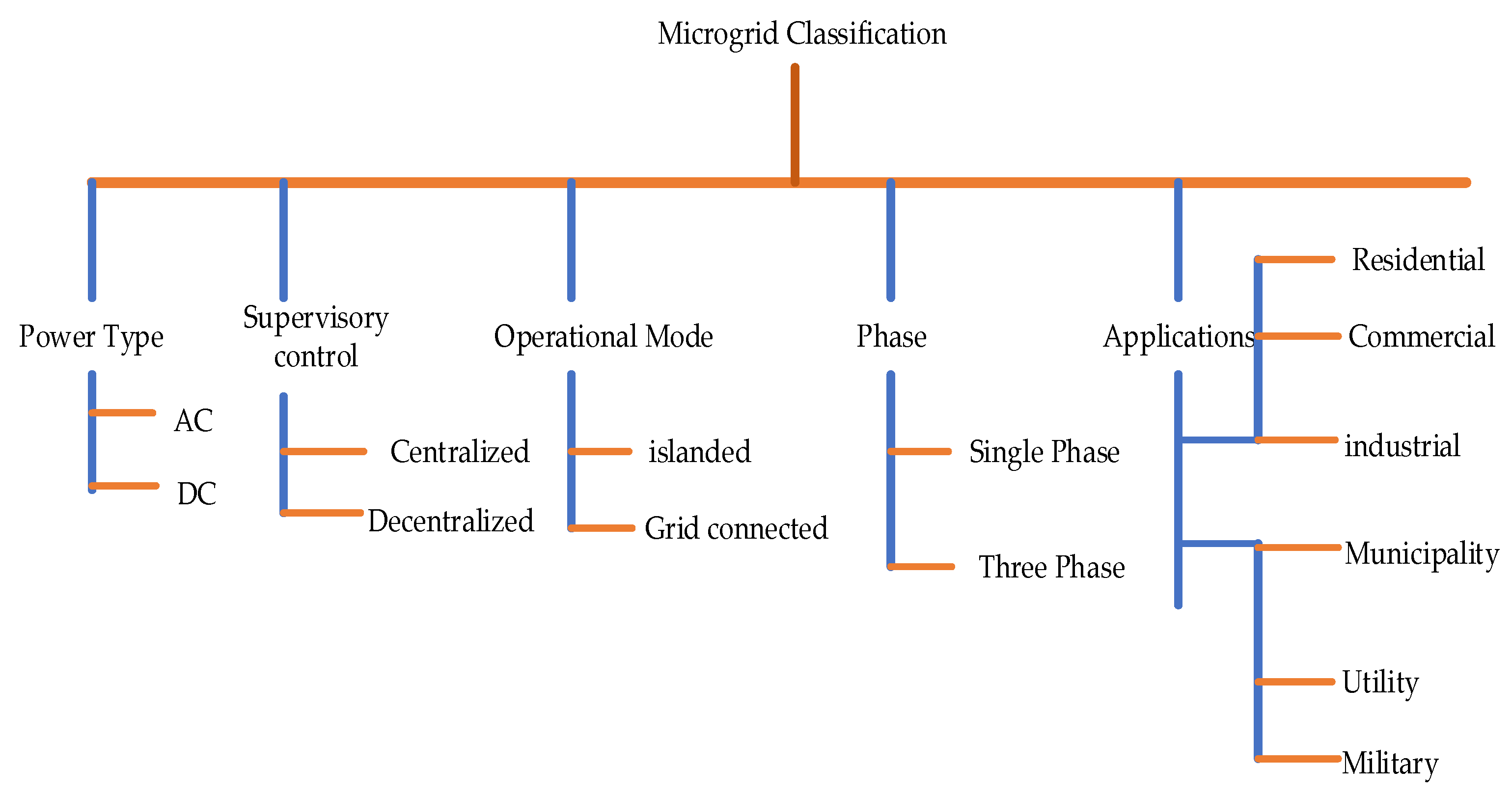
:1. Introduction
2. Problem Formulation
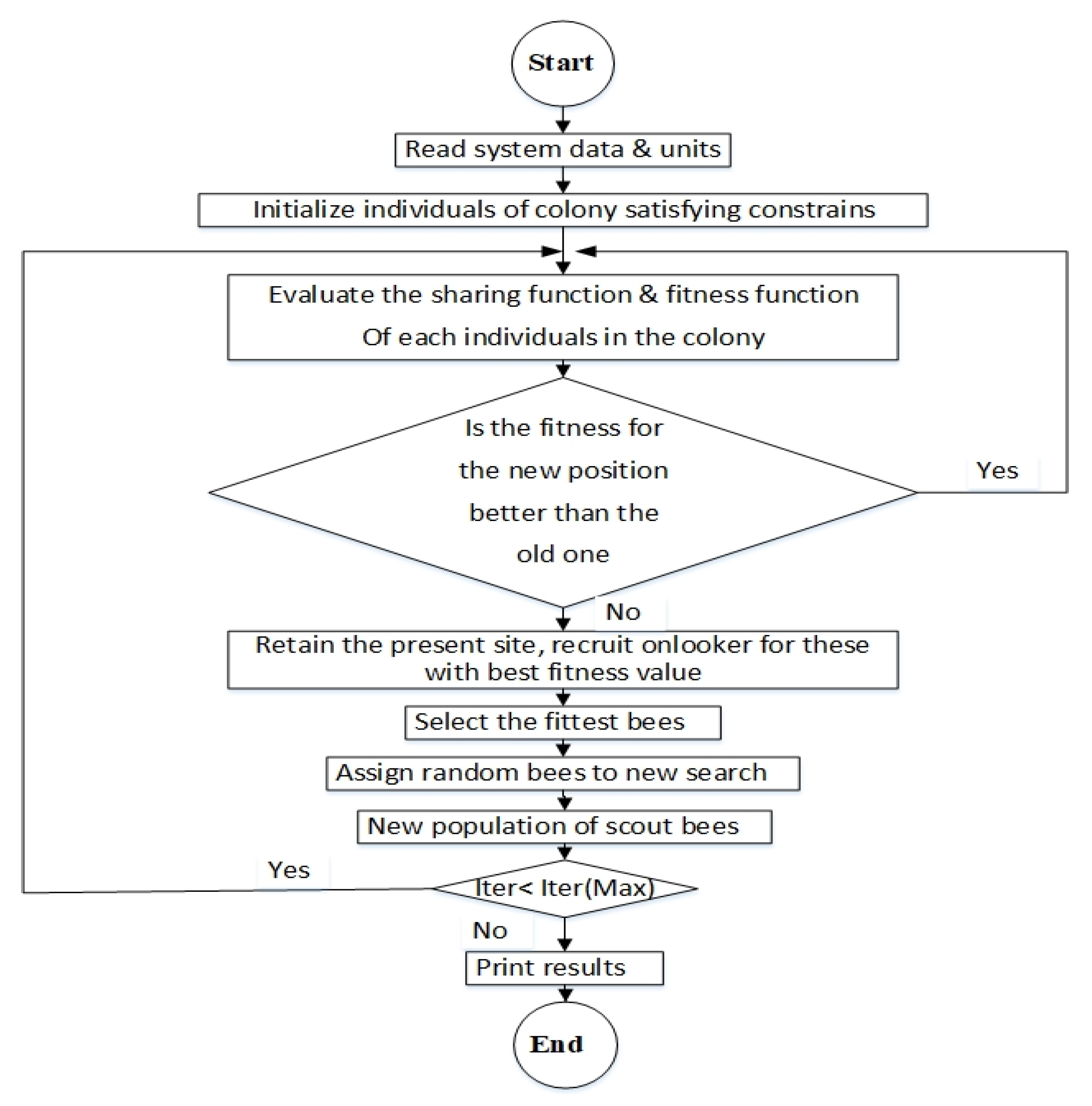
2.1. ABC Algorithm
ABC Algorithm Iteration Steps
3. Mathematical Modeling
3.1. Hybrid Wind/PV/Battery Storage/Gas Turbine
3.1.1. Wind Energy System
3.1.2. PV Energy System
3.1.3. Battery Storage
4. Mathematical Modeling of the Proposed Approach
4.1. Microgrids’ Net Load
4.2. Energy Management Strategy
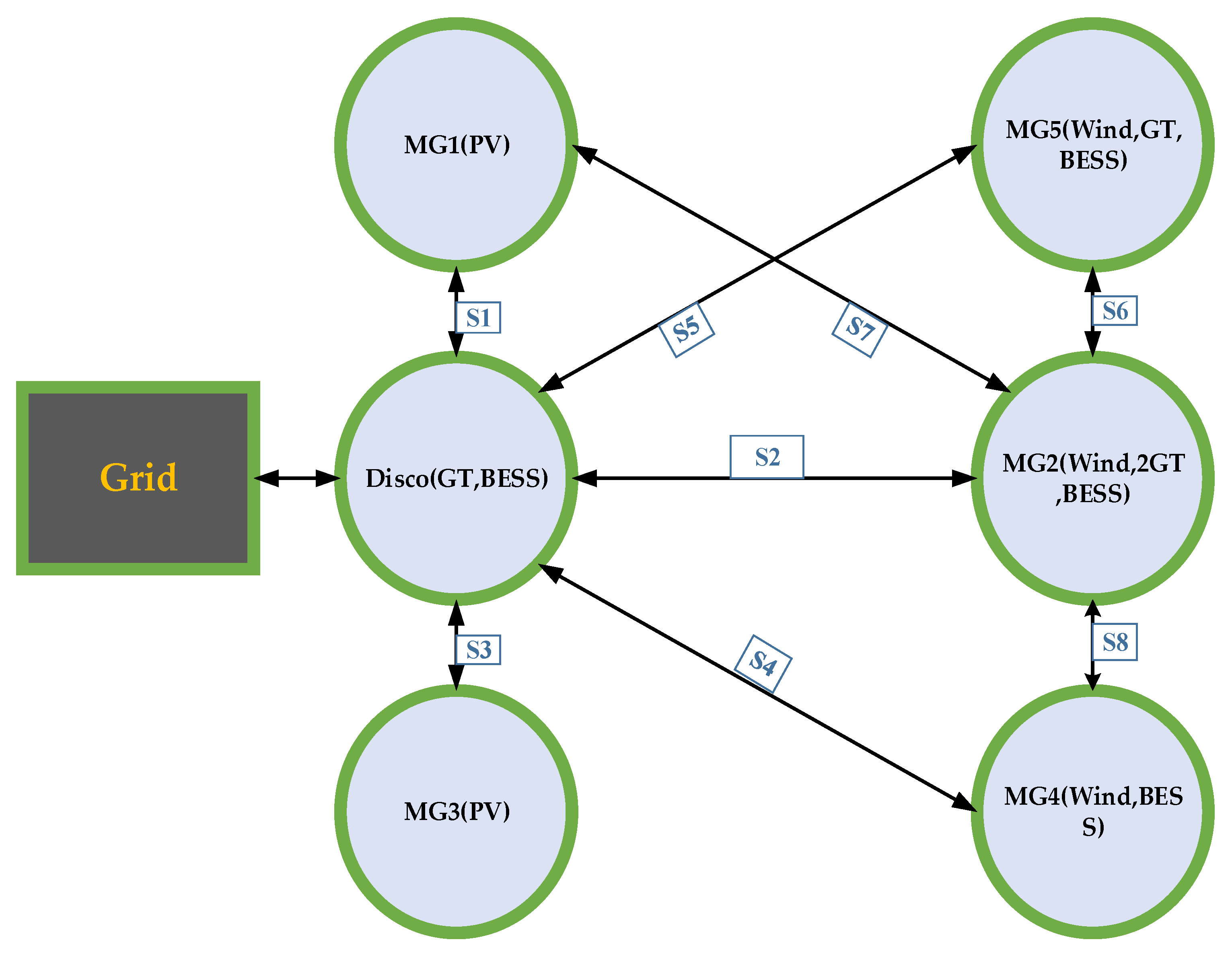
4.3. Microgrid Energy Sharing Problem
5. Power Balance
Objective Function
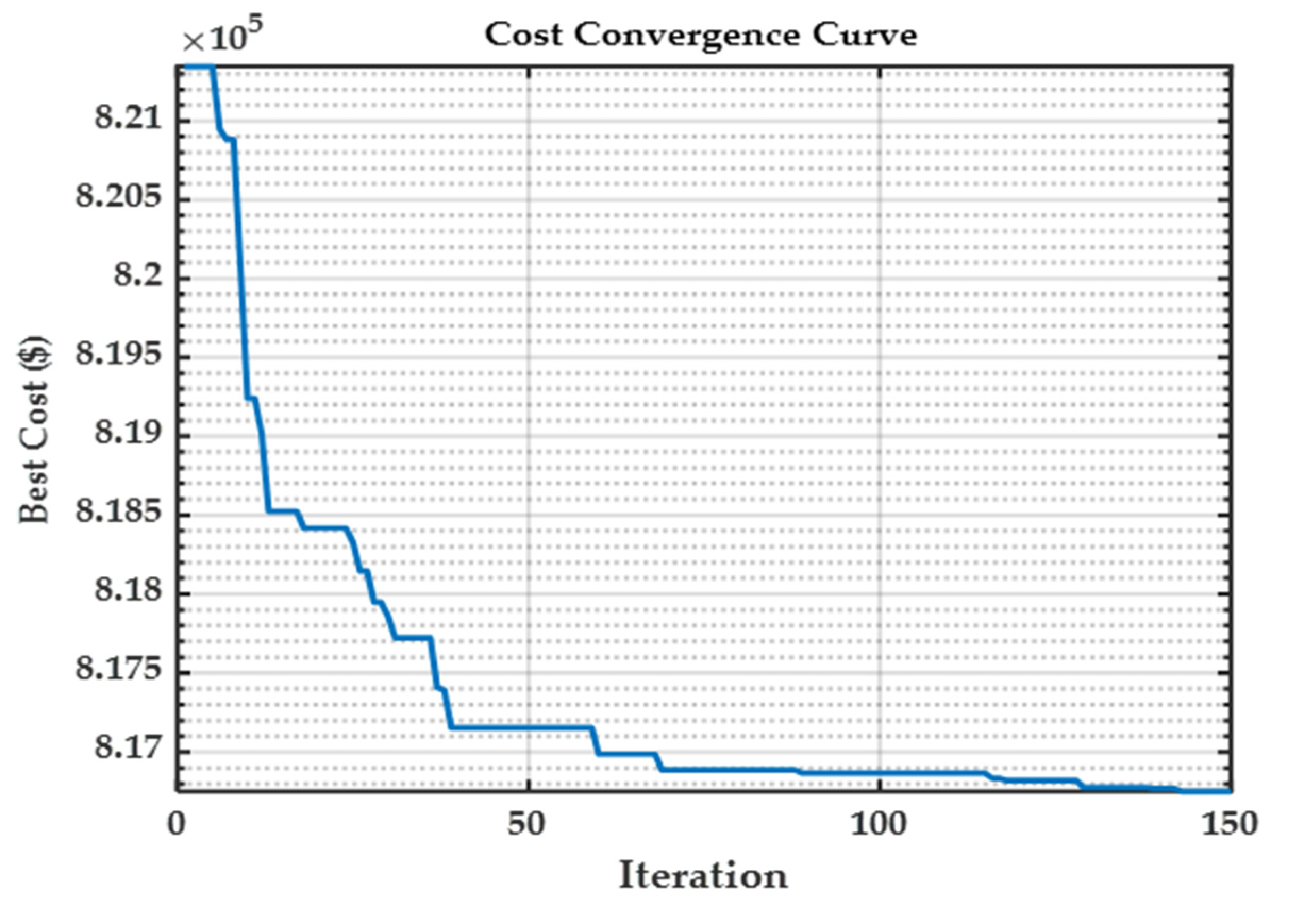
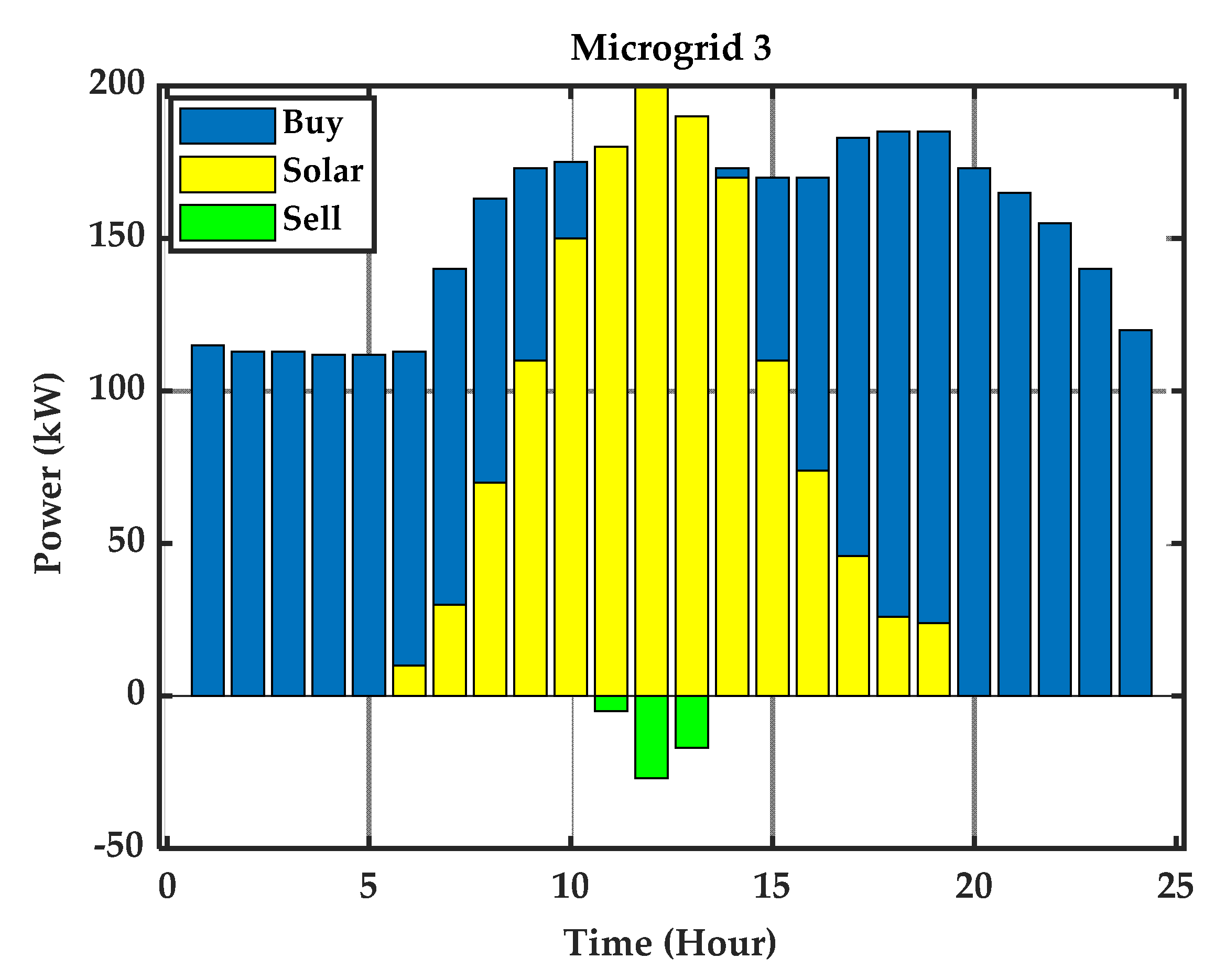
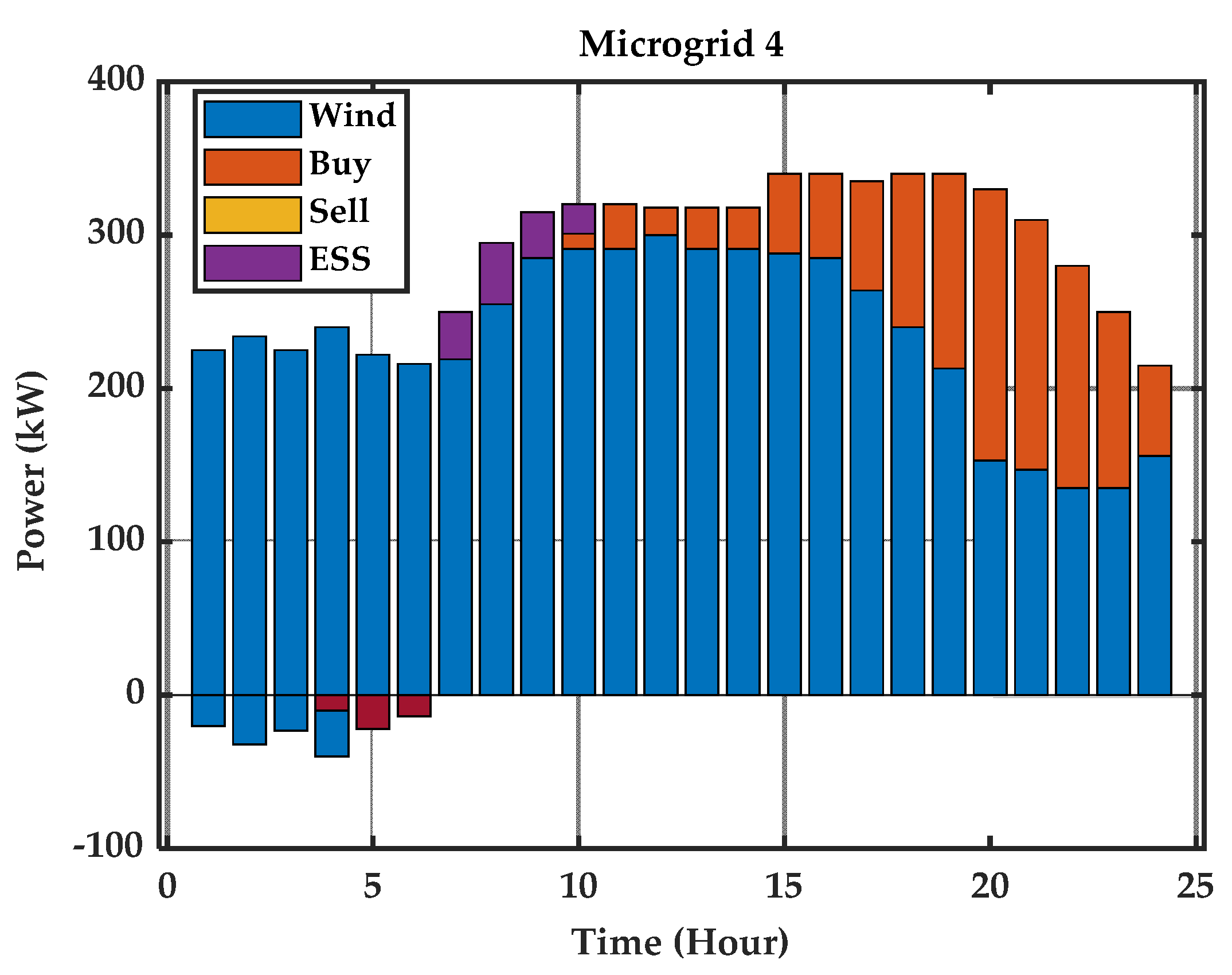
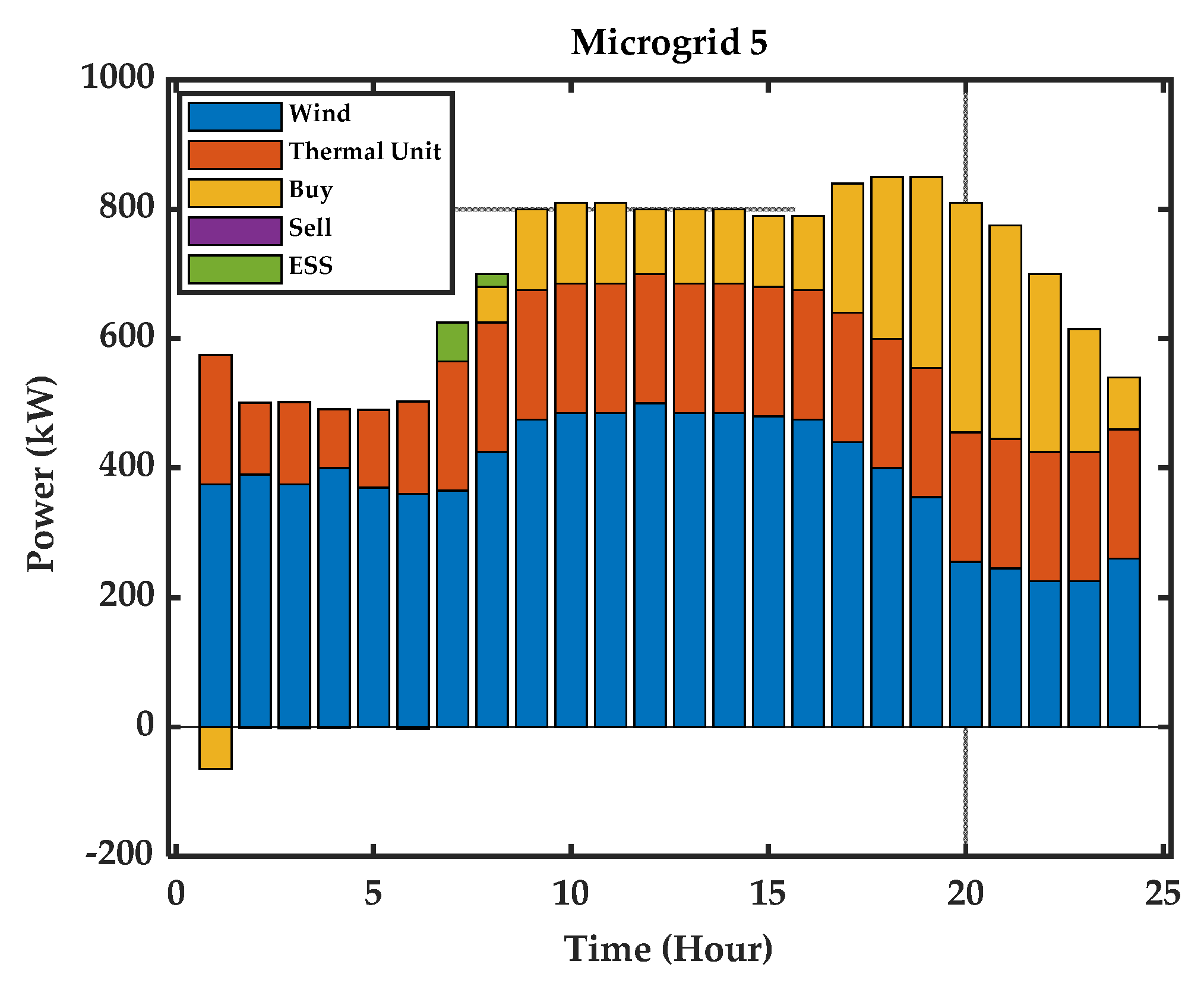
6. Simulations and Results Analysis
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohammed, O.H.; Amirat, Y.; Benbouzid, M.E.H.; Feld, G. Optimal Design and Energy Management of a Hybrid Power Generation System Based on Wind/Tidal/PV Sources: Case Study for the Ouessant French Island. In Smart Energy Grid Design for Island Countries: Challenges and Opportunities; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 9783319501970. [Google Scholar]
- Child, M.; Bogdanov, D.; Breyer, C. The role of storage technologies for the transition to a 100% renewable energy system in Europe. Energy Procedia 2018, 155, 44–60. [Google Scholar] [CrossRef]
- Aslam, S.; Herodotou, H.; Mohsin, S.M.; Javaid, N.; Ashraf, N.; Aslam, S. A survey on deep learning methods for power load and renewable energy forecasting in smart microgrids. Renew. Sustain. Energy Rev. 2021, 144, 110992. [Google Scholar] [CrossRef]
- Zhang, D.; Mu, S.; Chan, C.C.; Zhou, G.Y. Optimization of renewable energy penetration in regional energy system. Energy Procedia 2018, 152, 922–927. [Google Scholar] [CrossRef]
- Stroe, D.I.; Zaharof, A.; Iov, F. Power and energy management with battery storage for a hybrid residential PV-wind system—A case study for Denmark. Energy Procedia 2018, 155, 464–477. [Google Scholar] [CrossRef]
- Zhou, Z.; Benbouzid, M.E.H.; Charpentier, J.F.; Scuiller, F. Hybrid Diesel/MCT/Battery Electricity Power Supply System for Power Management in Small Island. In Smart Energy Grid Design for Island Countries: Challenges and Opportunities; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 9783319501970. [Google Scholar]
- Mohammed, O.H.; Amirat, Y.; Benbouzid, M.; Elbast, A. Optimal Design of a PV/Fuel Cell Hybrid Power System for the City of Brest in France. In Proceedings of the 2014 First International Conference on Green Energy ICGE 2014, Sfax, Tunisia, 25–27 March 2014. [Google Scholar]
- Zhang, J.; Huang, L.; Shu, J.; Wang, H.; Ding, J. Energy Management of PV-Diesel-Battery Hybrid Power System for Island Stand-Alone Micro-Grid. Energy Procedia 2017, 105, 2201–2206. [Google Scholar] [CrossRef]
- Khursheed, A.; Aslam, S.; Haider, S.I.; Mohsin, S.M.; ul Islam, S.; Khattak, H.A.; Shah, S. Energy forecasting using multiheaded convolutional neural networks in efficient renewable energy resources equipped with energy storage system. Trans. Emerg. Telecommun. Technol. 2019, e3837. [Google Scholar] [CrossRef]
- Toutounchi, A.N.; Seyedshenava, S.; Contreras, J.; Akbarimajd, A. A Stochastic Bilevel Model to Manage Active Distribution Networks with Multi-Microgrids. IEEE Syst. J. 2019, 13, 4190–4199. [Google Scholar] [CrossRef]
- Aboli, R.; Ramezani, M.; Falaghi, H. A hybrid robust distributed model for short-term operation of multi-microgrid distribution networks. Electr. Power Syst. Res. 2019, 177, 106011. [Google Scholar] [CrossRef]
- Lasseter, R.; Abbas, A.; Marnay, C.; Stevens, J.; Dagle, J.; Guttromson, R.; Meliopoulos, A.S.; Yinger, R.; Eto, J. Integration of Distributed Energy Resources: The CERTS Microgrid Concept. Consult. Rep. Prep. Calif. Energy Comm. 2003, 89. [Google Scholar]
- LI, Y.; Nejabatkhah, F. Overview of control, integration and energy management of microgrids. J. Mod. Power Syst. Clean Energy 2014, 2, 212–222. [Google Scholar] [CrossRef] [Green Version]
- Hatziargyriou, N.; Jenkins, N.; Strbac, G.; Pecas Lopes, J.A.; Ruela, J.; Engler, A.; Oyarzabal, J.; Kariniotakis, G.; Amorim, A. Microgrids—Large scale integration of microgeneration to low voltage grids. In Proceedings of the 41st International Conference on Large High Voltage Electric Systems 2006, CIGRE 2006, Paris, France, 27 August–1 September 2006. [Google Scholar]
- Li, M.; Zhang, X.; Li, G.; Jiang, C. A feasibility study of microgrids for reducing energy use and GHG emissions in an industrial application. Appl. Energy 2016, 176, 138–148. [Google Scholar] [CrossRef]
- Chaudhary, G.; Lamb, J.J.; Burheim, O.S.; Austbø, B. Review of energy storage and energy management system control strategies in microgrids. Energies 2021, 14, 4929. [Google Scholar] [CrossRef]
- Zhou, B.; Zou, J.; Chung, C.Y.; Wang, H.; Liu, N.; Voropai, N.; Xu, D. Multi-Microgrid Energy Management Systems: Architecture, Communication, and Scheduling Strategies. J. Mod. Power Syst. Clean Energy 2021, 9, 463–476. [Google Scholar] [CrossRef]
- Raghav, L.P.; Rangu, S.K.; Dhenuvakonda, K.R.; Singh, A.R. Optimal energy management of microgrids-integrated nonconvex distributed generating units with load dynamics. Int. J. Energy Res. 2021, 45, 18919–18934. [Google Scholar] [CrossRef]
- Restrepo, M.; Cañizares, C.A.; Simpson-Porco, J.W.; Su, P.; Taruc, J. Optimization- and Rule-Based Energy Management Systems at the Canadian Renewable Energy Laboratory Microgrid Facility. Appl. Energy 2021, 290, 116760. [Google Scholar] [CrossRef]
- Roslan, M.F.; Hannan, M.A.; Jern Ker, P.; Begum, R.A.; Indra Mahlia, T.M.; Dong, Z.Y. Scheduling controller for microgrids energy management system using optimization algorithm in achieving cost saving and emission reduction. Appl. Energy 2021, 292, 116883. [Google Scholar] [CrossRef]
- Li, F.F.; Qiu, J. Multi-objective optimization for integrated hydro-photovoltaic power system. Appl. Energy 2016, 167, 377–384. [Google Scholar] [CrossRef]
- Askarzadeh, A. A Memory-Based Genetic Algorithm for Optimization of Power Generation in a Microgrid. IEEE Trans. Sustain. Energy 2018, 9, 1081–1089. [Google Scholar] [CrossRef]
- Obara, S.; Kawai, M.; Kawae, O.; Morizane, Y. Operational planning of an independent microgrid containing tidal power generators, SOFCs, and photovoltaics. Appl. Energy 2013, 102, 1343–1357. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Reichle, R.H.; Peng, J.; Kerr, Y.; Castro, R.; Kim, E.J.; Liu, Q. Converting between SMOS and SMAP Level-1 Brightness Temperature Observations over Nonfrozen Land. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1908–1912. [Google Scholar] [CrossRef] [Green Version]
- Samuel, O.; Javaid, N.; Khalid, A.; Khan, W.Z.; Aalsalem, M.Y.; Afzal, M.K.; Kim, B.S. Towards Real-Time Energy Management of Multi-Microgrid Using a Deep Convolution Neural Network and Cooperative Game Approach. IEEE Access 2020, 8, 161377–161395. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Fazlhashemi, S.S.; Javadi, H.; Taghvaei, M. Multi-objective day-ahead energy management of a microgrid considering responsive loads and uncertainty of the electric vehicles. J. Clean. Prod. 2020, 267, 121562. [Google Scholar] [CrossRef]
- Arefifar, S.A.; Ordonez, M.; Mohamed, Y.A.R.I. Energy Management in Multi-Microgrid Systems—Development and Assessment. IEEE Trans. Power Syst. 2017, 32, 910–922. [Google Scholar] [CrossRef]
- Baboli, P.T.; Shahparasti, M.; Moghaddam, M.P.; Haghifam, M.R.; Mohamadian, M. Energy management and operation modelling of hybrid AC-DC microgrid. IET Gener. Transm. Distrib. 2014, 8, 1700–1711. [Google Scholar] [CrossRef]
- Hasankhani, A.; Hakimi, S.M. Stochastic energy management of smart microgrid with intermittent renewable energy resources in electricity market. Energy 2021, 219, 119668. [Google Scholar] [CrossRef]
- Querini, P.L.; Chiotti, O.; Fernádez, E. Cooperative energy management system for networked microgrids. Sustain. Energy Grids Netw. 2020, 23, 100371. [Google Scholar] [CrossRef]
- Lan, T.; Jermsittiparsert, K.; Alrashood, S.T.; Rezaei, M.; Al-Ghussain, L.; Mohamed, M.A. An advanced machine learning based energy management of renewable microgrids considering hybrid electric vehicles’ charging demand. Energies 2021, 14, 569. [Google Scholar] [CrossRef]
- Ghavifekr, A.A. Application of heuristic techniques and evolutionary algorithms in microgrids optimization problems. In Microgrids; Power Systems; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Chen, S.M.; Sarosh, A.; Dong, Y.F. Simulated annealing based artificial bee colony algorithm for global numerical optimization. Appl. Math. Comput. 2012, 219, 3575–3589. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, J.; Zhou, Y. Two modified Artificial Bee Colony algorithms inspired by Grenade Explosion Method. Neurocomputing 2015, 151, 1198–1207. [Google Scholar] [CrossRef]
- Mernik, M.; Liu, S.H.; Karaboga, D.; Črepinšek, M. On clarifying misconceptions when comparing variants of the Artificial Bee Colony Algorithm by offering a new implementation. Inf. Sci. 2015, 291, 115–127. [Google Scholar] [CrossRef]
- Li, L.; Yao, F.; Tan, L.; Niu, B.; Xu, J. A novel DE-ABC-based hybrid algorithm for global optimization. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Zhengzhou, China, 11–14 August 2011; Volume 6840. [Google Scholar]
- Mao, W.; Lan, H.Y.; Li, H.R. A New Modified Artificial Bee Colony Algorithm with Exponential Function Adaptive Steps. Comput. Intell. Neurosci. 2016, 2016, 9820294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Satapathy, S.C.; Naik, A. Modified Teaching-Learning-Based Optimization algorithm for global numerical optimization—A comparative study. Swarm Evol. Comput. 2014, 16, 28–37. [Google Scholar] [CrossRef]
- Xiang, Y.; Peng, Y.; Zhong, Y.; Chen, Z.; Lu, X.; Zhong, X. A particle swarm inspired multi-elitist artificial bee colony algorithm for real-parameter optimization. Comput. Optim. Appl. 2014, 57, 493–516. [Google Scholar] [CrossRef]
- Setiawan, A.A.; Zhao, Y.; Nayar, C.V. Design, economic analysis and environmental considerations of mini-grid hybrid power system with reverse osmosis desalination plant for remote areas. Renew. Energy 2009, 34, 374–383. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H. Power management of a stand-alone wind/photovoltaic/fuel cell energy system. IEEE Trans. Energy Convers. 2008, 23, 957–967. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Mohamed, M.A. A novel design and optimization software for autonomous PV/wind/battery hybrid power systems. Math. Probl. Eng. 2014, 2014, 637174. [Google Scholar] [CrossRef]
- Bernal-Agustín, J.L.; Dufo-López, R. Simulation and optimization of stand-alone hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2009, 13, 2111–2118. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Addoweesh, K.E.; Bawah, U.; Mohamed, M.A. New software for hybrid renewable energy assessment for ten locations in Saudi Arabia. J. Renew. Sustain. Energy 2013, 5, 033126. [Google Scholar] [CrossRef]
- Sreeraj, E.S.; Chatterjee, K.; Bandyopadhyay, S. Design of isolated renewable hybrid power systems. Sol. Energy 2010, 84, 1124–1136. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Eltamaly, A.M.; Alolah, A.I. Sizing and techno-economic analysis of stand-alone hybrid photovoltaic/wind/diesel/battery power generation systems. J. Renew. Sustain. Energy 2015, 7, 063128. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Mohamed, M.A. A novel software for design and optimization of hybrid power systems. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1299–1315. [Google Scholar] [CrossRef]
- Habib, M.A.; Said, S.A.M.; El-Hadidy, M.A.; Al-Zaharna, I. Optimization procedure of a hybrid photovoltaic wind energy system. Energy 1999, 24, 919–929. [Google Scholar] [CrossRef]
- Javanmard, B.; Tabrizian, M.; Ansarian, M.; Ahmarinejad, A. Energy management of multi-microgrids based on game theory approach in the presence of demand response programs, energy storage systems and renewable energy resources. J. Energy Storage 2021, 42, 102971. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Eltamaly, A.M.; Alolah, A.I. Swarm intelligence-based optimization of grid-dependent hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2017, 77, 515–524. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, W.; Lu, L.; Fang, Z. Optimal sizing method for stand-alone hybrid solar-wind system with LPSP technology by using genetic algorithm. Sol. Energy 2008, 82, 354–367. [Google Scholar] [CrossRef]








| References | Solar | WT | FC | CHP | EES | Biomass | Hydro | Tidal |
|---|---|---|---|---|---|---|---|---|
| [21] | ✓ | ✓ | ||||||
| [22] | ✓ | ✓ | ✓ | |||||
| [23] | ✓ | ✓ | ✓ | |||||
| [24] | ✓ | |||||||
| [25] | ✓ | |||||||
| [26] | ✓ | |||||||
| [27] | ✓ | ✓ | ✓ | |||||
| [28] | ✓ | ✓ | ✓ | ✓ | ||||
| [29,30,31] | ✓ |
| Parameters | Values | Unit |
|---|---|---|
| Go | 1000 | W/m2 |
| µ | 20 | % |
| TM,O | 25 | °C |
| NOCT | 44 | °C |
| ΠPV | 0 | Cent/kWh |
| Parameters | Values | Unit |
|---|---|---|
| Pgas | 5 | Cent/kWh |
| PMG | 15.75 | Cent/kWh |
| PDis | 15.3 | Cent/kWh |
| PB | 3 | Cent/kWh |
| Pp | 40 | Cent/kWh |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, K.; Jiang, Q.; Geng, G.; Rahim, S.; Khan, R.A. Optimal Power Sharing in Microgrids Using the Artificial Bee Colony Algorithm. Energies 2022, 15, 1067. https://doi.org/10.3390/en15031067
Ullah K, Jiang Q, Geng G, Rahim S, Khan RA. Optimal Power Sharing in Microgrids Using the Artificial Bee Colony Algorithm. Energies. 2022; 15(3):1067. https://doi.org/10.3390/en15031067
Chicago/Turabian StyleUllah, Kalim, Quanyuan Jiang, Guangchao Geng, Sahar Rahim, and Rehan Ali Khan. 2022. "Optimal Power Sharing in Microgrids Using the Artificial Bee Colony Algorithm" Energies 15, no. 3: 1067. https://doi.org/10.3390/en15031067
APA StyleUllah, K., Jiang, Q., Geng, G., Rahim, S., & Khan, R. A. (2022). Optimal Power Sharing in Microgrids Using the Artificial Bee Colony Algorithm. Energies, 15(3), 1067. https://doi.org/10.3390/en15031067







