Stacked LSTM Sequence-to-Sequence Autoencoder with Feature Selection for Daily Solar Radiation Prediction: A Review and New Modeling Results
Abstract
:1. Background Review
2. Review of Theoretical Framework for ML and DL Techniques
2.1. Manta Ray Foraging Optimization (MRFO)
- Chain foraging: When 50 or more manta rays begin foraging, they line up one after the other, forming an ordered line. Male manta rays are smaller than females and dive on top of their back stomachs to the beats of the female’s pectoral fins. As a result, plankton (prey or marine drifters) lost by past manta rays will be scooped up by those after them. Through working together in this manner, they can get the most plankton into their gills and increase their food rewards. This mathematical model of chain foraging is represented as follows [58]:where () = individual manta ray (m); r = random uniformly distributed number in . and MB = new or best position of manta ray in population, = weight coefficient as a function of each iteration.It is clear from Equation (1) that the previous manta ray in the chain and the spatial location of the strongest plankton clearly define the position update process in chain foraging.
- Cyclone foraging: When the abundance of plankton is very high, hundreds of manta rays group together in a cyclone foraging strategy. Their tail ends spiral along with the heads to form a spiraling vertex in the cyclone’s eye, and the purified water rises to the surface. This attracts plankton to their open mouths. Mathematically, this cyclone foraging is divided into two parts. The first half focuses on enhancing the exploration and is updated as [59]:where = individual created randomly:The adaptive weight coefficient () is varied as:where = current iteration and random uniformly distributed number, and is over .The second half concentrates on improving the exploitation, so the update is as per:
- Somersault foraging: This is the final foraging strategy with manta rays discovering the food supply and doing backwards somersaults to circle the plankton for attraction. Somersaulting is a spontaneous, periodic, local, and cyclical action that manta rays use to maximize their food intake. The third strategy is where an update of each individual occurs around an optimal position [60]:In Equation (7), S = somersault coefficient () controlling the domain of manta rays, and are random numbers within .
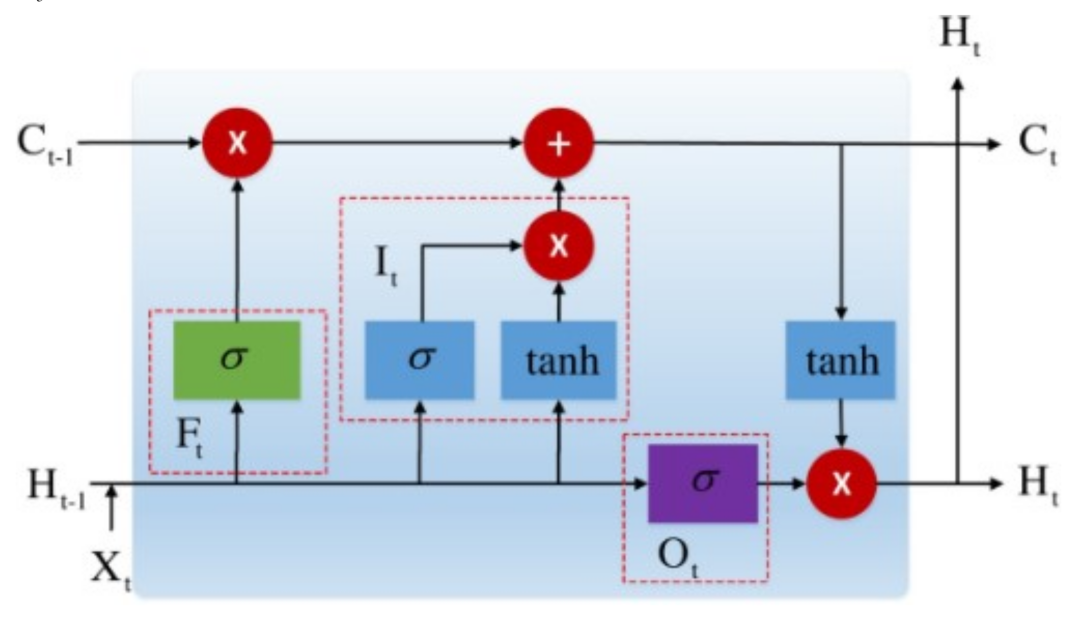
2.2. Long Short-Term Memory Network (LSTM)
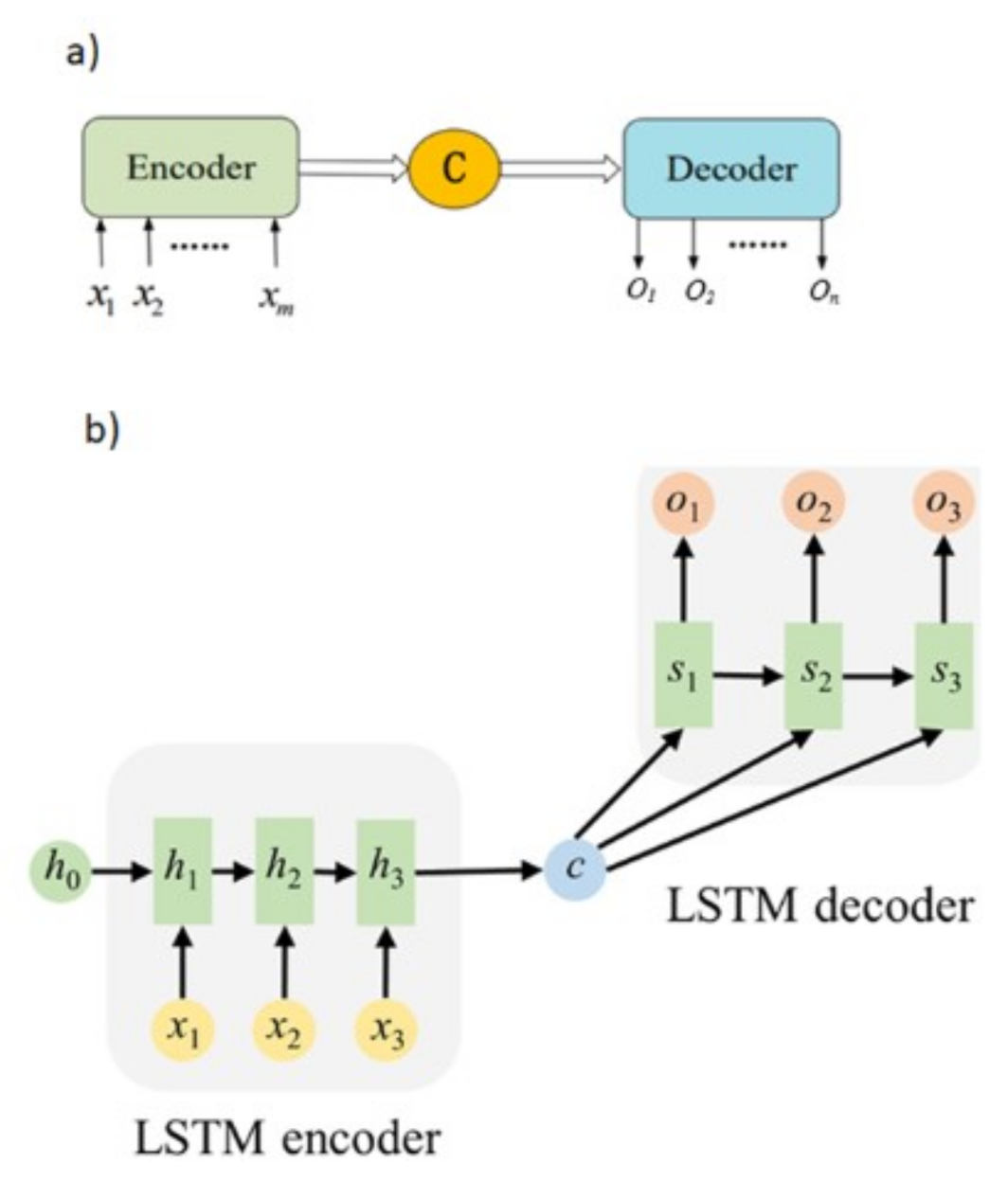
2.3. Stacked LSTM Sequence-to-Sequence Autoencoder (SAELSTM)
2.4. Benchmark Models
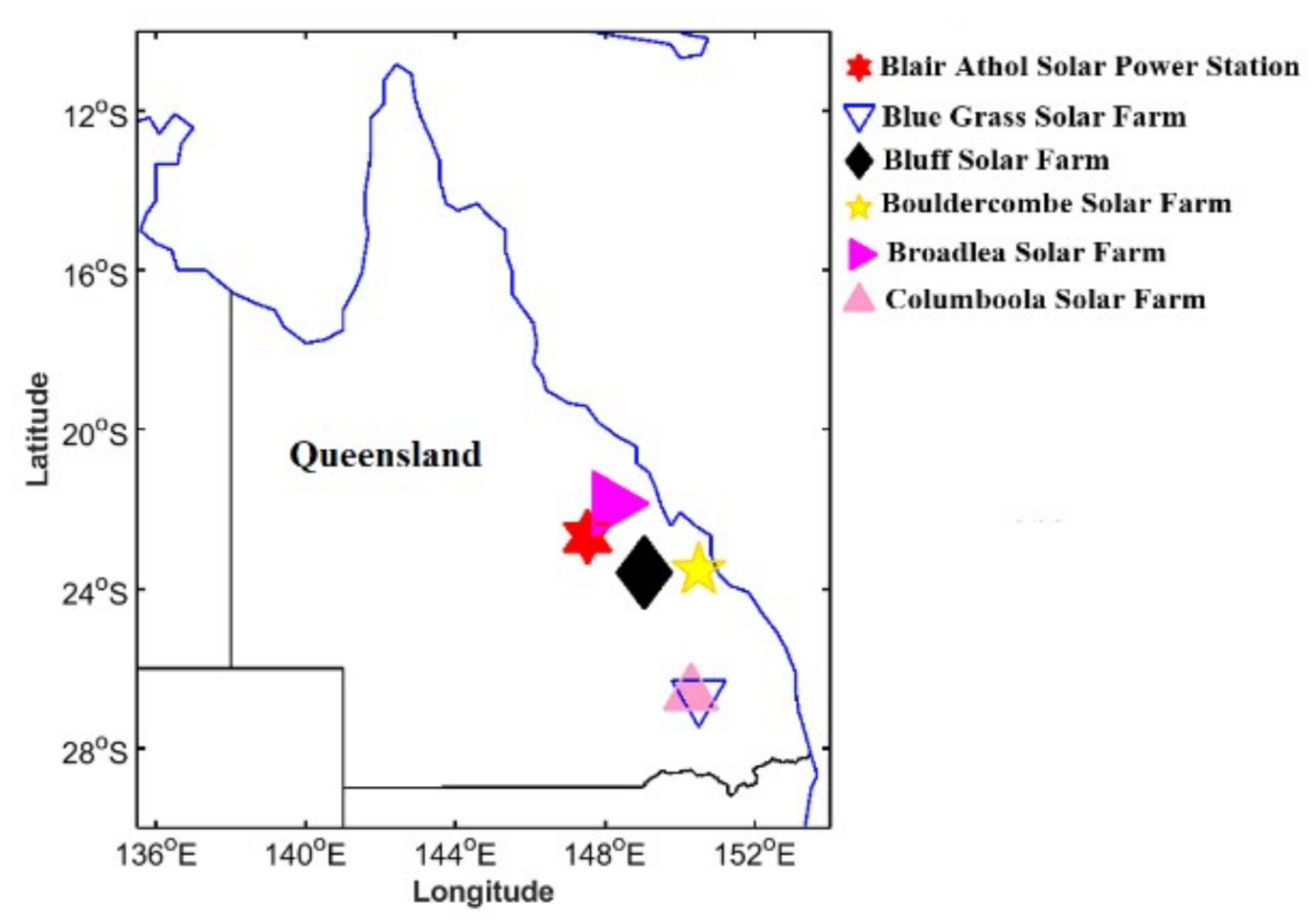
3. Study Area and Data Available
4. Predictive Model Development
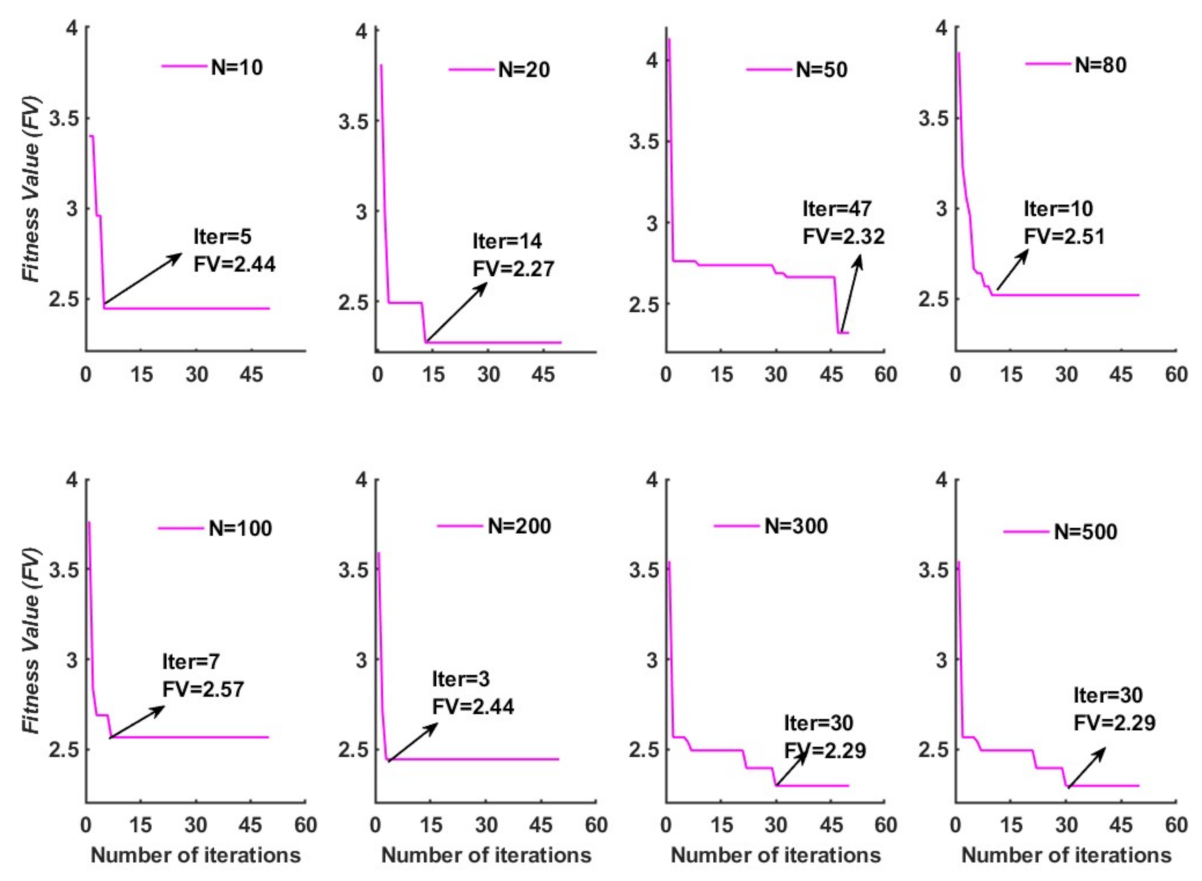
- Population size .
- The number of maximum iterations (T) = 50.
- Somersault coefficient (S) = 2.
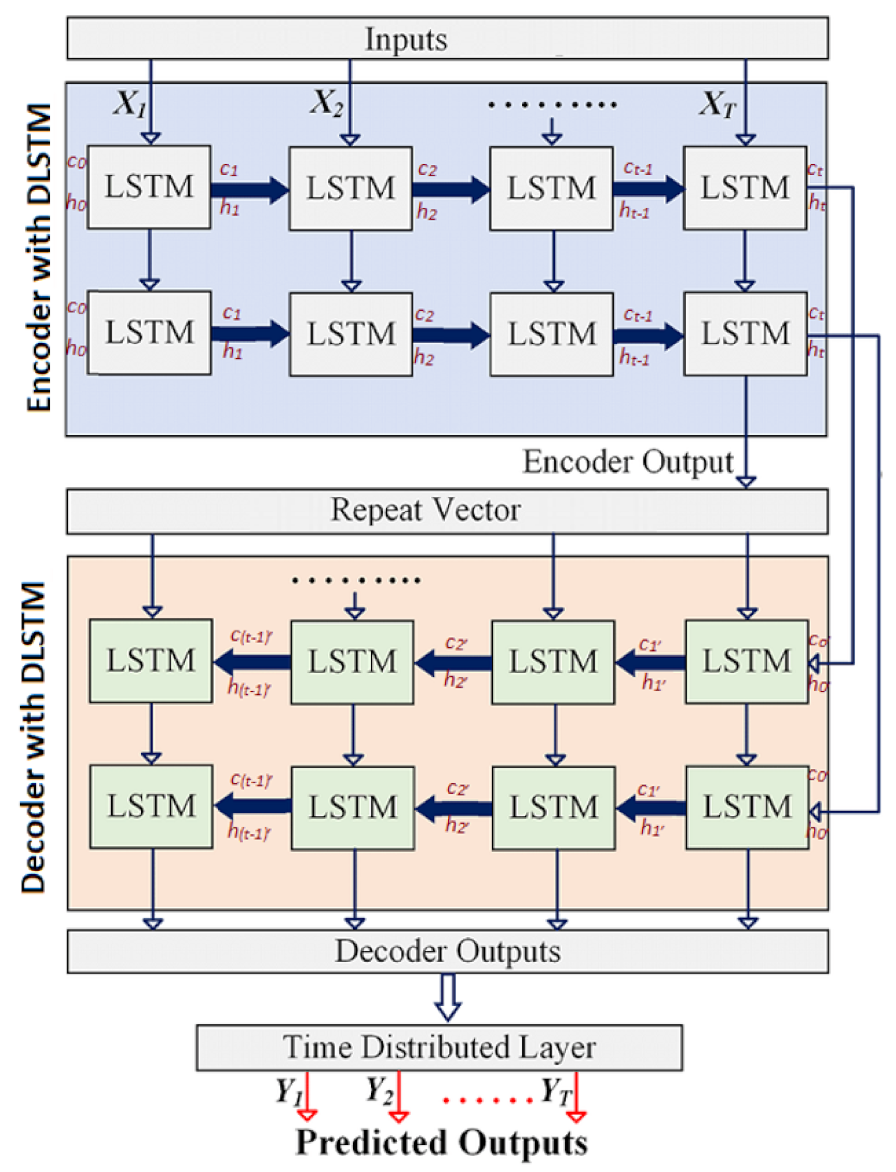
4.1. Stacked LSTM Sequence to Sequence Autoencoder Model Development
- The encoder layer of the SAELSTM receives as an input a sequence X of predictor variables after MRFO FS, which are represented as with terms to time series in time step.
- The encoder recursively handles the input sequence (X) of length t. Then, it updates the cell memory state vector and hidden state vector at time step t. Afterwards, the encoder summarizes the input sequence in and .
- An encoder output is fed through a repeat vector layer, which is then fed into a decoder layer.
- Afterwards, the decoder layer of SAELSTM adopts Ct and ht from an encoder as initial cell memory state vector. The initial hidden state vectors C0’ and h0’ for t’ length are at the respective time step.
- Afterwards, the decoder layer of SAELSTM uses the final vectors Ct and ht passed from the encoder as initial cell memory state vectors and initial hidden state vectors C0’ and h0’ for t’ length of time step.
- The learning of features is performed by the decoder as included in the original input to generate multiple outputs with N-time step ahead.
- Using a time-distributed dense layer, each time step has a fully connected layer that separates the outputs (GSR). The prediction accuracy of the SAELSTM model can be evaluated here.
4.2. Benchmark Model Development
4.3. Performance Evaluation Metrics Considered
- r can be in the range of and , MAE, RMSE = 0 (perfect fit) to ∞ (worst fit);
- RRMSE and RMAE ranges from 0% to 100%. For model evaluation, the precision is excellent if , good if , fair if , and poor if [122].
- WI, which is improvement to RMSE and MAE and overcomes the insensitivity issues with differences between observed and predicted not squared. We have from 0 (worst fit) to 1 (perfect fit) [123].
- NSE compares the variance of observed and predicted GSR and ranges from (the worst fit) to 1 (perfect fit) [124].
- LM is a more robust metric developed to address the limitations of both the WI and [119] and the value ranges between 0 and 1 (ideal value).
- uses biased variance for explaining the fraction of variance and ranges from 0 to 1.
4.4. Prediction Interval
5. Results and Discussion
6. Conclusions, Limitations, and Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Model Development Parameters
| Predictive Models | Model Hyperparameters | Hyperparameter Selection | Blair Athol Solar Power Station | Blue Grass Solar Farm | Bluff Solar Farm | Bouldercombe Solar Farm | Broadlea Solar Farm | Columboola Solar Farm |
|---|---|---|---|---|---|---|---|---|
| SAELSTM | Encoder LSTM cell 1 | [10,20,30,40,50,60] | 20 | 10 | 30 | 20 | 40 | 20 |
| Encoder LSTM cell 2 | [5,10,15,25] | 10 | 5 | 25 | 15 | 25 | 15 | |
| Encoder LSTM cell 3 | [6,8,10,15] | 6 | 6 | 10 | 15 | 15 | 10 | |
| Decoder LSTM cell 1 | [80,90,100,200] | 100 | 80 | 200 | 100 | 100 | 90 | |
| Decoder LSTM cell 2 | [40,50,60,70,100] | 70 | 60 | 50 | 100 | 60 | 50 | |
| Decoder LSTM cell 3 | [5,10,15,20,25,30] | 20 | 15 | 25 | 15 | 30 | 15 | |
| Activation function | ReLU | |||||||
| Epochs | [300,400,500,600,700] | 400 | 500 | 300 | 500 | 400 | 500 | |
| Drop rate | [0,0.1,0.2] | 0.1 | 0.2 | 0 | 0 | 0.2 | 0.1 | |
| Batch Size | [5,10,15,20,25,30] | 10 | 15 | 15 | 20 | 10 | 10 | |
| DNN | Hiddenneuron 1 | [100,200,300,400,50] | 300 | 100 | 100 | 200 | 100 | 200 |
| Hiddenneuron 2 | [20,30,40,50,60,70] | 60 | 70 | 40 | 50 | 30 | 20 | |
| Hiddenneuron 3 | [10,20,30,40,50] | 40 | 30 | 50 | 20 | 10 | 40 | |
| Hiddenneuron 4 | [5,6,7,8,12,15,18] | 15 | 18 | 7 | 12 | 15 | 18 | |
| Epochs | [100,200,400,500] | 500 | 200 | 100 | 200 | 100 | 400 | |
| Batch Size | [5,10,15,20,25,30] | 5 | 10 | 20 | 15 | 15 | 20 | |
| Predictive Models | Model hyperparameters | Hyperparameter Selection | Blair Athol Solar Power Station | Blue Grass Solar Farm | Bluff Solar Farm | Bouldercombe Solar Farm | Broadlea Solar Farm | Columboola Solar Farm |
| RFR | The maximum depth of the tree | [5,8,10,20,25] | 20 | 25 | 8 | 25 | 20 | 10 |
| The number of trees in the forest | [50,100,150,200] | 150 | 100 | 50 | 100 | 50 | 200 | |
| Minimum number of samples to split an internal node | [2,4,6,8,10] | 6 | 8 | 10 | 10 | 8 | 10 | |
| The number of features to consider when looking for the best split. | [’auto’, ’sqrt’, ’log2’] | auto | auto | auto | auto | auto | auto | |
| ADBR | The maximum number of estimators at which boosting is terminated | [50,100,150,200] | 150 | 200 | 100 | 150 | 200 | 150 |
| learning rate | [0.01,0.001,0.005] | 0.01 | 0.001 | 0.01 | 0.01 | 0.005 | 0.001 | |
| The loss function to use when updating the weights after each boosting iteration | [‘linear’, ‘square’, ‘exponential’] | square | square | square | square | square | square | |
| GBM | Number of neighbors | [5,10,20,30,50,100] | 50 | 30 | 20 | 30 | 50 | 20 |
| Algorithm used to compute the nearest neighbors | [‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’] | auto | auto | auto | auto | auto | auto | |
| Leaf size passed to BallTree or KDTree | [10,20,30,50,60,70] | 10 | 30 | 20 | 10 | 30 | 10 | |
| ETR | The number of trees in the forest | [10,20,30] | 30 | 10 | 10 | 20 | 30 | 20 |
| The maximum depth of the tree | [5,8,10,20,25] | 8 | 10 | 5 | 8 | 10 | 5 | |
| The number of features to consider when looking for the best split | [’auto’, ’sqrt’, ’log2’] | auto | auto | auto | auto | auto | auto | |
| Minimum number of samples to split an internal node | [5,10,15,20] | 15 | 10 | 20 | 15 | 20 | 15 |
References
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Gielen, D.; Gorini, R.; Wagner, N.; Leme, R.; Gutierrez, L.; Prakash, G.; Asmelash, E.; Janeiro, L.; Gallina, G.; Vale, G.; et al. Global Energy Transformation: A Roadmap to 2050; Hydrogen Knowledge Centre: Derby, UK, 2019; Available online: https://www.h2knowledgecentre.com/content/researchpaper1605 (accessed on 1 December 2021).
- Farivar, G.; Asaei, B. A new approach for solar module temperature estimation using the simple diode model. IEEE Trans. Energy Convers. 2011, 26, 1118–1126. [Google Scholar] [CrossRef]
- Pazikadin, A.R.; Rifai, D.; Ali, K.; Malik, M.Z.; Abdalla, A.N.; Faraj, M.A. Solar irradiance measurement instrumentation and power solar generation forecasting based on Artificial Neural Networks (ANN): A review of five years research trend. Sci. Total Environ. 2020, 715, 136848. [Google Scholar] [CrossRef]
- Amiri, B.; Gómez-Orellana, A.M.; Gutiérrez, P.A.; Dizène, R.; Hervás-Martínez, C.; Dahmani, K. A novel approach for global solar irradiation forecasting on tilted plane using Hybrid Evolutionary Neural Networks. J. Clean. Prod. 2021, 287, 125577. [Google Scholar] [CrossRef]
- Yang, K.; Koike, T.; Ye, B. Improving estimation of hourly, daily, and monthly solar radiation by importing global data sets. Agric. For. Meteorol. 2006, 137, 43–55. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Ghamisi, P.; Piles, M.; Werner, M.; Cuadra, L.; Moreno-Martínez, A.; Izquierdo-Verdiguier, E.; Muñoz-Marí, J.; Mosavi, A.; Camps-Valls, G. Machine learning information fusion in Earth observation: A comprehensive review of methods, applications and data sources. Inf. Fusion 2020, 63, 256–272. [Google Scholar] [CrossRef]
- García-Hinde, O.; Terrén-Serrano, G.; Hombrados-Herrera, M.; Gómez-Verdejo, V.; Jiménez-Fernández, S.; Casanova-Mateo, C.; Sanz-Justo, J.; Martínez-Ramón, M.; Salcedo-Sanz, S. Evaluation of dimensionality reduction methods applied to numerical weather models for solar radiation forecasting. Eng. Appl. Artif. Intell. 2018, 69, 157–167. [Google Scholar] [CrossRef]
- Jiang, Y. Computation of monthly mean daily global solar radiation in China using artificial neural networks and comparison with other empirical models. Energy 2009, 34, 1276–1283. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Adamowski, J.F.; Li, Y. Short-term electricity demand forecasting with MARS, SVR and ARIMA models using aggregated demand data in Queensland, Australia. Adv. Eng. Inform. 2018, 35, 1–16. [Google Scholar] [CrossRef]
- Huang, J.; Korolkiewicz, M.; Agrawal, M.; Boland, J. Forecasting solar radiation on an hourly time scale using a Coupled AutoRegressive and Dynamical System (CARDS) model. Sol. Energy 2013, 87, 136–149. [Google Scholar] [CrossRef]
- Shadab, A.; Said, S.; Ahmad, S. Box–Jenkins multiplicative ARIMA modeling for prediction of solar radiation: A case study. Int. J. Energy Water Resour. 2019, 3, 305–318. [Google Scholar] [CrossRef]
- Zang, H.; Liu, L.; Sun, L.; Cheng, L.; Wei, Z.; Sun, G. Short-term global horizontal irradiance forecasting based on a hybrid CNN-LSTM model with spatiotemporal correlations. Renew. Energy 2020, 160, 26–41. [Google Scholar] [CrossRef]
- Mishra, S.; Palanisamy, P. Multi-time-horizon solar forecasting using recurrent neural network. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 18–24. [Google Scholar]
- Elminir, H.K.; Areed, F.F.; Elsayed, T.S. Estimation of solar radiation components incident on Helwan site using neural networks. Sol. Energy 2005, 79, 270–279. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Adamowski, J.F.; Li, Y. Short-term electricity demand forecasting using machine learning methods enriched with ground-based climate and ECMWF Reanalysis atmospheric predictors in southeast Queensland, Australia. Renew. Sustain. Energy Rev. 2019, 113, 109293. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Deo, R.C.; Cornejo-Bueno, L.; Camacho-Gómez, C.; Ghimire, S. An efficient neuro-evolutionary hybrid modelling mechanism for the estimation of daily global solar radiation in the Sunshine State of Australia. Appl. Energy 2018, 209, 79–94. [Google Scholar] [CrossRef]
- Guijo-Rubio, D.; Durán-Rosal, A.; Gutiérrez, P.; Gómez-Orellana, A.; Casanova-Mateo, C.; Sanz-Justo, J.; Salcedo-Sanz, S.; Hervás-Martínez, C. Evolutionary artificial neural networks for accurate solar radiation prediction. Energy 2020, 210, 118374. [Google Scholar] [CrossRef]
- Bouzgou, H.; Gueymard, C.A. Minimum redundancy–maximum relevance with extreme learning machines for global solar radiation forecasting: Toward an optimized dimensionality reduction for solar time series. Sol. Energy 2017, 158, 595–609. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Li, Y. Electrical energy demand forecasting model development and evaluation with maximum overlap discrete wavelet transform-online sequential extreme learning machines algorithms. Energies 2020, 13, 2307. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Casanova-Mateo, C.; Pastor-Sánchez, A.; Sánchez-Girón, M. Daily global solar radiation prediction based on a hybrid Coral Reefs Optimization–Extreme Learning Machine approach. Sol. Energy 2014, 105, 91–98. [Google Scholar] [CrossRef]
- Aybar-Ruiz, A.; Jiménez-Fernández, S.; Cornejo-Bueno, L.; Casanova-Mateo, C.; Sanz-Justo, J.; Salvador-González, P.; Salcedo-Sanz, S. A novel grouping genetic algorithm–extreme learning machine approach for global solar radiation prediction from numerical weather models inputs. Sol. Energy 2016, 132, 129–142. [Google Scholar] [CrossRef]
- AlKandari, M.; Ahmad, I. Solar power generation forecasting using ensemble approach based on deep learning and statistical methods. Appl. Comput. Inform. 2020. [Google Scholar] [CrossRef]
- AL-Musaylh, M.S.; Al-Daffaie, K.; Prasad, R. Gas consumption demand forecasting with empirical wavelet transform based machine learning model: A case study. Int. J. Energy Res. 2021, 45, 15124–15138. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Casanova-Mateo, C.; Muñoz-Marí, J.; Camps-Valls, G. Prediction of daily global solar irradiation using temporal Gaussian processes. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1936–1940. [Google Scholar] [CrossRef]
- Chen, J.L.; Li, G.S. Evaluation of support vector machine for estimation of solar radiation from measured meteorological variables. Theor. Appl. Climatol. 2014, 115, 627–638. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Li, Y.; Adamowski, J.F. Two-phase particle swarm optimized-support vector regression hybrid model integrated with improved empirical mode decomposition with adaptive noise for multiple-horizon electricity demand forecasting. Appl. Energy 2018, 217, 422–439. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Li, Y. Particle swarm optimized–support vector regression hybrid model for daily horizon electricity demand forecasting using climate dataset. In Proceedings of the 3rd International Conference on Power and Renewable Energy, Berlin, Germany, 21–24 September 2018; Volume 64. [Google Scholar] [CrossRef]
- Hocaoğlu, F.O. Novel analytical hourly solar radiation models for photovoltaic based system sizing algorithms. Energy Convers. Manag. 2010, 51, 2921–2929. [Google Scholar] [CrossRef]
- Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Huertas-Tato, J.; Aler-Mur, R.; Galván-León, I.; Pozo-Vázquez, D. A short-term solar radiation forecasting system for the Iberian Peninsula. Part 1: Models description and performance assessment. Sol. Energy 2020, 195, 396–412. [Google Scholar] [CrossRef]
- Linares-Rodríguez, A.; Ruiz-Arias, J.A.; Pozo-Vázquez, D.; Tovar-Pescador, J. Generation of synthetic daily global solar radiation data based on ERA-Interim reanalysis and artificial neural networks. Energy 2011, 36, 5356–5365. [Google Scholar] [CrossRef]
- Sivamadhavi, V.; Selvaraj, R.S. Prediction of monthly mean daily global solar radiation using Artificial Neural Network. J. Earth Syst. Sci. 2012, 121, 1501–1510. [Google Scholar] [CrossRef] [Green Version]
- Khodayar, M.; Kaynak, O.; Khodayar, M.E. Rough deep neural architecture for short-term wind speed forecasting. IEEE Trans. Ind. Informatics 2017, 13, 2770–2779. [Google Scholar] [CrossRef]
- Bengio, Y. Learning Deep Architectures for AI; Now Publishers Inc.: Delft, The Netherlands, 2009; Available online: https://books.google.es/books?hl=es&lr=&id=cq5ewg7FniMC&oi=fnd&pg=PA1&dq=Learning+Deep+Architectures+for+AI%7D%3B+%5Chl%7BNow+Publishers+Inc.:city,+country&ots=Kpi7OXklKw&sig=JHafuLqX_O0_PsqA7BaPLFOY_zg&redir_esc=y#v=onepage&q&f=false (accessed on 1 December 2021).
- Sun, S.; Chen, W.; Wang, L.; Liu, X.; Liu, T.Y. On the depth of deep neural networks: A theoretical view. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Wang, F.; Zhang, Z.; Liu, C.; Yu, Y.; Pang, S.; Duić, N.; Shafie-Khah, M.; Catalão, J.P. Generative adversarial networks and convolutional neural networks based weather classification model for day ahead short-term photovoltaic power forecasting. Energy Convers. Manag. 2019, 181, 443–462. [Google Scholar] [CrossRef]
- Kawaguchi, K.; Kaelbling, L.P.; Bengio, Y. Generalization in deep learning. arXiv 2017, arXiv:1710.05468. [Google Scholar]
- Khodayar, M.; Wang, J. Spatio-temporal graph deep neural network for short-term wind speed forecasting. IEEE Trans. Sustain. Energy 2018, 10, 670–681. [Google Scholar] [CrossRef]
- Ziyabari, S.; Du, L.; Biswas, S. Short-term Solar Irradiance Forecasting Based on Multi-Branch Residual Network. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2000–2005. [Google Scholar]
- Abdel-Nasser, M.; Mahmoud, K.; Lehtonen, M. Reliable solar irradiance forecasting approach based on choquet integral and deep LSTMs. IEEE Trans. Ind. Informatics 2020, 17, 1873–1881. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, C.; Li, Q.; Tai, Y.; Gao, B.; Shi, J. A comparison of hour-ahead solar irradiance forecasting models based on LSTM network. Math. Probl. Eng. 2020, 2020, 4251517. [Google Scholar] [CrossRef]
- Gao, B.; Huang, X.; Shi, J.; Tai, Y.; Zhang, J. Hourly forecasting of solar irradiance based on CEEMDAN and multi-strategy CNN-LSTM neural networks. Renew. Energy 2020, 162, 1665–1683. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Long short term memory–convolutional neural network based deep hybrid approach for solar irradiance forecasting. Appl. Energy 2021, 295, 117061. [Google Scholar] [CrossRef]
- Ziyabari, S.; Du, L.; Biswas, S. A Spatio-temporal Hybrid Deep Learning Architecture for Short-term Solar Irradiance Forecasting. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, ON, Canada, 15 June–21 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 0833–0838. [Google Scholar]
- Srivastava, S.; Lessmann, S. A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data. Solar Energy 2018, 162, 232–247. [Google Scholar] [CrossRef]
- Aslam, M.; Lee, J.M.; Kim, H.S.; Lee, S.J.; Hong, S. Deep learning models for long-term solar radiation forecasting considering microgrid installation: A comparative study. Energies 2020, 13, 147. [Google Scholar] [CrossRef] [Green Version]
- Brahma, B.; Wadhvani, R. Solar irradiance forecasting based on deep learning methodologies and multi-site data. Symmetry 2020, 12, 1830. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, X.; Cao, J.; Wang, Z.; Wang, T.; Wang, H.; Zhang, Y. Anomaly detection in quasi-periodic time series based on automatic data segmentation and attentional lstm-cnn. IEEE Trans. Knowl. Data Eng. 2020. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhan, Z.H.; Wang, H.; Zhang, J. Data-driven evolutionary algorithm with perturbation-based ensemble surrogates. IEEE Trans. Cybern. 2020, 51, 3925–3937. [Google Scholar] [CrossRef] [PubMed]
- Bendali, W.; Saber, I.; Bourachdi, B.; Boussetta, M.; Mourad, Y. Deep learning using genetic algorithm optimization for short term solar irradiance forecasting. In Proceedings of the 2020 Fourth International Conference On Intelligent Computing in Data Sciences (ICDS), Fez, Morocco, 21–23 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–8. [Google Scholar]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms. Appl. Energy 2019, 253, 113541. [Google Scholar] [CrossRef]
- Husein, M.; Chung, I.Y. Day-ahead solar irradiance forecasting for microgrids using a long short-term memory recurrent neural network: A deep learning approach. Energies 2019, 12, 1856. [Google Scholar] [CrossRef] [Green Version]
- Deo, R.C.; Wen, X.; Qi, F. A wavelet-coupled support vector machine model for forecasting global incident solar radiation using limited meteorological dataset. Appl. Energy 2016, 168, 568–593. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Wavelet-based 3-phase hybrid SVR model trained with satellite-derived predictors, particle swarm optimization and maximum overlap discrete wavelet transform for solar radiation prediction. Renew. Sustain. Energy Rev. 2019, 113, 109247. [Google Scholar] [CrossRef]
- Attoue, N.; Shahrour, I.; Younes, R. Smart building: Use of the artificial neural network approach for indoor temperature forecasting. Energies 2018, 11, 395. [Google Scholar] [CrossRef] [Green Version]
- Bandara, K.; Shi, P.; Bergmeir, C.; Hewamalage, H.; Tran, Q.; Seaman, B. Sales demand forecast in e-commerce using a long short-term memory neural network methodology. In Proceedings of the International Conference on Neural Information Processing, Sydney, NSW, Australia, 12–15 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 462–474. [Google Scholar]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Ghoneim, S.S. Economic power and heat dispatch in cogeneration energy systems using manta ray foraging optimizer. IEEE Access 2020, 8, 208281–208295. [Google Scholar] [CrossRef]
- Elattar, E.E.; Shaheen, A.M.; El-Sayed, A.M.; El-Sehiemy, R.A.; Ginidi, A.R. Optimal operation of automated distribution networks based-MRFO algorithm. IEEE Access 2021, 9, 19586–19601. [Google Scholar] [CrossRef]
- Turgut, O.E. A novel chaotic manta-ray foraging optimization algorithm for thermo-economic design optimization of an air-fin cooler. SN Appl. Sci. 2021, 3, 1–36. [Google Scholar] [CrossRef]
- Sheng, B.; Pan, T.; Luo, Y.; Jermsittiparsert, K. System Identification of the PEMFCs based on Balanced Manta-Ray Foraging Optimization algorithm. Energy Rep. 2020, 6, 2887–2896. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Wang, J.Q.; Du, Y.; Wang, J. LSTM based long-term energy consumption prediction with periodicity. Energy 2020, 197, 117197. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, X. Predicting China’s energy consumption: Combining machine learning with three-layer decomposition approach. Energy Rep. 2021, 7, 5086–5099. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Jang, M.; Seo, S.; Kang, P. Recurrent neural network-based semantic variational autoencoder for sequence-to-sequence learning. Inf. Sci. 2019, 490, 59–73. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Haffari, G.; Norouzi, M. Sequence to sequence mixture model for diverse machine translation. arXiv 2018, arXiv:1810.07391. [Google Scholar]
- Huang, J.; Sun, Y.; Zhang, W.; Wang, H.; Liu, T. Entity Highlight Generation as Statistical and Neural Machine Translation. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1860–1872. [Google Scholar] [CrossRef]
- Hwang, S.; Jeon, G.; Jeong, J.; Lee, J. A novel time series based Seq2Seq model for temperature prediction in firing furnace process. Procedia Comput. Sci. 2019, 155, 19–26. [Google Scholar] [CrossRef]
- Golovko, V.; Kroshchanka, A.; Mikhno, E. Deep Neural Networks: Selected Aspects of Learning and Application. Pattern Recognit. Image Anal. 2021, 31, 132–143. [Google Scholar] [CrossRef]
- Mert, İ. Agnostic deep neural network approach to the estimation of hydrogen production for solar-powered systems. Int. J. Hydrog. Energy 2021, 46, 6272–6285. [Google Scholar] [CrossRef]
- Jallal, M.A.; Chabaa, S.; Zeroual, A. A novel deep neural network based on randomly occurring distributed delayed PSO algorithm for monitoring the energy produced by four dual-axis solar trackers. Renew. Energy 2020, 149, 1182–1196. [Google Scholar] [CrossRef]
- Pustokhina, I.V.; Pustokhin, D.A.; Gupta, D.; Khanna, A.; Shankar, K.; Nguyen, G.N. An effective training scheme for deep neural network in edge computing enabled Internet of medical things (IoMT) systems. IEEE Access 2020, 8, 107112–107123. [Google Scholar] [CrossRef]
- Srinidhi, C.L.; Ciga, O.; Martel, A.L. Deep neural network models for computational histopathology: A survey. Med Image Anal. 2021, 67, 101813. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.I.; Shah, J.L.; Bhat, M.M. CoroNet: A deep neural network for detection and diagnosis of COVID-19 from chest x-ray images. Comput. Methods Programs Biomed. 2020, 196, 105581. [Google Scholar] [CrossRef]
- Bau, D.; Zhu, J.Y.; Strobelt, H.; Lapedriza, A.; Zhou, B.; Torralba, A. Understanding the role of individual units in a deep neural network. Proc. Natl. Acad. Sci. USA 2020, 117, 30071–30078. [Google Scholar] [CrossRef]
- Wang, F.K.; Mamo, T. Gradient boosted regression model for the degradation analysis of prismatic cells. Comput. Ind. Eng. 2020, 144, 106494. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Ridgeway, G. Generalized Boosted Models: A guide to the gbm package. Update 2007, 1, 2007. [Google Scholar]
- Grape, S.; Branger, E.; Elter, Z.; Balkeståhl, L.P. Determination of spent nuclear fuel parameters using modelled signatures from non-destructive assay and Random Forest regression. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 969, 163979. [Google Scholar] [CrossRef]
- Desai, S.; Ouarda, T.B. Regional hydrological frequency analysis at ungauged sites with random forest regression. J. Hydrol. 2021, 594, 125861. [Google Scholar] [CrossRef]
- Hariharan, R. Random forest regression analysis on combined role of meteorological indicators in disease dissemination in an Indian city: A case study of New Delhi. Urban Clim. 2021, 36, 100780. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Wang, Y.; Zhang, K.; Hu, M.; Weng, Q.; Zhang, H. Spatial heterogeneity modeling of water quality based on random forest regression and model interpretation. Environ. Res. 2021, 202, 111660. [Google Scholar] [CrossRef] [PubMed]
- Sahani, N.; Ghosh, T. GIS-based spatial prediction of recreational trail susceptibility in protected area of Sikkim Himalaya using logistic regression, decision tree and random forest model. Ecol. Inform. 2021, 64, 101352. [Google Scholar] [CrossRef]
- Fouedjio, F. Exact Conditioning of Regression Random Forest for Spatial Prediction. Artif. Intell. Geosci. 2020, 1, 11–23. [Google Scholar] [CrossRef]
- Mohammed, S.; Al-Ebraheem, A.; Holb, I.J.; Alsafadi, K.; Dikkeh, M.; Pham, Q.B.; Linh, N.T.T.; Szabo, S. Soil management effects on soil water erosion and runoff in central Syria—A comparative evaluation of general linear model and random forest regression. Water 2020, 12, 2529. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Li, Y.; Wang, L.; Samui, P. Assessment of pile drivability using random forest regression and multivariate adaptive regression splines. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2021, 15, 27–40. [Google Scholar] [CrossRef]
- Babar, B.; Luppino, L.T.; Boström, T.; Anfinsen, S.N. Random forest regression for improved mapping of solar irradiance at high latitudes. Sol. Energy 2020, 198, 81–92. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Zhang, P.; Xie, M. A Joint Long Short-Term Memory and AdaBoost regression approach with application to remaining useful life estimation. Measurement 2021, 170, 108707. [Google Scholar] [CrossRef]
- Xia, T.; Zhuo, P.; Xiao, L.; Du, S.; Wang, D.; Xi, L. Multi-stage fault diagnosis framework for rolling bearing based on OHF Elman AdaBoost-Bagging algorithm. Neurocomputing 2021, 433, 237–251. [Google Scholar] [CrossRef]
- Jiang, H.; Zheng, W.; Luo, L.; Dong, Y. A two-stage minimax concave penalty based method in pruned AdaBoost ensemble. Appl. Soft Comput. 2019, 83, 105674. [Google Scholar] [CrossRef]
- Mehmood, Z.; Asghar, S. Customizing SVM as a base learner with AdaBoost ensemble to learn from multi-class problems: A hybrid approach AdaBoost-MSVM. Knowl.-Based Syst. 2021, 217, 106845. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Gong, J.; Chen, Z. Short and mid-term sea surface temperature prediction using time-series satellite data and LSTM-AdaBoost combination approach. Remote Sens. Environ. 2019, 233, 111358. [Google Scholar] [CrossRef]
- CEC. Clean Energy Australia Report; CEC: Melbourne, Australia, 2020. [Google Scholar]
- CEC. Clean Energy Australia Report 2021; CEC: Melbourne, Australia, 2021. [Google Scholar]
- List of Solar Farms in Queensland—Wikipedia. 2021. Available online: https://en.wikipedia.org/wiki/List_of_solar_farms_in_Queensland (accessed on 1 December 2021).
- Stone, G.; Dalla Pozza, R.; Carter, J.; McKeon, G. Long Paddock: Climate risk and grazing information for Australian rangelands and grazing communities. Rangel. J. 2019, 41, 225–232. [Google Scholar] [CrossRef]
- Centre for Environmental Data Analysis. CEDA Archive; Centre for Environmental Data Analysis: Leeds, UK, 2020; Available online: https://www.ceda.ac.uk/ (accessed on 1 December 2021).
- The Commonwealth Scientific and Industrial Research Organisation; Bureau of Meteorology. WCRP CMIP5: The CSIRO-BOM team ACCESS1-0 Model Output Collection; Centre for Environmental Data Analysis: Leeds, UK, 2017; Available online: https://www.csiro.au/ (accessed on 1 December 2021).
- Met Office Hadley Centre. WCRP CMIP5: Met Office Hadley Centre (MOHC) HadGEM2-CC Model Output Collection; Centre for Environmental Data Analysis: Leeds, UK, 2012; Available online: https://catalogue.ceda.ac.uk/uuid/2e4f5b3748874c61a265f58039898ea5 (accessed on 1 December 2021).
- Meteorological Research Institute of the Korean Meteorological Administration WCRP CMIP5: Meteorological Research Institute of KMA MRI-CGCM3 Model Output Collection; Centre for Environmental Data Analysis: Oxon, UK. 2013. Available online: https://data-search.nerc.ac.uk/geonetwork/srv/api/records/d8fefd3b748541e69e69154c7933eba1 (accessed on 1 December 2021).
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Global solar radiation prediction by ANN integrated with European Centre for medium range weather forecast fields in solar rich cities of Queensland Australia. J. Clean. Prod. 2019, 216, 288–310. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Self-adaptive differential evolutionary extreme learning machines for long-term solar radiation prediction with remotely-sensed MODIS satellite and Reanalysis atmospheric products in solar-rich cities. Remote Sens. Environ. 2018, 212, 176–198. [Google Scholar] [CrossRef]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow prediction using an integrated methodology based on convolutional neural network and long short-term memory networks. Sci. Rep. 2021, 11, 1–26. [Google Scholar]
- Gong, G.; An, X.; Mahato, N.K.; Sun, S.; Chen, S.; Wen, Y. Research on short-term load prediction based on Seq2seq model. Energies 2019, 12, 3199. [Google Scholar] [CrossRef] [Green Version]
- Cavalli, S.; Amoretti, M. CNN-based multivariate data analysis for bitcoin trend prediction. Appl. Soft Comput. 2021, 101, 107065. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Prechelt, L. Early stopping-but when? In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998; pp. 55–69. [Google Scholar]
- Chollet, F. Keras. 2017. Available online: https://keras.io/ (accessed on 1 December 2021).
- Brownlee, J. Time series prediction with lstm recurrent neural networks in python with keras. Mach. Learn. Mastery. 2016. Available online: https://machinelearningmastery.com/time-series-prediction-lstm-recurrent-neural-networks-python-keras/ (accessed on 1 December 2021).
- Goldsborough, P. A tour of tensorflow. arXiv 2016, arXiv:1610.01178. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. Available online: https://www.usenix.org/system/files/conference/osdi16/osdi16-abadi.pdf (accessed on 1 December 2021).
- ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology. II: Hydrologic applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar] [CrossRef]
- ASCE Task Committee on Definition of Criteria for Evaluation of Watershed Models of the Watershed Management Committee; Irrigation and Drainage Division. Criteria for evaluation of watershed models. J. Irrig. Drain. Eng. 1993, 119, 429–442. [Google Scholar] [CrossRef]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ. Model. Softw. 2007, 22, 1034–1052. [Google Scholar] [CrossRef] [Green Version]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep learning neural networks trained with MODIS satellite-derived predictors for long-term global solar radiation prediction. Energies 2019, 12, 2407. [Google Scholar] [CrossRef] [Green Version]
- Pan, T.; Wu, S.; Dai, E.; Liu, Y. Estimating the daily global solar radiation spatial distribution from diurnal temperature ranges over the Tibetan Plateau in China. Appl. Energy 2013, 107, 384–393. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Mandeville, A.; O’connell, P.; Sutcliffe, J.; Nash, J. River flow forecasting through conceptual models part III-The Ray catchment at Grendon Underwood. J. Hydrol. 1970, 11, 109–128. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Review and statistical analysis of different global solar radiation sunshine models. Renew. Sustain. Energy Rev. 2015, 52, 1869–1880. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- McKenzie, J. Mean absolute percentage error and bias in economic forecasting. Econ. Lett. 2011, 113, 259–262. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. Smart deep learning based wind speed prediction model using wavelet packet decomposition, convolutional neural network and convolutional long short term memory network. Energy Convers. Manag. 2018, 166, 120–131. [Google Scholar] [CrossRef]
- Sun, S.; Qiao, H.; Wei, Y.; Wang, S. A new dynamic integrated approach for wind speed forecasting. Appl. Energy 2017, 197, 151–162. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]
- Costantini, M.; Pappalardo, C. Combination of Forecast Methods Using Encompassing Tests: An Algorithm-Based Procedure; Technical Report; Reihe Ökonomie/Economics Series; Institute for Advanced Studies (IHS): Vienna, Austria, 2008; Available online: https://www.econstor.eu/handle/10419/72708 (accessed on 1 December 2021).
- Lian, C.; Zeng, Z.; Wang, X.; Yao, W.; Su, Y.; Tang, H. Landslide displacement interval prediction using lower upper bound estimation method with pre-trained random vector functional link network initialization. Neural Netw. 2020, 130, 286–296. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Y.; Qian, Z.; Zareipour, H.; Pei, Y.; Wang, J.Y. Performance assessment of photovoltaic modules using improved threshold-based methods. Sol. Energy 2019, 190, 515–524. [Google Scholar] [CrossRef]
- Bremnes, J.B. Probabilistic wind power forecasts using local quantile regression. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2004, 7, 47–54. [Google Scholar] [CrossRef]
- Naik, J.; Bisoi, R.; Dash, P. Prediction interval forecasting of wind speed and wind power using modes decomposition based low rank multi-kernel ridge regression. Renew. Energy 2018, 129, 357–383. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A.F. Lower upper bound estimation method for construction of neural network-based prediction intervals. IEEE Trans. Neural Netw. 2010, 22, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Shichang, D.; Shiyao, J.; Chen, Z.; Zhiyuan, X. Prognostic study of ball screws by ensemble data-driven particle filters. J. Manuf. Syst. 2020, 56, 359–372. [Google Scholar] [CrossRef]
- Lu, J.; Ding, J. Construction of prediction intervals for carbon residual of crude oil based on deep stochastic configuration networks. Inf. Sci. 2019, 486, 119–132. [Google Scholar] [CrossRef]
- Hora, J.; Campos, P. A review of performance criteria to validate simulation models. Expert Syst. 2015, 32, 578–595. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F. Proposed metric for evaluation of solar forecasting models. J. Sol. Energy Eng. 2013, 135, 011016. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Alessandrini, S.; Antonanzas, J.; Antonanzas-Torres, F.; Badescu, V.; Beyer, H.G.; Blaga, R.; Boland, J.; Bright, J.M.; Coimbra, C.F.; et al. Verification of deterministic solar forecasts. Sol. Energy 2020, 210, 20–37. [Google Scholar] [CrossRef]
| Property | Blair Athol Solar Power Station | Blue Grass Solar Farm | Bluff Solar Farm | Bouldercombe Solar Farm | Broadlea Solar Farm | Columboola Solar Farm |
|---|---|---|---|---|---|---|
| Latitude | 22°4128 S | 26°4048 S | 23°3553 S | 23°3130 S | 21°5143 S | 26°3810 S |
| Longitude | 147°3231 E | 150°2935 E | 149°0220 E | 150°2956 E | 148°1012 E | 150°1746 E |
| Capacity (MW) | 60 | 200 | 250 | 280 | 100 | 162 |
| Median | 20.00 | 19.00 | 20.00 | 20.00 | 20.00 | 19.00 |
| Mean | 20.02 | 19.28 | 19.76 | 19.57 | 19.85 | 19.33 |
| Standard deviation | 5.80 | 6.43 | 5.84 | 5.83 | 5.68 | 6.48 |
| Variance | 33.64 | 41.34 | 34.10 | 33.95 | 32.23 | 42.05 |
| Maximum | 32.00 | 32.00 | 32.00 | 32.00 | 31.00 | 33.00 |
| Minimum | 4.00 | 4.00 | 4.00 | 4.00 | 3.00 | 4.00 |
| Mode | 28.00 | 28.00 | 28.00 | 28.00 | 28.00 | 29.00 |
| Interquartile range | 8.00 | 9.00 | 8.00 | 8.00 | 8.00 | 9.00 |
| Skewness | −0.38 | −0.18 | −0.36 | −0.36 | −0.41 | −0.19 |
| Kurtosis | 2.65 | 2.34 | 2.57 | 2.54 | 2.65 | 2.34 |
| Variable | Description | Units | |
|---|---|---|---|
| Global Circulation Model Atmospheric Predictor Variables | clt | Cloud Area Fraction | % |
| hfls | Surface Upward Latent Heat Flux | wm | |
| hfss | Surface Upward Sensible Heat Flux | wm | |
| hur | Relative Humidity | % | |
| hus | Near-Surface Specific Humidity | gkg | |
| pr | Precipitation | kgms | |
| prc | Convective Precipitation | kgms | |
| prsn | Solid Precipitation | kgms | |
| psl | Sea Level Pressure | pa | |
| rhs | Near-Surface Relative Humidity | % | |
| rhsmax | Surface Daily Max Relative Humidity | % | |
| rhsmin | Surface Daily Min Relative Humidity | % | |
| sfcWind | Wind Speed | ||
| sfcWindmax | Daily Maximum Near-Surface Wind Speed | ms | |
| ta | Air Temperature | K | |
| tas | Near-Surface Air Temperature | K | |
| tasmax | Daily Max Near Surface Air Temperature | K | |
| tasmin | Daily Min Near Surface Air Temperature | K | |
| ua | Eastward Wind | ms | |
| uas | Eastern Near-Surface Wind | ms | |
| va | Northward Wind | ms | |
| vas | Northern Near-Surface Wind | ms | |
| wap | Omega (Lagrangian Tendency of Air Pressure) | pas | |
| zg | Geopotential Height | m | |
| Grnd.-based SILO | T.Max | Maximum Temperature | K |
| T.Min | Minimum Temperature | K | |
| Rain | Rainfall | mm | |
| Evap | Evaporation | mm | |
| VP | Vapor Pressure | Pa | |
| RHmaxT | Relative Humidity at Maximum Temperature | % | |
| RHminT | Relative Humidity at Minimum Temperature | % |
| Blair Athol Solar Power Station | Blue Grass Solar Farm | Bluff Solar Farm | Bouldercombe Solar Farm | Broadlea Solar Farm | Columboola Solar Farm |
|---|---|---|---|---|---|
| Evap | Evap | Evap | Evap | Evap | Evap |
| RHmaxT | RHmaxT | RHmaxT | RHmaxT | RHmaxT | RHmaxT |
| hfss | ua_1000 | hfss | hfss | hfss | ua_1000 |
| hur_1000 | hfls | hur_1000 | Rain | hur_1000 | hfls |
| ua_5000 | hfss | ua_5000 | ua_1000 | Rain | hfss |
| wap_1000 | hus_5000 | wap_1000 | zg_1000 | T.Max | hus_5000 |
| Rain | ta_25000 | hus_5000 | hus_5000 | RHminT | wap_1000 |
| T.Max | wap_1000 | sfcWindmax | wap_1000 | wap_85000 | ta_25000 |
| va_85000 | wap_85000 | Rain | va_85000 | wap_1000 | Rain |
| RHminT | sfcWindmax | T.Max | T.Max | va_85000 | hur_1000 |
| wap_85000 | zg_1000 | ta_25000 | hur_1000 | ua_5000 | ua_5000 |
| zg_5000 | Rain | wap_85000 | ta_25000 | va_50000 | wap_85000 |
| va_50000 | RHminT | zg_1000 | wap_85000 | zg_5000 | RHminT |
| sfcWindmax | ua_5000 | RHminT | ua_5000 | sfcWindmax | |
| hus_5000 | T.Max | va_50000 | sfcWindmax | T.Max | |
| hfls | va_25000 | zg_85000 | va_50000 | zg_1000 | |
| hur_1000 | va_25000 |
| Predictive Models | Blair Athol Solar Power Station | Blue Grass Solar Farm | Bluff Solar Farm | Bouldercombe Solar Farm | Broadlea Solar Farm | Columboola Solar Farm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r | RMSE | r | RMSE | r | RMSE | r | RMSE | r | RMSE | r | RMSE | |
| SAELSTM | 0.956 | 2.344 | 0.965 | 2.340 | 0.954 | 2.503 | 0.951 | 2.502 | 0.959 | 2.208 | 0.962 | 2.407 |
| DNN | 0.952 | 2.715 | 0.959 | 2.644 | 0.946 | 2.696 | 0.946 | 2.555 | 0.954 | 2.354 | 0.956 | 2.634 |
| ADBR | 0.952 | 2.436 | 0.958 | 2.601 | 0.944 | 2.674 | 0.938 | 2.748 | 0.954 | 2.377 | 0.957 | 2.664 |
| GBM | 0.953 | 2.441 | 0.956 | 2.671 | 0.948 | 2.580 | 0.945 | 2.620 | 0.957 | 2.295 | 0.953 | 2.759 |
| ETR | 0.953 | 2.445 | 0.959 | 2.592 | 0.947 | 2.619 | 0.939 | 2.733 | 0.953 | 2.426 | 0.955 | 2.716 |
| RFR | 0.952 | 2.456 | 0.955 | 2.660 | 0.940 | 2.760 | 0.939 | 2.724 | 0.952 | 2.420 | 0.953 | 2.744 |
| Predictive Models | Blair Athol Solar Power Station | Blue Grass Solar Farm | Bluff Solar Farm | Bouldercombe Solar Farm | Broadlea Solar Farm | Columboola Solar Farm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WI | NSE | WI | NSE | WI | NSE | WI | NSE | WI | NSE | WI | NSE | |
| SAELSTM | 0.918 | 0.834 | 0.930 | 0.863 | 0.916 | 0.820 | 0.885 | 0.799 | 0.926 | 0.845 | 0.925 | 0.854 |
| DNN | 0.885 | 0.785 | 0.904 | 0.828 | 0.881 | 0.791 | 0.881 | 0.788 | 0.910 | 0.824 | 0.911 | 0.826 |
| ADBR | 0.911 | 0.821 | 0.906 | 0.832 | 0.897 | 0.793 | 0.858 | 0.757 | 0.909 | 0.822 | 0.902 | 0.824 |
| GBM | 0.911 | 0.820 | 0.902 | 0.823 | 0.906 | 0.807 | 0.874 | 0.780 | 0.918 | 0.833 | 0.896 | 0.811 |
| ETR | 0.911 | 0.820 | 0.908 | 0.833 | 0.903 | 0.801 | 0.862 | 0.761 | 0.906 | 0.815 | 0.899 | 0.817 |
| RFR | 0.910 | 0.818 | 0.902 | 0.824 | 0.891 | 0.779 | 0.861 | 0.762 | 0.907 | 0.815 | 0.899 | 0.812 |
| Predictive Models | Blair Athol Solar Power Station | Blue Grass Solar Farm | Bluff Solar Farm | Bouldercombe Solar Farm | Broadlea Solar Farm | Columboola Solar Farm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SAELSTM | 0.630 | 0.835 | 0.665 | 0.867 | 0.595 | 0.827 | 0.600 | 0.817 | 0.644 | 0.845 | 0.659 | 0.856 |
| DNN | 0.573 | 0.817 | 0.628 | 0.846 | 0.577 | 0.798 | 0.583 | 0.799 | 0.605 | 0.824 | 0.628 | 0.831 |
| ADBR | 0.616 | 0.823 | 0.633 | 0.842 | 0.582 | 0.793 | 0.568 | 0.773 | 0.621 | 0.829 | 0.631 | 0.837 |
| GBM | 0.618 | 0.823 | 0.612 | 0.836 | 0.592 | 0.807 | 0.579 | 0.798 | 0.626 | 0.838 | 0.608 | 0.825 |
| ETR | 0.615 | 0.824 | 0.638 | 0.846 | 0.591 | 0.802 | 0.573 | 0.779 | 0.609 | 0.825 | 0.617 | 0.829 |
| RFR | 0.612 | 0.820 | 0.624 | 0.833 | 0.573 | 0.780 | 0.581 | 0.778 | 0.616 | 0.821 | 0.614 | 0.822 |
| Predictive Models | Blair Athol Solar Power Station | Blue Grass Solar Farm | Bluff Solar Farm | Bouldercombe Solar Farm | Broadlea Solar Farm | Columboola Solar Farm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RRMSE | RMAE | RRMSE | RMAE | RRMSE | RMAE | RRMSE | RMAE | RRMSE | RMAE | RRMSE | RMAE | |
| SAELSTM | 11.418 | 10.309 | 11.617 | 10.527 | 12.480 | 11.514 | 12.518 | 11.192 | 10.840 | 9.599 | 11.912 | 10.904 |
| DNN | 13.226 | 12.038 | 13.126 | 11.928 | 13.441 | 13.181 | 12.783 | 11.546 | 11.554 | 10.629 | 13.035 | 11.698 |
| ADBR | 11.867 | 10.519 | 12.910 | 11.895 | 13.334 | 12.329 | 13.749 | 12.125 | 11.668 | 10.305 | 13.188 | 11.955 |
| GBM | 11.894 | 10.465 | 13.259 | 12.441 | 12.866 | 12.044 | 13.106 | 12.035 | 11.266 | 10.041 | 13.657 | 12.706 |
| ETR | 11.910 | 10.371 | 12.868 | 11.790 | 13.060 | 12.218 | 13.671 | 12.045 | 11.911 | 10.501 | 13.440 | 12.225 |
| RFR | 11.967 | 10.496 | 13.208 | 12.166 | 13.763 | 12.542 | 13.630 | 11.828 | 11.881 | 10.252 | 13.579 | 12.337 |
| SAELSTM Compared Against | Blair Athol Solar Power Station | Blue Grass Solar Farm | Bluff Solar Farm | Bouldercombe Solar Farm | Broadlea Solar Farm | Columboola Solar Farm | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DNN | 13% | 11% | 10% | 8% | 4% | 8% | 2% | 4% | 3% | 7% | 11% | 7% | 9% | 9% | 9% | 16% | 16% | 11% |
| ADBR | 11% | 10% | 10% | 7% | 2% | 8% | 10% | 8% | 11% | 8% | 6% | 6% | 11% | 8% | 9% | 4% | 4% | 4% |
| GBM | 14% | 16% | 13% | 3% | 0% | 4% | 5% | 5% | 5% | 4% | 5% | 3% | 15% | 15% | 13% | 4% | 3% | 4% |
| ETR | 11% | 8% | 9% | 5% | 0% | 6% | 9% | 7% | 10% | 10% | 10% | 8% | 13% | 12% | 11% | 4% | 4% | 4% |
| RFR | 14% | 12% | 13% | 10% | 5% | 12% | 9% | 5% | 10% | 10% | 8% | 8% | 14% | 13% | 13% | 5% | 5% | 5% |
| (a) | ||||||
|---|---|---|---|---|---|---|
| Predictive Model | SAELSTM | DNN | ADBR | GBM | ETR | RFR |
| SAELSTM | 1.777 | 2.219 | 3.447 | 2.454 | 2.526 | |
| DNN | 0.365 | 1.491 | 1.012 | 1.318 | ||
| ADBR | 1.874 | 1.175 | 1.740 | |||
| GBM | −0.890 | −0.219 | ||||
| ETR | 0.533 | |||||
| (b) | ||||||
| Predictive Model | SAELSTM | DNN | ADBR | GBM | ETR | RFR |
| SAELSTM | 1.862 | 2.324 | 3.611 | 2.570 | 2.646 | |
| DNN | 0.383 | 1.562 | 1.060 | 1.381 | ||
| ADBR | 1.963 | 1.231 | 1.823 | |||
| GBM | −0.932 | −0.230 | ||||
| ETR | 0.558 | |||||
| (c) | ||||||
| Solar Energy Farm | SAELSTM | DNN | ADBR | GBM | ETR | RFR |
| Blair Athol Solar Power Station | 0.706 | 0.682 | 0.605 | 0.681 | 0.680 | 0.677 |
| Blue Grass Solar Farm | 0.730 | 0.666 | 0.655 | 0.648 | 0.668 | 0.651 |
| Bluff Solar Farm | 0.678 | 0.632 | 0.626 | 0.657 | 0.647 | 0.608 |
| Bouldercombe Solar Farm | 0.603 | 0.521 | 0.586 | 0.565 | 0.526 | 0.529 |
| Broadlea Solar Farm | 0.694 | 0.645 | 0.652 | 0.669 | 0.630 | 0.632 |
| Columboola Solar Farm | 0.715 | 0.651 | 0.659 | 0.625 | 0.637 | 0.630 |
| (d) | ||||||
| Predictive Model | SAELSTM | DNN | ADBR | GBM | ETR | RFR |
| SAELSTM | 1.862 | 2.324 | 3.611 | 2.570 | 2.646 | |
| DNN | 0.383 | 1.562 | 1.060 | 1.381 | ||
| ADBR | 1.963 | 1.231 | 1.823 | |||
| GBM | −0.932 | −0.230 | ||||
| ETR | 0.558 | |||||
| Predictive Models | SAELSTM | DNN | ADBR | GBM | ETR | RFR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PICP | MPIW | PICP | MPIW | PICP | MPIW | PICP | MPIW | PICP | MPIW | PICP | MPIW | |
| Blair Athol Solar Power Station | 92% | 7.732 | 93% | 10.134 | 95% | 12.208 | 92% | 10.407 | 92% | 8.892 | 90% | 10.088 |
| Blue Grass Solar Farm | 93% | 8.680 | 97% | 10.453 | 96% | 13.591 | 93% | 11.665 | 95% | 10.378 | 93% | 11.398 |
| Bluff Solar Farm | 90% | 7.702 | 95% | 10.791 | 96% | 12.239 | 91% | 10.683 | 91% | 9.338 | 91% | 10.436 |
| Bouldercombe Solar Farm | 95% | 9.483 | 93% | 10.685 | 96% | 13.511 | 94% | 11.656 | 93% | 9.852 | 93% | 11.250 |
| Broadlea Solar Farm | 93% | 8.411 | 97% | 9.260 | 95% | 11.637 | 93% | 9.815 | 92% | 8.443 | 91% | 9.515 |
| Columboola Solar Farm | 95% | 8.500 | 97% | 11.169 | 95% | 14.047 | 94% | 11.958 | 93% | 10.111 | 93% | 11.557 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghimire, S.; Deo, R.C.; Wang, H.; Al-Musaylh, M.S.; Casillas-Pérez, D.; Salcedo-Sanz, S. Stacked LSTM Sequence-to-Sequence Autoencoder with Feature Selection for Daily Solar Radiation Prediction: A Review and New Modeling Results. Energies 2022, 15, 1061. https://doi.org/10.3390/en15031061
Ghimire S, Deo RC, Wang H, Al-Musaylh MS, Casillas-Pérez D, Salcedo-Sanz S. Stacked LSTM Sequence-to-Sequence Autoencoder with Feature Selection for Daily Solar Radiation Prediction: A Review and New Modeling Results. Energies. 2022; 15(3):1061. https://doi.org/10.3390/en15031061
Chicago/Turabian StyleGhimire, Sujan, Ravinesh C. Deo, Hua Wang, Mohanad S. Al-Musaylh, David Casillas-Pérez, and Sancho Salcedo-Sanz. 2022. "Stacked LSTM Sequence-to-Sequence Autoencoder with Feature Selection for Daily Solar Radiation Prediction: A Review and New Modeling Results" Energies 15, no. 3: 1061. https://doi.org/10.3390/en15031061
APA StyleGhimire, S., Deo, R. C., Wang, H., Al-Musaylh, M. S., Casillas-Pérez, D., & Salcedo-Sanz, S. (2022). Stacked LSTM Sequence-to-Sequence Autoencoder with Feature Selection for Daily Solar Radiation Prediction: A Review and New Modeling Results. Energies, 15(3), 1061. https://doi.org/10.3390/en15031061










