Data-Driven Proxy Models for Improving Advanced Well Completion Design under Uncertainty
Abstract
1. Introduction
2. Data and Methods
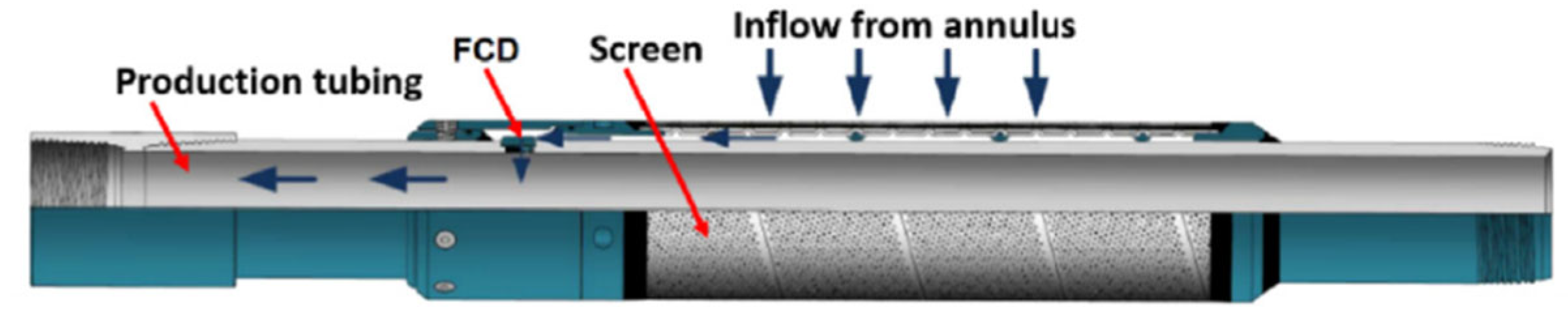
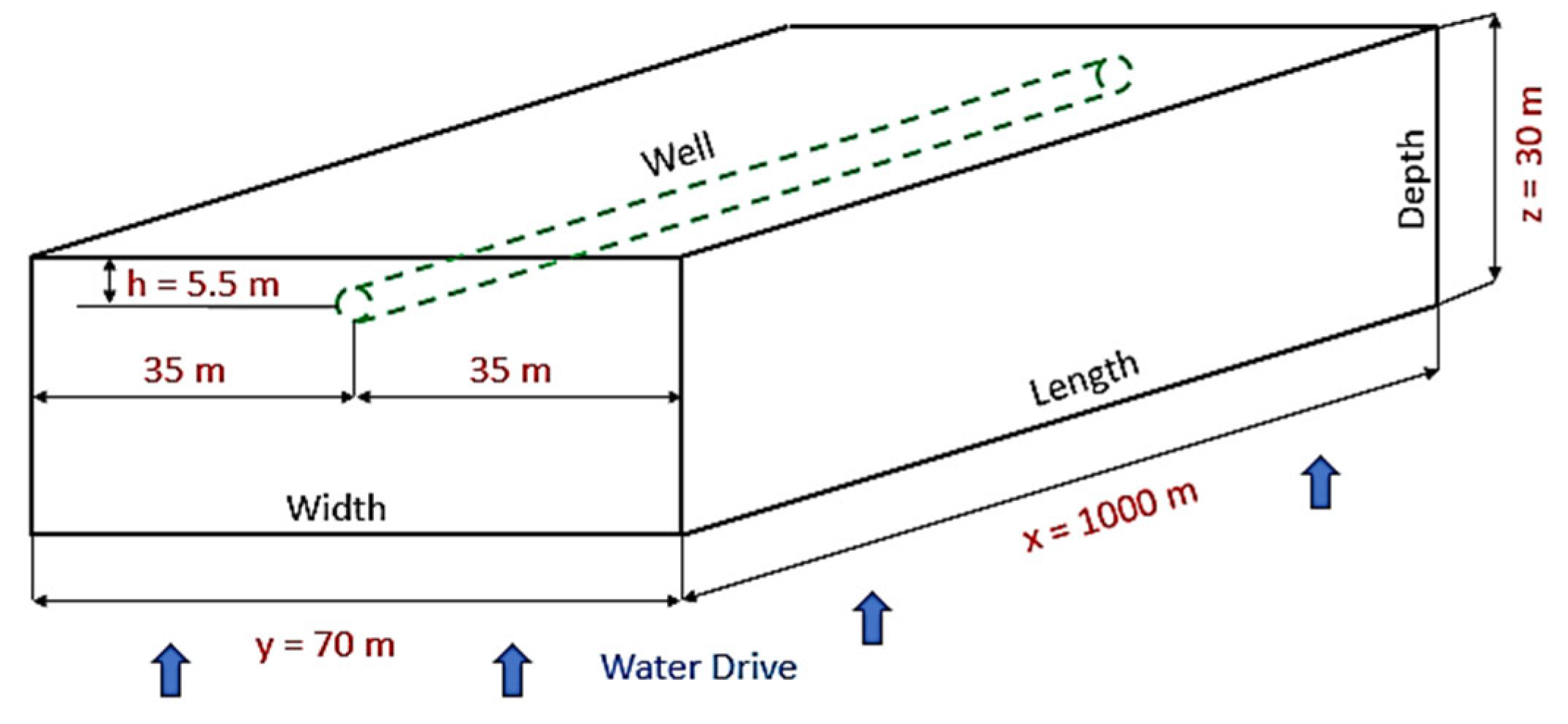
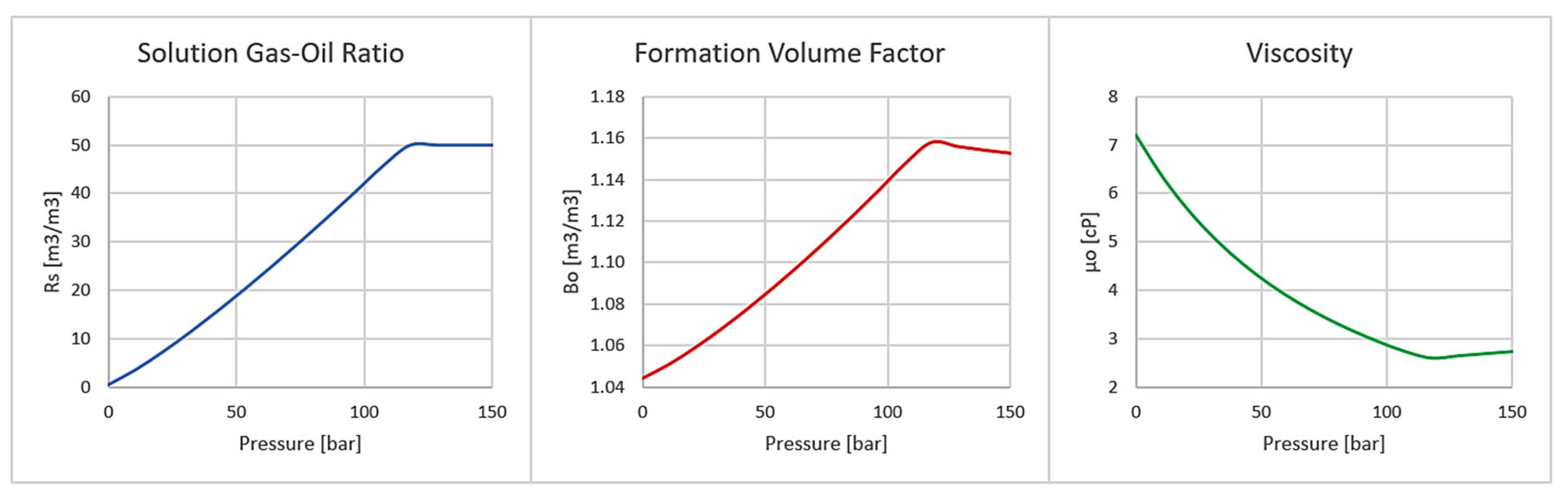
2.1. Development of the Physics-Based Integrated Well–Reservoir Model
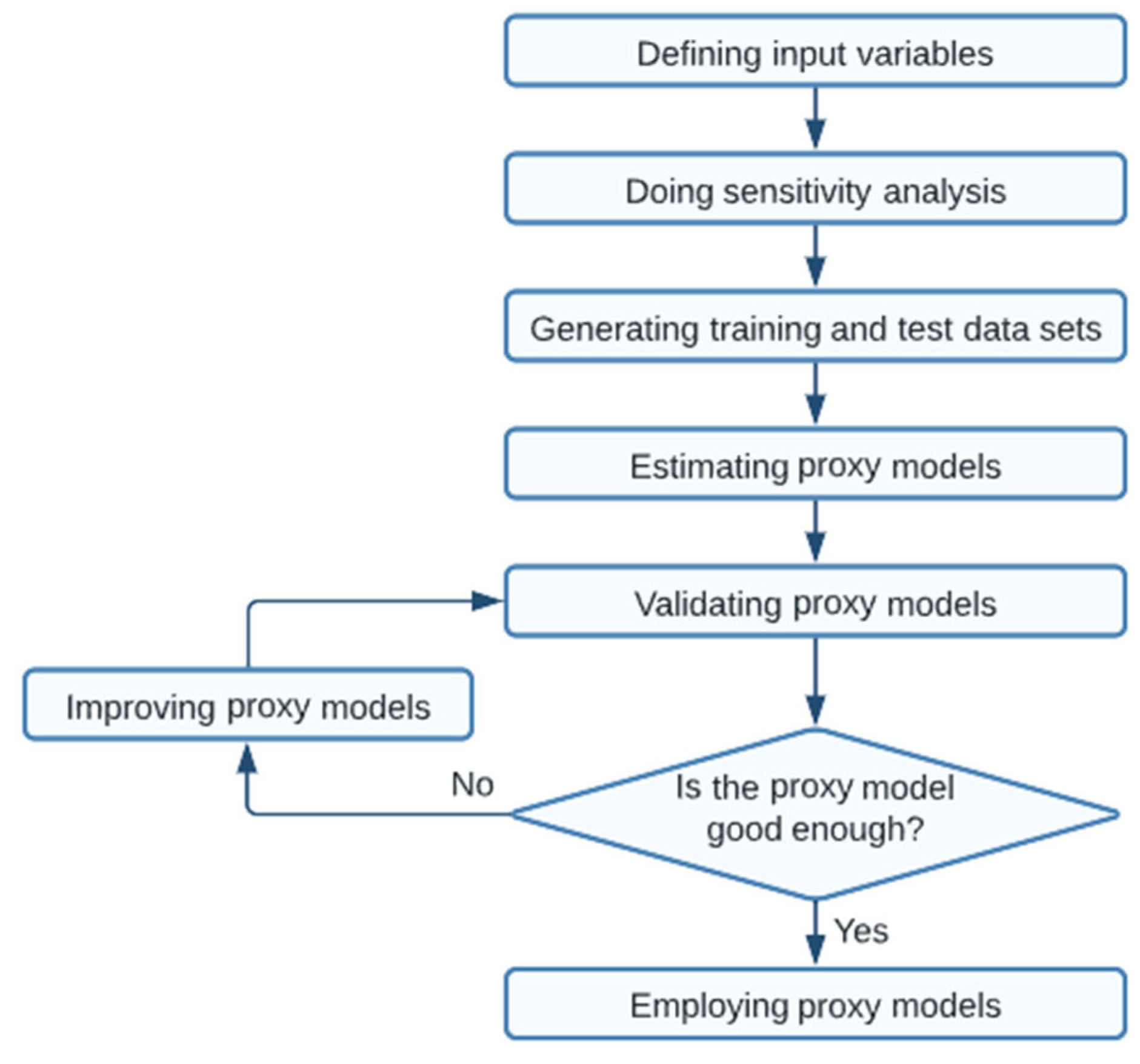
2.2. Development of the Data-Driven Proxy Model
2.2.1. Data Set Generation
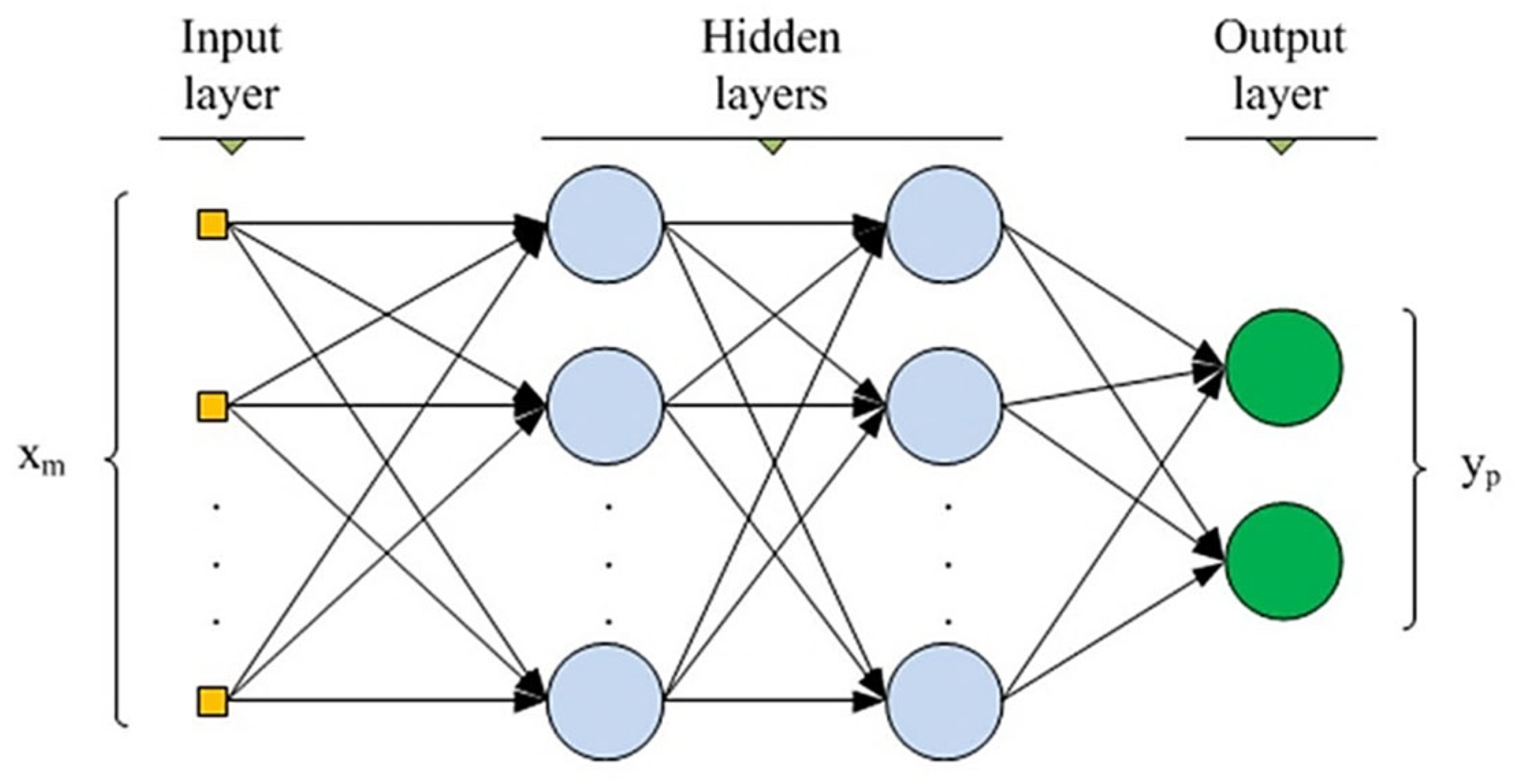
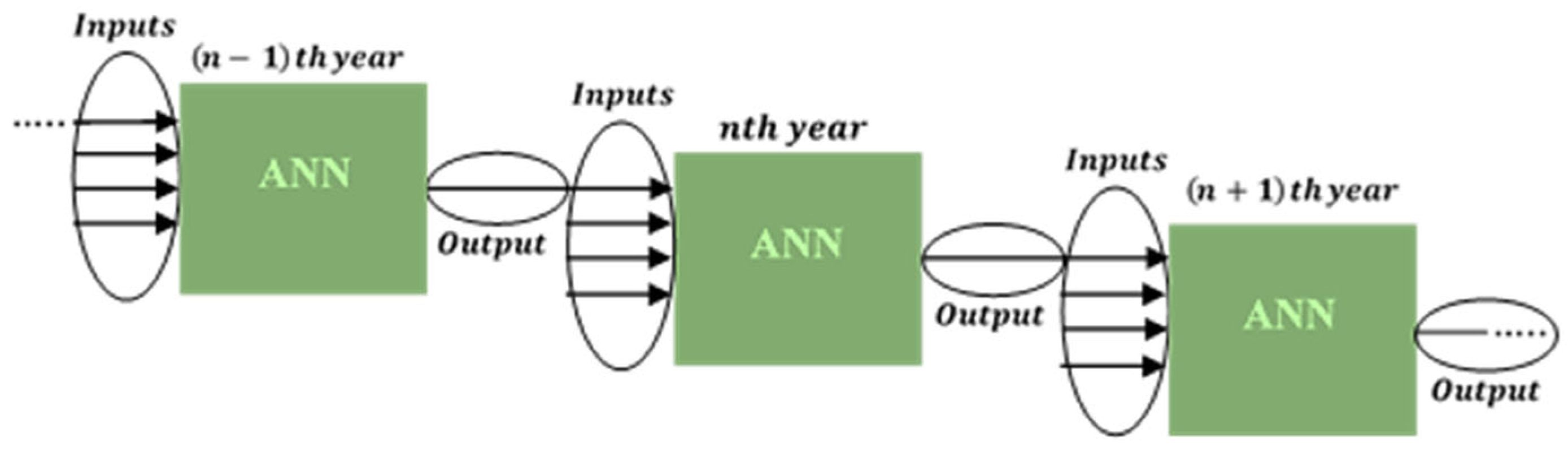
2.2.2. Architecture of the Proxy
2.2.3. Training and Testing the Proxy
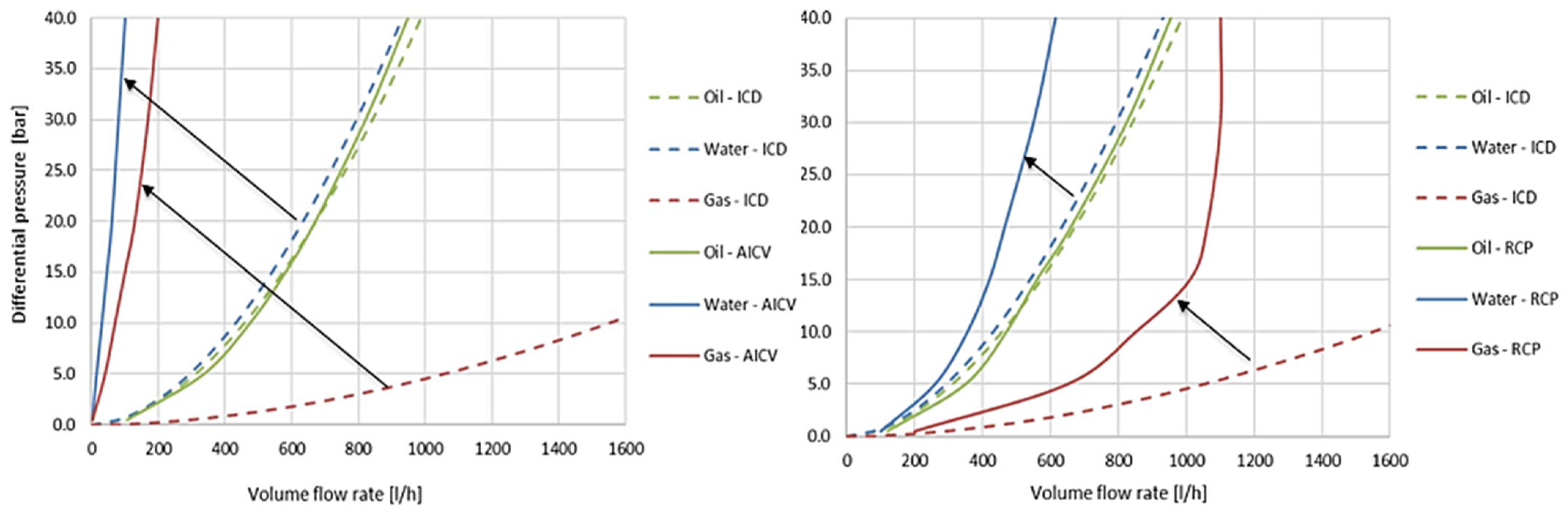
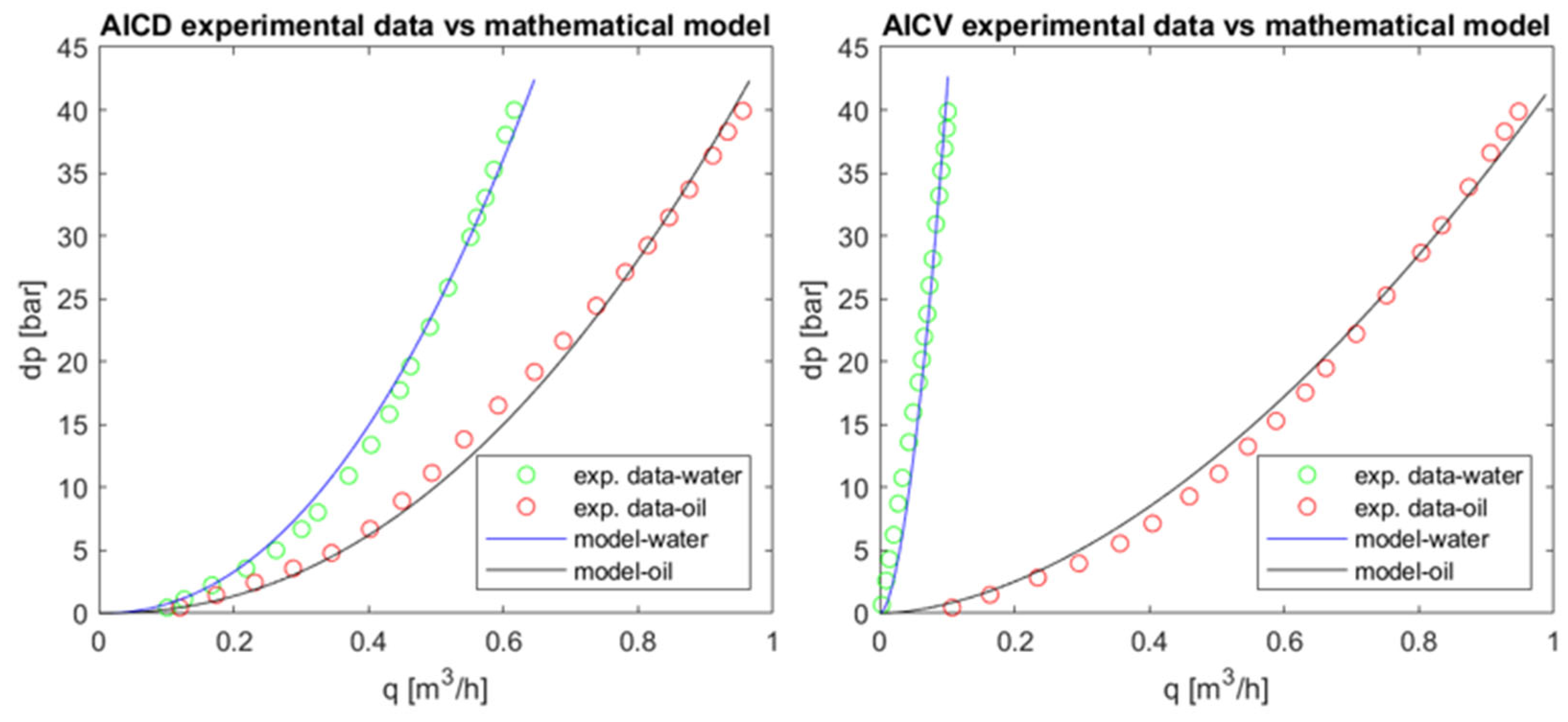
3. Results and Discussions
3.1. Performance of the Developed Proxy Models
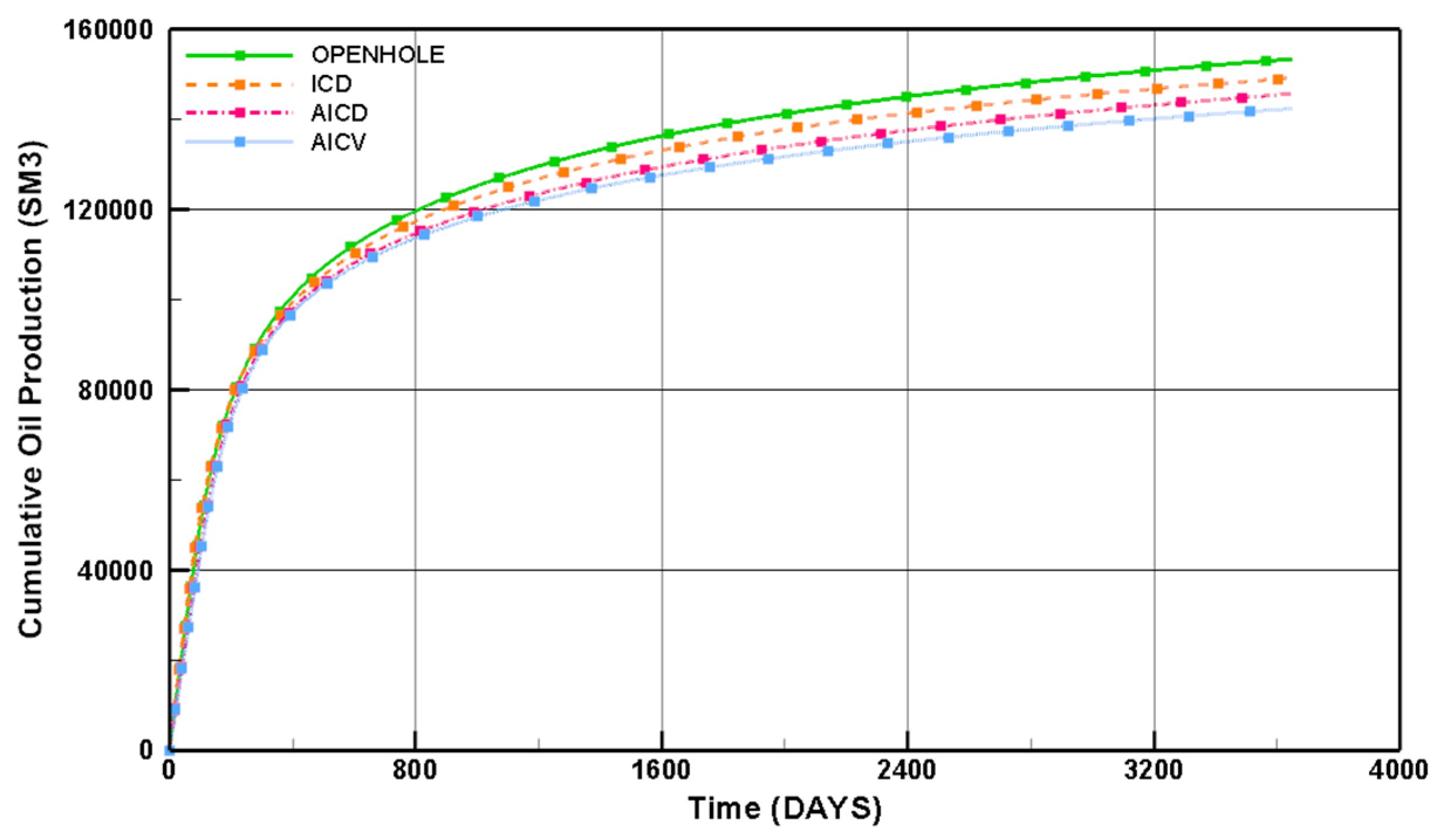
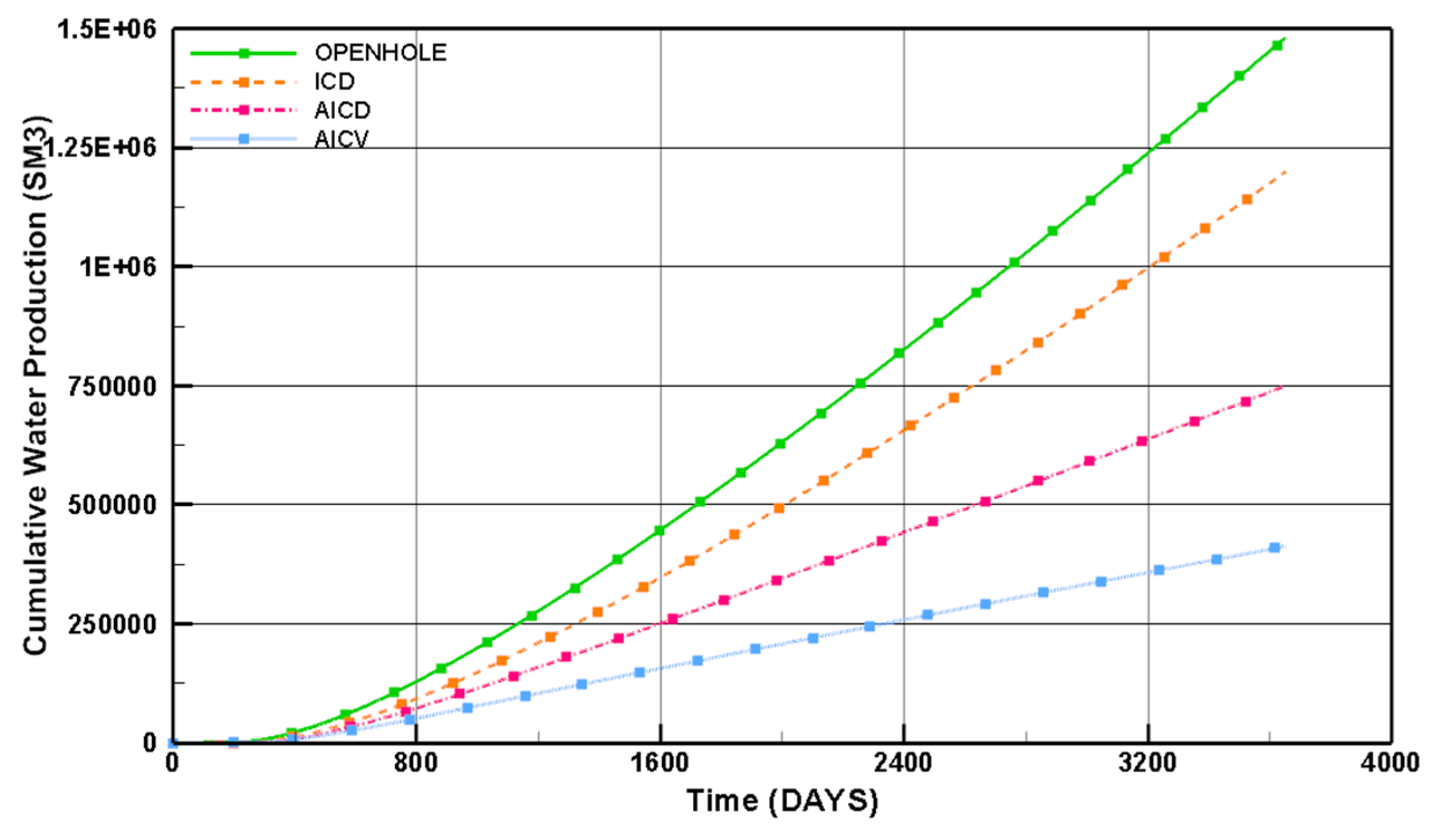
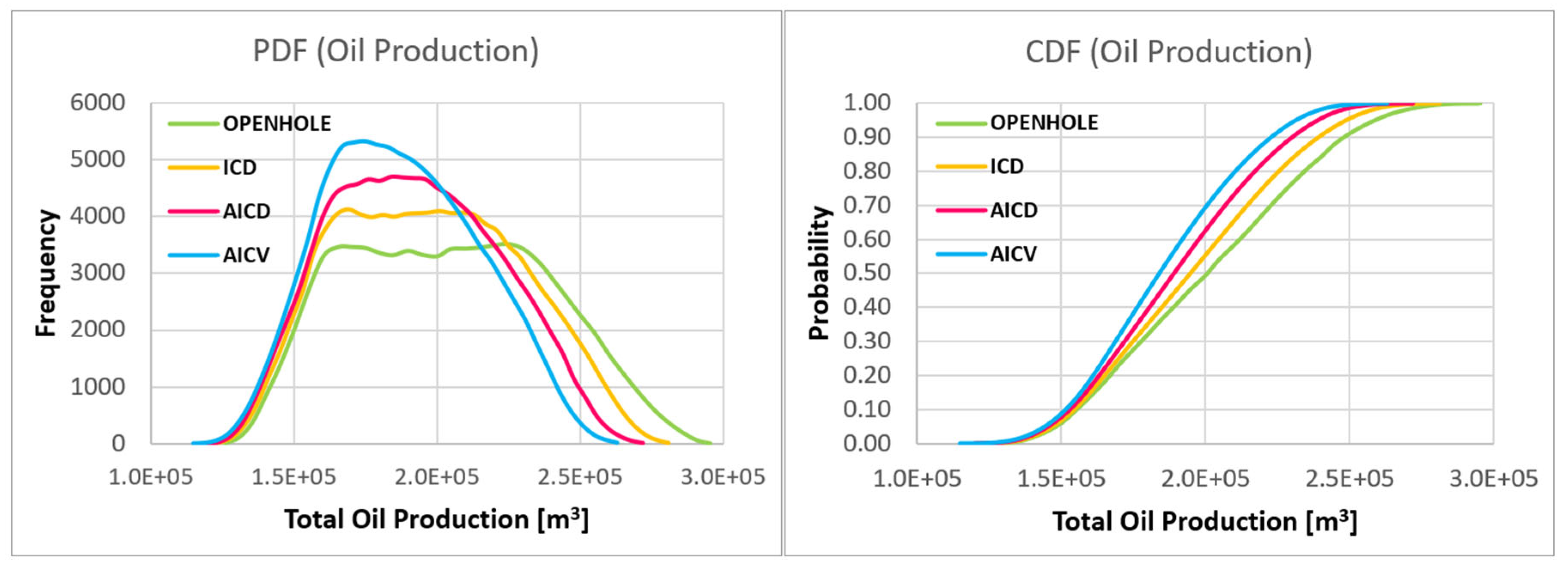
3.2. Evaluating the Performance of Advanced Wells under Uncertainty
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moradi, A.; Moldestad, B.M. Simulation of heavy oil production using smart wells. Scand. Simul. Soc. 2022, 263–270. [Google Scholar] [CrossRef]
- Triandi, M.; Chigbo, I.; Khunmek, T.; Ismail, I.M. Field Case: Use of Autonomous Inflow Control Devices To Increase Oil Production in a Thin Oil Rim Reservoir in the Gulf of Thailand. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 12–15 November 2018. [Google Scholar]
- Moradi, A.; Samani, N.A.; Kumara, A.S.; Moldestad, B.M. Evaluating the performance of advanced wells in heavy oil reservoirs under uncertainty in permeability parameters. Energy Rep. 2022, 8, 8605–8617. [Google Scholar] [CrossRef]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Alenezi, F.; Mohaghegh, S. A data-driven smart proxy model for a comprehensive reservoir simulation. In Proceedings of the 2016 4th Saudi International Conference on Information Technology (Big Data Analysis)(KACSTIT), Riyadh, Saudi Arabia, 6–9 November 2016; pp. 1–6. [Google Scholar]
- Yu, Y.; Liu, S.; Liu, Y.; Bao, Y.; Zhang, L.; Dong, Y. Data-driven proxy model for forecasting of cumulative oil production during the steam-assisted gravity drainage process. ACS Omega 2021, 6, 11497–11509. [Google Scholar] [CrossRef]
- Navrátil, J.; King, A.; Rios, J.; Kollias, G.; Torrado, R.; Codas, A. Accelerating physics-based simulations using end-to-end neural network proxies: An application in oil reservoir modeling. Front. Big Data 2019, 2, 33. [Google Scholar] [CrossRef] [PubMed]
- Guérillot, D.; Bruyelle, J. Uncertainty assessment in production forecast with an optimal artificial neural network. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Manama, Bahrain, 6–9 March 2017. [Google Scholar]
- Silva, C.; Maschio, C.; Schiozer, D.J. Use of neuro-simulation techniques as proxies to reservoir simulator: Application in production history matching. J. Pet. Sci. Eng. 2007, 57, 273–280. [Google Scholar] [CrossRef]
- Foroud, T.; Seifi, A.; AminShahidi, B. Assisted history matching using artificial neural network based global optimization method–Applications to Brugge field and a fractured Iranian reservoir. J. Pet. Sci. Eng. 2014, 123, 46–61. [Google Scholar] [CrossRef]
- Shaik, N.B.; Pedapati, S.R.; Dzubir, F.A.B. Remaining useful life prediction of a piping system using artificial neural networks: A case study. Ain Shams Eng. J. 2022, 13, 101535. [Google Scholar] [CrossRef]
- Otchere, D.A.; Ganat, T.O.A.; Gholami, R.; Ridha, S. Application of supervised machine learning paradigms in the prediction of petroleum reservoir properties: Comparative analysis of ANN and SVM models. J. Pet. Sci. Eng. 2021, 200, 108182. [Google Scholar] [CrossRef]
- Yuan, Z.; Huang, H.; Jiang, Y.; Li, J. Hybrid deep neural networks for reservoir production prediction. J. Pet. Sci. Eng. 2021, 197, 108111. [Google Scholar] [CrossRef]
- Mohaghegh, S. Virtual-Intelligence Applications in Petroleum Engineering: Part 1—Artificial Neural Networks. J. Pet. Technol. 2000, 52, 64–73. [Google Scholar] [CrossRef]
- Mohaghegh, S. Virtual-Intelligence Applications in Petroleum Engineering: Part 2—Evolutionary Computing. J. Pet. Technol. 2000, 52, 40–46. [Google Scholar] [CrossRef]
- Mohaghegh, S. Virtual-Intelligence Applications in Petroleum Engineering: Part 3—Fuzzy Logic. J. Pet. Technol. 2000, 52, 82–87. [Google Scholar] [CrossRef]
- Lie, K.-A. An Introduction to Reservoir Simulation Using MATLAB/GNU Octave: User Guide for the MATLAB Reservoir Simulation Toolbox (MRST); Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Bahadori, A. Fluid Phase Behavior for Conventional and Unconventional Oil and Gas Reservoirs; Gulf Professional Publishing: Woburn, MA, USA, 2016. [Google Scholar]
- ECLIPSE Reservoir Simulation Software: Reference Manual/Technical Description; Schlumberger: Houston, TX, USA, 2019.
- Raoufi, M.H.; Farasat, A.; Mohammadifard, M. Application of simulated annealing optimization algorithm to optimal operation of intelligent well completions in an offshore oil reservoir. J. Pet. Explor. Prod. Technol. 2015, 5, 327–338. [Google Scholar] [CrossRef][Green Version]
- Elverhøy, A.B.; Aakre, H.; Mathiesen, V. Autonomous Inflow Control for Reduced Water Cut and/or Gas Oil Ratio. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2018. [Google Scholar] [CrossRef]
- Teixeira, A.F.; Secchi, A.R. Machine learning models to support reservoir production optimization. IFAC-PapersOnLine 2019, 52, 498–501. [Google Scholar] [CrossRef]
- Zubarev, D.I. Pros and cons of applying proxy-models as a substitute for full reservoir simulations. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- Tripoppoom, S.; Ma, X.; Yong, R.; Wu, J.; Yu, W.; Sepehrnoori, K.; Miao, J.; Li, N. Assisted History Matching in Shale Gas Well Using Multiple-Proxy-Based Markov Chain Monte Carlo Algorithm: The Comparison of K-Nearest Neighbors and Neural Networks as Proxy Model. Fuel 2020, 262, 116563. [Google Scholar] [CrossRef]
- Wang, J.; Olson, J.E. Auto-Optimization of Hydraulic Fracturing Design with Three-Dimensional Fracture Propagation in Naturally Fractured Multi-Layer Formations. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Virtual, 20–22 July 2020. [Google Scholar] [CrossRef]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef] [PubMed]
- University of Oslo. Sampling Methods. Available online: https://www.uio.no/studier/emner/matnat/math/STK4400/v05/undervisningsmateriale/Sampling%20methods.pdf (accessed on 1 September 2022).
- Monteiro, D.D.; Ferreira-Filho, V.M.; Chaves, G.S.; De Santana, R.S.; Duque, M.M.; Granja-Saavedra, A.L.; Baioco, J.S.; Vieira, B.F.; Teixeira, A.F. Uncertainty analysis for production forecast in oil wells. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 17–19 May 2017. [Google Scholar]
- Geronimo, T.M.; Cruz, C.; Campos, F.D.; Aguiar, R.; Bianchi, E.C. MLP and ANFIS Applied to the Prediction of Hole Diameters in the Drilling Process. Artif. Neural Netw. —Archit. Appl. 2013, 27. [Google Scholar]
- Tendeka. Case Study: FloSure AICD Improves Heavy Oil Cold Production in Western Canada. Available online: https://www.tendeka.com/wp-content/uploads/AICDHeavy-Oil-Canada-update-2019.pdf (accessed on 1 September 2022).
- InflowControl. 68% Water Cut Reduction: 6 AICV® Wells within a Mature Heavy Oil Field. Available online: https://www.nsenergybusiness.com/wpcontent/uploads/sites/3/2020/10/Case-Study-3-AICV%C2%AE-Water-Shutoff_Control_2020_A4.pdf. (accessed on 1 September 2022).
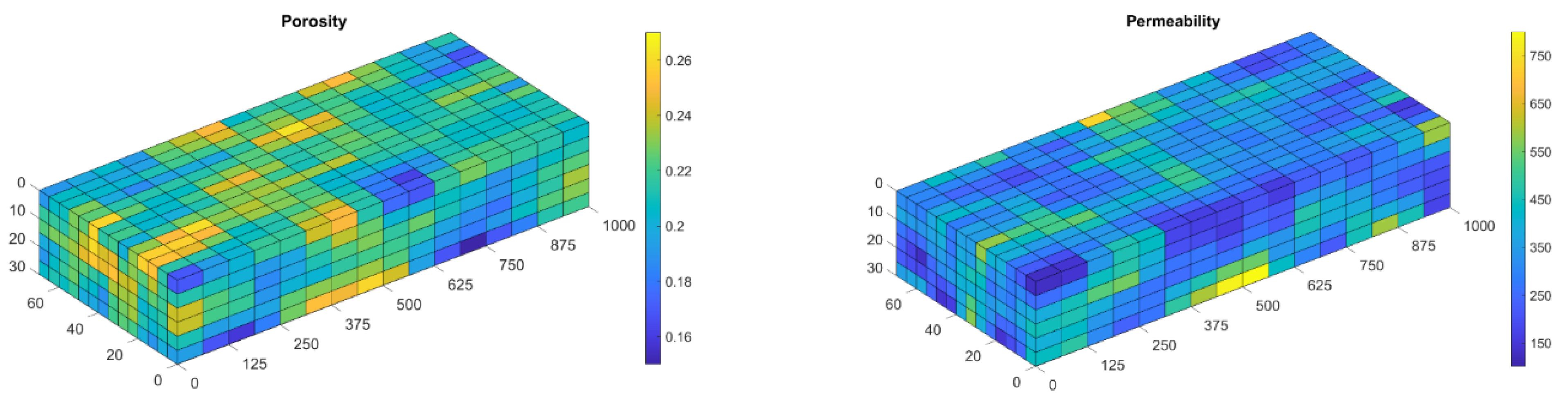




| Parameter | Min | Mean | Max | Unit |
|---|---|---|---|---|
| Porosity | 0.15 | 0.21 | 0.27 | - |
| Absolute permeability | 100 | 350 | 800 | mD |
| Irreducible water saturation | 0.1 | 0.15 | 0.2 | - |
| Residual oil saturation | 0.05 | 0.1 | 0.15 | - |
| Maximum relative permeability of water | 0.2 | 0.4 | 0.5 | - |
| Maximum relative permeability of oil | 0.85 | 0.95 | 1 | - |
| Permeability anisotropy | 0.7 | 0.3 | 0.1 | - |
| Initial water saturation | 0.12 | 0.2 | 0.25 | - |
| Capillary pressure | 2 | 2.7 | 4 | Bar |
| Aquifer productivity index | 2000 | 10,000 | 15,000 | m3/d/bar |
| Parameter | Min. | Mean | Max. |
|---|---|---|---|
| Porosity | 0.15 | 0.21 | 0.27 |
| Initial water saturation | 0.12 | 0.2 | 0.25 |
| Irreducible water saturation | 0.1 | 0.15 | 0.2 |
| Residual oil saturation | 0.05 | 0.1 | 0.15 |
| Maximum relative permeability of water | 0.2 | 0.4 | 0.5 |
| Absolute permeability | 100 | 350 | 800 |
| Case | Mean Error | |
|---|---|---|
| Oil | Water | |
| ICD | 0.96% | 3.79% |
| AICD | 0.48% | 1.98% |
| AICV | 0.46% | 1.98% |
| Case | Production [m3] | Mean | P10 | P50 | P90 | P10/P90 Range |
|---|---|---|---|---|---|---|
| OPENHOLE | Oil | 2.04 × 105 | 1.56 × 105 | 2.01 × 105 | 2.47 × 105 | 9.10 × 104 |
| Water | 1.72 × 106 | 1.24 × 106 | 1.74 × 106 | 2.01 × 106 | 7.70 × 105 | |
| ICD | Oil | 1.97 × 105 | 1.55 × 105 | 1.94 × 105 | 2.38 × 105 | 8.30 × 104 |
| Water | 1.43 × 106 | 1.14 × 106 | 1.42 × 106 | 1.58 × 106 | 4.40 × 105 | |
| AICD | Oil | 1.92 × 105 | 1.54 × 105 | 1.89 × 105 | 2.29 × 105 | 7.50 × 104 |
| Water | 1.06 × 106 | 9.36 × 105 | 1.04 × 106 | 1.10 × 106 | 8.26 × 104 | |
| AICV | Oil | 1.88 × 105 | 1.53 × 105 | 1.83 × 105 | 2.22 × 105 | 6.90 × 104 |
| Water | 5.70 × 105 | 4.98 × 105 | 5.30 × 105 | 5.66 × 105 | 6.80 × 104 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradi, A.; Tavakolifaradonbe, J.; Moldestad, B.M.E. Data-Driven Proxy Models for Improving Advanced Well Completion Design under Uncertainty. Energies 2022, 15, 7484. https://doi.org/10.3390/en15207484
Moradi A, Tavakolifaradonbe J, Moldestad BME. Data-Driven Proxy Models for Improving Advanced Well Completion Design under Uncertainty. Energies. 2022; 15(20):7484. https://doi.org/10.3390/en15207484
Chicago/Turabian StyleMoradi, Ali, Javad Tavakolifaradonbe, and Britt M. E. Moldestad. 2022. "Data-Driven Proxy Models for Improving Advanced Well Completion Design under Uncertainty" Energies 15, no. 20: 7484. https://doi.org/10.3390/en15207484
APA StyleMoradi, A., Tavakolifaradonbe, J., & Moldestad, B. M. E. (2022). Data-Driven Proxy Models for Improving Advanced Well Completion Design under Uncertainty. Energies, 15(20), 7484. https://doi.org/10.3390/en15207484








