Linear and Non-Linear Regression Analysis for the Adsorption Kinetics of SO2 in a Fixed Carbon Bed Reactor—A Case Study
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
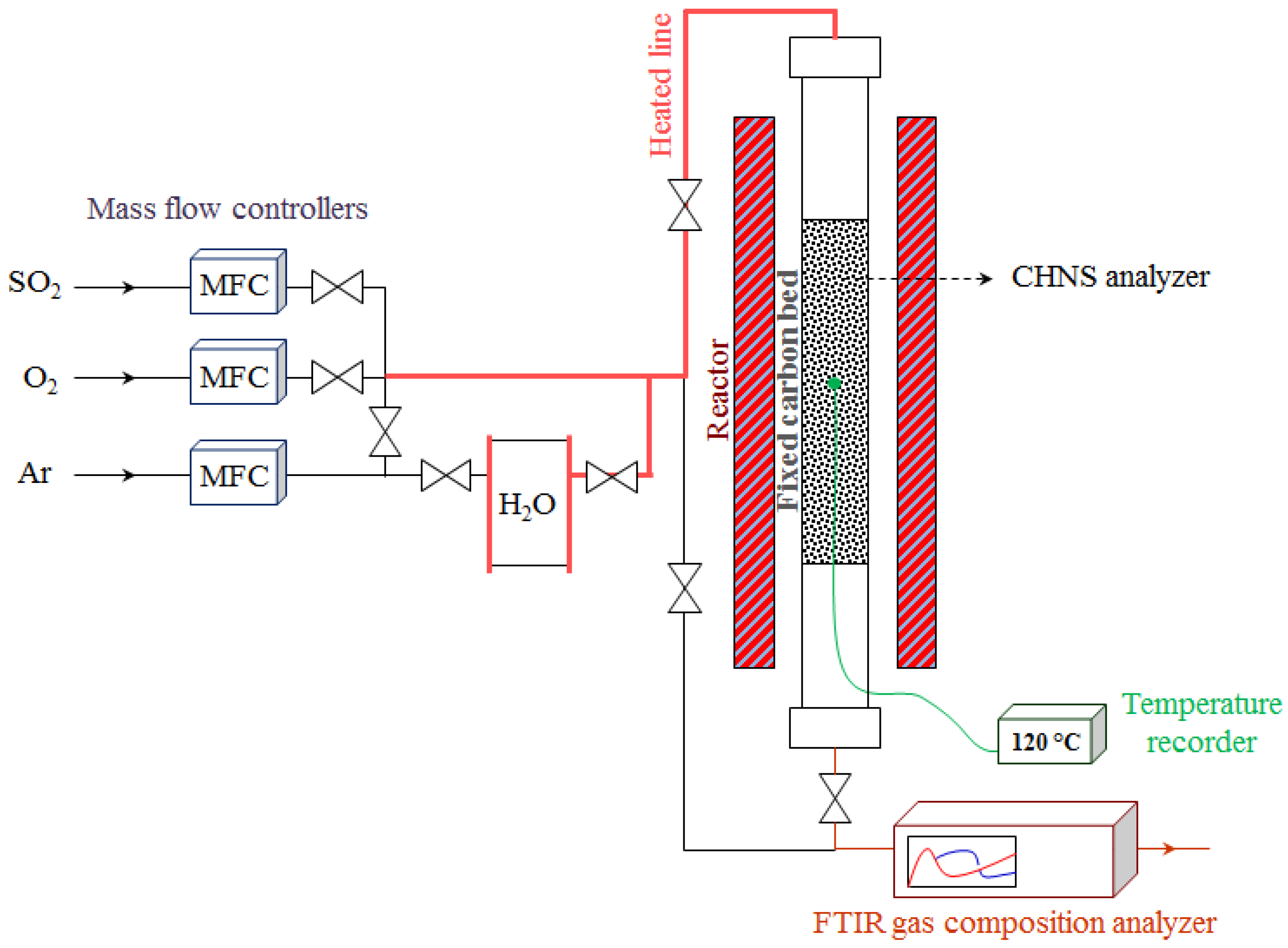
2.2. Experimental Studies
- 5% of sulfur dioxide and 95% of argon (as carrier gas) and a volumetric flow rate of 2 × 10−3 m3∙min−1;
- 2.5% of sulfur dioxide, 11% of water vapor, 20% of oxygen and 66.5% of argon (as carrier gas) and a volumetric flow rate of 2.05 × 10−3 m3∙min−1.
2.3. Modelling Studies
2.3.1. Reaction Kinetics Models
- pseudo first-order kinetic model developed by Legergren,
- pseudo second-order kinetic model developed by Ho i McKaya,
- Weber-Morris intraparticle diffusion model, and
- chemisorption on a heterogeneous surface called the Elovich or Roginski-Zeldowicz model,
Pseudo First-Order Kinetic Model (PFO)
Pseudo Second-Order Kinetic Model (PSO)
Model of Intraparticle Diffusion
Model of Chemisorption on a Heterogeneous Surface
2.3.2. Linear vs. Non-Linear Approach
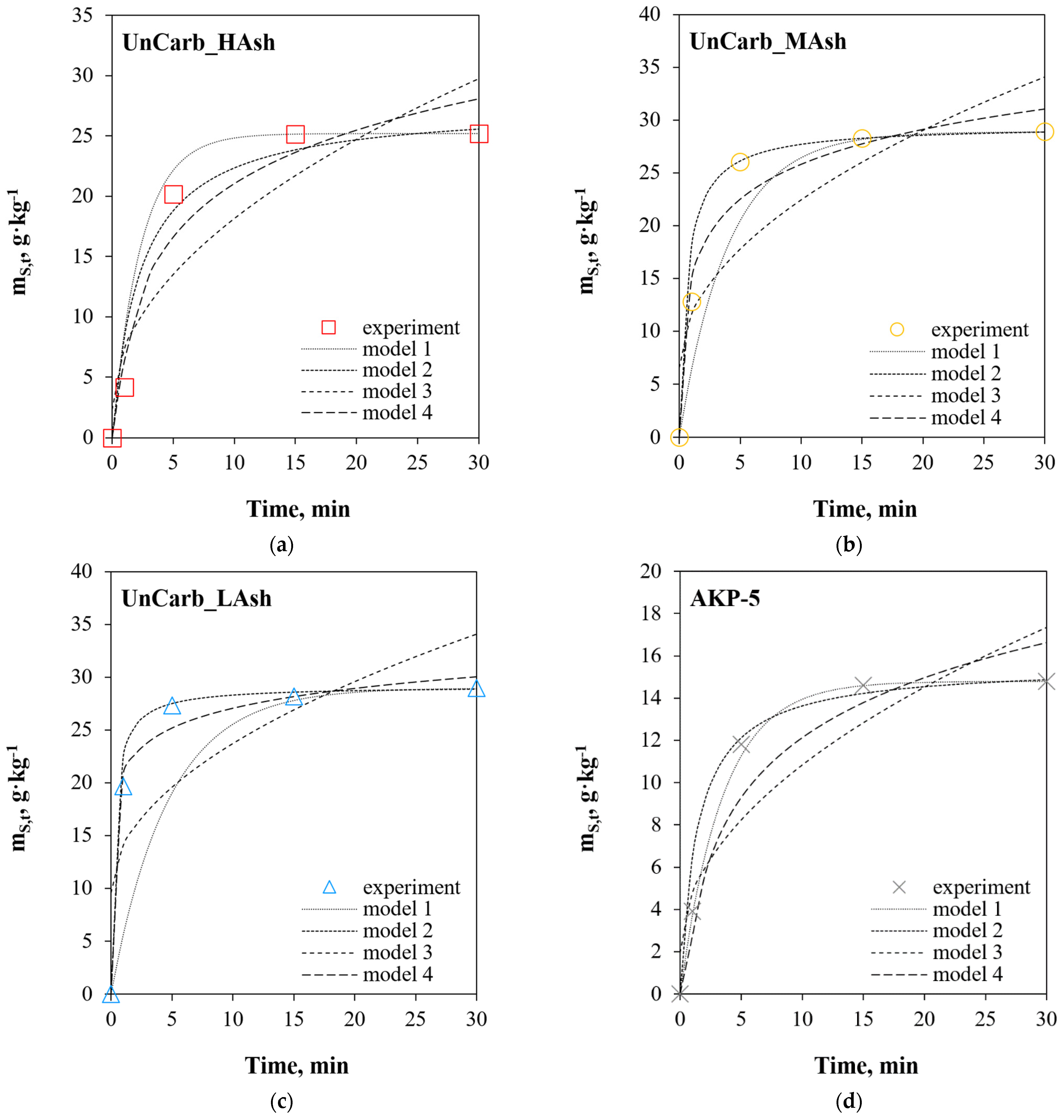
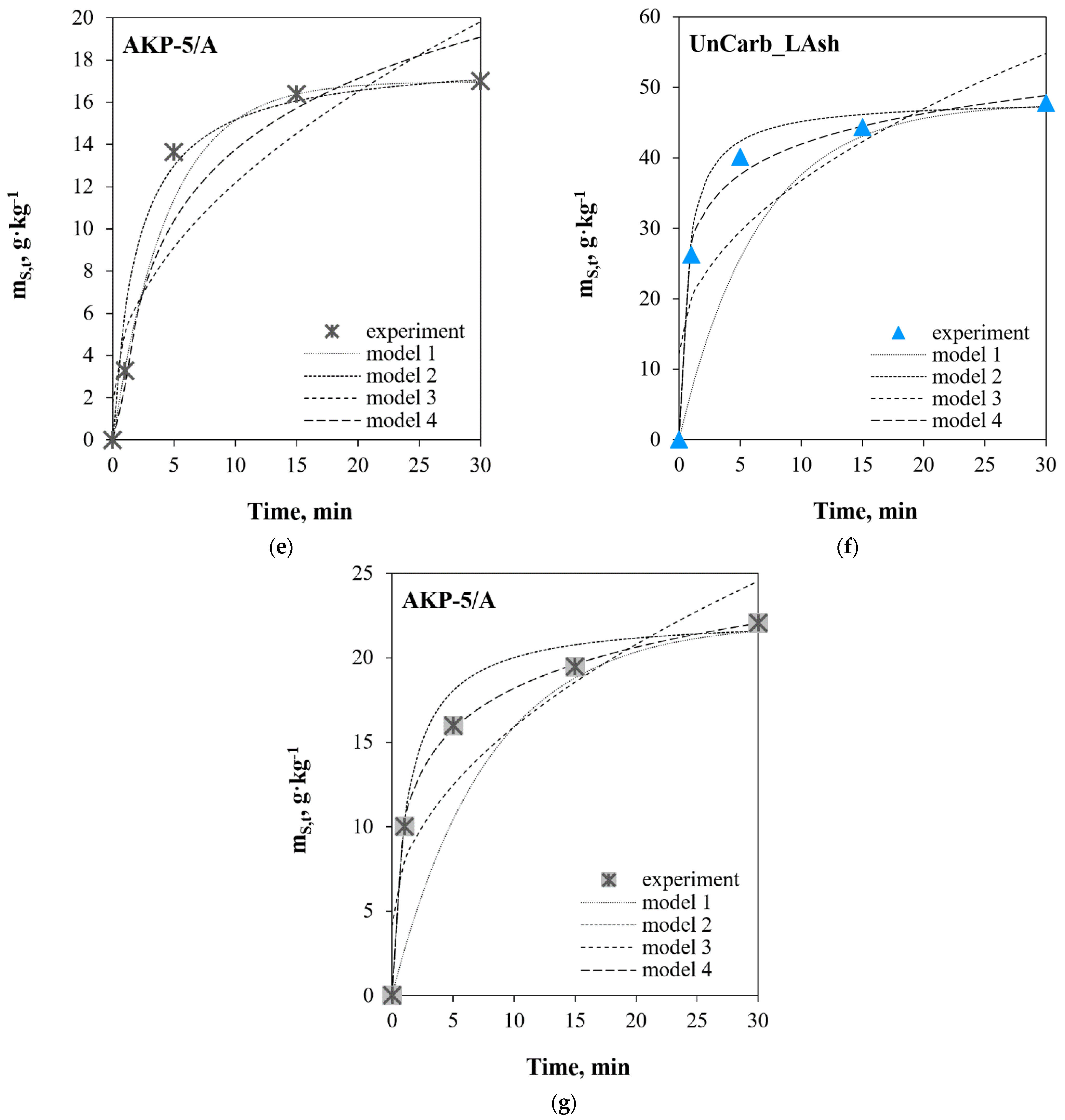
3. Results and Discussion
3.1. Linear Regression
3.2. Non-Linear Regression
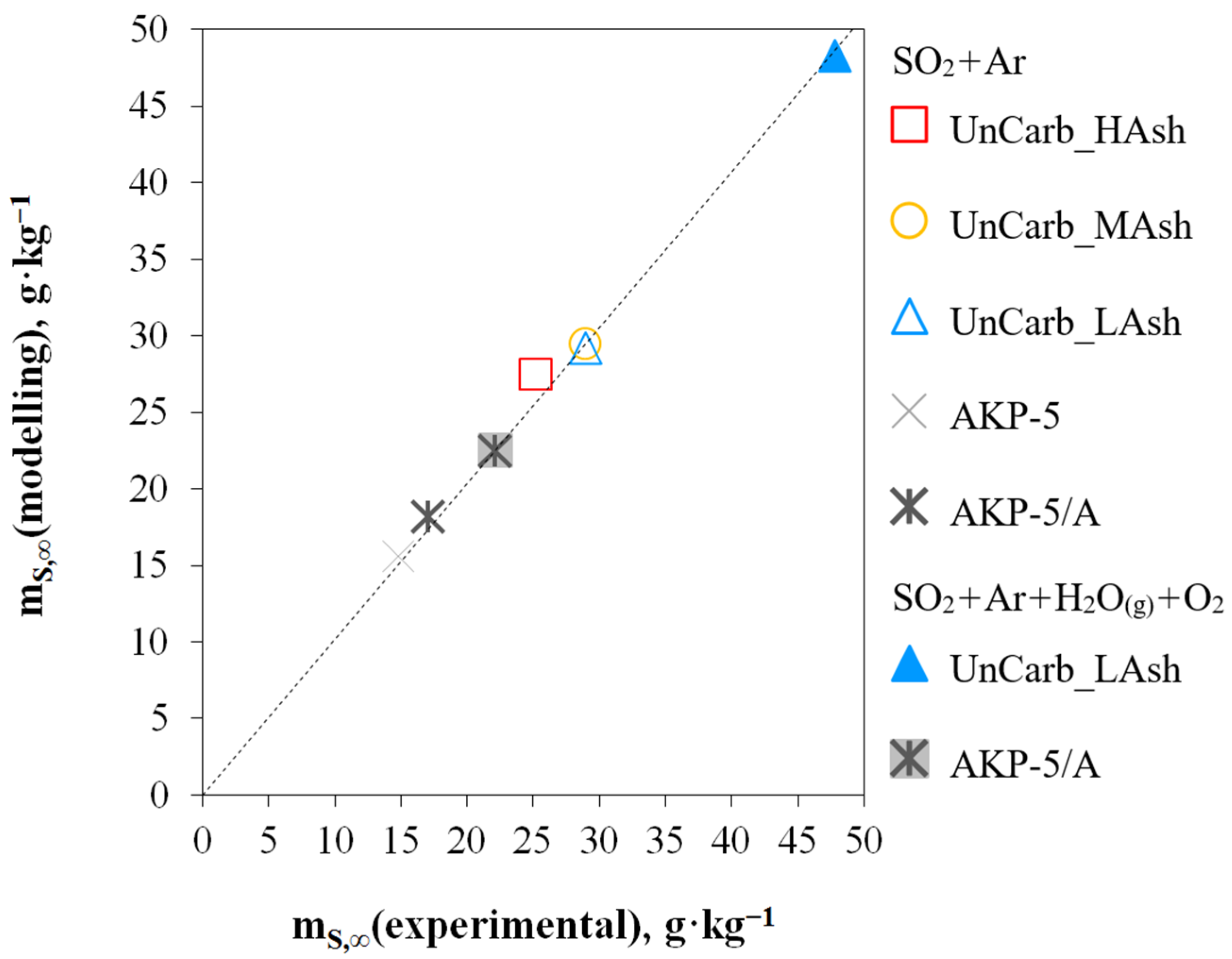
3.3. Comparative Analysis of Linear and Non-Linear Regression
4. Conclusions
- -
- confronting 9 statistical error functions for the models was the most reliable for linear and non-linear regression, respectively, leading to an unequivocal conclusion that it is the linear regression that more accurately reflects the behaviour of the adsorption system (regardless of the process conditions);
- -
- in the case of the SO2+Ar mixture, for commercial samples of activated carbons AKP-5 and AKP-5/A, regardless of the statistical error function, the quality of the results suggests that SO2 adsorption is a first-order kinetic reaction (model 1). However, it should be noted that fitting model data to experimental data for the systems close to the equilibrium state can only result from the mathematical foundations of model 1;
- -
- in the case of unburned carbons samples (UnCarb_HAsh, UnCarb_MAsh, UnCarb_LAsh), regardless of the process conditions, and the AKP-5/A (SO2 + Ar + H2O(g) + O2) sample, the quality of the results shows that the adsorption is compatible with the kinetic mechanism of chemisorption on the heterogeneous surface (according to model 4);
- -
- the sum of normalized errors, regardless of the tested sample and process conditions, reaches the lowest values for models 1 and 2 by minimizing the hybrid fractional error function (HYBRID), and for models 3 and 4 by the Marquardt’s percentage standard deviation (MPSD);
- -
- minimization of the determination coefficient (R2) and correlation (R) leads to high SNE values. Fitting data by any of the non-linear equations based on the R or R2 functions only cannot be treated as evidence or a prerequisite of the existence of a given mechanism determining the kinetics or dynamics of adsorption in a given system.
- -
- only in 1 case (UnCarb_MAsh) out of 7 possible, both linear and non-linear regression indicate the same mechanism of the adsorption phenomenon—identical to chemisorption on a heterogeneous surface (according to model 4).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Institute of Environmental Protection—The National Centre for Emissions Management (KOBiZE). National Emission Balance of SO2, NOx, CO, NH3, NMVOC, Dust, Heavy Metals and POPs in the SNAP and NFR Classification System. Warsaw, 2015. Available online: https://www.kobize.pl/uploads/materialy/materialy_do_pobrania/krajowa_inwentaryzacja_emisji/Bilans_emisji_za_2017.pdf (accessed on 7 July 2021).
- Lecomte, T.; de la Fuente, J.F.F.; Neuwahl, F.; Canova, M.; Pinasseau, A.; Jankov, I.; Brinkmann, T.; Roudier, S.; Sancho, L.D. Best Available Techniques (BAT) Reference Document for Large Combustion Plants; EUR 28836 EN; Publications Office of the European Union: Luxembourg, 2017. [Google Scholar]
- Common Format for a National Air Pollution Control Program under Art. 6 of Directive (EU) 2016/2284. Available online: https://ec.europa.eu/environment/air/pdf/reduction_napcp/PL%20final%20NAPCP%2027Jun19%20annexed%20report.pdf (accessed on 14 July 2021).
- Bartonova, L. Unburned carbon from coal combustion ash: An overview. Fuel Process. Technol. 2015, 134, 136–158. [Google Scholar] [CrossRef]
- Hower, J.C.; Groppo, J.G.; Graham, U.M.; Ward, C.R.; Kostova, I.J.; Maroto-Valer, M.M.; Dai, S. Coal-derived unburned carbons in fly ash: A review. Int. J. Coal Geol. 2017, 179, 11–27. [Google Scholar] [CrossRef]
- Musyoka, N.M.; Wdowin, M.; Rambau, K.M.; Franus, W.; Panek, R.; Madej, J.; Czarna-Juszkiewicz, D. Synthesis of activated carbon from high-carbon coal fly ash and its hydrogen storage application. Renew. Energy 2020, 155, 1264–1271. [Google Scholar] [CrossRef]
- Kisiela-Czajka, A.M.; Hull, S.; Albiniak, A. Investigation of the activity of unburned carbon as a catalyst in the decomposition of NO and NH3. Fuel 2022, 309, 122170. [Google Scholar] [CrossRef]
- Kisiela, A.M.; Czajka, K.M.; Moroń, W.; Rybak, W.; Andryjowicz, C. Unburned carbon from lignite fly ash as an adsorbent for SO2 removal. Energy 2016, 116, 1454–1463. [Google Scholar] [CrossRef]
- Rubio, B.; Izquierdo, M.T.; Mayoral, M.C.; Bona, M.T.; Andres, J.M. Unburnt carbon from coal fly ashes as a precursor of activated carbon for nitric oxide removal. J. Hazard. Mater. 2007, 143, 561–566. [Google Scholar] [CrossRef] [Green Version]
- Bansal, R.C.; Goyal, M. Activated Carbon Adsorption; CRC Press: Boca Raton FL, USA, 2005. [Google Scholar]
- Roy, P.; Sardar, A. SO2 emission control and finding a way to produce sulphuric acid from industrial SO2 emission. J. Chem. Eng. Process Technol. 2015, 6, 1000230. [Google Scholar] [CrossRef] [Green Version]
- Moroń, W.; Ferens, W.; Czajka, K.M. Explosion of different ranks coal dust in oxy-fuel atmosphere. Fuel Process. Technol. 2016, 148, 388–394. [Google Scholar] [CrossRef]
- Wang, J.; Yi, H.; Tang, X.; Zhao, S.; Gao, F. Simultaneous removal of SO2 and NOx by catalytic adsorption using γ-Al2O3 under the irradiation of non-thermal plasma: Competitiveness, kinetic, and equilibrium. Chem. Eng. J. 2020, 384, 123334. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Q.; Ma, C. Adsorption kinetics of SO2 on powder activated carbon. IOP Conf. Ser. Earth Environ. Sci. 2018, 121, 022019. [Google Scholar] [CrossRef]
- Zhangm, S.; Li, Z.; Yang, Y.; Jian, W.; Ma, D.; Jia, F. Kinetics and thermodynamics of SO2 adsorption on metal-loaded multiwalled carbon nanotubes. Open Phys. 2020, 18, 1201–1214. [Google Scholar] [CrossRef]
- Wang, H.; Duan, Y.; Ying, Z.; Xue, Y. Effects of SO2 on Hg adsorption by activated carbon in O2/CO2 conditions. Part 1: Experimental and kinetic study. Energy Fuels 2018, 32, 10773–10778. [Google Scholar] [CrossRef]
- Silalahi, D.D.; Midi, H.; Arasan, J.; Mustafa, M.S.; Caliman, J.-P. Kernel partial least square regression with high resistance to multiple outliers and bad leverage points on near-infrared spectral data analysis. Symmetry 2021, 13, 547. [Google Scholar] [CrossRef]
- Fehintola, E.O.; Amoko, J.S.; Obijole, O.A.; Oke, I.A. Pseudo second order kinetics model of adsorption of Pb2+ onto powdered corn cobs: Comparison of linear regression methods. Direct Res. J. Chem. Mater. Sci. 2015, 3, 1–10. [Google Scholar]
- Adnan, F.; Thanasupsin, S.P. Kinetic studies using a linear regression analysis for a sorption phenomenon of 17a-methyltestosterone by Salvinia cucullata in an active plant reactor. Environ. Eng. Res. 2016, 21, 384–392. [Google Scholar] [CrossRef] [Green Version]
- Moroń, W.; Czajka, K.M.; Ferens, W.; Babul, K.; Szydełko, A.; Rybak, W. NOx and SO2 emission during oxy-coal combustion. Chem. Process Eng. 2013, 34, 337–346. [Google Scholar] [CrossRef] [Green Version]
- Pilatau, A.; Czajka, K.M.; Filho, G.P.; Medeiros, H.S.; Kisiela, A.M. Evaluation criteria for the assessment of the influence of additives (AlCl3 and ZnCl2) on pyrolysis of sunflower oil cake. Waste Biomass Valorization 2017, 8, 2595–2607. [Google Scholar] [CrossRef]
- Hanna, O.T.; Sandall, O.C. Computational Methods in Chemical Engineering; Prentice Hall International Series in the Physical and Chemical Engineering Sciences; Prentice Hall: Hoboken, NJ, USA, 1995. [Google Scholar]
- Ngakou, C.S.; Anagho, G.S.; Ngomo, H.M. Non-linear regression analysis for the adsorption kinetics and equilibrium isotherm of phenacetin onto activated carbons. Curr. J. Appl. Sci. Technol. 2019, 36, 1–18. [Google Scholar] [CrossRef]
- Lin, J.; Wang, L. Comparison between linear and non-linear forms of pseudo-first-order and pseudo-second-order adsorption kinetic models for the removal of methylene blue by activated carbon. Front. Environ. Sci. Eng. 2009, 3, 320–324. [Google Scholar] [CrossRef]
- Kumar, K.V. Comparative analysis of linear and non-linear method of estimating the sorption isotherm parameters for malachite green onto activated carbon. J. Hazard. Mater. 2006, 136, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Lataye, D.H.; Mishra, I.M.; Mall, I.D. Adsorption of 2-picoline onto bagasse fly ash from aqueous solution. Chem. Eng. J. 2008, 138, 35–46. [Google Scholar] [CrossRef]
- Kumar, K.V.; Porkodi, K.; Rocha, F. Isotherms and thermodynamics by linear and non-linear regression analysis for the sorption of methylene blue onto activated carbon: Comparison of various error functions. J. Hazard. Mater. 2008, 151, 794–804. [Google Scholar] [CrossRef] [PubMed]
- Edgar, T.F.; Himmelblau, D.M. Optimization of Chemical Processes; McGraw-Hill College: New York, NY, USA, 1988. [Google Scholar]
- Rybak, W.; Moroń, W.; Czajka, K.M.; Kisiela, A.M.; Ferens, W.; Jodkowski, W.; Andryjowicz, C. Co-combustion of unburned carbon separated from lignite fly ash. Energy Procedia 2017, 120, 197–205. [Google Scholar] [CrossRef]
- Kisiela-Czajka, A.M. Adsorption behaviour of SO2 molecules on unburned carbon from lignite fly ash in the context of developing commercially applicable environmental carbon adsorbent. Preprint (SSRN/Elsevier). [CrossRef]
- Lagergren, S. About the theory of so-called adsorption of soluble substances. K. Sven. Vetensk. Akad. Handl. 1989, 241, 1–39. [Google Scholar]
- Ho, Y.S.; McKay, G. Pseudo-second order model for sorption processes. Process Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Weber, W.J.; Morris, J.C. Kinetics of adsorption on carbon from solutions. J. Sanit. Eng. Div. 1963, 89, 31–60. [Google Scholar] [CrossRef]
- Low, M.D. Kinetics of chemisorption of gases on solids. Chem. Rev. 1960, 60, 267–312. [Google Scholar] [CrossRef]
- Shafiq, M.; Alazba, A.A.; Amin, M.T. Kinetic and isotherm studies of Ni2+ and Pb2+ adsorption from synthetic wastewater using Eucalyptus camdulensis–derived biochar. Sustainability 2021, 13, 3785. [Google Scholar] [CrossRef]
- Ghaffari, H.R.; Pasalari, H.; Tajvar, A.; Dindarloo, K.; Goudarzi, B.; Alipour, V.; Ghanbarneajd, A. Linear and non-linear two-parameter adsorption isotherm modeling: A case-study. Int. J. Eng. Sci. 2017, 6, 1–11. [Google Scholar] [CrossRef]
- Sivarajasekar, N.; Baskar, R. Adsorption of basic magenta II onto H2SO4 activated immature Gossypium hirsutum seeds: Kinetics, isotherms, mass transfer, thermodynamics and process design. Arab. J. Chem. 2019, 12, 1322–1337. [Google Scholar] [CrossRef] [Green Version]
- Ho, Y.S.; Porter, J.F.; McKay, G. Equilibrium isotherm studies for the sorption of divalent metal ions onto peat: Copper, nickel and lead single component systems. Water Air Soil Pollut. 2002, 141, 1–33. [Google Scholar] [CrossRef]
- Anirudhan, T.S.; Radhakrishnan, P.G. Kinetic and equilibrium modelling of Cadmium (II) ions sorption onto polymerized tamarind fruit shell. Desalination 2009, 249, 1298–1307. [Google Scholar] [CrossRef]
- Soco, E.; Kalembkiewicz, J. Effect of chemical modification of the coal fly ash onto adsorption of lead (II) ions in the presence of cadmium (II) ions in a single- and bi-component system. Eng. Prot. Environ. 2016, 19, 81–95. [Google Scholar] [CrossRef]
- Płaziński, W.; Rudziński, W.; Płazińska, A. Theoretical models of sorption kinetics including a surface mechanism: A review. Adv. Colloid Interface Sci. 2009, 152, 2–13. [Google Scholar] [CrossRef]
- Płaziński, W.; Rudziński, W. Adsorption kinetics at solid/solution interfaces. The meaning of the pseudo-first and pseudo-second-order equations. Wiadomości Chem. 2011, 65, 1055–1067. [Google Scholar]
- Czajka, K.M.; Modliński, N.; Kisiela-Czajka, A.M.; Naidoo, R.; Peta, S.; Nyangwa, B. Volatile matter release from coal at different heating rates—Experimental study and kinetic modeling. J. Anal. Appl. Pyrolysis 2019, 139, 282–290. [Google Scholar] [CrossRef]
- Moore, D.S.; Notz, W.I.; Flinger, M.A. The Basic Practise of Statistics, 3rd ed.; W. H. Freeman and Company: New York, NY, USA, 2013. [Google Scholar]
- Hashem, A.; Badawy, S.M.; Farag, S.; Mohamed, L.A.; Fletcher, A.J.; Taha, G.M. Non-linear adsorption characteristics of modified pine wood sawdust optimized for adsorption of Cd(II) from aqueous systems. J. Environ. Chem. Eng. 2020, 8, 103966. [Google Scholar] [CrossRef]
- Saravanan, A.; Karishma, S.; Jeevanantham, S.; Jeyarsi, S.; Kiruthika, A.R.; Senthil Kumar, P.; Yaashikaa, P.R. Optimization and modeling of reactive yellow adsorption by surface modified Delonix regia seed: Study on nonlinear isotherm and kinetic parameters. Surf. Interfaces 2020, 20, 100520. [Google Scholar] [CrossRef]
- Mohammed, N.A.S.; Abu-Zurayk, R.A.; Hamadneh, I.; Al-Dujaili, A.H. Phenol adsorption on biochar prepared from the pine fruit shells: Equilibrium, kinetic and thermodynamics studies. J. Environ. Manag. 2018, 226, 377–385. [Google Scholar] [CrossRef]
- Módenes, A.N.; Scheufele, F.B.; Espinoza-Quiñones, F.R.; de Souza, P.S.C.; Cripa, C.R.B.; dos Santos, J.; Steffen, V.; Kroumov, A.D. Adsorption of direct of yellow ARLE dye by activated carbon of shell of coconut palm: Diffusional effects on kinetics and equilibrium states. Int. J. Bioautom. 2015, 19, 187–206. [Google Scholar]


| Function | Equation | |
|---|---|---|
| Determination coefficient (R2) | (12) | |
| Correlation coefficient (R) | (13) | |
| Relative standard deviation (Δq) | (14) | |
| Sum of squared deviations (SSE) | (15) | |
| Average Relative Error (ARE) | (16) | |
| Chi-square test (χ2) | (17) | |
| Hybrid fractional error function (HYBRID) | (18) | |
| Marquardt’s percent standard deviation (MPSD) | (19) | |
| Sum of absolute errors (EABS) | (20) |
| Sample | Model 1 | Model 2 | Model 3 | Model 4 | |||
|---|---|---|---|---|---|---|---|
| k1 | k2 | mS,∞ | kid | C | α | β | |
| min−1 | kg·g−1·min−1 | g·kg−1 | g·kg−1·min−0.5 | g·kg−1 | g·kg−1min−1 | kg·g−1 | |
| SO2 + Ar | |||||||
| UnCarb_HAsh | 0.423 | 0.0156 | 27.5 | 5.01 | 2.33 | 17.2 | 0.156 |
| UnCarb_MAsh | 0.247 | 0.0527 | 29.5 | 5.03 | 6.56 | 107 | 0.210 |
| UnCarb_LAsh | 0.214 | 0.114 | 29.2 | 4.47 | 9.56 | 5917 | 0.370 |
| AKP-5 | 0.286 | 0.0449 | 15.6 | 2.81 | 1.94 | 7.92 | 0.244 |
| AKP-5/A | 0.222 | 0.0273 | 18.2 | 3.30 | 1.76 | 8.24 | 0.206 |
| SO2 + O2 + H2O(g) + Ar | |||||||
| UnCarb_LAsh | 0.155 | 0.0293 | 48.3 | 7.77 | 12.1 | 515 | 0.160 |
| AKP-5/A | 0.123 | 0.0363 | 22.5 | 3.73 | 4.13 | 62.6 | 0.285 |
| Sample | R2 | R | Δq | SSE | ARE | χ2 | HYBRID | MPSD | EABS |
|---|---|---|---|---|---|---|---|---|---|
| Model 1 1 | |||||||||
| UnCarb_HAsh | 0.955 | 0.977 | 54.9 | 24.6 | 23.9 | 5.16 | 172 | 63.4 | 6.55 |
| UnCarb_MAsh | 0.906 | 0.952 | 27.6 | 73.6 | 14.5 | 4.51 | 150 | 31.8 | 12.2 |
| UnCarb_LAsh | 0.745 | 0.863 | 38.9 | 268 | 20.8 | 12.6 | 421 | 45.0 | 22.9 |
| AKP-5 | 0.998 | 0.999 | 3.72 | 0.346 | 2.10 | 0.0383 | 1.28 | 4.29 | 0.776 |
| AKP-5/A | 0.979 | 0.989 | 8.39 | 5.05 | 3.98 | 0.373 | 12.4 | 9.68 | 2.38 |
| Model 2 1 | |||||||||
| UnCarb_HAsh | 0.958 | 0.979 | 49.9 | 20.7 | 22.6 | 4.27 | 142 | 57.6 | 7.15 |
| UnCarb_MAsh | 0.958 | 0.979 | 19.9 | 26.2 | 8.06 | 2.04 | 67.9 | 23.0 | 5.23 |
| UnCarb_LAsh | 0.987 | 0.994 | 7.04 | 7.77 | 3.28 | 0.392 | 13.1 | 8.13 | 3.42 |
| AKP-5 | 0.961 | 0.980 | 31.1 | 6.52 | 14.0 | 1.62 | 54.1 | 37.0 | 3.27 |
| AKP-5/A | 0.962 | 0.981 | 42.4 | 8.24 | 18.4 | 2.38 | 79.5 | 48.9 | 3.84 |
| Model 3 1 | |||||||||
| UnCarb_HAsh | 0.840 | 0.917 | 43.2 | 92.0 | 28.3 | 5.91 | 197 | 49.9 | 20.1 |
| UnCarb_MAsh | 0.771 | 0.878 | 19.3 | 144.8 | 13.5 | 3.85 | 128 | 22.2 | 23.5 |
| UnCarb_LAsh | 0.647 | 0.804 | 22.1 | 211 | 15.9 | 4.77 | 159 | 25.5 | 29.4 |
| AKP-5 | 0.851 | 0.922 | 21.3 | 26.8 | 16.2 | 1.91 | 63.8 | 24.6 | 10.7 |
| AKP-5/A | 0.847 | 0.920 | 33.3 | 38.1 | 23.1 | 3.14 | 105 | 38.5 | 12.7 |
| Model 4 1 | |||||||||
| UnCarb_HAsh | 0.952 | 0.976 | 28.3 | 27.8 | 17.4 | 2.17 | 72.5 | 32.7 | 10.1 |
| UnCarb_MAsh | 0.966 | 0.983 | 11.0 | 21.5 | 7.70 | 0.961 | 32.0 | 12.7 | 8.24 |
| UnCarb_LAsh | 0.988 | 0.994 | 5.20 | 6.99 | 3.50 | 0.272 | 9.07 | 6.01 | 4.40 |
| AKP-5 | 0.945 | 0.972 | 20.0 | 11.8 | 14.0 | 1.18 | 39.3 | 23.1 | 6.36 |
| AKP-5/A | 0.944 | 0.972 | 17.4 | 16.0 | 12.4 | 1.22 | 40.6 | 20.1 | 6.74 |
| Model 1 2 | |||||||||
| UnCarb_LAsh | 0.776 | 0.881 | 41.1 | 587.4 | 22.7 | 19.6 | 653 | 47.5 | 35.6 |
| AKP-5/A | 0.824 | 0.908 | 40.8 | 86.3 | 22.8 | 7.42 | 247 | 47.1 | 14.1 |
| Model 2 2 | |||||||||
| UnCarb_LAsh | 0.992 | 0.996 | 5.17 | 12.4 | 3.69 | 0.355 | 11.8 | 5.97 | 6.59 |
| AKP-5/A | 0.982 | 0.991 | 7.33 | 6.14 | 4.46 | 0.361 | 12.0 | 8.46 | 3.90 |
| Model 3 2 | |||||||||
| UnCarb_LAsh | 0.978 | 0.876 | 19.5 | 354 | 14.0 | 5.48 | 183 | 22.6 | 38.2 |
| AKP-5/A | 0.867 | 0.931 | 16.6 | 41.1 | 11.9 | 1.57 | 52.3 | 19.2 | 13.2 |
| Model 4 2 | |||||||||
| UnCarb_LAsh | 0.994 | 0.997 | 4.14 | 9.15 | 2.75 | 0.245 | 8.17 | 4.78 | 5.03 |
| AKP-5/A | 1.00 | 1.00 | 0.898 | 0.0787 | 0.614 | 0.00494 | 0.165 | 1.04 | 0.471 |
| Sample | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| SO2 + Ar | ||||
| UnCarb_HAsh | HYBRID | HYBRID | EABS | χ2 |
| 5.40 | 4.84 | 4.39 | 5.06 | |
| UnCarb_MAsh | SSE | χ2 | χ2 | Δq |
| 8.16 | 7.13 | 5.37 | 5.00 | |
| UnCarb_LAsh | R2 | EABS | MPSD | EABS |
| 8.97 | 8.43 | 3.16 | 5.59 | |
| AKP-5 | HYBRID | HYBRID | EABS | HYBRID |
| 6.08 | 6.28 | 6.94 | 5.60 | |
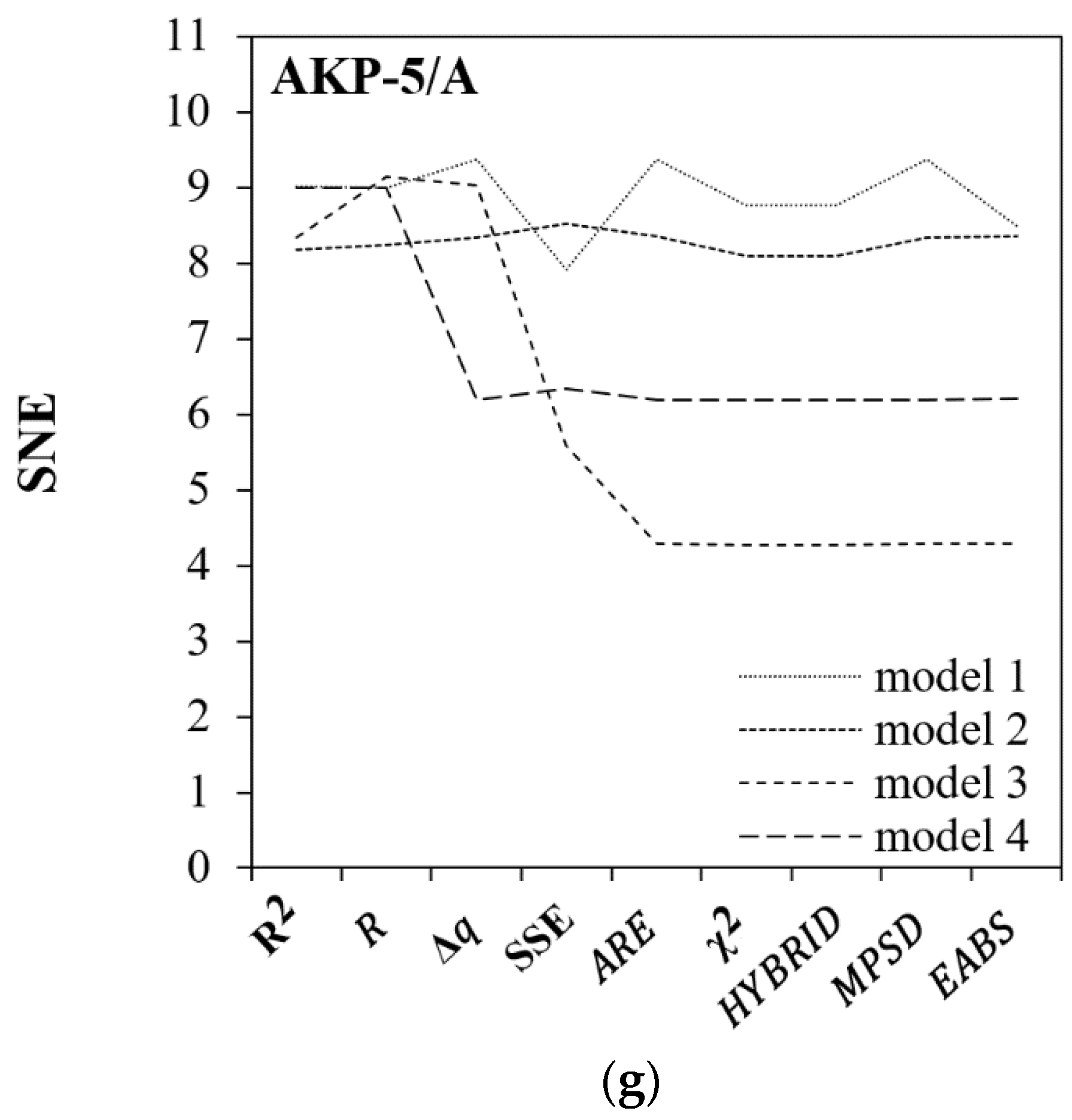
| AKP-5/A | HYBRID | χ2 | χ2 | MPSD |
| 5.42 | 4.97 | 6.77 | 4.84 | |
| SO2 + Ar + H2O(g) + O2 | ||||
| UnCarb_LAsh | SSE | R | χ2 | EABS |
| 8.92 | 7.55 | 4.04 | 5.52 | |
| AKP-5/A | SSE | χ2 | χ2 | χ2 |
| 7.91 | 8.09 | 4.27 | 6.18 | |
| Sample | Model 1 | Model 2 | Model 3 | Model 4 | |||
|---|---|---|---|---|---|---|---|
| k1 | k2 | mS,∞ | kid | C | α | β | |
| min−1 | kg·g−1·min−1 | g·kg−1 | g·kg−1·min−0.5 | g·kg−1 | g·kg−1min−1 | kg·g−1 | |
| SO2 + Ar | |||||||
| UnCarb_HAsh | 0.224 | 6.57E-03 | 31.8 | 4.59 | 0 | 13.6 | 0.123 |
| UnCarb_MAsh | 0.581 | 2.41E-02 | 31.0 | 5.38 | 7.48 | 54.4 | 0.175 |
| UnCarb_LAsh | 1.19 | 6.85E-02 | 29.4 | 1.97 | 18.2 | 3955 | 0.353 |
| AKP-5 | 0.312 | 1.97E-02 | 17.1 | 3.45 | 0.460 | 11.8 | 0.280 |
| AKP-5/A | 0.252 | 1.19E-02 | 20.6 | 3.52 | 0.775 | 9.44 | 0.213 |
| SO2 + O2 + H2O(g) + Ar | |||||||
| UnCarb_LAsh | 0.865 | 2.59E-02 | 47.5 | 4.80 | 24.3 | 390 | 0.153 |
| AKP-5/A | 0.578 | 3.71E-02 | 21.5 | 2.74 | 8.17 | 61.7 | 0.284 |
| Model | R2 | R | Δq | SSE | ARE | χ2 | HYBRID | MPSD | EABS |
|---|---|---|---|---|---|---|---|---|---|
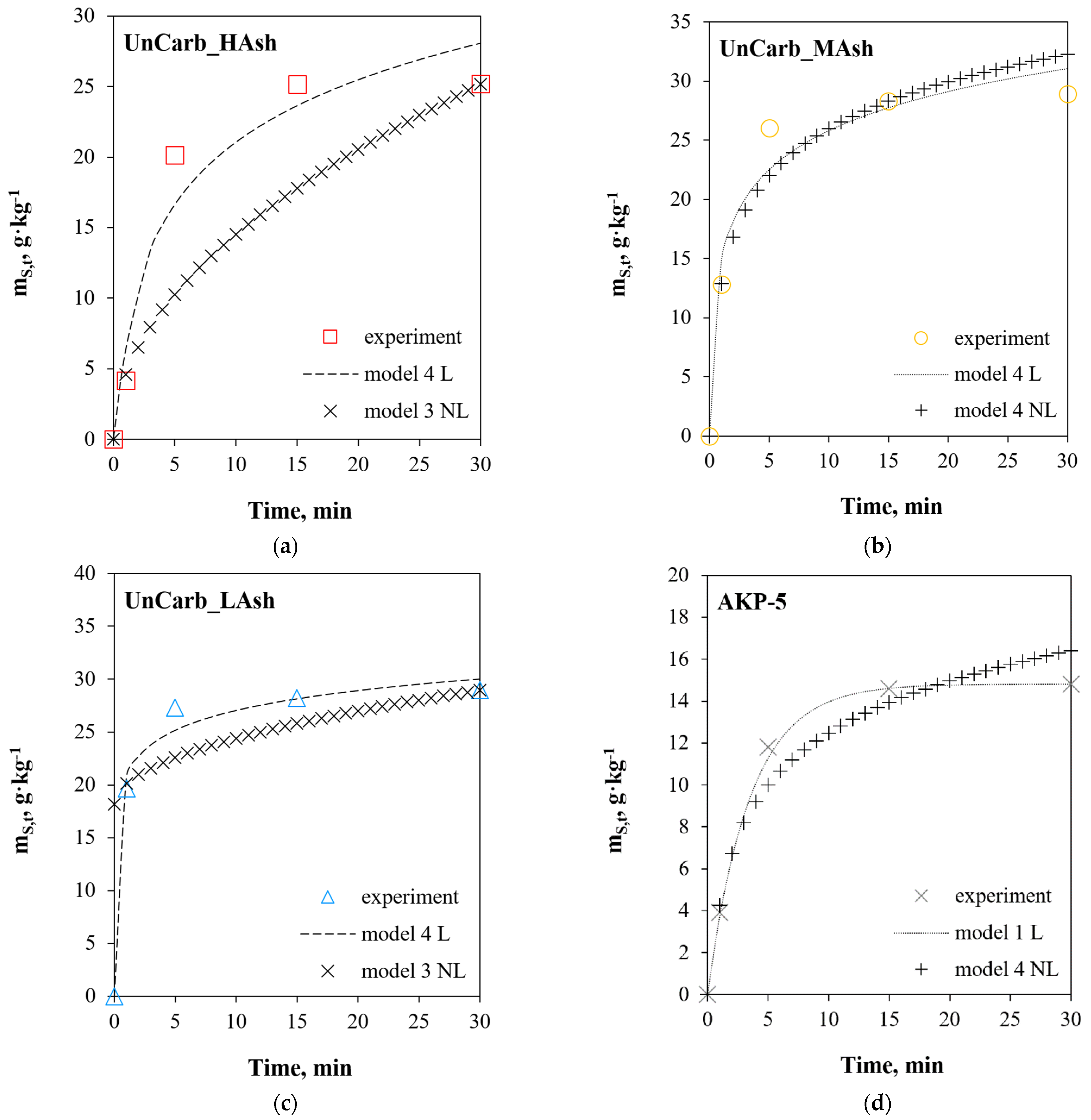
| UnCarb_HAsh 1 | |||||||||
| Model 4 L | 0.952 | 0.976 | 28.3 | 27.8 | 17.4 | 2.2 | 72.5 | 32.7 | 10.1 |
| Model 3 NL | 0.752 | 0.867 | 29.1 | 152.9 | 17.8 | 7.1 | 235.9 | 33.6 | 17.7 |
| UnCarb_Mash 1 | |||||||||
| Model 4L | 0.966 | 0.983 | 11.0 | 21.5 | 7.7 | 0.96 | 32.0 | 12.7 | 8.24 |
| Model 4NL | 0.961 | 0.980 | 9.6 | 27.4 | 5.4 | 1.01 | 33.6 | 11.1 | 7.4 |
| UnCarb_Lash 1 | |||||||||
| Model 4L | 0.988 | 0.994 | 5.2 | 7.0 | 3.5 | 0.3 | 9.1 | 6.0 | 4.4 |
| Model 3NL | 0.220 | 0.469 | 9.7 | 358.9 | 5.7 | 1.0 | 34.4 | 11.2 | 25.8 |
| AKP-5 1 | |||||||||
| Model 1L | 0.998 | 0.999 | 3.7 | 0.3 | 2.1 | 0.04 | 1.3 | 4.3 | 0.8 |
| Model 4NL | 0.967 | 0.983 | 10.6 | 6.4 | 7.9 | 0.5 | 17.0 | 12.2 | 4.4 |
| AKP-5/A 1 | |||||||||
| Model 1L | 0.979 | 0.989 | 8.4 | 5.1 | 4.0 | 0.4 | 12.4 | 9.7 | 2.4 |
| Model 4NL | 0.953 | 0.976 | 12.3 | 13.1 | 7.3 | 0.9 | 29.6 | 14.2 | 5.5 |
| UnCarb_Lash 2 | |||||||||
| Model 4L | 0.994 | 0.997 | 4.1 | 9.2 | 2.8 | 0.2 | 8.2 | 4.8 | 5.0 |
| Model 3 NL | 0.465 | 0.682 | 9.0 | 633.3 | 6.5 | 1.2 | 38.9 | 10.4 | 36.5 |
| AKP-5/A 2 | |||||||||
| Model 4L | 1.00 | 1.00 | 0.9 | 0.08 | 0.6 | 0.005 | 0.2 | 1.0 | 0.5 |
| Model 3NL | 0.686 | 0.828 | 7.5 | 72.1 | 5.6 | 0.3 | 11.2 | 8.7 | 12.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kisiela-Czajka, A.M.; Dziejarski, B. Linear and Non-Linear Regression Analysis for the Adsorption Kinetics of SO2 in a Fixed Carbon Bed Reactor—A Case Study. Energies 2022, 15, 633. https://doi.org/10.3390/en15020633
Kisiela-Czajka AM, Dziejarski B. Linear and Non-Linear Regression Analysis for the Adsorption Kinetics of SO2 in a Fixed Carbon Bed Reactor—A Case Study. Energies. 2022; 15(2):633. https://doi.org/10.3390/en15020633
Chicago/Turabian StyleKisiela-Czajka, Anna M., and Bartosz Dziejarski. 2022. "Linear and Non-Linear Regression Analysis for the Adsorption Kinetics of SO2 in a Fixed Carbon Bed Reactor—A Case Study" Energies 15, no. 2: 633. https://doi.org/10.3390/en15020633
APA StyleKisiela-Czajka, A. M., & Dziejarski, B. (2022). Linear and Non-Linear Regression Analysis for the Adsorption Kinetics of SO2 in a Fixed Carbon Bed Reactor—A Case Study. Energies, 15(2), 633. https://doi.org/10.3390/en15020633







