Research on the Relationship between Sediment Concentration and Centrifugal Pump Performance Parameters Based on CFD Mixture Model
Abstract
1. Introduction
2. Materials and Methods
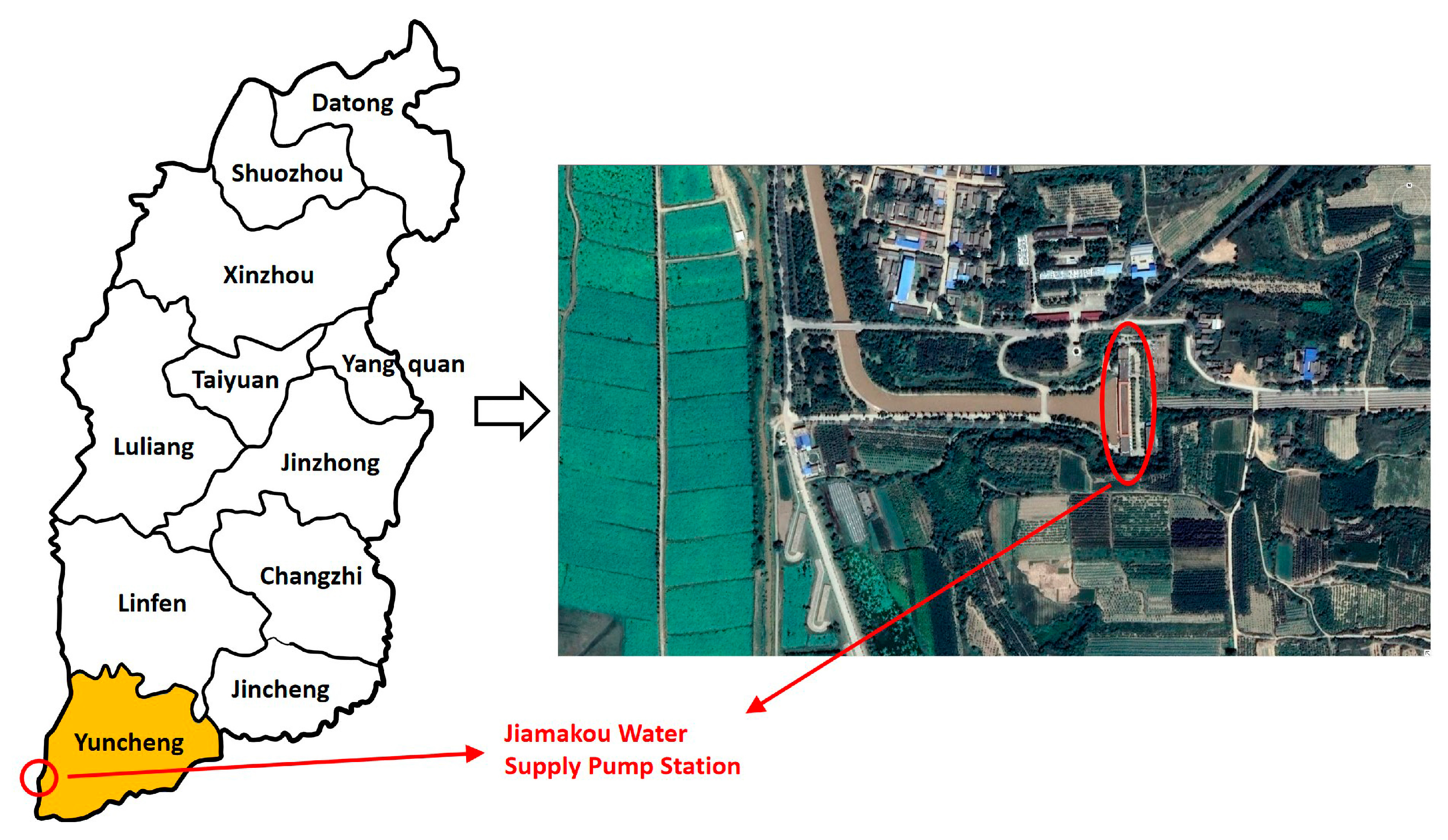
2.1. Research Object
2.2. Mixture Model
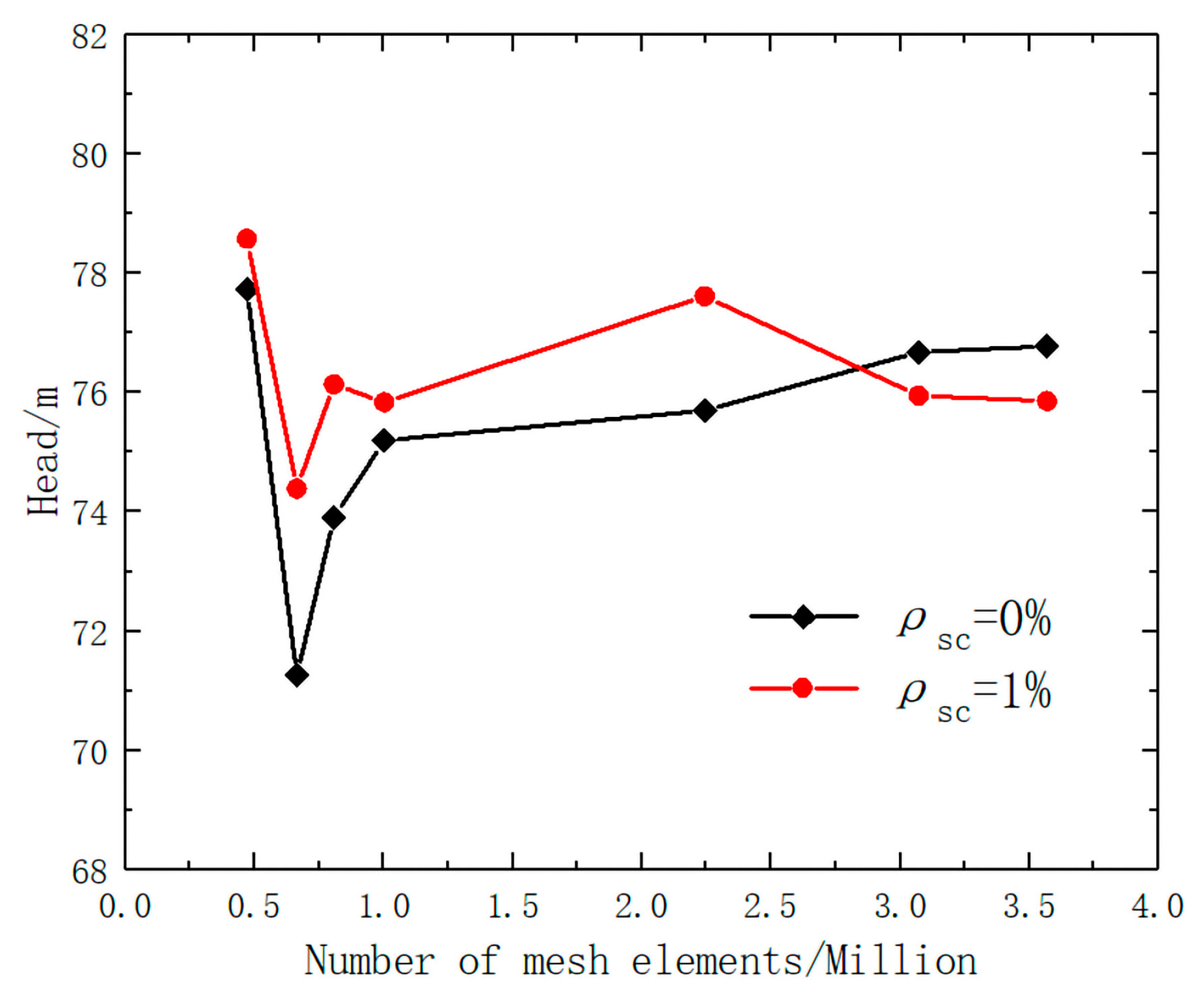
2.3. Meshing and Calculation Method
2.4. Polynomial Least-Squares Fitting Principle
3. Results and Discussion
3.1. Model Validation
3.2. Analysis of Simulated Results of Internal and External Characteristics of Centrifugal Pump with Sediment-Laden Flow
3.2.1. Internal Characteristic Analysis
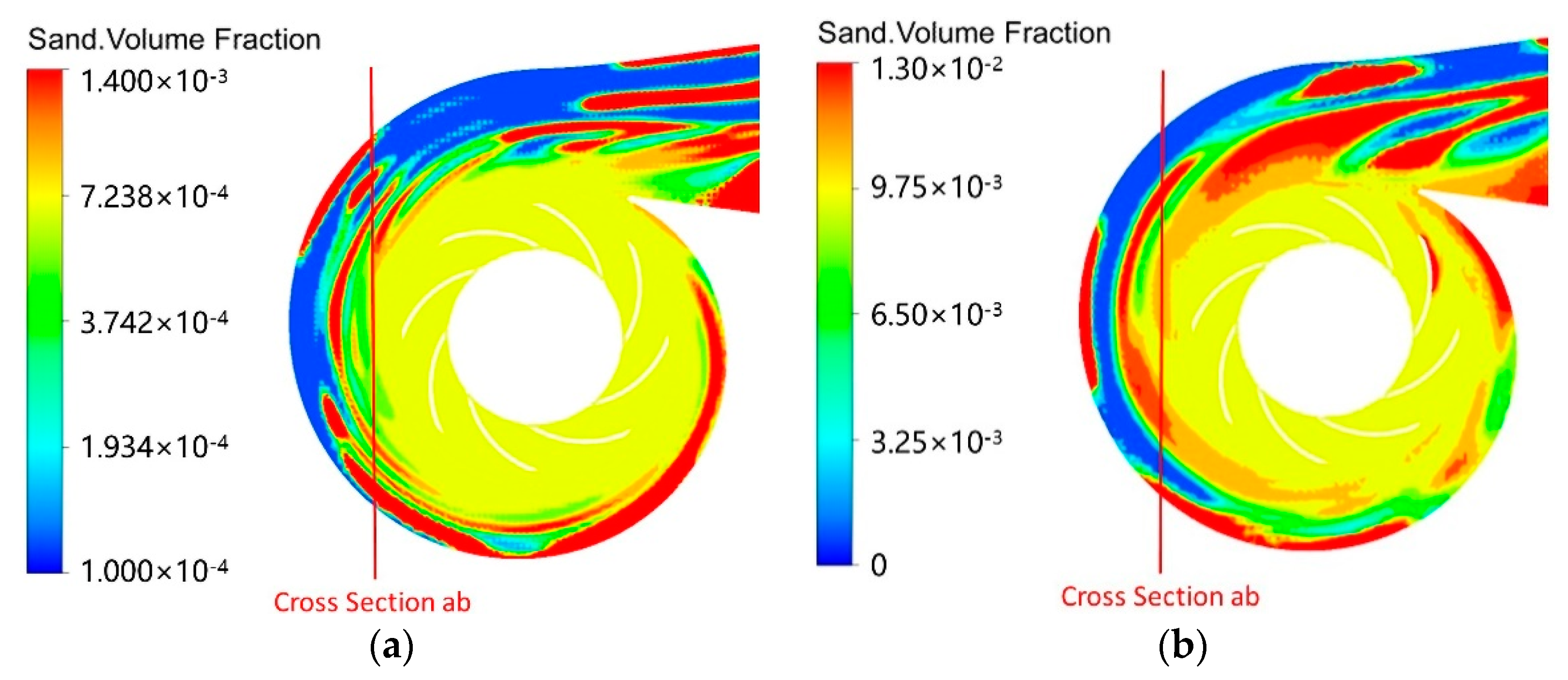
- Influence of sediment concentrations on solid particle distribution in the centrifugal pump
- (2)
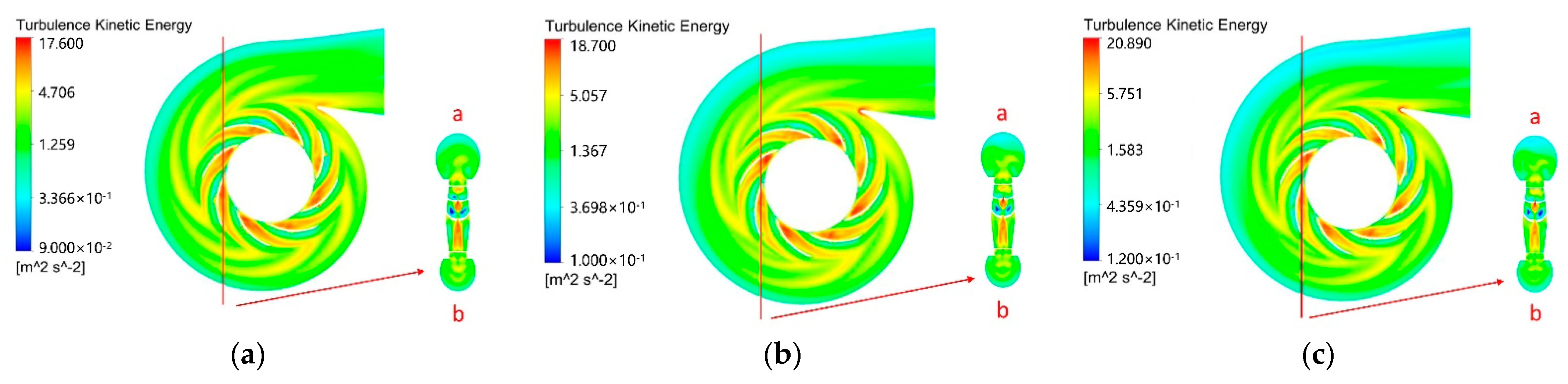
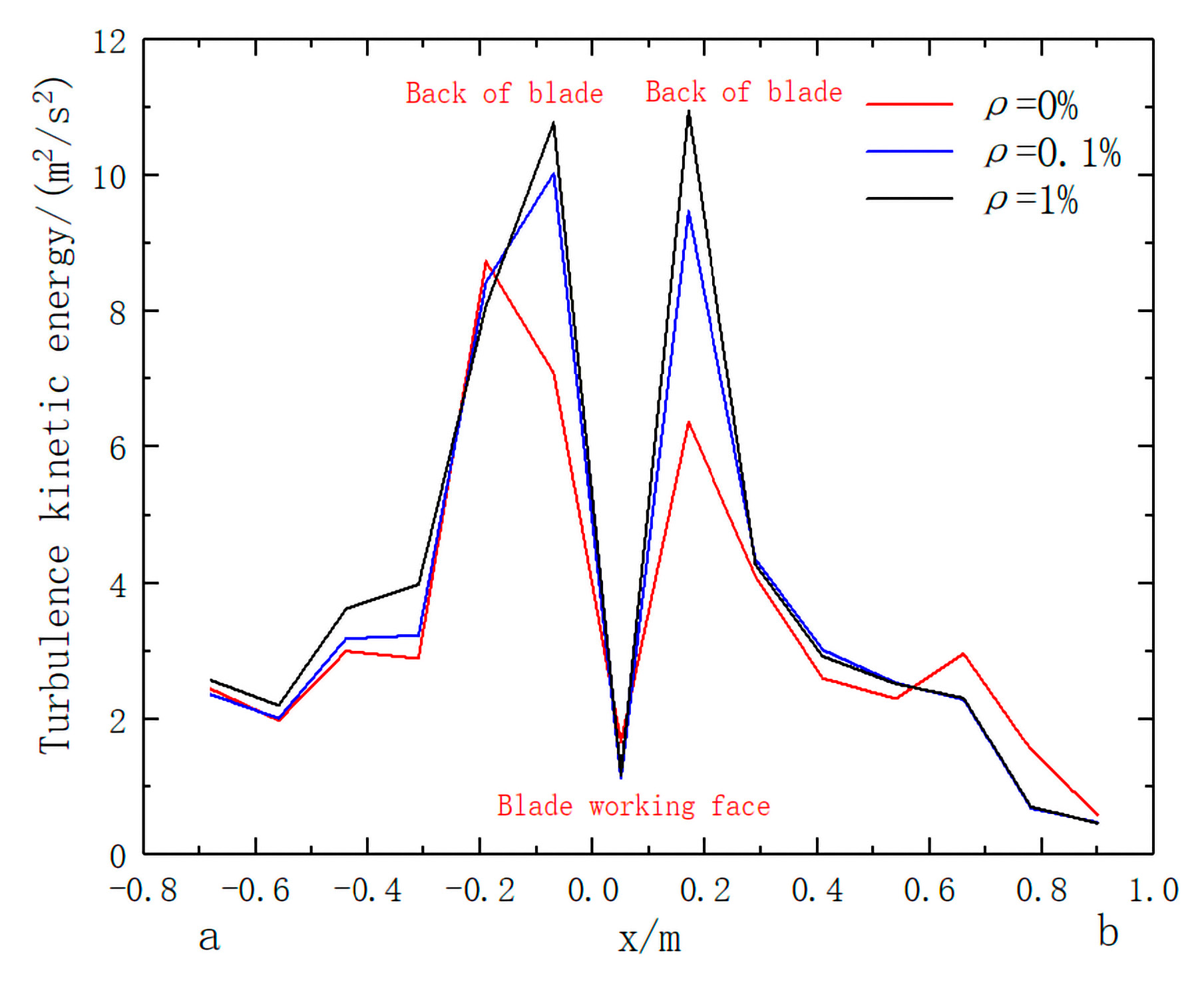
- Effect of sediment concentrations on the turbulent kinetic energy in centrifugal pump
3.2.2. External Characteristic Analysis
3.3. Establishment of Fitting Equations between Performance Parameters of Centrifugal Pump and Sediment Concentration at Different Working Conditions
3.4. Verification and Application of Fitting Equations
3.4.1. Comparison and Error Analysis of Measured Data and Calculated Values
3.4.2. Comparison of Similar Calculation Equations
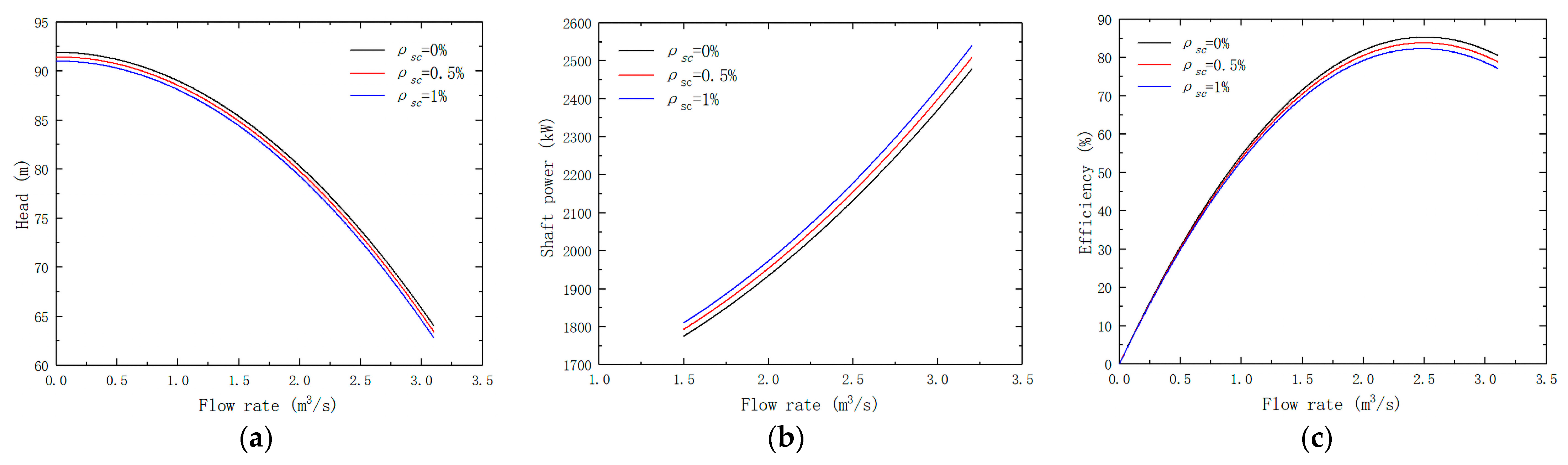
3.4.3. Characteristic Curves of Centrifugal Pump with Different Sediment Concentrations
4. Conclusions
- The volume fraction of sediment at impeller outlet and volute wall is relatively large under the condition of sediment-laden flow, leading to the wear of blade edge and volute wall being relatively serious. Moreover, the wear of blade edge and volute wall increases with the increase of sediment concentration.
- In the impeller inlet, blade back, impeller outlet, and cochlea tongue of the centrifugal pump, there are high turbulent kinetic energy regions in different degrees under the condition of sediment-laden flow, resulting in loss of pressure and energy in the centrifugal pump. With the increase of sediment concentration, the loss of pressure and energy in the centrifugal pump also increase.
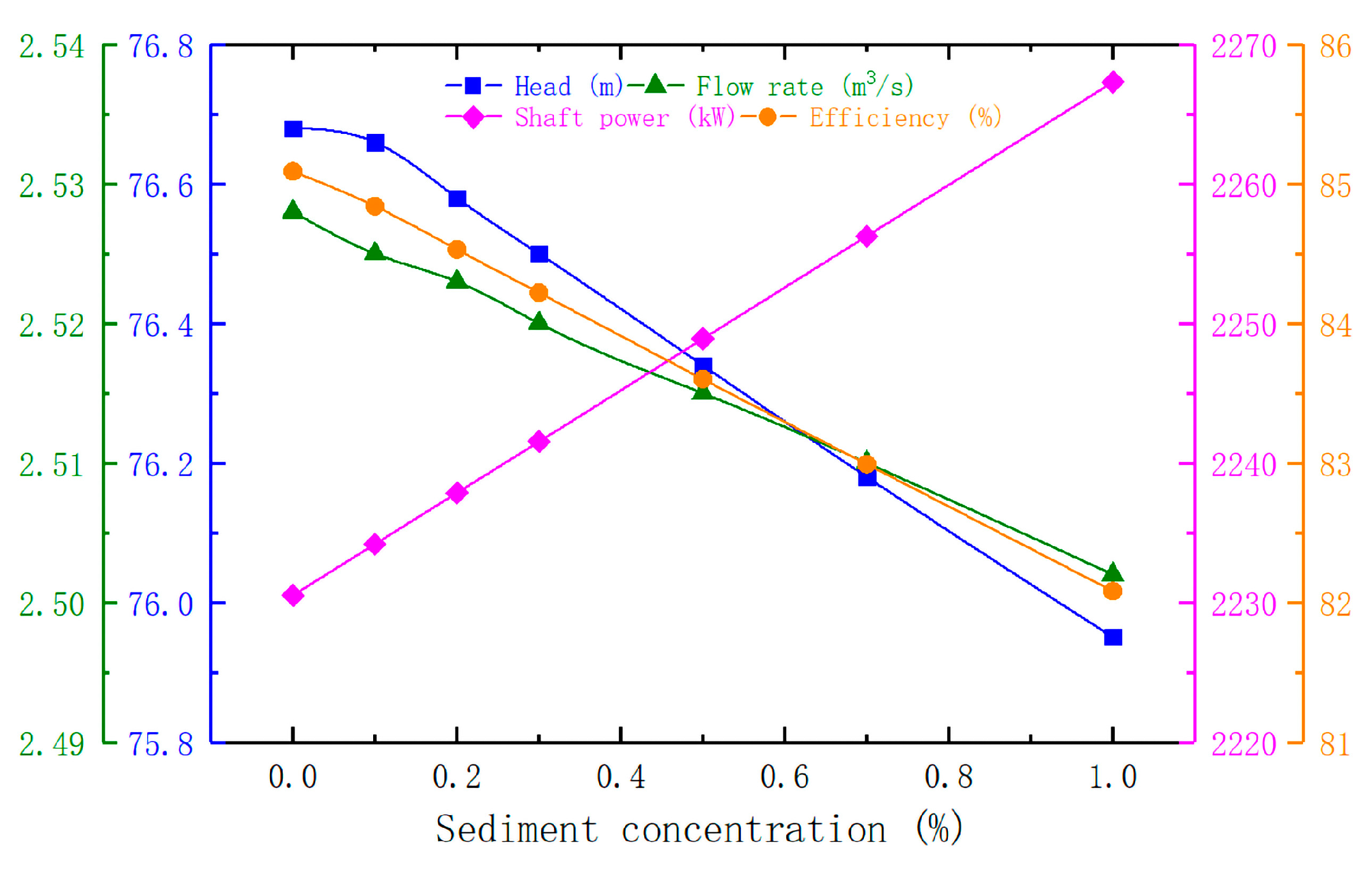
- With the increase of sediment concentration in the centrifugal pump, the head, flow rate, and efficiency of the centrifugal pump all show downward trends, while the shaft power shows a rising trend.
- The fitting equations are established between the performance parameters of the centrifugal pump and sediment concentration by the polynomial least-squares method, which can provide a simple and efficient method for the calculation of performance parameters of the centrifugal pump with different sediment concentrations. However, it can be seen from the error analysis results that, as the service time of the centrifugal pump increases, it is necessary to constantly calibrate fitting equations to ensure its calculation accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ρm | mixture density (kg/m3) |
| νm | mass average velocity (m/s) |
| μm | mixture viscous coefficient (Pa·s) |
| F | body force (Pa) |
| n | number of phases (there are only water phase and sediment phase, so n = 2) |
| αk | volume fraction of the kth phase (kg/m3) |
| ρk | density of the kth phase (kg/m3) |
| νdr,k | drift velocity of the kth phase (m/s) |
| τq,p | relaxation time of particles (s) |
| a | acceleration of second-phase particle (m/s2) |
| ρp | density of the second phase p (kg/m3) |
| dp | particle diameter of the second phase p (m) |
| μq | relative dynamic viscosity coefficient of the second phase p (Pa·s) |
| A | uncertainty of intercept a |
| B | uncertainty of slope b |
| ρsc | sediment concentration (%) |
| centrifugal pump head at 0.8 Q under the sediment concentration ρsc (m) | |
| centrifugal pump head at Q under the sediment concentration ρsc (m) | |
| centrifugal pump head at 1.2 Q under the sediment concentration ρsc (m) | |
| centrifugal pump flow rate at 0.8 Q under the sediment concentration ρsc (m3/s) | |
| centrifugal pump flow rate at Q under the sediment concentration ρsc (m3/s) | |
| centrifugal pump flow rate at 1.2 Q under the sediment concentration ρsc (m3/s) | |
| shaft power at 0.8 Q under the sediment concentration ρsc (kW) | |
| shaft power at Q under the sediment concentration ρsc (kW) | |
| shaft power at 1.2 Q under the sediment concentration ρsc (kW) | |
| centrifugal pump efficiency at 0.8 Q under the sediment concentration ρsc (%) | |
| centrifugal pump efficiency at Q under the sediment concentration ρsc (%) | |
| centrifugal pump efficiency at 1.2 Q under the sediment concentration ρsc (%) | |
| H0.8Q | centrifugal pump head at 0.8 Q under the condition of clean water (m) |
| HQ | centrifugal pump head at Q under the condition of clean water (m) |
| H1.2Q | centrifugal pump head at 1.2 Q under the condition of clean water (m) |
| Q0.8Q | centrifugal pump flow rate at 0.8 Q under the condition of clean water (m3/s) |
| centrifugal pump flow rate at Q under the condition of clean water (m3/s) | |
| Q1.2Q | centrifugal pump flow rate at 1.2 Q under the condition of clean water (m3/s) |
| N0.8Q | shaft power at 0.8 Q under the condition of clean water (kW) |
| NQ | shaft power at Q under the condition of clean water (kW) |
| N1.2Q | shaft power at 1.2 Q under the condition of clean water (kW) |
| η0.8Q | centrifugal pump efficiency at 0.8 Q under the condition of clean water (%) |
| ηQ | centrifugal pump efficiency at Q under the condition of clean water (%) |
| η1.2Q | centrifugal pump efficiency at 1.2 Q under the condition of clean water (%) |
| Qρ | flow rate of pumps with sediment-laden flow in old models (m3/s) |
| Hρ | head of pumps with sediment-laden flow in old models (m) |
| Nρ | shaft power of pumps with sediment-laden flow in old models (kW) |
| ρ | sediment concentration in old models (%) |
| Q0 | flow rate of pumps with clean water in old models (m3/s) |
| N0 | head of pumps with clean water in old models (m) |
| N0 | shaft power of pumps with clean water in old models (kW) |
References
- Hu, C.; Zhang, X.; Zhao, Y. Cause Analysis of the Centennial Trend and Recent Fluctuation of the Yellow River Sediment Load. Adv. Water Sci. 2020, 31, 725–733. (In Chinese) [Google Scholar] [CrossRef]
- Yue, J.; Huang, X.; Xing, X.; Zhao, L.; Kong, Q.; Yang, X.; Zhu, Y.; Zhang, J. Experimental Study on the Improvement of the Particle Gradation of the Yellow River Silt Based on MICP Technology. Adv. Eng. Sci. 2021, 53, 89–98. (In Chinese) [Google Scholar] [CrossRef]
- Shen, Z.; Chu, W.; Li, X.; Dong, W. Sediment erosion in the impeller of a double-suction centrifugal pump—A case study of the Jingtai Yellow River Irrigation Project, China. Wear 2019, 422–423, 269–279. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Cui, B.; Zhu, Z.; Dou, H. Numerical simulation and analysis of solid-liquid two-phase flow in centrifugal pump. Chin. J. Mech. Eng. 2013, 26, 53–60. [Google Scholar] [CrossRef]
- Wang, K.; Pan, Y.; Zheng, J.; Li, C.; Kim, K. A Numerical Study of the Impact of Fine Sand-particles on Centrifugal Pump Working Characteristics. Chin. Rural Water Hydropower 2013, 5, 129–132. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; He, T.; Han, C.; Zhu, Z.; Lin, Z. The effect of solid particle size and concentrations on internal flow and external characteristics of the dense fine particles solid–liquid two-phase centrifugal pump under low flow condition. Aip Adv. 2021, 11, 85309. [Google Scholar] [CrossRef]
- Lu, J.; Du, G. Study of the Influence of Silt on the Pump Performance. J. Drain. Irrig. Mach. Eng. 2003, 21, 13–16. (In Chinese) [Google Scholar] [CrossRef]
- Ding, H.; Visser, F.C.; Jiang, Y.; Furmanczyk, M. Demonstration and Validation of a 3D CFD Simulation Tool Predicting Pump Performance and Cavitation for Industrial Applications. J. Fluids Eng. 2011, 133, 11101. [Google Scholar] [CrossRef]
- Buratto, C.; Pinelli, M.; Spina, P.R.; Vaccari, A.; Verga, C. CFD study on special duty centrifugal pumps operating with viscous and non-Newtonian fluids. In Proceedings of the 11th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Madrid, Spain, 23–27 March 2015. [Google Scholar]
- Steinmann, A.; Wurm, H.; Otto, A. Numerical and experimental investigations of the unsteady cavitating flow in a vortex pump. J. Hydrodyn. Ser. B 2010, 22, 324–329. [Google Scholar] [CrossRef]
- Zhai, J.; Zhou, H. Model and Simulation on Flow and Pressure Characteristics of Axial Piston Pump for Seawater Desalination. Appl. Mech. Mater. 2012, 157–158, 1549–1552. [Google Scholar] [CrossRef]
- Thakkar, S.; Vala, H.; Patel, V.K.; Patel, R. Performance improvement of the sanitary centrifugal pump through an integrated approach based on response surface methodology, multi-objective optimization and CFD. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 24. [Google Scholar] [CrossRef]
- Wan, D.; Turek, S. An efficient multigrid-FEM method for the simulation of solid–liquid two phase flows. J. Comput. Appl. Math. 2007, 203, 561–580. [Google Scholar] [CrossRef]
- Pagalthivarthi, K.V.; Visintainer, R.J. Finite Element Prediction of Multi-Size Particulate Flow through Three-Dimensional Channel: Code Validation. J. Comput. Multiphase Flows 2013, 5, 57–72. [Google Scholar] [CrossRef]
- Kartashev, A.L.; Kartasheva, M.A.; Terekhin, A.A. Mathematical Models of Dynamics Multiphase Flows in Complex Geometric Shape Channels. Procedia Eng. 2017, 206, 121–127. [Google Scholar] [CrossRef]
- Zhou, W.; Chai, J.; Xu, Z.; Cao, C.; Wu, G.; Yao, X. Numerical Simulation of Solid-Liquid Two-Phase Flow and Wear Prediction of a Hydraulic Turbine High Sediment Content. Exp. Tech. 2022, 1–13. [Google Scholar] [CrossRef]
- Pathak, M. Computational investigations of solid-liquid particle interaction in a two-phase flow around a ducted obstruction. J. Hydraul. Res. 2011, 49, 96–104. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; He, Z.; He, W. Abrasion characteristic analyses of solid-liquid two-phase centrifugal pump. J. Therm. Sci. 2011, 20, 283–287. [Google Scholar] [CrossRef]
- Huang, S.; Su, X.; Qiu, G. Transient numerical simulation for solid-liquid flow in a centrifugal pump by DEM-CFD coupling. Eng. Appl. Comp. Fluid 2015, 9, 411–418. [Google Scholar] [CrossRef]
- Song, X.; Qi, D.; Xu, L.; Shen, Y.; Wang, W.; Wang, Z.; Liu, Y. Numerical Simulation Prediction of Erosion Characteristics in a Double-Suction Centrifugal Pump. Processes 2021, 9, 1483. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, H.; Deng, F.; Wang, C.; Si, Q. Effect of Short Blade Circumferential Position Arrangement on Gas-Liquid Two-Phase Flow Performance of Centrifugal Pump. Processes 2020, 8, 1317. [Google Scholar] [CrossRef]
- Noon, A.A.; Kim, M. Erosion wear on centrifugal pump casing due to slurry flow. Wear 2016, 364–365, 103–111. [Google Scholar] [CrossRef]
- Pagalthivarthi, K.V.; Gupta, P.K.; Tyagi, V.; Ravi, M.R. CFD Predictions of Dense Slurry Flow in Centrifugal Pump Casings. Int. J. Mech. Mechatron. Eng. 2011, 5, 538–550. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhu, Z.; Cui, B. Computational analysis of centrifugal pump delivering solid-liquid two-phase flow during startup period. Chin. J. Mech. Eng. 2014, 27, 178–185. [Google Scholar] [CrossRef]
- Fan, Y.; Gao, Z.; Wang, S.; Chen, H.; Liu, J. Evaluation of the Water Allocation and Delivery Performance of Jiamakou Irrigation Scheme, Shanxi, China. Water 2018, 10, 654. [Google Scholar] [CrossRef]
- Haavisto, S.; Syrjänen, J.; Koponen, A.; Manninen, M. UDV measurements and CFD simulation of two-phase flow in a stirred vessel. Prog. Comput. Fluid Dyn. 2009, 9, 375–382. [Google Scholar] [CrossRef]
- Pathak, M.; Khan, M.K. Inter-phase slip velocity and turbulence characteristics of micro particles in an obstructed two-phase flow. Environ. Fluid Mech. 2013, 13, 371–388. [Google Scholar] [CrossRef]
- Zi, D.; Wang, F.; Tao, R.; Hou, Y. Research for impacts of boundary layer grid scale on flow field simulation results in pumping station. J. Hydraul. Eng. 2016, 47, 139–149. (In Chinese) [Google Scholar] [CrossRef]
- Li, X.; Yuan, S.; Pan, Z.; Li, Y.; Yang, J. Realization and application evaluation of near-wall mesh in centrifugal pumps. Trans. Chin. Soc. Agric. Eng. 2012, 28, 67–72+293. (In Chinese) [Google Scholar] [CrossRef]
- Kim, S.; Kojima, M. Solving polynomial least squares problems via semidefinite programming relaxations. J. Glob. Optim. 2010, 46, 1. [Google Scholar] [CrossRef]
- Liang, S.; Doong, D.; Chao, W. Solution of Shallow-Water Equations by a Layer-Integrated Hydrostatic Least-Squares Finite-Element Method. Water 2022, 14, 530. [Google Scholar] [CrossRef]
- Jiang, H. Investigation on Turbulent Flow Characteristics in a Solid-Liquid Stirred Tank. Master’s Thesis, Beijing University of Chemical Technology, Beijing, China, 2010. [Google Scholar]
- Liu, Y.; Yang, D.; Gao, J.; Liu, C. Research on Characteristic Parameters of Jiamakou Pump Station under Condition of Sediment Flow. Water Resour. Power 2017, 35, 175–177. (In Chinese) [Google Scholar]




| Working Conditions | Head (m) | Flow Rate (m3/s) | Shaft Power (kW) | Efficiency (%) |
|---|---|---|---|---|
| 0.8 Q | 79 | 2 | 1886.82 | 82 |
| Q | 75 | 2.5 | 2160.08 | 85 |
| 1.2 Q | 64 | 3 | 2292.84 | 82 |
| Working Condition | Head (m) | Shaft Power (kW) | ||||
|---|---|---|---|---|---|---|
| Working Parameter | Simulated Value | Relative Error | Working Parameters | Simulated Value | Relative Error | |
| 0.8 Q | 79 | 79.64 | 0.81% | 1886.82 | 1921.66 | 1.85% |
| Q | 75 | 76.68 | 2.25% | 2160.08 | 2230.52 | 3.26% |
| 1.2 Q | 64 | 65.26 | 1.97% | 2292.84 | 2358.43 | 2.86% |
| ρsc (%) | Head (m) | Flow Rate (m3/s) | Shaft Power (kW) | Efficiency (%) |
|---|---|---|---|---|
| 0 | 76.68 | 2.528 | 2230.52 | 85.09 |
| 0.1 | 76.66 | 2.525 | 2234.17 | 84.84 |
| 0.2 | 76.58 | 2.523 | 2237.85 | 84.53 |
| 0.3 | 76.50 | 2.520 | 2241.52 | 84.22 |
| 0.5 | 76.34 | 2.515 | 2248.89 | 83.60 |
| 0.7 | 76.18 | 2.510 | 2256.25 | 82.99 |
| 1 | 75.95 | 2.502 | 2267.30 | 82.08 |
| Working Condition | Flow Rate (m3/s) | Efficiency (%) | ||||
|---|---|---|---|---|---|---|
| Performance Parameters | Simulated Value | Relative Error | Performance Parameters | Simulated Value | Relative Error | |
| 0.8 Q | 2 | 2.022 | 1.12% | 82 | 82.08 | 0.10% |
| Q | 2.5 | 2.528 | 1.10% | 85 | 85.09 | 0.11% |
| 1.2 Q | 3 | 3.033 | 1.09% | 82 | 82.18 | 0.22% |
| ρsc (%) | Shaft Power (kW) | ||
|---|---|---|---|
| Actual Data | Equation Calculated Value | Relative Error | |
| 0.15 | 1853.78 | 1891.52 | 2.04% |
| 0.16 | 1839.33 | 1891.83 | 2.85% |
| 0.22 | 1860.66 | 1893.71 | 1.78% |
| 0.27 | 1875.76 | 1895.28 | 1.04% |
| 0.39 | 1848.96 | 1899.04 | 2.71% |
| ρsc (%) | Head (m) | Flow Rate (m3/s) | Effective (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Actual Data | Equation Calculation | Relative Error | Actual Data | Equation Calculation | Relative Error | Actual Data | Equation Calculation | Relative Error | |
| 0.15 | 75.32 | 78.88 | 4.73% | 2.03 | 1.9969 | 1.63% | 80.77 | 81.57 | 0.99% |
| 0.16 | 74.59 | 78.87 | 5.74% | 2.07 | 1.9967 | 3.54% | 82.20 | 81.54 | 0.81% |
| 0.22 | 74.03 | 78.83 | 6.48% | 2.03 | 1.9955 | 1.70% | 79.09 | 81.36 | 2.87% |
| 0.27 | 75.16 | 78.79 | 4.83% | 2.02 | 1.9944 | 1.27% | 79.26 | 81.22 | 2.47% |
| 0.39 | 74.88 | 78.69 | 5.09% | 2.01 | 1.9920 | 0.90% | 79.71 | 80.87 | 1.46% |
| ρsc (%) | Head (m) | Flow Rate (m3/s) | ||||||
|---|---|---|---|---|---|---|---|---|
| Actual Data | Error of old Equations | Error of Fitting Equations | Difference Volume of Error | Actual Data | Error of Old Equations | Error of Fitting Equations | Difference Volume of Error | |
| 0.15 | 75.32 | 4.50% | 4.73% | 0.23% | 2.03 | 11.34% | 1.62% | 9.72% |
| 0.16 | 74.59 | 5.50% | 5.75% | 0.25% | 2.07 | 13.65% | 3.53% | 10.11% |
| 0.22 | 74.03 | 6.15% | 6.48% | 0.33% | 2.03 | 15.41% | 1.69% | 13.72% |
| 0.27 | 75.16 | 4.45% | 4.83% | 0.38% | 2.02 | 17.71% | 1.25% | 16.46% |
| 0.39 | 74.88 | 4.59% | 5.10% | 0.51% | 2.01 | 23.14% | 0.88% | 22.26% |
| ρsc (%) | Shaft Power (kW) | |||||||
| Actual Data | Error of OldEquations | Error of Fitting Equations | Difference Volume of Error | |||||
| 0.15 | 1853.78 | 1.81% | 2.03% | 0.22% | ||||
| 0.16 | 1839.33 | 2.61% | 2.85% | 0.23% | ||||
| 0.22 | 1860.66 | 1.47% | 1.77% | 0.29% | ||||
| 0.27 | 1875.76 | 0.69% | 1.03% | 0.33% | ||||
| 0.39 | 1848.96 | 2.28% | 2.69% | 0.41% | ||||
| ρsc (%) | Head (m) | Flow Rate (m3/s) | Shaft Power (kW) | Efficiency (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.8 Q | Q | 1.2 Q | 0.8 Q | Q | 1.2 Q | 0.8 Q | Q | 1.2 Q | 0.8 Q | Q | 1.2 Q | |
| 0 | 79 | 75 | 64 | 2 | 2.5 | 3 | 1886.82 | 2160.08 | 2292.84 | 82 | 85 | 82 |
| 0.5 | 78.61 | 74.63 | 63.68 | 1.99 | 2.487 | 2.985 | 1937.13 | 2178.01 | 2377.89 | 80.55 | 83.50 | 80.55 |
| 1 | 78.23 | 74.26 | 63.36 | 1.98 | 2.474 | 2.969 | 1952.60 | 2195.94 | 2397.34 | 79.11 | 82.00 | 79.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Su, P.; Wu, J.; Zhang, Y.; Wang, B. Research on the Relationship between Sediment Concentration and Centrifugal Pump Performance Parameters Based on CFD Mixture Model. Energies 2022, 15, 7228. https://doi.org/10.3390/en15197228
Wu X, Su P, Wu J, Zhang Y, Wang B. Research on the Relationship between Sediment Concentration and Centrifugal Pump Performance Parameters Based on CFD Mixture Model. Energies. 2022; 15(19):7228. https://doi.org/10.3390/en15197228
Chicago/Turabian StyleWu, Xinhao, Peilan Su, Jianhua Wu, Yusheng Zhang, and Baohe Wang. 2022. "Research on the Relationship between Sediment Concentration and Centrifugal Pump Performance Parameters Based on CFD Mixture Model" Energies 15, no. 19: 7228. https://doi.org/10.3390/en15197228
APA StyleWu, X., Su, P., Wu, J., Zhang, Y., & Wang, B. (2022). Research on the Relationship between Sediment Concentration and Centrifugal Pump Performance Parameters Based on CFD Mixture Model. Energies, 15(19), 7228. https://doi.org/10.3390/en15197228





