Machine Learning-Based Load Forecasting for Nanogrid Peak Load Cost Reduction
Abstract
:1. Introduction
- A multi-layer perceptron model with dynamic feature selection is developed for hour-ahead forecasting of a nanogrid;
- Peak loads of a nanogrid are identified fast and accurately based on the predicted load for potential energy cost saving through load shifting;
- Numerical testing results demonstrate the performance of the developed model with MSE of 0.03 kW, MAPE of 9%, and CV of 11.9%, and the achievement of 20% energy cost savings through shifting peak loads throughout the day.
2. Literature Review
2.1. Load Forecasting
2.2. Peak Load
3. Methodology
3.1. Pre-Processing
3.2. Feature Selection
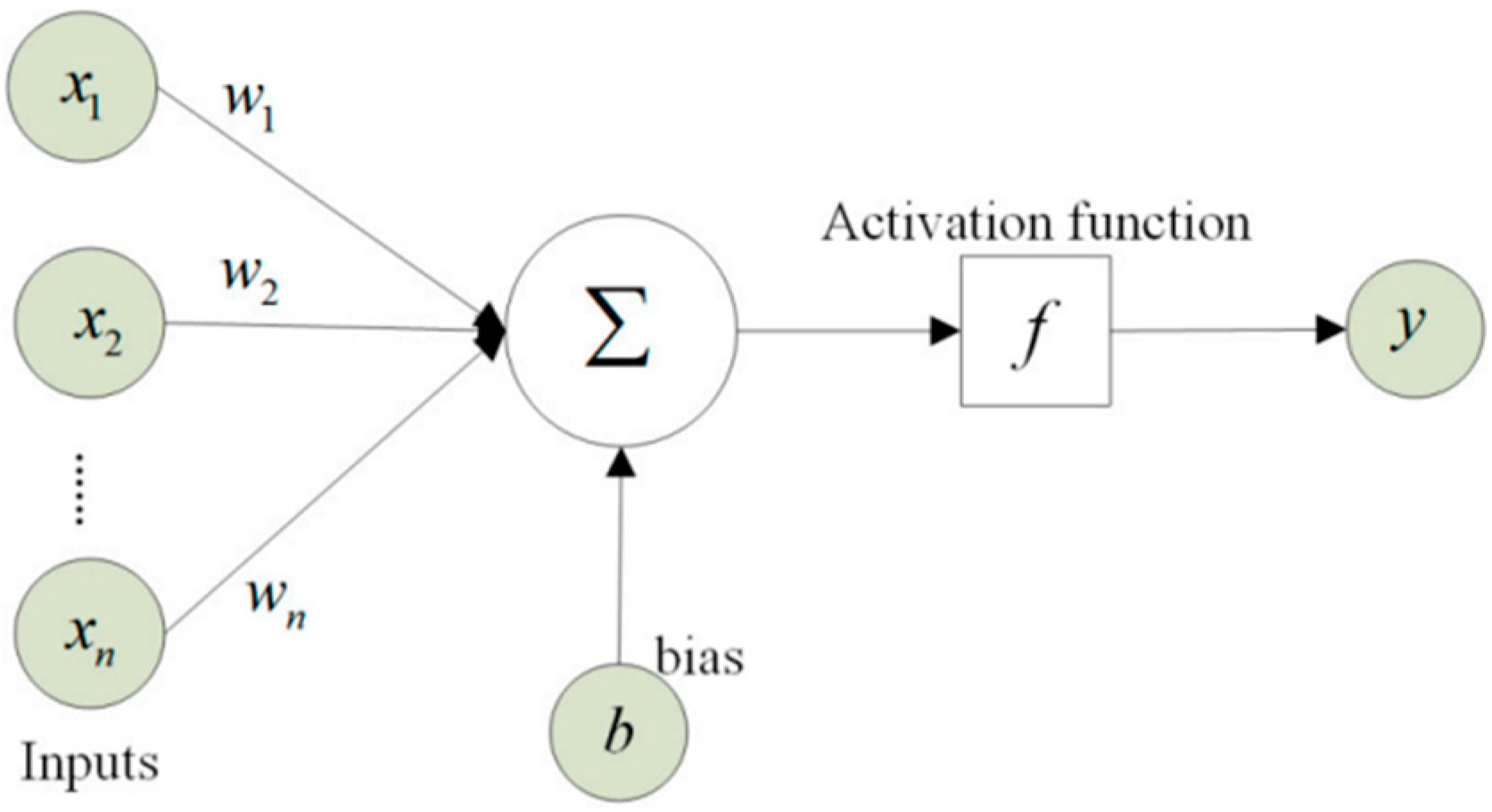
3.3. Network Modelling
3.4. Pseudocode
| Algorithm 1: for the ANN Model | |
| Input: Input features i.e., Meteorological data and Electric load | |
| Output: Hourly forecasted electric load and daily energy cost savings | |
| 1. | Get weather and electric load data |
| 2. | Pre-process the data by converting electric data into hourly electric data |
| 3. | Extract slope, t-1 load, and “rising or falling edge” parameter from the electric load |
| 4. | Get Pearson correlation Coefficients (µf) for weather data and its corresponding electric load |
| 5. | Apply K-means with K = 2 on the set of coefficients [µ1, µ2,...,µf] and determine the mid-point of two centroids (m) |
| 6. | for (t < Number of Potential features) |
| 7. | if (µf > m) |
| 8. | Feature (f) is selected as an input feature |
| 9. | else |
| 10. | Feature (f) is dropped |
| 11. | t = t + 1 |
| 12. | end for |
| 13. | Divide data (Input feature and electric load) into training and testing sets |
| 14. | Initialize ANN model |
| 15. | Training time starts |
| 16. | while (1) |
| 17. | Run the model |
| 18. | Losses are calculated |
| 19. | Tune the hyperparameters if needed |
| 20. | if1(Losses(t)-Losses(t-1)< ε) |
| 21. | count = count + 1 |
| 22. | if2 (count > β) |
| 23. | Break |
| 24. | end if2 |
| 25. | end if1 |
| 26. | end while |
| 27. | Training time stops and total training time is calculated (time) |
| 28. | Model tested on test data for hourly load forecasting (Lhour) |
| 29. | MAPE, MSE, CV, and RMSE are calculated |
| 30. | if (Lhour > 1.5*average (Lprevious_hours) & time is within range of peak hours) |
| 31. | Lhour is considered peak load |
| 32. | end if |
| 33. | Savings are calculated based on the potential shifting of Lhour to an off-peak hour. |
| 34. | Repeat from point 4 for load forecasting of the next hours |
3.5. Model Evaluation Criterion
4. Results
4.1. Dataset Description/Set-Up
4.2. Hyperparameters and Features
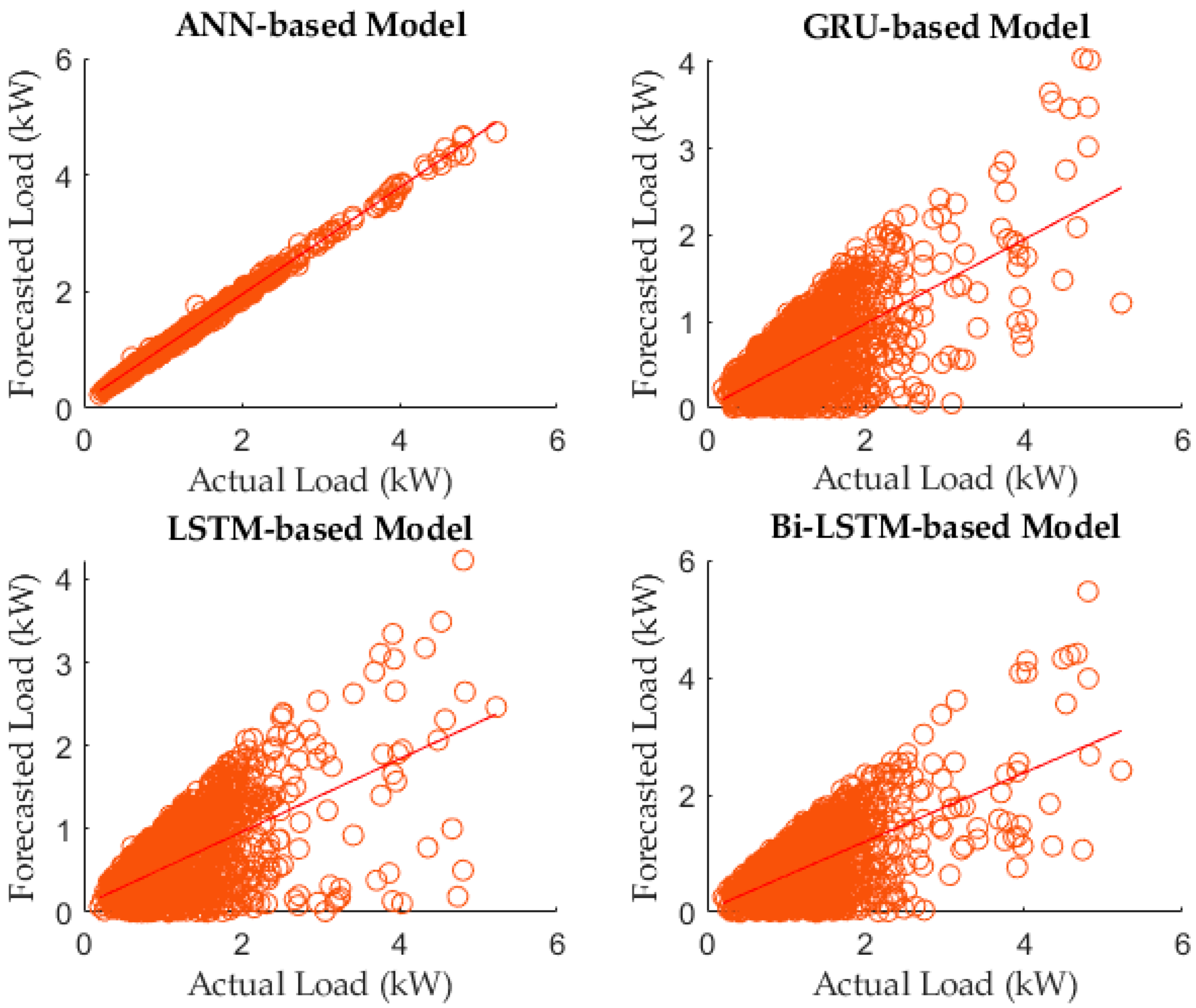
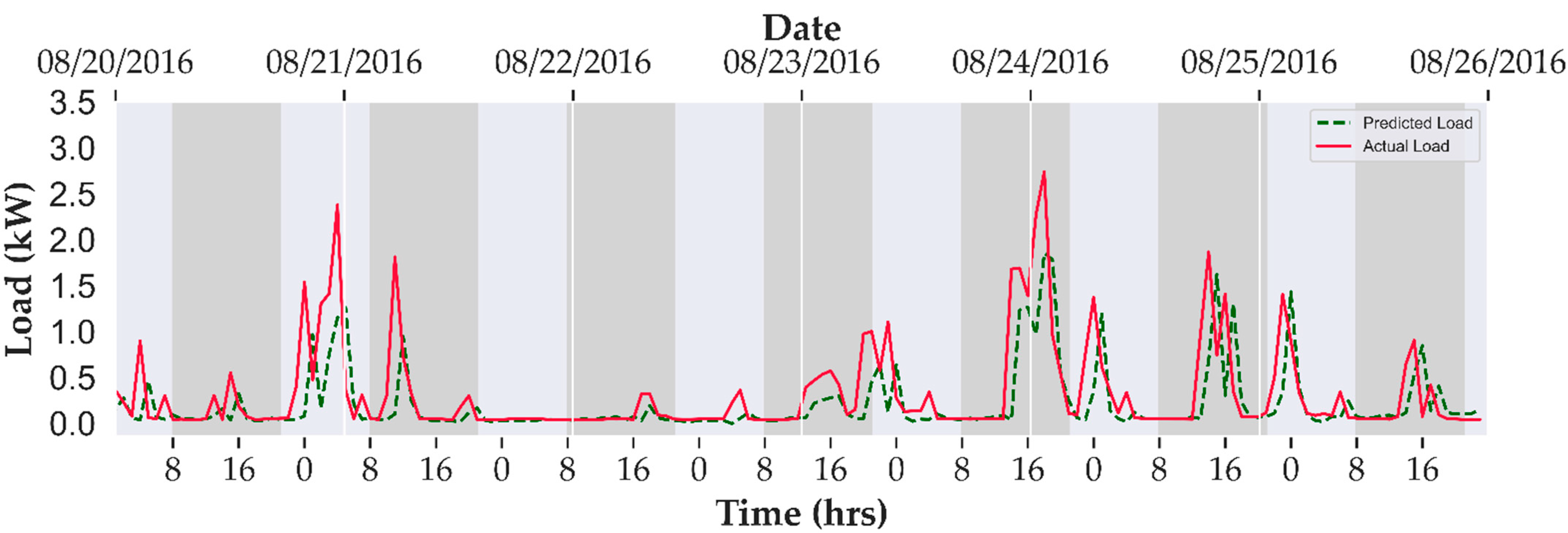
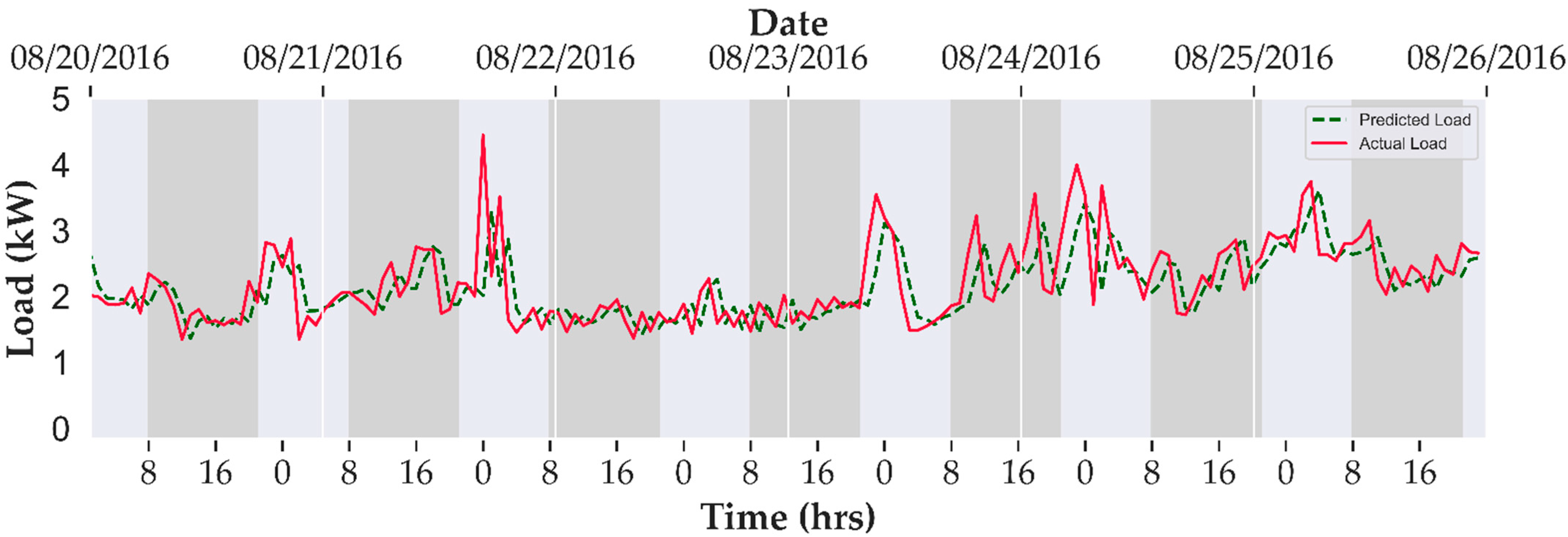
4.3. Load Forecasting
4.4. Cost Savings
5. Conclusions
- Apply optimization methods to decide load shifting strategies and, thus, to determine penitential energy cost savings for a nanogrid;
- Optimize the pricing mechanism for energy transactions within the nanogrid network by using the developed load forecasting model.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ARIMA | Autoregressive Integrated Moving Average |
| Bi-LSTM | Bi-directional Long Short-Term Memory |
| CNN | Convolutional Neural Network |
| CV | Co-efficient of variance |
| GRU | Gated Recurrent Unit |
| GBRT | Gradient Boosted Regression Trees |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MG | microgrid |
| MSE | Mean Squared Error |
| NG | nanogrid |
| PAR | Peak to Average Power Ratio |
| PSO | Particle Swarm Optimization |
| P2P | Peer-to-Peer |
| PV | Photovoltaic |
| RMSE | Root Mean Squared Error |
| ReLU | Rectified Linear Unit |
| RNN | Recurrent Neural Networks |
| STLF | Short-Term Load Forecasting |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| SARIMA | Seasonal Autoregressive Integrated Moving Average |
| WNN | Wavelet Neural Network |
Appendix A
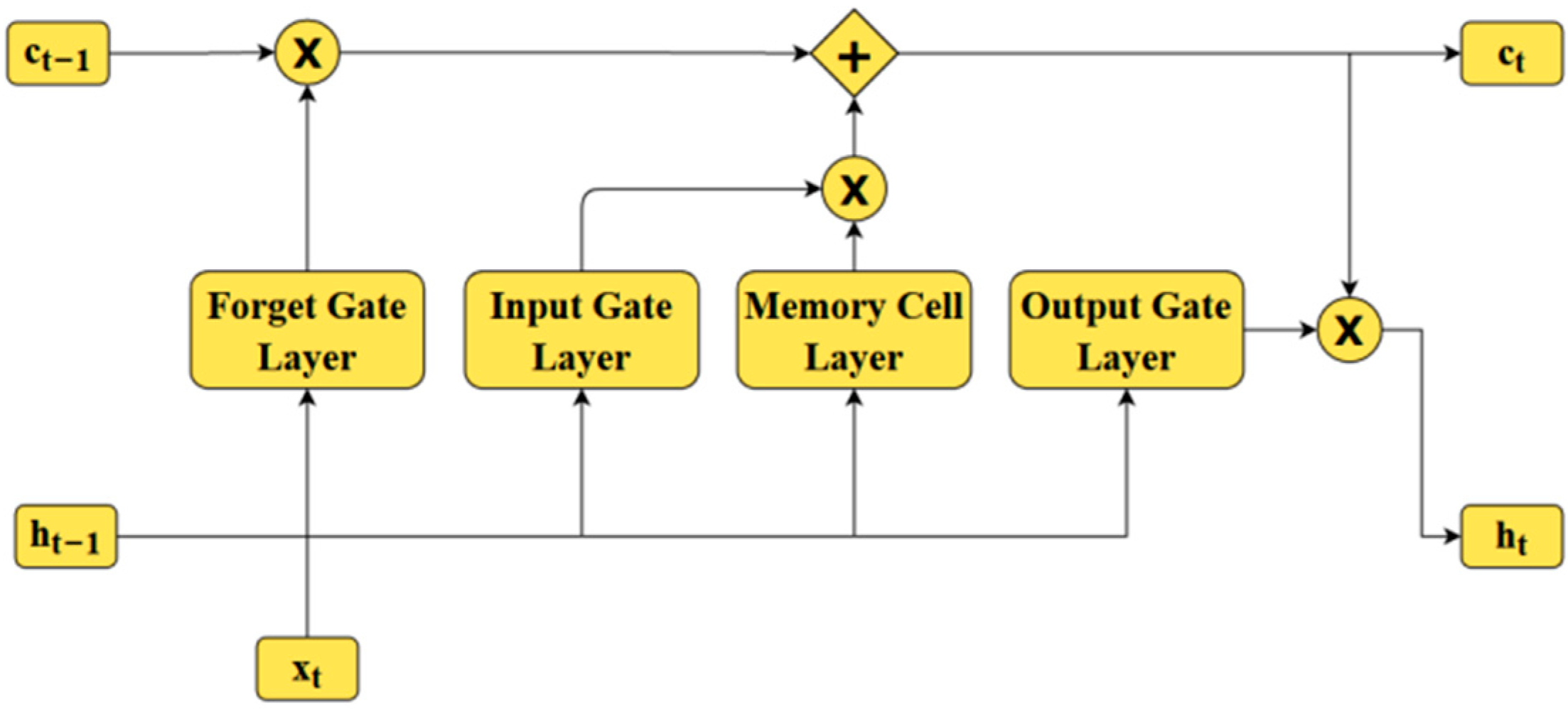
Appendix A.1. LSTM

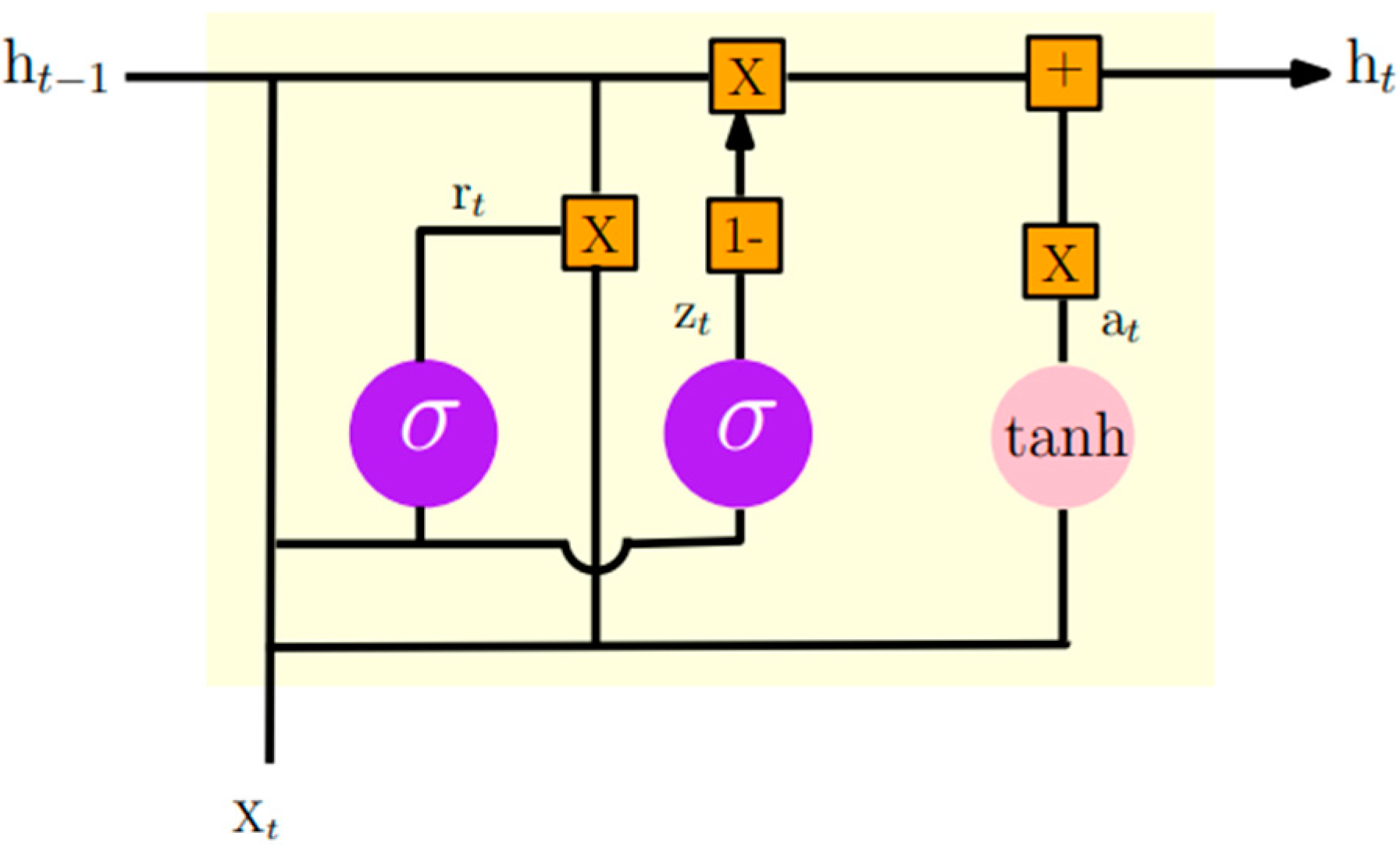
Appendix A.2. GRU

Appendix A.3. Bi-LSTM

Appendix B
Appendix C
| Algorithm A1: Pseudo-code for LSTM/GRU/Bi-LSTM Models | |
| Input: Electric load time series | |
| Output: Hourly forecasted electric load and daily energy cost savings | |
| 1. | Get Electric load data |
| 2. | Pre-process the data by converting electric data into hourly electric data |
| 3. | Divide data (Input feature and electric load) into training and testing sets |
| 4. | Initialize LSTM/GRU/Bi-LSTM model |
| 5. | Training time starts |
| 6. | while (1) |
| 7. | Run the model |
| 8. | Losses are calculated |
| 9. | Tune the hyperparameters if needed |
| 10. | if1(Losses(t)-Losses(t-1)< ε) |
| 11. | count = count + 1 |
| 12. | if2 (count > β) |
| 13. | Break |
| 14. | end if2 |
| 15. | end if1 |
| 16. | end while |
| 17. | Training time stops and total training time is calculated (time) |
| 18. | Model tested on test data for hourly load forecasting (Lhour) |
| 19. | MAPE, MSE, CV, and RMSE are calculated |
References
- Burmester, D.; Rayudu, R.; Seah, W.; Akinyele, D. A review of nanogrid topologies and technologies. Renew. Sustain. Energy Rev. 2017, 67, 760–775. [Google Scholar] [CrossRef]
- Yerasimou, Y.; Kynigos, M.; Efthymiou, V.; Georghiou, G. Design of a Smart Nanogrid for Increasing Energy Efficiency of Buildings. Energies 2021, 14, 3683. [Google Scholar] [CrossRef]
- Burgio, A.; Menniti, D.; Sorrentino, N.; Pinnarelli, A.; Motta, M. A compact nanogrid for home ap-plications with a behaviour-tree-based central controller. Appl. Energy 2018, 225, 14–26. [Google Scholar] [CrossRef]
- El-Shahat, A. Nanogrid Technology Increasing, Supplementing Microgrids. Nat. Gas Electr. 2016, 33, 1–7. [Google Scholar] [CrossRef]
- Ahmad, A.; Javaid, N.; Mateen, A.; Awais, M.; Khan, Z.A. Short-Term Load Forecasting in Smart Grids: An Intelligent Mod-ular Approach. Energies 2019, 12, 164. [Google Scholar] [CrossRef]
- Caro, E.; Juan, J.; Cara, J. Periodically correlated models for short-term electricity load forecasting. Appl. Math. Comput. 2019, 364, 124642. [Google Scholar] [CrossRef]
- Huang, Q.; Zheng, Y.; Xu, Y. Microgrid Load Forecasting Based on Improved Long Short-Term Memory Net-work. J. Electr. Comput. Eng. 2022, 2022, 4017708. [Google Scholar]
- Soman, A.; Trivedi, A.; Irwin, D.; Kosanovic, B.; McDaniel, B.; Shenoy, P. Peak Forecasting for Bat-tery-based Energy Optimizations in Campus Microgrids. In Proceedings of the Eleventh ACM International Conference on Future Energy Systems (e-Energy ‘20), Virtual Event, Australia, 22–26 June 2020; ACM: New York, NY, USA, 2010. [Google Scholar]
- Zuleta-Elles, I.; Bautista-Lopez, A.; Catano-Valderrama, M.J.; Marin, L.G.; Jimenez-Estevez, G.; Mendoza-Araya, P. Load Forecasting for Different Prediction Horizons using ANN and ARIMA models. In Proceedings of the 2021 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaíso, Chile, 6–9 December 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Arvanitidis, A.I.; Bargiotas, D.; Daskalopulu, A.; Laitsos, V.M.; Tsoukalas, L.H. Enhanced Short-Term Load Forecasting Using Artificial Neural Networks. Energies 2021, 14, 7788. [Google Scholar] [CrossRef]
- Ungureanu, S.; Topa, V.; Cziker, A.C. Deep Learning for Short-Term Load Forecasting—Industrial Consumer Case Study. Appl. Sci. 2021, 11, 10126. [Google Scholar] [CrossRef]
- Marzooghi, H.; Emami, K.; Wolfs, P.J.; Holcombe, B. Short-term Electric Load Forecasting in Microgrids: Issues and Challenges. In Proceedings of the 2018 Australasian Universities Power Engineering Conference (AUPEC), Auckland, New Zealand, 27–30 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recur-rent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Identifying Potential Markets for Behind-the-Meter Battery Energy Storage: A Survey of U.S. Demand Charges. Available online: https://www.nrel.gov/docs/fy17osti/68963.pdf (accessed on 30 June 2022).
- Rouzbahani, H.M.; Rahimnejad, A.; Karimipour, H. Smart Households Demand Response Management with Micro Grid. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies Conference, Washington, DC, USA, 18–21 February 2019; pp. 1–5. [Google Scholar]
- Uddin, M.; Romlie, M.F.; Abdullah, M.F.; Abd Halim, S.; Kwang, T.C. A review on peak load shaving strategies. Renew. Sustain. Energy Rev. 2018, 82, 3323–3332. [Google Scholar] [CrossRef]
- Rana, M.M.; Romlie, M.F.; Abdullah, M.F.; Uddin, M.; Sarkar, M.R. A novel peak load shav-ing algrithm for isolated microgrid using hybrid PV-BESS system. Energy 2021, 234, 121157. [Google Scholar] [CrossRef]
- Abdelsalam, A.A.; Zedan, H.A.; Eldesouky, A.A. Energy Management of Microgrids Using Load Shifting and Multi-agent System. J. Control. Autom. Electr. Syst. 2020, 31, 1015–1036. [Google Scholar] [CrossRef]
- Laboratory for Advanced Software Systems. Available online: https://lass.cs.umass.edu/projects/smart/ (accessed on 30 May 2022).
- Kondaiah, V.; Balasubramanian, S.; Sanjeevkumar, P.; Baseem, K. A Review on Short-Term Load Forecasting Models for Mi-cro-grid Application. J. Eng. 2022, 2022, 665–689. [Google Scholar] [CrossRef]
- Vivas, E.; Allende-Cid, H.; Salas, R. A Systematic Review of Statistical and Machine Learning Methods for Electrical Power Forecasting with Reported MAPE Score. Entropy 2020, 22, 1412. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, N.; Chen, X. A Short-Term Residential Load Forecasting Model Based on LSTM Recurrent Neural Network Considering Weather Features. Energies 2021, 14, 2737. [Google Scholar] [CrossRef]
- Singh, S.; Hussain, S.; Bazaz, M.A. Short term load forecasting using artificial neural network. In Proceedings of the 2017 Fourth International Conference on Image Information Processing (ICIIP), Shimla, India, 21–23 December 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, D.; Jiang, H.; Wang, L.; Chen, Y.; Xiao, Y.; Liu, J.; Zhang, Y.; Li, M. Load Forecasting Based on LSTM Neural Network and Applicable to Loads of “Re-placement of Coal with Electricity”. J. Electr. Eng. Technol. 2021, 16, 2333–2342. [Google Scholar] [CrossRef]
- Tayab, U.B.; Zia, A.; Yang, F.; Lu, J.; Kashif, M. Short-term load forecasting for microgrid energy management system using hybrid HHO-FNN model with best-basis stationary wavelet packet transform. Energy 2020, 203, 117857. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Zakeri, S.; Shoaran, M.; Mohammadi-Ivatloo, B.; Mohammadi, F. Short-Term Load Forecasting of Microgrid via Hybrid Support Vector Regression and Long Short-Term Memory Algorithms. Sustainability 2020, 12, 7076. [Google Scholar] [CrossRef]
- Quilumba, F.L.; Lee, W.-J.; Huang, H.; Wang, D.Y.; Szabados, R.L. Using Smart Meter Data to Improve the Accuracy of Intra-day Load Forecasting Considering Customer Behavior Similarities. IEEE Trans. Smart Grid 2015, 6, 911–918. [Google Scholar] [CrossRef]
- Lee, G.-C. Regression-Based Methods for Daily Peak Load Forecasting in South Korea. Sustainability 2022, 14, 3984. [Google Scholar] [CrossRef]
- Caliano, M.; Buonanno, A.; Graditi, G.; Pontecorvo, A.; Sforza, G.; Valenti, M. Consumption based-only load forecasting for individual households in nanogrids: A case study. In Proceedings of the 2020 AEIT International Annual Conference (AEIT), Catania, Italy, 23–25 September 2020. [Google Scholar] [CrossRef]
- Dong, H.; Gao, Y.; Fang, Y.; Liu, M.; Kong, Y. The Short-Term Load Forecasting for Special Days Based on Bagged Regression Trees in Qingdao, China. Comput. Intell. Neurosci. 2021, 2021, 3693294. [Google Scholar] [CrossRef] [PubMed]
- Kelo, S.; Dudul, S. A wavelet Elman neural network for short-term electrical load prediction under the influence of tempera-ture. Int. J. Electr. Power Energy Syst. 2012, 43, 1063–1071. [Google Scholar] [CrossRef]
- Khwaja, A.S.; Zhang, X.; Anpalagan, A.; Venkatesh, B. Boosted neural networks for improved short-term electric load fore-casting. Electr. Power Syst. Res. 2017, 143, 431–437. [Google Scholar] [CrossRef]
- Borghini, E.; Giannetti, C.; Flynn, J.; Todeschini, G. Data-Driven Energy Storage Scheduling to Minimise Peak Demand on Distribution Systems with PV Generation. Energies 2021, 14, 3453. [Google Scholar] [CrossRef]
- Szczepanik, W.; Niemiec, M. Heuristic Intrusion Detection Based on Traffic Flow Statistical Analysis. Energies 2022, 15, 3951. [Google Scholar] [CrossRef]
- Vairagade, N.; Logofatu, D.; Leon, F.; Muharemi, F. Demand Forecasting Using Random Forest and Artificial Neural Network for Supply Chain Management. In Computational Collective Intelligence, Proceedings of the 11th International Conference, ICCCI 2019, Hendaye, France, 4–6 September 2019; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; pp. 328–339. [Google Scholar] [CrossRef]
- Rahul, G.K.; Singh, S.; Dubey, S. Weather Forecasting Using Artificial Neural Networks. In Proceedings of the 2020 8th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), Noida, India, 4–5 June 2020; pp. 21–26. [Google Scholar] [CrossRef]
- Tran, T.; Bateni, S.; Ki, S.; Vosoughifar, H. A Review of Neural Networks for Air Temperature Forecasting. Water 2021, 13, 1294. [Google Scholar] [CrossRef]
- Radicioni, M.; Lucaferri, V.; De Lia, F.; Laudani, A.; Presti, R.L.; Lozito, G.; Fulginei, F.R.; Schioppo, R.; Tucci, M. Power Forecasting of a Photovoltaic Plant Located in ENEA Casaccia Research Center. Energies 2021, 14, 707. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Muthuramalingam, T.; Shanmugan, S.; Ibrahim, A.M.M.; Ramesh, B.; Khoshaim, A.B.; Moustafa, E.B.; Bedairi, B.; Panchal, H.; Sathyamurthy, R. Fine-tuned artificial intelligence model using pigeon optimizer for prediction of residual stresses during turning of Inconel 718. J. Mater. Res. Technol. 2021, 15, 3622–3634. [Google Scholar] [CrossRef]
- Moustafa, E.B.; Hammad, A.H.; Elsheikh, A.H. A new optimized artificial neural network model to predict thermal efficiency and water yield of tubular solar still. Case Stud. Therm. Eng. 2021, 30, 101750. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Panchal, H.; Ahmadein, M.; Mosleh, A.O.; Sadasivuni, K.K.; Alsaleh, N.A. Productivity forecasting of solar distiller integrated with evacuated tubes and external condenser using artificial intelligence model and moth-flame optimizer. Case Stud. Therm. Eng. 2021, 28, 101671. [Google Scholar] [CrossRef]
- Lizhen, W.; Yifan, Z.; Gang, W.; Xiaohong, H. A novel short-term load forecasting method based on mini-batch stochastic gradient descent regression model. Electr. Power Syst. Res. 2022, 211, 108226. [Google Scholar] [CrossRef]
- Phyo, P.-P.; Jeenanunta, C. Advanced ML-Based Ensemble and Deep Learning Models for Short-Term Load Forecasting: Comparative Analysis Using Feature Engineering. Appl. Sci. 2022, 12, 4882. [Google Scholar] [CrossRef]
- Kim, D.-H.; Lee, E.-K.; Qureshi, N. Peak-Load Forecasting for Small Industries: A Machine Learning Approach. Sustainability 2020, 12, 6539. [Google Scholar] [CrossRef]
- Hodo, E.; Bellekens, X.; Iorkyase, E.; Hamilton, A.; Tachtatzis, C.; Atkinson, R. Machine Learning Approach for Detection of nonTor Traffic. In Proceedings of the 12th International Conference on Availability, Reliability and Security, Reggio Calabria, Italy, 29 August–1 September 2017; p. 85. [Google Scholar] [CrossRef] [Green Version]
- Aponte, O.; McConky, K. Peak electric load days forecasting for energy cost reduction with and without behind the meter renewable electricity generation. Int. J. Energy Res. 2021, 45, 18735–18753. [Google Scholar] [CrossRef]
- Hernandez, L.; Baladrón, C.; Aguiar, J.M.; Carro, B.; Sanchez-Esguevillas, A.J.; Lloret, J. Short-Term Load Forecasting for Microgrids Based on Artificial Neural Networks. Energies 2013, 6, 1385–1408. [Google Scholar] [CrossRef]
- Li, R.; Sun, F.; Ding, X.; Han, Y.; Liu, Y.P.; Yan, J.R. Ultra short-term load forecasting for user-level integrated energy system considering multi-energy spatio-temporal coupling. Power Syst. Technol. 2020, 44, 4121–4134. [Google Scholar]
- Zhu, R.; Guo, W.; Gong, X. Short-Term Load Forecasting for CCHP Systems Considering the Correlation between Heating, Gas and Electrical Loads Based on Deep Learning. Energies 2019, 12, 3308. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, L.; Chen, J.; Wu, G.; Ni, S.; Hu, Z.; Weng, C.; Chen, Z. Multiple-Load Forecasting for Integrated Energy System Based on Copula-DBiLSTM. Energies 2021, 14, 2188. [Google Scholar] [CrossRef]
- Activation Functions. Available online: https://paperswithcode.com/methods/category/activation-functions (accessed on 25 June 2022).
- Publication Ready NN-Architecture Schematics. Available online: https://alexlenail.me/NN-SVG/ (accessed on 20 August 2022).
- Elsheikh, A.H.; Sharshir, S.W.; Elaziz, M.A.; Kabeel, A.; Guilan, W.; Haiou, Z. Modeling of solar energy systems using artificial neural network: A comprehensive review. Sol. Energy 2019, 180, 622–639. [Google Scholar] [CrossRef]
- Azeem, A.; Ismail, I.; Jameel, S.M.; Romlie, F.; Danyaro, K.U.; Shukla, S. Deterioration of Electrical Load Forecasting Models in a Smart Grid Environment. Sensors 2022, 22, 4363. [Google Scholar] [CrossRef] [PubMed]
- Greater Boston Rates. Available online: https://www.eversource.com/content/docs/default-source/rates-tariffs/ema-greater-boston-rates.pdf (accessed on 30 June 2022).
- Shohan, M.J.A.; Faruque, M.O.; Foo, S.Y. Forecasting of Electric Load Using a Hybrid LSTM-Neural Prophet Model. Energies 2022, 15, 2158. [Google Scholar] [CrossRef]
- Mahjoub, S.; Chrifi-Alaoui, L.; Marhic, B.; Delahoche, L. Predicting Energy Consumption Using LSTM, Multi-Layer GRU and Drop-GRU Neural Networks. Sensors 2022, 22, 4062. [Google Scholar] [CrossRef] [PubMed]
- Petrosanu, D.-M.; Pîrjan, A. Electricity Consumption Forecasting Based on a Bidirectional Long-ShortTerm Memory Artificial Neural Network. Sustainability 2021, 13, 104. [Google Scholar] [CrossRef]
- Complete guide to Bi-Directional LSTM (With Python Codes). Available online: https://analyticsindiamag.com/complete-guide-to-bidirectional-lstm-with-python-codes/ (accessed on 30 August 2022).








| Paper Title | Classification | Algorithm | Summary/Results | Area |
|---|---|---|---|---|
| [6] A novel hybrid forecasting scheme for electricity demand time series’ | Statistical | ARIMA | Spain’s grid load forecasting has been performed while incorporating non-linear effects of temperature and special days for hourly 1 to 10 days ahead demand. | Grid |
| [28] Regression-Based Methods for Daily Peak Load Forecasting in South Korea | Statistical | ARIMA | Implementation of ARIMA in a South Korean grid showed a MAPE of 1.95%. | Grid |
| [7] Microgrid Load Forecasting Based on Improved Long Short-Term Memory Network | ML | LSTM | The model has been implemented for a micro-grid utilizing 5 years of load data. Results show improvement by reduction of MAPE from 8% to within 4%. | Microgrid |
| [10] Enhanced Short-Term Load Forecasting Using Artificial Neural Networks | ML | ANN | This work predicts load forecasting for Greek Intercontinental Power System with various scaling methods for input data. Based on the scaling method, MAPE changes from 2.73% to 1.76%. | Grid |
| [11] Deep Learning for Short-Term Load Forecasting: Industrial Consumer Case Study | ML & Statistical | GRU, ARIMA, LSTM, RNN and their combinations | Woodworking factory’s load was predicted using numerous mentioned methods. Amongst these, GRU outperformed others with a MAPE of 4.82%. Exogenous and lagged load data were used as input features. | Factory (Microgrid) |
| [29] Short and mid-term load forecasting using machine learning models | ML & Statistical | LR, SVR, GBRT | New York Independent System Operators (NYISO) dataset was used for the implementation of these algorithms and a comparison, on basis of MAPE, was drawn. Previous load and meteorological data were used as input features. It was found that the hybrid model AdaBoost and GBRT showed improved results with the MAPE of 2.27%. | Grid |
| [9] Load Forecasting for Different Prediction Horizons using ANN and ARIMA models | ML & Statistical | ANN & ARIMA | Microgrid load has been trained using ANN and compared with ARIMA. ANN captures more random behavior which is corroborated by the results: ANN is 0.5% more accurate than ARIMA in day-ahead prediction and 3.5% more accurate in an hour-ahead prediction. | Microgrid |
| Parameters | ANN | LSTM | GRU | BI-LSTM |
|---|---|---|---|---|
| Input Features | Meteorological and electrical load features | Electric load time series | Electric load time series | Electric load time series |
| Output | Hourly load forecast | Hourly load forecast | Hourly load forecast | Hourly load forecast |
| Number of hidden layers | 3 | 1 | 1 | 1 |
| Number of neurons in 1st hidden layer | 30 | - | - | - |
| Number of neurons in 2nd hidden layer | 30 | - | - | - |
| Number of neurons in 3rd hidden layer | 20 | - | - | - |
| Number of internal nodes | - | 200 | 200 | 200 |
| Learning Rate | 0.0001 | 0.001 | 0.001 | 0.001 |
| Internal Optimizer | Adam | Adam | Adam | Adam |
| Epoch | 300 | 10 | 10 | 10 |
| Activation Function | ReLu | ReLu | ReLu | ReLu |
| Batch Size | 32 | 32 | 32 | 32 |
| Regularization | l-1 on 3rd hidden layer | - | - | - |
| Weight Initialization | Random | Random | Random | Random |
| Evaluation Parameters | ANN | LSTM | GRU | Bi-Directional LSTM |
|---|---|---|---|---|
| MSE (KW) | 0.03 | 0.37 | 0.34 | 0.35 |
| RMSE (KW) | 0.17 | 0.60 | 0.55 | 0.59 |
| MAPE (%) | 9.00 | 28.0 | 26.1 | 25.0 |
| CV (%) | 11.9 | 33.7 | 32.3 | 32.8 |
| Training Time (min) | 7.50 | 39.40 | 27.6 | 38.7 |
| Date | Hour Indices for Peak Load | Daily Energy Cost without Peak Shifting ($) | Daily Energy Cost with Peak Shifting ($) | Energy Cost Saving (%) |
|---|---|---|---|---|
| 2016 August 20 | 4:00 PM | 0.28 | 0.22 | 21.0% |
| 2016 August 21 | 12:00 PM | 0.77 | 0.58 | 24.3% |
| 2016 August 22 | 6:00 PM | 0.12 | 0.09 | 24.3% |
| 2016 August 23 | 2:00 PM, 3:00 PM, 4:00 PM, 5:00 PM, 9:00 PM | 0.51 | 0.41 | 19.2% |
| 2016 August 24 | 3:00 PM, 4:00 PM, 5:00 PM, 6:00 PM, 7:00 PM | 1.08 | 0.81 | 24.3% |
| 2016 August 25 | 2:00 PM, 3:00 PM, 5:00 PM | 0.75 | 0.56 | 25.0% |
| 2016 August 26 | 3:00 PM, 4:00 PM, 6:00 PM | 0.33 | 0.26 | 20.9% |
| Week | Weekly Energy Cost without Peak Shifting ($) | Weekly Energy Cost with Peak Shifting ($) | Cost Saving (%) | |
|---|---|---|---|---|
| Extreme Summer | 2016 July 15 to 2016 July 21 | 6.03 | 5.02 | 16.7 |
| Extreme Winter | 2016 February 1 to 2016 August 1 | 28.4 | 25.9 | 8.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Yan, B.; Bilton, A. Machine Learning-Based Load Forecasting for Nanogrid Peak Load Cost Reduction. Energies 2022, 15, 6721. https://doi.org/10.3390/en15186721
Kumar A, Yan B, Bilton A. Machine Learning-Based Load Forecasting for Nanogrid Peak Load Cost Reduction. Energies. 2022; 15(18):6721. https://doi.org/10.3390/en15186721
Chicago/Turabian StyleKumar, Akash, Bing Yan, and Ace Bilton. 2022. "Machine Learning-Based Load Forecasting for Nanogrid Peak Load Cost Reduction" Energies 15, no. 18: 6721. https://doi.org/10.3390/en15186721
APA StyleKumar, A., Yan, B., & Bilton, A. (2022). Machine Learning-Based Load Forecasting for Nanogrid Peak Load Cost Reduction. Energies, 15(18), 6721. https://doi.org/10.3390/en15186721







