1. Introduction
Even with the COVID-19-induced economic slowdown, the renewable power sector is continuously experiencing high growth in installed capacity, with more than 260 Gigawatts (GW) in 2021, mostly by solar photovoltaic (PV). This fact led to a total installed capacity of 3064 GW [
1]. The highest increase ever is due in large part to political support and cost reductions. In most countries, producing electricity from solar PV and wind is becoming increasingly more cost-effective than generating it from coal and gas power plants [
2]. The solar PV market increased in 2021 to a record 175 GWdc, for a total power capacity of 942 GWdc [
3]. A recent investigation by the BloombergNEF company shows that the global benchmark levelized cost of electricity (LCOE) [
4] for fixed-axis utility-scale PV is
$46 per megawatt-hour (MWh) in the first half of 2022, while some of the cheapest PV projects were able to achieve an LCOE of
$21/MWh for tracking PV farms in Chile with very competitive returns. In 2022, the solar PV market experienced strong competitiveness between PV module manufacturers with new yields of up to 22.8% [
5]. Despite this progress, numerous challenges remain to be solved before solar PV can become a significant source of power generation worldwide, leading to a sustainable energy future [
6].
Like all electricity production systems, solar PV systems are often subject to various faults and failures that significantly affect their components, such as PV modules, cables, protection circuits, inverters, etc. [
7]. The most general effect of faults is the loss of energy, which is caused by one or more independent anomalies and failures. Some electrical faults cause total shutdowns of PV plants, and other faults such as electric arcs can cause fires, which leads to shortfalls and loss of income. Early detection of such faults is crucial to prevent critical PV system failures and increase their reliability with a high quality of performance. Over the past few years, the Fault Detection and Diagnosis (FDD) of solar PV systems has become a topical research topic for many researchers [
8,
9]. Generally, anomalies or faults occurring in grid-connected PV systems can be classified primarily according to the side of the fault in the PV installation, either the DC side before the inverter or the AC side at the output of the inverter up to the point of injection [
8]. Faults in the DC side of PV systems, which are principally located in the PV array, include; temporary and permanent mismatches, hotspot, degradation, short circuit, open circuit, electrical arc, line–line, and line–ground faults, as well as the DC/DC converter fault inside the PV grid-tie inverter. On the AC side, total blackout and grid abnormalities (unbalanced voltage and lightning) are the types of faults commonly found in PV systems [
10]. A statistical study of the power loss evaluation and clustering of faults affecting PV systems installed in different climate zones in the world helps to decrease the number of faults in the new PV installations [
11]. The experimental data from PV installed systems show that a better operation and maintenance (O&M) service significantly improves the average performance ratio from 88% to 94%, and as a result, profits and environmental benefits are increased. Indeed, improvements of the PV O&M include the following: (1) increasing efficiency and energy production, (2) extending the lifetime of PV systems (25 to 40 years), (3) decreasing system downtime, (4) reducing the possible risks and ensuring safety and (5) reducing the cost of O&M [
12,
13].
Continuous and real-time monitoring of PV systems is essential during their working cycle to ensure the rapid detection of faults, reduce downtime, maintain long-term profitability, and exploit their full power. The key point of reliable monitoring and FDD strategy is related to the quality of measurement accuracy of both meteorological and electrical data of the PV system. Without a reliable monitoring system, the PV system is often expected to operate with poor performance for a limited time period before the fault is detected and identified. This fact generally results in a major loss of income [
13].
An FDD tool based on the Artificial Neural Network (ANN) algorithm using Laterally Primed Adaptive Resonance Theory (LAPART) was developed in [
14] in order to detect module-level faults with minimal error. The results showed that the LAPART algorithm can quickly learn PV performance data (only 4 days of one-minute data) and provide an accurate multi-level FDD tool. Other FDD methods include the k-Nearest Neighbors (kNN) algorithm, which is a non-parametric method used for regression models and fault classification [
15]. In [
16], four approaches made by EWMA (Exponentially Weighted Moving Average) schemes and kNN-based Shewhart with parametric and non-parametric models were used to detect faults. The results obtained showed a high capability for detecting short-circuit faults, open-circuit faults, and temporary shading, whereas this algorithm does not have the ability to distinguish the partial shading among faults occurring on the DC side of the PV array. A real-time detection and classification technique based on the clustering kNN rule was proposed in [
15]. This technique does not require any predefined threshold to classify the faults; the threshold values are unknown and difficult to choose for each PV system due to the strong dependence of the output power on the climatic conditions. In [
17], a C4.5 decision tree (DT) approach is proposed to detect and diagnose the faults in a Grid-Connected PV system (GCPV) using a non-parametric model by learning the task. In this work, a semi-empirical model by Sandia National Laboratories (SNL) was used to predict the power produced from the PV array under normal operation conditions (fault-free). Then, the supervised decision tree algorithm was exploited to classify four cases: (1) fault-free, (2) string fault, (3) short-circuit fault, and (4) line-line fault. The results obtained showed a high accuracy of around 99.86% for detection and 99.80% for diagnosis. This supervised learning method requires data from several sets of training examples to build a good classifier that can distinguish between different faults. The authors in [
18] used the ANN technique and FL (Fuzzy Logic) system interface to develop a PV FDD algorithm that has been tested to detect ten faults cases, such as a combination of four cases of faulty PV modules and two cases of low and high partial shading. In such a PV FDD algorithm, the voltage and power variations of the studied PV system were used as input for both the ANN technique and the FL system. An unsupervised monitoring approach for detecting anomalies and faults in PV installations using a one-class SVM technique is proposed in [
19], where the one-diode model is used under PSIMTM to simulate the normal operation of the PV array, while the one-class SVM technique is applied to calculate residuals between measured and simulation data for FDD. The use of machine learning techniques (MLT) is advantageous in the sense that they have rapid detection response, they allow distinguishing among faults of the same signature and classifying faults with high accuracy, and setting threshold limits is not required. Nevertheless, the FDD accuracy depends proportionally on the trained PV model to estimate the expected energy yield. Moreover, these techniques require more advanced skills for real-time hardware and software implementation, and obtaining a training dataset of all possible faults scenarios could be difficult.
Accurate monitoring of PV plants is necessary to meet the desired specifications regarding power production and safety and help avoid serious incidents. Machine learning techniques have demonstrated themselves as a prominent field of study within a data-driven framework over the last decade by addressing numerous challenging and complex real-world problems [
20,
21,
22,
23,
24]. Thus, this study aims to design a semi-supervised data-driven detector for anomaly detection in PV plants that do not require labeled data. Unlike supervised methods, semi-supervised anomaly detection methods aim to train the detection model using a normal event dataset only, which make them more attractive for detecting anomalies in PV plants, since it is not always easy to obtain accurately labeled data. Until now, very few research papers have investigated integrating machine learning models and statistical control charts for fault detection in multivariate data. The contribution of this work is threefold as summarized below.
This paper aims to develop flexible and efficient semi-supervised machine learning-driven methodologies to improve the operation and performance of PV plants. These semi-supervised approaches only employ normal events data without labeling to train the detection models, making them more attractive for detecting faults in practice. This study presents a semi-supervised monitoring approach for anomaly detection in PV plants by combining the advantages of the ensemble learning models and the Double Exponentially Weighted Moving Average (DEWMA) chart. In the last decade, ensemble learning-driven methods (e.g., boosting and bagging models), which combine several single models, have demonstrated a promising solution compared to traditional machine learning methods. Notably, ensemble models are characterized by their ability to reduce the model’s variance while achieving a low bias, making them appealing to improve prediction quality [
25]. Overall, an efficient monitoring strategy relies principally on the accuracy of the adopted modeling method and the sensitivity of the anomaly detection technique. Here, we employed ensemble learning methods to exploit their capability to enhance the modeling precision of the PV monitored system. On the other hand, the key characteristic of the DEWMA scheme resides in its capacity to enclose all of the information from past and actual samples in the detection statistic, which makes it sensitive for uncovering anomalies with small magnitudes. In the proposed approach, ensemble learning models are used for residual generation. Essentially, residuals are close to zero in the absence of anomalies, while residuals diverge from zero in the presence of anomalies. The DEWMA detector is employed to check the generated residuals to uncover possible anomalies in the inspected PV array.
Additionally, in this work, Bayesian optimization (BO) has been adopted to optimally tune hyperparameters of the boosted trees (BS) and bagged trees (BG) models. Specifically, the BO is used to find the optimal parameters of the ensemble models based on training data (anomaly-free data). This enables obtaining more accurate prediction models and improves the detection performance.
Note that the detection threshold in the DEWMA chart is computed based on the Gaussian assumption of data. Here, to extend further the flexibility of the proposed fault detection method, we employed kernel density estimation (KDE) to compute the detection threshold in a non-parametric way. We assessed the effectiveness of the considered fault detection approaches on real data from a 9.54 kWp photovoltaic system. The detection capacity of the proposed approaches is investigated in the presence of different types of faults. Six statistical scores are computed to judge the fault detection quality. Results revealed the promising performance of the proposed approaches in detecting various types of anomalies in a PV system.
This paper is structured as follows. The studied PV system is briefed in
Section 2. Then, the BS and BG models are introduced in
Section 3. In
Section 4, after presenting the DEWMA scheme, we introduce the proposed approach. The experimental results are provided In
Section 5. Lastly, conclusions are offered in
Section 6.
2. PV System Description
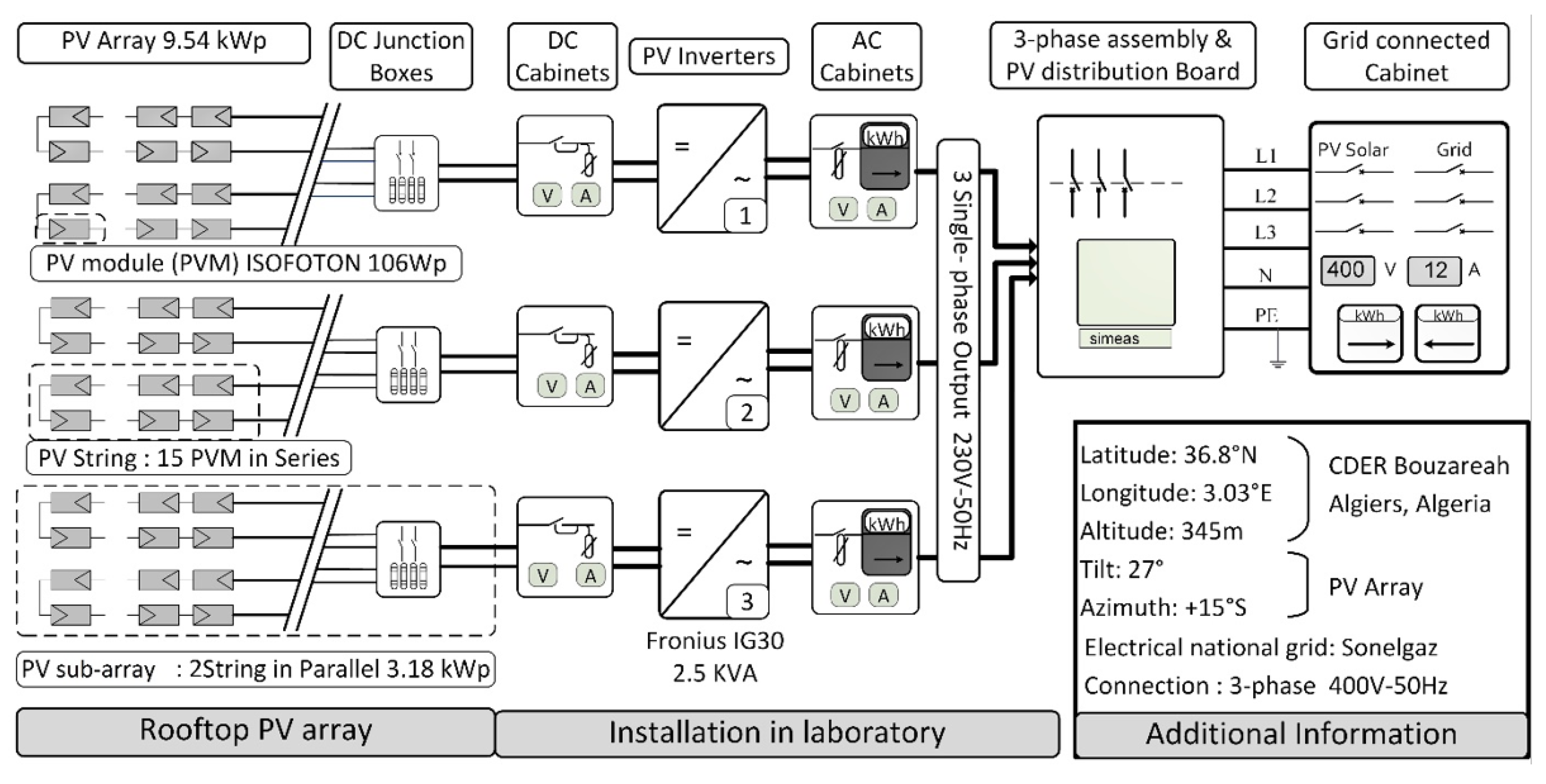
This section is devoted to presenting briefly the grid-tied PV system used in this study. Indeed, the proposed algorithm for fault detection in this work will be verified using the meteorological and electrical data measurement collected from a 9.54 kWp PV system at the Renewable Energy Development Center (CDER) in Algeria. This PV system contains 90 PV modules with a total power of 9.54 kWdc in operation since 2004; it is composed of three identical single-phase PV sub-systems (
Figure 1).
The entire produced PV energy is injected into the low-voltage electrical grid. As shown in
Figure 1, each PV sub-system consists of a 3.18 kW sub-array, grid-tie inverter, and electrical cabinets for protection. The sub-array contains two parallel strings of 15 PV modules (PVM) in a series.
Table 1 and
Table 2 display, respectively, the main technical specifications of the PV sub-array and the PV inverter.
Here, the STC refers to Standard Test Conditions (irradiance =1000 W/m, cell temperature =25 °C, air mass = 1.5) and MPP denotes Maximum Power Point. G is the received irradiance by the PV module during the flash test, TC is the temperature of the PV cell, and AM is the air mass. VOC is the open circuit voltage, ISC is the short circuit current, VMPP is the voltage at MPP, IMPP is the current at MPP, and PM is the maximum power.
The meteorological and electrical measured data used in this work are recovered by an external monitoring system composed essentially of sensors, data acquisition unit Agilent 34970A, and software under PC (
Figure 2).
For the measure of tilted irradiance at 27 °C, a pyranometer and a reference cell are used, and a thermocouple measures the ambient temperature. The DC voltage at the MPP of the PV sub-array is measured by a simple voltage divider circuit, while a voltage transformer measures the AC voltage at the inverter output. A hall-effect sensor was used to measure the current on both the DC and AC sides of the PV inverter.
Table 3 reviews the measured parameters with the main sensor information. Agilent 34970A provides the conditioning and the measure of the signal at the sensor’s output. While the monitoring user interface is designed under LabVIEW software, this interface can recover, display, record, and analyze the measured data. According to IEC 61724 standard, the sampling time was chosen at 1 min, which gives 1440 samples per 24 h.
5. EWMA and DEWMA Monitoring Schemes
This subsection presents the basic idea behind the EWMA and the DEWMA monitoring charts. Unlike Shewhart charts employing only the value of the actual measurement, the EWMA and DEWMA charts, as control charts with memory, are not very sensitive in detecting small and moderate changes. Thus, they are better than Shewhart charts in uncovering changes with small magnitude in the process mean.
5.1. EWMA Monitoring Scheme
Roberts introduced the EWMA chart as a memory chart to bypass the limitations of the Shewhart chart in detecting small changes [
50]. In short, the EWMA chart is characterized by its use of information from the past and actual data points, making it sensitive to small changes [
51]. Lucas et al. investigated the statistical properties of the EWMA scheme and showed it has similar performance to the CUmulative SUM (CUSUM) scheme in sensing small changes. It is more straightforward to implement and use in practice than the CUSUM chart [
52,
53,
54]. The EWMA statistic is derived as a weighted linear combination of current and past data.
where
denotes the smoothing parameter such that
, and
is usually selected to be equal to the mean of fault-free data. Using small values of
provides less weight to the most recent data points and larger weight to the past observations. In other words,
regulates the memory depth of the EWMA chart. Crucially, the use of small values of
enables a more significant influence of the past observations, enabling the EWMA chart to be more capable of sensing small changes [
52,
55,
56]. In practice,
is usually chosen within the interval [0.15 0.3] for detecting anomalies with small or medium magnitude. We observe that the EWMA chart becomes similar to the Shewhart chart if
.
From (
10), we obtain the following formula by recursively substituting
,
We observe from (
11) that the weights
are decreasing exponentially with time, and the sum of these weights is unity because:
The upper and lower detection thresholds of the EWMA scheme are computed using the following equation.
where the factor
L represents the width of the decision thresholds. From (
13), the asymptotic thresholds are expressed as:
As it can be noticed, the
in (
13) becomes closer to unity in case of larger
t. The EWMA chart signals a potential fault if the EWMA statistic exceeds the decision thresholds. Here, we used the one-sided EWMA chart by using the absolute value of the EWMA charting statistic and only an upper detection threshold. More details on the EWMA chart can be found in [
57].
DEWMA Monitoring Approach
The DEWMA chart was introduced in [
58,
59] to improve the capability of the conventional EWMA approach to sense small changes in the process mean. The basic concept of the DEWMA is founded on the double exponentially weighted moving average, which is a common forecasting technique in time-series analysis. Several authors investigated the performance of the DEWMA in the litterature [
60,
61,
62,
63]. It has been shown in [
64] that the DEWMA outperformed the EWMA scheme in the detection fault with small and moderate magnitude. The two charts deliver relatively similar results in the case of large and moderate changes [
65]. The DEWMA charting statistic,
is derived as follows,
As it can be noticed, in the DEWMA chart, the exponential smoothing is carried out two times, and the
values are extra smoothed (compared to the
). Here, we use DEWMA with equal smoothing constant when computing
and
as recommended in [
64]. We can compute the variance of
as,
The asymptotic variance when
t is large is computed as follows,
The DEWMA scheme declares an anomaly if the charting statistic
overpasses the decision thresholds, UCL, and LCL.
5.2. Monitoring PV Systems Using Ensemble Learning Techniques Based DEWMA Chart
As discussed above, there are several motivations for utilizing ensemble learning methods with monitoring charts for fault detection purposes. The main motivation consists in the capacity of ensemble learning methods to model multivariate input–output data, and they outperform their alternative single models in many practical situations. It is known that using ensemble models reduces the prediction error compared to single models. Furthermore, monitoring charts, such as the EWMA and DEWMA, assume that data are uncorrelated. Therefore, there is a consequent need for some ensemble-driven models for generating uncorrelated residuals to enable successful fault detection using monitoring charts. In addition, these integrated ensemble learning techniques-based monitoring charts only employ the data of normal events to train the detection model, making them more attractive for detecting faults in PV systems, since it is not always easy to obtain accurately labeled data.
The proposed ensemble learning (BS and BG)-based DEWMA chart to detect anomalies in PV systems is briefly explained in this section and depicted in
Figure 10. Specifically, this approach is implemented in two main stages: model construction using training data and fault detection. At first, the ensemble learning models are trained using training data. Here, Bayesian optimization is used to optimally find values of the hyperparameters of the BS and BG models based on training data. In addition, in this step, the detection threshold of the DEWMA and EWMA charts are computed when applied to the residuals obtained from the ensemble learning models. Residuals represent the deviation separating the real output measurements and the predicted values from the ensemble learning model. Under normal operating conditions of the inspected PV systems, the residuals are around zero due to noise measurements and model errors; however, in the case of faulty conditions, the residuals deviate significantly from zero. Here, the ensemble learning models (BS and BG) are trained using fault-free data and then employed for monitoring new data. Then, in the second stage, the constructed models are used for residuals generation, and the DEWMA chart with the previously computed detection threshold is applied to detect potential anomalies in the monitored PV systems.
Note that the decision threshold of the DEWMA and EWMA charts is derived based on the Gaussian distribution of data. However, often in practice, the underlying distribution of data deviates from Gaussianity or is unknown. In such cases, the monitoring results would be unsuitable. To bypass this limitation, in this paper, a non-parametric kernel density estimation (KDE) method was used to set a detection threshold of the DEWMA and EWMA for fault detection. For more details about KDE, refer to [
66]. Importantly, it has been shown that the use of KDE to set up the detection threshold does not need to assume that the data follow a Gaussian distribution [
67,
68], which extends the flexibility of the monitoring charts. Thus, KDE-based detection thresholds are widely employed for process monitoring. A non-parametric detection threshold of the DEWMA chart using KDE is carried out as follows. First, we used KDE to estimate the distribution of the DEWMA statistic based on fault-free data. Given the DEWMA statistic
w, the PDF through the KDE is computed as follows.
where
is the kernel function, and
h is the kernel bandwidth parameter and refers to the number of samples. It is mentioned that the Gaussian kernel function is commonly used.
Now, the threshold of the distribution-free DEWMA chart is derived as the ()-th quantile of the estimated distribution of the DEWMA statistic computed via the KDE. We signal the presence of a potential anomaly if the DEWMA charting statistic exceeds the KDE-based threshold.
The DEWMA with a non-parametric detection threshold is performed as follows:
Step 1: Computing the DEWMA charting statistic (Equation (
18)) for each observation.
Step 2: Estimating the probability density function for given DEWMA measurements via KDE.
Step 3: Setting up the detection threshold based on the previously estimated distribution of DEWMA in a non-parametric way as the ()-th quantile.
Step4: Flagging out a fault if the DEWMA statistic is above the detection threshold.
To assess the efficiency of the studied ensemble learning-based monitoring charts, we used six most commonly used performance measures: true positive rate (TPR), false positive rate (FPR), accuracy, recall, F1-score, and area under curve (AUC), and EER (equal error rate) [
69]. For a binary detection problem, the number of true positives (TP), false positives (FP), false negatives (FN), and true negatives (TN) is utilized to calculate the performance measures. The
confusion matrix is depicted in
Figure 11. The six performance measures are computed as the following.
6. Results and Discussion
As discussed above, ensemble learning-based monitoring charts enable automatically flagging anomalies in the inspected PV system while avoiding false alarms during normal operating conditions. In this section, the ability of the proposed ensemble learning-based DEWMA schemes to detect anomalies in the DC side of a PV system is assessed. Here, the experimental data were collected from an actual PV system described in
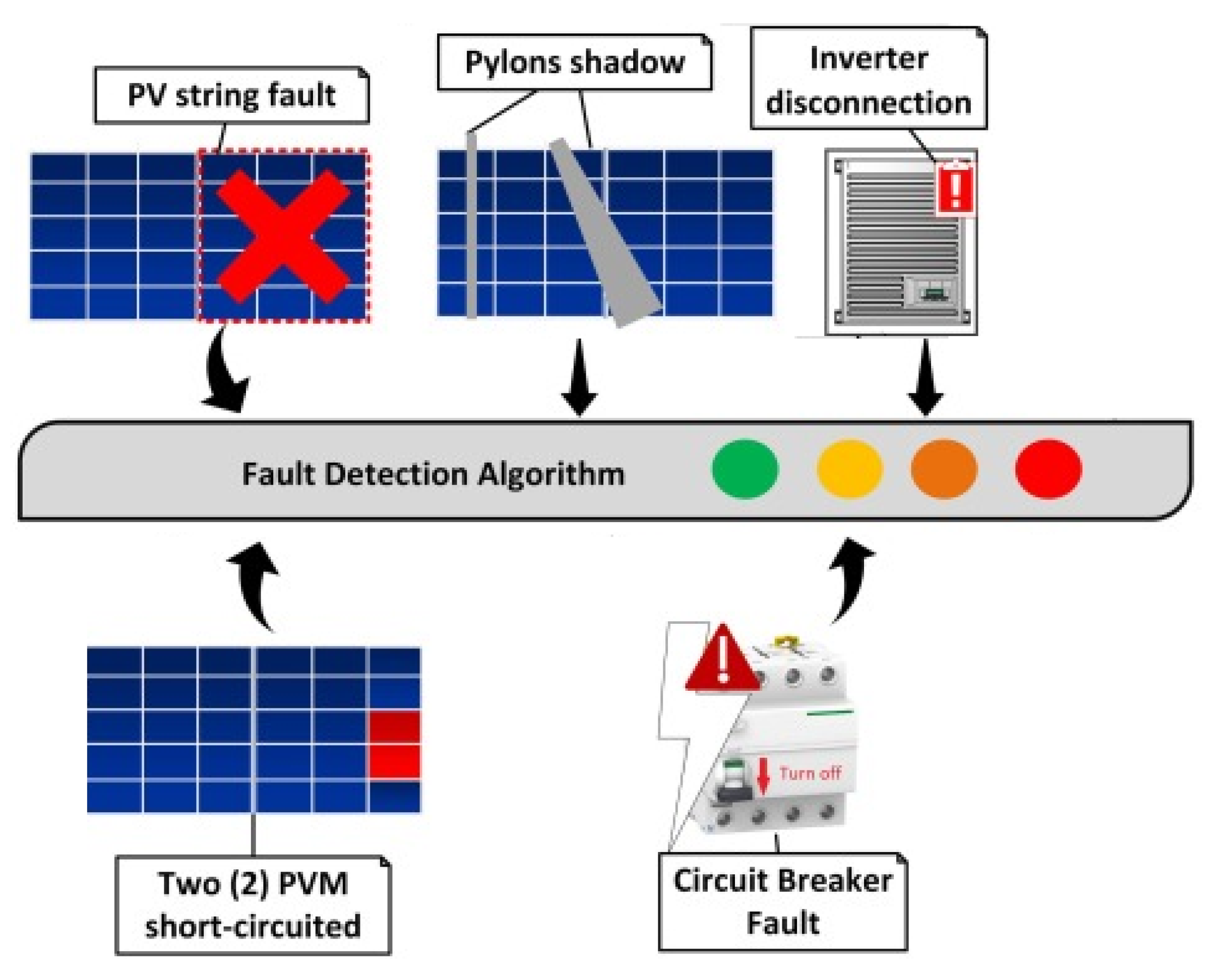
Section 2. This study considered five kinds of anomalies: PV string fault (F1), inverter disconnection (F2), circuit breaker faults (F3), partial shading of two pylons (F4), and two PV modules (PVM) short-circuited (F5), as they are represented in
Figure 12. For an effective fault detection approach, the TPR, accuracy, F1-score, and AUC values should be close to 1 so that all faulty data are detected. On the other hand, the FPR and EER values should be close to zero to avoid false alarms. For a fair comparison between the competing fault detection methods, in what follows, we used the optimized BG and BS models for each monitoring chart.
6.1. Scenarios with String Faults
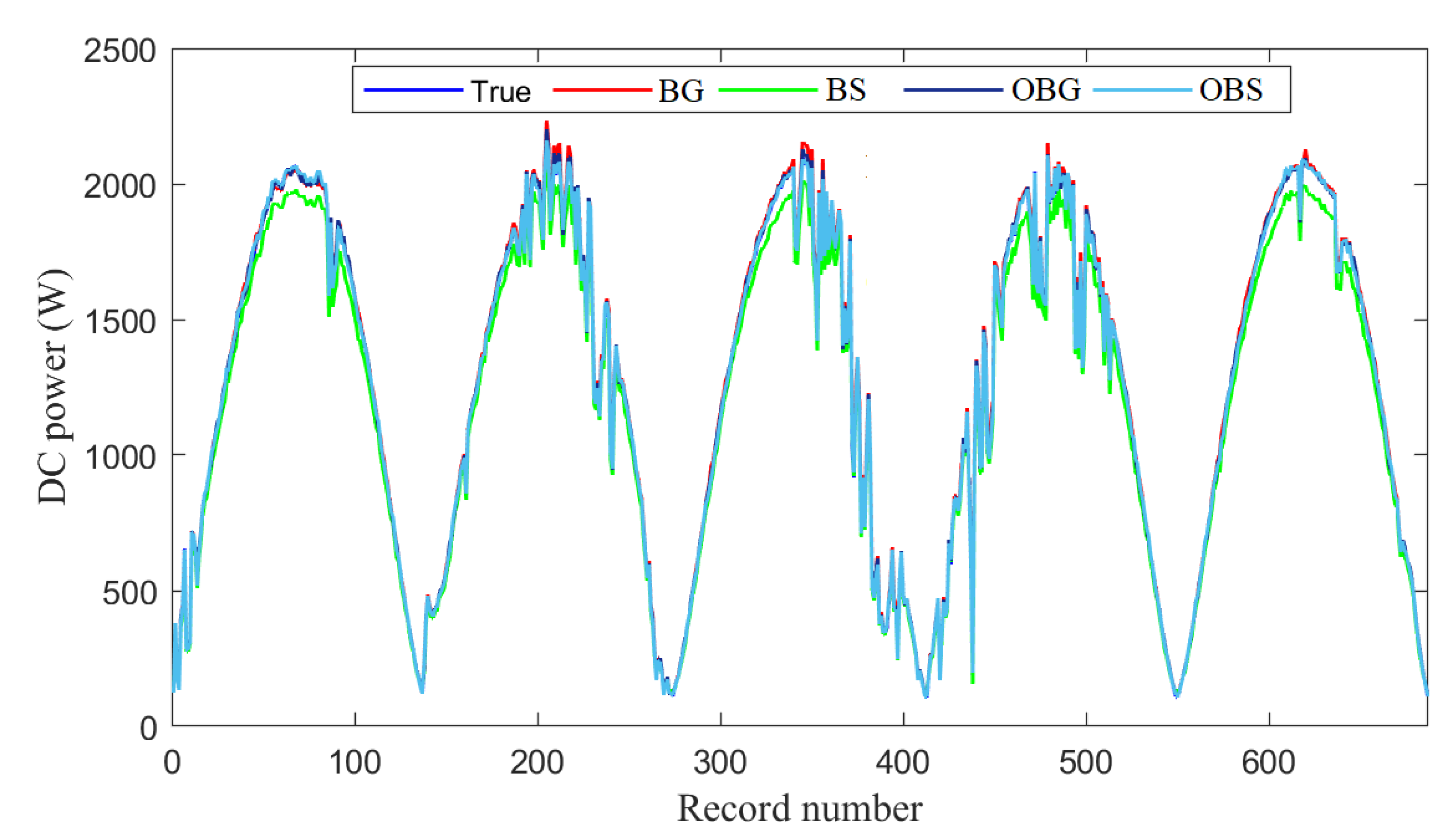
The aim of the first experiment is to study the efficiency of the proposed methods in detecting open-circuit faults in the monitored PV system. Broadly speaking, open-circuit faults could be caused by the deterioration of DC protection or the disconnection between PV modules in series. In this case, a string fault is intentionally generated by switching off the circuit breaker of the PV system. More specifically, we disconnect one string from the PV array. The results of the optimized ensemble models (BG)-based DEWMA and EWMA charts are provided in
Figure 13 and show the presence of energy losses in terms of DC power. The results based on BS-based schemes are omitted because they all provide relatively similar results. We observe that the considered monitoring charts with parametric and non-parametric thresholds perform similarly for detecting this severe fault that resulted in a decrease of relatively 50% of the rated power, making it easy to detect by the investigated models.
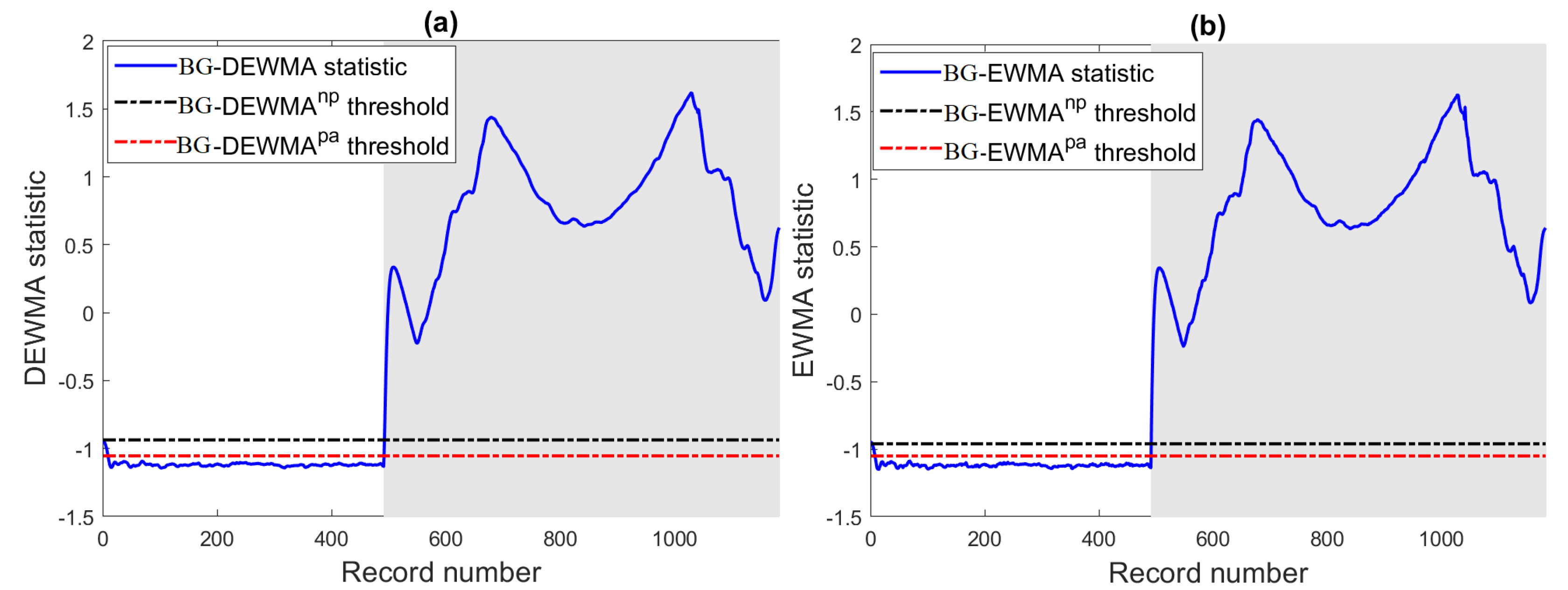
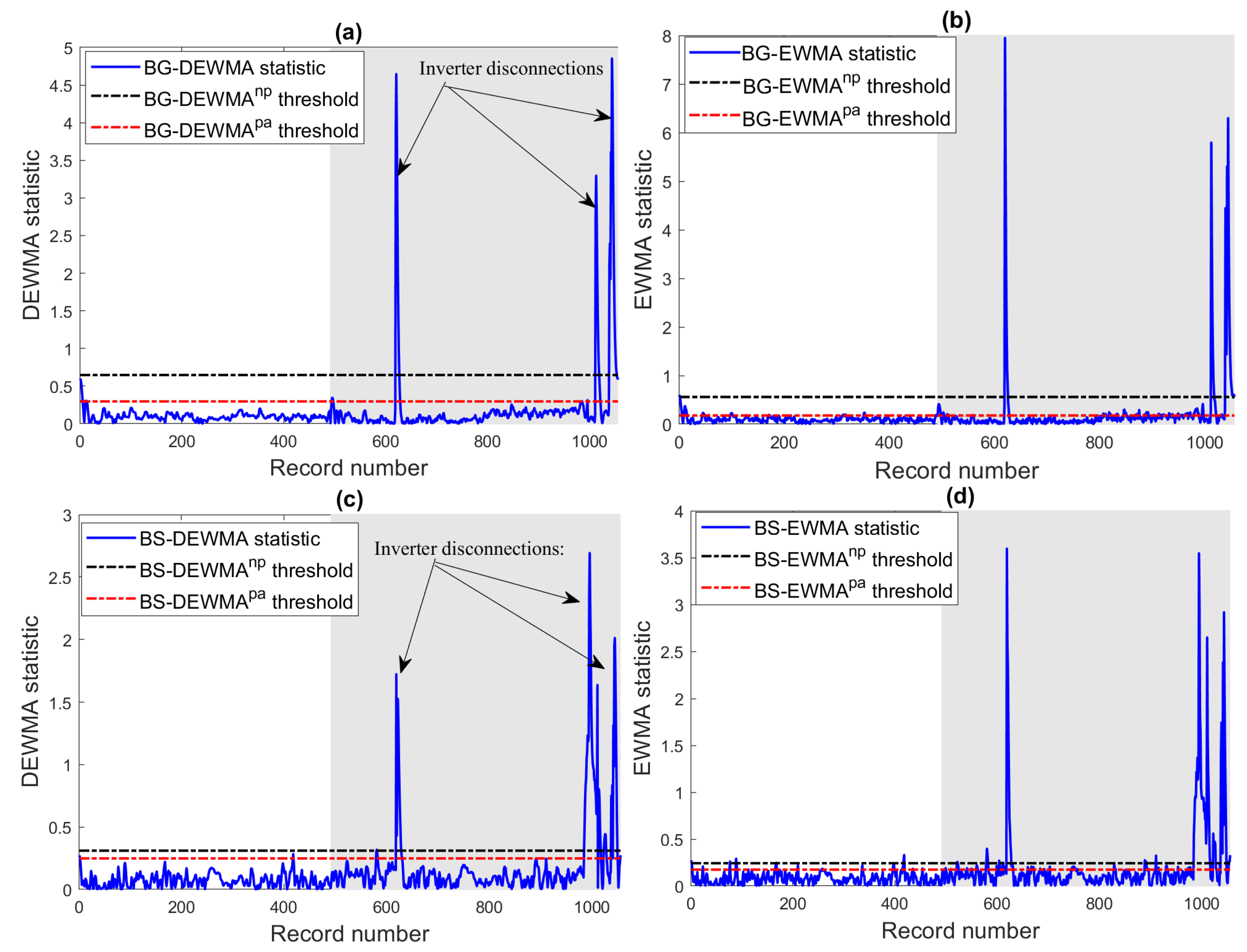
6.2. Scenarios with Inverter Disconnections
In the next experiments, the efficiency of the BG and BS-based DEWMA charts and the competing charts using both parametric and non-parametric thresholds have been investigated in the case of inverter disconnections. Broadly speaking, inverter disconnections are caused if the electrical characteristics exceed the operational limits of the inverter, which are usually given in the datasheet. Note that if inverter disconnections occur, the PV system will shut down until the re-connection of the inverter. In this case study, to verify the detection efficiency of the considered methods, we selected one day of data with inverter disconnection faults. Here, the inverter disconnections are caused by grid instability. More specifically, the voltage and frequency of the grid overpassed the inverter operating limits. Inverter disconnections can be recognized by their very short period and look like spikes, making them easy to discriminate from temporary shading and string faults.
The monitoring results of the investigated ensemble learning-based fault detection charts are depicted in
Figure 14. Visually,
Figure 14 indicates that these inverter disconnections have been recognized by the considered charts. In addition, we observe that residuals of DC power from the BG and BS models deviate significantly from zero (
Figure 14). This means that the constructed models describe well the fault-free data and diverge in the presence of faults.
Table 7 lists the detection performance of the considered charts in terms of the five commonly used evaluation scores. As the magnitude of this fault is large,
Table 7 clearly indicates that the considered charts easily detect this fault. The results in this table also revealed that the BG and BS-based DEWMA charts with non-parametric thresholds achieved the best performance compared to the other charts. Here, the BS-DEWMA obtained the best detection with an AUC of 0.99, which was followed by the BG-DEWMA chart with an AUC of 0.9881. This could be due to the use of non-parametric thresholds, allowing the DEWMA to be more sensitive than other considered charts. Note that for this fault with a large magnitude, the two types of DEWMA charts (parametric and non-parametric) have slightly similar performance.
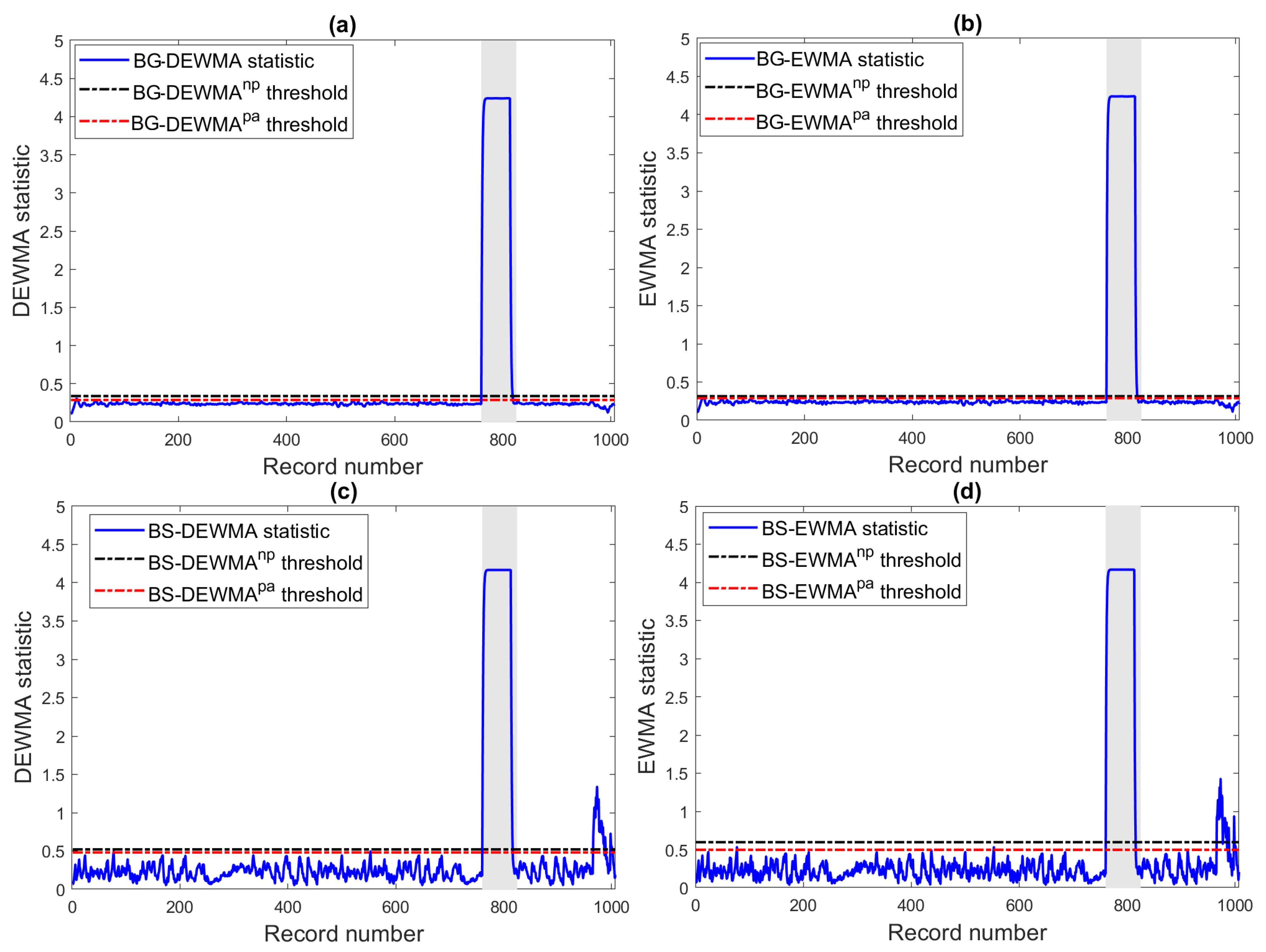
6.3. Scenario with Circuit Breaker Faults
The third experiment aimed to assess the ability of the proposed monitoring schemes in detecting circuit breaker fault failures. Crucially, the use of a residual current circuit breaker (RCCB) with a miniature circuit breaker (MCB) is necessary for ensuring the desired performance and protecting PV systems from sudden shock or electrical anomalies. The key role of RCCB is the protection of people from electric shock, and the principal MCB function consists of protecting a PV system against short circuits or overloads. More specifically, the RCCB immediately turns off the power in the presence of a potential electrical fault in the inspected PV system. In this scenario, we generate an RCCB fault within one hour using the collected data.
Figure 15 shows the detection performance of the eight investigated ensemble learning-based EWMA and DEWMA charts. We observe that this large fault has been recognized by all the studied charts (
Figure 15). We can also see that the BG-DEWMA chart can clearly uncover this fault with reduced false alarms compared to the other charts.
Table 8 presents the performance of the studied BS and BT-based monitoring schemes. From
Table 8, it can be clearly seen that BT-based schemes perform slightly better than BS-based schemes. Here, BG-based schemes achieved an AUC of around 0.98, and BS-based schemes obtained an AUC of around 0.97. This means that the considered schemes can efficiently detect this RCCB fault. Results showed that the BG-based EWMA and DEWMA schemes with non-parametric thresholds models reached the highest detection performance in terms of the five evaluation metrics. As the magnitude of the occurred RCCB fault is large, we can see that the BG-based EWMA and DEWMA schemes perform similarly.
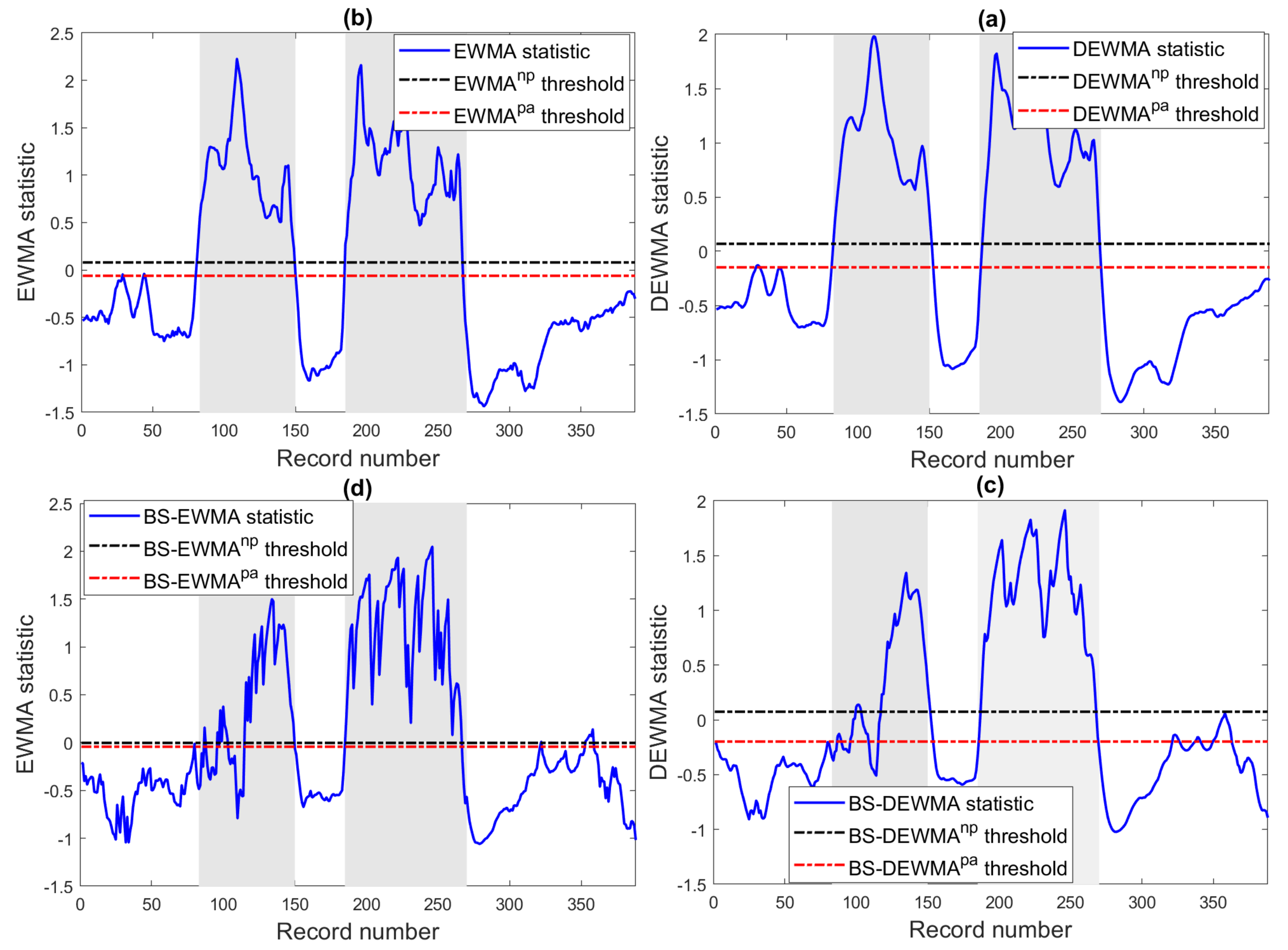
6.4. Scenario with Shaded Modules
Next, the capability of the ensemble learning-based techniques in detecting partial shading is demonstrated. Broadly speaking, different factors can cause shading losses, such as the installation of the PV system close to pylons and trees [
8]. Crucially, the production of a PV system exposed to partial shading will decrease from the desired production. Here, the monitored system is exposed to two communication pylons (
Figure 16), which can decrease the power output. The data are collected within a period of the day in the presence of partial shading.
The results of the BG and BS-based techniques are depicted in
Figure 17. From the plots in
Figure 17, we observe that the partial shading of the two pylons resulted in a significant power. It is observed from
Figure 17 that the considered charts can sense the presence of this partial shading. So, the proposed ensemble learning-based detection methods effectively flagged out this partial shading. Furthermore, we notice that the BS-based EWMA and DWEMA schemes detect this shading partially, i.e., with some missed detections. On the other hand, all BG-based schemes provide good detection results of this partial shading. Hence, we conclude that the BG model catches most of the variability in the data compared to the BS model, facilitating obtaining more sensitive residuals.
Table 9 shows that the non-parametric DEWMA performed better than the conventional DEWMA and single EWMA schemes with lower FPR and the highest TPR, accuracy, and precision. The non-parametric DEWMA reaches an AUC of 0.984, and the conventional DEWMA and EWMA schemes reached, respectively, AUC values of 0.932 and 0.65. The conventional schemes flag this shading but with some false alarms and missed detection. Such results may indicate the non-parametric DEWMA rather than the conventional DEWMA and EWMA charts for appropriately revealing partial shading in a PV array.
Table 9 lists the detection results of the BG and BS-based techniques in terms of the five evaluation scores. From
Table 9, it can be inferred that the BG-based EWMA and DEWMA schemes with non-parametric thresholds outperformed all other methods by providing the best detection performance with a TPR of 0.9805 and very few false alarms (FPR = 0.9869), and an accuracy of 0.9869. This highlights the capacity of these BG-based EWMA and DEWMA schemes in accurately detecting partial shading. Furthermore, it is worth observing that the BG-based schemes with non-parametric thresholds dominate the parametric BG-based schemes’ counterparts. In the parametric schemes, the detection thresholds are determined based on the assumption of the Gaussian distribution of data, which is not often valid. However, in the non-parametric counterparts, the threshold is automatically determined using the KDE approach, making them more effective and flexible. As expected for anomalies with a large magnitude as in this case of partial shading, the DEWMA and the EWMA perform similarly. In contrast, the BS-based monitoring schemes can sense the presence of power loss but with some missed detections. Here, the BS-based DEWMA and EWMA schemes are showing comparable performance with an AUC around 0.89 but with several missed detection (TPR around 0.8).
6.5. Short-Circuit Fault
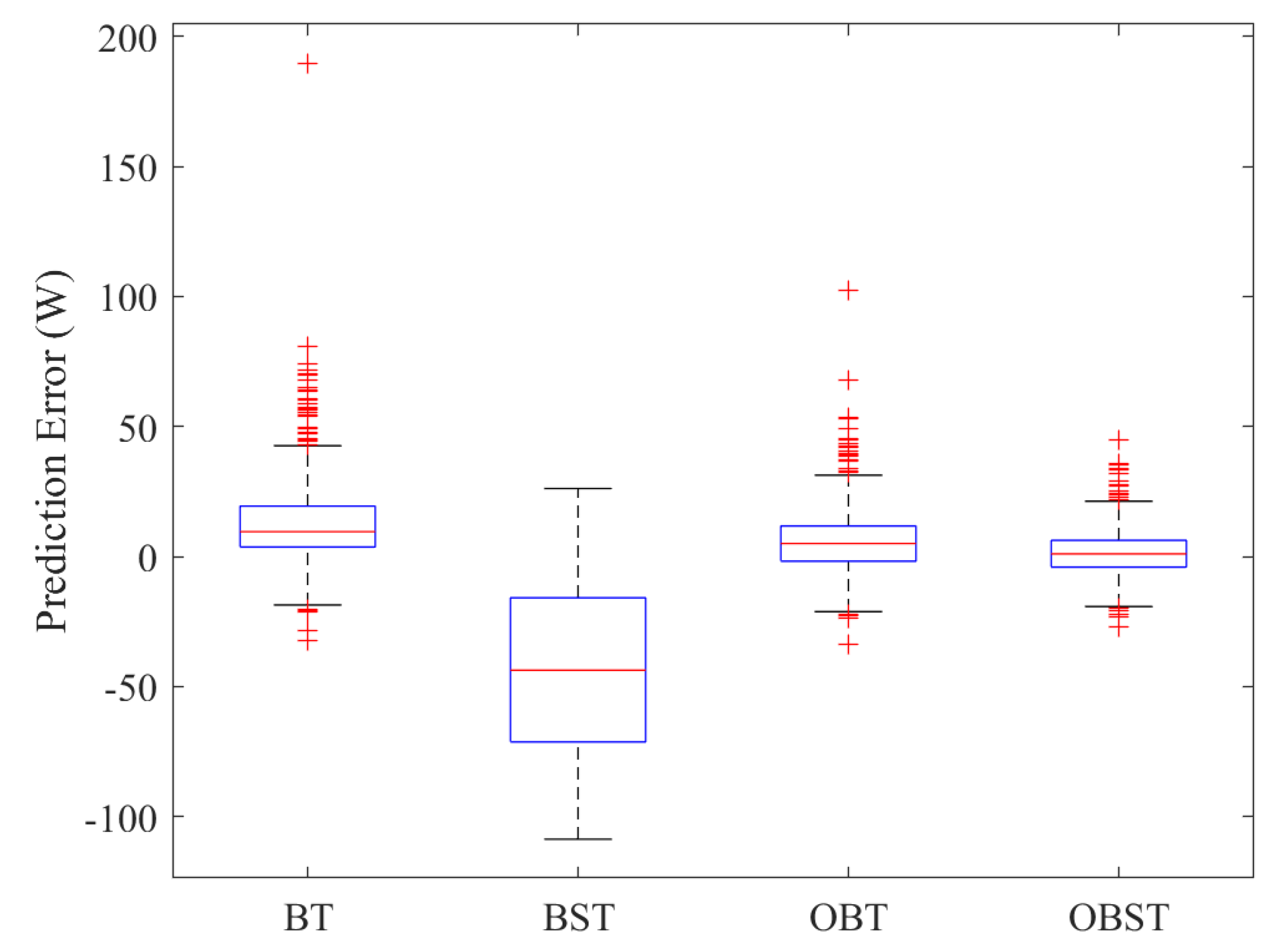
In this last investigation, we examine the performance of the proposed monitoring schemes in the presence of short-circuit faults. Short-circuit faults if not detected can induce degradation of the PV modules’ performance [
70]. In this scenario, the BG and BS-based monitoring schemes are verified in the case of two PV modules short-circuited. The monitoring results of BG and BS-based strategies are presented in
Figure 18. Here, the EWMA and DEWMa charts are applied to residual of DC power obtained from the already constructed ensemble learning models (i.e., BG and BT). We observe that the studied monitoring schemes can recognize this short-circuit fault (
Figure 18). The BS-based DEWMA and EWMA schemes flag this fault, but with several missed detection. In contrast, BG-based charts detect the fault with minimum false alarms and missed detection.
Table 10 quantitively summarizes the results of BG and BS-based monitoring techniques. From
Table 10, the results confirm that the BS-based schemes dominate the BG-based monitoring schemes. In addition, results revealed that the proposed BG-based DEWMA scheme with a non-parametric threshold provides the best results in this case study. It is followed by its parametric counterpart.
In summary, this work shows that merging ensemble learning models to capture describe DC power with the good detection capability of DEWMA enables an efficient detection of anomalies on the DC side of a PV system. The ensemble learning-based fault detection schemes presented in this paper can effectively detect the presence of potential anomalies on the DC sides of the PV system, but they do not identify the types of detected anomaly. Anomaly identification can be performed by the analysis of the DC current and DC voltage.
Table 11 lists the influence of the considered anomalies on DC current and DC voltage. Overall, anomaly identification could be conducted by employing semi-supervised anomaly detection methods, such as one-class SVM and isolation forest, to monitor DC current and DC voltage.