SENERGY: A Novel Deep Learning-Based Auto-Selective Approach and Tool for Solar Energy Forecasting
Abstract
:1. Introduction
- This paper proposes a novel approach and tool that uses deep learning to automatically predict the best-performing solar energy forecasting model. The approach is extensible to other performance metrics or user preferences and is applicable to other energy sources and problems.
- We provide an in-depth analysis of five deep learning models for solar energy forecasting using ten datasets from three continents. This is the first time that such a combination of models, datasets, and analyses has been reported. Particularly, none of the earlier works have reported forecasting based on five deep learning-based models with such many locations in Saudi Arabia and provided a comparison with locations abroad (Toronto and Caracas).
- We highlight the need for standardization in performance evaluation of machine and deep learning modelling in solar forecasting by providing extensive analysis and visualization of the tool and its comparison with other works using several performance metrics. We have not seen such an extensive evaluation of work earlier in solar energy forecasting. This paper is expected to open new avenues for higher depth and transparency in benchmarking of solar energy forecasting methods.
2. Literature Review
Research Gap
3. SENERGY: Methodology and Design
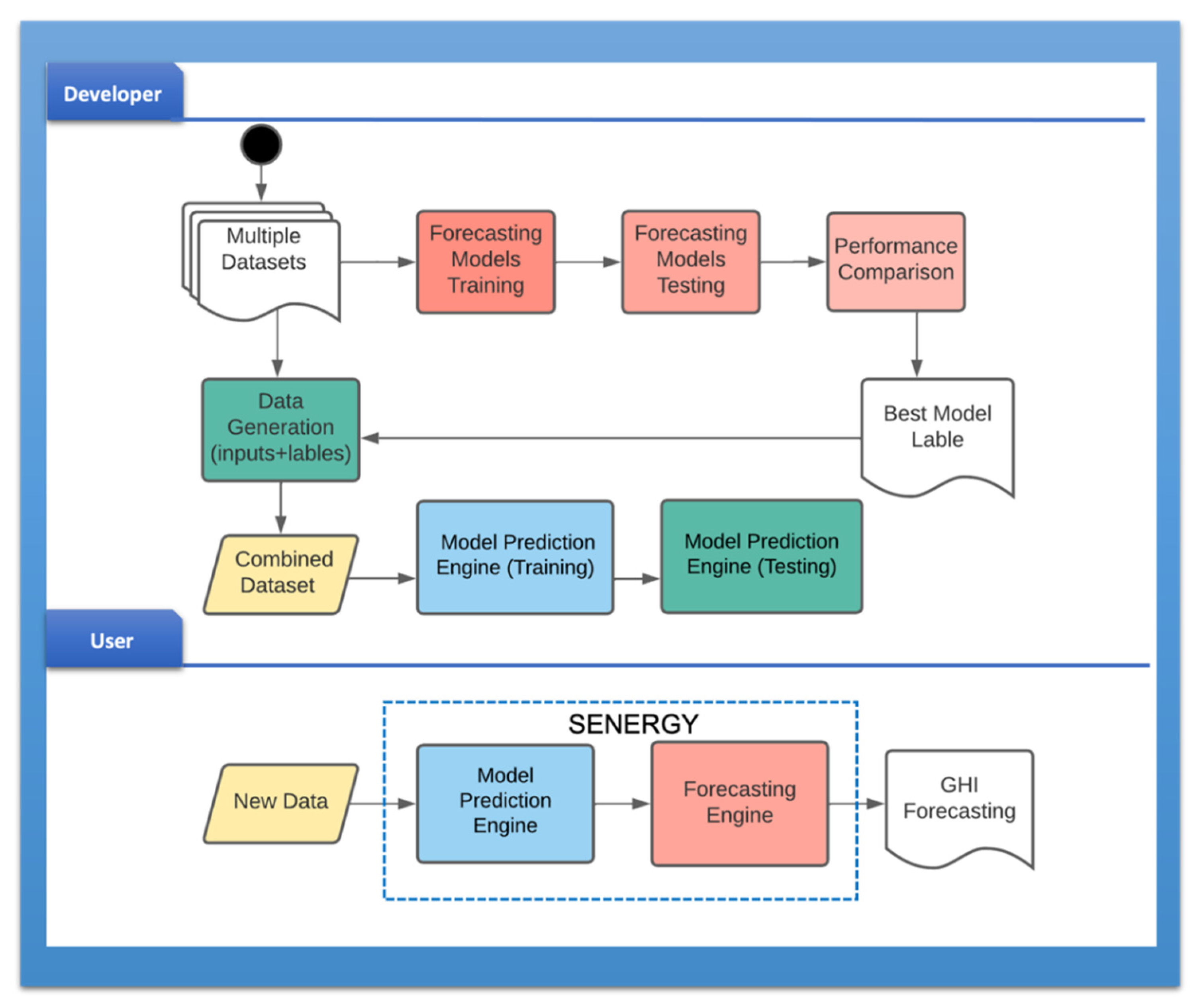
3.1. Tool Development Process
3.2. Datasets Development
3.2.1. Data Collection
3.2.2. Datasets for Forecasting
- GHI: the total amount of shortwave radiation received from sun by a surface horizontal to the ground. It is calculated using the following equation, which explains how GHI is related to DHI, DNI, and the Zenith Angle (ZA) [52];
- 2.
- DHI: solar radiation that does not come on a direct path from the sun, but has been spread by particles and molecules in the atmosphere and comes equally from all directions;
- 3.
- DNI: solar radiation that comes in a straight path from the direction of the sun at its current place in the sky. On a sunny day, GHI consists of 20% DHI and 80% DNI [52].
- 4.
- ZA: the angle between the sun’s rays and a vertical line;
- 5.
- 6.
- Wind speed (WS) and wind direction (WD) at 3 m;
- 7.
- Barometric pressure (BP);
- 8.
3.2.3. Datasets for Model Prediction
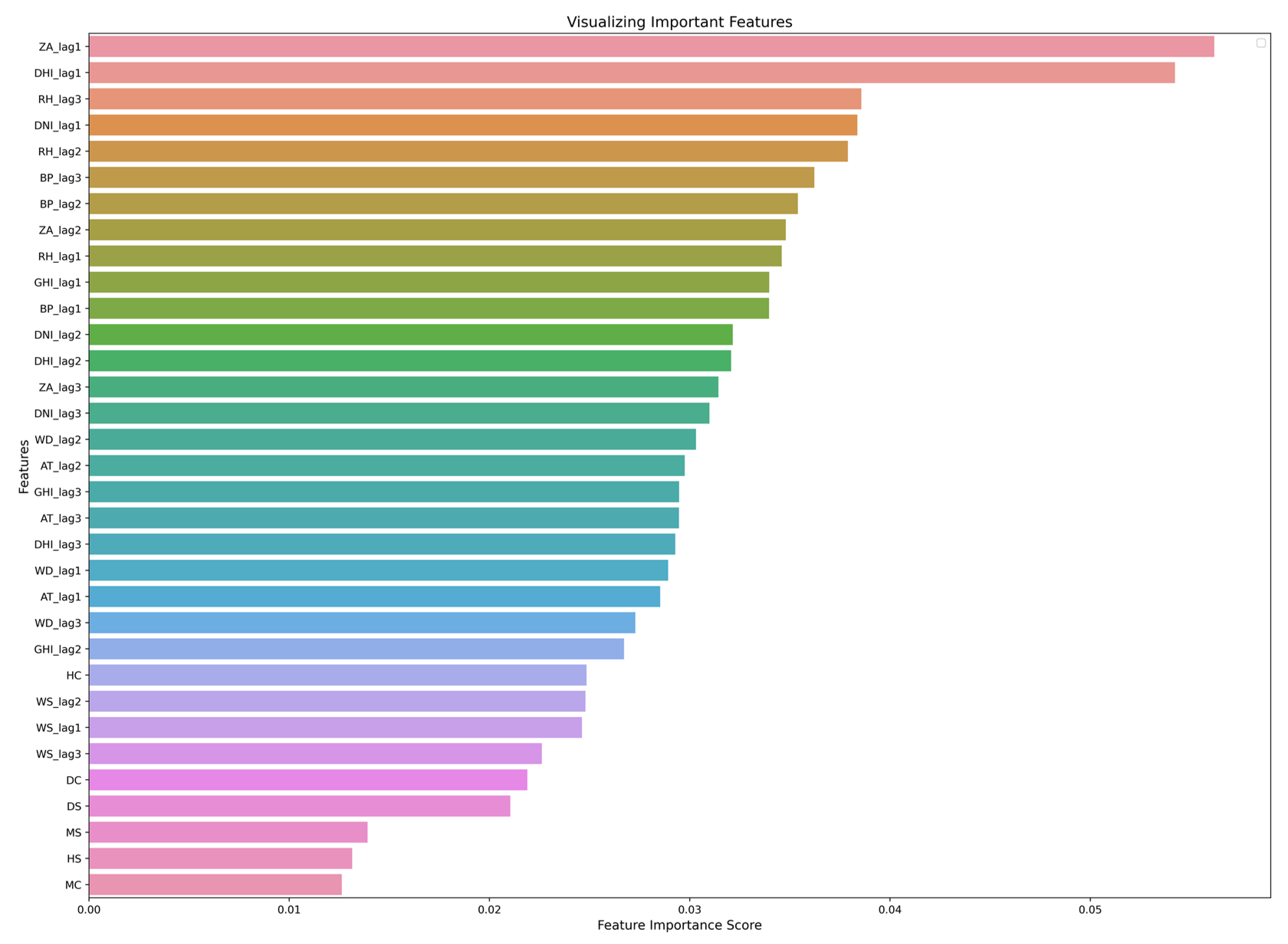
3.3. Feature Importance
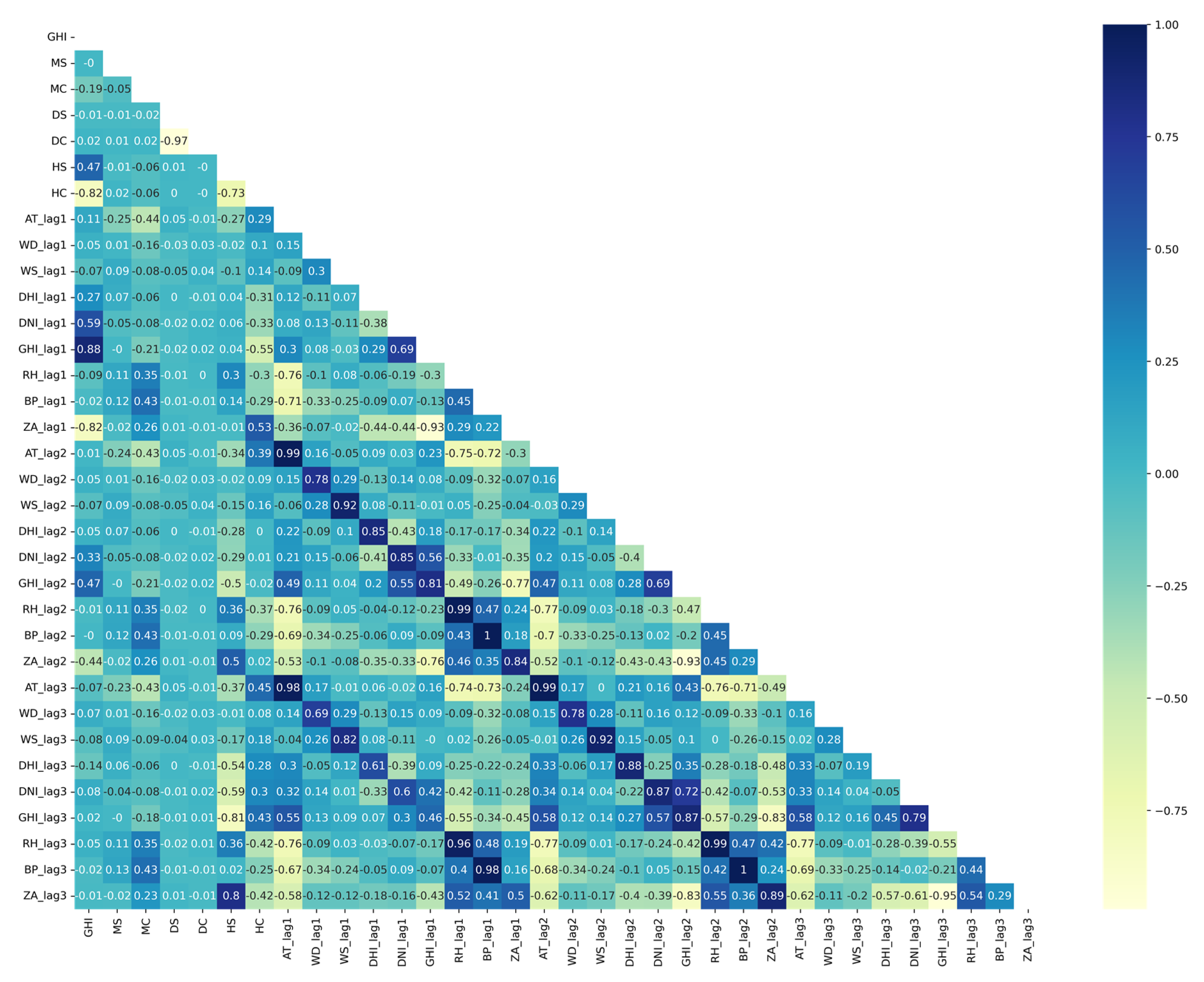
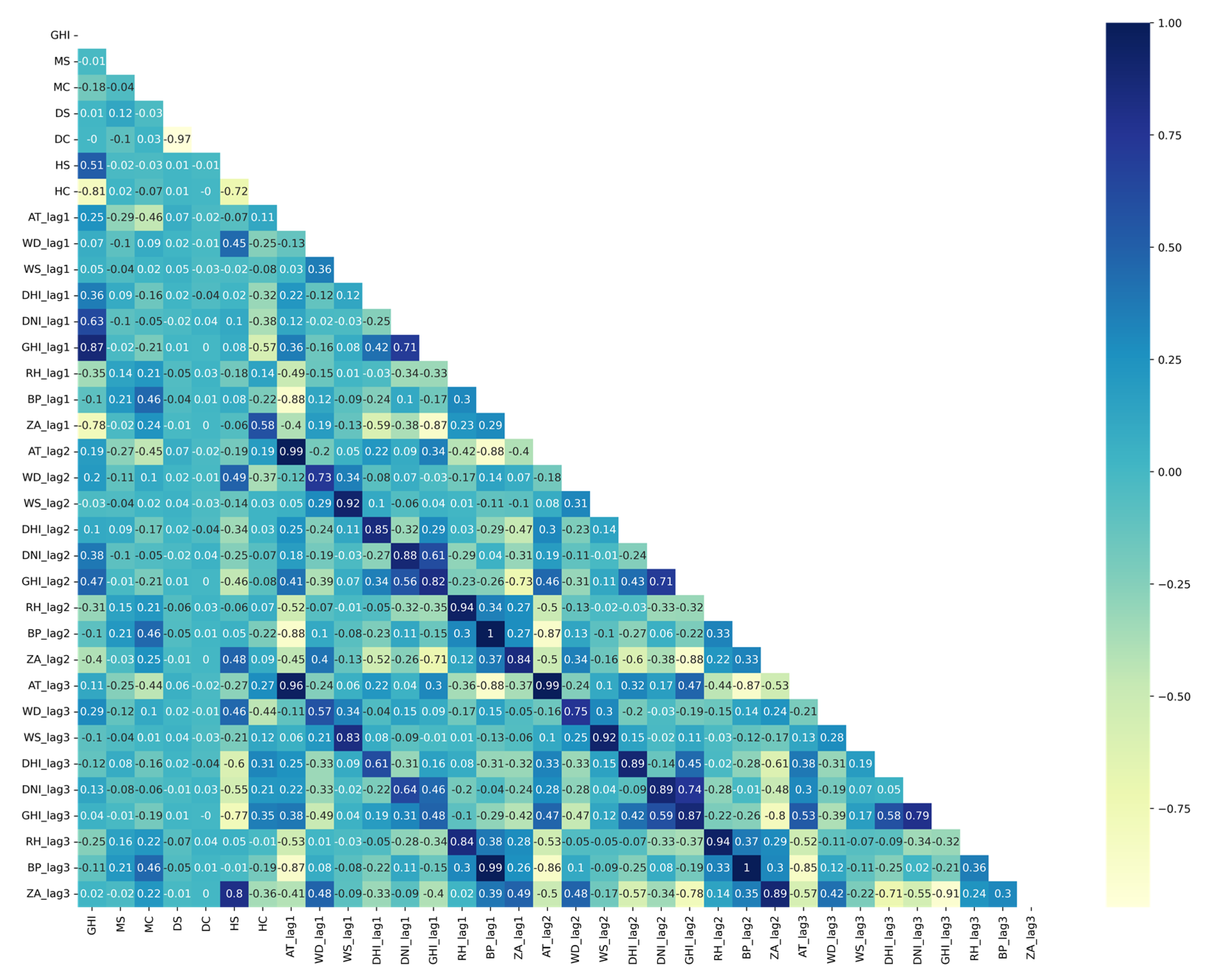
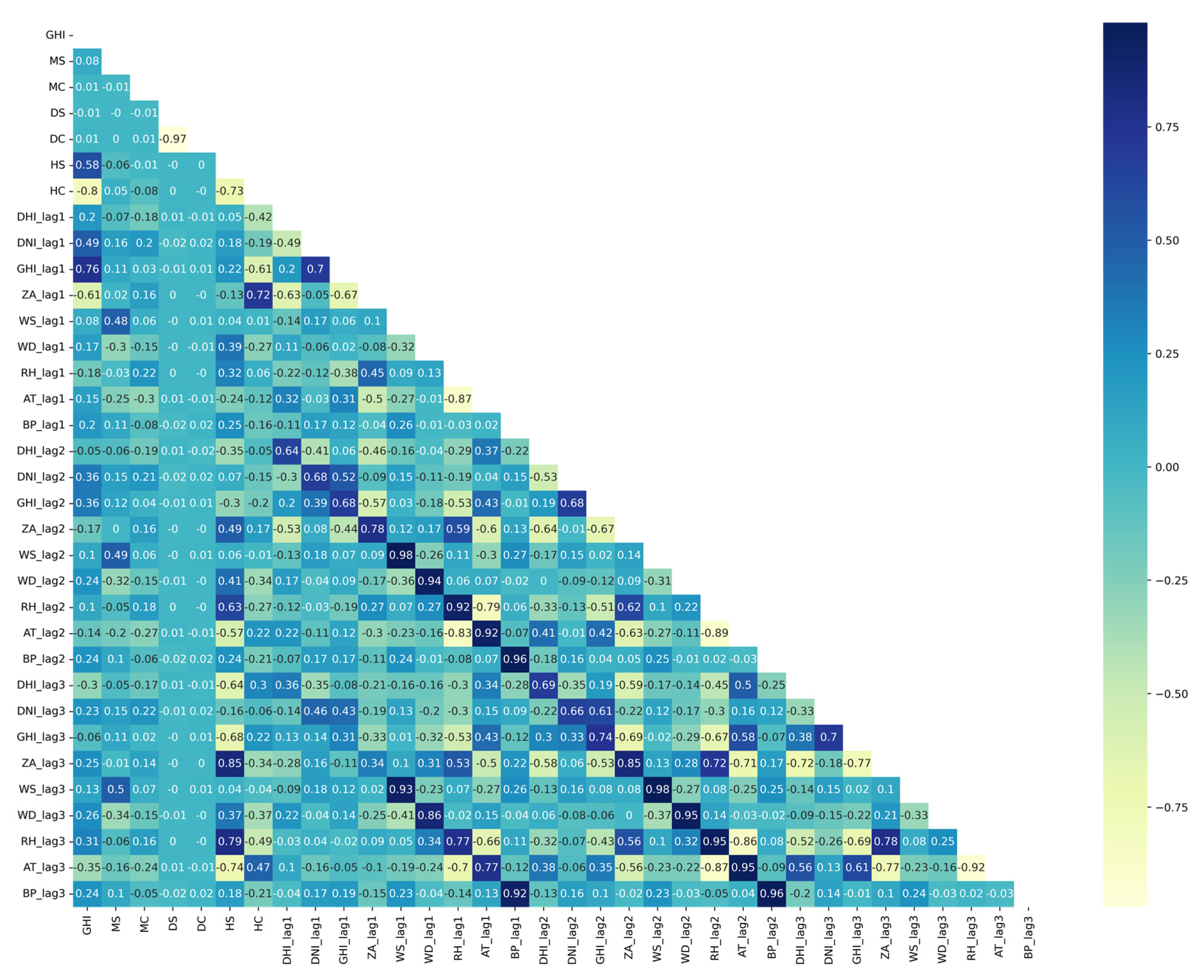
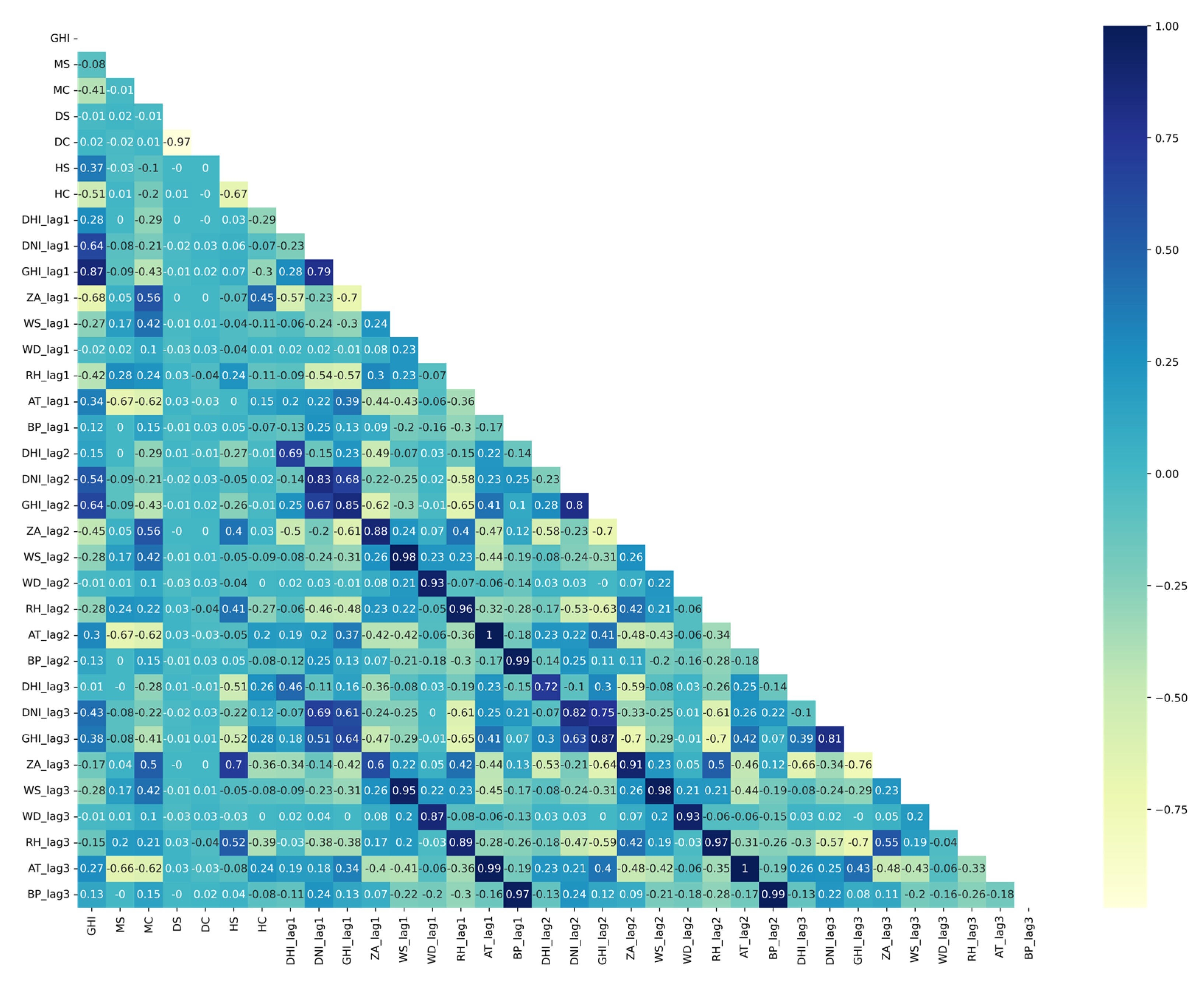
3.3.1. Pearson’s Correlation
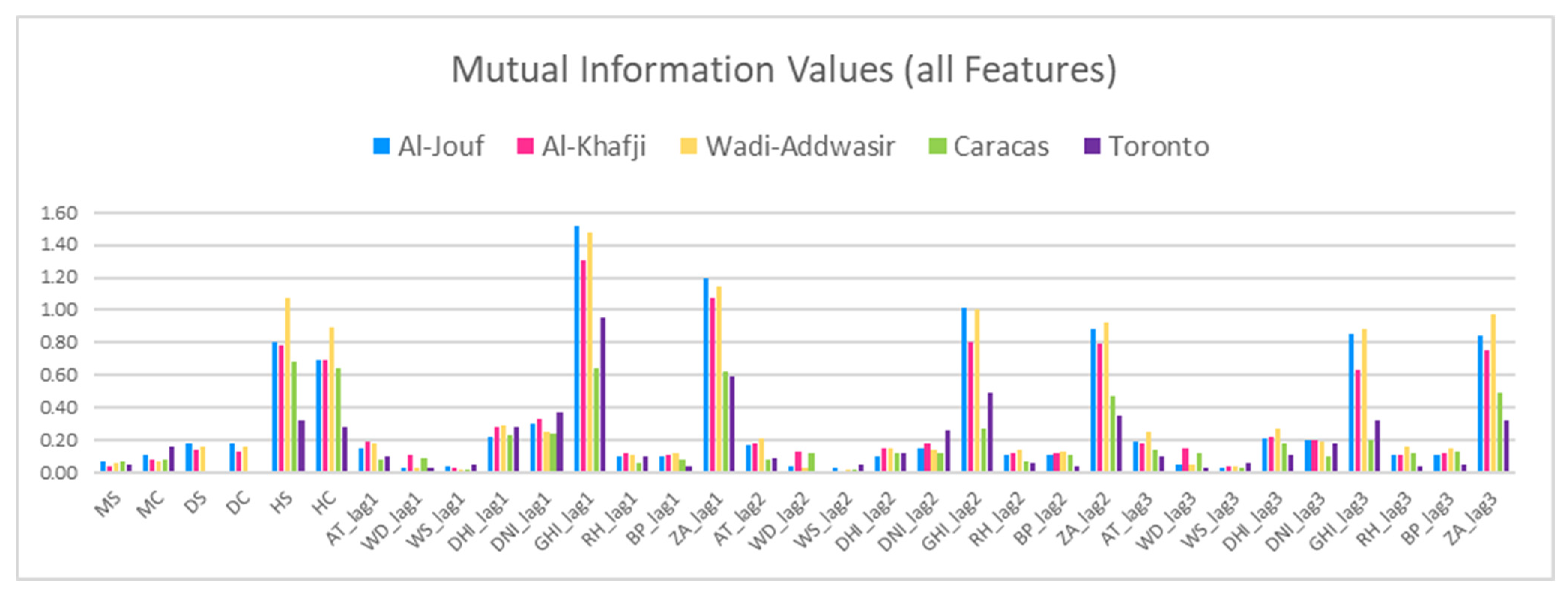
3.3.2. Mutual Information
3.3.3. Forward Feature Selection (FFS) and Backward Feature Elimination (BFE)
3.3.4. LASSO Feature Selection
3.4. Models’ Development
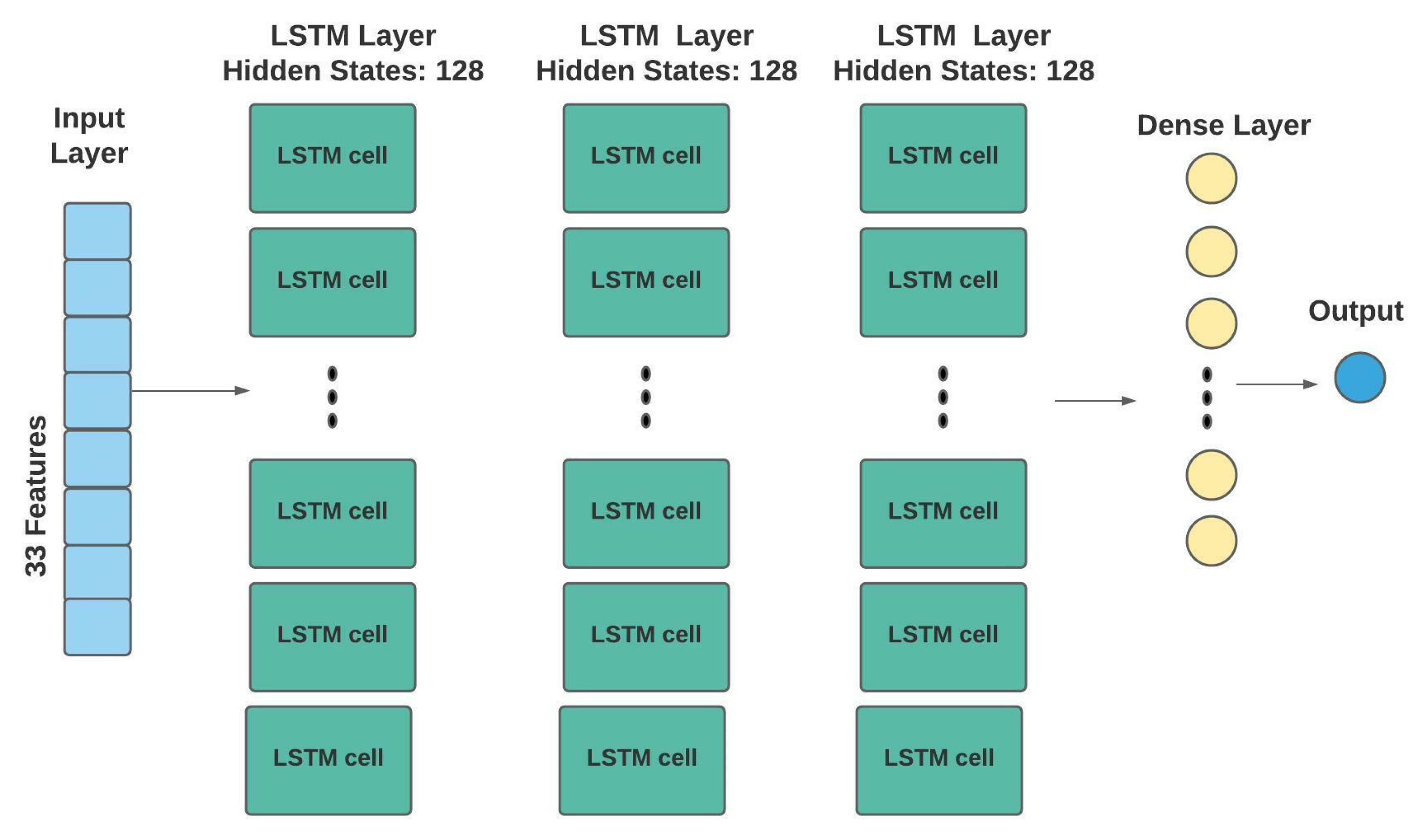
3.4.1. Long Short-Term Memory (LSTM)
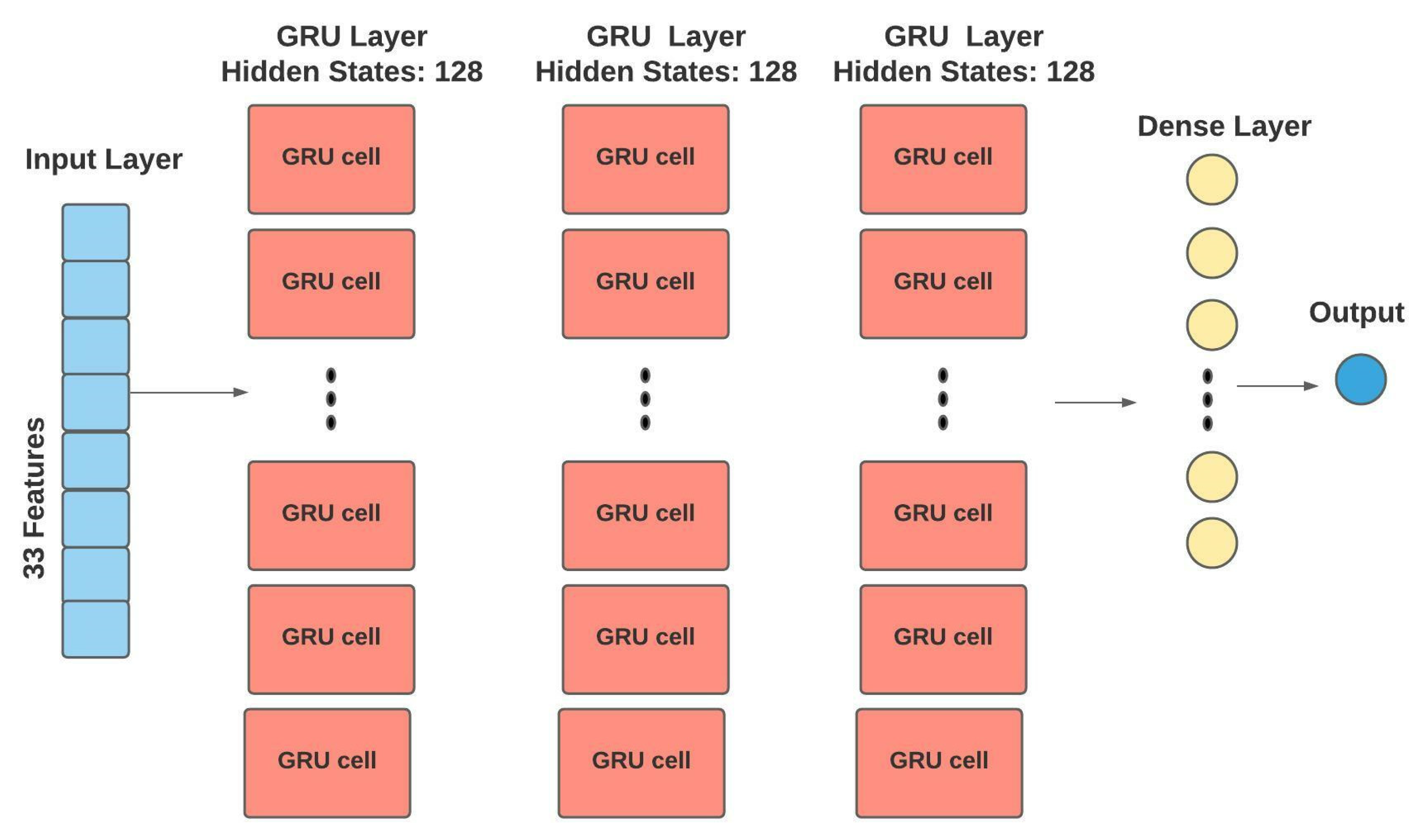
3.4.2. Gated Recurrent Unit (GRU)
3.4.3. Convolutional Neural Network (CNN)
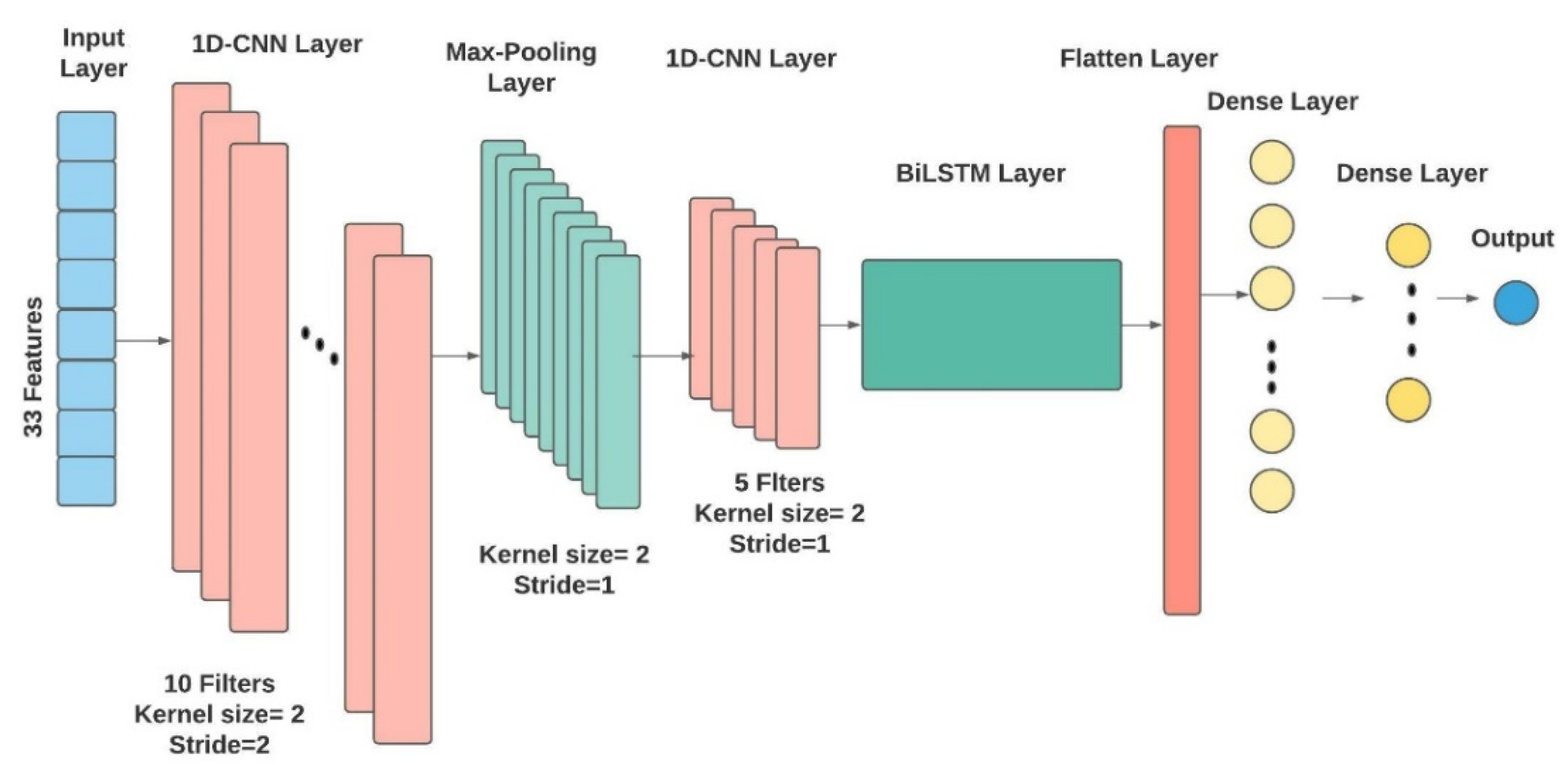
3.4.4. Hybrid CNN-Bidirectional LSTM (CNN-BiLSTM)
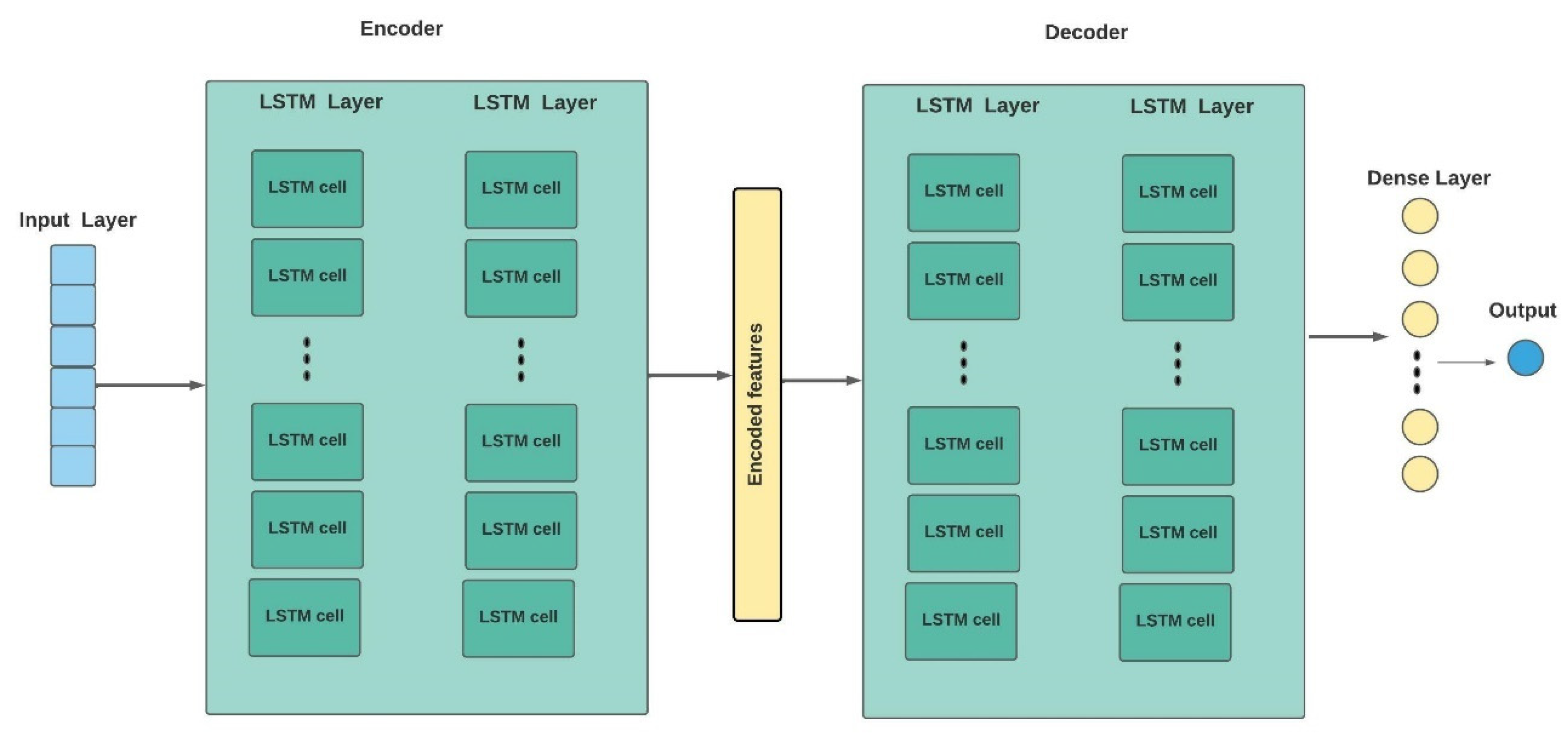
3.4.5. LSTM Autoencoder (LSTM-AE)
3.5. Performance Evaluation Metrics
3.6. Tool Implementation
4. SENERGY: Results and Evaluation
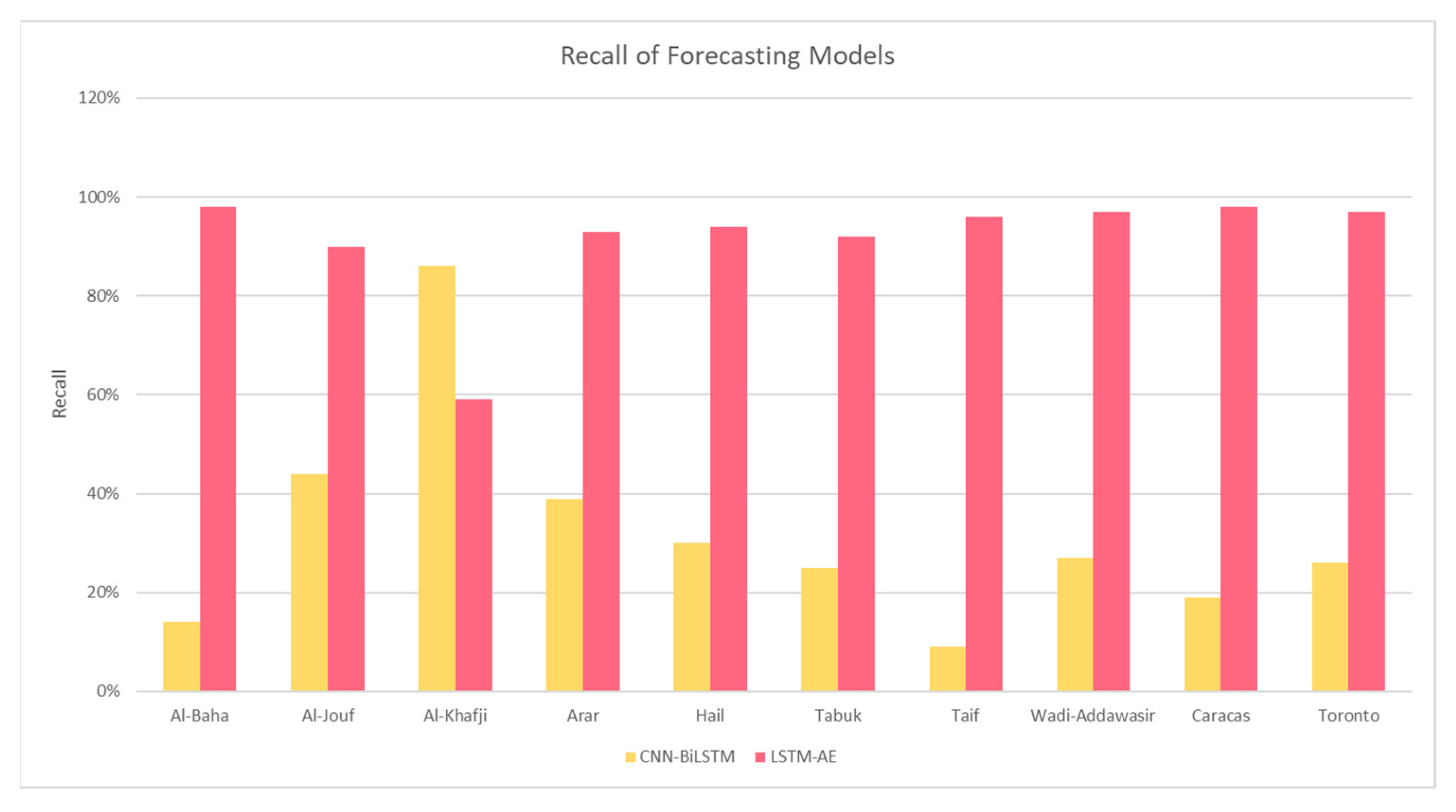
4.1. SENERGY: Forecasting Engine Performance
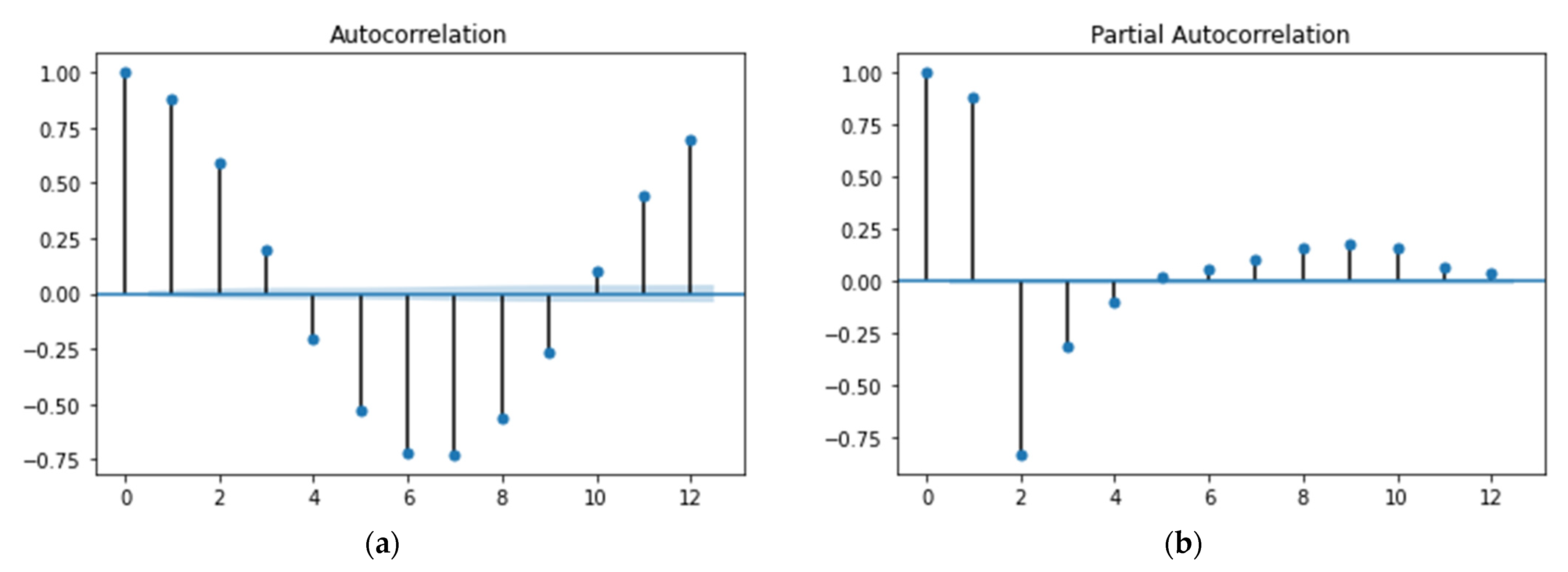
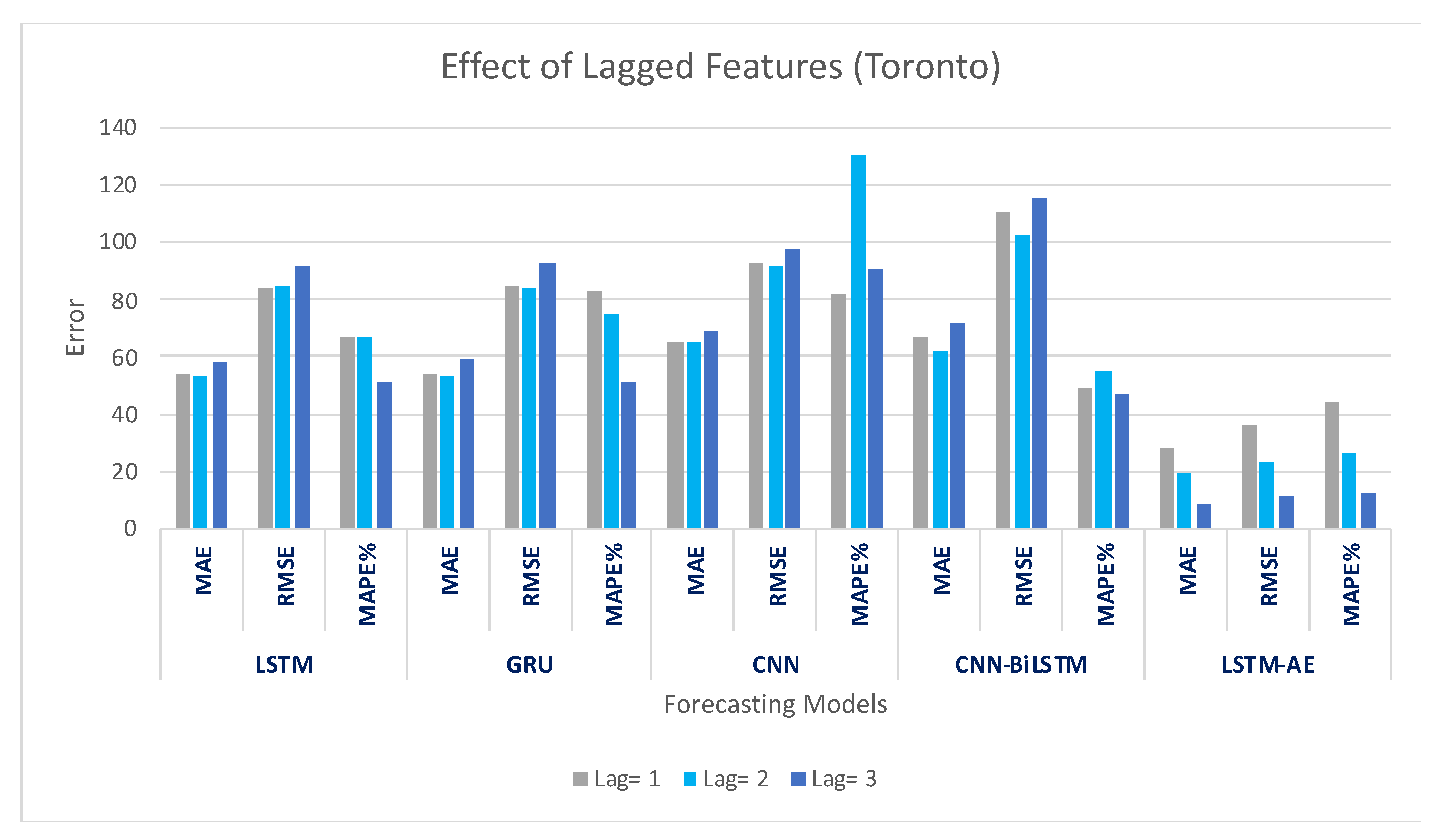
4.1.1. Effect of Lagged Features on Forecasting
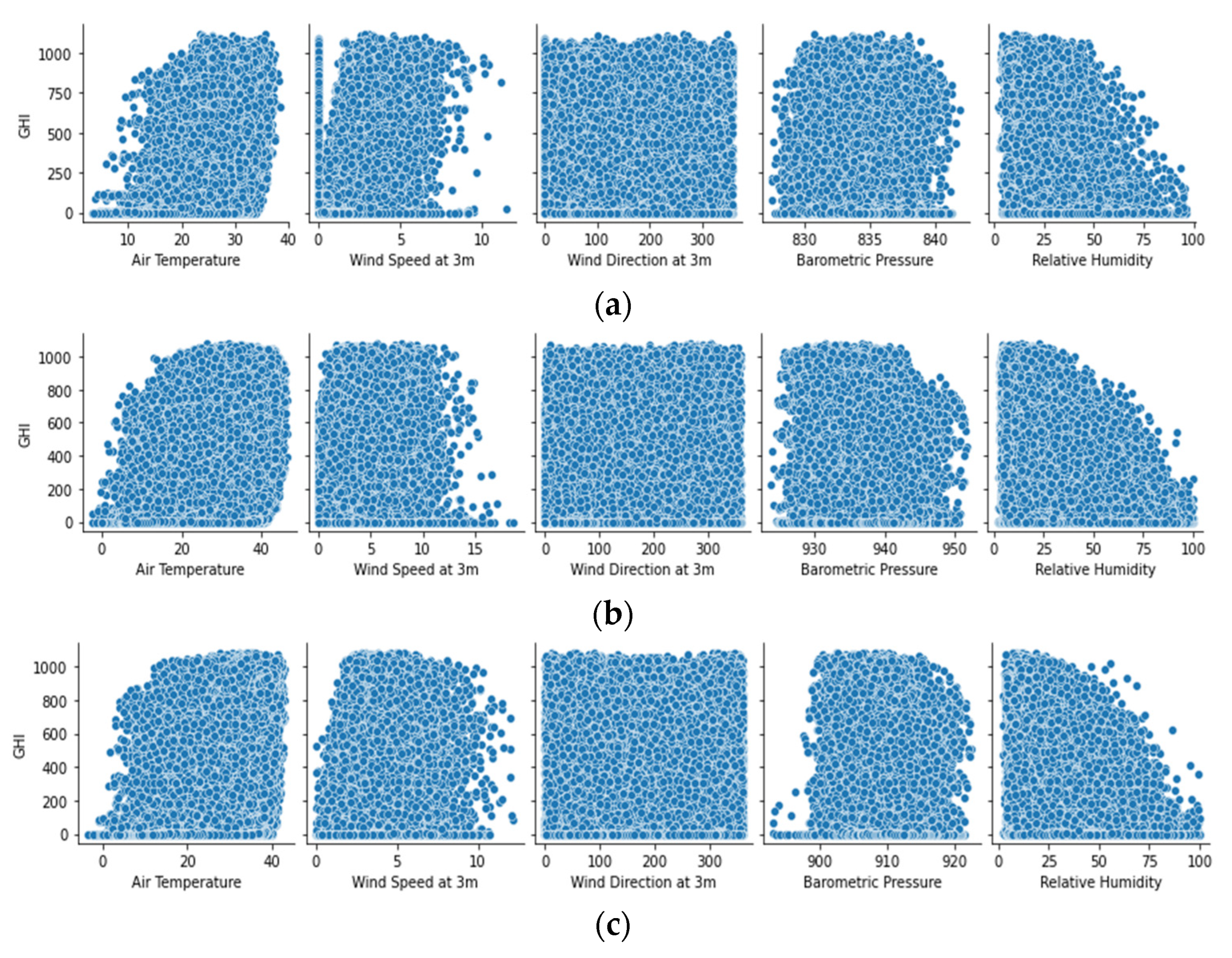
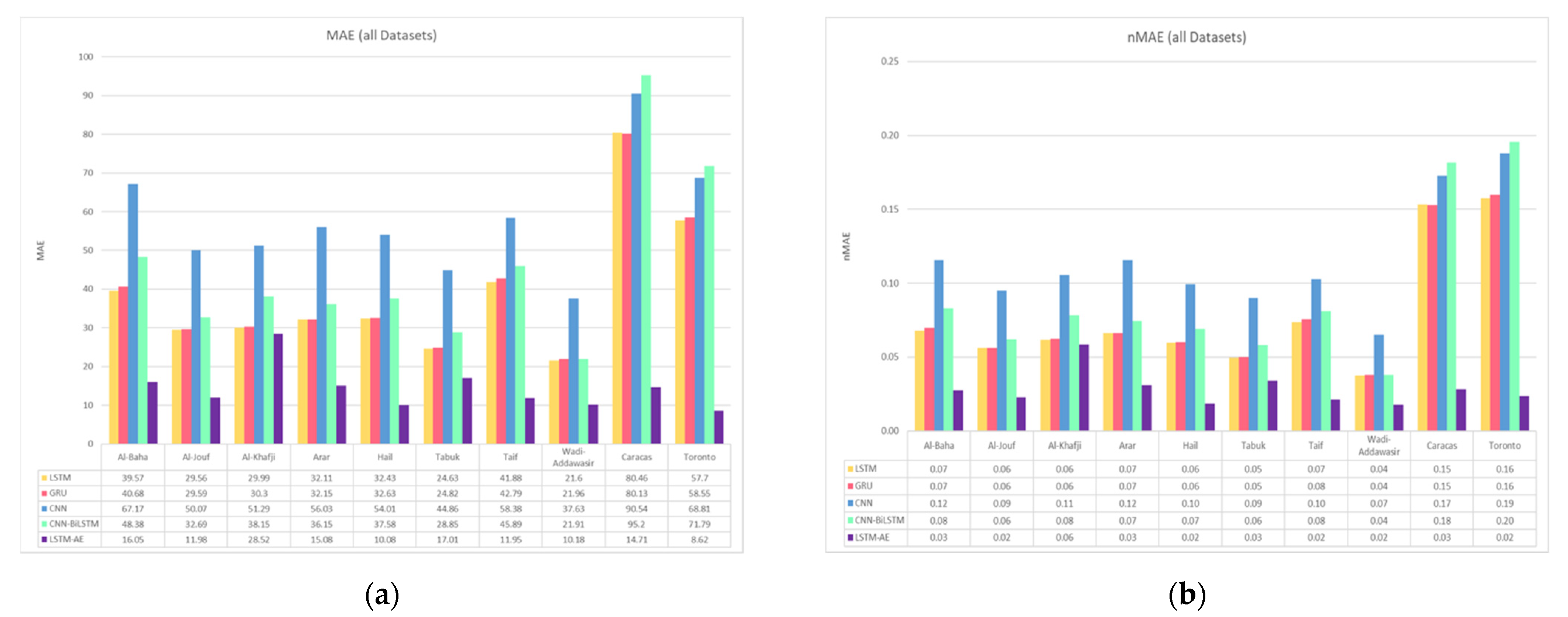
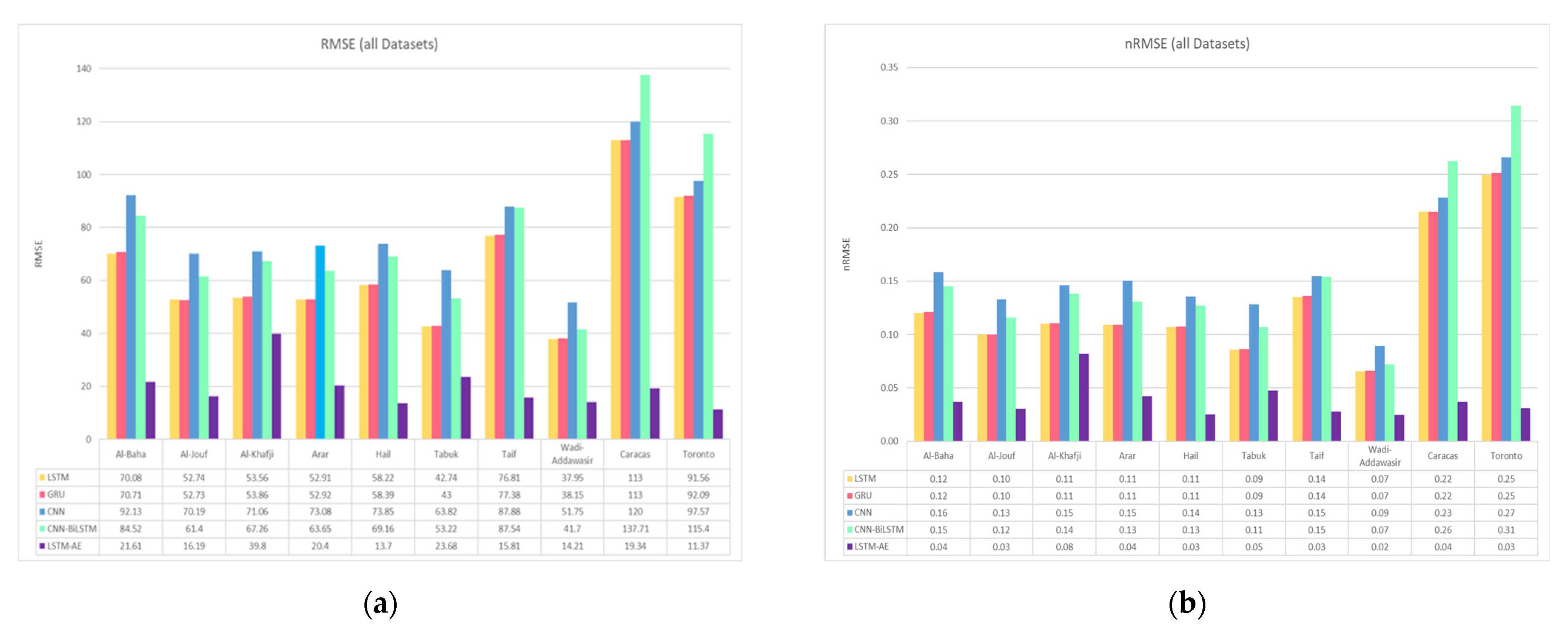
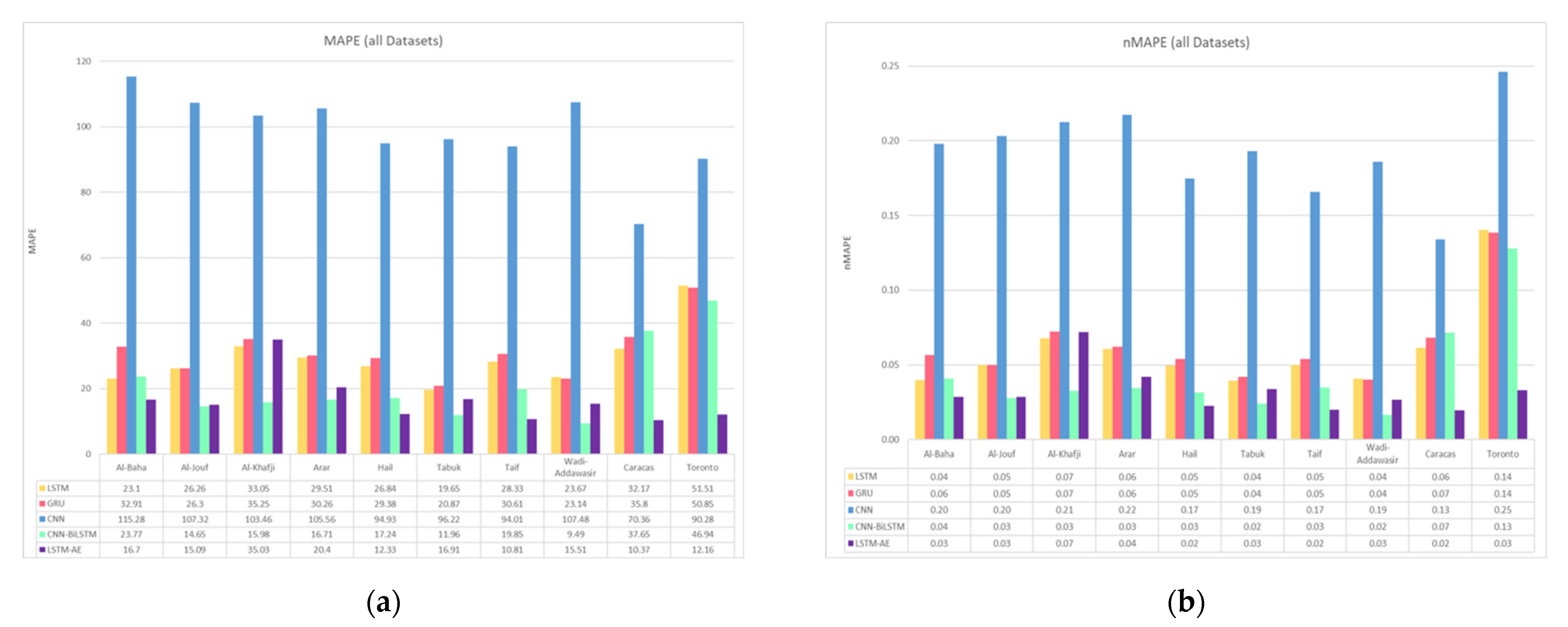
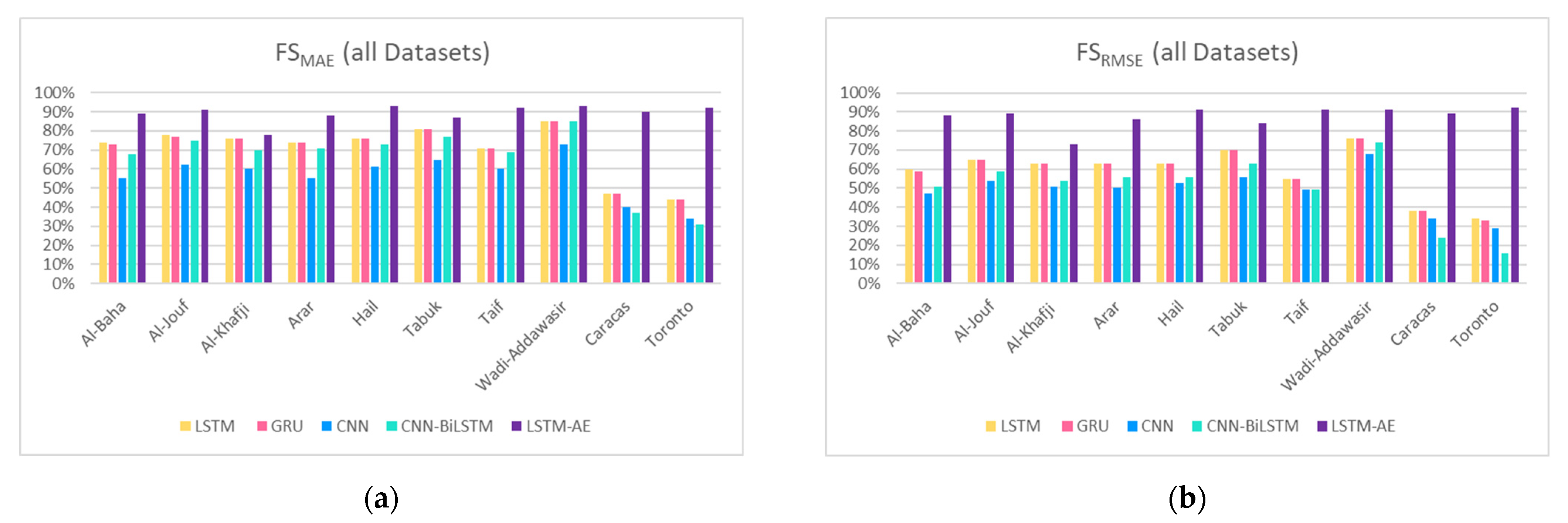
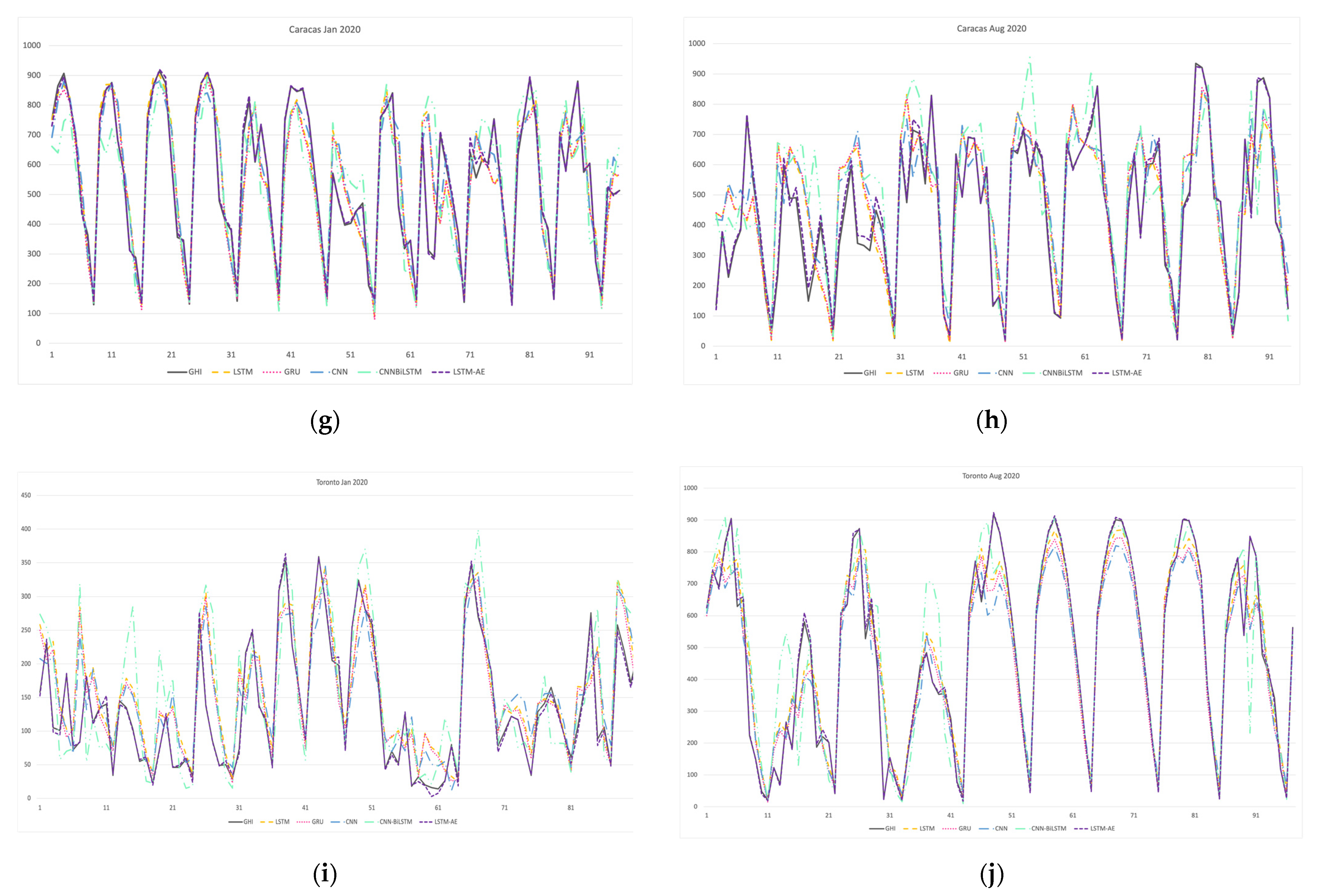
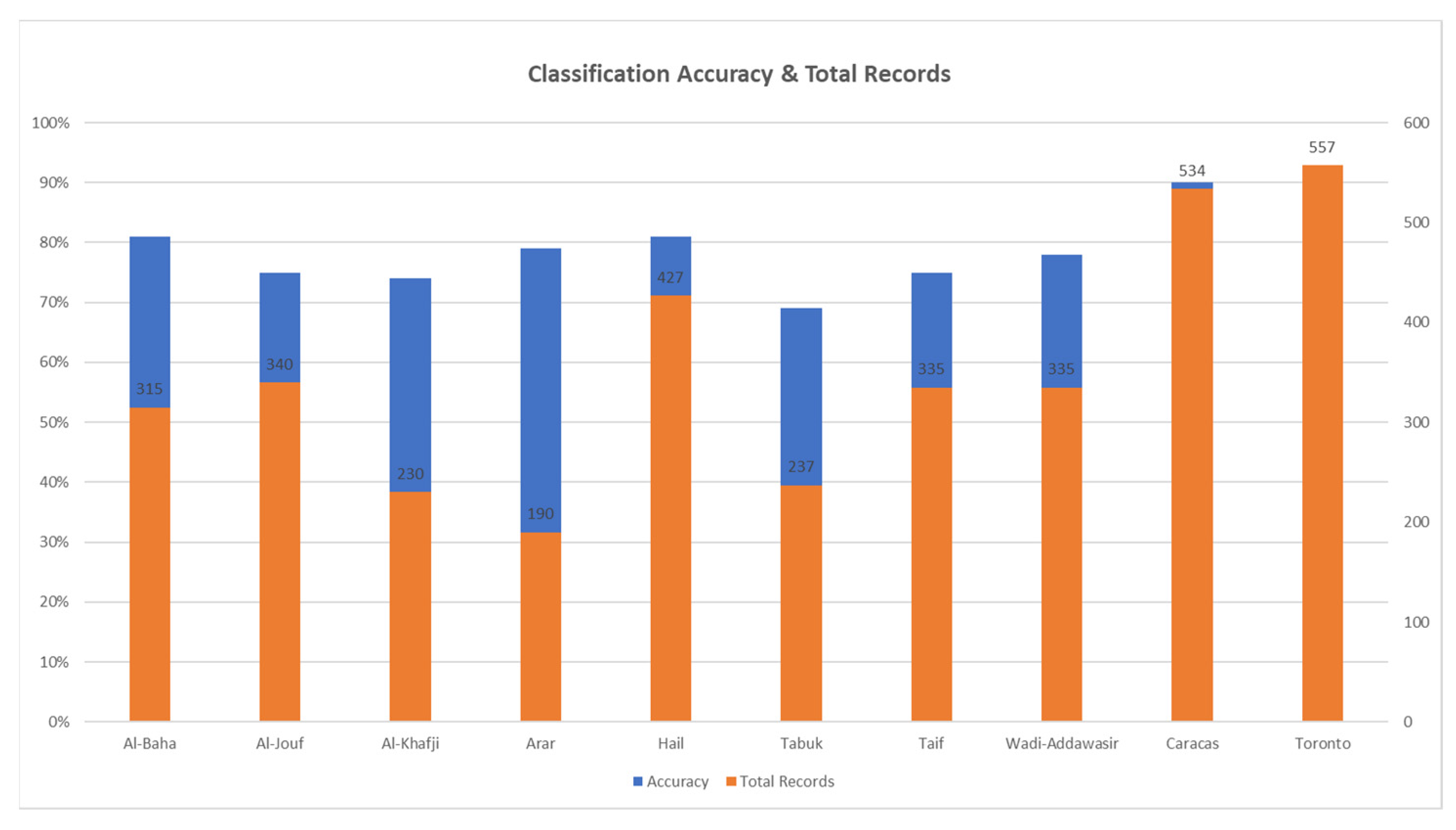
4.1.2. Effect of Climate and Location on Forecasting
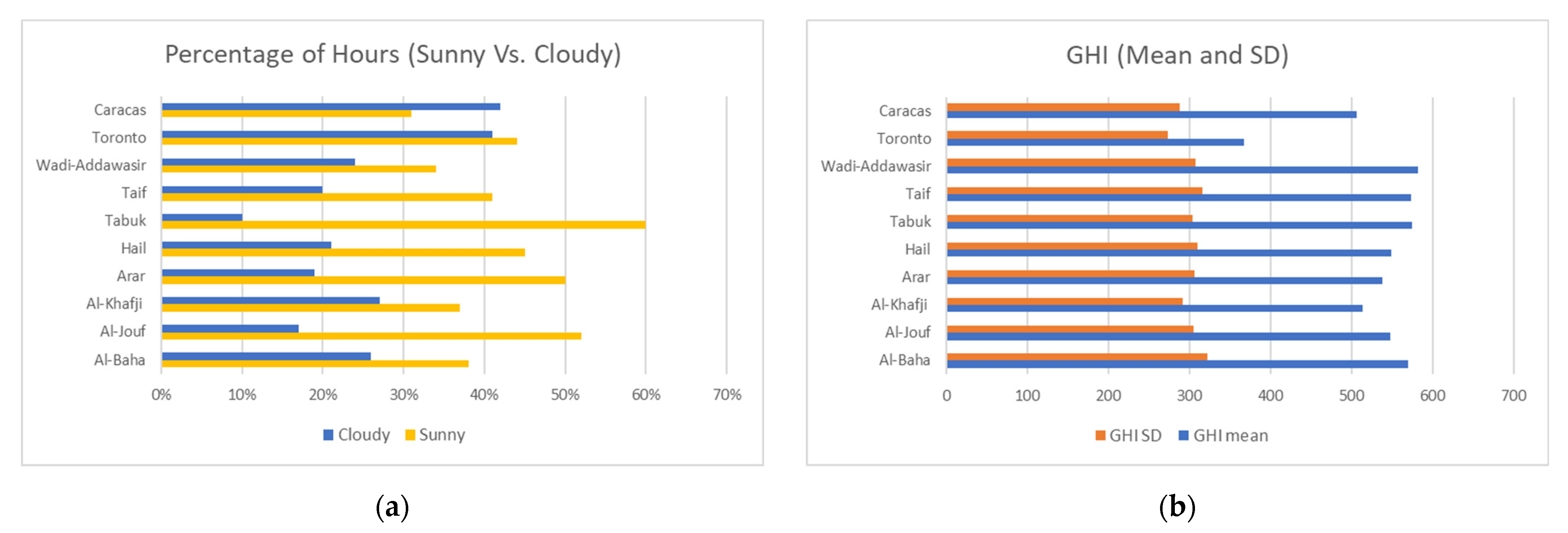
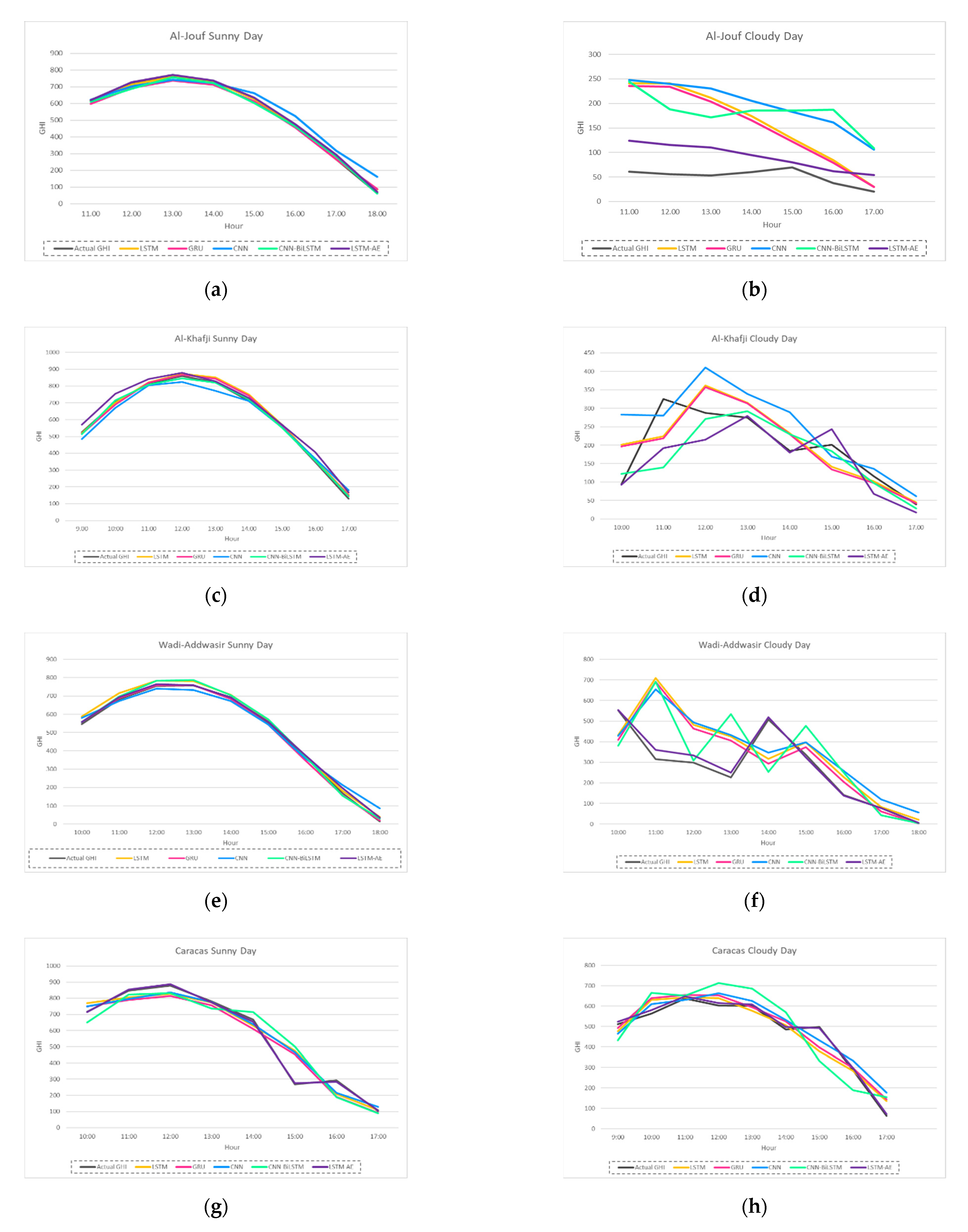
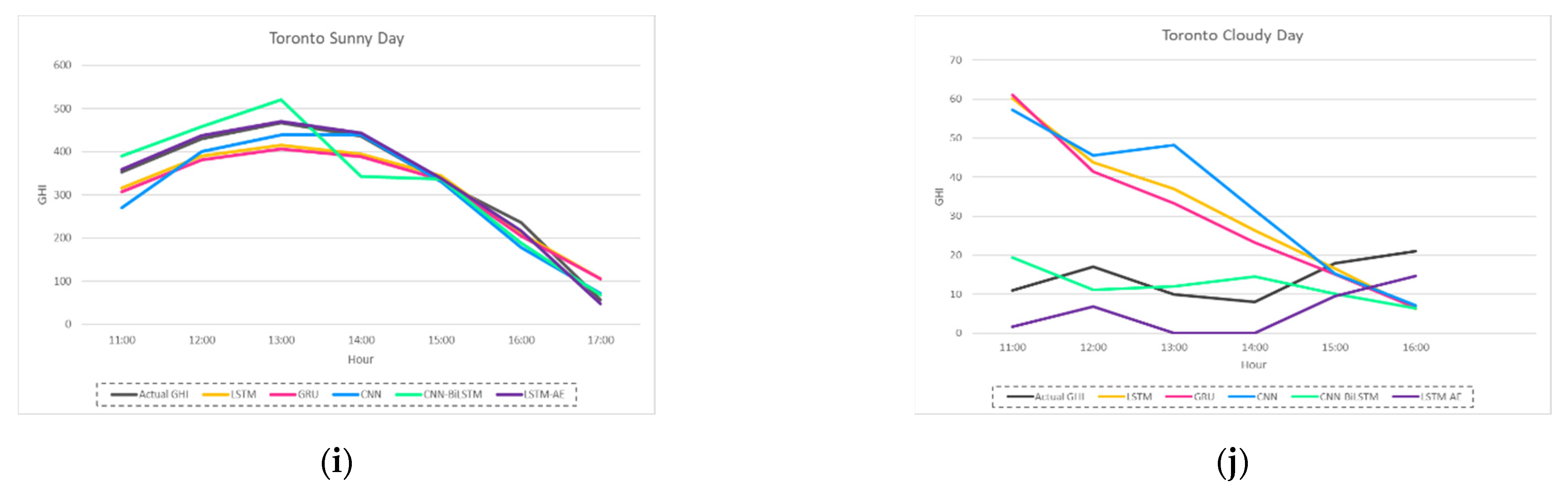
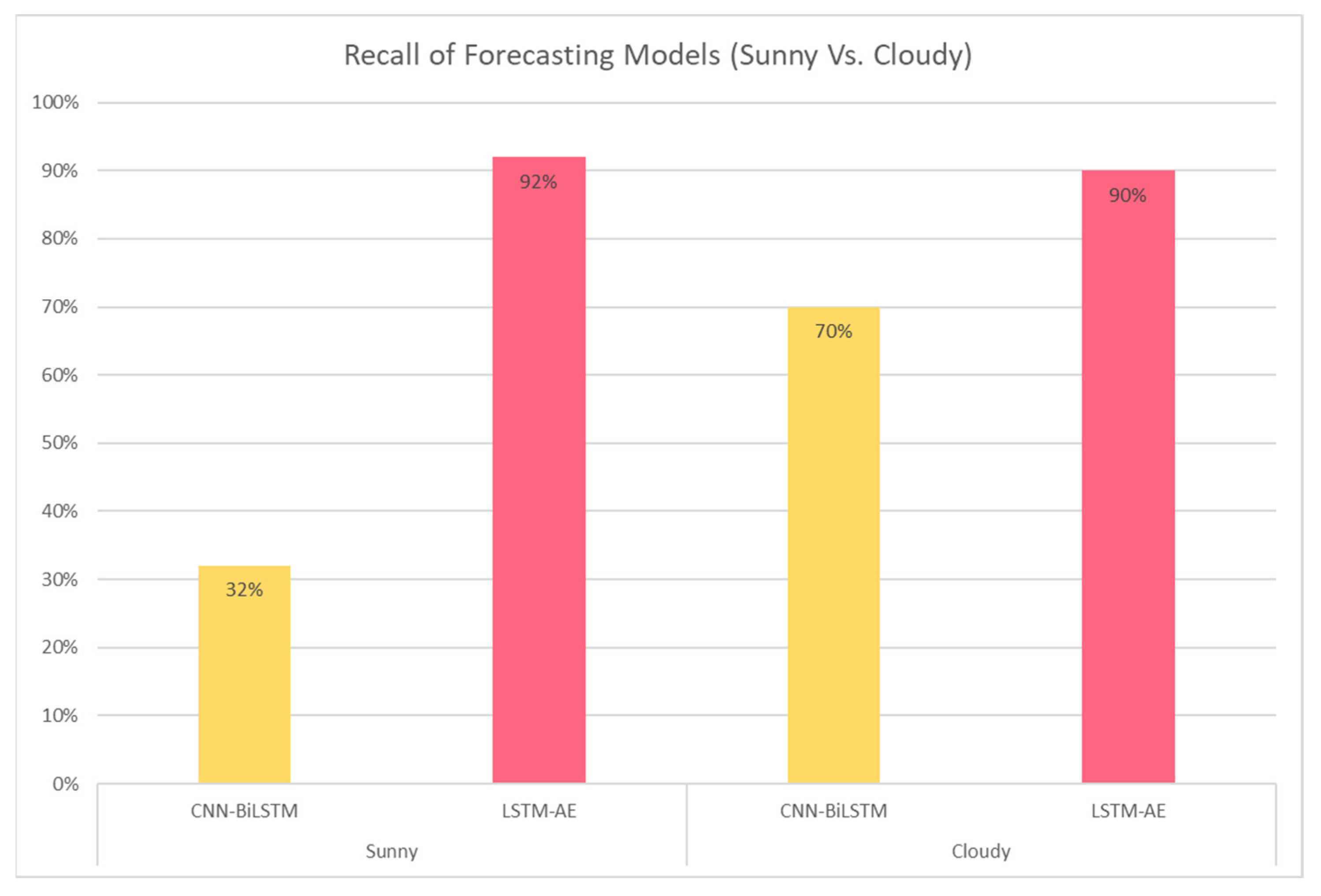
4.1.3. Effect of Sunny and Cloudy Weather on Forecasting
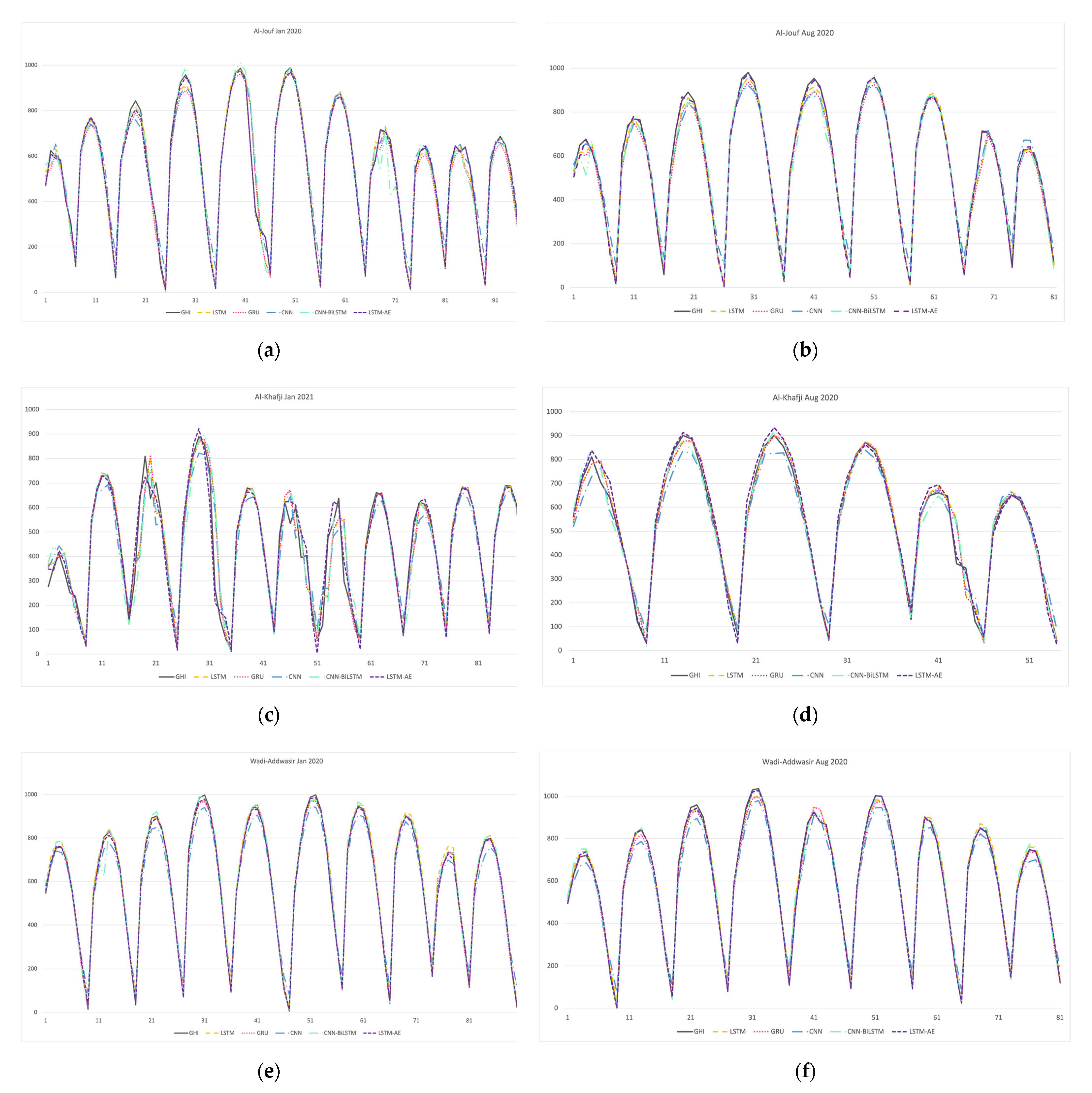
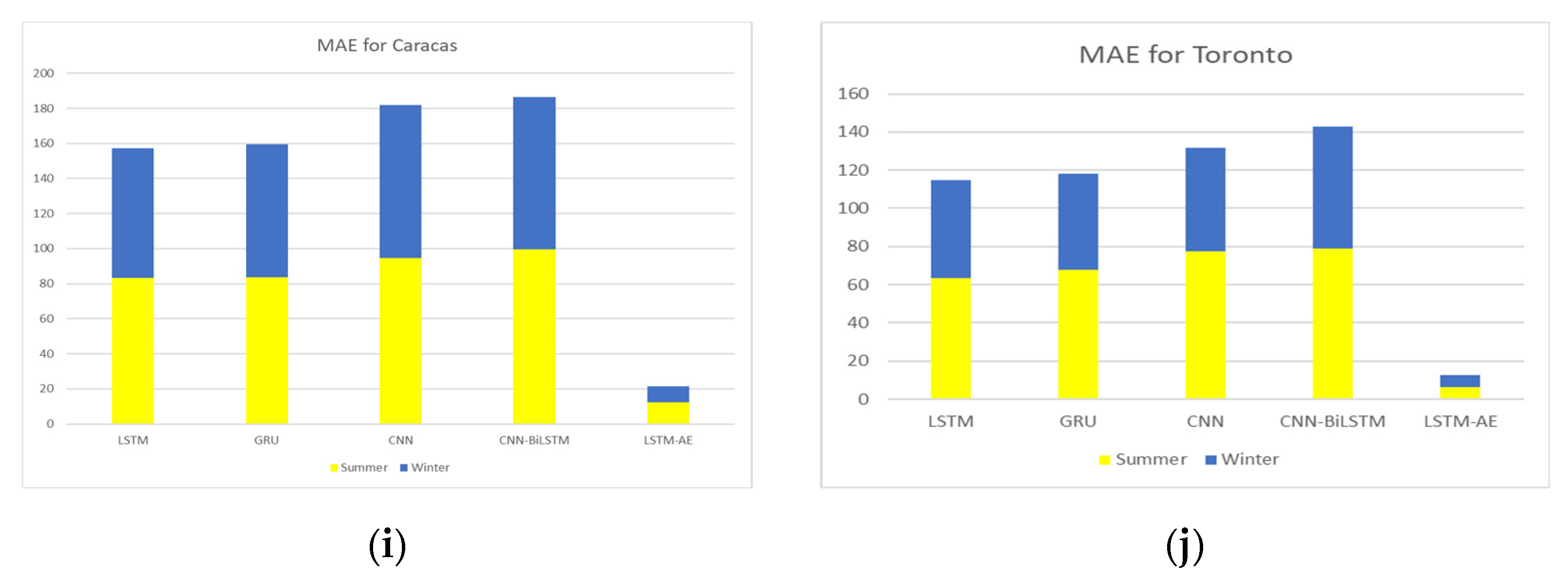
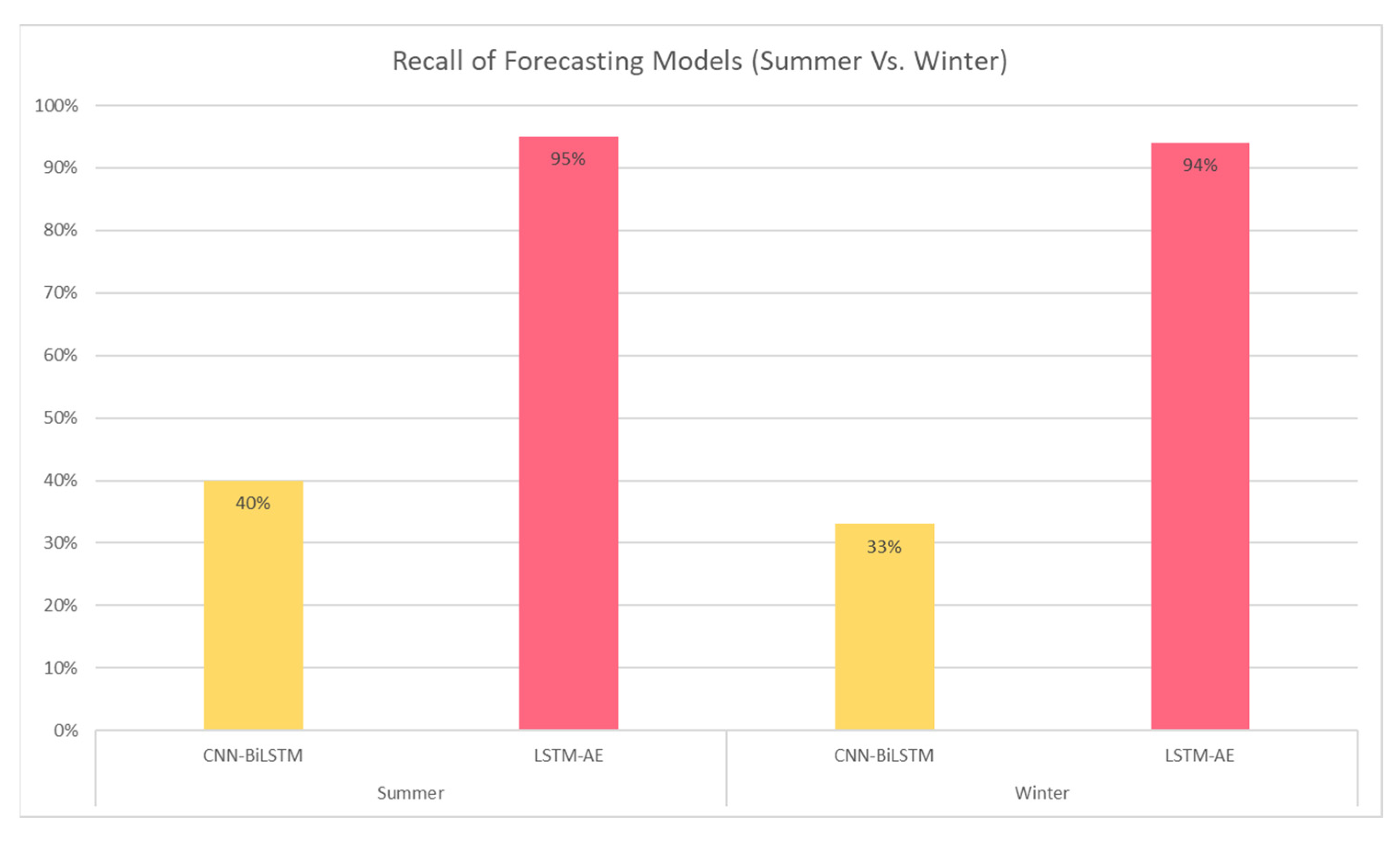
4.1.4. Effect of Summer and Winter Seasons on Forecasting
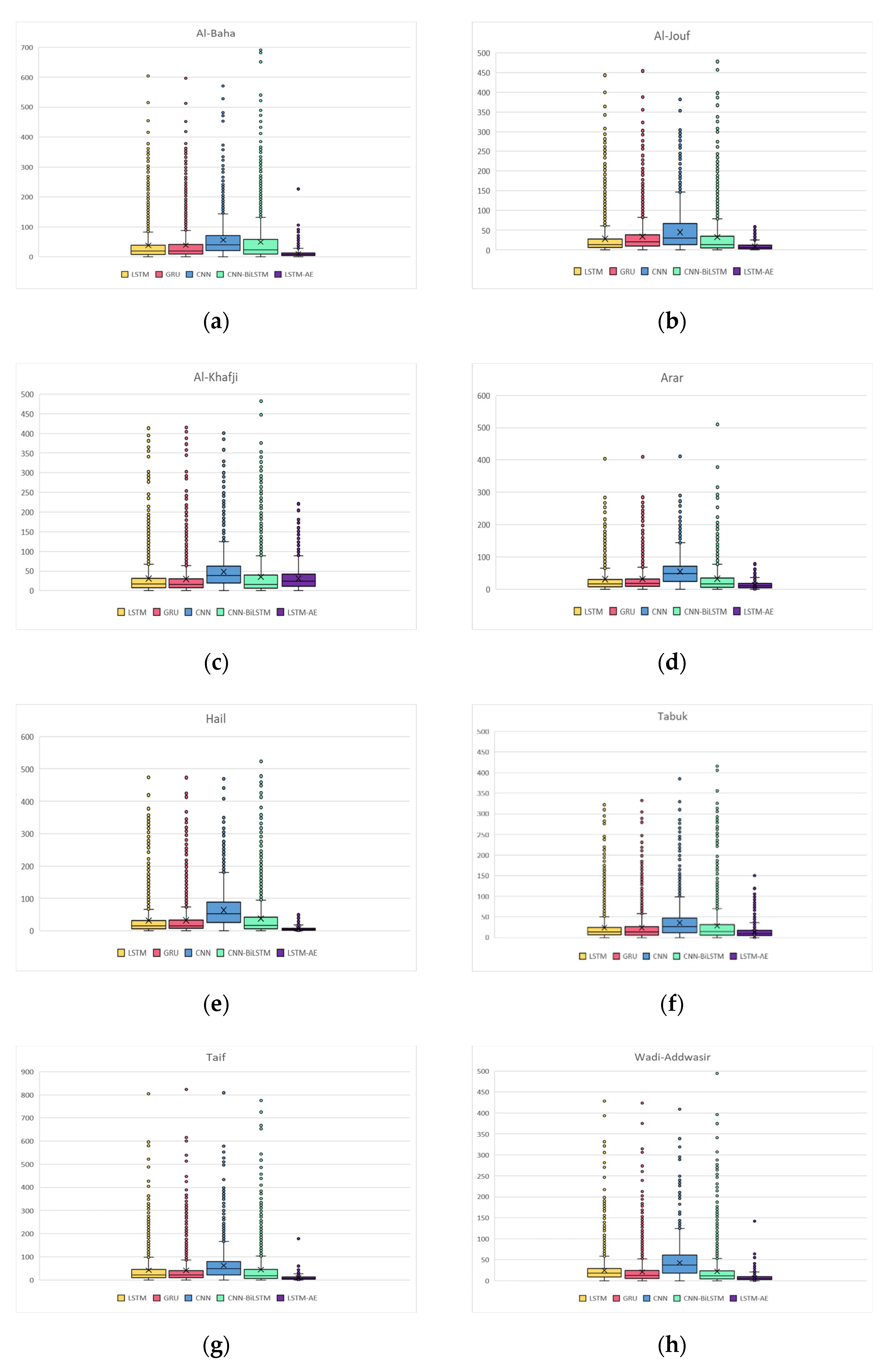
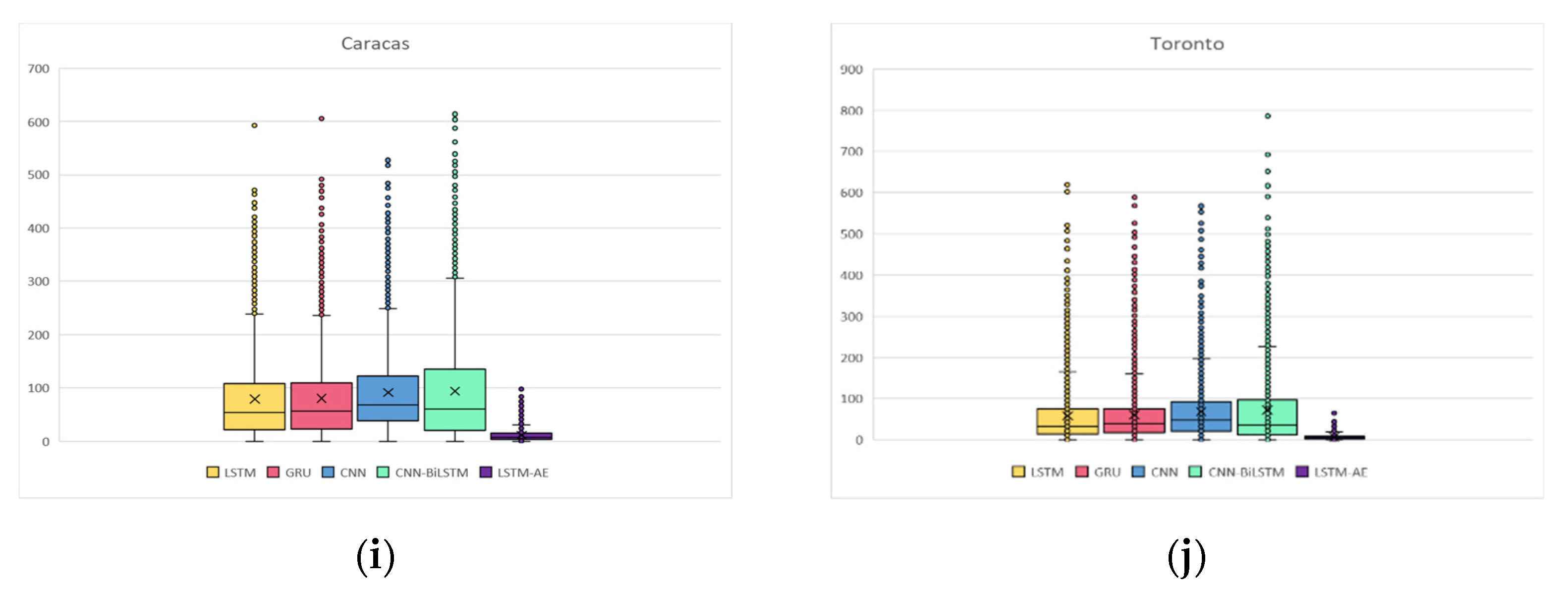
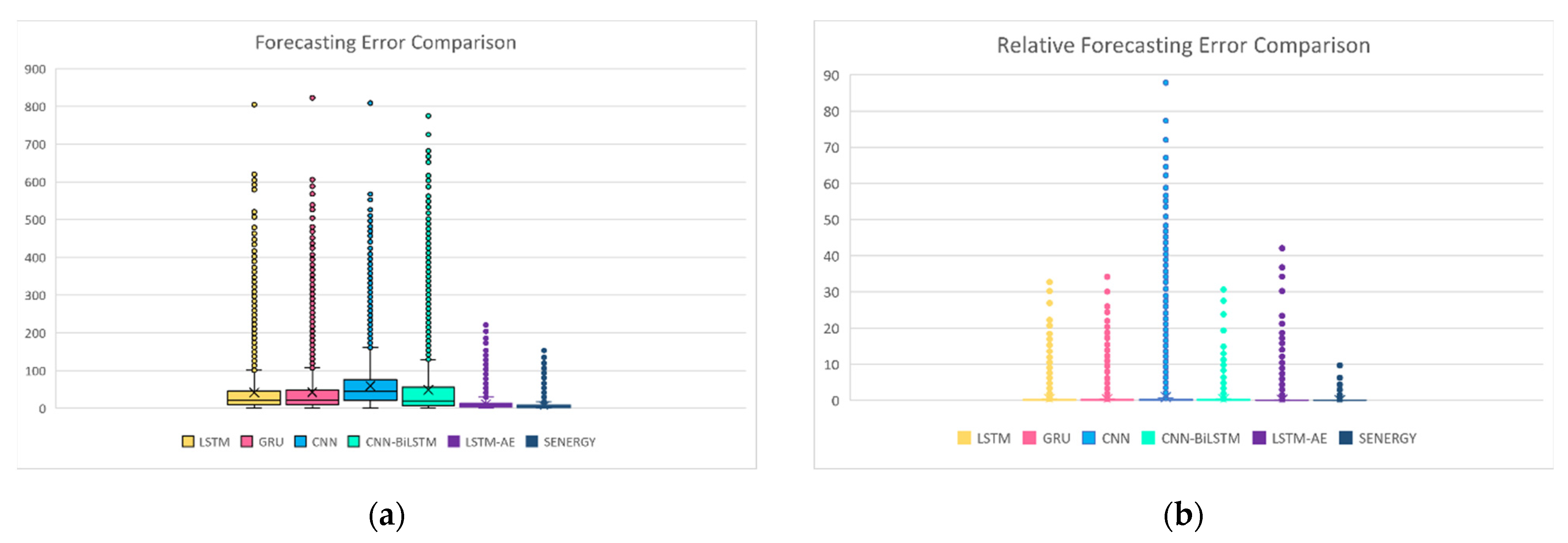
4.1.5. Digging Deeper into Forecasting Error for Each GHI Prediction
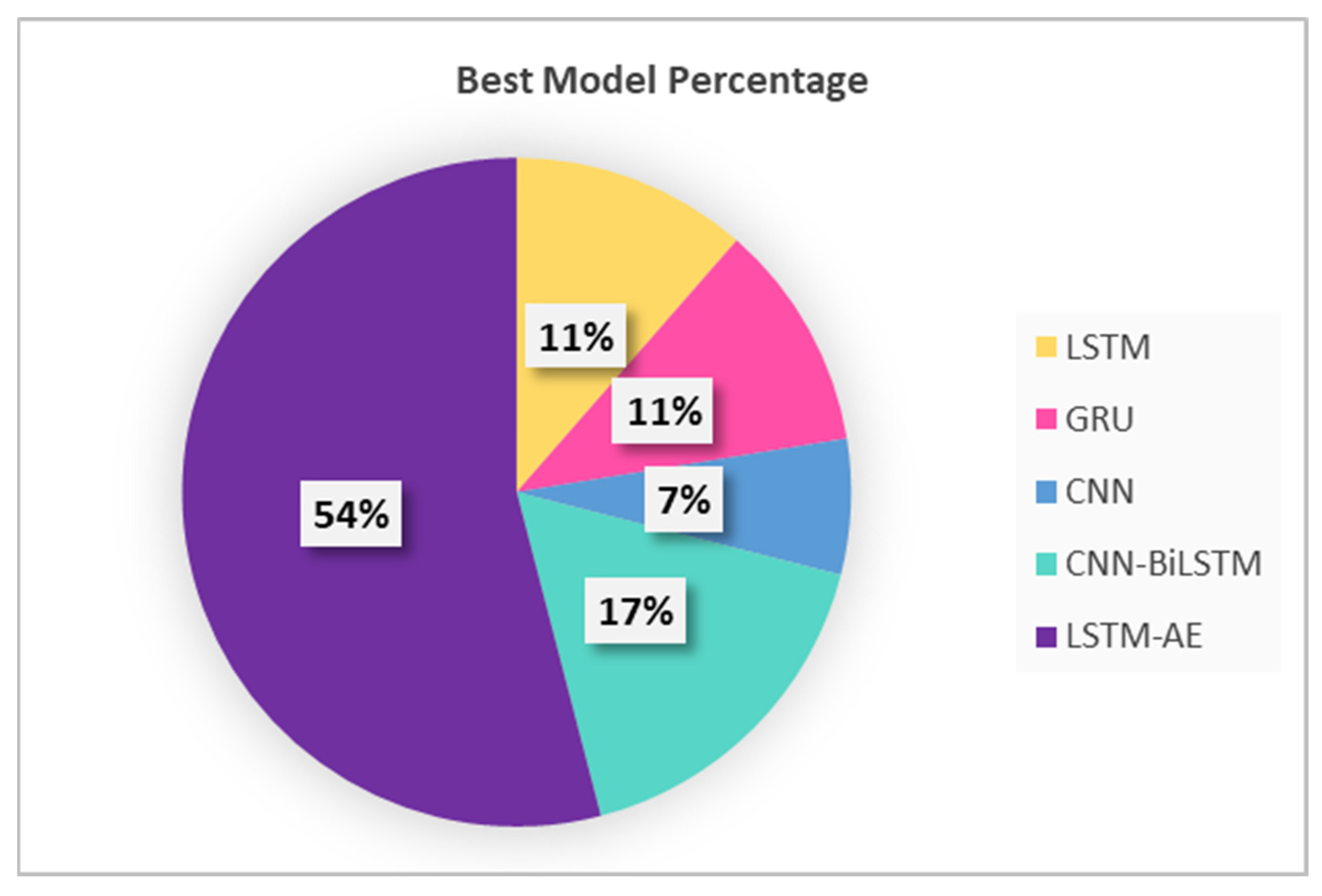
4.2. SENERGY: Auto-Selective Model Prediction Engine Performance
4.2.1. Model Prediction: Climate and Location
4.2.2. Model Prediction: Sunny and Cloudy Weathers
4.2.3. Model Prediction: Summer and Winter Seasons
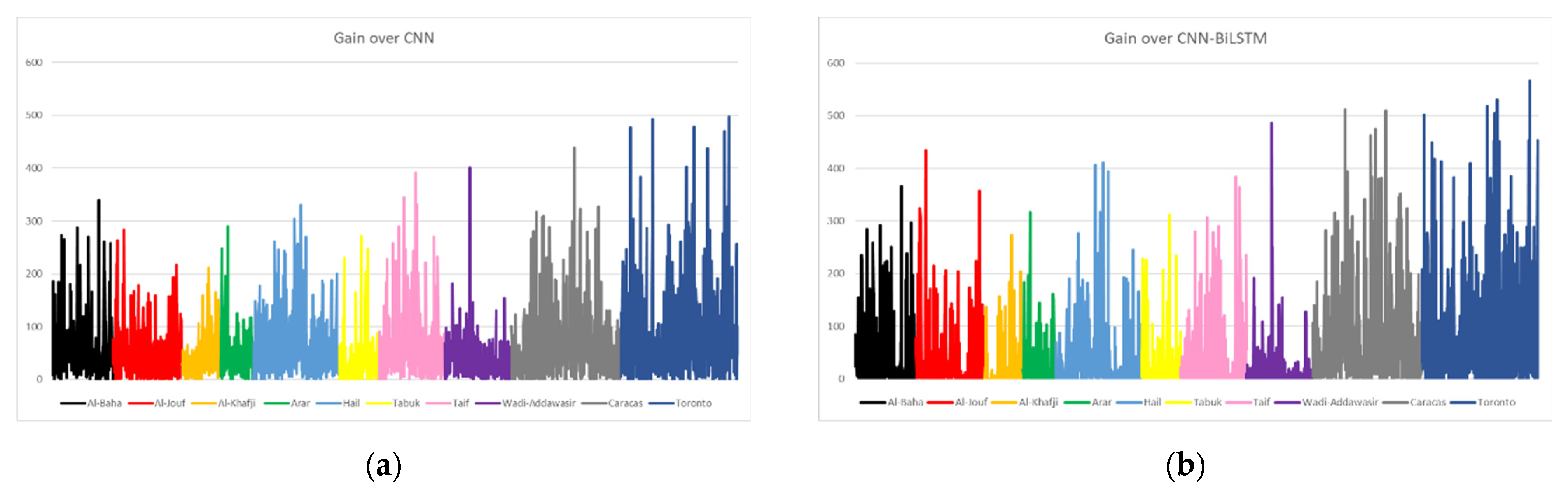
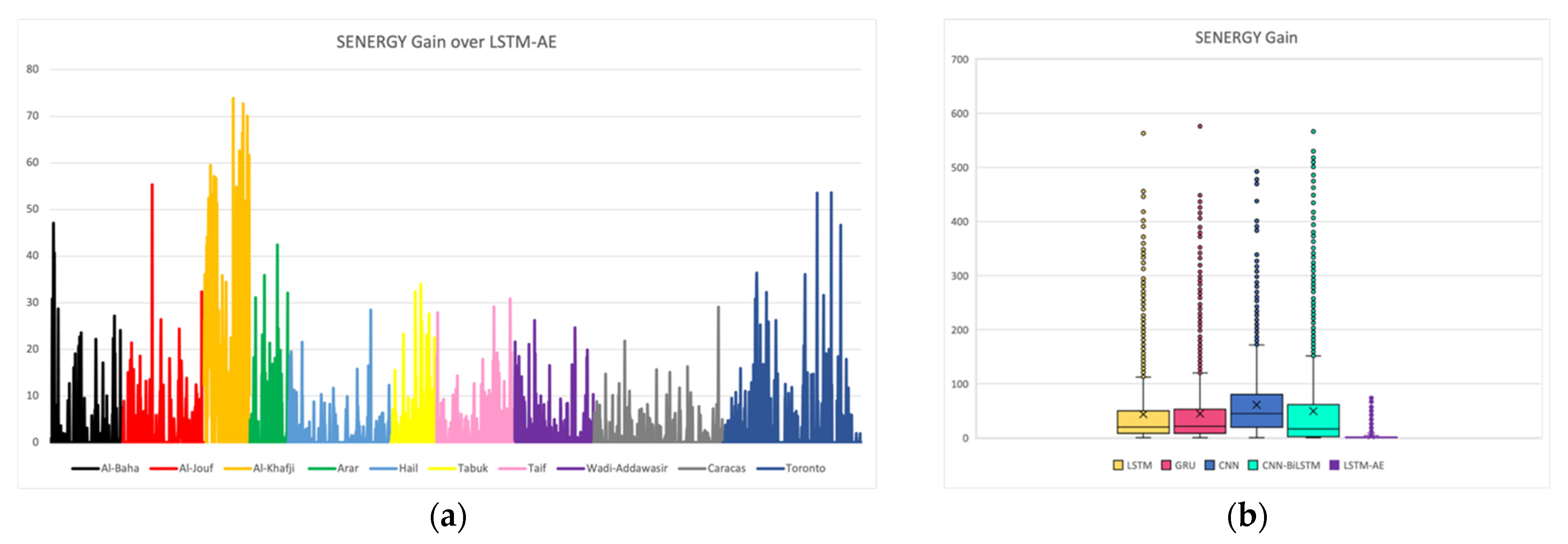
4.3. SENERGY: Performance Gain and Loss
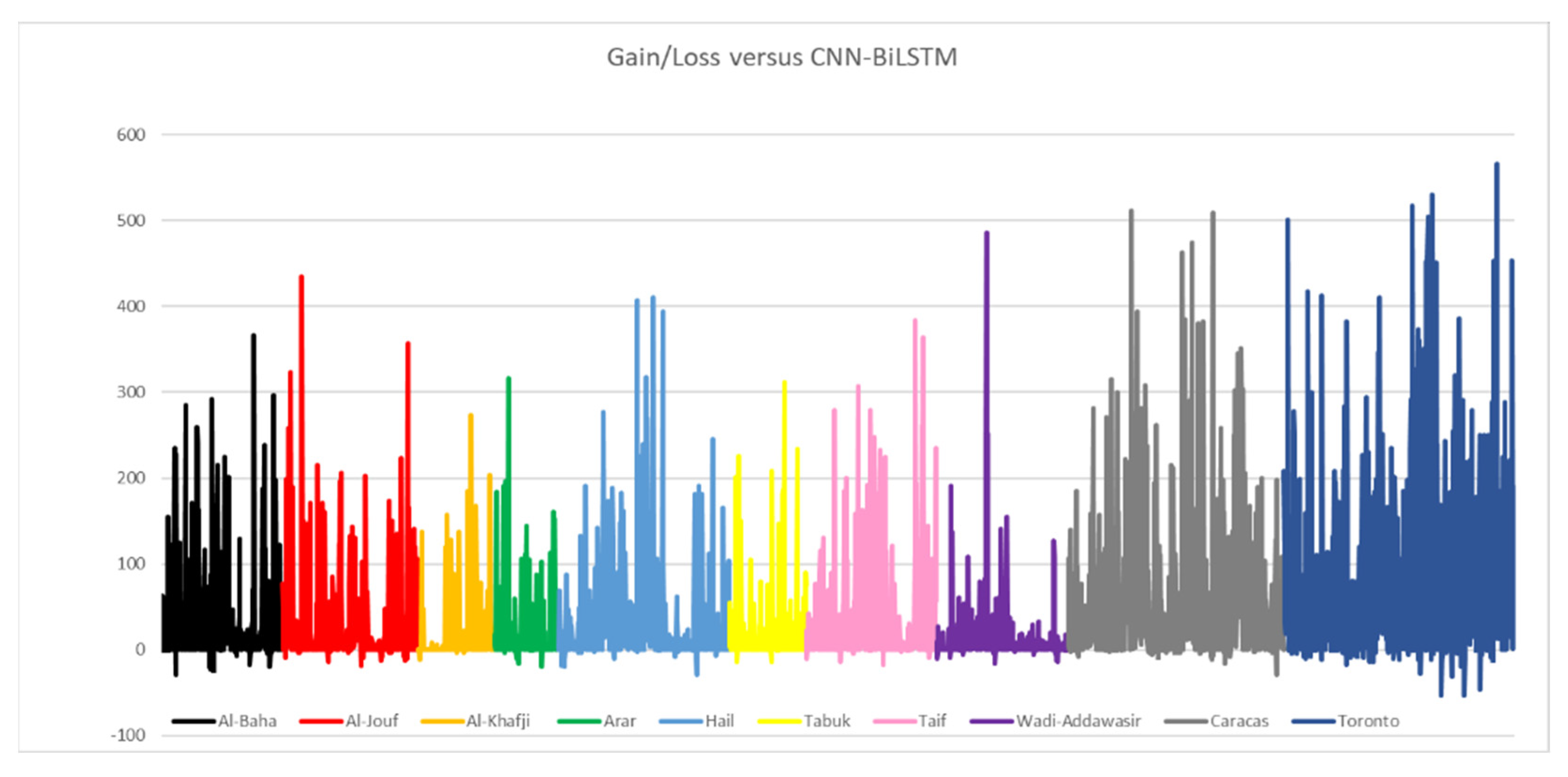
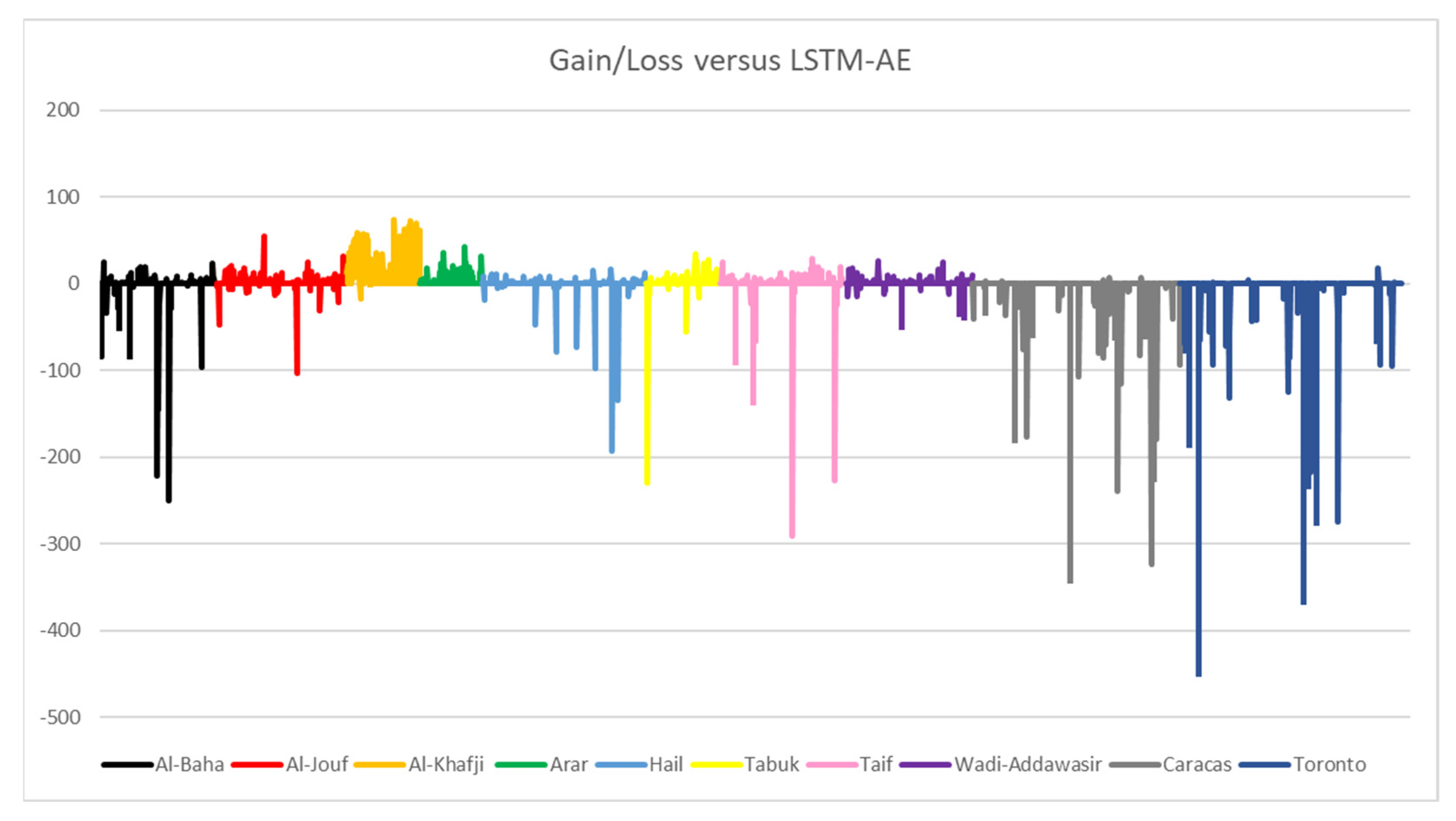
4.3.1. Actual Gains and Losses
4.3.2. Potential Performance
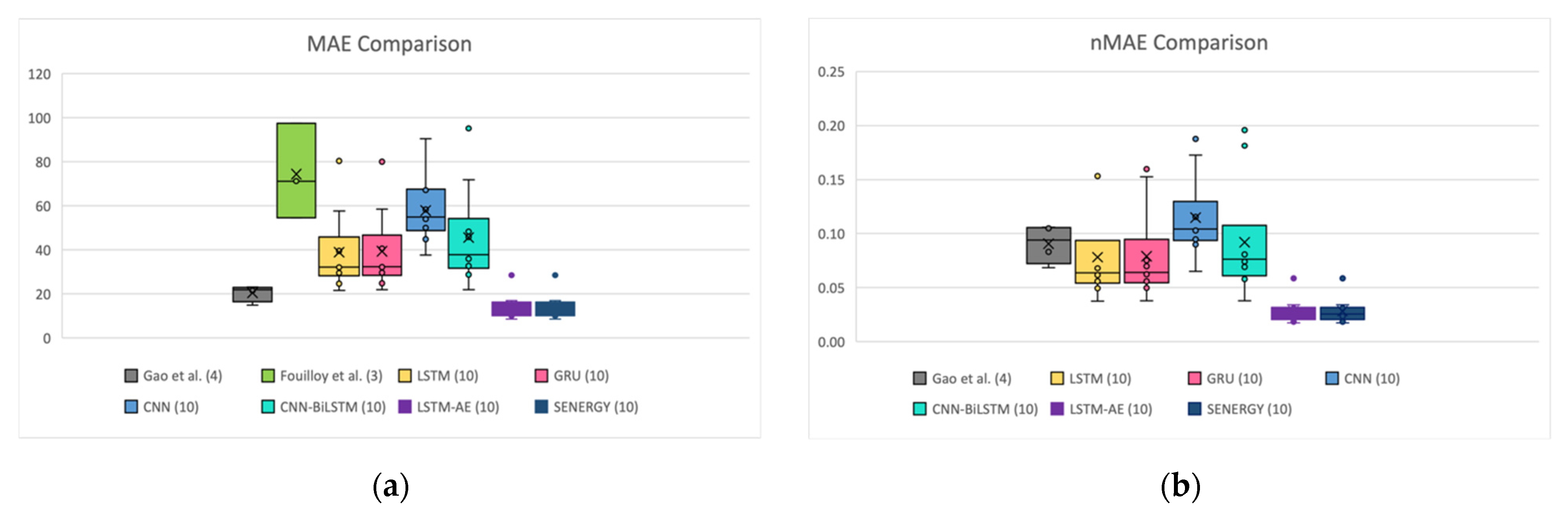
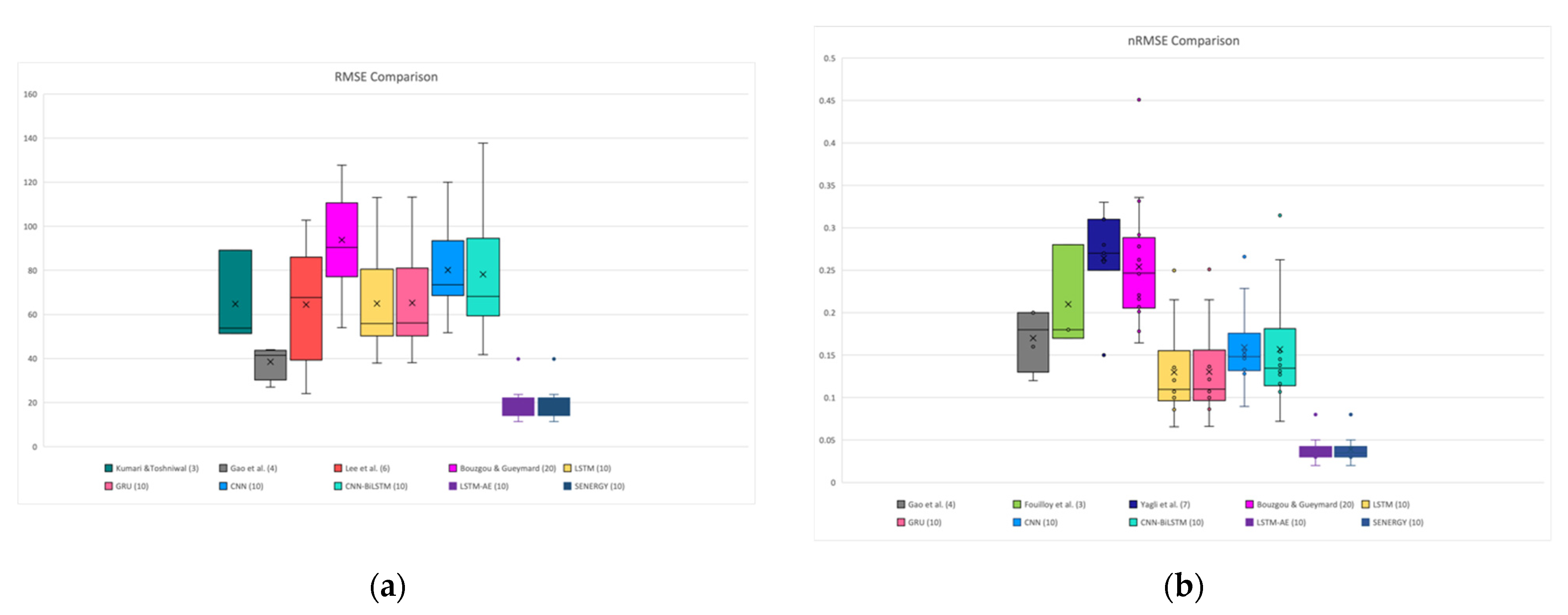
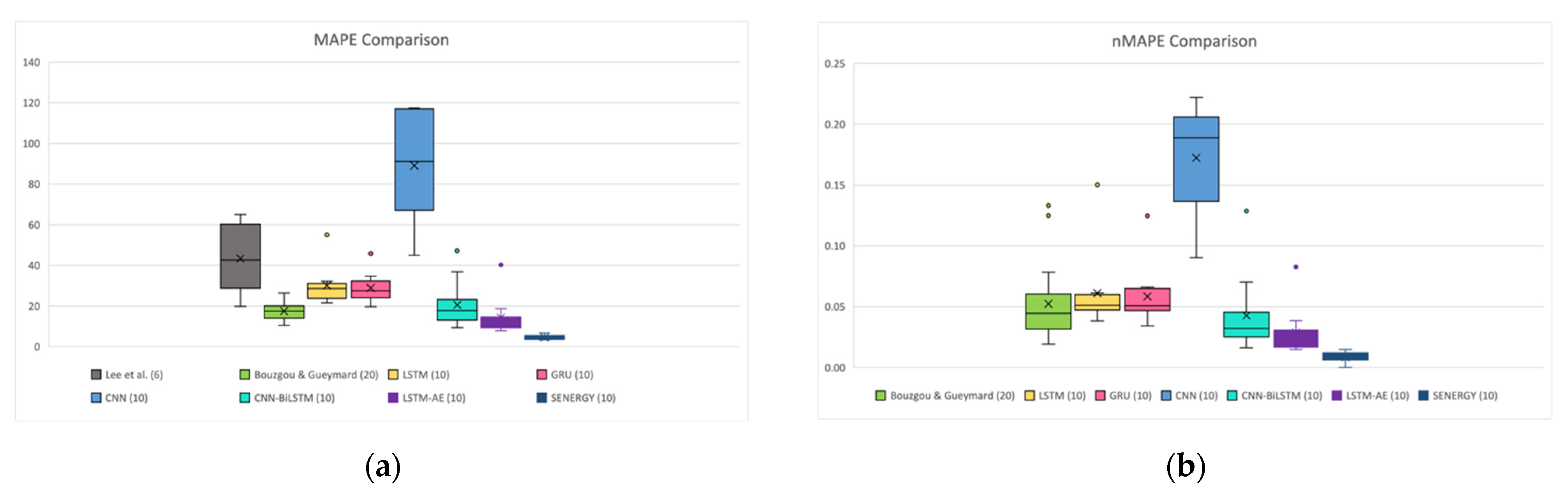
4.4. SENERGY: Comparison with Other Works
4.5. Results Summary
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NWP | Numerical Weather Prediction |
| RNN | Recurrent Neural Network |
| ANN | Artificial neural network |
| AE | Autoencoder |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| MI | Mutual Information |
| MLP | Multilayer Perceptron Network |
| ARMA | Autoregressive Moving Average |
| WT | Wavelet Transform |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| SVM | Support Vector Machine |
| RMSE | Root Mean Square Error |
| nRMSE | Normalized Root Mean Square Error |
| MAPE | Mean Absolute Percentage Error |
| nMAPE | Normalized Mean Absolute Percentage Error |
| MAE | Mean Absolute Error |
| nMAE | normalized Mean Absolute Error |
| MSE | Mean Squared Error loss |
| WS | Wind Speed |
| AT | Air Temperature |
| RH | Relative Humidity |
| ML | Machine Learning |
| CNN | Convolutional Neural Network |
| PV | Photovoltaic |
| AI | Artificial Intelligence |
| SVR | Support Vector machine Regression |
| FFNN | Feed Forward Neural Network |
| GHI | Global Horizontal Irradiation |
| RF | Random Forest |
| DNN | Deep Neural Network |
| ELM | Extreme Learning Machine |
| BPNN | Back Propagation Neural Network |
| ReLU | Rectified Linear Unit |
| DHI | Diffuse Horizontal Irradiation |
| DNI | Direct Normal Irradiance |
| BiLSTM | Bidirectional LSTM |
| FS | Forecast Skill |
| XGBoost | eXtreme Gradient Boosting |
| ACF | Autocorrelation Function |
| PACF | Partial Autocorrelation Function |
| WD | Wind Direction |
| BP | Barometric Pressure |
| ZA | Zenith Angle |
References
- Shining Brightly|MIT News|Massachusetts Institute of Technology. Available online: https://news.mit.edu/2011/energy-scale-part3-1026 (accessed on 14 August 2022).
- Kabir, E.; Kumar, P.; Kumar, S.; Adelodun, A.A.; Kim, K.-H. Solar energy: Potential and future prospects. Renew. Sustain. Energy Rev. 2018, 82, 894–900. [Google Scholar] [CrossRef]
- Shell Global, Global Energy Resources Database. Available online: https://www.shell.com (accessed on 26 June 2020).
- Elrahmani, A.; Hannun, J.; Eljack, F.; Kazi, M.-K. Status of renewable energy in the GCC region and future opportunities. Curr. Opin. Chem. Eng. 2021, 31, 100664. [Google Scholar] [CrossRef]
- Peng, T.; Zhang, C.; Zhou, J.; Nazir, M.S. An integrated framework of Bi-directional Long-Short Term Memory (BiLSTM) based on sine cosine algorithm for hourly solar radiation forecasting. Energy 2021, 221, 119887. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Deep learning models for solar irradiance forecasting: A comprehensive review. J. Clean. Prod. 2021, 318, 128566. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Zhou, B.; Li, C.; Cao, G.; Voropai, N.; Barakhtenko, E. Taxonomy research of artificial intelligence for deterministic solar power forecasting. Energy Convers. Manag. 2020, 214, 112909. [Google Scholar] [CrossRef]
- Ozcanli, A.K.; Yaprakdal, F.; Baysal, M. Deep learning methods and applications for electrical power systems: A comprehensive review. Int. J. Energy Res. 2020, 44, 7136–7157. [Google Scholar] [CrossRef]
- Said, Z.; Sharma, P.; Elavarasan, R.M.; Tiwari, A.K.; Rathod, M.K. Exploring the specific heat capacity of water-based hybrid nanofluids for solar energy applications: A comparative evaluation of modern ensemble machine learning techniques. J. Energy Storage 2022, 54, 105230. [Google Scholar] [CrossRef]
- Sharma, P.; Said, Z.; Kumar, A.; Nižetić, S.; Pandey, A.; Hoang, A.T.; Huang, Z.; Afzal, A.; Li, C.; Le, A.T. Recent advances in machine learning research for nanofluid-based heat transfer in renewable energy system. Energy Fuels 2022, 36, 6626–6658. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Reda, F.M. Deep Learning an Overview. Neural Netw. 2019, 12, 14–18. [Google Scholar]
- Shamshirband, S.; Rabczuk, T.; Chau, K.-W. A Survey of Deep Learning Techniques: Application in Wind and Solar Energy Resources. IEEE Access 2019, 7, 164650–164666. [Google Scholar] [CrossRef]
- Ahmad, I.; Alqurashi, F.; Abozinadah, E.; Mehmood, R. Deep Journalism and DeepJournal V1.0: A Data-Driven Deep Learning Approach to Discover Parameters for Transportation. Sustainability 2022, 14, 5711. [Google Scholar] [CrossRef]
- Alahmari, N.; Alswedani, S.; Alzahrani, A.; Katib, I.; Albeshri, A.; Mehmood, R.; Sa, A.A. Musawah: A Data-Driven AI Approach and Tool to Co-Create Healthcare Services with a Case Study on Cancer Disease in Saudi Arabia. Sustainability 2022, 14, 3313. [Google Scholar] [CrossRef]
- Alswedani, S.; Mehmood, R.; Katib, I. Sustainable Participatory Governance: Data-Driven Discovery of Parameters for Planning Online and In-Class Education in Saudi Arabia During COVID-19. Front. Sustain. Cities 2022, 4, 97. [Google Scholar] [CrossRef]
- Janbi, N.; Mehmood, R.; Katib, I.; Albeshri, A.; Corchado, J.M.; Yigitcanlar, T.; Sa, A.A. Imtidad: A Reference Architecture and a Case Study on Developing Distributed AI Services for Skin Disease Diagnosis over Cloud, Fog and Edge. Sensors 2022, 22, 1854. [Google Scholar] [CrossRef] [PubMed]
- Alkhayat, G.; Mehmood, R. A review and taxonomy of wind and solar energy forecasting methods based on deep learning. Energy AI 2021, 4, 100060. [Google Scholar] [CrossRef]
- Abualigah, L.; Zitar, R.A.; Almotairi, K.H.; Hussein, A.M.; Elaziz, M.A.; Nikoo, M.R.; Gandomi, A.H. Wind, Solar, and Photovoltaic Renewable Energy Systems with and without Energy Storage Optimization: A Survey of Advanced Machine Learning and Deep Learning Techniques. Energies 2022, 15, 578. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Extreme gradient boosting and deep neural network based ensemble learning approach to forecast hourly solar irradiance. J. Clean. Prod. 2021, 279, 123285. [Google Scholar] [CrossRef]
- Lima, M.A.F.B.; Carvalho, P.C.M.; Fernández-Ramírez, L.M.; Braga, A.P.S. Improving solar forecasting using Deep Learning and Portfolio Theory integration. Energy 2020, 195, 117016. [Google Scholar] [CrossRef]
- AlKandari, M.; Ahmad, I. Solar power generation forecasting using ensemble approach based on deep learning and statistical methods. Appl. Comput. Informatics 2020. ahead-of-print. [Google Scholar] [CrossRef]
- Gao, B.; Huang, X.; Shi, J.; Tai, Y.; Zhang, J. Hourly forecasting of solar irradiance based on CEEMDAN and multi-strategy CNN-LSTM neural networks. Renew. Energy 2020, 162, 1665–1683. [Google Scholar] [CrossRef]
- Fouilloy, A.; Voyant, C.; Notton, G.; Motte, F.; Paoli, C.; Nivet, M.-L.; Guillot, E.; Duchaud, J.-L. Solar irradiation prediction with machine learning: Forecasting models selection method depending on weather variability. Energy 2018, 165, 620–629. [Google Scholar] [CrossRef]
- Lago, J.; De Brabandere, K.; De Ridder, F.; De Schutter, B. Short-term forecasting of solar irradiance without local telemetry: A generalized model using satellite data. Sol. Energy 2018, 173, 566–577. [Google Scholar] [CrossRef]
- Lee, J.; Wang, W.; Harrou, F.; Sun, Y. Reliable solar irradiance prediction using ensemble learning-based models: A comparative study. Energy Convers. Manag. 2020, 208, 112582. [Google Scholar] [CrossRef]
- Yagli, G.M.; Yang, D.; Srinivasan, D. Automatic hourly solar forecasting using machine learning models. Renew. Sustain. Energy Rev. 2019, 105, 487–498. [Google Scholar] [CrossRef]
- Srivastava, S.; Lessmann, S. A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data. Sol. Energy 2018, 162, 232–247. [Google Scholar] [CrossRef]
- Bouzgou, H.; Gueymard, C.A. Minimum redundancy–Maximum relevance with extreme learning machines for global solar radiation forecasting: Toward an optimized dimensionality reduction for solar time series. Sol. Energy 2017, 158, 595–609. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Review and statistical analysis of different global solar radiation sunshine models. Renew. Sustain. Energy Rev. 2015, 52, 1869–1880. [Google Scholar] [CrossRef]
- Behar, O.; Khellaf, A.; Mohammedi, K. Comparison of solar radiation models and their validation under Algerian climate—The case of direct irradiance. Energy Convers. Manag. 2015, 98, 236–251. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S.; Zareipour, H.; Troccoli, A.; Hyndman, R.J. Probabilistic energy forecasting: Global energy forecasting competition 2014 and beyond. Int. J. Forecast. 2016, 32, 896–913. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, T.; Albeshri, A.; Katib, I.; Mehmood, R. DIESEL: A Novel Deep Learning based Tool for SpMV Computations and Solving Sparse Linear Equation Systems. J. Supercomput. 2020, 77, 6313–6355. [Google Scholar] [CrossRef]
- Usman, S.; Mehmood, R.; Katib, I.; Albeshri, A.; Altowaijri, S.M. ZAKI: A Smart Method and Tool for Automatic Performance Optimization of Parallel SpMV Computations on Distributed Memory Machines. Mob. Networks Appl. 2019, 1–20. [Google Scholar] [CrossRef]
- Usman, S.; Mehmood, R.; Katib, I.; Albeshri, A. ZAKI+: A Machine Learning Based Process Mapping Tool for SpMV Computations on Distributed Memory Architectures. IEEE Access 2019, 7, 81279–81296. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, H.; Zhang, Z.; Pei, S.; Wang, C.; Yu, X.; Jiang, Z.; Zhou, J. Ensemble spatiotemporal forecasting of solar irradiation using variational Bayesian convolutional gate recurrent unit network. Appl. Energy 2019, 253, 113596. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, H.; Dai, Y.; Wang, B.; Zheng, T.; Liao, Q.; Liang, Y.; Zhang, F.; Song, X. Time series prediction for output of multi-region solar power plants. Appl. Energy 2020, 257, 114001. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Lu, S.; Hamann, H.F.; Hodge, B.M.; Lehman, B. A Solar Time Based Analog Ensemble Method for Regional Solar Power Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 268–279. [Google Scholar] [CrossRef]
- Huertas-Tato, J.; Aler, R.; Galván, I.M.; Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Pozo-Vázquez, D. A short-term solar radiation forecasting system for the Iberian Peninsula. Part 2: Model blending approaches based on machine learning. Sol. Energy 2020, 195, 685–696. [Google Scholar] [CrossRef]
- Brahma, B.; Wadhvani, R. Solar irradiance forecasting based on deep learning methodologies and multi-site data. Symmetry 2020, 12, 1830. [Google Scholar] [CrossRef]
- Khan, W.; Walker, S.; Zeiler, W. Improved solar photovoltaic energy generation forecast using deep learning-based ensemble stacking approach. Energy 2022, 240, 122812. [Google Scholar] [CrossRef]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, K.; Wang, T.; Shi, M. A day-ahead PV power forecasting method based on LSTM-RNN model and time correlation modification under partial daily pattern prediction framework. Energy Convers. Manag. 2020, 212, 112766. [Google Scholar] [CrossRef]
- Singla, P.; Duhan, M.; Saroha, S. An ensemble method to forecast 24-h ahead solar irradiance using wavelet decomposition and BiLSTM deep learning network. Earth Sci. Informatics 2022, 15, 291–306. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Tan, J. Day-ahead hourly forecasting of solar generation based on cluster analysis and ensemble model. IEEE Access 2019, 7, 112921–112930. [Google Scholar] [CrossRef]
- El-Kenawy, E.-S.M.; Mirjalili, S.; Ghoneim, S.S.M.; Eid, M.M.; El-Said, M.; Khan, Z.S.; Ibrahim, A. Advanced Ensemble Model for Solar Radiation Forecasting Using Sine Cosine Algorithm and Newton’s Laws. IEEE Access 2021, 9, 115750–115765. [Google Scholar] [CrossRef]
- Kaba, K.; Sarıgül, M.; Avcı, M.; Kandırmaz, H.M. Estimation of daily global solar radiation using deep learning model. Energy 2018, 162, 126–135. [Google Scholar] [CrossRef]
- Jeon, B.K.; Kim, E.J. Next-Day Prediction of Hourly Solar Irradiance Using Local Weather Forecasts and LSTM Trained with Non-Local Data. Energies 2020, 13, 5258. [Google Scholar] [CrossRef]
- Renewable Resource Atlas- King Abdullah City for Atomic and Renewable Energy. Available online: https://rratlas.energy.gov.sa (accessed on 1 December 2021).
- Zepner, L.; Karrasch, P.; Wiemann, F.; Bernard, L. ClimateCharts.net—An interactive climate analysis web platform. Int. J. Digit. Earth 2021, 14, 338–356. [Google Scholar] [CrossRef]
- Sengupta, M.; Habte, A.; Xie, Y.; Lopez, A.; Buster, G. National Solar Radiation Database (NSRDB). United States. Renew. Sustain. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Vignola, F. GHI Correlations with DHI and DNI and the Effects of Cloudiness on One-Minute Data; ASES: Schaumburg, IL, USA, 2012. [Google Scholar]
- Yazdani, M.G.; Salam, M.A.; Rahman, Q.M. Investigation of the effect of weather conditions on solar radiation in Brunei Darussalam. Int. J. Sustain. Energy 2016, 35, 982–995. [Google Scholar] [CrossRef]
- Petneházi, G. Recurrent neural networks for time series forecasting. arXiv 2019, arXiv:1901.00069. [Google Scholar]
- Marchesoni-Acland, F.; Alonso-Suárez, R. Intra-day solar irradiation forecast using RLS filters and satellite images. Renew. Energy 2020, 161, 1140–1154. [Google Scholar] [CrossRef]
- Pereira, G.M.S.; Stonoga, R.L.B.; Detzel, D.H.M.; Küster, K.K.; Neto, R.A.P.; Paschoalotto, L.A.C. Analysis and Evaluation of Gap Filling Procedures for Solar Radiation Data. In Proceedings of the 2018 IEEE 9th Power, Instrumentation and Measurement Meeting (EPIM), Salto, Uruguay, 14–16 November 2018; IEEE: Salto, Uruguay, 2018; pp. 1–6. [Google Scholar]
- Mohamad, N.B.; Lai, A.-C.; Lim, B.-H. A case study in the tropical region to evaluate univariate imputation methods for solar irradiance data with different weather types. Sustain. Energy Technol. Assessments 2022, 50, 101764. [Google Scholar] [CrossRef]
- Abreu, E.F.M.; Canhoto, P.; Prior, V.; Melicio, R. Solar resource assessment through long-term statistical analysis and typical data generation with different time resolutions using GHI measurements. Renew. Energy 2018, 127, 398–411. [Google Scholar] [CrossRef]
- KAPSARC Data Portal. Available online: https://datasource.kapsarc.org/pages/home/ (accessed on 1 March 2022).
- Tang, X.; Yao, H.; Sun, Y.; Aggarwal, C.; Mitra, P.; Wang, S. Joint modeling of local and global temporal dynamics for multivariate time series forecasting with missing values. Proc. AAAI Conf. Artif. Intell. 2020, 34, 5956–5963. [Google Scholar] [CrossRef]
- Hadeed, S.J.; O’Rourke, M.K.; Burgess, J.L.; Harris, R.B.; Canales, R.A. Imputation methods for addressing missing data in short-term monitoring of air pollutants. Sci. Total Environ. 2020, 730, 139140. [Google Scholar] [CrossRef]
- Venkatesh, B.; Anuradha, J. A review of feature selection and its methods. Cybern. Inf. Technol. 2019, 19, 3–26. [Google Scholar] [CrossRef]
- Memarzadeh, G.; Keynia, F. A new short-term wind speed forecasting method based on fine-tuned LSTM neural network and optimal input sets. Energy Convers. Manag. 2020, 213, 112824. [Google Scholar] [CrossRef]
- Shilaskar, S.; Ghatol, A. Feature selection for medical diagnosis: Evaluation for cardiovascular diseases. Expert Syst. Appl. 2013, 40, 4146–4153. [Google Scholar] [CrossRef]
- Fonti, V.; Belitser, E. Feature selection using lasso. VU Amsterdam Res. Pap. Bus. Anal. 2017, 30, 1–25. [Google Scholar]
- Zhou, H.; Zhang, Y.; Yang, L.; Liu, Q.; Yan, K.; Du, Y. Short-term photovoltaic power forecasting based on long short term memory neural network and attention mechanism. IEEE Access 2019, 7, 78063–78074. [Google Scholar] [CrossRef]
- Sorkun, M.C.; Paoli, C.; Incel, Ö.D. Time series forecasting on solar irradiation using deep learning. In Proceedings of the 2017 10th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 30 November–2 December 2017; IEEE: Bursa, Turkey, 2017; pp. 151–155. [Google Scholar]
- Zang, H.; Liu, L.; Sun, L.; Cheng, L.; Wei, Z.; Sun, G. Short-term global horizontal irradiance forecasting based on a hybrid CNN-LSTM model with spatiotemporal correlations. Renew. Energy 2020, 160, 26–41. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Liang, Z.; Wei, Z.; Sun, G. Hybrid method for short-term photovoltaic power forecasting based on deep convolutional neural network. IET Gener. Transm. Distrib. 2018, 12, 4557–4567. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef] [Green Version]
- Dolatabadi, A.; Abdeltawab, H.; Mohamed, Y.A.-R.I. Hybrid Deep Learning-Based Model for Wind Speed Forecasting Based on DWPT and Bidirectional LSTM Network. IEEE Access 2020, 8, 229219–229232. [Google Scholar] [CrossRef]
- Boubaker, S.; Benghanem, M.; Mellit, A.; Lefza, A.; Kahouli, O.; Kolsi, L. Deep Neural Networks for Predicting Solar Radiation at Hail Region, Saudi Arabia. IEEE Access 2021, 9, 36719–36729. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Tran, K.P.; Thomassey, S.; Hamad, M. Forecasting and Anomaly Detection approaches using LSTM and LSTM Autoencoder techniques with the applications in supply chain management. Int. J. Inf. Manage. 2021, 57, 102282. [Google Scholar] [CrossRef]
- Sagheer, A.; Kotb, M. Unsupervised pre-training of a deep LSTM-based stacked autoencoder for multivariate time series forecasting problems. Sci. Rep. 2019, 9, 19038. [Google Scholar] [CrossRef]
- Li, G.; Xie, S.; Wang, B.; Xin, J.; Li, Y.; Du, S. Photovoltaic Power Forecasting With a Hybrid Deep Learning Approach. IEEE Access 2020, 8, 175871–175880. [Google Scholar] [CrossRef]
- Hossain, M.S.; Mahmood, H. Short-term photovoltaic power forecasting using an LSTM neural network and synthetic weather forecast. IEEE Access 2020, 8, 172524–172533. [Google Scholar] [CrossRef]
- Alrashidi, M.; Alrashidi, M.; Rahman, S. Global solar radiation prediction: Application of novel hybrid data-driven model. Appl. Soft Comput. 2021, 112, 107768. [Google Scholar] [CrossRef]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Meenal, R.; Selvakumar, A.I. Assessment of SVM, empirical and ANN based solar radiation prediction models with most influencing input parameters. Renew. Energy 2018, 121, 324–343. [Google Scholar] [CrossRef]
- Gigoni, L.; Betti, A.; Crisostomi, E.; Franco, A.; Tucci, M.; Bizzarri, F.; Mucci, D. Day-Ahead Hourly Forecasting of Power Generation from Photovoltaic Plants. IEEE Trans. Sustain. Energy 2018, 9, 831–842. [Google Scholar] [CrossRef] [Green Version]
- Deo, R.C.; Şahin, M. Forecasting long-term global solar radiation with an ANN algorithm coupled with satellite-derived (MODIS) land surface temperature (LST) for regional locations in Queensland. Renew. Sustain. Energy Rev. 2017, 72, 828–848. [Google Scholar] [CrossRef]
- Marzo, A.; Trigo-Gonzalez, M.; Alonso-Montesinos, J.; Martínez-Durbán, M.; López, G.; Ferrada, P.; Fuentealba, E.; Cortés, M.; Batlles, F.J. Daily global solar radiation estimation in desert areas using daily extreme temperatures and extraterrestrial radiation. Renew. Energy 2017, 113, 303–311. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Wang, H.; Al-Musaylh, M.S.; Casillas-Pérez, D.; Salcedo-Sanz, S. Stacked LSTM Sequence-to-Sequence Autoencoder with Feature Selection for Daily Solar Radiation Prediction: A Review and New Modeling Results. Energies 2022, 15, 1061. [Google Scholar] [CrossRef]
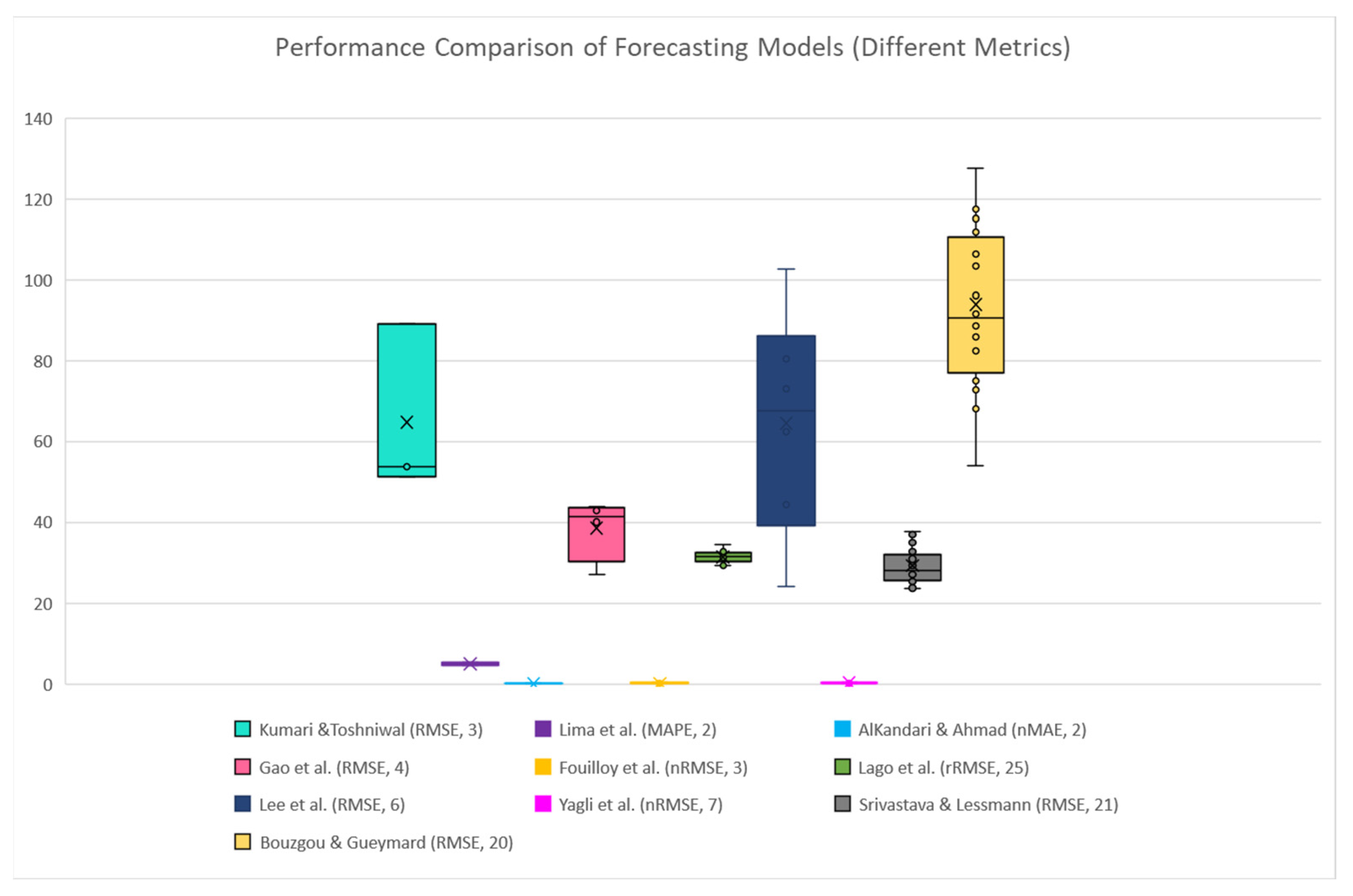










| Ref No. | Ensemble Model | Multiple Climates | Results | Main Findings |
|---|---|---|---|---|
| [21] | ✓ | ✓ | The ensemble model (XGBF-DNN) performed better than smart persistence, SVR, random forest (RF), XGBoost, and DNN models in hourly GHI prediction for all three locations in India and can be used for other locations. | The ensemble model (XGBF-DNN) attained RMSE = 53.79 for Jaipur, RMSE = 51.35 for New Delhi, and RMSE = 89.13 for Gangtok. |
| [22] | ✓ | ✓ | Integrating of LSTM, MLP, RBF, and SVR forecasting techniques provided better performance than the individual models for Brazil and Spain in 1 h ahead PV power forecasting. | The ensemble model of LSTM, MLP, RBF, and SVR achieved MAPE = 5.36% for Spain and 4.52% for Brazil. |
| [42] | ✓ | The ensemble model of ANN, LSTM, and XGBoost performed better than ANN and LSTM models alone in PV power forecast. | The ensemble model of ANN, LSTM, and XGBoost achieved RMSE = 0.74 and MAE = 0.47 with 15 min data resolution and RMSE = 0.78 and MAE = 0.59 with 1 h data resolution. | |
| [23] | ✓ | ✓ | The ensemble model of GRU, LSTM, and Theta achieved better performance with Shagaya dataset than with Cocoa because of the additional weather data and it achieved better accuracy than single ML algorithms and theta model in day-ahead solar power forecast for both locations. | The ensemble model of GRU, LSTM, and Theta achieved nMAE = 0.0317 for Shagaya in Kuwait while LSTM model alone achieved nMAE = 0.0739 for Cocoa in USA, which is slightly better than the ensemble model performance with nMAE = 0.0877. |
| [43] | ✓ | The ensemble model of LSTMs attained better performance than back propagation neural network (BPNN), SVM, and persistent models in day-ahead PV power forecasting. | The ensemble model of LSTMs attained RMSE = 5.68. | |
| [44] | ✓ | The ensemble model of WT and bidirectional LSTM outperformed the naïve predictor, LSTM, BiLSTM, GRU and two different WT based BiLSTM models in 24 h ahead solar irradiance forecast. | The ensemble model of WT and bidirectional LSTM attained annual average RMSE = 45.61 and MAPE = 6.48%. | |
| [45] | ✓ | The ensemble model of RF with cluster analysis for day-ahead solar forecasting performed better than RF alone and gradient boosted regression trees because weather classification improved the accuracy. | The ensemble model of RF with cluster analysis attained nRMSE = 8.8. | |
| [46] | ✓ | The ensemble model of LSTM, NN, and SVM for solar radiation forecasting, optimized using advanced sine and cosine algorithm, outperformed all the reference models. | The ensemble model of LSTM, NN, and SVM achieved RMSE = 0.0018. | |
| [24] | ✓ | The hybrid model of complete ensemble empirical mode decomposition adaptive noise (CEEMD), CNN, and LSTM to forecast hourly irradiance performed better compared to LSTM, BPNN, and SVM models as well as the hybrid CEEMDAN-LSTM, CEEMDAN-BPNN, and CEEMDAN-SVM models. | The hybrid model of CEEMD, CNN, and LSTM achieved annual RMSE = 42.84 for Tamanrasset, 43.98 for Hawaii’s Big Island, 40.60 for Denver, and 27.09 for Los Angeles. | |
| [47] | ✓ | The DNN model for daily GHI prediction showed good performance with 34 cities in Turkey using all inputs (extraterrestrial radiation, sunshine duration, cloud cover, and maximum and minimum temperature). | The DNN achieved RMSE ranges from 0.52 to 1.29 for 34 cities, which represent all climatic conditions in Turkey. | |
| [25] | ✓ | Statistical models’ performance of hourly solar irradiation forecasting with low to medium meteorological variabilities data is efficient while with high variability or longer forecasting horizons, bagged regression tree and RF approaches performed better. | For a medium and low variability dataset (Tilos and Ajaccio), the best 1 h ahead forecasting is MAE = 71.27 and 54.58 achieved by SVR model, whereas for a high variability dataset (Odeillo), the best result is 97.48 achieved by RF. | |
| [26] | ✓ | The global DNN for hourly GHI forecasting, which was trained using data from 25 locations in the Netherlands (satellite-based measurements and weather-based forecasts) has a better average performance than other four local models. | The global DNN attained average relative RMSE = 31.31%, where the lowest relative RMSE = 29.24 for Hoek v. H. site and the highest relative RMSE = 34.55 for Deelen site. | |
| [27] | ✓ | ✓ | The ensemble models (boosted trees, bagged trees, RF, and generalized RF) for short-term solar irradiance forecast outperformed SVR and Gaussian process regression. | The ensemble model achieved the best MAPE results for 4 out of 6 datasets (MAPE equals to 19.76, 42.27, 31.79, and 58.58 for CA, TX, WA, and MN respectively). |
| [28] | ✓ | For hourly solar forecasting, tree-based methods were better in all-sky conditions, whereas variants of MLP and SVR were better in clear-sky and RF with quantile regression in overcast sky conditions. | Tree-based methods are superior for all-sky conditions with nRMSE ranges from 15.46% to 33.36% based on location. | |
| [29] | ✓ | The LSTM model outperformed persistence, FFNN, and gradient boosting regression methods in day-ahead GHI forecasting. | The LSTM model achieved RMSE ranges from 23.6 to 37.78 for 21 locations. | |
| [48] | ✓ | The global LSTM model, which was trained with international data for next-day GHI prediction, was able to predict GHI in Korea. | The global LSTM model achieved RMSE = 30 with Inchon in Korea. | |
| [30] | ✓ | The ELM model, which was trained with data from 20 locations, has good performance for 15 min, 1 h, and 24 h ahead forecasting. | The ELM model achieved average RMSE = 93.82 for 20 locations for 1 h ahead forecast. |
| Station No. | Station Name | Latitude (N) | Longitude (E) | Elevation (m) |
|---|---|---|---|---|
| 1 | Al-Baha University | 20.1794 | 41.6357 | 1680 |
| 2 | Al-Jouf College of Technology | 29.77634 | 40.02318 | 680 |
| 3 | Saline Water Conversion Corporation (Al-Khafji) | 28.50676 | 48.45513 | 13 |
| 4 | Arar Technical Institute | 31.0274 | 40.90642 | 583 |
| 5 | Hail College of Technology | 27.65261 | 41.70826 | 928 |
| 6 | Tabuk University | 28.38287 | 36.48396 | 781 |
| 7 | Taif University | 21.43278 | 40.49173 | 1518 |
| 8 | Wadi-Addawasir College of Technology | 20.43008 | 44.89433 | 671 |
| Location | Latitude (N) | Longitude (E) | Elevation (m) | Climate Class |
|---|---|---|---|---|
| Caracas, Venezuela | 10.49 | −66.9 | 942 | A |
| Toronto, Canada | 43.65 | −79.38 | 93 | Dfb |
| Time t Features | Time t−1 Features | Time t−2 Features | Time t−3 Features | Unit |
|---|---|---|---|---|
| GHI (output) | GHI_lag1 | GHI_lag2 | GHI_lag3 | Wh/m2 |
| Hour_sin (HS) | DNI_lag1 | DNI_lag2 | DNI_lag3 | Wh/m2 |
| Hour_cos (HC) | DHI_lag1 | DHI_lag2 | DHI_lag3 | Wh/m2 |
| Day_sin (DS) | AT_lag1 | AT_lag2 | AT_lag3 | °C |
| Day_cos (DC) | ZA_lag1 | ZA_lag2 | ZA_lag3 | ° |
| Month_sin (MS) | WS_lag1 | WS_lag2 | WS_lag3 | m/s |
| Month_cos (MC) | WD_lag1 | WD_lag2 | WD_lag3 | ° |
| RH_lag1 | RH_lag2 | RH_lag3 | % | |
| BP_lag1 | BP_lag2 | BP_lag3 | Pa (Saudi data)/Millibar (others) |
| Tim Stamp e | GHI at t | GHI at t−1 | GHI at t−2 | GHI at t−3 |
|---|---|---|---|---|
| 01/01/2016 7:00 | 0 | 0 | 0 | 0 |
| 01/01/2016 8:00 | 35.3 | 0 | 0 | 0 |
| 01/01/2016 9:00 | 236.2 | 35.3 | 0 | 0 |
| 01/01/2016 10:00 | 468.8 | 236.2 | 35.3 | 0 |
| 01/01/2016 11:00 | 609.6 | 468.8 | 236.2 | 35.3 |
| 01/01/2016 12:00 | 688.7 | 609.6 | 468.8 | 236.2 |
| 01/01/2016 13:00 | 686.8 | 688.7 | 609.6 | 468.8 |
| 01/01/2016 14:00 | 635.6 | 686.8 | 688.7 | 609.6 |
| 01/01/2016 15:00 | 522.7 | 635.6 | 686.8 | 688.7 |
| 01/01/2016 16:00 | 361.3 | 522.7 | 635.6 | 686.8 |
| 01/01/2016 17:00 | 166.2 | 361.3 | 522.7 | 635.6 |
| 01/01/2016 18:00 | 15.6 | 166.2 | 361.3 | 522.7 |
| Location | Total Hourly Records | Missing Days | GHI Mean | GHI SD | GHI Var |
|---|---|---|---|---|---|
| Al-Baha | Train: 6227 | 635 days | 574.67 | 323.90 | 104,896.29 |
| Val: 3056 | 552.10 | 325.90 | 106,176.30 | ||
| Test: 2247 | 582.09 | 311.16 | 96,780.11 | ||
| Al-Jouf | Train: 8600 | 363 days | 554.11 | 307.66 | 94,643.25 |
| Val: 2991 | 547.92 | 306.49 | 93,901.92 | ||
| Test: 2554 | 528.14 | 296.47 | 87,858.12 | ||
| Al-Khafji | Train: 4618 | 970 days (Year 2019) | 504.81 | 288.56 | 83,245.88 |
| Val: 2363 | 555.17 | 308.66 | 95,231.29 | ||
| Test: 2110 | 486.59 | 275.73 | 75,991.13 | ||
| Arar | Train: 8339 | 575 days | 546.71 | 310.06 | 96,128.23 |
| Val: 3589 | 537.73 | 300.20 | 90,097.23 | ||
| Test: 1357 | 485.46 | 295.04 | 86,983.40 | ||
| Hail | Train: 8723 | 271 days | 552.26 | 311.69 | 97,140.65 |
| Val: 3260 | 544.05 | 310.67 | 96,486.20 | ||
| Test: 2561 | 543.77 | 303.82 | 92,270.30 | ||
| Tabuk | Train: 7576 | 542 days | 593.27 | 310.35 | 96,307.42 |
| Val: 3100 | 579.62 | 303.93 | 92,342.88 | ||
| Test: 1937 | 498.03 | 261.73 | 68,465.05 | ||
| Taif | Train: 8618 | 272 days | 580.83 | 321.62 | 103,424.30 |
| Val: 3386 | 562.14 | 308.42 | 95,094.37 | ||
| Test: 2543 | 567.62 | 308.47 | 95,115.01 | ||
| Wadi-Addawasir | Train: 9199 | 242 days | 584.98 | 309.00 | 95,474.22 |
| Val: 3450 | 579.24 | 306.12 | 93,684.80 | ||
| Test: 2551 | 578.02 | 301.69 | 90,982.42 | ||
| Caracas | Train: 10,112 | 0 days | 499.28 | 284.48 | 80,922.07 |
| Val: 3428 | 505.95 | 288.71 | 83,327.90 | ||
| Test: 3428 | 524.82 | 297.12 | 88,255.24 | ||
| Toronto | Train: 9892 | 0 days | 381.15 | 273.39 | 74,732.91 |
| Val: 3392 | 336.74 | 266.95 | 71,242.70 | ||
| Test: 3388 | 366.77 | 278.11 | 77,322.36 | ||
| All | Train: 81,904 | 3870 days | - | - | - |
| Val: 32,015 | |||||
| Test: 24,676 |
| Al-Jouf | Al-Khafji | Wadi-Addawasir | Caracas | Toronto | |||||
|---|---|---|---|---|---|---|---|---|---|
| Feature | PC | Feature | PC | Feature | PC | Feature | PC | Feature | PC |
| GHI_lag1 | 0.88 | GHI_lag1 | 0.87 | HC | −0.91 | HC | −0.80 | GHI_lag1 | 0.87 |
| HC | −0.82 | HC | −0.81 | GHI_lag1 | 0.86 | GHI_lag1 | 0.76 | ZA_lag1 | −0.68 |
| ZA_lag1 | −0.82 | ZA_lag1 | −0.78 | ZA_lag1 | −0.80 | ZA_lag1 | −0.61 | DNI_lag1 | 0.64 |
| DNI_lag1 | 0.59 | DNI_lag1 | 0.63 | HS | 0.53 | HS | 0.58 | GHI_lag2 | 0.64 |
| HS | 0.47 | HS | 0.51 | DNI_lag1 | 0.53 | DNI_lag1 | 0.49 | DNI_lag2 | 0.54 |
| GHI_lag2 | 0.47 | GHI_lag2 | 0.47 | HC | −0.51 | ||||
| Al-Jouf | Al-Khafji | Wadi-Addawasir | Caracas | Toronto | |||||
|---|---|---|---|---|---|---|---|---|---|
| FFS | BFE | FFS | BFE | FFS | BFE | FFS | BFE | FFS | BFE |
| HS | HS | HS | HS | HS | HS | HS | HS | MS | HS |
| HC | HC | WS_lag1 | DHI_lag1 | HC | HC | HC | HC | HS | DHI_lag1 |
| DHI_lag1 | DHI_lag1 | DHI_lag1 | DNI_lag1 | DHI_lag1 | DHI_lag1 | DHI_lag1 | DHI_lag1 | GHI_lag1 | DNI_lag1 |
| DNI_lag1 | DNI_lag1 | DNI_lag1 | GHI_lag1 | DNI_lag1 | DNI_lag1 | DNI_lag1 | DNI_lag1 | ZA_lag1 | GHI_lag1 |
| GHI_lag1 | GHI_lag1 | GHI_lag1 | BP_lag1 | GHI_lag1 | GHI_lag1 | GHI_lag1 | GHI_lag1 | WS_lag1 | AT_lag1 |
| ZA_lag1 | ZA_lag1 | ZA_lag1 | DHI_lag2 | DHI_lag2 | DHI_lag2 | RH_lag1 | RH_lag1 | WS_lag3 | ZA_lag2 |
| DHI_lag2 | DHI_lag2 | DHI_lag2 | DNI_lag2 | ZA_lag3 | ZA_lag3 | GHI_lag2 | DNI_lag2 | DNI_lag2 | DHI_lag3 |
| DNI_lag2 | DNI_lag2 | DHI_lag3 | GHI_lag2 | GHI_lag3 | GHI_lag2 | ZA_lag2 | ZA_lag2 | GHI_lag3 | DNI_lag3 |
| GHI_lag3 | GHI_lag2 | DNI_lag3 | ZA_lag2 | ZA_lag1 | ZA_lag2 | WS_lag3 | WS_lag3 | ZA_lag3 | GHI_lag3 |
| ZA_lag3 | AT_lag1 | GHI_lag3 | GHI_lag3 | RH_lag1 | DNI_lag2 | AT_lag3 | AT_lag3 | RH_lag3 | AT_lag3 |
| Model | Batch Size | Layers | Learning Rate | Number of Epochs | Optimization |
|---|---|---|---|---|---|
| LSTM | 256 | 3 hidden layers with 128 hidden states, 1 dense layer | 0.001 | 100 | Dropout = 0.2, ReLU function, Weight decay = 0.000001, Adam |
| GRU | 256 | 3 hidden layers with 128 hidden states,1 dense layer | 0.001 | 100 | Dropout = 0.2, ReLU function, Weight decay = 0.000001, Adam |
| CNN | 64 | 2 conv layers with 10 and 5 filters, 1 max-pooling layer, 2 dense layers | 0.001 | 100 | Dropout = 0.2, ReLU function, Adam, batch normalization |
| CNN-BiLSTM | 64 | 2 conv layers with 10 and 5 filters, 1 max-pooling layer, 1 BiLSTM layer, 2 dense layers | 0.001 | 100 | Dropout = 0.2, ReLU function, Adam, batch normalization |
| LSTM-AE | 256 | 4 LSTM layers with 128 hidden states, 1 dense layer | 0.001 | 100 | ReLU function, weight decay = 0.000001, Adam |
| Model | Precision | Recall | F1-score | Support |
|---|---|---|---|---|
| CNN-BiLSTM | 66% | 36% | 47% | 809 |
| LSTM-AE | 83% | 94% | 88% | 2691 |
| Accuracy | 81% | 3500 | ||
| Macro average | 75% | 65% | 68% | 3500 |
| Weighted average | 79% | 81% | 79% | 3500 |
| FE CNN-BiLSTM | FE LSTM-AE | FE Best Model | G/L CNN-BiLSTM | G/L LSTM-AE |
|---|---|---|---|---|
| 67.73 | 4.83 | 4.83 | 62.90 | 0 |
| 128.60 | 44.41 | 128.60 | 0 | −84.19 |
| 0.47 | 29.12 | 29.12 | −28.65 | 0 |
| Ref No. | Location | GHI Mean | GHI SD | Climate | Weather Data | Model |
|---|---|---|---|---|---|---|
| [21] | Jaipur | NA | NA |
| ✓ | Ensemble model of XGBF-DNN |
| New Delhi | ||||||
| Gangtok | ||||||
| [24] | Los Angeles | 217.37 | 291.73 |
| ✗ | Hybrid model of CEEMDAN-CNN-LSTM |
| Denver | 203.33 | 276.40 | ||||
| Hawaii’s Big Island | 220.12 | 307.79 | ||||
| Tamanrasset | 269.98 | 361.83 | ||||
| [25] | Ajaccio | NA | NA |
| ✗ | ARMA RF |
| Tilos | ||||||
| Odeillo | ||||||
| [27] | CA | NA | NA |
| ✓ | Generalized random forest |
| TX | ||||||
| WA | ||||||
| FL | ||||||
| PA | ||||||
| MN | ||||||
| [28] | Bondville | 398.04 | 284.66 |
| ✗ | 68 machine learning algorithms (Cubist model is the best in most cases) |
| Desert Rock | 517.72 | 314.73 | ||||
| Fort Peck | 368.17 | 277.33 | ||||
| Goodwin Creek | 442.77 | 289 | ||||
| Penn. State Uni | 384.31 | 277.24 | ||||
| Sioux Falls | 406.94 | 277.55 | ||||
| Table Mountain | 412.19 | 287.97 | ||||
| [30] | Tucson | 532.5 | NA |
| ✗ | ELM |
| Bermuda | 417.1 | |||||
| Brasilia | 475.6 | |||||
| Sonnblick | 347.2 | |||||
| Solar Village | 580.9 | |||||
| Golden | 459.4 | |||||
| Darwin | 516.4 | |||||
| Ny-Alesund | 184.3 | |||||
| Toravere | 256.9 | |||||
| Lerwick | 198.3 | |||||
| This work | Al-Baha | 582.09 | 311.16 |
| ✓ | LSTM GRU CNN CNN-BiLSTM LSTM-AE |
| Al-Jouf | 528.14 | 296.47 | ||||
| Al-Khafji | 486.59 | 275.73 | ||||
| Arar | 485.46 | 295.04 | ||||
| Hail | 543.77 | 303.82 | ||||
| Tabuk | 498.03 | 261.73 | ||||
| Taif | 567.62 | 308.47 | ||||
| Wadi-Addawasir | 578.02 | 301.69 | ||||
| Caracas | 366.77 | 271.11 | ||||
| Toronto | 524.82 | 297.12 | ||||
| Ref [30] has 20 locations, we present data from 10 locations from various climates for simplicity. NA: Not available. | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkhayat, G.; Hasan, S.H.; Mehmood, R. SENERGY: A Novel Deep Learning-Based Auto-Selective Approach and Tool for Solar Energy Forecasting. Energies 2022, 15, 6659. https://doi.org/10.3390/en15186659
Alkhayat G, Hasan SH, Mehmood R. SENERGY: A Novel Deep Learning-Based Auto-Selective Approach and Tool for Solar Energy Forecasting. Energies. 2022; 15(18):6659. https://doi.org/10.3390/en15186659
Chicago/Turabian StyleAlkhayat, Ghadah, Syed Hamid Hasan, and Rashid Mehmood. 2022. "SENERGY: A Novel Deep Learning-Based Auto-Selective Approach and Tool for Solar Energy Forecasting" Energies 15, no. 18: 6659. https://doi.org/10.3390/en15186659
APA StyleAlkhayat, G., Hasan, S. H., & Mehmood, R. (2022). SENERGY: A Novel Deep Learning-Based Auto-Selective Approach and Tool for Solar Energy Forecasting. Energies, 15(18), 6659. https://doi.org/10.3390/en15186659











