Optimization of Proton Exchange Membrane Electrolyzer Cell Design Using Machine Learning
Abstract
:Highlights
- A dataset of PEM water electrolysis was constructed for machine learning purposes.
- Machine learning can be used for optimal PEM water electrolyzer cell design.
- Adaptive degree prediction can be employed to optimize the polynomial regression models.
- The proposed model can predict the cell design parameters for small-scale and commercial-scale PEM water electrolyzer cells.
- Optimal PEM water electrolyzer cell design can be modeled using polynomial regression and logistic regression machine learning models.
Abstract
1. Introduction
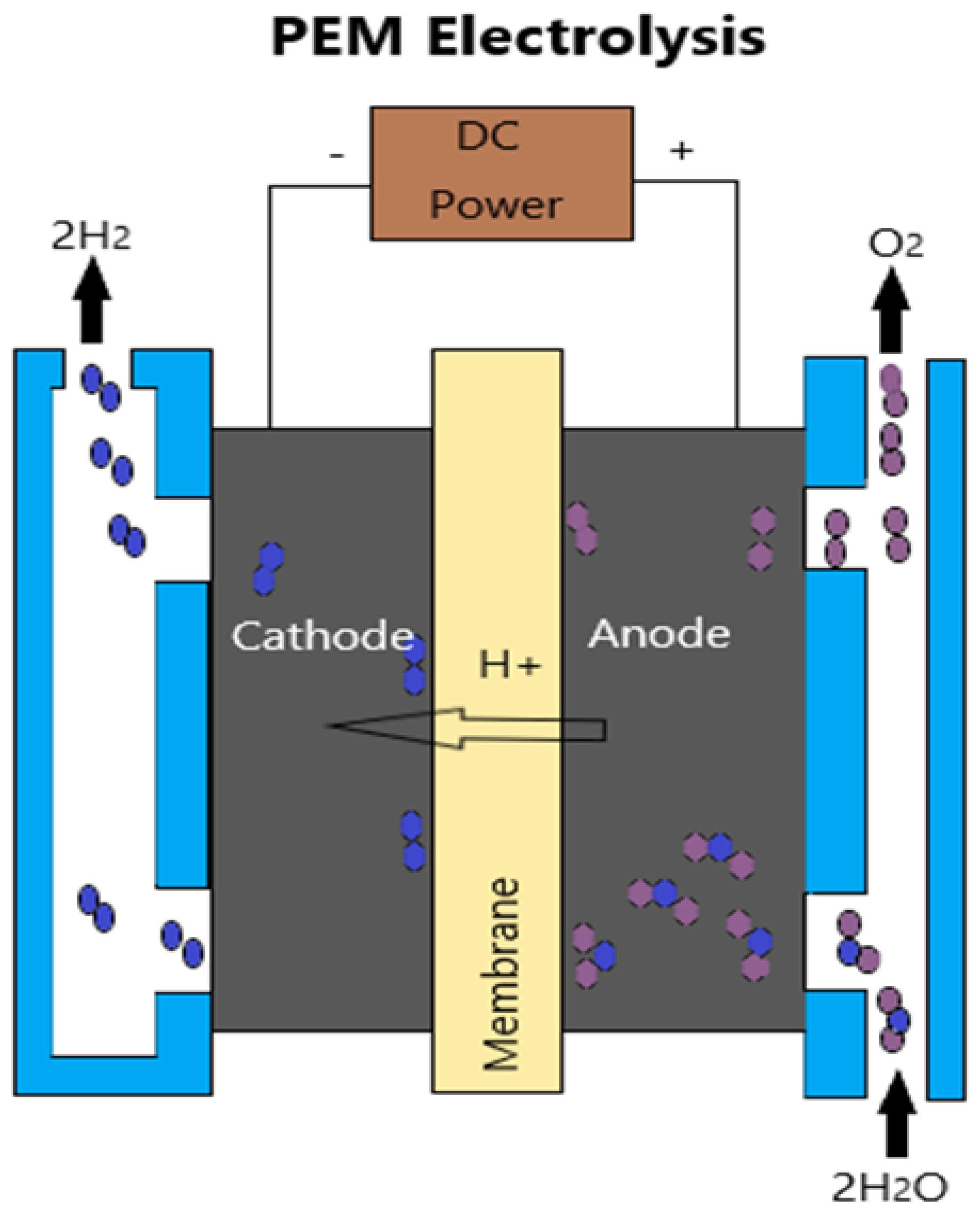
2. Theory and Calculation
3. Dataset Collection
4. Machine Learning Models Training and Validation
5. Laboratory Experiments for Validating Models
5.1. Preparation of the Catalysts
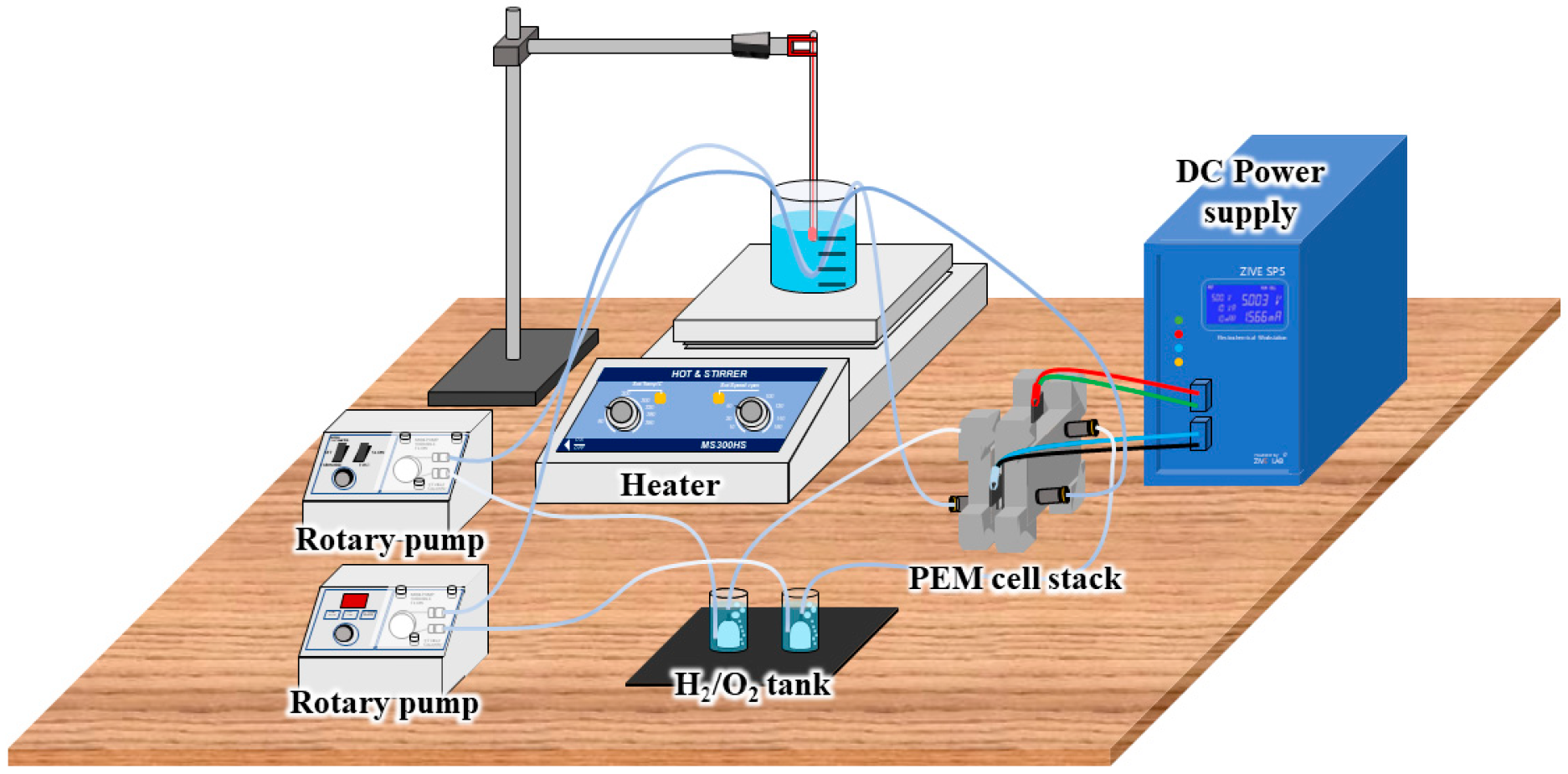
5.2. Experimental Method
6. Results and Discussion
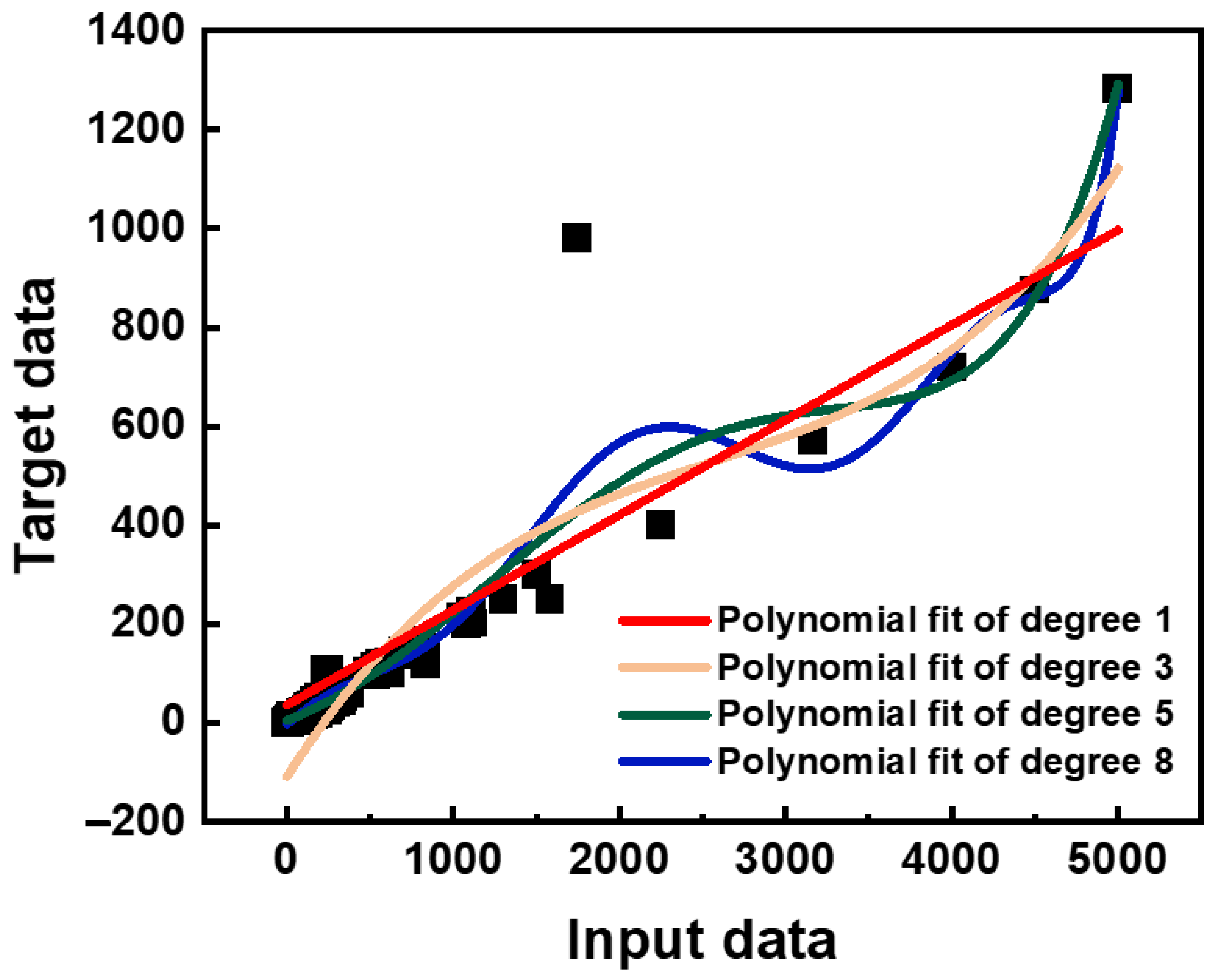
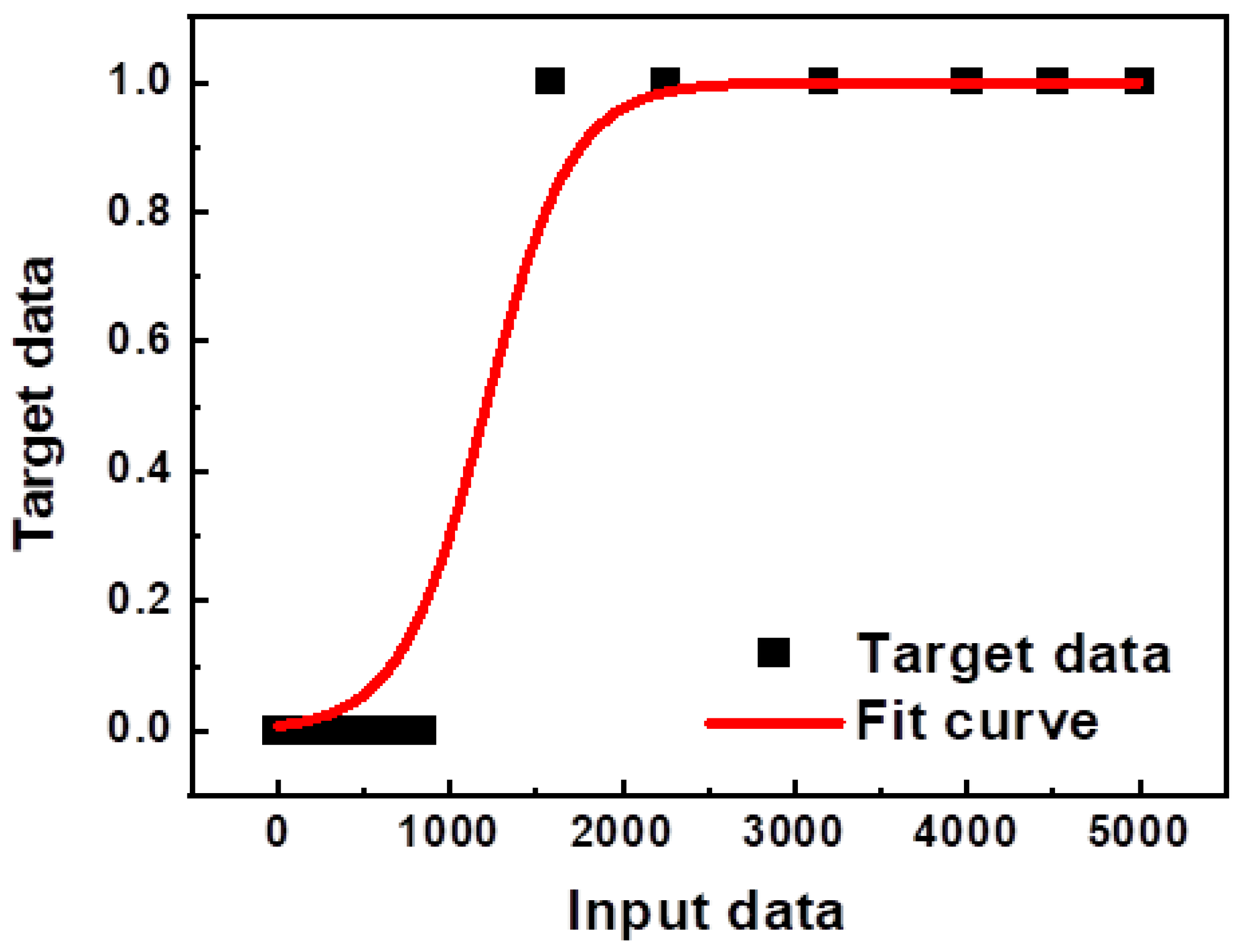
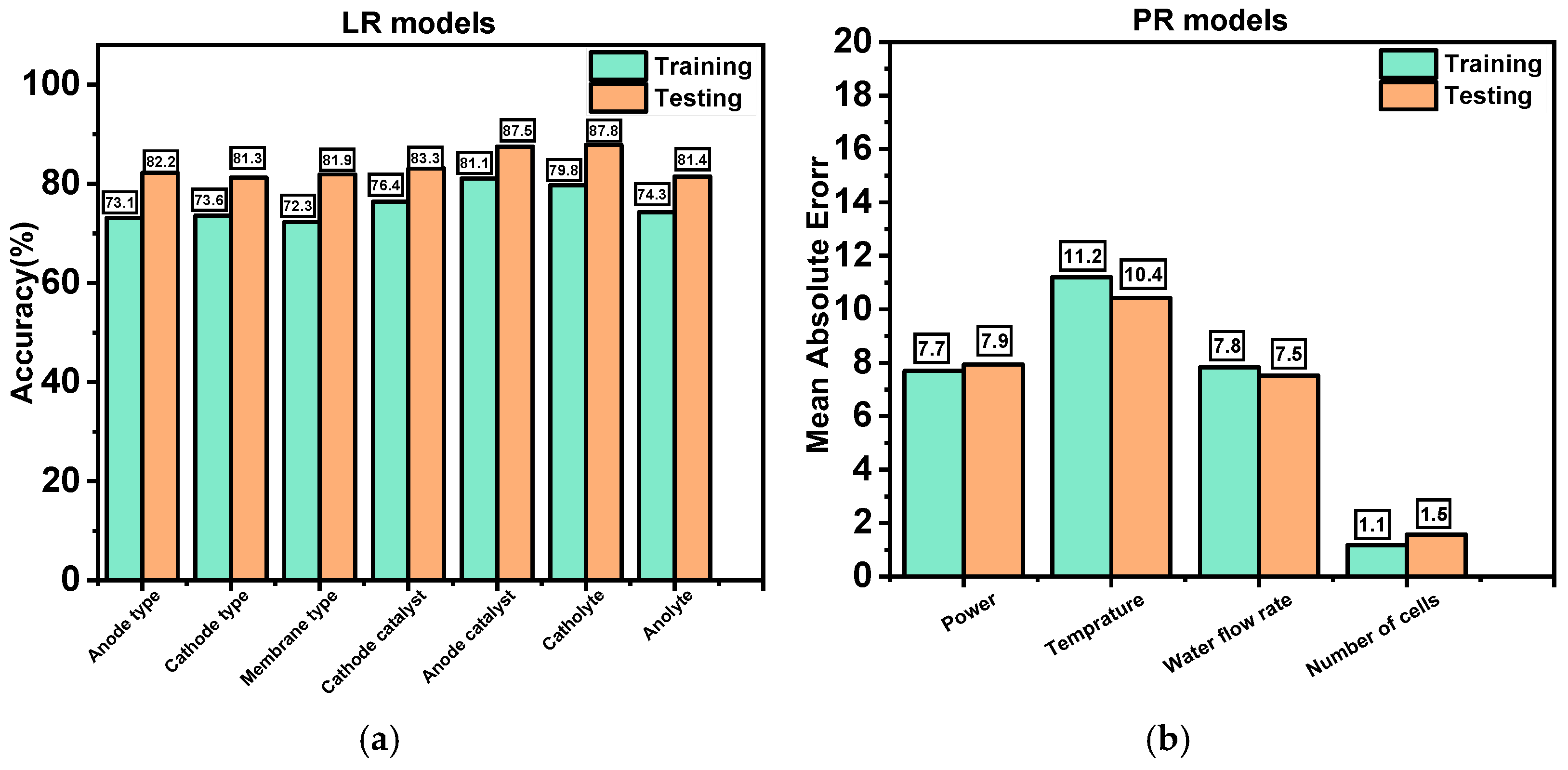
6.1. Performance of the Machine Learning Models
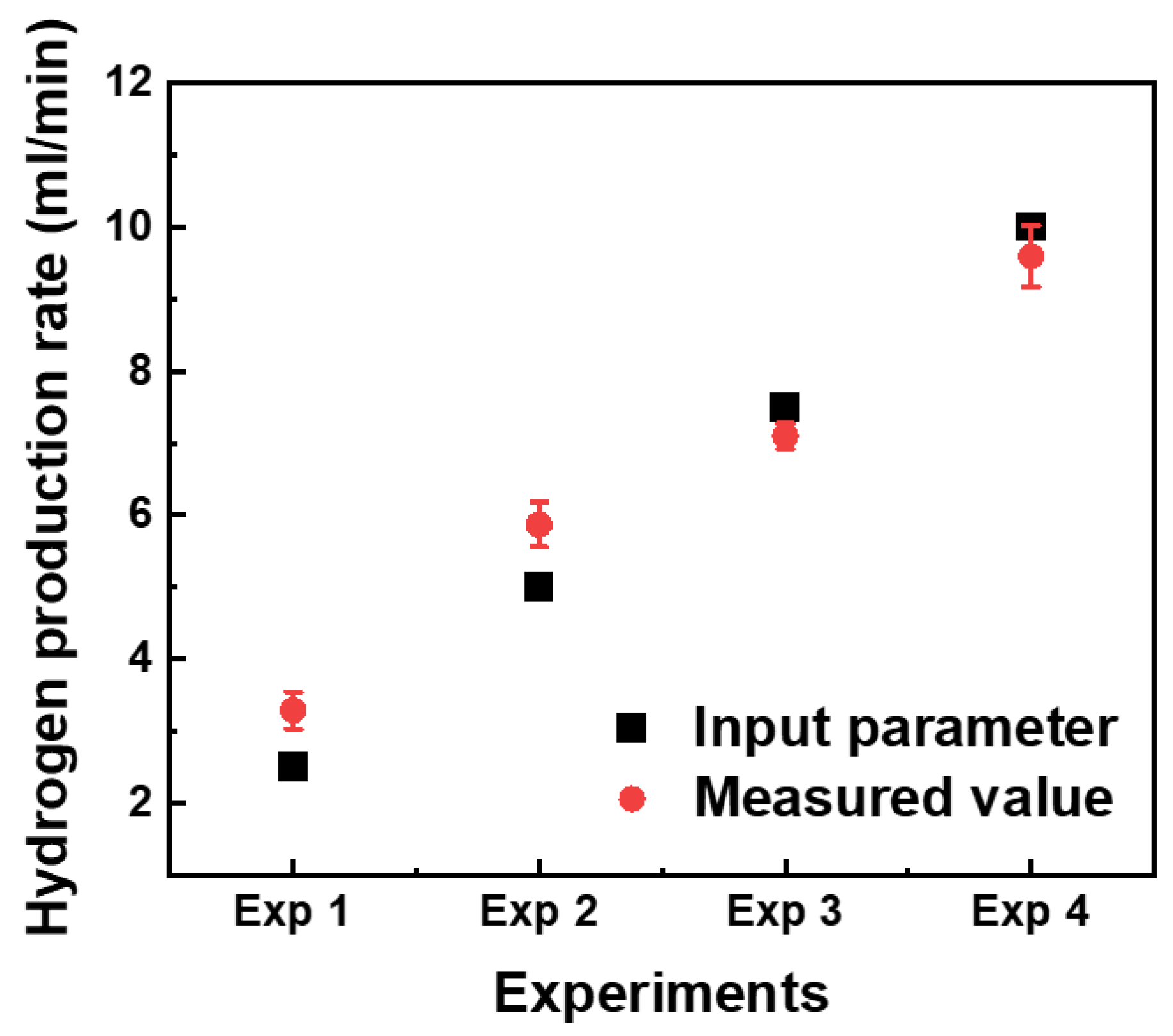
6.2. Model Validation Using Laboratory Experiments
6.3. ML Model Performance for a Commercial-Scaled PEM Water Electrolyzer Cell Design
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| LR Model | Number of Categories | Number of Learnable Weights | Learnt Weight Values as a Python List |
| Anode type | 4 | 4 × 4 | [[1.44462466 × 10−1 −6.12298768 × 10−2 6.13973935 × 10−2 3.64800267 × 10−1] [1.46054452 × 10−1 −7.60564943 × 10−4 1.38269198 × 10−4 1.21432242 × 10−2] [−4.31161394 × 10−1 1.00330176 × 10−1 −1.00065339 × 10−1 −2.70354882 × 10−2] [1.40644477 × 10−1 −3.83397333 × 10−2 3.85296768 × 10−2 −3.49908003 × 10−1]] |
| Cathode type | 5 | 4 × 5 | [[1.44462466 × 10−1 −6.12298768 × 10−2 6.13973935 × 10−2 3.64800267 × 10−1] [1.46054452 × 10−1 −7.60564943 × 10−4 1.38269198 × 10−4 1.21432242 × 10−2] [−4.31161394 × 10−1 1.00330176 × 10−1 −1.00065339 × 10−1 −2.70354882 × 10−2] [1.40644477 × 10−1 −3.83397333 × 10−2 3.85296768 × 10−2 −3.49908003 × 10−1]] |
| Membrane type | 4 | 4 × 4 | [[−3.61453160 × 10−2 7.37919754 × 10−3 9.38431838 × 10−3 7.59994519 × 10−2] [−3.63925709 × 10−2 −3.34377249 × 10−2 5.02725002 × 10−2 1.14175043 ] [−3.81851194 × 10−2 5.23432817 × 10−2 −3.53771847 × 10−2 −1.21776783 ] [1.10723006 × 10−1 −2.62847497 × 10−2 −2.42796289 × 10−2 1.79419465 × 10−5]] |
| Cathode catalyst | 9 | 4 × 9 | [[4.62538696 × 10−1 −1.73429684 × 10−1 −1.72194908 × 10−1 9.44123724 × 10−5] [8.74550852 × 10−3 2.07860659 × 10−2 2.20208426 × 10−2 −4.41194136 × 10−2] [−2.34382706 × 10−1 9.27164067 × 10−2 −4.67910927 × 10−2 −1.36263928 ] [−7.60384199 × 10−3 2.19398429 × 10−2 2.31746196 × 10−2 −1.10382521 × 10−1] [4.66713125 × 10−3 −4.21039516 × 10−2 8.78954152 × 10−2 2.20360246 × 10−1] [−1.96806895 × 10−1 1.90339303 × 10−2 2.02687069 × 10−2 −2.88371268 × 10−2] [8.17614369 × 10−3 2.19340870 × 10−2 2.40335601 × 10−2 1.32154990 ] [−2.23215768 × 10−2 1.95596857 × 10−2 2.07944624 × 10−2 2.05992475 × 10−3] [−2.30124632 × 10−2 1.95636123 × 10−2 2.07983889 × 10−2 1.91386035 × 10−3]] |
| Anode catalyst | 9 | 4 × 9 | [[5.59937140 × 10−1 −1.34767419 × 10−1 −1.34974607 × 10−1 1.14946617 × 10−4] [2.48528231 × 10−2 1.90093734 × 10−2 1.88021862 × 10−2 −2.74401454 × 10−2] [−4.51294267 × 10−1 3.15581162 × 10−2 9.32589281 × 10−3 −1.19339127 ] [1.79141511 × 10−2 9.65845025 × 10−3 3.11238126 × 10−2 2.23865612 ] [−1.90096227 × 10−1 1.49808056 × 10−2 1.96494875 × 10−2 −1.98781788 × 10−2] [2.18144668 × 10−2 2.07939216 × 10−2 1.91745657 × 10−2 1.09433554 ] [−2.68433462 × 10−3 1.78404022 × 10−2 1.76332512 × 10−2 −6.46443455 × 10−3] [1.95562480 × 10−2 2.09263455 × 10−2 1.92654063 × 10−2 −2.08593258 ]] |
| Anolyte | 8 | 4 × 8 | [[8.41818183 × 10−2 −3.77899754 × 10−4 1.03837844 × 10−3 −2.30651817 × 10−1] [9.34764020 × 10−2 −9.71012939 × 10−4 4.45506477 × 10−4 −2.65266069 × 10−1] [6.89813505 × 10−2 −1.59102629 × 10−3 −1.74836248 × 10−4 −1.19477921 × 10−2] [8.80060005 × 10−2 −1.08905169 × 10−3 3.26999016 × 10−4 −3.86594484 × 10−1] [9.39022060 × 10−2 −1.12957815 × 10−1 1.13610766 × 10−1 1.29855994 ] [−2.81643536 × 10−1 −6.00417095 × 10−4 1.36202923 × 10−3 −1.90252849 × 10−1] [−2.27920956 × 10−1 1.18191783 × 10−1 −1.17420389 × 10−1 −1.59723081 × 10−1] [8.10167126 × 10−2 −6.04560766 × 10−4 8.11546336 × 10−4 −5.41238514 × 10−2]] |
| Catholyte | 8 | 4 × 8 | [[0.07478746 0.04592284 −0.04188776 −0.23696409] [0.07708628 0.00384208 −0.00328621 0.12424417] [0.05464852 0.00182964 −0.00529848 0.01823618] [0.0727397 0.00466682 −0.00245757 0.1467709 ] [0.08341487 −0.12855017 0.13257934 0.99461289] [−0.21004092 0.07089918 −0.06678267 −1.08327702] [−0.21321721 −0.00277489 −0.00990302 0.01055434] [0.0605813 0.0041645 −0.00296362 0.02582262]] |
Appendix B
References
- Ursua, A.; Gandia, L.M.; Sanchis, P. Hydrogen production from water electrolysis: Current status and future trends. Proc. IEEE 2012, 100, 410–426. [Google Scholar] [CrossRef]
- Zeng, K.; Zhang, D. Recent progress in alkaline water electrolysis for hydrogen production and applications. Prog. Energy Combust. 2010, 36, 307–326. [Google Scholar] [CrossRef]
- Manabe, A.; Kashiwase, M.; Hashimoto, T.; Hayashida, T.; Kato, A.; Hirao, K.; Shimomura, I.; Nagashima, I. Basic study of alkaline water electrolysis. Electrochim. Acta 2013, 100, 249–256. [Google Scholar] [CrossRef]
- Marini, S.; Salvi, P.; Nelli, P.; Pesenti, R.; Villa, M.; Berrettoni, M.; Zangari, G.; Kiros, Y. Advanced alkaline water electrolysis. Electrochim. Acta 2012, 82, 384–391. [Google Scholar] [CrossRef]
- Hauch, A.; Ebbesen, S.D.; Jensen, S.H.; Mogensen, M. Highly efficient high temperature electrolysis. J. Mater. Chem. 2008, 18, 2331–2340. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.H.; Leung, D.Y.C. Technological development of hydrogen production by solid oxide electrolyzer cell (SOEC). Int. J. Hydrogen Energy 2008, 33, 2337–2354. [Google Scholar] [CrossRef]
- Laguna-Bercero, M.A. Recent advances in high temperature electrolysis using solid oxide fuel cells: A review. J. Power Sources 2012, 203, 4–16. [Google Scholar] [CrossRef]
- Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. A comprehensive review on PEM water electrolysis. Int. J. Hydrogen Energy 2013, 38, 4901–4934. [Google Scholar] [CrossRef]
- Aricò, A.S.; Siracusano, S.; Briguglio, N.; Baglio, V.; di Blasi, A.; Antonucci, V. Polymer electrolyte membrane water electrolysis: Status of technologies and potential applications in combination with renewable power sources. J. Appl. Electrochem. 2013, 43, 107–118. [Google Scholar] [CrossRef]
- Grigoriev, S.A.; Mamat, M.S.; Dzhus, K.A.; Walker, G.S.; Millet, P. Platinum and palladium nano-particles supported by graphitic nano-fibers as catalysts for PEM water electrolysis. Int. J. Hydrogen Energy 2011, 36, 4143–4147. [Google Scholar] [CrossRef]
- Khan, M.A.; Zhao, H.; Zou, W.; Chen, Z.; Cao, W.; Fang, J.; Xu, J.; Zhang, L.; Zhang, J. Recent progresses in electrocatalysts for water electrolysis. Electrochem. Energy Rev 2018, 1, 483–530. [Google Scholar] [CrossRef]
- Liu, C.; Carmo, M.; Bender, G.; Everwand, A.; Lickert, T.; Young, J.L.; Smolinka, T.; Stolten, D.; Lehnert, W. Performance enhancement of PEM electrolyzers through iridium-coated titanium porous transport layers. Electrochem. Commun. 2018, 97, 96–99. [Google Scholar] [CrossRef]
- Tang, C.; Pu, Z.; Liu, Q.; Asiri, A.M.; Luo, Y.; Sun, X. Ni3S2 nanosheets array supported on Ni foam: A novel efficient three-dimensional hydrogen-evolving electrocatalyst in both neutral and basic solutions. Int. J. Hydrogen Energy 2015, 40, 4727–4732. [Google Scholar] [CrossRef]
- Saha, S.; Rajbongshi, B.M.; Ramani, V.; Verma, A. Titanium carbide: An emerging electrocatalyst for fuel cell and electrolyser. Int. J. Hydrogen Energy 2021, 46, 12801–12821. [Google Scholar] [CrossRef]
- Shi, H.; Yu, Q.; Liu, G.; Hu, X. Promoted electrocatalytic hydrogen evolution performance by constructing Ni12P5–Ni2P heterointerfaces. Int. J. Hydrogen Energy 2021, 46, 17097–17105. [Google Scholar] [CrossRef]
- Lee, H.-O.; Yoon, J.-S.; Kim, K. Influence of uniform deposition of molybdenum disulfide particles on electrochemical reaction. Electrochim. Acta 2020, 353, 136480. [Google Scholar] [CrossRef]
- Lee, H.O.; Yesuraj, J.; Kim, K. Parametric study to optimize proton exchange membrane electrolyzer cells. Appl. Energy 2022, 314, 118928. [Google Scholar] [CrossRef]
- Lee, S.-H.; Lee, H.-O.; Kim, K. Micromachined dimples on carbon electrode for enhancing electrochemical reaction. Energy Convers. Manag. 2022, 255, 115320. [Google Scholar] [CrossRef]
- Voronova, A.; Kim, H.J.; Jang, J.H.; Park, H.Y.; Seo, B. Effect of low voltage limit on degradation mechanism during high-frequency dynamic load in proton exchange membrane water electrolysis. Int. J. Energy Res. 2022, 46, 11867–11878. [Google Scholar] [CrossRef]
- Menesy, A.S.; Sultan, H.M.; Korashy, A.; Kamel, S.; Jurado, F.L. A modified farmland fertility optimizer for parameters estimation of fuel cell models. Neural Comput. Appl. 2021, 33, 12169–12190. [Google Scholar] [CrossRef]
- Bahr, M.; Gusak, A.; Stypka, S.; Oberschachtsiek, B. Artificial Neural Networks for Aging Simulation of Electrolysis Stacks. Chem. Ing. Technol. 2020, 92, 1610–1617. [Google Scholar] [CrossRef]
- Curteanu, S.; Piuleac, C.G.; Godini, K.; Azaryan, G. Modeling of electrolysis process in wastewater treatment using different types of neural networks. Chem. Eng. J. 2011, 172, 267–276. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Kong, H.; Kim, J.; Choi, S.; Ciucci, F.; Hao, Y.; Yang, S.; Shao, Z.; Lim, J. Non-precious-metal catalysts for alkaline water electrolysis: Operando characterizations, theoretical calculations, and recent advances. Chem. Soc. Rev. 2020, 49, 9154–9196. [Google Scholar] [CrossRef] [PubMed]
- Tapan, N.A.; Günay, M.E.; Yildirim, R. Constructing global models from past publications to improve design and operating conditions for direct alcohol fuel cells. Chem. Eng. Res. Des. 2016, 105, 162–170. [Google Scholar] [CrossRef]
- Satjaritanun, P.; O’Brien, M.; Kulkarni, D.; Shimpalee, S.; Capuano, C.; Ayers, K.E.; Danilovic, N.; Parkinson, D.Y.; Zenyuk, I.V. Observation of preferential pathways for oxygen removal through porous transport layers of polymer electrolyte water electrolyzers. iScience 2020, 23, 101783. [Google Scholar] [CrossRef]
- Hossain, S.S.; Ali, S.S.; Rushd, S.; Ayodele, B.V.; Cheng, C.K. Interaction effect of process parameters and Pd-electrocatalyst in formic acid electro-oxidation for fuel cell applications: Implementing supervised machine learning algorithms. Int. J. Energy Res. 2022. [Google Scholar] [CrossRef]
- Lee, B.; Park, K.; Kim, H.M. Dynamic simulation of PEM water electrolysis and comparison with experiments. Int. J. Electrochem. Sci. 2013, 8, 235–248. [Google Scholar]
- Navarro-Solís, I.; Villalba-Almendra, L.; Alvarez-Gallegos, A. H2 production by PEM electrolysis, assisted by textile effluent treatment and a solar photovoltaic cell. Int. J. Hydrogen Energy 2010, 35, 10833–10841. [Google Scholar] [CrossRef]
- Sarno, M.; Ponticorvo, E. High hydrogen production rate on RuS2@MoS2 hybrid nanocatalyst by PEM electrolysis. Int. J. Hydrogen Energy 2019, 44, 4398–4405. [Google Scholar] [CrossRef]
- Gibson, T.L.; Kelly, N.A. Optimization of solar powered hydrogen production using photovoltaic electrolysis devices. Int. J. Hydrogen Energy 2008, 33, 5931–5940. [Google Scholar] [CrossRef]
- Caravaca, A.; Sapountzi, F.M.; de Lucas-Consuegra, A.; Molina-Mora, C.; Dorado, F.; Valverde, J.L. Electrochemical reforming of ethanol–water solutions for pure H2 production in a PEM electrolysis cell. Int. J. Hydrogen Energy 2012, 37, 9504–9513. [Google Scholar] [CrossRef]
- Siracusano, S.; Baglio, V.; Briguglio, N.; Brunaccini, G.; Di Blasi, A.; Stassi, A.; Ornelas, R.; Trifoni, E.; Antonucci, V.; Aricò, A.S. An electrochemical study of a PEM stack for water electrolysis. Int. J. Hydrogen Energy 2012, 37, 1939–1946. [Google Scholar] [CrossRef]
- Garcia-Valverde, R.; Espinosa, N.; Urbina, A. Simple PEM water electrolyser model and experimental validation. Int. J. Hydrogen Energy 2011, 37, 1927–1938. [Google Scholar] [CrossRef]
- Selamet, Ö.F.; Becerikli, F.; Mat, M.D.; Kaplan, Y. Development and testing of a highly efficient proton exchange membrane (PEM) electrolyzer stack. Int. J. Hydrogen Energy 2011, 36, 11480–11487. [Google Scholar] [CrossRef]
- Garcia, A.L.T.; Mirzaeian, M.; Chisholm, G.; Olabi, A.G. Design and testing of a single-cell PEM electrolyser for small-scale hydrogen production under mild conditions. In Proceedings of the 10th International Conference on Sustainable Energy and Environmental Protection: Mechanical Engineering, Bled, Slovenia, 27–30 June 2017. [Google Scholar]
- Mahesh, K.N.; Prasad, J.S.; Rao, M.V.; Himabindu, V.; Yerramilli, A.; Rao, P.R. Performance of Pd on activated carbon as hydrogen electrode with respect to hydrogen yield in a single cell proton exchange membrane (PEM) water electrolyser. Int. J. Hydrogen Energy 2009, 34, 6085–6088. [Google Scholar] [CrossRef]
- Tebibel, H.; Medjebour, R. Comparative performance analysis of a grid connected PV system for hydrogen production using PEM water, methanol and hybrid sulfur electrolysis. Int. J. Hydrogen Energy 2018, 43, 3482–3498. [Google Scholar] [CrossRef]
- Siracusano, S.; Baglio, V.; Briguglio, N.; Brunaccini, G.; Di Blasi, A.; Stassi, A.; Ornelas, R.; Trifoni, E.; Antonucci, V.; Aricò, A.S. Optimization of components and assembling in a PEM electrolyzer stack. Int. J. Hydrogen Energy 2011, 36, 3333–3339. [Google Scholar] [CrossRef]
- Ostertagová, E. Modelling using Polynomial Regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef] [Green Version]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
| Parameter | Category/Value Range |
|---|---|
| Anode/Cathode type | Porous titanium, titanium, porous carbon, 304 stainless steel, carbon plate |
| Membrane type | nafion112, nafion115, nafion117, nafion110 |
| Cathode catalyst | 4 mg/cm2 platinum, (0.5) mg/cm2 platinum, nano sheets of MoS2/RuS2,10% platinum, 20% platinum, 30% platinum, 5% Palladium, 10% Palladium |
| Anode catalyst | Using 2 (mg/cm2) platinum and 2 (mg/cm2) iridium oxide (IrO2),1 (mg/cm2) iridium oxide (IrO2), ruthenium oxide or iridium oxide, 40% platinum and 20% ruthenium, iridium oxide (IrO2), Ruthenium (RuO2), Platinum and ruthenium (RuO2), platinum and iridium oxide (IrO2) |
| Anolyte/Catholyte | hybrid sulfur (SO2), 4 mol methanol, pure water, normal water, Deionized water, wastewater + 2 L of (0.1) mol of Sulfuric acid (H2SO4), wastewater + 2 L OF (0.05) Na2SO5, (0.5) mol Sulfuric acid H2SO4 |
| Cell design type | Single or bipolar |
| Number of cells | 1–20 cells |
| Hydrogen flow rate (mL/min) | 0–5000 |
| Power (w) | 0–1300 |
| Water flow rate (mL/min) | 5–750 |
| cell Temperature (k) | 298–359 |
| Pressure (atm) | 1 |
| Input Parameters | Exp 1 | Exp 2 | Exp 3 | Exp 4 |
|---|---|---|---|---|
| Hydrogen production rate (mL/min) | 2.5 | 5 | 7.5 | 10 |
| Cathode area (mm2) | 900 | 900 | 900 | 900 |
| Anode area (mm2) | 900 | 900 | 900 | 900 |
| Type of cell design | single | single | single | single |
| Predicted Parameters | ||||
| Anode type | Carbon plate | Carbon plate | Carbon plate | Carbon plate |
| Cathode type | Carbon plate | Carbon plate | Carbon plate | Carbon plate |
| Membrane type | nafion115 | nafion115 | nafion115 | nafion115 |
| Cathode catalyst | Pt/C (20% Pt) | Pt/C (20% Pt) | Pd/C (10% Pd) | Pd/C (10% Pd) |
| Anode catalyst | Ruthenium (RuO2) | Ruthenium (RuO2) | Ruthenium (RuO2) | Ruthenium (RuO2) |
| Anolyte | pure water | pure water | pure water | pure water |
| Catholyte | pure water | pure water | pure water | pure water |
| Power (W) | 2.15 | 2.68 | 3.21 | 3.75 |
| Water flow rate (mL/min) | 12.62 | 13.6 | 14.62 | 15.61 |
| Cell Temperature (K) | 332.75 | 332.95 | 333.15 | 333.36 |
| Number of cells | 1 | 1 | 1 | 1 |
| No. | Exp 1 | Exp 2 | Exp 3 | Exp 4 |
|---|---|---|---|---|
| 1 | 3.1 | 6.0 | 6.9 | 9.2 |
| 2 | 2.9 | 5.5 | 7.2 | 9.6 |
| 3 | 3.3 | 5.6 | 6.7 | 10.0 |
| 4 | 3.4 | 5.9 | 7.0 | 9.7 |
| 5 | 3.3 | 6.0 | 7.3 | 9.5 |
| Average value | 3.2 | 5.8 | 7.0 | 9.6 |
| Design Parameters | (500 mL/min) Hydrogen Production Rate | (1000 mL/min) Hydrogen Production Rate | (3000 mL/min) Hydrogen Production Rate | (4500 mL/min) Hydrogen Production Rate |
|---|---|---|---|---|
| Anode type | Titanium | Titanium | Titanium | Titanium |
| Cathode type | Titanium | Titanium | Titanium | Titanium |
| Membrane type | Nafion 115 | Nafion 115 | Nafion 115 | Nafion 115 |
| Cathode catalyst | Pt/C (10% Pt) | Pt/C (10% Pt) | Pt/C (30% Pt) | Pt/C (30% Pt) |
| Anode catalyst | Ruthenium (RuO2) or Iridium oxide (IrO2) | Ruthenium (RuO2) or Iridium oxide (IrO2) | Iridium oxide (IrO2) | Iridium oxide (IrO2) |
| Anolyte | Deionized Water | Deionized Water | Deionized Water | Deionized Water |
| Catholyte | Deionized Water | Deionized Water | Deionized Water | Deionized Water |
| Power (W) | 98.9 | 190.5 | 531.7 | 874.8 |
| Water flow rate (mL/min) | 18.8 | 30.6 | 69 | 53.7 |
| Cell Temperature(K) | 304 | 311 | 339 | 359 |
| Number of cells | 18 | 15 | 6 | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.; Ibrahem, H.; Yang, R.; Kim, K. Optimization of Proton Exchange Membrane Electrolyzer Cell Design Using Machine Learning. Energies 2022, 15, 6657. https://doi.org/10.3390/en15186657
Mohamed A, Ibrahem H, Yang R, Kim K. Optimization of Proton Exchange Membrane Electrolyzer Cell Design Using Machine Learning. Energies. 2022; 15(18):6657. https://doi.org/10.3390/en15186657
Chicago/Turabian StyleMohamed, Amira, Hatem Ibrahem, Rui Yang, and Kibum Kim. 2022. "Optimization of Proton Exchange Membrane Electrolyzer Cell Design Using Machine Learning" Energies 15, no. 18: 6657. https://doi.org/10.3390/en15186657
APA StyleMohamed, A., Ibrahem, H., Yang, R., & Kim, K. (2022). Optimization of Proton Exchange Membrane Electrolyzer Cell Design Using Machine Learning. Energies, 15(18), 6657. https://doi.org/10.3390/en15186657









