Rotating Flow and Heat Transfer of Single-Wall Carbon Nanotube and Multi-Wall Carbon Nanotube Hybrid Nanofluid with Base Fluid Water over a Stretching Sheet
Abstract
:1. Introduction
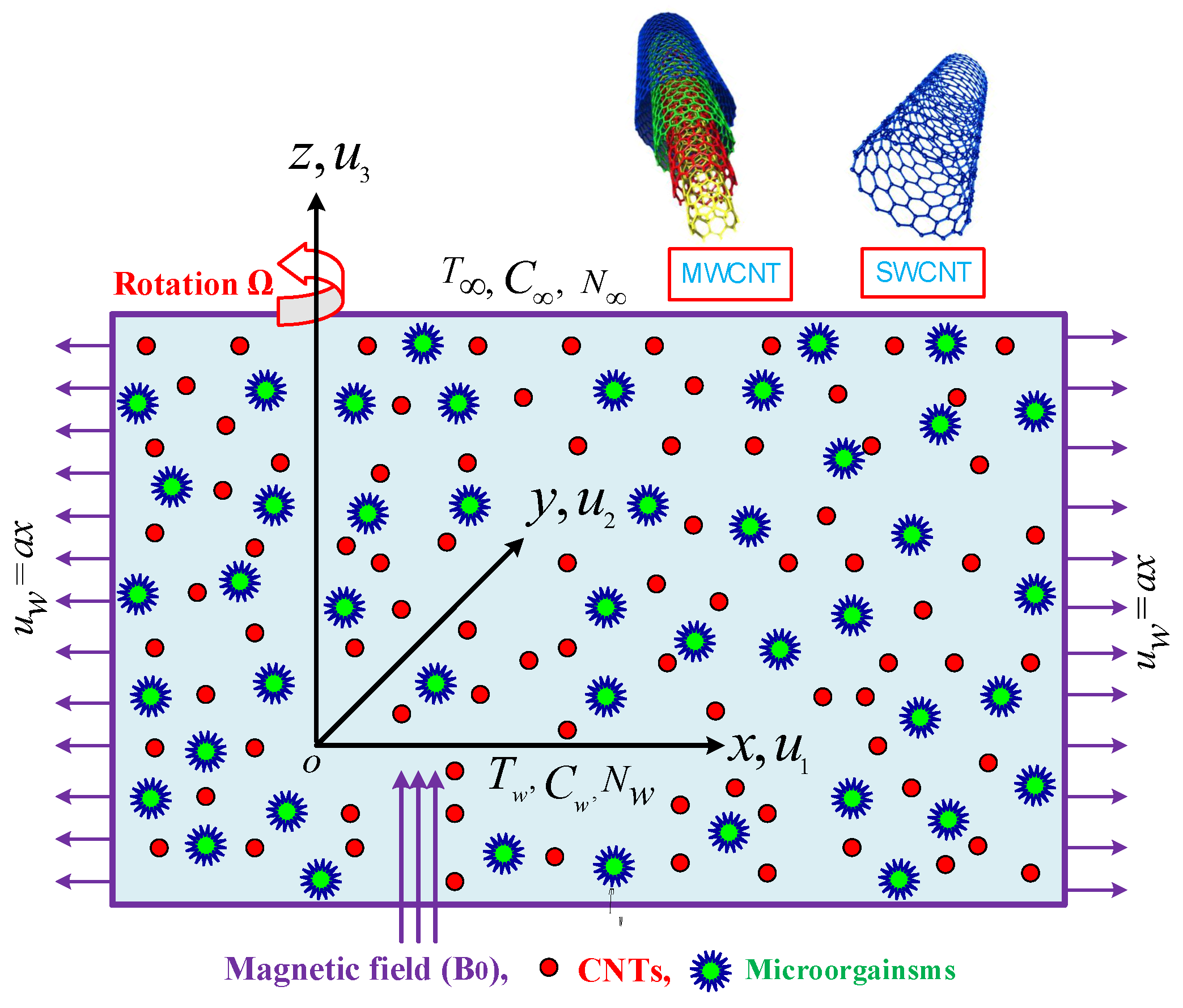
2. Description of the Problem
| Physical Properties | ||||
|---|---|---|---|---|
| 4179 | 997.1 | 0.613 | ||
| 425 | 2600 | 6600 | ||
| 796 | 1600 | 3000 |
| Properties | Nanofluid | Hybrid Nanofluid |
|---|---|---|
| (viscosity) | = | = |
| (density) | = | = |
| (Heat capacity) | = | = |
| (Thermal conductivity) | = | |
| where = |
3. Physical Quantities
4. Implementation of Method
5. Results and Discussion
6. Conclusions
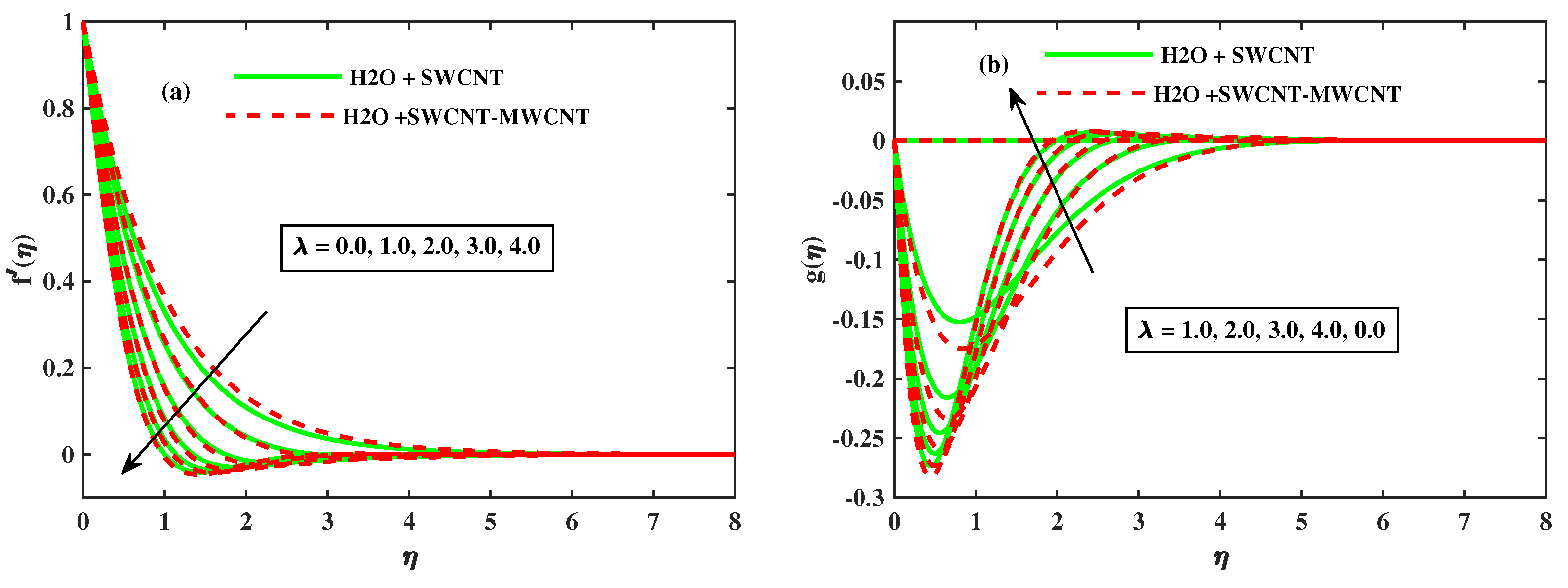
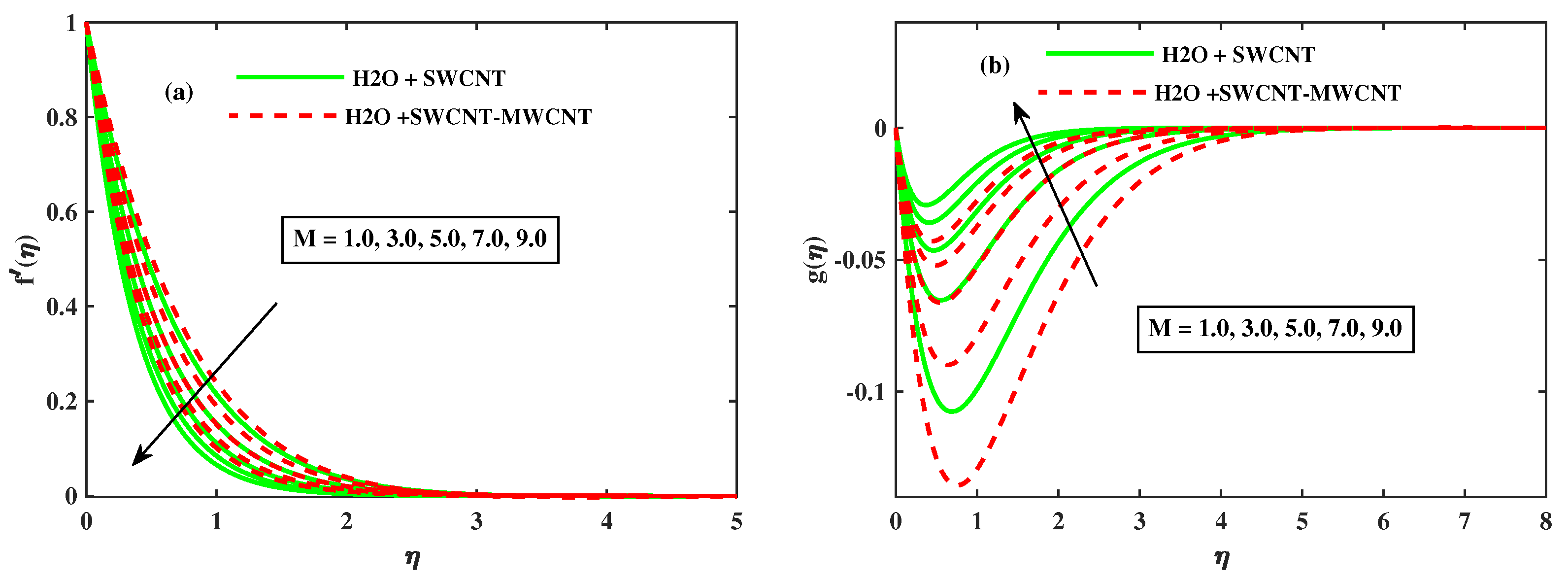
- When and M for nanofluid are increased, the velocity component along the x-axis decreases monotonically, while the amplitude of velocity along the y-axis increases significantly. It is also worth noting that the velocity fields of the hybrid phase and are faster than the nano phase.
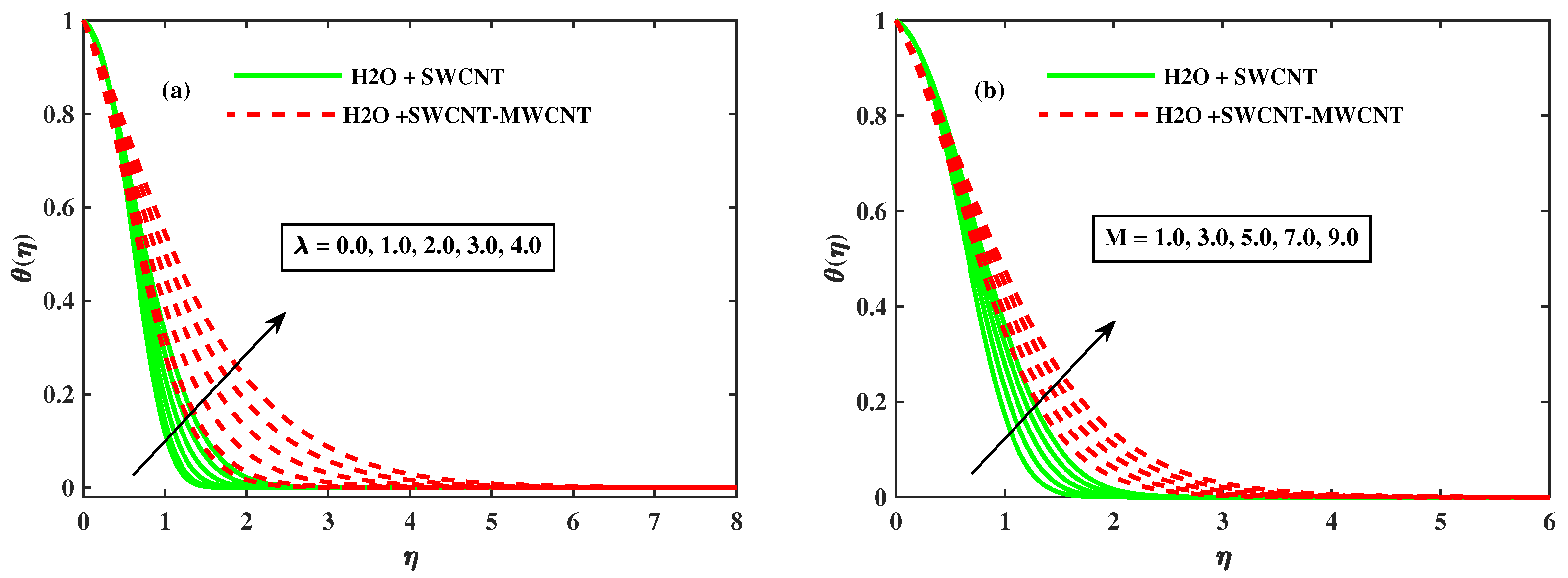
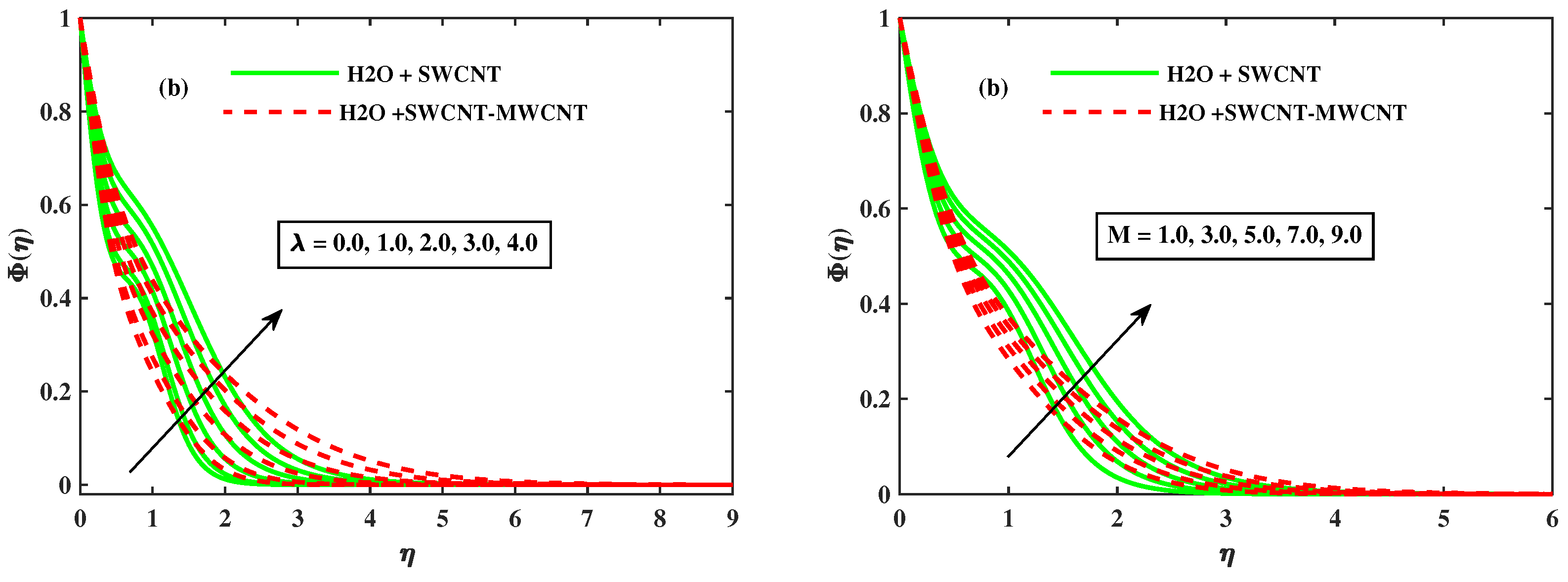
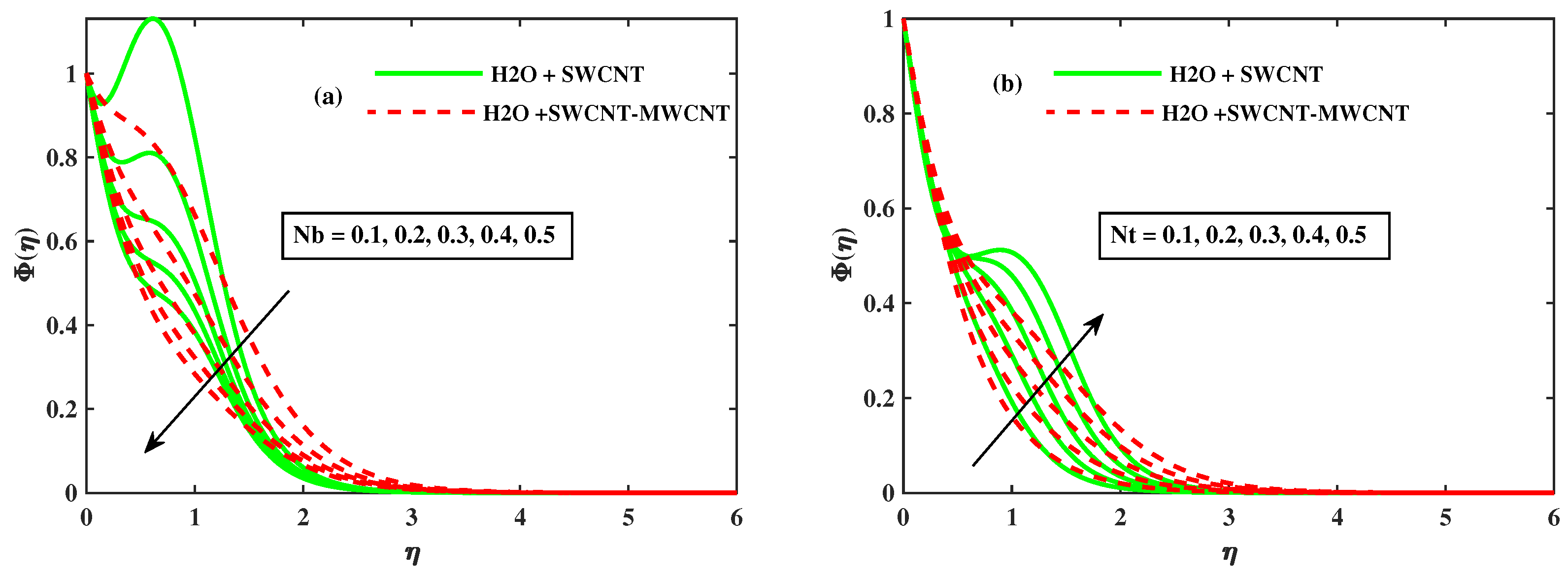
- The growing strength of rotating (), magnetic (M), Brownian motion (), and thermophoresis (), the temperature of fluid enhanced, and hybrid phase fluid enhanced the thermal boundary layer as compared to mono-nanofluid .
- The concentration profile rises when the rotational parameter , magnetic parameter M, and thermophoresis parameter rise, but falls as the Brownian motion parameter rises, and hybrid nano liquids exhibit a slower concentration profile .
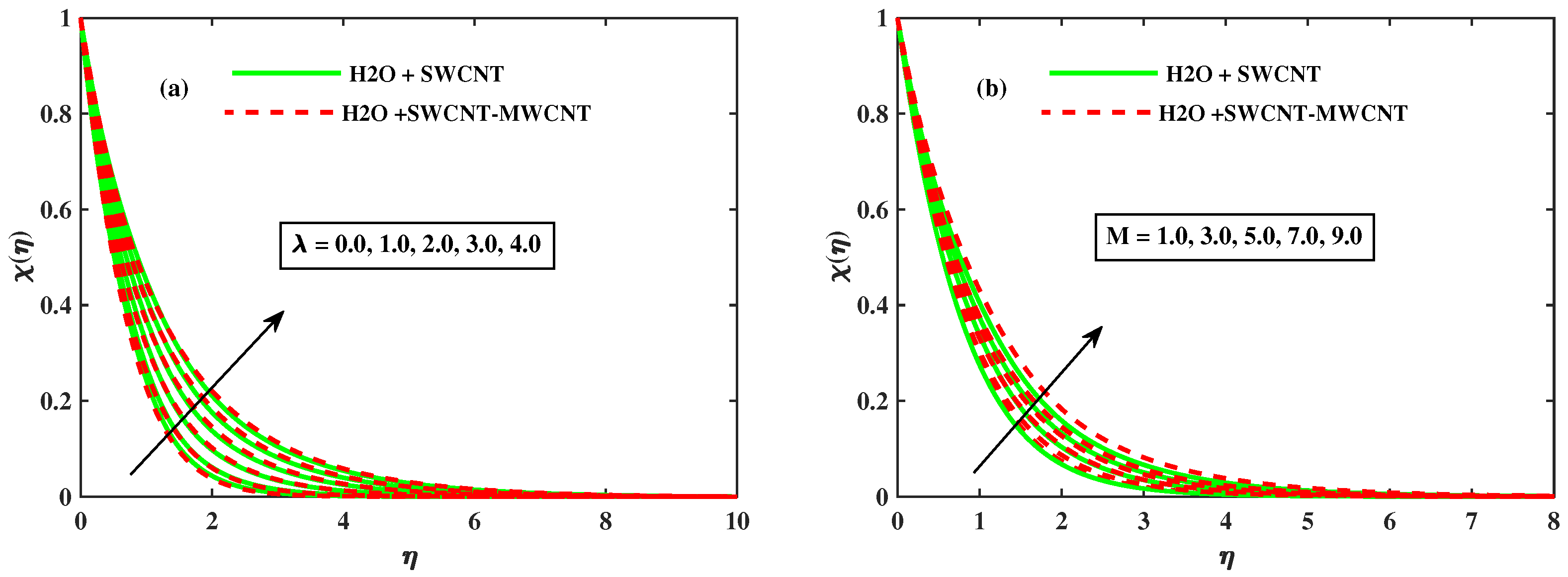
- The motile concentration profile of the nano fluid grows as the rotational parameter and magnetic parameter M increase, and hybrid phase have a stronger motile concentration profile over the mono phase.
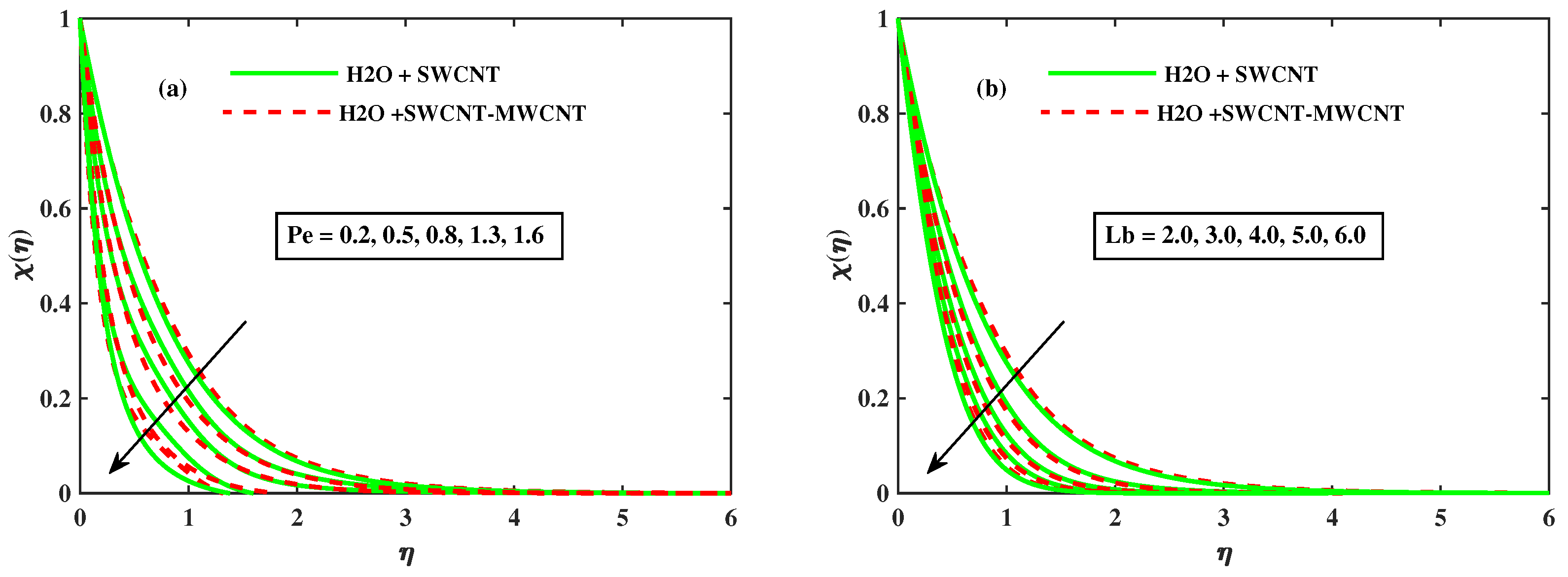
- The motile concentration profile drops as and increase.
- The rising values of rotational parameter increases the skin friction coefficients (, ) in both the x and y directions, and the skin friction coefficients is larger in values for hybrid nanofluid than nanofluid.
- The heat transfer rate and wall mass transfer rate drops, by means of growing values of and magnetic (M).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mebarek-Oudina, F.; Bessaih, R. Oscillatory magnetohydrodynamic natural convection of liquid metal between vertical coaxial cylinders. J. Appl. Fluid Mech. 2016, 9, 1655–1665. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018, 9, 1201–1214. [Google Scholar] [CrossRef]
- Fukumori, Y.; Ichikawa, H. Nanoparticles for cancer therapy and diagnosis. Adv. Powder Technol. 2006, 17, 1–28. [Google Scholar] [CrossRef]
- Ahmadi, A.; Zahmatkesh, A.; Hatami, M.; Ganji, D. A comprehensive analysis of the flow and heat transfer for a nanofluid over an unsteady stretching flat plate. Powder Technol. 2014, 258, 125–133. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. Int. J. Heat Mass Transf. 2011, 54, 4410–4428. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Li, J.; Koo, J. Microfluidics of nano-drug delivery. Int. J. Heat Mass Transf. 2008, 51, 5590–5597. [Google Scholar] [CrossRef]
- Choi, S. Enhancing thermal conductivity of fluids with nanoparticle, in: Development and Applications of Non-Newtonian Flow. ASME Fluids Eng. Div. 1995, 231, 99–105. [Google Scholar]
- Eastman, J.A.; Phillpot, S.; Choi, S.; Keblinski, P. Thermal transport in nanofluids. Annu. Rev. Mater. Res. 2004, 34, 219–246. [Google Scholar] [CrossRef]
- Khairul, M.; Shah, K.; Doroodchi, E.; Azizian, R.; Moghtaderi, B. Effects of surfactant on stability and thermo-physical properties of metal oxide nanofluids. Int. J. Heat Mass Transf. 2016, 98, 778–787. [Google Scholar] [CrossRef]
- Rehman, S.U.; Fatima, N.; Ali, B.; Imran, M.; Ali, L.; Shah, N.A.; Chung, J.D. The Casson dusty nanofluid: Significance of Darcy–forchheimer law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics 2022, 10, 2877. [Google Scholar] [CrossRef]
- Ahmad, B.; Ahmad, M.O.; Ali, L.; Ali, B.; Hussein, A.K.; Shah, N.A.; Chung, J.D. Significance of the Coriolis force on the dynamics of Carreau–Yasuda rotating nanofluid subject to Darcy–forchheimer and gyrotactic microorganisms. Mathematics 2022, 10, 2855. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Rehman, S.U.; Habib, D.; Abdal, S.; Shah, N.A.; Chung, J.D. Micropolar dusty fluid: Coriolis force effects on dynamics of mhd rotating fluid when Lorentz force is significan. Mathematics 2022, 10, 2630. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Ahammad, N.A.; Din, E.M.T.E.; Gamaoun, F.; Awan, A.U.; Ali, B. Bio-convection effects on prandtl hybrid nanofluid flow with chemical reaction and motile microorganism over a stretching sheet. Nanomaterials 2022, 12, 2174. [Google Scholar] [CrossRef] [PubMed]
- Sheikholeslami, M.; Shah, Z.; Shafee, A.; Khan, I.; Tlili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019, 9, 1196. [Google Scholar] [CrossRef] [Green Version]
- Sheikholeslami, M. Numerical approach for MHD Al2O3-water nanofluid transportation inside a permeable medium using innovative computer method. Comput. Methods Appl. Mech. Eng. 2019, 344, 306–318. [Google Scholar] [CrossRef]
- Masuda, H.; Ebata, A.; Teramae, K.; Hishinuma, N.; Ebata, Y. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles (dispersion of γ-Al2O3, SiO2 and TiO2 ultra-fine particles). Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Ali, B.; Siddique, I.; Khan, I.; Masood, B.; Hussain, S. Magnetic dipole and thermal radiation effects on hybrid base micropolar CNTs flow over a stretching sheet: Finite element method approach. Results Phys. 2021, 25, 104145. [Google Scholar] [CrossRef]
- Haq, R.U.; Rashid, I.; Khan, Z. Effects of aligned magnetic field and CNTs in two different base fluids over a moving slip surface. J. Mol. Liq. 2017, 243, 682–688. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Giannopoulos, F.; Chronopoulou, N.; Bai, J.; Zhao, H.; Pantelis, D.; Pavlatou, E.; Karantonis, A. Nickel/MWCNT-Al2O3 electrochemical co-deposition: Structural properties and mechanistic aspects. Electrochim. Acta 2016, 207, 76–86. [Google Scholar] [CrossRef]
- Tseluikin, V.; Koreshkova, A. Deposition of zinc-carbon nanotube composite coatings in the pulse-reverse mode. Russ. J. Appl. Chem. 2014, 87, 1251–1253. [Google Scholar] [CrossRef]
- Ali, B.; Naqvi, R.A.; Ali, L.; Abdal, S.; Hussain, S. A comparative description on time-dependent rotating magnetic transport of a water base liquid H2O with hybrid nano-materials Al2O3-Cu and Al2O3-TiO2 over an extending sheet using Buongiorno model: Finite element approach. Chin. J. Phys. 2021, 70, 125–139. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Ellahi, R.; Alamri, S.Z. Convective Poiseuille flow of Al2O3-EG nanofluid in a porous wavy channel with thermal radiation. Neural Comput. Appl. 2018, 30, 3371–3382. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Moghaddam, M.E.; Asadi, A.; Mogharrebi, A.; Ganji, D. Effect of internal fins along with hybrid nano-particles on solid process in star shape triplex latent heat thermal energy storage system by numerical simulation. Renew. Energy 2020, 154, 497–507. [Google Scholar] [CrossRef]
- Aziz, A.; Muhammad, T.; Alsaedi, A.; Hayat, T. An optimal study for 3D rotating flow of Oldroyd-B nanofluid with convectively heated surface. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–11. [Google Scholar] [CrossRef]
- Mustafa, M.; Ahmad, R.; Hayat, T.; Alsaedi, A. Rotating flow of viscoelastic fluid with nonlinear thermal radiation: A numerical study. Neural Comput. Appl. 2018, 29, 493–499. [Google Scholar] [CrossRef]
- Wang, C. Stretching a surface in a rotating fluid. Z. Angew. Math. Phys. 1988, 39, 177–185. [Google Scholar] [CrossRef]
- Takhar, H.S.; Chamkha, A.J.; Nath, G. Flow and heat transfer on a stretching surface in a rotating fluid with a magnetic field. Int. J. Therm. Sci. 2003, 42, 23–31. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Filip, D.; Pop, I. Unsteady boundary layer flow in the region of the stagnation point on a stretching sheet. Int. J. Eng. Sci. 2004, 42, 1241–1253. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.; Salahuddin, T.; Yousaf, M.M.; Khan, F.; Hussain, A. Variable diffusion and conductivity change in 3d rotating Williamson fluid flow along with magnetic field and activation energy. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 2467–2484. [Google Scholar] [CrossRef] [Green Version]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Bahar, A.; Salah, F. Slip role for unsteady MHD mixed convection of nanofluid over stretching sheet with thermal radiation and electric field. Indian J. Phys. 2020, 94, 195–207. [Google Scholar] [CrossRef]
- Ellahi, R.; Bhatti, M.M.; Khalique, C. Three-dimensional flow analysis of Carreau fluid model induced by peristaltic wave in the presence of magnetic field. J. Mol. Liq. 2017, 241, 1059–1068. [Google Scholar] [CrossRef]
- Waqas, M.; Farooq, M.; Khan, M.I.; Alsaedi, A.; Hayat, T.; Yasmeen, T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Transf. 2016, 102, 766–772. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A. A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J. Colloid Interface Sci. 2017, 498, 85–90. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Khan, M.I.; Qayyum, S.; Alsaedi, A. Entropy generation in flow with silver and copper nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2018, 539, 335–346. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rokni, H.B. CVFEM for effect of Lorentz forces on nanofluid flow in a porous complex shaped enclosure by means of non-equilibrium model. J. Mol. Liq. 2018, 254, 446–462. [Google Scholar] [CrossRef]
- Yu, S.; Ameel, T.A. Slip-flow heat transfer in rectangular microchannels. Int. J. Heat Mass Transf. 2001, 44, 4225–4234. [Google Scholar] [CrossRef]
- Pedley, T.; Hill, N.; Kessler, J.O. The growth of bioconvection patterns in a uniform suspension of gyrotactic micro-organisms. J. Fluid Mech. 1988, 195, 223–237. [Google Scholar] [CrossRef] [Green Version]
- Ashraf, E.E. Advected Bioconvection and the Hydrodynamics of Bounded Biflagellate Locomotion. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2011. [Google Scholar]
- Mondal, S.K.; Pal, D. Computational analysis of bioconvective flow of nanofluid containing gyrotactic microorganisms over a nonlinear stretching sheet with variable viscosity using HAM. J. Comput. Des. Eng. 2020, 7, 251–267. [Google Scholar] [CrossRef] [Green Version]
- Ullah, M.Z.; Jang, T. An efficient numerical scheme for analyzing bioconvection in von-Kármán flow of third-grade nanofluid with motile microorganisms. Alex. Eng. J. 2020, 59, 2739–2752. [Google Scholar] [CrossRef]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S. Finite Element Simulation of Multi-Slip Effects on Unsteady MHD Bioconvective Micropolar nanofluid Flow Over a Sheet with Solutal and Thermal Convective Boundary Conditions. Coatings 2019, 9, 842. [Google Scholar] [CrossRef]
- Khan, W.; Makinde, O.; Khan, Z. MHD boundary layer flow of a nanofluid containing gyrotactic microorganisms past a vertical plate with Navier slip. Int. J. Heat Mass Transf. 2014, 74, 285–291. [Google Scholar] [CrossRef]
- Mutuku, W.N.; Makinde, O.D. Hydromagnetic bioconvection of nanofluid over a permeable vertical plate due to gyrotactic microorganisms. Comput. Fluids 2014, 95, 88–97. [Google Scholar] [CrossRef]
- Nadeem, S.; Khan, M.N.; Muhammad, N.; Ahmad, S. Mathematical analysis of bio-convective micropolar nanofluid. J. Comput. Des. Eng. 2019, 6, 233–242. [Google Scholar] [CrossRef]
- Pedley, T.J.; Kessler, J. The orientation of spheroidal microorganisms swimming in a flow field. Proc. R. Soc. Lond. Ser. B. Biol. Sci. 1987, 231, 47–70. [Google Scholar]
- Ghorai, S.; Hill, N. Gyrotactic bioconvection in three dimensions. Phys. Fluids 2007, 19, 054107. [Google Scholar] [CrossRef] [Green Version]
- Zeng, L.; Pedley, T. Distribution of gyrotactic micro-organisms in complex three-dimensional flows. Part 1. Horizontal shear flow past a vertical circular cylinder. J. Fluid Mech. 2018, 852, 358–397. [Google Scholar] [CrossRef]
- Kessler, J.O. Co-operative and concentrative phenomena of swimming micro-organisms. Contemp. Phys. 1985, 26, 147–166. [Google Scholar] [CrossRef]
- Ashraf, M.Z.; Rehman, S.U.; Farid, S.; Hussein, A.K.; Ali, B.; Shah, N.A.; Weera, W. Insight into significance of bioconvection on mhd tangent hyperbolic nanofluid flow of irregular thickness across a slender elastic surface. Mathematics 2022, 10, 2592. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Ali, B.; Siddique, I.; Ahmadian, A.; Senu, N.; Ali, L.; Haider, A. Significance of Lorentz and Coriolis forces on dynamics of water based silver tiny particles via finite element simulation. Ain Shams Eng. J. 2022, 13, 101572. [Google Scholar] [CrossRef]
- Wang, F.; Asjad, M.I.; Rehman, S.U.; Ali, B.; Hussain, S.; Gia, T.N.; Muhammad, T. MHD Williamson Nanofluid Flow over a Slender Elastic Sheet of Irregular Thickness in the Presence of Bioconvection. Nanomaterials 2021, 11, 2297. [Google Scholar] [CrossRef] [PubMed]
- Tayyab, M.; Siddique, I.; Jarad, F.; Ashraf, M.K.; Ali, B. Numerical solution of 3D rotating nanofluid flow subject to Darcy-Forchheimer law, bio-convection and activation energy. S. Afr. J. Chem. Eng. 2022, 40, 48–56. [Google Scholar] [CrossRef]
- Ramaiah K, D.; Kotha, G.; Thangavelu, K. MHD rotating flow of a Maxwell fluid with Arrhenius activation energy and non-Fourier heat flux model. Heat Transf. 2020, 49, 2209–2227. [Google Scholar] [CrossRef]
- Ahmad, S.; Nadeem, S. Cattaneo–Christov-based study of SWCNT–MWCNT/EG Casson hybrid nanofluid flow past a lubricated surface with entropy generation. Appl. Nanosci. 2020, 10, 5449–5458. [Google Scholar] [CrossRef]
- Saba, F.; Ahmed, N.; Khan, U.; Mohyud-Din, S.T. A novel coupling of (CNT-Fe3O4/H2O) hybrid nanofluid for improvements in heat transfer for flow in an asymmetric channel with dilating/squeezing walls. Int. J. Heat Mass Transf. 2019, 136, 186–195. [Google Scholar] [CrossRef]
- Gul, H.; Ramzan, M.; Chung, J.D.; Chu, Y.M.; Kadry, S. Multiple slips impact in the MHD hybrid nanofluid flow with Cattaneo–Christov heat flux and autocatalytic chemical reaction. Sci. Rep. 2021, 11, 14625. [Google Scholar] [CrossRef]
- Bilal, M.; Arshad, H.; Ramzan, M.; Shah, Z.; Kumam, P. Unsteady hybrid-nanofluid flow comprising ferrousoxide and CNTs through porous horizontal channel with dilating/squeezing walls. Sci. Rep. 2021, 11, 12637. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Hussain, S.; Manan, A.; Sadiq, M.T. Unsteady magneto-hydrodynamic transport of rotating Maxwell nanofluid flow on a stretching sheet with Cattaneo–Christov double diffusion and activation energy. Therm. Sci. Eng. Prog. 2020, 20, 100720. [Google Scholar] [CrossRef]
- Ali, L.; Liu, X.; Ali, B. Finite Element Analysis of Variable Viscosity Impact on MHD Flow and Heat Transfer of Nanofluid Using the Cattaneo–Christov Model. Coatings 2020, 10, 395. [Google Scholar] [CrossRef] [Green Version]



| Bagh et al. [60] | Nazar et al. [29] | (Our Results) | ||||
|---|---|---|---|---|---|---|
| 0 | 1.0000 | 0.0000 | 1.000 | 0.000 | 1.0000 | 0.0000 |
| 0.5 | 1.13844 | 0.51283 | 1.1384 | 0.5128 | 1.13842 | 0.51284 |
| 1 | 1.32501 | 0.83715 | 1.3250 | 0.8371 | 1.32502 | 0.83717 |
| 2 | 1.65232 | 1.28732 | 1.6523 | 1.2873 | 1.65233 | 1.28730 |
| 5 | 2.39026 | 2.15024 | - | - | 2.39024 | 2.15025 |
| Ali et al. [61] | (Our Results) | |||||
|---|---|---|---|---|---|---|
| Pr = 0.7 | Pr = 2.0 | Pr = 7.0 | Pr = 0.7 | Pr = 2.0 | Pr = 7.0 | |
| 0.0 | 0.4552 | 0.9108 | 1.8944 | 0.4551 | 0.9112 | 1.8941 |
| 0.5 | 0.3901 | 0.8525 | 1.8500 | 0.3902 | 0.8522 | 1.8501 |
| 1.0 | 0.3214 | 0.7703 | 1.7877 | 0.3212 | 0.7705 | 1.7876 |
| 2.0 | 0.2420 | 0.6381 | 1.6642 | 0.2421 | 0.6383 | 1.6643 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haider, S.M.A.; Ali, B.; Wang, Q.; Zhao, C. Rotating Flow and Heat Transfer of Single-Wall Carbon Nanotube and Multi-Wall Carbon Nanotube Hybrid Nanofluid with Base Fluid Water over a Stretching Sheet. Energies 2022, 15, 6060. https://doi.org/10.3390/en15166060
Haider SMA, Ali B, Wang Q, Zhao C. Rotating Flow and Heat Transfer of Single-Wall Carbon Nanotube and Multi-Wall Carbon Nanotube Hybrid Nanofluid with Base Fluid Water over a Stretching Sheet. Energies. 2022; 15(16):6060. https://doi.org/10.3390/en15166060
Chicago/Turabian StyleHaider, Syed Muhammad Ali, Bagh Ali, Qiuwang Wang, and Cunlu Zhao. 2022. "Rotating Flow and Heat Transfer of Single-Wall Carbon Nanotube and Multi-Wall Carbon Nanotube Hybrid Nanofluid with Base Fluid Water over a Stretching Sheet" Energies 15, no. 16: 6060. https://doi.org/10.3390/en15166060
APA StyleHaider, S. M. A., Ali, B., Wang, Q., & Zhao, C. (2022). Rotating Flow and Heat Transfer of Single-Wall Carbon Nanotube and Multi-Wall Carbon Nanotube Hybrid Nanofluid with Base Fluid Water over a Stretching Sheet. Energies, 15(16), 6060. https://doi.org/10.3390/en15166060









