Rotating Flow and Heat Transfer of Single-Wall Carbon Nanotube and Multi-Wall Carbon Nanotube Hybrid Nanofluid with Base Fluid Water over a Stretching Sheet

Abstract

In this article, numerical simulations of the rotational flow of water-based magnetohydrodynamic (MHD) nanofluid containing single-wall carbon nanotube (SWCNT) and hybrid nanofluid containing single- and multiple-wall carbon nanotube (SWCNT-MWCNT) over a stretching sheet are performed. The primary goal is to improve thermal transport efficiency due to CNTs extraordinary thermal conductivity. The 3D governing equations for microorganism concentration, energy, momentum, concentration, and mass conservation are transformed into 1D ordinary differentiation via similarity transformations. In a MATLAB environment, the resultant system of equations (ODEs) are then solved using Runge–Kutta fourth order with the shooting process. Tables and graphs were used to show the results of physical parameters. According to our findings, enhancing the rotational parameter $\lambda$ and the magnetic field M reduce the base fluid velocity along the x-axis, and on the other hand, the opposite tendency is shown along the y-axis. Furthermore, the velocities, temperature, and microorganism concentration profiles of hybrid nanofluid ($SWCNT-MWCNT$/H₂O) are found to be higher than those of mono nanofluid ($H_{2}O+SWCNT$), while the concentration profile is found to be lower.

1. Introduction

Nanofluids contain suspended nanoparticles of fewer than a hundred nano-meters in size, which are utilized to improve heat conductivity. Nanofluids are usually made of oxide, metals, carbides and nano-metals such as carbon nanotubes or graphite. In the last ten years, the research of nanoparticles has gained important significance because of its applications in the areas of modern sciences and technological industry, such as industrial cooling, biomedical sciences, solar absorption, nano drug delivery, electromechanical systems, nuclear reactors, transportation, and many more [1,2,3,4,5,6]. Furthermore, nanofluids are now being developed for medical applications, such as safe cooling operations, cancer therapy, heart surgery, and brain tumor treatment. Firstly, Choi et al. [7] introduced the ultrafine particle suspension in the base fluid as nanofluids. According to Phillpot et al. [8], the essential factor of nanofluids is their capability to improve the efficiency of heat transmission apparatuses. Khairul et al. [9] studied the results of the spectacular thermal characteristics of nanofluids. Numerous notable works have examined the scope of the nanofluid flow, including [10,11,12]. Shah et al. [13] explored the role of nanoparticles Brownian motion subject to chemical reaction and motile microorganisms, and he obtained that thermophoresis and Brownian motion of nanoparticles enhanced the base fluid temperature profile. Sheikholeslami et al. [14,15] explored nanofluid with various base fluids numerically in different geometries. Masuda et al. [16] pioneered research on fine particles dispersed and gradually suspended in a traditional fluid.

The single-wall and multi-wall carbon nanotubes are allotropes of carbon having wide scope of practical applications, such as optics, chemical production, microelectronics cooling, ultra-capacitors and many types of industry [17,18]. Firstly, Iijima [19] introduced the Carbon nanotubes, and Iijima divided the Carbon nanotubes into two types as: SWCNT (single-walled carbon nanotubes) and MWCNT (multi-walled carbon nanotubes). The mechanistic and structural properties aspect subject to multi-wall carbon nanotubes incorporated with Nickel and Al₂O₃ investigated by Giannopoulos et al. [20]. The composite coatings of Zinc-carbon nanotubes were studied by Tseluikin et al. [21]. Researchers have explored composite nanoparticles in recent years in order to improve or increase the thermal conductivity of traditional fluids. Fluids made up of hybrid nanoparticles are known as hybrid nanofluids. These fluids are utilized for a wide range of applications, such as cooling automobile engines, manufacturing, transportation, medical, naval structures, and so on. In a comparative investigation, Ali et al. [22] explore the MHD rotating flow of hybrid nanofluids over a horizontally planar sheet in a comparative study. Zeeshan et al. [23] published a study on the convective Poiseuille flow of an Al${}_2$O${}_3$/C${}_2$H${}_6$O${}_2$ nanofluid. Hosseinzadeh et al. [24] analyzed the performance of internal fins on the flow of hybrid nanofluids.

The study of heat transportation difficulties in a rotating frame is a fascinating topic. It is an outcome of their widespread use in food handling, computer stockpiling devices, crystal development, diffusive filtering processes, viscometry, thermal power stations, gas turbine rotors, and rotating machinery [25,26]. Wang et al. [27] finished the major effort toward this approach. Takhar et al. [28] concentrate on the magnetohydrodynamics (MHD) influence on rotating fluids. Nazar et al. [29] investigated the time-dependent flow in a revolving frame caused by a moving sheet. Khan et al. [30] explore the effect of mutable heat transmission on a 3D Williamson revolving fluid. Magnetohydrodynamic (MHD) fluids are critical in the following fields: advanced plane design, medicine, astronomy, and successfully managing the rate of heat transfer in turbulent pumps, energy generators, various machines, and cylinders. Daniel et al. [31] investigated the influence of the slip condition over stretching sheet on the time-dependent mixed convective of hydro-magnetic and electrically conducting nano liquid, and Ellahi et al. [32] used homotopy analysis to explore the 3D flow of Carreau fluid with (MHD). Recently, numerous researchers [33,34,35,36,37] have studied the impacts of MHD with mass and heat transfer.

Biological transport has made a significant contribution to current fluid mechanics. The term bioconvection can be described as a form of development in suspensions of microorganisms, specifically algae and bacteria, because of upswimming the microorganisms in the direction of particular taxis, for example, oxygen, chemicals, gravity, light, and magnetic fields [38]. The applications of bioconvection include the field of biofuels, ethanol, fertilizers, bio-medicine (e.g., cancer therapeutics and nano drug delivery), and so on [39,40]. Bioconvection is critical for the formation of microbial oil and meteorological events, such as hot springs colonized by motile microorganisms known as thermophiles [41]. Ali et al. [42] reported the MHD bioconvective nanofluid flow restraining microorganisms by the finite element (FE) technique. Khan et al. [43] use the Oberbeck–Boussinesq approximation to discuss gyrotactic microorganisms on a vertical plate. In the literature review, different analysts have investigated highlights of bioconvection [44,45,46,47,48,49,50].

In light of the above-mentioned literature, less consideration is paid toward the significance of Lorentz force on the dynamic of water-based nanofluids over a stretch surface subject to rotating frame and gyrotactic microorganisms. The two types of CNTs are incorporated due to their extraordinary viscosity, thermal conductivity, density, heat transfer capacity, etc., which are very useful in modern technology, material sciences, and electronics cooling. Moreover, to avoid the sedimentation of solid particles and improve the base fluid stability, we involved motile microorganisms. To the authors’ knowledge, these aspects of the topic have not been addressed in previous research. Motivated by the above-mentioned numerous applications of nanofluids in the literature, we select the elaborated fluid model. The formulated fluid problem in three dimensions are transformed into one-dimensional ODEs via similarity transformation, and then ODEs are solved using a well-known Runge–Kutta fourth order simulation with shooting approach, which is then coded and implemented in a Matlab environment. The results for temperature, micro-organism concentration, skin friction coefficients, Nusselt number, and velocity components are analyzed. The numerical technique of Runge–Kutta fourth order has produced consistent results to validate our findings, we compare our results with existing data in the literature.

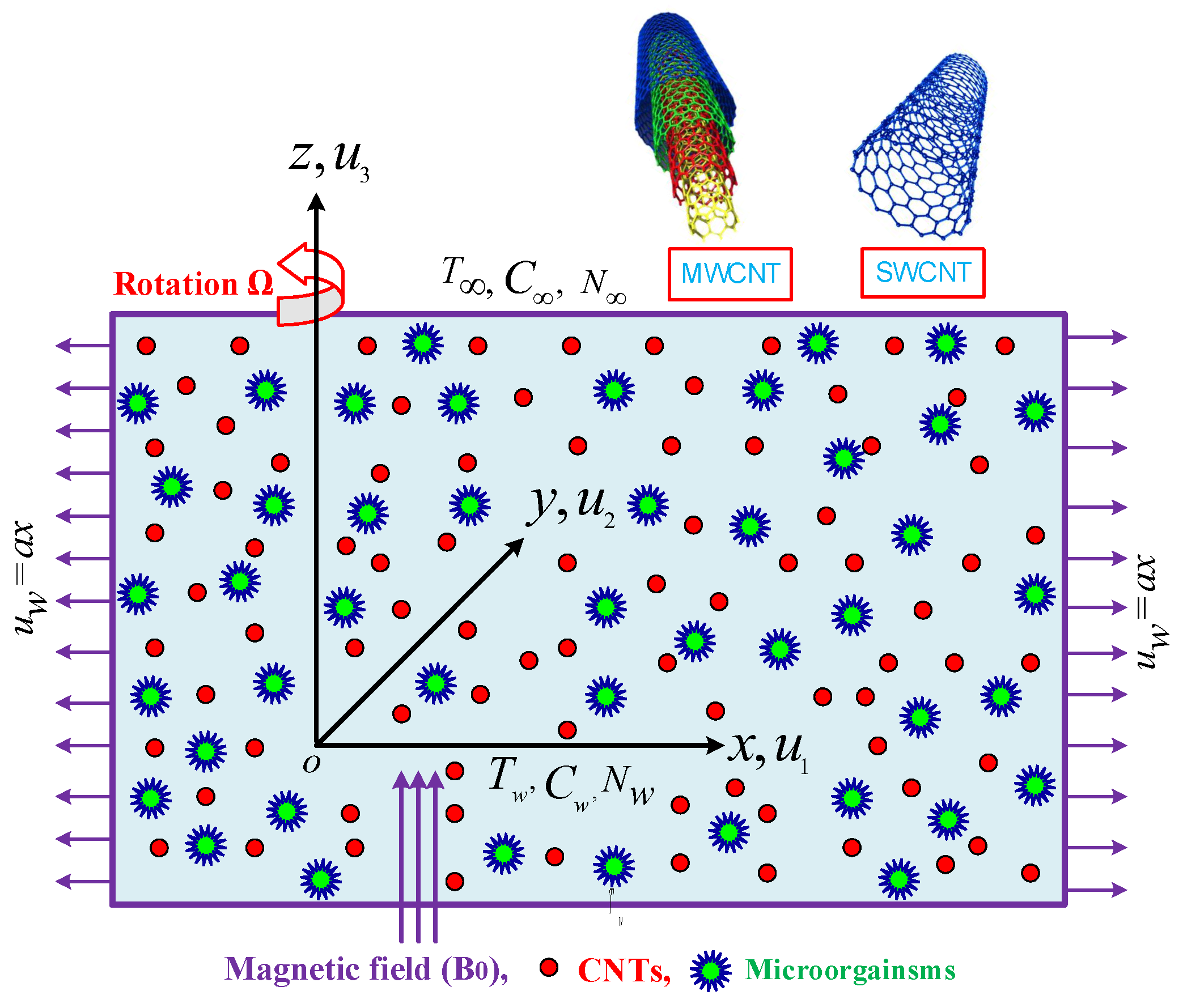
2. Description of the Problem

In the current study, we examined the rotating incompressible nanofluid flow of water-based carbon nanotubes (CNTs) with an angular velocity $\mathsf{\Omega }$ over a stretched sheet with a xy-plane and a z-axis perpendicular to the plate. The rate of sheet stretching is defined as $ax(a>0)$ along the x-axis. The velocity structure of the fluid has been estimated as $U(u_1,u_2,u_3)$ along the $(x,y,z)$-axis, respectively. Additionally, we assume that $N_w$, $C_w$, and $T_w$ represent the density of surface microorganisms, nanoparticle volume friction, and temperature, respectively, and that $N_{\infty }$, $T_{\infty }$, and $C_{\infty }$ represent the density of ambient microorganisms, temperature, and nanoparticle volume friction, respectively, as shown in Figure 1. $B_0$ is the strength of the uniform magnetic force applied parallel to the z-axis. Magnetic Reynolds numbers have been considered to be extremely modest in comparison to induced magnetic fields. We based our research on the physical premise that neither radiative heat transfer or chemical reaction occurs between water and carbon nanotubes, and that no slips (velocity slip or thermal jump) occur between them. The impacts of viscous dissipation or joule heating are not taken into account. All body forces are neglected. The fundamental components of our investigation have been investigated utilizing two distinct carbon nanotubes, namely MWCNT and SWCNT. The thermophysical properties are listed in Table 1 and Table 2. The governing equations are as follows, based on the principles stated above and Tiwari [51,52,53]:

$${\partial }_x{u}_1+{\partial }_y{u}_2+{\partial }_z{u}_3=0,$$

(1)

$${\rho }_{hnf}\left(u_3{\partial }_z{u}_1+u_1{\partial }_x{u}_1+u_2{\partial }_y{u}_1-2\mathsf{\Omega }{u}_2\right)={\mu }_{hnf}{\partial }_{zz}{u}_1-\sigma B_0^2{u}_1,$$

(2)

$${\rho }_{hnf}\left(u_3{\partial }_z{u}_2+u_1{\partial }_x{u}_2+u_2{\partial }_y{u}_2+2\mathsf{\Omega }{u}_1\right)={\mu }_{hnf}{\partial }_{zz}{u}_2-\sigma B_0^2{u}_2,$$

(3)

$$u_1{\partial }_{x}T+u_2{\partial }_{y}T+u_3{\partial }_{z}T={\alpha }_{hnf}{\partial }_{zz}T+\tau \left[D_B{\partial }_{z}C{\partial }_{z}T+\frac{D_T}{T_{\infty }}\left({\partial }_z{T)}^2\right)\right],$$

(4)

$$u_1{\partial }_{x}C+u_2{\partial }_{y}C+u_3{\partial }_{z}C=D_B{\partial }_{zz}C+\frac{D_T}{T_{\infty }}{\partial }_{zz}T,$$

(5)

$$u_1{\partial }_{x}N+u_2{\partial }_{y}N+u_3{\partial }_{z}N+\frac{b{W}_c}{C_w-C_{\infty }}\left[{\partial }_z\left(N{\partial }_{z}C\right)\right]=D_m{\partial }_{zz}N.$$

(6)

Here, the factors of flow along the x, y, and z axes are denoted by $u_1$, $u_2$, and $u_3$, respectively, whereas $(N,C,T)$ denote the concentration of microorganisms, the nanoparticle volume concentration, and the fluid temperature, respectively. The subscript “$h_{nf}$” denots hybrid nanofluid. We also have ${\mu }_{hnf}$, ${\rho }_{hnf}$, and ${\alpha }_{hnf}$ signifies the dynamic viscosity, density, and thermal diffusivity of the hybrid nanofluid, b, $D_B$, $D_T$, $W_c$, $\sigma$, and $D_m$ are chemotaxis constant, Brownian diffusion coefficient, thermophoretic diffusion coefficient, maximum cell swimming speed, electrical conductivity and the microorganisms diffusion coefficient, respectively. The above elaborated model boundary conditions are [54,55]:

$$u_1=a\left(x\right),u_2=0,u_3=0,T=T_w,C=C_w,N=N_{w}asz=0,$$

(7)

$$u_1\to 0,u_2\to 0,T\to T_{\infty },C\to C_{\infty },N\to N_{\infty }asz\to \infty .$$

(8)

Table 1. Thermophysical properties of H${}_2$O and CNTs [56,57].

Physical Properties	${\mathit{C}}_{\mathit{p}}(\mathbf{J}\left({\mathbf{kg}}^{-1}{\mathbf{K}}^{-1}\right)$	$\mathit{\rho }(\mathbf{kg}·{\mathbf{m}}^{-3})$	$\mathit{\kappa }\left({\mathbf{W}(\mathbf{m}}^{-1}{\mathbf{K}}^{-1}\right)$	$\mathit{\sigma }(\mathbf{S}·{\mathbf{m}}^{-1})$
$H_{2}O$	4179	997.1	0.613	$5.5\times {10}^{-6}$
$SWCNT$	425	2600	6600	${10}^6$
$MWCNT$	796	1600	3000	${10}^7$

Table 1. Thermophysical properties of H${}_2$O and CNTs [56,57].

Physical Properties	${\mathit{C}}_{\mathit{p}}(\mathbf{J}\left({\mathbf{kg}}^{-1}{\mathbf{K}}^{-1}\right)$	$\mathit{\rho }(\mathbf{kg}·{\mathbf{m}}^{-3})$	$\mathit{\kappa }\left({\mathbf{W}(\mathbf{m}}^{-1}{\mathbf{K}}^{-1}\right)$	$\mathit{\sigma }(\mathbf{S}·{\mathbf{m}}^{-1})$
$H_{2}O$	4179	997.1	0.613	$5.5\times {10}^{-6}$
$SWCNT$	425	2600	6600	${10}^6$
$MWCNT$	796	1600	3000	${10}^7$

Table 2. Thermophysical aspects of nanofluid and hybrid nanofluid [58,59].

Properties	Nanofluid	Hybrid Nanofluid
$\mu$ (viscosity)	${\mu }_{nf}$ = $\frac{{\mu }_f}{{(1-\varphi )}^{2.5}}$	${\mu }_{hnf}$ = $\frac{{\mu }_f}{{(1-{\varphi }_1)}^{2.5}{(1-{\varphi }_2)}^{2.5}}$
$\rho$ (density)	${\rho }_{nf}$ = $(1-\varphi ){\rho }_f+\varphi {\rho }_{CNT}$	${\rho }_{hnf}$ = $[{\rho }_f(1-{\varphi }_1)+{\varphi }_1{\rho }_{MWCNT}](1-{\varphi }_2)+{\varphi }_2{\rho }_{SWCNT}$
$\rho$$C_p$ (Heat capacity)	$\left(\rho C_p\right)nf$ = $(1-\varphi ){\left(\rho C_p\right)}_f+\varphi {\left(\rho C_p\right)}_{CNT}$	${\left(\rho C_p\right)}_{hnf}$ = $[{\left(\rho C_p\right)}_f(1-{\varphi }_1)+{\varphi }_1{\left(\rho C_p\right)}_{MWCNT}](1-{\varphi }_2)+{\varphi }_2{\left(\rho C_p\right)}_{SWCNT}$
$\kappa$ (Thermal conductivity)	$\frac{{\kappa }_{nf}}{{\kappa }_f}=\frac{(1-\varphi )+2\varphi \left(\frac{{\kappa }_{SWCNT}}{{\kappa }_{SWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_f}{{\kappa }_f}\right)}{(1-\varphi )+2\varphi \left(\frac{{\kappa }_f}{{\kappa }_{SWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_f}{{\kappa }_f}\right)}$	$\frac{{\kappa }_{hnf}}{{\kappa }_{bf}}$ = $\frac{(1-{\varphi }_2)+2{\varphi }_2\left(\frac{{\kappa }_{SWCNT}}{{\kappa }_{SWCNT}-{\kappa }_{bf}}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_{bf}}{{\kappa }_{bf}}\right)}{(1-{\varphi }_2)+2{\varphi }_2\left(\frac{{\kappa }_{bf}}{{\kappa }_{SWCNT}-{\kappa }_{bf}}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_{bf}}{{\kappa }_{bf}}\right)}$
		where $\frac{{\kappa }_{bf}}{{\kappa }_f}$ = $\frac{(1-{\varphi }_1)+2{\varphi }_1\left(\frac{{\kappa }_{MWCNT}}{{\kappa }_{MWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{MWCNT}+{\kappa }_f}{{\kappa }_f}\right)}{(1-{\varphi }_1)+2{\varphi }_1\left(\frac{{\kappa }_f}{{\kappa }_{MWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{MWCNT}+{\kappa }_f}{{\kappa }_f}\right)}$

Table 2. Thermophysical aspects of nanofluid and hybrid nanofluid [58,59].

Properties	Nanofluid	Hybrid Nanofluid
$\mu$ (viscosity)	${\mu }_{nf}$ = $\frac{{\mu }_f}{{(1-\varphi )}^{2.5}}$	${\mu }_{hnf}$ = $\frac{{\mu }_f}{{(1-{\varphi }_1)}^{2.5}{(1-{\varphi }_2)}^{2.5}}$
$\rho$ (density)	${\rho }_{nf}$ = $(1-\varphi ){\rho }_f+\varphi {\rho }_{CNT}$	${\rho }_{hnf}$ = $[{\rho }_f(1-{\varphi }_1)+{\varphi }_1{\rho }_{MWCNT}](1-{\varphi }_2)+{\varphi }_2{\rho }_{SWCNT}$
$\rho$$C_p$ (Heat capacity)	$\left(\rho C_p\right)nf$ = $(1-\varphi ){\left(\rho C_p\right)}_f+\varphi {\left(\rho C_p\right)}_{CNT}$	${\left(\rho C_p\right)}_{hnf}$ = $[{\left(\rho C_p\right)}_f(1-{\varphi }_1)+{\varphi }_1{\left(\rho C_p\right)}_{MWCNT}](1-{\varphi }_2)+{\varphi }_2{\left(\rho C_p\right)}_{SWCNT}$
$\kappa$ (Thermal conductivity)	$\frac{{\kappa }_{nf}}{{\kappa }_f}=\frac{(1-\varphi )+2\varphi \left(\frac{{\kappa }_{SWCNT}}{{\kappa }_{SWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_f}{{\kappa }_f}\right)}{(1-\varphi )+2\varphi \left(\frac{{\kappa }_f}{{\kappa }_{SWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_f}{{\kappa }_f}\right)}$	$\frac{{\kappa }_{hnf}}{{\kappa }_{bf}}$ = $\frac{(1-{\varphi }_2)+2{\varphi }_2\left(\frac{{\kappa }_{SWCNT}}{{\kappa }_{SWCNT}-{\kappa }_{bf}}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_{bf}}{{\kappa }_{bf}}\right)}{(1-{\varphi }_2)+2{\varphi }_2\left(\frac{{\kappa }_{bf}}{{\kappa }_{SWCNT}-{\kappa }_{bf}}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_{bf}}{{\kappa }_{bf}}\right)}$
		where $\frac{{\kappa }_{bf}}{{\kappa }_f}$ = $\frac{(1-{\varphi }_1)+2{\varphi }_1\left(\frac{{\kappa }_{MWCNT}}{{\kappa }_{MWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{MWCNT}+{\kappa }_f}{{\kappa }_f}\right)}{(1-{\varphi }_1)+2{\varphi }_1\left(\frac{{\kappa }_f}{{\kappa }_{MWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{MWCNT}+{\kappa }_f}{{\kappa }_f}\right)}$

Now, using the following similarity transformation to convert the above elaborated mathematical model to its dimensionless form [54,55]:

$$\begin{array}{c}\hfill \eta =z\sqrt{\frac{a}{{\nu }_f}},u_3=-\sqrt{a{\nu }_f}f\left(\eta \right),u_1=ax{f}^{\prime }\left(\eta \right),u_2=axg\left(\eta \right),\frac{T-T_{\infty }}{T_w-T_{\infty }}=\theta \left(\eta \right)\\ \hfill \frac{C-C_{\infty }}{C_w-C_{\infty }}=\mathsf{\Phi }\left(\eta \right),\frac{N-N_{\infty }}{N_w-N_{\infty }}=\chi \left(\eta \right).\end{array}$$

(9)

where $CNT$, $\varphi$, f, $\mu$, ${\rho }_f$, ${\rho }_{CNT}$,${\left(\rho C_p\right)}_{CNT}$, ${\left(\rho C_p\right)}_f$, ${\kappa }_{CNT}$, and ${\kappa }_f$ are the carbon nanotube, solid volume fraction, fluid, viscosity of the fluid, density of the fluid, density of the carbon nanotube, specific heat parameters of the nanotubes, specific heat of the fluid, the thermal conductivities of the carbon nanotube, and thermal conductivities of the fluid, respectively. The equation of continuity (1) is achieved by the use of the similarity transformation described above. In view of Equation (9), the following Equations (2)–(6) are transformed as:

$$\frac{1}{{\chi }_1{\chi }_2}{f}^{‴}-\frac{1}{{\chi }_2}M{f}^{\prime }+2\lambda g-f^{\prime 2}+f{f}^{″}=0,$$

(10)

$$\frac{1}{{\chi }_1{\chi }_2}{g}^{″}-\frac{1}{{\chi }_2}Mg-2\lambda f^{\prime }+f{g}^{\prime }-f^{\prime }g=0,$$

(11)

$$Pr\left[f{\theta }^{\prime }+Nb{\mathsf{\Phi }}^{\prime }{\theta }^{\prime }+Nt{{\theta }^{\prime }}^2\right]+\frac{{\chi }_3}{{\chi }_4}{\theta }^{″}=0,$$

(12)

$${\mathsf{\Phi }}^{″}+Le{\mathsf{\Phi }}^{\prime }+\frac{Nt}{Nb}{\theta }^{″}=0,$$

(13)

$${\chi }^{″}-Pe\left[{\chi }^{\prime }{\mathsf{\Phi }}^{\prime }+({\delta }_1+\chi ){\mathsf{\Phi }}^{″}\right]+Lbf{\chi }^{\prime }=0.$$

(14)

The modified boundary condition of Equations (7) and (8) are as follows:

$$f^{\prime }\left(0\right)=1,g\left(0\right)=0,f\left(0\right)=0,\theta \left(0\right)=1,\mathsf{\Phi }\left(0\right)=1,\chi \left(0\right)=1,at\eta =0$$

(15)

$$f^{\prime }(\infty )\to 0,g(\infty )\to 0,\theta (\infty )\to 0,\mathsf{\Phi }(\infty )\to 0,\chi (\infty )\to 0,as\eta \to \infty .$$

(16)

In the above Equations (10)–(14), the ${\chi }_1$, ${\chi }_2$, ${\chi }_3$, and ${\chi }_4$ are:

$$\begin{array}{c}{\chi }_1=\left[{(1-{\varphi }_1)}^{\frac{5}{2}}{(1-{\varphi }_2)}^{\frac{5}{2}}\right],{\chi }_2=(1-{\varphi }_2)[(1-{\varphi }_1)+{\varphi }_1\frac{{\rho }_{MWCNT}}{{\rho }_f}]+{\varphi }_2\frac{{\rho }_{SWCNT}}{{\rho }_f},\\ {\chi }_3=\left[\frac{(1-{\varphi }_1)+2{\varphi }_1\left(\frac{{\kappa }_{MWCNT}}{{\kappa }_{MWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{MWCNT}+{\kappa }_f}{{\kappa }_f}\right)}{(1-{\varphi }_1)+2{\varphi }_1\left(\frac{{\kappa }_f}{{\kappa }_{MWCNT}-{\kappa }_f}\right)ln\left(\frac{{\kappa }_{MWCNT}+{\kappa }_f}{{\kappa }_f}\right)}\right].\left[\frac{(1-{\varphi }_2)+2{\varphi }_2\left(\frac{{\kappa }_{SWCNT}}{{\kappa }_{SWCNT}-{\kappa }_{bf}}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_{bf}}{{\kappa }_{bf}}\right)}{(1-{\varphi }_2)+2{\varphi }_2\left(\frac{{\kappa }_{bf}}{{\kappa }_{SWCNT}-{\kappa }_{bf}}\right)ln\left(\frac{{\kappa }_{SWCNT}+{\kappa }_{bf}}{{\kappa }_{bf}}\right)}\right],\\ {\chi }_4=(1-{\varphi }_2)[(1-{\varphi }_1)+{\varphi }_1\frac{{\left(\rho C_p\right)}_{MWCNT}}{{\left(\rho C_p\right)}_f}]+{\varphi }_2\frac{{\left(\rho C_p\right)}_{SWCNT}}{{\left(\rho C_p\right)}_f}.\end{array}$$

and the dimensionless form of involved parameters in Equations (10)–(14) are: $\lambda =\frac{\mathsf{\Omega }}{a}$, $M=\frac{\sigma B_0^2}{a{\rho }_f}$, $Pr=\frac{{\mu }_f{\left(\rho C_p\right)}_f}{{\kappa }_f{\rho }_f}$, $Nb=\frac{\tau D_B(C_w-C_{\infty })}{{\nu }_f}$, $Nt=\frac{\tau D_T(T_w-T_{\infty })}{T_{\infty }{\nu }_f}$, $Le=\frac{{\nu }_f}{D_B}$, $Pe=\frac{b{W}_c}{D_m}$, ${\delta }_1=\frac{N_{\infty }}{N_w-N_{\infty }}$, $Lb=\frac{{\nu }_f}{D_m}$. where $Nt$, $\lambda$, $Lb$, ${\delta }_1$, $Pr$, $Nb$, M, $Le$, and $Pe$ are the thermophoresis parameter, rotational parameter, bioconvection Lewis number, microorganism concentration difference parameter, prandtl number, Brownian motion, magnetic parameter, Lewis number, and Peclet number, respectively.

3. Physical Quantities

The most important relationships for the current investigation are the local skin friction coefficient expressions, the local Nusselt number, the local Sherwood number, and the local motile number. These relationships are defined as follows:

$$C{f}_x=\frac{{\tau }_w^x}{{\rho }_f{u}_1^2},C{f}_y=\frac{{\tau }_w^y}{{\rho }_f{u}_1^2},N{u}_x=\frac{x{q}_w}{{\kappa }_f(T_w-T_{\infty })},S{h}_r=\frac{x{q}_m}{D_B(C_w-C_{\infty })},N{n}_x=\frac{x{q}_s}{D_m(N_w-N_{\infty })}.$$

(17)

where the skin friction tensor along the x- and y-direction at a wall are ${\tau }_w^x={\mu }_{nf}.{\left({\partial }_z{u}_1\right)}_{z=0}$ and ${\tau }_w^y={\mu }_{nf}.{\left({\partial }_z{u}_2\right)}_{z=0}$, respectively. Moreover, the heat transfer at wall $q_w=-{\kappa }_{nf}.{\left({\partial }_{z}T\right)}_{z=0}$, $q_m=-D_B.{\left({\partial }_{z}C\right)}_{z=0}$ is the mass flux, and the wall motile microorganisms flux is $q_s=-D_m.{\left({\partial }_{z}N\right)}_{z=0}$. By using similarity transformation Equation (9), we get:

$$\begin{array}{c}\hfill \sqrt{R{e}_x}C{f}_x=\frac{1}{{\chi }_1}{f}^{″}\left(0\right),\sqrt{R{e}_x}C{f}_y=\frac{1}{{\chi }_1}{g}^{\prime }\left(0\right),N{u}_{x}R{e}_x^{\frac{-1}{2}}=-{\chi }_3{\theta }^{\prime }\left(0\right),\\ \hfill S{h}_{r}R{e}_x^{\frac{-1}{2}}=-{\mathsf{\Phi }}^{\prime }\left(0\right),N{n}_{x}R{e}_x^{\frac{-1}{2}}=-{\chi }^{\prime }\left(0\right).\end{array}$$

(18)

4. Implementation of Method

A set of ODEs with definite boundary conditions was obtained in the preceding section. As a result, the coupled system is highly non-linear, therefore, an exact solution is difficult. A well-known Runge–Kutta fourth order has been used, combined with the shooting technique for a numerical solution. This method is well known to solve the boundary value problem. First, we convert the higher order derivatives of Equations (10)–(16) to first-order as follows:

$U_1^{\prime }=U_2$,

$U_2^{\prime }=U_3$,

$U_3^{\prime }={\chi }_1{\chi }_2\left[U_2^2-U_1{U}_3-2\lambda U_4+\frac{1}{{\chi }_2}M{U}_2\right]$,

$U_4^{\prime }=U_5$,

$U_5^{\prime }={\chi }_1{\chi }_2\left[U_2{U}_4+2\lambda U_2-U_1{U}_5+\frac{1}{{\chi }_2}M{U}_4\right]$,

$U_6^{\prime }=U_7$

$U_7^{\prime }=-\frac{Pr{\chi }_4}{{\chi }_3}\left[U_1{U}_7+Nb{U}_7{U}_9+Nt{U}_7^2\right]$,

$U_8^{\prime }=U_9$,

$U_9^{\prime }=-\left[\frac{Nt}{Nb}{U}_7^{\prime }+Le{U}_9\right]$,

$U_{10}^{\prime }=U_{11}$,

$U_{11}^{\prime }=Pe\left[U_9{U}_{11}+({\delta }_1+U_{10})U_9^{\prime }\right]-U_{1}Lb{U}_{11}$.

The boundary conditions are:

$U_1=0,U_2=1,U_4=0,U_6=1,U_8=1,U_{10}=1at\eta =0,$

$U_2\to 0,U_4\to 0,U_6\to 0,U_8\to 0,U_{10}\to 0 as \eta \to \infty ,$

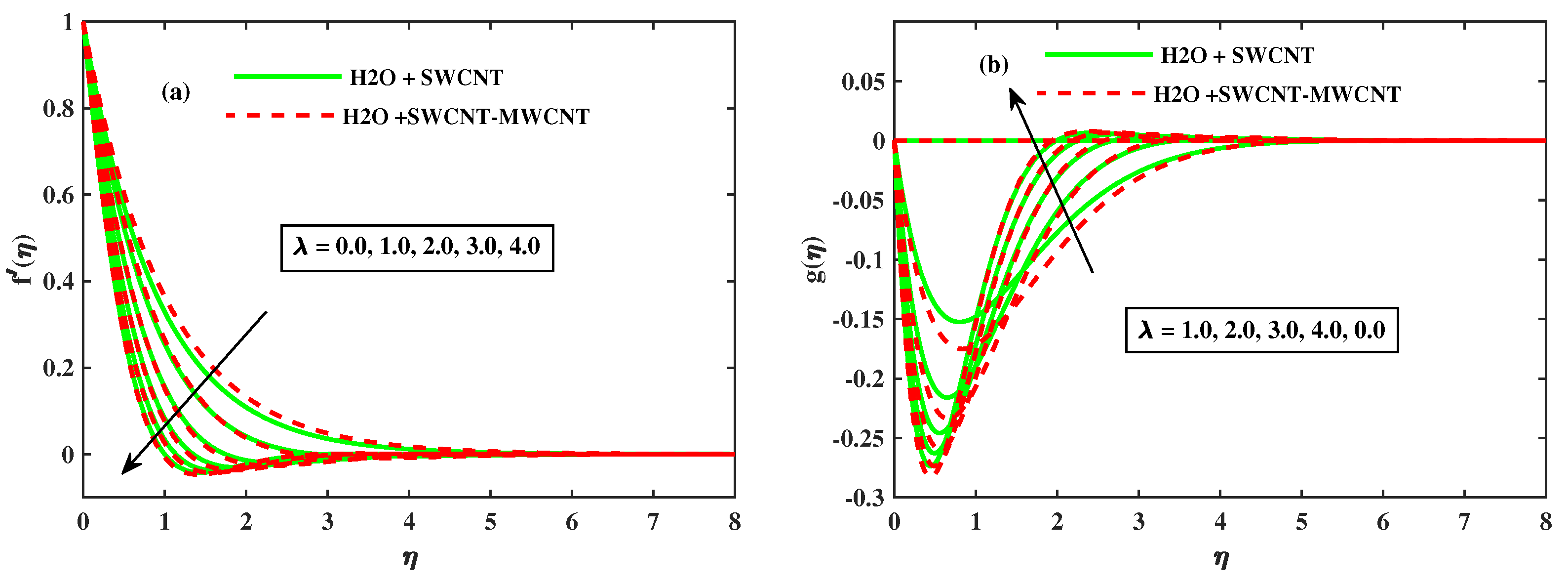
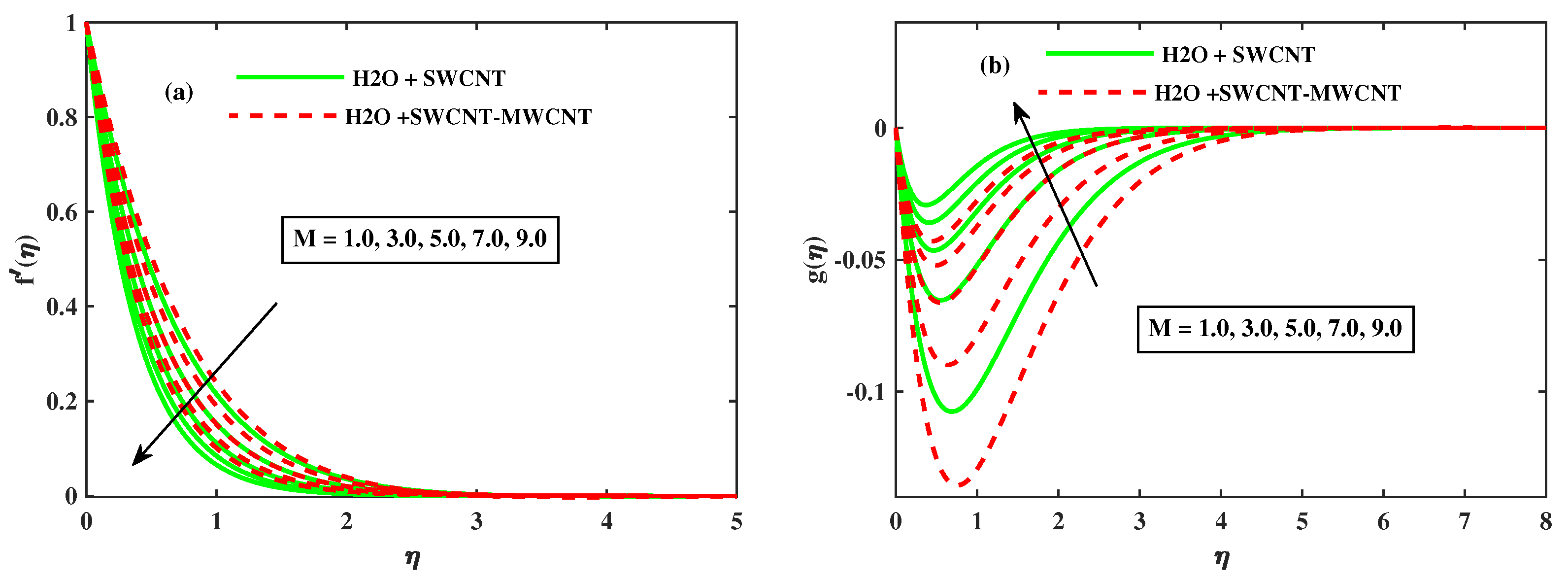
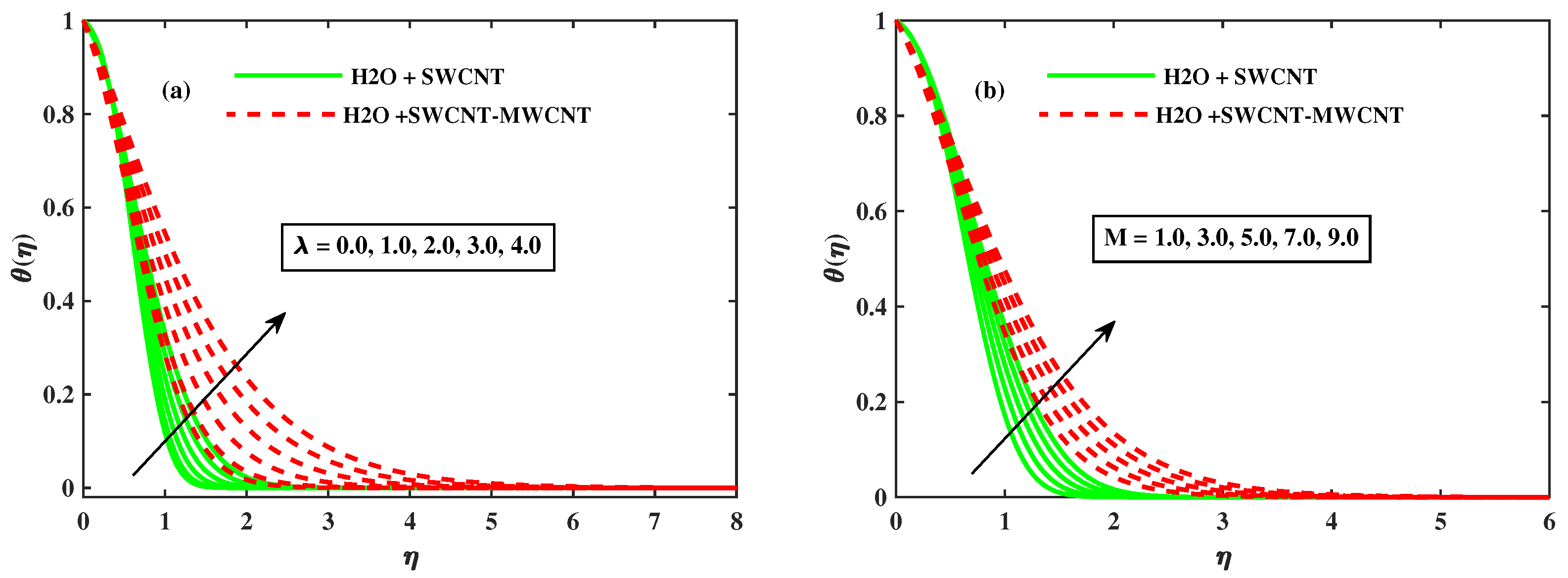
5. Results and Discussion

In this section, we examined the numerical findings of dimensionless velocities ($f^{\prime }\left(\eta \right)$, $g\left(\eta \right)$), concentration of microorganism $\chi \left(\eta \right)$, nanoparticle concentration $\varphi \left(\eta \right)$, and temperature $\theta \left(\eta \right)$ for various physical parameters. For validity of present findings, first, we compared our results with earlier investigations, and found that the Runge–Kutta approach is effectively carried out, and confirmed the validity (see

Table 3. $g^{\prime }\left(0\right)$ and $f^{″}\left(0\right)$ values along with distinct values of $\lambda$.

$\mathit{\lambda }$	Bagh et al. [60]		Nazar et al. [29]		(Our Results)
	$-{\mathit{f}}^{″}\left(\mathbf{0}\right)$	$-{\mathit{g}}^{\prime }\left(\mathbf{0}\right)$	$-{\mathit{f}}^{″}\left(\mathbf{0}\right)$	$-{\mathit{g}}^{\prime }\left(\mathbf{0}\right)$	$-{\mathit{f}}^{″}\left(\mathbf{0}\right)$	$-{\mathit{g}}^{\prime }\left(\mathbf{0}\right)$
0	1.0000	0.0000	1.000	0.000	1.0000	0.0000
0.5	1.13844	0.51283	1.1384	0.5128	1.13842	0.51284
1	1.32501	0.83715	1.3250	0.8371	1.32502	0.83717
2	1.65232	1.28732	1.6523	1.2873	1.65233	1.28730
5	2.39026	2.15024	-	-	2.39024	2.15025

and

Table 4. $-{\theta }^{\prime }\left(0\right)$ value along with distinct values of $\lambda$.

$\mathit{\lambda }$	Ali et al. [61]			(Our Results)
	Pr = 0.7	Pr = 2.0	Pr = 7.0	Pr = 0.7	Pr = 2.0	Pr = 7.0
0.0	0.4552	0.9108	1.8944	0.4551	0.9112	1.8941
0.5	0.3901	0.8525	1.8500	0.3902	0.8522	1.8501
1.0	0.3214	0.7703	1.7877	0.3212	0.7705	1.7876
2.0	0.2420	0.6381	1.6642	0.2421	0.6383	1.6643

). The fixed physical parameter values are as follows: $Le=5$, $M=2$, $\lambda =1$, ${\delta }_1=0.1$, $Pe=0.2$, $Lb=2$, $Pr=6.2$, ${\mathsf{\Phi }}_1=0.04\&{\mathsf{\Phi }}_2=0.0$ $\left(SWCNTs\right)$, and ${\mathsf{\Phi }}_1=0.02\&{\mathsf{\Phi }}_2=0.02$ $(SWCNTs-MWCNTs)$.

Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show the behavior of physical parameters on the dynamics of a water-based fluid subject to a higher input value of parameters. Figure 2a,b exhibits the impact of the rotational parameter $\lambda$ on the flow velocities in the $x,y$-direction, and the results show that as the $\lambda$ rises, the momentum along the x-direction $f^{\prime }\left(\eta \right)$ decreases, while the transverse momentum $g\left(\eta \right)$ increases. The reason behind this outcomes is $\lambda =\frac{\mathsf{\Omega }}{a}$, rising $\lambda$ values raise the stretching rate, which is why the momentum along the x-direction is inversely proportional to rotational parameter $\lambda$, while $g\left(\eta \right)$ increases. Additionally, the hybrid nanofluid $(SWCNTs-MWCNTs)$ case increases the magnitude of the velocity distribution more rapidly than nanofluid $\left(SWCNTs\right)$. The influence of magnetic field parameter M on the velocity profile $f^{\prime }\left(\eta \right)$ and $g\left(\eta \right)$ is demonstrated in Figure 2a,b. When M is increased, the velocity profile along the x-direction $f^{\prime }\left(\eta \right)$ declines monotonically, while the magnitude of the velocity along the y-direction $g\left(\eta \right)$ decreases dramatically. This decrease in velocity is connected to an increase in the resistive force recognized as Lorentz force, which is created when magnetic and electric fields interact. This phenomenon aids to control the thickness of the boundary layer. Furthermore, the velocity distribution of hybrid nanofluid improves more rapidly than the velocity distribution of the nanofluid.

Figure 4a,b exhibited the temperature distribution of several values of the rotational parameter $\lambda$, and the magnetic field M. It is demonstrated that the temperature curve for both the parameters is enhanced. On the other hand, the figure also shows that the hybrid nanofluid has a better temperature distribution than the nanofluid. Figure 5a,b shows that $\theta \left(\eta \right)$ for various values of Brownian motion parameter $Nb$, and thermophoresis parameter $Nt$. Figure 5a depicts the influence of the Brownian motion. In fact, Brownian motion helps heat the boundary layer fluid and inhibits particle development on the surface. As a result, the profile of temperature rises as $Nb$ rises. The effect of $Nt$ on the $\theta \left(\eta \right)$ profile is depicted in Figure 5b. As the thermophoresis parameter rises, the thermal boundary layer thickness grows as $Nt$ increments. The boundary layer’s temperature increases as nanoparticles move from a hot surface to a cold ambient liquid. This influences the growth of the thermal boundary layer thickness. Furthermore, the hybrid phase nano particle temperature is higher than that of the nano phase.

Figure 6a,b illustrates the behavior of the nanoparticle concentration profile as a function of the rotational parameter $\lambda$ and the magnetic field parameter M. As seen in Figure 4a,b, the behavior of $\lambda$ and M is identical to that of the temperature profile. Additionally, hybrid nano liquids have a lower concentration profile than nano liquids. Figure 7a,b illustrates the behavior of the nanoparticle’s concentration $\mathsf{\Phi }\left(\eta \right)$ as a function of $Nb$ and $Nt$. The influence of $Nb$ on the concentration distribution exists in Figure 7a. The $\mathsf{\Phi }\left(\eta \right)$ profile diminishes with rising values of $Nb$. The thermophoresis parameter $Nt$ has the same trend as Figure 5b. Moreover, the values of the concentration profile for hybrid nanofluids are reduced as compared to nanofluid. Figure 8a,b shows the behavior of the nanoparticle motile concentration profile $\chi \left(\eta \right)$ with several values of the rotational parameter $\lambda$ and the magnetic field parameter M. It has been noticed that the behavior of $\lambda$ and M is the same as the nano particle concentration profile $\mathsf{\Phi }\left(\eta \right)$, which can be shown in Figure 6a,b. Figure 9a,b present the effect of the motile concentration profile on Peclet number $Pe$ and bioconvection Lewis number $Lb$. An enhancement in the values of $Pe$ and $Lb$ causes the $\chi \left(\eta \right)$ concentration profile to decline. Furthermore, with hybrid nanofluid, the motile concentration distribution improves more quickly than for nanofluids.

Figure 10a,b represents the fluctuation of skin friction coefficients ($C{f}_x·{R{e}_x}^{0.5}$, $C{f}_y·{R{e}_x}^{0.5}$) with respect to the x, y-direction, respectively, under the influence of the parameters M and $\lambda$. It has been discovered that skin friction coefficients rise as $\lambda$ increases. It is to be noted that the skin friction coefficients is larger in values for hybrid nano fluid than nanofluid. Figure 11a,b demonstrates the effect of $N{u}_x·{R{e}_x}^{-0.5}$ and $Sh{r}_x·{R{e}_x}^{0.5}$ when the parameters $\lambda$ and M are supplied with different inputs. These numbers endure a significant decrease with $\lambda$ and M increases.

6. Conclusions

The Runge–Kutta fourth order with shooting approach is used to explore the enhancement of thermal distribution for the MHD rotating flow of hybrid-nanofluids over a stretched sheet. The numerical results for Nusselt number, microorganism concentration, skin friction coefficients, momentum, concentration, and also temperature profiles are determined for the mono and hybrid-phases. The following are some of the most important results that were obtained:

• When $\lambda$ and M for nanofluid are increased, the velocity component along the x-axis $f^{\prime }\left(\eta \right)$ decreases monotonically, while the amplitude of velocity along the y-axis $g\left(\eta \right)$ increases significantly. It is also worth noting that the velocity fields of the hybrid phase $f^{\prime }\left(\eta \right)$ and $g\left(\eta \right)$ are faster than the nano phase.
• The growing strength of rotating ($\lambda$), magnetic (M), Brownian motion ($Nb$), and thermophoresis ($Nt$), the temperature $\theta \left(\eta \right)$ of fluid enhanced, and hybrid phase fluid $(SWCNTs-MWCNTs)$ enhanced the thermal boundary layer as compared to mono-nanofluid $\left(SWCNTs\right)$.
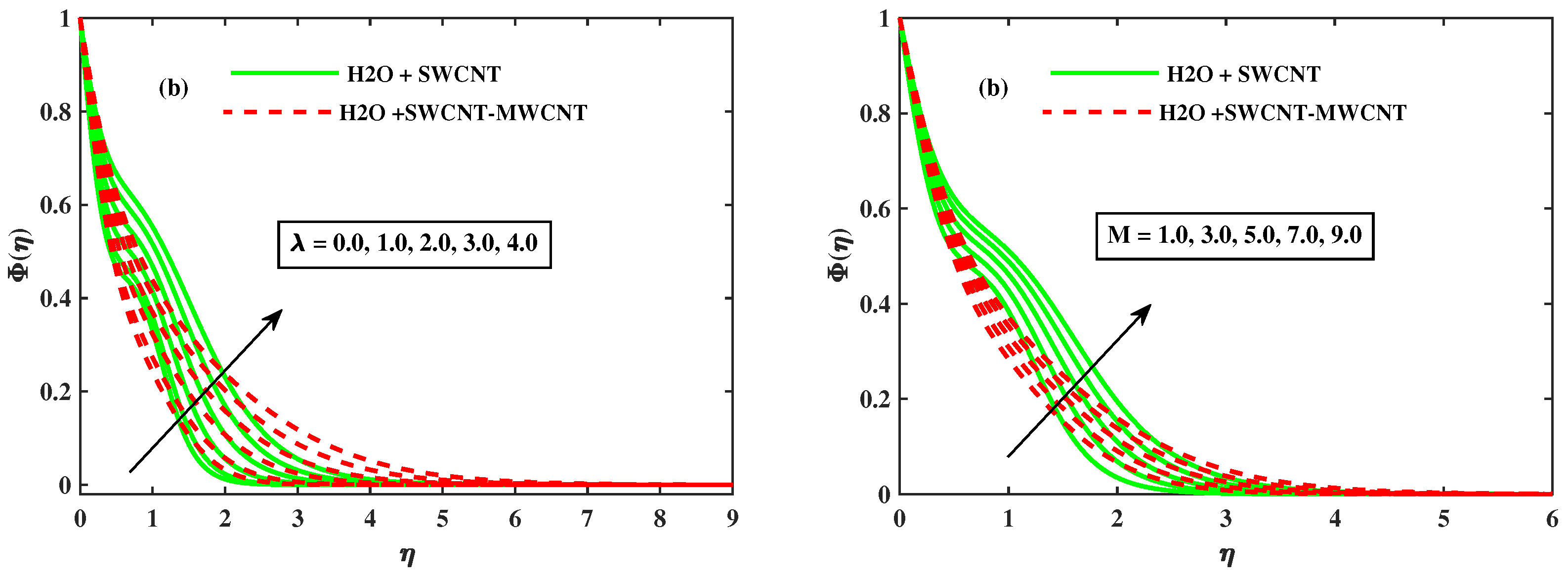
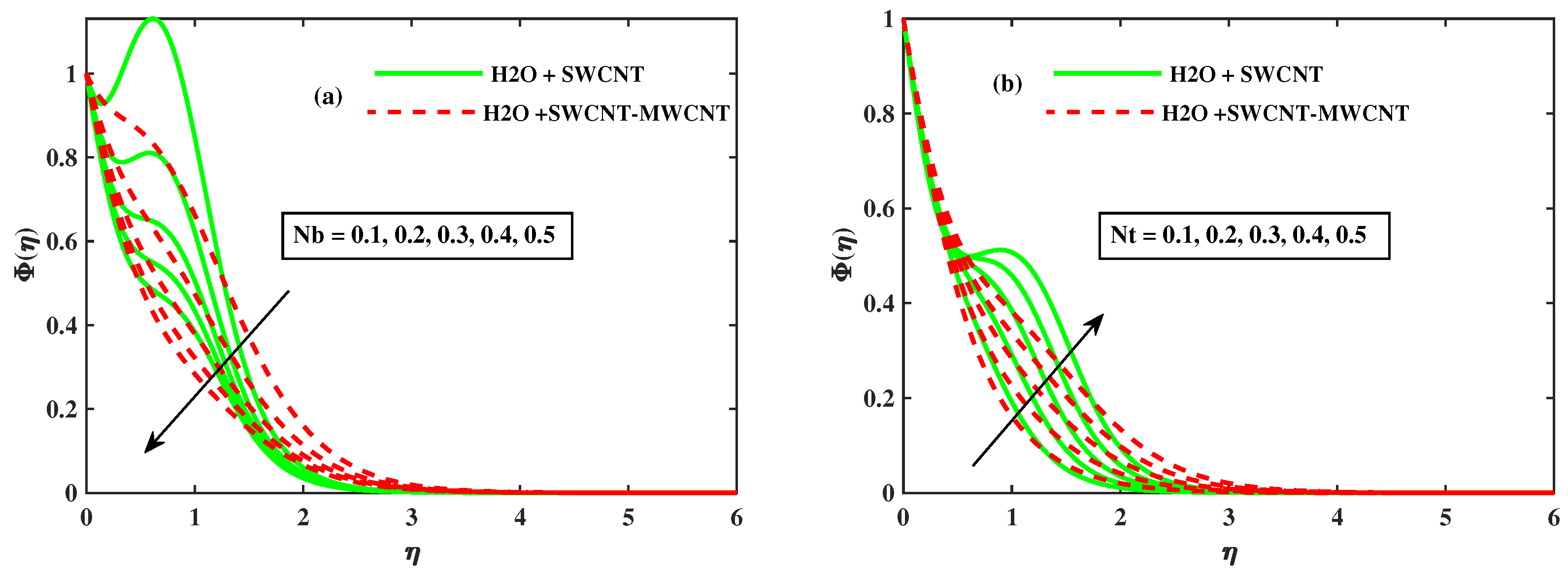
• The concentration profile $\varphi \left(\eta \right)$ rises when the rotational parameter $\lambda$, magnetic parameter M, and thermophoresis parameter $Nt$ rise, but falls as the Brownian motion parameter $Nb$ rises, and hybrid nano liquids exhibit a slower concentration profile $\varphi \left(\eta \right)$.
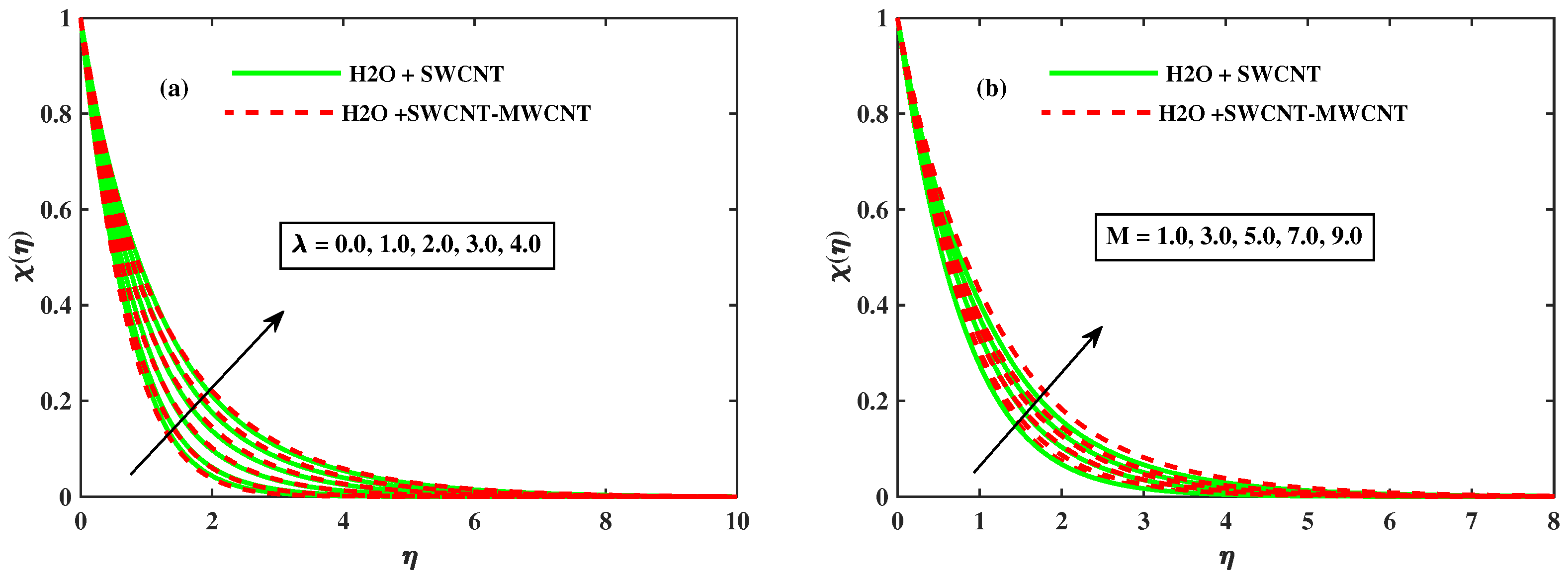
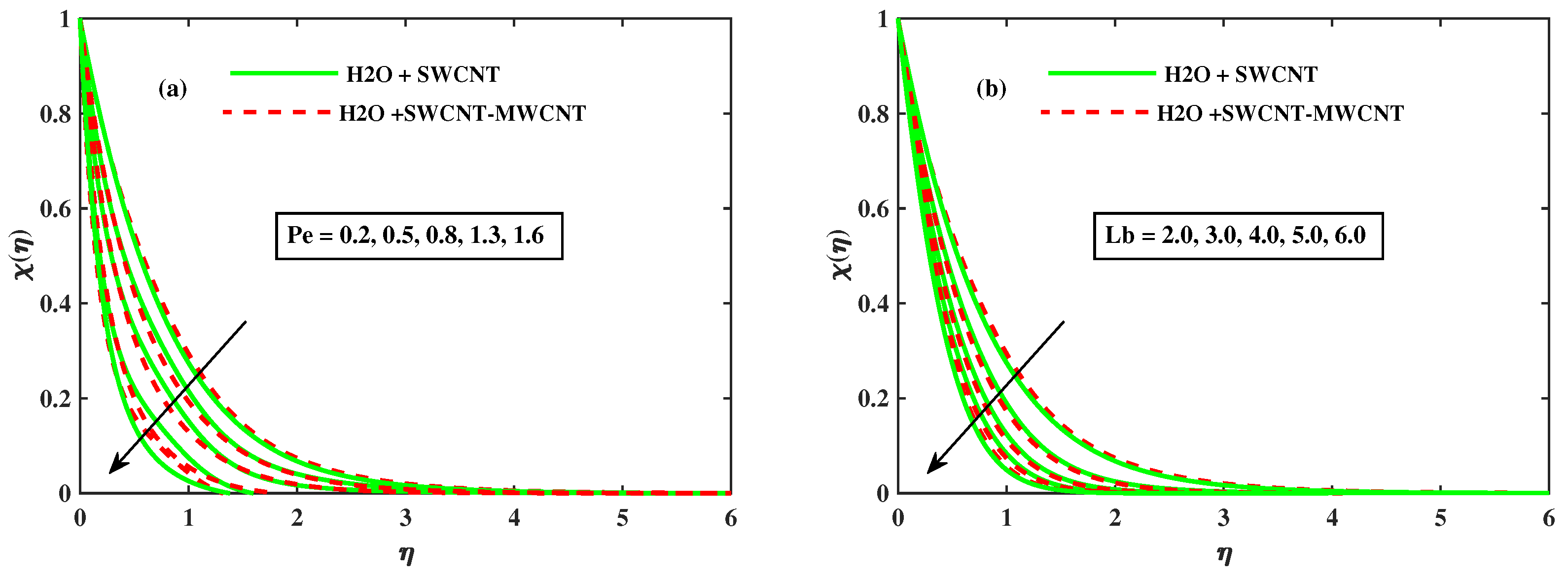
• The motile concentration profile $\chi \left(\eta \right)$ of the nano fluid grows as the rotational parameter $\lambda$ and magnetic parameter M increase, and hybrid phase have a stronger motile concentration profile over the mono phase.
• The motile concentration profile $\chi \left(\eta \right)$ drops as $Pe$ and $Lb$ increase.
• The rising values of rotational parameter $\lambda$ increases the skin friction coefficients ($C{f}_x·{R{e}_x}^{0.5}$, $C{f}_y·{R{e}_x}^{0.5}$) in both the x and y directions, and the skin friction coefficients is larger in values for hybrid nanofluid than nanofluid.
• The heat transfer rate and wall mass transfer rate drops, by means of growing values of $\lambda$ and magnetic (M).

After successful numerical computation of this elaborated fluid problem, we can extend this study for Casson CNTs nanofluid, Oldroyd-B CNTs nanofluid, and Maxwell CNTs nanofluid. This numerical investigation has many industrials and engineering applications such as optics, chemical production, microelectronics cooling, ultra-capacitors, and many types of industry. Further, applications of the study arise in advanced nano-mechanical bioconvection energy conversion devices, bio-nano-coolant deployment systems, and present results are relevant to improving the performance of microbial fuel cells deploying nanofluids.