Influence of Local Gas Sources with Variable Density and Momentum on the Flow of the Medium in the Conduit
Abstract
:1. Introduction
2. Considered Flow Cases and Calculation Results
3. Results of Numerical Calculations for the Mathematical Flow Models
4. Distribution of Static Pressure and Mechanical Energy Losses on the Resistance of Motion in the Duct
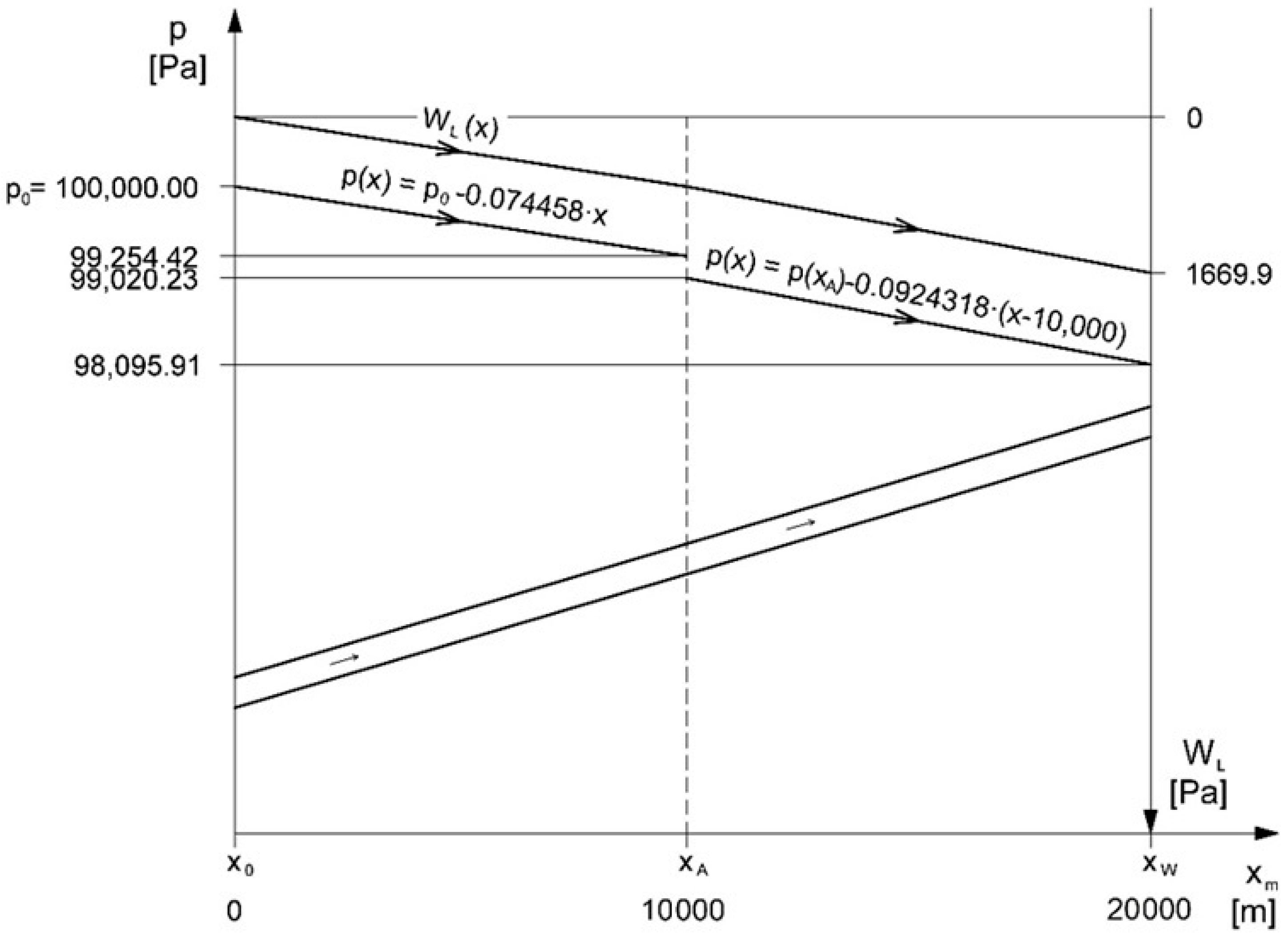
- For section <> of duct:
- For section <> of the duct, the dependence on the pressure profile is also the decreasing linear function:
5. Conclusions
- If there is a local source of gas mass with a density of 1.6 kg/m3 entering a duct containing gas flowing at a rate of 1.2 kg/m3, the pressure increases in the fan are also loaded by the energy spent to provide the required kinetic energy to this gas mixture with the resultant density.
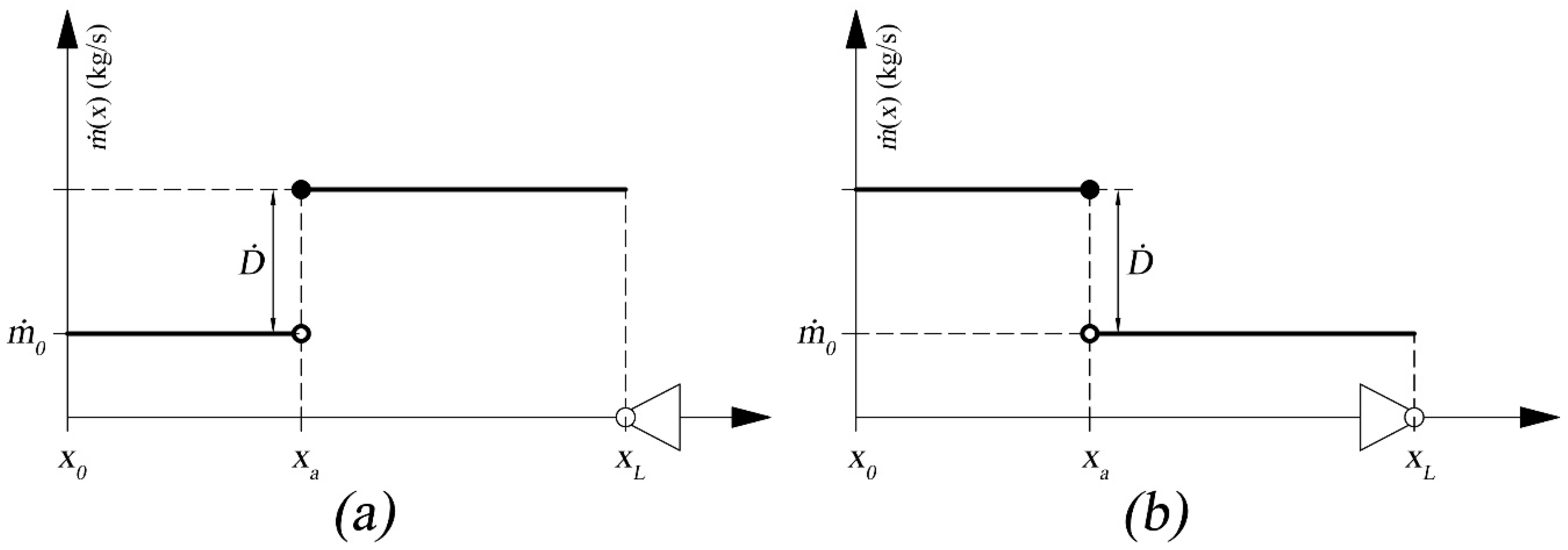
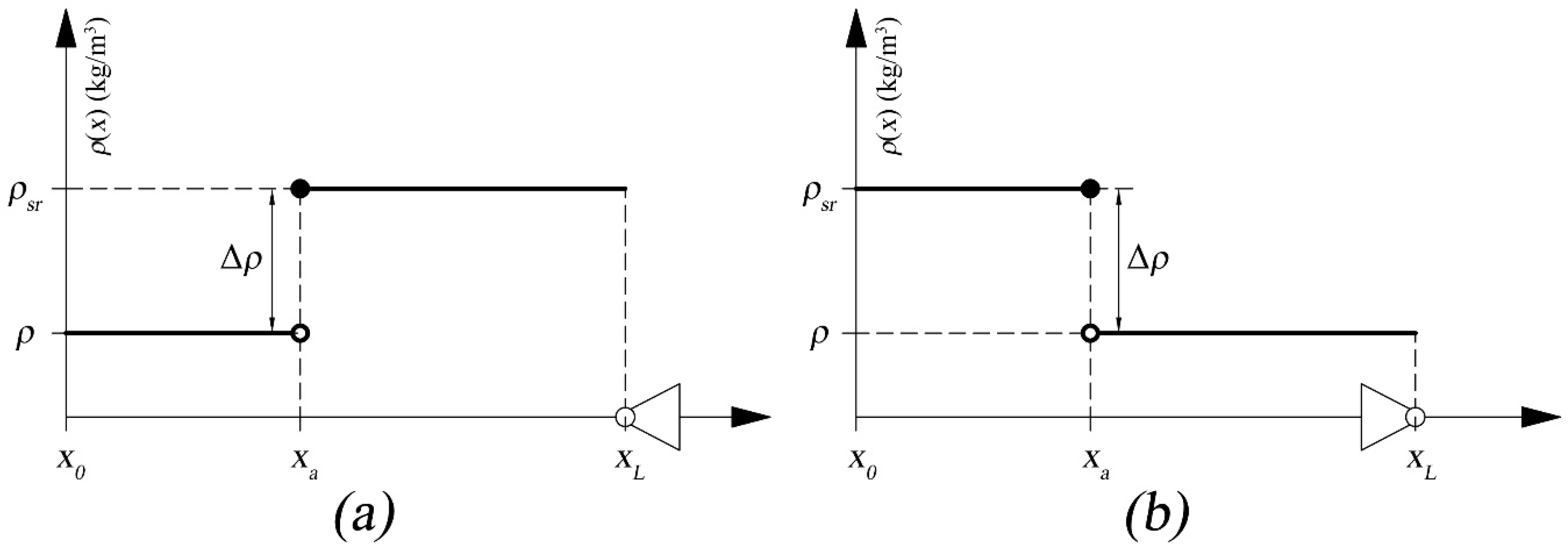
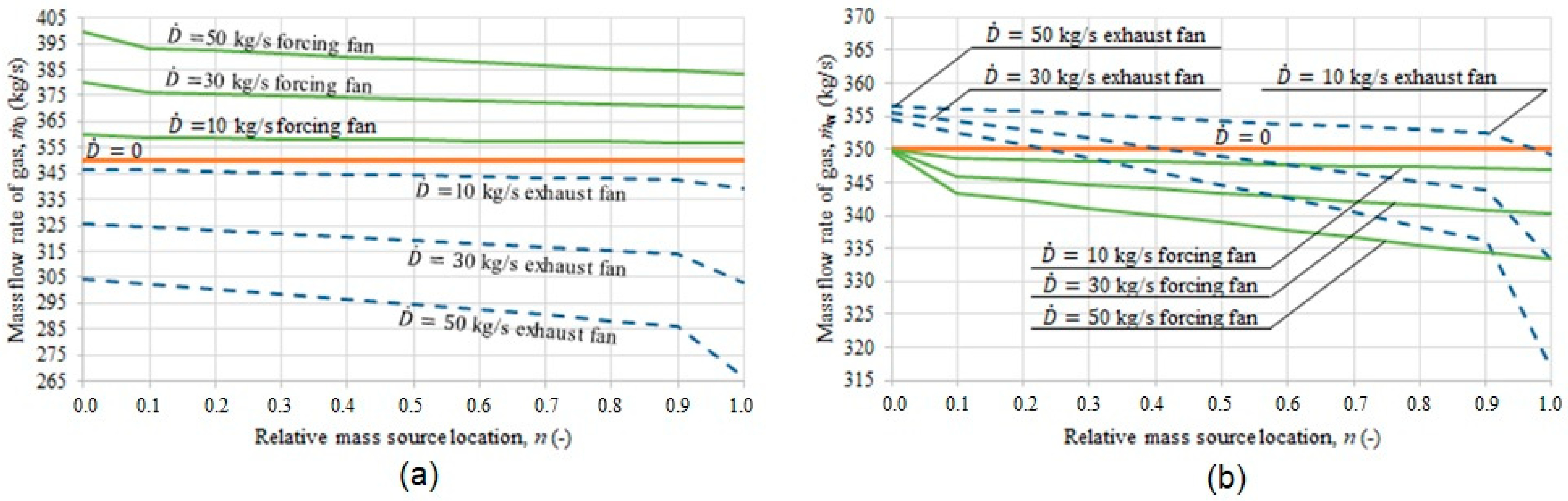
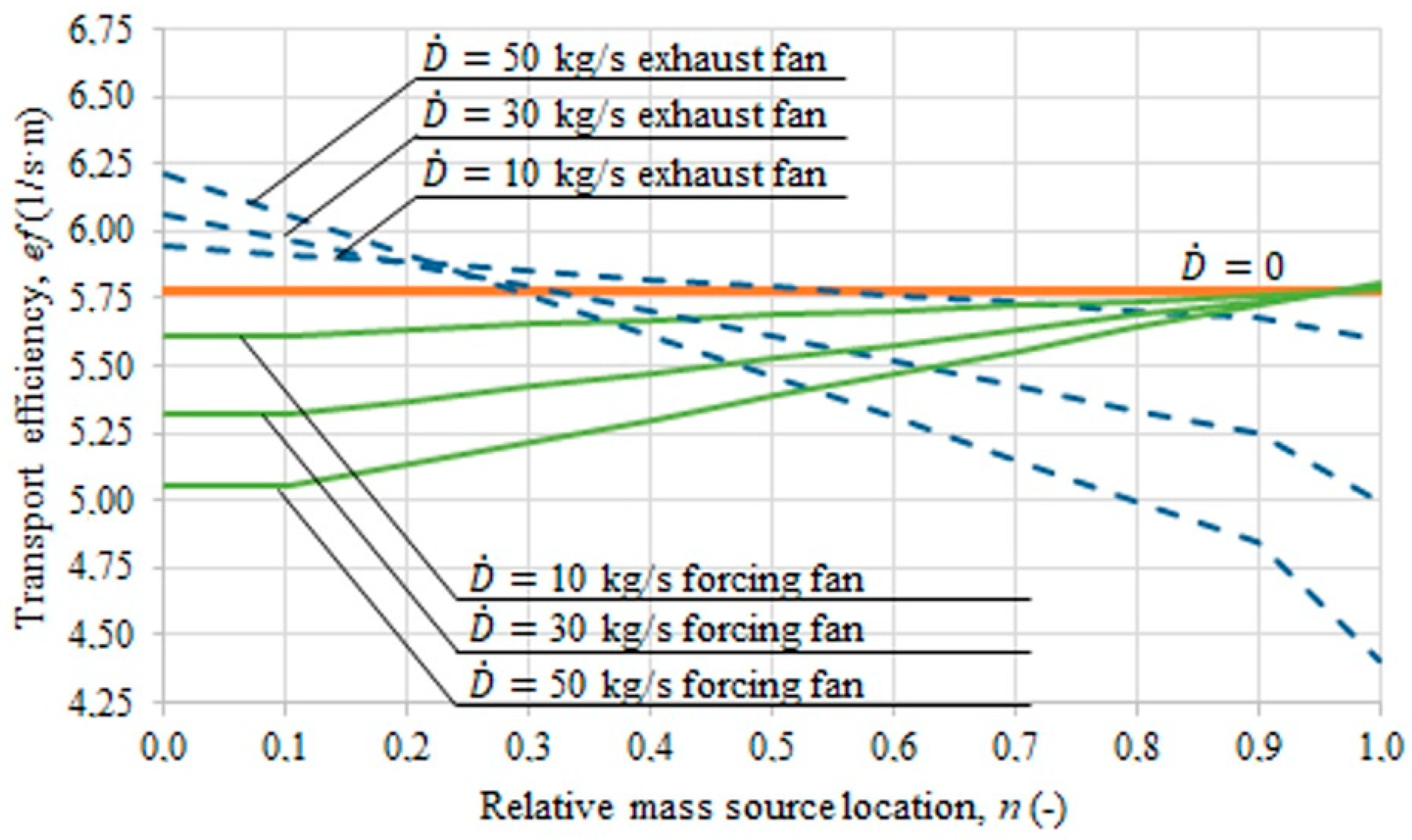
- If there is a source of gas mass with a different (higher) density, the different duct sections will be passed through by gas with varying density (steady within a range) (Figure 3). If the duct fan is working in the suction mode, the fan will be passed through by gas with an average density of more than 1.2 kg/m3.
- If the duct fan is working in the blowing mode, gas with a density of 1.2 kg/m3 will be flowing through the fan, regardless of where the local source of gas with a higher density is situated.
- Changes in the density of gas flowing through the fan require the recalculation of the fan characteristic curve from the catalogue density of 1.2 kg/m3. This means that if the fan is working in the suction mode, the local inflow of gas with varying densities causes changes in the parameters of the mechanical energy source (no such changes occur when the duct fan is working in the blowing mode).
- Differences in gas densities in different duct sections do not change the relationship between the losses of mechanical energy due to forces of opposing motion. However, these differences do affect the values of these relationships by making it necessary to recalculate the drag values for these duct sections, as shown in Formulas (35) and (36). An increase in density of gas flowing through the duct causes a reduction in the duct’s existing drag.
- Such differences in gas density between duct sections due to the presence of local sources of gas with varying densities generate mechanical energy in the inclined parts of the duct through which average-density gas is flowing. This energy is associated with a change in the existing buoyancy in this section. This value is defined as natural head and is included for the suction mode of the fan in Formula (29). The local natural head can be negative or positive, depending on the height difference of a duct in which an average-density gas mixture is flowing. This value may differ between duct sections, due to an exhaust or forcing fan. For the same local source of gas mass with a steady flow density, the local natural head for the suction mode is slightly lower than for the blowing mode, as follows from Formulas (31), (32), (37) and (38) for ∆z = 0. The source of gas mass is located at the end of the duct, with the fan working in the suction mode, and conversely, if the source is located at the entry of the duct, with the fan working in the blowing mode, the local natural head is equal to zero.
- The gas transport efficiency is higher with the suction mode of the fan if the gas source of higher density is located closer to the beginning of the duct. Gas transport with greater efficiency requires a greater expenditure of mechanical energy of the fan.
- The presented mathematical model allows for the determination of the static pressure distribution and mechanical energy loss in the conduit.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Parameter |
| d | hydraulic diameter of the duct, m |
| mass efficiency of the gas source (steady value), kg/s | |
| ef | energy efficiency for the observed medium’s flow, (m·s)−1 |
| F | cross-sectional area of the duct, m2 |
| gravity, m/s2 | |
| mass flow rate of gas, kg/s | |
| mass flow rate of gas entering the duct, the opposite end of which features a mechanical suction source (mass flow rate of gas leaving the duct, the opposite end of which features a mechanical a suction source), kg/s | |
| mass flow rate of gas flowing through the fan, kg/s | |
| p | absolute static pressure, Pa |
| R | specific drag, Ns2/m8 or kg/m7 |
| R* | specific drag of the duct, 1/(kg·m) |
| duct equivalent drag per unit, kg/m8 | |
| duct equivalent drag per unit, 1/(kg·m2) | |
| loss of mechanical energy (total head), N/m2 | |
| x | current coordinate measured along the duct’s axis, m |
| za | spot heights at a point of the current coordinates xa, m |
| zw | spot heights at a point of the current coordinates xw, m |
| δ(x–xa), δ(x–xw) | Dirac delta function distribution, 1/m |
| δ(x–xL) | Dirac delta function distribution at the point of local resistance xL, 1/m |
| Δpc(ρ) | fan’s pressure increase when gas with the density ρ is flowing through the fan, Pa |
| Δpc(ρw) | fan’s total pressure increase with the fan flow rate of gas with density ρ, ρ(x) = ρ(xw), Pa |
| λ | dimensionless coefficient of distributed resistance, - |
| ξ | dimensionless coefficient of local resistance, - |
| ρd | density of local-source gas stream, kg/m3 |
| ρ(x) | gas density at a point with the current coordinate x, kg/m3 |
References
- Bergander, M.J. Fluid Mechanics Vol. 1. Basic Principles; AGH University of Science and Technology Press: Krakow, Poland, 2010. [Google Scholar]
- McPherson, M.J. Subsurface Ventilation and Environmental Engineering; Chapman & Hall: London, UK, 1992. [Google Scholar]
- Pawiński, J.; Roszkowski, J.; Strzemiński, J. Przewietrzanie Kopalń; Śląskie Wydawnictwo Techniczne: Katowice, Poland, 1995. [Google Scholar]
- Wacławik, J. Mechanika Płynów i Termodynamika; Wydawnictwo AGH: Krakow, Poland, 1993. [Google Scholar]
- Yamaguchi, H. Engineering Fluid Mechanics; Springer: Cham, The Netherlands, 2010. [Google Scholar]
- Ptaszyński, B. Charakterystyka przepływowa przewodu transportującego różne media. In Proceedings of the 8 Szkoła Aerologii Górniczej. Sekcja Aerologii Górniczej: Nowoczesne Metody Zwalczania Zagrożeń Aerologicznych w Podziemnych Wyrobiskach Górniczych, Jaworze, Poland, 13–16 October 2015; Dziurzyński, W., Ed.; Główny Instytut Górnictwa: Katowice, Poland, 2015. [Google Scholar]
- Ptaszyński, B.; Łuczak, R.; Życzkowski, P.; Kuczera, Z. Transport Efficiency of a Homogeneous Gaseous Substance in the Presence of Positive and Negative Gaseous Sources of Mass and Momentum. Energies 2022. in print. [Google Scholar]
- Wacławik, J. Wentylacja Kopalń, Tom I, II; Wydawnictwo AGH: Krakow, Poland, 2010. [Google Scholar]
- Bunko, T.; Shyshov, M.; Myroshnychenko, V.; Kokoulin, I.; Dudnyk, M. Estimation and use materials of the airily-depressed surveys on the coal mines of Ukraine. International Conference Essays of Mining Science and Practice. E3S Web Conf. 2019, 109, 13. [Google Scholar] [CrossRef]
- Zmrhal, V.; Boháč, J. Pressure loss of flexible ventilation ducts for residential ventilation: Absolute roughness and compression effect. J. Build. Eng. 2021, 44, 103320, ISSN 2352-7102. [Google Scholar] [CrossRef]
- Dziurzyński, W.; Krach, A.; Pałka, T. Airflow Sensitivity Assessment Based on Underground Mine Ventilation Systems Modeling. Energies 2017, 10, 1451. [Google Scholar] [CrossRef]
- Szmuk, A.; Kuczera, Z.; Badylak, A.; Cheng, J.; Borowski, M. Regulation and control of ventilation in underground workings with the use of VentSim software. In Proceedings of the International Conference on Energy, Resources, Environment and Sustainable Development, Xuzhou, China, 26–27 May 2022; p. 102. [Google Scholar]
- Dziurzyński, W.; Krawczyk, J. Możliwości obliczeniowe wybranych programów symulacyjnych stosowanych w górnictwie światowym, opisujących przepływ powietrza, gazów pożarowych i metanu w sieci wyrobisk kopalni. Przegląd Górniczy Miesięcznik Stowarzyszenia Inżynierów Tech. Górnictwa 2012, 68, 1–11. [Google Scholar]
- Semin, M.A.; Levin, L.Y. Stability of air flows in mine ventilation networks. Process Saf. Environ. Prot. 2019, 124, 167–171. [Google Scholar] [CrossRef]
- Onder, M.; Cevik, E. Statistical model for the volume rate reaching the end of ventilation duct. Tunn. Undergr. Space Technol. 2008, 23, 179–184. [Google Scholar] [CrossRef]
- Auld, G. An estimation of fan performance for leaky ventilation ducts. Tunn. Undergr. Space Technol. 2004, 19, 539–549. [Google Scholar] [CrossRef]
- Jiang, H.; Lu, L.; Sun, K. Experimental study and numerical investigation of particle penetration and deposition in 90 bent ventilation ducts. Build. Environ. 2011, 46, 2195–2202. [Google Scholar] [CrossRef]
- Sleiti, A.K.; Zhai, J.; Idem, S. Computational Fluid Dynamics to Predict Duct Fitting Losses: Challenges and Opportunities. HVAC&R Res. 2013, 19, 2–9. [Google Scholar] [CrossRef]
- Akhtar, S.; Kumral, M.; Sasmito, A.P. Correlating variability of the leakage characteristics with the hydraulic performance of an auxiliary ventilation system. Build. Environ. 2017, 121, 200–214. [Google Scholar] [CrossRef]
- Sharma, S.K.; Kalamkar, V.R. Computational Fluid Dynamics approach in thermo-hydraulic analysis of flow in ducts with rib roughened walls—A review. Renew. Sustain. Energy Rev. 2016, 55, 756–788. [Google Scholar] [CrossRef]
- Yu, H.; Xu, H.; Fan, J.; Zhu, Y.; Wang, F.; Wu, H. Transport of Shale Gas in Microporous/Nanoporous Media: Molecular to Pore-Scale Simulations. Energy Fuels 2021, 35, 911–943. [Google Scholar] [CrossRef]
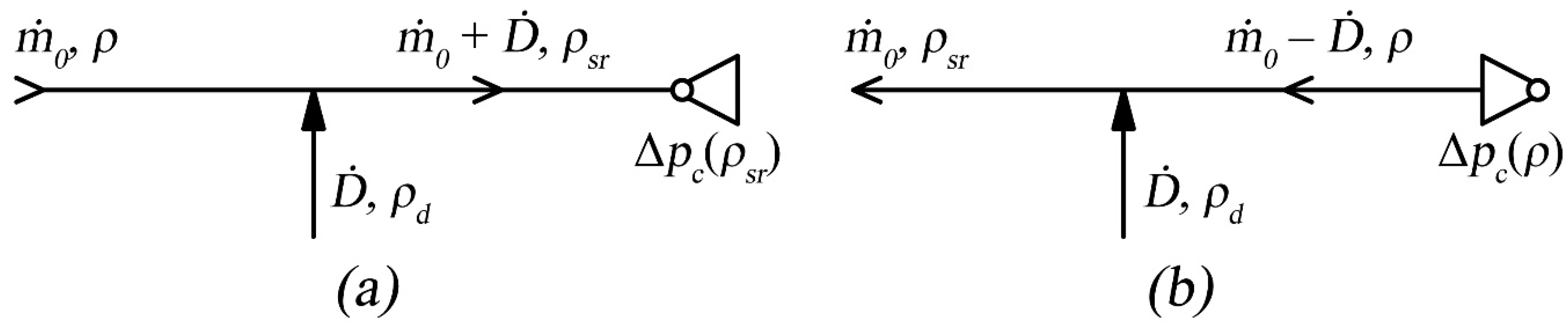
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ptaszyński, B.; Łuczak, R.; Kuczera, Z.; Życzkowski, P. Influence of Local Gas Sources with Variable Density and Momentum on the Flow of the Medium in the Conduit. Energies 2022, 15, 5834. https://doi.org/10.3390/en15165834
Ptaszyński B, Łuczak R, Kuczera Z, Życzkowski P. Influence of Local Gas Sources with Variable Density and Momentum on the Flow of the Medium in the Conduit. Energies. 2022; 15(16):5834. https://doi.org/10.3390/en15165834
Chicago/Turabian StylePtaszyński, Bogusław, Rafał Łuczak, Zbigniew Kuczera, and Piotr Życzkowski. 2022. "Influence of Local Gas Sources with Variable Density and Momentum on the Flow of the Medium in the Conduit" Energies 15, no. 16: 5834. https://doi.org/10.3390/en15165834
APA StylePtaszyński, B., Łuczak, R., Kuczera, Z., & Życzkowski, P. (2022). Influence of Local Gas Sources with Variable Density and Momentum on the Flow of the Medium in the Conduit. Energies, 15(16), 5834. https://doi.org/10.3390/en15165834





