Investigation into Power Line Supporting Structure Dynamic Properties by Means of Impulse Test
Abstract
1. Introduction
2. Methods of Testing Large, Full-Scale Structures
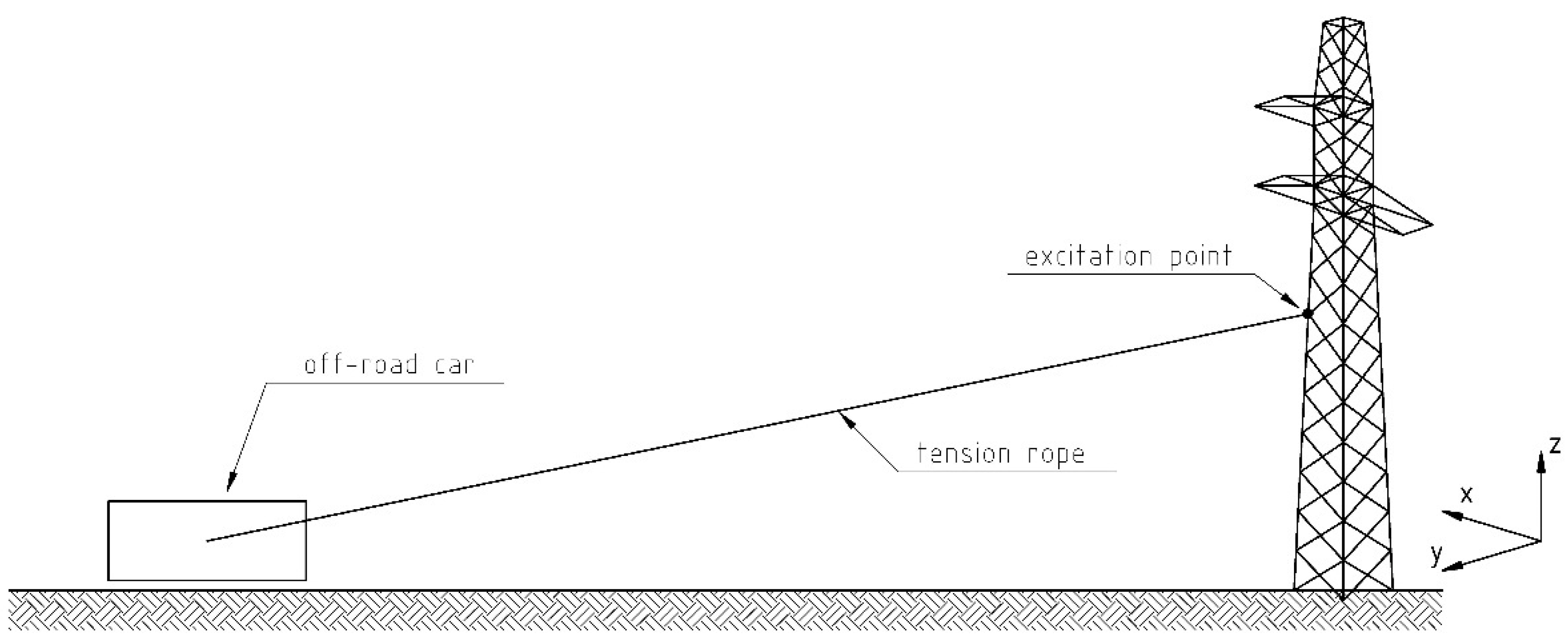
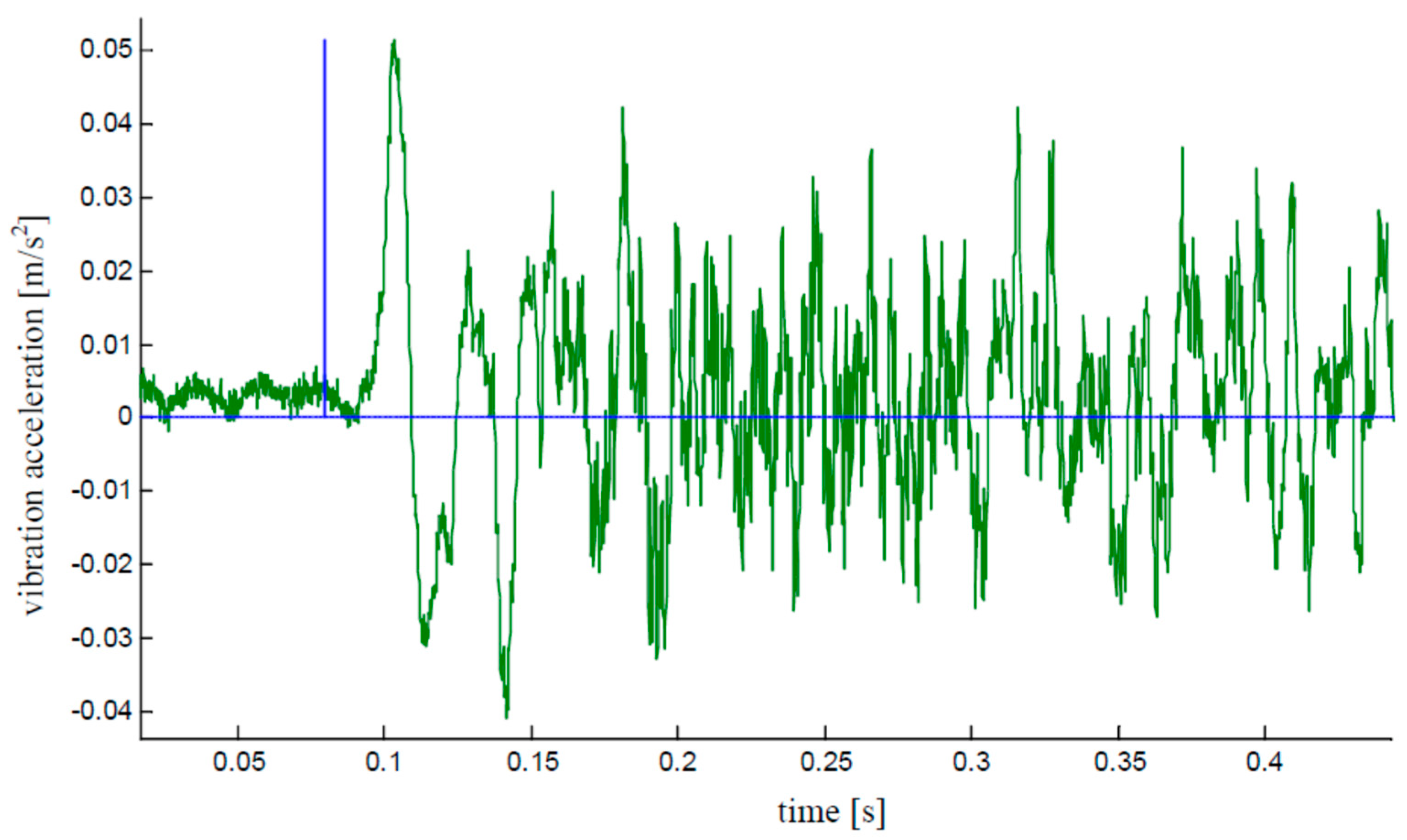
3. Identification Experiment
4. Proposed Method
4.1. Classical Modal Analysis Methods
4.2. Proposed Pseudo-Impulse Approach
- Selection of the reference signal, on the basis of which synchronisation is carried out;
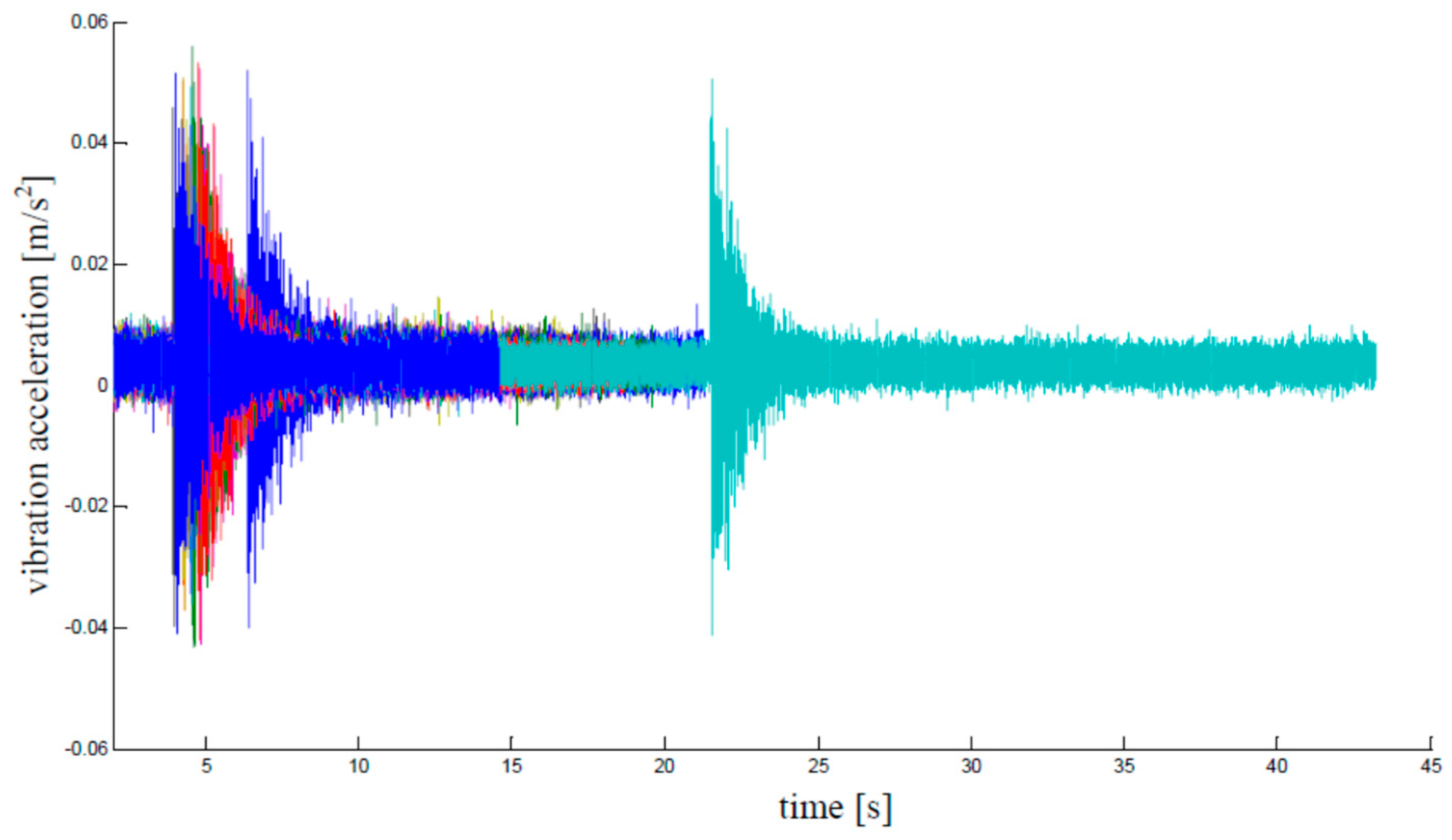
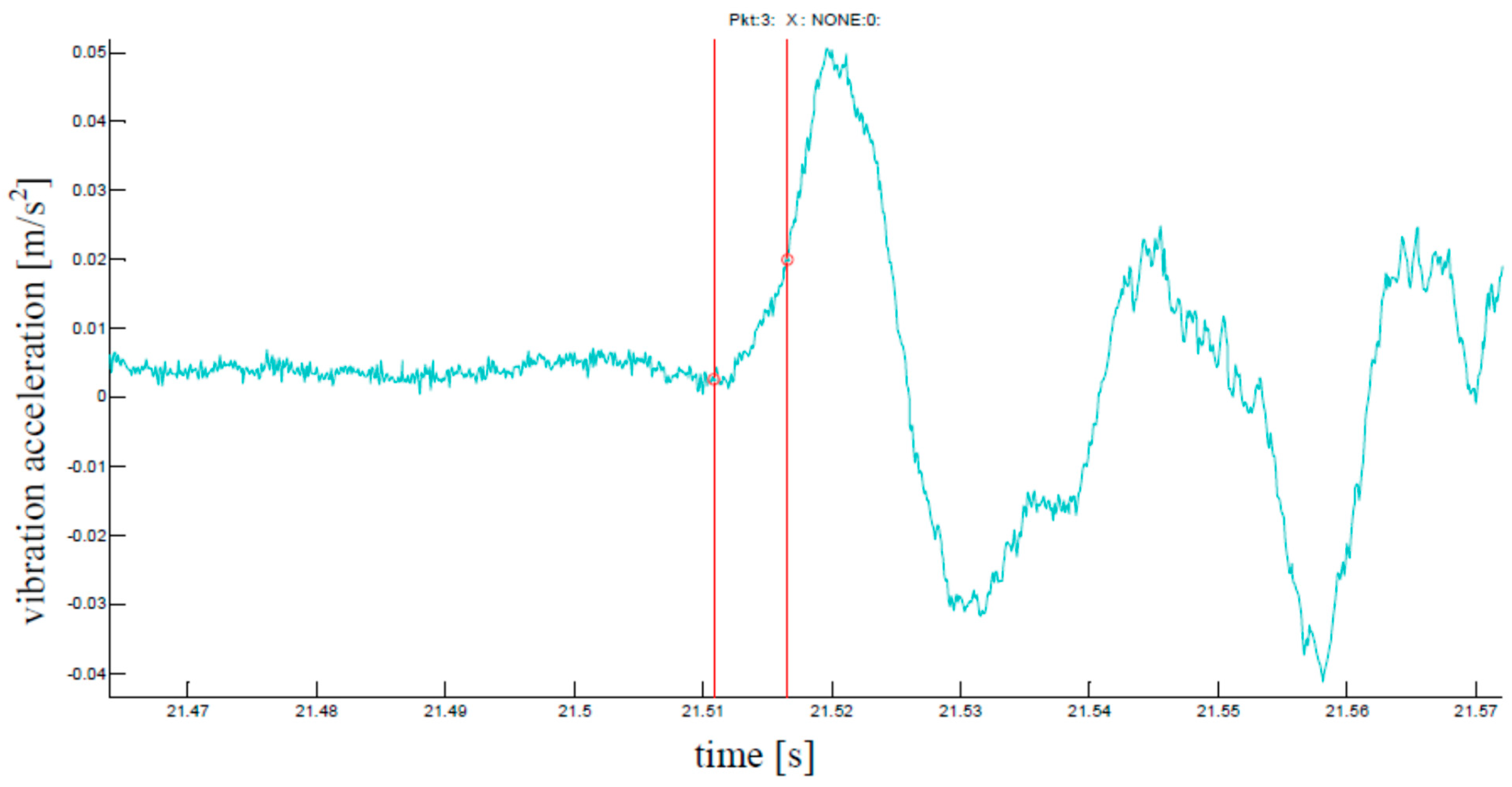
- Determination of synchronisation points (cutting times);
- Signal decimation [53];
- Addition of a pseudo-impulse;
- Estimation of the pseudo-frequency response function.
- -
- The best signal-to-noise ratio;
- -
- The steepest slope associated with the increase in response amplitude after the rope releasing.
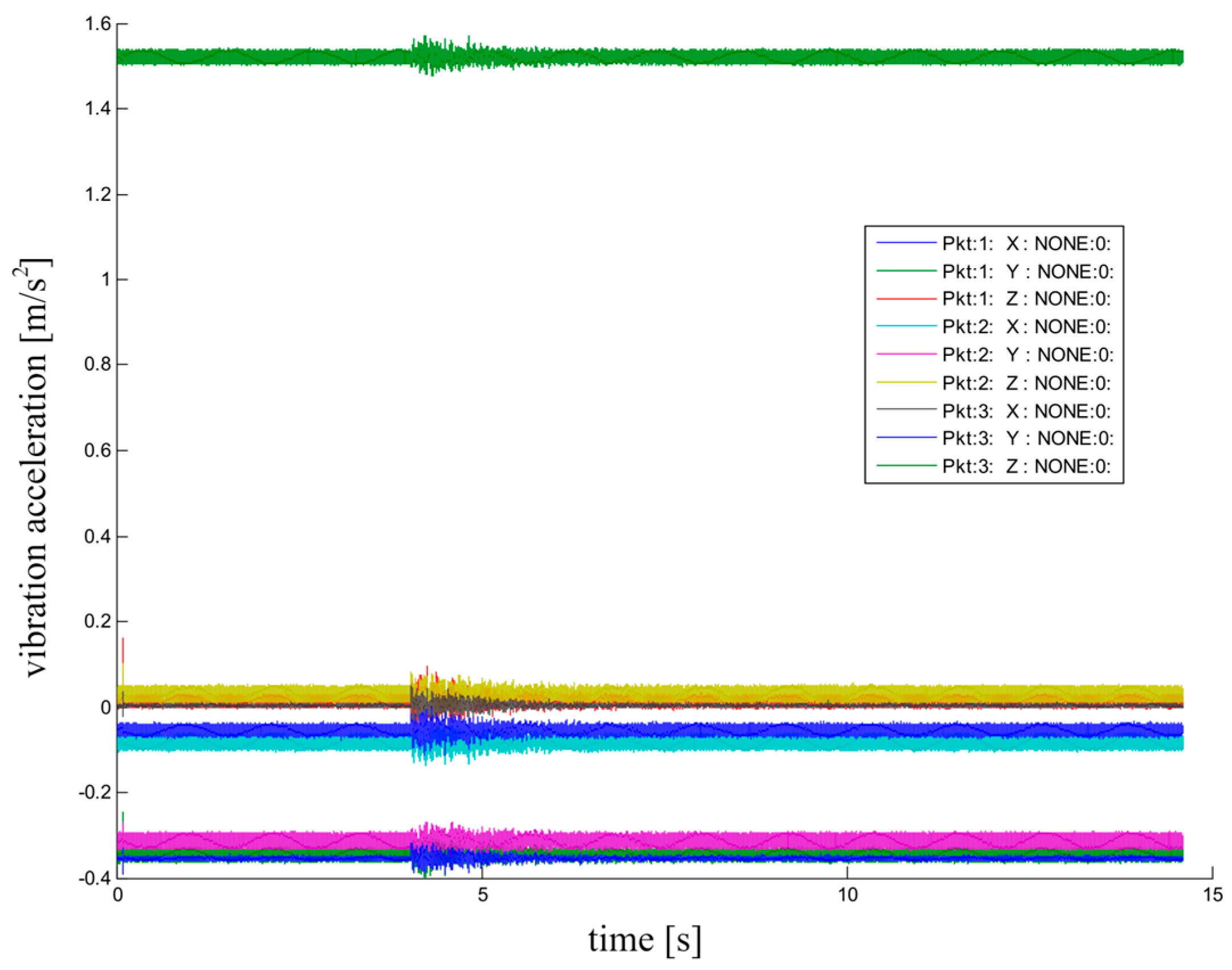
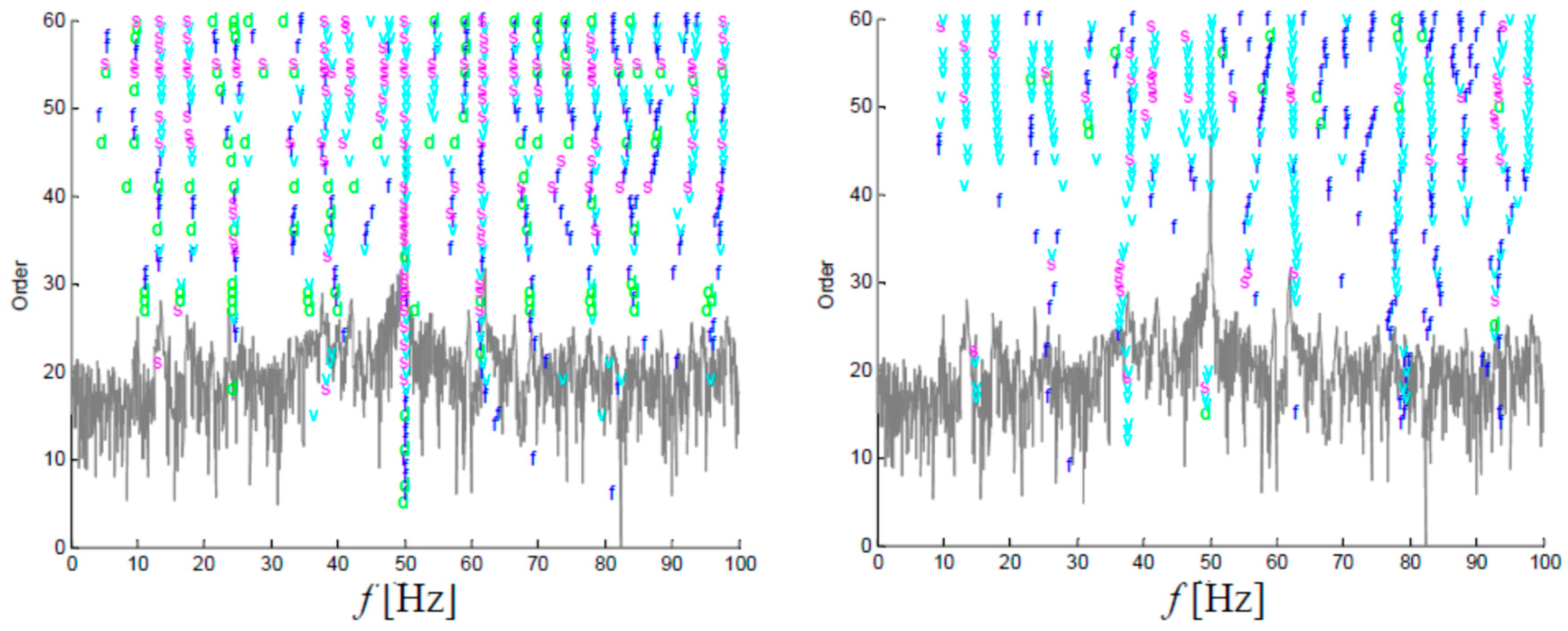
5. Estimation Results
5.1. Exploitational Approach
5.2. Application of Pseudo-Impulse
6. Discussion
7. Conclusions
- The proposed method is suitable for investigation into dynamic properties of large, lightly damped mechanical structures, such as supporting structures of power lines.
- In comparison to the methods in which operational excitation is used, in the proposed approach vibrations of the structure of interest are forced by means of wide-frequency-band excitation, providing enough energy to excite individual natural mode shapes in the tested range. A single measurement series is short and there is no need to wait for the appropriate operating conditions (e.g., wind).
- The input parameters (rope release time and pulling force) are unknown and different in each test. The pseudo-impulse method is independent of the excitation parameters.
- The most important steps of the developed algorithm are the synchronisation of the output signals in the time domain and the amplitude normalisation, which enable averaging the characteristics from individual measurements.
- The stabilisation diagrams show that the usage of the pseudo-impulse results in stabilisation of the pole lines for the lower order and appearance of the stable pole lines, which allows for the visualisation of poles that are non-detectable in cases of classical analyses.
- The modal parameters obtained by the application of the proposed method can be used for the purposes of non-destructive diagnostics and monitoring of the technical condition of the large, full-scale constructions in order to improve the safety and reliability of their exploitation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Uhl, T. Computer Aided Identification of Models of Mechanical Structures; WNT: Warsaw, Poland, 1997. [Google Scholar]
- Nguyen, K.D.; Chan, T.H.; Thambiratnam, D.P.; Nguyen, A. Damage identification in a complex truss structure using modal characteristics correlation method and sensitivity-weighted search space. Struct. Health Monit. 2019, 18, 49–65. [Google Scholar] [CrossRef]
- Iwaniec, J.; Iwaniec, M.; Kasprzyk, S. Transverse vibrations of transmission tower of variable geometrical structure. J. Low Freq. Noise Vib. Act. Control 2019, 38, 774–786. [Google Scholar] [CrossRef]
- Szopa, K.; Iwaniec, M.; Iwaniec, J. Identification of technical condition of the overhead power line supporting structure. Eksploat. Niezawodn.–Maint. Reliab. 2019, 21, 115–124. [Google Scholar] [CrossRef]
- Panth, D. Reasons for Failure of Transmission Lines and Their Prevention Strategies. Int. J. Electr. Electron. Data Commun. 2014, 2, 1–4. [Google Scholar]
- Yang, S.; Zhou, W.; Zhu, S.; Wang, L.; Ye, L.; Xia, X.; Li, H. Failure probability estimation of overhead transmission lines considering the spatial and temporal variation in severe weather. J. Mod. Power Syst. Clean Energy 2019, 7, 131–138. [Google Scholar] [CrossRef]
- Haes Alhelou, H.; Hamedani-Golshan, M.E.; Njenda, T.C.; Siano, P. A Survey on Power System Blackout and Cascading Events: Research Motivations and Challenges. Energies 2019, 12, 682. [Google Scholar] [CrossRef]
- Karamitsos, I.; Konstantinos, O. Blackouts in electric power transmission systems. In Proceedings of the 5th WSEAS International Conference on Applications of Electrical Engineering, Prague, Czech Republic, 12–14 March 2006; pp. 44–47. [Google Scholar]
- Gan, J.; Li, L. Research on the Technical Reliability of the Overhead Transmission Lines Based on the Life Cycle Technology. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 558, p. 052037. [Google Scholar] [CrossRef]
- Chiachío, J.; Chiachío, M.; Derriso, M.M.; Goebel, K.; Hong, M.; Huang, W.; Jiang, X.; Li, F.; Lim, Y.Y.; Liu, P.; et al. Structural Health Monitoring (SHM) in Aerospace Structures; Yuan, F.-G., Ed.; Woodhead Publishing: Cambridge, UK, 2016; ISBN 9780081001486. [Google Scholar] [CrossRef]
- Markus, G.; Sause, R.; Jasiūnienė, E. (Eds.) Structural Health Monitoring Damage Detection Systems for Aerospace; Springer Aerospace Technology; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Sroka, K.; Złotecka, D. The risk of large blackout failures in power systems. Arch. Electr. Eng. 2019, 68, 411–426. [Google Scholar]
- Esfandiari, A.; Bakhtiari-Nejad, F.; Rahai, A. Theoretical and experimental structural damage diagnosis method using natural frequencies through an improved sensitivity equation. Int. J. Mech. Sci. 2013, 70, 79–89. [Google Scholar] [CrossRef]
- Jassim, Z.; Ali, N.; Mustapha, F.; Abdul Jalil, N. A review on the vibration analysis for a damage occurrence of a cantilever beam. Eng. Fail. Anal. 2013, 31, 442–461. [Google Scholar] [CrossRef]
- Maia, N.M.M.; Almeida, R.A.B.; Urgueira, A.P.V.; Sampaio, R.P.C. Damage detection and quantification using transmissibility. Mech. Syst. Signal Process. 2011, 25, 2475–2483. [Google Scholar] [CrossRef]
- Pascual, R.; Golinval, J.C.; Razeto, M. A Frequency Domain Correlation Technique for Model Correlation and updating. In Proceedings of the 15th International Modal Analysis Conference, Orlando, FL, USA, 3–6 February 1997; pp. 587–592. [Google Scholar]
- Worden, K. Structural Fault Detection Using a Novelty Measure. J. Sound Vib. 1997, 201, 85–101. [Google Scholar] [CrossRef]
- Lang, Z.Q.; Park, G.; Farrar, C.R.; Todd, M.D.; Mao, Z.; Zhao, L.; Worden, K. Transmissibility of non-linear output frequency response functions with application in detection and location of damage in MDOF structural systems. Int. J. Non-Linear Mech. 2011, 46, 841–853. [Google Scholar] [CrossRef]
- Yan, W.-J.; Chronopoulos, D.; Yuen, K.-V.; Zhu, Y.-C. Structural anomaly detection based on probabilistic distance measures of transmissibility function and statistical threshold selection scheme. Mech. Syst. Signal Process. 2022, 162, 108009. [Google Scholar] [CrossRef]
- Taajobian, M.; Mohammadzaheri, M.; Doustmohammadi, M.; Amouzadeh, A.; Emadi, M. Fault diagnosis of an automobile cylinder head using low frequency vibrational data. J. Mech. Sci. Technol. 2018, 32, 3037–3045. [Google Scholar] [CrossRef]
- Kaewniam, P.; Cao, M.; Alkayem, N.F.; Li, D.; Manoach, E. Recent advances in damage detection of wind turbine blades: A state-of-the-art review. Renew. Sustain. Energy Rev. 2022, 167, 112723. [Google Scholar] [CrossRef]
- Mohammadzaheri, M.; Amouzadeh, A.; Doustmohammadi, M.; Emadi, M.; Jamshidi, E.; Ghodsi, M.; Soltani, P. Fuzzy Analysis of Resonance Frequencies for Structural Inspection of an Engine Cylinder Block. Fuzzy Inf. Eng. 2021, 13, 266–276. [Google Scholar] [CrossRef]
- Li, X.Y.; Guan, Y.H.; Law, S.S.; Zhao, W. Monitoring abnormal vibration and structural health conditions of an in-service structure from its SHM data. J. Sound Vib. 2022, 537, 117185. [Google Scholar] [CrossRef]
- Eiras, J.N.; Payan, C.; Rakotonarivo, S.; Garnier, V. Experimental modal analysis and finite element model updating for structural health monitoring of reinforced concrete radioactive waste packages. Constr. Build. Mater. 2018, 180, 531–543. [Google Scholar] [CrossRef]
- Pallarés, F.J.; Betti, M.; Bartoli, G.; Pallaré, L. Structural health monitoring (SHM) and Nondestructive testing (NDT) of slender masonry structures: A practical review. Constr. Build. Mater. 2021, 297, 123768. [Google Scholar] [CrossRef]
- Mironovs, D.; Ručevskis, S.; Dzelzītis, K. Prospects of Structural Damage Identification Using Modal Analysis and Anomaly Detection. Procedia Struct. Integr. 2022, 37, 410–416. [Google Scholar] [CrossRef]
- Li, Q.; He, Y.; Zhou, K.; Han, X.; He, Y.; Shu, Z. Structural health monitoring for a 600 m high skyscraper. Struct. Des. Tall Spec. Build. 2018, 27, e1490. [Google Scholar] [CrossRef]
- Svendsen, B.T.; Frøseth, G.T.; Øiseth, O.; Rønnquist, A. A data-based structural health monitoring approach for damage detection in steel bridges using experimental data. J. Civ. Struct. Health Monit. 2022, 12, 101–115. [Google Scholar] [CrossRef]
- Chojnacki, A.L. Assessment of the Risk of Damage to 110 kV Overhead Lines Due to Wind. Energies 2021, 14, 556. [Google Scholar] [CrossRef]
- Paiva, F.; Henriques, J.; Barros, R.C. Review of Transmission Tower Testing Stations around the World. Procedia Eng. 2013, 57, 859–868. [Google Scholar] [CrossRef][Green Version]
- Szafran, J. An experimental investigation into failure mechanism of a full-scale 40 m high steel telecommunication tower. Eng. Fail. Anal. 2015, 54, 131–145. [Google Scholar] [CrossRef]
- Szopa, K.; Iwaniec, M.; Iwaniec, J. Modelling and identification of bolted truss structure with the use of design of experiment approach. Structures 2020, 27, 462–473. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. High accuracy measurement of deflections of an electricity transmission line tower. Eng. Struct. 2014, 80, 418–425. [Google Scholar] [CrossRef]
- Denoon, R.O.; Kwok, K.C.S. Full-scale measurements of wind-induced response of an 84 m high concrete control tower. J. Wind Eng. Ind. Aerodyn. 1996, 60, 155–165. [Google Scholar] [CrossRef]
- Fu, J.Y.; Wu, J.R.; Xu, A.; Li, Q.S.; Xiao, Y.Q. Full-scale measurements of wind effects on Guangzhou West Tower. Eng. Struct. 2012, 35, 120–139. [Google Scholar] [CrossRef]
- Guo, Y.L.; Kareem, A.; Ni, Y.Q.; Liao, W.Y. Performance evaluation of Canton Tower under winds based on full-scale data. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 116–128. [Google Scholar] [CrossRef]
- Wang, H.; Ke, S.T.; Ge, Y.J. Research on non-stationary wind-induced effects and the working mechanism of full scale super-large cooling tower based on field measurement. J. Wind Eng. Ind. Aerodyn. 2019, 184, 61–76. [Google Scholar] [CrossRef]
- Experimental Modal Analysis; Brüel & Kjær Sound & Vibration Measurement A/S: Nærum, Denmark, 2003.
- Shin, J.; Scott, D.W.; Stewart, L.K.; Yang, C.-S.; Wright, T.R.; DesRoches, R. Dynamic response of a full-scale reinforced concrete building frame retrofitted with FRP column jackets. Eng. Struct. 2016, 125, 244–253. [Google Scholar] [CrossRef]
- Baqersad, J.; Bharadwaj, K. Strain expansion-reduction approach. Mech. Syst. Signal Process. 2018, 101, 156–167. [Google Scholar] [CrossRef]
- Reiland, M.; Kane, B.; Modarres-Sadeghi, Y.; Ryan, H.D.P. The effect of cables and leaves on the dynamic properties of red oak (Quercus rubra) with co-dominant stems. Urban For. Urban Green. 2015, 14, 844–850. [Google Scholar] [CrossRef]
- Weissteiner, C.; Rauch, H.P. The architecture and dynamic properties of young Salix purpurea trees in the context of riparian engineering systems. Ecol. Eng. 2018, 123, 161–167. [Google Scholar] [CrossRef]
- Desjardins, S.; Poitras, G. In-operation performance evaluation of damped light poles using fatigue life estimations. Eng. Struct. 2022, 258, 114081. [Google Scholar] [CrossRef]
- Pagnini, L.C.; Solari, G. Damping measurements of steel poles and tubular towers. Eng. Struct. 2001, 23, 1085–1095. [Google Scholar] [CrossRef]
- Janeliukstis, R. Continuous wavelet transform-based method for enhancing estimation of wind turbine blade natural frequencies and damping for machine learning purposes. Measurement 2021, 172, 108897. [Google Scholar] [CrossRef]
- Heylen, W.; Lammens, S.; Sas, P. Modal Analysis Theory and Testing; KUL: Leuven, Belgium, 1994. [Google Scholar]
- Worden, K.; Burrows, A.P. Optimal sensor placement for fault detection. Eng. Struct. 2001, 23, 885–901. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W. An Overview of modal-based damage identification methods. In Proceedings of the DAMAS Conference, Sheffield, UK, 30 June–2 July 1997. [Google Scholar]
- Iwaniec, J.; Kurowski, P. Experimental verification of selected methods sensitivity to damage size and location. J. Vib. Control 2017, 23, 1133–1151. [Google Scholar] [CrossRef]
- Naidu, P.S. Modern Spectrum Analysis of Time Series; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Inman, D.J. Engineering Vibration, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2001. [Google Scholar]
- Ewins, D.J. Modal Testing: Theory and Practice; Research Studies Press: Letchworth, UK, 1984. [Google Scholar]
- Antoniou, A. Digital Signal Processing; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Bendat, J.S.; Piersol, A.G. Random Data, 2nd ed.; John Wiley: New York, NY, USA, 1986. [Google Scholar]
- Welch, P.D. The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]







| No. | Frequency (Hz) | Damping (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Classical Method | Pseudo-Impulse | Classical Method | Pseudo-Impulse | |||||
| LSCE | BR | LSCE | LSCF | LSCE | BR | LSCE | LSCF | |
| 1. | - | - | - | 1.50 | - | - | - | 32.90 |
| 2. | - | - | 5.85 | - | - | - | 9.89 | - |
| 3. | - | - | 5.99 | 6.16 | - | - | 7.61 | 1.12 |
| 4. | 9.82 | 9.77 | 10.02 | 9.94 | 5.19 | 3.74 | 3.90 | 0.72 |
| 5. | - | - | - | 11.41 | - | - | - | 0.23 |
| 6. | 13.52 | 13.22 | 13.55 | 13.47 | 4.64 | 1.68 | 2.00 | 1.27 |
| 7. | - | - | - | 14.79 | - | - | - | 0.05 |
| 8. | 17.80 | 17.63 | 17.41 | 17.53 | 3.06 | 1.72 | 2.19 | 0.25 |
| 9. | - | - | 17.63 | - | - | - | 1.73 | - |
| 10. | 21.92 | - | 21.28 | - | 5.21 | - | 3.05 | - |
| 11. | 24.92 | 23.17 | 23.53 | 23.68 | 3.81 | 1.00 | 3.30 | 0.15 |
| 12. | - | 26.02 | 24.84 | 25.61 | - | 2.55 | 2.55 | 0.13 |
| 13. | 33.64 | 31.76 | 33.46 | - | 3.44 | 3.31 | 3.20 | - |
| 14. | 38.13 | 36.68 | 34.48 | 36.27 | 2.03 | 4.27 | 1.07 | 0.38 |
| 15. | 38.80 | 38.43 | 38.36 | 37.78 | 3.48 | 1.93 | 1.70 | 0.28 |
| 16. | 39.07 | - | - | 39.83 | 4.33 | - | - | 0.26 |
| 17. | 41.70 | 41.68 | 41.89 | 41.93 | 2.72 | 3.70 | 1.75 | 0.33 |
| 18. | - | - | - | 43.16 | - | - | - | 0.12 |
| 19. | 46.86 | 46.57 | 45.31 | 44.57 | 3.35 | 3.35 | 2.66 | 0.04 |
| 20. | - | - | 47.77 | 48.03 | - | - | 2.61 | 0.34 |
| 21. | 50.05 | 49.81 | 49.83 | 48.95 | 0.038 | 0.44 | 0.45 | 0.12 |
| 22. | 54.33 | 55.96 | 53.76 | 52.57 | 1.70 | 3.64 | 1.52 | 0.14 |
| No. | Frequency (Hz) | Damping (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Classical Method | Pseudo-Impulse | Classical Method | Pseudo-Impulse | |||||
| LSCE | BR | LSCE | LSCF | LSCE | BR | LSCE | LSCF | |
| 23. | - | - | 54.52 | 53.85 | - | - | 1.74 | 0.06 |
| 24 | - | - | 54.62 | 55.88 | - | - | 1.24 | 0.12 |
| 25. | 57.08 | 57.50 | 56.29 | 57.71 | 5.10 | 1.38 | 2.59 | 0.17 |
| 26. | - | - | 58.95 | - | - | - | 1.14 | - |
| 27. | 61.71 | 62.31 | 61.83 | 61.95 | 1.08 | 0.45 | 0.55 | 0.10 |
| 28. | 66.42 | - | 66.28 | 66.50 | 0.83 | - | 0.49 | 0.04 |
| 29. | 69.94 | 70.28 | 69.70 | 69.03 | 0.88 | 0.30 | 0.79 | 0.03 |
| 30. | - | - | 69.72 | 70.52 | - | - | 0.78 | 0.11 |
| 31. | 74.30 | - | 74.35 | 75.19 | 0.92 | - | 1.04 | 0.06 |
| 32. | - | - | 74.45 | - | - | - | 0.82 | - |
| 33. | 78.03 | 78.52 | 77.52 | 77.84 | 1.52 | 0.50 | 0.75 | 0.11 |
| 34. | - | - | 80.93 | - | - | - | 0.76 | - |
| 35. | - | - | 81.04 | - | - | - | 0.93 | - |
| 36. | 82.66 | 83.14 | 83.78 | 83.54 | 1.17 | 0.58 | 0.86 | 0.10 |
| 37. | 84.28 | - | 83.99 | - | 2.86 | - | 0.84 | - |
| 38. | - | - | 85.11 | - | - | - | 1.23 | - |
| 39. | 87.89 | 87.49 | 86.83 | - | 1.59 | 0.80 | 1.27 | - |
| 40. | - | - | 88.61 | - | - | - | 1.34 | - |
| 41. | - | - | 91.64 | 90.76 | - | - | 1.84 | 0.05 |
| 42. | 92.97 | 93.42 | 93.09 | 92.98 | 1.06 | 1.88 | 1.90 | 0.12 |
| 43. | - | - | 93.45 | 94.52 | - | - | 0.75 | 0.06 |
| 44. | 97.62 | 97.72 | - | 97.23 | 0.71 | 0.13 | - | 0.03 |
| 45. | - | - | 98.09 | 98.22 | - | - | 0.67 | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwaniec, J.; Iwaniec, M.; Kurowski, P.; Szopa, K. Investigation into Power Line Supporting Structure Dynamic Properties by Means of Impulse Test. Energies 2022, 15, 5707. https://doi.org/10.3390/en15155707
Iwaniec J, Iwaniec M, Kurowski P, Szopa K. Investigation into Power Line Supporting Structure Dynamic Properties by Means of Impulse Test. Energies. 2022; 15(15):5707. https://doi.org/10.3390/en15155707
Chicago/Turabian StyleIwaniec, Joanna, Marek Iwaniec, Piotr Kurowski, and Krystian Szopa. 2022. "Investigation into Power Line Supporting Structure Dynamic Properties by Means of Impulse Test" Energies 15, no. 15: 5707. https://doi.org/10.3390/en15155707
APA StyleIwaniec, J., Iwaniec, M., Kurowski, P., & Szopa, K. (2022). Investigation into Power Line Supporting Structure Dynamic Properties by Means of Impulse Test. Energies, 15(15), 5707. https://doi.org/10.3390/en15155707







