Electromagnetic Design and Analysis of Permanent Magnet Linear Synchronous Motor
Abstract
:1. Introductions
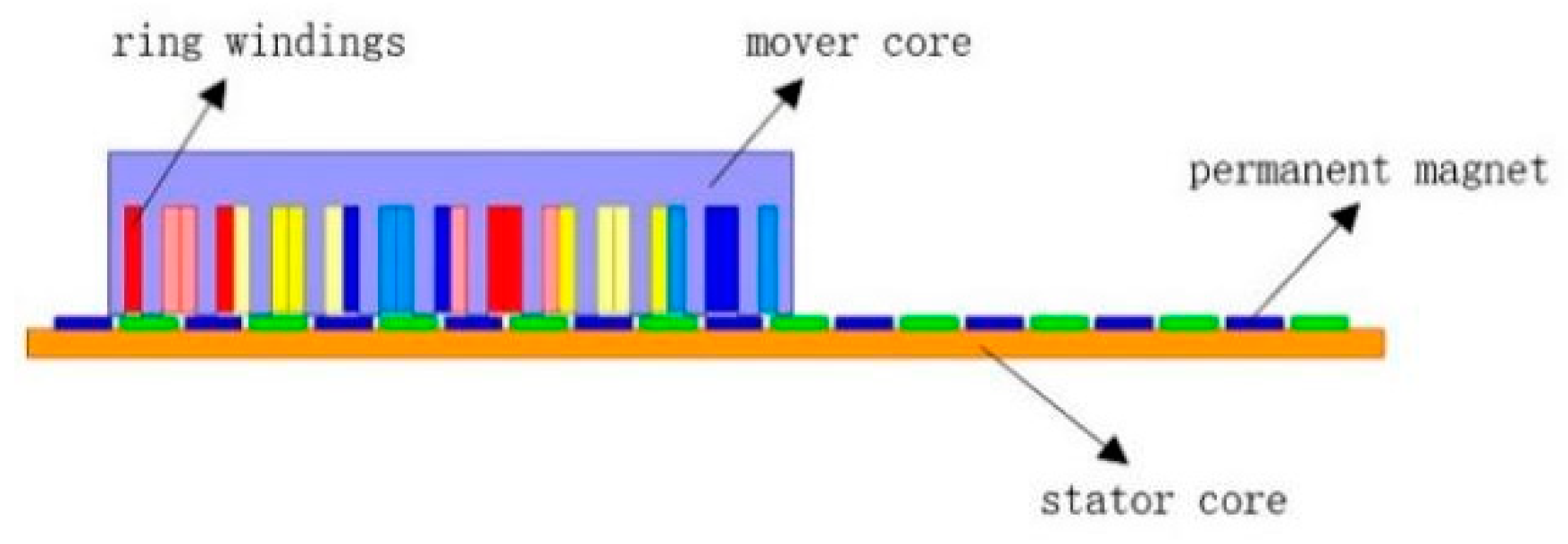
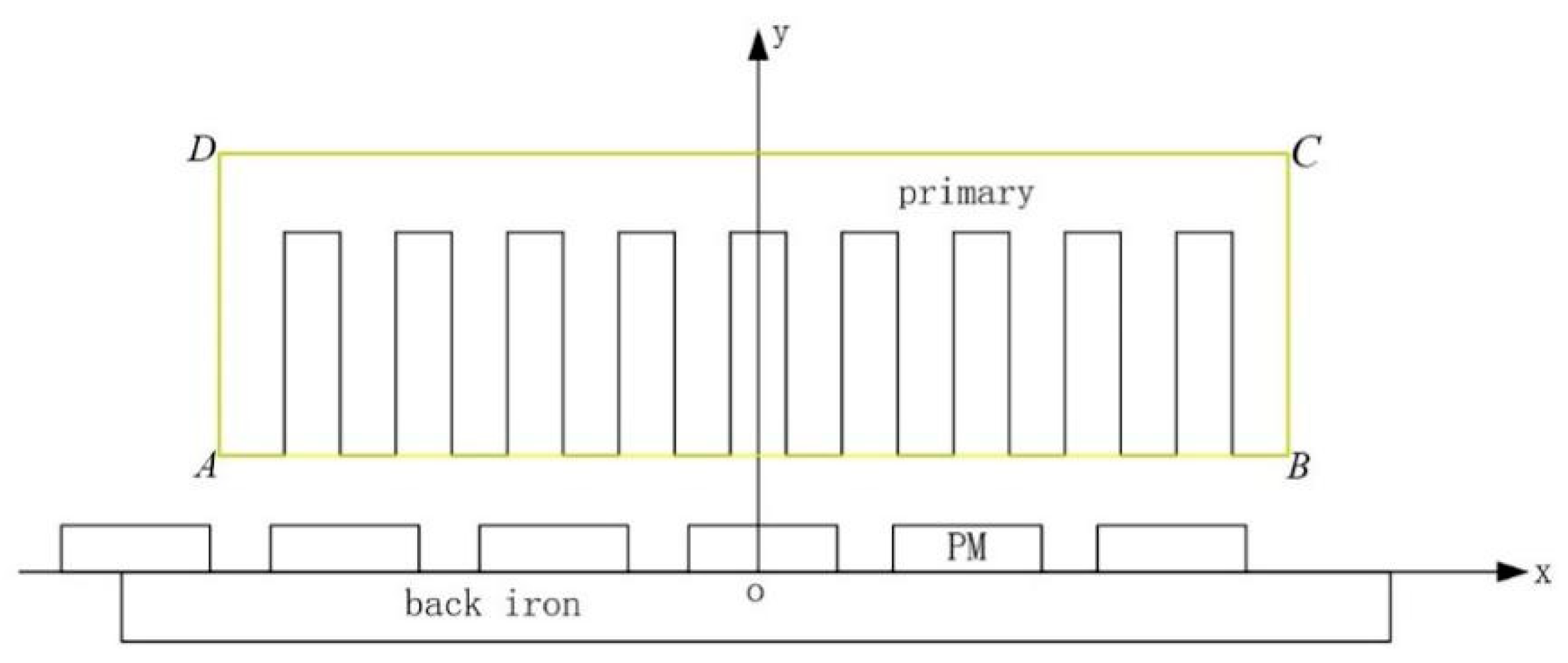
2. PMLSM Structure and Parameters
3. PMLSM Theoretical Analysis
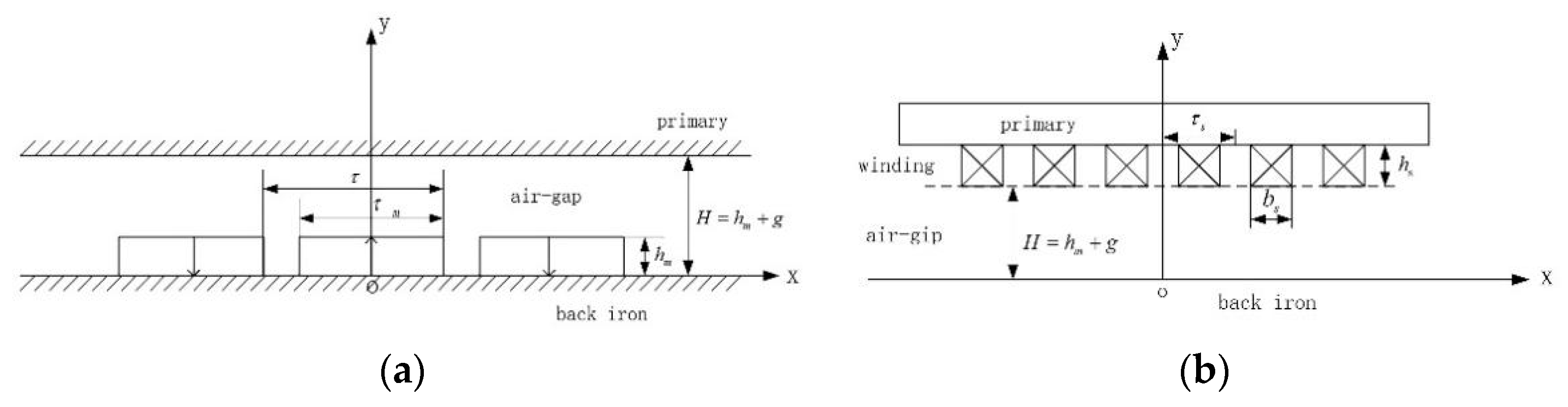
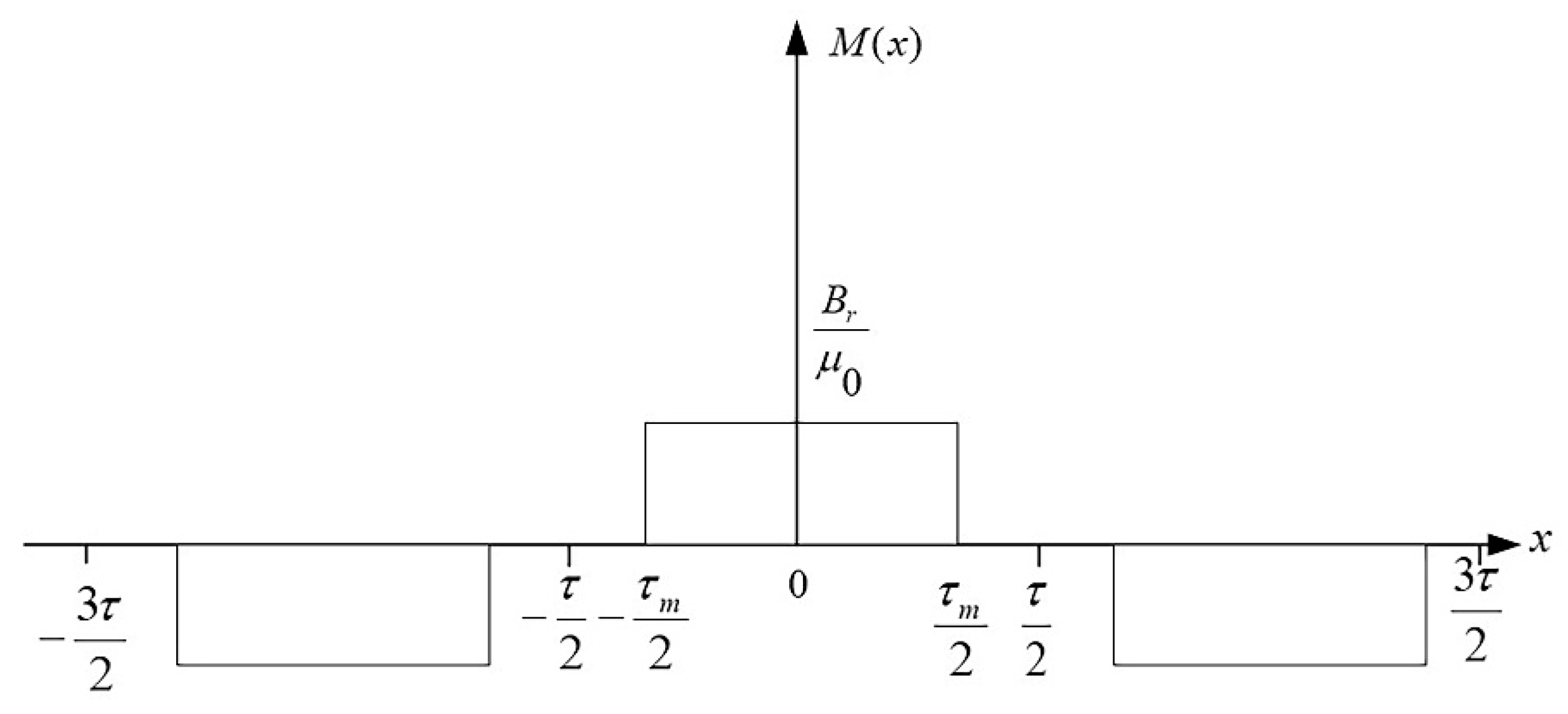
3.1. Magnetic Field Analysis
3.2. Electromagnetic Thrust Calculation
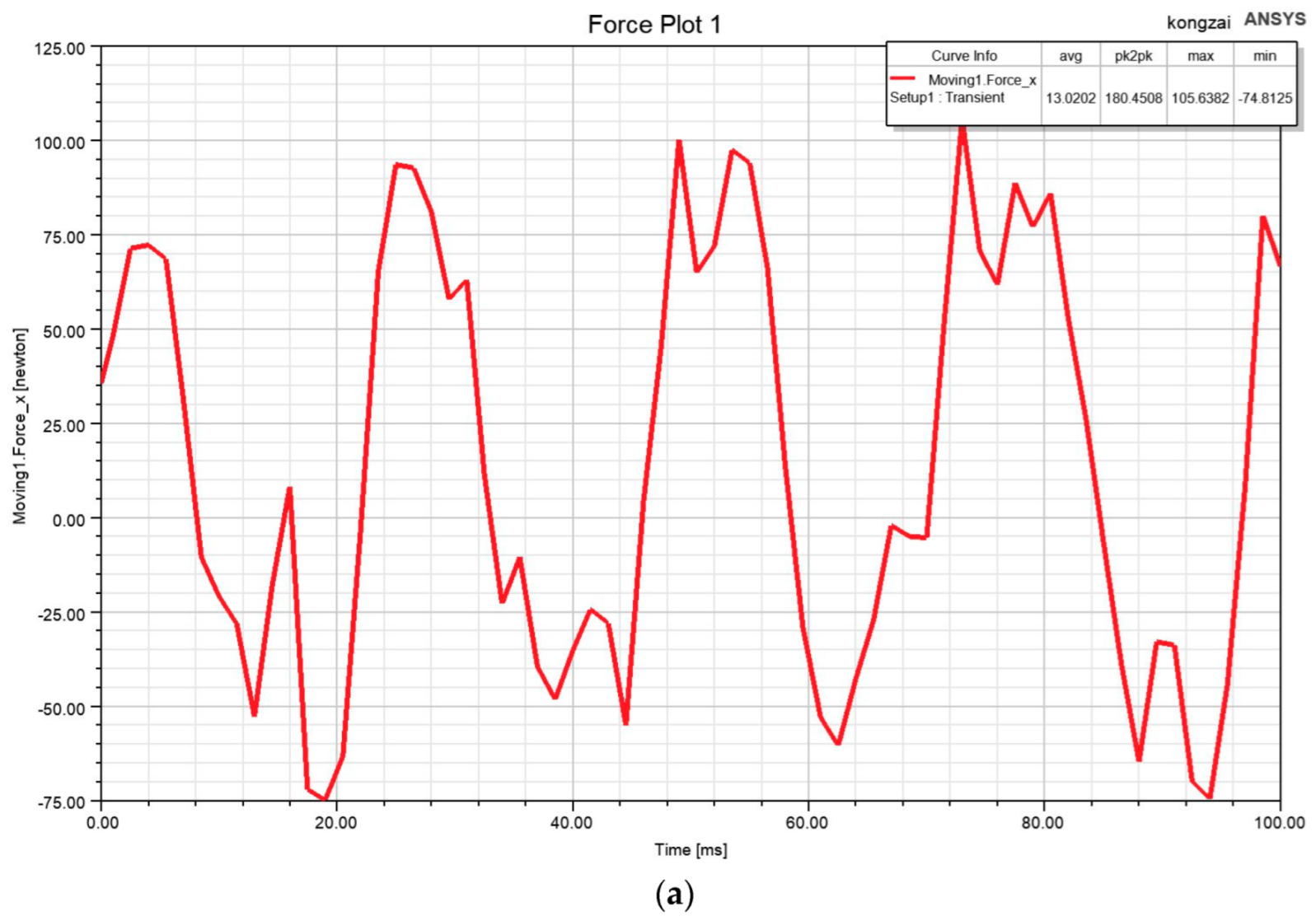
3.3. Vibration Analysis
4. Finite Element Analysis
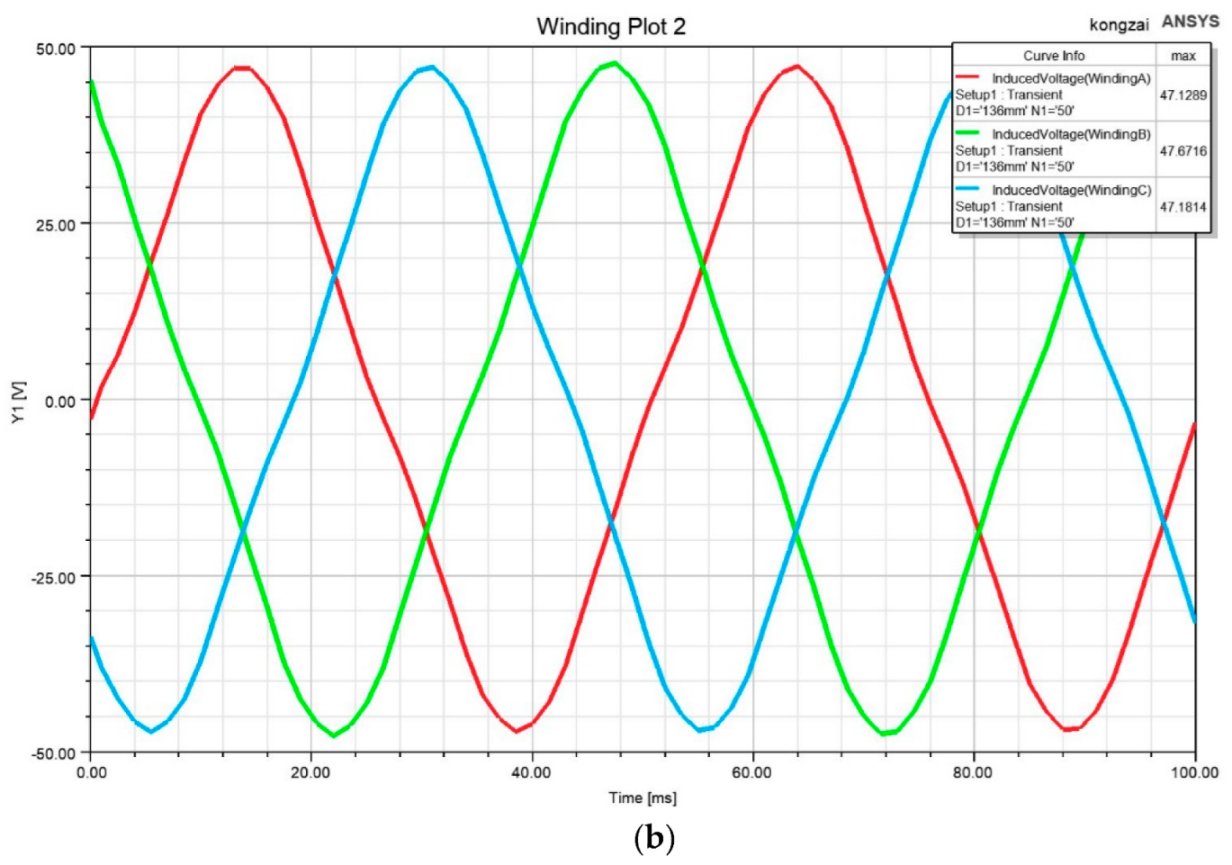
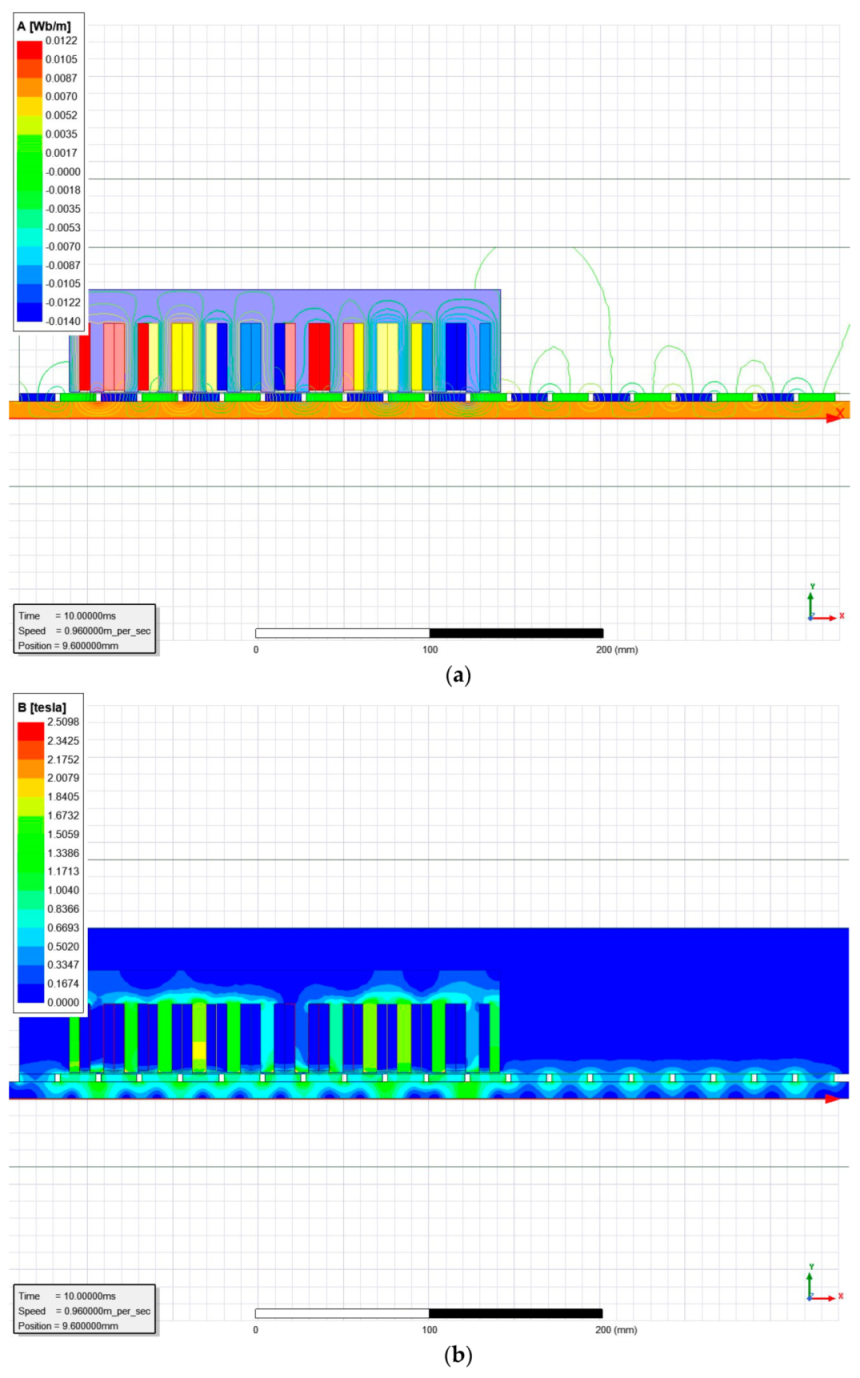
4.1. Analysis of No-Load Simulation Results
4.2. Analysis of Load Simulation Results
5. Experimental Analysis
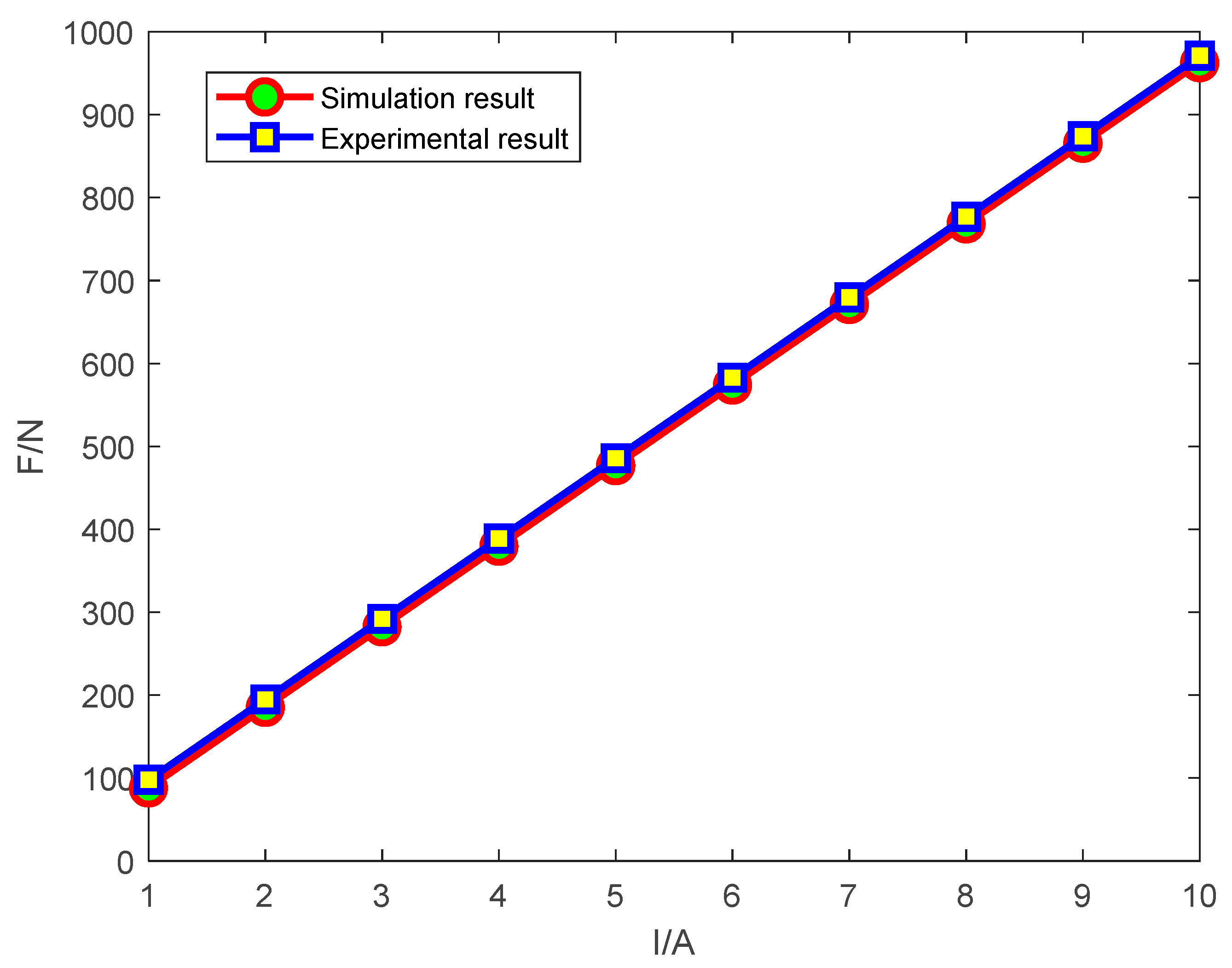
5.1. Thrust Constant Test
5.2. Resonance Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, X.Z.; Li, J.; Zhang, C.; Qian, Z.Y.; Li, L.; Gerada, D. Electromagnetic and Thrust Characteristics of Double-sided Permanent Magnet Linear Synchronous Motor Adopting Staggering Primaries Structure. IEEE Trans. Ind. Electron. 2019, 66, 4826–4836. [Google Scholar] [CrossRef]
- Huang, X.Z.; Yu, H.C.; Zhou, B.; Li, L.Y.; Gerada, D.; Gerada, C.; Qian, Z.Y. Detent-Force Minimization of Double-Sided Permanent Magnet Linear Synchronous Motor by Shifting One of the Primary Components. IEEE Trans. Ind. Electron. 2020, 67, 180–191. [Google Scholar] [CrossRef]
- Shen, Y.; Lu, Q.; Li, H.; Cai, J.; Huang, X.; Fang, Y. Analysis of a Novel Double-Sided Yokeless Multitooth Linear Switched-Flux PM Motor. IEEE Trans. Ind. Electron. 2018, 65, 1837–1845. [Google Scholar] [CrossRef]
- Luu, P.T.; Lee, J.-Y.; Kim, J.-W.; Chung, S.-U.; Kwon, S.-M. Magnetic Sensor Design for a Permanent Magnet Linear Motor Considering Edge-Effect. IEEE Trans. Ind. Electron. 2020, 67, 5768–5777. [Google Scholar] [CrossRef]
- Tan, Q.; Huang, X.Z.; Li, L.; Wang, M. Magnetic Field Analysis and Flux Barrier Design for Modular Permanent Magnet Linear Synchronous Motor. IEEE Trans. Ind. Electron. 2020, 67, 3891–3900. [Google Scholar] [CrossRef]
- Cui, F.; Sun, Z.; Xu, W.; Zhou, W.; Liu, Y. Comparative analysis of bilateral permanent magnet linear synchronous motors with different structures. CES Trans. Electr. Mach. Syst. 2020, 4, 142–150. [Google Scholar] [CrossRef]
- Kang, G.-H.; Hong, J.-P.; Kim, G.-T. A novel design of an air-core type permanent magnet linear brushless motor by space harmonics field analysis. IEEE Trans. Magn. 2001, 37, 3732–3736. [Google Scholar] [CrossRef]
- Kim, J.; Joo, S.; Hahn, S.; Hong, J.; Kang, D.; Koo, D. Static Characteristics of Linear BLDC Motor Using Equivalent Magnetic Circuit and Finite Element Method. IEEE Trans. Magn. 2004, 40, 742–745. [Google Scholar] [CrossRef]
- Liu, X.; Gao, J.; Huang, S.; Lu, K. Magnetic Field and Thrust Analysis of the U-Channel Air-Core Permanent Magnet Linear Synchronous Motor. IEEE Trans. Magn. 2017, 53, 8201504. [Google Scholar] [CrossRef]
- Hu, H.; Zhao, J.; Liu, X.; Guo, Y. Magnetic Field and Force Calculation in Linear Permanent-Magnet Synchronous Machines Accounting for Longitudinal End Effect. IEEE Trans. Ind. Electron. 2016, 63, 7632–7643. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.Q.; Wu, L.J.; Xia, Z.P. An Accurate Subdomain Model for Magnetic Field Computation in Slotted Surface-Mounted Permanent-Magnet Machines. IEEE Trans. Magn. 2010, 46, 1100–1115. [Google Scholar] [CrossRef]
- Virtic, P.; Stumberger, B. Analytical Analysis of Magnetic Field and Force Calculation in a Slotless-Type Permanent Magnet Linear Synchronous Machine; Verification with Numerical Analysis. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Cracow, Poland, 6–8 September 2007; pp. 963–968. [Google Scholar]
- Bao-Quan, K.; Hong-Xing, W.; Li-Yi, L.; Liang-Liang, Z.; Zhe, Z.; Hai-Chuan, C. The Thrust Characteristics Investigation of Double-Side Plate Permanent Magnet Linear Synchronous Motor for EML. IEEE Trans. Magn. 2009, 45, 501–505. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, L.; Wang, K.; Li, Y. Characteristics investigation of single-sided ironless pmlsm based on Halbach array for medium-speed Maglev train. CES Trans. Electr. Mach. Syst. 2017, 1, 375–382. [Google Scholar] [CrossRef]
- Li, C.; Kou, B. Research on Electromagnetic Force of Large Thrust Force PMLSM Used in Space Electromagnetic Launcher. IEEE Trans. Plasma Sci. 2013, 41, 1209–1213. [Google Scholar]
- Song, J.; Dong, F.; Zhao, J.; Lu, S.; Li, L.; Pan, Z. A New Design Optimization Method for Permanent Magnet Synchronous Linear Motors. Energies 2016, 9, 992. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Cheng, M.; Ji, J.; Cao, R.; Du, Y.; Li, F. Design and Analysis of a New Fault-Tolerant Linear Permanent-Magnet Motor for Maglev Transportation Applications. IEEE Trans. Appl. Supercond. 2012, 22, 5200204. [Google Scholar] [CrossRef]
- Zhang, X.M.; Cheng, C.Y.; Lu, Q.F.; Ye, Y.Y.; Tao, X.S. Design and Electromagnetic Analysis of a Double-Sided Permanent Magnet Linear Synchronous Motor. Appl. Mech. Mater. 2013, 416–417, 270–275. [Google Scholar] [CrossRef]
- Li, L.; Zhu, G.; Liu, X.; Chen, H.; Jiang, W.; Xue, M. Design and Optimization of a Novel HTS Flux-Modulated Linear Motor Using Halbach Permanent Magnet Arrays. IEEE Trans. Appl. Supercond. 2021, 31, 5203104. [Google Scholar] [CrossRef]
- Yue, F.; Sun, Z.; Xu, W.; Li, X. Calculation and analysis of electromagnetic vibration of transverse flux linear oscillation motor with moving stator. In Proceedings of the 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Yue, F.; Sun, Z.; Xu, W.; Yang, X. Structure Optimization Design and Analysis of Transverse Flux Linear Oscillation Motor with Moving Stator. In Proceedings of the 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Mao, Y.; Sun, Z.; Zhou, W.; Zhuang, Z.; Qian, H. Electromagnetic Design of Toroidal Permanent Magnet Linear Synchronous Motor. IEEE Access 2021, 9, 98005–98012. [Google Scholar] [CrossRef]










| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Slot width | 12 | mm | |
| Slot depth | 40 | mm | |
| Tooth width | 8 | mm | |
| The length of the mover core | 252 | mm | |
| The thickness of the mover yoke | 20 | mm | |
| Permanent magnet width | 21 | mm | |
| Permanent magnet height | 4.4 | mm | |
| Air gap height | 1 | mm | |
| Stator core length | 500 | mm | |
| Stator iron yoke thickness | 10 | mm | |
| Polar pitch | 24 | mm | |
| Number of coil turns | 50 | ||
| Number of permanent magnets | 20 | ||
| Number of slots | 12 |
| Current RMS A | Simulate Output Thrust N | Simulation Thrust Constant N/A | Experimental Output Thrust N | Experimental Thrust Constant N/A |
|---|---|---|---|---|
| 1 | 99 | 99 | 89 | 89 |
| 2 | 205 | 102.5 | 196 | 98 |
| 3 | 295 | 98.3 | 291 | 97 |
| 4 | 390 | 97.5 | 392 | 98 |
| 5 | 485 | 97 | 489 | 97.8 |
| 6 | 579 | 96.5 | 589 | 98.1 |
| 7 | 674 | 96.2 | 676 | 96.5 |
| 8 | 765 | 95.6 | 772 | 96.5 |
| 9 | 860 | 95.5 | 881 | 97.8 |
| 10 | 948 | 94.8 | 966 | 96.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Chang, S.; He, J.; Sun, H.; Huang, J.; Tian, H. Electromagnetic Design and Analysis of Permanent Magnet Linear Synchronous Motor. Energies 2022, 15, 5441. https://doi.org/10.3390/en15155441
Yu L, Chang S, He J, Sun H, Huang J, Tian H. Electromagnetic Design and Analysis of Permanent Magnet Linear Synchronous Motor. Energies. 2022; 15(15):5441. https://doi.org/10.3390/en15155441
Chicago/Turabian StyleYu, Lijuan, Shuyuan Chang, Jialong He, Huilu Sun, Jie Huang, and Hailong Tian. 2022. "Electromagnetic Design and Analysis of Permanent Magnet Linear Synchronous Motor" Energies 15, no. 15: 5441. https://doi.org/10.3390/en15155441
APA StyleYu, L., Chang, S., He, J., Sun, H., Huang, J., & Tian, H. (2022). Electromagnetic Design and Analysis of Permanent Magnet Linear Synchronous Motor. Energies, 15(15), 5441. https://doi.org/10.3390/en15155441






