Comparison of Interleaving Methods of Parallel Connected Three-Level Bi-Directional Converters
Abstract
:1. Introduction
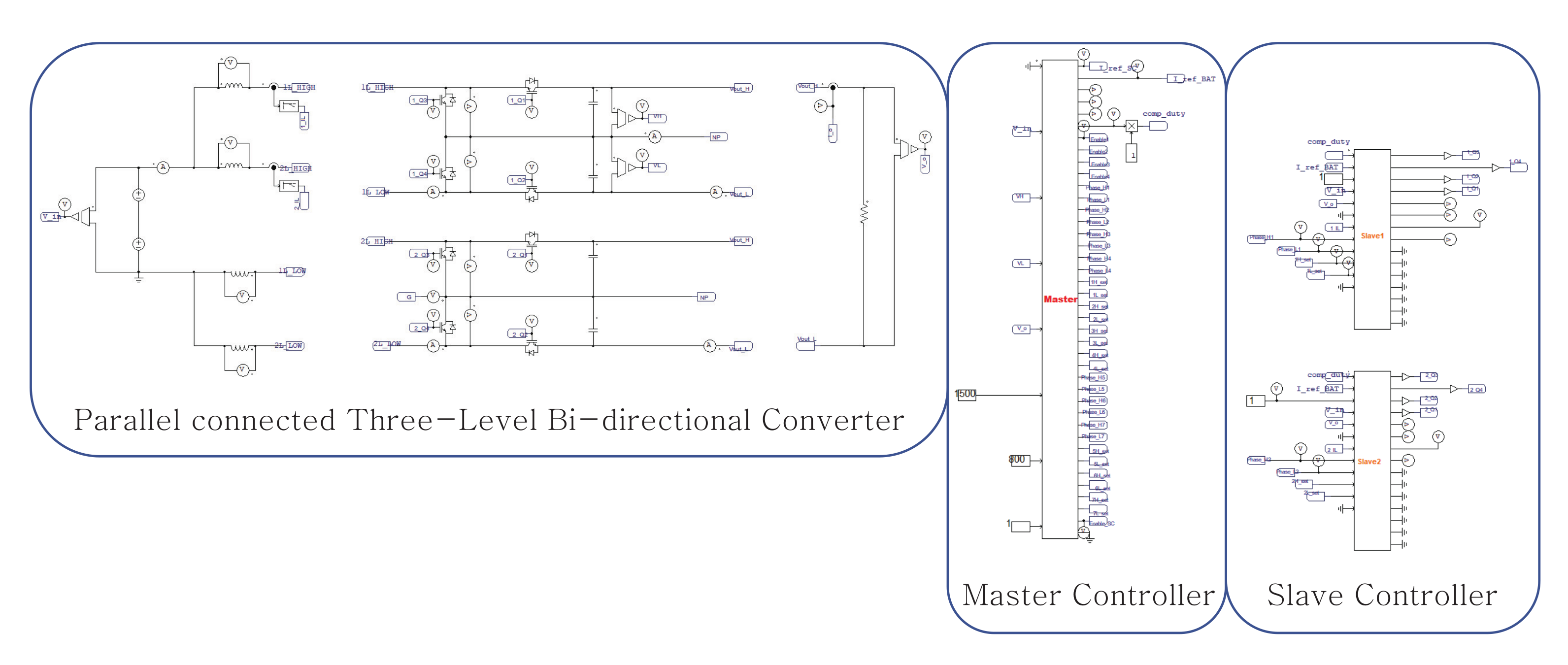
2. Parallel Operation of Two-Phase Parallel TLBC
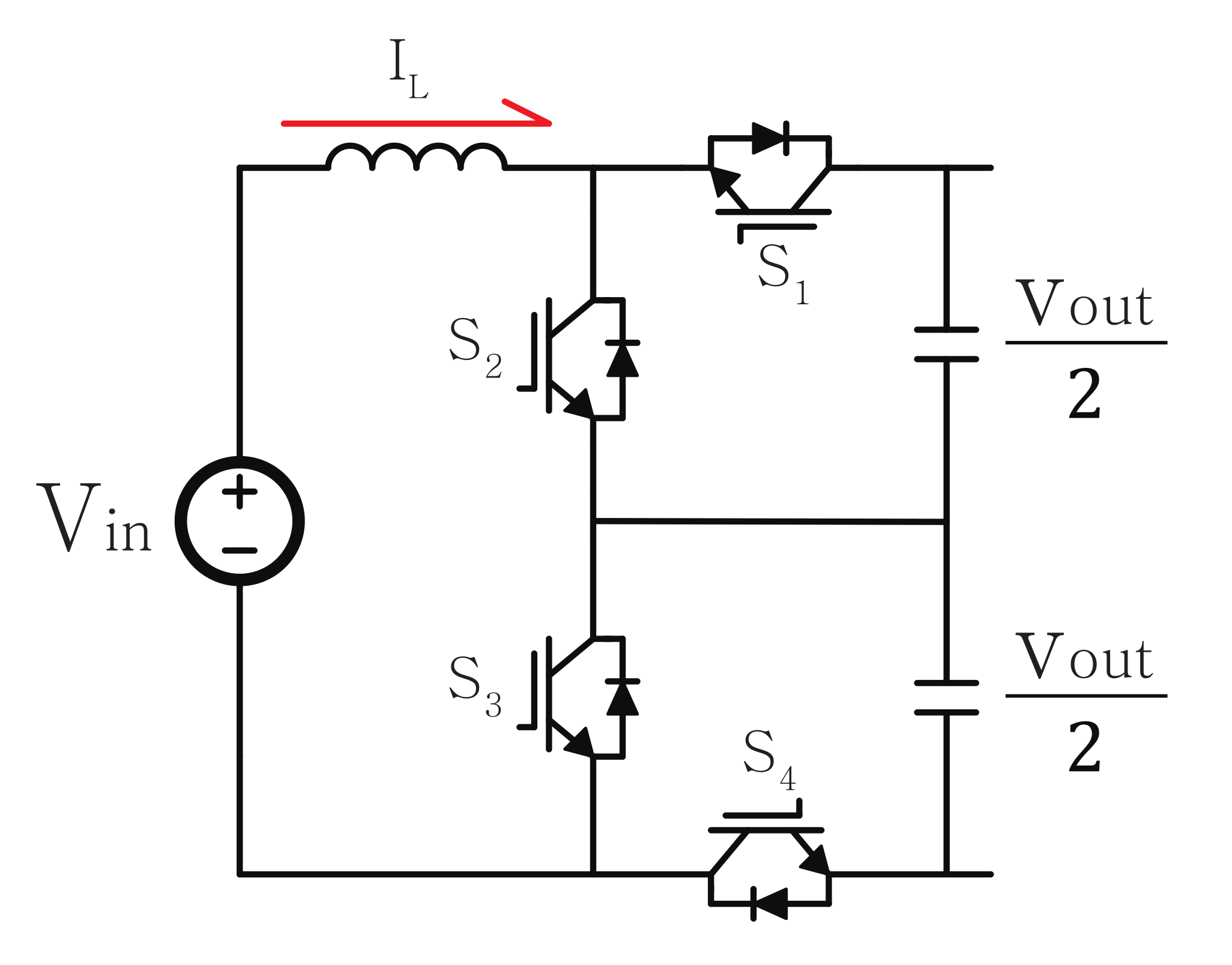
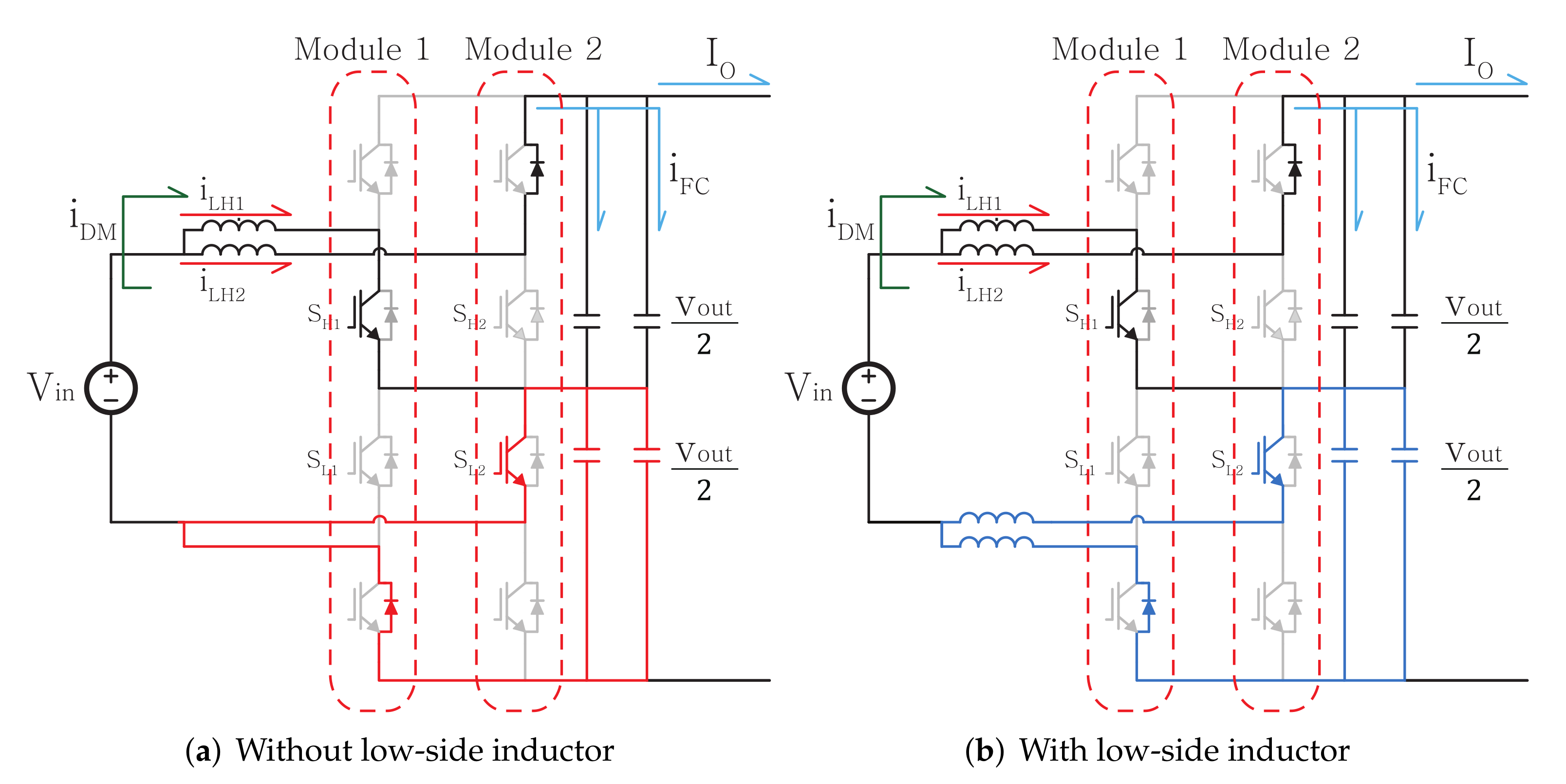
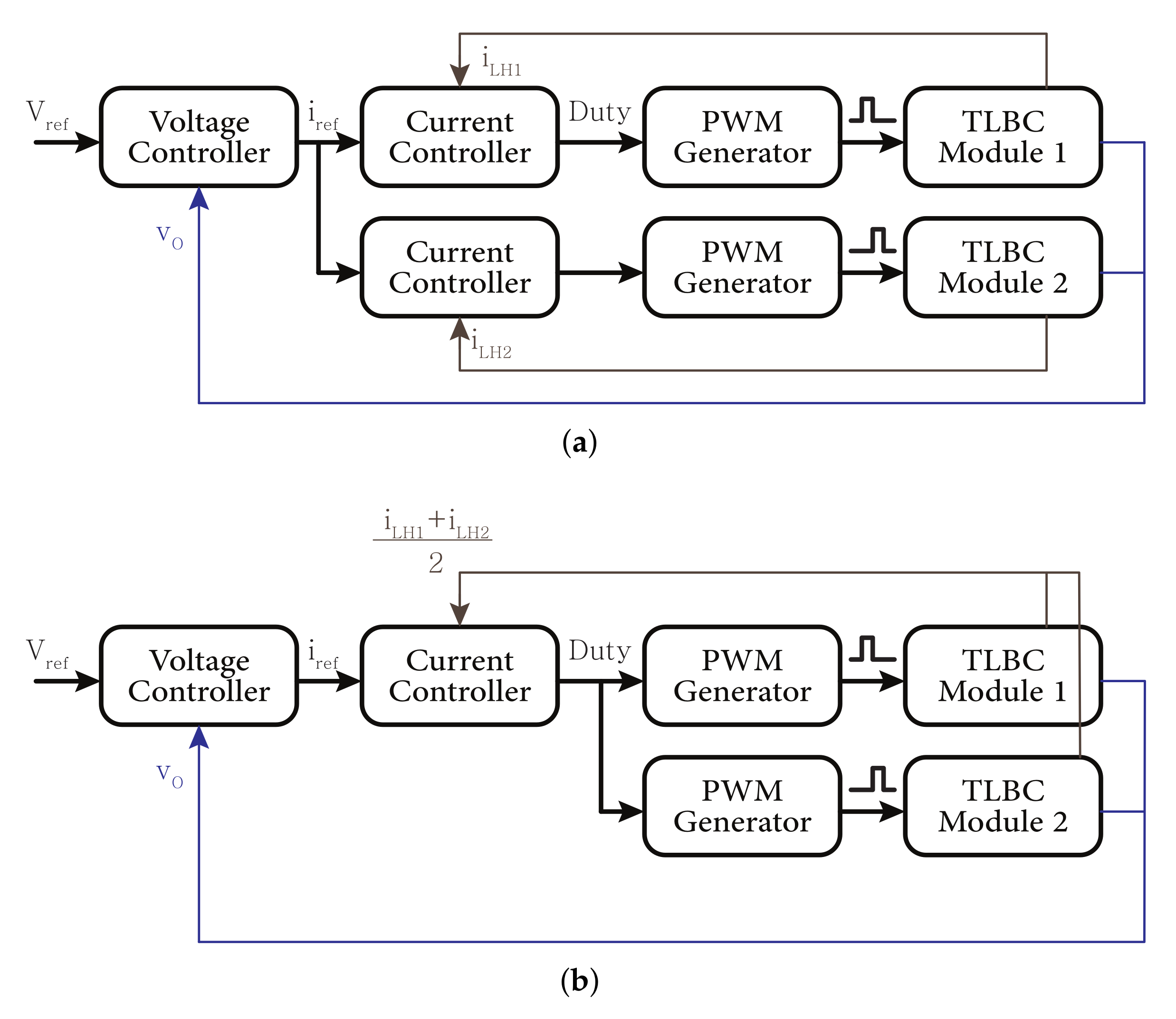
2.1. Circuit of Two-Phase Parallel TLBC
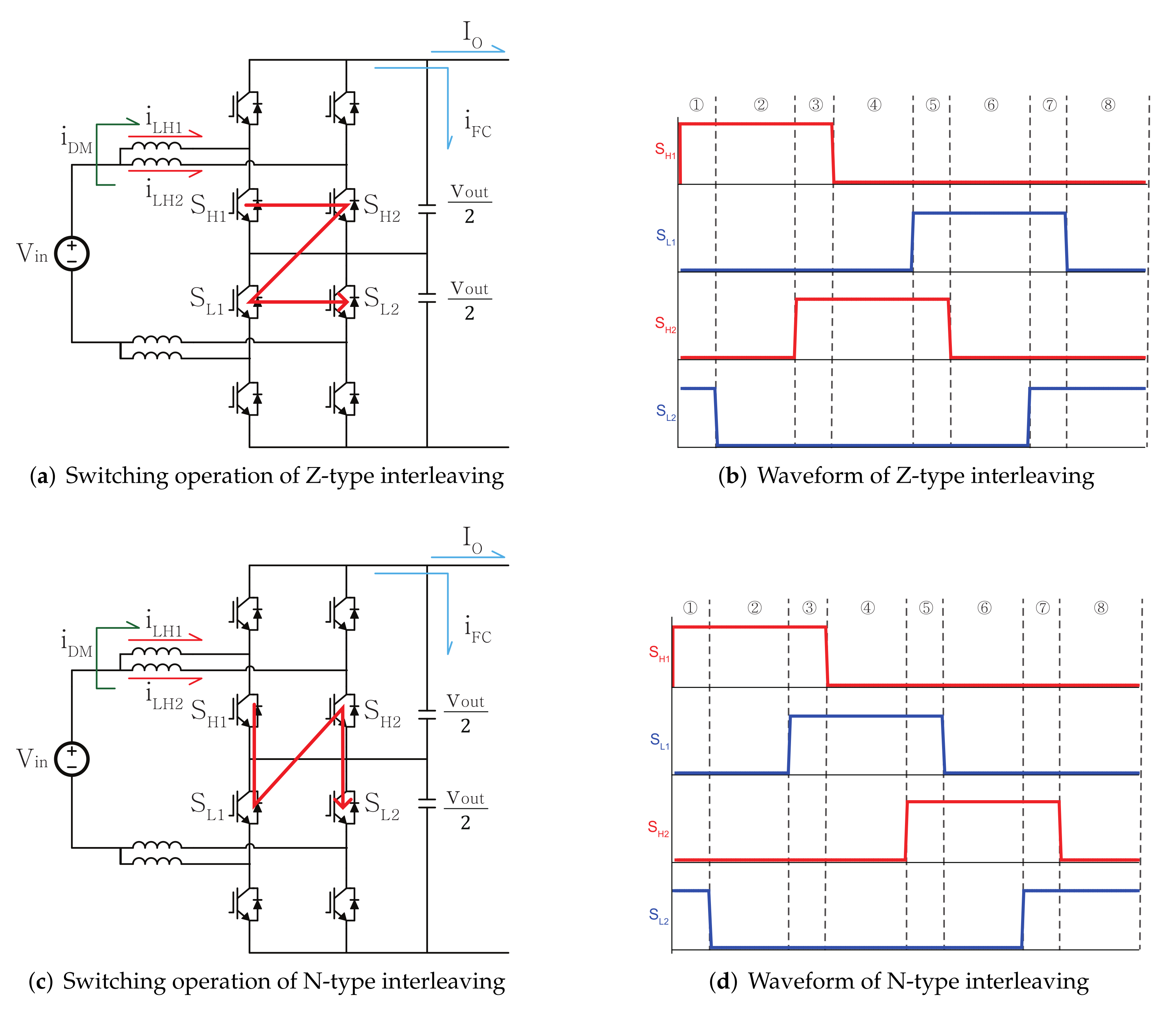
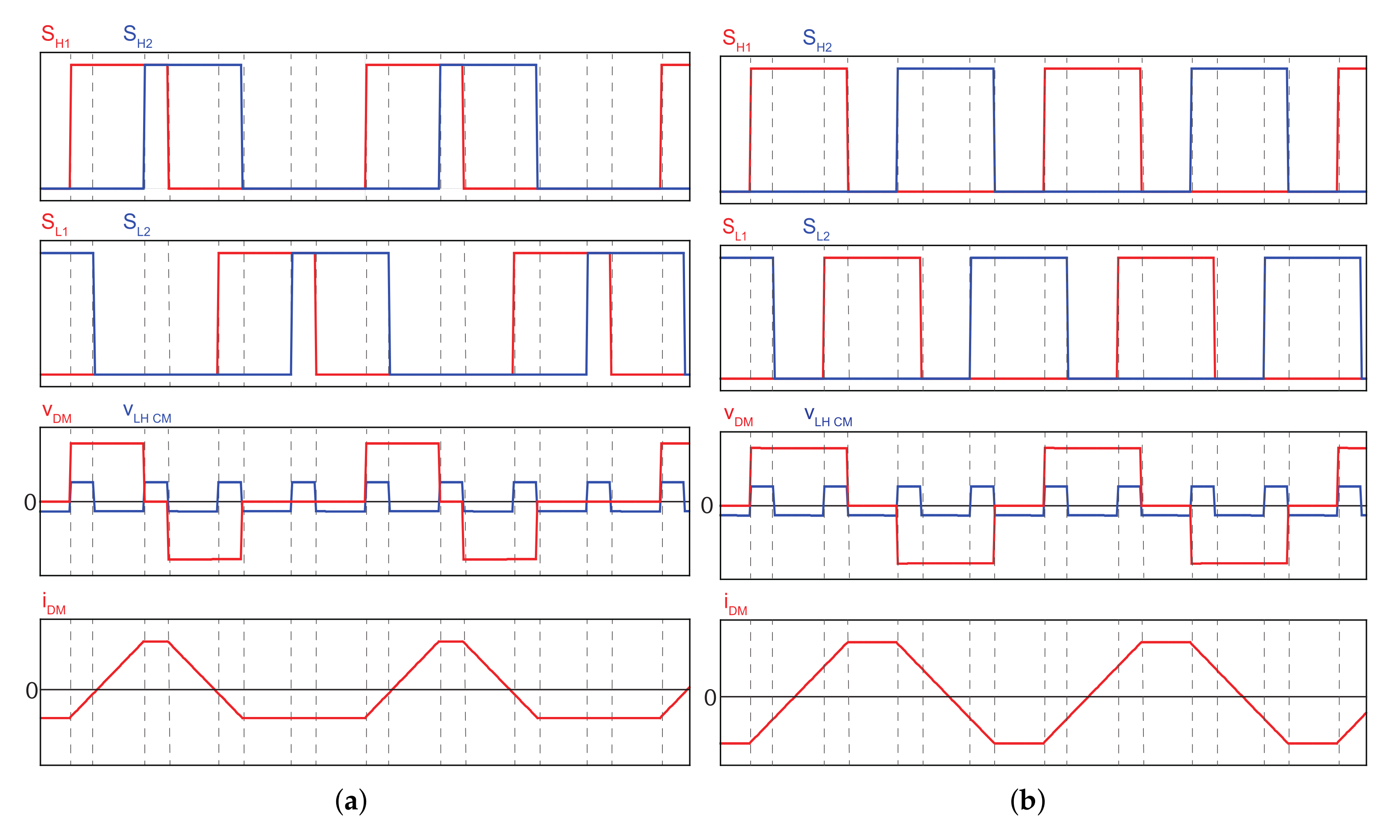
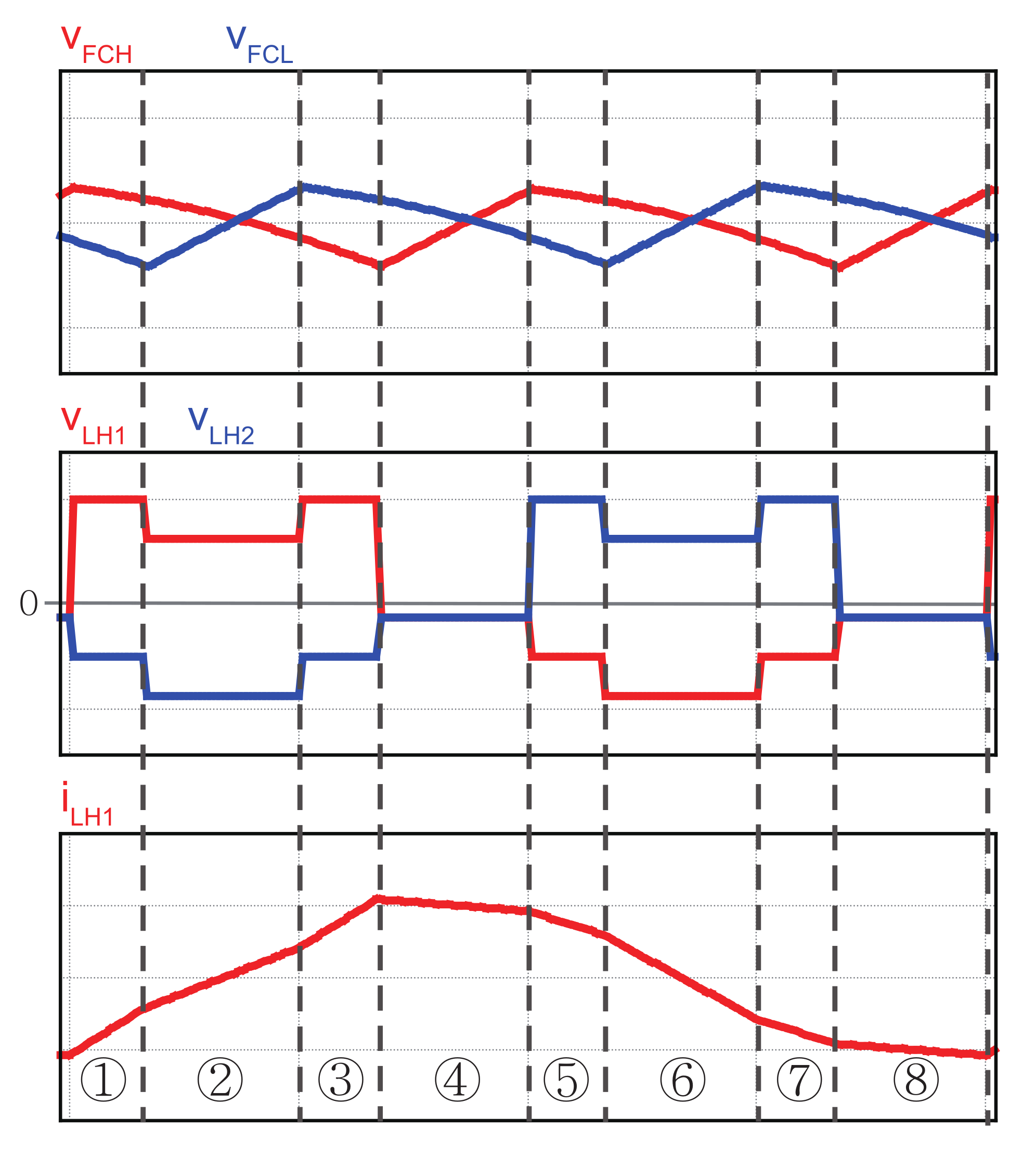
2.2. Interleaving Methods of 2 Parallel Three-Level Bi-Directional Converters
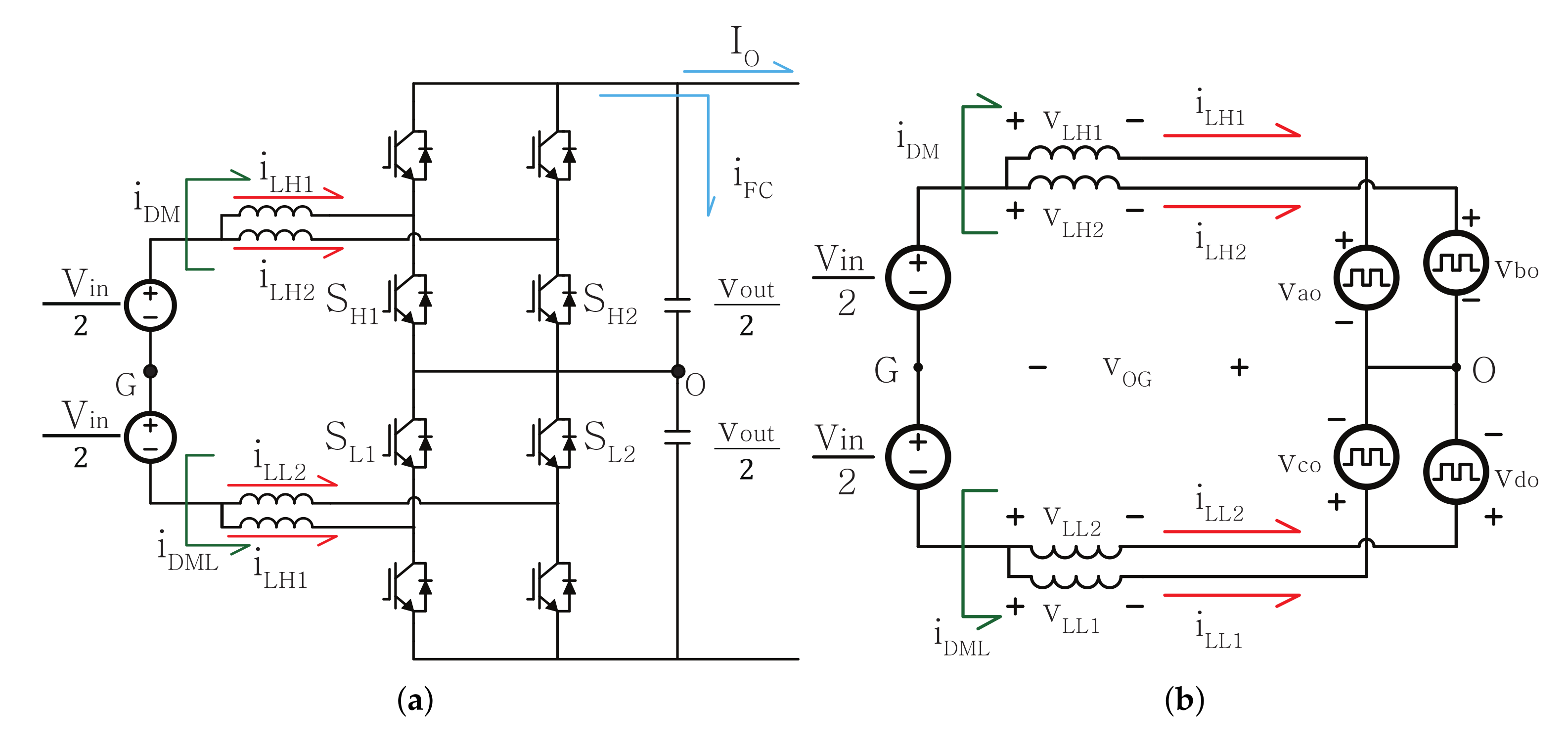
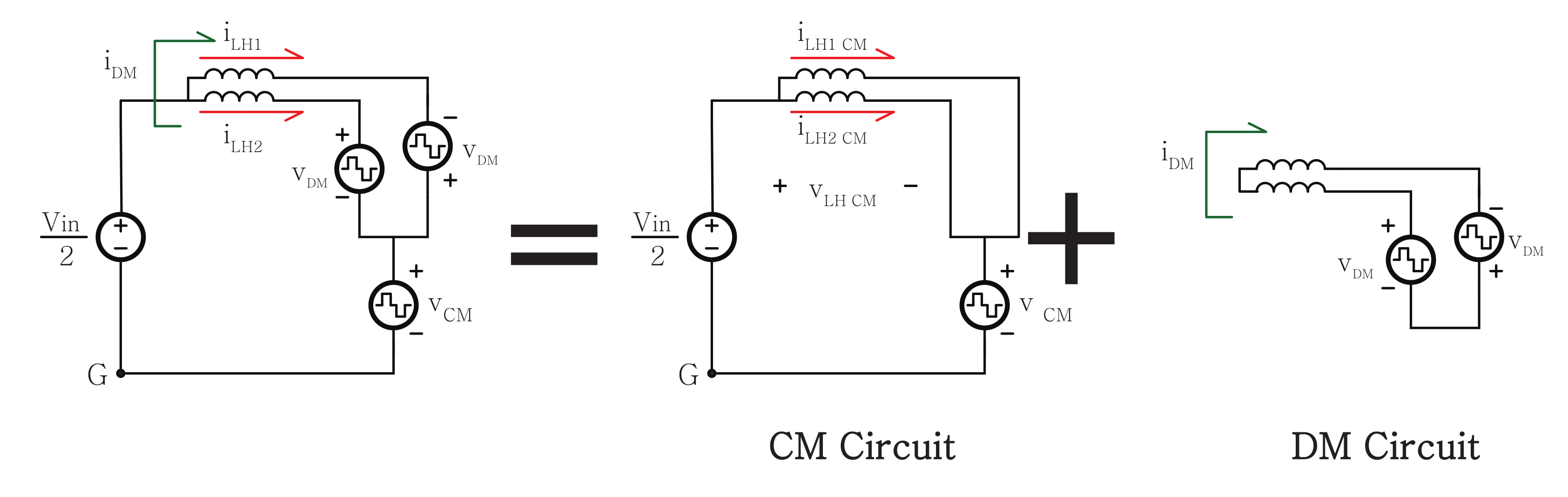
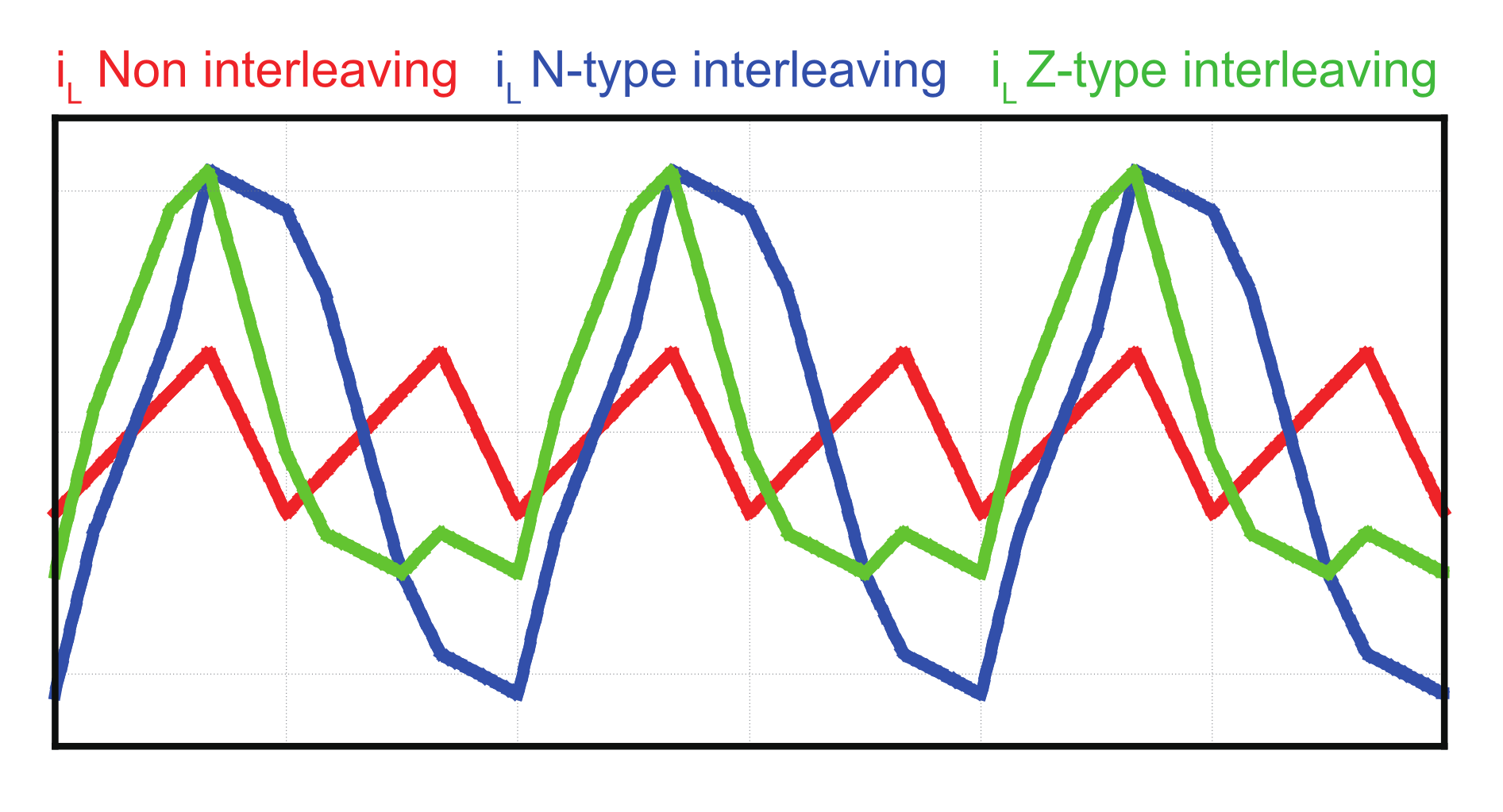
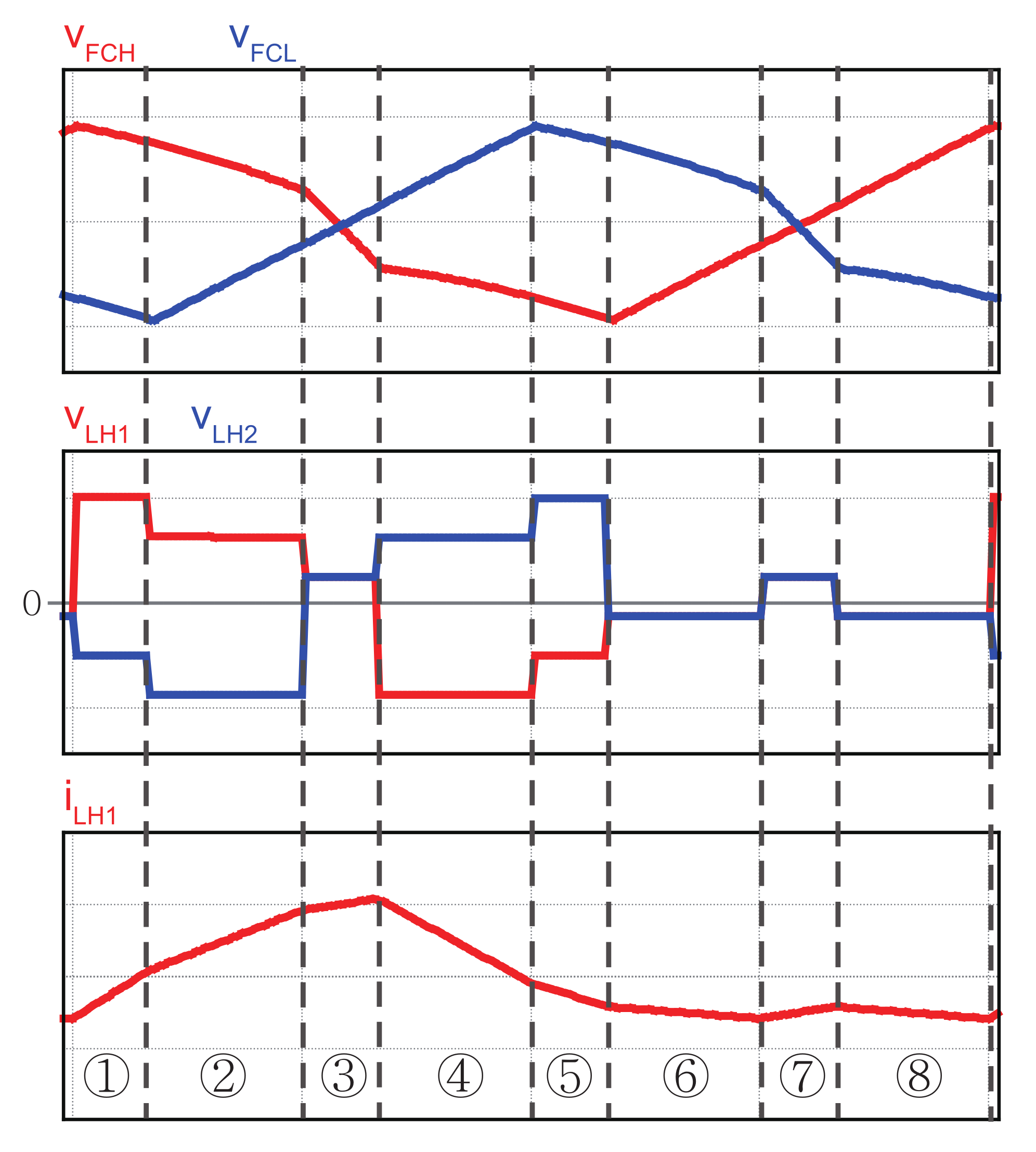
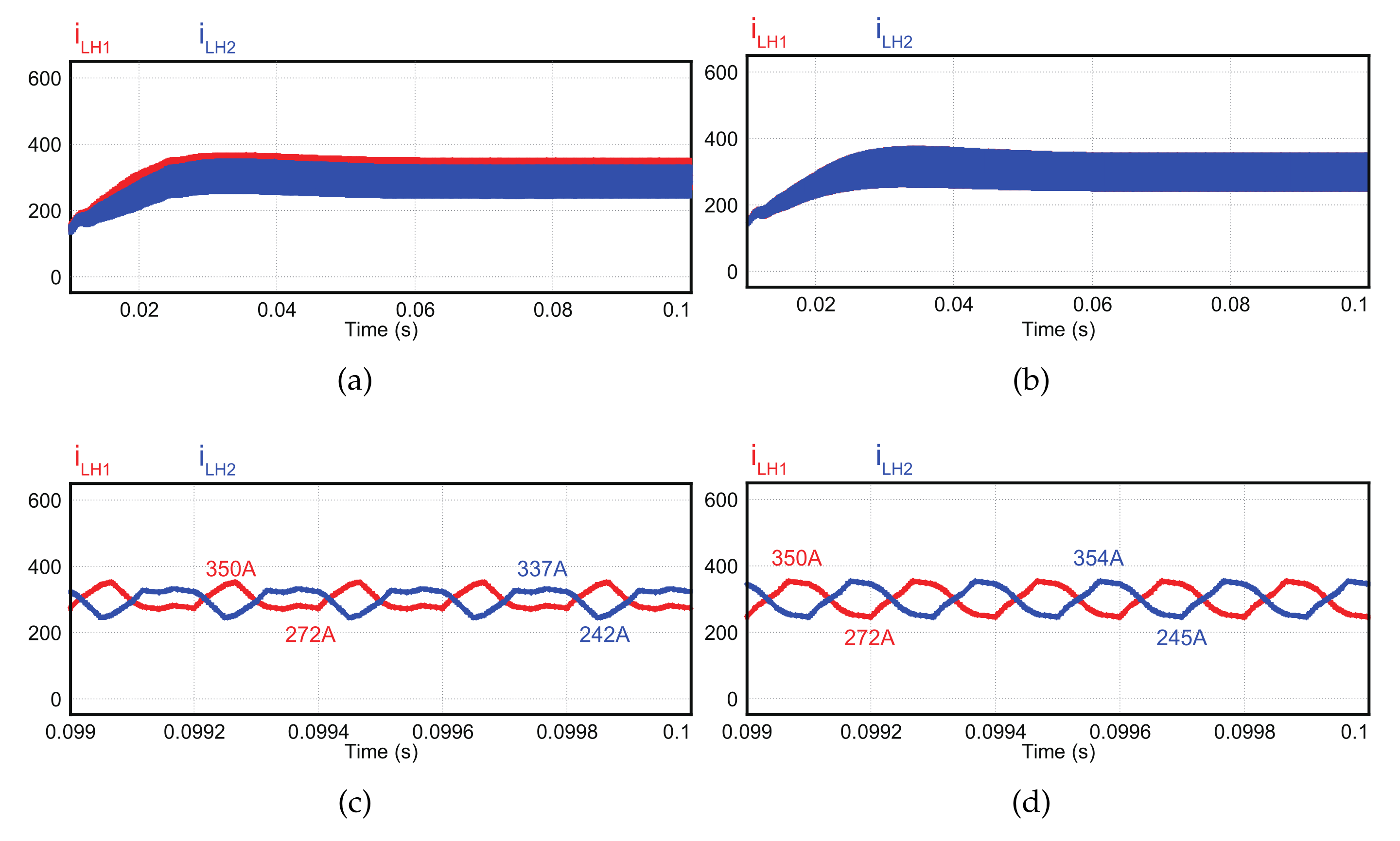
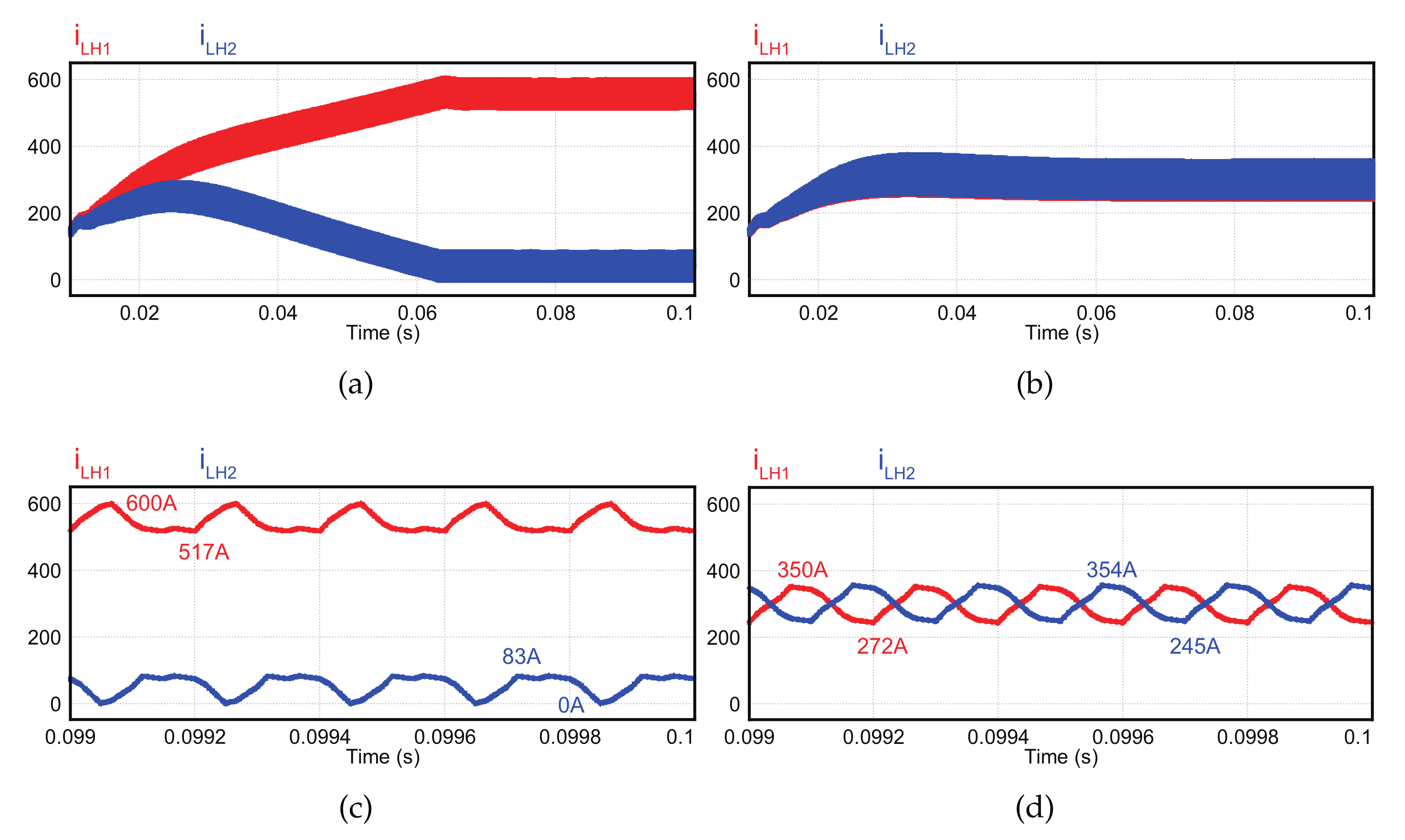
2.3. Circulating Current Variation with an Interleaving Method
3. Comparison of Interleaving Methods for Capacitor’s Current and Voltage
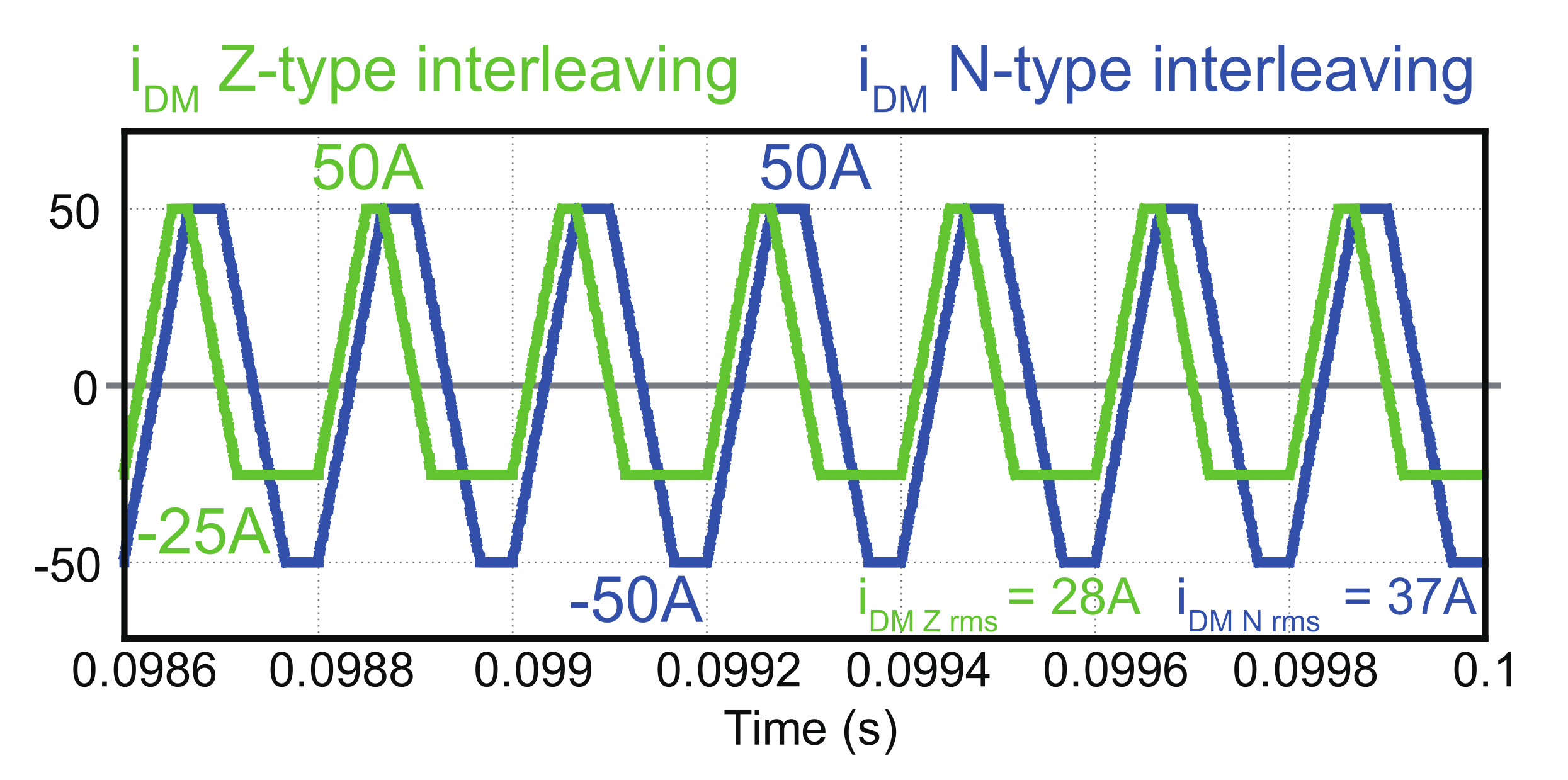
3.1. Impact of Interleaving on Capacitor Current Ripple of Parallel TLBC
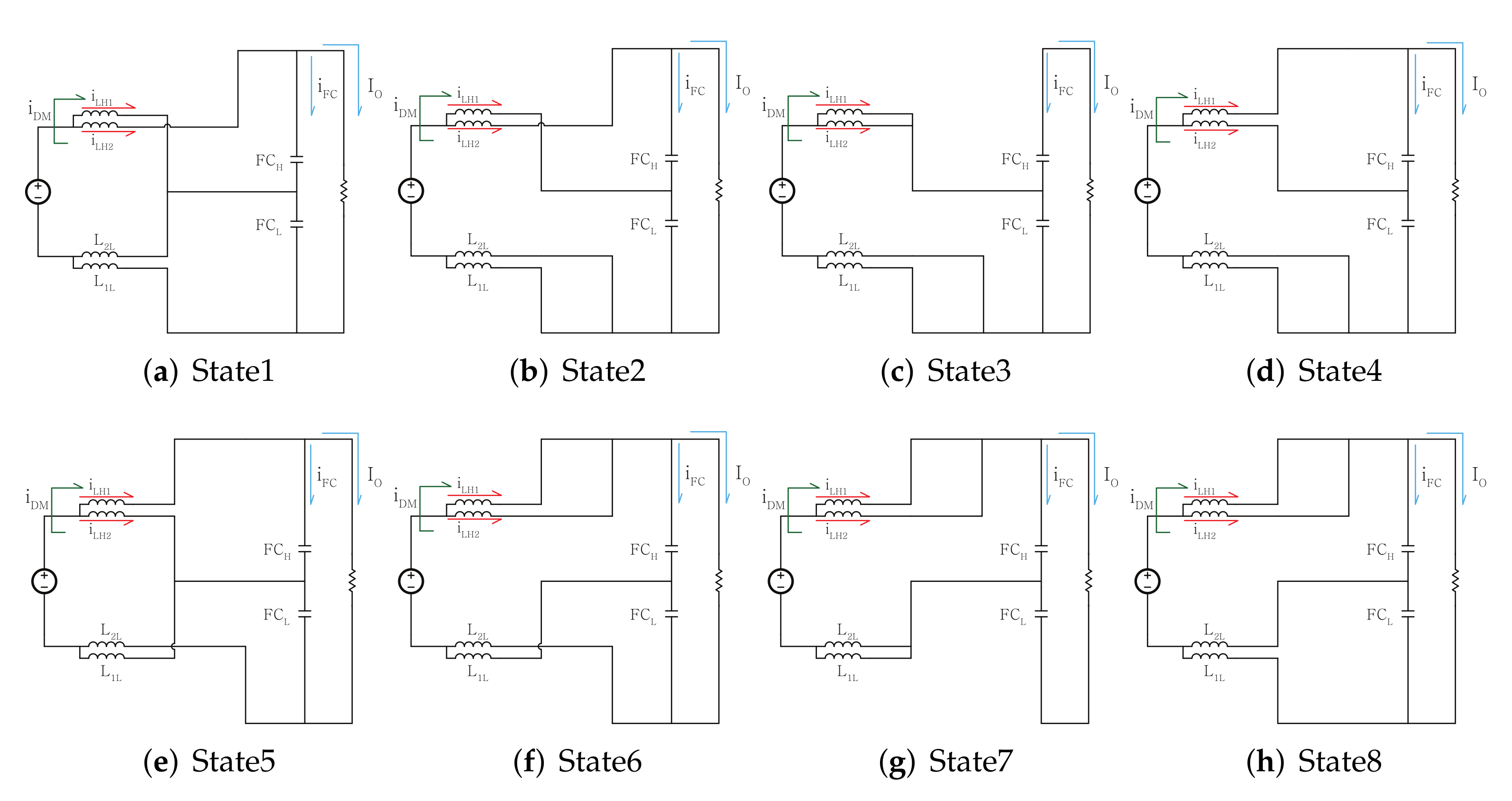
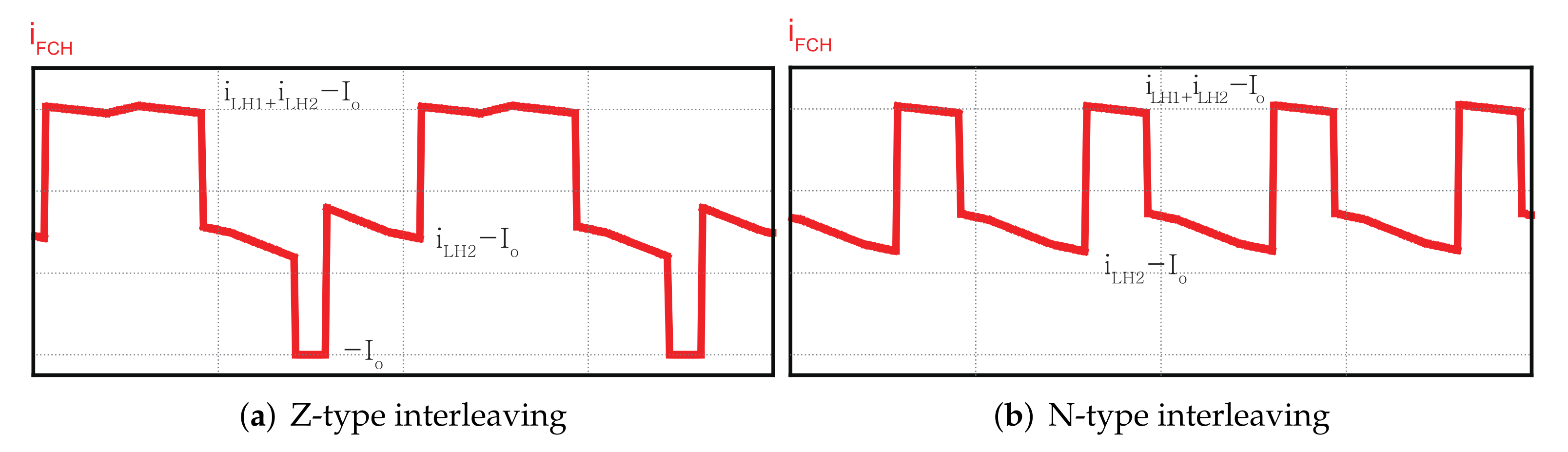
3.1.1. Capacitor Current for Z-Type Interleaving
3.1.2. Capacitor Current for N-Type Interleaving
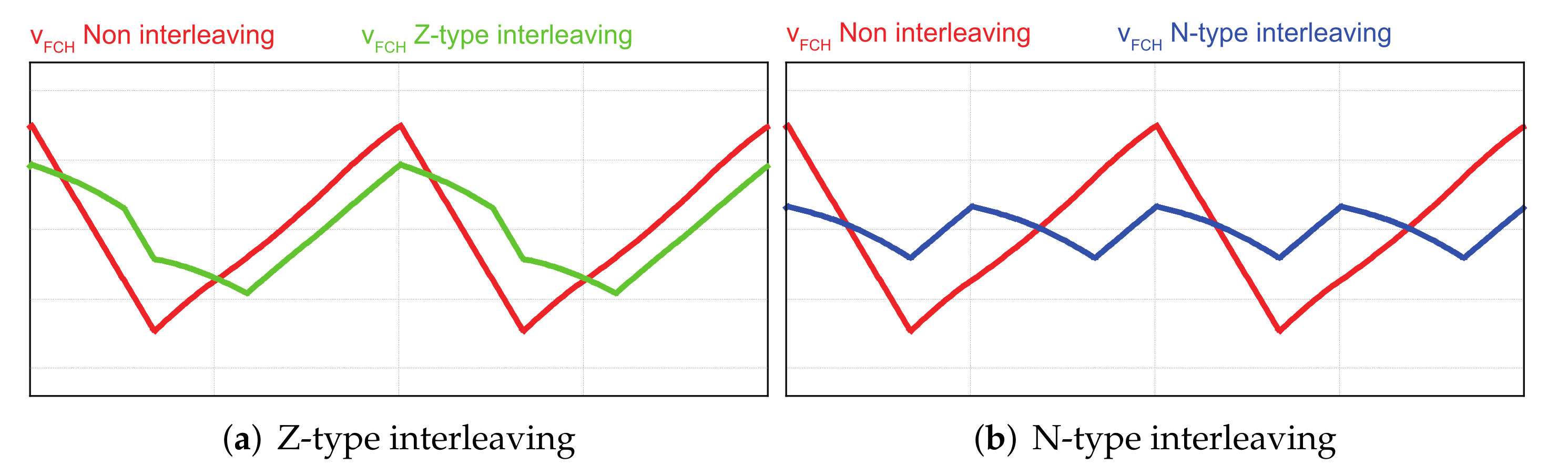
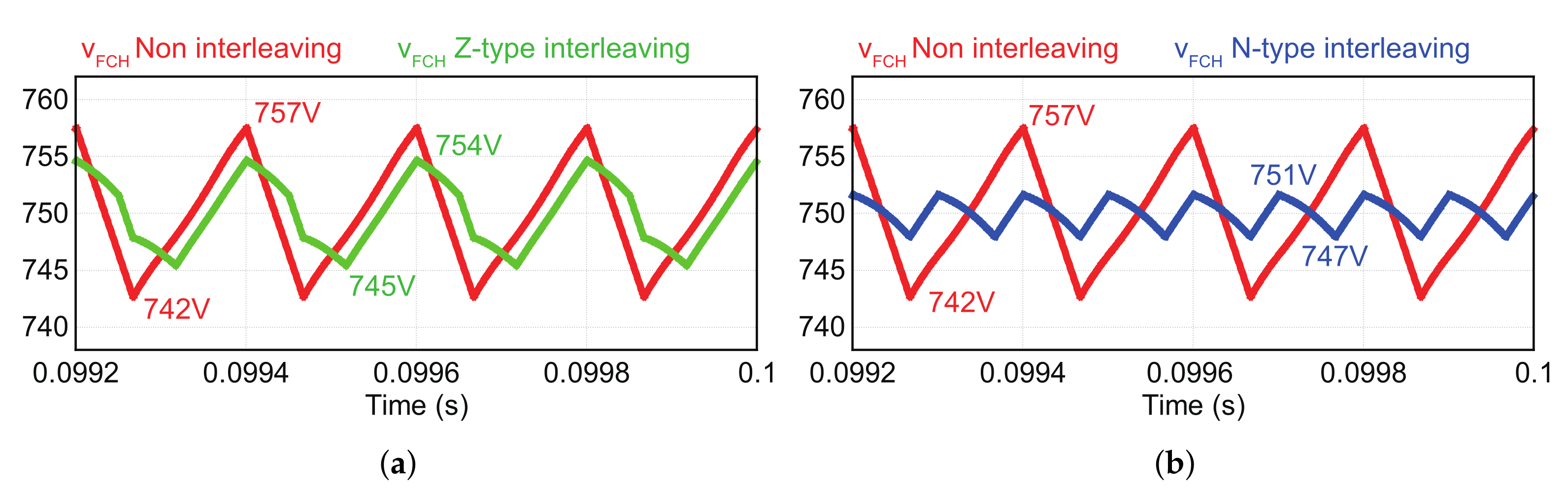
3.2. Comparative Analysis of Capacitor Voltage
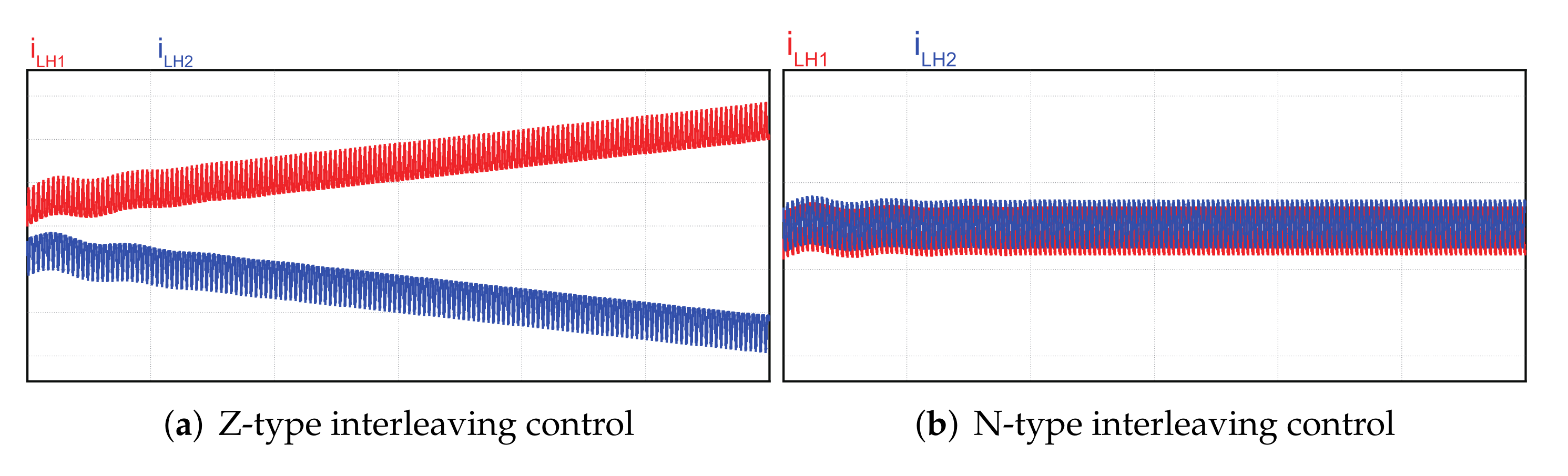
3.3. Current Imbalance with Z-Type Interleaving by the Capacitor Voltage
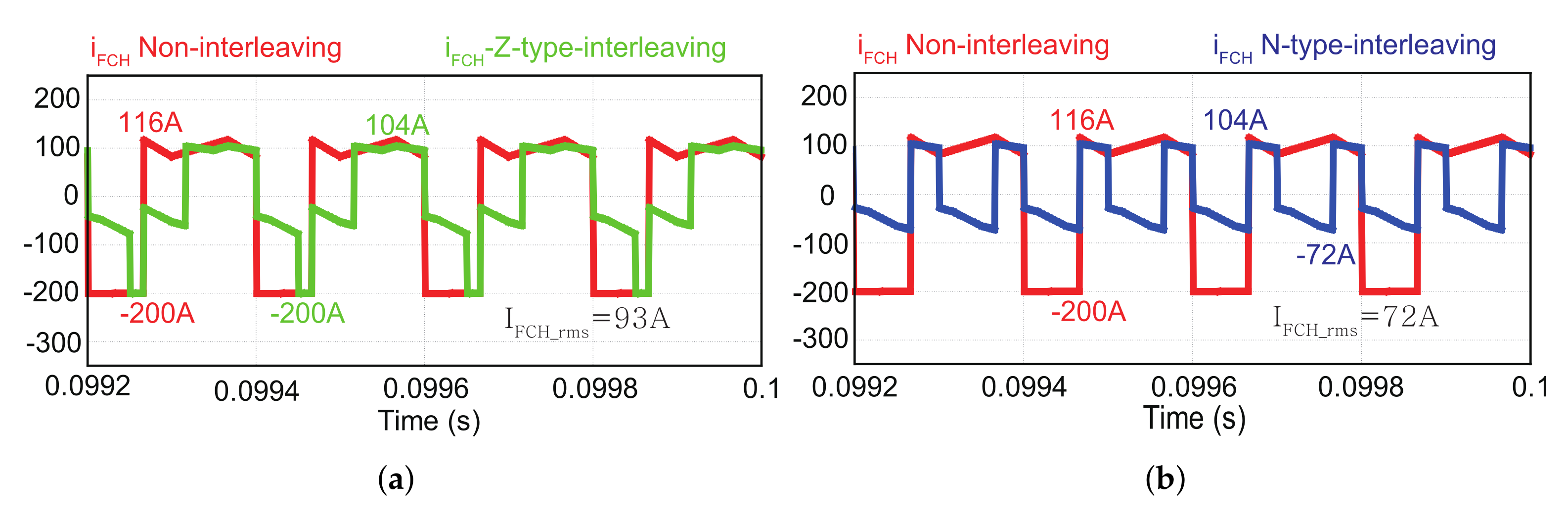
4. Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, X.L.; Liang, D.Q.; Zhang, W.D. Braking energy recovery for electric traction based on super-capacitor and bidirectional dc-dc converter. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; Volume 2, pp. 879–883. [Google Scholar] [CrossRef]
- Lianfu, T.; Lixin, W. Research on the integrated braking energy recovery strategy based on super-capacitor energy storage. In Proceedings of the 2017 International Conference on Smart Grid and Electrical Automation (ICSGEA), Changsha, China, 27–28 May 2017; pp. 175–178. [Google Scholar] [CrossRef]
- Wang, F.; Zhuo, F.; Wang, X.; Guo, H.; Wang, Z. Bi-directional interleaving dc/dc converter used in dual voltage system for vehicle. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 1335–1339. [Google Scholar] [CrossRef]
- Meleshin, V.; Zhiklenkov, D.; Ganshin, A. Efficient three-level boost converter for various applications. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. DS1e.9-1–DS1e.9-8. [Google Scholar] [CrossRef]
- Kan, Z.; Li, P.; Yuan, R.; Zhang, C. Interleaved three-level bi-directional dc-dc converter and power flow control. In Proceedings of the 2018 3rd International Conference on Intelligent Green Building and Smart Grid (IGBSG), Yilan, Taiwan, 22–25 April 2018; pp. 1–4. [Google Scholar]
- Dusmez, S.; Hasanzadeh, A.; Khaligh, A. Comparative analysis of bidirectional three-level dc–dc converter for automotive applications. IEEE Trans. Ind. Electron. 2015, 62, 3305–3315. [Google Scholar] [CrossRef]
- Mei, Y.; Li, X.; Qi, Y. A model predictive control method for three-level bi-directional dc-dc converter in renewable generation system. In Proceedings of the 2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015; pp. 417–421. [Google Scholar] [CrossRef]
- Haddad, K. Three level dc-dc converters as efficient interface in two stage PV power systems. In Proceedings of the 2012 IEEE Energytech, Cleveland, OH, USA, 29–31 May 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Yao, G.; Hu, L.; Liu, Y.; Chen, A.; He, X. Interleaved three-level boost converter with zero diode reverse-recovery loss. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition (APEC ’04), Anaheim, CA, USA, 22–26 February 2004; Volume 2, pp. 1090–1095. [Google Scholar] [CrossRef]
- Bilgin, M.S.; Poyrazoglu, G.; Aktem, M.; Er, E. DC-link capacitor lifetime under various operating conditions. In Proceedings of the 2019 IEEE 13th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Sonderborg, Denmark, 23–25 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Basu, S.; Undeland, T.M. Voltage and current ripple considerations for improving lifetime of ultra-capacitors used for energy buffer applications at converter inputs. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 244–247. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, S.M.; Lee, K.B. A switching method for improving lifetime of dc-link capacitors in hybrid ANPC inverters. In Proceedings of the 2019 IEEE Student Conference on Electric Machines and Systems (SCEMS 2019), Busan, Korea, 1–3 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, H.; Zhang, Z.; Zheng, T.Q.; Shang, Z.; Qiu, Z.; Yuan, L.; Ding, Y. A parallel-resonant isolated bidirectional dc-dc converter with low current ripple for battery storage systems. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 5548–5553. [Google Scholar] [CrossRef]
- ElMenshawy, M.; Massoud, A. Multimodule dc-dc converters for high-voltage high-power renewable energy sources. In Proceedings of the 2019 2nd International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 19–21 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Shanthi, N.; Deepalaxmi, R. Performance analysis of three level interleaved boost converter with coupled inductor. In Proceedings of the 2019 Fifth International Conference on Electrical Energy Systems (ICEES), Chennai, India, 21–22 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Itoh, J.i.; Abe, T. Circulation current reduction for a motor simulator system using a power converter with a common mode transformer. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 1662–1667. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Z.; Chen, Q. Research and simulation of circulation current control for grid tied inverters connected in parallel. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 6036–6041. [Google Scholar] [CrossRef]
- Lu, S.; Mu, M.; Jiao, Y.; Lee, F.C.; Zhao, Z. Coupled inductors in interleaved multiphase three-level dc-dc converter for high-power applications. IEEE Trans. Power Electron. 2016, 31, 120–134. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Kim, J.S. A study on the reliability of a hot-swap applied DVR power supply using fault tree analysis. In Proceedings of the Korean Power Electronics Society Conference, Sono Belle Byeonsan, Buan-Gun Jeollabuk-Do, Korea, 6–8 July 2021; pp. 412–413. [Google Scholar]
- Lee, K.M.; Baek, S.W.; Kim, H.W.; Cho, K.Y.; Kang, J.W. 3-level boost converter having lower inductor for interleaving operation. Trans. Korean Inst. Electron. 2021, 26, 96–105. [Google Scholar]
- Wang, R.R. High Power Density and High Temperature Converter Design for Transportation Applications; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2012. [Google Scholar]

| State | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
| State | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
| Parameter | Value | Unit |
|---|---|---|
| Rated Power | 300 | kW |
| Input Voltage | 1000 | V |
| Output Voltage | 1500 | V |
| Load Resistor | 3.75 | |
| Inductance () | 0.25 | mH |
| Capacitance () | 900 | uF |
| Switching Frequency | 5 | kHz |
| Number of Modules | 2 | - |
| Non-Interleaving | Z-type | N-type | Unit | |
|---|---|---|---|---|
| Interleaving | Interleaving | |||
| ine i | 323 | 325 | 328 | A |
| i | 140 | 93 | 72 | A |
| 15 | 9 | 4 | V | |
| open loop drive | possible | impossible | possible | |
| Efficiency | 91.5 | 92.2 | 92.7 | % |
| ine | : better | |||
| : worse |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.-I.; Kim, S.-H.; Baek, S.-W.; Kim, H.-W.; Cho, K.-Y.; Kim, G.-D. Comparison of Interleaving Methods of Parallel Connected Three-Level Bi-Directional Converters. Energies 2022, 15, 6. https://doi.org/10.3390/en15010006
Kim H-I, Kim S-H, Baek S-W, Kim H-W, Cho K-Y, Kim G-D. Comparison of Interleaving Methods of Parallel Connected Three-Level Bi-Directional Converters. Energies. 2022; 15(1):6. https://doi.org/10.3390/en15010006
Chicago/Turabian StyleKim, Hae-In, Su-Hwan Kim, Seung-Woo Baek, Hag-Wone Kim, Kwan-Yuhl Cho, and Gil-Dong Kim. 2022. "Comparison of Interleaving Methods of Parallel Connected Three-Level Bi-Directional Converters" Energies 15, no. 1: 6. https://doi.org/10.3390/en15010006
APA StyleKim, H.-I., Kim, S.-H., Baek, S.-W., Kim, H.-W., Cho, K.-Y., & Kim, G.-D. (2022). Comparison of Interleaving Methods of Parallel Connected Three-Level Bi-Directional Converters. Energies, 15(1), 6. https://doi.org/10.3390/en15010006






