An Open Circuit Voltage Model Fusion Method for State of Charge Estimation of Lithium-Ion Batteries
Abstract
1. Introduction
- An OCV model fusion method is proposed to obtain fusional OCV model which may match the characteristic of OCV curve in complete SOC range. The OCV model fusion method is applied for a LiNiMnCoO2 (NMC) battery and a LiFePO4 (LFP) battery. OCV fitting curves with high precision are obtained at temperature of 10 °C, 25 °C and 40 °C, respectively.
- CKF and ACKF are utilized to estimate SOC and capacity, and the effect of the fusional OCV model on SOC and capacity estimation is evaluated by comparing with the OCV curve model. Besides, the adaptability of the ACKF algorithm for OCV model errors is verified.
2. Battery Modeling and Open Circuit Voltage (OCV) Curve Fusion Method
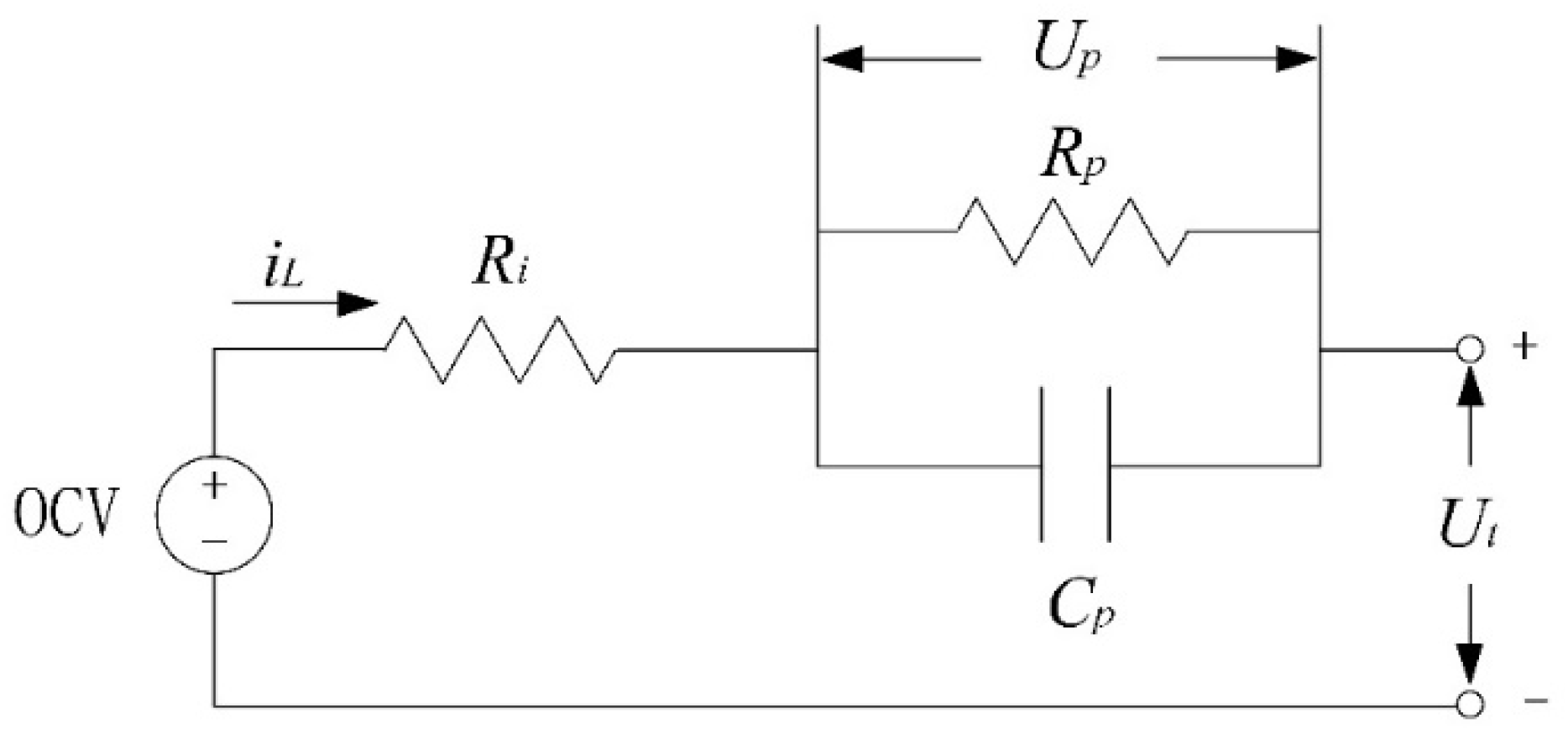
2.1. Battery Modelling
2.2. OCV Model Fusion Method
- From the perspective of battery characteristics, the marginal region of some OCV curves may be polarized, and the changing trend of the OCV curves may be transformed within a small SOC range. It is difficult for the OCV model to fully take into account the characteristics of the OCV curve.
- From the perspective of practical application, some algorithms are sensitive to the error of OCV fitting curve. For example, the OCV curve of a LFP battery may have several large flat regions. If SOC is inferred from the OCV based on OCV fitting curve which is stored in a table, the error of OCV will lead to larger error of the SOC due to the deviation of flat regions. Therefore, the requirement for the OCV model’s accuracy is strengthened.
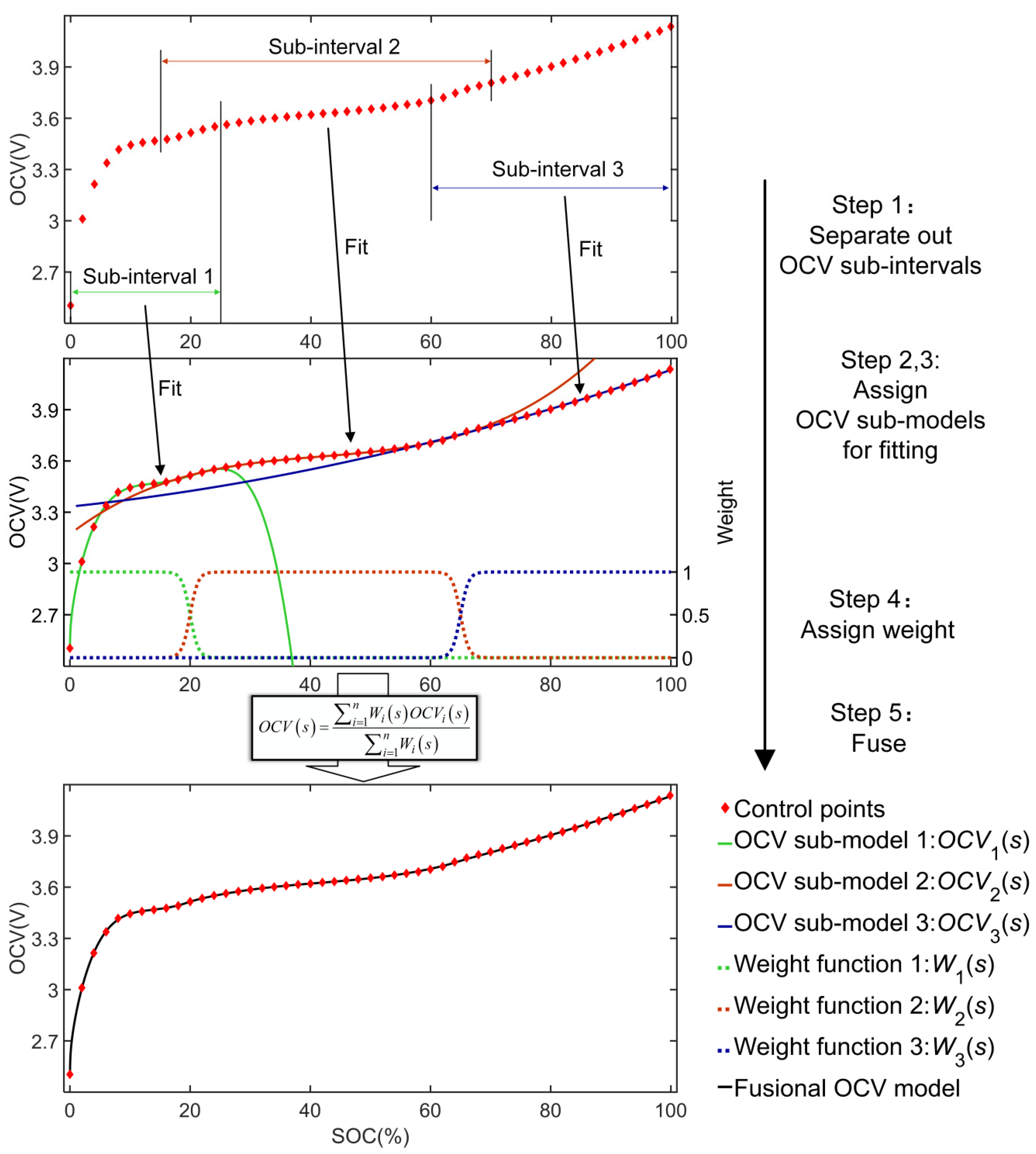
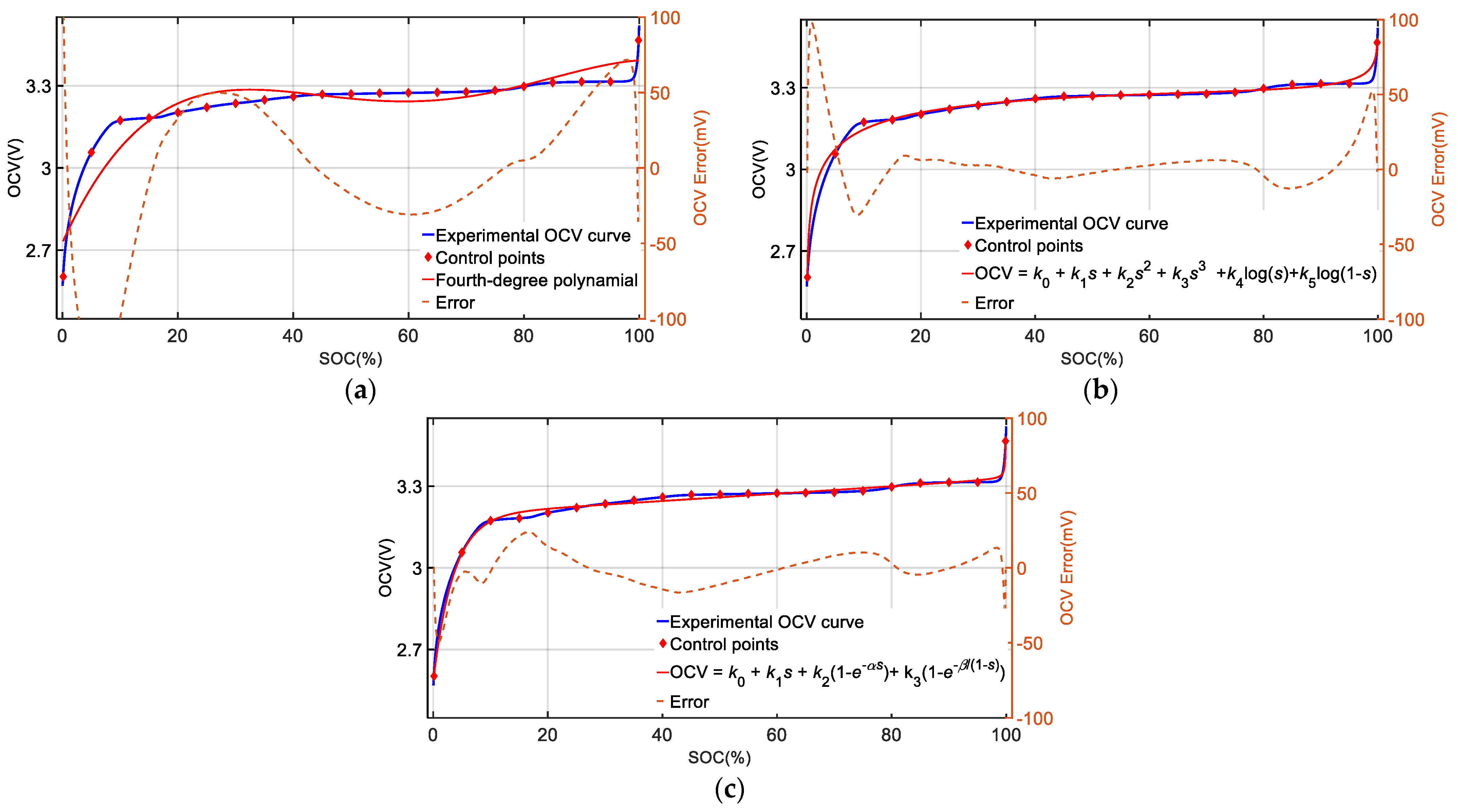
- Separate out OCV sub-intervals: according to the characteristics of OCV curve, the global SOC interval (0, 100%) can be divided into several local sub-intervals. In order to ensure the smoothness of fusional curve, each sub-interval exists overlap with neighboring sub-intervals.
- Assign OCV sub-models: according to the characteristics of the OCV curve in the local SOC sub-interval, each sub-interval corresponds to a specific OCV sub-model.
- Curve segment fitting: according to practical conditions, collecting the control points in each sub-interval. After fitting, the OCV fitting curve segments of all sub-models are obtained.
- Assign weight: different global weight functions are assigned to corresponding OCV sub-models. The function should convert weight from high to low continually when the SOC gradually away from sub-interval in the overlapped region. Logistic function is suitable for defining conversion above.
- Fuse: according to weight functions, all OCV sub-models can fuse into a fusional OCV model. The final OCV fitting curve can be expressed by using equation as follows:where s denotes SOC, OCVi(s) denotes the OCV value of sub-model i at s, Wi(s) denotes the corresponding weight at s. The final fusional OCV model can be directly used for subsequent algorithms.
2.2.1. Method for LiNiMnCoO2 (NMC) Battery Cell
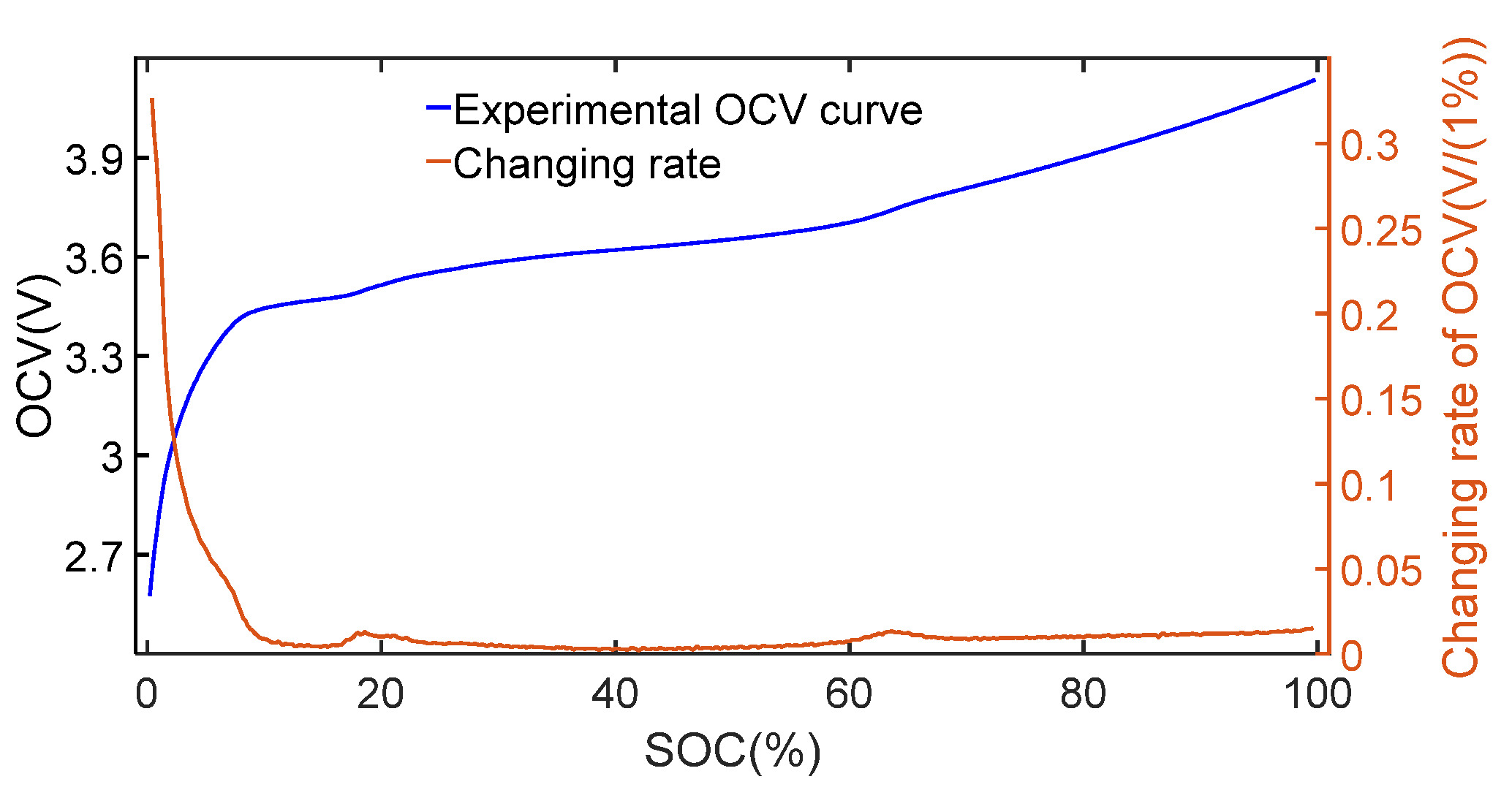
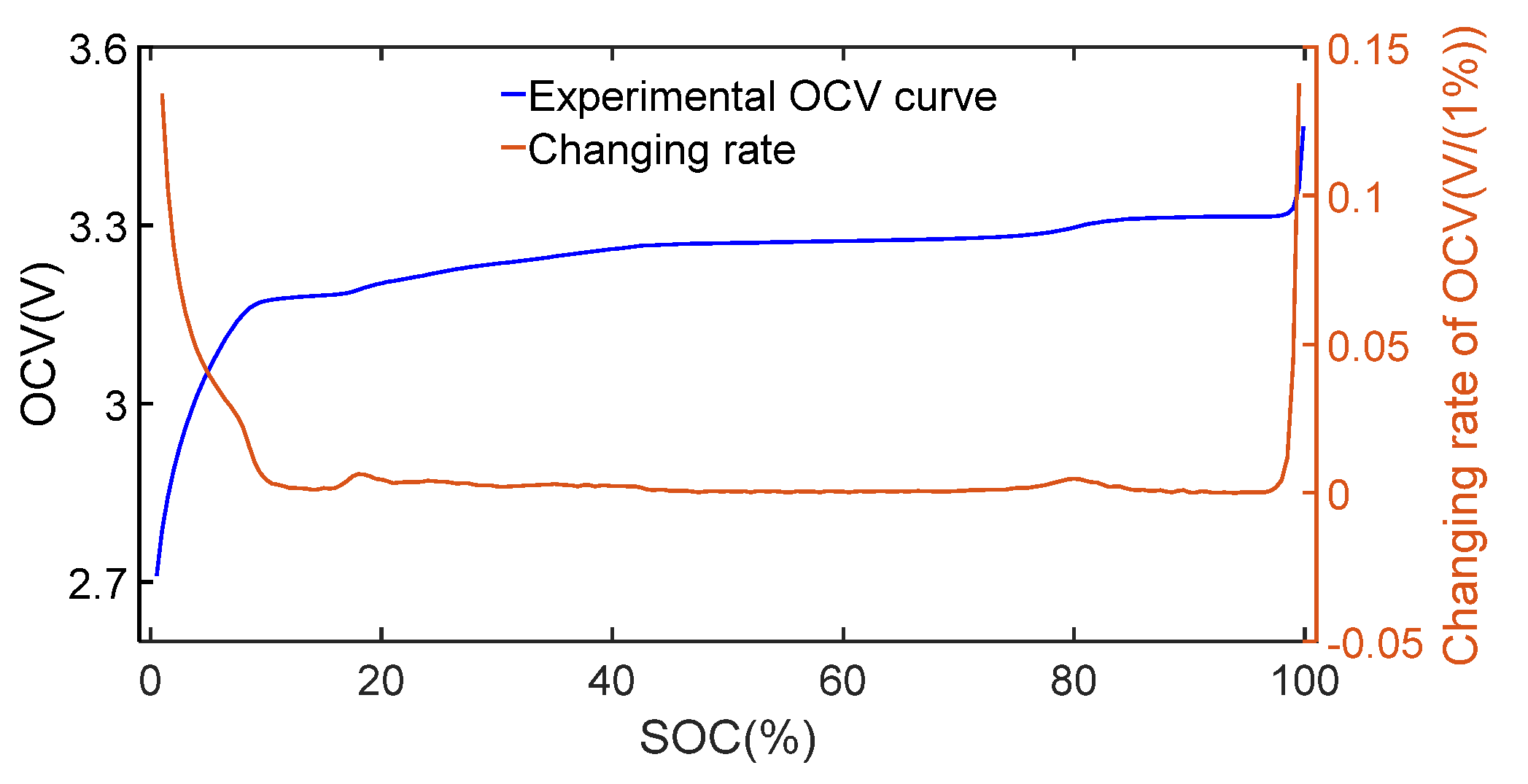
- The OCV curve is clearly monotonous, and OCV changes dramatically when SOC drops to 0%.
- By approximately calculating the changing rate of the OCV with SOC, it is obvious that the changing rate of OCV curve has bumps around 20% SOC and 65% SOC.
2.2.2. Method for LiFePO4 (LFP) Battery Cell
- The OCV curve is monotonous, and the OCV changes dramatically when SOC drops to 0% and rises to 100%. Moreover, the OCV curve has flat regions where the changing rate of OCV is close to zero.
- By approximately calculating the changing rate of OCV with SOC, it is obvious that the changing rate of the OCV curve has bumps around 20% SOC and 80% SOC.
- Although the fusional results are deduced from two examples, the steps of fusion method are generalized.
- According to practical condition, parameters like sub-intervals, sub-models and weight function can be explored freely.
- It is not suitable to select a sub-interval with too short a length, otherwise the number of control points need to be increased.
3. State of Charge (SOC) and Capacity Estimation Algorithm
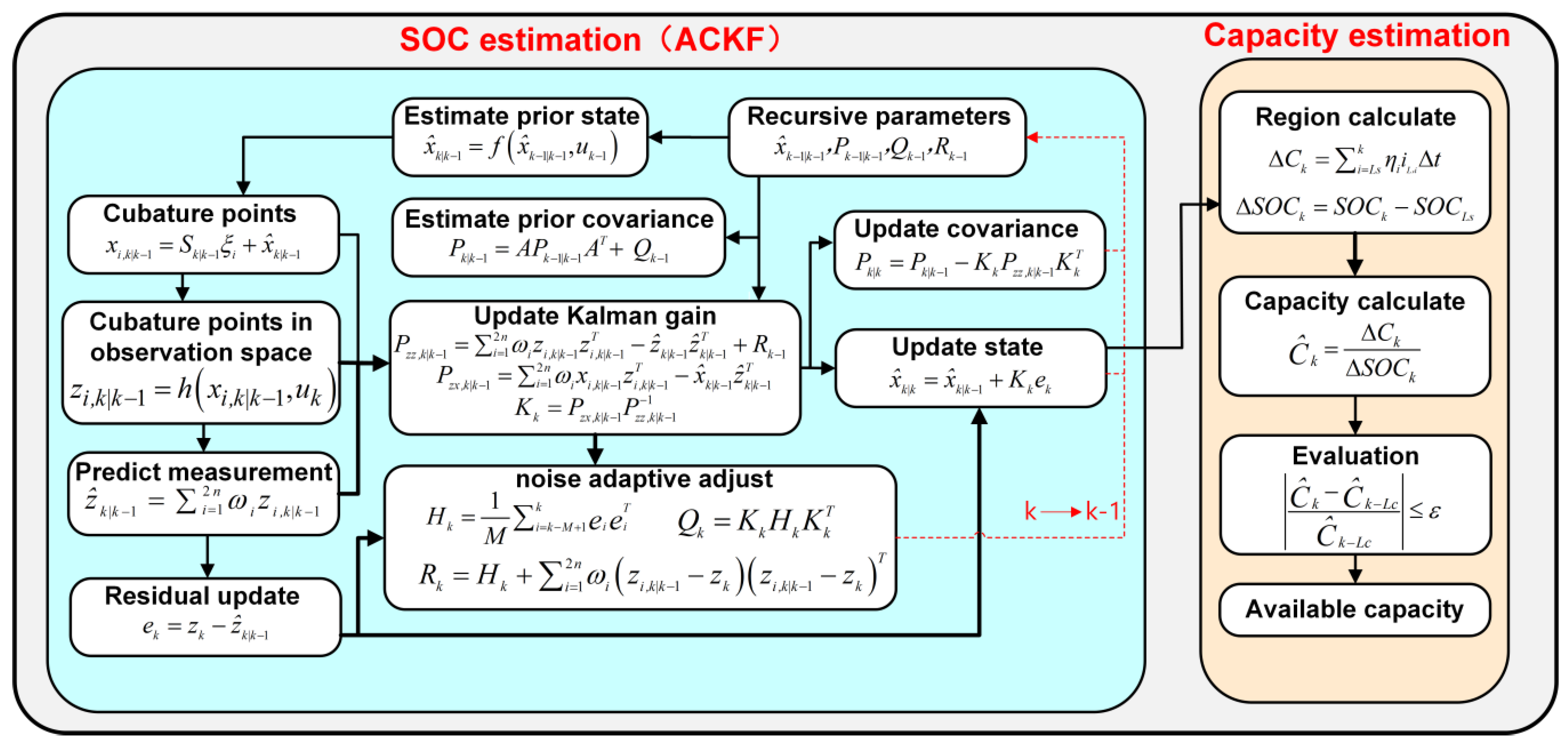
3.1. Adaptive Cubature Kalman Filter
3.2. Process of SOC Estimation
3.2.1. Initialization
3.2.2. Time Update
3.2.3. Measurement Update
- Generate cubature points:where Sk|k−1 is the Cholesky decomposition result of Pk|k−1.
- Calculate propagated cubature points in observation space:
- Calculate the predicted measurement:
- Calculate the measurement innovation covariance:
- Calculate the cross-covariance:
- Calculate the Kalman gain:
- Calculate the updated state:
- Calculate the updated covariance:
3.2.4. Adaptive Update of Noise
- The innovation covariance matrix:where M denotes the window size which is defaulted as 60, ei denotes residual which is calculated by:
- The process noise covariance Qk is updated as follows:
- The measurement noise covariance Rk is updated as follows:
3.3. Capacity Estimation Based on Estimated SOC
4. Experiment and Discussion
4.1. Experiment
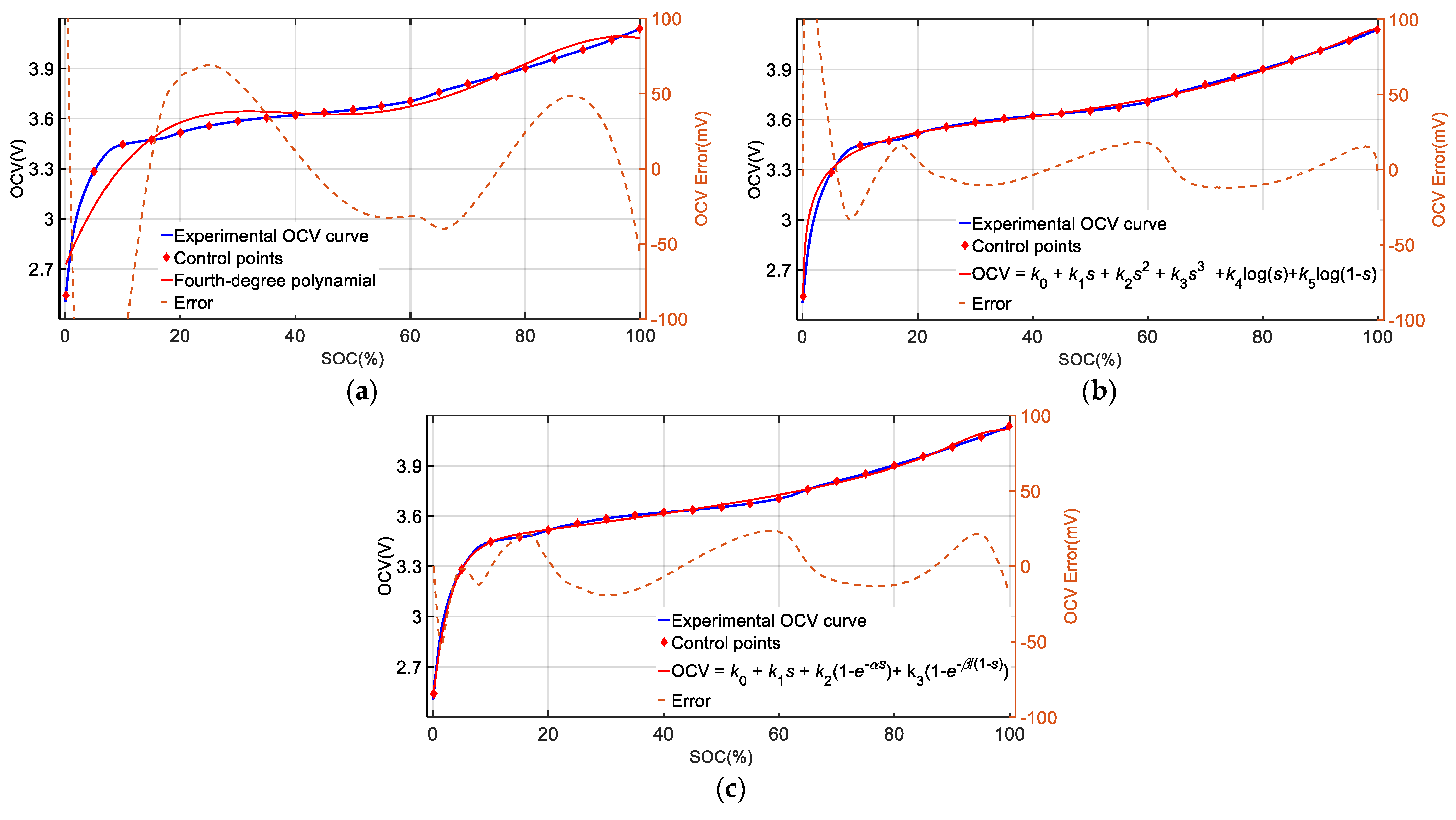
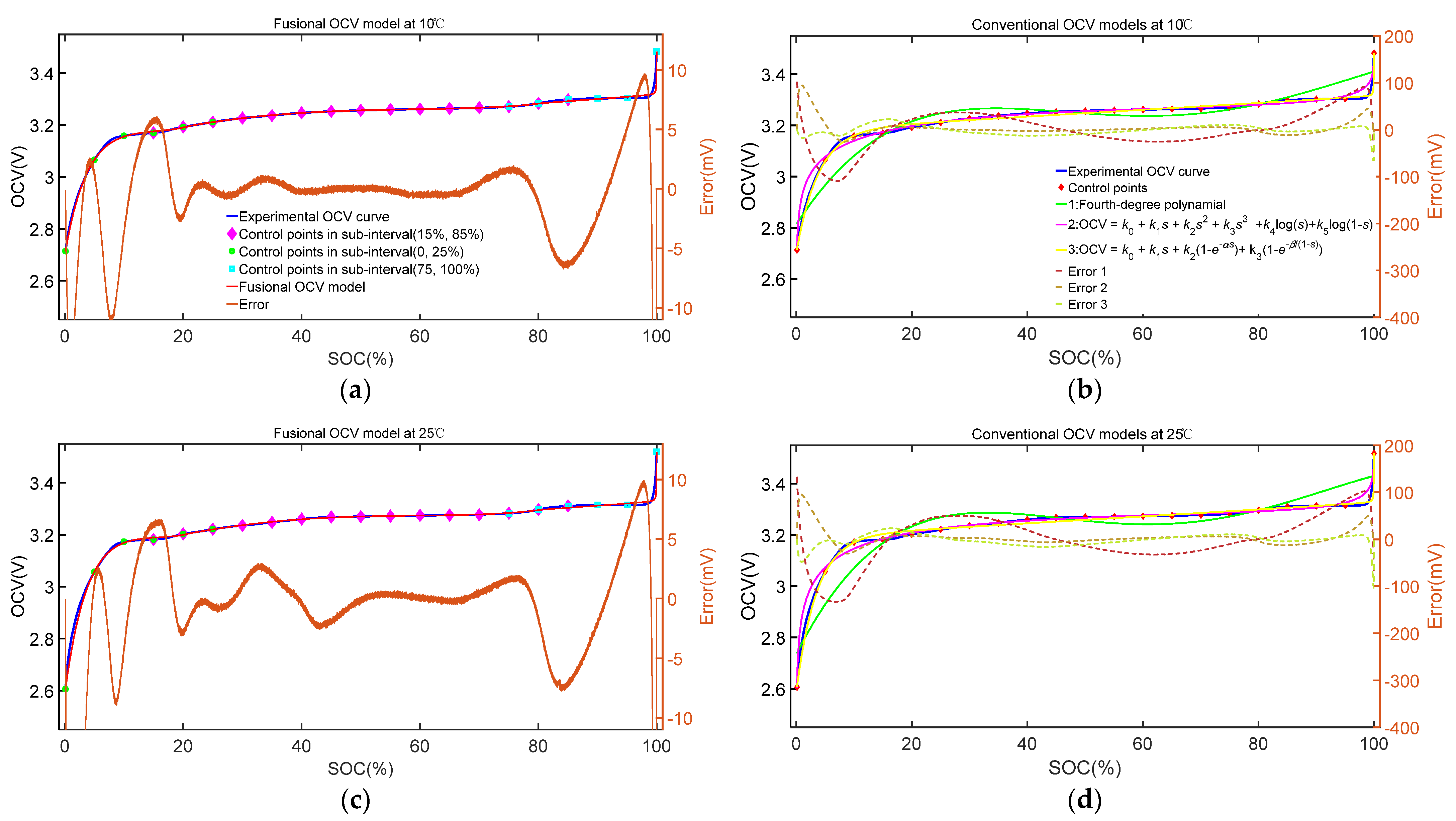
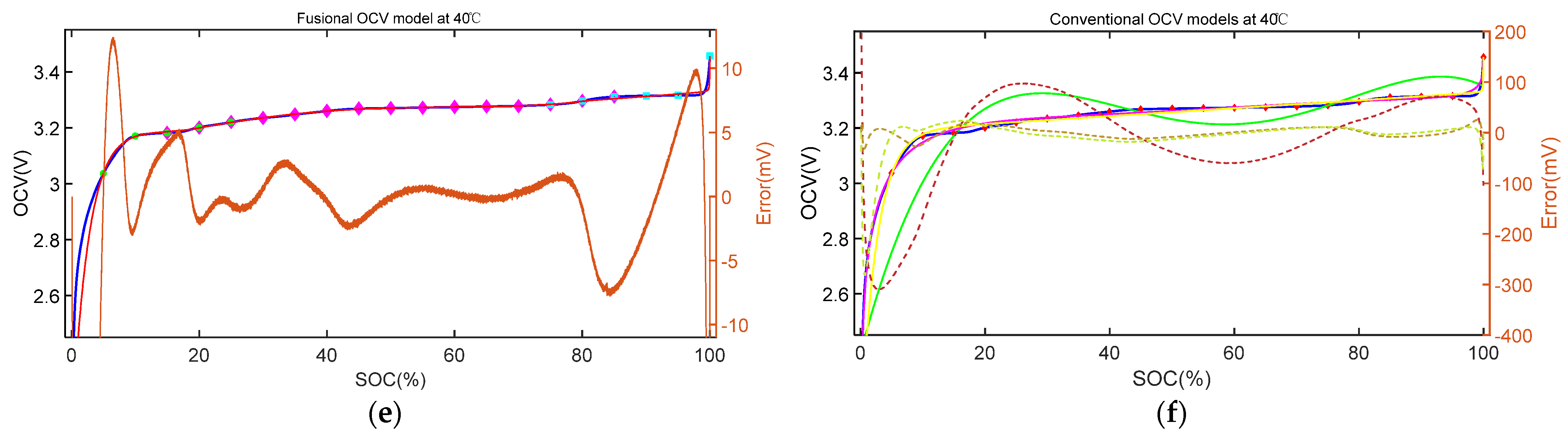
4.2. The Fusional OCV Model
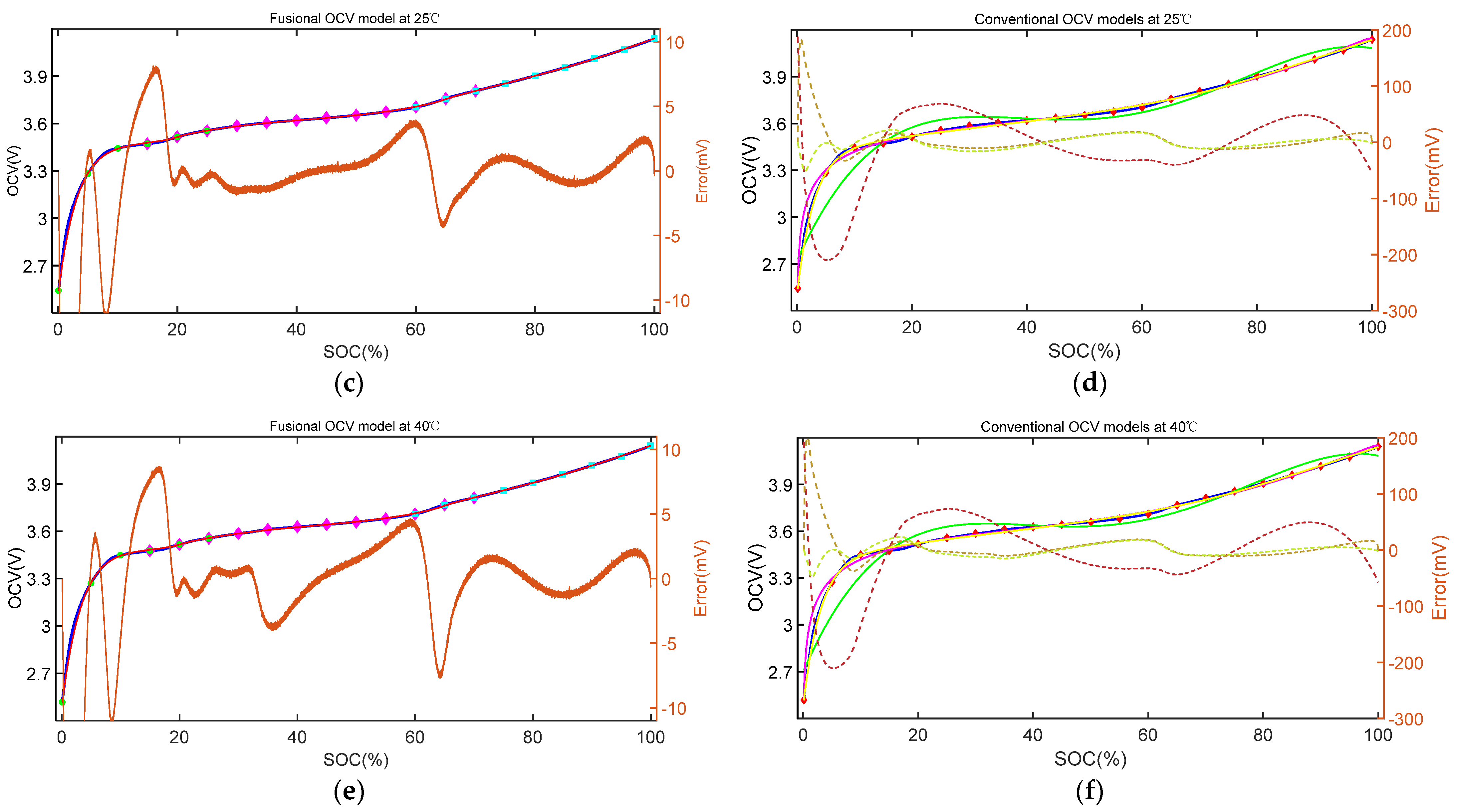
4.2.1. Fusional OCV Model of NMC Battery
4.2.2. Fusional OCV Model of LFP Battery
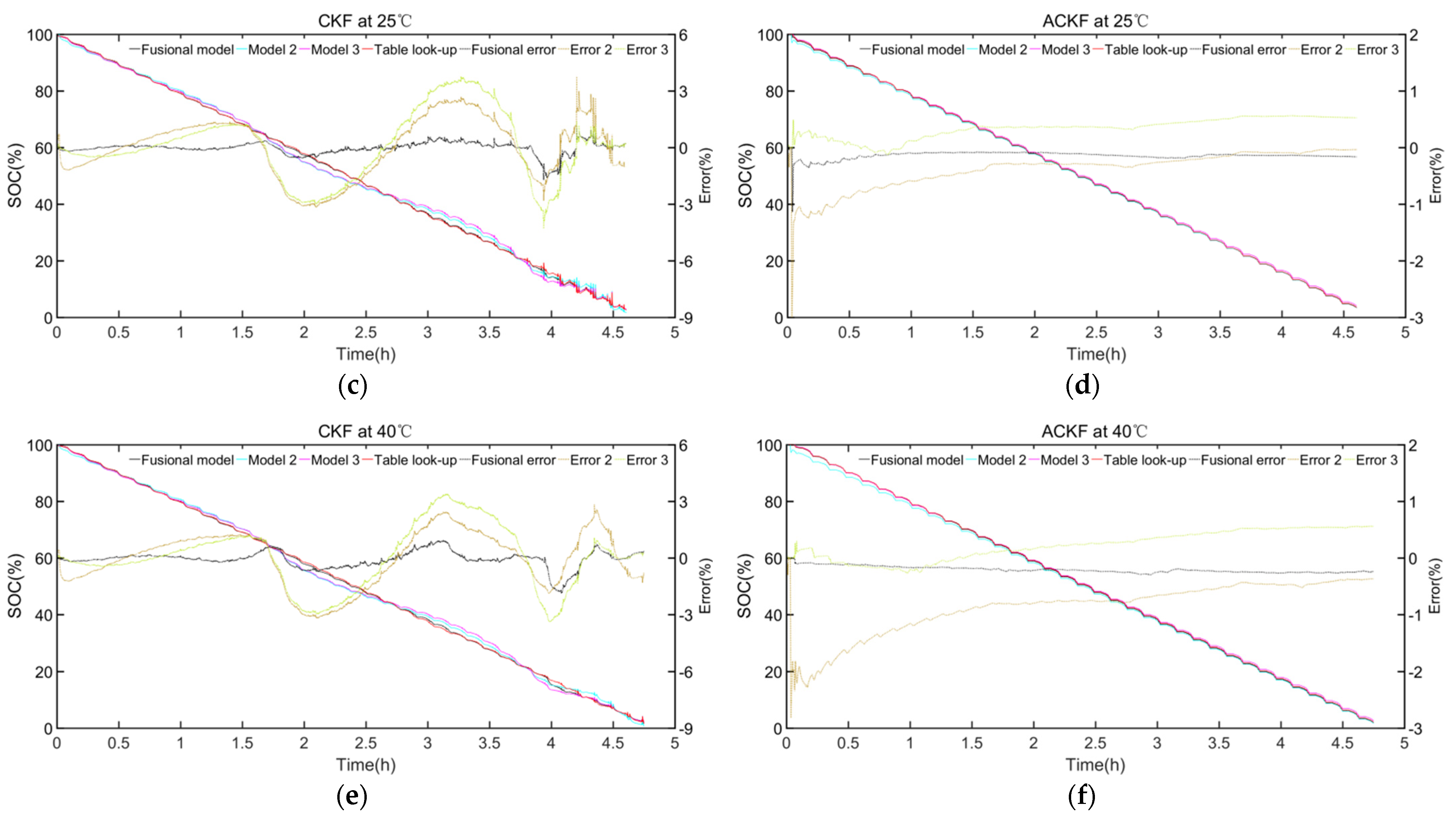
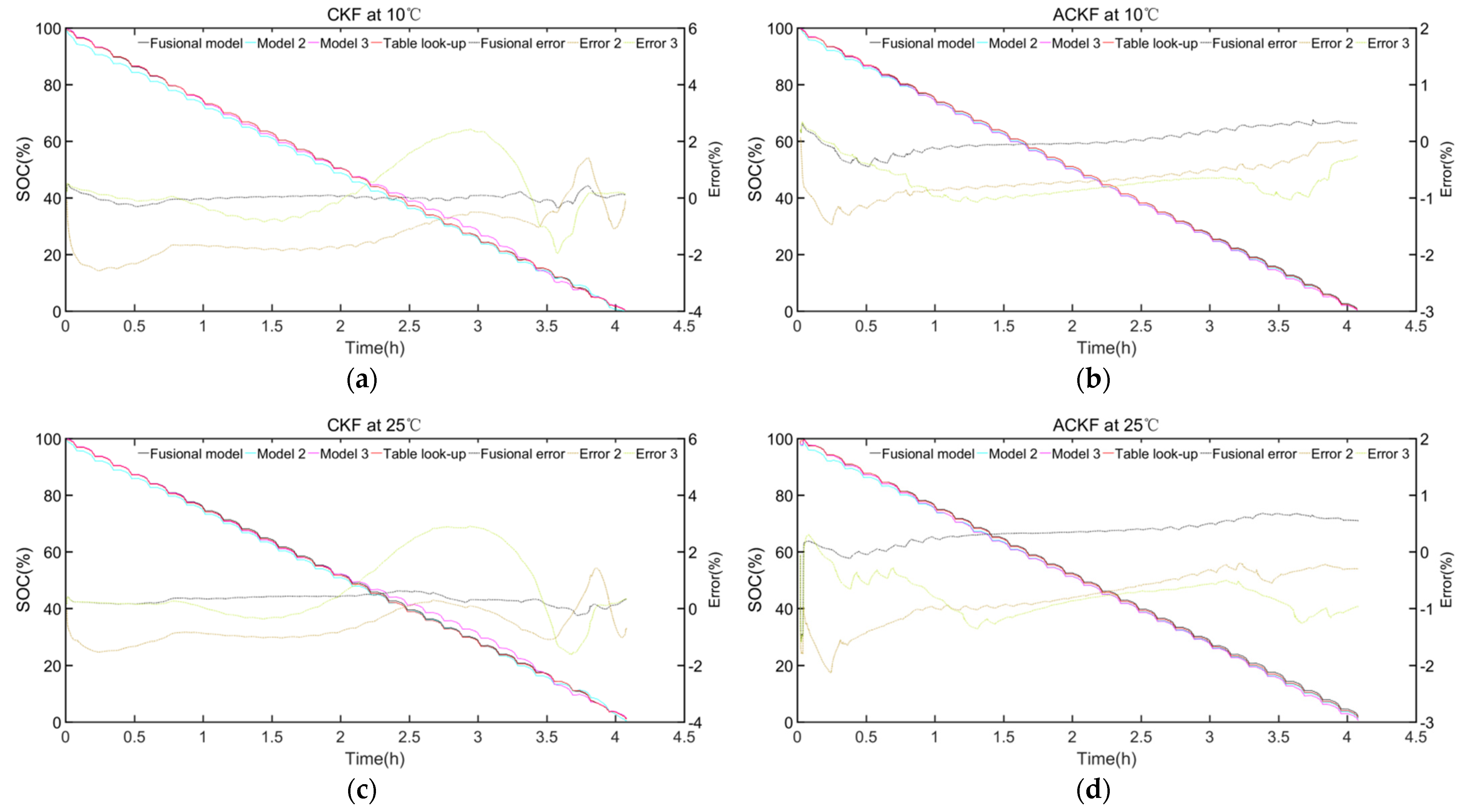
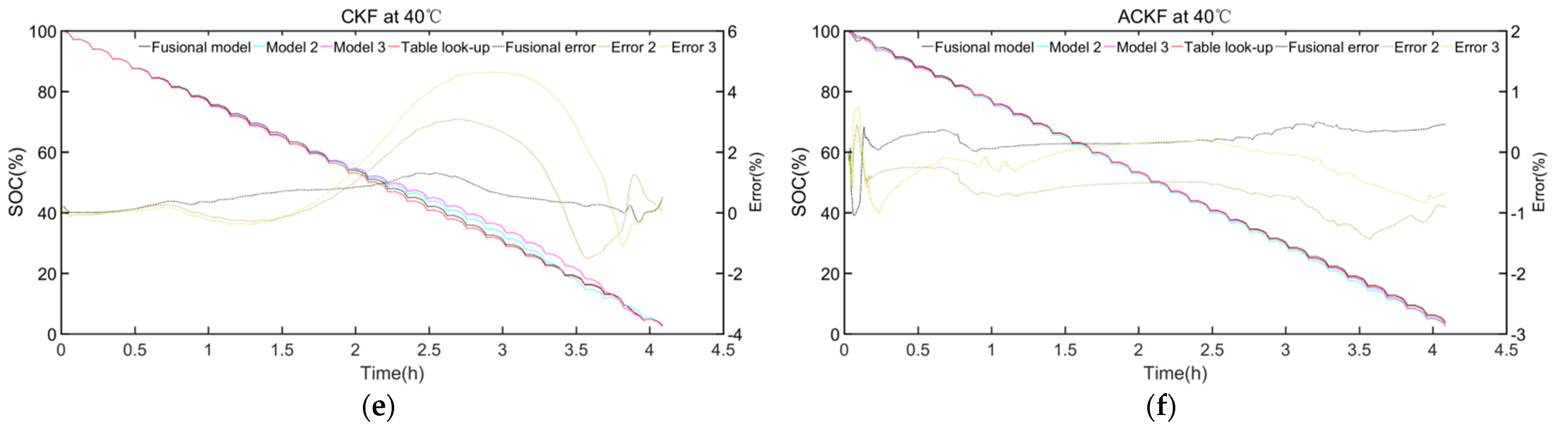
4.3. The Result of SOC Estimation with Different OCV Models
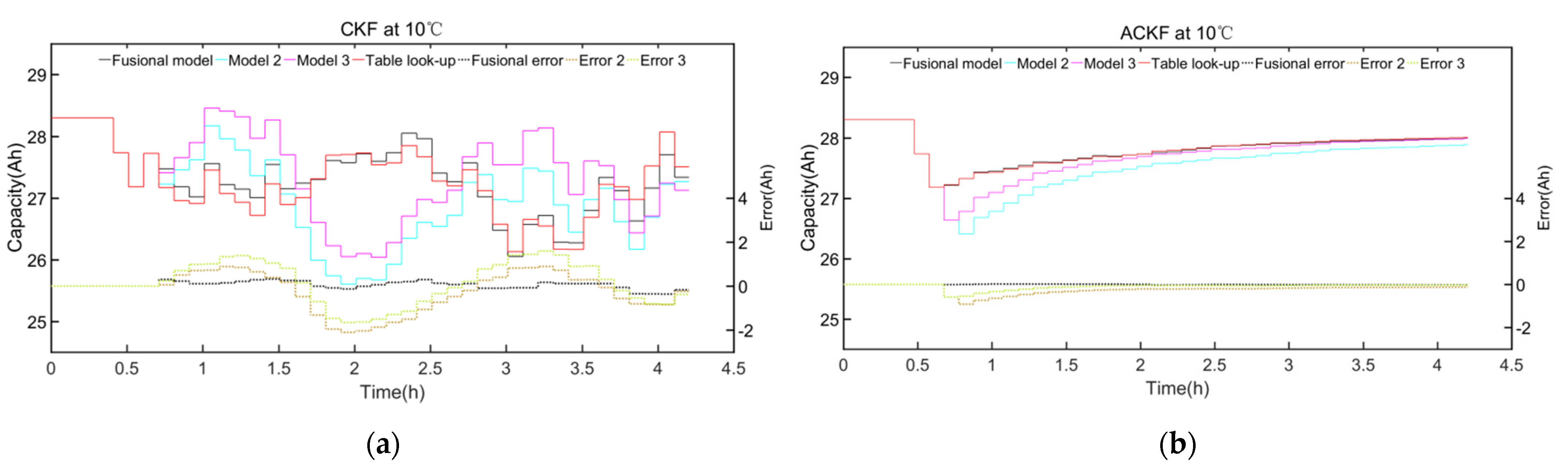
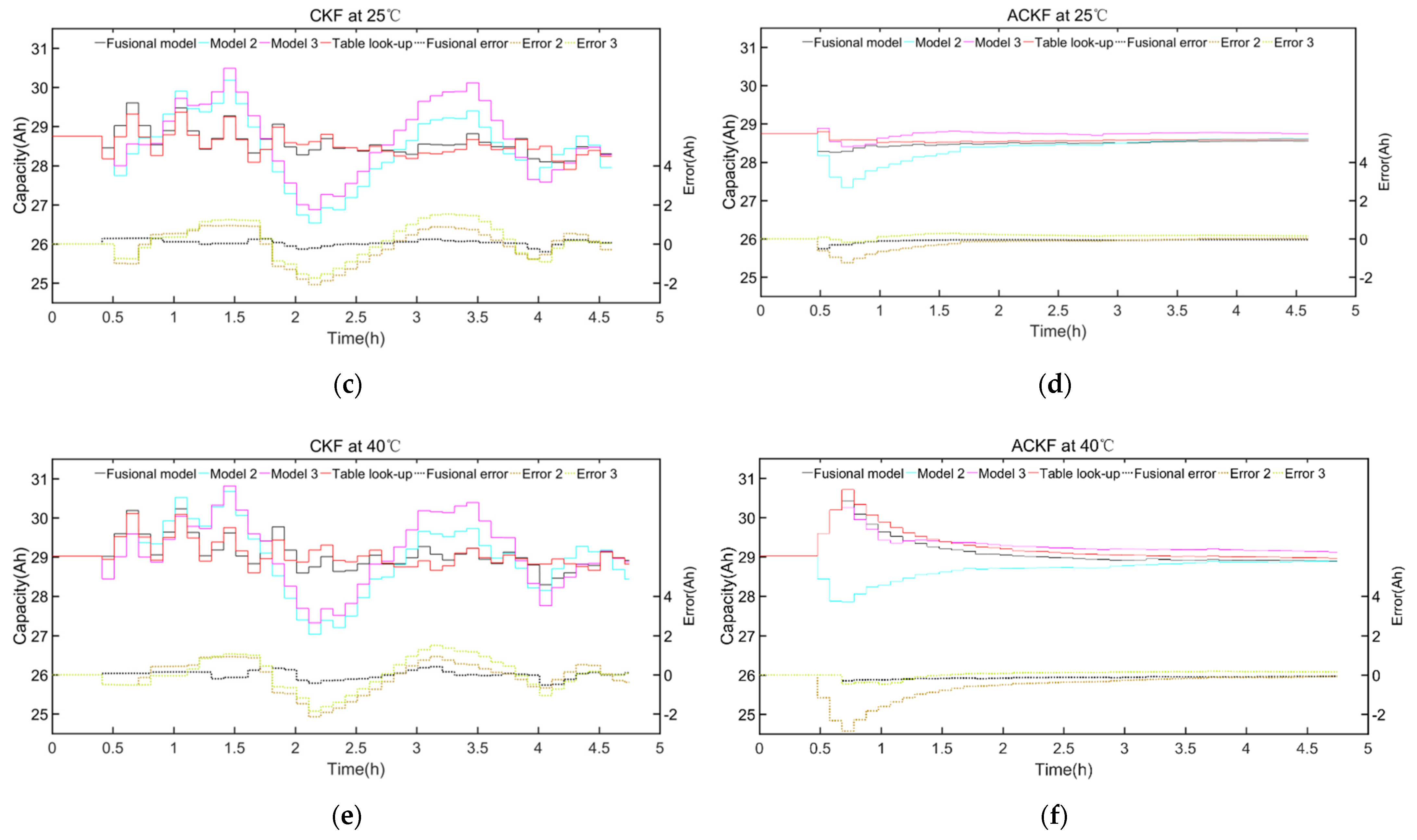
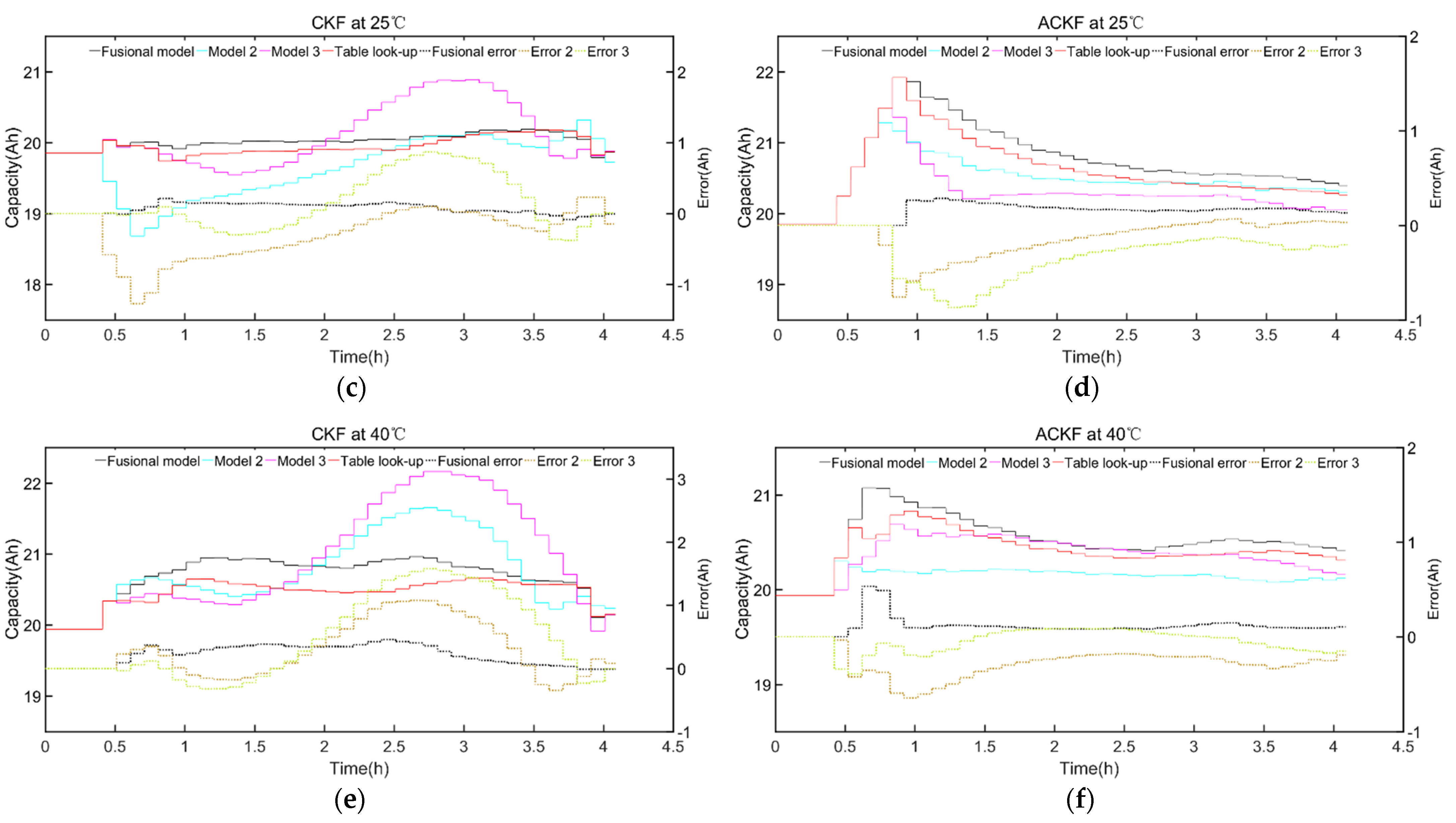
4.4. The Result of Capacity Estimation with Different OCV Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abada, S.; Marlair, G.; Lecocq, A.; Petit, M.; Sauvant-Moynot, V.; Huet, F. Safety focused modeling of lithium-ion batteries: A review. J. Power Sources 2016, 306, 178–192. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.J.; Sun, T. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries. Electrochim. Acta 2018, 259, 566–577. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; Shen, W.; Lin, X. Extreme Learning Machine Based Thermal Model for Lithium-ion Batteries of Electric Vehicles under External Short Circuit. Engineering 2020. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Yang, R.; Pecht, M. Online capacity estimation for lithium-ion batteries through joint estimation method. Appl. Energy 2019, 255, 113817. [Google Scholar] [CrossRef]
- Xing, Y.J.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S. Battery cell state-of-charge estimation using linear parameter varying system techniques. J Power Sources 2012, 198, 338–350. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Yu, Q.Q.; Xiong, R.; Wang, L.Y.; Lin, C. A Comparative Study on Open Circuit Voltage Models for Lithium-ion Batteries. Chin. J. Mech. Eng. 2018, 31, 64. [Google Scholar] [CrossRef]
- Fang, Y.; Xiong, R.; Wang, J. Estimation of Lithium-Ion Battery State of Charge for Electric Vehicles Based on Dual Extended Kalman Filter. Energy Procedia 2018, 152, 574–579. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Source 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.; Wang, L.Y. Open circuit voltage and state of charge online estimation for lithium ion batteries. Energy Procedia 2017, 142, 1902–1907. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.C.; He, H.W. Data-driven state-of-charge estimator for electric vehicles battery using robust extended Kalman filter. Int. J. Automot. Technol. 2014, 15, 89–96. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman filtering for INS/GPS. J. Geodesy 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Han, J.; Kim, D.; Sunwoo, M. State-of-charge estimation of lead-acid batteries using an adaptive extended Kalman filter. J. Power Sources 2009, 188, 606–612. [Google Scholar] [CrossRef]
- Sun, F.C.; Hu, X.S.; Zou, Y.; Li, S.G. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. J. Power Sources 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Zheng, F.D.; Xing, Y.J.; Jiang, J.C.; Sun, B.X.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]
- Petzl, M.; Danzer, M. Advancements in OCV Measurement and Analysis for Lithium-Ion Batteries. IEEE Trans. Energy Convers. 2013, 28, 675–681. [Google Scholar] [CrossRef]
- Zhu, J.G.; Knapp, M.; Darma, M.S.D.; Fang, Q.H.; Wang, X.Y.; Dai, H.F.; Wei, X.Z.; Ehrenberg, H. An improved electro-thermal battery model complemented by current dependent parameters for vehicular low temperature application. Appl. Energy 2019, 248, 149–161. [Google Scholar] [CrossRef]
- Lavigne, L.; Sabatier, J.; Francisco, M.; Guillemard, F.; Noury, A. Lithium-ion Open Circuit Voltage (OCV) curve modelling and its ageing adjustment. J. Power Sources 2016, 324, 694–703. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Yu, Q.; Jin, Q.; Yang, R. A set membership theory based parameter and state of charge co-estimation method for all-climate batteries. J. Clean. Prod. 2020, 249, 11389. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.C.; Chen, C.; He, H.W. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Dong, G.Z.; Wei, J.W.; Zhang, C.B.; Chen, Z.H. Online state of charge estimation and open circuit voltage hysteresis modeling of LiFePO4 battery using invariant imbedding method. Appl. Energy 2016, 162, 163–171. [Google Scholar] [CrossRef]
- Zhang, C.P.; Jiang, J.C.; Zhang, L.J.; Liu, S.J. A generalized SOC-OCV model for lithium-ion batteries and the SOC estimation for LNMCO battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Hu, X.S.; Li, S.B.; Peng, H.; Sun, F.C. Robustness analysis of state-of-charge estimation methods for two types of Li-ion batteries. J. Power Sources 2012, 217, 209–219. [Google Scholar] [CrossRef]
- Ganesan, N.; Basu, S.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.; Sohn, D.K.; Doo, S. Physics based modeling of a series parallel battery pack for asymmetry analysis, predictive control and life extension. J. Power Sources 2016, 322, 57–67. [Google Scholar] [CrossRef]
- Widanage, W.D.; Barai, A.; Chouchelamane, G.H.; Uddin, K.; McGordon, A.; Marco, J.; Jennings, P. Design and use of multisine signals for Li-ion battery equivalent circuit modelling. Part 2: Model estimation. J. Power Sources 2016, 324, 61–69. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Lin, C.; Shen, W.X.; Deng, J. Lithium-ion battery parameters and state-of-charge joint estimation based on H-infinity and unscented Kalman filters. IEEE Trans. Veh. Technol. 2017, 66, 8693–8701. [Google Scholar] [CrossRef]
- Hu, X.S.; Li, S.B.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.; Wang, L.; Lin, C. A novel method to obtain the open circuit voltage for the state of charge of lithium ion batteries in electric vehicles by using H infinity filter. Appl. Energy 2017, 207, 346–353. [Google Scholar] [CrossRef]
- Xiong, R. Estimation of Battery Pack State for Electric Vehicles Using Model-Data Fusion Approach. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, June 2014. [Google Scholar]
- Liu, M.; Lai, J.Z.; Li, Z.M.; Liu, J.Y. An adaptive cubature Kalman filter algorithm for inertial and land-based navigation system. Aerosp. Sci. Technol. 2016, 51, 52–60. [Google Scholar] [CrossRef]




| Sub-Interval | Sub-Model |
|---|---|
| (0, 25%) | |
| (15, 70%) | |
| (60, 100%) |
| Sub-Interval | Sub-Model |
|---|---|
| (0, 25%) | |
| (15, 85%) | |
| (75, 100%) |
| Material | Type | Nominal Capacity (Ah) | Available Capacity (Ah) | ||
|---|---|---|---|---|---|
| 10 °C | 25 °C | 40 °C | |||
| NMC | cylinder | 25.00 | 28.30 | 28.75 | 29.02 |
| LFP | pouch | 20.00 | 19.72 | 19.85 | 19.94 |
| Label | Model |
|---|---|
| 1 | |
| 2 | |
| 3 |
| 10 °C | 25 °C | 40 °C | |
|---|---|---|---|
| Fusional model | 0.0022 | 0.0027 | 0.0031 |
| Model 1 | 0.0473 | 0.0575 | 0.0596 |
| Model 2 | 0.0106 | 0.0115 | 0.0117 |
| Model 3 | 0.0109 | 0.0105 | 0.0101 |
| 10 °C | 25 °C | 40 °C | |
|---|---|---|---|
| Fusional model | 0.0032 | 0.0033 | 0.0033 |
| Model 1 | 0.0386 | 0.0482 | 0.0782 |
| Model 2 | 0.0088 | 0.0101 | 0.0100 |
| Model 3 | 0.0090 | 0.0096 | 0.0106 |
| 10 °C | 25 °C | 40 °C | ||||
|---|---|---|---|---|---|---|
| CKF | ACKF | CKF | ACKF | CKF | ACKF | |
| Fusional model | 0.3277 | 0.0725 | 0.3385 | 0.1555 | 0.4465 | 0.2125 |
| Model 2 | 1.6378 | 0.6027 | 1.5454 | 0.5056 | 1.4508 | 0.9889 |
| Model 3 | 1.9407 | 0.1843 | 1.7782 | 0.3828 | 1.6261 | 0.3358 |
| 10 °C | 25 °C | 40 °C | ||||
|---|---|---|---|---|---|---|
| CKF | ACKF | CKF | ACKF | CKF | ACKF | |
| Fusional model | 0.6462 | 0.2049 | 0.3530 | 0.4179 | 0.6506 | 0.2905 |
| Model 2 | 1.6222 | 0.7526 | 0.8740 | 0.9157 | 1.4714 | 0.7377 |
| Model 3 | 1.2080 | 0.7656 | 1.3779 | 0.8355 | 2.4103 | 0.3655 |
| 10 °C | 25 °C | 40 °C | ||||
|---|---|---|---|---|---|---|
| CKF | ACKF | CKF | ACKF | CKF | ACKF | |
| Fusional model | 0.1833 | 0.0138 | 0.1718 | 0.1556 | 0.2226 | 0.1427 |
| Model 2 | 0.9395 | 0.3558 | 0.8801 | 0.4317 | 0.8161 | 0.9693 |
| Model 3 | 0.9877 | 0.1973 | 0.9414 | 0.1940 | 0.8499 | 0.1866 |
| 10 °C | 25 °C | 40 °C | ||||
|---|---|---|---|---|---|---|
| CKF | ACKF | CKF | ACKF | CKF | ACKF | |
| Fusional model | 0.1523 | 0.1866 | 0.1073 | 0.1791 | 0.2808 | 0.1240 |
| Model 2 | 0.6295 | 0.4062 | 0.4753 | 0.2461 | 0.5442 | 0.3240 |
| Model 3 | 0.3775 | 0.4850 | 0.4307 | 0.4102 | 0.8465 | 0.1283 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Wan, C.; Li, J.; E, L.; Zhang, X.; Huang, Y.; Liu, T. An Open Circuit Voltage Model Fusion Method for State of Charge Estimation of Lithium-Ion Batteries. Energies 2021, 14, 1797. https://doi.org/10.3390/en14071797
Yu Q, Wan C, Li J, E L, Zhang X, Huang Y, Liu T. An Open Circuit Voltage Model Fusion Method for State of Charge Estimation of Lithium-Ion Batteries. Energies. 2021; 14(7):1797. https://doi.org/10.3390/en14071797
Chicago/Turabian StyleYu, Quanqing, Changjiang Wan, Junfu Li, Lixin E, Xin Zhang, Yonghe Huang, and Tao Liu. 2021. "An Open Circuit Voltage Model Fusion Method for State of Charge Estimation of Lithium-Ion Batteries" Energies 14, no. 7: 1797. https://doi.org/10.3390/en14071797
APA StyleYu, Q., Wan, C., Li, J., E, L., Zhang, X., Huang, Y., & Liu, T. (2021). An Open Circuit Voltage Model Fusion Method for State of Charge Estimation of Lithium-Ion Batteries. Energies, 14(7), 1797. https://doi.org/10.3390/en14071797








