Optimal Adaptive Gain LQR-Based Energy Management Strategy for Battery–Supercapacitor Hybrid Power System
Abstract
1. Introduction
- Robust control ensures a good energy quality provided to the load side and an extended Hybrid Energy Storage System (HESS) component lifetime;
- Combination of different methods to achieve an optimal performance.
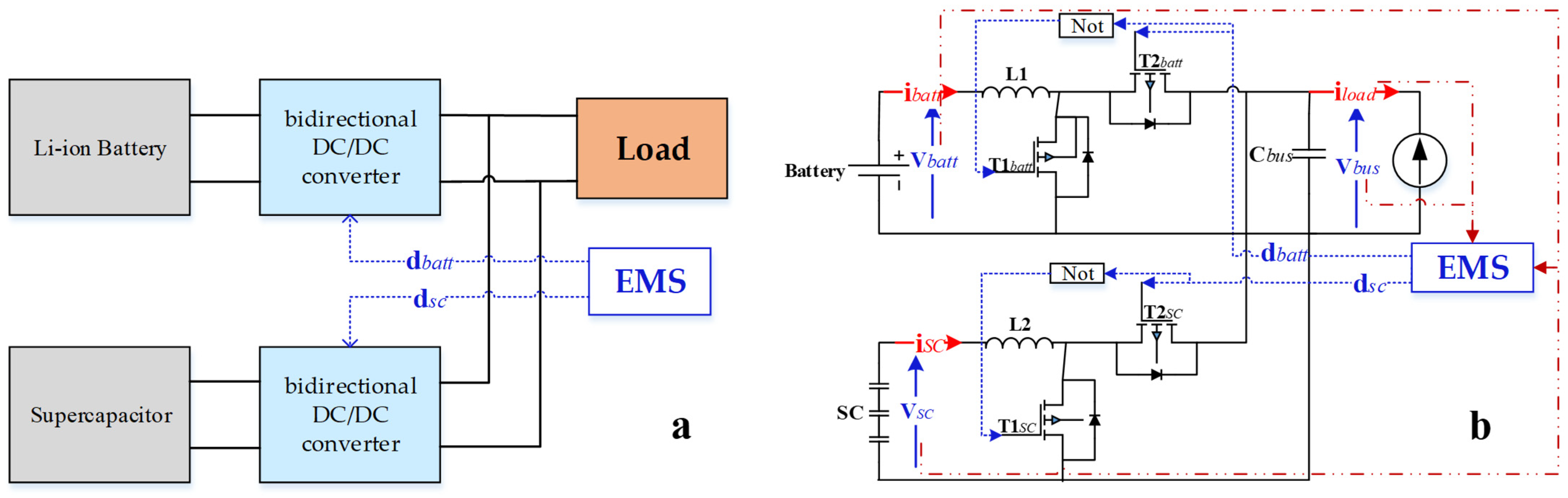
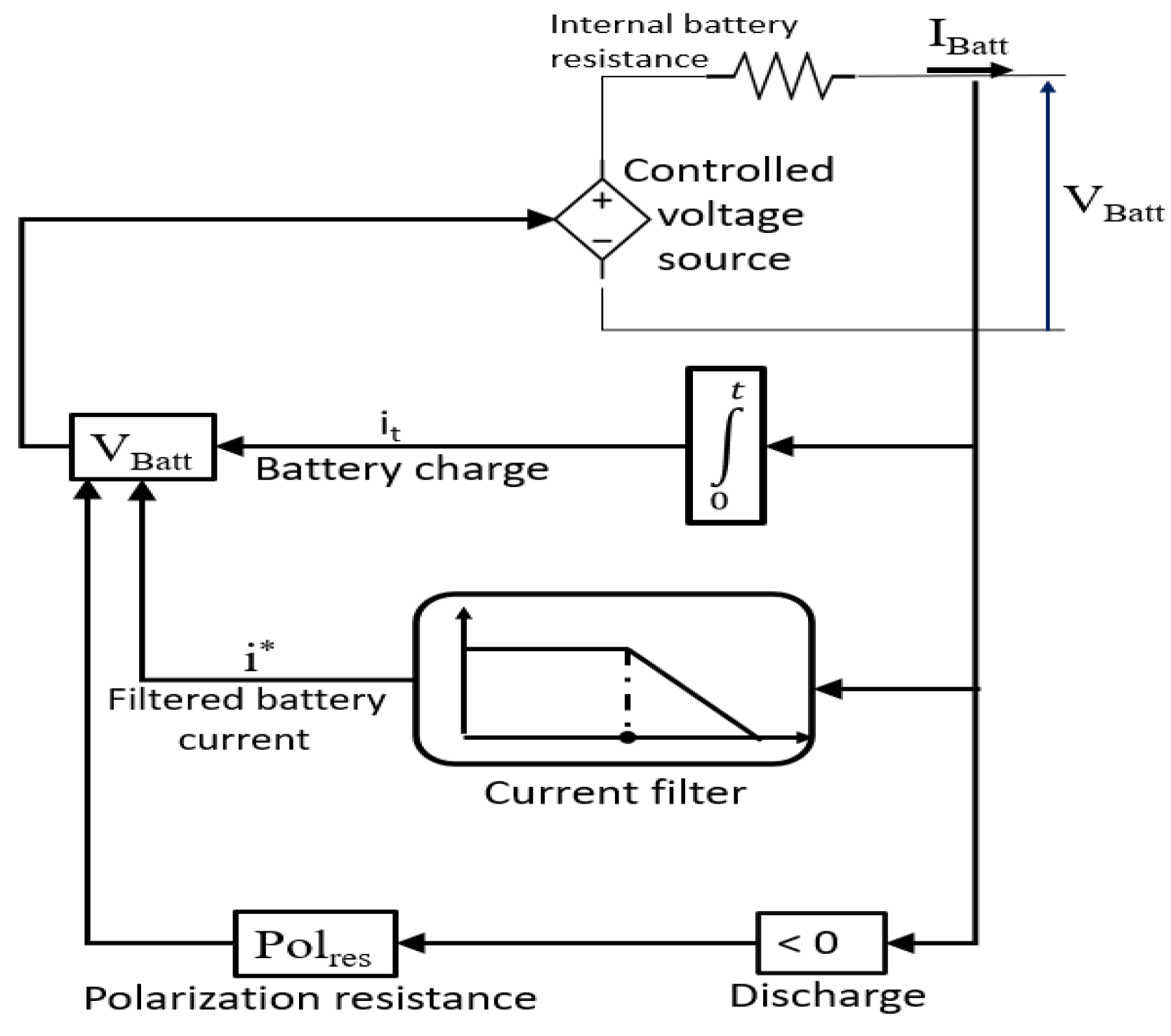
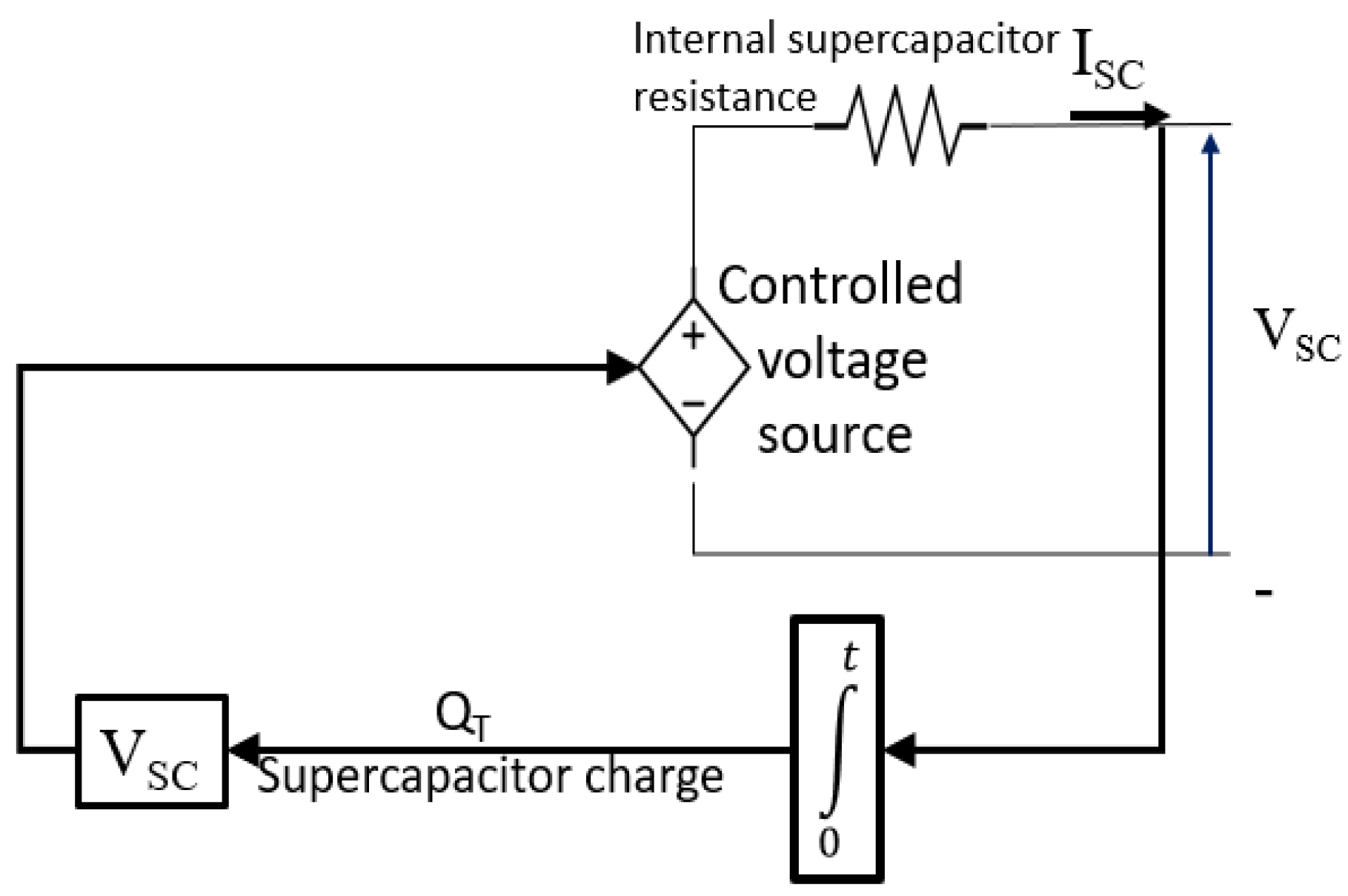
2. HPS Topology Structure and Modeling
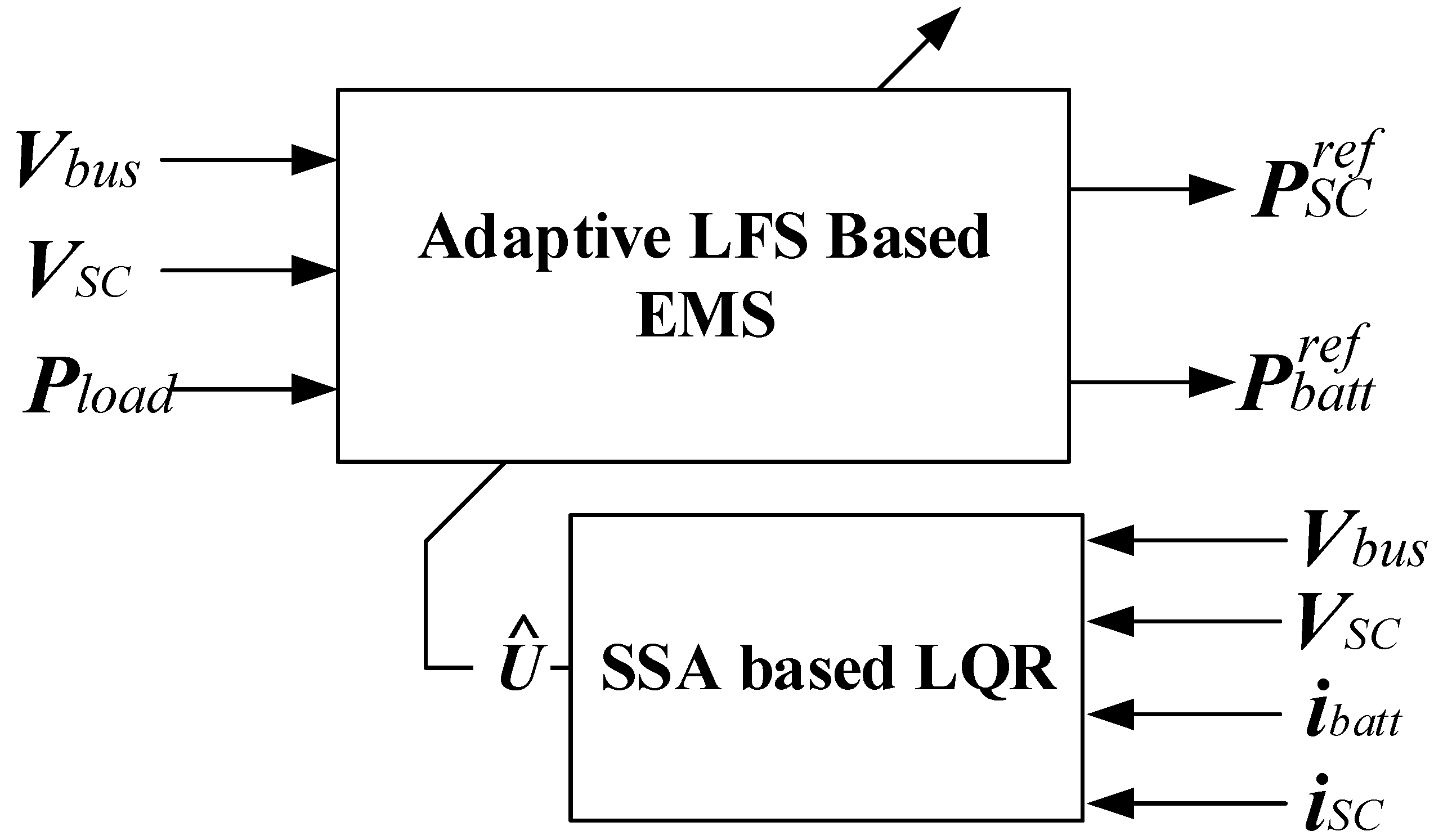
3. The Proposed EMS
3.1. LQR Controller
3.2. SSA Optimizer
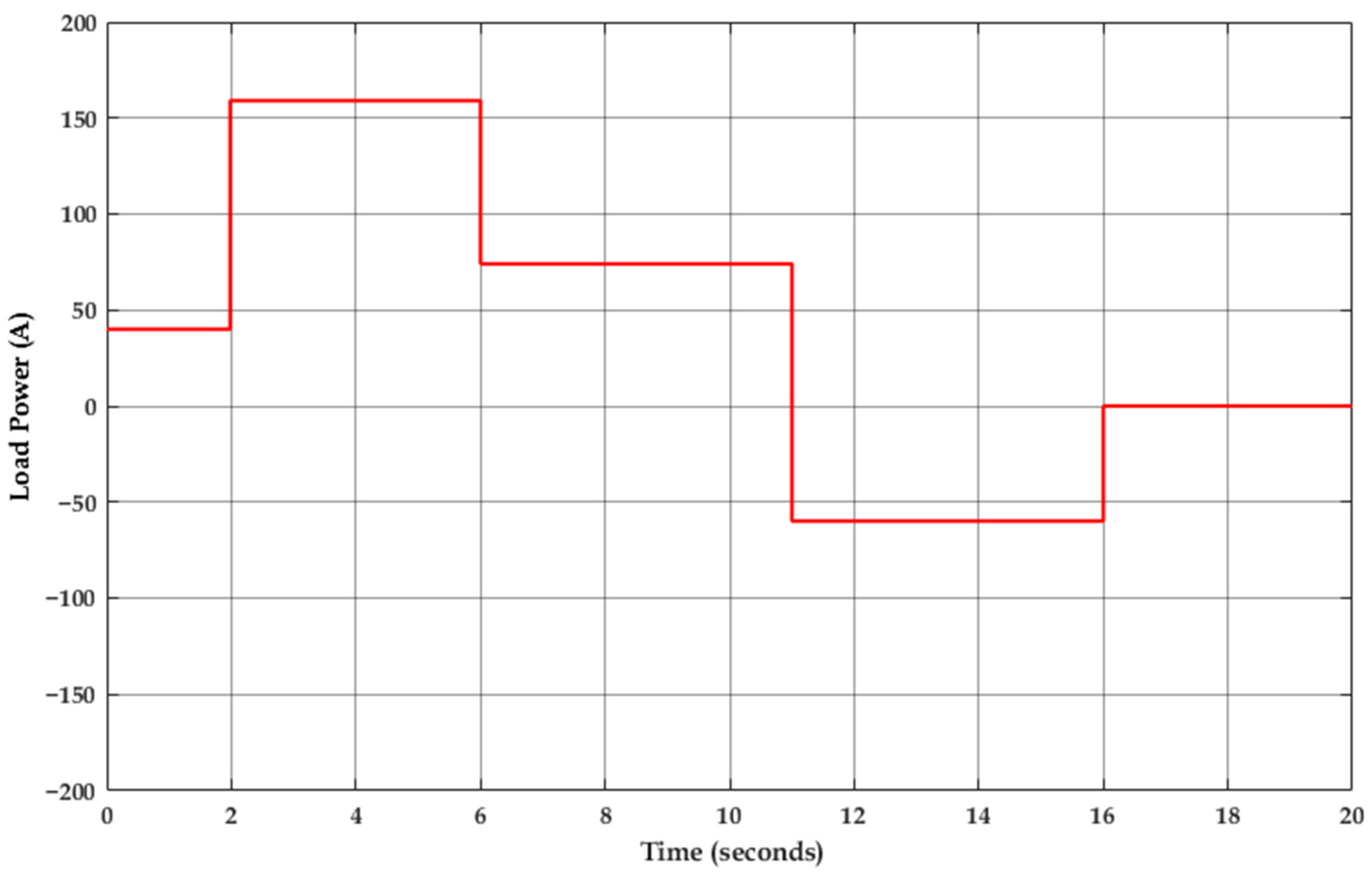
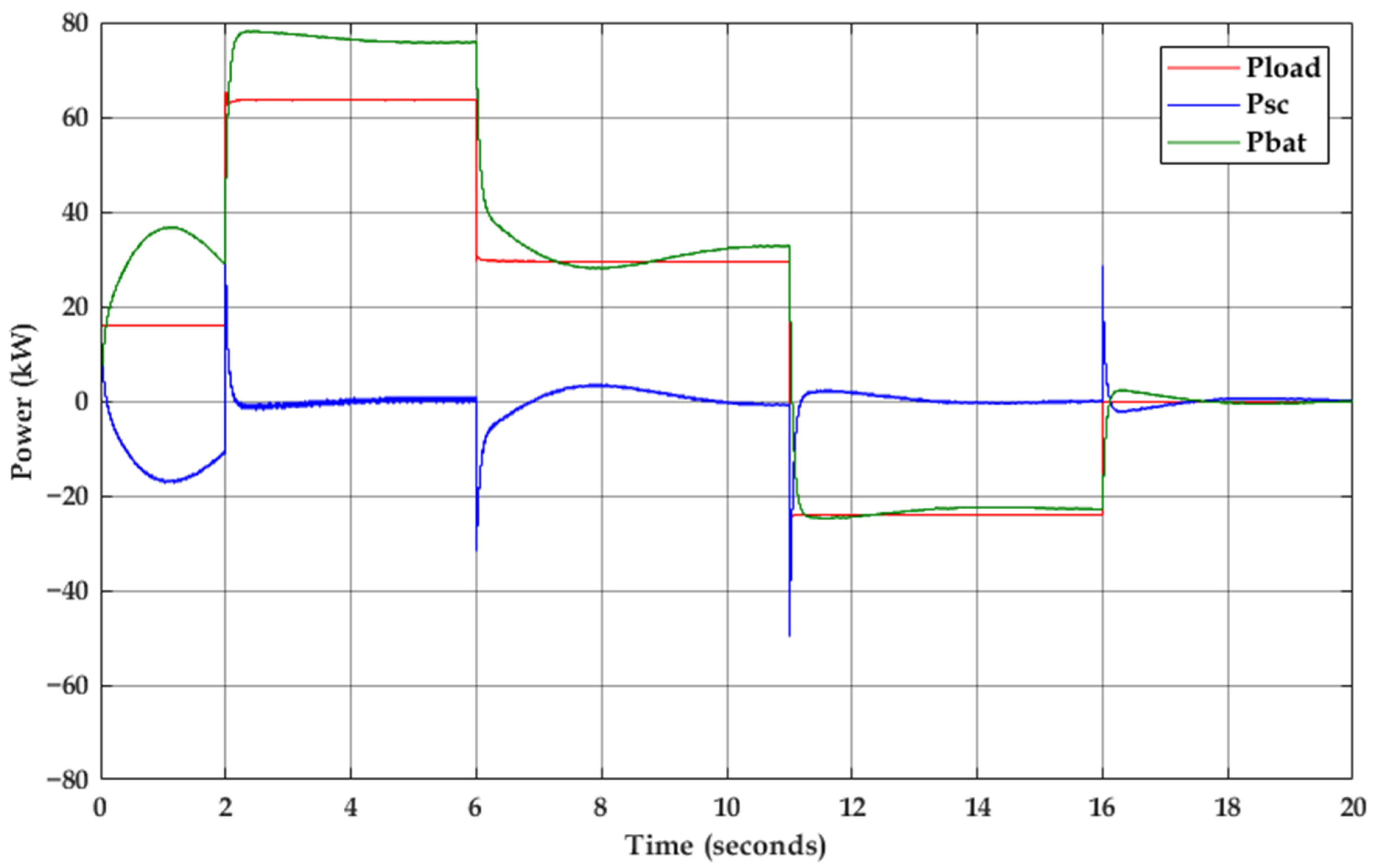
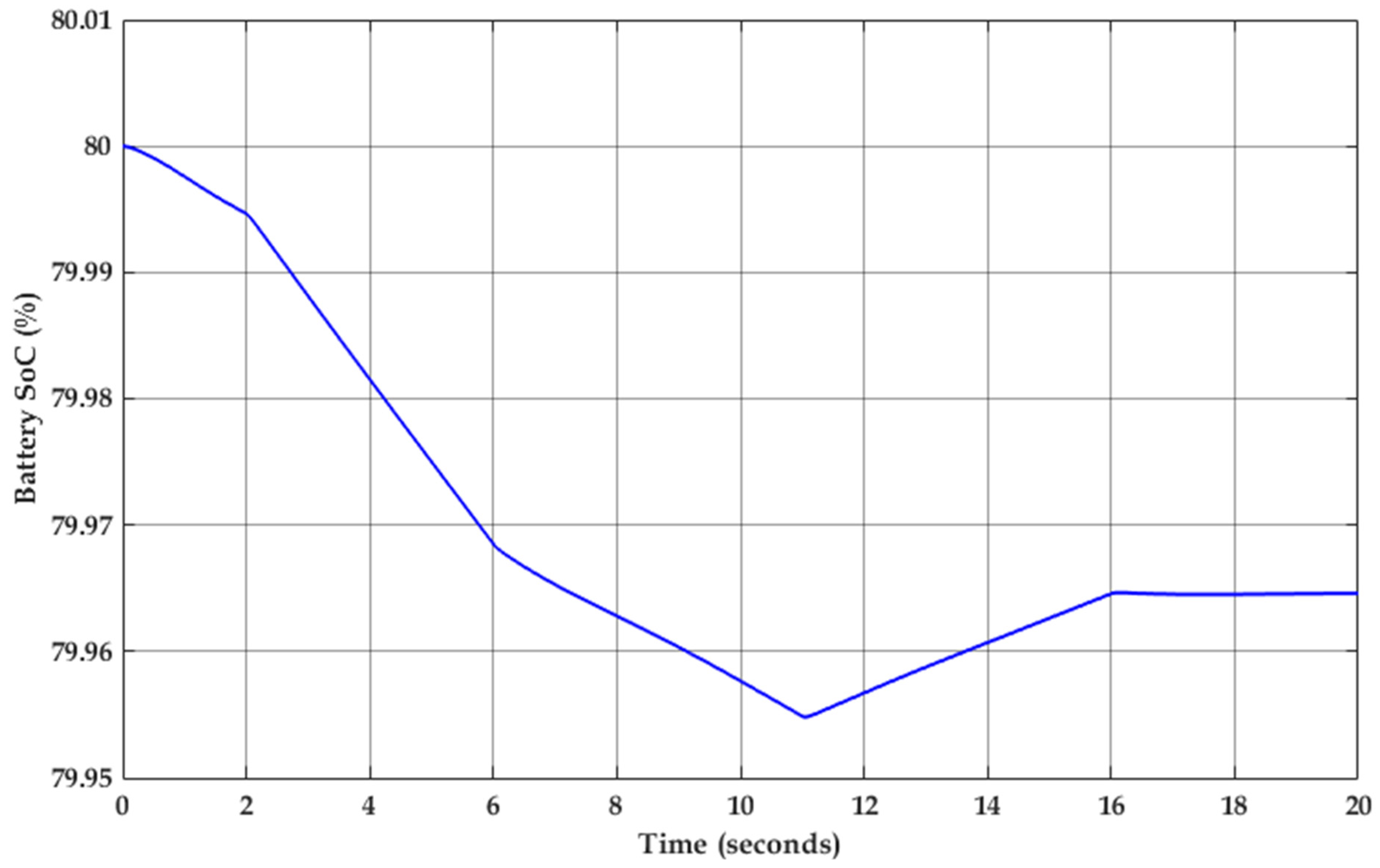
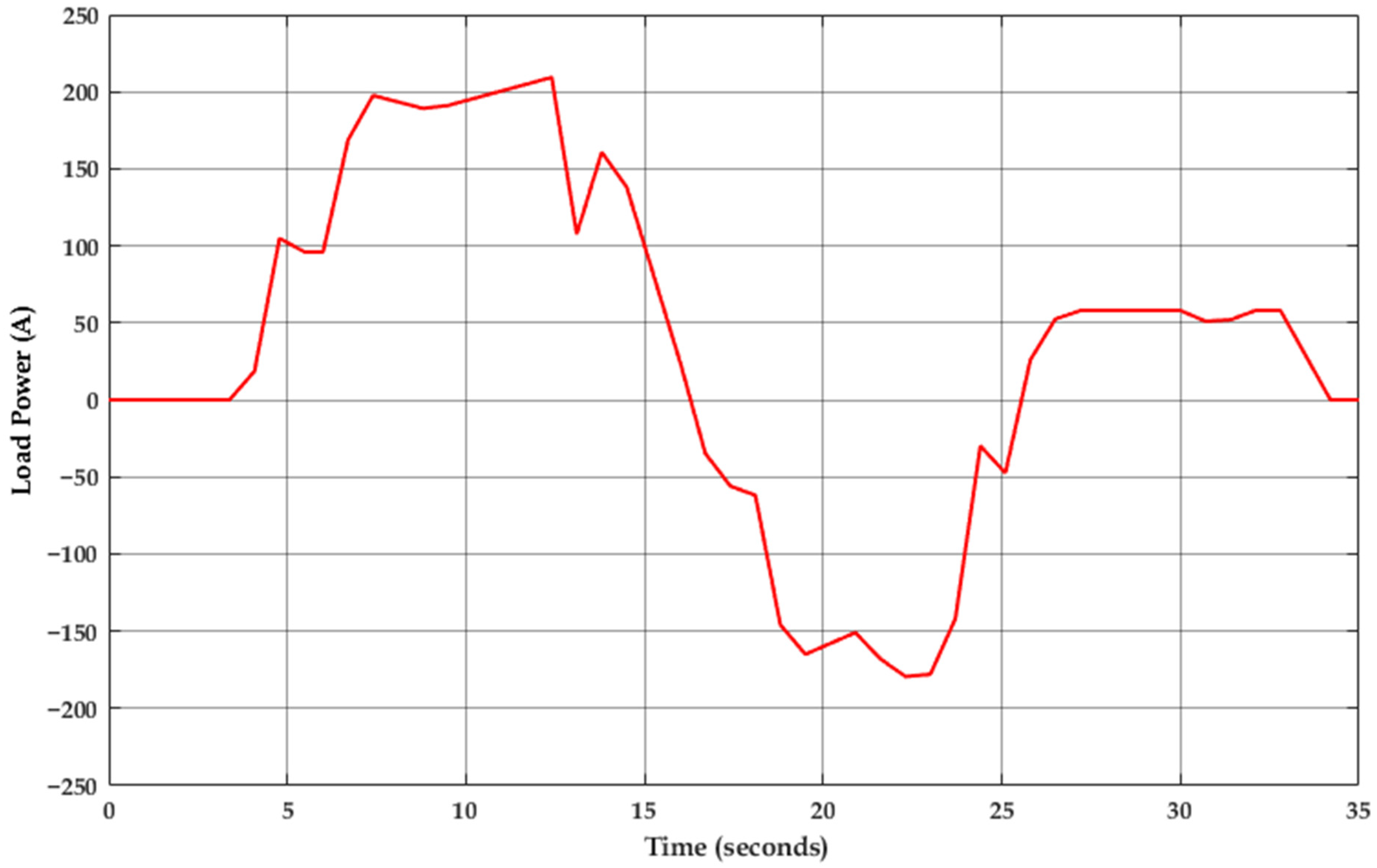
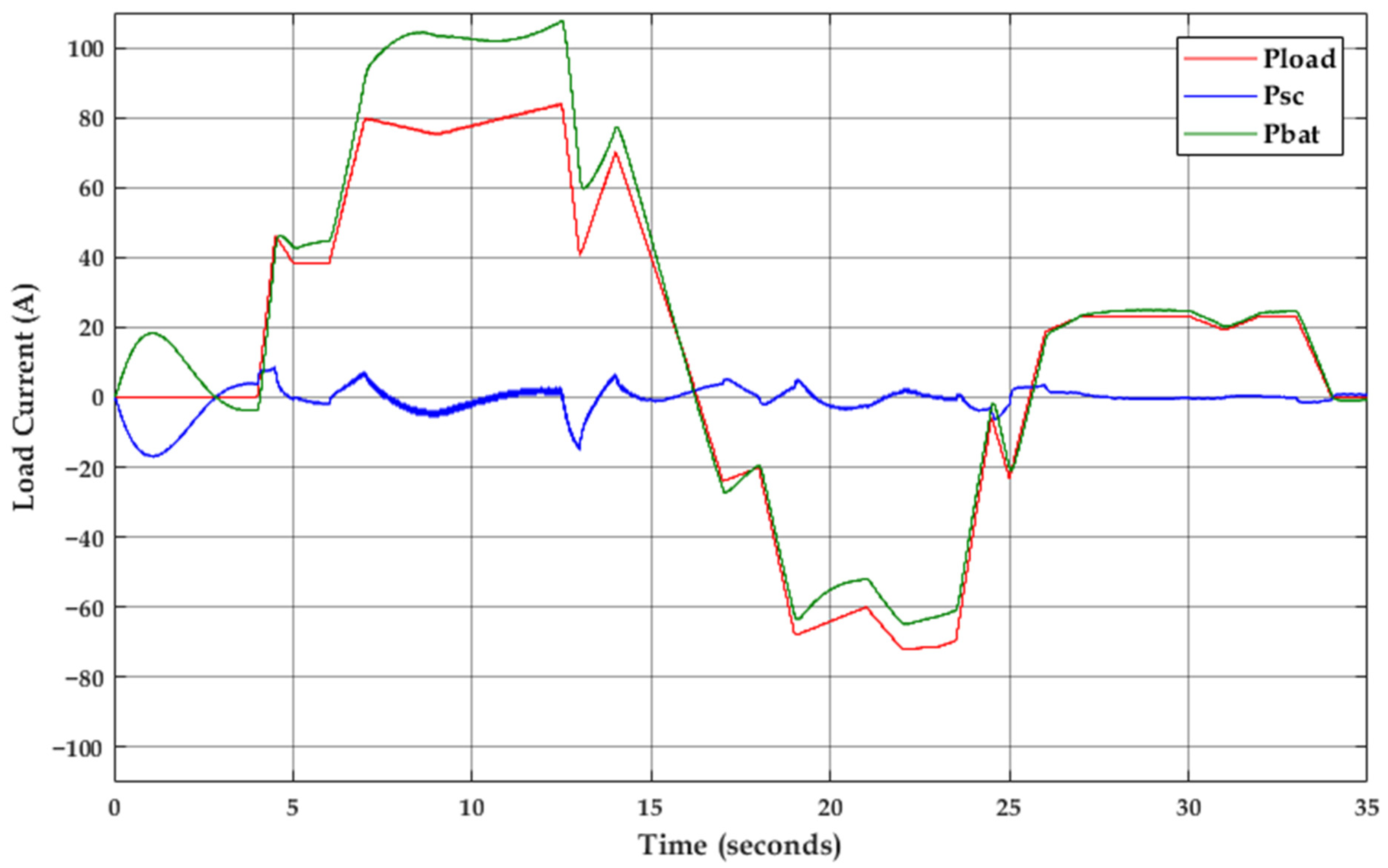
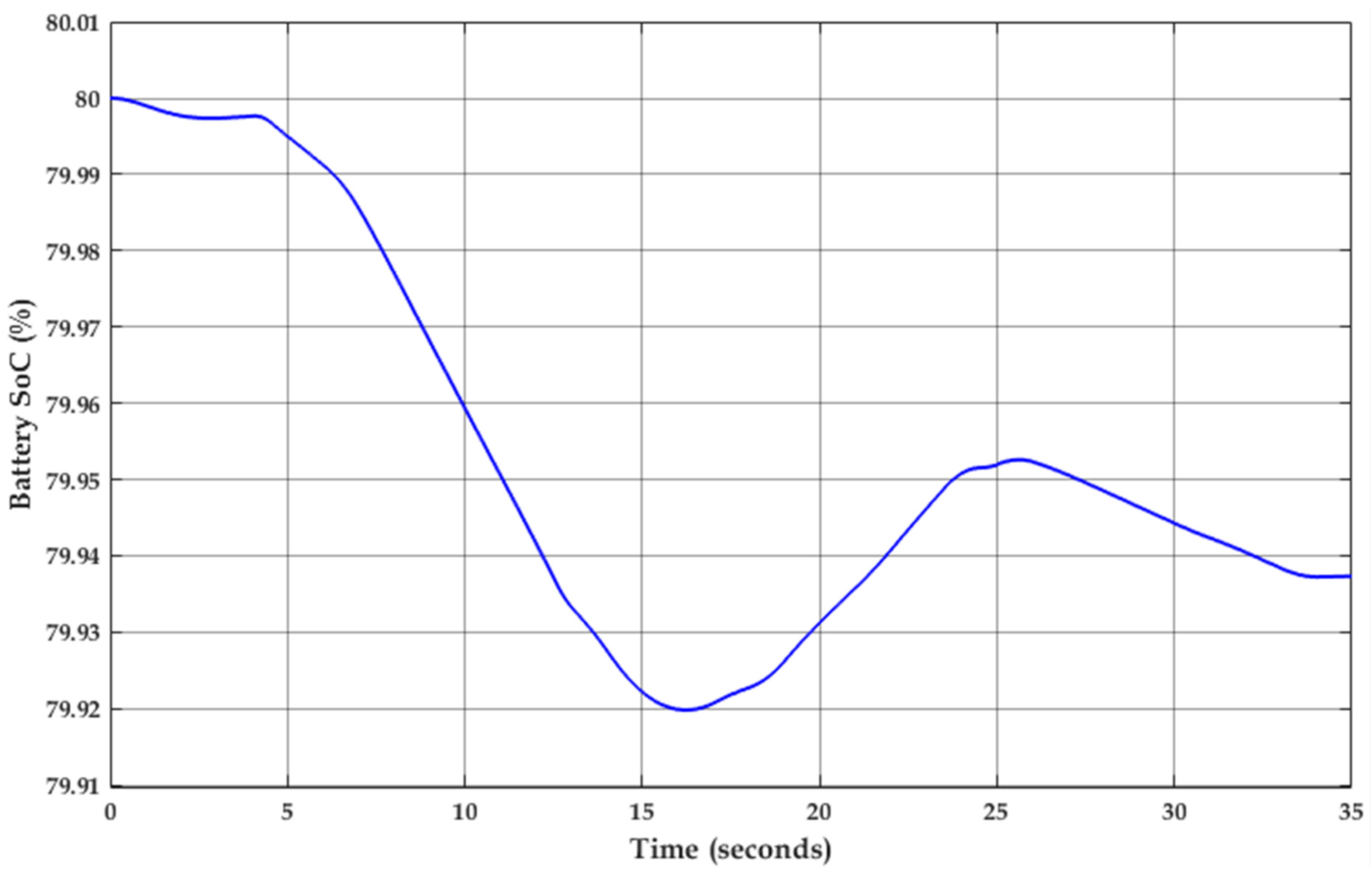
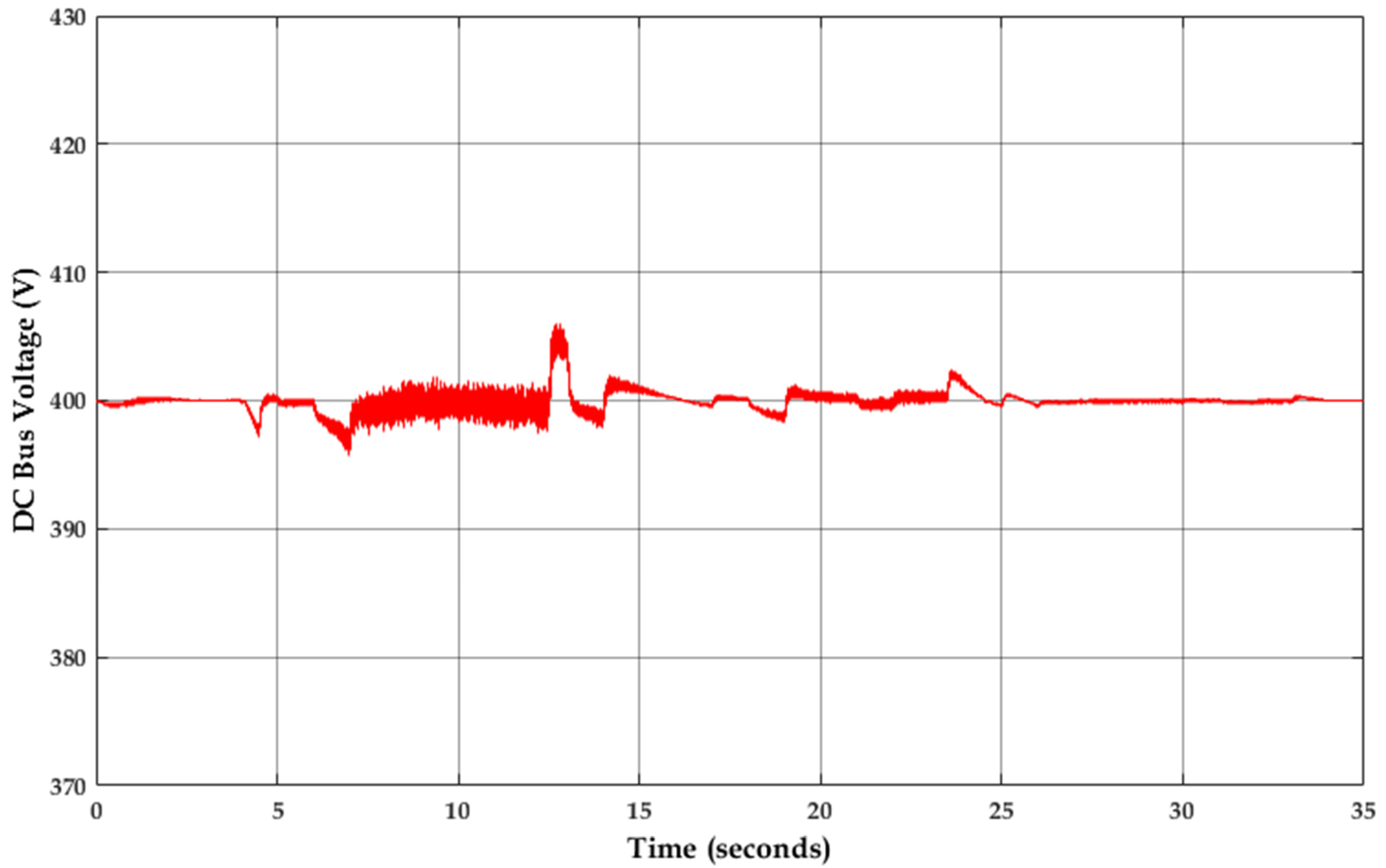
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. LQR Matrices
References
- Paska, J.; Biczel, P.; Kłos, M. Hybrid power systems—An effective way of utilising primary energy sources. Renew. Energy 2009, 34, 2414–2421. [Google Scholar] [CrossRef]
- Lü, X.; Wu, Y.; Lian, J.; Zhang, Y.; Chen, C.; Wang, P.; Meng, L. Energy management of hybrid electric vehicles: A review of energy optimization of fuel cell hybrid power system based on genetic algorithm. Energy Convers. Manag. 2020, 205, 112474. [Google Scholar] [CrossRef]
- Sorlei, I.-S.; Bizon, N.; Thounthong, P.; Varlam, M.; Carcadea, E.; Culcer, M.; Iliescu, M.; Raceanu, M. Fuel Cell Electric Vehicles—A Brief Review of Current Topologies and Energy Management Strategies. Energies 2021, 14, 252. [Google Scholar] [CrossRef]
- Shigeta, N.; Hosseini, S.E. Sustainable Development of the Automobile Industry in the United States, Europe, and Japan with Special Focus on the Vehicles’ Power Sources. Energies 2020, 14, 78. [Google Scholar] [CrossRef]
- Ou, K.; Yuan, W.-W.; Choi, M.; Yang, S.; Jung, S.; Kim, Y.-B. Optimized power management based on adaptive-PMP algorithm for a stationary PEM fuel cell/battery hybrid system. Int. J. Hydrogen Energy 2018, 43, 15433–15444. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A. Fuel cell application in the automotive industry and future perspective. Energy 2021, 214, 118955. [Google Scholar] [CrossRef]
- Ferahtia, S.; Djerioui, A.; Zeghlache, S.; Houari, A. A hybrid power system based on fuel cell, photovoltaic source and supercapacitor. SN Appl. Sci. 2020, 2, 940. [Google Scholar] [CrossRef]
- Xun, Q.; Liu, Y.; Holmberg, E. A Comparative Study of Fuel Cell Electric Vehicles Hybridization with Battery or Supercapacitor. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalf, Italy, 20–22 June 2018; pp. 389–394. [Google Scholar]
- Hemi, H.; M’Sirdi, N.K.; Naamane, A. A new proposed shepherd model of a li-ion open circuit battery based on data fitting. In Proceedings of the 12th International Conference and Analysis in Applied Control and Automation, IMAACA 2019, Lisbon, Portugal, 18–20 September 2019; pp. 83–92. [Google Scholar]
- Qi, W.; Li, Y.; Li, H.; Wayne, S.W.; Lin, X. The development and numerical verification of a compromised real time optimal control algorithm for hybrid electric vehicle. J. Power Sources 2019, 443, 227272. [Google Scholar] [CrossRef]
- Zhang, Z.; Guan, C.; Liu, Z. Real-Time Optimization Energy Management Strategy for Fuel Cell Hybrid Ships Considering Power Sources Degradation. IEEE Access 2020, 8, 87046–87059. [Google Scholar] [CrossRef]
- Wang, X.; Huang, Y.; Guo, F.; Zhao, W. Energy Management Strategy based on Dynamic Programming Considering Engine Dynamic Operating Conditions Optimization. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5485–5492. [Google Scholar]
- Zhang, S.; Xiong, R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming. Appl. Energy 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Sun, L.; Jin, Y.; Shen, J.; You, F. Sustainable Residential Micro-Cogeneration System Based on a Fuel Cell Using Dynamic Programming-Based Economic Day-Ahead Scheduling. ACS Sustain. Chem. Eng. 2021. [Google Scholar] [CrossRef]
- Leroy, T.; Vidal-Naquet, F.; Tona, P. Stochastic Dynamic Programming based Energy Management of HEV’s: An Experimental Validation. IFAC Proc. Vol. 2014, 47, 4813–4818. [Google Scholar] [CrossRef]
- Panday, A.; Bansal, H.O. Energy management strategy for hybrid electric vehicles using genetic algorithm. J. Renew. Sustain. Energy 2016, 8, 015701. [Google Scholar] [CrossRef]
- Shi, W.; Li, N.; Chu, C.C.; Gadh, R. Real-Time Energy Management in Microgrids. IEEE Trans. Smart Grid 2017, 8, 228–238. [Google Scholar] [CrossRef]
- Borhan, H.; Member, S.; Vahidi, A.; Phillips, A.M.; Kuang, M.L.; Kolmanovsky, I.V.; Cairano, S. Di MPC-Based Energy Management of a Power-Split Hybrid Electric Vehicle. IEEE Trans. Control Syst. Technol. 2012, 20, 593–603. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Khajepour, A.; He, H.; Ji, J. Model predictive control power management strategies for HEVs: A review. J. Power Sources 2017, 341, 91–106. [Google Scholar] [CrossRef]
- Motapon, S.N.; Dessaint, L.A.; Al-Haddad, K. A robust H2-consumption-minimization-based energy management strategy for a fuel cell hybrid emergency power system of more electric aircraft. IEEE Trans. Ind. Electron. 2014, 61, 6148–6156. [Google Scholar] [CrossRef]
- Lei, Z.; Qin, D.; Hou, L.; Peng, J.; Liu, Y.; Chen, Z. An adaptive equivalent consumption minimization strategy for plug-in hybrid electric vehicles based on traffic information. Energy 2020, 190, 116409. [Google Scholar] [CrossRef]
- Dhifli, M.; Jawadi, S.; Lashab, A.; Guerrero, J.M.; Cherif, A. An Efficient External Energy Maximization-based Energy Management Strategy for a Battery/Supercapacitor of a Micro Grid System. Int. J. Comput. Sci. Netw. Secur. 2020, 20, 196–203. [Google Scholar]
- Han, Y.; Chen, W.; Li, Q. Energy management strategy based on multiple operating states for a photovoltaic/fuel cell/energy storage DC microgrid. Energies 2017, 10, 136. [Google Scholar] [CrossRef]
- Konara, K.M.S.Y.; Kolhe, M.L.; Sharma, A. Power dispatching techniques as a finite state machine for a standalone photovoltaic system with a hybrid energy storage. AIMS Energy 2020, 8, 214–230. [Google Scholar] [CrossRef]
- Corcau, J.I.; Dinca, L. Fuzzy Energy Management Scheme for a Hybrid Power Sources of High-Altitude Pseudosatellite. Model. Simul. Eng. 2020, 2020, 5459098. [Google Scholar] [CrossRef]
- Al-Sakkaf, S.; Kassas, M.; Khalid, M.; Abido, M.A. An energy management system for residential autonomous DC microgrid using optimized fuzzy logic controller considering economic dispatch. Energies 2019, 12, 1457. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, T.; Liu, D.; Sun, F. Reinforcement learning-based real-time energy management for a hybrid tracked vehicle. Appl. Energy 2016, 171, 372–382. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Gooi, H.B. Optimization strategy based on deep reinforcement learning for home energy management. CSEE J. Power Energy Syst. 2020, 6, 572–582. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Z.; Li, W.; Wang, Y.; Li, Y.; Sauer, D. Battery Thermal- and Health-Constrained Energy Management for Hybrid Electric Bus based on Soft Actor-Critic DRL Algorithm. IEEE Trans. Ind. Inform. 2021. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Z.; Liu, K.; Quan, Z.; Li, Y. Battery-Involved Energy Management for Hybrid Electric Bus Based on Expert-Assistance Deep Deterministic Policy Gradient Algorithm. IEEE Trans. Veh. Technol. 2020, 69, 12786–12796. [Google Scholar] [CrossRef]
- Hemi, H.; Ghouili, J.; Cheriti, A. A real time fuzzy logic power management strategy for a fuel cell vehicle. Energy Convers. Manag. 2014, 80, 63–70. [Google Scholar] [CrossRef]
- Jia, Z.; Jiang, J.; Lin, H.; Cheng, L. A Real-time MPC-based Energy Management of Hybrid Energy Storage System in Urban Rail Vehicles. Energy Procedia 2018, 152, 526–531. [Google Scholar] [CrossRef]
- Bizon, N.; Oproescu, M. Experimental Comparison of Three Real-Time Optimization Strategies Applied to Renewable/FC-Based Hybrid Power Systems Based on Load-Following Control. Energies 2018, 11, 3537. [Google Scholar] [CrossRef]
- Bizon, N. Real-time optimization strategies of Fuel Cell Hybrid Power Systems based on Load-following control: A new strategy, and a comparative study of topologies and fuel economy obtained. Appl. Energy 2019, 241, 444–460. [Google Scholar] [CrossRef]
- Zhang, C.; Ordóñez, R. Extremum-Seeking Control and Applications; Advances in Industrial Control; Springer: London, UK, 2012; ISBN 978-1-4471-2223-4. [Google Scholar]
- Li, A. Analyse Expérimentale et Modélisation D’éléments de Batterie et de leurs Assemblages: Application aux Véhicules Electriques et Hybrides. Ph.D. Thesis, Universite Claude Bernard Lyon 1, Villeurbanne, France, 2015. [Google Scholar]
- Wang, T.; Li, Q.; Chen, W.; Liu, T. Application of energy management strategy based on state machine in fuel cell hybrid power system. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Chicago, IL, USA, 22–24 June 2017; pp. 1–5. [Google Scholar]
- Zhang, Q.; Deng, W.; Zhang, S.; Wu, J. A Rule Based Energy Management System of Experimental Battery/Supercapacitor Hybrid Energy Storage System for Electric Vehicles. J. Control Sci. Eng. 2016, 1–17. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| R1, R2 (Ω) | 0.1 |
| L1, L2 (mH) | 2 |
| (V) | 200 |
| (V) | 400 |
| CSC (F) | 120 |
| Cbus (µF) | 2000 |
| Cbatt (Ah) | 1500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferahtia, S.; Djeroui, A.; Mesbahi, T.; Houari, A.; Zeghlache, S.; Rezk, H.; Paul, T. Optimal Adaptive Gain LQR-Based Energy Management Strategy for Battery–Supercapacitor Hybrid Power System. Energies 2021, 14, 1660. https://doi.org/10.3390/en14061660
Ferahtia S, Djeroui A, Mesbahi T, Houari A, Zeghlache S, Rezk H, Paul T. Optimal Adaptive Gain LQR-Based Energy Management Strategy for Battery–Supercapacitor Hybrid Power System. Energies. 2021; 14(6):1660. https://doi.org/10.3390/en14061660
Chicago/Turabian StyleFerahtia, Seydali, Ali Djeroui, Tedjani Mesbahi, Azeddine Houari, Samir Zeghlache, Hegazy Rezk, and Théophile Paul. 2021. "Optimal Adaptive Gain LQR-Based Energy Management Strategy for Battery–Supercapacitor Hybrid Power System" Energies 14, no. 6: 1660. https://doi.org/10.3390/en14061660
APA StyleFerahtia, S., Djeroui, A., Mesbahi, T., Houari, A., Zeghlache, S., Rezk, H., & Paul, T. (2021). Optimal Adaptive Gain LQR-Based Energy Management Strategy for Battery–Supercapacitor Hybrid Power System. Energies, 14(6), 1660. https://doi.org/10.3390/en14061660










