The Investigation of Fracture Networks on Heat Extraction Performance for an Enhanced Geothermal System
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Assumptions
- (1)
- Any individual fracture is assumed to be uniform and isotropic within the same fracture conductivity. The length and conductivity can vary for different fractures. The rock matrix is assumed to be homogeneous. The embedded discrete fracture model is employed to model fractured EGS. The mass flow in matrix and fractures obeys Darcy’s law.
- (2)
- Water is used as circulating fluid and kept as in the state of liquid under reservoir conditions and the dry hot rock is saturated with single-phase water.
- (3)
- The process of heat convection and conduction is considered and the local thermal equilibrium is instantaneously reached.
2.2. Governing Equations
2.3. The Discretization of Mathematical Models
2.4. Solution to Mathematical Models
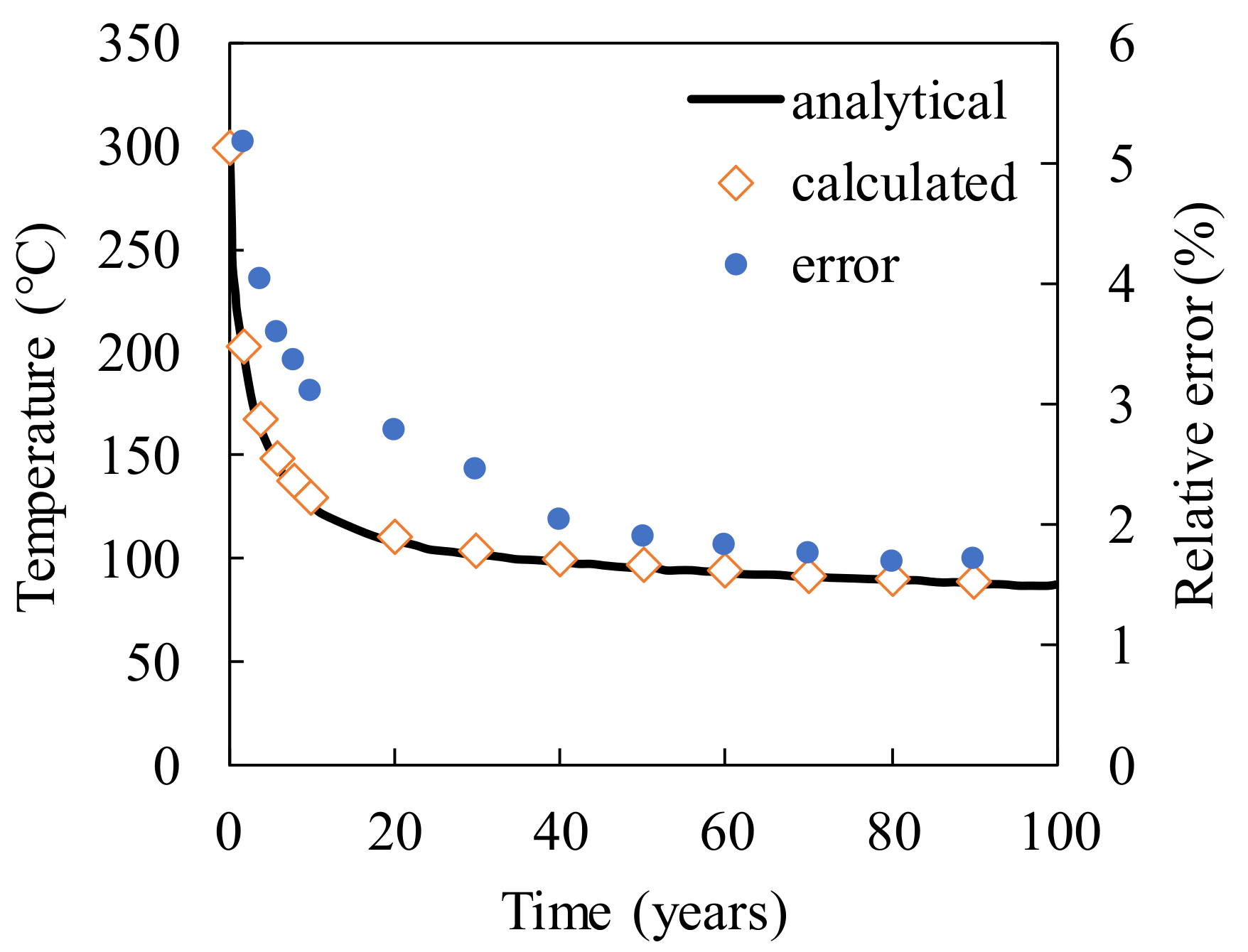
3. The Verification of the Mathematical Solution
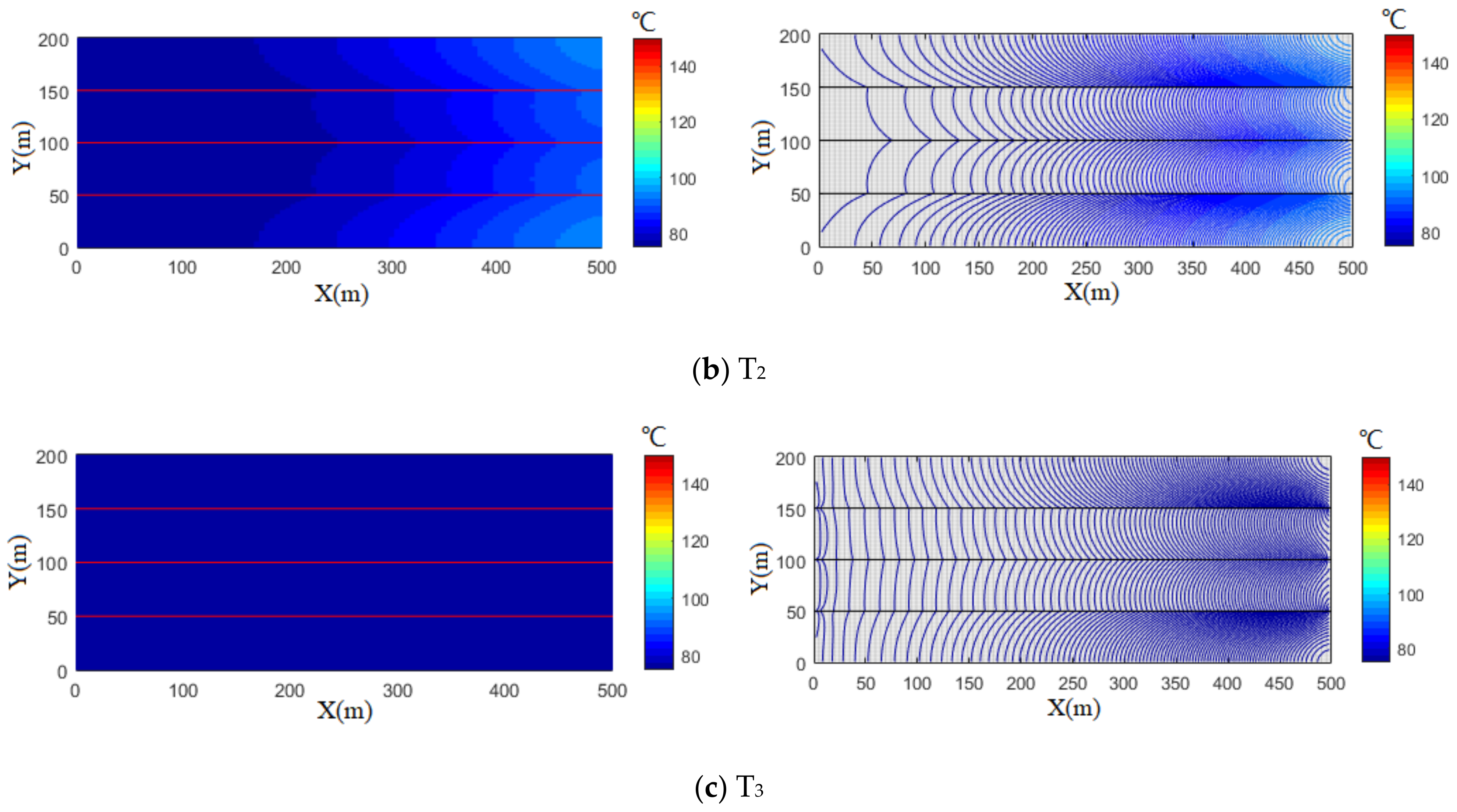
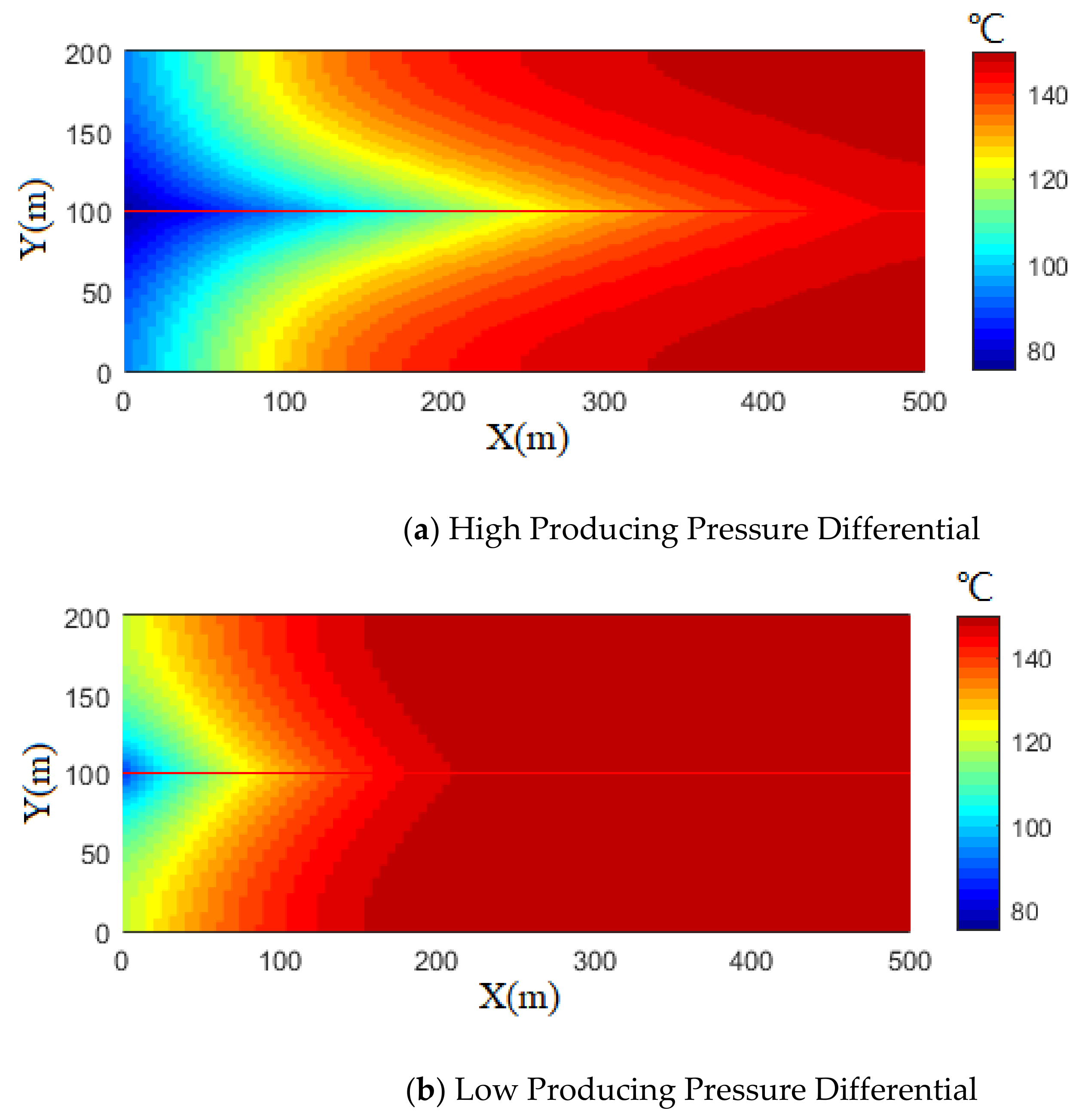
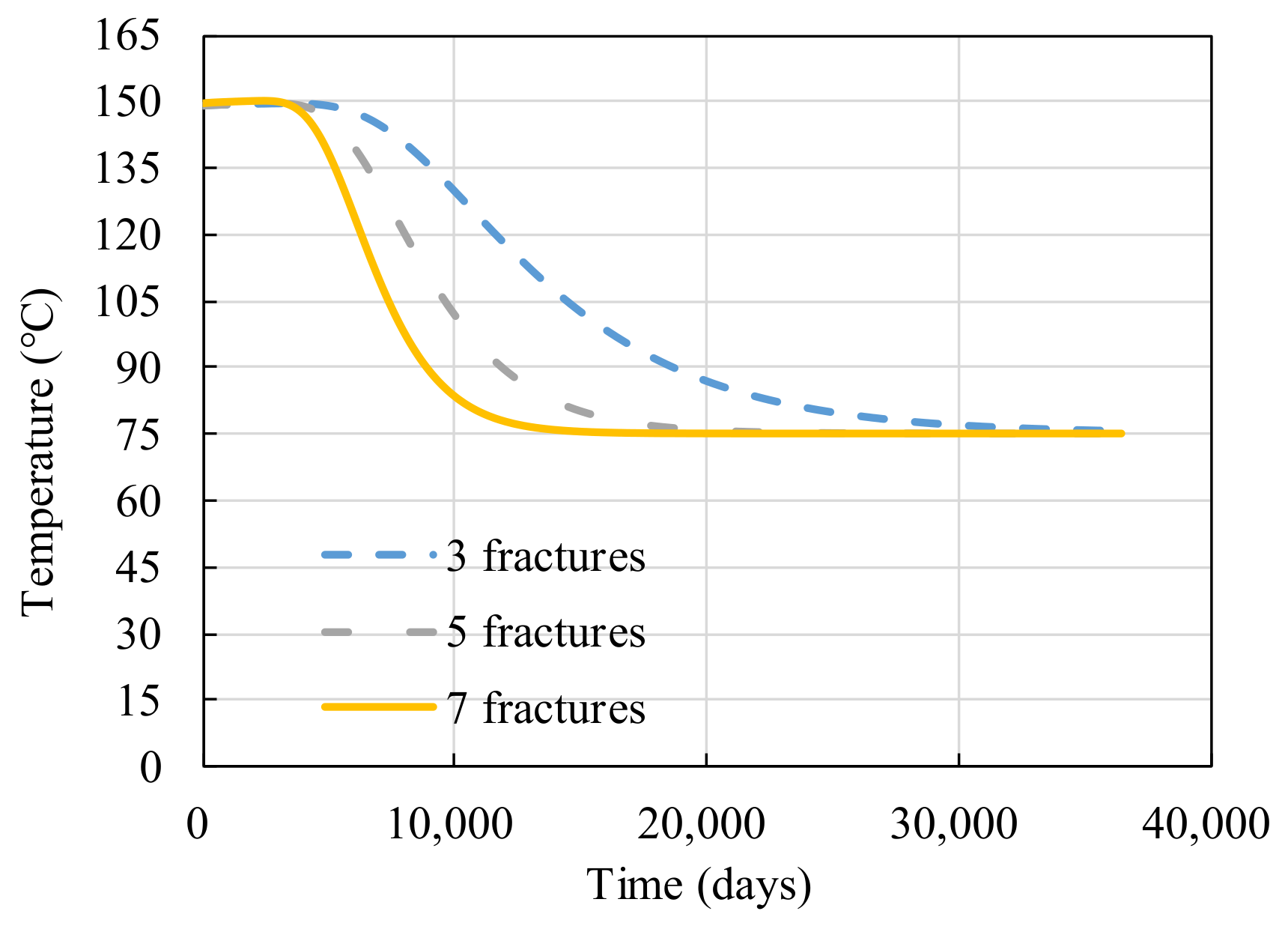
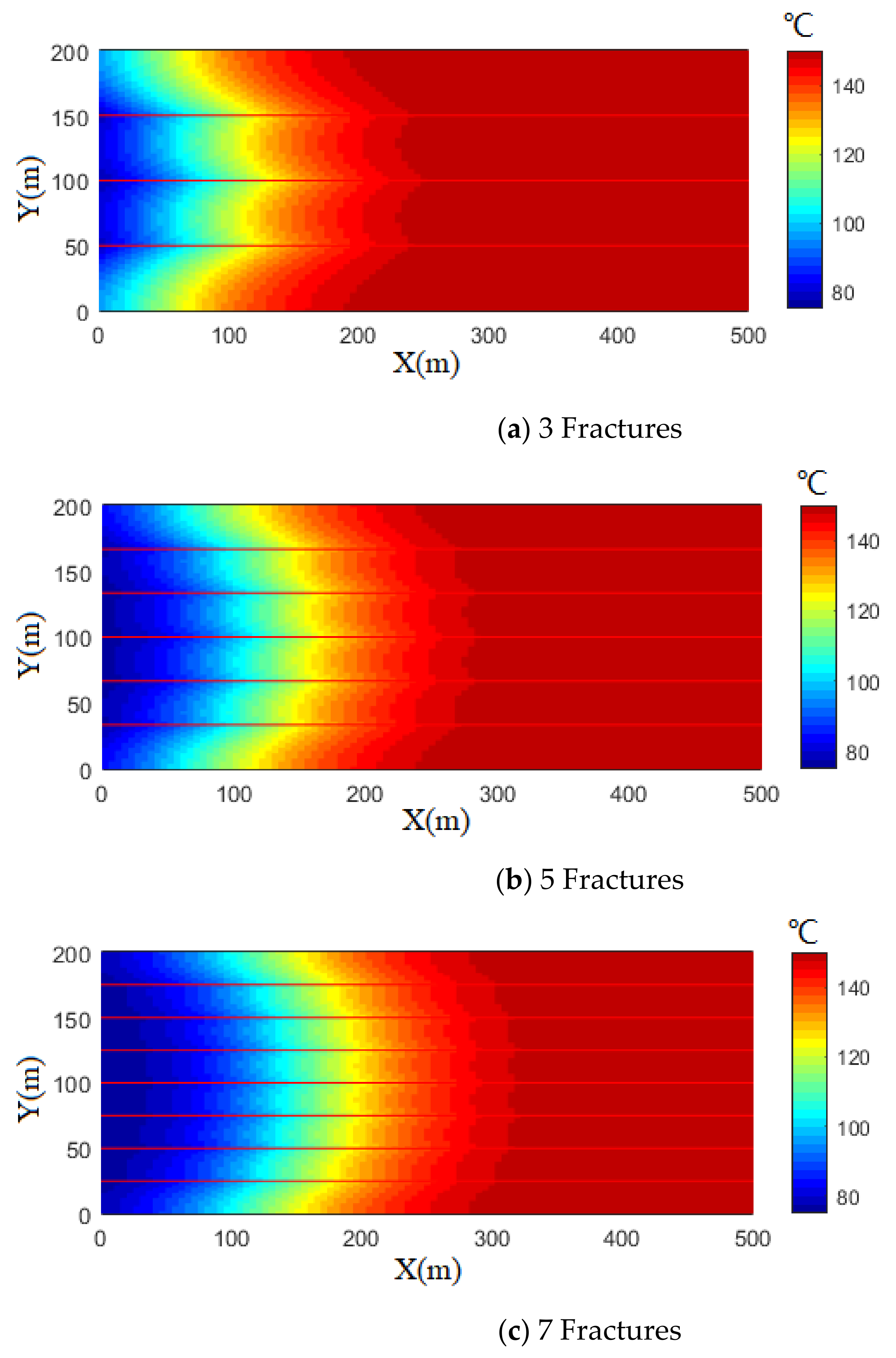
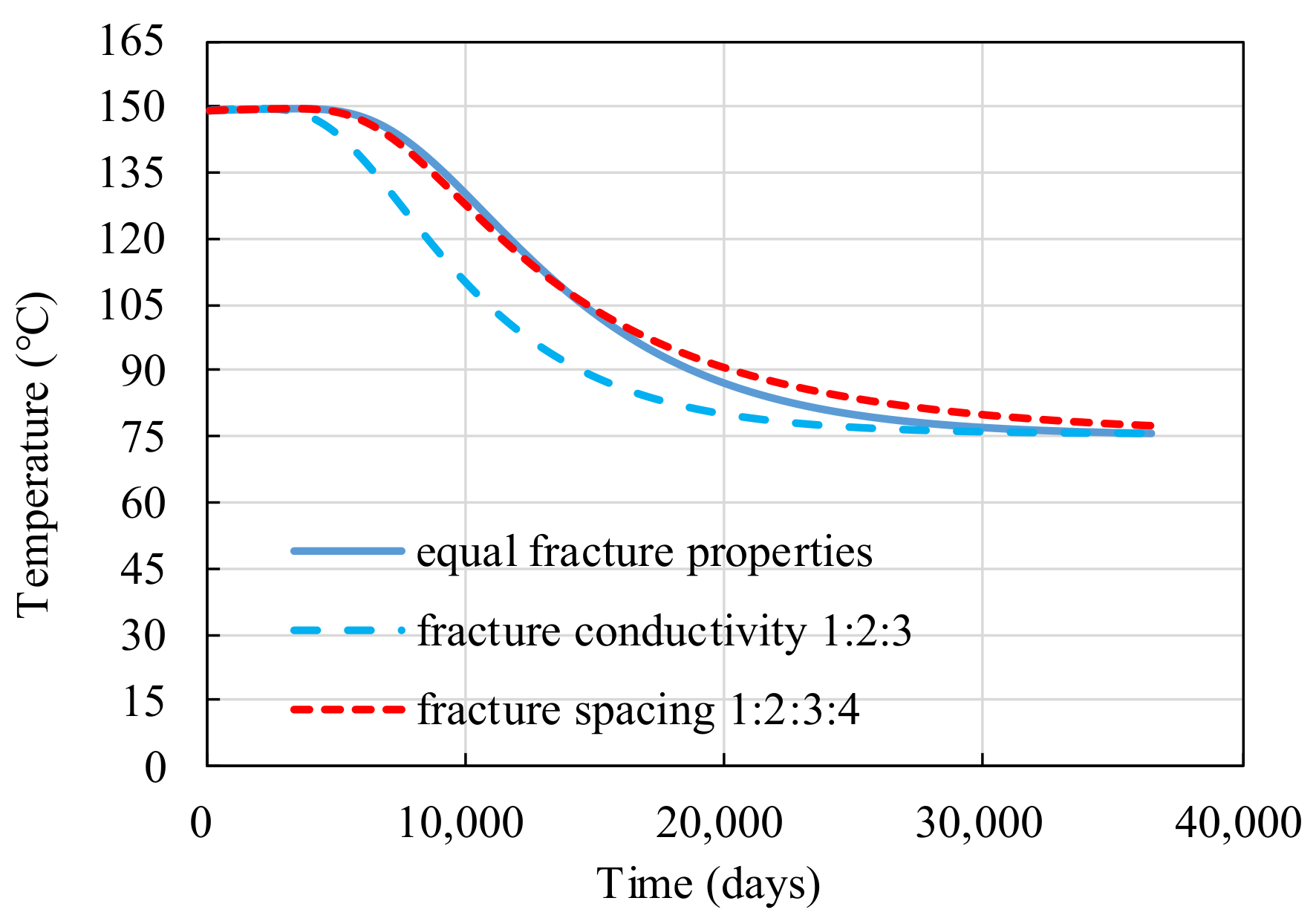
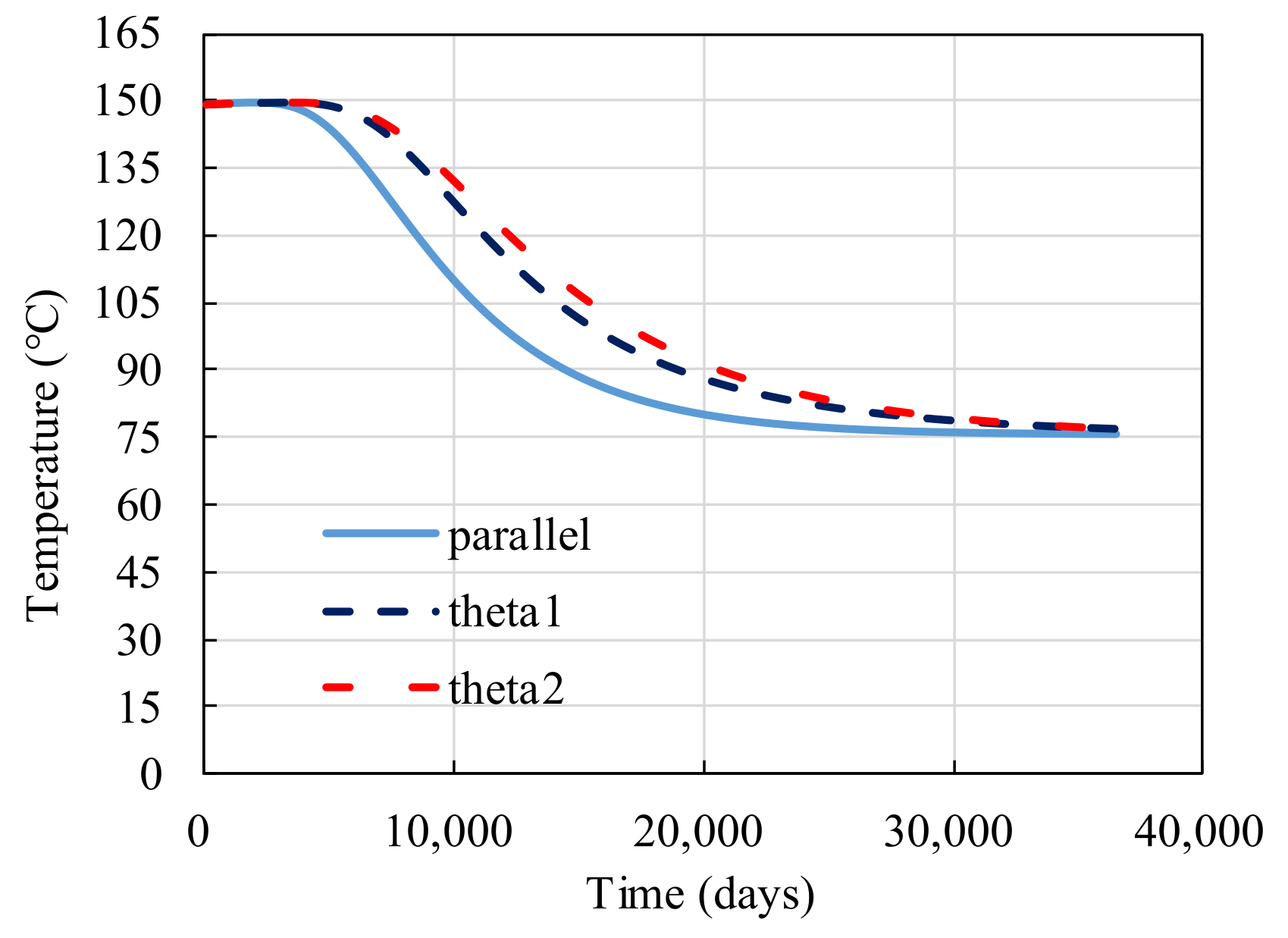
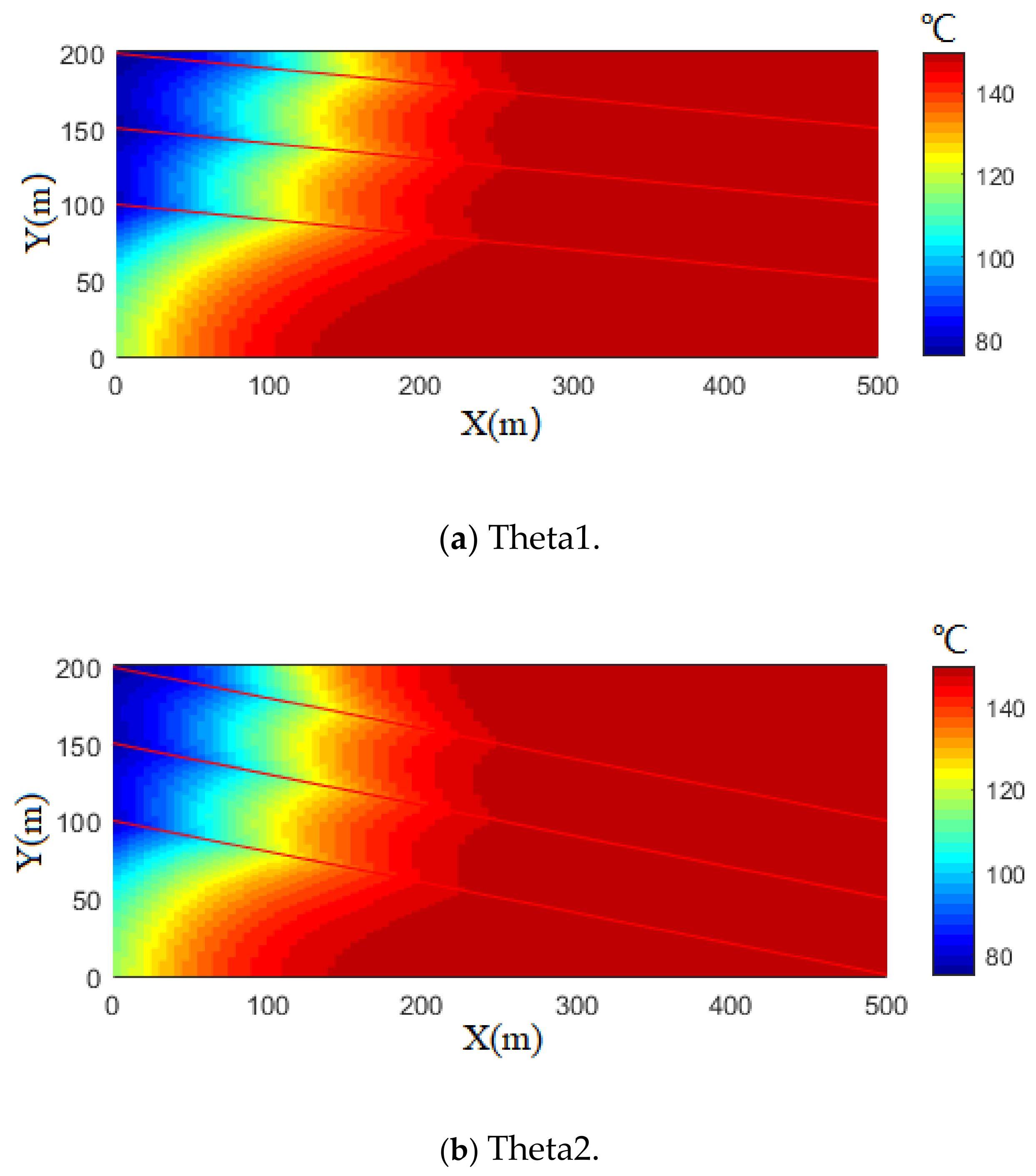
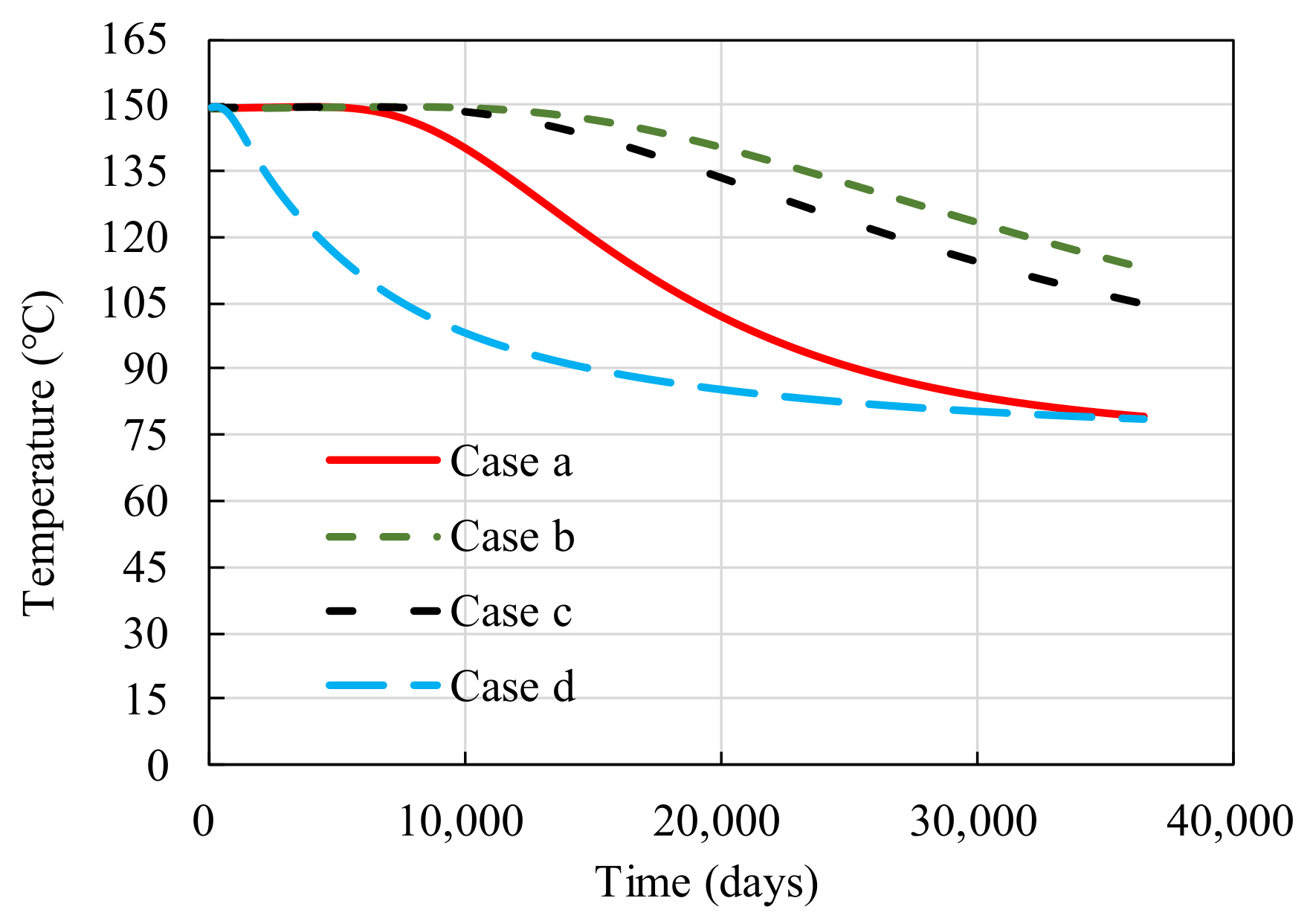
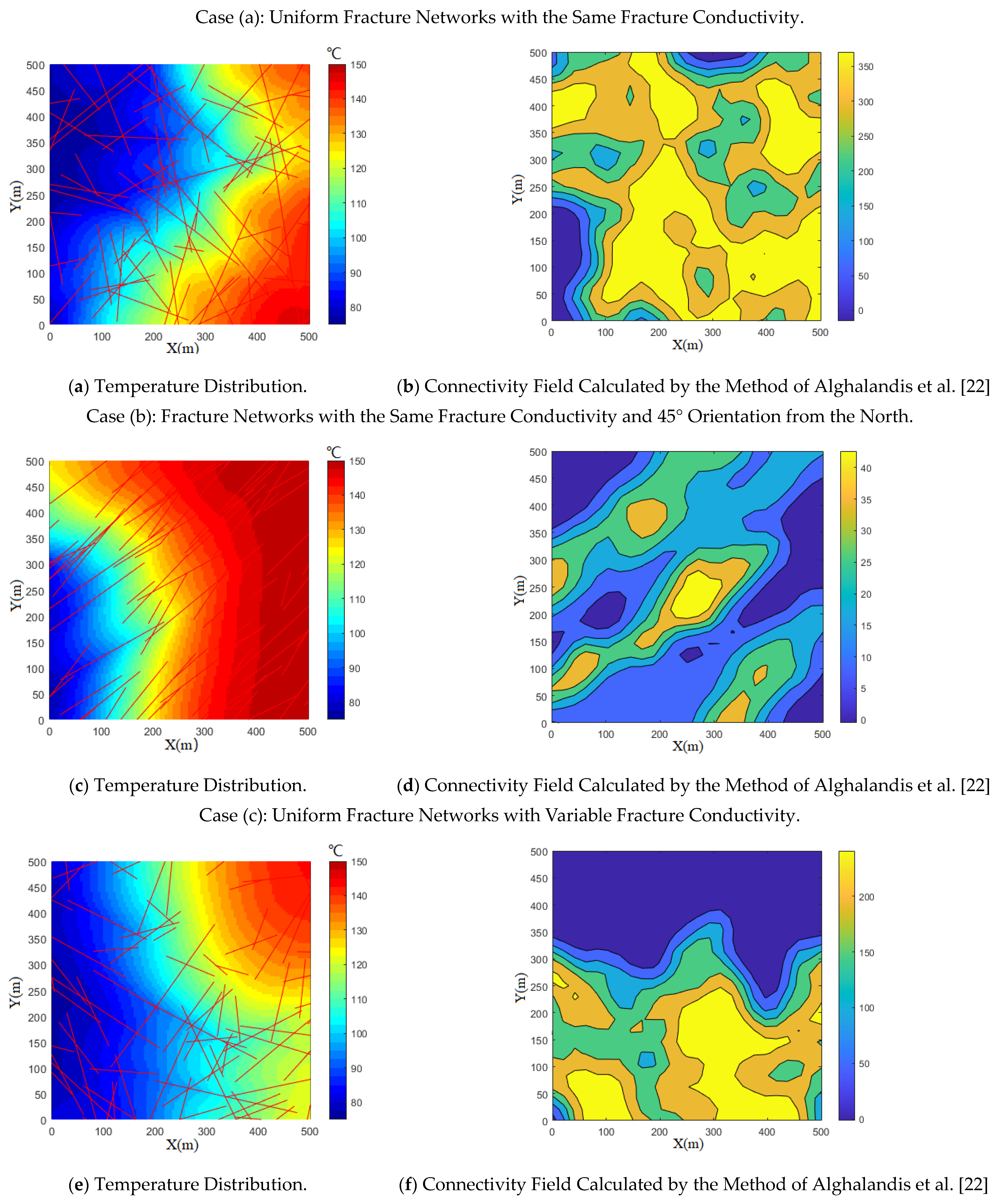
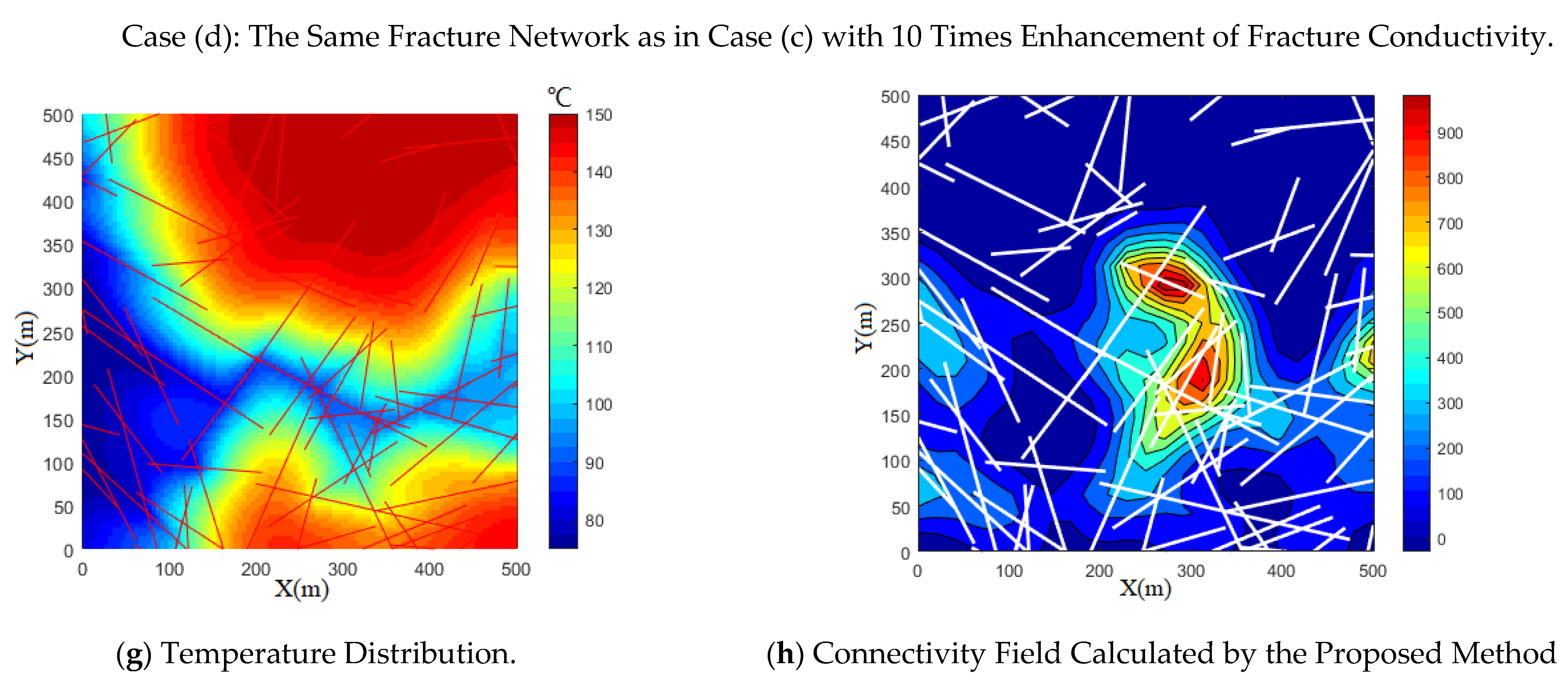
4. The Effects of Fracture Networks on the Heat Extraction Performance
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blackwell, D.D.; Negraru, P.T.; Richards, M.C. Assessment of the Enhanced Geothermal System Resource Base of the United States. Nat. Resour. Res. 2007, 15, 283–308. [Google Scholar] [CrossRef]
- Lu, S.-M. A global review of enhanced geothermal system (EGS). Renew. Sustain. Energy Rev. 2018, 81, 2902–2921. [Google Scholar] [CrossRef]
- Song, X.; Shi, Y.; Li, G.; Yang, R.; Wang, G.; Zheng, R.; Li, J.; Lyu, Z. Numerical simulation of heat extraction performance in enhanced geothermal system with multilateral wells. Appl. Energy 2018, 218, 325–337. [Google Scholar] [CrossRef]
- Sun, Z.; Xin, Y.; Yao, J.; Zhang, K.; Zhuang, L.; Zhu, X.; Wang, T.; Jiang, C. Numerical Investigation on the Heat Extraction Capacity of Dual Horizontal Wells in Enhanced Geothermal Systems Based on the 3-D THM Model. Energies 2018, 11, 280. [Google Scholar] [CrossRef]
- Olasolo, P.; Juárez, M.C.; Morales, M.P.; Liarte, I.A. Enhanced geothermal systems (EGS): A review. Renew. Sust. Energ. Rev. 2016, 56, 133–144. [Google Scholar] [CrossRef]
- Isaka, B.A.; Ranjith, P.G.; Rathnaweera, T.D. The use of super-critical carbon dioxide as the working fluid in enhanced geo-thermal systems (EGSs): A review study. Sustain. Energy Techm. 2019, 36, 100547. [Google Scholar]
- Song, W.; Wang, C.; Du, Y.; Shen, B.; Chen, S.; Jiang, Y. Comparative analysis on the heat transfer efficiency of supercritical CO2 and H2O in the production well of enhanced geothermal system. Energy 2020, 205, 118071. [Google Scholar] [CrossRef]
- Li, J.; Yuan, W.; Zhang, Y.; Cherubini, C.; Scheuermann, A.; Torres, S.A.G.; Li, L. Numerical investigations of CO2 and N2 miscible flow as the working fluid in enhanced geothermal systems. Energy 2020, 206, 118062. [Google Scholar] [CrossRef]
- Karmakar, S.; Ghergut, J.; Sauter, M. Early-flowback tracer signals for fracture characterization in an EGS developed in deep crystalline and sedimentary formations: A parametric study. Geothermics 2016, 63, 242–252. [Google Scholar] [CrossRef]
- Ma, Y.; Li, S.; Zhang, L.; Liu, S.; Liu, Z.; Li, H.; Shi, E.; Zhang, H. Numerical simulation study on the heat extraction performance of multi-well injection enhanced geothermal system. Renew. Energy 2020, 151, 782–795. [Google Scholar] [CrossRef]
- Cipolla, C.L.; Lolon, E.P.; Erdle, J.C.; Rubin, B. Reservoir Modeling in Shale-Gas Reservoirs. SPE Reserv. Eval. Eng. 2010, 13, 638–653. [Google Scholar] [CrossRef]
- Mukuhira, Y.; Ito, T.; Asanuma, H.; Häring, M. Evaluation of flow paths during stimulation in an EGS reservoir using micro-seismic information. Geothermics 2020, 87, 101843. [Google Scholar] [CrossRef]
- Chilès, J.P. Fractal and geostatistical methods for modeling of a fracture network. Math. Geol. 1988, 20, 631–654. [Google Scholar] [CrossRef]
- Davy, P.; Sornette, A. Some consequences of a proposed fractal nature of continental faulting. Nat. Cell Biol. 1990, 348, 56–58. [Google Scholar] [CrossRef]
- Darcel, C.; Bour, O.; Davy, P.; De Dreuzy, J.R. Connectivity properties of two-dimensional fracture networks with stochastic fractal correlation. Water Resour. Res. 2003, 39, 39. [Google Scholar] [CrossRef]
- Kim, T.H.; Schechter, D.S. Estimation of Fracture Porosity of Naturally Fractured Reservoirs With No Matrix Porosity Using Fractal Discrete Fracture Networks. SPE Reserv. Evaluation Eng. 2009, 12, 232–242. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P. A new computer code for discrete fracture network modelling. Comput. Geosci. 2010, 36, 292–301. [Google Scholar] [CrossRef]
- Boyle, E.J.; Sams, W.N. NFFLOW: A Reservoir Simulator Incorporating Explicit Fractures. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 19–23 March 2012. [Google Scholar]
- La Pointe, P. A method to characterize fracture density and connectivity through fractal geometry. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1988, 25, 421–429. [Google Scholar] [CrossRef]
- Berkowitz, B. Analysis of fracture network connectivity using percolation theory. Math. Geol. 1995, 27, 467–483. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A.; Mardia, K.V.; Fowell, R.J. A Connectivity Index for Discrete Fracture Networks. Math. Geol. 2006, 38, 611–634. [Google Scholar] [CrossRef]
- Alghalandis, Y.F.; Dowd, P.A.; Xu, C. Connectivity Field: A Measure for Characterising Fracture Networks. Math. Geol. 2014, 47, 63–83. [Google Scholar] [CrossRef]
- Li, L.; Jiang, H.; Wu, K.; Li, J.; Chen, Z. An analysis of tracer flowback profiles to reduce uncertainty in fracture-network ge-ometries. J. Petrol. Sci. Eng. 2019, 173, 246–257. [Google Scholar] [CrossRef]
- Barenblatt, G.; Zheltov, I.; Kochina, I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Warren, J.; Root, P. The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Pruess, K.; Narasimhan, T.N. A practical method for modeling fluid and heat flow in fractured porous media. SPE J. 1982, 25, 14–26. [Google Scholar] [CrossRef]
- Sarda, S.; Jeannin, L.; Basquet, R.; Bourbiaux, B. Hydraulic Characterization of Fractured Reservoirs: Simulation on Discrete Fracture Models. SPE Reserv. Eval. Eng. 2002, 5, 154–162. [Google Scholar] [CrossRef]
- Karimifard, M.; Durlofsky, L.J.; Aziz, K. An Efficient Discrete-Fracture Model Applicable for General-Purpose Reservoir Simulators. SPE J. 2004, 9, 227–236. [Google Scholar] [CrossRef]
- Li, L.; Lee, S.H. Efficient Field-Scale Simulation of Black Oil in a Naturally Fractured Reservoir Through Discrete Fracture Networks and Homogenized Media. SPE Reserv. Eval. Eng. 2008, 11, 750–758. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Witherspoon, P.A.; Ohnishi, Y. Theory of heat extraction from fractured hot dry rock. J. Geophys. Res. Space Phys. 1975, 80, 1120–1124. [Google Scholar] [CrossRef]
- Doe, T.; McLaren, R.; Dershowitz, W. Discrete fracture network simulations of enhanced geothermal systems. In Proceedings of the Thirty-Ninth Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, CA, USA, 24–26 February 2014; pp. 24–26. [Google Scholar]
- Gan, Q.; Elsworth, D. Production optimization in fractured geothermal reservoirs by coupled discrete fracture network mod-eling. Geothermics 2016, 62, 131–142. [Google Scholar] [CrossRef]
- Gong, F.; Guo, T.; Sun, W.; Li, Z.; Yang, B.; Chen, Y.; Qu, Z. Evaluation of geothermal energy extraction in Enhanced Geothermal System (EGS) with multiple fracturing horizontal wells (MFHW). Renew. Energy 2020, 151, 1339–1351. [Google Scholar] [CrossRef]
- Asai, P.; Panja, P.; McLennan, J.; Moore, J. Efficient workflow for simulation of multifractured enhanced geothermal systems (EGS). Renew. Energy 2019, 131, 763–777. [Google Scholar] [CrossRef]
- Asai, P.; Panja, P.; McLennan, J.; Moore, J. Performance evaluation of enhanced geothermal system (EGS): Surrogate models, sensitivity study and ranking key parameters. Renew. Energy 2018, 122, 184–195. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of well-block pressures in numerical reservoir simulation with nonsquare grid blocks and ani-sotropic permeability. SPE J. 1983, 23, 531–543. [Google Scholar]
- Lie, K.A.; Krogstad, S.; Ligaarden, I.S.; Natvig, J.R.; Nilsen, H.M.; Skaflestad, B. Open-source matlab implementation of con-sistent discretisations on complex grids. Comput. Geosci. 2012, 16, 297–322. [Google Scholar] [CrossRef]
- Lie, K.A. An Introduction to Reservoir Simulation Using MATLAB/GNU Octave: User Guide for the MATLAB Reservoir Simulation Toolbox (MRST); Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]




| Parameters | Value |
|---|---|
| Rock density | 2.65 g/cm3 |
| Water density | 1.0 g/cm3 |
| Rock thermal conductivity | 2.595 × 10−2 J/(m·s·°C) |
| Rock specific heat capacity | 1.05 J/(g·°C) |
| Water specific heat capacity | 4.186 J/(g·°C) |
| Fracture porosity | 1, decimal |
| Rock porosity | 0, decimal |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Guo, X.; Zhou, M.; Xiang, G.; Zhang, N.; Wang, Y.; Wang, S.; Landjobo Pagou, A. The Investigation of Fracture Networks on Heat Extraction Performance for an Enhanced Geothermal System. Energies 2021, 14, 1635. https://doi.org/10.3390/en14061635
Li L, Guo X, Zhou M, Xiang G, Zhang N, Wang Y, Wang S, Landjobo Pagou A. The Investigation of Fracture Networks on Heat Extraction Performance for an Enhanced Geothermal System. Energies. 2021; 14(6):1635. https://doi.org/10.3390/en14061635
Chicago/Turabian StyleLi, Linkai, Xiao Guo, Ming Zhou, Gang Xiang, Ning Zhang, Yue Wang, Shengyuan Wang, and Arnold Landjobo Pagou. 2021. "The Investigation of Fracture Networks on Heat Extraction Performance for an Enhanced Geothermal System" Energies 14, no. 6: 1635. https://doi.org/10.3390/en14061635
APA StyleLi, L., Guo, X., Zhou, M., Xiang, G., Zhang, N., Wang, Y., Wang, S., & Landjobo Pagou, A. (2021). The Investigation of Fracture Networks on Heat Extraction Performance for an Enhanced Geothermal System. Energies, 14(6), 1635. https://doi.org/10.3390/en14061635






