Lithodynamic Processes along the Seashore in the Area of Planned Nuclear Power Plant Construction: A Case Study on Lubiatowo at Poland

Abstract

The Polish government has made a decision to build a nuclear power plant (NPP) in the South Baltic coastal zone. This means that three major types of structures will be located in the nearshore: (1) breakwaters and a wharf where ships may dock to load and unload cargo (harbor), (2) seawalls protecting the shore against erosion and storm surge floods, and (3) an underwater piping system for cold water intake and heated water discharge. This study determines the dominant directions and rate of sediment transport for the coastline section in the vicinity of the projected Polish NPP (ca. 100,000 m³/year), as well as assesses current changes at this coastline location on the basis of field measurements and mathematical modeling.

1. Introduction

The first nuclear power plant was connected to the power grid in 1954. At present, there are 442 reactors in operation, with a total net installed capacity of 392,335 MW and 53 reactors under construction with a total net installed capacity of 56,276 MW. More than a quarter of all nuclear power plants are located in the coastal zone of seas and oceans [1]. Moreover, all nuclear power plants in China, including both the completed ones and those under construction, are coastal plants [2]. Coastal location has many advantages. Seawater can be used to cool reactors, and sea ports facilitate, among other things, the transport of prefabricated units during construction and of fresh and spent fuel during operation. However, such a location of a power plant requires a very careful assessment of potential flood and erosion risks from the sea.

The flood-related quantities and parameters needed for the selection of a location for a nuclear power plant are put together in

Table 1. Ocean flood prediction and prevention for coastal nuclear power plant infrastructure [3,4,5,6,7].

Events/Hazards/Phenomena	Design Basis Parameter
Storm surges	Max. still water, if a deterministic method is used; Hazard curve (still water level vs. annual frequency of exceedance), if a probabilistic method is used
Wind-induced waves	Increase in water level due to wind above still water; Wave run-up height
Tsunami	Max. water level at the shoreline; Run-up height; Inundation range horizontal flood Max. water level at the site; Min. water level at the shoreline; The duration of the drawdown below the intake
Seiches	Max. and min. run up height

, in compliance with the international guidelines and scientific publications [3,4,5,6,7].

Studies complying with the above recommendations contain all situations for nuclear power plants erected on rocky coasts. The situation is different for plants erected on sandy, erosive coasts. Every technical object (e.g., pipeline, provisional pier for delivery of materials to the site) erected on a sandy coastal segment causes disturbance in natural sediment transport processes and produces local areas of coastline erosion/accretion [8]. Disregard of the scale, extent and intensity of natural alongshore sediment transport or failure to evaluate possible shoreline change in investigating a potential location for a nuclear power plant on a sandy coast may have serious consequences for its safety [9,10].

In 2009, the Polish government made a decision to launch the Polish Nuclear Energy Programme. Consequently, environmental and location surveys were commenced in 2013. They have been conducted in three communes: Choczewo, Gniewino and Krokowa (in Pomerania Province, which borders on the Baltic Sea), but the final location of the first Polish NPP is still unknown. Given the coastal location of these communes, it can be assumed that seawater will be used in the reactor cooling system (Figure 1). This involves the construction of large and crucial coastal engineering structures. Three major types of structures can be distinguished, which, depending on the design of the plant, will be located in the coastal zone [9,10]:

• breakwaters and a wharf, where ships may dock to load and unload cargo (harbor),
• seawalls protecting the shore against erosion and storm surge floods,
• an underwater piping system for cold water intake and heated water discharge.

The Baltic Sea is dominated by low pressure systems moving from west to east [11,12]. As a result, offshore wind waves generally move from west to east. In addition to the prevailing direction of wind waves, the longshore transport of sediment in the coastal zone is significantly affected by the orientation of the coastline relative to the average annual wind direction [13,14]. The eastern section of the Polish Baltic coast (from the Koszalin Bay to the Hel Peninsula) is oblique from SW to NW, while its western section (from the Koszalin Bay to Świnoujście) is approximately latitudinal. As a result, the eastern section of the Polish seashore is dominated by west-to-east sediment transport, while the western section is dominated by transport in the opposite direction. Consequently, the accretion of the shore (sediment accumulation) on the western side of the breakwaters and the retreat of the shore (sediment erosion) on the eastern side are expected after the possible construction of a port in the Lubiatowo area.

The scale, range and intensity of these changes depend on the prevailing directions and intensity of sediment transport, the local and regional geological structure (thickness and distribution of sand layers), the type of geomorphological structures, as well as the type and geometry of structures founded in the coastal zone [15,16].

The cognitive aim of this study was to determine the dominant directions and rate of sediment transport for the coastline section in the vicinity of the Coastal Research Station (CRS) in Lubiatowo, where a nuclear power plant is likely to be built, as well as to assess current changes in this coastline location on the basis of field measurements and theoretical considerations.

The current article, based on a case study of a plant to be erected on the sandy, dissipative south Baltic Sea coast of Poland, presents a methodology of conducting this type of analysis. The same methodology can be applied to all such analyses performed for locations of NPPs on sandy coasts worldwide.

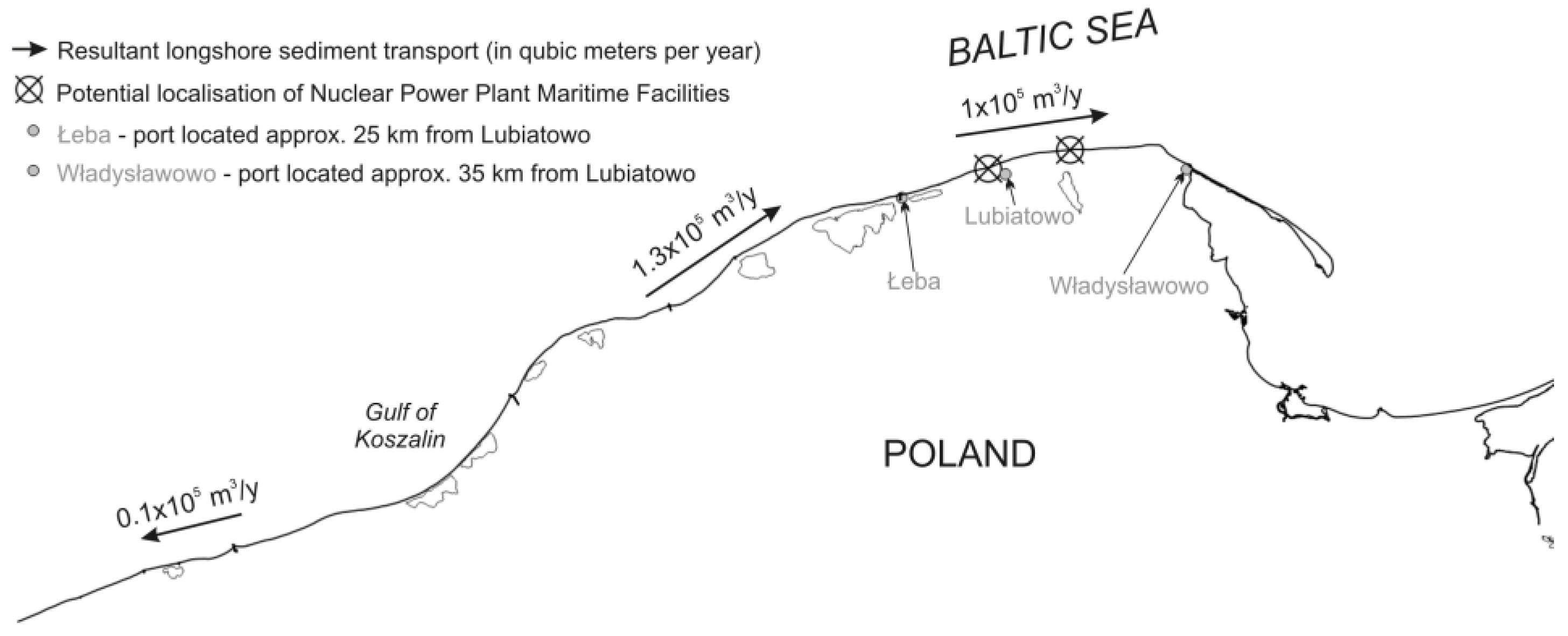
2. Assessment of Sediment Transport along the Shore Section between Łeba and Władysławowo Based on Archival Data

A comprehensive review of discussions on large-scale sediment movement along the entire Polish coast started with the first coherent concepts put forward in the late 1950s by Zenkowicz [17] and ended with research by Kaczmarek et al. [18].

In the past, research and assessment of the longshore sediment transport volume on large spatial scales were carried out by various marker methods, i.e., petrographic-mineralogical, geomorphological, energetic, and hydrometeorological methods. That work has led to the identification of a general scheme of large-scale sediment movement along the Polish coast, which shows two main sediment streams originating in the Gulf of Koszalin (divergence zone): an eastward transport of higher intensity (about 105 m³/year), and a westward transport of lower intensity (about 104 m³/year) (Figure 1). In the Oder estuary, the latter meets an opposite stream of sediments moving eastwards from Rügen and forms a convergence zone in this area. A similar situation occurs in the Gulf of Gdańsk, where sediments moving from Sambia (to the west) coincide.

Schwarzer et al. [19] observed a system of sediment streams covering various directions in the nearshore zone of Western Pomerania. Similar conclusions about the heterogeneity and varying saturation of streams, with one dominant direction of sediment movement, were presented by Subotowicz [20] for the seashore section stretching from the Hel Peninsula promontory to the town of Dziwnów. According to Furmańczyk et al. [21], a further detailing of this general sediment movement pattern along the Polish shore suggests the existence of two opposite directions of sediment transport and the presence of a number of discontinuities, which leads to a cellular structure of sediment transport.

The volume of the transported sediment is very difficult to measure in nature. It can be inferred indirectly on the basis of wave parameters measured in a given area, seabed currents, changes in the seabed topography visible on bathymetric plans, changes in the coastline position and the width of the beach in subsequent years. There are a number of mathematical and numerical models to compute the volume of transported sediments—based on calculated hydrodynamic parameters (velocities of longshore and cross-shore currents, waves, etc.) and the present-day bathymetric-tachymetric topographic features of the surveyed area, assuming an unlimited thickness of the dynamic layer.

In the past, an assessment of the sediment transport volume was conducted in the eastern and western parts of the Lubiatowo seashore section, i.e., in the vicinity of the port in Łeba (approximately 25 km west of Lubiatowo) and in Władysławowo (approximately 35 km east of Lubiatowo). Kaczmarek et al. [18] compared the amount of sand deposited in a fairway leading to the Łeba port (approximately 20 km west of Lubiatowo) in the average statistical year with average annual dredging works carried out in 1949–1974. The volume and rate of the sediment transported along the seashore were calculated using a three-layer graded sediment transport model [22,23]. The calculations showed that the average annual sedimentation volume in the fairway was 83,000 m³/year [24]. On the other hand, the data obtained from the Maritime Office in Słupsk showed that the average annual output from the fairway was 70,000 m³/year [24,25]. The calculated annual transport volumes are relatively consistent with their equivalents presented in reports on dredging works carried out in the past. This is not surprising, since in this case the calculated sediment transport included only sediment dragged along sandbars II, III and IV.

On the other hand, a papers by Kaczmarek et al. [25] and Szmytkiewicz et al. [26] present calculated longshore sediment transport values in the whole coastal zone in the area of the Łeba port. The calculations were made with Bijker’s [27] model and indicated that the transport of sediment in the eastern direction amounted to 103,000 m³/year.

The transport calculated with Bijker’s model accounts for both bedload and suspended transport, whereas transport calculated with the model by Kaczmarek et al. [22] takes into account only bedload transport. This indirectly confirms the findings of Zenkovich [17] and other researchers [19,20,21] that the longshore sediment transport in the Łeba area is diverted towards the east and amounts to 100,000 m³/year.

The most detailed calculations of the longshore sediment transport for the Polish coast have so far been performed for the port area in Władysławowo [28]. The accuracy of the calculated longshore sediment transport values was evaluated by comparing the calculated evolution of the coastline with the actual coastline measured in 1936 (initial position before the breakwater construction began), 1937 and 1938 (completion of the breakwater construction), 1962, 1964, 1965, 1968, 1976, 1988, 1991, and 1997 on both sides of the port. The calculated resultant (net) longshore sediment transport rates in the vicinity of the western port breakwaters ranged from 40,000 to 65,000 m³/year towards the east. The calculated values should be interpreted mainly as part of the total sediment stream moving eastwards, which was blocked by the western breakwater. The total resultant (net) sediment transport calculated with the three-layer model in the bathymetric profile on the western side of the port breakwaters was 115,000 m³/year in the average statistical year. On the other hand, the resultant (net) longshore sediment transport calculated with Bijker’s model [27] for the seawards shore of the Hel Peninsula in the Jastarnia region was 128,000 m³/year. Other computations of this type and estimations based on measurements of the amount of material deposited in the western part of the Władysławowo port were collated in the study [28,29]. Depending on the computational methodology adopted by various authors, the volume of sediment transport ranged from 90,000 to about 150,000 m³/year, while that determined on the basis of measurements of sediment deposited in the western part of the port varied from 70,000 to 120,000 m³/year.

3. Lubiatowo Study Site

In the present study, calculations of sediment transport are carried out for the Lubiatowo site. In this area, observations and measurements of hydro-, litho- and morphodynamics phenomena occurring in the coastal zone have been performed since the 1970s. A complementary analysis, such as the one presented in this paper, has not been available until now.

The following steps were carried out to determine the dominant directions and rate of sediment transport for the coastline section:

-

geological and geomorphological structures occurring in the backshore and foreshore zones were described based on the available literature,

-

trends and rates of seashore modifications were determined based on long-term (multiannual) data on changes in the coastline and dune foot position,

-

intensity of hydrodynamic processes occurring in the coastal zone was described based on long-term wave-current data collected over many years through direct measurements,

-

rate and volume of longshore sediment transport were calculated for a typical bathymetric profile based on wave conditions occurring in the average statistical year.

3.1. Geological Structure and Morphodynamic Features

The seabed within this area slopes mildly towards NNW. The angle of the seabed inclination is about 9° up to the 10 m isobath. Isobaths up to a depth of 15 m are approximately parallel to the shore (Figure 2).

There are 3–4 stable submerged sandbars in the coastal zone. The first sandbar is located at a distance of about 80–100 m from the coastline, the second at a distance of about 150–180 m, and the third at about 300–350 m, whereas the fourth, situated at about 500–550 m, and possibly the fifth one form one larger dynamic structure located at a distance of about 800–900 m from the shore (Figure 3). Beyond the sandbar zone, there is a N-S depression in the seabed at a depth of 9–10 m in the western part of the area.

The seabed is composed mainly of fine-grained quartz sand with an average diameter oscillating around D50 ≈ 0.22 mm. The statistical grain size analysis was performed by the sieving method [30] on 46 samples. Two isolated fields of medium-grained sand are found only a few hundred metres from the shore. Glacial till of the Weichselian glaciation is deposited in the onshore area near Lubiatowo, 10 m below sea level (b.s.l.), and is overlain by a series of sand-gravel fluvioglacial Pleistocene deposits. The top layer of the sediments descends in the N direction, where it occurs under the seabed at about 7–8 m below sea level, partly as a substrate for contemporary marine sand, while in the onshore part it reaches an altitude of up to 5–7 m above sea level (a.s.l.). Biogenic deposits (peat, alluvium/mud, gyttja) form a discontinuous cover on their surface, both in the onshore area and under the seabed [31,32,33]. The surface of the area is built of aeolian sands, both in the dunes and covers [31,32,33] (Figure 4).

The width of the beach is up to 50 m along erosive stretches and more than 50 m in depositional sections. There are three generations of dunes along the depositional section: the oldest stabilized dune overgrown with forest, the younger, partly stabilized dune and the frontal dune, currently being formed. In order to protect the shores, biological reinforcement has been implemented, e.g., fascine fences and dune consolidation by planting sand ryegrass. The dunes are characterized by height differences of about 5–6 m. The dune toe ordinate in the profile analyzed is about 2 m. The dunes in this region are protected by twig fences and reinforcing plants [33]. The dune system of that stretch of the shore is built of sand with grain diameters ranging from 0.16 to 0.25 mm. As a result of selection during sediment transport, finer and more rounded sediment grains reach the dune ridge, while coarser aeolian material is deposited in depressions [33].

3.2. Trends and Rate of Seashore Modifications

Routine monthly measurements of the coastline and dune foot position have been carried out since 1983 in 29 tachymetric profiles located at 100 m intervals at the Lubiatowo site. The measurements basically show that the shore is in a relative dynamic equilibrium. The analysis of coastline oscillations does not indicate either long-term erosion or accumulation trends [34].

Seasonal and long-term changes in the coastline location range from about 10 to 100 m—Figure 5 [35]. Changes in the seabed level (ordinate) from a depth of about 4–6 m to the shoreline, due the onshore and offshore migration of sandbars, amount to about 5 m over the last 30 years.

On the other hand, the analysis of changes in the coastline position in 1983–1998 performed by the statistical method Singular Spectrum Analysis (SSA) for the same 2.9 km section of the seashore in the Lubiatowo area showed that long-term changes in the coastline position resemble a standing wave with an amplitude of ±10 m and a period of T = 8 years [35,36,37].

4. Calculation of Longshore Sediment Transport for Wave Conditions Occurring in the Average Statistical Year

Calculation of the sediment transport rate in the average statistical year requires prior knowledge of wave parameters in that year. Data from the wave forecast model of the Baltic Sea developed by Cieślikiewicz and Paplińska-Swerpel [38] were used to reconstruct long-term wind-generated waves. The input data for this model were archival wind data from the regional atmospheric model REMO (Regional Climate Model 2001). Based on these data, wind-generated waves were calculated with the spectral model WAM4. The results of these calculations made it possible to reconstruct waves in the Baltic Sea for a period of 44 years (1958–2001). The resolution of the computational numerical grid was approximately 9 km. The calculations produced representative wave parameters, i.e., significant wave heights, periods and azimuths of wave approach angles for each forecast point and each consecutive hour.

For the purposes of the present study,

-

forecast points, obtained through wave reconstruction and located as close as possible to the Lubiatów shore, were analyzed; this criterion was met by a point located at a distance of approximately 10 km at a depth of h ≈ 21 m.

-

wave scenarios were developed, i.e., wave parameters were determined for the average statistical year; in order to determine the durations of specific wave heights for individual onshore wind directions, wave height intervals of 0.5 m were assumed and for each of them average significant wave heights, average peak periods, average azimuths of wave approach directions, and their duration were calculated. The results of this analysis are presented in

Table 2. Total statistics of wind-generated waves determined for a forecast point corresponding to the bathymetric profile in Lubiatowo.

Direction	Wave Intervals	Hs (m)	Wave Peak Period Tp (s)	Wave Direction Θ (0)	Duration (Days)
W	0.0–0.5	0.28	4.03	76.4	26.81
	0.5–1.0	0.71	5.34	75.9	21.68
	1.0–1.5	1.20	6.47	74.3	8.89
	1.5–2.0	1.68	7.28	72.8	2.79
	2.0–2.5	2.17	7.93	71.5	0.60
	2.5–3.0	2.66	8.86	71.2	0.09
	3.0–3.5	3.15	8.97	71.1	0.01
WNW	0.0–0.5	0.31	3.88	60.0	24.01
	0.5–1.0	0.72	5.04	60.0	29.23
	1.0–1.5	1.22	6.18	60.4	16.58
	1.5–2.0	1.72	7.07	60.0	0.73
	2.0–2.5	2.22	7.84	59.4	4.31
	2.5–3.0	2.71	8.50	57.8	2.10
	3.0–3.5	3.20	9.07	56.1	0.84
	3.5–4.0	3.70	9.66	54.7	0.30
	4.0–4.5	4.19	10.25	53.1	0.11
	4.5–5.0	4.70	10.72	51.3	0.06
	5.0–5.5	5.23	11.10	49.2	0.02
	5.5–6.0	5.68	11.70	47.7	0.01
NW	0.0–0.5	0.29	3.68	37.0	9.68
	0.5–1.0	0.71	4.88	37.1	8.50
	1.0–1.5	1.21	6.03	37.6	3.84
	1.5–2.0	1.72	6.86	38.3	1.98
	2.0–2.5	2.22	7.59	38.5	1.01
	2.5–3.0	2.71	8.23	38.7	0.54
	3.0–3.5	3.21	8.79	38.7	0.28
	3.5–4.0	3.73	9.40	39.3	0.13
	4.0–4.5	4.22	9.82	38.3	0.07
	4.5–5.0	4.68	10.44	37.6	0.02
	5.0–5.5	5.19	10.66	36.5	0.01
NNW	0.0–0.5	0.29	4.13	13.0	5.95
	0.5–1.0	0.71	5.26	12.8	5.28
	1.0–1.5	1.21	5.90	12.5	2.43
	1.5–2.0	1.72	6.40	12.1	0.95
	2.0–2.5	2.21	6.89	12.0	0.49
	2.5–3.0	2.71	7.37	11.8	0.22
	3.0–3.5	3.22	7.82	11.9	0.08
	3.5–4.0	3.71	7.94	9.0	0.04
	4.0–4.5	4.22	8.26	6.1	0.02
	4.5–5.0	4.68	8.58	6.6	0.01
N	0.0–0.5	0.29	4.37	−10.8	8.28
	0.5–1.0	0.72	5.89	−11.1	8.99
	1.0–1.5	1.22	7.13	−11.7	5.12
	1.5–2.0	1.72	7.95	−12.0	3.11
	2.0–2.5	2.22	8.67	−12.3	1.55
	2.5–3.0	2.72	9.28	−12.2	0.94
	3.0–3.5	3.22	9.77	−12.1	0.49
	3.5–4.0	3.72	10.24	−12.3	0.28
	4.0–4.5	4.22	10.70	−12.1	0.14
	4.5–5.0	4.72	11.14	−10.8	0.07
	5.0–5.5	5.21	11.55	−11.0	0.04
	5.5–6.0	5.70	11.83	−14.4	0.02
	6.0–6.5	6.15	11.89	−17.0	0.01
NNE	0.0–0.5	0.30	4.45	−33.1	14.74
	0.5–1.0	0.72	5.82	−32.1	15.43
	1.0–1.5	1.21	6.98	−30.6	6.91
	1.5–2.0	1.71	7.82	−30.0	2.96
	2.0–2.5	2.20	8.49	−29.6	1.32
	2.5–3.0	2.71	9.17	−28.2	0.57
	3.0–3.5	3.21	9.75	−27.4	0.30
	3.5–4.0	3.72	10.20	−26.6	0.12
	4.0–4.5	4.21	10.57	−27.1	0.05
	4.5–5.0	4.70	10.71	−27.0	0.02
	5.0–5.5	5.17	11.32	−26.72	0.01
	5.5–6.0	5.68	11.86	−22.2	0.01
	6.0–6.5	6.21	12.70	−18.0	0.01
NE	0.0–0.5	0.30	3.95	−53.8	14.07
	0.5–1.0	0.70	5.22	−54.0	10.69
	1.0–1.5	1.20	6.47	−53.4	3.13
	1.5–2.0	1.70	7.41	−52.9	1.02
	2.0–2.5	2.21	8.23	−52.1	0.37
	2.5–3.0	2.68	8.86	−51.1	0.12
	3.0–3.5	3.15	9.22	−51.1	0.06
	3.5–4.0	3.67	9.74	−44.7	0.02
	4.0–4.5	4.31	10.09	−41.3	0.02
ENE	0.0–0.5	0.29	3.85	−76.5	9.41
	0.5–1.0	0.68	5.15	−76.5	7.12
	1.0–1.5	1.17	6.59	−75.3	1.61
	1.5–2.0	1.67	7.73	−74.8	0.36
	2.0–2.5	2.18	7.92	−71.7	0.16
	2.5–3.0	2.65	8.30	−65.0	0.06
	3.0–3.5	3.06	8.76	−62.5	0.01

.

The scenarios presented in Table 2 served as a starting point to calculate the wave transformation, longshore currents and longshore sediment transport rate as a function of distance from the shore along a characteristic bathymetric profile selected from survey measurements taken in March 2019 (Figure 4).

Calculations were performed with the numerical package SAND94 developed and verified by Szmytkiewicz [38] and the software UNIBEST-LT, version 4.0 [39]. In both models, calculations were performed in representative bathymetric profiles selected by the user and for specific, characteristic diameters of sediment grains (D50, D90) representative of the shore section analyzed. The rate and volume of the longshore sediment transport can be calculated with various models: according to Ackers and White [40], Bailard [41], Bijker [26], Engelund-Hansen [42], and van Rijn [43]. It appears that, in the case of the UNIBEST numerical package, the most versatile and most frequently used models for hydro- and lithodynamic conditions occurring in the Baltic coastal zone are Bijker’s and van Rijn’s calculation formulas. They are considered to be the most accurate among the so-called “engineering models”.

The value of roughness coefficients has a major impact on calculated transport values. According to Bijker’s and van Rijn’s models, they are defined by a roughness height of approximately 2–3 heights of seabed forms. These models distinguish between two types of roughness associated with waves and flow velocities: rc—the height of “current” roughness; rw—the height of “wave” roughness.

UNI-LT recommends applying roughness heights from the range of 0.01–0.10 m. At the Lubiatowo site, for storm conditions, ripples in the breaker zone are almost completely washed away. For these conditions (sheet flow), a recommended value of r_c = r_w = 0.01 m was used. On the basis of data from a study by Ostrowski [25], characteristic diameters of grains D₅₀ = 0.22 mm and D₉₀ = 0.35 mm and their settling velocity w_s = 2.78 cm/s were applied. The calculated annual totals of longshore sediment transport for each direction of wave approach to the shore, the total amounts of sediments transported from west to east and from east to west, and the annual transport during the year in individual bathymetric profiles are presented in

Table 3. Calculated longshore sediment transport in the average statistical year in the bathymetric profile at 163.5 km near Lubiatowo. The calculated transport values are given in m³/year.

Directions	Bijker	Van Rijn	Directions	Bijker	Van Rijn
	rc = rw = 0.01 m
W	6000	4000	N	−31,000	−21,000
WNW	130,000	155,000	NNE	−18,000	−15,000
NW	23,000	23,000	NE	−6000	−5000
NNW	7000	4000	ENE	~0	~0
Total from west to east	167,000	186,000	Total from east to west	−56,000	−41,000
Resultant Bijker	111,000
Resultant van Rijn	145,000

.

According to the convention adopted in Poland, transport from west to east is regarded as positive, and from east to west as negative.

The total values of longshore sediment transport (Table 3) indicate that

-

the resultant annual transport of sediment is oriented from west to east, totaling 111,000 m³/year according to Bijker’ model and 145,000 m³/year according to van Rijn’ model,

-

the largest sediment transport from westerly directions occurs with waves coming from the WNW direction,

-

the east–west sediment transport is much smaller, accounting for 34% to 22% of the sediment transported from west to east according to Bijker’s and van Rijn’s models, respectively,

-

the largest transport from easterly directions occurs with waves approaching from the NNE direction.

The calculated total amounts of sediment transport do not provide information on how this transport is distributed in the coastal zone, where its intensity is the highest and how far it reaches from the shore. In order to answer these questions, Figure 6 and Figure 7 show the calculated distributions of the longshore sediment transport as a function of distance from the shore for the total west–east transport, the total transport in the opposite direction and the resultant transport in the bathymetric profile shown in Figure 3.

These figures show that the longshore sediment transport distributions calculated by the two models are similar, whereby

-

the transport of sediment takes place mainly up to a distance of about 600 m from the shore, where five streams of moving sediments can be distinguished,

-

the so-called “tail” of the transported sediment is observed at a distance of approximately 800–1200 m from the shore, with the east–west direction of the resultant transport; the tail accounts for about 1% of the total transport,

-

the first coastal sediment stream moves on the nearshore slope, within a zone of 0–50 m from the shore,

-

the remaining sediment streams are located near the other ridges of coastal longshore bars, with the highest intensity of sediment transport on the crests of the first and second bars,

-

sediment transport decreases basically to zero in the depressions between the bars.

For the purpose of comparison, Figure 8 shows the resultant sediment transport calculated with Bijker’s and van Rijn’s models. It follows from the figure that the distributions obtained are almost identical, only the maximum values are different.

Based on the calculated distributions of the sediment transport rate as a function of distance from the shore (Figure 8), the percentage of the transported sediment was determined within zones of increasing width measured from the shore. The results of these calculations are presented in

Table 4. Percentage of sediment transported in each zone in the average statistical year calculated with Bijker’s and van Rijn’s models.

Distance from the Shore (m)	Bijker’s Model	Van Rijn’s Model
0–50	10%	3%
0–100	42%	29%
0–200	86%	83%
0–400	97%	97%
0–650	99%	99%
0–1200	100%	100%

.

Table 3 shows that more than 80% of sediment transport takes place in a zone of less than 200 m width. The comparison of this result with the bathymetric profile shown in Figure 4 indicates that the main longshore sediment transport takes place near the first and second longshore bars.

5. Discussion

Environmental studies have been conducted to facilitate the final decision on the location of a nuclear power plant on the Polish coast. One of the two locations selected initially for the power plant is the Lubiatowo site, and the other potential site is located 15 km east of Lubiatowo on a shore that is very similar (in terms of geology, geomorphology and oceanographic conditions) to that in Lubiatowo. Environmental factors that have a significant impact on the selection of a power plant location include, among others, the rate of erosion processes occurring within the shore section under consideration. These are especially important, since it is initially assumed that a parking berth for ships transporting structural elements for power plant construction will have to be built with breakwaters.

The calculated resultant (net) sediment transport in the vicinity of the Łeba port (approximately 20 km west of Lubiatowo) is 103,000 m³/year, directed from west to east. On the other hand, the calculated amount of sand material deposited during the year in the fairway leading to the port of Łeba amounted to 83,000 m³/year.

For the region of Władysławowo (about 35 km east of Lubiatowo), the volume of sediment transport varied considerably: from 90,000 to about 150,000 m³/year, depending on the computational methodology, while the sediment deposition determined for the western side of the port breakwaters ranged from 70,000 to 120,000 m³/year.

In the present study, the annual resultant (net) longshore sediment transport for the Lubiatowo site was calculated with two different models, which yielded values ranging from 111,000 to 145,000 m³/year, moving from west to east. This transport takes place in five main zones extending up to approximately 650 m from the shore, with more than 80% of sediment transport taking place in a zone with a width of up to 200 m from the shore.

Routine monthly measurements of the coastline and dune foot position have been carried out in the vicinity of the Coastal Research Station (CRS) since 1983 in 29 tachymetric profiles at intervals of 100 m. The measurements basically show that seasonal and long-term changes in the coastline location range from about 10 to 100 m. The analysis of changes in the coastline position in 1983–1998 showed that the long-term changes in the coastline position resemble a standing wave with an amplitude of ±10 m and a period of T = 8 years. Changes in the seabed level (ordinate) from a depth of about 4–6 m to the shoreline, due to the onshore and offshore migration of the sandbars, amounted to about 5 m over the last 30 years.

The calculations of the longshore sediment transport show that, if a jetty/port is built, certain modifications of the shore in its vicinity must be expected. Accretion of the shore (sediment accumulation) will occur on the western side of the structure, while the shore on its eastern side will retreat (erode). A similar situation will take place during the construction of seawater intake and discharge pipelines. Such a construction is usually carried out in a trench protected with sheet pile walls. This effect will, of course, only be temporary and will disappear when the pipelines are completed and the sheet pile walls protecting the trench are removed.

The methodology presented in this paper for the determination of the annual mean longshore sediment transport at Lubiatowo and for the analysis of shoreline changes is an appropriate approach to assess possible negative changes associated with shoreline modification in the vicinity of a nuclear power plant constructed on the seashore. The intensity of sediment transport on sandy shores is a key factor in determining the magnitude of this modification. Calculations of this transport are based on the knowledge of wave-current fields. Since these processes are characterized by high variability in time and a completely random nature, it is impossible to determine their exact values. As a rule, their numerical values are determined on the basis of specific statistical and stochastic distribution functions.

The application of even very long recurrence periods to determine design values of individual parameters is not sufficient to predict extreme events, as demonstrated by the disaster at the Fukushima Nuclear Power Plant in March 2011 [44]. The Fukushima power plant was protected against various natural disasters, including earthquakes and hurricanes. The plant was protected from the ocean by a concrete storm surge wall, which was also supposed to protect the plant from tsunami waves. The wall was designed to stop a tsunami wave of 6.1 m height, while the actual wave height was about 15 m. As a result, the waves overtopped the wall, which led to the flooding of the generators and consequently to the melting of cores in three out of the six reactors installed in the plant.

The plant had an extensive safety system that worked flawlessly. The design tsunami height was determined from statistical distributions based on existing historical measurement data. However, no provision was made for the possibility of an extreme event, such as an earthquake of this magnitude. Consequently, the possibility of a wave approximately twice the height of the design wave was not foreseen either. If the monstrous tsunami wave had not arrived, the catastrophe would not have occurred, because both the reactors and the antistorm wall withstood the earthquake shocks.

This example shows that marine hydrodynamic processes are random, and therefore it is impossible to accurately determine their extreme values. It also clearly indicates that when assessing the flood risk for a nuclear power plant located close to the sandy shores of nontidal seas, one should consider not only the main recommendations of the IAEA, but also the local conditions. On the other hand, one is tempted to oversize facilities to eliminate the risk of failure, which is also undesirable. It is important to bear in mind that artificially inflated safety coefficients are economically unjustified. Moreover, modern knowledge of litho- and morphodynamic processes in sandy nontidal seas is so well grounded that a potential hazard can be mitigated by appropriate protection measures. This primarily involves monitoring the shore (through regular bathymetric and tacheometric measurements in the area of the power plant, as well continuous measurements of deep-water waves). Such an approach makes it possible to monitor in situ the coastal processes occurring on the seashore in the vicinity of the power plant and to apply appropriate mitigation measures (e.g., beach nourishment) if a dangerous change is identified.

It is not possible to completely eliminate the risk of construction failure. However, the methodology presented in this paper and calculations performed with a calibrated and verified theoretical model make it possible to determine the mean annual intensity of sediment transport in Lubiatowo. Such calculations can also be performed for sandy shores of other nontidal dissipative seas.