Comparing Exergy Analysis and Physical Optimum Method Regarding an Induction Furnace
Abstract
1. Introduction
2. Materials and Methods
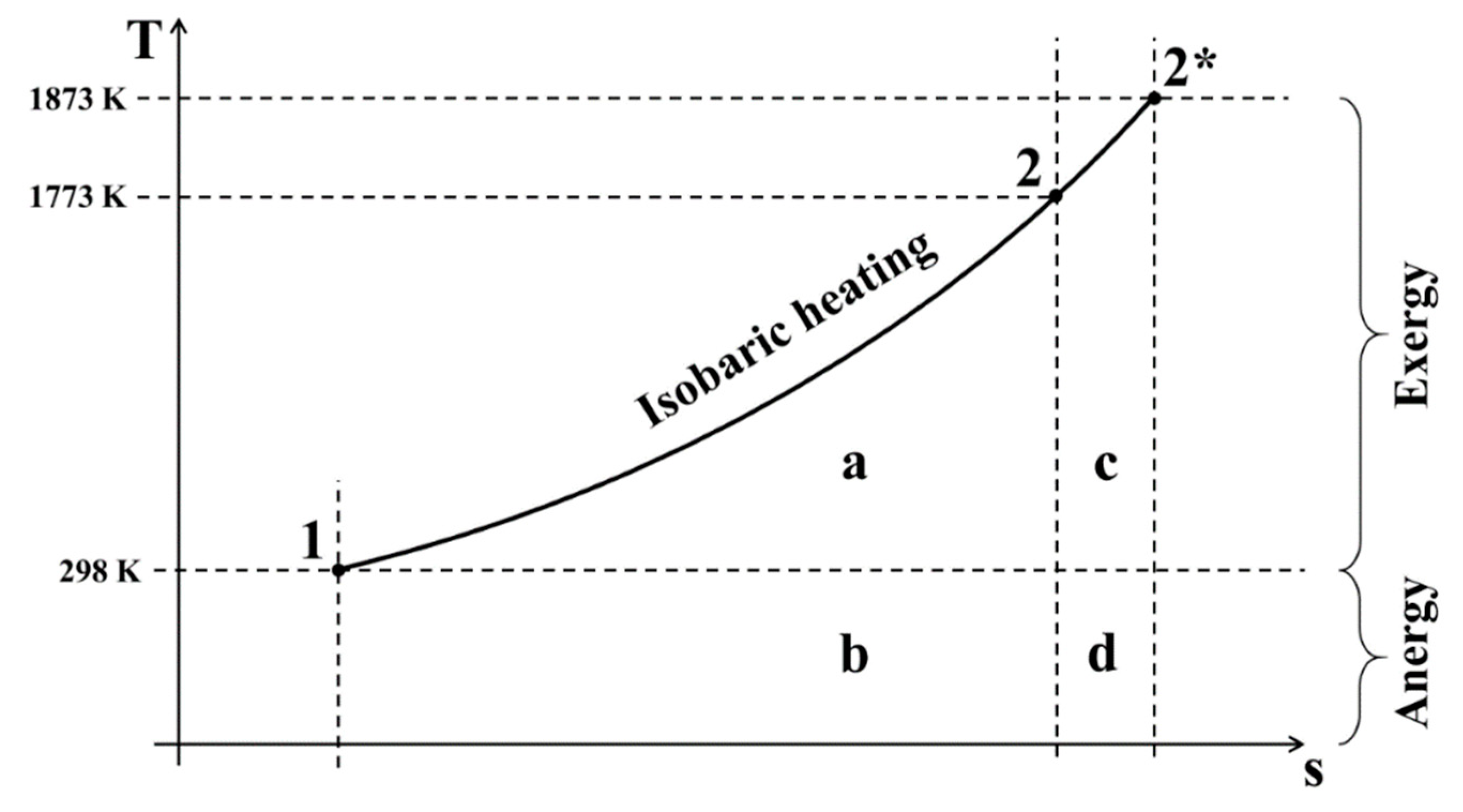
2.1. Exergy Analysis
| Energy Components | Exergy Percentage 1 | Exergy Calculation | ||
|---|---|---|---|---|
| Material-free | Electrical energy Wel | 100% | ||
| Magnetic energy Wmag | 100% | |||
| Mechanical energy Wmech | 100% | |||
| Therm. | Heat Q | 0% ≤ < 100% | ||
| Ambient heat Qamb | 0% (100% anergy) | |||
| Stream of substance | Kinetic energy Ekin | 100% | ||
| Potential energy Epot | 100% | |||
| Physical/thermomechanical energy | 0% ≤ < 100% | |||
| Chemical | Non-reactive (standard chemical exergy) | 0% ≤ < 100% | Tabulated for standard conditions [7] | |
| Reactive | 0% ≤ < 100% | Tabulated for reference reactions [7] | ||
| Mixing | ||||
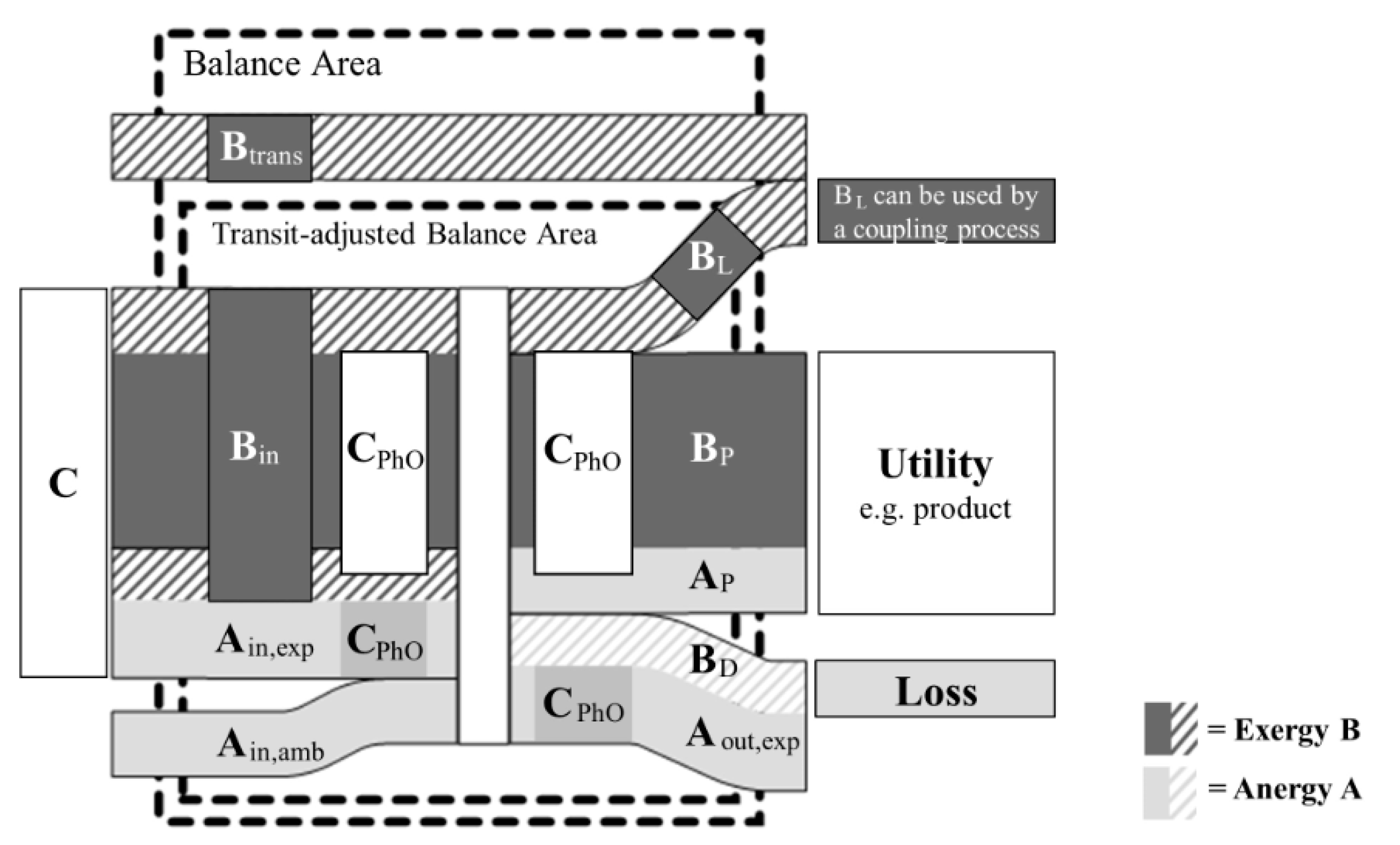
2.2. Physical Optimum (PhO) Method
2.3. Data and Assumptions
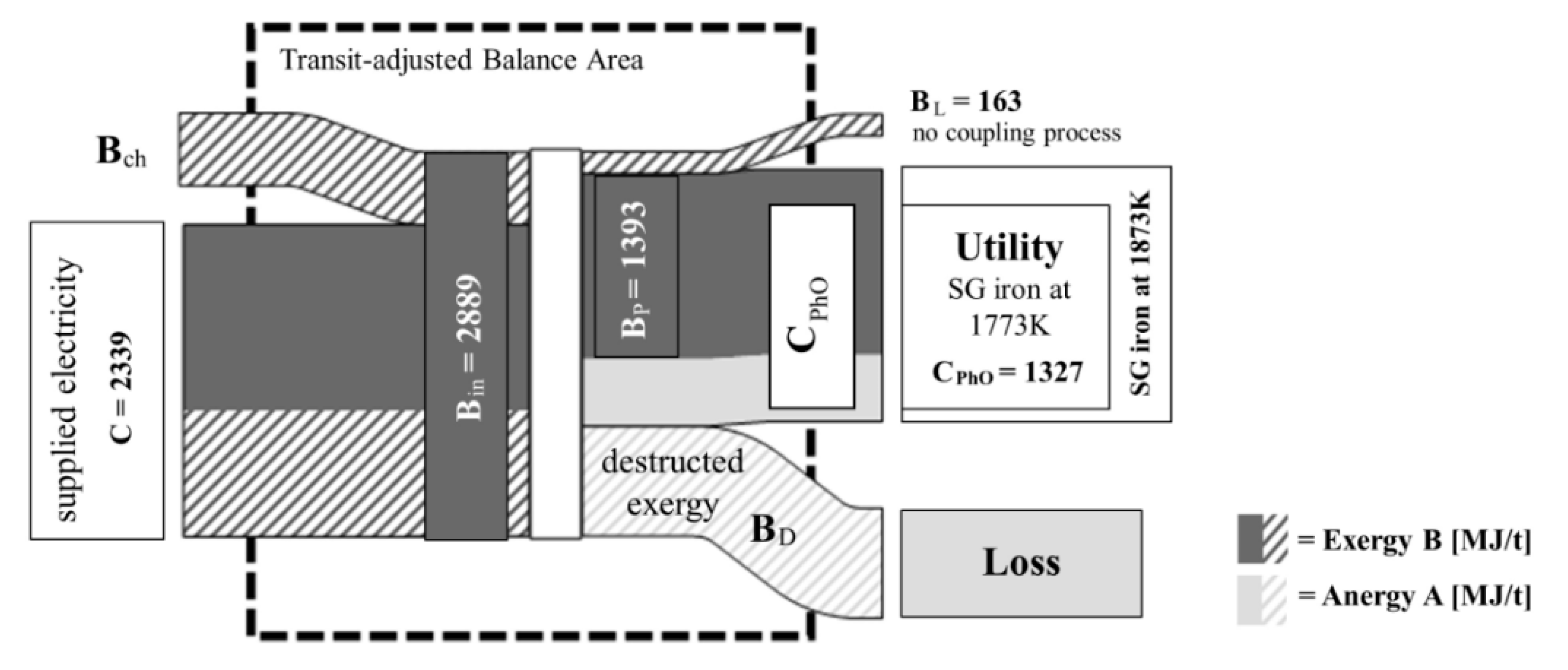
2.3.1. System Boundaries and Utility Definition
2.3.2. General Assumptions
2.3.3. Physical Input–Output Table
| Parameter | Value | Ref. | Comment | |
|---|---|---|---|---|
| Input | Electrical Energy | 2339 MJ | [15] | per ton output, measured, averaged over one year (2018) |
| Stack of Sheets | 358.0 kg | [14] | 35.8% stack of sheets of total metal input | |
| Fe (α) | 354.4 kg | (p. 98) | Assumption: 1% carbon | |
| C | 3.6 kg | |||
| Recycled Metal | 625.0 kg | [14] (p. 98) [18] (p. 16) | 24.6% circulation, 37.1% cuttings | |
| Fe (α) | 590.6 kg | 94.5% Fe | ||
| C (graphite) | 23.1 kg | 3.7% C | ||
| Si | 11.2 kg | 1.8% Si | ||
| Alloying Materials | 17.1 kg | [14] (p. 98) | calculated based on the literature data of the output materials (mass conservation) and values compared and reviewed on the basis of [14] | |
| C (graphite) | 7.5 kg | |||
| SiC (hexagonal) | 9.6 kg | |||
| Impurities (Sand, Rust) | 20.9 kg | |||
| SiO2 (quartz) | 11.0 kg | |||
| Al2O3 (α corundum) | 2.9 kg | |||
| CaO | 6.5 kg | |||
| Fe2O3 (hematite) | 0.6 kg | |||
| Drawn-in Air | 6300 kg | [15,19] | Approximation calculated based on a batch time of 1.75 h, unthrottled suction [15], 30,000 Nm3/h per ton of melt [19], density of dry air: 1.2 kg/Nm3 | |
| Dry Air | 6206 kg | |||
| H2O (gaseous) | 94.5 kg | assumption of absolute humidity of 15 gH2O/kgair, 298 K, 101,325 Pa | ||
| Coolant Inductor (H2O at 313 K [10]) | 5811 kg | [10] (pp. 50–51) | Cooling capacity: 26 to 30% of the inverter capacity [10], transformer efficiency: 98.5% Assumption based on this approximation: | |
| Coolant Electric (H2O at 307 K [10]) | 5505 kg | Cooling capacity: 6% of the inverter capacity [10], transformer efficiency: 98.5% Assumption based on this approximation: | ||
| Output | Liquid SG iron at 1873 K | 1000 kg | [18] (p. 16) | Reference value |
| Fe (α) | 945 kg | 94.5% Fe | ||
| C (graphite) | 37 kg | 3.7% C | ||
| Si | 18 kg | 1.8% Si | ||
| Slag | 20.0 kg | [13,19] | 10 to 30 kg slag per ton of iron at 1573 K [19] | |
| SiO2 (amorphous) | 10.7 kg | 45 to 55% | ||
| CaO | 6.5 kg | 25 to 40% [13] (p. 274) | ||
| Al2O3 (α corundum) | 2.8 kg | 8 to 20% | ||
| Exhaust Air | 1.0 kg | [13,20] (p. 41) | 0.06 to 1 kg dust emission per ton of iron | |
| Fe2O3 (hematite) | 0.6 kg | 30 to 60% | ||
| SiO2 (amorphous) | 0.3 kg | ~25% [13] (p. 274) | ||
| C (graphite) | 0.1 kg | 3 to 10% | ||
| Al2O3 (α corundum) | 0.1 kg | 3 to 10% | ||
| dry air | 6206 kg | Equals input of dry air and moisture (H2O) | ||
| H2O (gaseous) | 94.5 kg | |||
| Coolant Inductor | 5811 kg | Equals input of coolant: H2O at 340 K [10] (p. 51) and H2O at 313 K [10] (p. 54) | ||
| Coolant Electric | 5505 kg | |||
| Energy Output | to be analyzed |
3. Results
3.1. Exergy Analysis
3.2. PhO Method
- No ohmic resistances of transformer, inverter, capacitor, coil, and power lines;
- No magnetic scattering or no magnetic resistance of the environment;
- No iron losses of the transformer and the coil;
- No friction due to coil vibrations (due to ideal fixing of the coil (rigid body) or friction coefficient equal to zero);
- No heat loss of the furnace (adiabatic crucible or zero melting time).
3.3. Method Comparison
4. Discussion
4.1. Analysis of the Induction Furnace
4.2. Method Comparison
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | Subscripts | ||
| PhO | physical optimum | amb | ambient (reference state, components) |
| PIOT | physical input-output table | ch | chemical |
| SG iron | spheroidal graphite cast iron | D | internal loss, destruction |
| VDI | Verein Deutscher Ingenieure | el | related to electricity |
| Symbols | exp | ||
| A | anergy [J] | i | component, parameter |
| B | exergy [J] | in | input |
| C | amount of a resource (e.g., energy [J]) | kin | kinetic |
| c | heat capacity [kJ/(kgK)] | L | external loss |
| f | factor [−] | mag | related to magnetism |
| H | enthalpy [J] | mech | mechanical |
| p | pressure [Pa] | out | output |
| Q | heat [J] | P | product |
| S | entropy [J/K] | ph | physical |
| T | temperature [K] | PhO | physical optimum |
| V | volume [m3] | pot | potential |
| W | work [J] | th | thermal |
| x | mass fraction [kg/kg] | trans | transit |
| y | mole fraction [mol/mol] | ||
| ζ | exergy efficiency [%] | ||
Appendix A
| PIOT | Chemical Exergy | Physical Exergy | Transit-Adjusted | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter i | Value xi | Molar mass | bch,I [kJ/mol] [7] | Bch [MJ/tP] | T [K] | cp [kJ/kgK] | Bph [MJ/tP] | Bch,trans [MJ/tP] | Bph,trans [MJ/tP] | |
| Input | Electrical Energy | 2339 MJ | ||||||||
| Stack of Sheets | 358.0 kg | 2511 | 0 | 0 | ||||||
| Fe (α) | 354.4 kg | 55.85 | 376 | 2389 | ||||||
| C | 3.6 kg | 12.01 | 410 | 122 | ||||||
| Recycled metal | 625.0 kg | 4881 | 0 | 0 | ||||||
| Fe (α) | 590.6 kg | 55.85 | 376.4 | 3980 | ||||||
| C (graphite) | 23.1 kg | 12.01 | 410.3 | 634 | ||||||
| Si | 11.2 kg | 28.09 | 854.6 | 266 | ||||||
| Alloying materials | 17.1 kg | 546 | 0 | 546 | 0 | |||||
| C (graphite) | 7.5 kg | 12.01 | 410.3 | 257 | ||||||
| SiC (hexag.) | 9.6 kg | 40.10 | 1204.6 | 290 | ||||||
| Impurities | 20.9 kg | 20.0 | 0 | 0 | 0 | |||||
| SiO2 (quartz) | 11.0 kg | 60.09 | 7.9 | 1.4 | ||||||
| Al2O3 (α cor.) | 2.9 kg | 101.96 | 200.4 | 5.7 | ||||||
| CaO | 6.5 kg | 56.08 | 110.2 | 12.8 | ||||||
| Fe2O3 (hem.) | 0.6 kg | 159.69 | 16.5 | 0.1 | ||||||
| Intake Air | 6300 kg | 0 | 0 | 0 | 0 | |||||
| dry air | 6206 kg | 1.29 | ||||||||
| H2O (gaseous) | 94.5 kg | 18.02 | ||||||||
| Coolant Inductor | 5811 kg | 18.02 | 0.9 | 290 | 313 | 4.19 | 9 | 0 | 0 | |
| Coolant Electric | 5505 kg | 18.02 | 0.9 | 275 | 307 | 4.19 | 3 | 0 | 0 | |
| Output | Liquid SG iron | 1000 kg | 7810 | 1873 | 0.949 | 975.0 | 418 | 975 | ||
| Fe (α) | 945 kg | 55.85 | 376.4 | 6369 | ||||||
| C (graphite) | 37 kg | 12.01 | 410.3 | 1015 | ||||||
| Si | 18 kg | 28.09 | 854.6 | 426.4 | ||||||
| Slag | 20.0 kg | 19.7 | 1573 | 14.8 | 0 | 15 | ||||
| SiO2 (amorph.) | 10.7 kg | 60.09 | 7.9 | 1.4 | 1573 | 0.98 | 8.2 | |||
| CaO | 6.5 kg | 56.08 | 110.2 | 12.8 | 1573 | 0.90 | 4.6 | |||
| Al2O3 (α cor.) | 2.8 kg | 102 | 200.4 | 5.5 | 1573 | 0.96 | 2.1 | |||
| Exhaust Air | 1.0 kg | 3.7 | 393 | 82.7 | 3.4 | 83 | ||||
| Fe2O3 (hem.) | 0.6 kg | 159.7 | 16.5 | 0.1 | 393 | 0.71 | 0.0 | |||
| SiO2 (amorph.) | 0.3 kg | 60.09 | 7.9 | 0.0 | 393 | 0.86 | 0.0 | |||
| C (graphite) | 0.1 kg | 12.01 | 410.3 | 3.4 | 393 | 1.11 | 0.0 | |||
| Al2O3 (α cor.) | 0.1 kg | 102 | 200.4 | 0.2 | 393 | 0.93 | 0.0 | |||
| dry air | 6206 kg | 0.0 | 393 | 1.00 | 77.8 | |||||
| H2O (gaseous) | 94.5 kg | 18.02 | 9.5 | 49.8 | 393 | 4.19 | 5.0 | |||
| Coolant Inductor | 5811 kg | 18.02 | 0.9 | 290.3 | 340 | 4.19 | 65.8 | 0 | 57 | |
| Coolant Electric | 5505 kg | 18.02 | 0.9 | 275.0 | 313 | 4.19 | 8.4 | 0 | 5 | |
| Exergy Destr. BD | 1329 MJ | 7810 | 1873 | 0.949 | 975.0 | 418 | 975 | |||
References
- Volta, D. Das Physikalische Optimum als Basis von Systematiken zur Steigerung der Energie- und Stoffeffizienz von Produktionsprozessen. Ph.D. Thesis, Universitätsbibliothek Clausthal, Technische Universität Clausthal, Clausthal-Zellerfeld, Germany, 2014. [Google Scholar]
- Keichel, C. Methode der Grenzwertorientierten Bewertung. Ph.D. Thesis, Universitätsbibliothek Clausthal, Technische Universität Clausthal, Clausthal-Zellerfeld, Germany, 2017. [Google Scholar]
- Beckmann, N. Wechselwirkungsanalyse Zwischen dem Physikalischen Optimum, dem Betriebswirtschaftlichen Optimum und dem Carbon-Footprint-Optimum (PhO-BwO-CFO). Ph.D. Thesis, Universitätsbibliothek Clausthal, Technische Universität Clausthal, Clausthal-Zellerfeld, Germany, 2017. [Google Scholar]
- Sankol, B.; Keichel, C.; Volta, D.; Pauksztat, A.; Kohn, D.; Kretschmer, L.; Meyer, S.; Girbig, P.; Kastner, H.-J. (Eds.) Verein Deutscher Ingenieure. Bewertung von Energie- und Stoffeffizienz Methodische Anwendung des Physikalischen Optimums; Beuth Verlag GmbH: Berlin, Germany, 2019; ISC 27.015 (4663-1). [Google Scholar]
- Szargut, J. International progress in second law analysis. Energy 1980, 5, 709–718. [Google Scholar] [CrossRef]
- Gutowski, T.G.P.; Sekulić, D.P. Thermodynamic Analysis of Resources Used in Manufacturing Processes. In Thermodynamics and the Destruction of Resources; Bakshi, B.R., Sekulić, D.P., Gutowski, T.G.P., Eds.; Cambridge University Press: Cambridge, UK, 2011; ISBN 9780511976049. [Google Scholar]
- Szargut, J.; Morris, D.R.; Steward, F.R. Exergy Analysis of Thermal, Chemical and Metallurgical Processes; Hemisphere Publ. Corp: New York, NY, USA, 1988; ISBN 9780891165743. [Google Scholar]
- Fratzscher, W.; Brodjanskij, V.M.; Michalek, K. Exergie. Theorie und Anwendung, 1st ed.; Deutscher Verlag für Grundstoffindustrie: Leipzig, Germany, 1986; ISBN 3-342-00091-0. [Google Scholar]
- Riedl, K. Exergetische und Exergoökonomische Bewertung von Verfahren der Energie- und Stoffwandlung. Ph.D. Thesis, Martin-Luther-Universität Halle-Wittenberg, Merseburg, Germany, 2007. [Google Scholar]
- Dötsch, E. Induktives Schmelzen und Warmhalten. Grundlagen, Anlagenaufbau, Verfahrenstechnik, 3rd ed.; Vulkan Verlag: Essen, Germany, 2019; ISBN 9783802731075. [Google Scholar]
- Dötsch, E. Induktionsofentechnologie und Energieeffizienz. GIESSEREI 98 2011, 6, 158–170. [Google Scholar]
- ETSU. Efficient Melting in Coreless Induction Furnaces. Good Practice Guide 50. 2000. Available online: https://lists.man.lodz.pl/pipermail/odlew-pl/2012/10/att-0003/guide_coreless_induction_furnaces.pdf (accessed on 12 October 2020).
- Neumann, F. Gußeisen. Schmelztechnik, Metallurgie, Schmelzbehandlung, 2nd ed.; Expert-Verl.: Renningen-Malmsheim, Germany, 1999; ISBN 3816917283. [Google Scholar]
- Schwanke, W. Schmelzen in Hochleistungsinduktionsöfen. In Elektrische Prozeßwärme für Aluminium, Gußeisen, Stahl: Tagung Essen, July 1993, 1st ed.; VDI, Ed.; VDI-Verl.: Düsseldorf, Germany, 1993; pp. 97–100. ISBN 3-18-091057-7. [Google Scholar]
- Wenzel, P. Exergetische Analyse und Physikalisches Optimum zur Bewertung und Steigerung der Ressourceneffizienz am Beispiel Eines Mittelfrequenzofens. Master‘s Thesis, Universität Stuttgart, Stuttgart, Germany, 2019. [Google Scholar]
- Frenzel, P. Bewertung von Syntheserouten auf Basis von Exergiebilanzen. Ph.D. Thesis, Technische Hochschule Aachen, Aachen, Germany, 2014. [Google Scholar]
- Trauzeddel, D. Spezielle Anwendungen der Induktiven Schmelz- und Gießtechnik. Einsatzgebiete—Anlagenbau—Prozesstechnik, 1st ed.; Vulkan: Essen, Germany, 2018; ISBN 978-3-8027-3093-1. [Google Scholar]
- Hack, K. Stoffwerte von Metallen und Berechnung von Wärmebilanzen. In Praxishandbuch Thermoprozess-Technik, 1st ed.; Starck, A.V., Mühlbauer, A., Kramer, C., Eds.; Vulkan-Verl.: Essen, Germany, 2003; ISBN 3-8027-2923-4. [Google Scholar]
- Trauzeddel, D. (Otto Junker GmbH, Simmerath, Germany). Personal communication, 6 May 2019.
- Neumann, F.; Schneider, W.-D.; Herfurth, K. Der Schmelzprozess für Eisenguß (GG/GGG/GT) aus der Sicht der Umwelt- und Klimabelastung in Zusammenhang mit dem Energieverbrauch. In Elektrische Prozeßwärme für Aluminium, Gußeisen, Stahl: Tagung Essen, July 1993, 1st ed.; VDI, Ed.; VDI-Verl.: Düsseldorf, Germany, 1993; ISBN 3-18-091057-7. [Google Scholar]
- Verein Deutscher Ingenieure. VDI-Wärmeatlas, 11th ed.; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-19980-6. [Google Scholar]
- Svehla, J.; Krutzler, T.; Schindler, I. Stand der Technik der Österreichischen Gießereien. Gesetzliche Rahmenbedingungen, Technische Möglichkeiten und Gießereibetriebe in Österreich. 2012. Available online: https://www.umweltbundesamt.at/fileadmin/site/publikationen/REP0389.pdf (accessed on 12 October 2020).
- Gonzalez Hernandez, A.; Paoli, L.; Cullen, J.M. How resource-efficient is the global steel industry? Resour. Conserv. Recycl. 2018, 133, 132–145. [Google Scholar] [CrossRef]
- Lally, B.; Biegler, L.; Henein, H. Finite difference heat-transfer modeling for continuous casting. MTB 1990, 21, 761–770. [Google Scholar] [CrossRef]
- Bosse, M.; Frost, E.; Hazrat, M.; Riemeier, J.-M.; Wolff, H. Ermittlung von Branchenspezifischen Potentialen zum Einsatz von Erneuerbaren Energien in Besonders Energieintensiven Industriesektoren am Beispiel der Gießerei-Industrie. UBA-FB 00. 2013. Available online: https://www.bmu.de/fileadmin/Daten_BMU/Pools/Forschungsdatenbank/fkz_3712_44_347_erneuerbare_energien_bf.pdf (accessed on 12 January 2020).




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wenzel, P.M.; Radgen, P.; Westermeyer, J. Comparing Exergy Analysis and Physical Optimum Method Regarding an Induction Furnace. Energies 2021, 14, 1621. https://doi.org/10.3390/en14061621
Wenzel PM, Radgen P, Westermeyer J. Comparing Exergy Analysis and Physical Optimum Method Regarding an Induction Furnace. Energies. 2021; 14(6):1621. https://doi.org/10.3390/en14061621
Chicago/Turabian StyleWenzel, Paula Marlene, Peter Radgen, and Jan Westermeyer. 2021. "Comparing Exergy Analysis and Physical Optimum Method Regarding an Induction Furnace" Energies 14, no. 6: 1621. https://doi.org/10.3390/en14061621
APA StyleWenzel, P. M., Radgen, P., & Westermeyer, J. (2021). Comparing Exergy Analysis and Physical Optimum Method Regarding an Induction Furnace. Energies, 14(6), 1621. https://doi.org/10.3390/en14061621






