An Optimal Power Flow Algorithm for the Simulation of Energy Storage Systems in Unbalanced Three-Phase Distribution Grids †
Abstract
1. Introduction
2. Dynamic Optimal Power Flow Algorithm
3. Solving the Optimization Problem
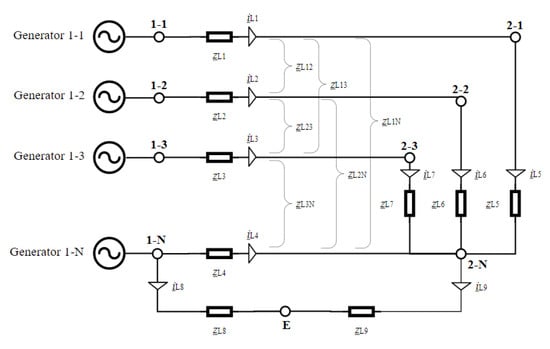
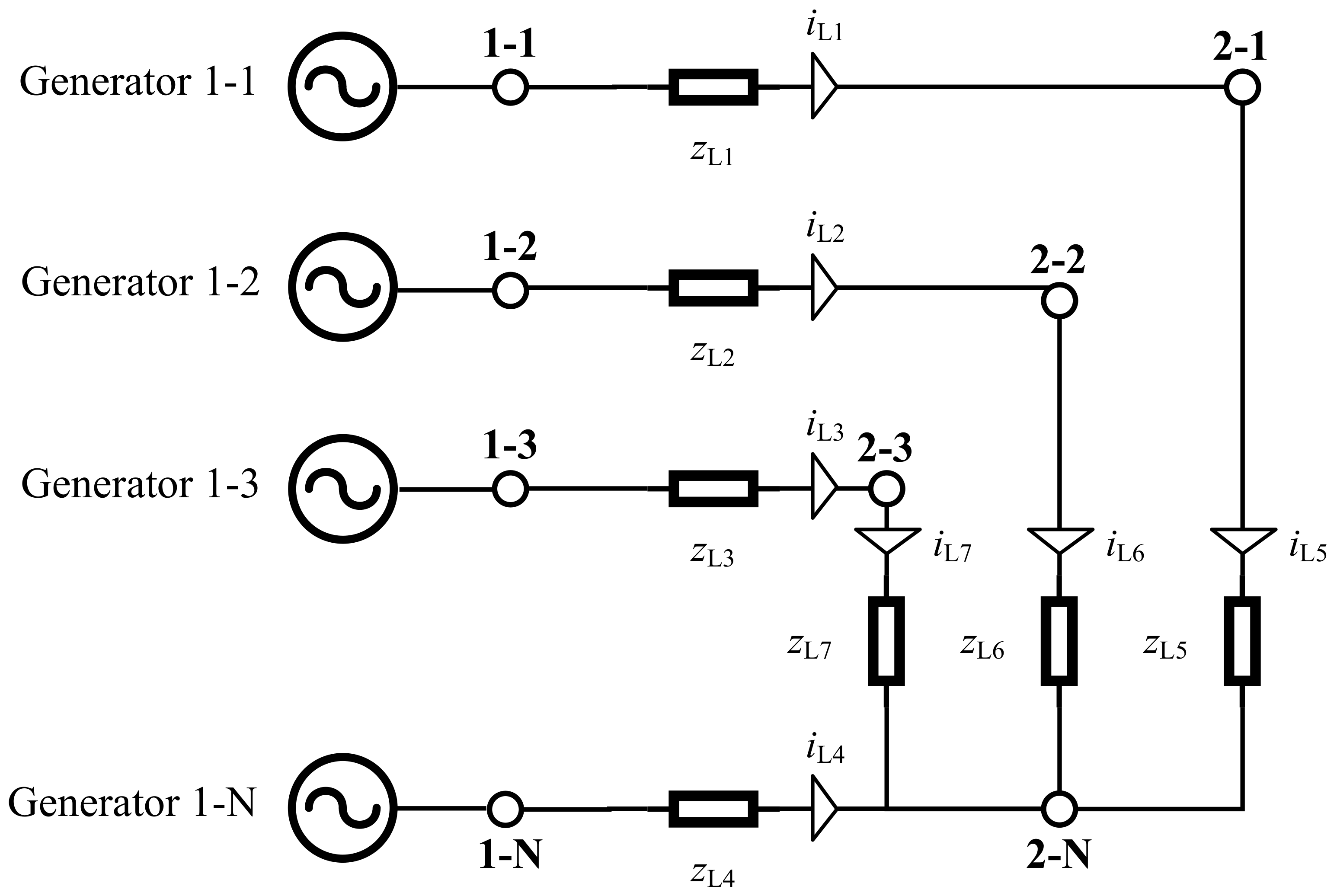
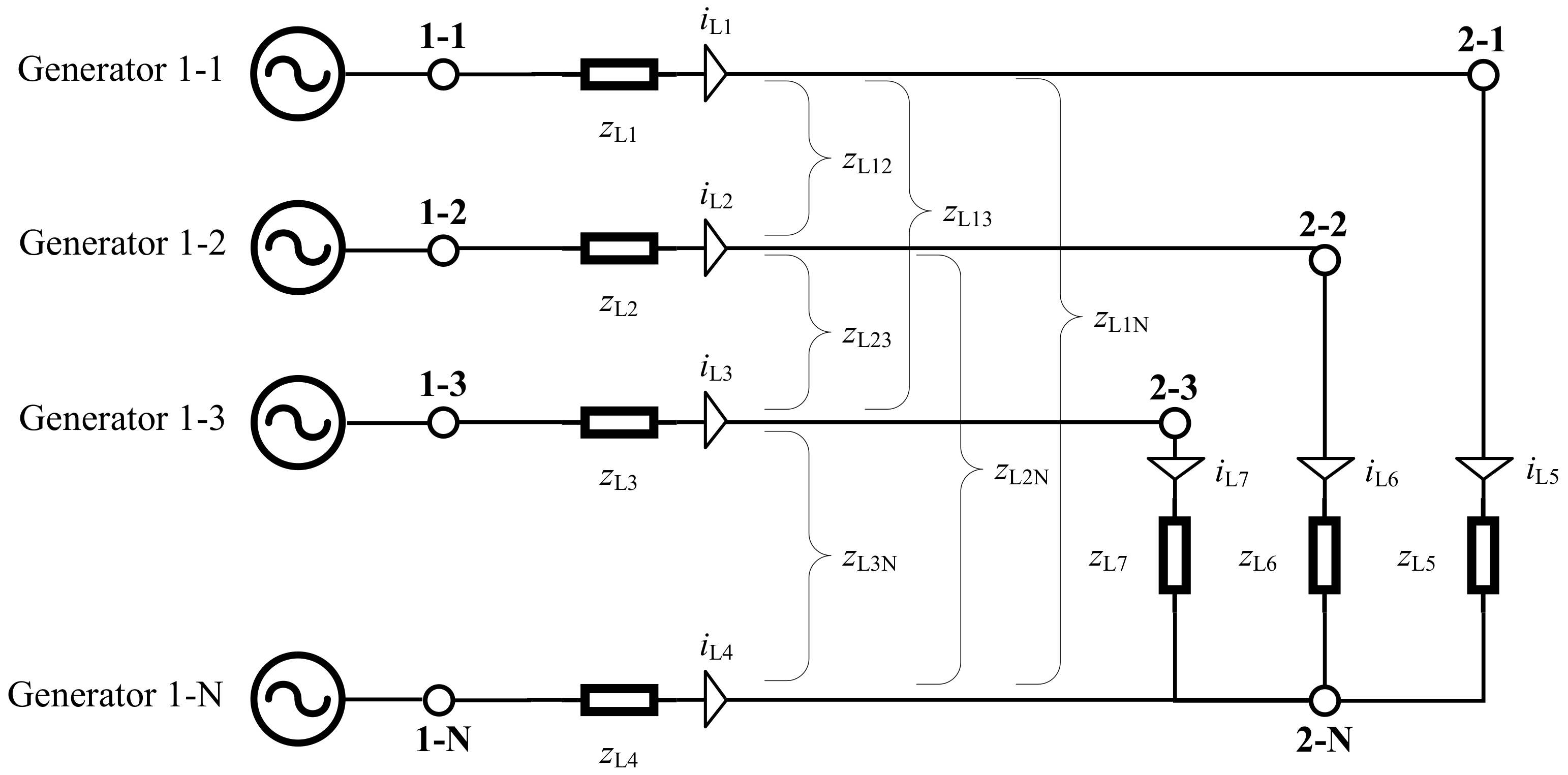
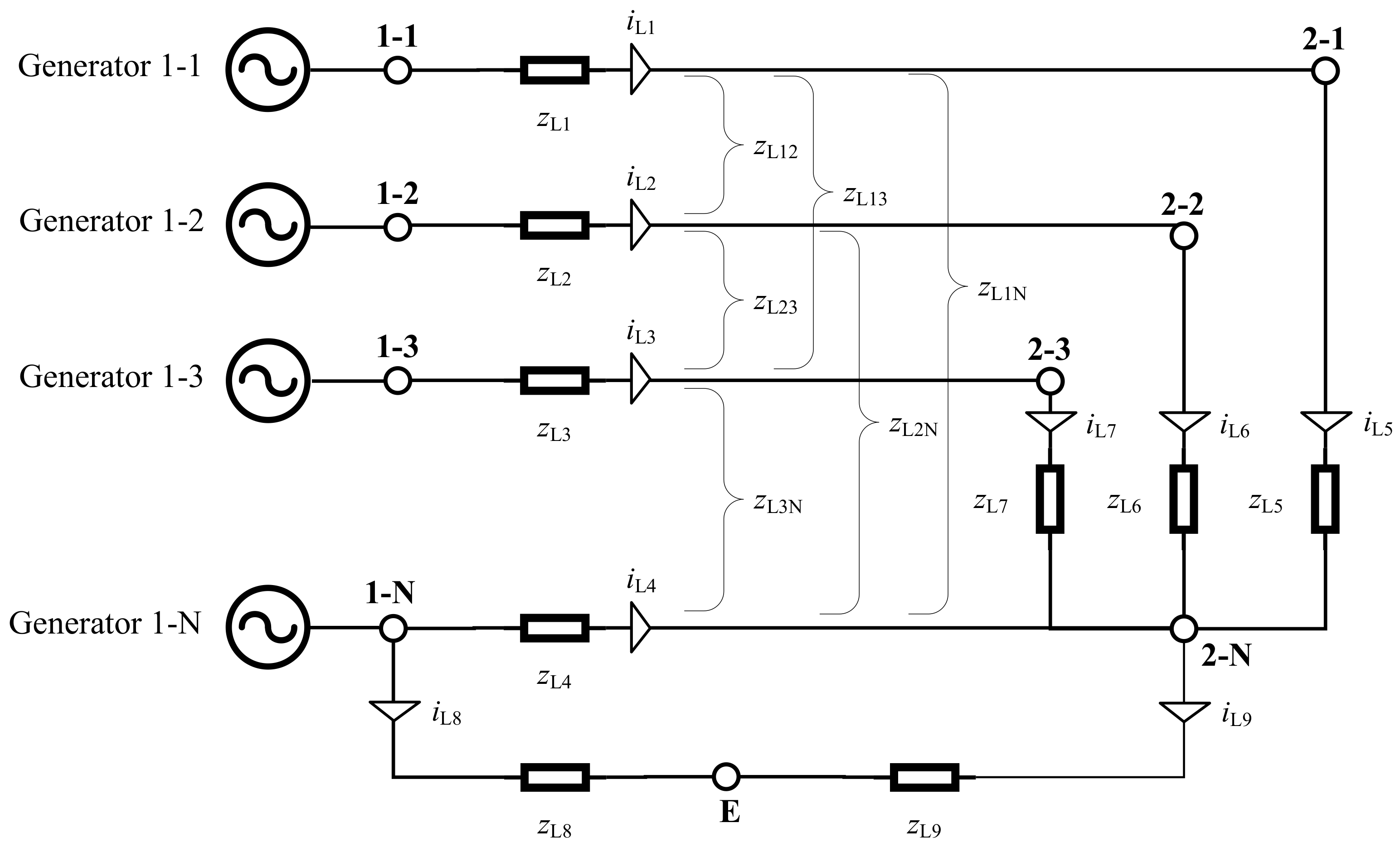
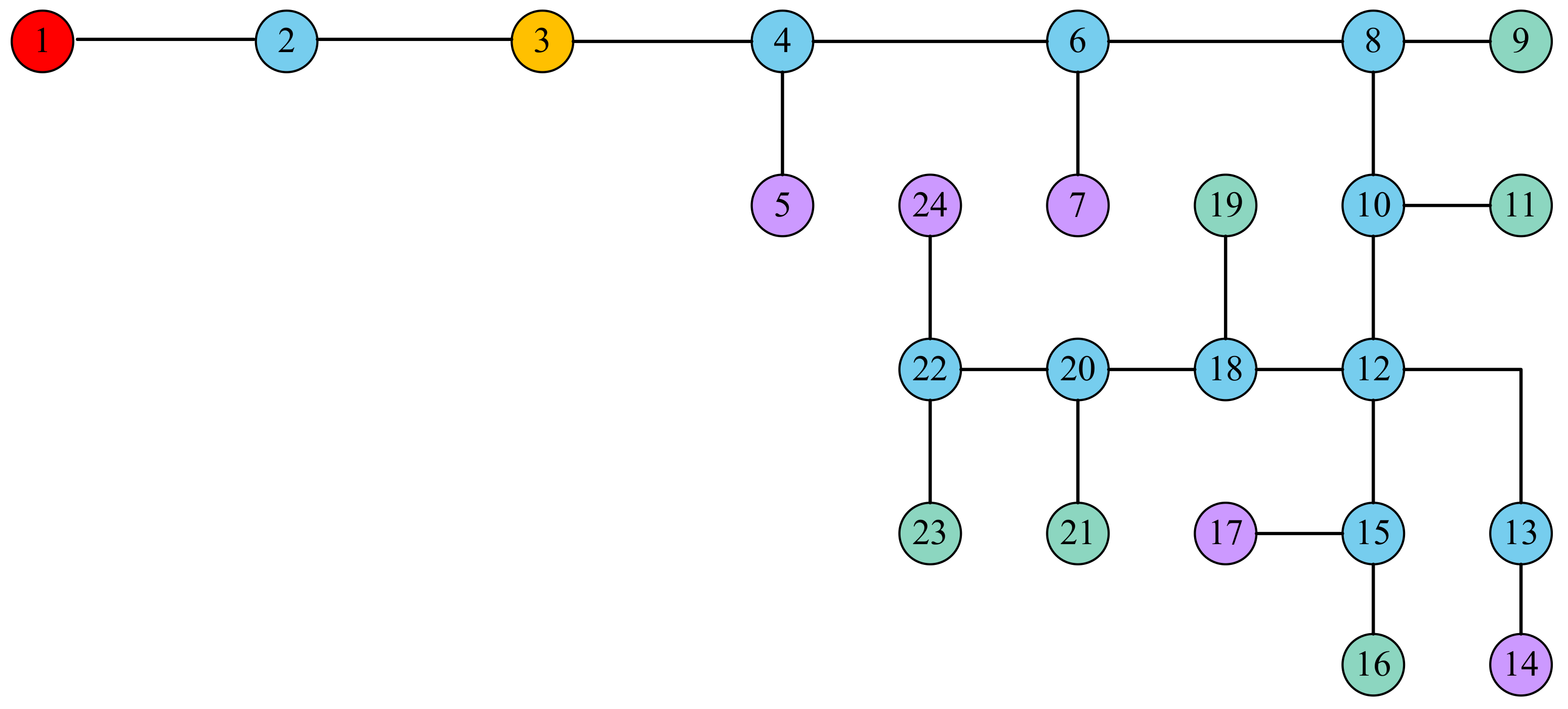
4. Model for the Three-Phase Low Voltage Grid
4.1. Representation of a Load as Impedance
4.2. The Impedance Matrix
4.3. The Nodal Impedance Matrix
5. Optimization Variables
6. Cost Function
7. Constraints for the Formulation of the Optimization Problem
7.1. Voltage at the Slack Bus
7.2. Power Flow Equation
7.3. Current Equation
7.4. Limits for the Voltages in the Grid
7.5. Limit for Voltage Unbalance
7.6. Current Limits of the Lines
7.7. Power Limits of the Generator
7.8. Power Limits of the Storage
7.9. Energy Capacity Limits of the Storage
7.10. Storage Equation
7.11. Total Number of Constraints
8. Validation of the OPF Algorithm Using Simulink
9. Exemplary Results for the Dynamic TOPF Using a Battery Storage
9.1. Input Data for the Simulations
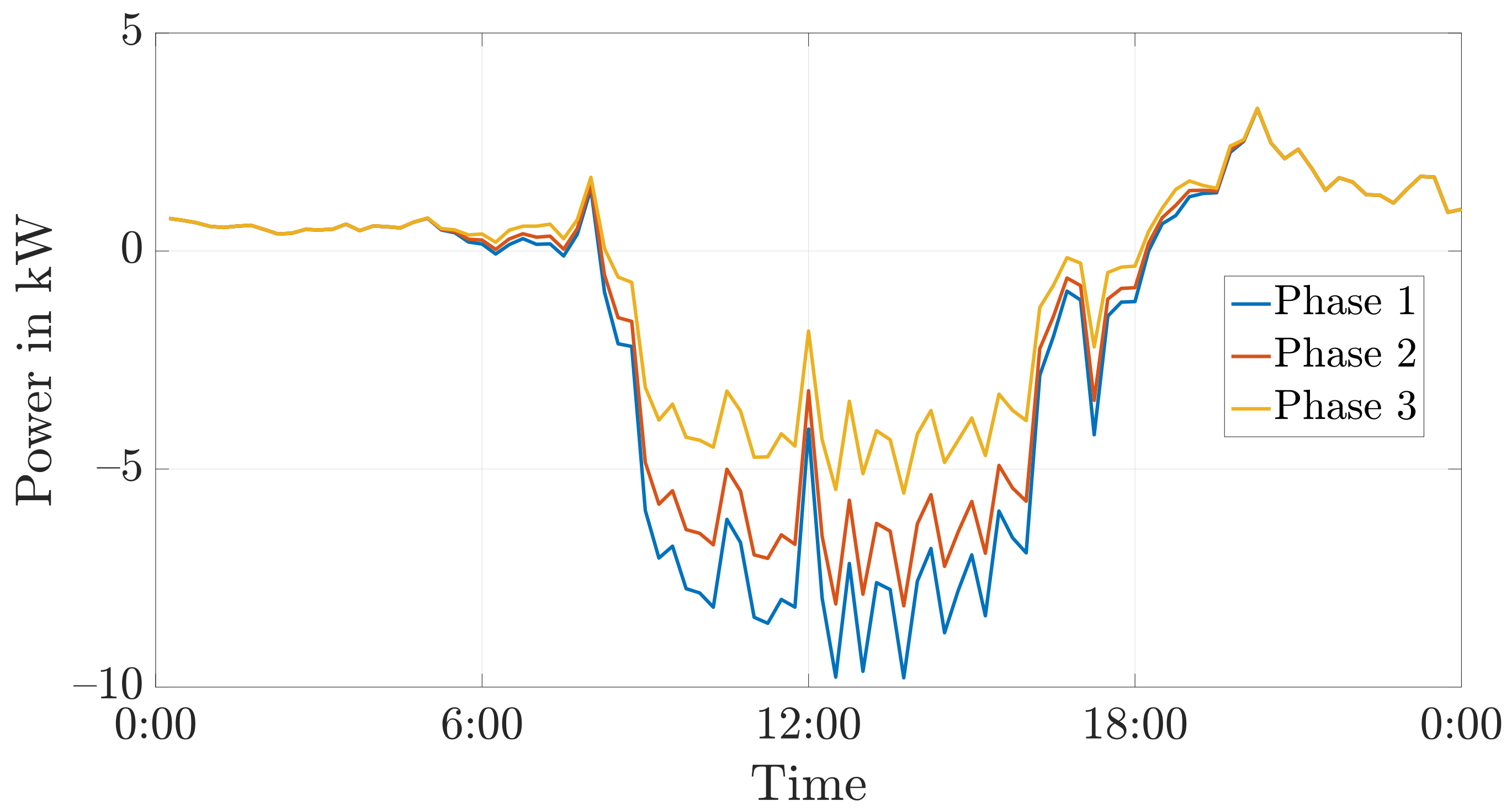
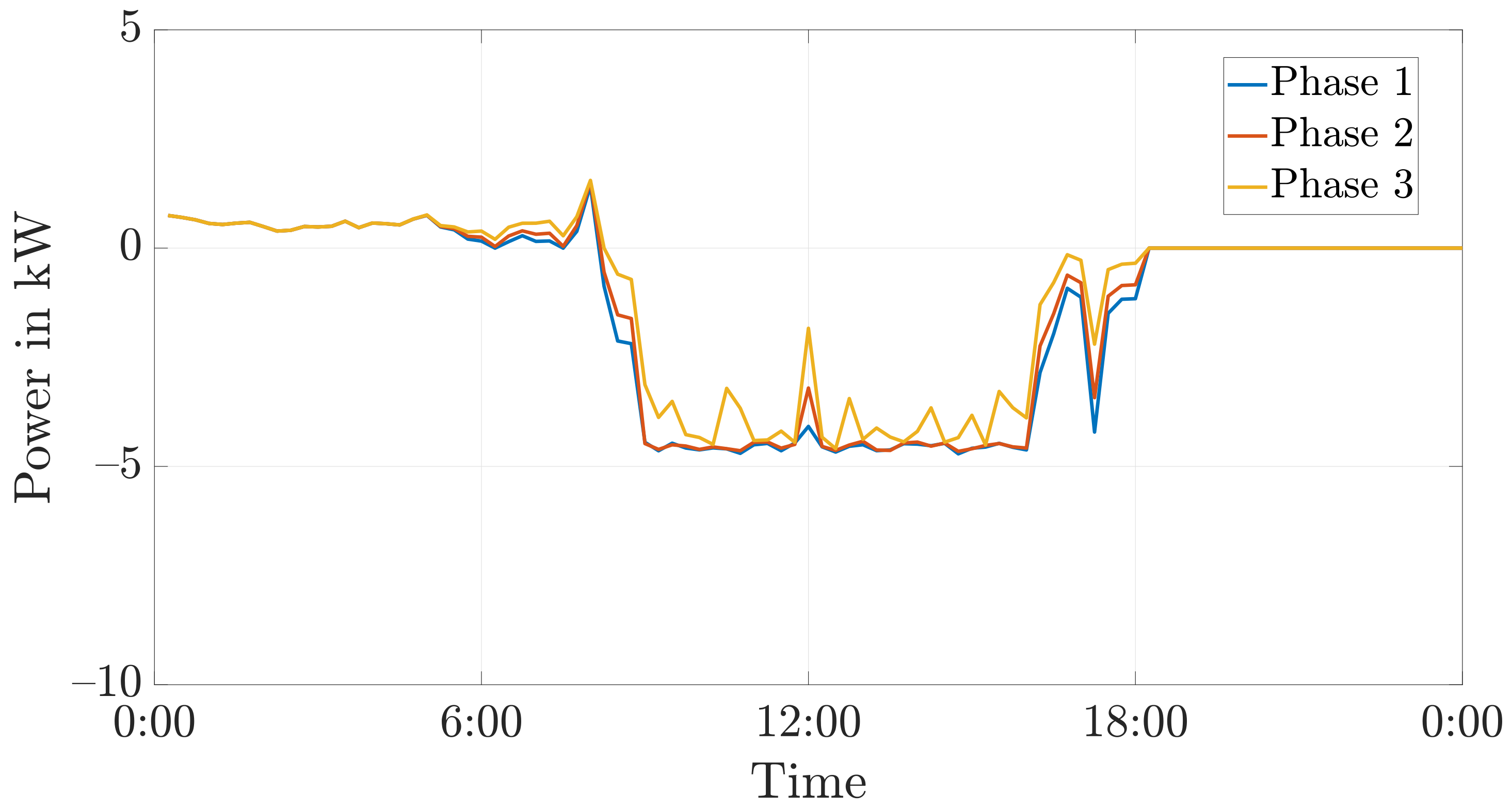
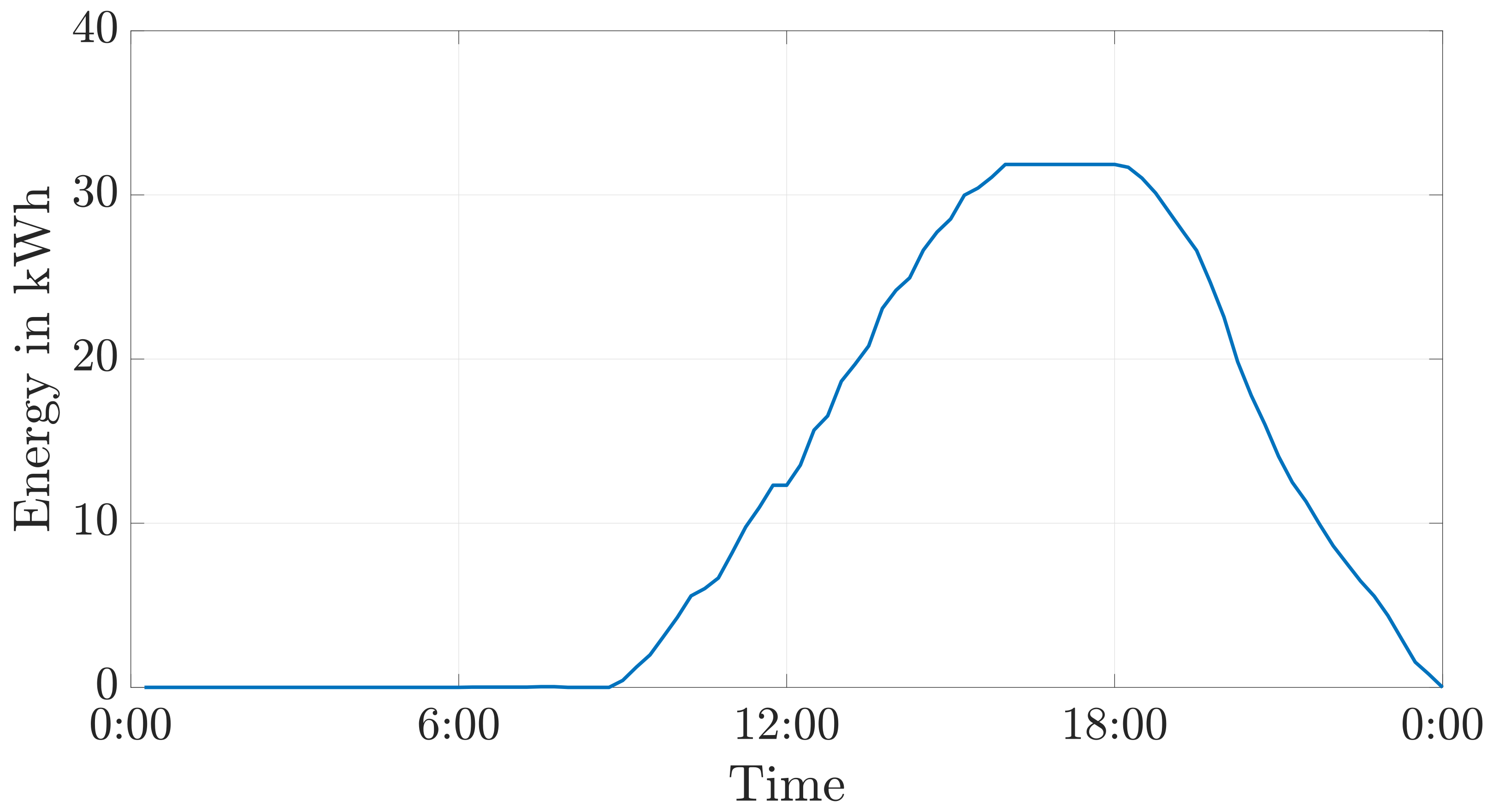
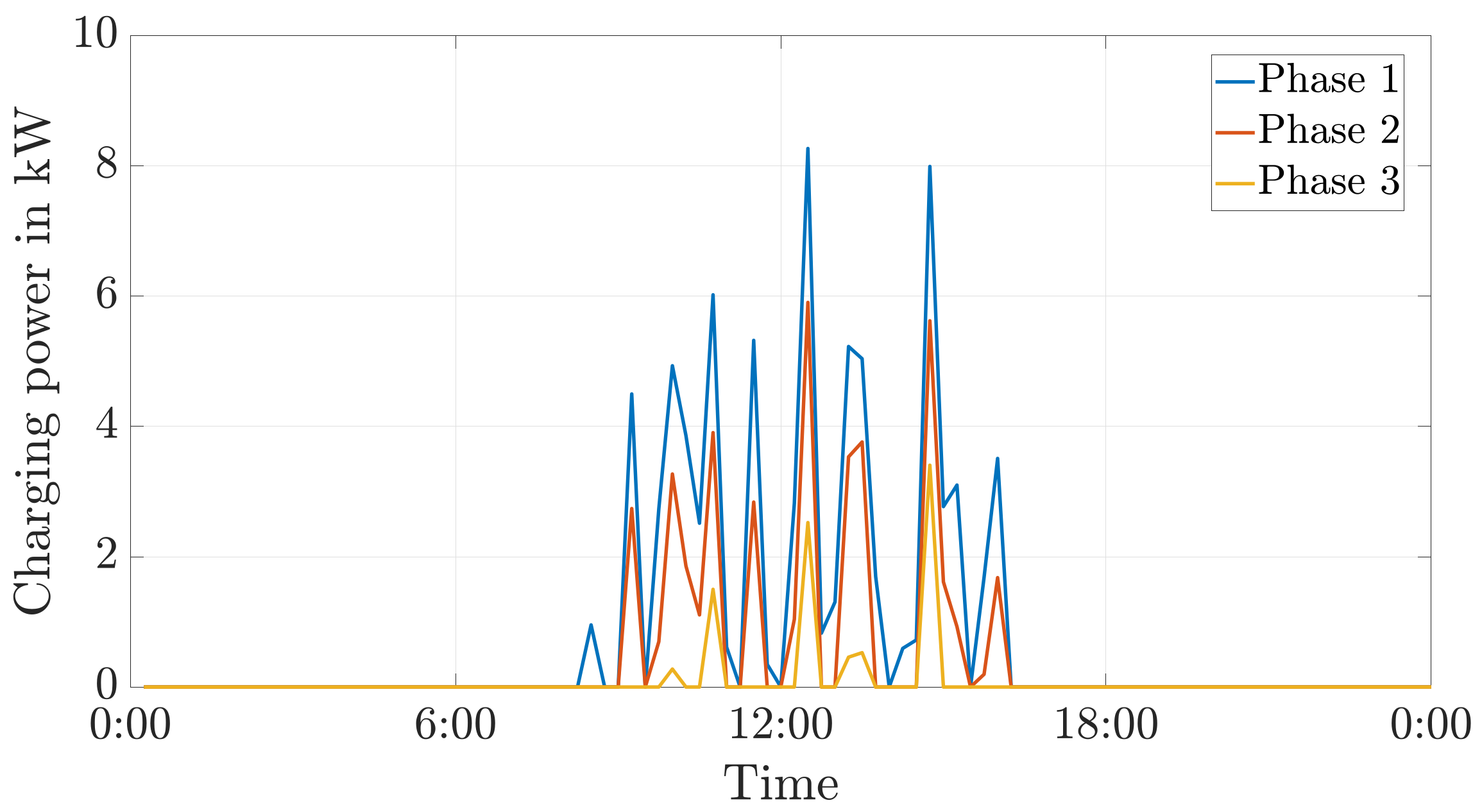
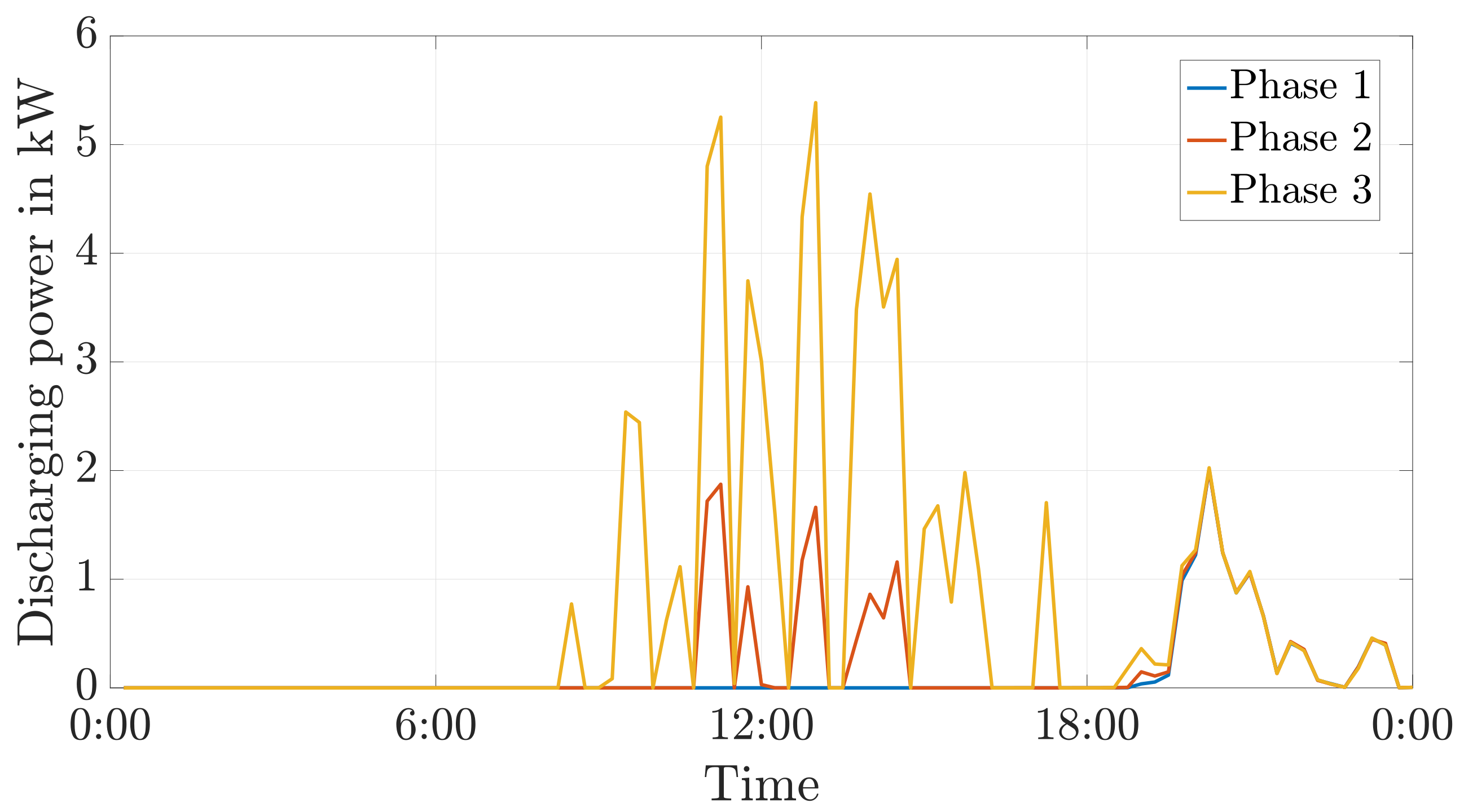
9.2. Increasing Self-Consumption Using a Battery Storage
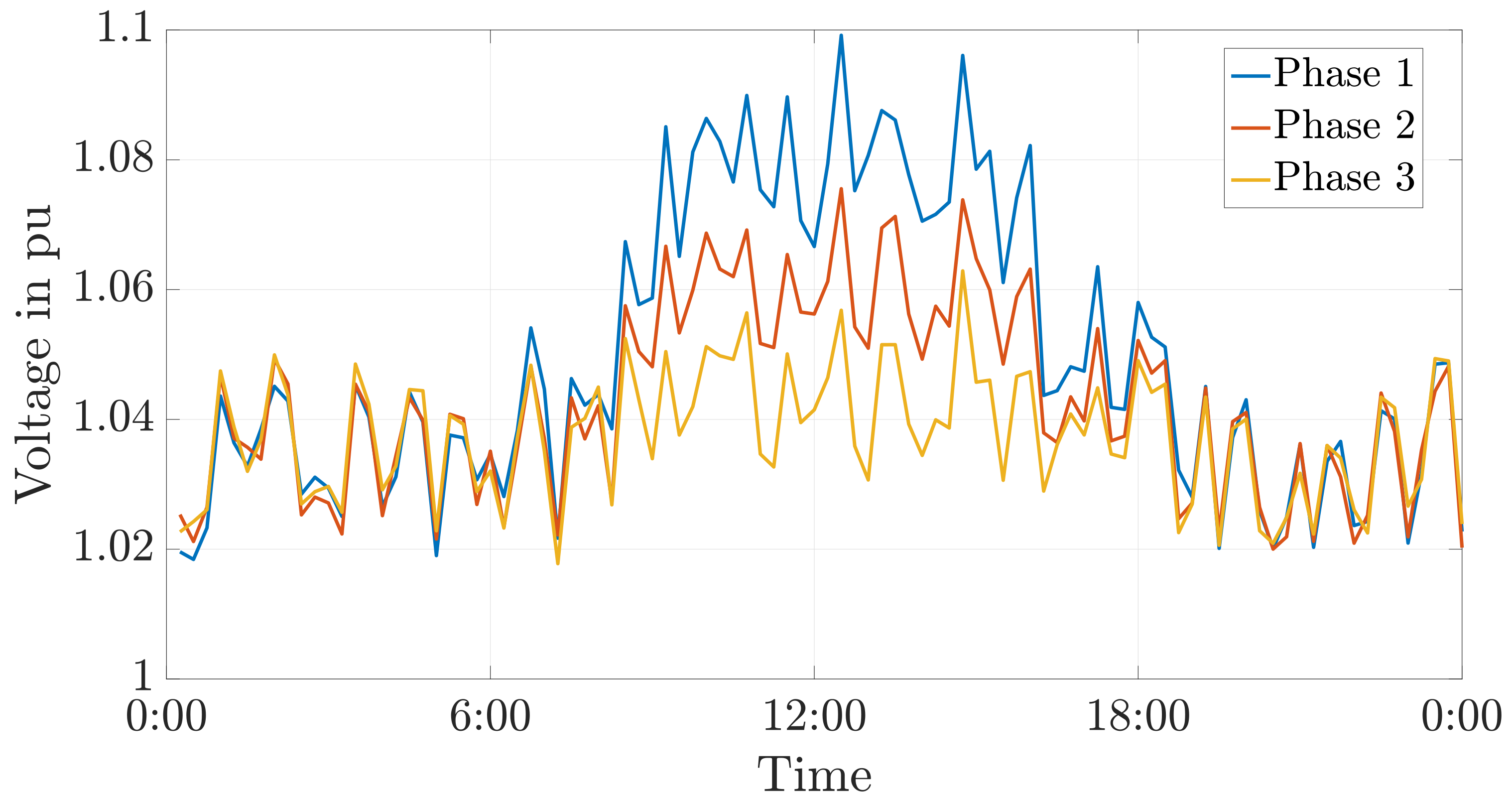
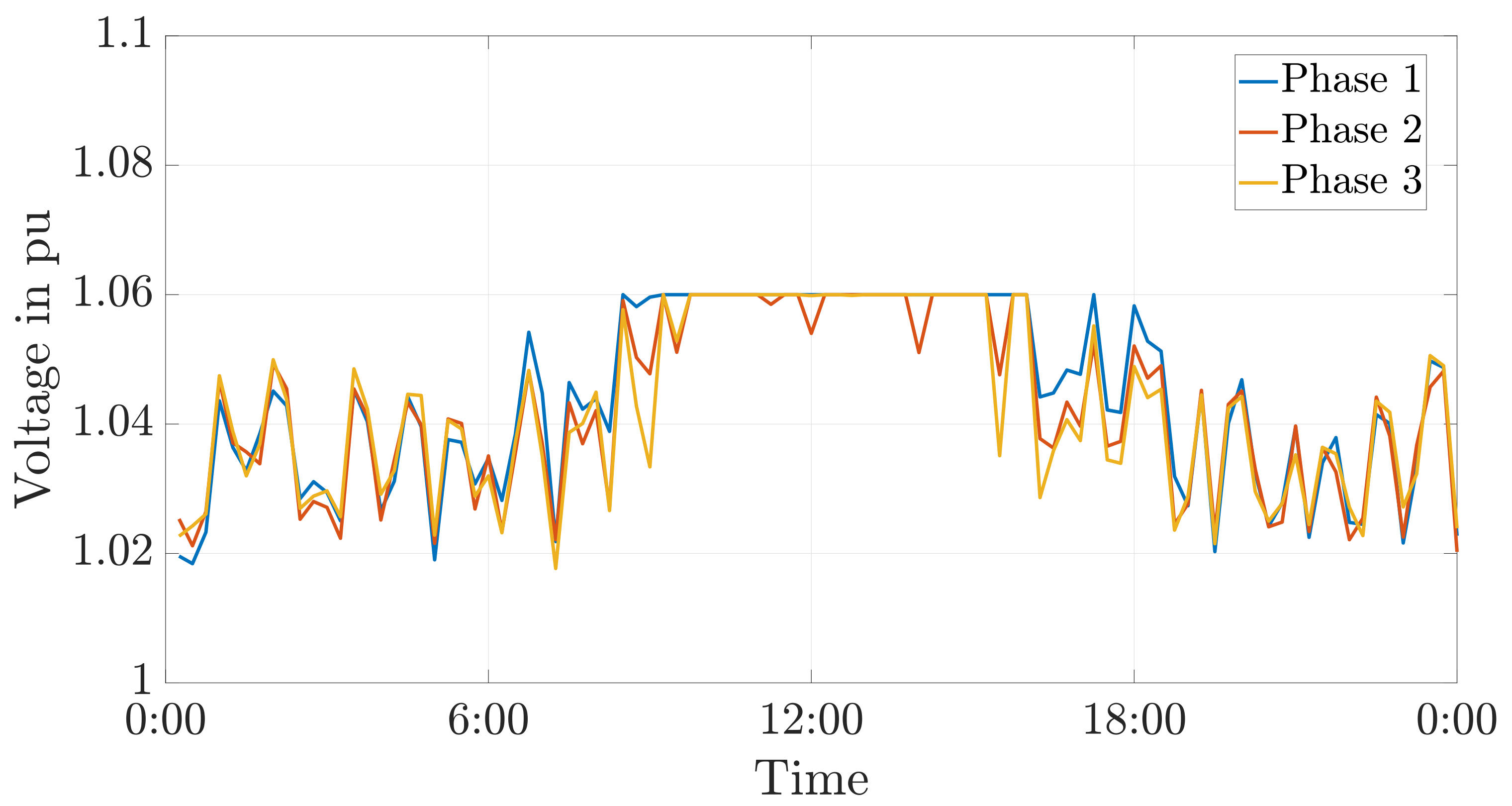
9.3. Ensuring Compliance with the Voltage Limits Using a Battery Storage
9.4. Ensuring Compliance with the Voltage Unbalance Limit Using a Battery Storage
9.5. Discussion of the Simulation Results
10. Summary & Outlook
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DG | Distributed generation |
| LV | Low voltage |
| MV | Medium voltage |
| OPF | Optimal power flow |
| PDIPM | Primal-Dual Interior Point Method |
| PV | Photovoltaic |
| TOPF | Three-phase optimal power flow |
| The following symbols are used in this manuscript: | |
| a | Real part of the admittance matrix |
| Real part of the nodal admittance matrix | |
| b | Imaginary part of the admittance matrix |
| Imaginary part of the nodal admittance matrix | |
| B | Bus |
| c | Cost factor |
| C | C = (1, 2, 3 or N) |
| CP = (1, 2 or 3) | |
| Auxiliary variable | |
| Real part of the voltage at point B-C at time step t | |
| Real part of the negative sequence voltage at bus B at time step t | |
| Real part of the positive sequence voltage at bus B at time step t | |
| Vector containing the real part of all voltages at time step t | |
| E | Earth |
| Energy stored in the storage at bus B at time step t | |
| Total energy capacity of the storage at bus B | |
| Charging efficiency | |
| Discharging efficiency | |
| Imaginary part of the voltage at Point B-C at time step t | |
| Imaginary part of the negative sequence voltage at bus B at time step t | |
| Imaginary part of the positive sequence voltage at bus B at time step t | |
| Vector containing the imaginary part of all voltages at time step t | |
| F | Cost function |
| g | Equality constraint |
| Barrier coefficient | |
| h | Inequality constraint |
| Sum of the currents at point B-C at time step t | |
| Sum of the currents at point Earth at time step t | |
| Current that is inserted at point B-CP at time step t | |
| Real part of the current that is inserted at point B-CP at time step t | |
| Imaginary part of the current that is inserted at point B-CP at time step t | |
| Current on Line Y at time step t | |
| Maximum current on Line Y | |
| Vector containing flowing from one bus B to other buses at time step t | |
| Real part of the current that is inserted at all points at time step t | |
| Imaginary part of the current that is inserted at all points at time step t | |
| Vector containing all currents at time step t | |
| j | imaginary unit |
| k | Any real part or imaginary part of a voltage |
| l | Any real part or imaginary part of a voltage |
| Langrangian | |
| Langrangian multiplier for equality constraints | |
| Langrangian multiplier for inequality constraints | |
| Number of inequality constraints | |
| N | Neutral |
| Sum of the active power flowing from point B-C to other points | |
| Active power of the generator at point B-C at time step t | |
| Minimum active power of the generator at point B-C | |
| Maximum active power of the generator at point B-C | |
| Active charging power of the storage at point B-CP at time step t | |
| Maximum active charging power of the storage at point B-CP | |
| Minimum active charging power of the storage at point B-CP | |
| Active discharging power of the storage at point B-CP at time step t | |
| Maximum active discharging power of the storage at point B-CP | |
| Minimum active discharging power of the storage at point B-CP | |
| Rated active power of the transformer at bus B | |
| Vector containing the sum of the active power flowing from one point to | |
| other points | |
| Vector containing the sum of the active power generated by generators, | |
| storage systems or constant power loads at all points in the grid at time step t | |
| Sum of the reactive power flowing from point B-C to other points at time step t | |
| Reactive power of the generator at point B-C at time step t | |
| Minimum reactive power of the generator at point B-C | |
| Maximum reactive power of the generator at point B-C | |
| Reactive power of the storage at point B-CP at time step t | |
| Maximum reactive power of the storage at point B-CP | |
| Rated reactive power of the transformer at bus B | |
| Vector containing the sum of the reactive power flowing from one point to other points | |
| Vector containing the sum of the reactive power generated by generators, storage systems or constant power loads at all points in the grid at time step t | |
| S | Auxiliary matrix |
| Power consumed at time step t at bus B | |
| Constant power share of the power consumed at time step t at bus B | |
| Constant impedance share of the power consumed at time step t at bus B | |
| Sum of the power flowing from point B-C to other points | |
| Vector containing the sum of the power flowing from one point to other points | |
| t | Actual time step |
| T | Horizon |
| Nominal voltage | |
| Maximum allowed voltage | |
| Minimum allowed voltage | |
| Voltage at point B-C at time step t | |
| Voltage at point Earth at time step t | |
| Negative sequence voltage at bus B at time step t | |
| Positive sequence voltage at bus B at time step t | |
| Voltage unbalance at bus B at time step t | |
| Maximum allowed voltage unbalance | |
| Vector containing all voltages at time step t | |
| x | Vector containing optimization variables |
| Admittance matrix | |
| Nodal admittance matrix | |
| Impedance matrix | |
| Mutual impedance | |
| Nodal Impedance matrix | |
| Series impedance | |
| Impedance of Line Y at time step t | |
| Slack variable n | |
| Vector of slack variables | |
References
- Held, L.; Koenig, S.; Uhrig, M.; Leibfried, T.; Hoeche, R.; Buschmann, H.; Woessner, R.; Neu, C.; Nikolic, L. Hybrid-Optimal: Demonstration project of the cellular approach. In Proceedings of the International ETG Congress 2017, Bonn, Germany, 28–29 November 2017. [Google Scholar]
- Held, L.; Märtz, A.; Krohn, D.; Wirth, J.; Zimmerlin, M.; Suriyah, M.R.; Leibfried, T.; Jochem, P.; Fichtner, W. The Influence of Electric Vehicle Charging on Low Voltage Grids with Characteristics Typical for Germany. World Electr. Veh. J. 2019, 10, 88. [Google Scholar] [CrossRef]
- Carpentier, J. Contribution to the economic dispatch problem. Bull. Soc. Fr. Des. Electr. 1962, 3, 431–447. (In French) [Google Scholar]
- Pandya, K.; Joshi, S. A survey of optimal power flow methods. J. Theor. Appl. Inf. Technol. 2008, 4, 762–770. [Google Scholar]
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal power flow: A bibliographic survey I. Energy Syst. 2012, 3, 221–258. [Google Scholar] [CrossRef]
- Harrison, G.P.; Piccolo, A.; Siano, P.; Wallace, R. Hybrid GA and OPF evaluation of network capacity for distributed generation connections. Electr. Power Syst. Res. 2008, 78, 392–398. [Google Scholar] [CrossRef]
- Zhu, Y.; Tomsovic, K. Optimal distribution power flow for systems with distributed energy resources. Int. J. Electr. Power Energy Syst. 2007, 29, 260–267. [Google Scholar] [CrossRef]
- Khodr, H.M.; Matos, M.A.; Pereira, J. Distribution Optimal Power Flow. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007. [Google Scholar]
- Ochoa, L.F.; Harrison, G.P. Minimizing Energy Losses: Optimal Accommodation and Smart Operation of Renewable Distributed Generation. IEEE Trans. Power Syst. 2011, 26, 198–205. [Google Scholar] [CrossRef]
- Ahmadi, A.R.; Green, T.C. Optimal power flow for autonomous regional active network management system. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Ochoa, L.F.; Dent, C.J.; Harrison, G.P. Distribution Network Capacity Assessment: Variable DG and Active Networks. IEEE Trans. Power Syst. 2010, 25, 87–95. [Google Scholar] [CrossRef]
- Dolan, M.J.; Davidson, E.M.; Ault, G.W.; Coffele, F.; Kockar, I.; McDonald, J.R. Using optimal power flow for management of power flows in active distribution networks within thermal constraints. In Proceedings of the 2009 44th International Universities Power Engineering Conference, Glasgow, UK, 1–4 September 2009. [Google Scholar]
- O’Connell, A.; Keane, A. Multi-period three-phase unbalanced optimal power flow. In Proceedings of the 2014 IEEE PES Innovative Smart Grid Technologies Europe, Istanbul, Turkey, 12–15 October 2014. [Google Scholar]
- Araujo, L.R.; Penido, D.R.R.; Alcantara Vieira, F. A multiphase optimal power flow algorithm for unbalanced distribution systems. Int. J. Electr. Power Energy Syst. 2013, 53, 632–642. [Google Scholar] [CrossRef]
- Paudyal, S.; Canizares, C.A.; Bhattacharya, K. Optimal Operation of Distribution Feeders in Smart Grids. IEEE Trans. Ind. Electron. 2011, 58, 4495–4503. [Google Scholar] [CrossRef]
- Bruno, S.; Lamonaca, S.; Rotondo, G.; Stecchi, U.; La Scala, M. Unbalanced Three-Phase Optimal Power Flow for Smart Grids. IEEE Trans. Ind. Electron. 2011, 58, 4504–4513. [Google Scholar] [CrossRef]
- Araujo, L.R.; Penido, D.R.R.; Carneiro, S.; Pereira, J.L.R. A Three-Phase Optimal Power-Flow Algorithm to Mitigate Voltage Unbalance. IEEE Trans. Power Deliv. 2013, 28, 2394–2402. [Google Scholar] [CrossRef]
- O’Connell, A. Unbalanced distribution system voltage optimisation. In Proceedings of the 2016 IEEE PES Innovative Smart Grid Technologies Conference Europe, Ljubljana, Slovenia, 9–12 October 2016. [Google Scholar]
- Cao, Y.; Tan, Y.; Li, C.; Rehtanz, C. Chance-Constrained Optimization-Based Unbalanced Optimal Power Flow for Radial Distribution Networks. IEEE Trans. Power Deliv. 2013, 28, 1855–1864. [Google Scholar]
- Ju, Y.; Wu, W.; Lin, Y.; Ge, F.; Ye, L. Three-phase optimal load flow model and algorithm for active distribution networks. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Watson, J.D.; Watson, N.R.; Lestas, I. Optimized Dispatch of Energy Storage Systems in Unbalanced Distribution Networks. IEEE Trans. Sustain. Energy 2018, 9, 639–650. [Google Scholar] [CrossRef]
- Meng, X.; Wang, L.; Wang, J.; Wang, Y.; Meng, Y. Distributed Generation Optimal Placing Approach Considering Low-voltage Control in Low-voltage Distribution Network. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020. [Google Scholar]
- Bazrafshan, M.; Gatsis, N.; Dall’Anese, E. Placement and Sizing of Inverter-Based Renewable Systems in Multi-Phase Distribution Networks. IEEE Trans. Power Syst. 2019, 34, 918–930. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, W.; Lin, C.; Li, L.; Yang, Y. Asynchronous Distributed Optimal Load Scheduling Algorithm. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020. [Google Scholar]
- Wei, J.; Corson, L.; Srivastava, A.K. Three-phase optimal power flow based distribution locational marginal pricing and associated price stability. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Anwar, A.; Pota, H.R. Optimum capacity allocation of DG units based on unbalanced three-phase optimal power flow. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Giraldo, J.S.; Vergara, P.P.; Lopez, J.C.; Nguyen, P.H.; Paterakis, N.G. A Novel Linear Optimal Power Flow Model for Three-Phase Electrical Distribution Systems. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020. [Google Scholar]
- Paudyal, S.; Cañizares, C.A.; Bhattacharya, K. Three-phase distribution OPF in smart grids: Optimality versus computational burden. In Proceedings of the 2011 2nd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies, Manchester, UK, 5–7 December 2011. [Google Scholar]
- Gan, L.; Low, S.H. Chordal relaxation of OPF for multiphase radial networks. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems, Melbourne, Australia, 1–5 June 2014. [Google Scholar]
- Liu, Y.; Li, J.; Wu, L. ACOPF for three-phase four-conductor distribution systems: Semidefinite programming based relaxation with variable reduction and feasible solution recovery. IET Gener. Transm. Distrib. 2019, 13, 266–276. [Google Scholar] [CrossRef]
- Usman, M.; Cervi, A.; Coppo, M.; Bignucolo, F.; Turri, R. Convexified OPF in Multiphase Low Voltage Radial Distribution Networks including Neutral Conductor. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019. [Google Scholar]
- Alsenani, T.R.; Paudyal, S. Distributed Approach for Solving Optimal Power Flow Problems in Three-phase Unbalanced Distribution Networks. In Proceedings of the 2018 Australasian Universities Power Engineering Conference, Auckland, New Zealand, 27–30 November 2018. [Google Scholar]
- Geth, F.; Coffrin, C.; Fobes, D.M. A Flexible Storage Model for Power Network Optimization. In Proceedings of the Eleventh ACM International Conference on Future Energy Systems (e-Energy ’20), Melbourne, Australia, 22–26 June 2020. [Google Scholar]
- Held, L.; Kràmer, H.; Zimmerlin, M.; Suriyah, M.R.; Leibfried, T.; Ratajczak, L.; Lossau, S.; Konermann, M. Dimensioning of battery storage as temporary equipment during grid reinforcement caused by electric vehicles. In Proceedings of the 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018. [Google Scholar]
- Held, L.; Gerhardt, N.; Zimmerlin, M.; Suriyah, M.R.; Leibfried, T.; Armbruster, M. Grid-friendly Operation of a Hybrid Battery Storage System. In Proceedings of the CIRED 2019 Conference, Madrid, Spain, 3–6 June 2019. [Google Scholar]
- Held, L.; Uhrig, M.; Suriyah, M.R.; Leibfried, T.; Junge, E.; Lossau, S.; Konermann, M. Impact of electric vehicle charging on low-voltage grids and the potential of battery storage as temporary equipment during grid reinforcement. In Proceedings of the 1st E-Mobility Power System Interation Symposium, Berlin, Germany, 23 October 2017. [Google Scholar]
- Held, L.; Barakat, M.; Müller, F.; Suriyah, M.R.; Leibfried, T. An Optimal Power Flow Algorithm for the Simulation of Energy Storage Systems in Unbalanced Three-Phase Distribution Grids. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Torino, Italy, 1–4 September 2020. [Google Scholar]
- Fobes, D.M.; Claeys, S.; Geth, F.; Coffrin, C. PowerModelsDistribution.jl: An Open-Source Framework for Exploring Distribution Power Flow Formulations. Electr. Power Syst. Res. 2020, 189, 106664. [Google Scholar] [CrossRef]
- Rigoni, V.; Keane, A. Open-DSOPF: An open-source optimal power flow formulation integrated with OpenDSS. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sanchez, C.E. MATPOWER (Version 6.0). Available online: https://matpower.org (accessed on 12 March 2021).
- Meyer-Hùbner, N.; Haas, M.; Suriyah, M.; Leibfried, T. Dynamic Optimal Power Flow for Dimensioning and Operating Quarter Based Storage in Low Voltage Grids. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe, Torino, Italy, 26–29 September 2017. [Google Scholar]
- Wang, H.; Murillo-Sanchez, C.; Zimmermann, R.; Thomas, R. On computational issues of market-based optimal power flow. IEEE Trans. Power Syst. 2007, 22, 1185–1193. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Geis-Schroer, J.; Hubschneider, S.; Held, L.; Gielnik, F.; Armbruster, M.; Suriyah, M.; Leibfried, T. Modeling of German Low Voltage Cables with Ground Return Path. Energies 2021, 14, 1265. [Google Scholar] [CrossRef]
- Stenzel, D.; Viernstein, L.; Hewes, D.; Würl, T.; Witzmann, R. Modelling of Stationary and Dynamic Demand Behavior considering Sectoral and Regional Characteristics. In Proceedings of the CIRED 2019 Conference, Madrid, Spain, 3–6 June 2019. [Google Scholar]
- CENELEC - European Committee for Electrotechnical Standardization. EN 50160:2010/A1:2015—Voltage Characteristics of Electricity Supplied by Public Electricity Networks; CEN-CENELEC Management Centre: Brussels, Belgium, 2015. [Google Scholar]
- Held, L.; Armbruster, M.; Zimmerlin, M.; Suriyah, M.R.; Leibfried, T.; Höche, R. The Operation of a Battery Storage System to Avoid Overvoltages in a Low Voltage Grid. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Tunis, Tunisia, 28 September–1 October 2020. [Google Scholar]
- Armbruster, M.; Höche, R.; Held, L.; Zimmerlin, M.; Suriyah, M.R.; Leibfried, T. The Influence of Energy Cell’s Size and Generation-Load-Ratio on Economic Benefits. In Proceedings of the 13th International Renewable Energy Storage Conference 2019 (IRES 2019), Düsseldorf, Germany, 12–15 March 2019. [Google Scholar]
- Uhrig, M. Lastprofilgenerator zur Modellierung von Wirkleistungsprofilen Privater Haushalte. Available online: http://doi.org/10.5281/zenodo.803261 (accessed on 12 March 2021).








| Equipment | Earthing Resistance |
|---|---|
| Transformer | 6 |
| Household | 2 |
| Cable distribution cabinet | 2 |
| Balanced | Unbalanced | |||
|---|---|---|---|---|
| Constraints | No Storage | Storage | No Storage | Storage |
| Linear Equality | ||||
| Slack constraints | 2 | 2 | 8 | 8 |
| Linear Inequality | ||||
| Power limits generator | 4 | 4 | 16 | 16 |
| Energy capacity limits | 0 | 2 | 0 | 2 |
| Power limits storage | 0 | 6 | 0 | 18 |
| Nonlinear Equality | ||||
| Power flow equation | 4 | 4 | 14 | 14 |
| Current equation | 0 | 0 | 4 | 4 |
| Storage equation | 0 | 1 | 0 | 1 |
| Nonlinear Inequality | ||||
| Power limits lines | 2 | 2 | 18 | 18 |
| Voltage limits | 4 | 4 | 12 | 12 |
| Voltage unbalance | 0 | 0 | 2 | 2 |
| Total | 16 | 25 | 74 | 95 |
| Starting Bus | End Bus | Distance in m | rS in pu | rM in pu | xS in pu | xM in pu |
|---|---|---|---|---|---|---|
| 1 | 2 | 1010.9 | 0.394 | 0.630 | 0.000 | 0.506 |
| OPF | Simulink | Deviation | |
|---|---|---|---|
| point 2-1 | 0.951536 pu | 0.951482 pu | 0.000054 pu |
| point 2-2 | 0.930303 pu | 0.930227 pu | 0.000076 pu |
| point 2-3 | 0.952876 pu | 0.952820 pu | 0.000054 pu |
| point 2-N | 0.022397 pu | 0.022415 pu | 0.000018 pu |
| point E | 0.005599 pu | 0.005604 pu | 0.000005 pu |
| Starting Bus | End Bus | Distance in m | rS in pu | rM in pu | xS in pu | xM in pu |
|---|---|---|---|---|---|---|
| 1 | 2 | 721.3 | 0.281 | 0.450 | 0.000 | 0.361 |
| 2 | 3 | 138.7 | 0.054 | 0.086 | 0.000 | 0.069 |
| 3 | 4 | 150.9 | 0.059 | 0.094 | 0.000 | 0.076 |
| 4 | 5 | 36.2 | 0.059 | 0.093 | 0.000 | 0.074 |
| 4 | 6 | 46.7 | 0.018 | 0.029 | 0.000 | 0.023 |
| 6 | 7 | 19.2 | 0.016 | 0.025 | 0.000 | 0.020 |
| 6 | 8 | 14.0 | 0.005 | 0.009 | 0.000 | 0.007 |
| 8 | 9 | 12.9 | 0.021 | 0.033 | 0.000 | 0.026 |
| 8 | 10 | 23.1 | 0.009 | 0.014 | 0.000 | 0.012 |
| 10 | 11 | 25.0 | 0.021 | 0.033 | 0.000 | 0.026 |
| 10 | 12 | 17.6 | 0.007 | 0.011 | 0.000 | 0.009 |
| 12 | 13 | 22.1 | 0.018 | 0.029 | 0.000 | 0.023 |
| 13 | 14 | 50.5 | 0.042 | 0.066 | 0.000 | 0.053 |
| 12 | 15 | 32.3 | 0.027 | 0.042 | 0.000 | 0.034 |
| 15 | 16 | 9.1 | 0.015 | 0.023 | 0.000 | 0.019 |
| 15 | 17 | 15.6 | 0.013 | 0.020 | 0.000 | 0.016 |
| 12 | 18 | 16.6 | 0.006 | 0.010 | 0.000 | 0.008 |
| 18 | 19 | 13.9 | 0.012 | 0.018 | 0.000 | 0.015 |
| 18 | 20 | 5.1 | 0.002 | 0.003 | 0.000 | 0.003 |
| 20 | 21 | 9.9 | 0.008 | 0.013 | 0.000 | 0.010 |
| 20 | 22 | 43.8 | 0.017 | 0.027 | 0.000 | 0.022 |
| 22 | 23 | 33.8 | 0.028 | 0.044 | 0.000 | 0.035 |
| 23 | 24 | 13.7 | 0.011 | 0.018 | 0.000 | 0.014 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Held, L.; Mueller, F.; Steinle, S.; Barakat, M.; Suriyah, M.R.; Leibfried, T. An Optimal Power Flow Algorithm for the Simulation of Energy Storage Systems in Unbalanced Three-Phase Distribution Grids. Energies 2021, 14, 1623. https://doi.org/10.3390/en14061623
Held L, Mueller F, Steinle S, Barakat M, Suriyah MR, Leibfried T. An Optimal Power Flow Algorithm for the Simulation of Energy Storage Systems in Unbalanced Three-Phase Distribution Grids. Energies. 2021; 14(6):1623. https://doi.org/10.3390/en14061623
Chicago/Turabian StyleHeld, Lukas, Felicitas Mueller, Sina Steinle, Mohammed Barakat, Michael R. Suriyah, and Thomas Leibfried. 2021. "An Optimal Power Flow Algorithm for the Simulation of Energy Storage Systems in Unbalanced Three-Phase Distribution Grids" Energies 14, no. 6: 1623. https://doi.org/10.3390/en14061623
APA StyleHeld, L., Mueller, F., Steinle, S., Barakat, M., Suriyah, M. R., & Leibfried, T. (2021). An Optimal Power Flow Algorithm for the Simulation of Energy Storage Systems in Unbalanced Three-Phase Distribution Grids. Energies, 14(6), 1623. https://doi.org/10.3390/en14061623