Abstract
Owing to the increases of energy loads and penetration of renewable energy with variability, it is essential to determine the optimum capacity of the battery energy storage system (BESS) and demand response (DR) within the microgrid (MG). To accomplish the foregoing, this paper proposes an optimal MG operation approach with a hybrid method considering the game theory for a multi-agent system. The hybrid method operation includes both BESS and DR methods. The former is presented to reduce the sum of the MG operation and BESS costs using the game theory, resulting in the optimal capacity of BESS. Similarly, the DR method determines the optimal DR capacity based on the trade-off between the incentive value and capacity. To improve optimization operation, multi-agent guiding particle swarm optimization (MAG-PSO) is implemented by adjusting the best global position and position vector. The results demonstrate that the proposed approach not only affords the most economical decision among agents but also reduces the utilization cost by approximately 8.5%, compared with the base method. Furthermore, it has been revealed that the proposed MAG-PSO algorithm has superiority in terms of solution quality and computational time with respect to other algorithms. Therefore, the optimal hybrid method operation obtains a superior solution with the game theory strategy.
1. Introduction
Over the last decade, renewable energy (RE) such as solar and wind energy has attracted more attention than traditional power generation due to the increases in power loads and greenhouse gas emission [,]. However, depending on the fluctuation and unpredictability of weather conditions, RE may create difficulty in the management and operation of power systems. To minimize the complexities and technical challenges of bidirectional power flow through the distribution line on existing power systems, a microgrid (MG) consisting of RE, energy storage devices, and loads has been introduced []. The MG operator (MGO) should be able to realize the self-use of distributed energy and even achieve low cost and high stability.
Recently, multi-agent systems (MASs) have attracted interest as an effective means of flexible operation within the MG []. The MAS model is a distributed system consisting of numerous intelligent agents that have been introduced for efficient performance and burden distribution. The agents of the MAS can be classified into: Load agent, generation agent, central agent, and battery agent [,,,]. In [], the load and battery agents coordinated with the generation agent to address complex objectives by dividing the main problem into sequential subproblems. The aggregation agent minimized the energy cost by receiving information from the load agent, production agent, and storage agent by using sensors. Among the four, the storage agent was used to control the electricity storage, such as batteries and electric vehicles []. The MAS in [] was focused on the building energy management system via cooperation with the RE agent, central coordinator agent, and battery bank agent. In [], by employing the incentive-based demand response (DR), MG-affiliated agents were implemented in order to minimize operation cost, environmental cost, and operation risk. Furthermore, the coordination and scheduling of the various agent units made the final decision. Energy hubs minimized the total operation costs through decentralized management using agent systems instead of centralized management in IEEE 30-bus systems that include ESS and DR []. In addition, MAS accounted for the complex behavior using the management and control strategies []. However, the agents did not have clear roles and decision-making authority. The capability of the agents can be noted in autonomous decision-making. Energy management in a distributed energy resource system may be conducted by using the decision-making capacity of agents. The MAS in [] enables decision-making and promotes competition among agents to achieve the global goal. The decision-making of agents widely applies game theory to MG energy management []. Game theory can provide economic and mathematical tools, allowing the action of each agent to interact with other decision-makers, and is characterized into two categories: Cooperative and non-cooperative game theories. The cooperative game theory requires players to make binding commitments, thus that legal regulations maintain their promises. Conversely, non-cooperative game theory does not allow binding contracts or solidarity but permits agents to pursue their own purposes. The game model exhibits different objective functions of the consumers and utility []. The Stackelberg game has been applied to handle non-cooperative game theory based on the payoff of each agent []. It is essential to predict individual strategies and find the Nash equilibrium that can satisfy all players.
In general, a battery energy storage system (BESS) has been proven to reduce the cost, not only by charging energy during the low electricity price period but also by discharging the energy during the high price period []. Since BESS is considered a dispatchable source, it has operational benefits for stable and economical operation. It is necessary to install BESS with the appropriate capacity for optimal MG operation. In [], the BESS sizing was addressed using a non-cooperative game approach in order to minimize electricity price and increase self-energy consumption. However, battery costs, such as installation and operation costs, were not considered. The objective function in [] was calculated to minimize the sum of the cost of the power imported from the main grid and BESS. However, the state of charge (SOC) and depth of discharge (DOD), which are important lifetime factors, were not considered. Thus, in considering the MG operation and BESS costs as well as lifetime, a multi-dimensional complex objective function would be required. Meanwhile, the DR program has also been expected to improve both reliability and economics by reducing the peak load. The MGO encourages consumers to participate in DR when power load reduction is required because DR is a flexible and inexpensive resource. In [], a confidence-based incentive DR strategy was applied to attract more DR participation during the peak period by offering different incentives at different periods. A relationship certainly exists between DR participation and incentive value. The authors studied the principles of pay-as-bid, which presented that aggregators bid for the incentive value and DR capacity offered by customers to receive the incentive []. Combining game theory with the original pay-as-bid, in which only the winner obtains the monopoly, the study proceeded with decision-making and concluded that the load aggregators gained the maximum benefit. The results demonstrated a reasonable price at which to sell the power stored in the residential battery, but MG operation was not considered. The microgrid clusters were employed to consider the balance of collective and individual interests under transactive energy management []. However, the optimal capacities of BESS and DR were not applied. In [,], the optimal BESS capacity was solved by considering the installation and operation costs of BESS using various programming techniques, and in [,,], the incentive value of DR was determined using non-cooperative game theory or Nash equilibrium. Although a multi-agent based energy management system was presented to solve the main objective in division into subproblem and to schedule the DR program, autonomous decision-making and BESS allocation through agents were not considered []. However, these studies did not consider both BESS and DR allocation simultaneously. During the process, it is essential to determine the optimal capacities of BESS and DR and consider them for the economic MG operation.
Although the optimal operation of MG with BESS and DR was extensively studied, optimal capacity allocation of BESS and determining DR incentive payment solved by game theory has not been widely investigated. In this regard, this study proposes an optimal hybrid method optimization method for a grid-connected MG by determining the BESS and DR capacities using the non-cooperative game theory. Due to the trade-off characteristics between optimal BESS capacity and microgrid utilization cost, as well as between optimal DR capacity and incentive payments, game theory has been used. To this end, game theory strategies are expected to minimize the MG utilization cost and aid in coordinating BESS and DR, as the BESS operation can curtail DR participation. The objective function comprises the electricity price purchased from the utility, BESS cost, and DR cost. In addition, the problem is successfully performed using multi-agent guiding particle swarm optimization (MAG-PSO), which adjusts the best global position and position vector of a particle.
The main contributions of this paper are listed as follows:
- The proposed two-layer MAS model is constructed with an MGO agent, an RE agent, a Battery agent, and a Load agent. It achieves coordinated and efficient MG operation by considering BESS and DR. It enables autonomous game theory based on communication among agents to optimize the MG operation.
- The effectiveness of applying BESS allocation is evaluated by the sum of the MG operation cost and BESS cost considering depreciation, whereas the superiority of DR allocation is demonstrated by comparison with different DR strategies.
- The proposed optimal hybrid method operation can improve the utilization costs, including operation, BESS, and DR costs. It assists the MGO in formulating reasonable and economical decisions in the MAS model.
- MAG-PSO, which adjusts the best global position and position vector of the particle, is formulated in the proposed MG model to prevent the curtailment of DR participation. By using the MAG-PSO, the solution is improved with the optimal capacity of BESS and DR and exhibits better performance. The solution can be applied to larger power systems.
The remainder of this paper is organized as follows. Section 2 describes the construction of a grid-connected MG system. In Section 3, the proposed MAS model and game theory strategy are introduced, and the formulation and solution method of the optimization problem is presented. Section 4 discusses the simulation results, and finally, Section 5 summarizes the conclusions.
2. Overall Scheme of the Microgrid
2.1. Grid-Connected Microgrid
The MG is an electrical power system situated at a distributed level, consisting of decentralized energy systems, i.e., photovoltaic (PV), wind turbine (WT), and BESS. In MG, the RE resources can reduce the gas turbine power or thermal power generations, but intermittent power generation can destabilize the power system. Thus, the MGO should consider the security and economics of the power supply using adjustable power while monitoring the RE and power load.
In general, there are two MG operating modes, such as islanded and grid-connected modes. The islanded mode dispatches electrical power independently from the utility. The generators should have the power capacity to satisfy the energy balance. This mode requires more capacity for renewable sources that do not cause environmental problems. However, the variability of power sources reduces the reliability of the system. According to a high proportion of volatile power sources, the MGO may prioritize resiliency. In contrast, the MG operating in the grid-connected mode supplies/purchases surplus/deficient electric power to/from the utility, depending on the electricity price determined by a fixed or variable market price. Unlike the islanded mode, the grid-connected mode ensures the security of the system because it can easily supply power based on the reserve power of the utility.
In order to provide the reliability of power to load, our work focuses on the grid-connected mode with the assumption that the utility is a power supplier. Figure 1 shows the structure of the proposed MG model consisting of PV, WT, BESS, and responsive loads. The DC/AC inverter is a component of the system because intermittent RE sources cause high-level fluctuations and disturbances in the system []. For the primary use of the RE, the MGO decides whether to receive electrical power from the utility. The electricity prices are also communicated to users regarding each time slot and BESS aids in reducing the load by storing surplus power and using it during peak demand times.
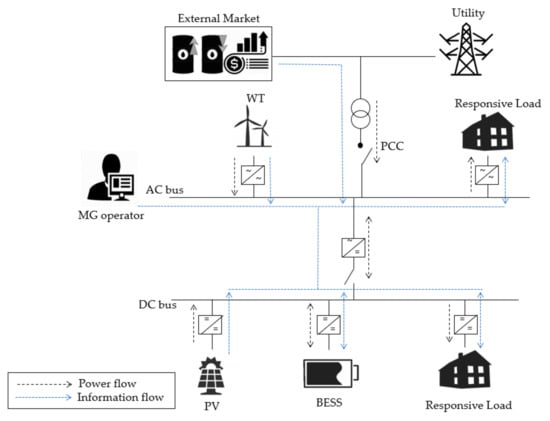
Figure 1.
Structure of grid-connected microgrid.
2.2. Modeling of PV
PV panels convert solar power into DC electricity. The output of a PV generator depends on the size and efficiency of PV panels. The power output can then be calculated as a function of solar irradiation [].
where ηs and A are the efficiency (%) and area of the panels (m2), respectively. β denotes the temperature coefficient of the maximum output power, and SI represents solar irradiation (kW/m2). β denotes a negative percentage per Kelvin or degree Celsius and is considered as −0.005/°C in this study. Tt represents the output air temperature.
The total generated solar power can be extracted as follows:
where Ns is the number of solar generators.
2.3. Modeling of WT
The electric power of a WT is generated by the rotating turbine blades mounted on the tower. The wind speed-generated power can be expressed as a piecewise function [].
where Pr and vr represent the rated electrical power and rated wind speed, respectively. v and ηw denote wind speed and efficiency. vc and vf represent the cut-in and cut-off wind speeds, respectively.
For a number of wind generators, the total power can be given by
where Nw is the number of wind generators.
2.4. Modeling of BESS
The BESS is one of the most important microgrid units for minimizing the effect of the intermittent property of renewable sources. This study selects an electrochemical battery because it is known to be capable of storing energy over an extended time. In time slot t, Pb(t) is negative if it is discharged or positive if it is charged []. The BESS power can be expressed as follows:
where Pb(t) is the discharging or charging power on the AC side of BESS. Pbdch,max and Pbch,max denote the maximum discharging power and maximum charging power, respectively.
The state of charge (SOC) of the BESS in time slot t is represented as SOC(t).
subject to
where PbDC(t) is the power on the DC side of BESS and Eb is the capacity of BESS. Δt and Pbloss(t) denote the interval of the time period and power loss in the converter, respectively.
To avoid over-discharging and over-charging, the maximum and minimum SOCs are determined []. The battery energy level limits can be represented as
The behavior of BESS can be mathematically described through the following equations.
where Pbdch(t) and Pbch(t) are the discharging charging power at time t, respectively. SOC(t) is the battery SOC at each time step, tstep, bounded by an upper limit, SOCmax and lower limit, SOCmin. EESS denotes the battery capacity in kWh.
The charging/discharging power of the BESS is also bounded due to the following constraints.
where ηch and ηdch are the charging and discharging efficiencies of the battery, respectively. ub is a binary variable denoting the charging (“1”) or discharging (“0”) status at each time step.
Assuming that the BESS cannot discharge and charge simultaneously, its formulation is as follows:
2.5. Load and Utility
A fluctuating residential load profile, Pd(t), is taken as a continuous function with a time step of 1 h. The electricity price information invigorates the consumer to be active in power trading and to manage power demand.
where Pg(t) represents the net load and PDR(t) is the capacity of DR in time slot t, respectively.
The power supplied by the utility is Pg(t), which is positive if the power is imported from the grid because of deficient power generation or negative if the power is exported to the grid []. In our work, the power exported to the grid is zero, and the financial benefits caused by excess electricity are also zero. Pb(t) is on the right side because BESS power is negative when it is discharging and positive when it is charging.
3. Proposed Optimal Operation for Multi-Agent System
3.1. Two-Layer MAS Model
The MAS is composed of numerous distributed intelligent agents that communicate and cooperate within the environment for each agent in order to solve the multifaceted optimization problems. The MAS characteristics can be summarized as capable of dealing with complex and large problems, extendibility and flexibility, intelligence and autonomy, handling distributed data and expertise, and modularity and cooperation [,,]. For the MAS model to work effectively, the organization of the communication among agents and operation is important. Hierarchical systems need to optimize different types of energy management systems. The smart grid architecture model has been used as a typical power management system consisting of the hierarchical layers for implementing information exchange and technical functions. In order to communicate between each agent in MAS, addressing communication networks or links is also a huge research area. In this regard, we assumed that the communication is based on basic Ethernet communication, and the database is the blackboard [].
In this paper, based on the smart grid architecture model, a two-layer MAS is conducted to achieve the coordinated and efficient management of energy considering BESS and DR. Figure 2 illustrates the proposed MAS model, including the communication method between agents. Our work constructs a two-layer MAS consisting of an MGO agent on the upper layer and RE, Battery, and Load agents on the lower layer. MGO agent receives information regarding the RE agent in only one direction and conducts two-way communication with Battery and Load agents. The RE agent monitors the WT and PV states and predicts renewable power generations based on the environment, such as wind speed or solar radiation. Meanwhile, the Battery agent perceives the current BESS SOC and participates in the game theory. Load agent recognizes the DR capacity and is involved in incentive pricing based on game theory. Agents in the lower layer have distributed relationships because they do not communicate with each other. Consequently, the upper layer should send out an economic dispatch, whereas the lower layer provides data concerning the state of the unit or reacts to the response from MGO agent.
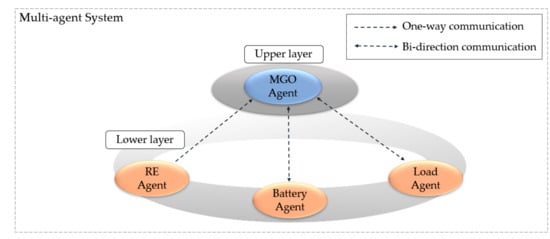
Figure 2.
Proposed two-layer multi-agent system (MAS) model.
The goals of the optimization operation are not only to reduce the MG operation cost, but also to supply power safely, considering the balancing problem between generation and load. The optimal steps of the proposed MAS model are explained as follows:
- RE agent includes PV and WT power generation. The agent recognizes the environment, such as solar radiation or wind speed, and delivers information on renewable power generation to the MGO agent in a time slot.
- Because BESS is mainly used to adjust the peak power, the Battery agent monitors the SOC and determines the optimal BESS sizing based on the game theory with the operation schedule of the MGO agent.
- The load agent recognizes the available capacity to reduce the peak load during the time slot. This agent makes a decision with differential incentives based on a pay-as-bid pricing mechanism using game theory.
- The MGO agent receives the market price, load demand, and operation information from agents in the lower layer. After receiving the communication, the agent solves the game theory, which is discussed in Section 3.2. MGO operates to minimize MG operation costs through determined capacities of the BESS and DR.
3.2. Game Theory Strategy
3.2.1. Non-Cooperative Game Formulation
Game theory is a decision-making strategy involving a number of cooperative or non-cooperative players. The communication between MG and users has been proposed using the Stackelberg game model, which combines energy storage capacity and consumption by applying a non-cooperative game-theoretic method based on the Nash equilibrium, which is defined as a stable decision based on the payoffs received by players after their best choices []. In the process of finding satisfaction, each player responds to the other opponents’ choices with its best decision. In a non-cooperative game, the players aim to maximize/minimize their profit/cost and then search for the Nash equilibrium. Their strategies are directed with their own purposes, assuming that the players in the game theory are rational. Our work formulates a game theory that minimizes the MG operating cost.
The non-cooperative game among users can be formulated as follows:
- (1)
- Players: Agents in the set N participates in the game theory strategy;
- (2)
- Strategies: Each agent n∈N decides its strategy by determining the usable power capacity and setting the cost to maximize its payoff;
- (3)
- Payoff: Pn(xn, x-n, yn) is a cost function for user n.
Based on the payoff function, agents set their capacity or incentive value until the Nash equilibrium is achieved. Let (x−n*, …, x1*, …, xn*) denote the Nash equilibrium, and the optimal output is yn*, then:
Here, xn* and x−n* are represented as the BESS and MG operation cost or DR capacity and cost during the time slot at the Nash equilibrium. yn* indicates the optimal BESS sizing or DR incentive value, which are the intermediate solutions, after achieving the optimal point.
Proposition 1.
For each agent n∈
N, the daily cost function Pn is continuously differentiable in xn. Thus, the space of agent cost function is a non-empty convex compact subset of Euclidean space in xn.
Proof.
Due to the continuous characteristics of the daily cost function Pn(xn, x−n, yn), it is continuously differentiable in xn. Because the Hessian of Pn(xn, x−n, yn) is a positive semi-definite, Pn(xn, x−n, yn) is convex []. Proposition 1 is a prerequisite for Proposition 2. □
Proposition 2.
For∀n∈N, the Nash equilibrium of the non-cooperative game exists and is also unique.
Proof.
Since the cost function Pn is convex in xn, the Nash equilibrium is proved to be present and also unique []. □
Proposition 3.
The uniqueness of Nash equilibrium, proven in Proposition 2 is Pareto optimality.
Proof.
According to Proposition 2, the non-cooperative game has the Nash equilibrium among all agents. No one can change their payoff without the permission to change the strategies of other agents, and then Pareto optimality is defined as the opted strategy state when no one can increase their payoff by modifying the strategies of users without affecting other agents’ payoff []. Consequently, it is noted that the Nash equilibrium in the game is the Pareto optimality. □
Proposition 4.
For the optimal output yn as the BESS capacity or DR incentive, there is a unique yn that can minimize MG cost. It is comprehended that there is a specific cost value with a certain BESS capacity or DR incentive.
Proof.
In the BESS strategy, MG operating cost function is expressed as Equation (16).
where CGrid(t) and kh denote the electricity price and parameter of discharging/charging of BESS, respectively.
The parenthesis function on the right side is the polynomial, and BESS cost and xn is the primary function []. Therefore, the function Pn is convex in yn and exists as an optimal BESS capacity, yn*. Conversely, in DR strategy, the cost function, Pn can be written as follow:
where kh represents the parameter of the expected DR incentive price considered in MGO.
The parenthesis function is the primary function and the consumer benefit, xn is a secondary function. The optimal DR incentive value exists, hence, the proof is complete. □
From Propositions 1–4, it can be seen that the non-cooperative game certainly depends upon the payoff function. For the optimal strategy to minimize MG cost, our work formulates the payoff function using a payoff matrix with game theory strategy.
3.2.2. BESS Strategy
The battery of MG is scheduled based on the game theory between MGO and Battery agents. In the BESS, the Nash equilibrium is formed at the economic optimal trade-off point between the MG operation and BESS costs. Generally, higher BESS capacity could level the power load, reducing operating costs. The BESS cost (SCn) is a function of the storage size in terms of rated power and energy.
where cp and cE are the specific costs of the BESS adopted technology, depending on the rating power, Pnrated and the nominal capacity, Enrated, of the nth BESS. cfixedO&M and cvariO&M are the coefficients of fixed and variable operation and maintenance costs, respectively.
Considering the lifetime, Equation (19) is reformulated.
where Ks denotes a capital recovery factor with a value of 0.1, considering that the BESS lifetime is 10 years.
The cycle life of the lithium-ion battery refers to the number of discharge and charge cycles, which is a function of DOD. The aging relationship between cycle life and DOD is as follow:
Here, β0 = 2731.7, β1 = 0.679, β2 = 1.614.
To ensure the lifetime of Ks used in Equation (19), the battery constraint that the DOD should be 80% or less is satisfied. In the first part of the BESS strategy, the Battery agent presents the BESS maximum capacity, which is set as equal to five times the peak load.
3.2.3. DR Strategy
Our study proposes a pay-as bid strategy to determine DR incentives while game theory between MGO and Load agents increases the participation of DR. The purpose of DR bidding and incentives is to optimize the general satisfactions of MGO and Load agents. Assuming that the agent in the game theory is rational, the Load agent submits bids that are ordered pairs of the proposed incentives and capacities. Because participation and incentives have a positive correlation, it is critical to find the perfect competition in the operation concept. The payoff factor of the DR game is expressed, accounting for the residential battery cost function of the Load agent.
where αtbat and ΔEDR denote the cost of the battery in house as a function of stored energy and DR capacity, respectively. at is a pricing coefficient determined by utility. B represents a parameter and also serves as the maximum value of |ΔEDR|.
Since ΔEDR/B < 1, the quadratic equation can be understood from its Taylor expansion.
The total load can be rewritten as PDR, assuming that the load is constant for an hour. Thus, the DR’s payoff factor can be represented by a quadratic function.
The DR incentive is obtained between the cost of the residential battery and market pricing. Under the assumption that a higher incentive value corresponds to higher participation, MGO agent should find the Nash equilibrium that can satisfy both DR capacity and economics. When the DR is not needed, the MGO agent suggests a lower price than the minimum incentive of the Load agent, thus that game theory does not start. During DR strategy, the Load agent presents the maximum power market price as an incentive value with the maximum capacity. Consumers pay the market price consumed regardless of their bids and submission, assuming that the market price does not depend upon the DR strategy.
3.3. Optimization Technique
3.3.1. MG Formulation
The MGO aims to determine the operation of the MG, including the market price, DR incentives, and BESS cost by the maximum use of renewable energy. Referring to the objective functions [,], the objective function that minimizes the utilization cost is as follow:
where CDR(t) denotes the determined incentive in time slot t.
The following constraints are imposed to determine the feasible solutions of the cost function.
- Power balance constraint
Equation (25) is the equality constraint, which is the premise of the stable operation of the MG energy management. The reason for Pb on the right-hand side is that BESS discharging is negative, whereas charging is positive.
- Generation limit constraints for PV, WT, and BESS
Equations (26) and (27) are the PV and WT power constraints, respectively. Equation (28) ensures that the power between the utility and MG does not exceed the transmission capacity limitation. The constraint of Equation (29) implies that the total usable capacity of DR during the day is limited.
3.3.2. Multi-Agent Guiding PSO
PSO is a population-based stochastic optimization method inspired by the social behavior of bird flocking and results in optimal solutions via repeated simulations to improve candidate solutions []. This can be viewed as a distributed behavioral algorithm that can perform n-dimensional searches to find solutions to various optimization problems. In the PSO algorithm, the kth individual of the population in the n-dimensional search space is evaluated based on the objective function at its current position. Each particle consists of an n-dimensional position vector, Xk = [xk1, xk2, …, xkn]T and velocity vector, Vk = [vk1, vk2, …, vkn]T. The velocity and position of a particle, k, can be expressed at the (i + 1)th iteration.
subject to
where r1 and r2 are two different random numbers of the uniform distribution within the range [0 1], and c1 and c2 represent learning rates with positive constants. pbesti is the best solution, and gbesti is the best global position at the ith iteration. iwi+1 denotes the inertia weight for the (i + 1)th iteration to control the velocity in the PSO algorithm. iwmax and iwmin are the initial and final inertia weights, respectively, and imax is the maximum number of iterations.
Since PSO has no evolutionary algorithms, it affords the advantage of convergence speed in power systems []. The fast convergence rate and accuracy are suitable for real-time optimization processes. However, while processing some model functions, the PSO can become trapped in local optima. Dynamic Guiding PSO (DG-PSO) ensures particle swarm migration and prevents entrapment by the local optima with the limiting absolute value of the global position []. If the values of the global position are not changed at the end of each iteration, the algorithm is triggered by using two tuning factors: Contraction and expansion. However, the limitations of gbest are changed in the process of the algorithm and the user-defined tuning factors do not randomly control the global position. Hence, DG- PSO cannot ultimately solve the local optima. Therefore, an improved algorithm is required to find global optima and effectively reflect the decision-making of the agents. Our work proposes the Multi-agent Guiding PSO (MAG-PSO), which adjusts the best global position based on the results implemented through the game theory among the agents.
where gbestmax represents the absolute maximum vector value of n-dimensional gbest1 in the operation with the optimal BESS capacity and gbestmin denotes the absolute minimum vector values of gbest2 derived during operations with incentives determined by the game theory.
In order to prevent entrapment by the local optima, the updating position vector is obtained follows.
subject to
where wi+1 and r3 are the weight and random number ranging from 0 to 1, respectively.
The advantages of the proposed MAG-PSO are as follows: It can prevent the DR curtailment effect and achieve satisfactory optimization results by inhibiting particles from entering the local optima. The convergence speed also increases because the gbest maximal and minimal limits reduce the range in which particles should move, and agent guiding aids the PSO to quickly search for the optimal solution.
3.3.3. Hybrid Optimization Process
In the MAS, each agent tries to find the optimum BESS capacity and DR incentive to satisfy their own purposes. After comparing the daily cost corresponding to the BESS capacity or DR incentive, each of the two game theory strategies may reach a Nash equilibrium. Then, the MGO agent selects the final optimal strategy that minimizes the daily cost. The process of MG operation with game theory is performed in the following steps.
- Step 1:
- Construct the two-layer MAS model and initialize the MG input parameters, such as PV, WT, BESS, and Load.
- Step 2:
- Define an objective function as (16) and (17) with the following constraints (24)–(29). Obtain the intermediate solutions derived from Method 1 and 2. Further details of the process are as follows:
| Method 1: Game Theory Strategy for BESS |
| 1 Set yn = ynmax |
| 2 Calculate initial xn and x-n |
| 3 repeat |
| 4 Define objective function as Equation (16) and solve cost function in Equation (15) |
| 5 if xn changes then |
| 6 Update and broadcast xn |
| 7 end |
| 8 if A new update is received then |
| 9 Update x-n accordingly |
| 10 end |
| 11 until No user changes its strategy |
| 12 Select minimal daily cost Pn(xn*, x-n*, yn*) |
| Method 2: Game Theory Strategy for DR |
| 1 for h = 1:24 |
| 2 Set yn = yninitial |
| 3 Calculate initial xn and x-n |
| 4 repeat |
| 5 Define objective function as Equation (17) and solve cost function in Equation (15) |
| 6 if yn changes then |
| 7 Update and broadcast yn |
| 8 end |
| 9 until No user changes its strategy 10 end |
| 11 Select minimal daily cost Pn(xn*, x-n*, yn*) at each time slot h |
- Step 3:
- Establish the objective function and constraints given by Equations (24–29).
- Step 4:
- In the MAG-PSO, set the required input parameters to initialize the algorithm.
- Step 5:
- Obtain the best global particle position sets at the optimal capacity of BESS and DR, respectively, and store them in the repository.
- Step 6:
- Start iteration
- Step 7:
- Implement Multi-Agent Guiding. Update the maximum and minimum values of the global particle positions.
- Step 8:
- Update the velocity and position of each particle according to Equations (30) and (34). Calculate the fitness value of each particle.
- Step 9:
- Determine whether the stopping criteria is satisfied. If the number of iterations reaches the maximum, go to the next step. If not, repeat the iteration.
- Step 10:
- Output the iteration results based on MAG-PSO.
- Step 11:
- Step 11: Obtain BESS charge/discharge operation and DR scheduling during the time slot.
The overall optimization procedure of the proposed hybrid method is shown in Figure 3.
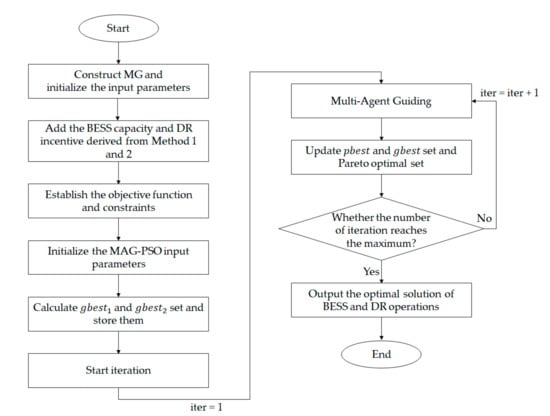
Figure 3.
Overall procedure of the proposed optimal hybrid method operation.
4. Simulation Results
In order to validate the superiority of the optimal operation, a hybrid method is demonstrated considering a grid-connected MG. Our work not only demonstrates the BESS strategy results but also simulates the DR incentive using the dual-game theory strategy. Moreover, it proves that the optimization problem of minimizing the MG operation cost is solved by the MAG-PSO algorithm. The simulations have been implemented in MATLAB R2020a installed on a personal laptop with Intel®® Core i5-8400 CPU @ 2.80 GHz and 16 GB RAM.
4.1. Data Description
To evaluate the feasibility of the proposed hybrid method, the parameters of the PV and wind generators are given in Table 1. Here, the six WT and five PV systems are installed in the MG and take on the role of RE sources. Figure 4 depicts the wind velocity, solar irradiation data, residential load, and utility grid electricity price, which are taken from []. Regardless of the capacity of the BESS, the maximum and minimum SOC values are set equal to 10% and 90%, respectively []. In addition, the initial SOC level at the start of the day is always set to 50% of the BESS capacity. For conducting the proposed MAG-PSO algorithm, the number of particles, the maximum number of iterations, and learning rates have been set as 3000, 250, and 2, respectively [,].

Table 1.
Input parameters.
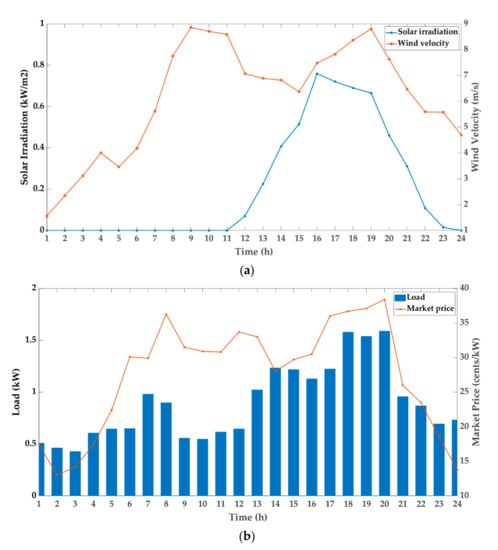
Figure 4.
Input data over a 24 h horizon. (a) Wind velocity and solar irradiation. (b) Power load and market price.
4.2. Optimal Operation Results
4.2.1. Method 1: BESS Strategy
The game theory strategy for BESS is based on a trade-off, which can be used to find the optimal sizing of BESS. The sum of the MG operation and BESS cost is plotted for the BESS capacity in kWh. However, plotting the operating costs for all capacities requires considerable time. Table 2 represents the calculation of MG operating costs based on the capacities of 200 kWh, 100 kWh, and 35 kWh. The Battery agent justly satisfies the condition that the DOD should be less than 80% to ensure its lifetime. Honestly, the MG operating cost without BESS and DR scheduling are also the highest. As shown in Table 2, the MG operating cost decreases as the BESS capacity increases. This is because a sufficient BESS capacity becomes the resource to take more responsibility for the load of MG. Meanwhile, the BESS cost also increases as the BESS capacity increases. Since the MG operating cost is expressed as a polynomial and the BESS cost as a linear function, the optimal BESS capacity to minimize the objective function is unique. According to the results of Method 1, the BESS capacity for the proposed MG model is 32 kWh.

Table 2.
Microgrid (MG) operating and battery energy storage system (BESS) costs according to BESS capacity.
Figure 5 illustrates the amount of energy purchased without the BESS and with 32 kWh and 200 kWh BESS. Comparing the amounts of power purchased from 8 to 20 h when the electricity price is high, note that purchased energy is lower using BESS. In particular, the 200 kWh BESS significantly curtails the MG operating cost by reducing the amount of purchased power at 8 h and from 13 to 16 h, when the electricity price is high.
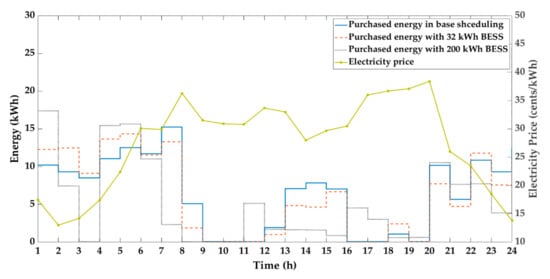
Figure 5.
Energy purchased from the utility grid.
Figure 6 shows the charging/discharging energy and SOC of BESS. The 32 kWh BESS supplies power from 6 to 15 h, and the volatility of SOC is greater than when the capacity is 200 kWh. This means that the appropriate BESS capacity is obtained for the balance of power supply and demand. Finally, MG operation cost decreases to 3486.86¢, and the utilization cost is 3754.238¢.
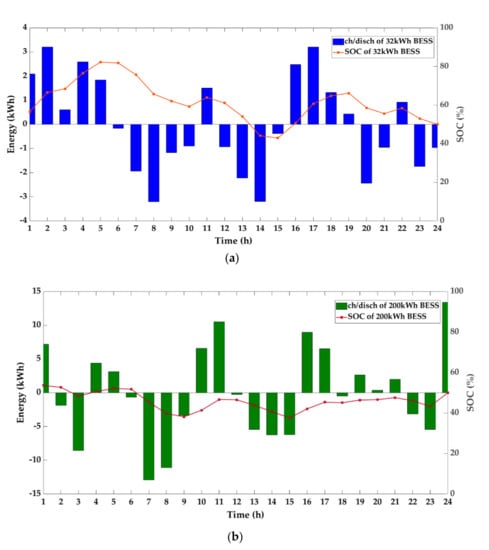
Figure 6.
Optimal charging/discharging cycles and state of charge (SOC) of BESS. (a) 32 kWh BESS. (b) 200 kWh BESS.
4.2.2. Method 2: DR Strategy
The DR strategy is applied to the incentive decisions that decrease the MG utilization costs while increasing consumer participation. This strategy, which is similar to that of BESS, is based on the trade-off between the DR capacity and incentive price. In the game theory between MGO and Load agents, the former has data on renewable power generation and market prices. On the premise that a higher incentive value increases the participation rate, each agent makes a rational decision. The maximum DR participation per hour is 4 kWh, and the total DR participation per day is limited to 25 kWh. In order to reflect Australia’s actual market operations, the conventional DR program has been taken from [], which is engaged through the aggregator with 18.82¢ incentives value for 1 to 4 h a day.
Figure 7 illustrates the power load profiles with and without the DR program. The DR game strategy intends to reduce power regardless of the peak energy time. If there is an RE that can satisfy the power load, the incentive value is fixed at 0 to preclude the game theory from being established. The conventional DR can only participate for up to 4 h a day, thus, it should reduce energy when the power market prices are high.
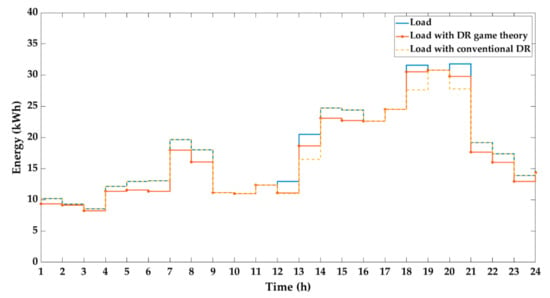
Figure 7.
Load patterns of each demand response (DR) strategy.
Table 3 shows the operation results of the conventional DR program and Method 2. To ensure the feasibility of Method 2, the total DR cost, capacity, MG operating cost, and utilization cost are expressed. The conventional DR reduces the load by 14 kWh because of the time limit. The DR cost is also low by 262.51¢ due to its low capacity. In contrast, the game theory DR strategy intends to reduce power by a total of 22.96 kWh, which curtails the operating costs to 3126.13¢. As a result, the utilization cost is 7.1% less than that without the DR program and 3.8% less than that with the conventional DR program.

Table 3.
Comparison of the DR programs.
Figure 8 depicts the hourly DR capacity and incentive values derived from Method 2. Here, the average incentive value for one day is calculated as 16.8 ¢/kWh. Certainly, the higher the capacity, the higher the incentive value.
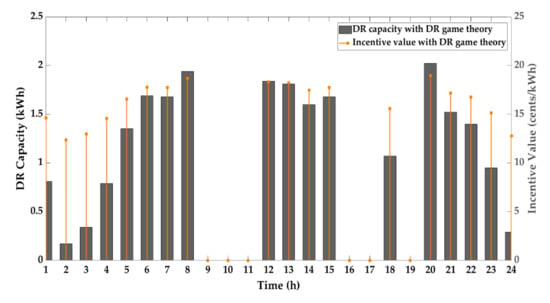
Figure 8.
Proposed DR strategy results.
4.2.3. Hybrid Method
The hybrid method focuses on minimizing the MG operating cost using BESS and DR strategies. Table 4 represents the DR capacity and utilization costs for each strategy. The proposed hybrid method reduces the operating cost by 8.5%, whereas the Battery agent satisfies the lifetime constraint. The daily DR capacity is 15.94 kWh, and the total incentive value is 263.12¢. Then, the average incentive value is 16.5 ¢/kWh, which is less than that of Method 2. This means that the proposed hybrid method utilizes a more cost-effective DR because it reduces the utilization cost. Furthermore, the synergy between BESS and DR can be seen by deriving costs lower than those of Method 1 and 2. In addition, to investigate whether a higher DR capacity results in a lower utilization cost, the decision intention of the Load agent is limited to increasing the DR capacity. It can be seen from Table 4 that the total DR is 18.55 kWh, and the utilization cost is 3503.047¢. In this supposition, the utilization cost excluding the DR incentive cost is 10.46¢ less, but the DR cost is 43.401¢ more expensive, which not only spoils the autonomy of the agent but also fails to minimize the MG cost. Therefore, it should be noted that the proposed operation strategy can produce economically optimal results.

Table 4.
Comparison of each operation method.
Figure 9 illustrates the purchased energy from the utility, which is associated with the MG operating costs. BESS shifts the required energy in Method 1, and DR curtails the power load in Method 2. The hybrid method requires the least amount of energy from 5 to 18 h, indicating the impact of BESS and DR. In the proposed optimal operation, the purchased energy capacity during the high-cost period has the largest reduction. Consequently, it is clear that the hybrid method applies the most economical decision among agents and also reduces the MG utilization cost.
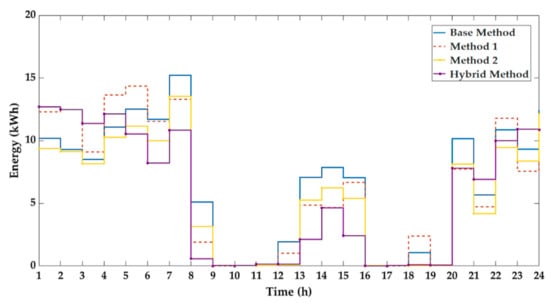
Figure 9.
Comparison of optimal purchased energy.
In order to demonstrate the superiority of the MAG-PSO, performance tests have been implemented through a comparison with PSO and DG-PSO []. The MAG-PSO has been proposed to prevent BESS operations and DR participation from contracting each other. For a fair comparison, the simulation was conducted 20 times, and the results for the best, worst, and average solutions were obtained, along with computation times for each algorithm. Table 5 presents the simulation results for the different algorithms. The error between the best and average values of the MAG-PSO algorithm is approximately 0.085%, reaching an optimal solution compared with the other algorithms. These quantitative results demonstrate the efficiency of the MAG-PSO algorithm in providing the optimal hybrid method results, accounting for the economic and computational factors and without being trapped in the local optima.

Table 5.
Results of the best, worst, and average solutions.
Table 6 shows the detailed optimal operation results for each of the three algorithms. It can be observed that the MAG-PSO has the lowest utilization cost of 3470.106¢ and adopts a higher DR capacity compared with the other algorithms. The PSO without the guiding global position and weighting position vector does not use sufficient DR capacity, and as a result, the total cost is high. Although the DG-PSO adopted more DR capacity than the PSO, the average incentive price per kWh is slightly higher than that of the other algorithms, at 16.7¢. The MAG-PSO performs better than the PSO and DG-PSO in terms of simulation time due to the limitations on the best global position and the adjustment of the position vector. Considering that the maximum peak power is only 32 kWh, note that the run time benefit would be improved in larger power systems. Based on the comparative results, our work concludes that the proposed optimal operation method is appropriate for minimizing the utilization cost and ensuring game theoretical decisions among agents.

Table 6.
Comparison of results.
5. Conclusions
This paper proposed an optimal hybrid method operation for grid-connected MG based on game theory. The hybrid method consisted of BESS and DR strategies based on the game theory for the MAS model. BESS method determined the optimal BESS sizing based on the trade-off between operation cost and BESS cost considering depreciation. Meanwhile, the DR method was formulated to minimize the utilization cost by proposing an hourly incentive value to determine the optimal DR capacity. The optimization problem was constructed considering the electricity price from the utility, ESS, and DR costs and was solved using MAG-PSO, which adjusted the best global position and position vector of the particle in order to prevent the curtailment of DR participation. The results demonstrated that the proposed method was reasonable compared with the conventional method and even presented the synergy between BESS and DR with lower utilization costs than Method 1 and 2. In addition, the superiority of the proposed MAG-PSO in terms of utilization cost and performance was confirmed through comparison with other algorithms. Therefore, the proposed optimal hybrid method operation provided the MGO not only a solution to reduce the utilization cost but also reasonable and economic decisions in the MAS model with autonomy. Our future work is underway to focus on not only solving hybrid method with game theory considering uncertainties of renewables sources, loads, and market prices by combining data-driven approach but also improving efficient information transmission and processing in the situation of adopting short-term power operations.
Author Contributions
J.-W.L. proposed the main idea of this paper and H.-J.K. provided essential information and supported manuscript preparation. M.-K.K. coordinated the proposed approach and thoroughly reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Korea Electric Power Corporation (grant number: R19XO01-37). This research was also supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2020R1A2C1004743).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The Authors declare no conflict of interest.
References
- Ding, Z.; Hou, H.; Yu, G.; Hu, E.; Duan, L.; Zhao, J. Performance analysis of a wind-solar hybrid power generation system. Energy Convers. Manag. 2019, 181, 223–234. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Hossain, M.J.; Haruni, A.M.O. Active power management in a low-voltage islanded microgrid. Int. J. Electr. Power Energy Syst. 2018, 98, 36–47. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Issa, W.; Hossain, M.J. Overview of AC microgrid controls with inverter-interfaced generations. Energies 2017, 10, 1300. [Google Scholar] [CrossRef]
- Dou, C.X.; An, X.G.; Yue, D. Multi-agent system based energy management strategies for microgrid by using renewable energy source and load forecasting. Electr. Power Compon. Syst. 2016, 44, 2059–2072. [Google Scholar] [CrossRef]
- Sharma, S.; Panigrahi, B.K.; Verma, A. A smarter method for self-sustainable buildings: Using multiagent systems as an effective alternative for managing energy operations. IEEE Trans. Consum. Electron. Mag. 2018, 7, 32–41. [Google Scholar] [CrossRef]
- Mets, K.; Strobbe, M.; Verschueren, T.; Roelens, T.; De Turck, F.; Develder, C. Distributed multi-agent algorithm for residential energy management in smart grids. In Proceedings of the 2012 IEEE Network Operations and Management Symposium, Maui, HI, USA, 16–20 April 2012; pp. 435–443. [Google Scholar]
- Kan, E.M.; Kan, S.L.; Soh, Y.; Zi, D.; Yadanar, K. Multi-agent control system with intelligent optimisation for building energy and comfort management. Int. J. Autom. Logist. 2016, 2, 60–77. [Google Scholar] [CrossRef]
- Liu, J.; Xu, F.; Lin, S.; Cai, H.; Yan, S. A Multi-agent-based optimization model for microgrid operation using dynamic guiding chaotic search particle swarm optimization. Energies 2018, 11, 3286. [Google Scholar] [CrossRef]
- Oskouei, M.Z.; Mohammadi-Ivatloo, B.; Abapour, M.; Shafiee, M.; Anvari-Moghaddam, A. Privacy-preserving mechanism for collaborative operation of high-renewable power systems and industrial energy hubs. Appl. Energy 2020, 283, 116338. [Google Scholar] [CrossRef]
- Yu, J.; Dou, C.; Li, X. MAS-based energy management strategies for a hybrid energy generation system. IEEE Trans. Ind. Electron. 2016, 63, 3756–3764. [Google Scholar] [CrossRef]
- Hedjazi, D.; Layachi, F.; Boubiche, D.E. A multi-agent system for distributed maintenance scheduling. Comput. Electr. Eng. 2019, 77, 1–11. [Google Scholar] [CrossRef]
- Naz, A.; Javaid, N.; Rasheed, M.B.; Haseeb, A.; Alhussein, M.; Aurangzeb, K. Game theoretical energy management with storage capacity optimization and photo-voltaic cell generated power forecasting in micro grid. Sustainability 2019, 11, 2763. [Google Scholar] [CrossRef]
- Belhaiza, S.; Baroudi, U. A game theoretic model for smart grids demand management. IEEE Trans. Smart Grid 2014, 6, 1386–1393. [Google Scholar] [CrossRef]
- Ji, X.; Yang, K.; Na, X.; Lv, C.; Liu, Y. Shared steering torque control for lane change assistance: A stochastic game-theoretic approach. IEEE Trans. Ind. Electron. 2018, 66, 3093–3105. [Google Scholar] [CrossRef]
- Oudalov, A.; Cherkaoui, R.; Beguin, A. Sizing and optimal operation of battery energy storage system for peak shaving application. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 621–625. [Google Scholar]
- Pilz, M.; Ellabban, O.; Al-Fagih, L. On optimal battery sizing for households participating in demand-side management schemes. Energies 2019, 12, 3419. [Google Scholar] [CrossRef]
- Sukumar, S.; Mokhlis, H.; Mekhilef, S.; Naidu, K.; Karimi, M. Mix-mode energy management strategy and battery sizing for economic operation of grid-tied microgrid. Energy 2017, 118, 1322–1333. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, M.K. Multi-objective based optimal energy management of grid-connected microgrid considering advanced demand response. Energies 2019, 12, 4142. [Google Scholar] [CrossRef]
- Motalleb, M.; Ghorbani, R. A game theoretic model of demand response aggregator competition for selling stored energy in regulated and unregulated power markets. arXiv 2016, arXiv:1612.00716. [Google Scholar]
- Daneshvar, M.; Mohammadi-Ivatloo, B.; Asadi, S.; Anvari-Moghaddam, A.; Rasouli, M.; Abapour, M.; Gharehpetian, G.B. Chance-constrained models for transactive energy management of interconnected microgrid clusters. J. Clean. Prod. 2020, 271, 122177. [Google Scholar] [CrossRef]
- Zhang, X.; Tan, S.C.; Li, G.; Li, J.; Feng, Z. Components sizing of hybrid energy systems via the optimization of power simulations. Energy 2013, 52, 165–172. [Google Scholar] [CrossRef]
- Koohi-Kamali, S.; Rahim, N.A.; Mokhlis, H.J.E.C. Smart power management algorithm in microgrid consisting of photovoltaic, diesel, and battery storage plants considering variations in sunlight, temperature, and load. Energy Convers. Manag. 2014, 84, 562–582. [Google Scholar] [CrossRef]
- Gao, B.; Liu, X.; Wu, C.; Tang, Y. Game-theoretic energy management with storage capacity optimization in the smart grids. J. Mod. Power Syst. Clean Energy 2018, 6, 656–667. [Google Scholar] [CrossRef]
- Sheikhi, A.; Rayati, M.; Bahrami, S.; Ranjbar, A.M. Integrated demand side management game in smart energy hubs. IEEE Trans. Smart Grid 2015, 6, 675–683. [Google Scholar] [CrossRef]
- Anvari-Moghaddam, A.; Rahimi-Kian, A.; Mirian, M.S.; Guerrero, J.M. A multi-agent based energy management solution for integrated buildings and microgrid system. Appl. Energy 2017, 203, 41–56. [Google Scholar] [CrossRef]
- Fan, H.; Yuan, Q.; Cheng, H. Multi-objective stochastic optimal operation of a grid-connected microgrid considering an energy storage system. Appl. Sci. 2018, 8, 2560. [Google Scholar] [CrossRef]
- Kim, H.Y.; Kim, M.K.; Kim, S. Multi-objective scheduling optimization based on a modified non-dominated sorting genetic algorithm-II in voltage source Converter—Multi-terminal high voltage DC grid-connected offshore wind farms with battery energy storage systems. Energies 2017, 10, 986. [Google Scholar] [CrossRef]
- Lai, X.; He, L.; Wang, S.; Zhou, L.; Zhang, Y.; Sun, T.; Zheng, Y. Co-estimation of state of charge and state of power for lithium-ion batteries based on fractional variable-order model. J. Clean. Prod. 2020, 255, 120203. [Google Scholar] [CrossRef]
- Sycara, K.P. Multiagent systems. AI Mag. 1998, 19, 79. [Google Scholar]
- McArthur, S.D.; Davidson, E.M.; Catterson, V.M.; Dimeas, A.L.; Hatziargyriou, N.D.; Ponci, F.; Funabashi, T. Multi-agent systems for power engineering applications—Part I: Concepts, approaches, and technical challenges. IEEE Trans. Power Syst. 2017, 22, 1743–1752. [Google Scholar] [CrossRef]
- Catterson, V.M.; Davidson, E.M.; McArthur, S.D. Practical applications of multi-agent systems in electric power systems. Eur. Trans. Electr. Power 2012, 22, 235–252. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Stephens, E.R.; Smith, D.B.; Mahanti, A. Game theoretic model predictive control for distributed energy demand-side management. IEEE Trans. Smart Grid 2014, 6, 1394–1402. [Google Scholar] [CrossRef]
- Yang, L.; Su, H.; Wen, Z. Improved PLS and PSO methods-based back analysis for elastic modulus of dam. Adv. Eng. Softw. 2019, 131, 205–216. [Google Scholar] [CrossRef]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Huang, K.Y.; Hutomo, M. Multiobjective dynamic-guiding PSO for optimizing work shift schedules. J. Constr. Eng. Manag. 2018, 144, 04018089. [Google Scholar] [CrossRef]
- ComED, USA. Available online: http://www.thewattspot.com/ (accessed on 14 September 2020).
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Abdou, A.F. Modified PSO algorithm for real-time energy management in grid-connected microgrids. Renew. Energy 2019, 136, 746–757. [Google Scholar] [CrossRef]
- Energy Australia. Available online: https://www.energyaustralia.com.au/ (accessed on 10 September 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).