The Effect of Insulation Characteristics on Thermal Instability in HVDC Extruded Cables
Abstract
:1. Introduction
- The insulation material characteristics, focusing here on the electrical conductivity coefficients of both temperature and electrical stress, a and b, respectively.
- The electric field variation as a result of the applied voltage variation. This might happen during testing at very high and/or increasing voltage levels, e.g., during thermal stability tests [12].
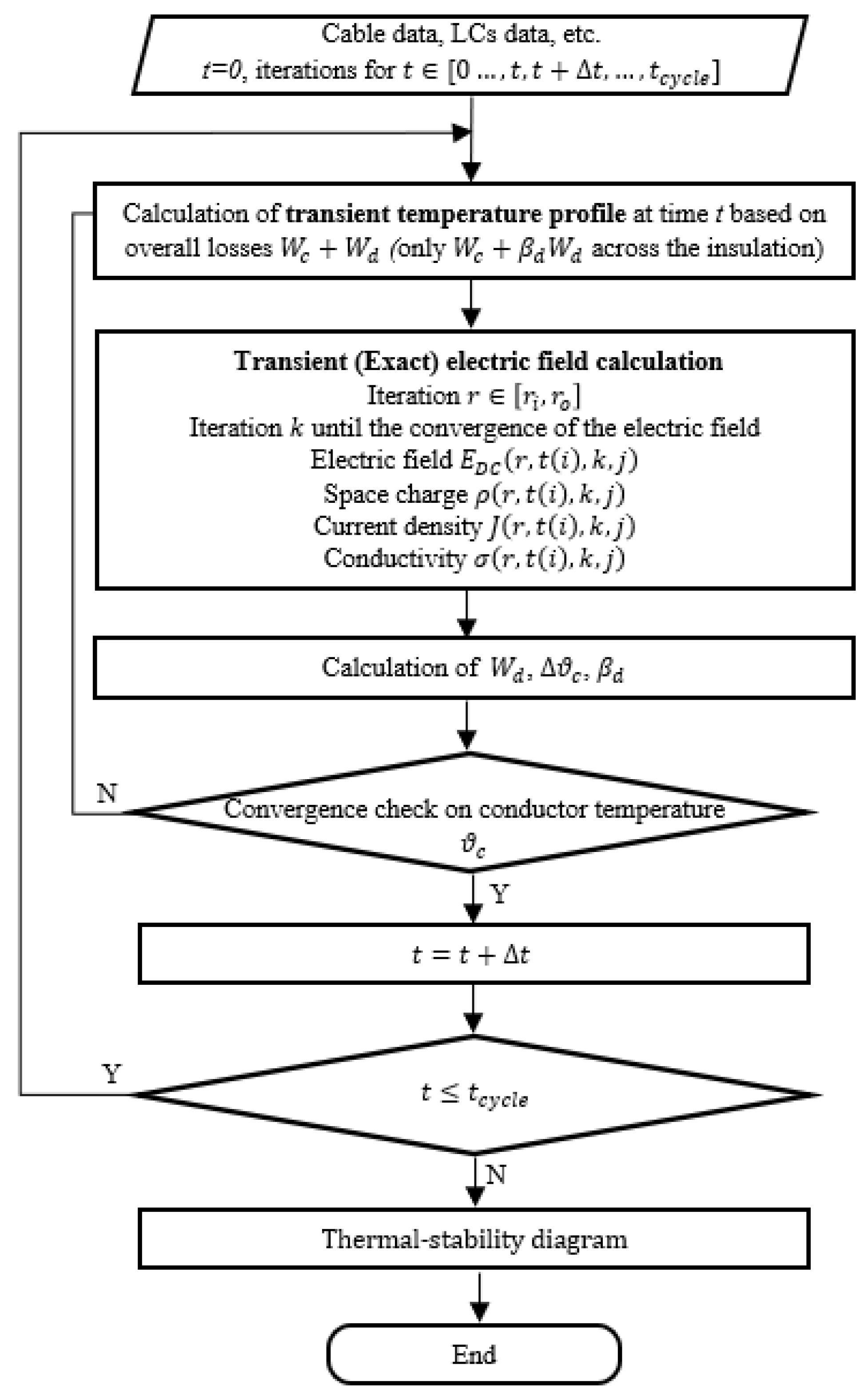
2. Theoretical Background
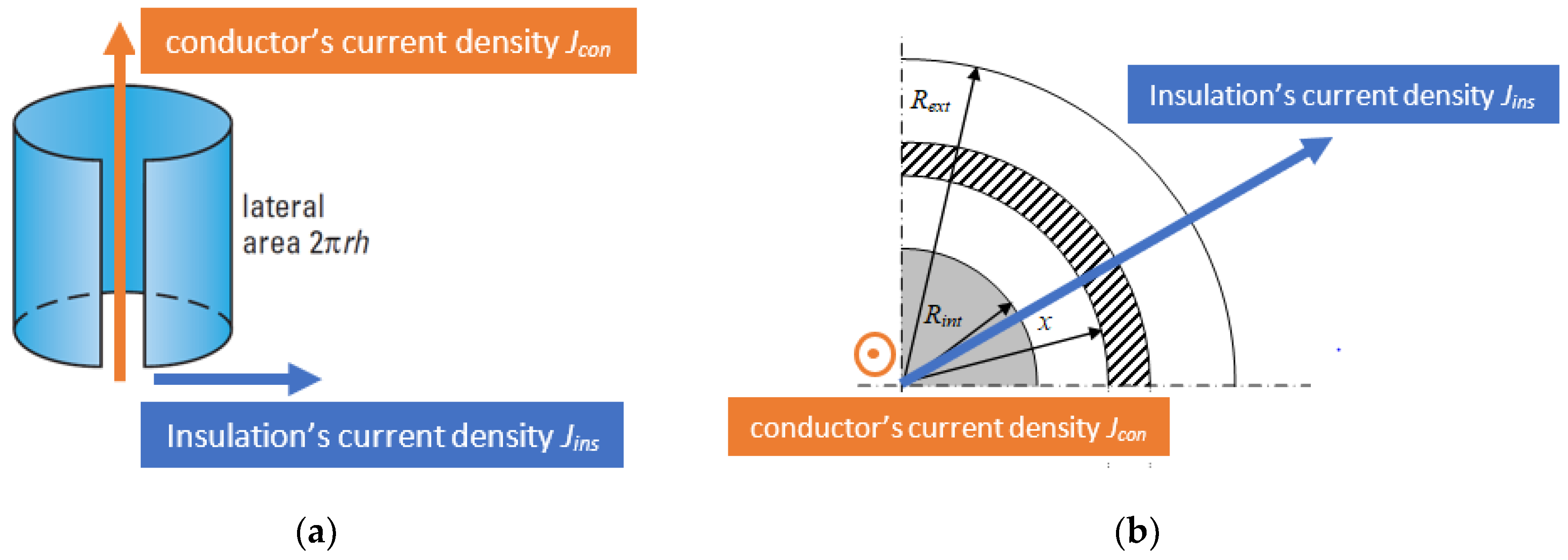
2.1. Temperature Profile and Electric Field Calculation
2.2. Calculation of Insulation Losses
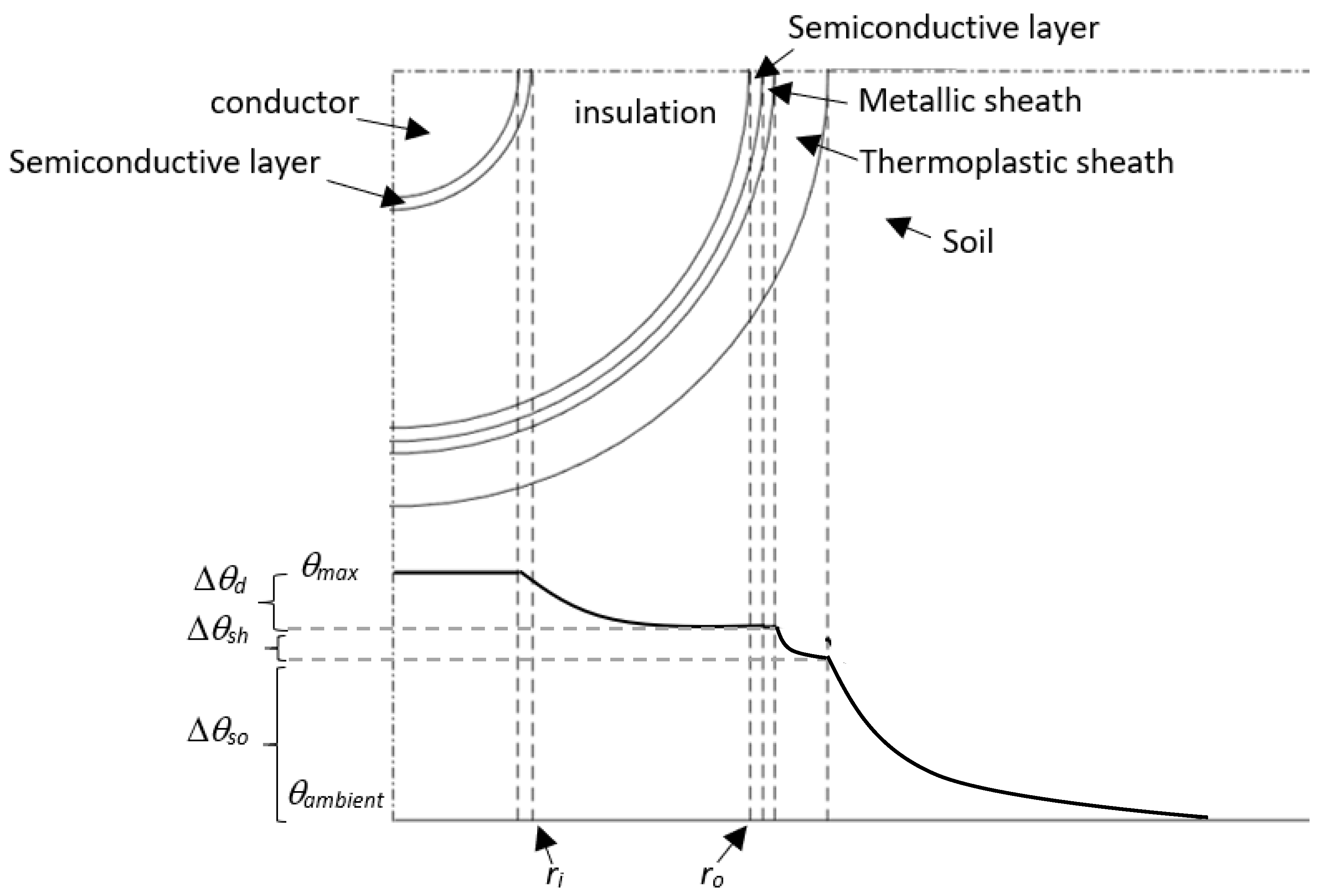
- Inner boundary conditions: Neumann boundary conditions are applied to the inner insulation near the conductor surface. The RHS of (10) refers to the heat flowing from the conductor to the insulation due to conductor losses in the r axis where the temperature drop takes place.where T1 and T2 are the temperatures at the first and second points of the mesh in the inner insulation.
- Outer boundary conditions: Neumann boundary conditions are applied to the outer insulation, where the heat flow in the direction of the r axis consists of both the heat generated due to conductor losses and the heat generated due to insulation losses. A ghost point n + 1 is placed at the metallic/screen sheath whose temperature is calculated using (13). This gives a more realistic simulation of heat flow in the thermoplastic sheath (which, contrary to the metallic sheath, has a non-negligible thermal resistance [18]) and in the surrounding soil resulting in a more realistic metallic sheath temperature (see both Appendix A and Appendix B).where is the thermal resistance of the thermoplastic sheath, is the thermal resistance of the surrounding soil.
2.3. Calculation of Dielectric Loss Coefficient
2.4. Calculation of De-Rating Factor
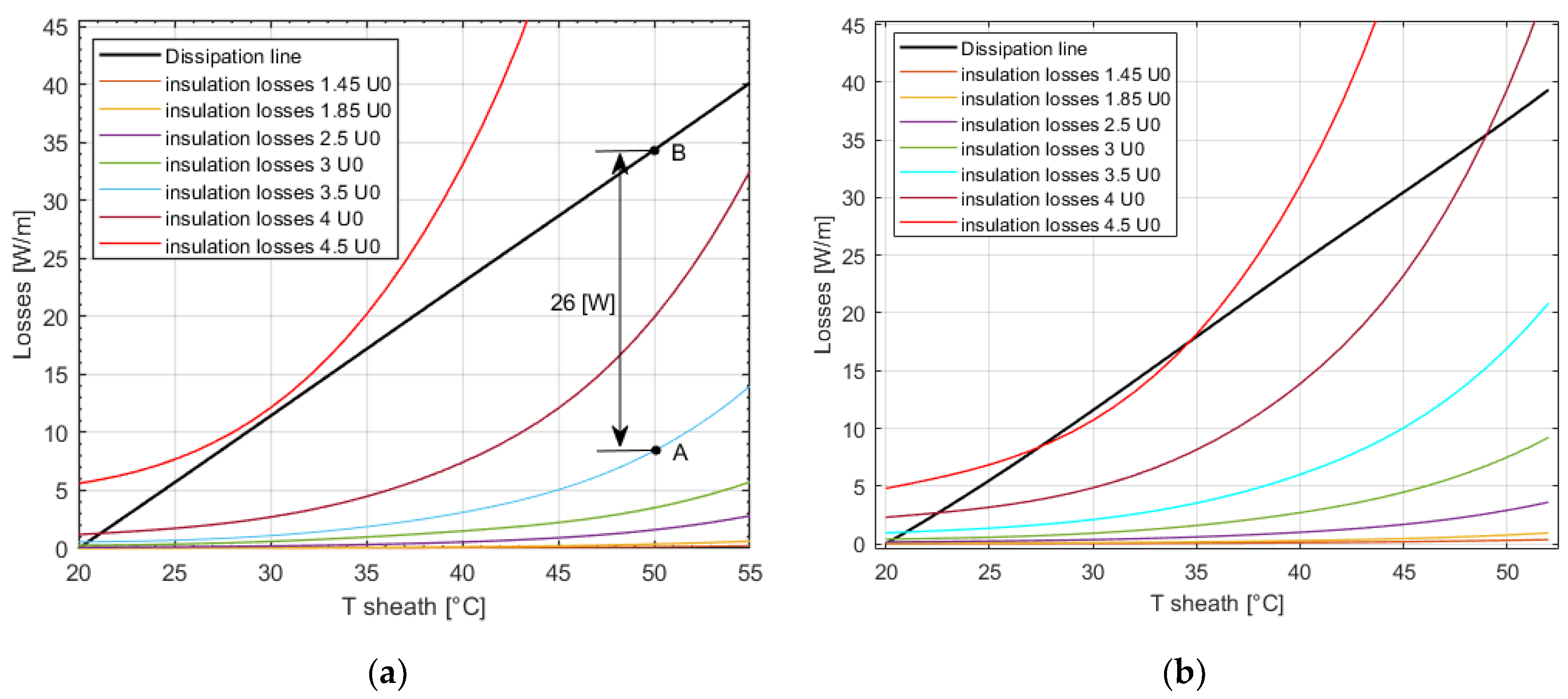
2.5. Thermal Stability
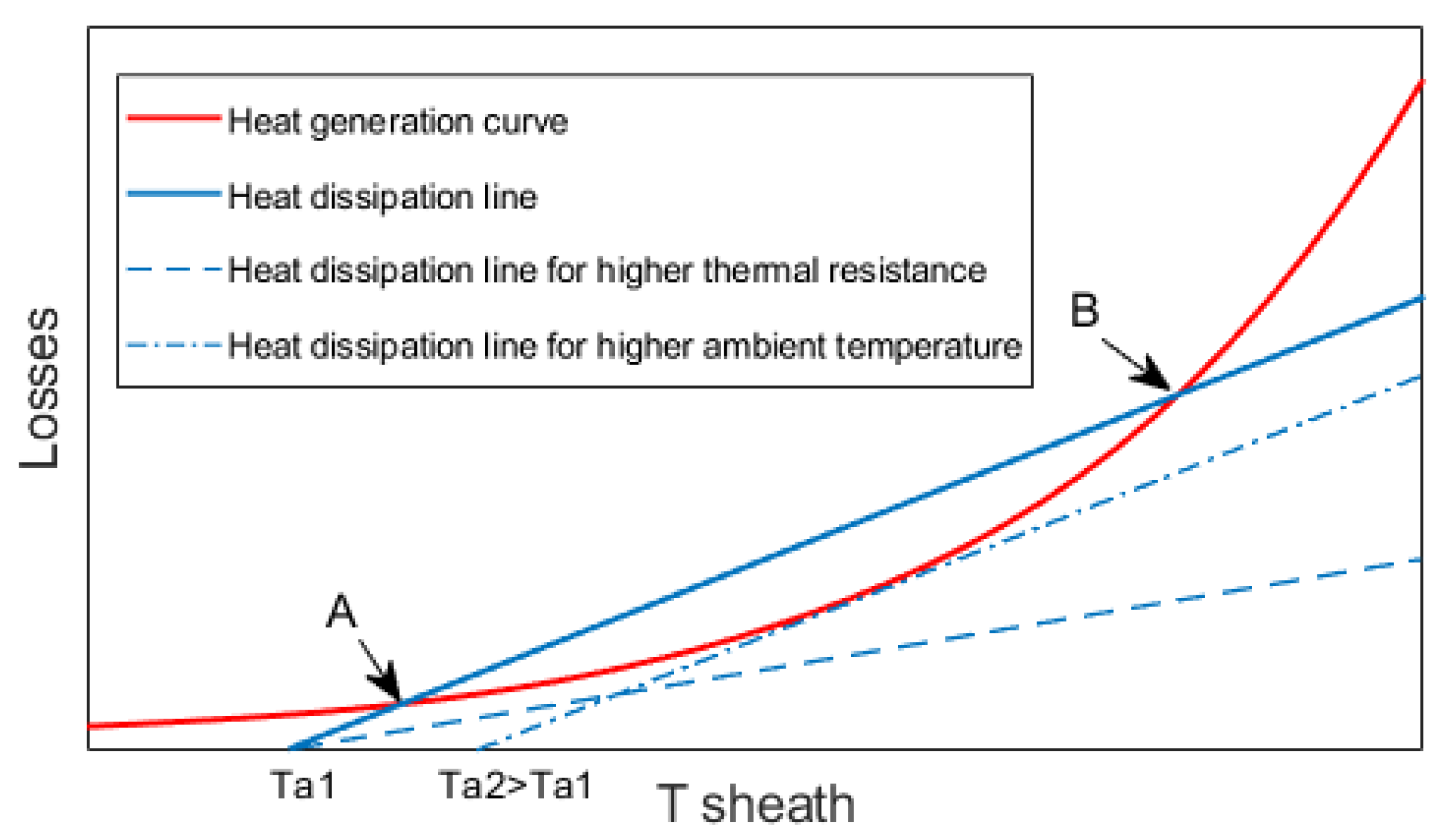
- The heat generation curve (red solid curve in Figure 4) refers to the heat generated within the cable due to both insulation losses and conductor losses .
- The heat dissipation line (blue solid line in Figure 4) refers to the heat dissipated outside the cable through the insulation, thermoplastic sheath and soil, . This full straight line is defined using two parameters:
- (1)
- The thermal resistance of the insulation, thermoplastic sheath and soil, represented by the reciprocal of the slope of the dissipation line. The higher the thermal resistance, the lower the slope, resulting in a higher temperature w.r.t the same losses, see dashed blue line in Figure 4;
- (2)
- The ambient temperature, the intersection of the dissipation line with the temperature axis. As the ambient temperature rises, the dissipation line shifts in the direction of the temperature rise without variation in the slope, see dash-dotted blue line in Figure 4.
- Intrinsic thermal instability:
- 2.
- Interactive thermal instability:
- (i)
- for a value of the ambient temperature ≥Ta2 (dash-dotted line), equilibrium cannot occur, and thermal instability takes place;
- (ii)
- the increase in the thermal resistance of the surrounding soil (dashed line) leads to inevitable thermal instability because the equilibrium cannot exist.
3. Case Study
3.1. Cable Characteristics
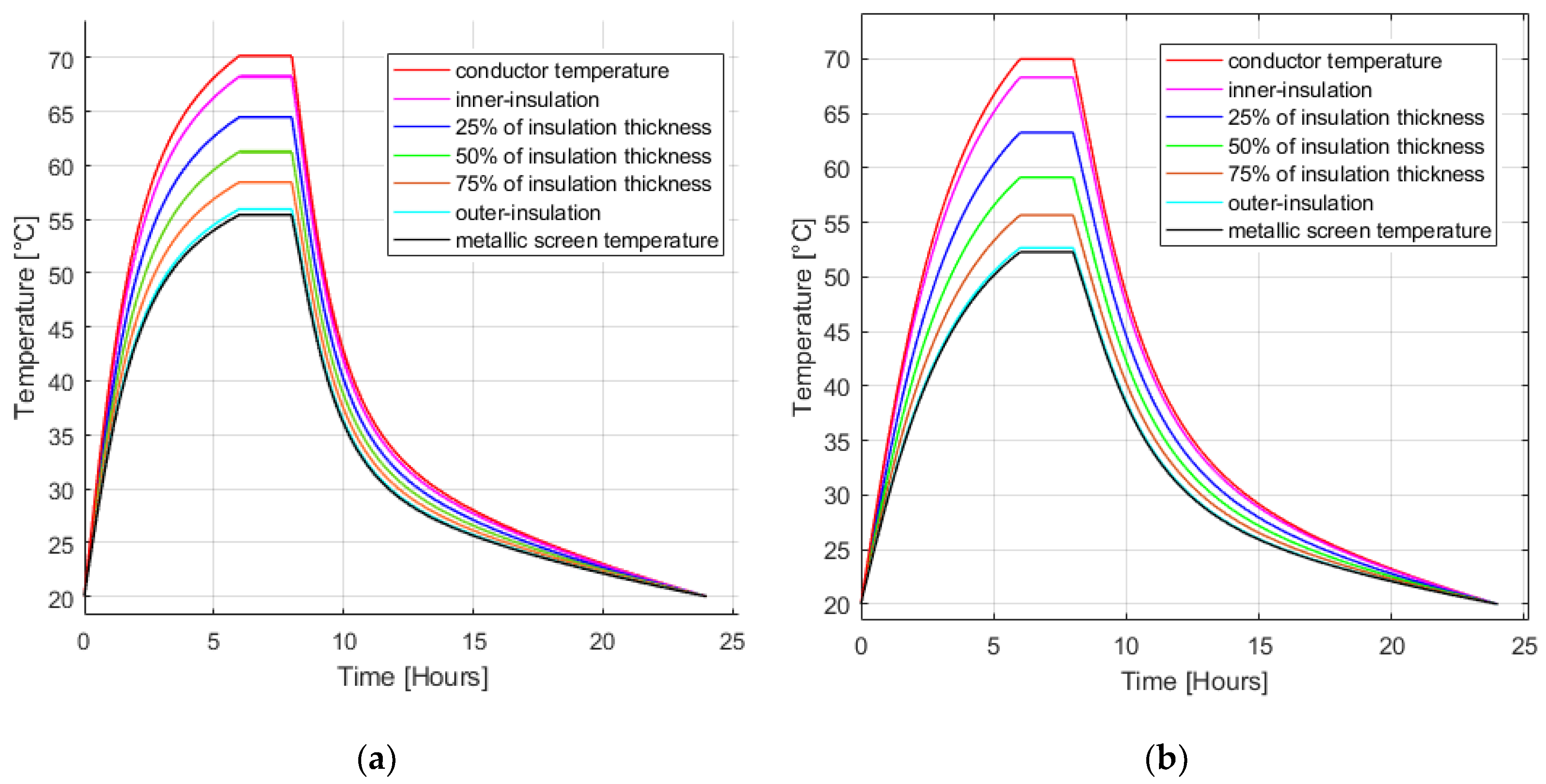
3.2. Temperature Profile Calculations
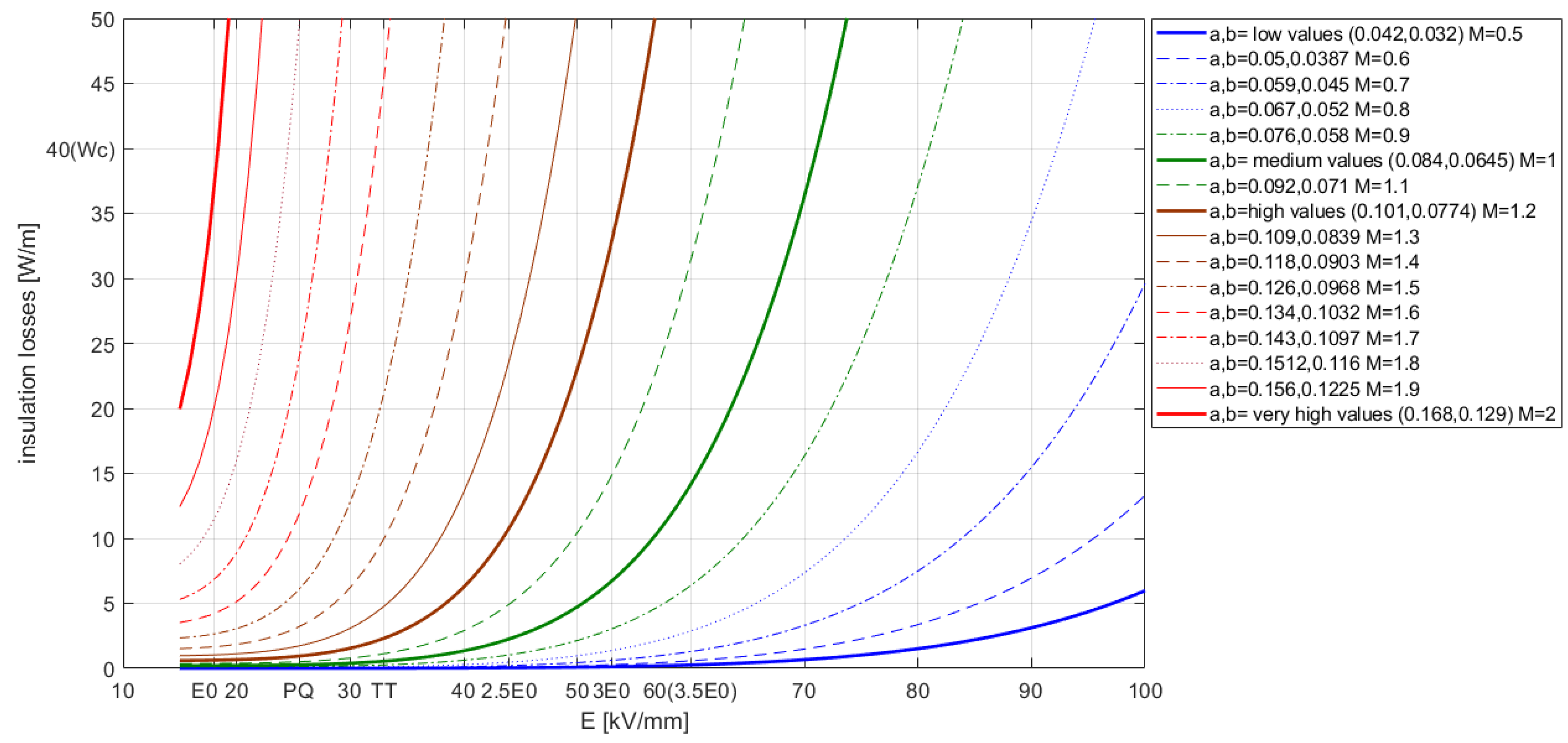
3.3. Temperature and Stress Coefficients of Electrical Conductivity a, b
- -
- An extremely low set, aL, bL, is obtained by multiplying aM, bM by M = 0.5;
- -
- An extremely high set, aVH, bVH, is obtained by multiplying aM, bM by M = 2;
- -
- The interval [aL, bL ÷ aVH, bVH] is divided into 16 equally distributed sets of a, b values, each identified in Table 4 by the corresponding value of the multiplier M of the medium set aM, bM.
4. Results
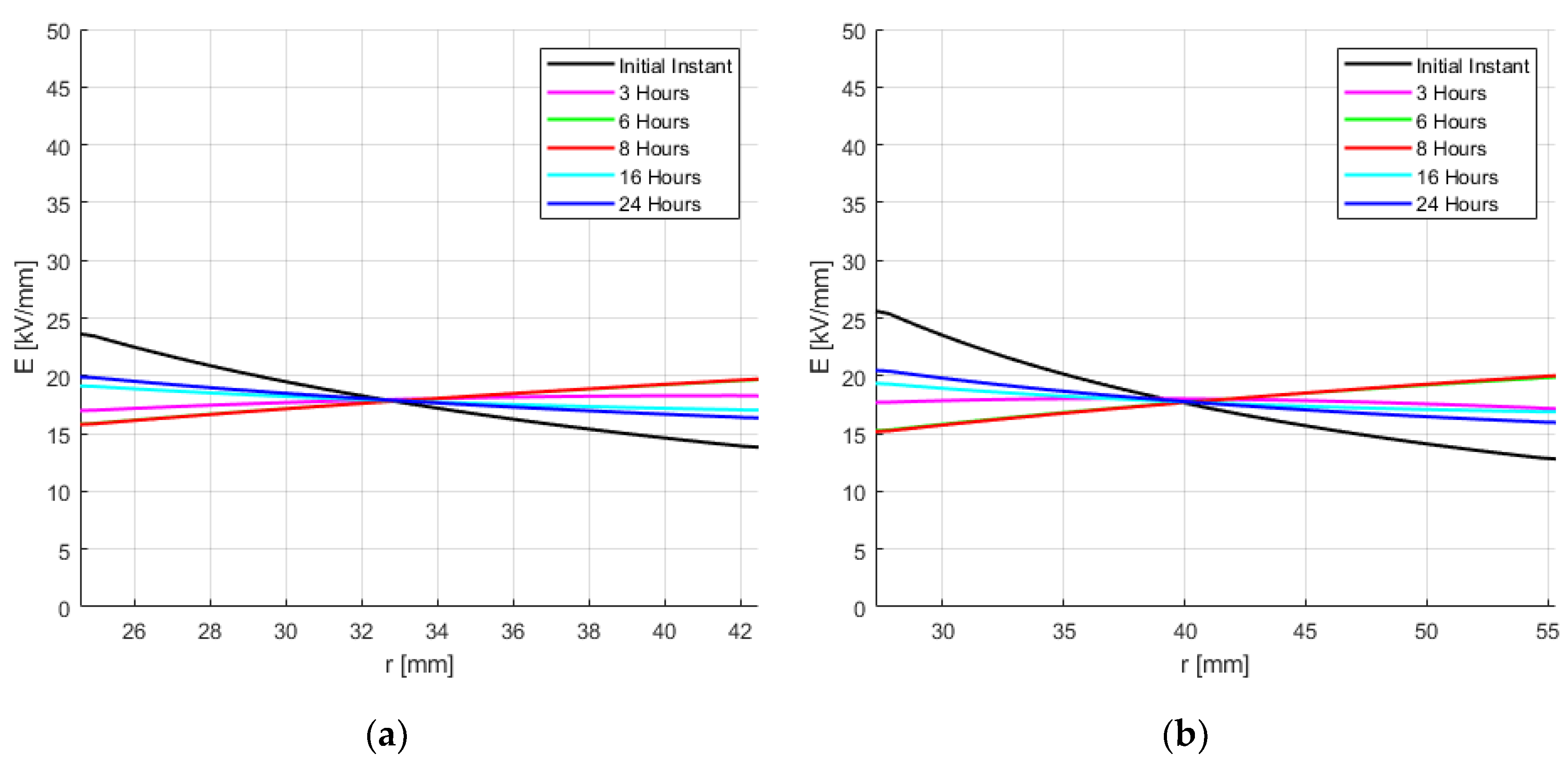
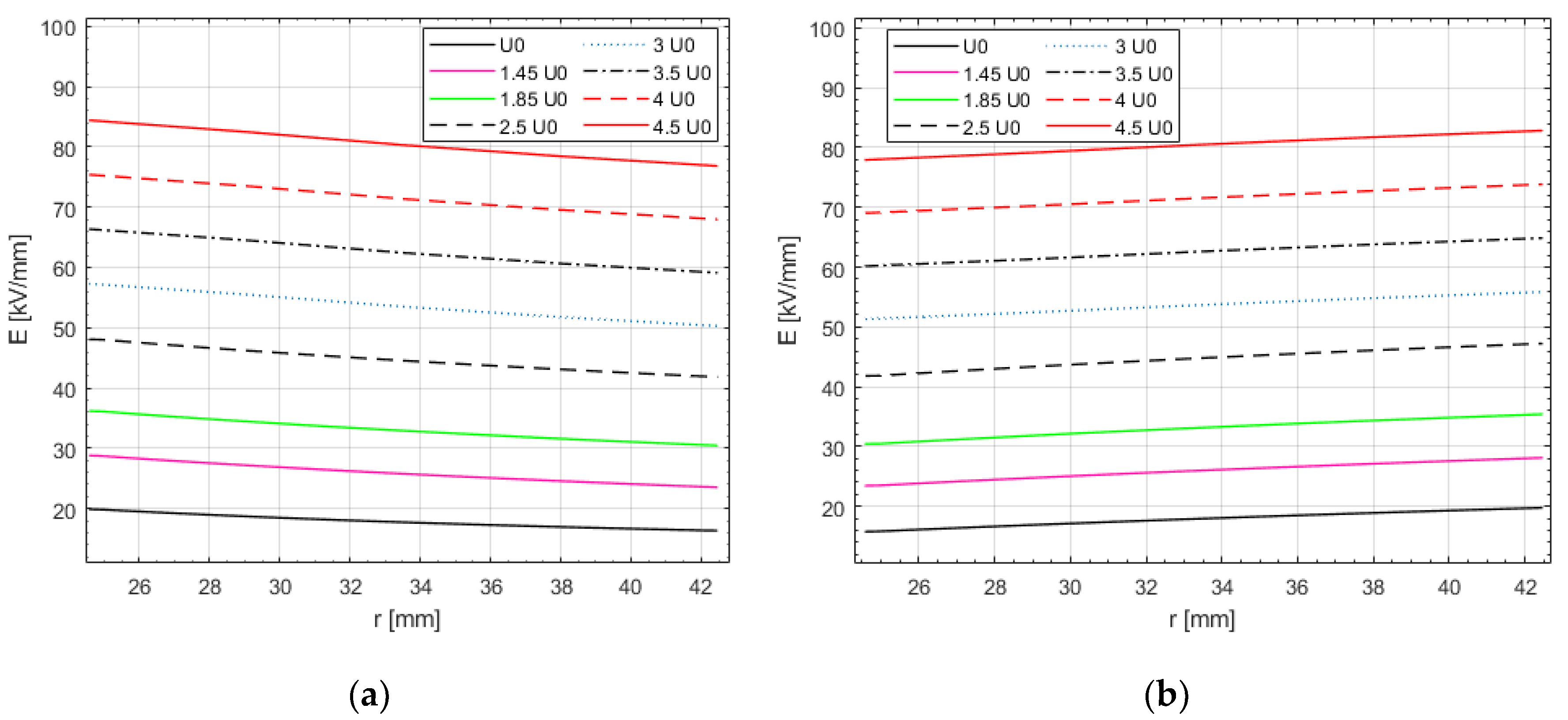
4.1. Electric Field Distribution
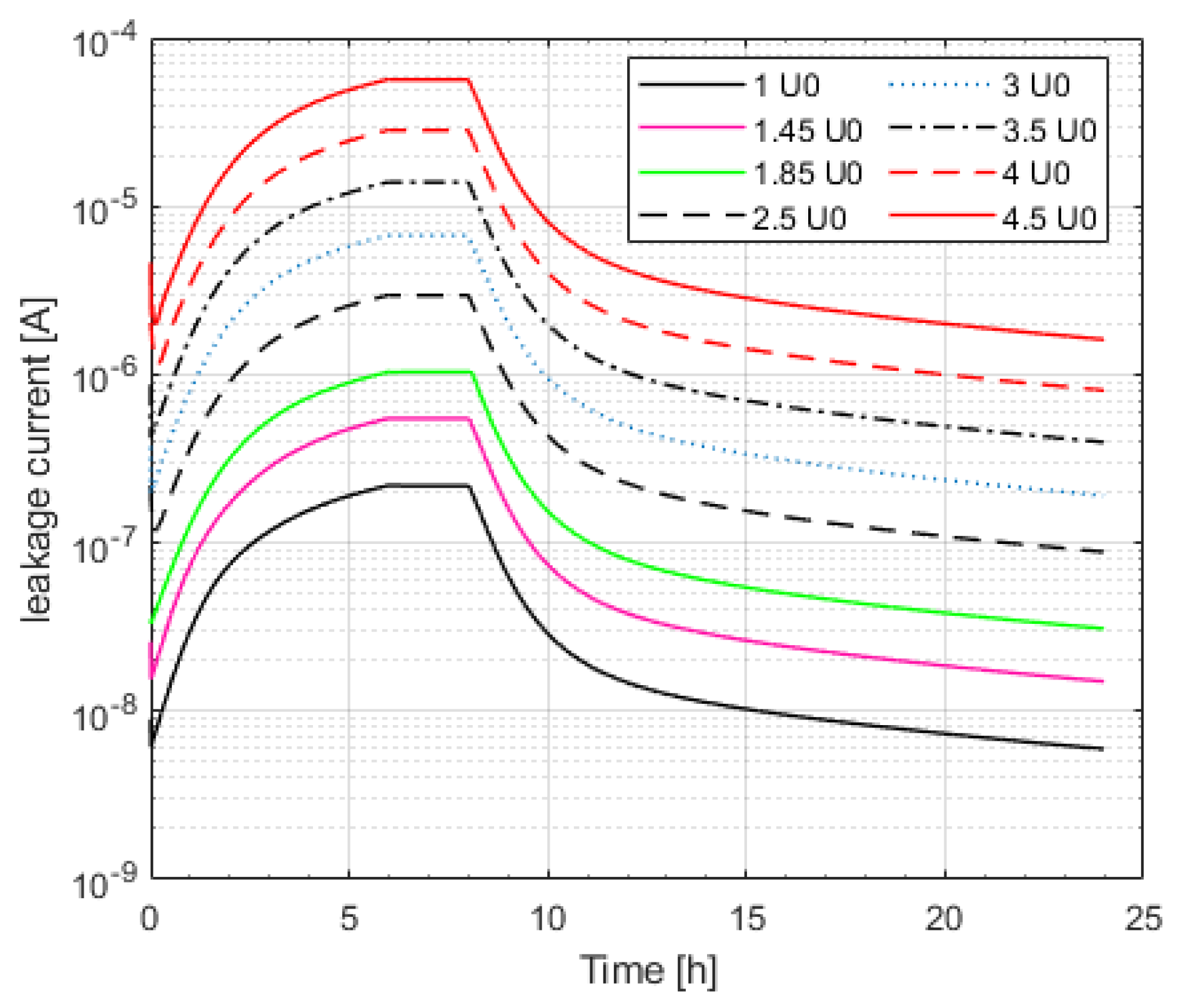
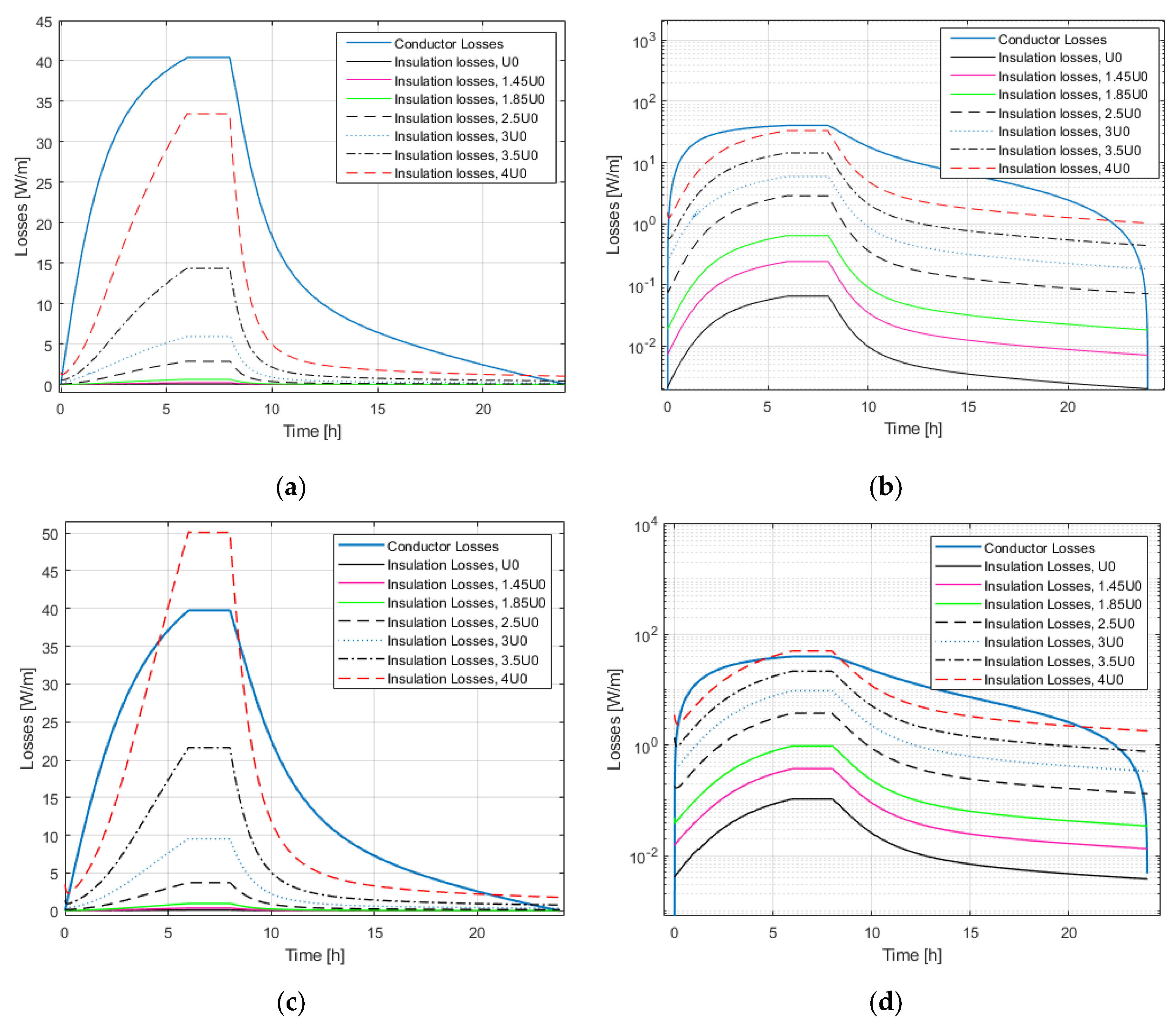
4.2. Insulation Losses
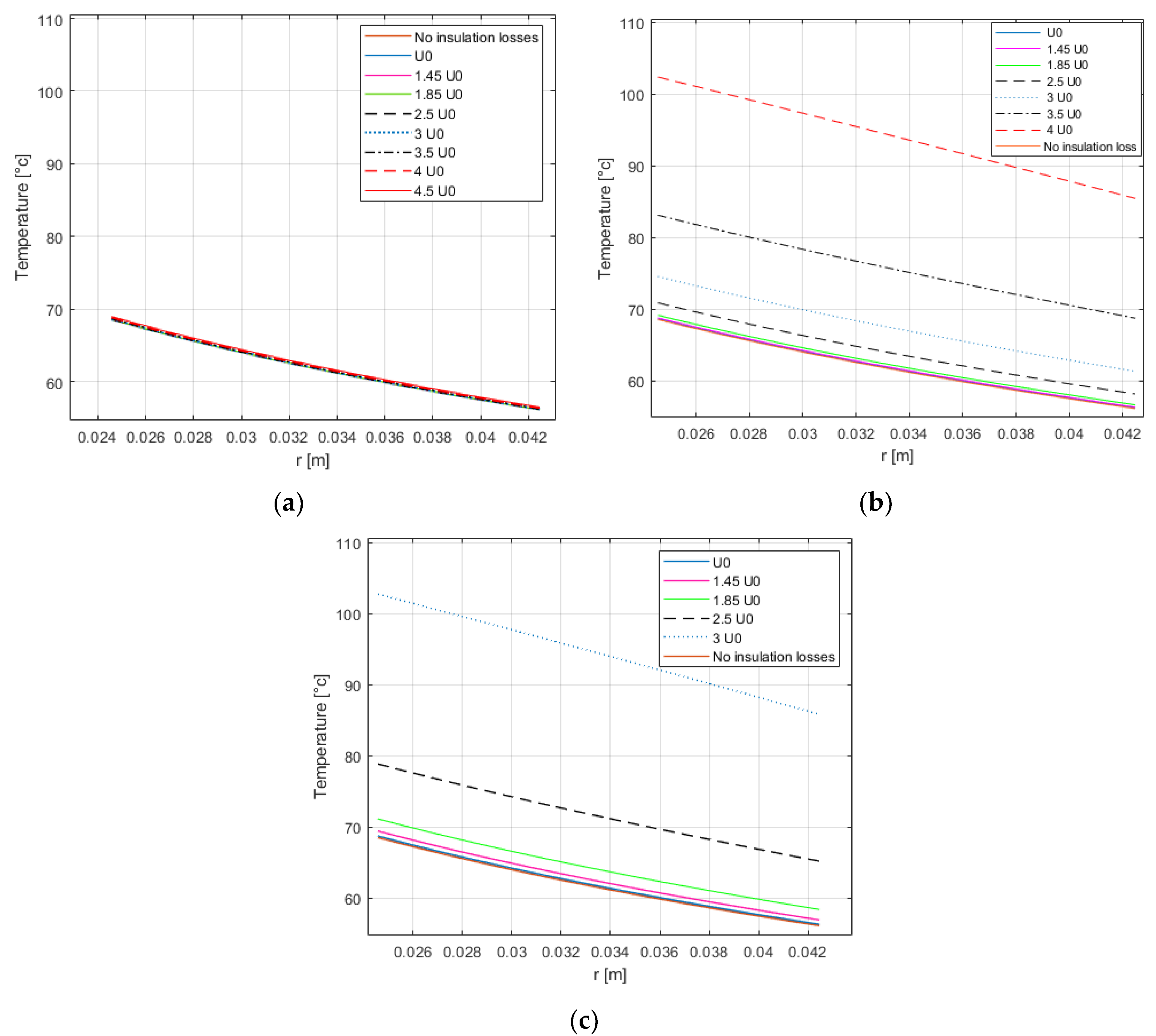
4.3. Temperature Rise
4.4. Calculation of
4.5. Thermal Stability Diagram
4.6. Thermal Instability for Different Cable Characteristics and Applied Voltages
4.7. De-Rating Factor
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- At the conductor
- (2)
- At the metallic sheath
Appendix B
References
- Mazzanti, G.; Marzinotto, M. Extruded Cables for High Voltage Direct Current Transmission: Advance in Research and Development; Power Engineering Series; Wiley-IEEE Press: Hoboken, NJ, USA, 2013. [Google Scholar]
- Jeroense, M. Fully Qualified 640 Kv Underground Extruded DC Cable System; Paper B1-309, CIGRÉ: Paris, France, 2018. [Google Scholar]
- Diban, B.; Mazzanti, G.; Troia, I. Preliminary Estimation of The Effect of Insulation Losses on HVDC Cable Reliability. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena CEIDP, Virtual Event, Piscataway, NJ, USA, 18–30 October 2020. [Google Scholar]
- Whitehead, S. Dielectric Breakdown of Solids; Oxford University Press: London, UK, 1951. [Google Scholar]
- O’Dwyer, J.J. The Theory of Dielectric Breakdown of Solids; Oxford University Press: London, UK, 1964. [Google Scholar]
- CIGRÉ. Recommendations for Testing DC Extruded Cable Systems for Power Transmission at a Rated Voltage up to 500 kV; CIGRÉ Technical Brochure 496; CIGRÉ: Paris, France, 1 April 2012. [Google Scholar]
- Fallou, M.M. Perforration dielectrique par instabilite thermique des cables a courant continu. Rev. Gen. De L’Electricite 1959, 693–695. [Google Scholar]
- Brazier, L.G. The breakdown of cables by thermal instability. J. Inst. Electr. Eng. 1935, 77, 104–115. [Google Scholar] [CrossRef]
- Jeroense, M.J.P.; Morshuis, P.H.F. Electric fields in HVDC paper insulated cables. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 225–236. [Google Scholar] [CrossRef]
- Eoll, C.K. Theory of Stress Distribution in Insulation of High Voltage DC Cables: Part, I. IEEE Trans. Electr. Insul. 1975, 10, 27–35. [Google Scholar] [CrossRef]
- Reddy, C.C.; Ramu, T.S. On the intrinsic thermal stability in HVDC cables. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1509–1515. [Google Scholar] [CrossRef] [Green Version]
- CIGRÉ. Diagnostic and Accelerated Life Endurance Testing of Polymeric Materials for HVDC Application; CIGRÉ Technical Brochure 636; CIGRÉ: Paris, France, 2015. [Google Scholar]
- Mazzanti, G. Life estimation of HVDC cables under the time-varying electro-thermal stress associated with load cycles. IEEE Trans. Power Del. 2015, 30, 931–939. [Google Scholar] [CrossRef]
- Mazzanti, G. Including the calculation of transient electric field in the life estimation of HVDC cables subjected to load cycles. IEEE Electr. Insul. Mag. 2018, 34, 27–37. [Google Scholar] [CrossRef]
- Diban, B.; Mazzanti, G. The effect of temperature and stress coefficients of electrical conductivity on the life of HVDC extruded cable insulation subjected to type test conditions. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1295–1302. [Google Scholar] [CrossRef]
- IEC 60853-2. Calculation of the Cyclic and Emergency Current Rating of Cables, Part 2: Cyclic Rating of Cables Greater Than 18/30 (36) kV and Emergency Ratings for Cables of All Voltages; Ed. 1.0; International Electrotechnical Commission IEC: Geneva, Switzerland, January 1989. [Google Scholar]
- Klein, N. Electrical Breakdown in Solids. Adv. Electr. Electron. Phys. 1969, 26, 309–424. [Google Scholar]
- IEC 60287. Electric cables—Calculation of the Current Rating Equations (100% Load Factor) and Calculations of Losses; Part 1-1; 1-2, 1-3, 2-1, 3-1, Series (Ed.2-2020); International Electrotechnical Commission IEC: Geneva, Switzerland, 2020. [Google Scholar]
- Fukagawa, H.; Imajo, T.; Sakamoto, Y. Thermal Breakdown and Thermal Runaway Phenomena in EHV Cables. IEEE Trans. Power Syst. 1978, PAS-97, 1885–1892. [Google Scholar] [CrossRef]
- Mazzanti, G.; Diban, B. Parametric Analysis of HVDC Extruded Cable Reliability for Different Cable Designs. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena CEIDP, Virtual Event, Piscataway, NJ, USA, 18–30 October 2020. [Google Scholar]
- Hampton, R.N. Some of the considerations for materials operating under high-voltage, direct-current stresses. IEEE Electr. Insul. Mag. 2008, 24, 5–13. [Google Scholar] [CrossRef]
- Dissado, L.A.; Fothergill, J.C. Electrical Degradation and Breakdown in Polymers; Peter Peregrinus: London, UK, 1992. [Google Scholar]
- Riechert, U.; Vogelsang, R.; Kindersberger, J. Temperature Effect on DC Breakdown of Polyethylene Cables. In Proceedings of the 12th International Symposium on High Voltage Engineering, Bangalore, India, 20–24 August 2001. [Google Scholar]
- Tanaka, T.; Greenwood, A. Advanced Power Cable Technology Vol. I Basic Concepts and Testing; CRC Press: Boca Raton, FL, USA, 1983. [Google Scholar]




| Parameter | 500 kV Cable | 320 kV Cable |
|---|---|---|
| Rated power (bipolar scheme) (MW) | 1715 | 1105 |
| Rated voltage (kV) | 500 | 320 |
| Conductor Material | Cu | Cu |
| Insulation Material | DC-XLPE | DC-XLPE |
| relative permittivity | 2.3 | 2.3 |
| Rated conductor temperature (°C) | 70 | 70 |
| Ambient temperature a (°C) | 20 | 20 |
| Conductor cross-section (mm2) | 2000 | 1600 |
| inner insulation radius ri (mm) | 27.2 | 24.6 |
| Insulation thickness (mm) | 28.1 | 17.9 |
| outer insulation radius ro (mm) | 55.3 | 42.5 |
| Design life LD (years) | 40 | 40 |
| Design failure probability PD (%) | 1 | 1 |
| Rated or design current (ampacity) Ic,n (A) | 1715 | 1727 |
| Thermal Resistivity | Thermal Resistance | ||
|---|---|---|---|
| 500 kV | 320 kV | ||
| insulation | 3.5 | 0.447 | 0.365 |
| Thermoplastic sheath | 3.5 | 0.0421 | 0.054 |
| Soil | 1.3 | 0.769 | 0.818 |
| Type of Dielectric | a (1/°C) | b (mm/kV) |
|---|---|---|
| Paper | 0.074 | 0.018 ÷ 0.029 |
| Thermoset | 0.084 ÷ 0.101 | 0.0645 |
| Thermoplastic | 0.104 ÷ 0.115 | 0.034 ÷ 0.128 |
| Classification | Symbols of the a, b Set | M (Multiplier of aM, bM) | a (1/°C) | b (mm/kV) |
|---|---|---|---|---|
| Low set | aL, bL | 0.5 | 0.042 | 0.032 |
| 0.6 | 0.05 | 0.0387 | ||
| 0.7 | 0.059 | 0.045 | ||
| 0.8 | 0.067 | 0.052 | ||
| 0.9 | 0.076 | 0.058 | ||
| Medium set | aM, bM | 1 | 0.084 | 0.0645 |
| 1.1 | 0.092 | 0.071 | ||
| High set | aH, bH | 1.2 | 0.101 | 0.0774 |
| 1.3 | 0.109 | 0.0839 | ||
| 1.4 | 0.118 | 0.0903 | ||
| 1.5 | 0.126 | 0.0968 | ||
| 1.6 | 0.134 | 0.1032 | ||
| 1.7 | 0.143 | 0.1097 | ||
| 1.8 | 0.1512 | 0.116 | ||
| 1.9 | 0.156 | 0.1225 | ||
| Very high set | aVH, bVH | 2 | 0.168 | 0.129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diban, B.; Mazzanti, G. The Effect of Insulation Characteristics on Thermal Instability in HVDC Extruded Cables. Energies 2021, 14, 550. https://doi.org/10.3390/en14030550
Diban B, Mazzanti G. The Effect of Insulation Characteristics on Thermal Instability in HVDC Extruded Cables. Energies. 2021; 14(3):550. https://doi.org/10.3390/en14030550
Chicago/Turabian StyleDiban, Bassel, and Giovanni Mazzanti. 2021. "The Effect of Insulation Characteristics on Thermal Instability in HVDC Extruded Cables" Energies 14, no. 3: 550. https://doi.org/10.3390/en14030550






