1. Introduction
In thermal response measurements, a system is exposed to a change in heating or cooling power and the response of the system, i.e. the resulting temperature change, is monitored. Typically, the impulse response or the step response is measured with the goal to reconstruct the relevant thermal properties of the system. For the one-dimensional case, this corresponds to the construction of an equivalent Cauer network with known resistances and capacitances. One method to achieve this is known as the “network identification by deconvolution” method [
1]. The method is regularly used as an analysis tool for transient thermal analysis [
2,
3,
4]. The methodology itself is also subject to intense discussions [
5,
6,
7,
8].
As a first step in this procedure, the measured thermal step response of a device under test, called thermal impedance, is plotted on a logarithmic time scale and differentiated to obtain the logarithmic impulse response. Subsequently, a deconvolution is performed to retrieve the time constant spectrum, which gives the parameters for a Foster-type thermal equivalence network. As the last step, a Foster-to-Cauer transformation is performed to identify the thermal resistances and capacities of the heat path and to construct the thermal structure function.
Network identification by deconvolution is a challenging technique both with respect to measurement setup and evaluation procedure. In their book, Lasance and Poppe state that “
curves must be extremely noise free” ([
9], p. 129). An industry standard for the thermal characterization of electronic devices, the JEDEC standard JESD51-14, reports that the solution is “extremely sensitive to noise” ([
10], p. 16). Ezzahri and Shakouri note in their paper that the thermal transient should ideally be sampled at least 10 to 15 times faster than the smallest time constant in the signal [
11]. A study at Infineon Technologies warns against misinterpretation of numerical artifacts in the structure function, highlighting the importance of accurate algorithms and careful interpretation of the results [
12].
The input signal is typically recorded at a constant rate on a linear timescale. The conversion from a linear to a logarithmic scale,
, presents a first challenge as it leaves the thermal impedance sparsely sampled in the beginning and dense at the end. The result is a relatively low accuracy for the derivative at short times, which is particularly detrimental for the subsequent, noise sensitive deconvolution. The final step, the Foster-to-Cauer transformation, typically introduces a divergence to the structure function. In principle, the divergence in thermal capacitance reflects the infinite heat capacity of the ambient. In practice, the divergence is significantly smeared out and masks the true behavior of the structure function at the end, which is an artifact of the algorithm [
13]. A detailed analysis of the numerical challenges during network identification by deconvolution and suggestions to systematically improve its performance are given in [
8].
In this work, an alternative approach is used for the task of network identification. The idea of the so-called optimization-based network identification is to avoid the numerically challenging steps by solving the inverse problem to network identification repeatedly. When solving the equations in this direction, an integration and convolution has to be performed instead of a differentiation and deconvolution. This promises a higher accuracy, as these tasks are numerically much simpler. In optimization-based network identification, an initial estimate for the thermal equivalence network, i.e., the thermal structure function, is first generated by conventional network identification by deconvolution. Next, the solution is refined by a multi-dimensional optimization to find a good match between optimization and measurement data. In this way, the algorithm does not rely on the differentiation and deconvolution of noisy data only.
2. Inverse Calculations
The goal of network identification by deconvolution is to derive a thermal equivalence network, i.e., the thermal structure function, from a thermal transient measurement. In this context, an inverse calculation means to derive a step response from a thermal equivalence network, i.e., a structure function.
The thermal structure function describes a system via numerous small sections with constant resistance and capacitance density,
and
. However, real physical systems comprise significantly fewer components. Most of the
and
represent the same layer or component. Thus, the relevant information is also captured by a simplified thermal equivalence network, which is constructed from the full thermal structure function. As a model for the simplified thermal network, a chain of uniform RC transmission lines is used [
14]. Its corresponding structure function is called piecewise uniform structure function. A comprehensive treatment of non-uniform RC lines can be found in [
15,
16]. Once the total resistances,
, and the total capacitances,
, of each section of the piecewise uniform transmission line are known, its total impedance can be constructed. The impedance up to each section,
, can be calculated via
Here,
denotes the load impedance of section
i and
s the complex frequency. The total impedance of the entire transmission line,
, is calculated sequentially by using the input impedance of the previous section as the load impedance of the next. The calculation begins at the short-circuited end with a vanishing load impedance. In
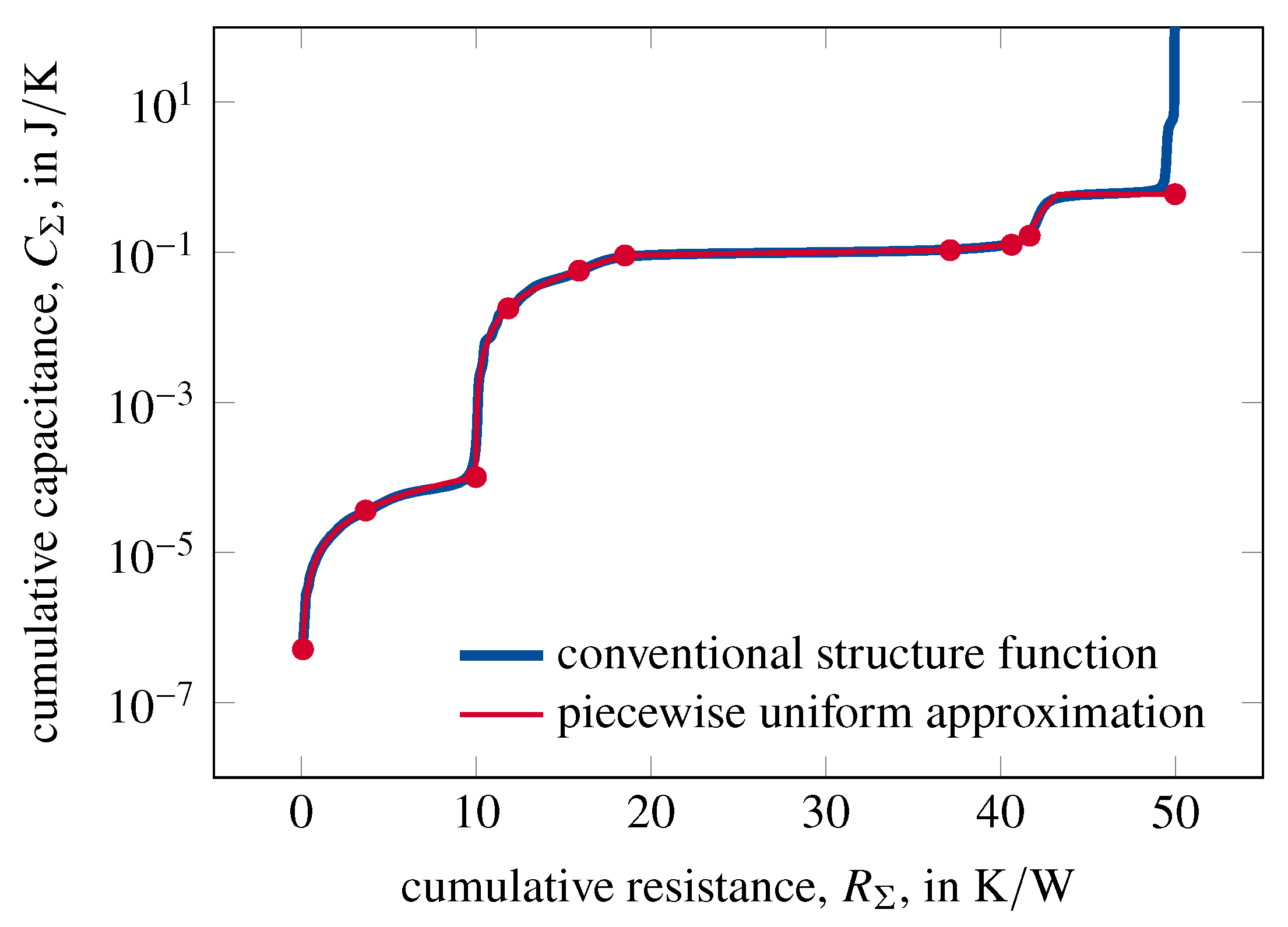
Figure 1, a structure function calculated via network identification by deconvolution is shown together with a piecewise uniform approximation comprising ten sections. Note that due to the decadic logarithmic scaling of the cumulative capacitance the sections do not appear linear.
Once
is known, the logarithmic time constant spectrum,
, is calculated. It is proportional to the imaginary part,
ℑ, of
on a path along the negative real axis,
Due to poles on this path, Equation (
2) cannot be evaluated directly. Instead, a small angle,
, is introduced which rotates the path into the complex plane,
This has the effect of smoothing the poles, making them finite as described in [
17]. The smaller
is, the more accurate the calculations become. However, a small angle of
produces high and narrow peaks, which requires a dense sampling of
s to be captured correctly. Moreover, for accurate calculations it is required to capture all side lobes of the time constant spectrum. This means, that for small angles of
the time constant spectrum has to be sampled densely over a wide range. In effect, calculating theoretical thermal impedances with very high accuracy becomes computationally demanding, requiring calculation times of up to several minutes on an ordinary desktop computer. In the literature, it is stated that the angle,
, should not exceed 5
[
17]. Typically, the time constant spectrum is sampled at approximately 30 points per decade [
18,
19].
Ideally, the asymptotic value of the thermal impedance, , should match the total thermal resistance of the structure function, , exactly. In this case, the relation is exactly satisfied. However, due to the discretization error and the finite angle, , the asymptotic thermal impedance, , is different from . The absolute difference between them is denoted as , i.e., .
In the following, an analysis is performed to determine appropriate parameters for inverse calculations. The accuracy is mainly determined by the angle
and the sampling parameters. The computational workload depends significantly on the number of points used for
. To strike a balance between computation time and accuracy,
points in the range
are used. To determine an optimum value of
for this sampling rate, a test series is performed.
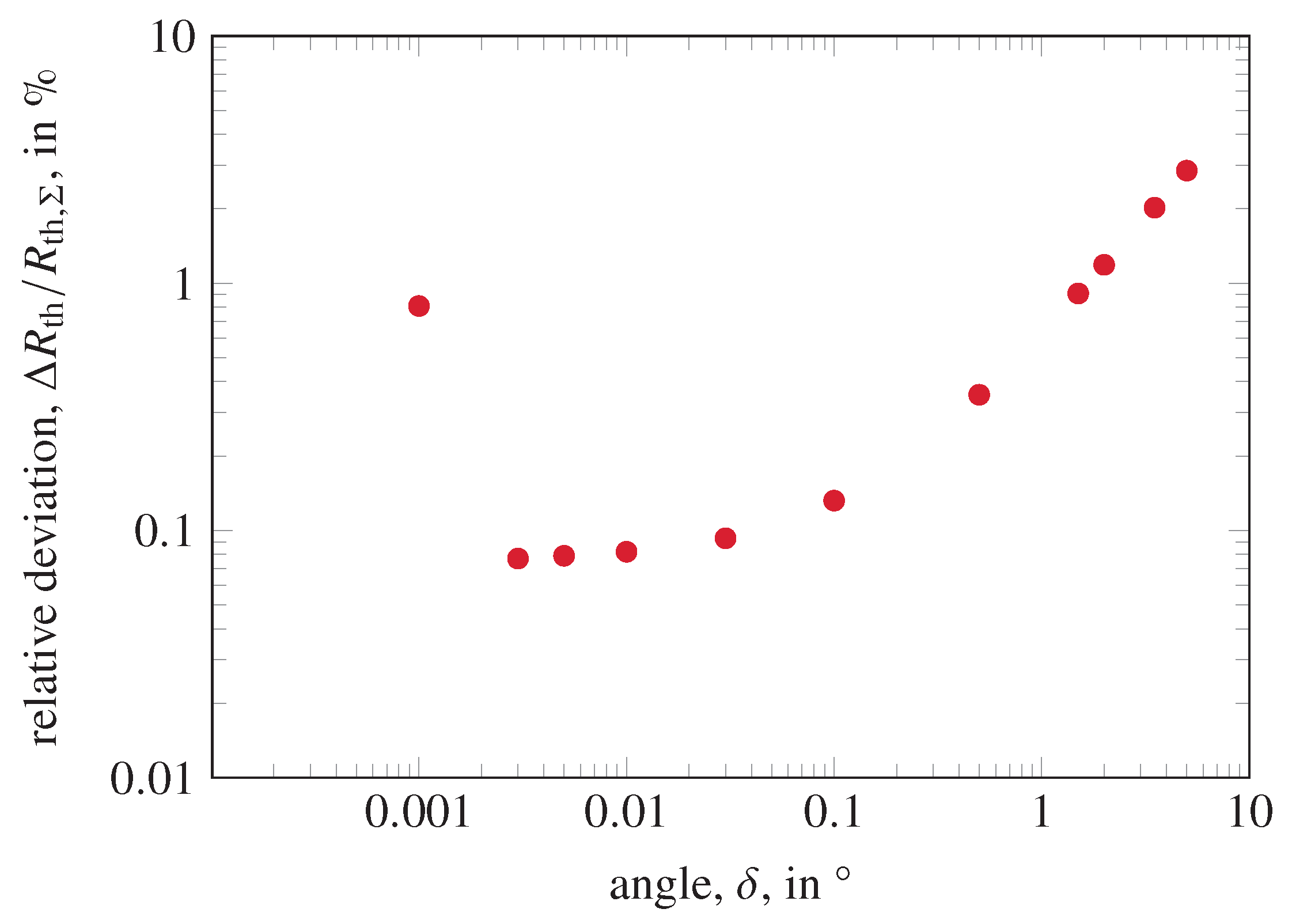
Figure 2 shows the relative deviation,
for different values of
and fixed sampling frequency. As a test case, structure 1 (see
Table 1) is used. At high angles, the accuracy is relatively low due to the error made in Equation (
3). At very low angles of
, the peaks are too narrow to be captured correctly, given the sampling frequency. A value of
limits the error made in Equation (
3) while making sure that all peaks are captured correctly. For smaller angles and higher sampling frequencies, the error is also limited by the width of the chosen interval.
3. Optimization-Based Network Identification
The idea of optimization-based network identification is to find a piecewise uniform structure function via multi-dimensional optimization, which has a thermal impedance which matches well with the measured thermal impedance. In this way, a structure function belonging to the system is known by definition and the associated time constant spectrum can be readily calculated with high accuracy.
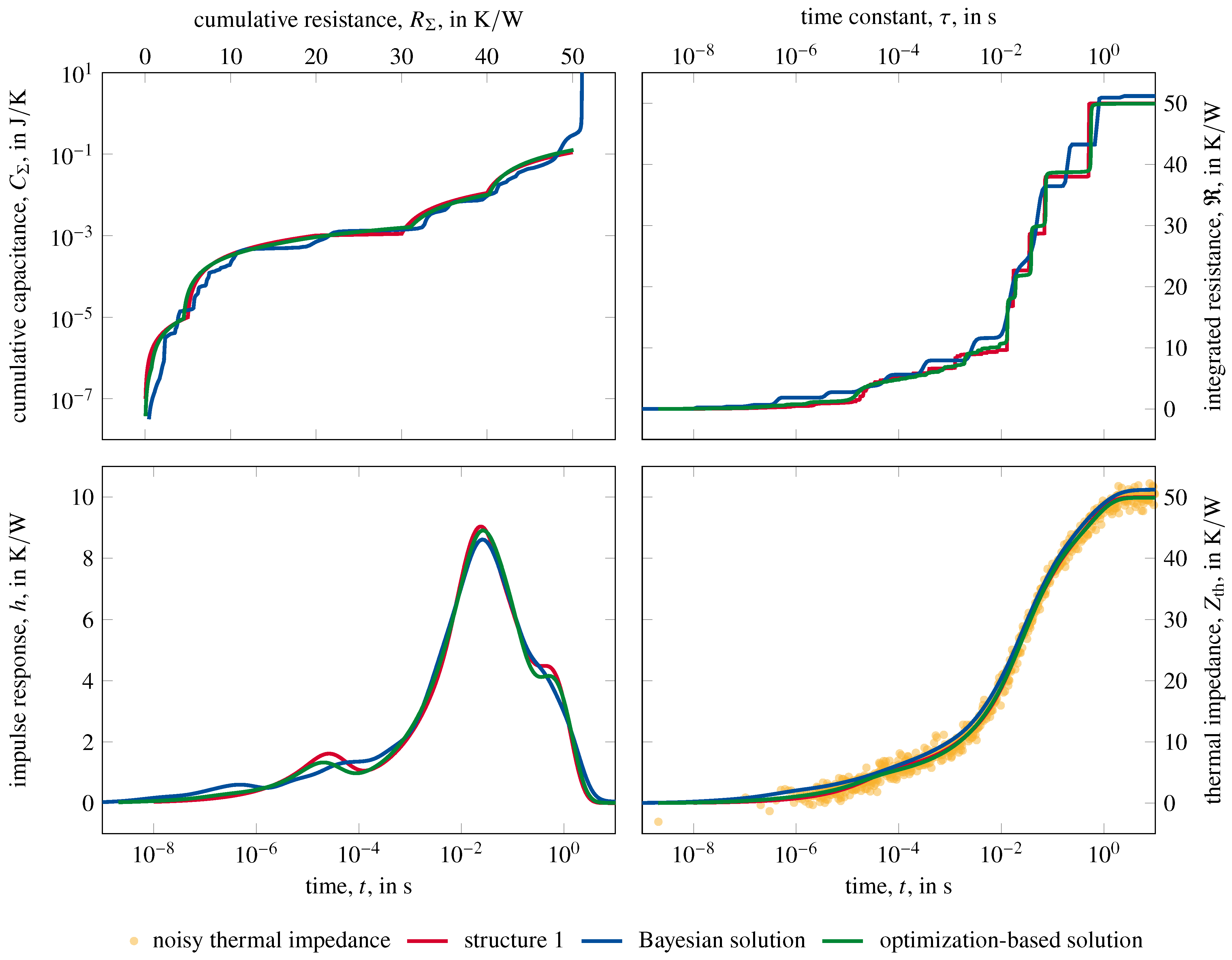
The scheme of
Figure 3 visualizes the procedure of optimization-based network identification. Starting from the measured step response (top left), a conventional network identification by deconvolution is performed first. Then, a network simplification is performed (see
Figure 1). In this step, the thermal structure function resulting from network identification by deconvolution is approximated by a piecewise uniform structure function, truncating the divergence at the end. A multi-dimensional optimization is performed, which optimizes the resistance and capacitance of each section. The goal is to minimize the discrepancy between the conventional thermal network and the simplified thermal network with a given number of sections. As a last step, an optimization-based network identification is performed. In this step, the simplified thermal network is optimized to best match the measured thermal impedance. The result is the optimized thermal network. For each function evaluation during the optimization, an inverse calculation is performed. Once the optimized thermal network is in good agreement with the measured thermal impedance, the optimization is successful.
For the success of optimization-based network identification, it is important to have good initial values. A strategy to obtain good initial values is to perform a conventional network identification by deconvolution first. To ensure a good fit between the intermediate thermal network,
, and the thermal structure function,
, an optimization is performed during network simplification. The number of piecewise uniform sections,
, in the step of network simplification is chosen manually. Typically, a suitable number of sections lies between 2 and 20. The number of sections has to be high enough to provide a sufficient number of degrees of freedom while keeping the optimization as simple as possible. Each section is completely defined by the thermal resistance and the thermal capacitance it contributes to the structure function. For the optimization, the best-performing objective function is the square root of the integral of the squared logarithmic deviations, i.e.,
The initial intermediate thermal network, i.e., the starting values for the optimization during the network simplification, are given by points, , evenly spaced along the arc length of the forward structure function. In addition, truncating the divergence at high , which is a numerical artifact of the Foster-to-Cauer transformation, increases the accuracy and the stability of the convergence. For a good convergence, it should be ensured that the total thermal resistance of the initial intermediate thermal network is identical to the total thermal resistance of the measured thermal impedance.
The degrees of freedom provided to the solver are the cumulative resistances and the cumulative capcitances, , of the piecewise uniform structure function. In this way, the total thermal resistance represented by the piecewise uniform structure function is only determined by and does not change when modifying the other .
The objective function employed for the main optimization is given in (
5). It has the form of an
-norm, i.e., it is the square root of the integral of the squared difference between optimized and measured step response,
Note that
is typically not evenly spaced. The optimized thermal impedance,
, is interpolated to be defined on the same set of
as the measurement data.
To compare the optimized thermal impedance to results from a network identification by deconvolution, the time constant spectrum, which appears during network identification by deconvolution, is reconvolved. Subsequently, it is integrated to reproduce a thermal impedance. This impedance is henceforth called backwards thermal impedance. It is the impedance represented by the time constant spectrum, i.e., it reflects the effects of differentiation and deconvolution. To have a valid solution, the discrepancy (as measured by ) between the optimized thermal impedance and the measured thermal impedance must be similar or even smaller than the discrepancy between the optimized thermal impedance and the backwards thermal impedance.
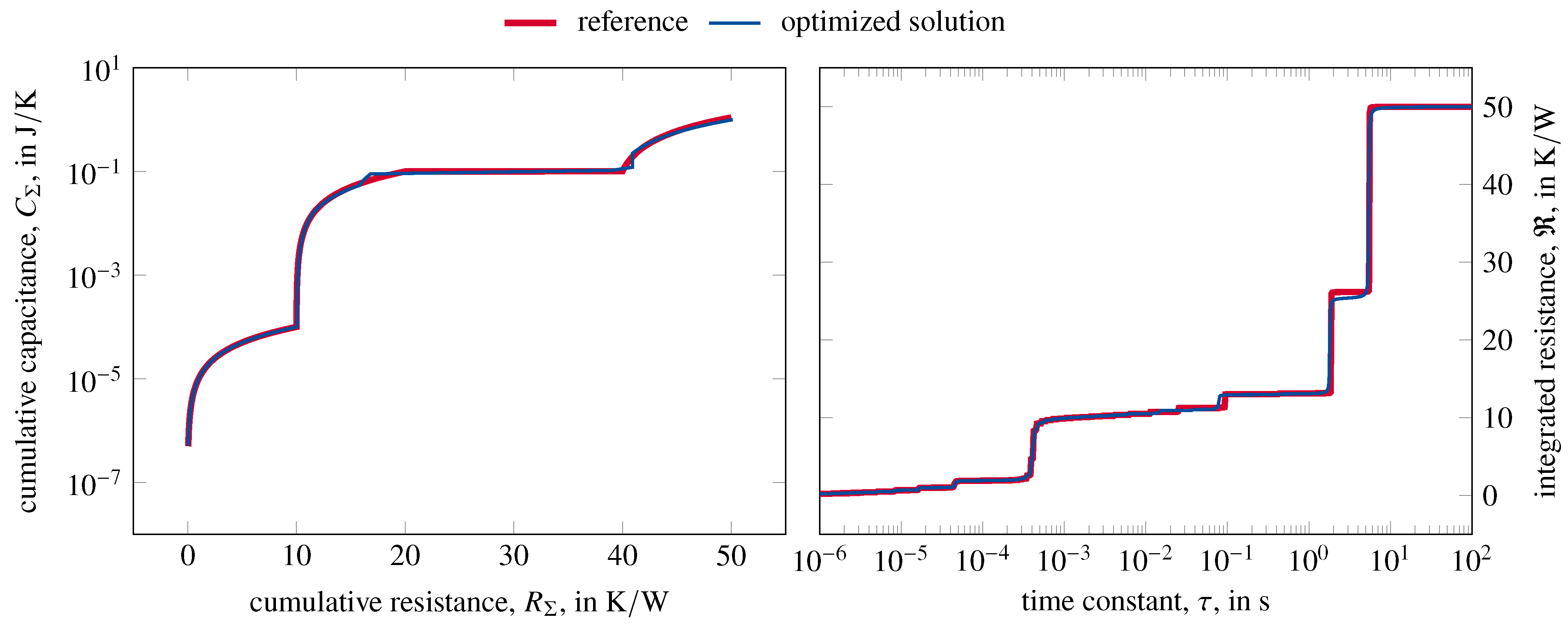
For network simplification as shown exemplarily in
Figure 1, the results of the following optimization-based network identification are shown in
Figure 4. The value of the objective function resulting from the initial simplified thermal network is
. After the main optimization, the value of the objective function is reduced to
. For comparison, the value of the objective function for the backwards thermal impedance is
. To calculate accurate structure functions, a low value of
is an important sanity check and suitable to validate solutions. However, it is not a sufficient measure of accuracy for a solution. A holistic comparison of the accuracy of various methods is performed in the following section.
For optimization of the objective function (
5), two solvers yield good results. Powell’s conjugate direction method provides a good convergence [
20], while constrained Optimization BY Linear Approximations, abbreviated COBYLA, is also suitable [
21]. A common feature of both solvers is that they do not calculate derivatives of the objective function and are therefore suitable for problems with complicated objective functions.
Moreover, both solvers are able to respect boundary conditions which is used here to restrict the search space to physically possible values. For example, it is required that all cumulative resistances and capacitances are positive. Additionally, the total thermal resistance, , is unlikely to significantly exceed .
As a physical constraint, the structure function must be monotonically increasing. This means that both the list of resistances, , and capacitances, , should be strictly monotonically increasing, i.e., each and has to be greater than its left neighbor and smaller than its right neighbor. However, the solvers do not uphold these conditions during the optimization strictly. There has to be a mechanism to repair unphysical structure functions that appear during the optimization. This is done by sorting the and in each evaluation. Furthermore, a minimum size for and is set to avoid numerical instability.
In general, the COBYLA solver is able to accept constraints, that force the parameters to fulfill certain boundary conditions. This can be used to restrict the solution to remain physically meaningful in the sense explained above. Still, validity should be checked every function evaluation because of possible constraint violations. Furthermore, significant speed increases for the Powell solver are achieved by using an LRU (least recently used) cache on parts of Equation (
1). On the computer used in this work (Windows 10, Intel Core i7-8665U CPU with 1.90 GHz, 16 GB RAM), the computation time for an optimization-based network identification is on the order of a few minutes depending on the speed of convergence for the specific problem. The conventional network identification by deconvolution, which is performed at first, takes a few seconds.
4. Methodology
Three reference structures are defined to compare the performance of optimization-based network identification with that of other methods such as network identification using Fourier or Bayesian deconvolution (
Table 1). To judge the accuracy of each method, the exact thermal impedance of each reference structure is calculated as described in
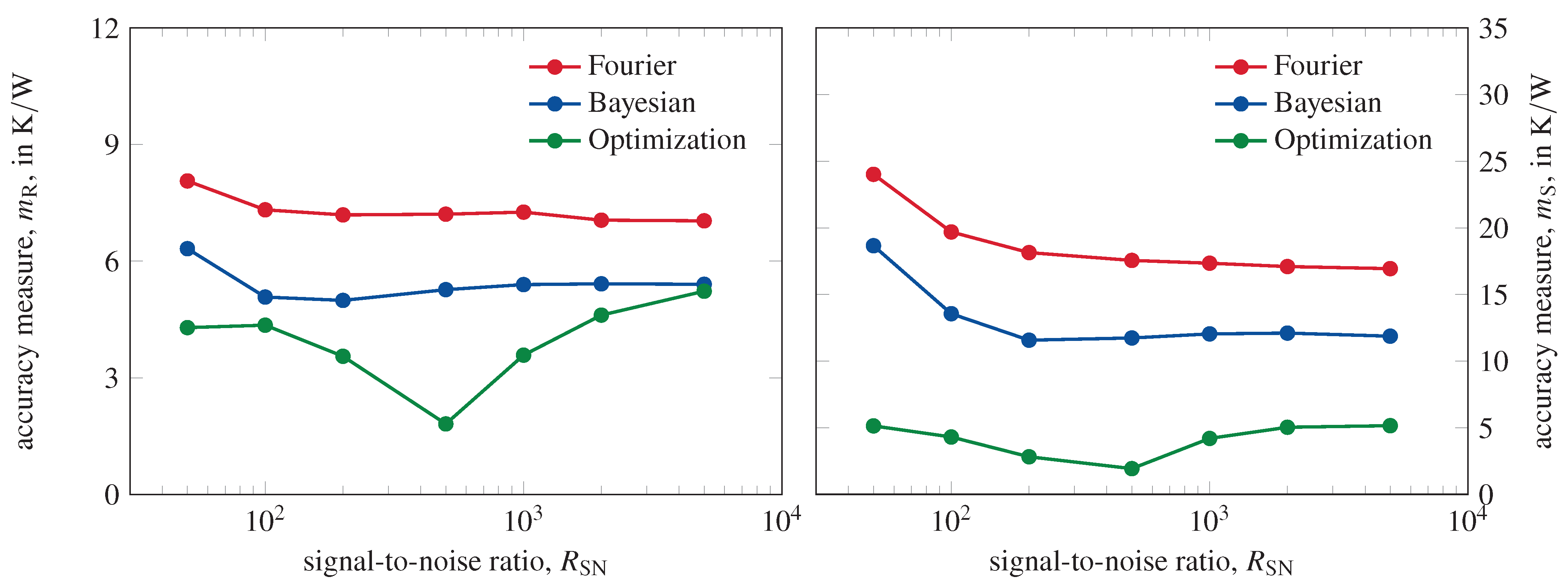
Section 2. This thermal impedance is then used as input data for a network identification algorithm. The accuracy of each method is measured by comparing the recovered structure functions and time constant spectra with the reference.
To evaluate the algorithms under different conditions, the sampling rate and the signal-to-noise ratio of the reference thermal impedances are artificially degraded. As a first test case, the exact thermal impedance is provided to the algorithm without noise and with a high sampling rate. This allows to judge the performance of the algorithms for perfect input data. Second, an imperfect measurement is simulated by a reduction of the sampling rate and the addition of Gaussian noise. The corresponding standard deviation,
, is defined by the signal-to-noise ratio,
, and the asymptotic thermal impedance,
, via
Third, in addition to the introduction of noise, the thermal impedance is resampled with a constant sampling rate in linear time, t. This results in unevenly spaced points in logarithmic time, z.
For the comparison of the recovered solutions with the theoretically ideal reference, several measures of accuracy are defined. For a derivation and discussion of these measures of accuracy, the reader is referred to ([
8] Section 3.1—Measures of Accuracy). There, also an analysis of network identification algorithms using Fourier and Bayesian deconvolution on the basis of these measures is given (Section 6—Performance Quantification). The calculations presented here are conducted as similarly as possible to allow a fair comparison.
To quantify differences between two time constant spectra, the integrated spectrum,
, is used, i.e.,
The measure of accuracy for time constant spectra,
, is then defined as an L
-norm of the differences between the integrated spectra,
When comparing two structure functions, a suitable definition for the integration limits is crucial, as there are divergences in the structure function and potentially different domains. The lower integration limit,
, and the upper integration limit,
, are defined as
where
is the theoretical reference structure function and
is the structure function it is compared to. Using these definitions, the measure of accuracy for structure functions,
, is
Here,
is measured in units of
. To assess the absolute accuracy of the total thermal resistance, a third measure of accuracy,
, is required [
8], as the upper integration limit,
, is defined by the recovered structure function itself,
Here,
is the exact thermal resistance.