1. Introduction
Currently, the environment is facing critical challenges that threaten numerous life forms on the planet. These challenges come as a result of the energy-related activities adopted by mankind over the last few decades. Therefore, there has been a growing effort to push energy systems towards sustainability and clean energy sources. Among the forms of this effort is the development of energy harvesters. Energy harvesters are devices that can absorb the energy wasted in the surroundings and change it to more useful forms [
1,
2]. These harvesters may rely—among other types of materials—on piezoelectric materials to change the captured energy from one form to another.
Piezoelectric materials are materials that can develop electric charges on their surfaces in response to applied mechanical pressure [
3,
4]. Hence, it has acquired its name “piezoelectric” from the Greek language, where the word “piezo” means to push [
5]. Piezoelectric materials were discovered in 1880 by the brothers Curie in naturally existing materials [
6,
7].
The ability of piezoelectric materials to interchange electric and mechanical energy is a result of its material structure that allows the motion of electrons upon being pressed. When this structure is subjected to mechanical pressure, electrons will be displaced, creating polarization between the negatively charged electron cloud and the positively charged nucleus. This polarization eventually forms an electric field [
8,
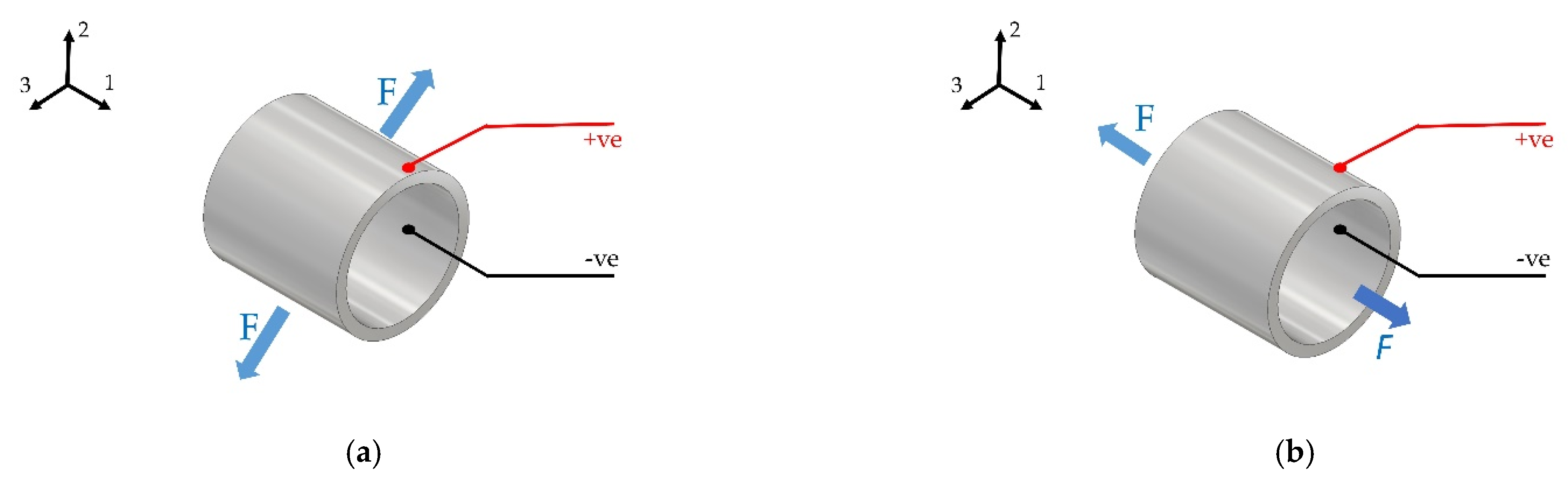
9]. It is necessary to mention that the direction of the applied pressure relative to the material structure is significant. Therefore, piezoelectric materials may be used in two modes: mode 33 and mode 31. As shown in
Figure 1a, mode 33 is the mode when the applied pressure is parallel to the material poling direction, while mode 31 is the mode when the pressure is applied perpendicular to the poling direction as shown in
Figure 1b [
10].
Hassan et al. [
11] compared different transduction technologies based on energy density—as energy converted per unit volume of the transducer—showing that piezoelectric transduction is the technology with the highest efficiency and the smallest size. Such facts make piezoelectric materials a favorable option during the process of designing energy harvesters where they have been used in several applications of energy harvesting. For example, research has been conducted on the use of piezoelectric transducers to harvest the energy of flow-induced vibrations. These vibrations are induced by putting a cylinder—a non–piezoelectric one—across the flow of a fluid. Being interrupted by the cylinder, the flow moves around the cylinder, inducing a wake region from which a vortex train is shed [
12]. Gao at al. [
13] developed a harvester of flow energy based on a piezoelectric cantilever with a cylindrical extension. The harvester managed to continuously operate an electronic thermometer chip MCP9700 using an airflow of velocity of 5.2 m/s. In addition to harvesting flow energy, piezoelectric materials have been used to harvest acoustic energy. Examples of piezoelectric energy harvesters shall be presented later in
Section 4.2.
To assess the quality by which an energy harvester can harvest vibration energy, it is necessary to define a qualitative measure that would describe such a process. Mostly, researchers tend to use efficiency , which is the ratio of the harvested electric energy to the supplied mechanical vibration energy. This number stands as the resultant final efficiency of the overall harvester taking into account all the factors governing its performance such as the electromechanical coupling factor of the material, the geometry of the transducer, the inhibited mechanical damping in the system, and the electrical damping characteristics of the load as well as of the whole circuit. Despite how simple the definition of efficiency is, it is quite challenging to agree on a strict way to evaluate efficiency because of the practical constraints on measuring the input energy. Therefore, large discrepancies can be found in the value of efficiency reported in the literature, where it can be estimated to be as high as 80% by some researchers, while others claim that it can never be more than 50%.
Yang et al. [
14] presented an overview of work conducted studying the efficiency by which piezoelectric energy harvesters convert energy. They reported that PZT (lead zirconate titanate)-based energy harvesters harvesting vibrational energy had the highest theoretical efficiency in the range of 50–90%. Richards et al. [
15] derived a formula to calculate the efficiency in the case of a system operating at the resonance frequency with impedance matched to the load’s. They considered systems of low damping and high mechanical coupling. Their theoretical study predicted that efficiency may be higher than 90%. However, high values of coupling are rarely achieved experimentally to justify this result. Shu et al. [
16] also devised a formula for the calculation of efficiency that was based on the material coupling coefficient, mechanical damping, and normalized values of each of the harvested sound frequency as well as the electric resistance. A maximum efficiency of 46% was reported for harvesters of weak coupling, while a maximum efficiency of more than 80% was reported for harvesters of strong coupling.
Liao et al. [
17] have proposed a different way to assess the performance of piezoelectric energy harvesters, where they derive a new efficiency that is analogous to the material loss factor. This efficiency is calculated as the ratio between the strain energy over each cycle and the power output. They validated this new quantity by numerical simulations, and it was estimated that harvesters would have a maximum efficiency of 2.5% around the resonance frequency.
Yuan et al. [
18] also compared various designs of acoustic energy harvesters reported in the literature. They did not base their comparison on the efficiency of energy conversion of these harvesters; however, they derived their own parameter and called it “Metric”. Their parameter is set to give a higher score for a smaller harvester that is able to harvest more power at a lower input sound power. Therefore, they devised their Metric according to Equation (1), where it is set to be the ratio between the harvested power and the product of the harvester volume and the square of the involved sound pressure, where
and
are the harvested power in
, the harvester volume in
, and the involved sound pressure in Pascals, respectively. Their motivation behind using a squared value of sound pressure is that sound intensity is proportional to the square of sound pressure as shown in Equation (2) which relates sound intensity
to the sound pressure
via the acoustic impedance
.
Using their parameter (i.e., Metric), the authors rated seventeen different designs of acoustic energy harvesters from the literature. The harvesters’ operating conditions—sound frequency and pressure—spanned over a wide range. The list included harvesters operating at a sound frequency in the range of 146–13,570 Hz, with most of the list targeting frequencies under 1 kHz. On the other hand, the operating sound pressure ranged over 1–563.7 Pa which corresponds to an SPL (sound pressure level) of 94–149 dB. Sixteen designs out of the presented seventeen achieved a value of Metric in the range of , while one last design achieved 14.536.
The goal of this work was to study the potential of cylindrical piezoelectric transducers for the application of high-frequency acoustic energy harvesting. Piezoelectric transducers have already been used in many shapes such as circular disks, plates, annular disks, and bending elements. Considering planar harvesters, such as plate-based and ring-based designs, the harvester’s dimension that is in the direction of acoustic wave propagation is the transducer thickness. Since this thickness is much smaller than the wavelength of the acoustic wave, the waves apply almost equal pressure on the two sides of the transducer which may reduce the transducer output [
19]. However, a cylindrical geometry might have its advantages over planar geometries due to the bigger dimension—diameter as opposed to thickness in planar geometries— in the direction of the acoustic wave propagation. Moreover, this work targets noise in the high-frequency range up to 20 kHz. According to a study presented by Fletcher at al. [
20], it was found that noises with a sound pressure level of 100 dB and a frequency near 20 kHz often exist in public places. Interestingly, a hand drier can produce a noise with an SPL of 84 dB at 40 kHz.
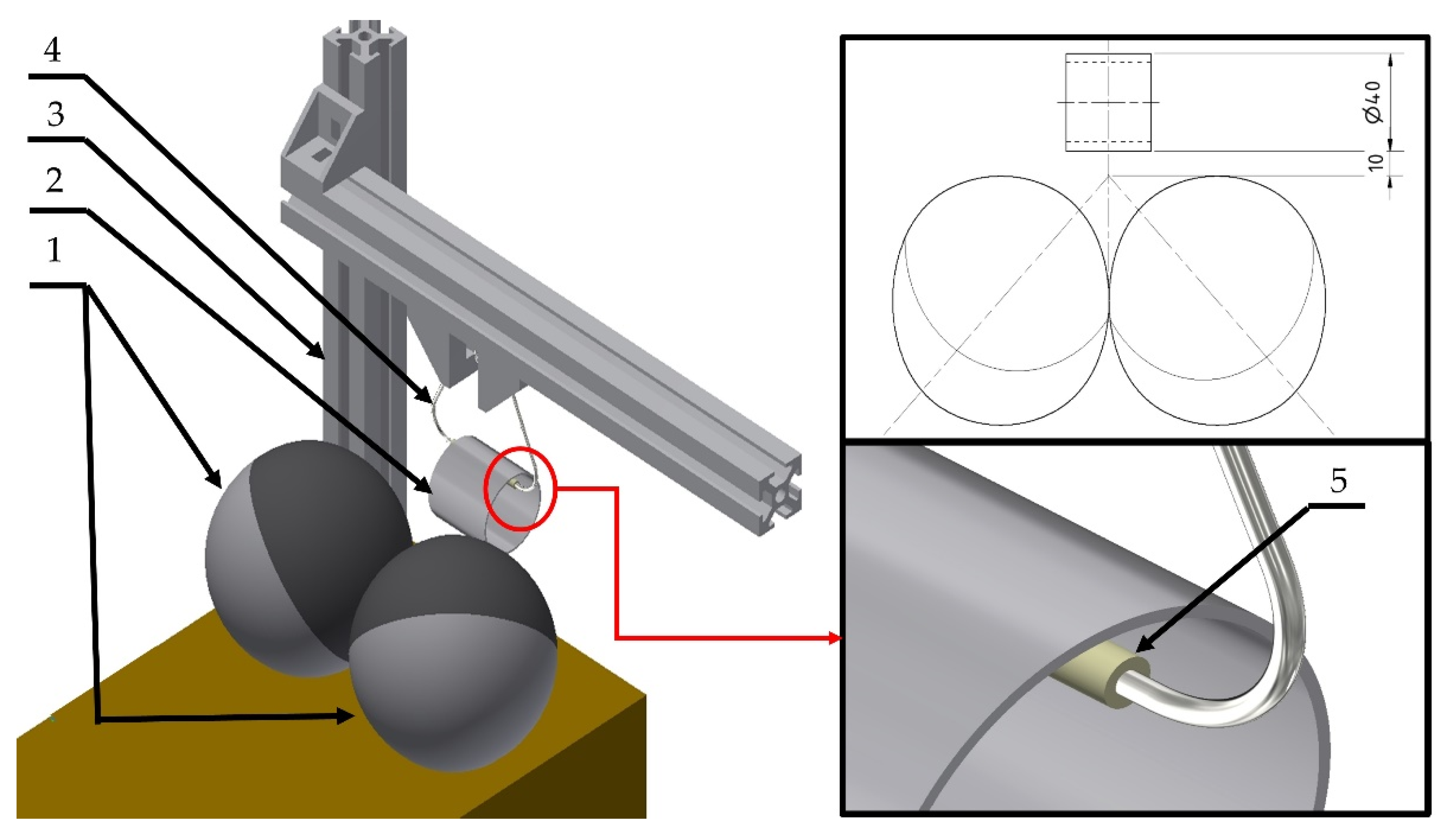
The cylinder under study was made of PZT which is a suitable material for the application of energy harvesting thanks to its high piezoelectric constant [
21]. The electrical impedance of the cylinder was already studied over a wide frequency spectrum in [
22], and it was found that the cylinder impedance tended to drop as the frequency increased, and this drop happened almost exponentially in the acoustic spectrum. Moreover, it was found that the cylinder has a capacitive nature. The work in this paper can be divided into two parts. The first part studied the effect of sound frequency and, hence, the sound wavelength on the energy harvesting process. Then, the second part demonstrates the operation of the cylinder in a complete energy harvester, harvesting sound waves with a frequency of 20 kHz.
3. Results
3.1. Case (0)
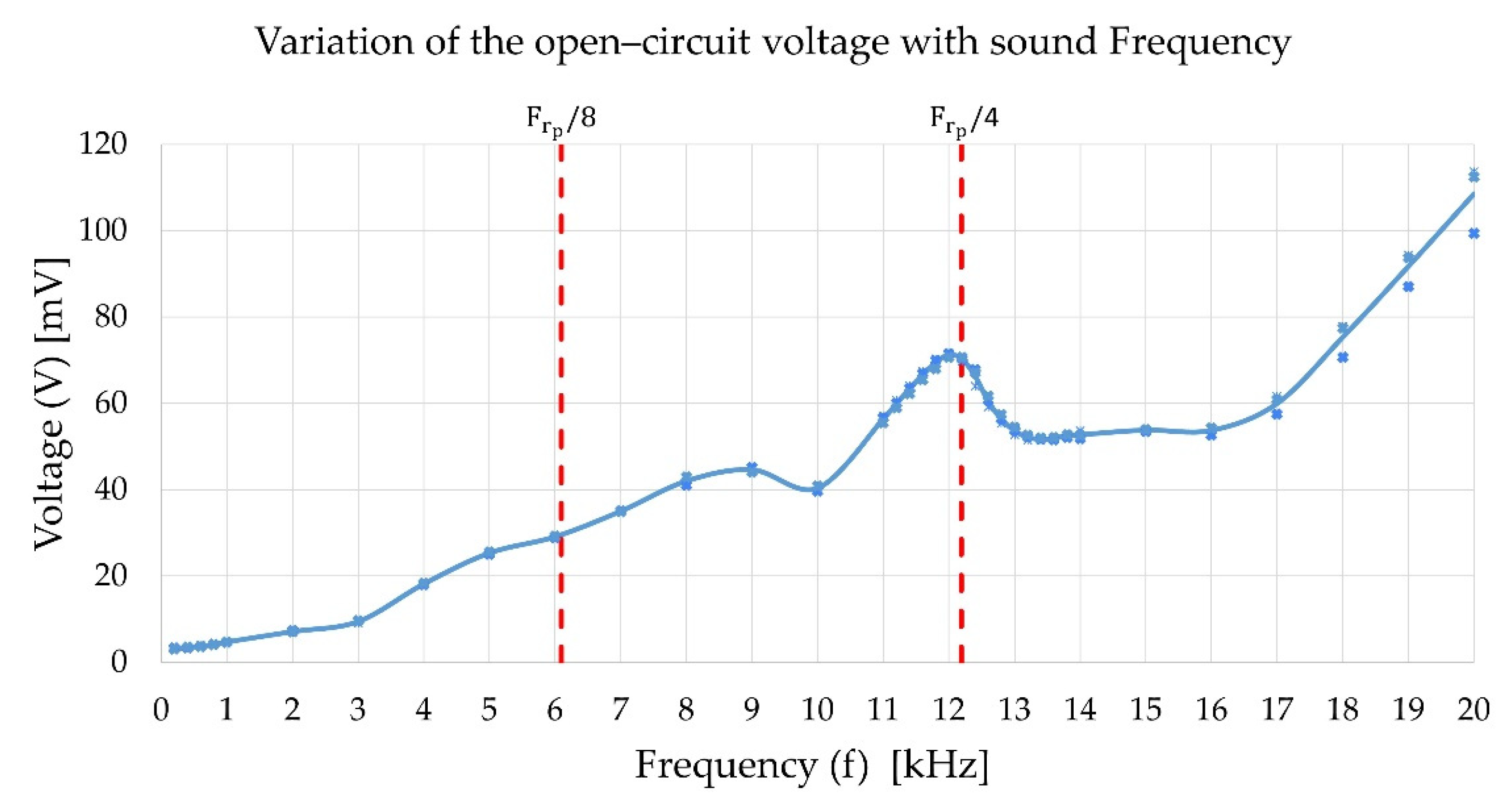
Figure 7 shows the raw data of the measured voltage across the harvester. It can be noticed that the voltage tended to generally increase with the increase in the sound frequency, achieving a maximum voltage of 110 mV at the ceiling of the acoustic spectrum. However, it can be noticed that a peak voltage formed at a frequency of 12.2 kHz despite the absence of a similar peak in the cylinder impedance at such a value of frequency.
To investigate this peak, it was necessary to recall the data of the resonance frequencies presented in
Table 3, where it can be noticed that this peak frequency represents 0.25025 of the radial resonance frequency
where that the radial resonance frequency itself lies outside of the acoustic range.
A possible explanation of this peak was that the sound waves applied from the speakers with a frequency 12.2 kHz would form other overtones with harmonic number, n, equals 2–4. Such overtones would be sufficient to create vibrations in the cylinder with its resonance frequency,
. Moreover, a similar behavior could be expected at the sound frequency
/8, where the eighth overtones of such waves could be able to achieve vibrations with the natural frequency. To furtherly investigate this observation, dashed red lines are plotted in
Figure 7 at each of the frequencies representing
/4 and
/8. However, no peak in the voltage was found at the frequency
/8.
In addition to the peak at /4, the voltage tended to increase, starting from the frequency 16 kHz up to the end of the acoustic range. Considering the frequency value /2 situated at 24.375 kHz—outside of the acoustic range, this increase in voltage could be attributed to the left side of a peak that was centered at a frequency of 24.375 kHz. Unfortunately, it was not possible to expand this measurement outside of the acoustic range to verify this hypothesis, since the used speakers were rated up to 20 kHz only. Moreover, it would not have been possible to measure the power of the ultrasonic waves to carry out Phase (2).
To investigate the potential relationship between the cylinder size and the frequency of the harvested sound waves, the data presented above were replotted in
Figure 8 using a dimensionless frequency,
. This dimensionless number was defined to be the ratio between the cylinder diameter and the sound wavelength as shown in Equation (10), where
is the outer diameter of the cylinder, f is the sound frequency, and U is the sound speed in air taken to be 343 m/s.
By representing the data using the new dimensionless parameter, it was possible to divide
Figure 8 into two parts separated by a green separation line at
= 1. The part on the left of the separation line represents the case when the cylinder diameter was less than the sound wavelength, and the part on the right of the separation line represents the case when the cylinder diameter was greater than the sound wavelength.
It can be noticed that the voltage tended to increase in the left part with increasing frequency up until the separation line exactly. On the other hand, the trend in the right part was different. By examining the right part, one would find that it was composed of four main sections: a, b, c, and d. Section (a) extended over the range of = 1–1.16, where the voltage tended to drop with increasing frequency. Then, Section (b)—the aforementioned peak—extended over the range = 1.17–1.52. Then, Section (c) extended over = 1.52–1.87, where the voltage was almost constant. Then, Section (d), where the voltage tended to increase with increasing frequency, forming what was thought to be a peak centered at /2 outside of the acoustic range.
The difference in the trends of the two halves may be attributed to the relation between the sound wavelength and the cylinder size. In the left half, where the sound wavelength was larger than the cylinder diameter, the sound waves tended to diffract off the cylinder without transporting its energy into the cylinder. In other words, the cylinder was not able to well capture the mechanical energy of sound waves of large wavelength and small frequency. As the frequency increased and the wavelength decreased, the sound waves gradually lost their ability to diffract off the cylinder and more energy was transferred from the acoustic waves to the cylinder. This may justify the direct proportionality between the generated voltage and sound frequency in the left half.
When the sound wavelengths reached a critical value that was equal to the cylinder diameter, acoustic waves were no longer able to diffract and were rather either absorbed or reflected off the cylinder. In such a case, energy transfer between the waves and the cylinder depended only on the difference between the acoustic impedance of the two media—the cylinder and the air. Therefore, it would be expected that the right half of the scale would have a constant voltage level which agreed with the obtained data, ignoring Sections (b) and (d), since they are altered by the resonance of the cylinder. However, the drop in voltage in Section (a) remains unjustified.
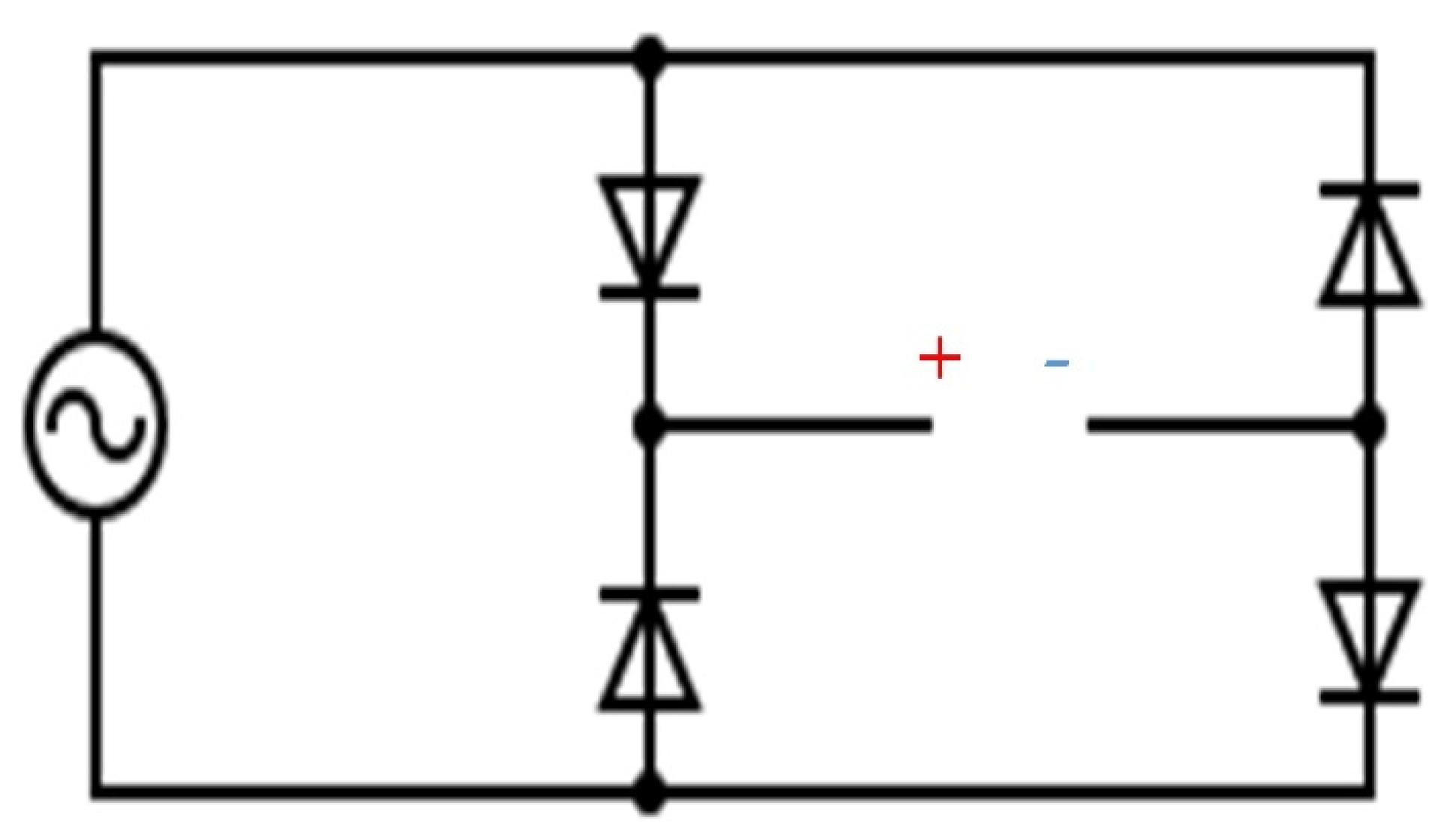
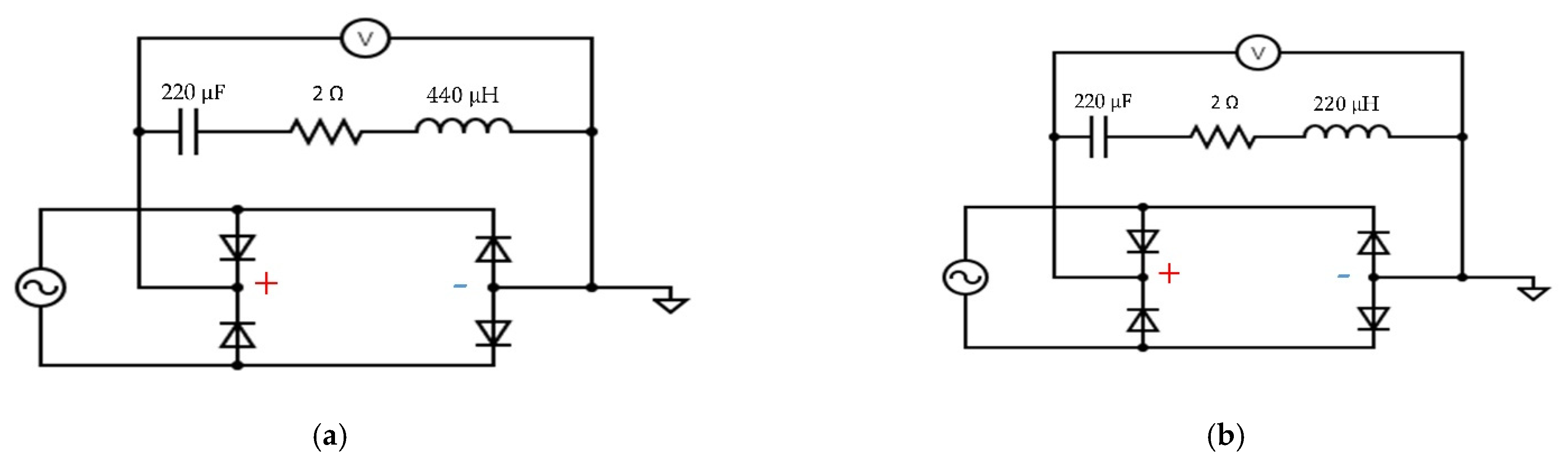
3.2. Case (1)
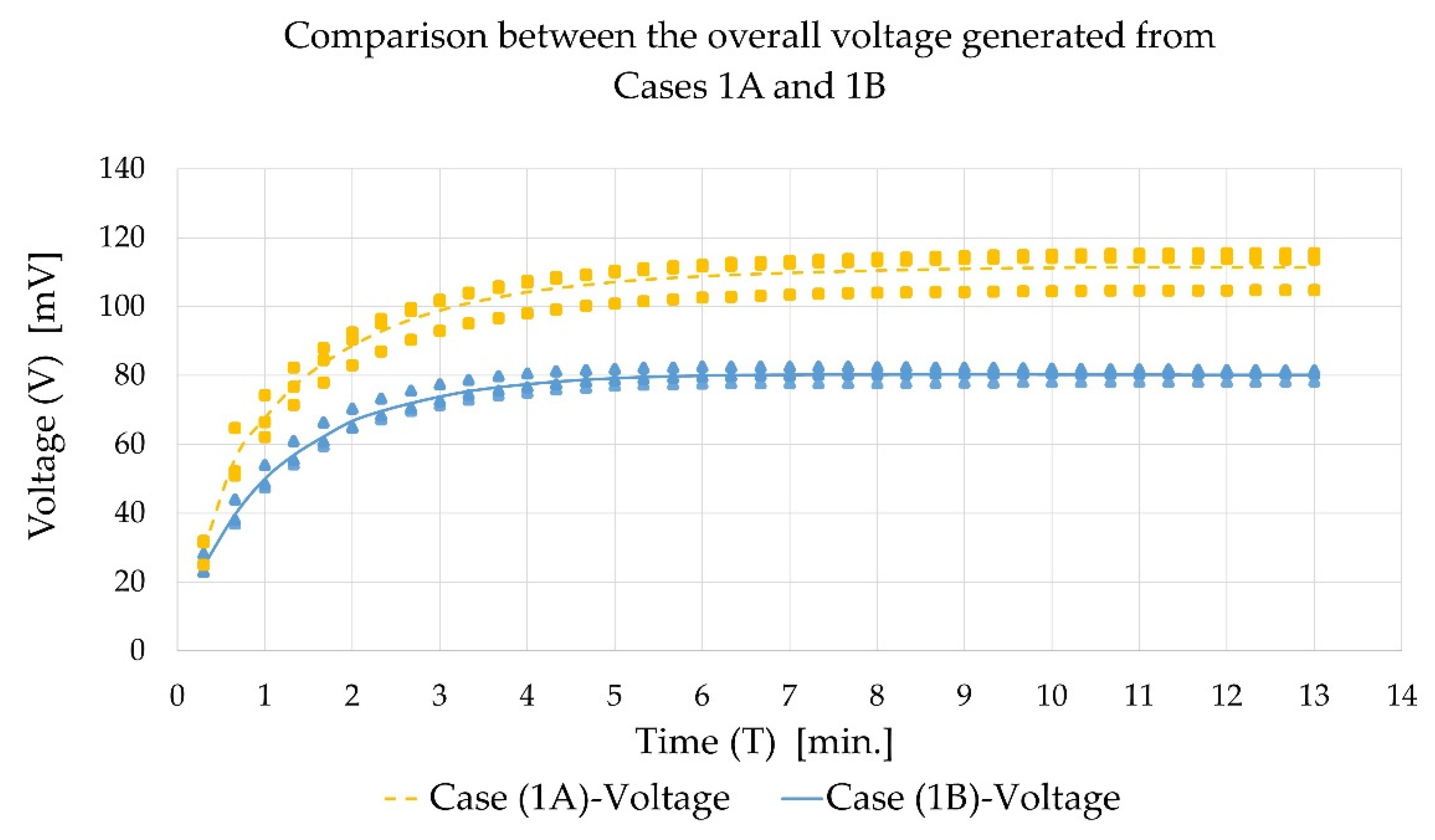
Figure 9 shows the voltage generated over time in both Cases (1A) and (1B). From
Figure 9, it can be noticed that it took 13 min to reach the steady-state voltage across the load. Moreover, it was noticed that Case (1A) achieved a high steady-state value of 115.6 mV. Unfortunately, it was not possible to measure the flowing electric current. Therefore, the electric power, P, dissipated in the load was determined using Equation (11).
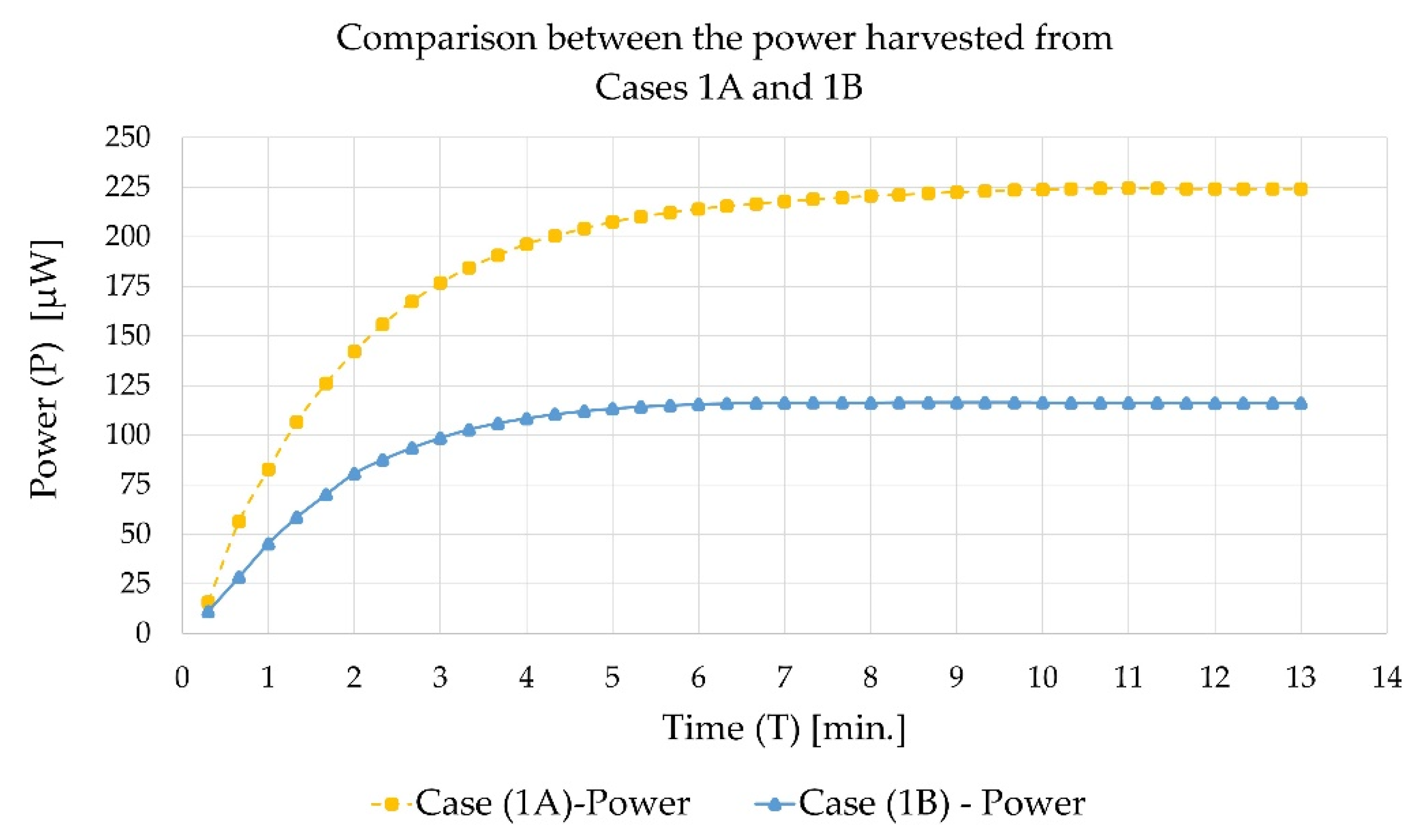
Figure 10 shows the power generated in the two cases, where 224
of power was harvested by the circuit of Case (1A), while only 116
of power was harvested by the circuit of Case (1B).
3.3. Case (2)
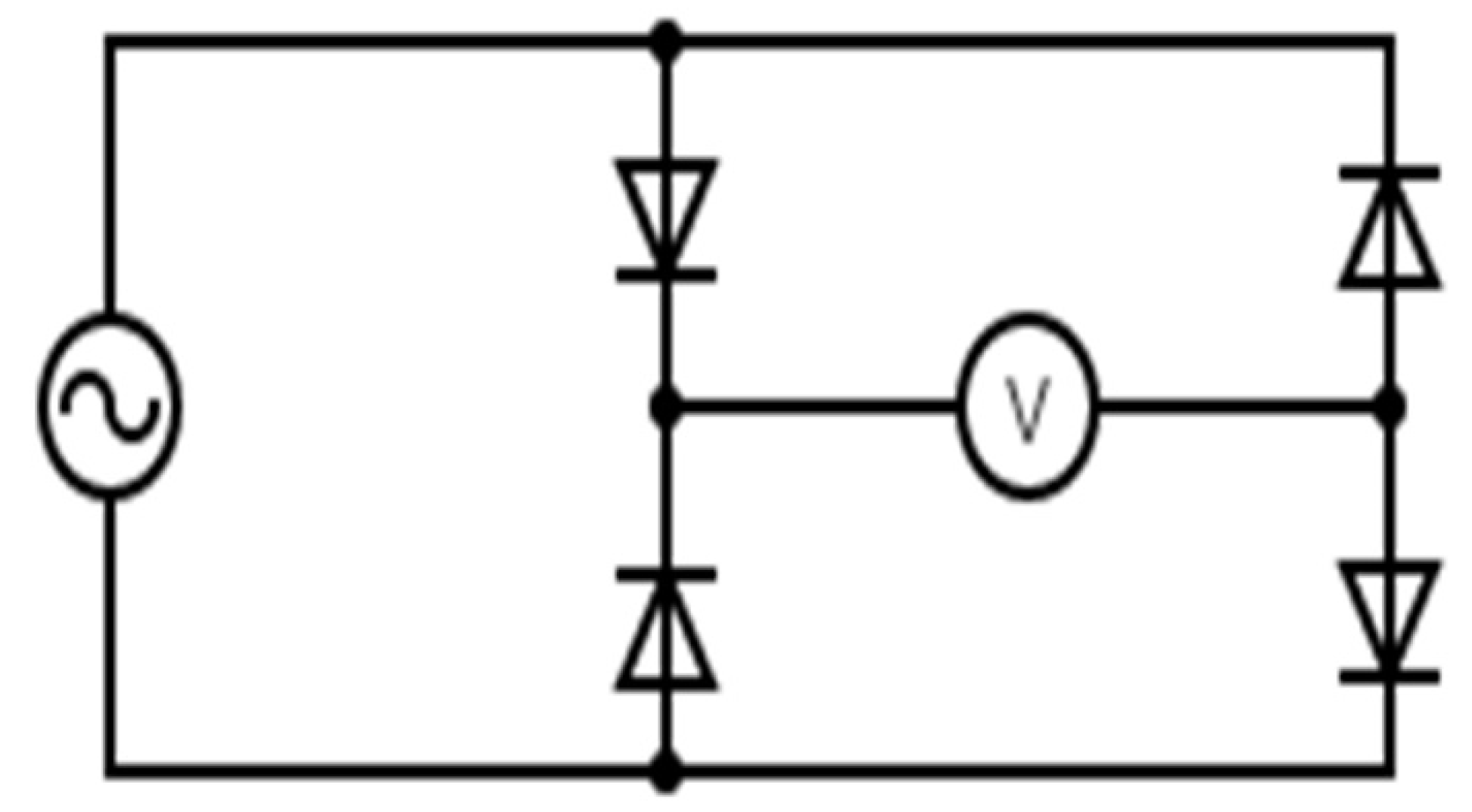
3.3.1. Results of Measuring the Electric Power
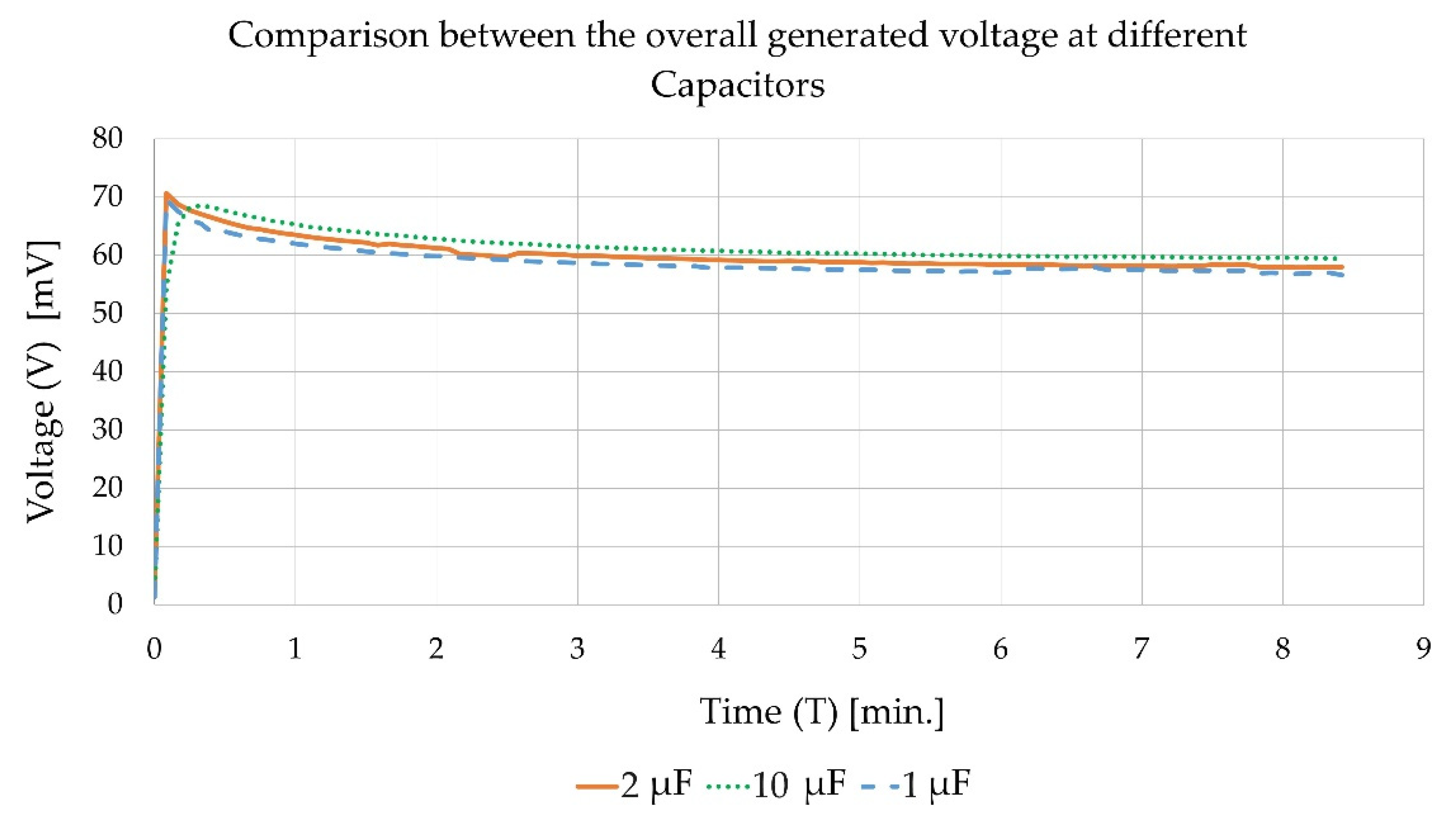
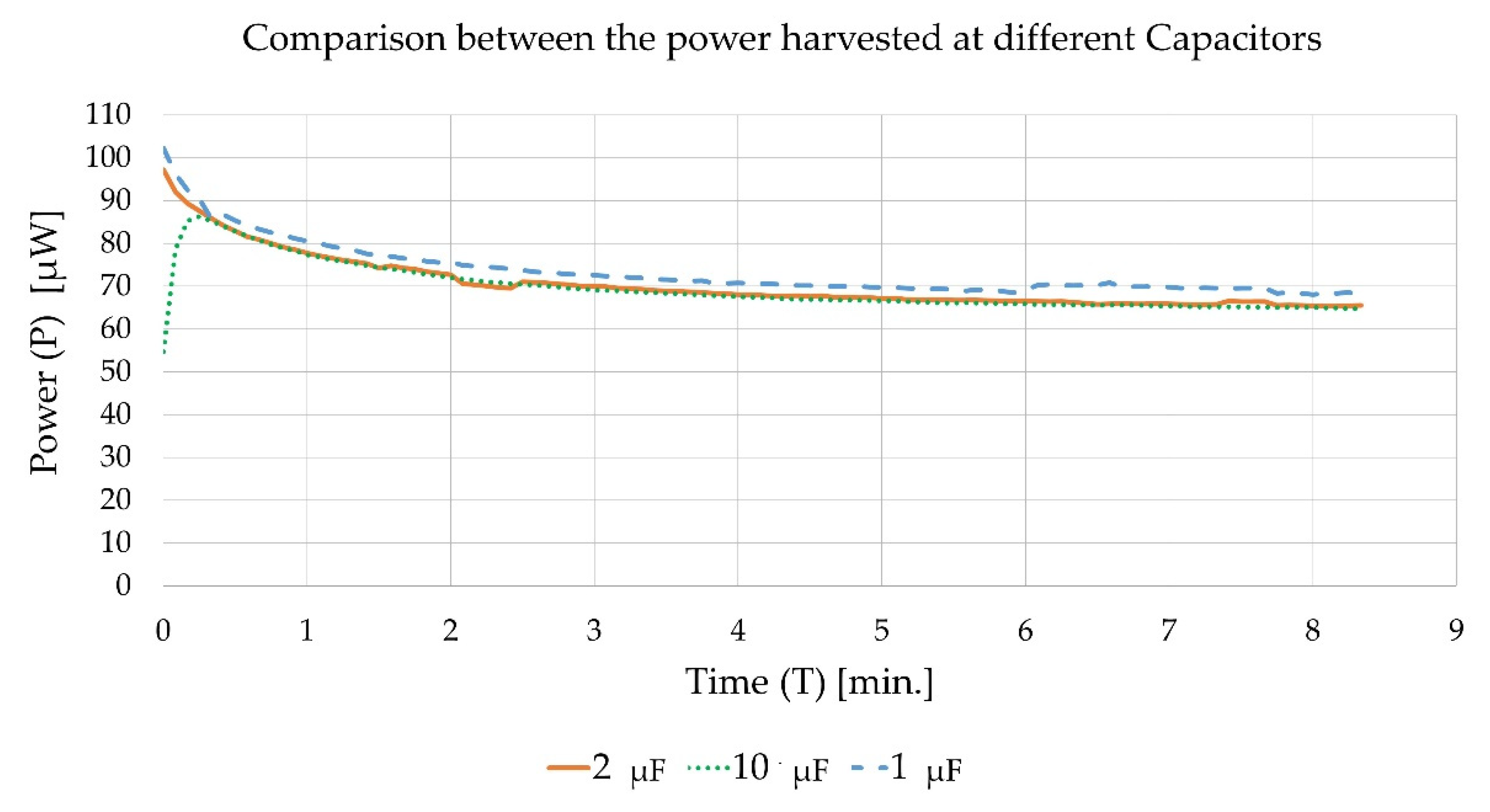
Figure 11 shows the developed voltage across the load circuit over time in the case of using different capacitors, while
Figure 12 shows the dissipated power in the load for each case. It was found that the load circuit with the 10
capacitor achieved the highest steady-state voltage. However, the circuit with the 1
capacitor dissipated the most power. This agrees with the data shown in
Table 5, where it was expected that the circuit with the 1
capacitor would dissipate the most power since it had the best impedance match among the three circuits.
3.3.2. Results of Measuring the Acoustic Power
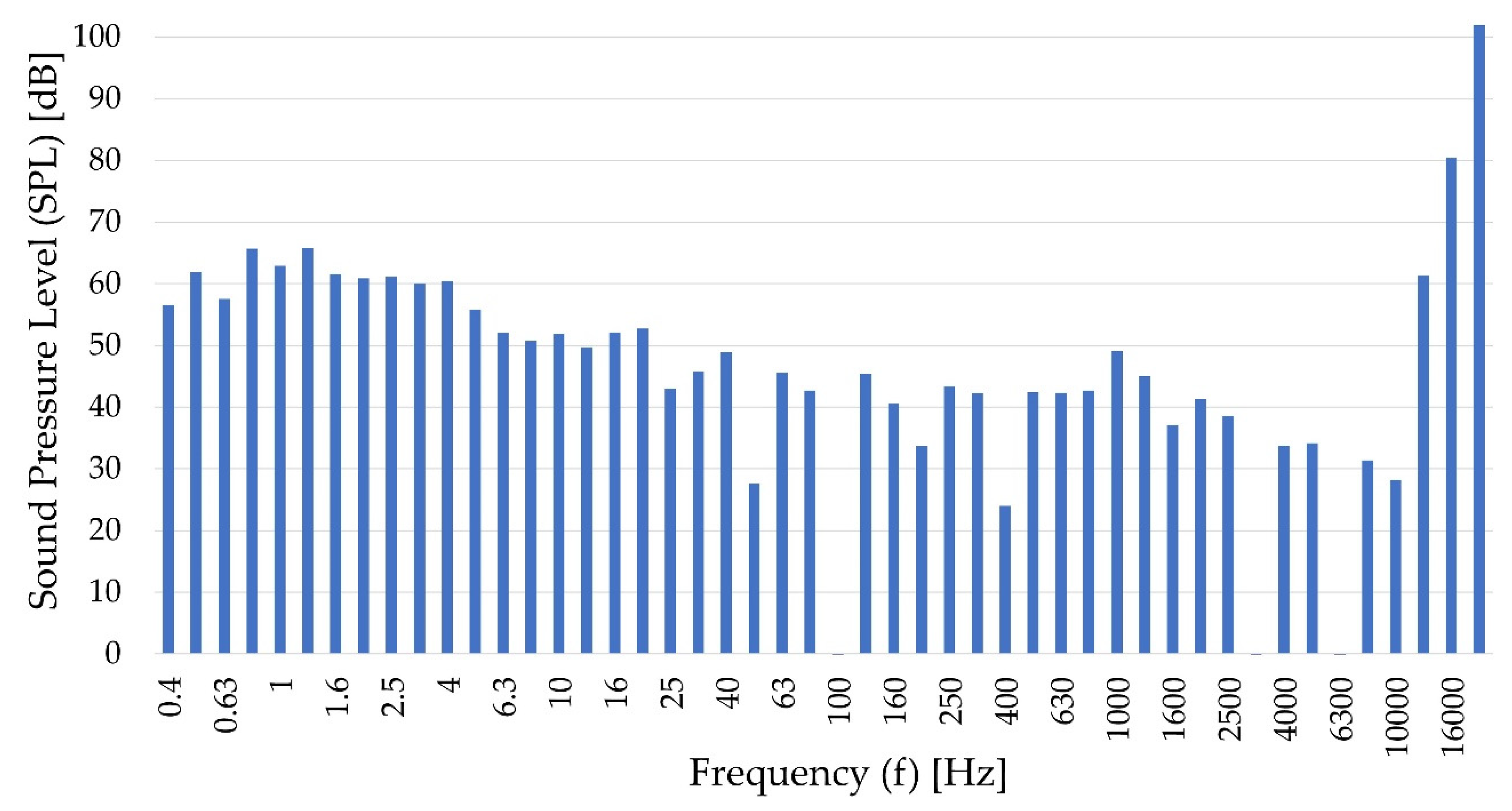
The mentioned measurement was conducted at several points at different distances from the speakers. For reference, the FFT (fast Fourier transform) of the sound pressure level measured at a distance of three centimeters is shown in
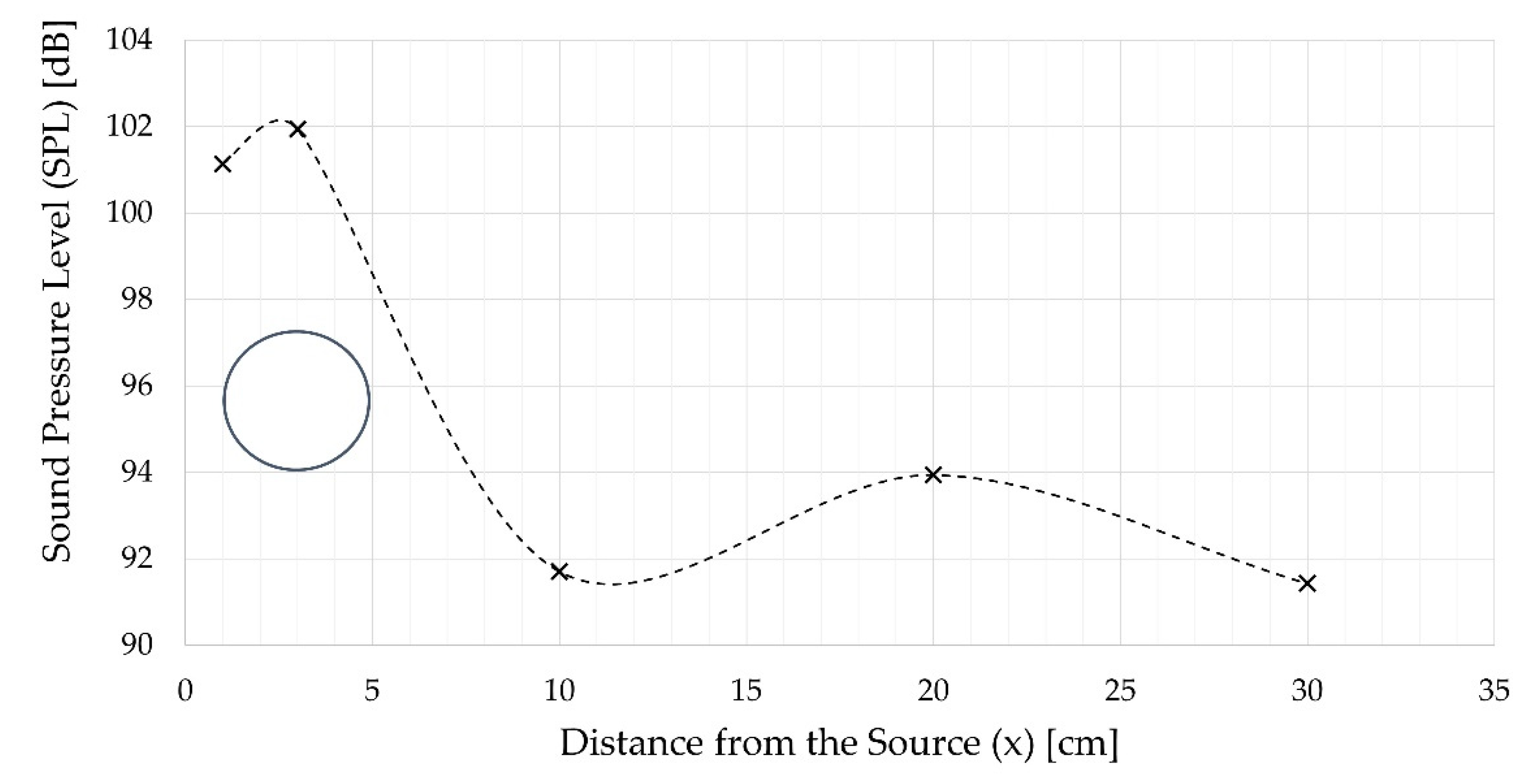
Figure 13, while
Figure 14 plots the variation in the 20 kHz component with the distance from the source compared to the diameter of the cylinder. From
Figure 14, it can be noticed that there were points of local maxima and local minima which is a property of the near–field sound. The highest pressure level,
, was achieved at a distance of three centimeters with a value of 102 dB. Using Equations (8) and (9) together with the
value at a distance of three centimeters, it would be possible to calculate the total acoustic power collected by the cylinder to be 78.5
.
3.3.3. Estimation of the Energy Conversion Efficiency
To evaluate the performance of the considered energy harvester, it was possible to use Equations (12) and (13) to calculate the harvesting efficiency,
, and energy harvesting density, p, respectively. The results obtained from the data of the three capacitor cases are summarized in
Table 6, where it was found that the optimized harvester with the capacitor of 1
achieved a harvesting efficiency of 86.1% with an energy-harvesting density of 1.3455
per unit squared centimeter of the cylinder’s surface area.
3.3.4. Estimation of the Effect of the Electric Circuit
To evaluate the voltage drop imposed by the electric circuit, Equation (14) was devised to calculate the voltage rectification efficiency,
, where
is the steady-state voltage across the load, and
is the voltage drop across the bridge. As was mentioned previously in
Section 2.3.2, the full-wave rectifier bridge imposed a total voltage drop,
, of 432 mV. Therefore, it would be possible to calculate
for the different load circuits as summarized in
Table 6. It is worth mentioning that the voltage rectification efficiency depended mainly on the forward voltage drop of the used diodes and the steady-state voltage generated by the cylinder. The steady-state voltage itself was related to—via the voltage constant of the piezoelectric material—the mechanical pressure applied on the harvester. In applications of acoustic energy harvesting, the magnitude of the pressure of the involved vibrations is relatively small. Therefore, the generated steady-state voltage will also be small, lowering the value of the voltage rectification efficiency.