Obtaining Robust Performance of a Current fed Voltage Source Inverter for Virtual Inertia Response in a Low Short Circuit Ratio Condition
Abstract
:1. Introduction
2. Modeling and Validation
2.1. Validation of Detailed Switching Model
2.2. Small Signal Model of the CFVSI

3. Transfer Functions Verification
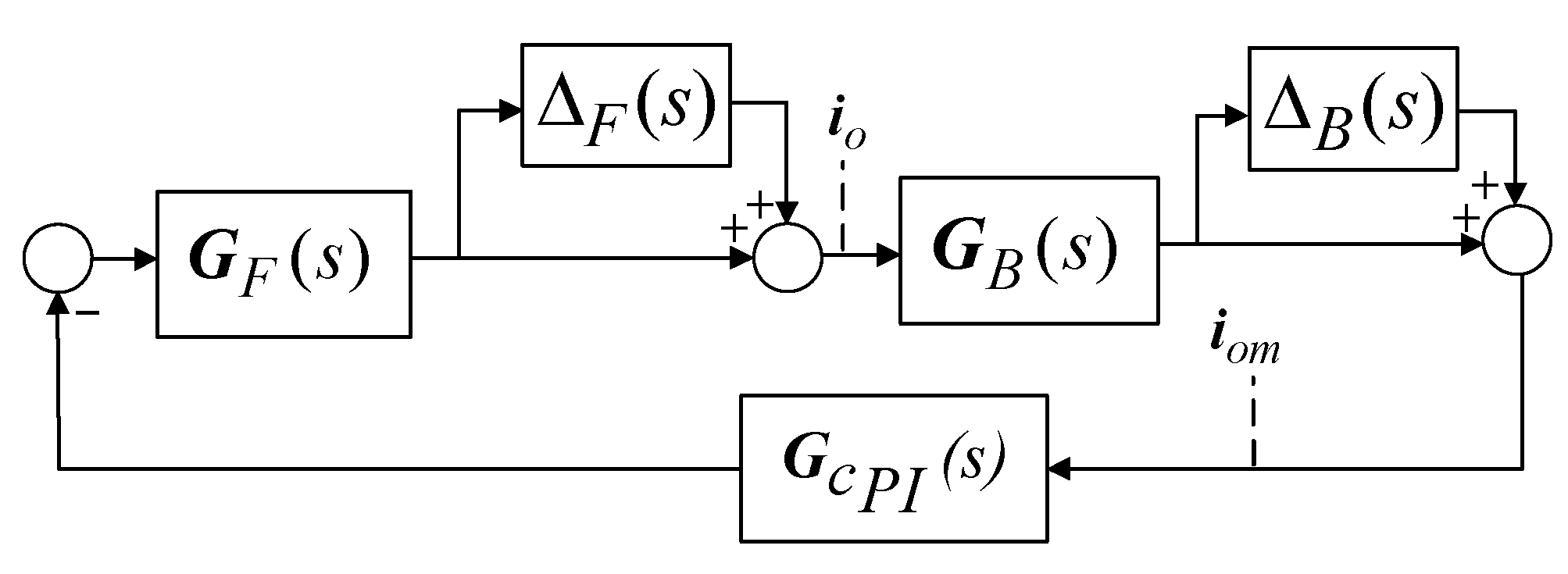
4. Generalized Representation and Controller Design
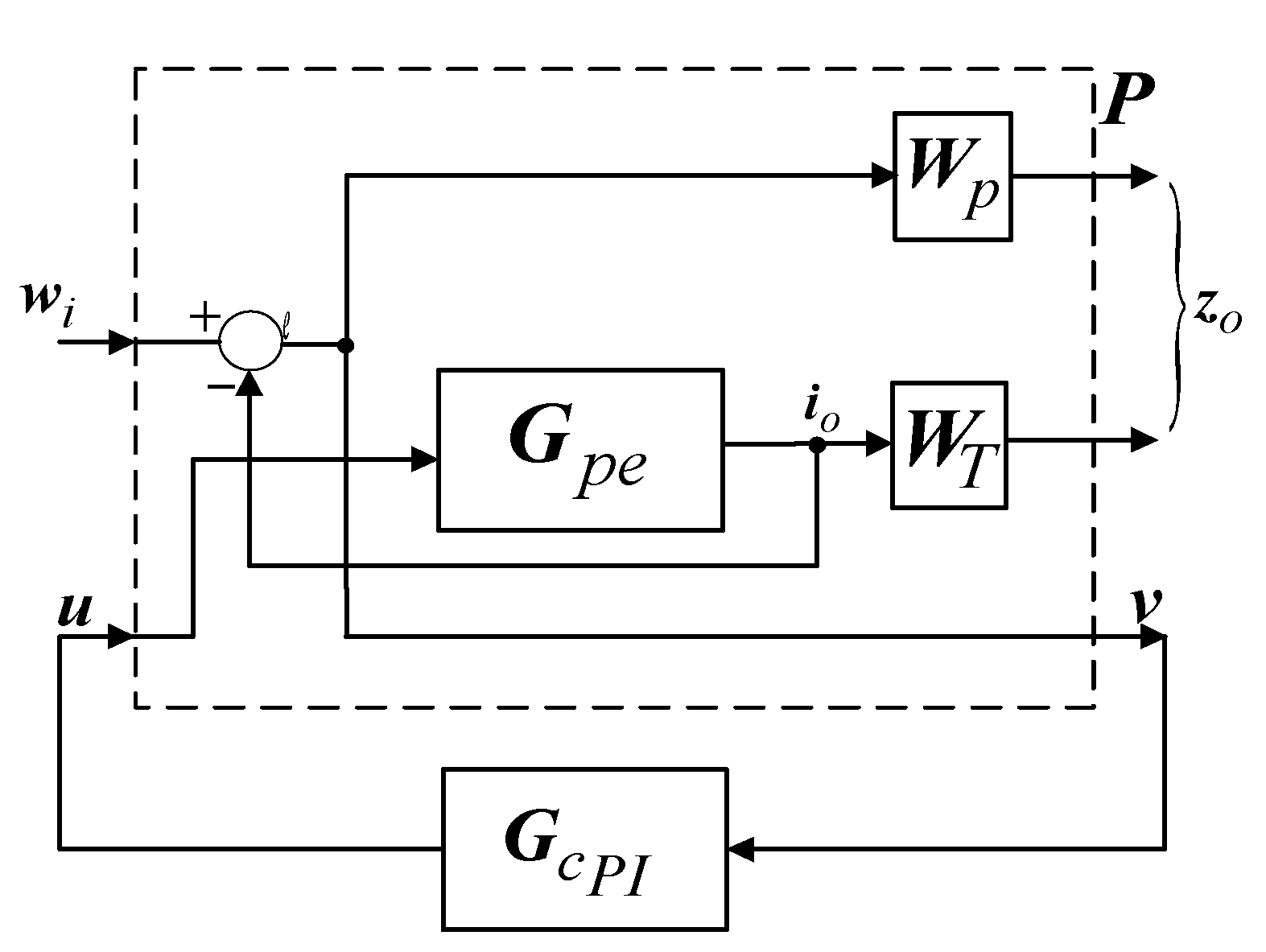
4.1. Generalized Representation
4.2. Weighting Functions
5. Results
5.1. Synthesized Robust Controller
5.2. Sensitivity Analysis
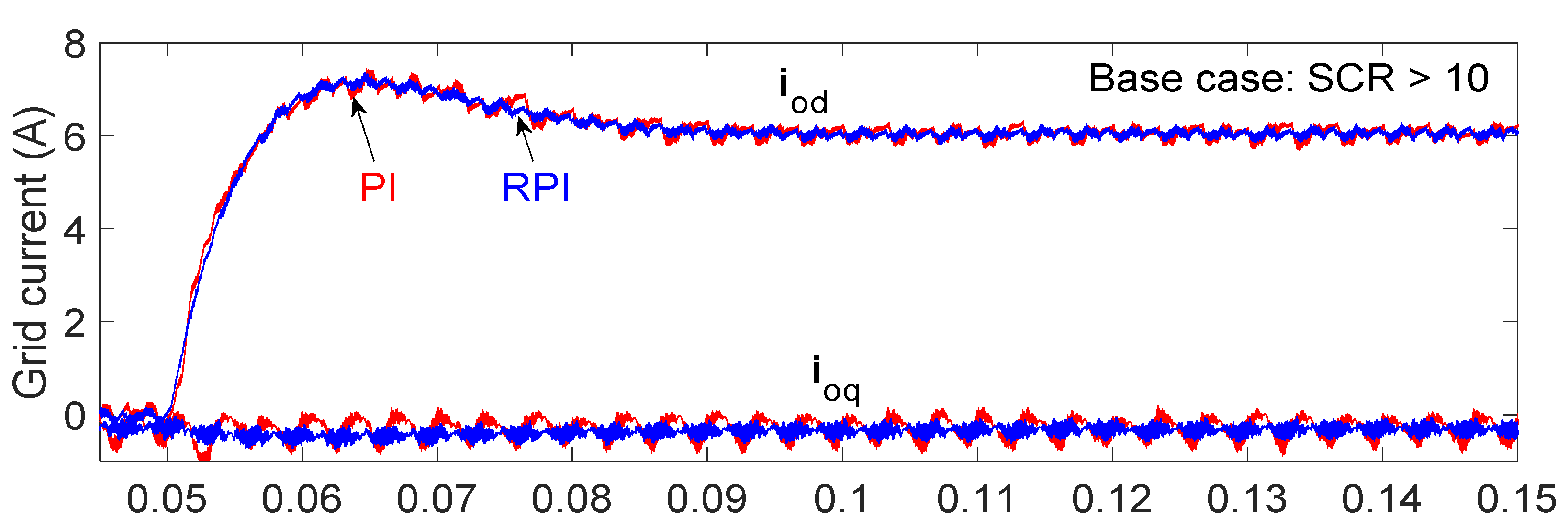
5.3. Time Domain Simulations
6. Conclusions
- While the regular loop-shaping method for tuning the inner-loop PI current controller is appropriate when the inverter-grid connection is strong (SCR > 10), it is inadequate in weak conditions (SCR < 3), even when the PLL-grid coupling dynamics are included in the loop transfer function.
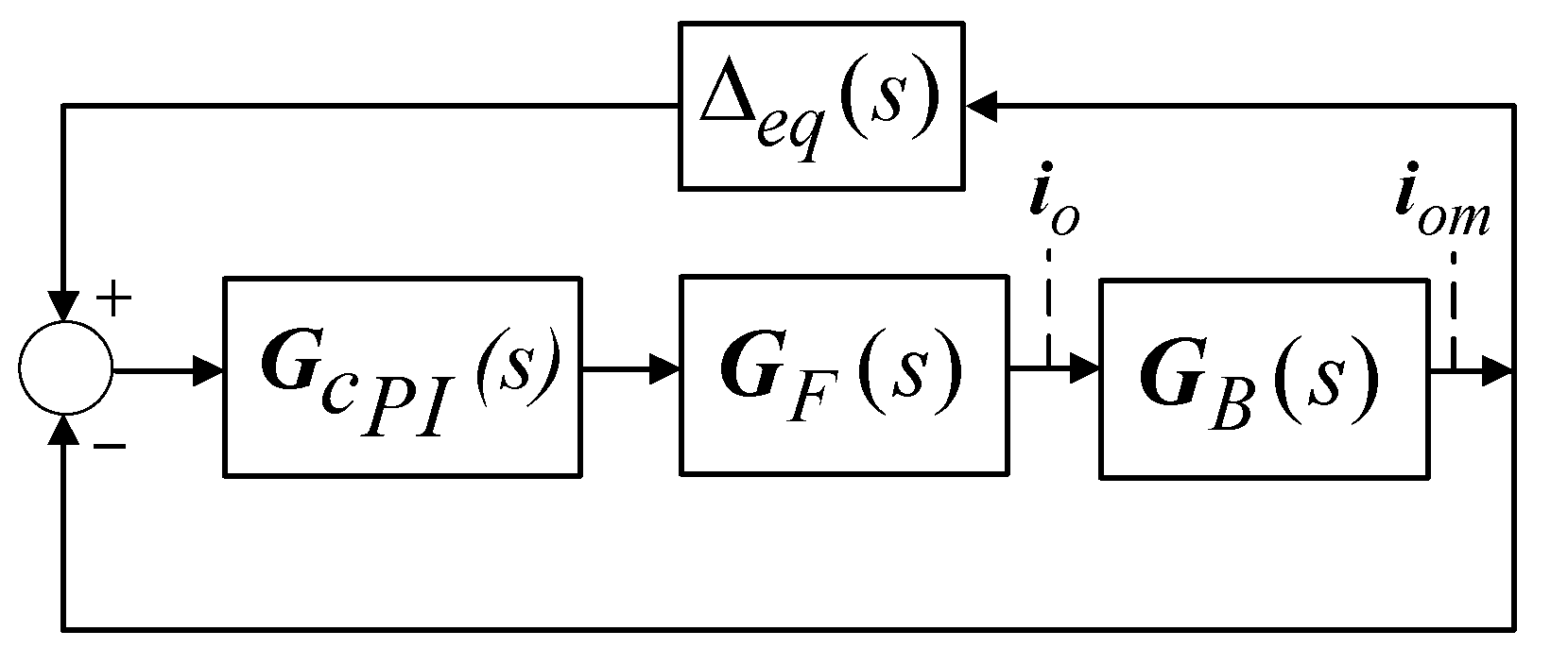
- The proposed alternative solution, whereby the PLL-grid coupling was formulated as a single perturbation on the dynamics of the inverter system, allowed for easy translation of the problem into the H∞ robust control framework. Adequate inverter dynamics in the presence of a strong PLL-grid impedance coupling can then be achieved by tuning the controller to minimize the H∞ norm.
- The structured H∞ method [30] can be applied to tune the inner-loop PI controller against the PLL-grid impedance coupling, thereby avoiding an H∞ controller with higher order dynamics.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| System matrix A: | Input matrix B: |
| Output matrix C: | Feedforward matrix D = 0. |
| Input vector U: | Output vector Y: |
References
- Wright, P.S.; Davis, P.N.; Johnstone, K.; Rietveld, G.; Roscoe, A.J. Field Measurement of Frequency and ROCOF in the Presence of Phase Steps. IEEE Trans. Instrum. Meas. 2019, 68, 1688–1695. [Google Scholar] [CrossRef]
- Sun, Y.; De Jong, E.C.W.; Wang, X.; Yang, D.; Blaabjerg, F.; Cuk, V.; Cobben, J.F.G. The Impact of PLL Dynamics on the Low Inertia Power Grid: A Case Study of Bonaire Island Power System. Energies 2019, 12, 1259. [Google Scholar] [CrossRef] [Green Version]
- REE, Terna, TransnetBW, 50Hz, Transmission, Swissgrid, Energienet.dk. Frequency Stability Evaluation Criteria for the Synchronous Zone of Continental Europe; ENTSO-E: Brussels, Belgium, 2016. [Google Scholar]
- DNV KEMA Energy & Sustainability. RoCoF An Independent Analysis on the Ability of Generators to Ride through Rate of Change of Frequency Values Up to 2 Hz/s; DNV KEMA Ltd: London, UK, 2013. [Google Scholar]
- Yan, R.; Masood, N.-A.; Saha, T.K.; Bai, F.; Gu, H. The Anatomy of the 2016 South Australia Blackout: A Catastrophic Event in a High Renewable Network. IEEE Trans. Power Syst. 2018, 33, 5374–5388. [Google Scholar] [CrossRef]
- ElectraNet. ESCRI-SA Battery Energy Storage—Final Knowledge Sharing Report; ElectraNet: Adelaide, Australia, 2021. [Google Scholar]
- Hawaii Natural Energy Institute. Hawaii Natural Energy Institute Research Highlights Fast Frequency Response Battery on a Low-Inertia Grid. 2020. Available online: https://www.hnei.hawaii.edu/wp-content/uploads/Fast-Frequency-Response-Battery-on-a-Low-Inertia-Grid.pdf (accessed on 1 September 2021).
- Vandermeer, J.; Glassmire, J.; Bitaraf, H.; Pike, C.; Wilber, M.; Whitney, E. Multi-Stage Flywheel Battery Energy Storage System at Chugach Electric Utility: A Performance Assessment. 2020. Available online: https://acep.uaf.edu/media/298261/MultiStage-Energy-Storage-System-Chugach_Final.pdf (accessed on 1 September 2021).
- Goud, R.D.; Rayudu, R.; Mantha, V.; Moore, C.P. Impact of Short-circuit Ratio on Grid Integration of Wind Farms-A New Zealand Perspective. In Proceedings of the 2nd International Conference Large-Scale Grid Integration of Renewable Energy in India, New Delhi, India, 4–6 September 2019. [Google Scholar]
- Zhang, C.; Wang, X.; Blaabjerg, F. Analysis of phase-locked loop influence on the stability of single-phase grid-connected inverter. In Proceedings of the 2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 22–25 June 2015; pp. 1–8. [Google Scholar]
- Huang, Z. Revisiting Stability Criteria for DC Power Distribution Systems Based on Power Balance. CPSS Trans. Power Electron. Appl. 2017, 2, 76–85. [Google Scholar] [CrossRef]
- He, Y.; Wang, X.; Ruan, X.; Pan, D.; Xu, X.; Liu, F. Capacitor-Current Proportional-Integral Positive Feedback Active Damping for LCL-Type Grid-Connected Inverter to Achieve High Robustness Against Grid Impedance Variation. IEEE Trans. Power Electron. 2019, 34, 12423–12436. [Google Scholar] [CrossRef]
- JXu, J.; Qian, Q.; Xie, S. Adaptive control method for enhancing the stability of grid-connected inverters under very weak grid condition. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1141–1146. [Google Scholar]
- Jang, Y.; Erickson, R. Physical origins of input filter oscillations in current programmed converters. IEEE Trans. Power Electron. 1992, 7, 725–733. [Google Scholar] [CrossRef]
- Huang, X.; Wang, K.; Fan, B.; Yang, Q.; Li, G.-J.; Xie, D.; Crow, M.L. Robust Current Control of Grid-Tied Inverters for Renewable Energy Integration Under Non-Ideal Grid Conditions. IEEE Trans. Sustain. Energy 2020, 11, 477–488. [Google Scholar] [CrossRef]
- Wang, J.; Tyuryukanov, I.; Monti, A. Design of a novel robust current controller for grid-connected inverter against grid impedance variations. Int. J. Electr. Power Energy Syst. 2019, 110, 454–466. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, B.; Qian, Q.; Meng, X.; Xie, S. Robust control and design based on impedance-based stability criterion for improving stability and harmonics rejection of inverters in weak grid. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 3619–3624. [Google Scholar]
- Kaura, V.; Blasko, V. Operation of a phase locked loop system under distorted utility conditions. IEEE Trans. Ind. Appl. 1997, 33, 58–63. [Google Scholar] [CrossRef]
- Yang, S.; Lei, Q.; Peng, F.Z.; Qian, Z. A Robust Control Scheme for Grid-Connected Voltage-Source Inverters. IEEE Trans. Ind. Electron. 2010, 58, 202–212. [Google Scholar] [CrossRef]
- Gryning, M.P.S.; Wu, Q.; Blanke, M.; Niemann, H.H.; Andersen, K.P.H. Wind Turbine Inverter Robust Loop-Shaping Control Subject to Grid Interaction Effects. IEEE Trans. Sustain. Energy 2015, 7, 41–50. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, J.; Zeng, W.; Liu, H.; Chai, Y. H∞ Robust Control of an LCL-Type Grid-Connected Inverter with Large-Scale Grid Impedance Perturbation. Energies 2018, 11, 57. [Google Scholar] [CrossRef] [Green Version]
- Osório, C.R.D.; Borin, L.C.; Koch, G.G.; Montagner, V.F. Optimization of Robust PI Controllers for Grid-Tied Inverters. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; pp. 1–6. [Google Scholar]
- Zhou, S.; Zou, X.; Zhu, D.; Tong, L.; Zhao, Y.; Kang, Y.; Yuan, X. An Improved Design of Current Controller for LCL-Type Grid-Connected Converter to Reduce Negative Effect of PLL in Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 648–663. [Google Scholar] [CrossRef]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and Control of an LCL-Filter-Based Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Messo, T.; Aapro, A.; Suntio, T. Generalized multivariable small-signal model of three-phase grid-connected inverter in dq-domain. In Proceedings of the 2015 IEEE 16th Workshop on Control and Modeling for Power Electronics (COMPEL), Vancouver, BC, Canada, 12-15 July 2015; pp. 1–8. [Google Scholar]
- Wang, X.; Harnefors, L.; Blaabjerg, F. Unified Impedance Model of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2018, 33, 1775–1787. [Google Scholar] [CrossRef] [Green Version]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-Admittance Calculation and Shaping for Controlled Voltage-Source Converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- The MathWorks, Inc. Simulink ® Control Design TM Getting Started Guide R2021a; The Mathworks, Inc.: Natick, MA, USA, 2021. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design, 2nd ed.; Wiley: New York, NY, USA, 2007; Volume 2. [Google Scholar]
- Gahinet, P.; Apkarian, P. Decentralized and fixed-structure H∞ control in MATLAB. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 8205–8210. [Google Scholar]
- Balas, G.; Chiang, R.; Packard, A.; Safonov, M. Robust Control Toolbox TM Getting Started Guide R2020b, 6.9; The Mathworks, Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Peña-Alzola, R.; Blaabjerg, F. Design and Control of Voltage Source Converters With LCL -Filters. In Control of Power Electronic Converters and Systems; Academic Press: Cambridge, MA, USA, 2018; pp. 207–242. [Google Scholar]


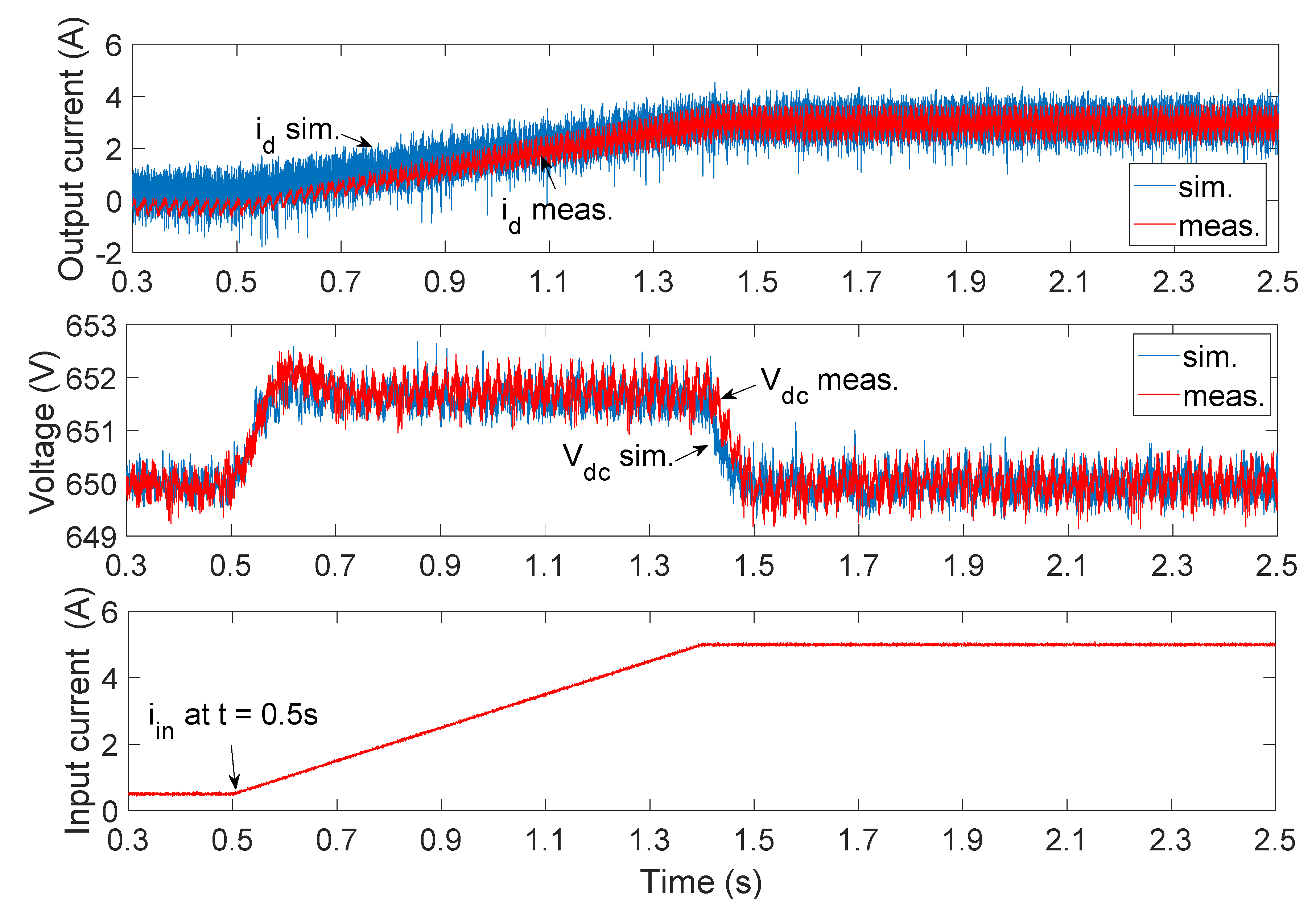
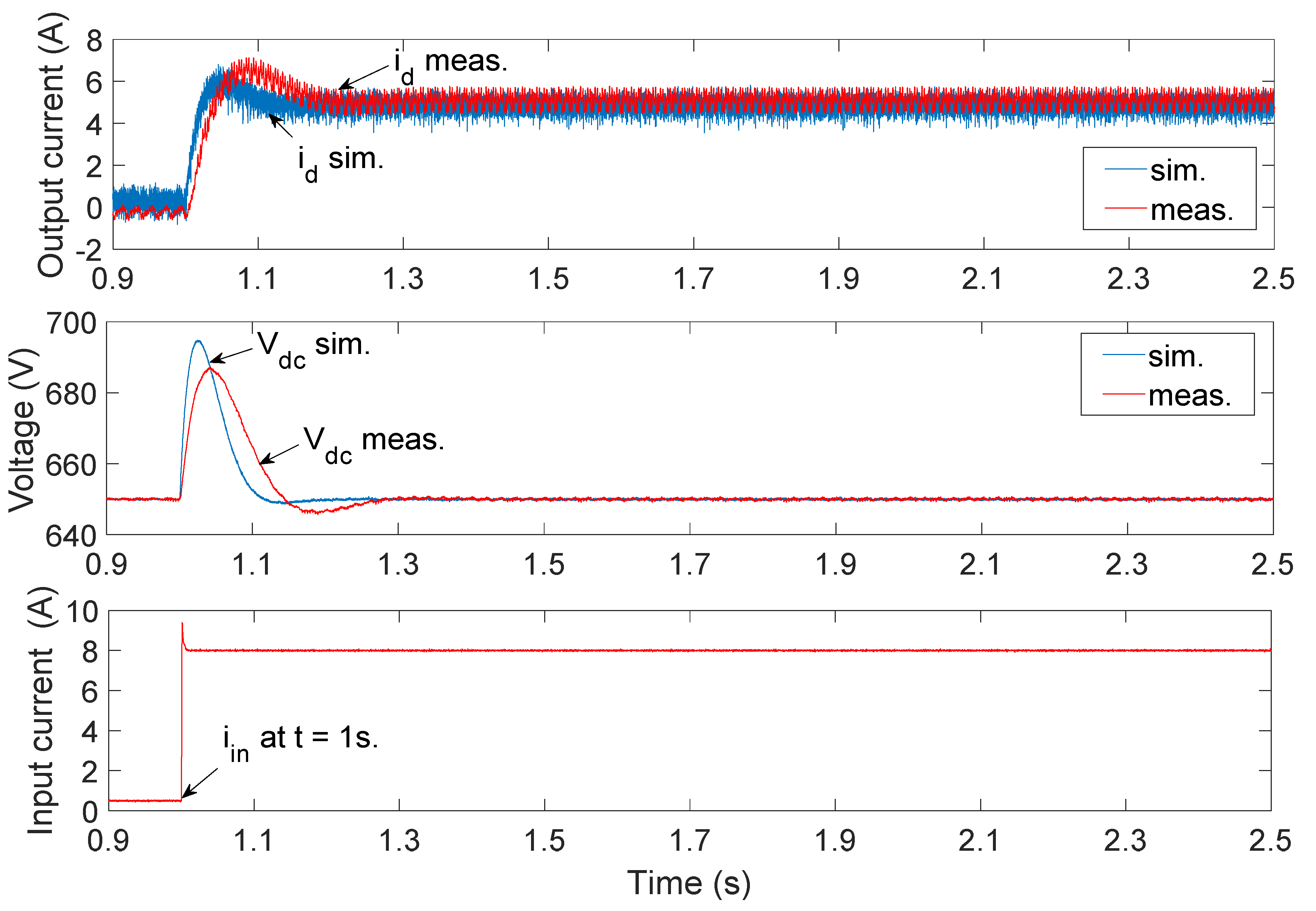

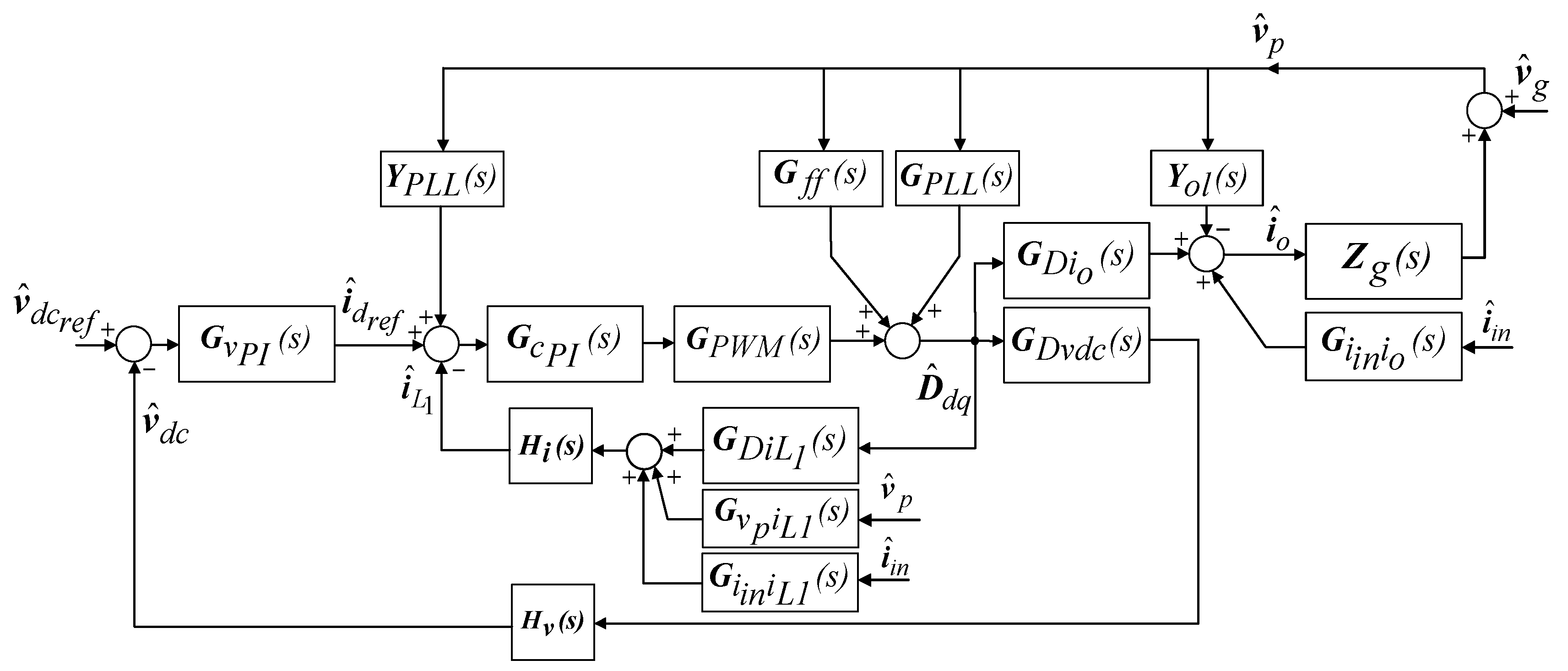
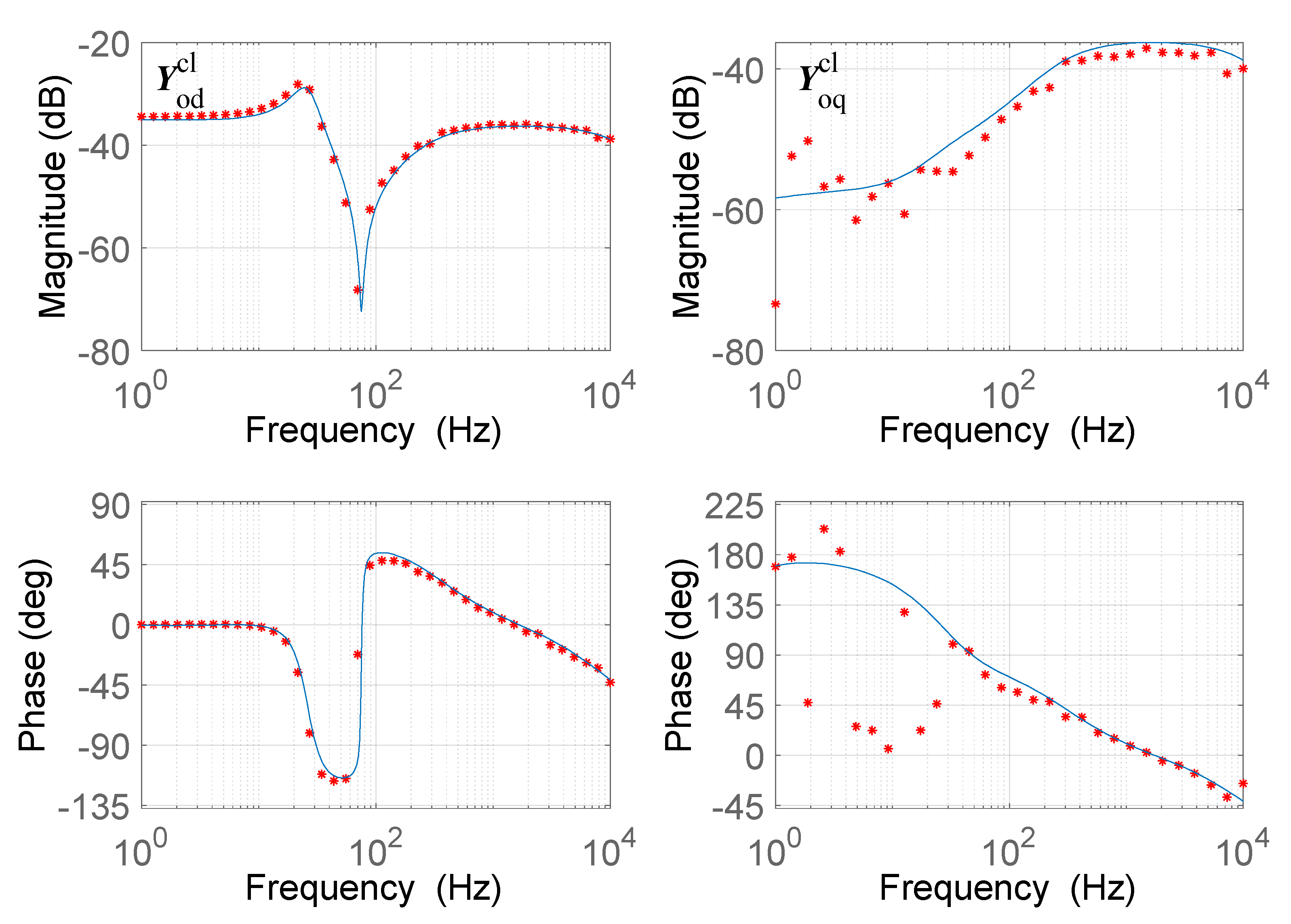



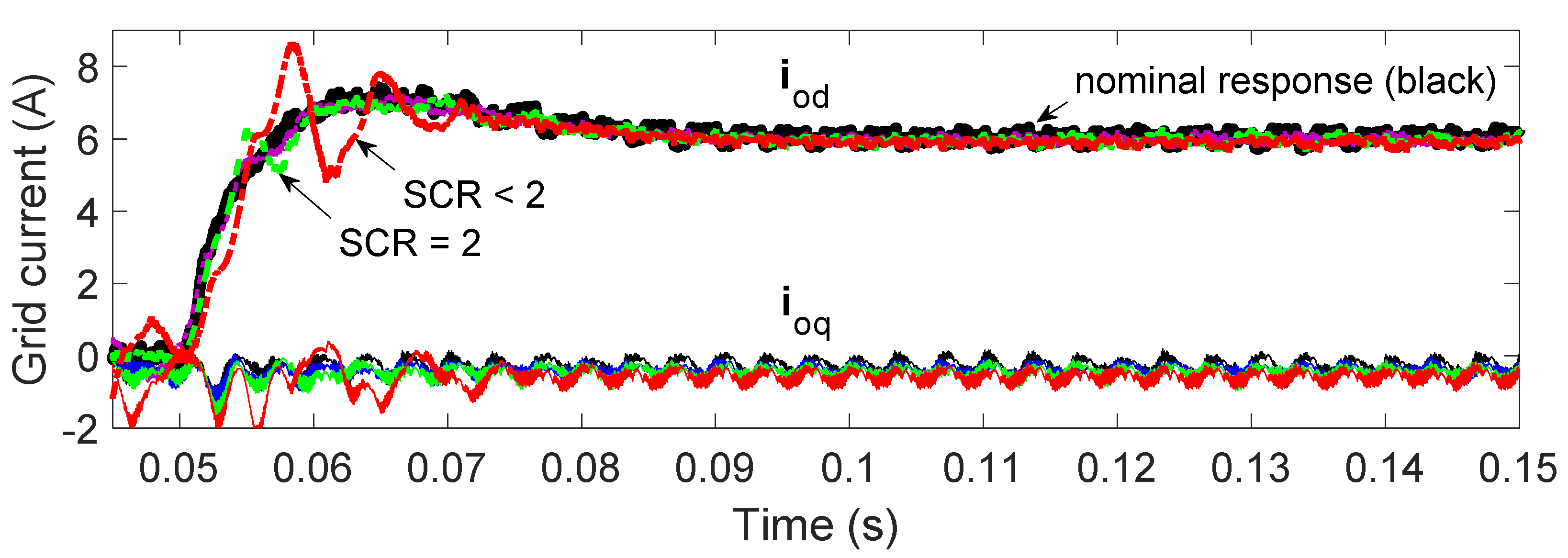
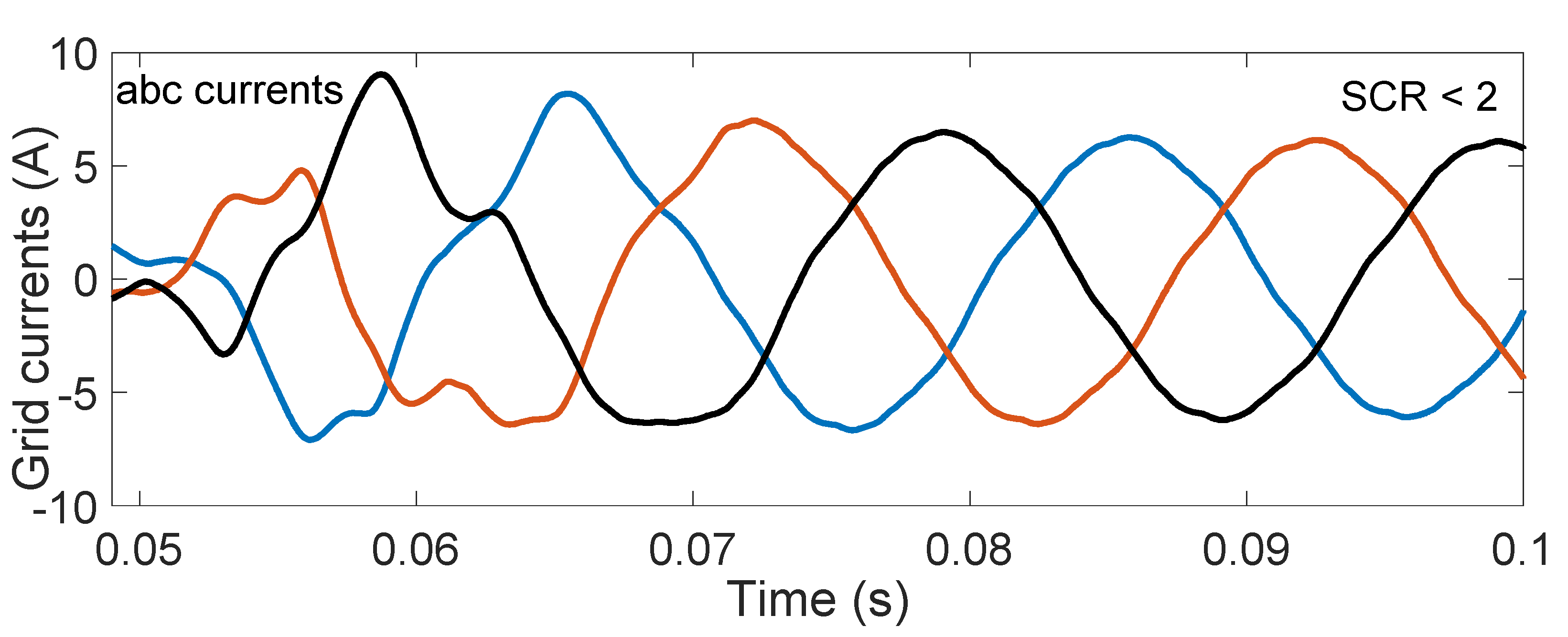


| Parameter | Value | Unit |
|---|---|---|
| Rated power | 17 | kVA |
| Rated voltage | 400 | V |
| DC link voltage | 650–750 | V |
| DC link capacitance C | 0.75 | |
| Filter inductance L1; L2 | 22.3; 1.28 | |
| Filter resistance RL1; RL2 | 200 | |
| Filter capacitance Cf | 8.8 | |
| Switching frequency, fs | 8–20 | kHz |
| Fundamental frequency | 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ally, C.Z.; de Jong, E.C.W. Obtaining Robust Performance of a Current fed Voltage Source Inverter for Virtual Inertia Response in a Low Short Circuit Ratio Condition. Energies 2021, 14, 5546. https://doi.org/10.3390/en14175546
Ally CZ, de Jong ECW. Obtaining Robust Performance of a Current fed Voltage Source Inverter for Virtual Inertia Response in a Low Short Circuit Ratio Condition. Energies. 2021; 14(17):5546. https://doi.org/10.3390/en14175546
Chicago/Turabian StyleAlly, Clint Z., and Erik C. W. de Jong. 2021. "Obtaining Robust Performance of a Current fed Voltage Source Inverter for Virtual Inertia Response in a Low Short Circuit Ratio Condition" Energies 14, no. 17: 5546. https://doi.org/10.3390/en14175546
APA StyleAlly, C. Z., & de Jong, E. C. W. (2021). Obtaining Robust Performance of a Current fed Voltage Source Inverter for Virtual Inertia Response in a Low Short Circuit Ratio Condition. Energies, 14(17), 5546. https://doi.org/10.3390/en14175546






