Microsecond Enhanced Indirect Model Predictive Control for Dynamic Power Management in MMC Units
Abstract
1. Introduction
2. MMC Modeling
2.1. Mathematical Model of the MMC
2.2. RSCAD Model of the MMC
2.3. Comparison between Mathematical and RSCAD Model of the MMC
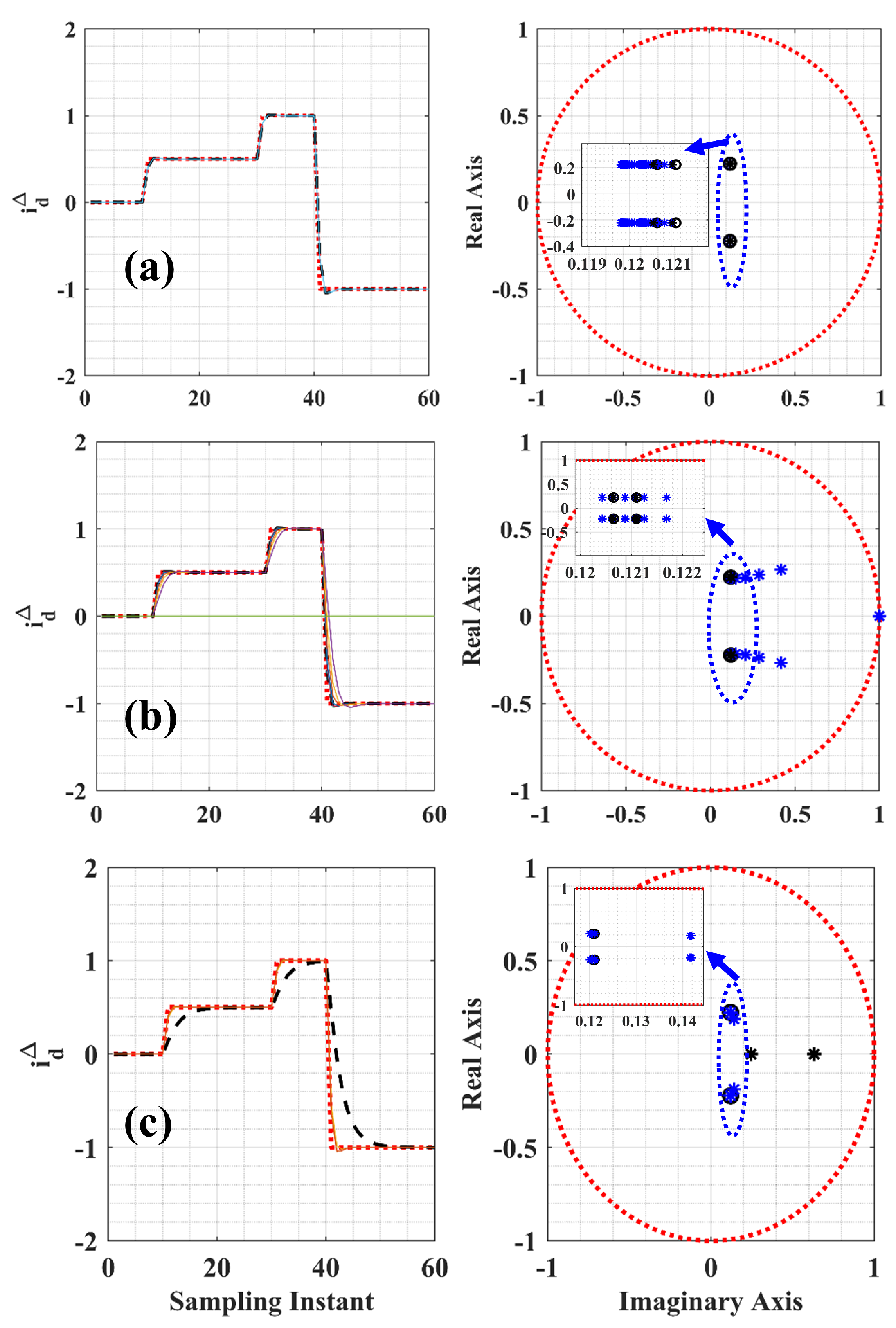
2.3.1. Small Signal Analysis
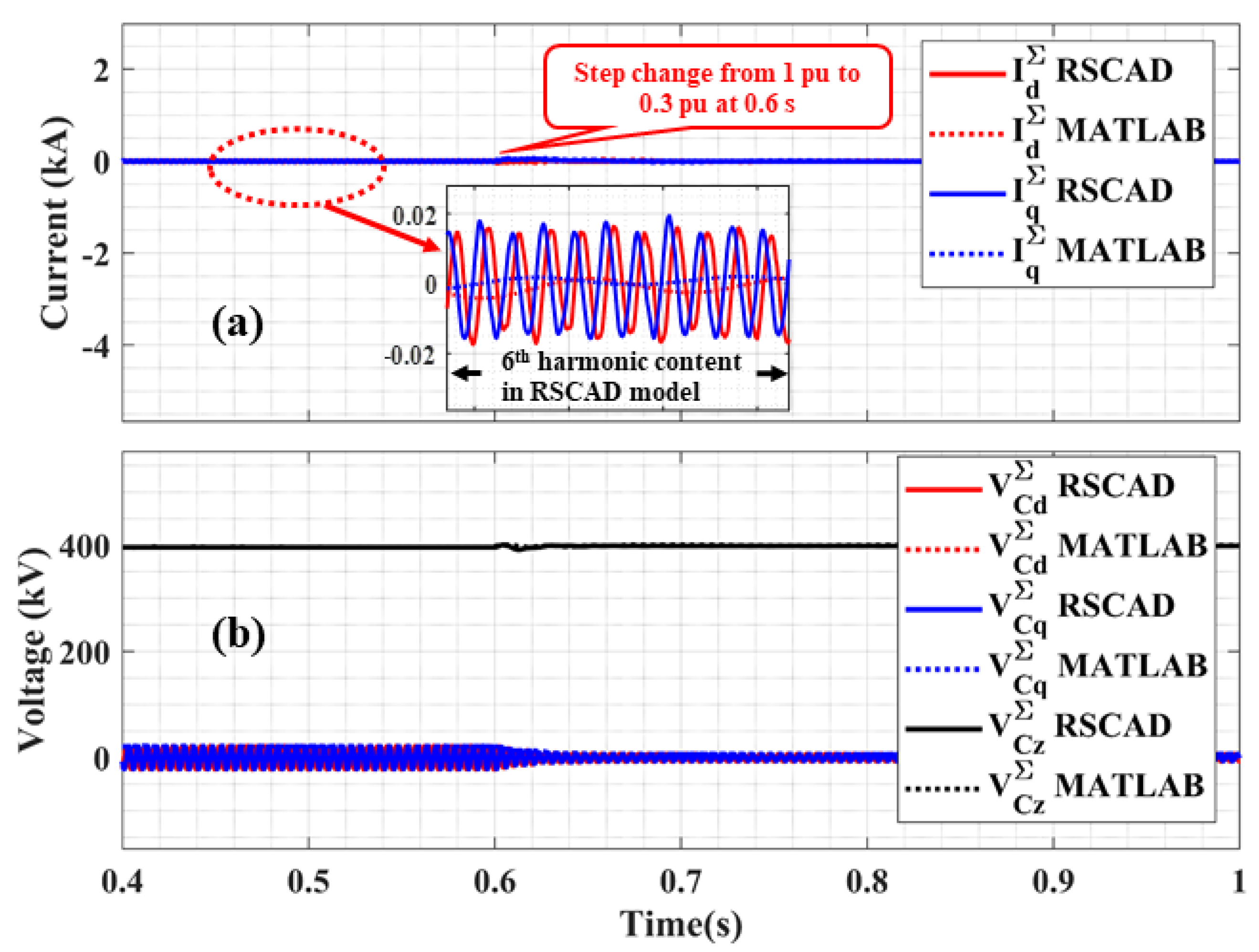
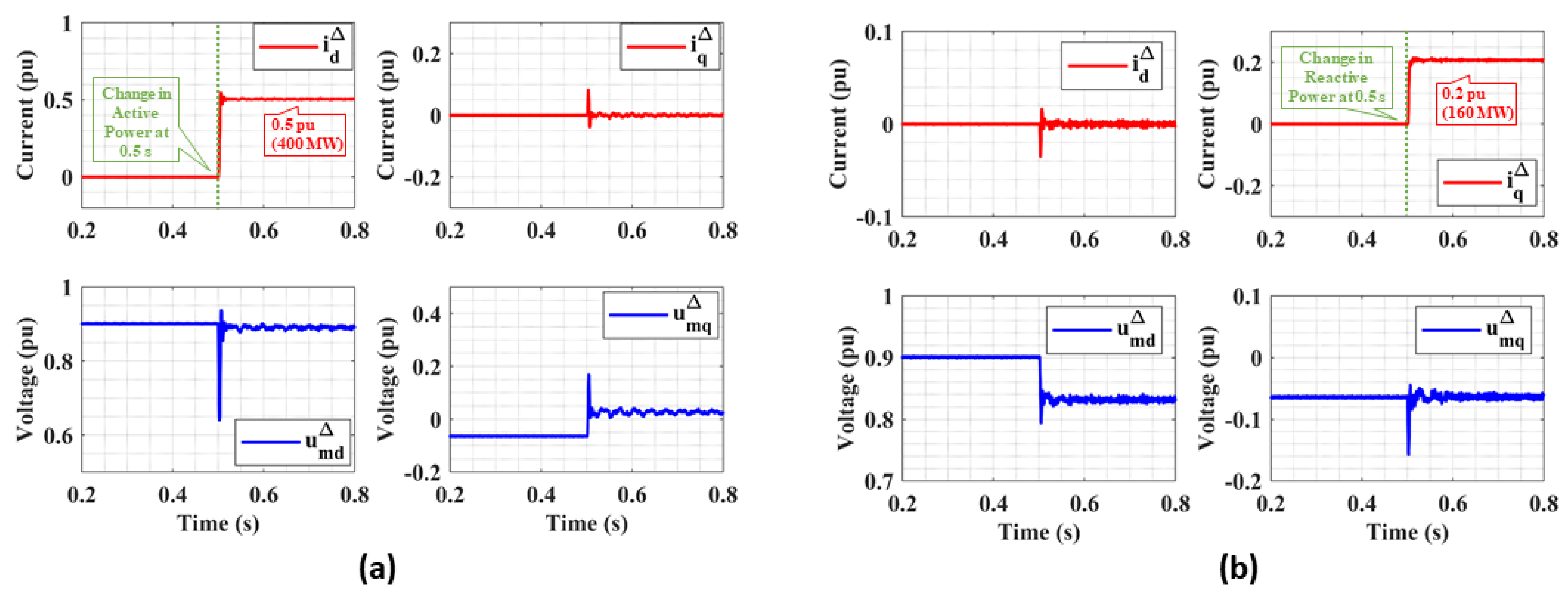
Active Power Step Change
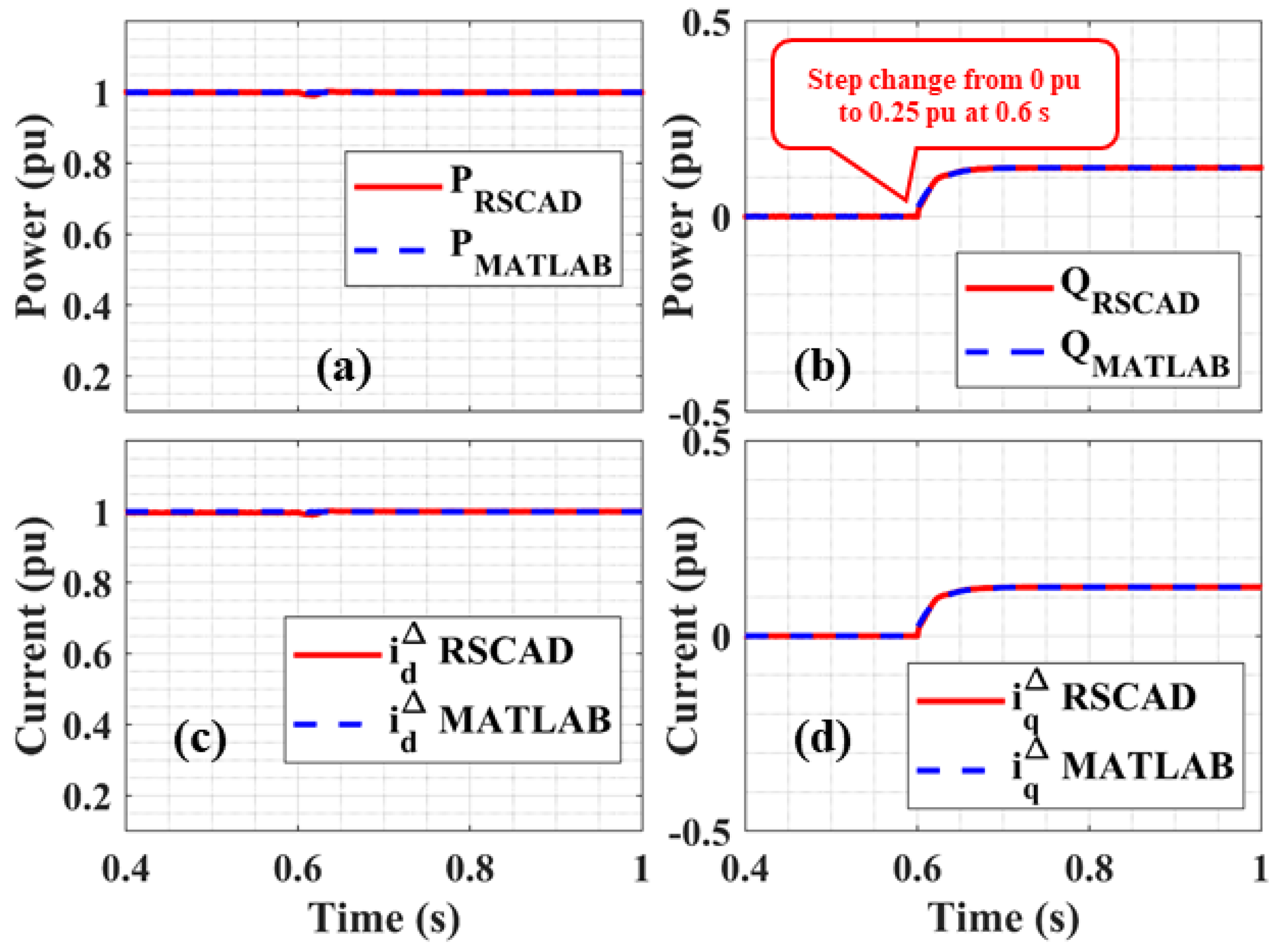
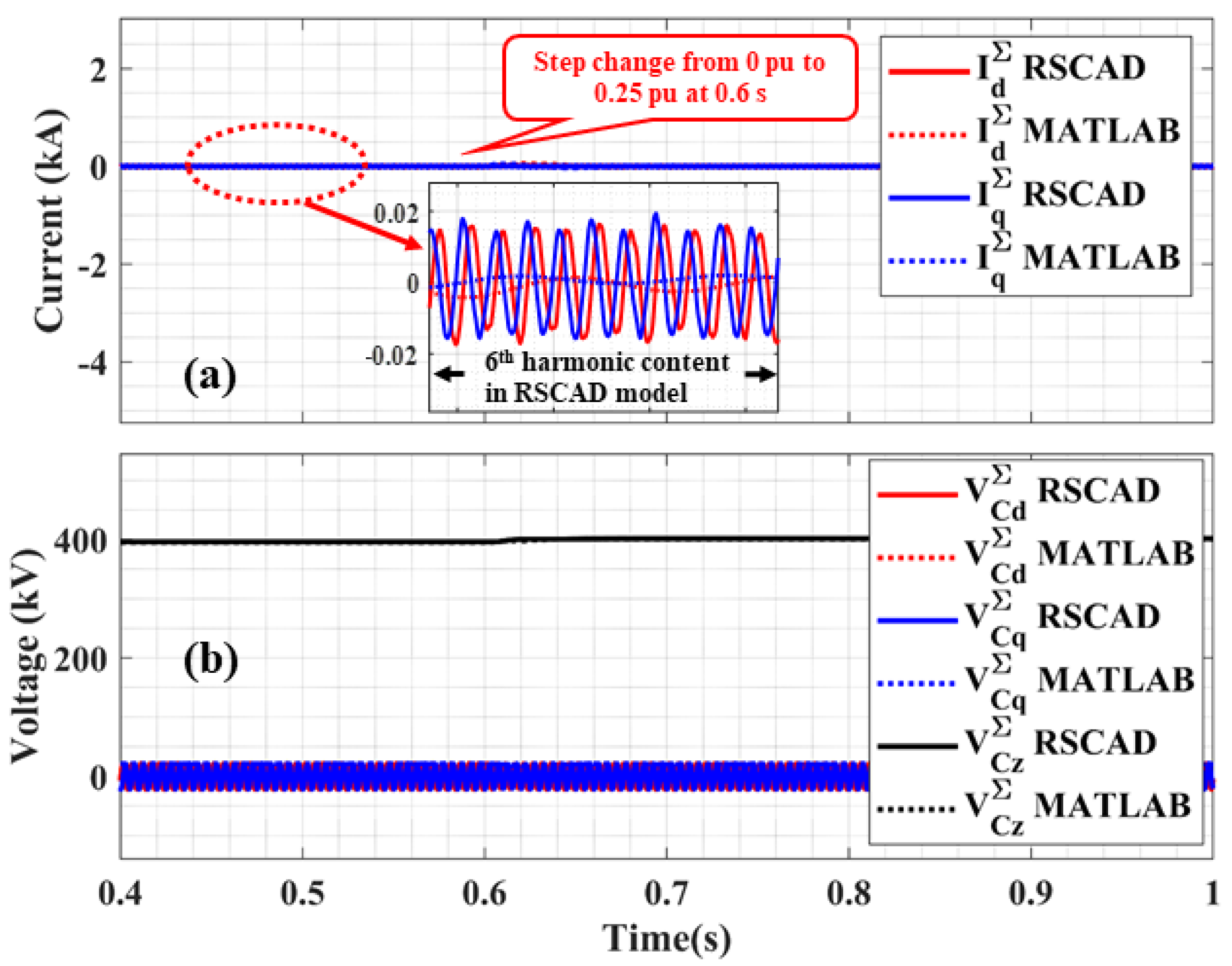
Reactive Power Step Change
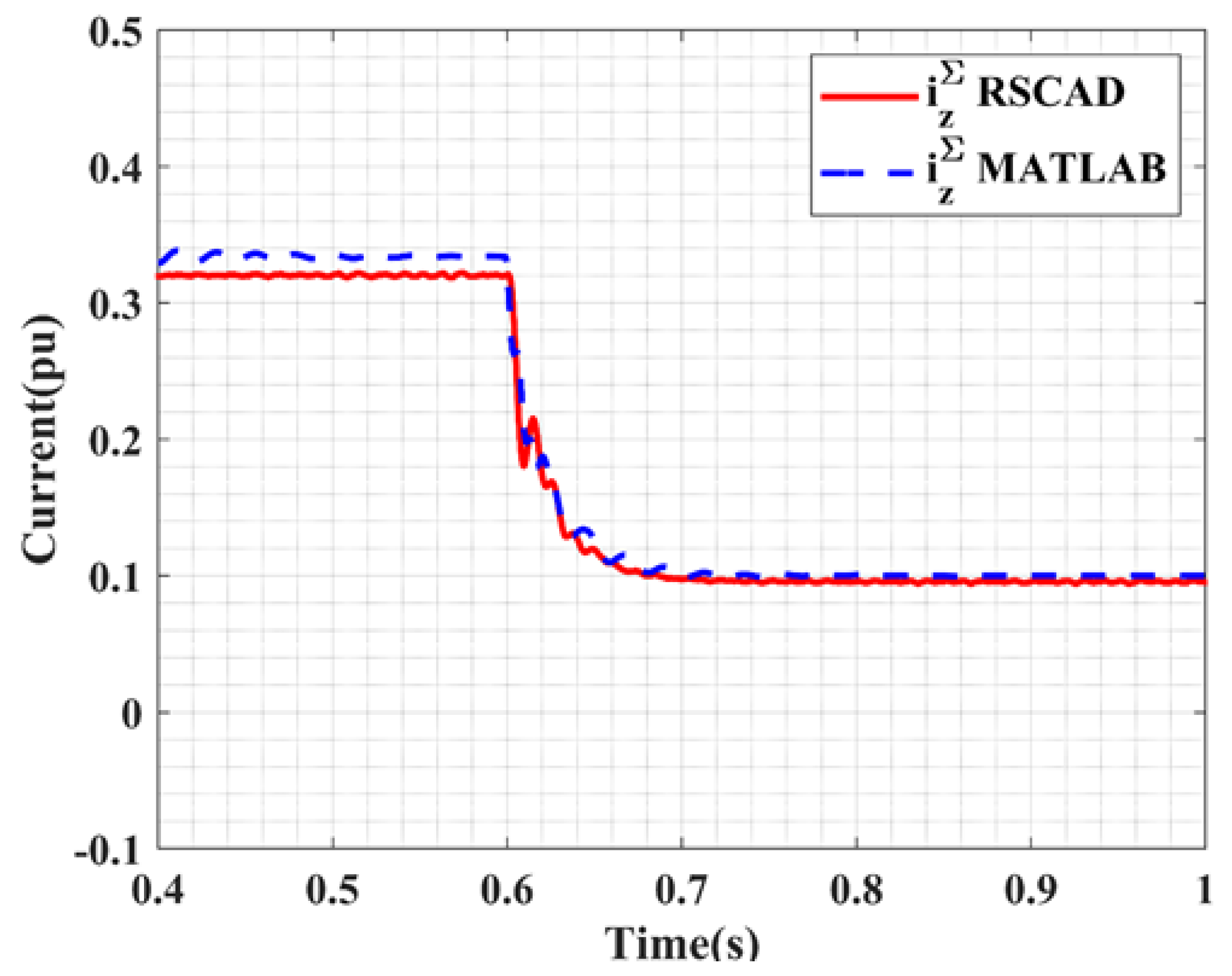
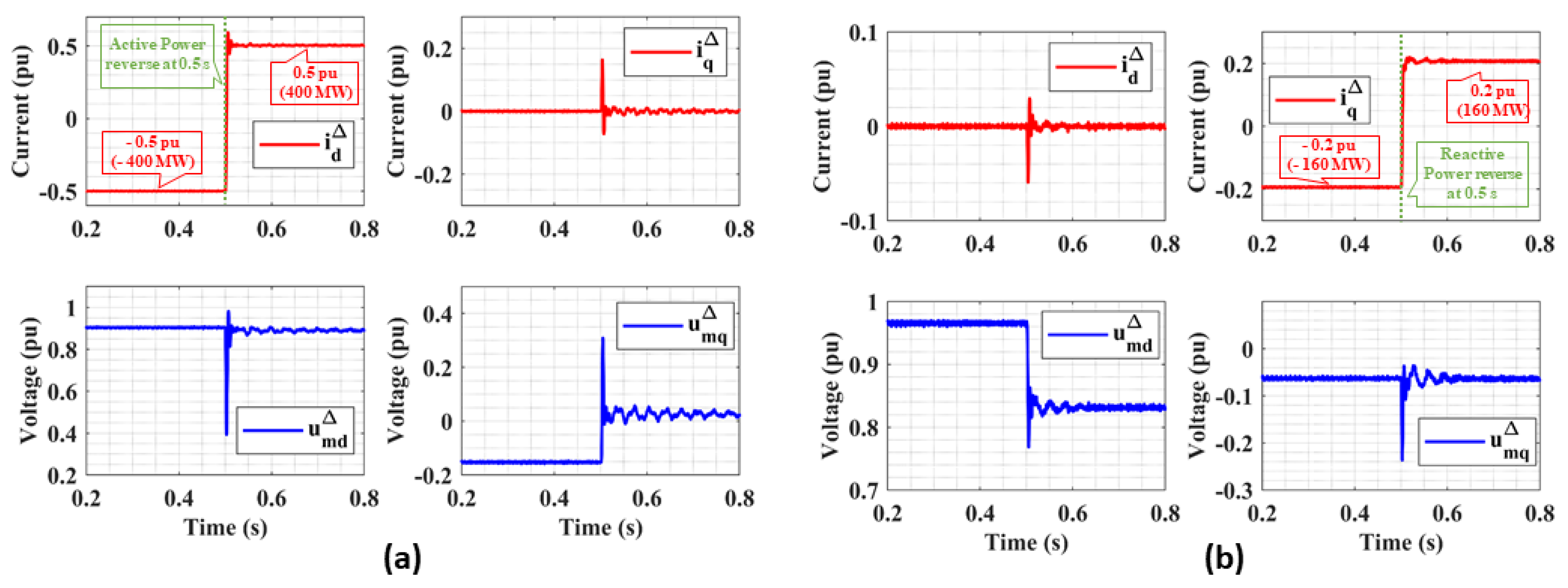
Active Power Reversal
2.3.2. Model Error Analysis
3. Indirect Implicit MPC with Laguerre’s Function
3.1. Discrete Mathematical Model of MMC
3.2. MPC Definition
| Algorithm 1: MPC using Laguerre’s function |
| Initialization: Augmented model (), , N, a, A, and b. Step 1: Measure at k-th instance. Step 2: Compute optimal by minimising the quadratic cost function (11a) using Hildreth’s Quadratic programming procedure considering the constraints. Step 3: Compute using with from step 2 to calculate equations (10). Step 4: Using the receding horizon principle, apply corresponding to kth instance and neglecting the inputs at other sampling instances. Step 5: Go to step 1. |
3.3. Indirect Implicit MPC Simulation Results in Matlab
3.3.1. Constraint Satisfaction Problem
Rate Constraint
Amplitude Constraint
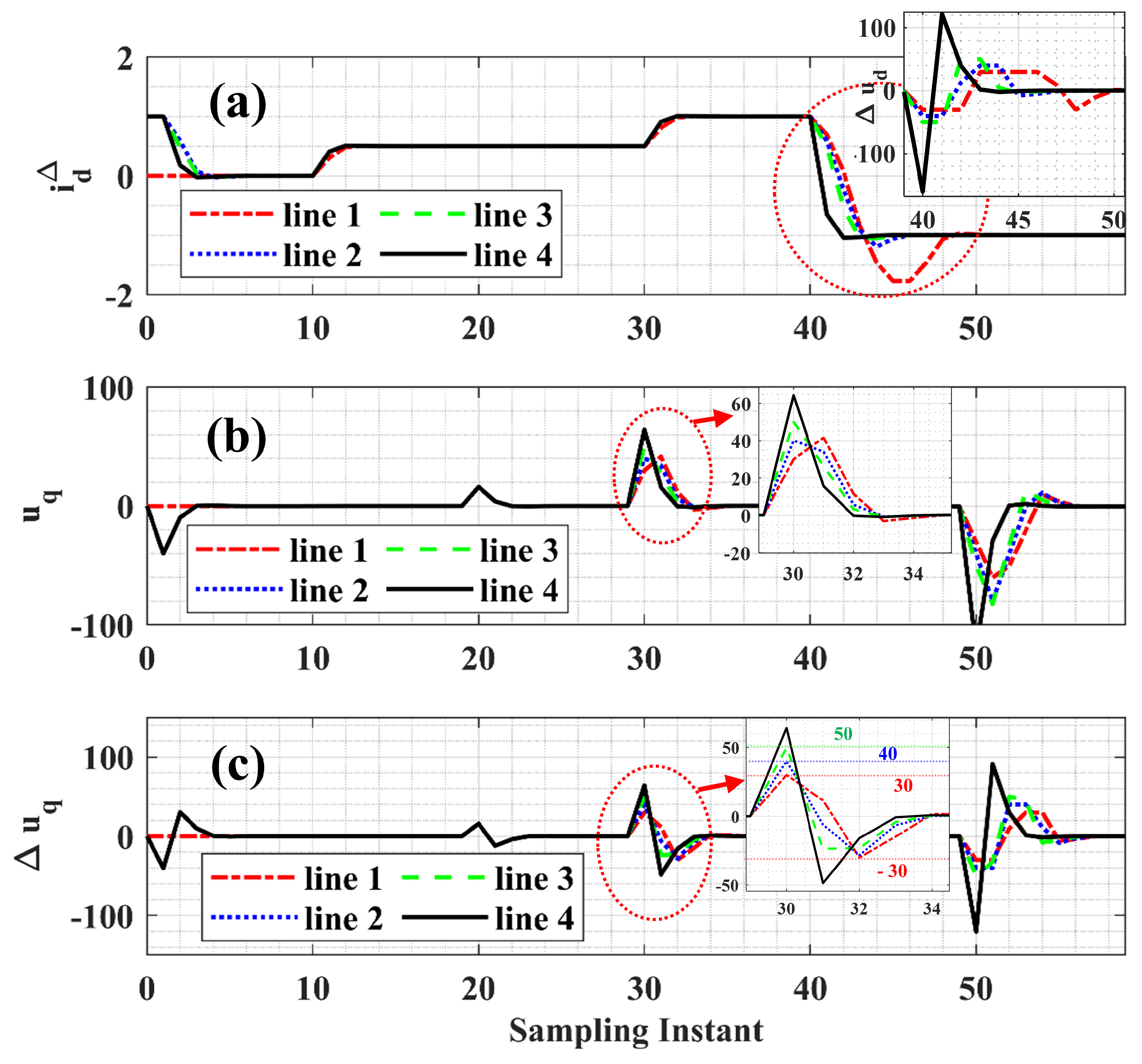
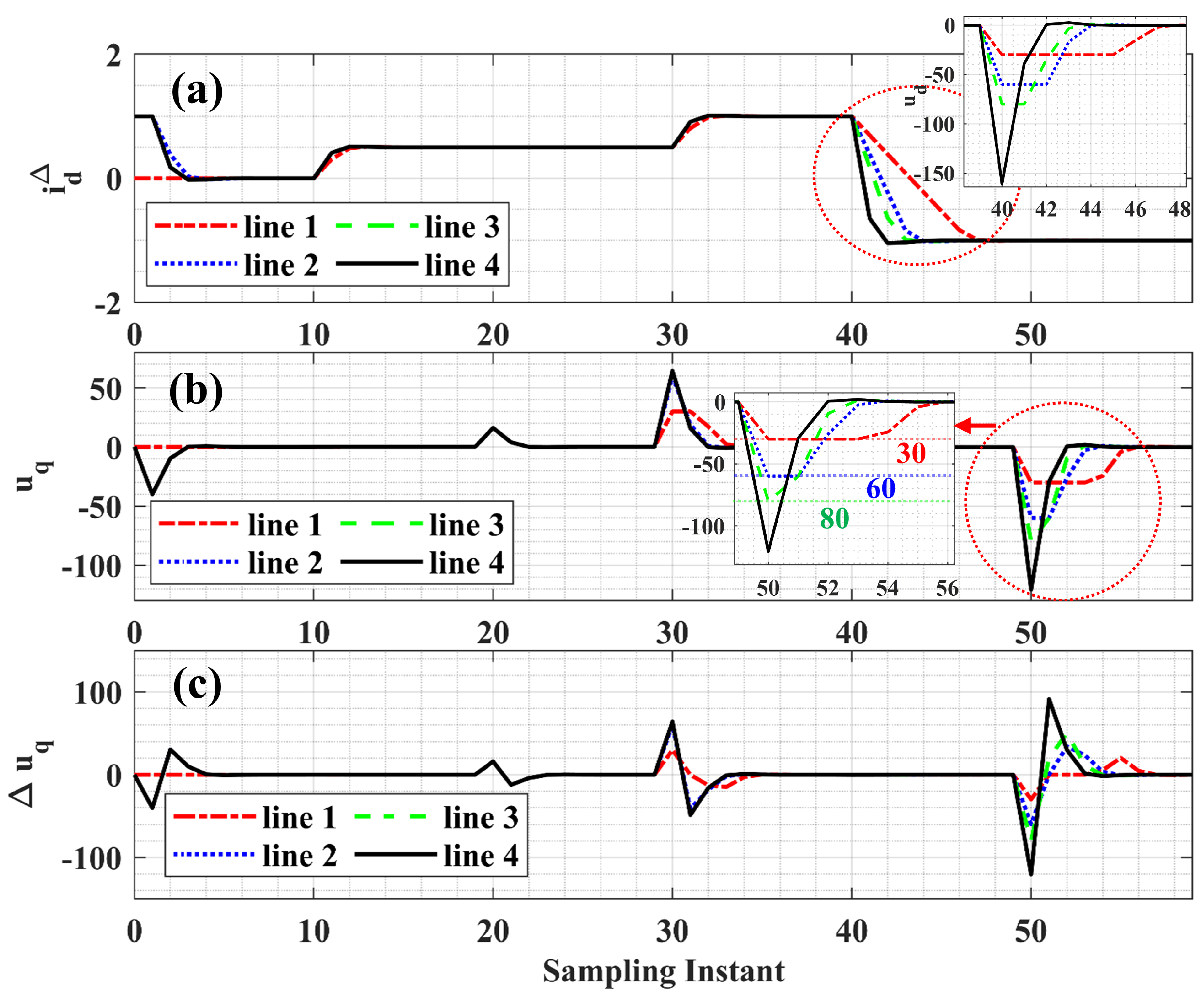
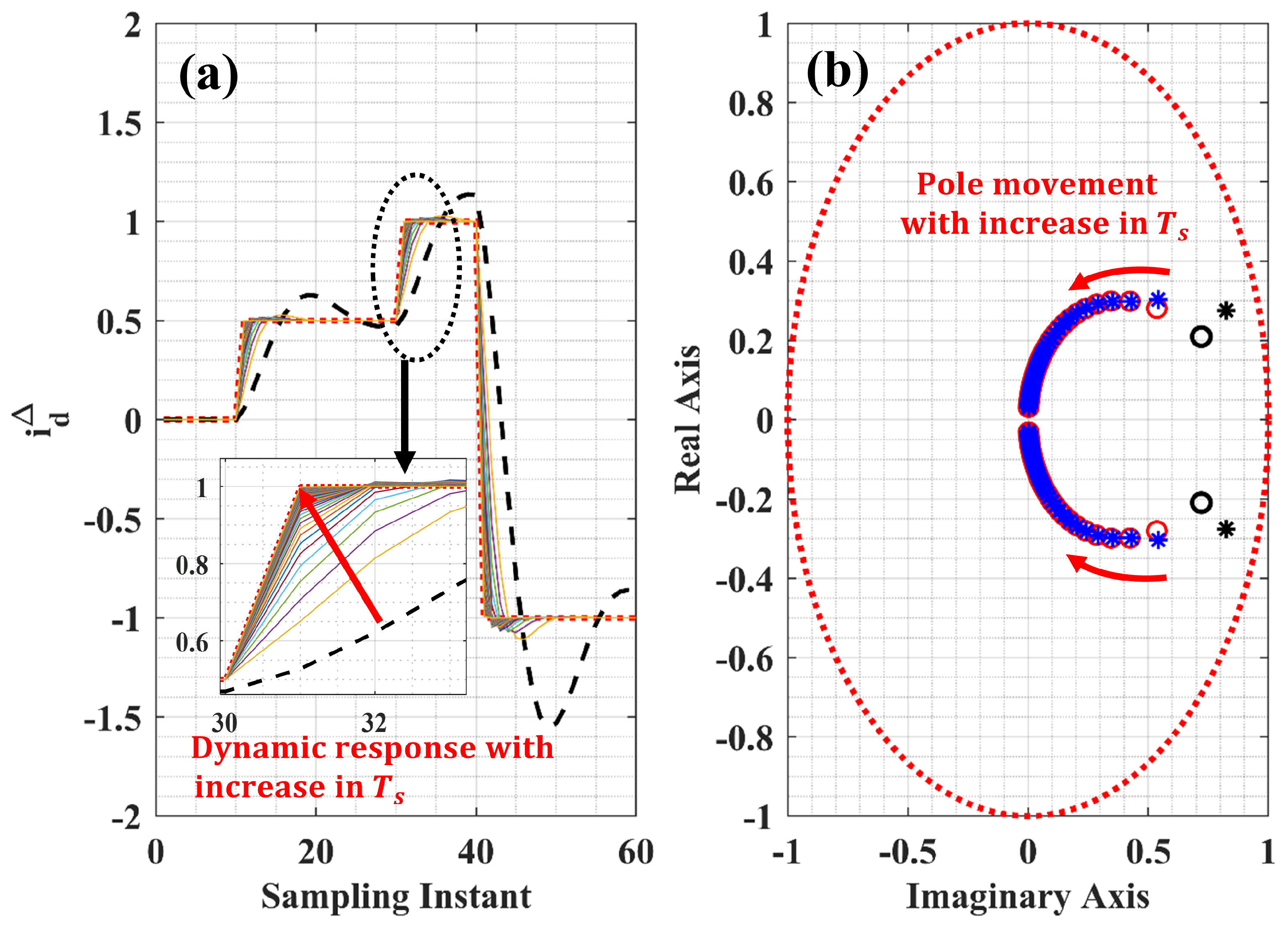
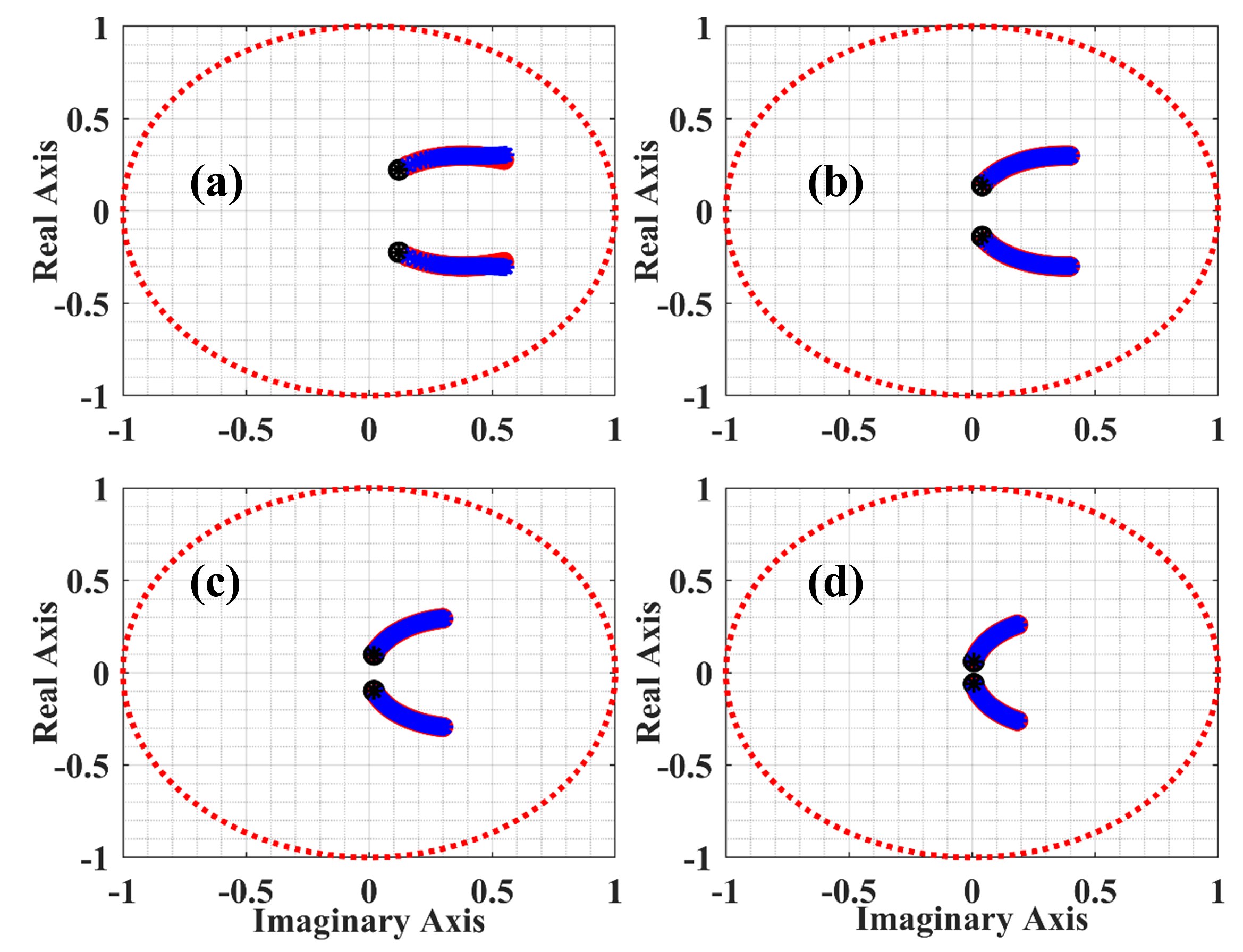
3.3.2. Sensitivity Analysis
Sample Time ()
Weighting, Predictive Horizon and Laguerre’s Parameter
3.4. Indirect Implicit MPC Simulations in RSCAD
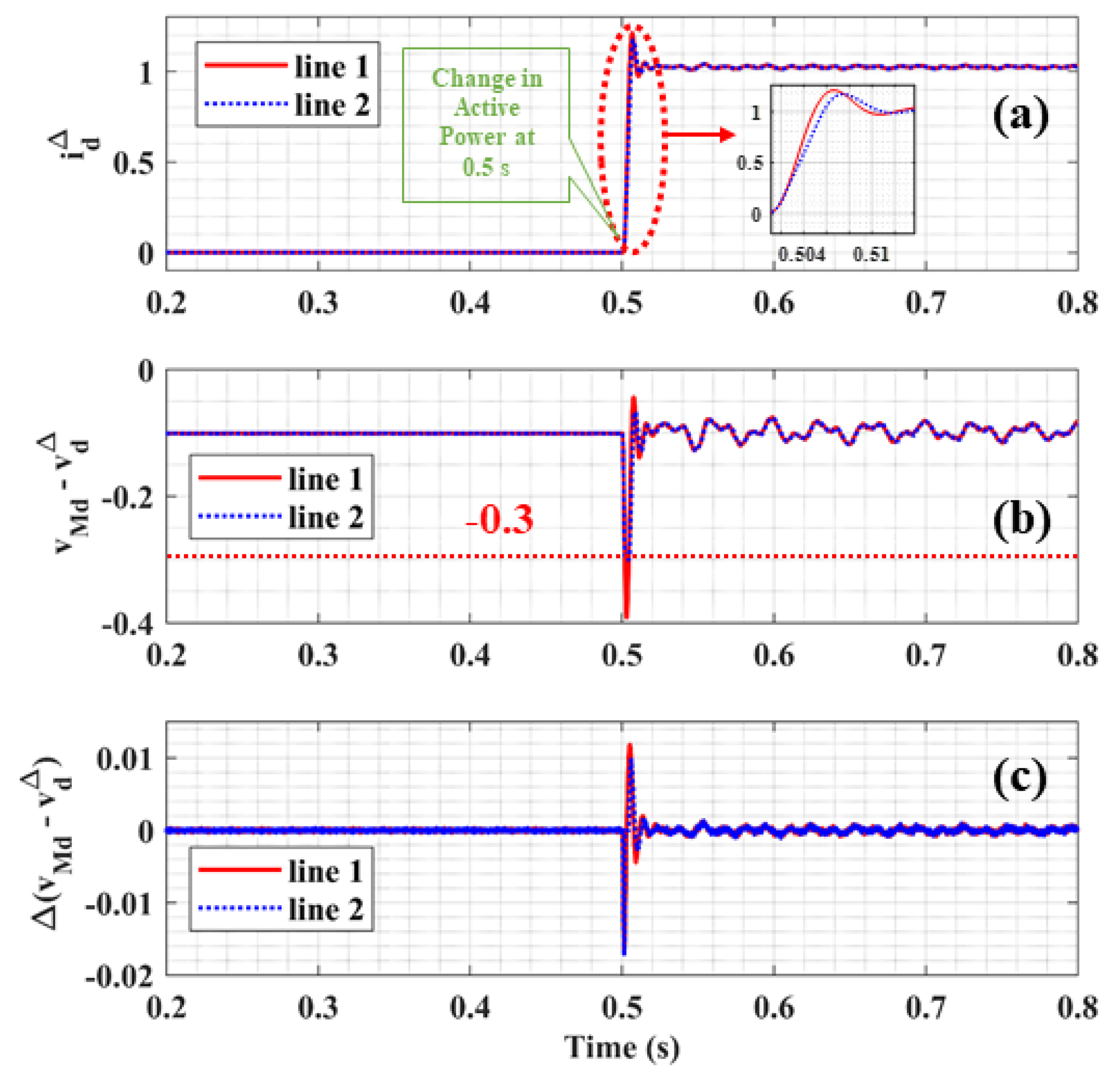
3.4.1. Simulations of Disturbance in Active and Reactive Power
3.4.2. Constrained Satisfaction Problem in RSCAD
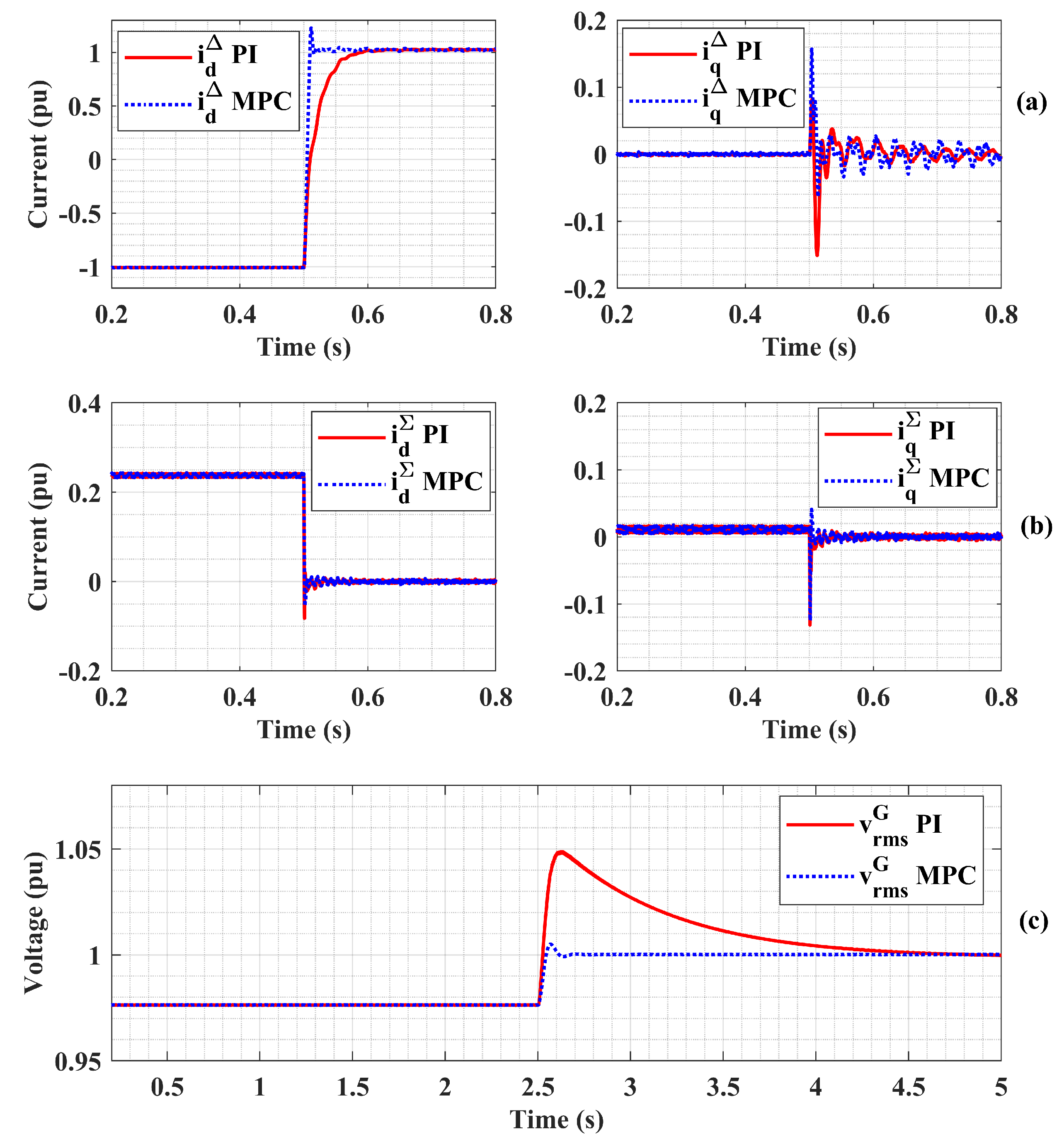
4. Comparison of PI and MPC Controls for the MMC in RTDS
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- United Nations. Paris Agreement. In United Nations Treaty Collection; United Nations: New York, NY, USA, 2015; pp. 1–27. [Google Scholar]
- Lesnicar, A.; Marquardt, R. An innovative modular multilevel converter topology suitable for a wide power range. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 3, p. 6. [Google Scholar] [CrossRef]
- Toghani Holari, Y.; Taher, S.A.; Mehrasa, M. Power management using robust control strategy in hybrid microgrid for both grid-connected and islanding modes. J. Energy Storage 2021, 39, 102600. [Google Scholar] [CrossRef]
- Bessegato, L.; Harnefors, L.; Ilves, K.; Norrga, S. A Method for the Calculation of the AC-Side Admittance of a Modular Multilevel Converter. IEEE Trans. Power Electron. 2019, 34, 4161–4172. [Google Scholar] [CrossRef]
- Beza, M.; Bongiorno, M.; Stamatiou, G. Analytical Derivation of the AC-Side Input Admittance of a Modular Multilevel Converter With Open- and Closed-Loop Control Strategies. IEEE Trans. Power Deliv. 2018, 33, 248–256. [Google Scholar] [CrossRef]
- Stamatiou, G.; Beza, M.; Bongiorno, M.; Harnefors, L. Analytical derivation of the DC-side input admittance of the direct-voltage controlled modular multilevel converter. IET Gener. Transm. Distrib. 2017, 11, 4018–4030. [Google Scholar] [CrossRef]
- Sakinci, O.C.; Beerten, J. Generalized Dynamic Phasor Modeling of the MMC for Small-Signal Stability Analysis. IEEE Trans. Power Deliv. 2019, 34, 991–1000. [Google Scholar] [CrossRef]
- Lyu, J.; Zhang, X.; Cai, X.; Molinas, M. Harmonic State-Space Based Small-Signal Impedance Modeling of a Modular Multilevel Converter with Consideration of Internal Harmonic Dynamics. IEEE Trans. Power Electron. 2019, 34, 2134–2148. [Google Scholar] [CrossRef]
- Sun, J.; Liu, H. Sequence Impedance Modeling of Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1427–1443. [Google Scholar] [CrossRef]
- De Rua, P.; Sakinci, O.C.; Beerten, J. Comparative Study of Dynamic Phasor and Harmonic State-Space Modeling for Small-Signal Stability Analysis. Electr. Power Syst. Res. 2020, 189, 106626. [Google Scholar] [CrossRef]
- Bergna-Diaz, G.; Freytes, J.; Guillaud, X.; D’Arco, S.; Suul, J.A. Generalized Voltage-Based State-Space Modeling of Modular Multilevel Converters With Constant Equilibrium in Steady State. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 707–725. [Google Scholar] [CrossRef]
- Cigré, W. Guide for the Development of Models for HVDC Converters in a HVDC Grid; Technical Brochures B4.57; CIGRÉ: Paris, France, 2014; Volume 604, pp. 1–222. [Google Scholar]
- Hosseinzadeh, M.; Schenato, L.; Garone, E. A distributed optimal power management system for microgrids with plug&play capabilities. Adv. Control Appl. Eng. Ind. Syst. 2021, 3, e65. [Google Scholar]
- Kang, W.; Chen, M.; Lai, W.; Luo, Y. Distributed real-time power management for virtual energy storage systems using dynamic price. Energy 2021, 216, 119069. [Google Scholar] [CrossRef]
- Aguilera, R.P.; Acuna, P.; Su, X.; Lezana, P.; McGrath, B. Sequential Phase-Shifted Model Predictive Control for multicell power converters. In Proceedings of the 2017 IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Yaramasu, V.; Fuentes, R.L.; Zargari, N.R. Model Predictive Control of High-Power Modular Multilevel Converters—An Overview. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 168–183. [Google Scholar] [CrossRef]
- Stanojev, O.; Markovic, U.; Vrettos, E.; Aristidou, P.; Callaway, D.; Hug, G. Enhanced MPC for Fast Frequency Control in Inverter-Dominated Power Systems. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Stanojev, O.; Markovic, U.; Aristidou, P.; Hug, G.; Callaway, D.S.; Vrettos, E. MPC-Based Fast Frequency Control of Voltage Source Converters in Low-Inertia Power Systems. IEEE Trans. Power Syst. 2020, 1. [Google Scholar] [CrossRef]
- Zheng, C.; Dragicevic, T.; Blaabjerg, F. Model Predictive Control Based Virtual Inertia Emulator for an Islanded AC Microgrid. IEEE Trans. Ind. Electron. 2020, 1. [Google Scholar] [CrossRef]
- Rodriguez-Bernuz, J.M.; Junyent-Ferré, A. Model predictive circulating current regulator for single-phase modular multilevel converter. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4824–4830. [Google Scholar]
- Rodriguez-Bernuz, J.M.; Junyent-Ferré, A. Operating Region Extension of a Modular Multilevel Converter using Model Predictive Control: A Single Phase Analysis. IEEE Trans. Power Deliv. 2019, 35, 171–182. [Google Scholar] [CrossRef]
- Tavakoli, S.D.; Fekriasl, S.; Prieto-Araujo, E.; Beerten, J.; Gomis-Bellmunt, O. Optimal H Infinity Control Design for MMC-based HVDC Links. IEEE Trans. Power Deliv. 2021. [Google Scholar] [CrossRef]
- Darivianakis, G.; Geyer, T.; van der Merwe, W. Model predictive current control of modular multilevel converters. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 5016–5023. [Google Scholar]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2016, 64, 935–947. [Google Scholar] [CrossRef]
- Ou, K.; Maguire, T.; Warkentin, B.; Chen, Y.; Zhang, Y.; Kuffel, R.; Cai, Z.; Guan, L. Research and application of small time-step simulation for MMC VSC-HVDC in RTDS. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 877–882. [Google Scholar] [CrossRef]
- Real-Time Digital Simulator. VSC Small Time-Step Modeling; Technical Report October; RTDS Technologies: Winnipeg, MB, Canada, 2006. [Google Scholar]
- Wu, H.; Wang, X. Dynamic impact of zero-sequence circulating current on modular multilevel converters: Complex-valued AC impedance modeling and analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 1947–1963. [Google Scholar] [CrossRef]
- Sammut, C.; Webb, G.I. (Eds.) Mean Absolute Error. In Encyclopedia of Machine Learning; Springer US: Boston, MA, USA, 2010; p. 652. [Google Scholar] [CrossRef]
- Zama, A.; Benchaib, A.; Bacha, S.; Frey, D.; Silvant, S. High Dynamics Control for MMC Based on Exact Discrete-Time Model With Experimental Validation. IEEE Trans. Power Deliv. 2018, 33, 477–488. [Google Scholar] [CrossRef]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB®; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
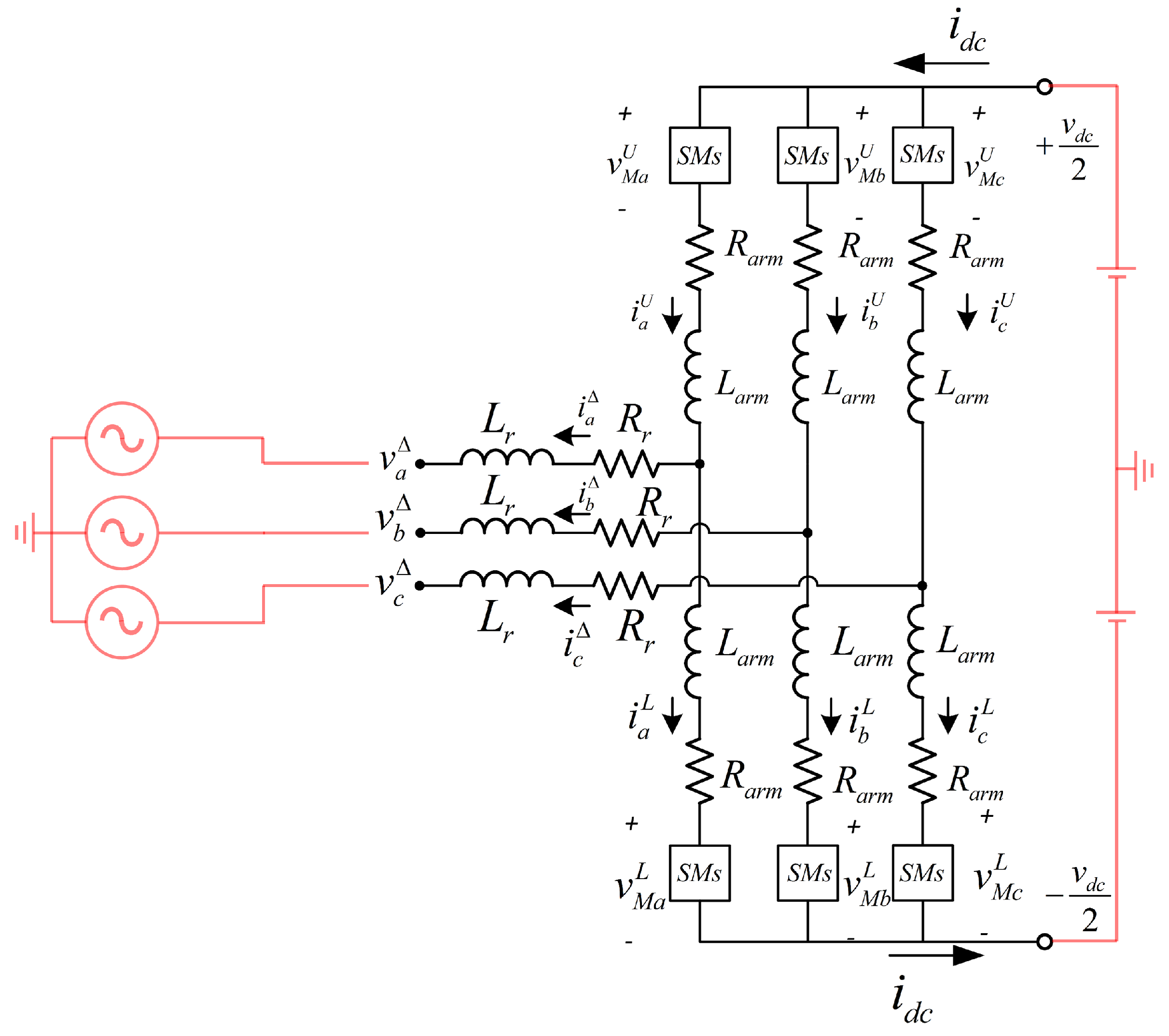
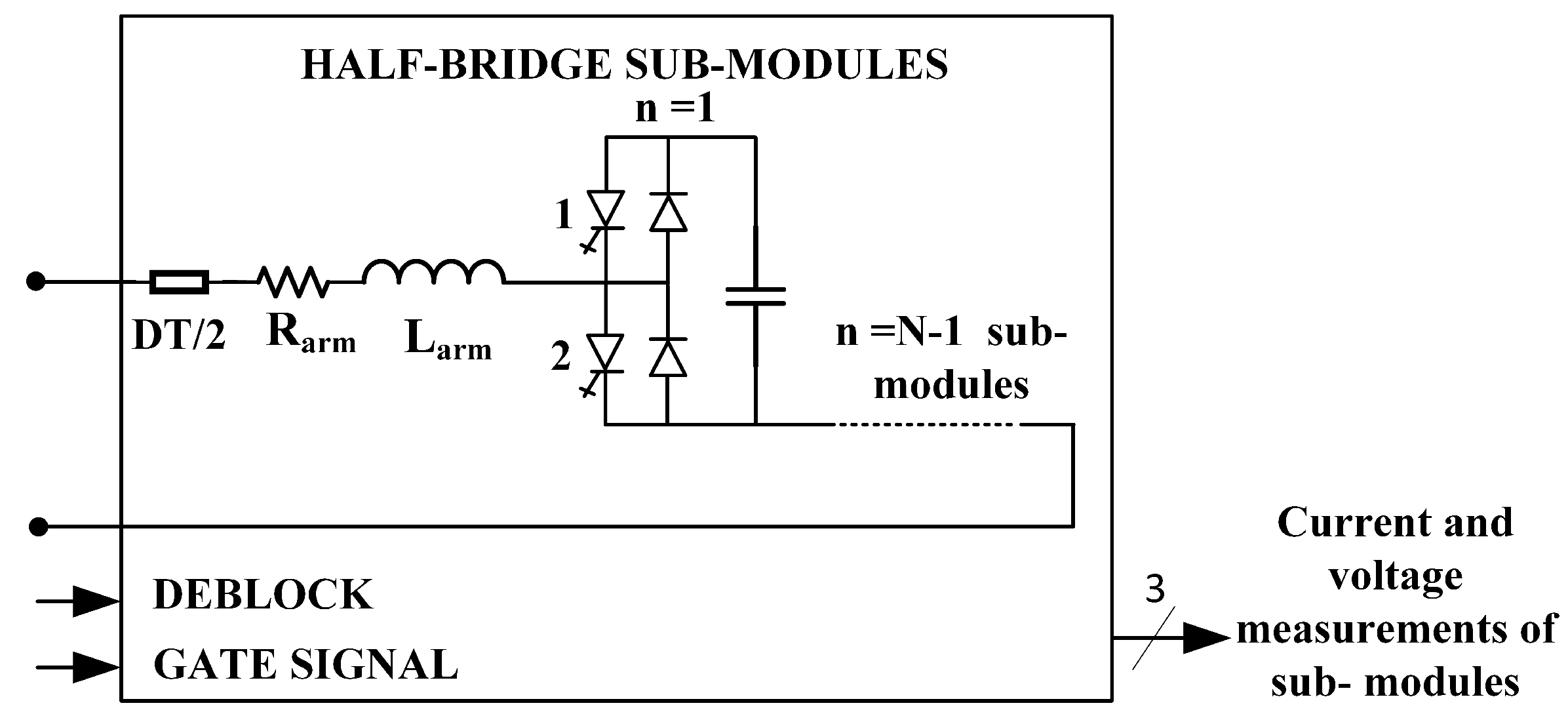

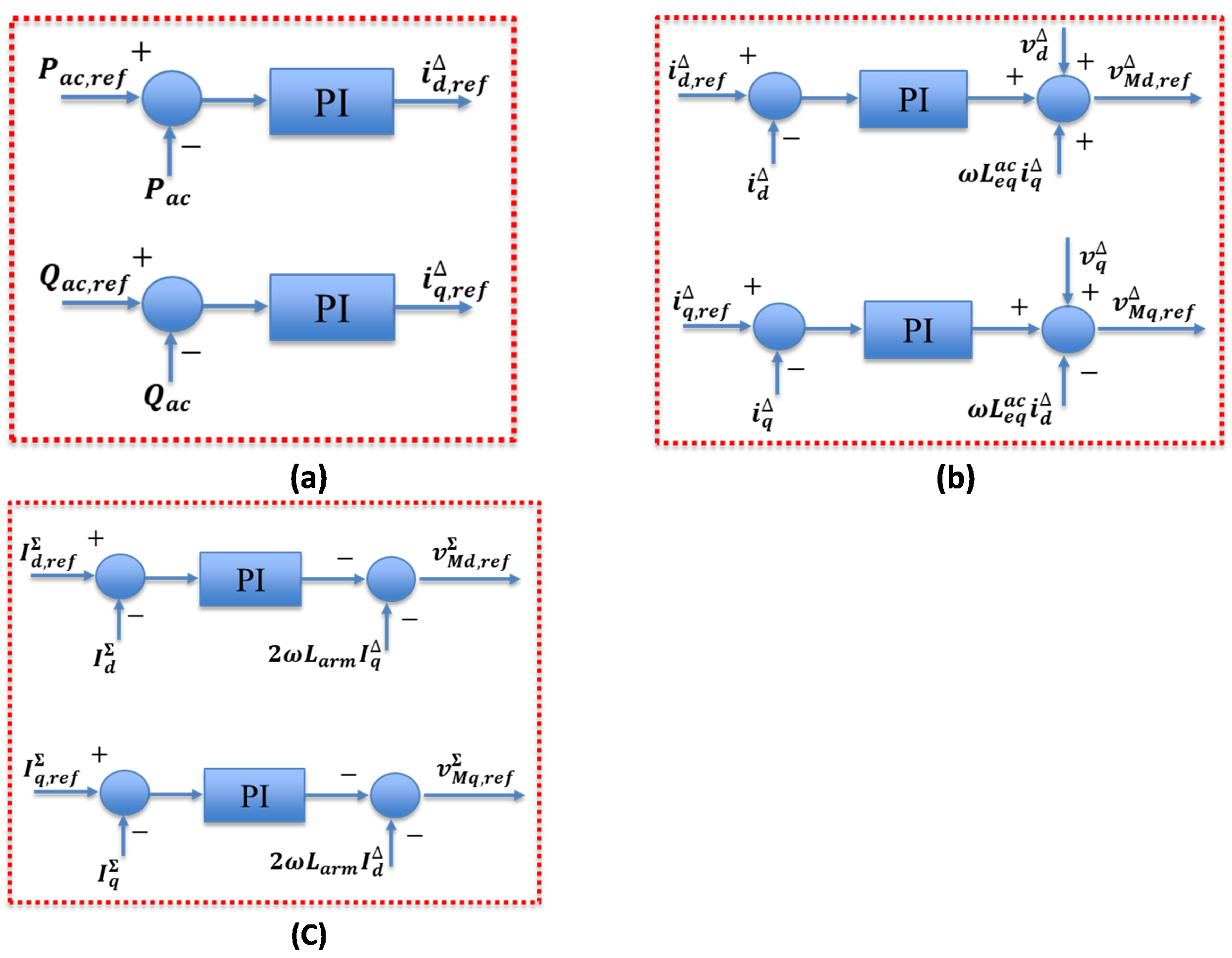
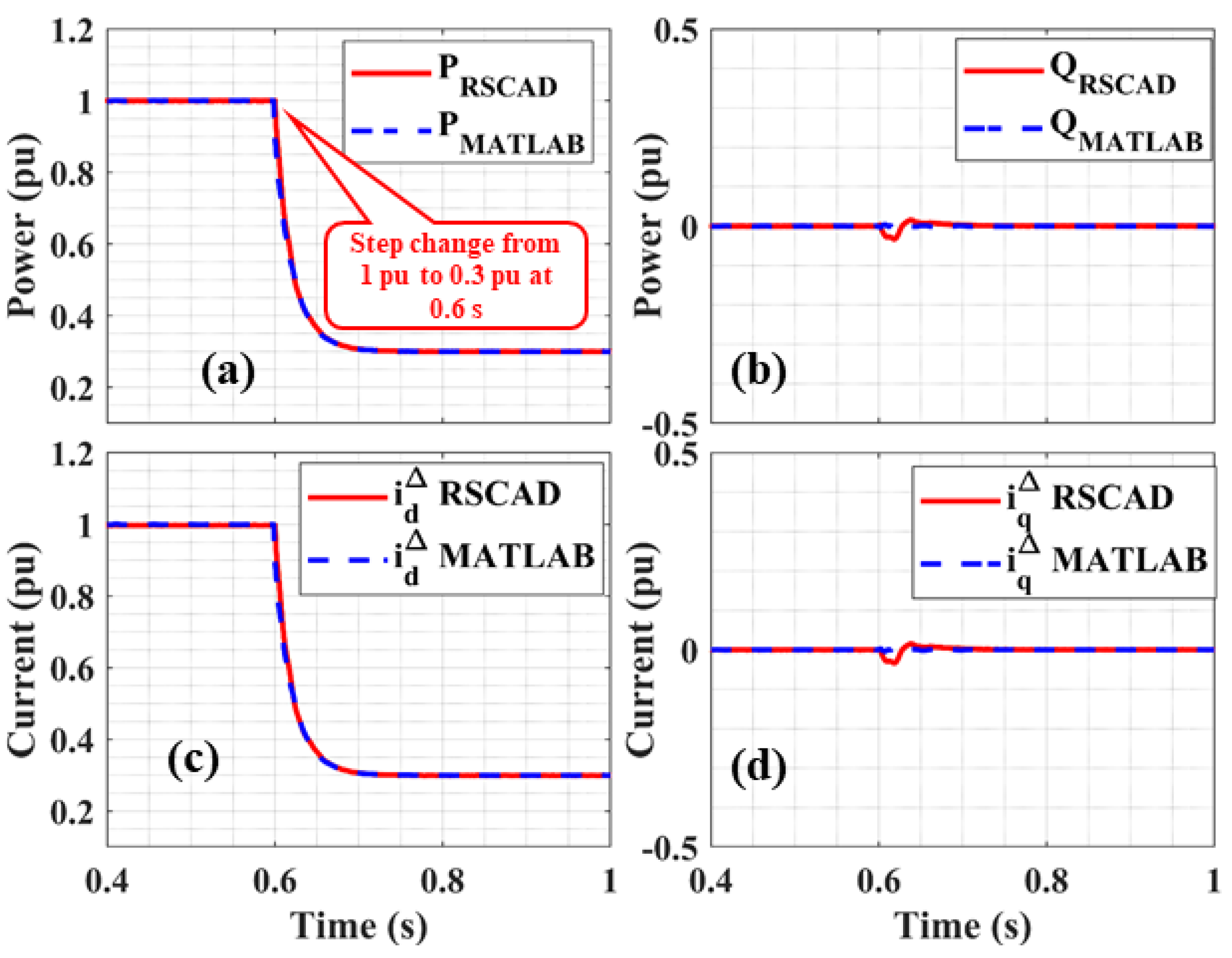
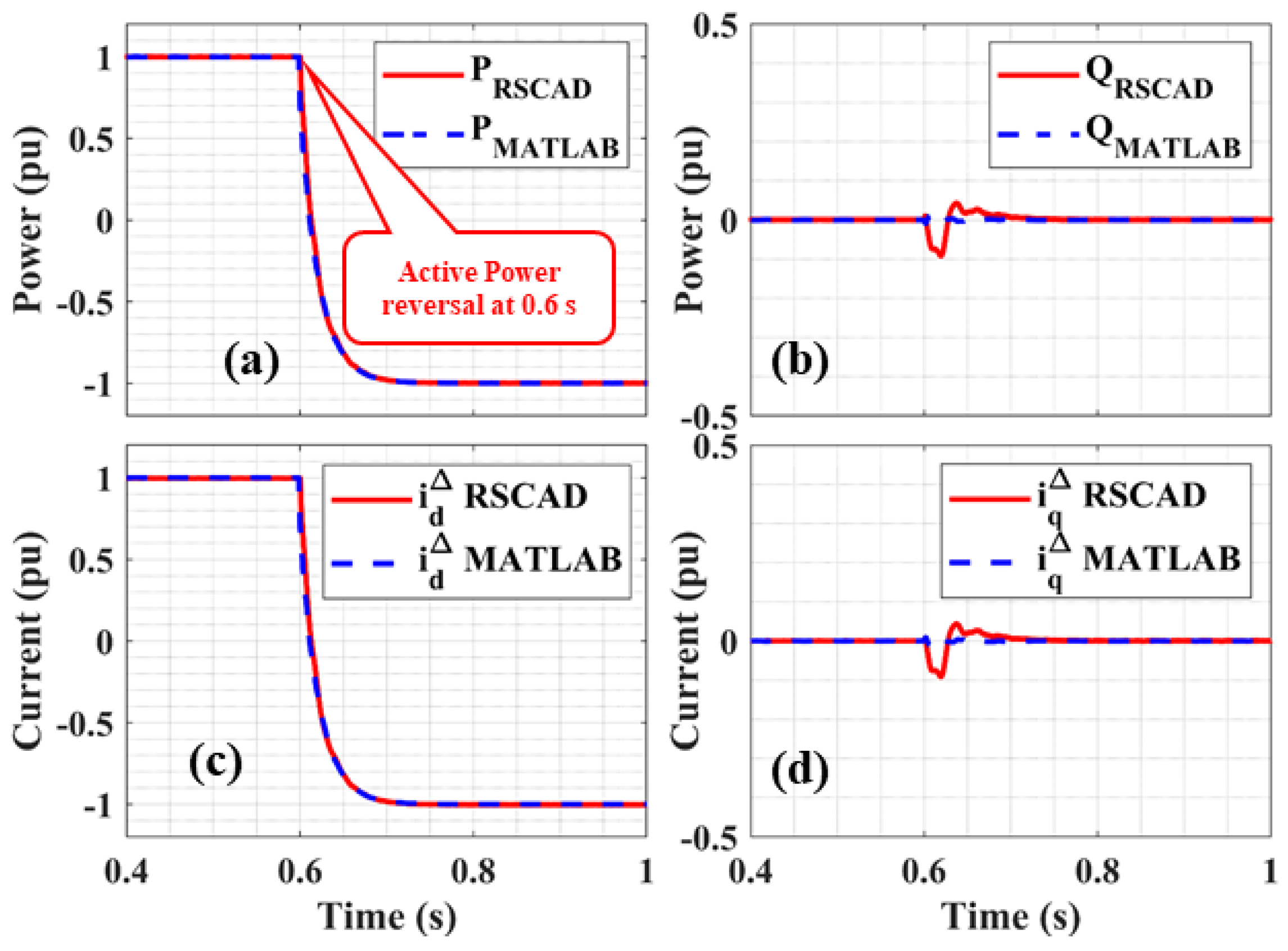
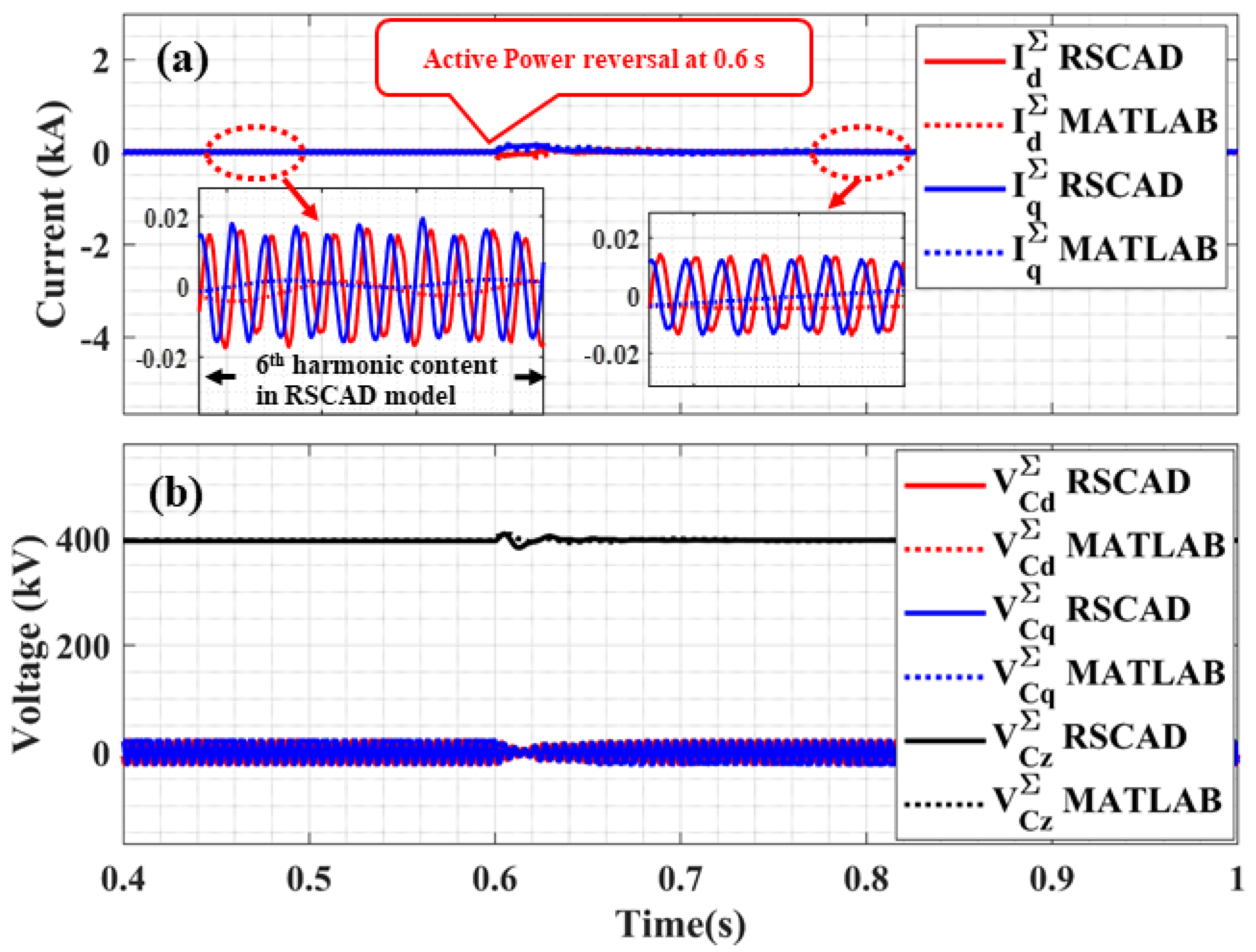
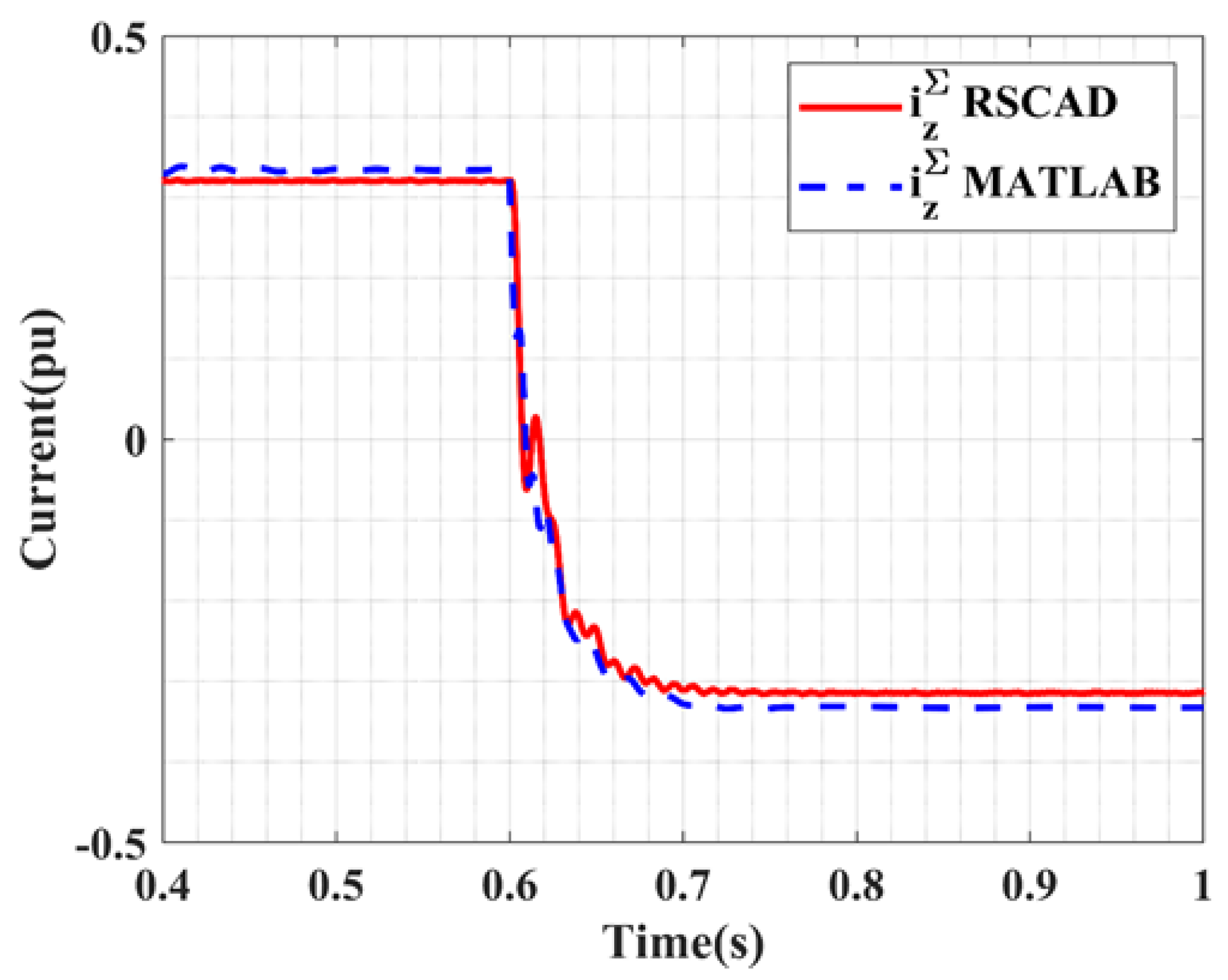
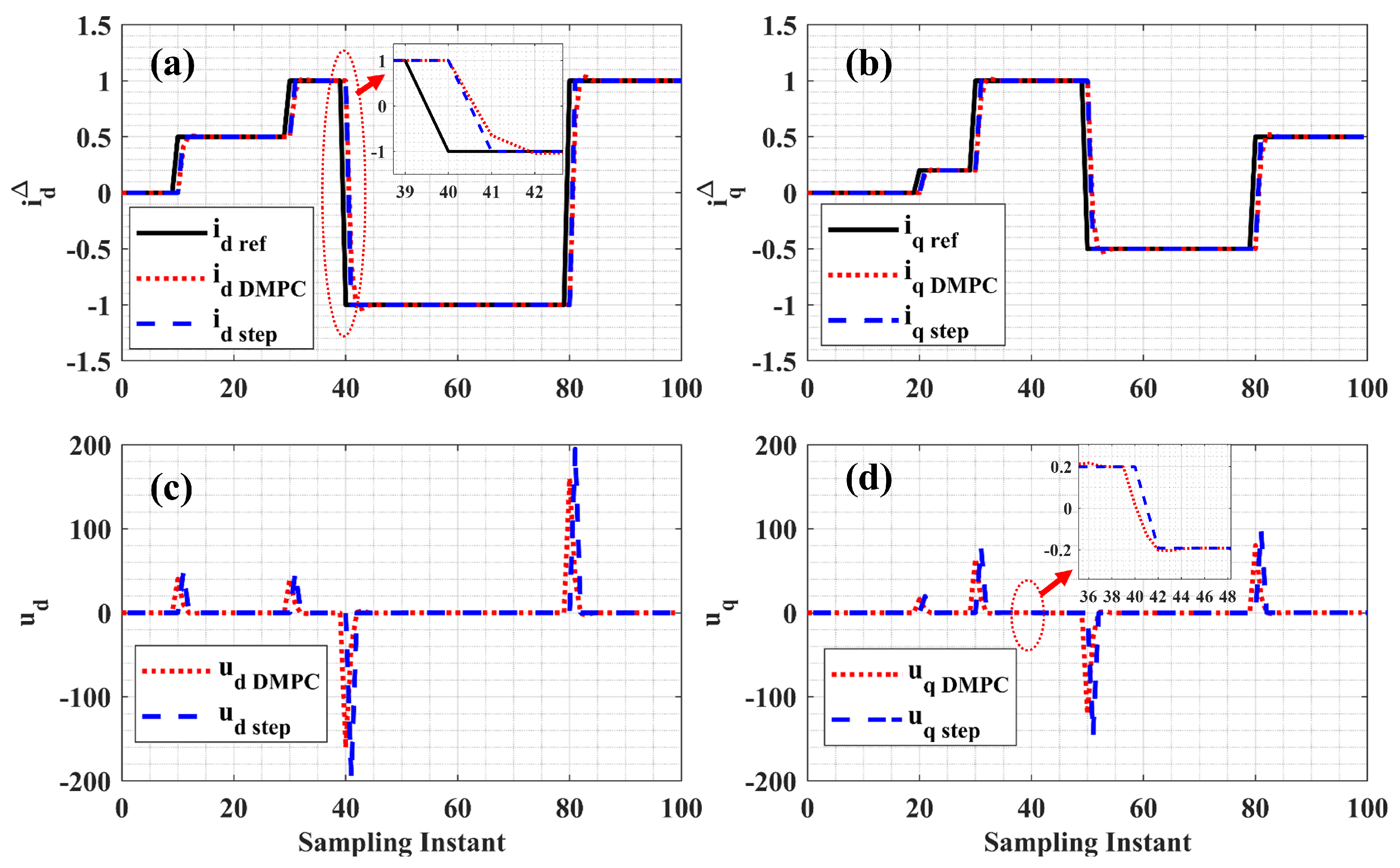
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Base power | P | 800 | MVA |
| Arm resistance | 0 | ||
| Equivalent transformer inductance | 35 | mH | |
| Equivalent transformer resistance | 0.363 | ||
| Submodule capacitance | C | 10 | mF |
| Number of submodules | 400 | - | |
| Fundamental grid frequency | f | 50 | Hz |
| Rated pole to pole DC voltage | 400 | kV | |
| Rated line to line primary voltage | 380 | kV | |
| Rated line to line secondary voltage | 220 | kV |
| Parameter | Value |
|---|---|
| Active and reactive power controller proportional gain | 0.08 [pu] |
| Active and reactive power controller integral gain | 4 [p.u.] |
| Output current controller proportional gain | 0.8 [p.u.] |
| Output current controller integral gain | 80 [p.u.] |
| Circulating current suppression controller proportional gain | 0.8 [p.u.] |
| Circulating current suppression controller integral gain | 80 [p.u.] |
| Signals | Error in Percentage | ||
|---|---|---|---|
| Pre-Disturbance | During-Disturbance | Post-Disturbance | |
| 0.05 | 0.48 | 0.02 | |
| 0.04 | 0.91 | 0.04 | |
| 1.37 | 0.92 | 0.43 | |
| 1.05 | 1.78 | 0.42 | |
| 1.00 | 1.55 | 0.39 | |
| 0.15 | 0.74 | 0.57 | |
| Signals | Error in Percentage | ||
|---|---|---|---|
| Pre-Disturbance | During-Disturbance | Post-Disturbance | |
| 0.04 | 0.16 | 0.03 | |
| 0.03 | 0.22 | 0.02 | |
| 1.50 | 1.52 | 1.49 | |
| 0.98 | 1.85 | 0.95 | |
| 0.98 | 0.79 | 0.97 | |
| 0.25 | 0.32 | 0.24 | |
| Signals | Error in Percentage | ||
|---|---|---|---|
| Pre-Disturbance | During-Disturbance | Post-Disturbance | |
| 0.05 | 1.28 | 0.05 | |
| 0.06 | 2.55 | 0.11 | |
| 1.35 | 2.33 | 1.79 | |
| 1.02 | 3.74 | 1.34 | |
| 0.99 | 3.96 | 1.25 | |
| 0.52 | 1.41 | 0.22 | |
| Name | Symbol | Value |
|---|---|---|
| Arm inductance | 0.15 [p.u.] | |
| Arm resistance | 0.0015 [p.u.] | |
| AC filter inductance | 0.12 [p.u.] | |
| AC filter resistance | 0.003 [p.u.] | |
| Sample time | 2 [ms] |
| Cases | Variables | Value (Sampling Instance) | Value (Sampling Instance) |
|---|---|---|---|
| Small Disturbance | Active power | 0.5 p.u. (10) | 1 p.u. (30) |
| Reactive power | 0.2 p.u. (20) | 1 p.u. (30) | |
| Large Disturbance | Active power reversal | −1 p.u. (40) | 1 p.u. (80) |
| Reactive power reversal | −1 p.u. (50) | 0.5 p.u. (80) |
| MPC | DLQR | Relative Error |
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shetgaonkar, A.; Lekić, A.; Rueda Torres, J.L.; Palensky, P. Microsecond Enhanced Indirect Model Predictive Control for Dynamic Power Management in MMC Units. Energies 2021, 14, 3318. https://doi.org/10.3390/en14113318
Shetgaonkar A, Lekić A, Rueda Torres JL, Palensky P. Microsecond Enhanced Indirect Model Predictive Control for Dynamic Power Management in MMC Units. Energies. 2021; 14(11):3318. https://doi.org/10.3390/en14113318
Chicago/Turabian StyleShetgaonkar, Ajay, Aleksandra Lekić, José Luis Rueda Torres, and Peter Palensky. 2021. "Microsecond Enhanced Indirect Model Predictive Control for Dynamic Power Management in MMC Units" Energies 14, no. 11: 3318. https://doi.org/10.3390/en14113318
APA StyleShetgaonkar, A., Lekić, A., Rueda Torres, J. L., & Palensky, P. (2021). Microsecond Enhanced Indirect Model Predictive Control for Dynamic Power Management in MMC Units. Energies, 14(11), 3318. https://doi.org/10.3390/en14113318








