A New Solar Assisted Heat Pump System with Underground Energy Storage: Modelling and Optimisation
Abstract
:1. Introduction
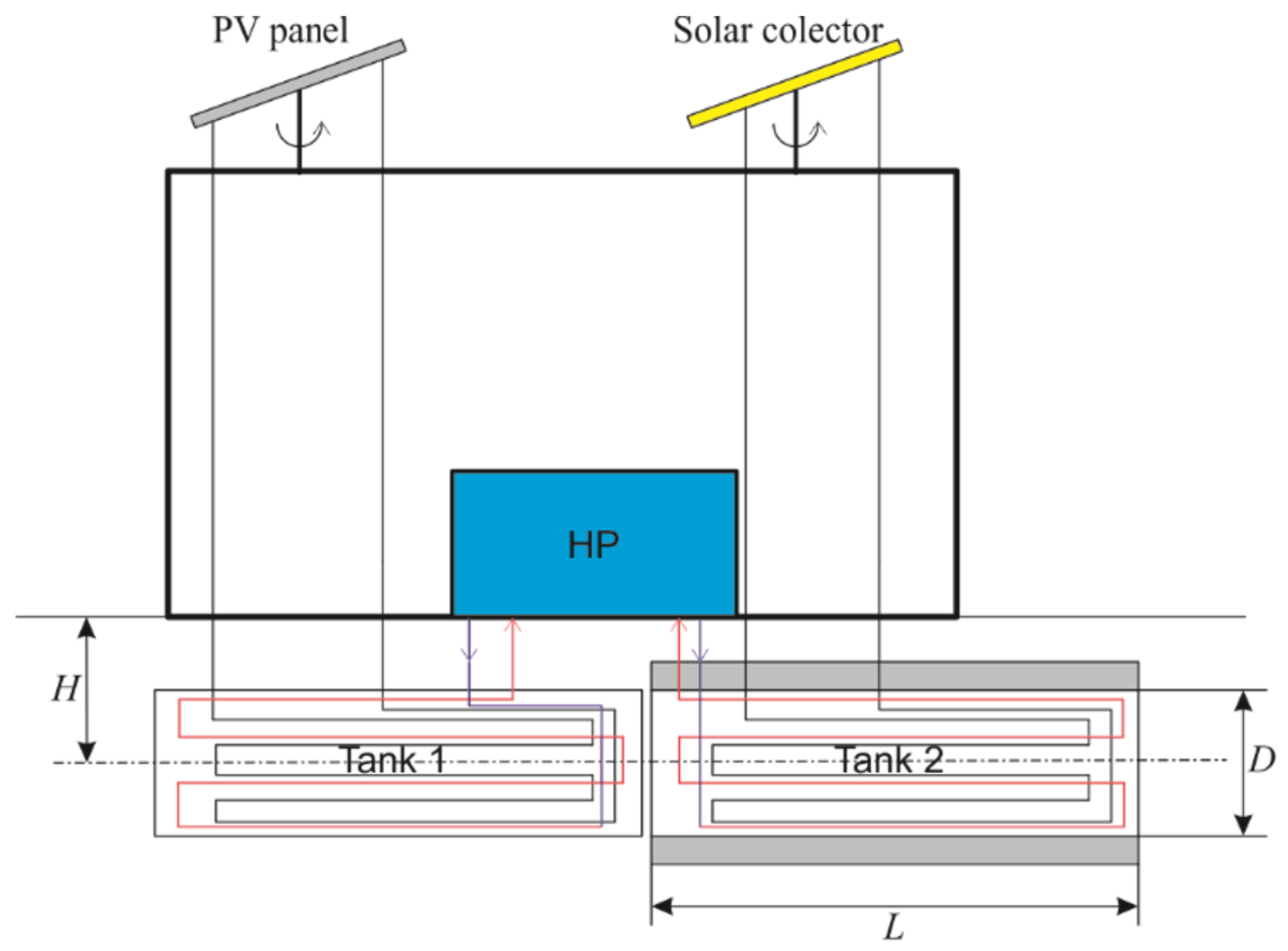
2. A Heating System Based on a Photovoltaic Panel and a Solar Collector
2.1. Process Description
2.2. Comparison with Other Systems
2.3. Process Modelling
- D is the tank diameter (3 m);
- L is length of the tank (10 m);
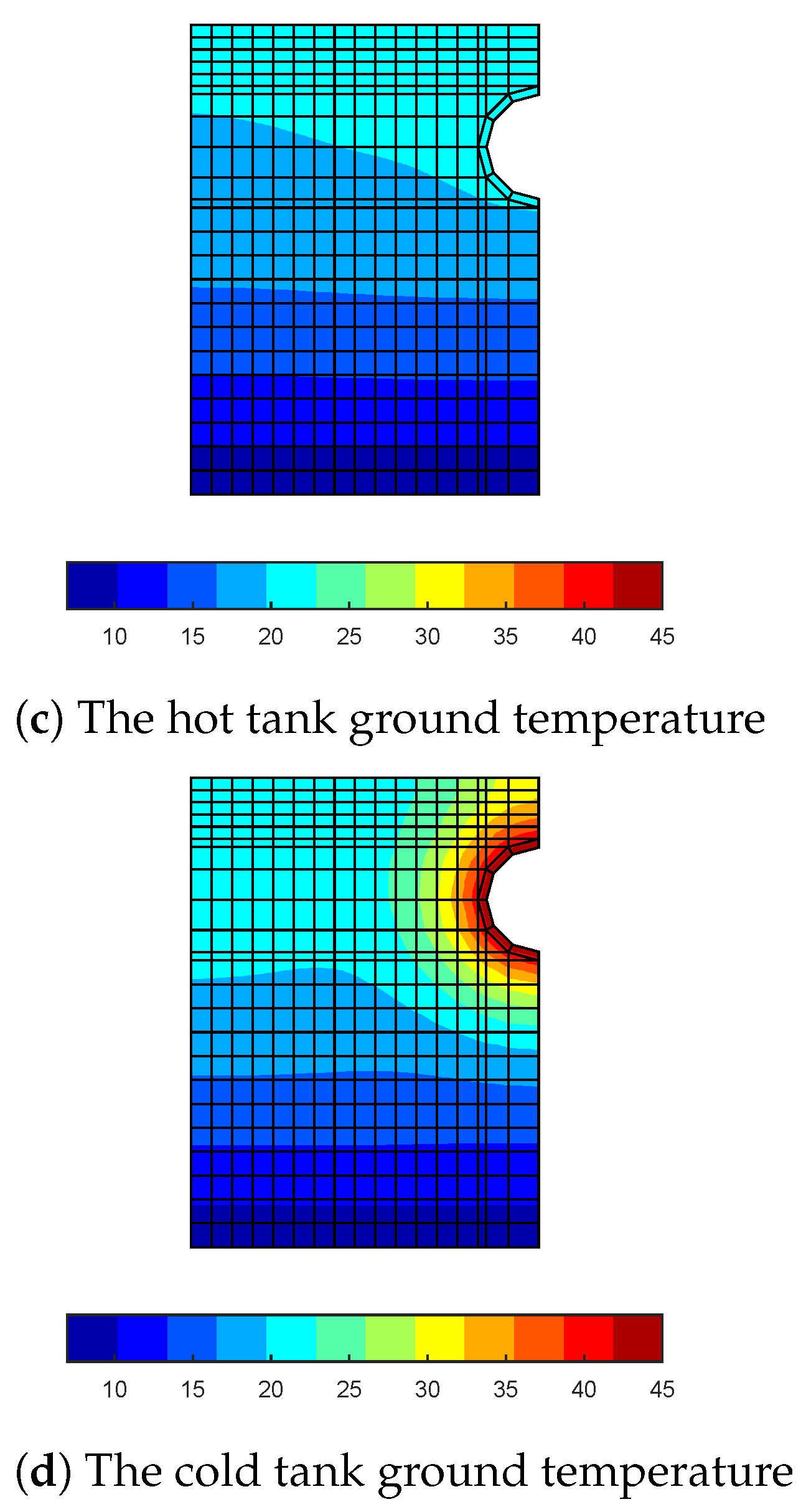
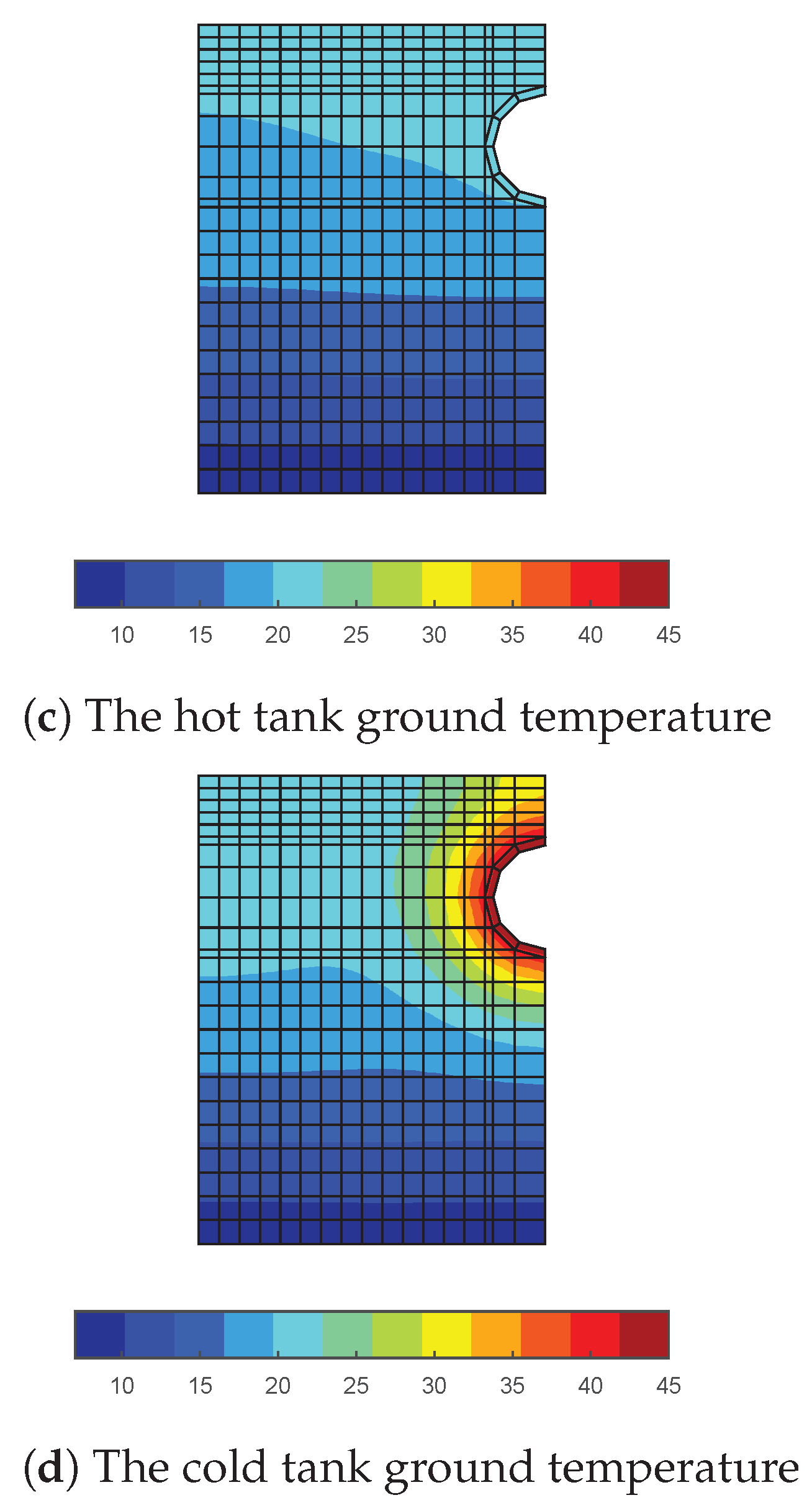
- and are ground heat transfer to the first and the second tank, respectively;
- is heat transferred through the heat pump to the building;
- is solar heat flow from PVT panels cooling;
- is solar heat flow from solar collectors;
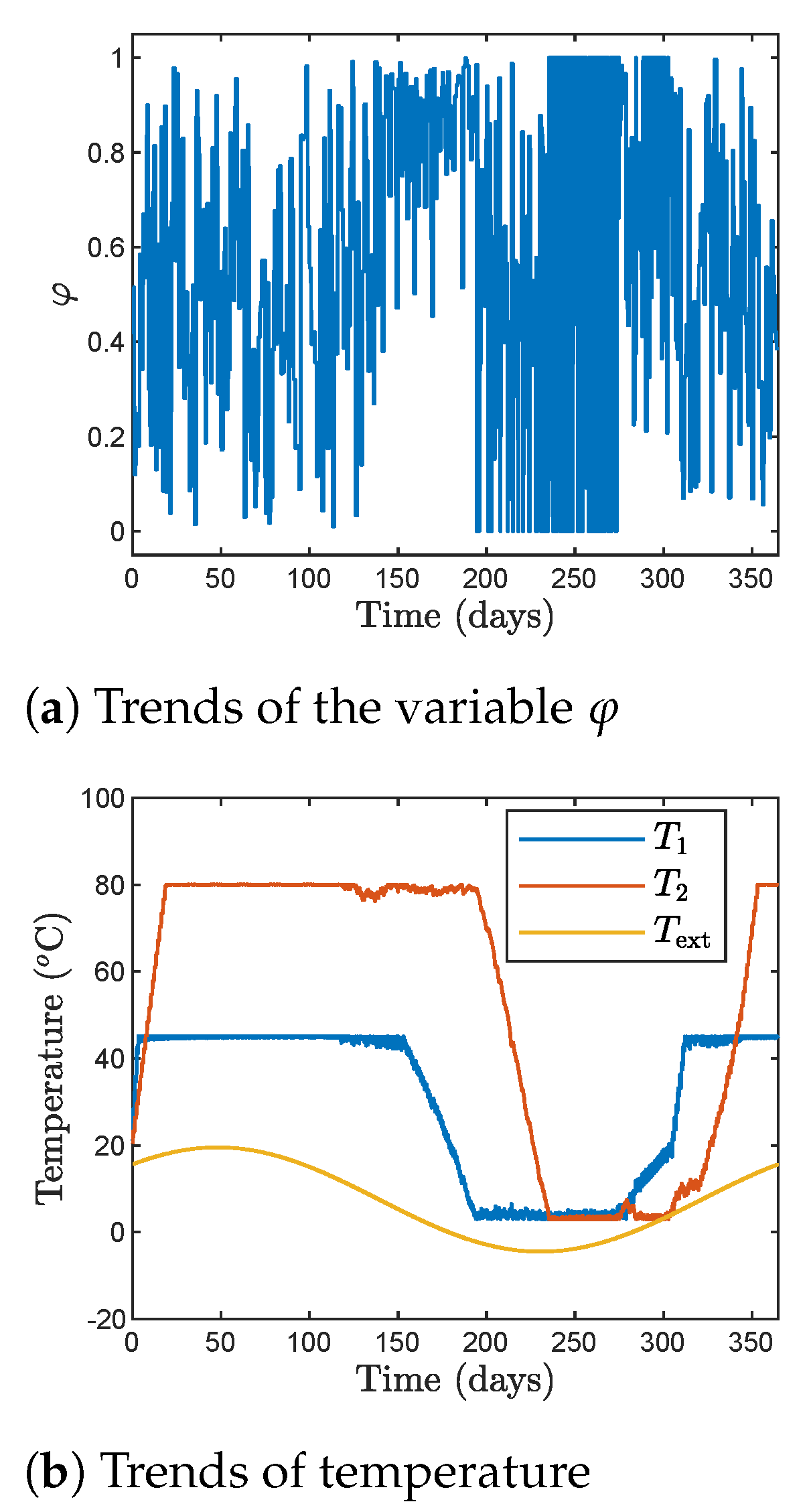
- , are water temperatures in the storages tanks 1 and 2, respectively;
- is specific heat of water;
- is the ratio of heat taken from the tank 1 to the entire heat taken by the heat pump;
- is density of water.
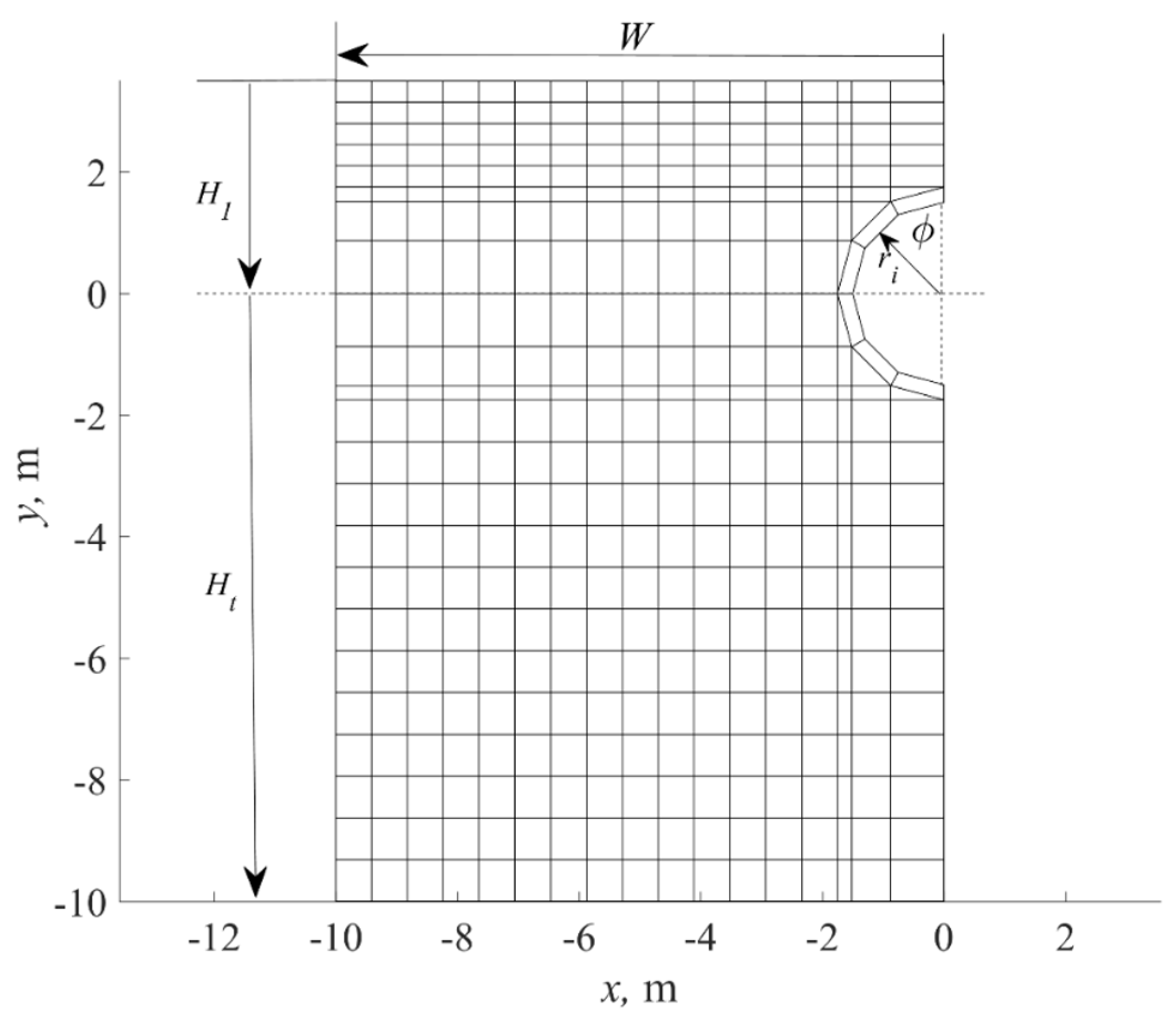
- is the total height of the domain assumed as 13 m;
- is the yearly average ground temperature, assumed to be equal to 7.5 ;
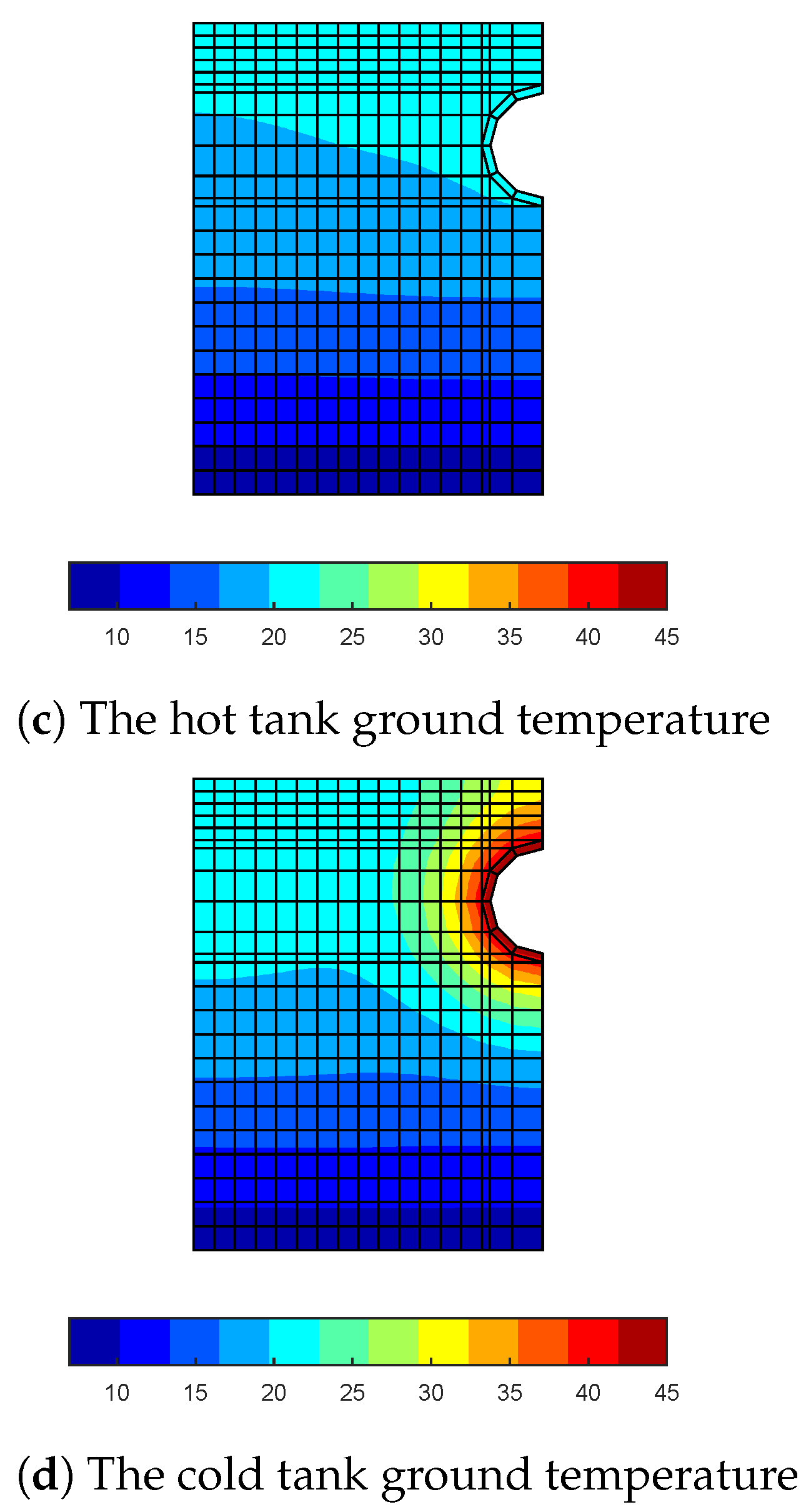
- is the ground temperature, the initial ground temperature is assumed to be equal to 20 ;
- is the overall heat transfer coefficient from the ground top layer to the external environment, equal to ;
- W is the width of the domain, assumed as 10 m;
- c is specific heat capacity of the ground;
- and are the heat transfer coefficients from the tank 1 and tank 2, respectively;
- k is thermal conductivity of the ground;
- x and y are Cartesian coordinates;
- is density of the ground.
2.4. Optimisation Objective
- To use less electrical energy due to the increase in the overall COP of the heat pump;
- To use mostly the underground energy storage unit instead of a borehole heat exchanger to allow efficient ground regeneration.
3. Optimisation Methods Used
3.1. Gradient-Based Optimisation Algorithm
3.2. Genetic Algorithm
3.3. Particle Swarm Optimisation Algorithm
3.4. Jaya Algorithm
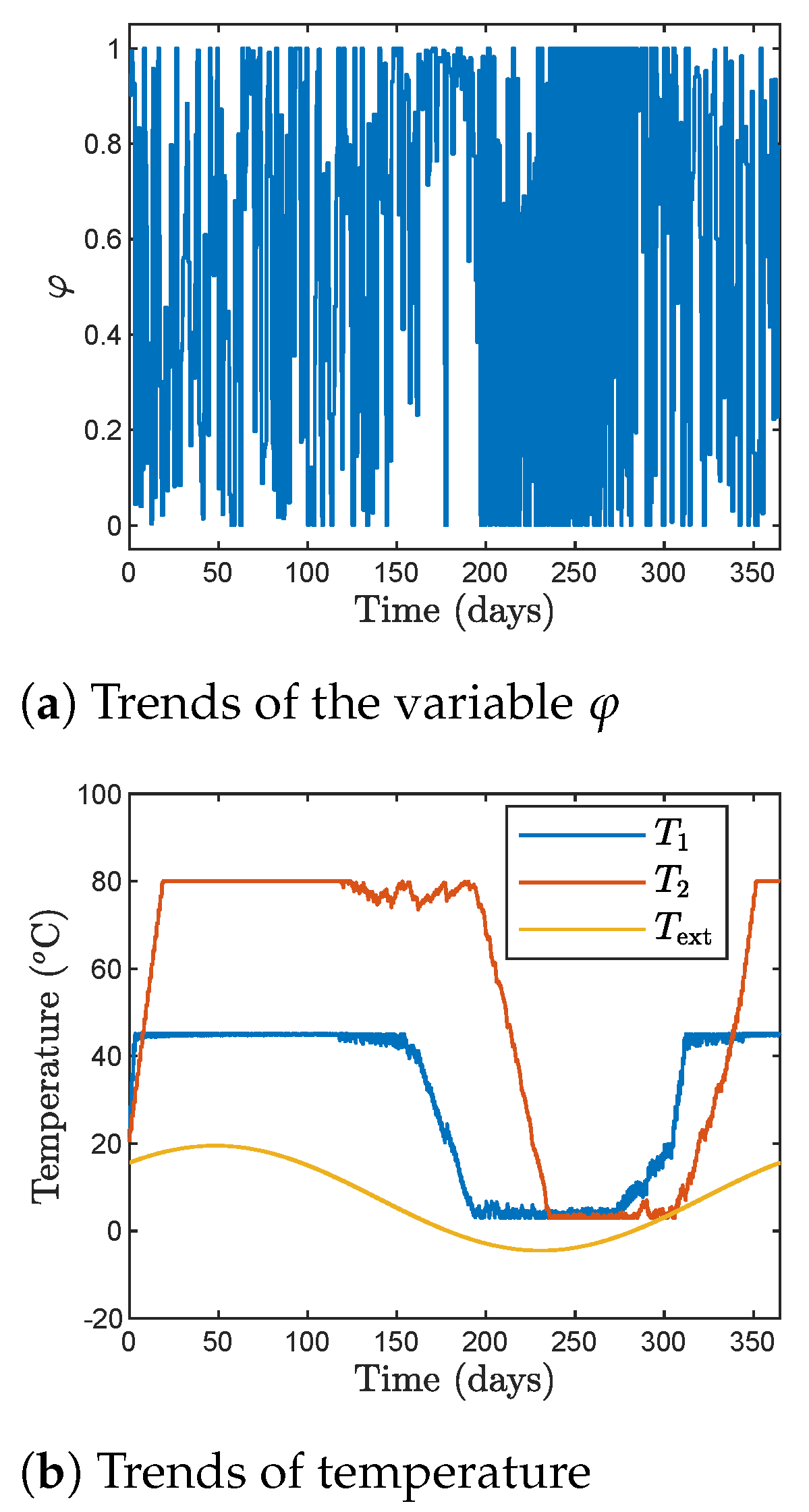
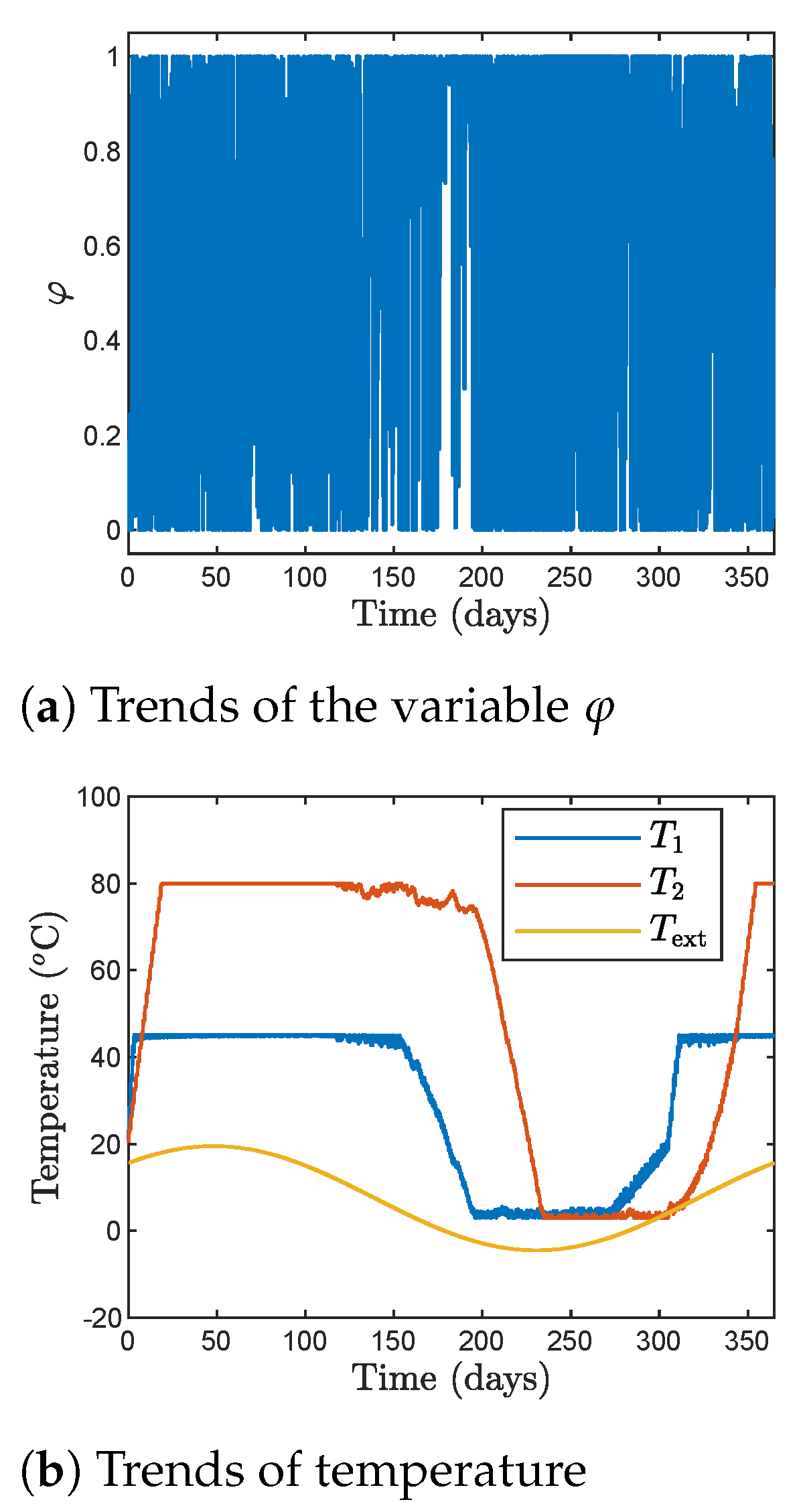
4. Results of Simulations
- In spite of the fact that in the gradient-based SQP algorithm relatively high number of iterations is used, it gives the worst results. Probably, the obtained results are shallow local minima.
- All three tested heuristic optimisation methods give better results than the SQP one.
- The PSO algorithm is the worst one in the group of the heuristic optimisation methods. Numerous attempts have been made to improve the results by using a larger population of individuals or by increasing the number of possible iterations, but such approaches do not lead to any better results. Typically, after some 50–80% of the allowed iterations, the optimised cost-function is practically constant and calculations are terminated.
- In comparison with the PSO algorithm, better results, in particular for the sampling time equal to 24 h, 12 h, or 6 h, are obtained by the genetic algorithm, although we may observe that as the sampling time is reduced, the genetic algorithm gives worse results. For the sampling time equal to 3 h, 2 h, or 1 h, the obtained results are only slightly better than those obtained by the PSO algorithm. Similarly to the PSO algorithm, also in the case of the genetic algorithm, increasing the number of individuals or the number of possible iterations does not yield better results.
- Generally, the Jaya algorithm gives the best results, the only exception is for = 24 h in which the genetic algorithm is better, but the difference is really insignificant.
- It is important that the Jaya algorithm finds good solutions for all tested values of the sampling time , which is not true in the case of the second-best approach, i.e., the genetic algorithm.
- As far as heuristic optimisation algorithms are concerned, the presented results have been achieved for exactly the same number of maximal iterations (as specified in Table 2 for the consecutive values of the sampling time , the only exception is for the sampling time 1 h, the Jaya algorithm needs a lower number of iterations) and population size (30 individuals).
- Decreasing the sampling instant leads to increasing the number of decision variables in the optimization problem. The more the decision variables, the more difficult the optimization task. Hence, more iterations of the optimization algorithms are necessary as shown in Table 2. It greatly increases the resulting calculation time.
- Since decreasing the sampling time does not improve the final value of the cost-function but only makes calculations more time-consuming, it is recommended to use quite long sampling periods, e.g., 24 h or 12 h.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Acronyms
| COP | Coefficient Of Performance |
| DHW | Domestic Hot Water |
| GA | Genetic Algorithm |
| MPC | Model Predictive Control |
| PSO | Particle Swarm Optimisation |
| PVT | Photovoltaic Thermal Hybrid Solar Panels |
| RES | Renewable Energy Sources |
| SAGSHP | Solar-Assisted Ground Source Heat Pump |
| SQP | Sequential Quadratic Programming |
References
- Vallati, A.; Ocłoń, P.; Colucci, C.; Mauri, L.; de Lieto Vollaro, R.; Taler, J. Energy analysis of a thermal system composed by a heat pump coupled with a PVT solar collector. Energy 2019, 174, 91–96. [Google Scholar] [CrossRef]
- Sun, T.; Yang, L.; Jin, L.; Luo, Z.; Zhang, Y.; Liu, Y.; Wang, Z. A novel solar-assisted ground-source heat pump (SAGSHP) with seasonal heat-storage and heat cascade utilization: Field test and performance analysis. Sol. Energy 2020, 201, 362–372. [Google Scholar] [CrossRef]
- Naranjo-Mendoza, C.; Oyinlola, M.A.; Wright, A.J.; Greenough, R.M. Experimental study of a domestic solar-assisted ground source heat pump with seasonal underground thermal energy storage through shallow boreholes. Appl. Therm. Eng. 2019, 162, 114218. [Google Scholar] [CrossRef]
- Sakellariou, E.I.; Axaopoulos, P.J.; Wright, A.J. Energy and economic evaluation of a solar assisted ground source heat pump system for a north Mediterranean city. Energy Build. 2021, 231, 110640. [Google Scholar] [CrossRef]
- Fine, J.P.; Nguyen, H.V.; Friedman, J.; Leong, W.H.; Dworkin, S.B. A simplified ground thermal response model for analyzing solar-assisted ground source heat pump systems. Energy Convers. Manag. 2018, 165, 276–290. [Google Scholar] [CrossRef]
- Nouri, G.; Noorollahi, Y.; Yousefi, H. Designing and optimization of solar assisted ground source heat pump system to supply heating, cooling and hot water demands. Geothermics 2019, 82, 212–231. [Google Scholar] [CrossRef]
- Verma, V.; Murugesan, K. Experimental study of solar energy storage and space heating using solar assisted ground source heat pump system for Indian climatic conditions. Energy Build. 2017, 139, 569–577. [Google Scholar] [CrossRef]
- Dai, L.; Li, S.; Mu, L.D.; Li, X.; Shang, Y.; Dong, M. Experimental performance analysis of a solar assisted ground source heat pump system under different heating operation modes. Appl. Therm. Eng. 2015, 75, 325–333. [Google Scholar] [CrossRef]
- Verma, V.; Murugesan, K. Optimization of solar assisted ground source heat pump system for space heating application by Taguchi method and utility concept. Energy Build. 2014, 82, 296–309. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer: Berlin, Germany; New York, NY, USA, 2006. [Google Scholar]
- Powell, M.J.D. A fast algorithm for nonlinearly constrained optimization calculations. In Numerical Analysis; Lecture Notes in Mathematics; Watson, G.A., Ed.; Springer: Dundee, UK, 1978; Volume 630, pp. 144–157. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Rao, R.V. A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar]
- Ocłoń, P.; Cisek, P.; Kozak-Jagieła, E.; Taler, J.; Taler, D.; Skrzyniowska, D.; Fedorczak-Cisak, M. Modeling and experimental validation and thermal performance assessment of a sun-tracked and cooled PVT system under low solar irradiation. Energy Convers. Manag. 2020, 222, 113289. [Google Scholar] [CrossRef]
- Zima, W.; Cisek, P.; Cebula, P. Mathematical model of an innovative double U-tube sun-tracked PTC and its experimental verification. Energy 2021, 235, 121293. [Google Scholar] [CrossRef]
- Ławryńczuk. Identification of Wiener models for dynamic and steady-state performance with application to solid oxide fuel cell. Asian J. Control. 2019, 21, 1836–1846. [Google Scholar] [CrossRef]
- Ławryńczuk, M. Computationally Efficient Model Predictive Control Algorithms: A Neural Network Approach. In Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2014; Volume 3. [Google Scholar]
- Aji, S.S.; Kim, Y.S.; Ahn, K.Y.; Lee, Y.D. Life-cycle cost minimization of gas turbine power cycles for distributed power generation using sequential quadratic programming method. Energies 2018, 11, 3511. [Google Scholar] [CrossRef] [Green Version]
- Białoń, T.; Pasko, M.; Niestrój, R. Developing induction motor state observers with increased robustness. Energies 2020, 13, 5487. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, C.; Li, K.; Zhan, Y.; Sun, B. Hybrid adaptive control for PEMFC gas pressure. Energies 2020, 13, 5334. [Google Scholar] [CrossRef]
- Narayanan, M.; de Lima, A.F.; de Azevedo Dantas, A.F.O.; Commerell, W. Development of a coupled TRNSYS-MATLAB simulation framework for model predictive control of integrated electrical and thermal residential renewable energy system. Energies 2020, 13, 5761. [Google Scholar] [CrossRef]
- Stoumpos, S. Multiobjective optimisation of a marine dual fuel engine equipped with exhaust gas recirculation and air bypass systems. Energies 2020, 13, 5021. [Google Scholar] [CrossRef]
- Torres-Madroñero, J.L.; Nieto-Londoño, C.; Sierra-Pérez, J. Hybrid energy systems sizing for the colombian context: A genetic algorithm and particle swarm optimization approach. Energies 2020, 13, 5648. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Yao, J. Multi-objective optimization of integrated process planning and scheduling considering energy savings. Energies 2020, 13, 6181. [Google Scholar] [CrossRef]
- Ding, T.; Chang, L.; Li, C.; Feng, C.; Zhang, N. A mixed-strategy-based whale optimization algorithm for parameter identification of hydraulic turbine governing systems with a delayed water hammer effect. Energies 2018, 11, 2367. [Google Scholar] [CrossRef] [Green Version]
- Lamedica, R.; Ruvio, A.; Palagi, L.; Mortelliti, N. Optimal siting and sizing of wayside energy storage systems in a D.C. railway line. Energies 2020, 13, 6271. [Google Scholar] [CrossRef]
- Liu, J.; Bai, M.; Long, Z.; Liu, J.; Ma, Y.; Yu, D. Early fault detection of gas turbine hot components based on exhaust gas temperature profile continuous distribution estimation. Energies 2020, 13, 5950. [Google Scholar] [CrossRef]
- Vishnu, M.; Sunil Kumar, T.K. An improved solution for reactive power dispatch problem using diversity-enhanced particle swarm optimization. Energies 2020, 13, 2862. [Google Scholar] [CrossRef]
- Chakraborty, U.K. Proton exchange membrane fuel cell stack design optimization using an improved Jaya algorithm. Energies 2019, 12, 3176. [Google Scholar] [CrossRef] [Green Version]
- Rao, R.V.; More, K.C.; Taler, J.; Ocłoń, P. Dimensional optimization of a micro-channel heat sink using Jaya algorithm. Appl. Therm. Eng. 2016, 103, 572–582. [Google Scholar] [CrossRef]
- Rao, R.V.; Saroj, A.; Ocłoń, P.; Taler, J.; Lakshmi, J. A posteriori multiobjective self-adaptive multipopulation Jaya algorithm for optimization of thermal devices and cycles. IEEE Access 2019, 7, 4113–4134. [Google Scholar] [CrossRef]
| Month | Monthly Averaged Daily Solar Irradiation Flux | Irradiation Hours |
|---|---|---|
| January | 400 | 2.8 |
| February | 400 | 3.6 |
| March | 500 | 4.8 |
| April | 600 | 7 |
| May | 800 | 7.7 |
| June | 800 | 7.9 |
| July | 900 | 8.8 |
| August | 900 | 7.5 |
| September | 700 | 6.1 |
| October | 500 | 4.8 |
| November | 400 | 3.4 |
| December | 400 | 2.5 |
| SQP Algorithm | PSO Algorithm | Genetic Algorithm | Jaya Algorithm | |
|---|---|---|---|---|
| 24 h | 200 | 500 | 500 | 500 |
| 12 h | 200 | 1000 | 1000 | 1000 |
| 6 h | 300 | 1500 | 1500 | 1500 |
| 3 h | 500 | 2000 | 2000 | 2000 |
| 2 h | 500 | 2500 | 2500 | 2500 |
| 1 h | 700 | 3000 | 3000 | 2500 |
| SQP Algorithm | PSO Algorithm | Genetic Algorithm | Jaya Algorithm | |
|---|---|---|---|---|
| 24 h | 0.8984 | 0.9045 | 0.9328 | 0.9318 |
| 12 h | 0.8986 | 0.9033 | 0.9289 | 0.9330 |
| 6 h | 0.8984 | 0.9018 | 0.9192 | 0.9317 |
| 3 h | 0.8984 | 0.9006 | 0.9054 | 0.9298 |
| 2 h | 0.8982 | 0.8997 | 0.9046 | 0.9306 |
| 1 h | 0.8984 | 0.9000 | 0.9035 | 0.9280 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ocłoń, P.; Ławryńczuk, M.; Czamara, M. A New Solar Assisted Heat Pump System with Underground Energy Storage: Modelling and Optimisation. Energies 2021, 14, 5137. https://doi.org/10.3390/en14165137
Ocłoń P, Ławryńczuk M, Czamara M. A New Solar Assisted Heat Pump System with Underground Energy Storage: Modelling and Optimisation. Energies. 2021; 14(16):5137. https://doi.org/10.3390/en14165137
Chicago/Turabian StyleOcłoń, Paweł, Maciej Ławryńczuk, and Marek Czamara. 2021. "A New Solar Assisted Heat Pump System with Underground Energy Storage: Modelling and Optimisation" Energies 14, no. 16: 5137. https://doi.org/10.3390/en14165137
APA StyleOcłoń, P., Ławryńczuk, M., & Czamara, M. (2021). A New Solar Assisted Heat Pump System with Underground Energy Storage: Modelling and Optimisation. Energies, 14(16), 5137. https://doi.org/10.3390/en14165137








