Heterogeneous Inertia Estimation for Power Systems with High Penetration of Converter-Interfaced Generation
Abstract
:1. Introduction
2. System Frequency Dynamics
2.1. Synchronous Generators Dynamics
2.2. Frequency Dynamics of Grid-Forming Converter-Interfaced Generation
2.3. Aggregated Frequency Dynamics
3. Parameterization and Regression
4. Simulation-Based Analysis
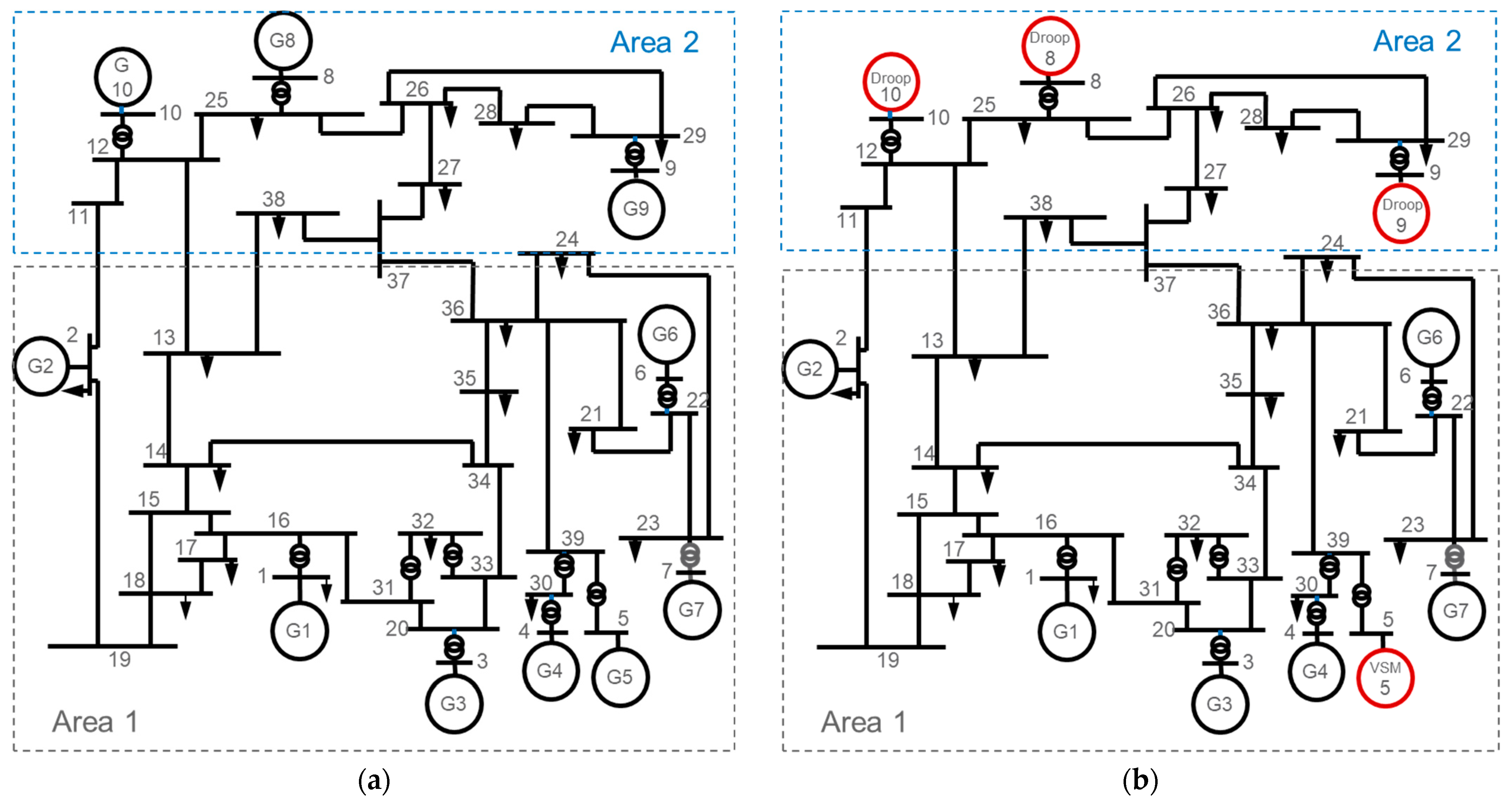
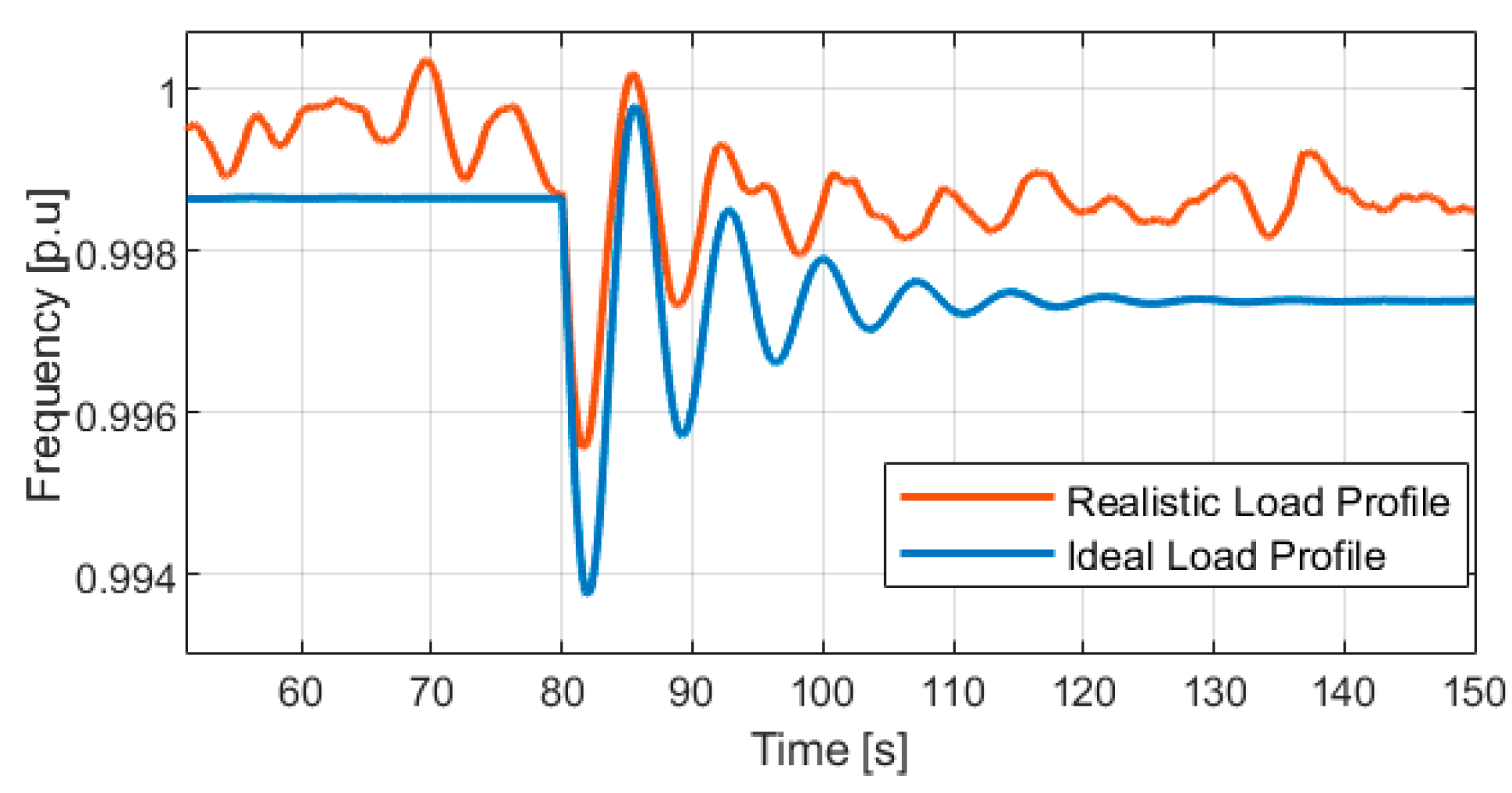
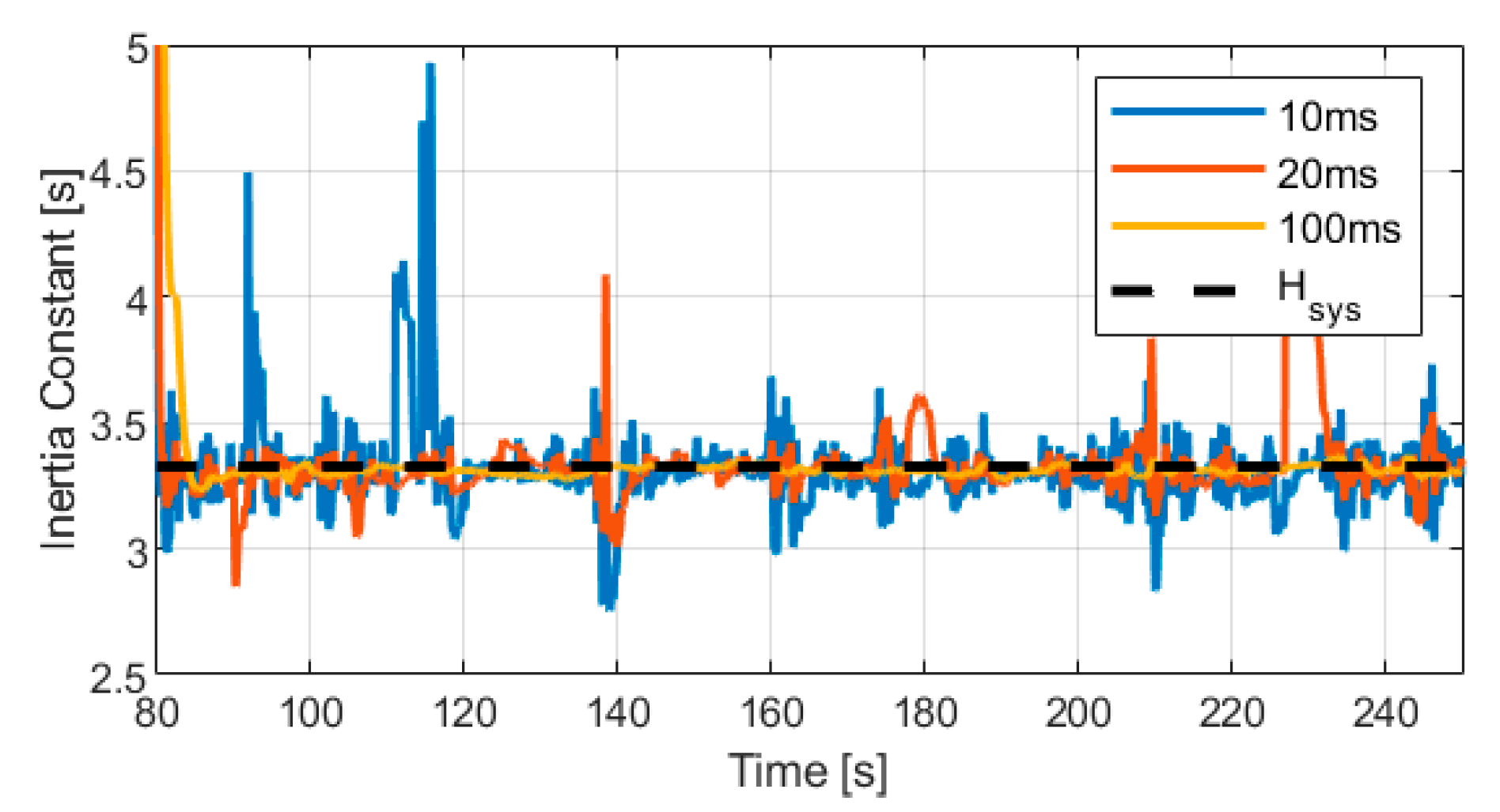
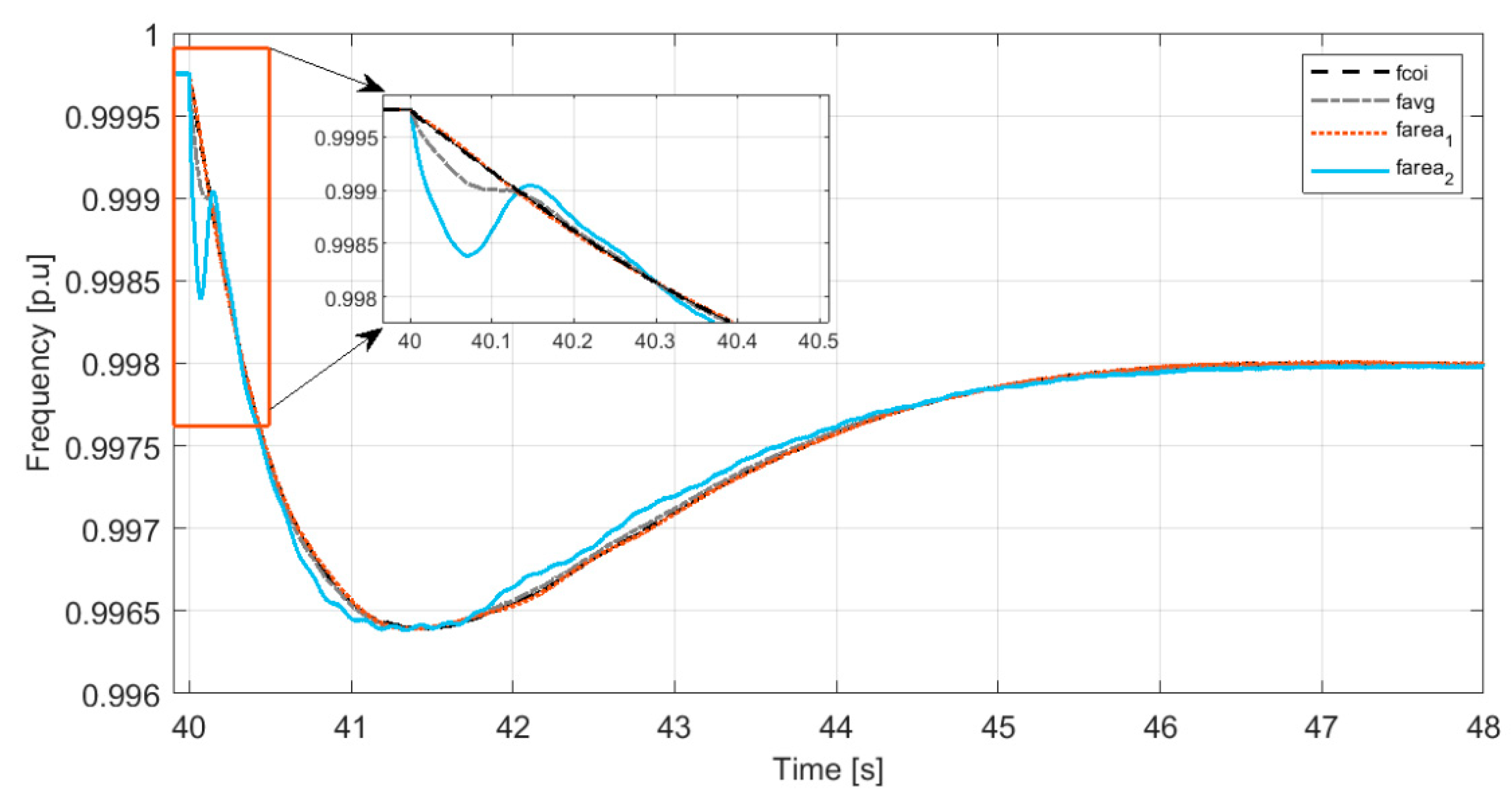
4.1. Case Study I: Estimation Performance and Validation
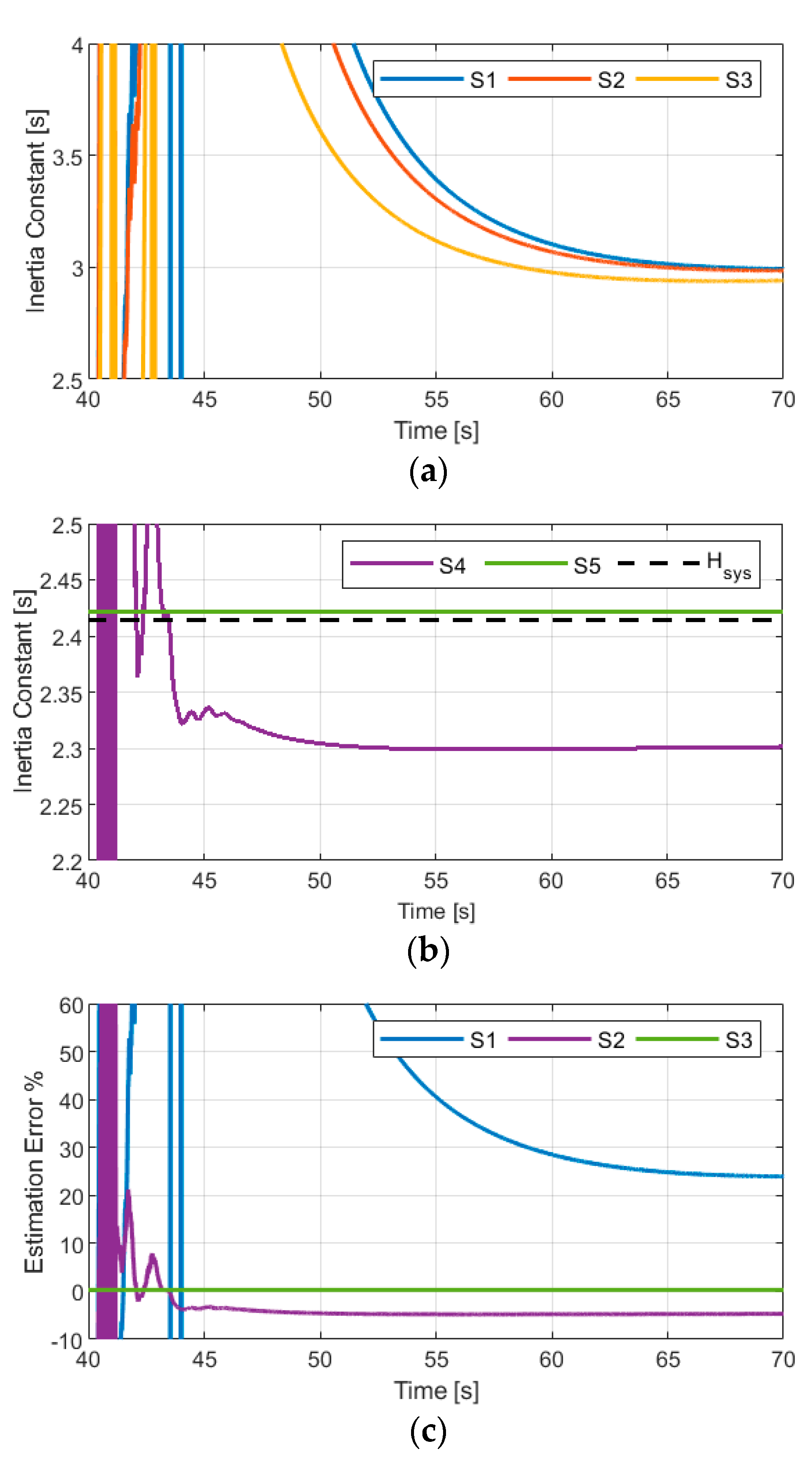
4.2. Case Study II: Effect of Inertia Heterogeneity on the Inertia Estimation
- A.
- Inertia and damping estimation at the machine level: machine parameters identification
- B.
- System inertia estimation with mixed generation
5. Discussion and Conclusions
- The proposed estimation method, has very high accuracy. It is demonstrated that, in real-world scenarios with stochastic load variations, the estimation still works with an estimation error of less than 1%.
- The estimation method can be applied during normal operation and hence it can provide continuous online estimations.
- The estimation method can be used for identifying the inertia and damping coefficients of both SGs and converter-interfaced generation with high accuracy. The estimation errors are less than 0.5% and 3% for SGs and converter-interfaced generation, respectively.
- The estimation method successfully estimates the amount of virtual inertia provided by the low-pass filter used in droop controllers. This result confirms the relationship between droop controllers and VSM and shows that the swing equation can be used for modelling the droop control. Furthermore, additional control parameters can be identified, i.e., using Equation (13), the cut-off frequency of the low pass filter of the converter can be calculated.
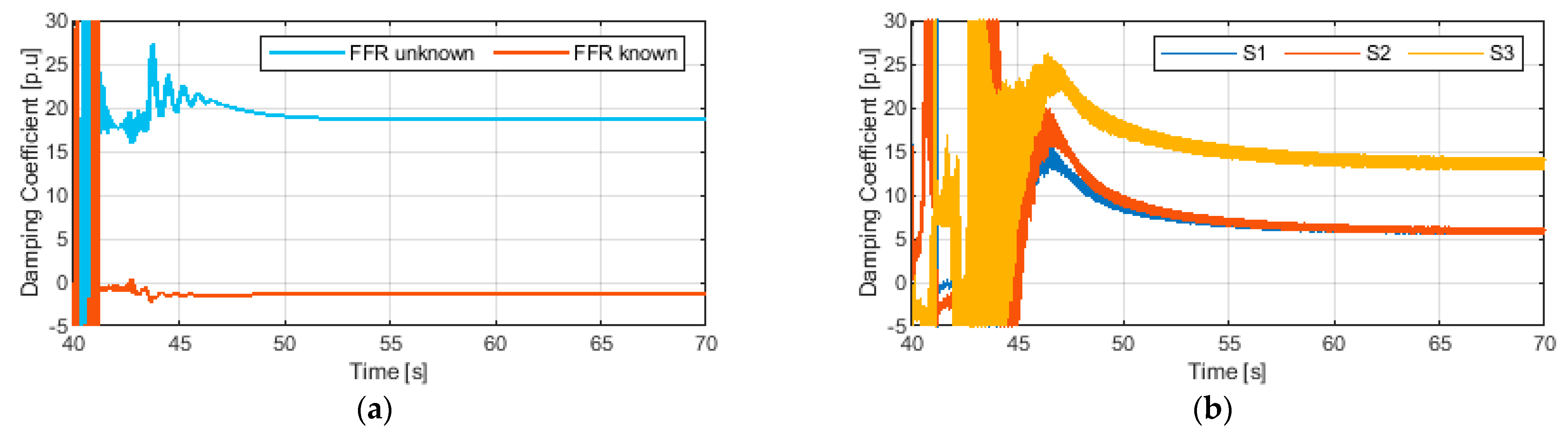
- The proposed approach eliminates the impact of damping, including PFC and FFR, on the accuracy of inertia estimation. Hence, the knowledge of PFC and FFR models is not required.
- When it comes to systems with heterogeneous inertia, estimating the overall system inertia at the system level results in large estimation errors. Hence, it is crucial to estimate the local inertia at an area level. This approach would be desirable by SOs not only to achieve accurate estimation results but also because the local inertia values per area are needed for protective actions and regional ancillary markets. Moreover, a distributed approach, considerably reduces the amount of data that needs to be centrally processed.
- The time scale difference between FFR and PFC affects the convergence time of the inertia estimation of systems with mixed generation.
- The inertia estimation accuracy can be further improved by performing the estimation at a machine level, in contrast to at an area level, and then calculate the overall system inertia.
- The timescale difference between the FFR and PFC affects the damping coefficient estimation accuracy. Hence, for the damping coefficient estimation it is crucial to either perform the estimation per area with resources of similar control timescales or in case the knowledge of the PFC models is available, include the PFC models into the parameterization and estimate the damping resulting from the faster controls, i.e., converter-interfaced generation.
Author Contributions
Funding
Conflicts of Interest
References
- Ulbig, A.; Borsche, T.S.; Andersson, G. Impact of Low Rotational Inertia on Power System Stability and Operation. IFAC Proc. 2014, 47, 7290–7297. [Google Scholar] [CrossRef] [Green Version]
- ENTSO-E. Fast Frequency Reserve—Solution to the Nordic Inertia Challenge. Available online: https://www.fingrid.fi/globalassets/dokumentit/fi/sahkomarkkinat/reservit/fast-frequency-reserve-solution-to-the-nordic-inertia-challenge.pdf (accessed on 16 August 2021).
- ENTSO-E. Future System Inertia. 2018. Available online: https://eepublicdownloads.entsoe.eu/clean-documents/Publications/SOC/Nordic/Nordic_report_Future_System_Inertia.pdf (accessed on 16 August 2021).
- Cai, G.; Wang, B.; Yang, D.; Sun, Z.; Wang, L. Inertia Estimation Based on Observed Electromechanical Oscillation Response for Power Systems. IEEE Trans. Power Syst. 2019, 34, 4291–4299. [Google Scholar] [CrossRef]
- Wall, P.; Gonzalez-Longatt, F.; Terzija, V. Estimation of generator inertia available during a disturbance. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar] [CrossRef]
- Ashton, P.M.; Taylor, G.A.; Carter, A.M.; Bradley, M.E.; Hung, W. Application of phasor measurement units to estimate power system inertial frequency response. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar] [CrossRef]
- Zografos, D.; Ghandhari, M. Estimation of power system inertia. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016. [Google Scholar] [CrossRef]
- Zografos, D.; Ghandhari, M. Power system inertia estimation by approaching load power change after a disturbance. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar] [CrossRef]
- Cao, X.; Stephen, B.; Abdulhadi, I.F.; Booth, C.D.; Burt, G.M. Switching Markov Gaussian Models for Dynamic Power System Inertia Estimation. IEEE Trans. Power Syst. 2016, 31, 3394–3403. [Google Scholar] [CrossRef] [Green Version]
- Tuttelberg, K.; Kilter, J.; Wilson, D.; Uhlen, K. Estimation of Power System Inertia from Ambient Wide Area Measurements. IEEE Trans. Power Syst. 2018, 33, 7249–7257. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Guillamón, A.; Vigueras-Rodríguez, A.; Molina-Garcia, Á. Analysis of power system inertia estimation in high wind power plant integration scenarios. IET Renew. Power Gener. 2019, 13, 2807–2816. [Google Scholar] [CrossRef]
- H2020n Migrate Project. Deliverable D2.1 Requirements for Monitoring & Forecasting PE-Based KPIs. Available online: https://www.h2020-migrate.eu/_Resources/Persistent/7c5fc3e4d17b17ca2e3ea78815bfd35998cf2ae0/D2.1%20-%20Requirements%20for%20Monitoring%20and%20Forecasting%20PE-based%20KPIs.pdf (accessed on 16 August 2021).
- Liu, M.; Chen, J.; Milano, F. On-Line Inertia Estimation for Synchronous and Non-Synchronous Devices. IEEE Trans. Power Syst. 2021, 36, 2693–2701. [Google Scholar] [CrossRef]
- Schiffer, J.; Aristidou, P.; Ortega, R. Online Estimation of Power System Inertia Using Dynamic Regressor Extension and Mixing. IEEE Trans. Power Syst. 2019, 34, 4993–5001. [Google Scholar] [CrossRef] [Green Version]
- Andersson, G. Dynamics and Control of Electric Power Systems. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.471.7315&rep=rep1&type=pdf (accessed on 16 August 2021).
- Athay, T.; Podmore, R.; Virmani, S. A Practical Method for the Direct Analysis of Transient Stability. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 573–584. [Google Scholar] [CrossRef]
- Derviškadić, A.; Zuo, Y.; Frigo, G.; Paolone, M. Under Frequency Load Shedding based on PMU Estimates of Frequency and ROCOF. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018. [Google Scholar] [CrossRef] [Green Version]
- Beltran, O.; Peña, R.; Segundo, J.; Esparza, A.; Muljadi, E.; Wenzhong, D. Inertia Estimation of Wind Power Plants Based on the Swing Equation and Phasor Measurement Units. Appl. Sci. 2018, 8, 2413. [Google Scholar] [CrossRef] [Green Version]
- D’Arco, S.; Suul, J.A. Virtual synchronous machines—Classification of implementations and analysis of equivalence to droop controllers for microgrids. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013. [Google Scholar] [CrossRef]

| Generator | Inertia Constant H (s) | Generator | Inertia Constant H (s) |
|---|---|---|---|
| SG1 | 5 | SG6 | 3.48 |
| SG2 | 3.03 | SG7 | 2.64 |
| SG3 | 3.58 | SG8 | 2.43 |
| SG4 | 2.86 | SG9 | 3.45 |
| SG5 | 2.6 | SG10 | 4.2 |
| Machine | Estimated Inertia Constant H (s) | Relative Estimation Error | Estimated Damping Coefficient D (p.u) | Relative Estimation Error |
|---|---|---|---|---|
| SG1 | 5.0127 | 0.25% | 19.9579 | −0.21% |
| SG2 | 3.0162 | −0.46% | 19.9386 | −0.0031% |
| SG3 | 3.5856 | 0.16% | 19.9966 | −0.017% |
| SG4 | 2.8659 | 0.21% | 19.9962 | −0.015% |
| VSM5 | 2.6187 | 0.72% | 19.5195 | −2.40% |
| SG6 | 3.4865 | 0.19% | 19.9987 | −0.007% |
| SG7 | 2.6469 | 0.26% | 19.9994 | −0.003% |
| Droop8 | 0.3275 | 2.91% | 19.8112 | −0.94% |
| Droop9 | 0.3275 | 2.91% | 18.6245 | −6.88% |
| Droop10 | 0.3275 | 2.91% | 19.9257 | −0.37% |
| Scenario | Inertia Estimation Manner | FFR Parameters Known | PFC Parameters Known |
|---|---|---|---|
| S1 | at system level | X | X |
| S2 | at system level | X | |
| S3 | at system level | ||
| S4 | at area level | X | X |
| S5 | at machine level |
| Scenario | Inertia Constant Estimation Error |
|---|---|
| S1 | 23.96% |
| S2 | 23.45% |
| S3 | 21.80% |
| S4 | 4.69% |
| S5 | 0.29% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nouti, D.; Ponci, F.; Monti, A. Heterogeneous Inertia Estimation for Power Systems with High Penetration of Converter-Interfaced Generation. Energies 2021, 14, 5047. https://doi.org/10.3390/en14165047
Nouti D, Ponci F, Monti A. Heterogeneous Inertia Estimation for Power Systems with High Penetration of Converter-Interfaced Generation. Energies. 2021; 14(16):5047. https://doi.org/10.3390/en14165047
Chicago/Turabian StyleNouti, Diala, Ferdinanda Ponci, and Antonello Monti. 2021. "Heterogeneous Inertia Estimation for Power Systems with High Penetration of Converter-Interfaced Generation" Energies 14, no. 16: 5047. https://doi.org/10.3390/en14165047
APA StyleNouti, D., Ponci, F., & Monti, A. (2021). Heterogeneous Inertia Estimation for Power Systems with High Penetration of Converter-Interfaced Generation. Energies, 14(16), 5047. https://doi.org/10.3390/en14165047








