Author Contributions
Conceptualization, A.B. (Aswin Balasubramanian); methodology, A.B. (Aswin Balasubramanian), F.M. and A.B. (Anouar Belahcen); software, A.B. (Aswin Balasubramanian), F.M. and A.B. (Anouar Belahcen); validation, A.B. (Aswin Balasubramanian) and F.M.; writing—original draft preparation, A.B. (Aswin Balasubramanian); writing—review and editing, A.B. (Aswin Balasubramanian), F.M., O.O., M.M.B. and A.B. (Anouar Belahcen); visualization, A.B. (Aswin Balasubramanian) and M.M.B.; supervision, A.B. (Anouar Belahcen); project administration, A.B. (Anouar Belahcen); funding acquisition, A.B. (Anouar Belahcen). All authors have read and agreed to the published version of the manuscript.
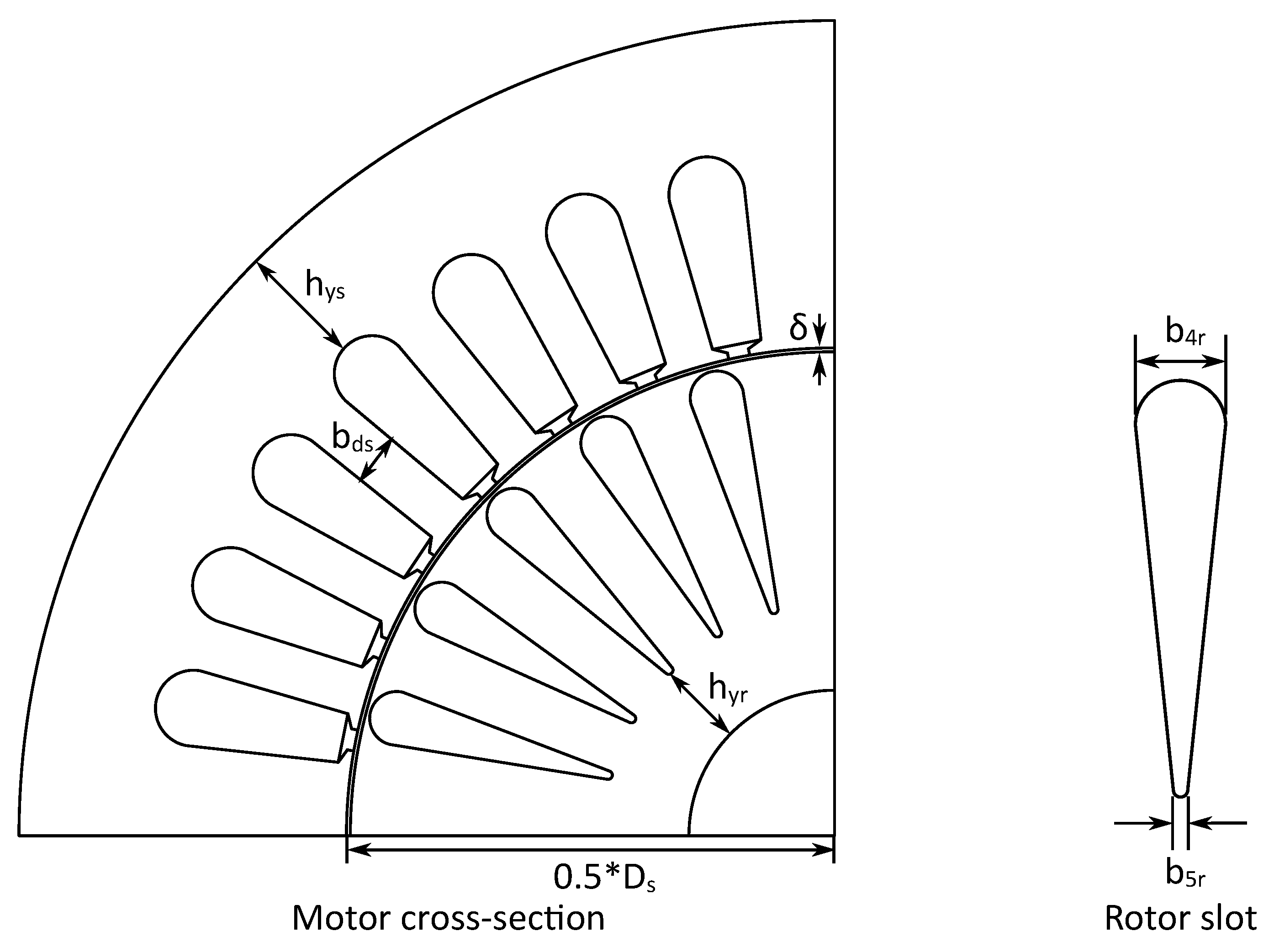
Figure 1.
Optimization variables of the induction motor.
Figure 1.
Optimization variables of the induction motor.
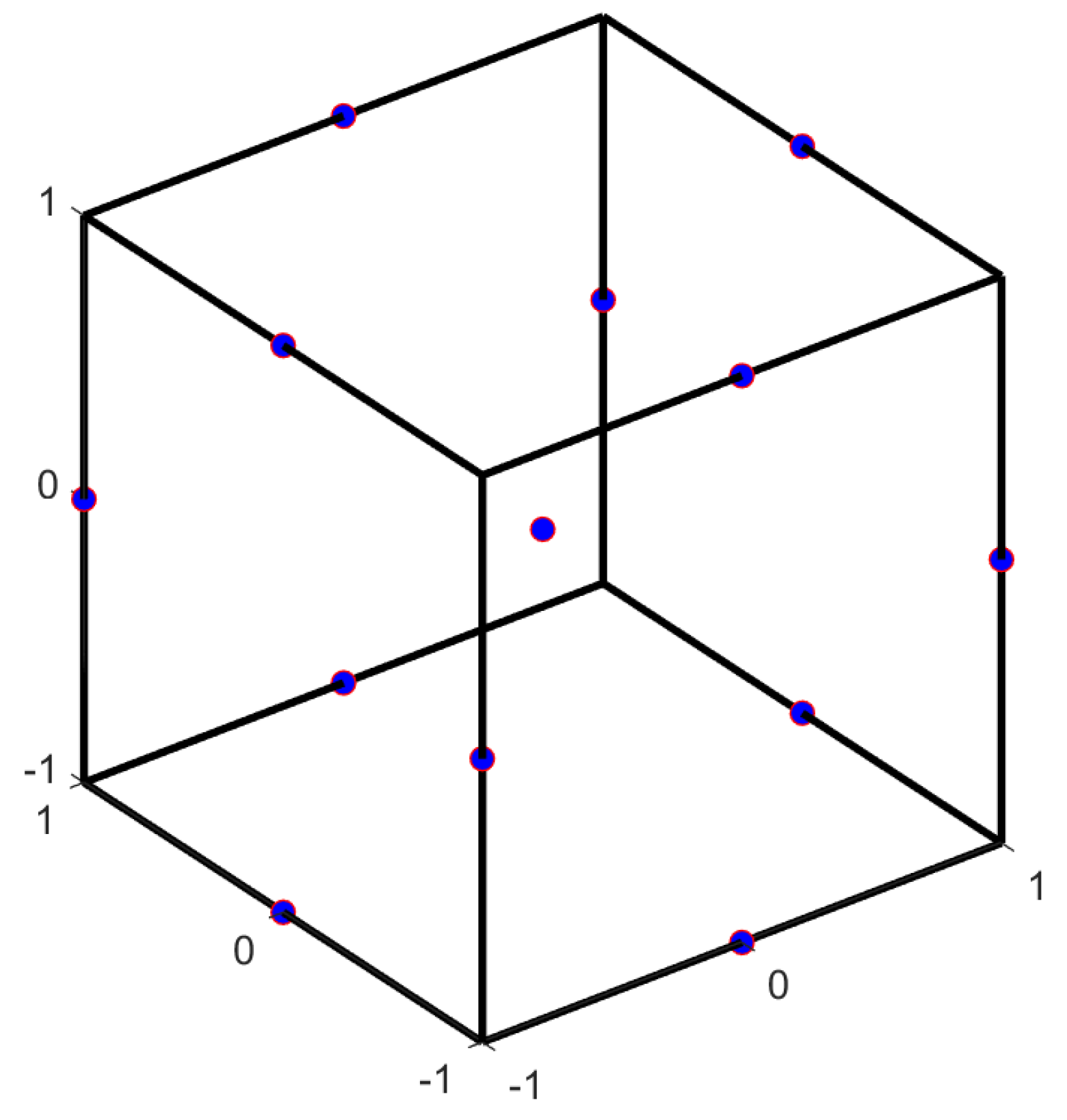
Figure 2.
Box–Behnken design represented for a 3-dimensional variable space.
Figure 2.
Box–Behnken design represented for a 3-dimensional variable space.
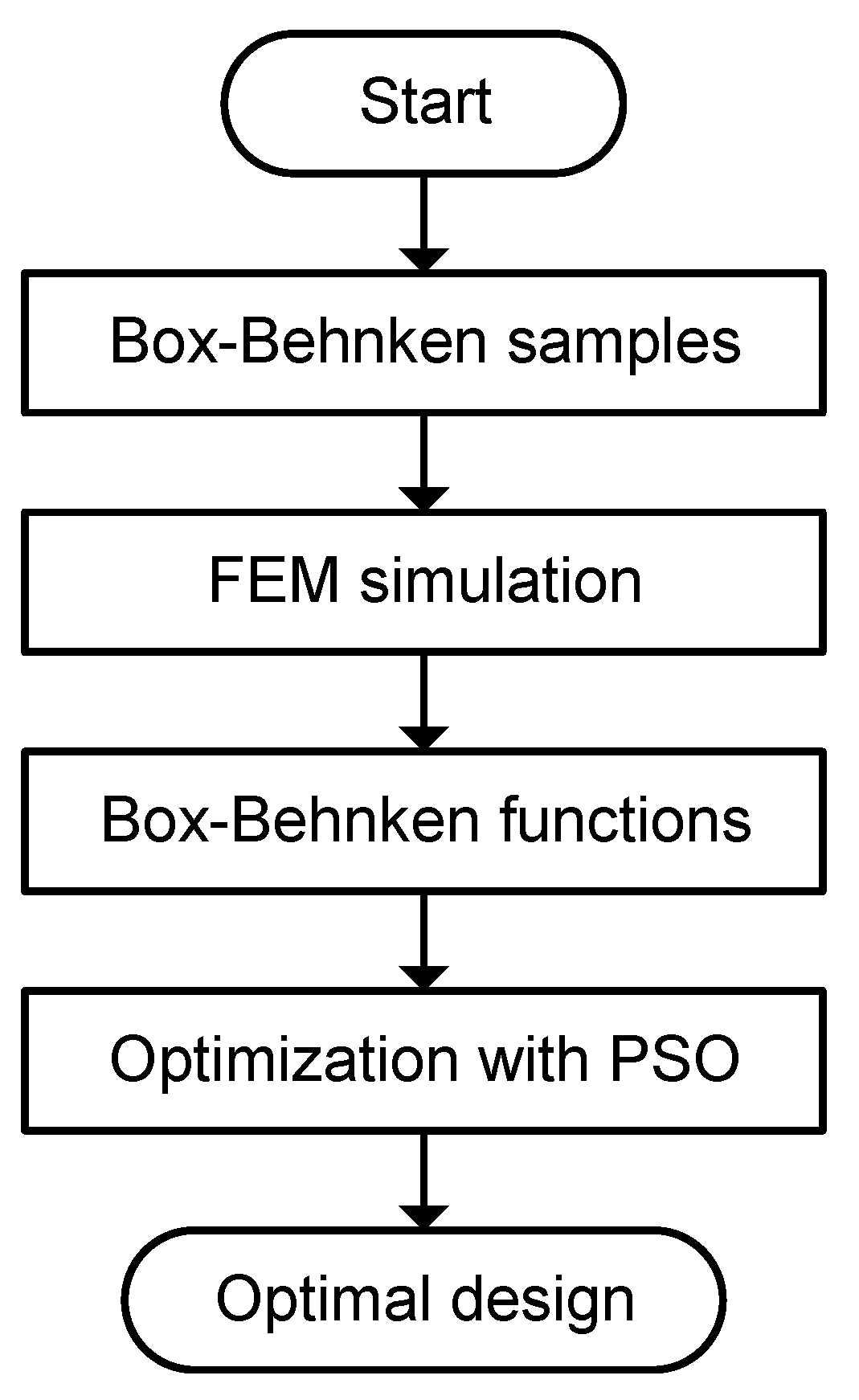
Figure 3.
Flow chart: optimization with Box–Behnken design.
Figure 3.
Flow chart: optimization with Box–Behnken design.
Figure 4.
Latin-hypercube sampling.
Figure 4.
Latin-hypercube sampling.
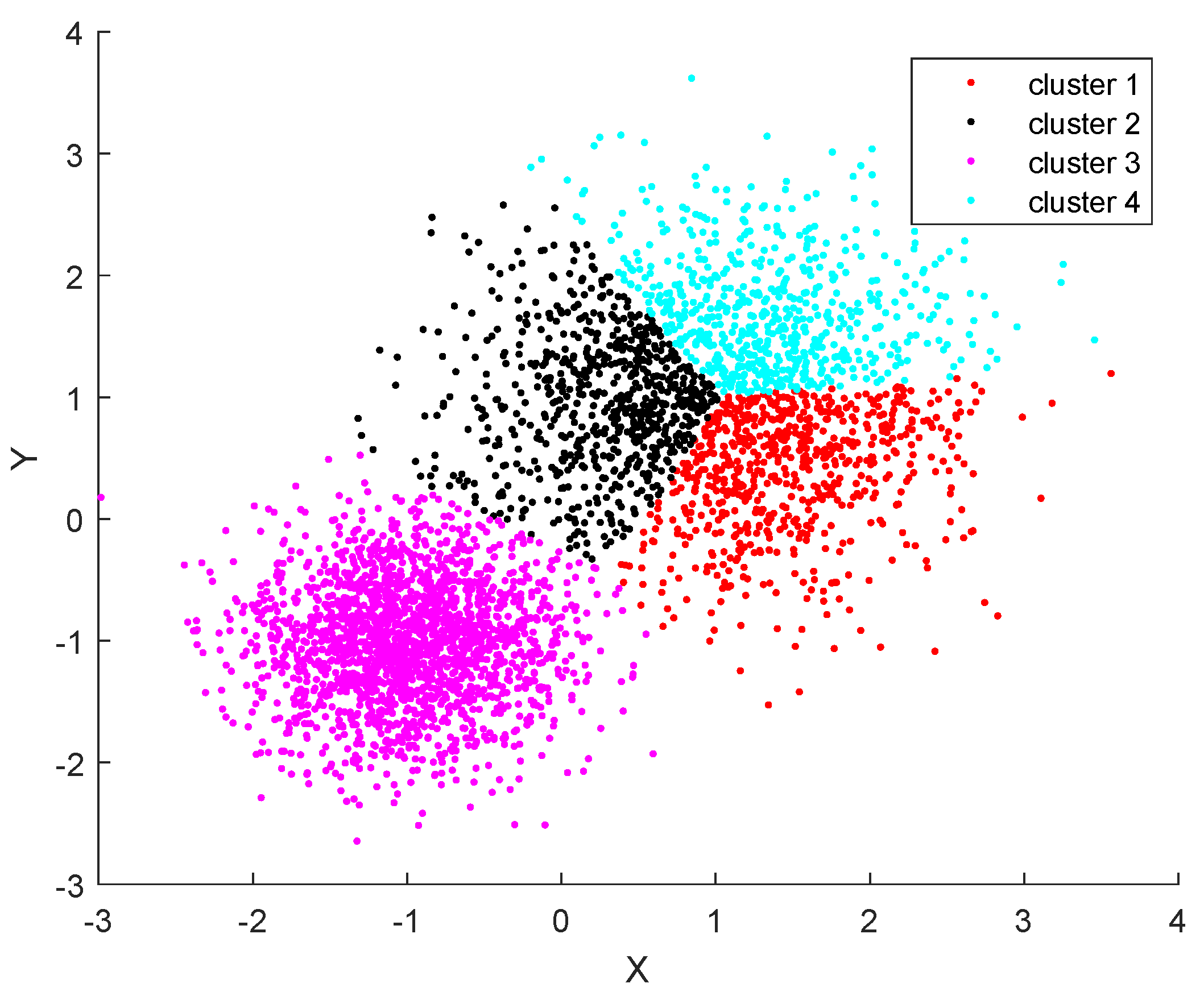
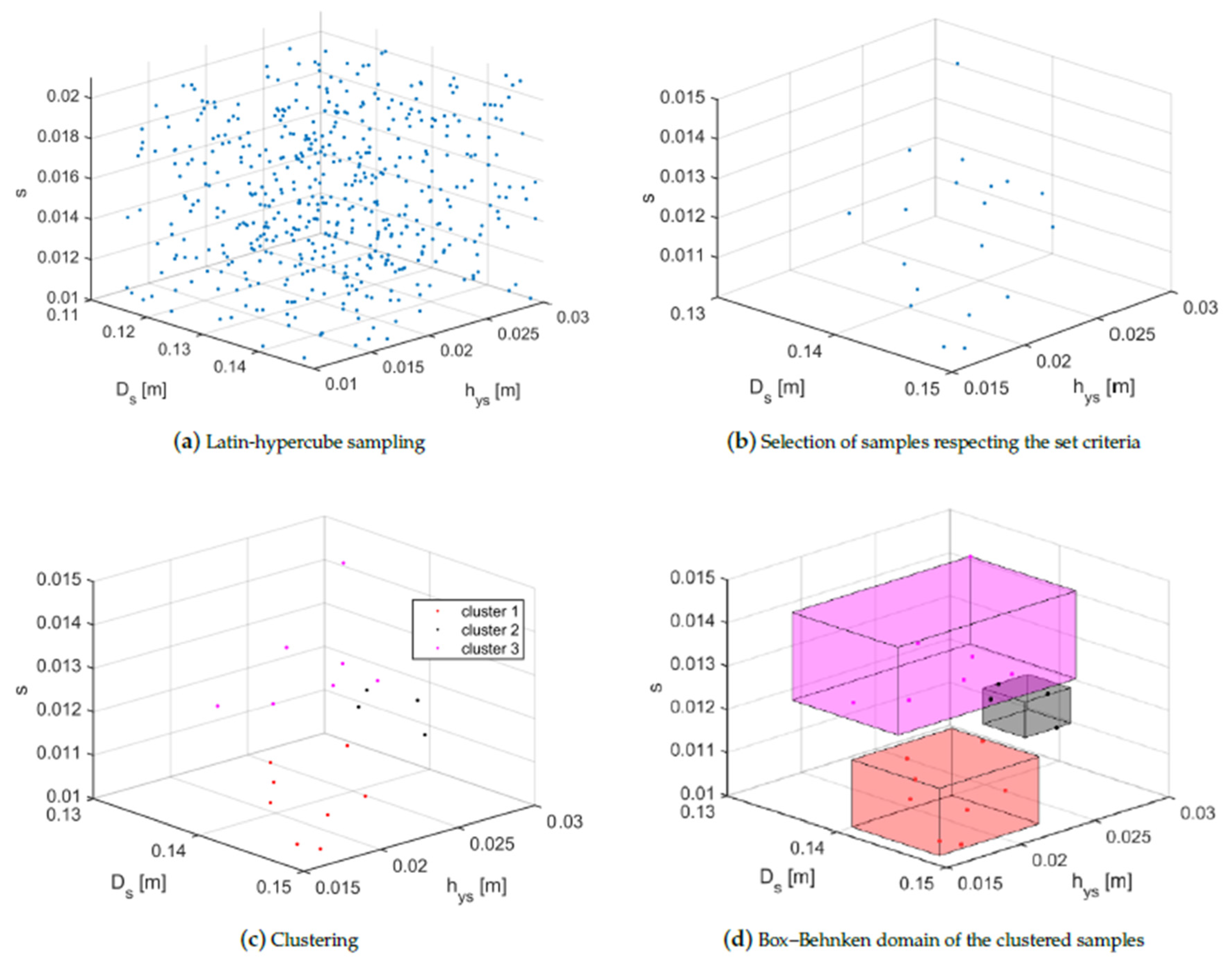
Figure 5.
A set of randomly generated samples clustered with the k-means++ algorithm.
Figure 5.
A set of randomly generated samples clustered with the k-means++ algorithm.
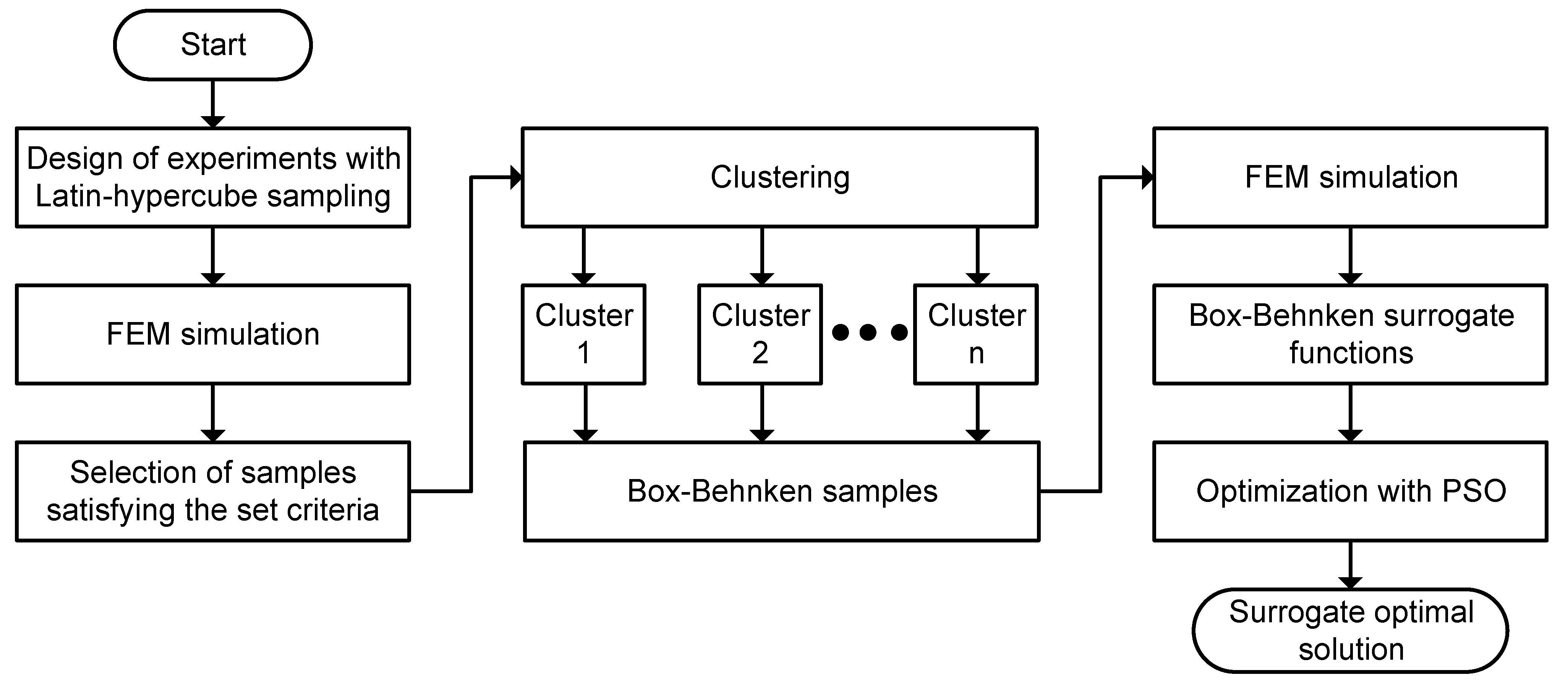
Figure 6.
Flow chart: proposed optimization routine—part 1 (surrogate optimization).
Figure 6.
Flow chart: proposed optimization routine—part 1 (surrogate optimization).
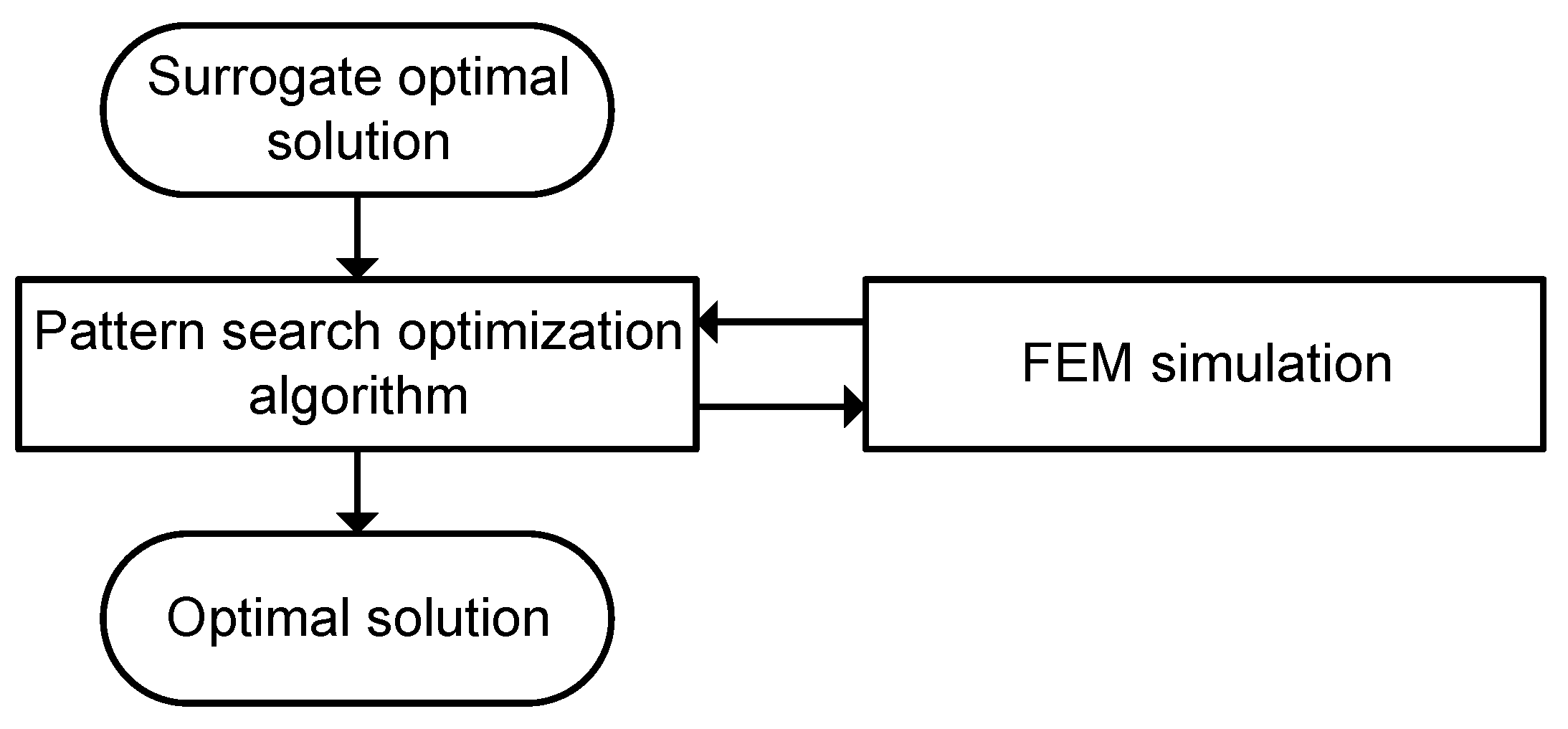
Figure 7.
Flow chart: proposed optimization routine—part 2 (pattern search).
Figure 7.
Flow chart: proposed optimization routine—part 2 (pattern search).
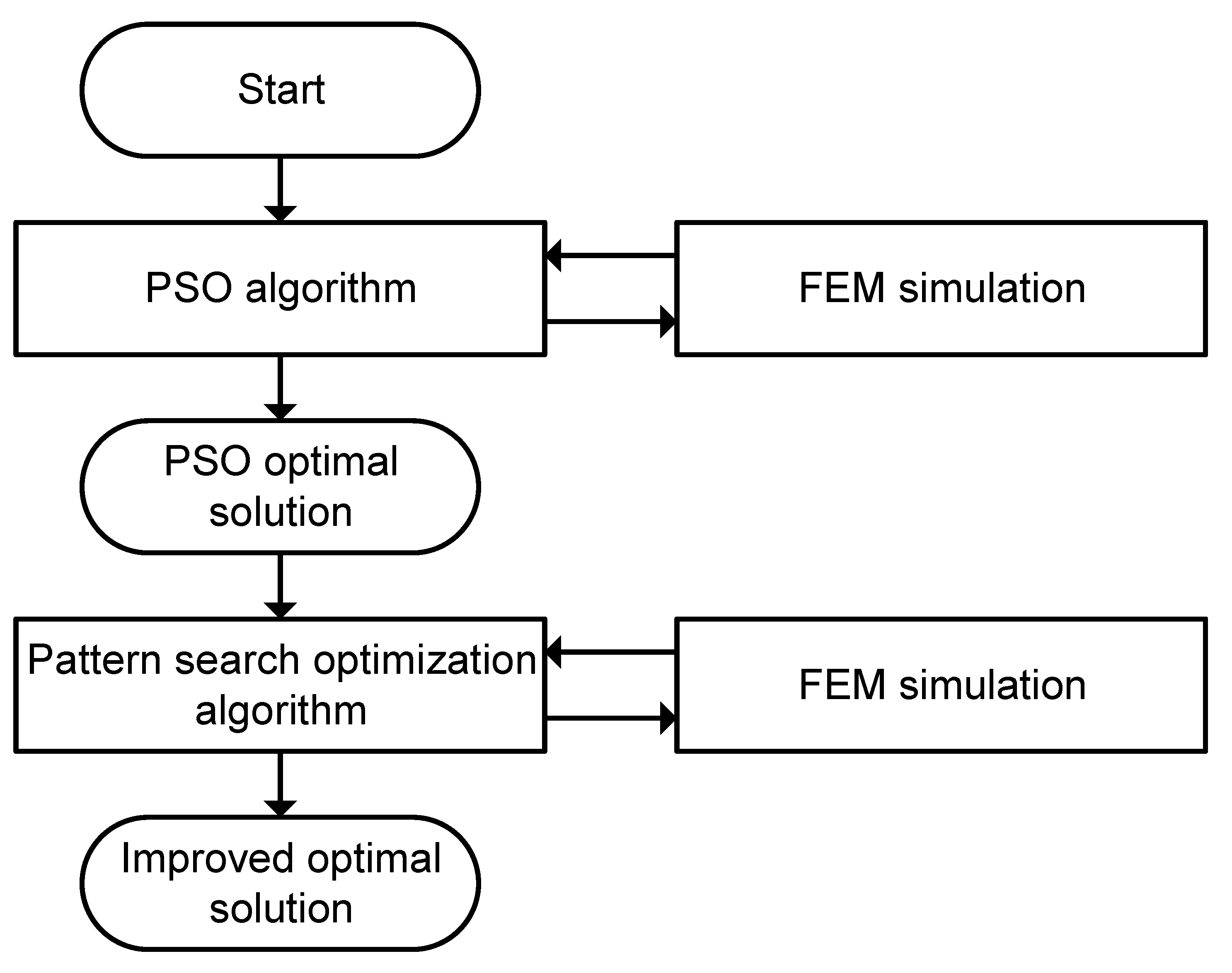
Figure 8.
Visualization of the process involved in the proposed surrogate optimization routine.
Figure 8.
Visualization of the process involved in the proposed surrogate optimization routine.
Figure 9.
Flux density distribution of the optimal solution from the proposed surrogate optimization routine–multivariate optimization problem.
Figure 9.
Flux density distribution of the optimal solution from the proposed surrogate optimization routine–multivariate optimization problem.
Figure 10.
Flow chart: direct optimization routine with FEM as the cost function.
Figure 10.
Flow chart: direct optimization routine with FEM as the cost function.
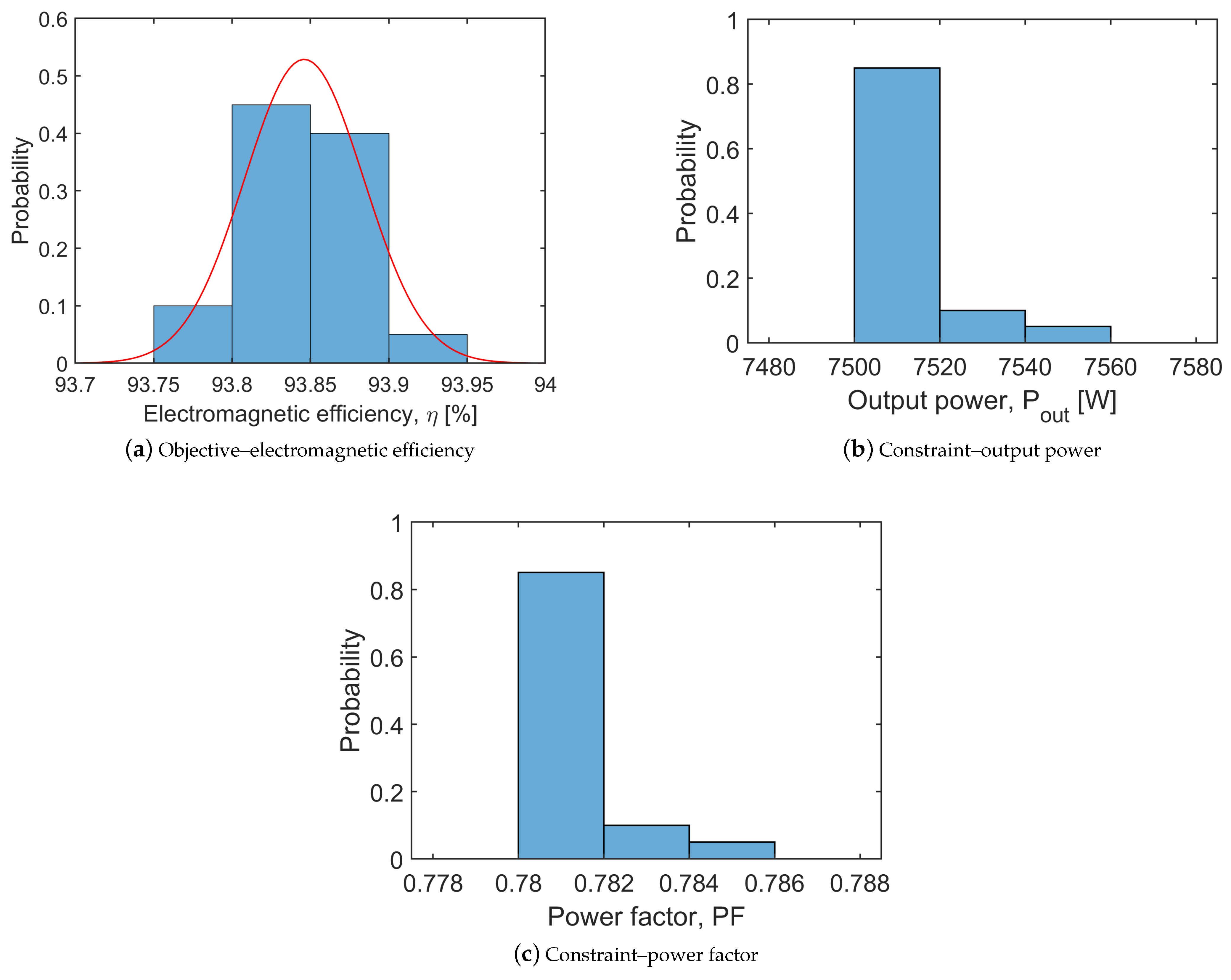
Figure 11.
Probability distribution of the objective and constraints from 20 runs of the proposed surrogate optimization routine.
Figure 11.
Probability distribution of the objective and constraints from 20 runs of the proposed surrogate optimization routine.
Table 1.
Specifications and fixed parameters of the induction motor.
Table 1.
Specifications and fixed parameters of the induction motor.
| Parameter | Value |
|---|
| Output power, [W] | 7500 |
| Line voltage, [V] | 400 |
| Frequency, f [Hz] | 50 |
| Number of poles, p | 4 |
| Filling factor-stator slot, | 0.6 |
| Number of conductors-stator slots, | 28 |
| Number of parallel paths-stator windings, a | 2 |
| Number of stator slots, | 48 |
| Number of rotor slots, | 44 |
| Axial length of the machine, l (mm) | 220 |
| Stator outer diameter, (mm) | 227.7 |
| Rotor inner (shaft) diameter, (mm) | 48.98 |
| End-ring overhang length, (mm) | 40 |
| Conductivity—aluminum (20 °C), [S/m] | |
| Conductivity—copper (20 °C), [S/m] | |
Table 2.
Objective and constraints of the optimization problem.
Table 2.
Objective and constraints of the optimization problem.
| Objective | Goal |
|---|
| Electromagnetic efficiency, (%) | To maximize the electromagnetic efficiency, |
| Constraints | Range |
| Output power, [W] | 7500 ≤ ≤ 7600 |
| Power factor, | ≥ 0.78 |
Table 3.
Optimization variables and their range.
Table 3.
Optimization variables and their range.
| Optimization Variables | Range |
|---|
| Stator inner diameter, (mm) | 120 ≤ ≤ 150 |
| Stator tooth width, (mm) | 2 ≤ ≤ 4 |
| Stator yoke width, (mm) | 10 ≤ ≤ 30 |
| Slip, s (%) | 1 ≤ s ≤ 2.1 |
| Air gap width, (mm) | 0.4 ≤ ≤ 0.7 |
| Rotor slot upper width, (mm) | 3 ≤ ≤ 6 |
| Rotor slot lower width, (mm) | 0.5 ≤ ≤ 2 |
| Rotor yoke width, (mm) | 2 ≤ ≤ 15 |
Table 4.
FEM validation of the optimal solution from Box–Behnken design.
Table 4.
FEM validation of the optimal solution from Box–Behnken design.
| Output Response | Box–Behnken Design | FEM Validation | Difference |
|---|
| Electromagnetic efficiency, | 95.30% | 93.31% | 2.13% |
| Output power, | 7500.28 W | 7131.98 W | 5.18% |
| Power factor, | 0.7860 | 0.7267 | 8.16% |
Table 5.
Sample selection criteria from the Latin-hypercube sampling method.
Table 5.
Sample selection criteria from the Latin-hypercube sampling method.
| Output Response | Sample Selection Criteria |
|---|
| Electromagnetic efficiency, (%) | ≥ 91 |
| Output power, [W] | 7000 ≤ ≤ 8000 |
| Power factor, | ≥ 0.75 |
Table 6.
Validation of surrogate optimal solution of the proposed optimization routine (part 1—surrogate optimization) with FEM simulation 3-variable optimization problem.
Table 6.
Validation of surrogate optimal solution of the proposed optimization routine (part 1—surrogate optimization) with FEM simulation 3-variable optimization problem.
| Output Response | Surrogate Optima | FEM Validation | Difference |
|---|
| Electromagnetic efficiency, | 93.63% | 93.64% | 0.01% |
| Output power, | 7599.97 W | 7614.76 W | 0.19% |
| Power factor, | 0.7800 | 0.7825 | 0.32% |
Table 7.
Surrogate optimal solution compared with the improved optimal solution (part 1—surrogate optimization vs. part 2—pattern search) of the proposed optimization routine 3-variable optimization problem.
Table 7.
Surrogate optimal solution compared with the improved optimal solution (part 1—surrogate optimization vs. part 2—pattern search) of the proposed optimization routine 3-variable optimization problem.
| Output Response | Optimal Solution (Part 1) | Optimal Solution (Part 2) | % Increase |
|---|
| Electromagnetic efficiency, | 93.64% | 93.66% | 0.021% |
| Output power, | 7614.76 W | 7572.32 W | −0.56% |
| Power factor, | 0.7825 | 0.7801 | −0.31% |
Table 8.
Comparison of design variables of the optimal solution (part 1—surrogate optimization vs. part 2—pattern search) from the proposed surrogate optimization routine 3-variable optimization problem.
Table 8.
Comparison of design variables of the optimal solution (part 1—surrogate optimization vs. part 2—pattern search) from the proposed surrogate optimization routine 3-variable optimization problem.
| Design Variables | Optimal Solution (Part 1) | Optimal Solution (Part 2) |
|---|
| Stator inner diameter, (mm) | 147.54 | 146.65 |
| Stator yoke width, (mm) | 17.01 | 17.27 |
| Slip, s (%) | 1.12 | 1.12 |
Table 9.
Comparison of electromagnetic efficiency and power factor for various load points of the optimal design 3-variable optimization problem.
Table 9.
Comparison of electromagnetic efficiency and power factor for various load points of the optimal design 3-variable optimization problem.
| Output Response | Load (100%) | Load (75%) | Load (50%) |
|---|
| Electromagnetic efficiency, | 93.66% | 93.74% | 92.97% |
| Power factor, | 0.7801 | 0.7122 | 0.5888 |
Table 10.
Comparison of losses for various load points of the optimal design 3-variable optimization problem.
Table 10.
Comparison of losses for various load points of the optimal design 3-variable optimization problem.
| Losses | Load (100%) | Load (75%) | Load (50%) |
|---|
| Stator losses, | 335.81 W | 251.63 W | 195.66 W |
| Rotor losses, | 177.18 W | 124.02 W | 88.06 W |
| Total electromagnetic losses, | 512.99 W | 375.65 W | 283.72 W |
Table 11.
Validation of surrogate optimal solution of the proposed optimization routine (part 1—surrogate optimization) with FEM simulationdesign–multivariate optimization problem.
Table 11.
Validation of surrogate optimal solution of the proposed optimization routine (part 1—surrogate optimization) with FEM simulationdesign–multivariate optimization problem.
| Output Response | Surrogate Optima | FEM Validation | Difference |
|---|
| Electromagnetic efficiency, | 93.48% | 93.54% | 0.064% |
| Output power, | 7500.16 W | 7514.74 W | 0.194% |
| Power factor, | 0.7964 | 0.7970 | 0.075% |
Table 12.
Surrogate optimal solution compared with the improved optimal solution (part 1—surrogate optimization vs. part 2—pattern search) of the proposed optimization routine–multivariate optimization problem.
Table 12.
Surrogate optimal solution compared with the improved optimal solution (part 1—surrogate optimization vs. part 2—pattern search) of the proposed optimization routine–multivariate optimization problem.
| Output Response | Optimal Solution (Part 1) | Optimal Solution (Part 2) | % Increase |
|---|
| Electromagnetic efficiency, | 93.54% | 93.90% | 0.385% |
| Output power, | 7514.74 W | 7502.62 W | −0.161% |
| Power factor, | 0.7970 | 0.7803 | −2.095% |
Table 13.
Comparison of design variables of the optimal solution (part 1—surrogate optimization vs. part 2—pattern search) from the the proposed surrogate optimization routine–multivariate optimization problem.
Table 13.
Comparison of design variables of the optimal solution (part 1—surrogate optimization vs. part 2—pattern search) from the the proposed surrogate optimization routine–multivariate optimization problem.
| Design Variables | Optimal Solution (Part 1) | Optimal Solution (Part 2) |
|---|
| Stator inner diameter, (mm) | 142.77 | 142.77 |
| Stator tooth width, (mm) | 3.28 | 3.30 |
| Stator yoke width, (mm) | 19.65 | 15.80 |
| Slip, s (%) | 1.26 | 1.26 |
| Air gap width, (mm) | 0.68 | 0.70 |
| Rotor slot upper width, (mm) | 5.78 | 5.78 |
| Rotor slot lower width, (mm) | 0.88 | 0.88 |
| Rotor yoke width, (mm) | 6.81 | 6.81 |
Table 14.
Comparison of electromagnetic efficiency and power factor for various load points of the optimal design–multivariate optimization problem.
Table 14.
Comparison of electromagnetic efficiency and power factor for various load points of the optimal design–multivariate optimization problem.
| Output Response | Load (100%) | Load (75%) | Load (50%) |
|---|
| Electromagnetic efficiency, | 93.90% | 93.95% | 93.19% |
| Power factor, | 0.7803 | 0.7164 | 0.5944 |
Table 15.
Comparison of losses for various load points of the optimal design 3-variable optimization problem.
Table 15.
Comparison of losses for various load points of the optimal design 3-variable optimization problem.
| Losses | Load (100%) | Load (75%) | Load (50%) |
|---|
| Stator losses, | 305.44 W | 234.83 W | 185.66 W |
| Rotor losses, | 181.89 W | 127.15 W | 88.77 W |
| Total electromagnetic losses, | 487.33 W | 361.98 W | 274.43 W |
Table 16.
Optimal design from the proposed surrogate optimization routine compared with the direct optimization routine.
Table 16.
Optimal design from the proposed surrogate optimization routine compared with the direct optimization routine.
| Output Response | Proposed Surrogate Optimization Routine | Direct Optimization Routine |
|---|
| Electromagnetic efficiency, | 93.90% | 93.89% |
| Output power, | 7502.62 W | 7505.29 W |
| Power factor, | 0.7803 | 0.7801 |
Table 17.
Design variables of the optimal solution from the the proposed surrogate optimization routine compared with direct optimization routine.
Table 17.
Design variables of the optimal solution from the the proposed surrogate optimization routine compared with direct optimization routine.
| Design Variables | Proposed Surrogate Optimization Routine | Direct Optimization Routine |
|---|
| Stator inner diameter, (mm) | 142.77 | 142.09 |
| Stator tooth width, (mm) | 3.30 | 3.40 |
| Stator yoke width, (mm) | 15.80 | 15.28 |
| Slip, s (%) | 1.26 | 1.30 |
| Air gap width, (mm) | 0.70 | 0.70 |
| Rotor slot upper width, (mm) | 5.78 | 5.80 |
| Rotor slot lower width, (mm) | 0.88 | 1.34 |
| Rotor yoke width, (mm) | 6.81 | 9.50 |
Table 18.
Comparison of electromagnetic efficiency and power factor for various load points of the optimal design—proposed surrogate optimization routine vs. direct optimization routine.
Table 18.
Comparison of electromagnetic efficiency and power factor for various load points of the optimal design—proposed surrogate optimization routine vs. direct optimization routine.
| Load | Output Response | Proposed Surrogate Optimization Routine | Direct Optimization Routine |
|---|
| 100% | Electromagnetic efficiency, | 93.90% | 93.89% |
| 100% | Power factor, | 0.7803 | 0.7801 |
| 75% | Electromagnetic efficiency, | 93.95% | 93.94% |
| 75% | Power factor, | 0.7164 | 0.7159 |
| 50% | Electromagnetic efficiency, | 93.19% | 93.16% |
| 50% | Power factor, | 0.5944 | 0.5926 |
Table 19.
Comparison of losses for various load points of the optimal design-proposed surrogate optimization routine vs. direct optimization routine.
Table 19.
Comparison of losses for various load points of the optimal design-proposed surrogate optimization routine vs. direct optimization routine.
| Load | Losses | Proposed Surrogate Optimization Routine | Direct Optimization Routine |
|---|
| 100% | Stator losses, | 305.44 W | 302.42 W |
| 100% | Rotor losses, | 181.89 W | 185.6 W |
| 100% | Total electromagnetic losses, | 487.33 W | 488.01 W |
| 75% | Stator losses, | 234.83 W | 233.65 W |
| 75% | Rotor losses, | 127.15 W | 129.37 W |
| 75% | Total electromagnetic losses, | 361.98 W | 363.03 W |
| 50% | Stator losses, | 185.66 W | 185.60 W |
| 50% | Rotor losses, | 88.77 W | 89.78 W |
| 50% | Total electromagnetic losses, | 274.43 W | 275.38 W |
Table 20.
Comparison of the number of FEM simulations in proposed surrogate optimization routine and direct optimization routine.
Table 20.
Comparison of the number of FEM simulations in proposed surrogate optimization routine and direct optimization routine.
| Parameter | Proposed Surrogate Optimization Routine | Direct Optimization Routine |
|---|
| Number of FEM simulations | 1364 | 75,208 |