Active Distribution Networks Planning Considering Multi-DG Configurations and Contingency Analysis
Abstract
:1. Introduction
1.1. Motivation and Background
1.2. Literature Review and Research Gap
1.3. Contributions
- Propose a novel approach for the planning of weakly meshed distribution networks with an ANM scheme that considers multi-DG configurations.
- Analyse the impact of ANM on the planning of weakly meshed ADNs with considerations for contingency analysis and multi-DG configurations.
1.4. Paper Organisation
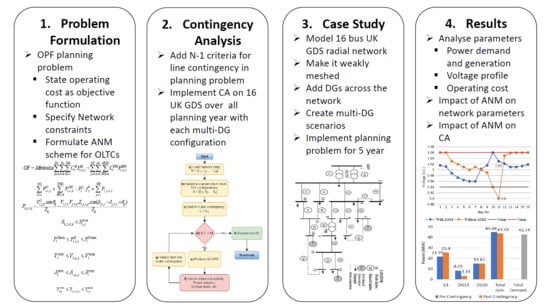
2. Methodology
3. Problem Formulation
3.1. Objective Function
3.2. Network Constraints
3.2.1. Equality Constraints
- Active and reactive power balance
- Active and reactive power flow
3.2.2. Inequality Constraints
- Active and reactive power generation
- Apparent power flow limits
- Voltage and angle limits
- OLTC Tap limits
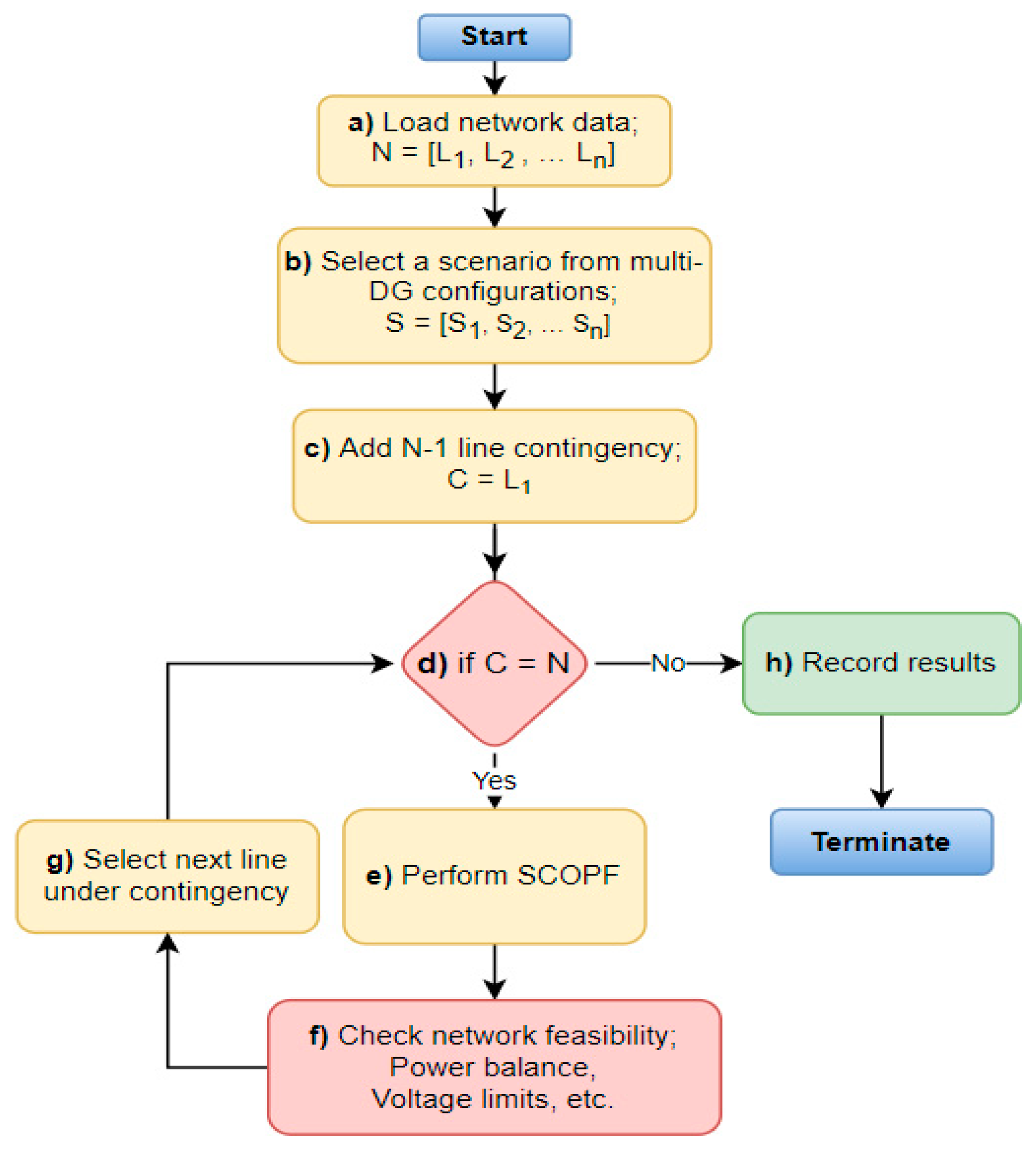
3.3. Proposed Algorithm for N-1 Line Contingency Analysis
- (a)
- Load network data: After formulating the problem and specifying scenarios, start by loading all available network parameters for generating units, buses, lines, transformers, and network constraints. N is a set of all lines in the network, from line 1, L1, to line N, Ln.
- (b)
- Select a scenario: As different scenarios are considered based on multi-DG configuration, each scenario will be selected one by one to perform SCOPF on all scenarios. If S is the set of all multi-DG configuration scenarios, Sn represents the nth scenario. A specific scenario will be selected at this stage to perform SCOPF.
- (c)
- Add line contingency: For N-1 line contingency analysis, there is only one line in contingency at an instant. Here, a line from Ln lines will be specified representing line contingency. Initially, line 1, L1, is considered in a contingency state, where C is a variable that represents the line under contingency.
- (d)
- Conditional statement: As C represents which line is in contingency, this stage verifies whether C represents a line from the N set lines of the network. If “yes”, move to step (e) to perform SCOPF, otherwise go to step (h) and terminate.
- (e)
- Perform SCOPF: After selecting a specific scenario and a line for N-1 contingency, this stage will perform SCOPF, using the formulation described in Section 3.1 and Section 3.2.
- (f)
- Check network feasibility: It is important to validate the feasibility of the network in a post-contingency condition against all network constraints including equality and inequality constraints. If the network meets all the constraints, it is in feasible conditions, otherwise infeasible.
- (g)
- Selected next line: After performing SCOPF with L1 representing a line in contingency, the next line, L2 will be selected for N-1 line contingency. The value of C will be updated and redirected to step (d). The loop will continue until SCOPF is performed for each line, from L1 to Ln, one by one.
- (h)
- Record results: Once SCOPF is performed for all N-1 line contingencies on a specific scenario, the results are recorded before terminating the program.
4. Case Study and Scenarios
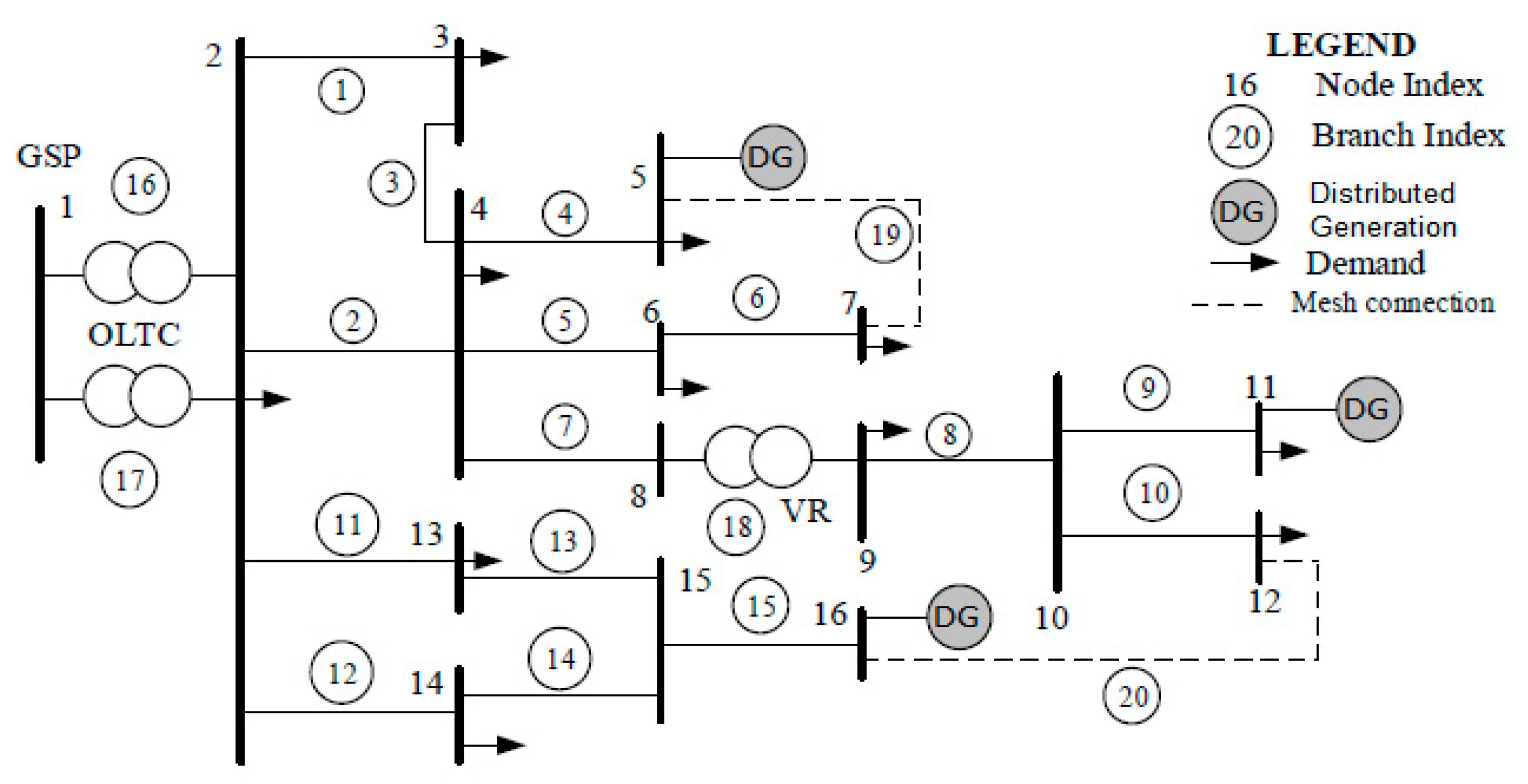
4.1. Network Description
4.2. Case Study
4.3. Multi-DG Configuration Scenarios
4.4. Radial and Meshed Topology Comparison under N-1 Contingency
5. Results and Discussion
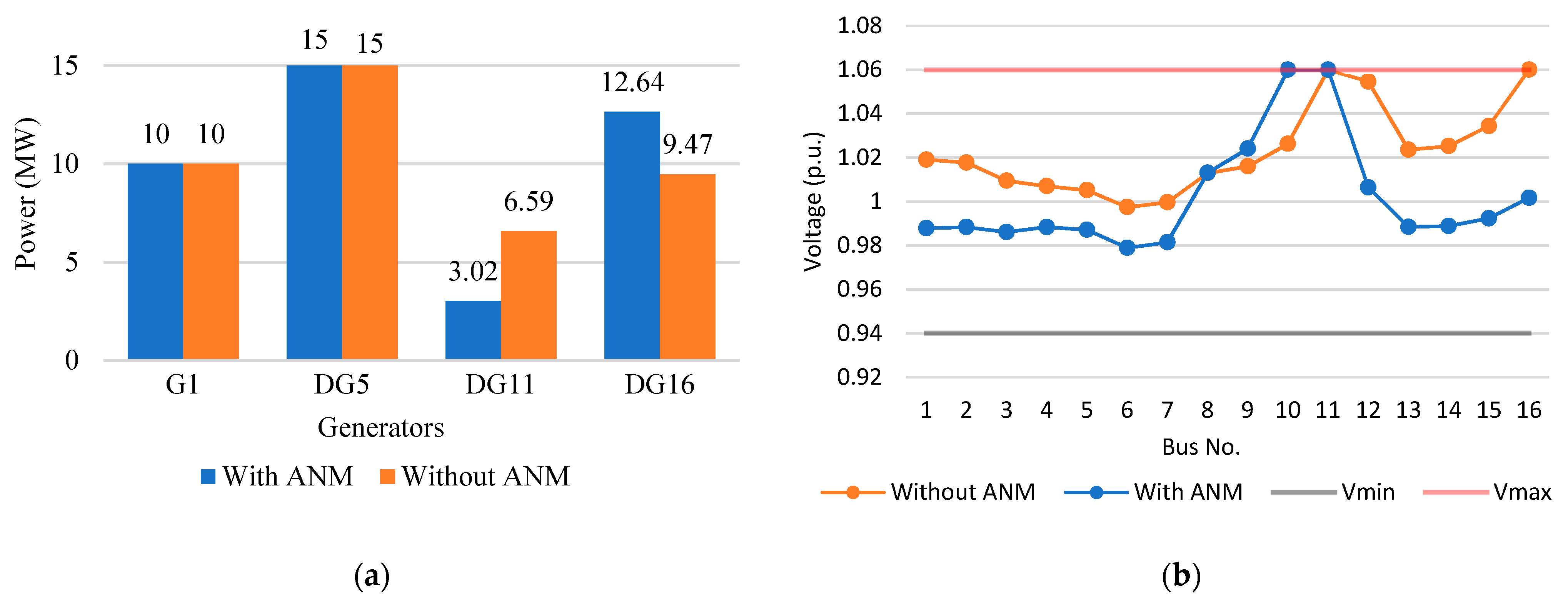
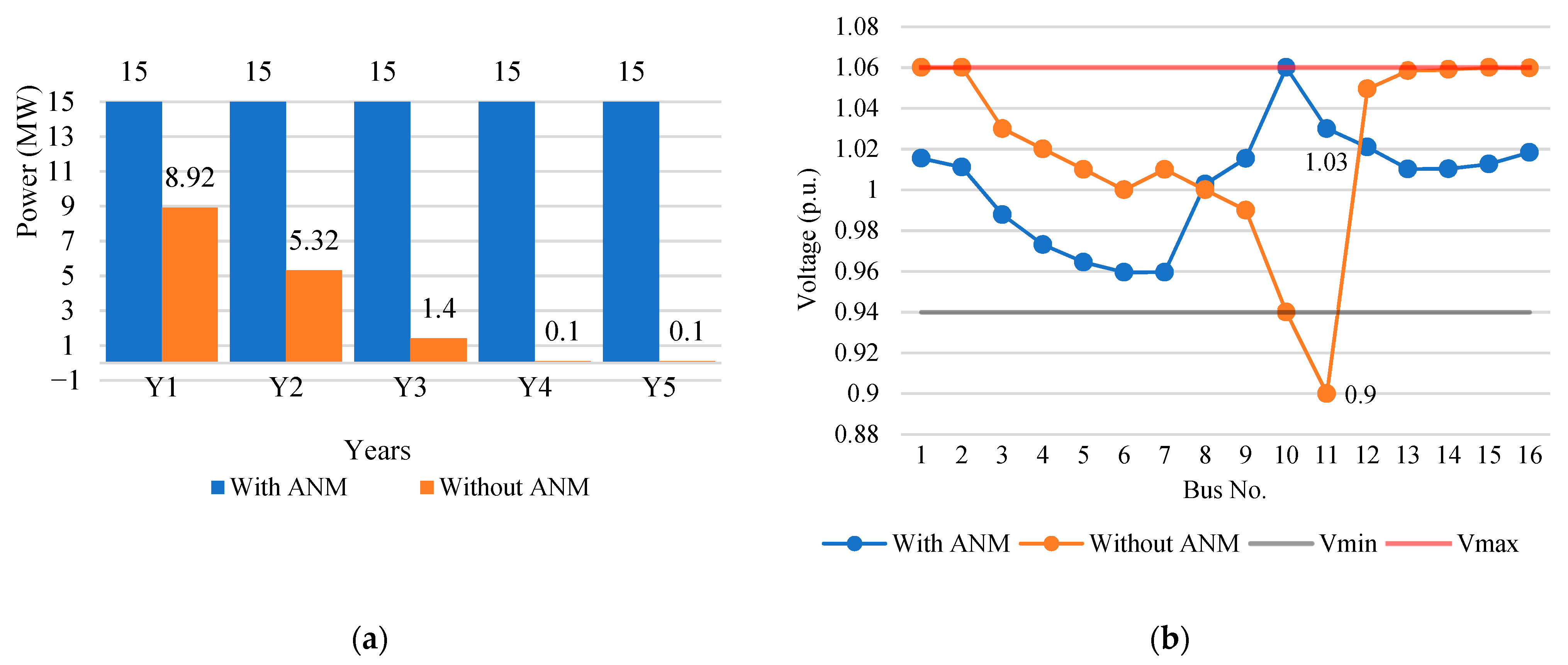
5.1. Power Generation and Voltage
5.1.1. Scenario S7
5.1.2. Scenario S3
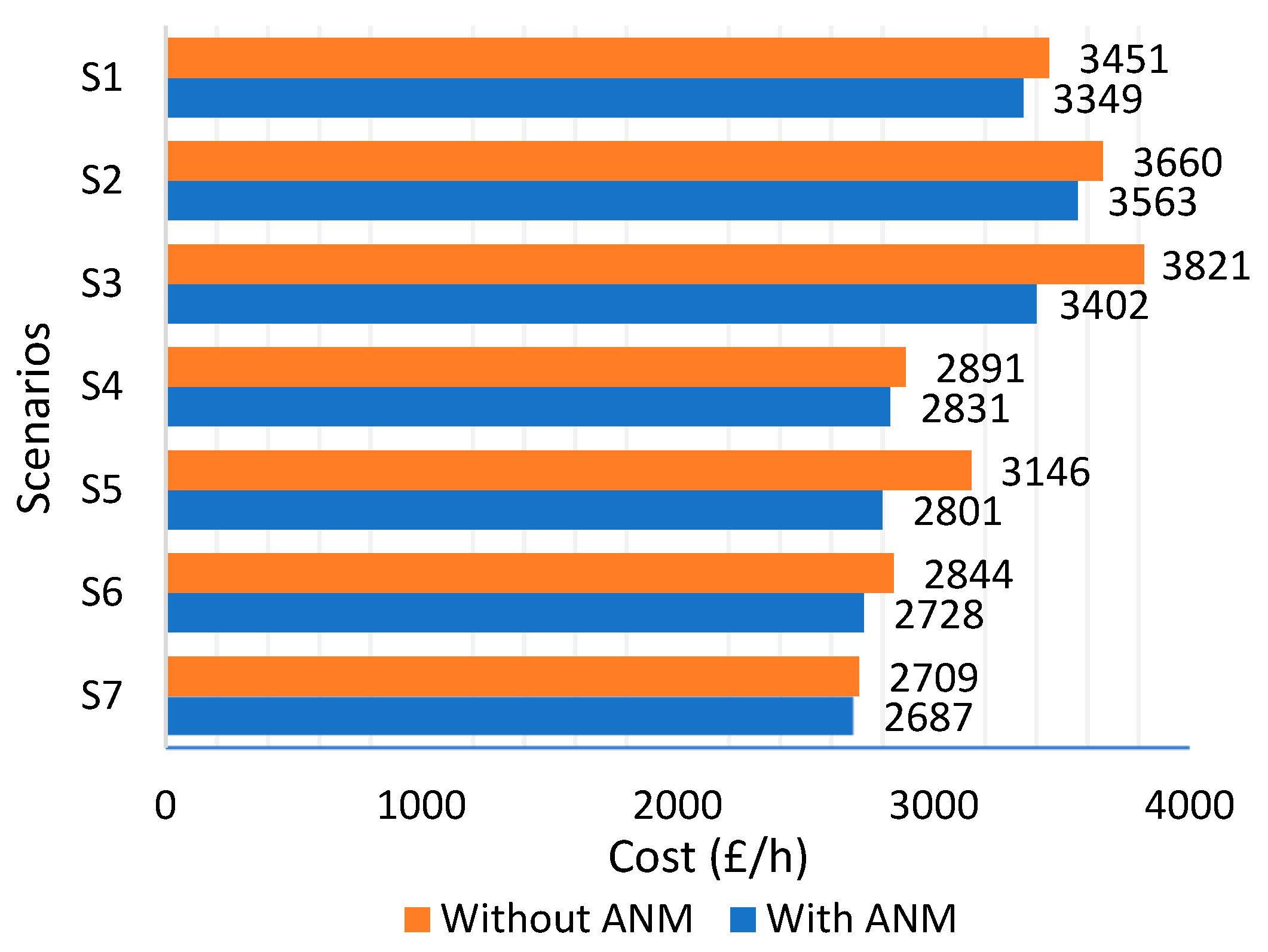
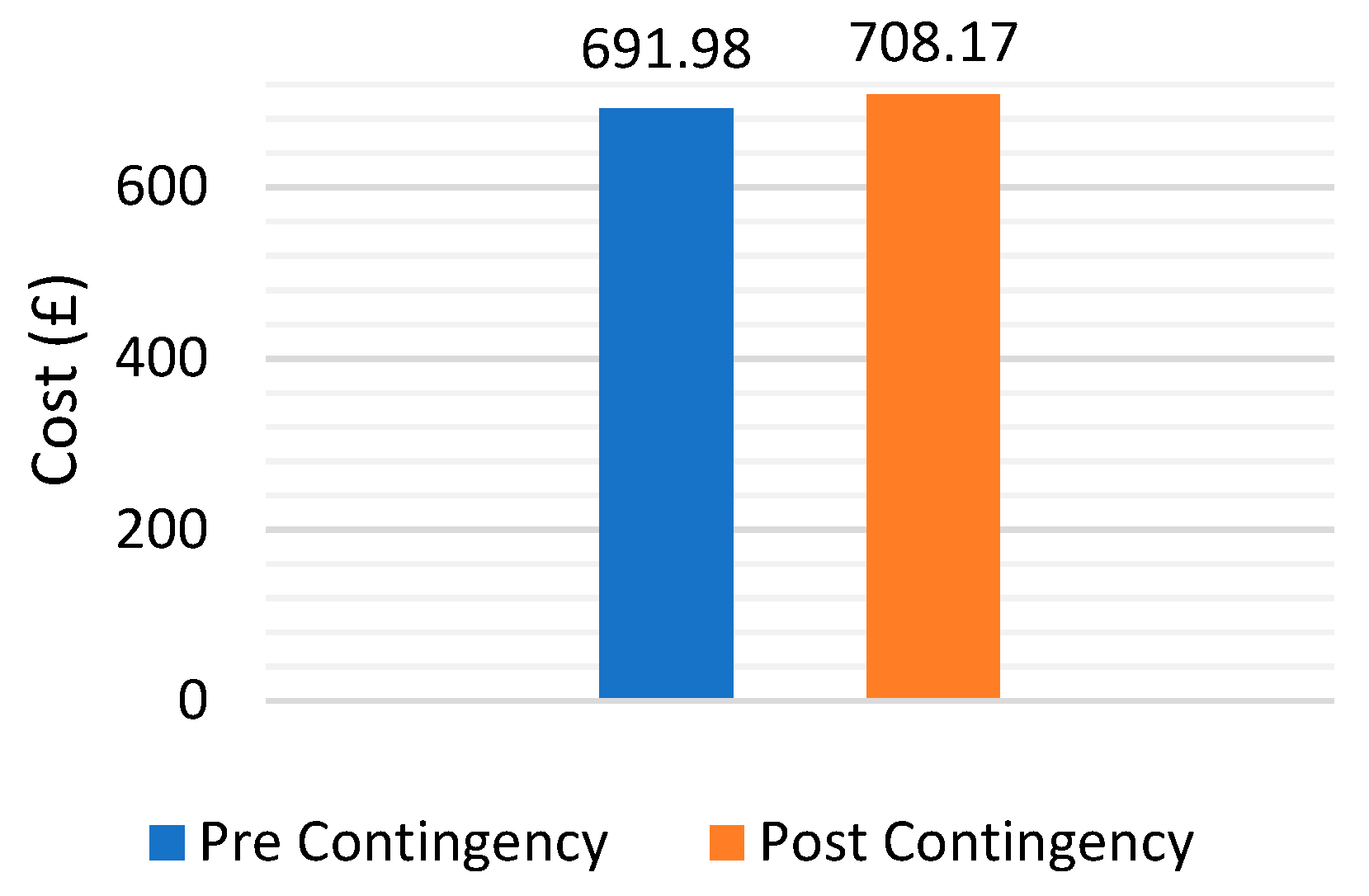
5.2. Network Operational Cost
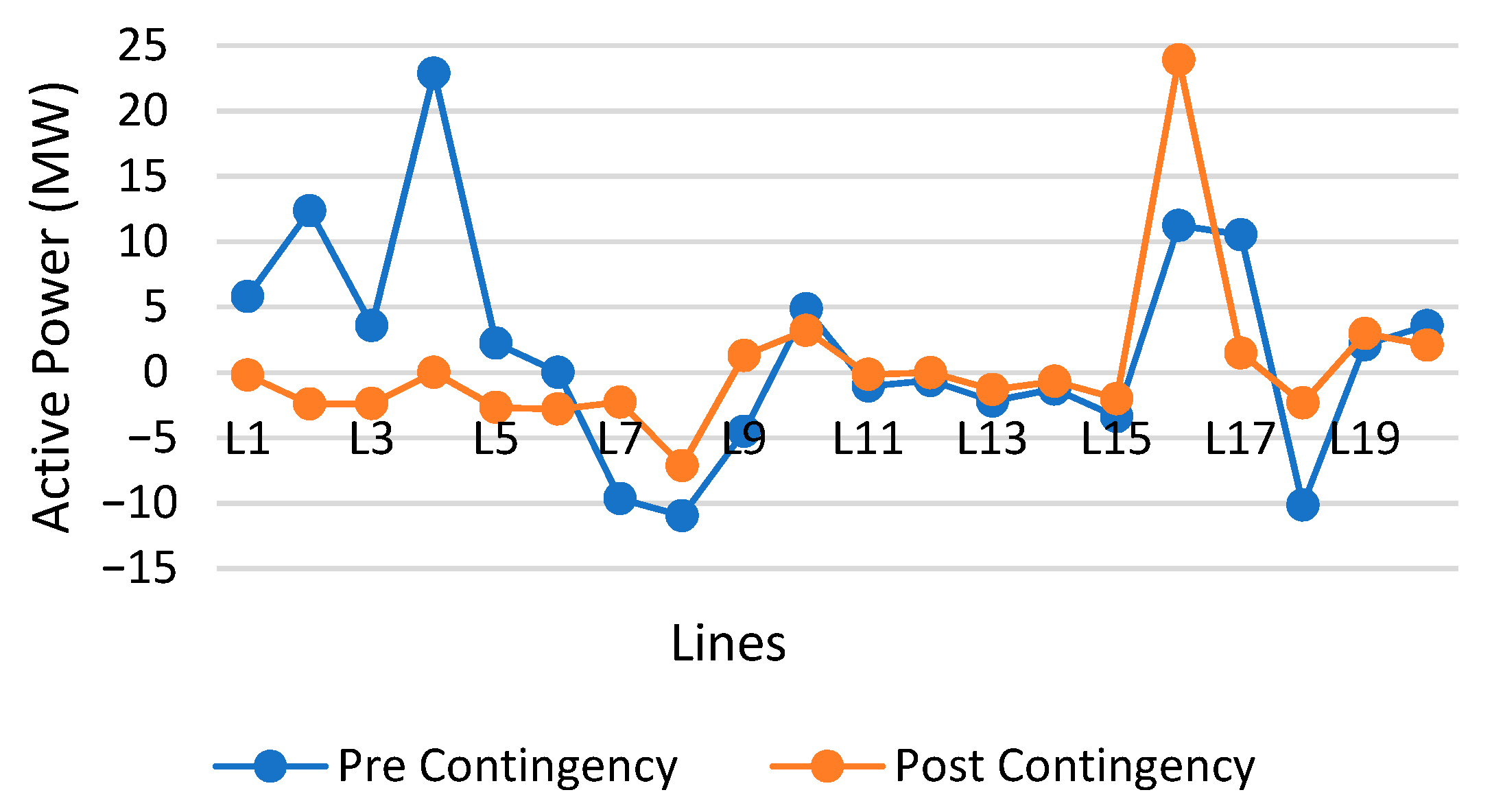
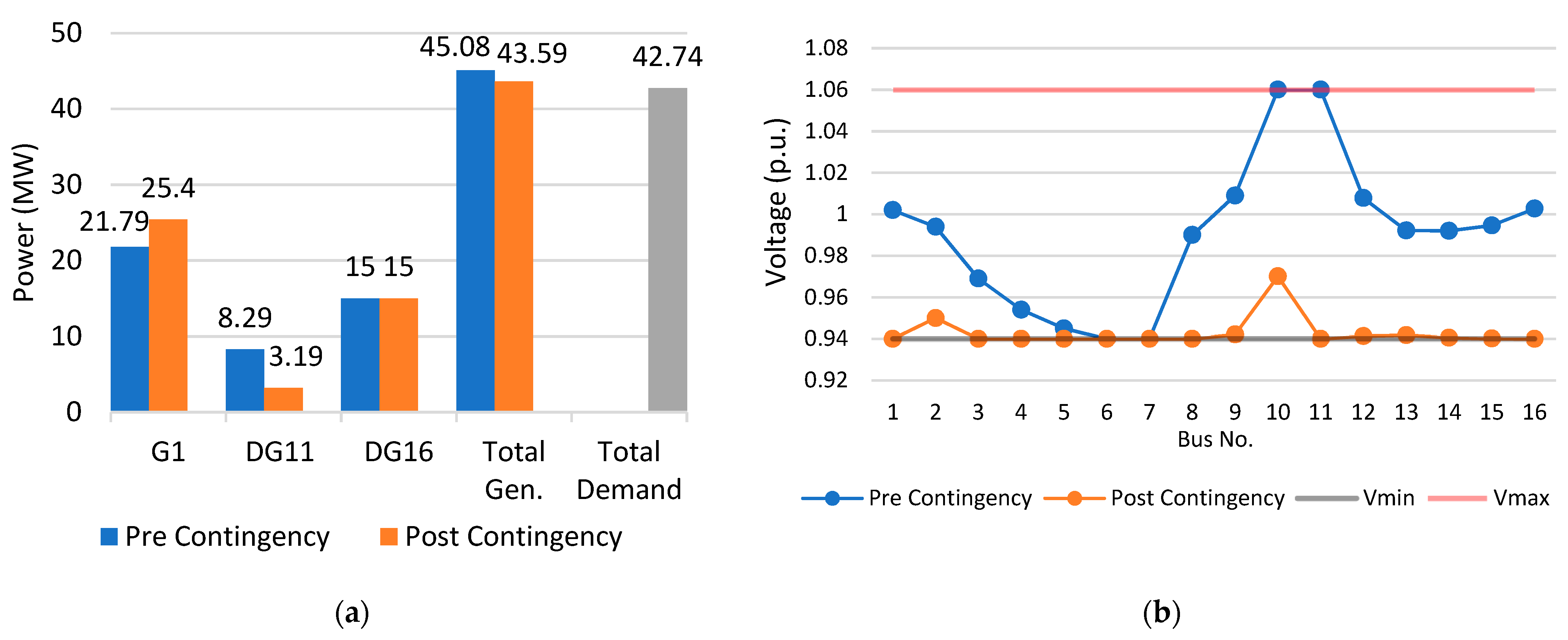
5.3. Contingency Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baruah, P.J.; Eyre, N.; Qadrdan, M.; Chaudry, M.; Blainey, S.; Hall, J.W.; Jenkins, N.; Tran, M. Energy system impacts from heat and transport electrification. Proc. Inst. Civ. Eng. Energy 2014, 167, 139–151. [Google Scholar] [CrossRef]
- Xinyu, C.; McElroy, M.B.; Qiuwei, W.U.; Yinbiao, S.H.U.; Yusheng, X.U.E. Transition towards higher penetration of renewables: An overview of interlinked technical, environmental and socio-economic challenges. J. Mod. Power Syst. Clean Energy 2019, 7, 1–8. [Google Scholar]
- Orkney ANM Live. Available online: https://www.ssen.co.uk/ANMGeneration/ (accessed on 4 May 2021).
- Powergrid, N. What Is Northern Powergrid Doing to Enable Active Network Management (ANM). Available online: https://northernpowergrid.custhelp.com/app/answers/detail/a_id/285/related/1 (accessed on 4 May 2021).
- Ochoa, L.F.; Mancarella, P. Low-carbon LV networks: Challenges for planning and operation. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–2. [Google Scholar]
- Weedy, B.M.; Cory, B.J.; Jenkins, N.; Ekanayake, J.B.; Strbac, G. Electric Power Systems; John Wiley & Sons: Sussex, UK, 2012. [Google Scholar]
- Al-Jaafreh, M.A.A.; Mokryani, G. Planning and operation of LV distribution networks: A comprehensive review. IET Energy Syst. Integr. 2019, 1, 133–146. [Google Scholar] [CrossRef]
- Satya, J.P.; Bhatt, N.; Pasumarthy, R.; Rajeswaran, A. Identifying Topology of Power Distribution Networks Based on Smart Meter Data. arXiv 2016, arXiv:1609.02678. [Google Scholar]
- Taibi, E.; Nikolakakis, T.; Gutierrez, L.; Fernandez del Valle, C.; Kiviluoma, J.; Lindroos, T.; Rissanen, S. Power System Flexibility for the Energy Transition; IRENA: Abu Dhabi, United Arab Emirates, 2018. [Google Scholar]
- Liew, S.N.; Strbac, G. Maximising penetration of wind generation in existing distribution networks. IEE Proc. Gener. Transm. Distrib. 2002, 149, 256–262. [Google Scholar] [CrossRef]
- Ochoa, L.F.; Dent, C.J.; Harrison, G.P. Distribution network capacity assessment: Variable DG and active networks. IEEE Trans. Power Syst. 2009, 25, 87–95. [Google Scholar] [CrossRef] [Green Version]
- Al Kaabi, S.S.; Zeineldin, H.H.; Khadkikar, V. Planning active distribution networks considering multi-DG configurations. IEEE Trans. Power Syst. 2013, 29, 785–793. [Google Scholar] [CrossRef]
- Mokryani, G.; Siano, P. Strategic placement of distribution network operator owned wind turbines by using market-based optimal power flow. IET Gener. Transm. Distrib. 2014, 8, 281–289. [Google Scholar] [CrossRef]
- Mokryani, G.; Siano, P.; Piccolo, A. Optimal allocation of wind turbines in microgrids by using genetic algorithm. J. Ambient Intell. Humaniz. Comput. 2013, 4, 613–619. [Google Scholar] [CrossRef]
- Abapour, S.; Babaei, E.; Khanghah, B.Y. Application of active management on distribution network with considering technical issues. In Proceedings of the 2nd Iranian Conference on Smart Grids, Tehran, Iran, 24 May 2012; pp. 1–6. [Google Scholar]
- Barr, J.; Majumder, R. Integration of Distributed Generation in the Volt/VAR Management System for Active Distribution Networks. IEEE Trans. Smart Grid 2015, 6, 576–586. [Google Scholar] [CrossRef]
- Hashim, T.J.T.; Mohamed, A.; Shareef, H. A review on voltage control methods for active distribution networks. Prz. Elektrotechniczny (Electr. Rev.) 2012, 88, 304–312. [Google Scholar]
- Collinson, A.; Dai, F.; Beddoes, A.; Crabtree, J. Solutions for the connection and operation of distributed generation. In DTI Distributed Generation Programme; Department of Trade and Industry: London, UK, July 2003. [Google Scholar]
- Shukla, A.; Verma, K.; Siddiqui, S.A. Optimal voltage regulation of a distribution network by output power management of DGs. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Sansawatt, T.; O’Donnell, J.; Ochoa, L.F.; Harrison, G.P. Decentralised voltage control for active distribution networks. In Proceedings of the 2009 44th International Universities Power Engineering Conference (UPEC), Glasgow, UK, 1–4 September 2009; pp. 1–5. [Google Scholar]
- Conti, S.; Greco, A.M. Active MV distribution network planning coordinated with advanced centralized voltage regulation system. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 2105–2109. [Google Scholar]
- Mokryani, G.; Hu, Y.F.; Pillai, P.; Rajamani, H.-S. Active distribution networks planning with high penetration of wind power. Renew. Energy 2017, 104, 40–49. [Google Scholar] [CrossRef] [Green Version]
- Zubo, R.H.; Mokryani, G. Active distribution network operation: A market-based approach. IEEE Syst. J. 2019, 14, 1405–1416. [Google Scholar] [CrossRef]
- Zubo, R.H.A.; Mokryani, G.; Rajamani, H.-S.; Aghaei, J.; Niknam, T.; Pillai, P. Operation and planning of distribution networks with integration of renewable distributed generators considering uncertainties: A review. Renew. Sustain. Energy Rev. 2017, 72, 1177–1198. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.; Chen, H.; Zheng, X.; Wu, B. Framework planning of active distribution network considering active management. J. Eng. 2017, 2017, 2093–2097. [Google Scholar] [CrossRef]
- Agalgaonkar, Y.P.; Pal, B.C.; Jabr, R.A. Distribution voltage control considering the impact of PV generation on tap changers and autonomous regulators. IEEE Trans. Power Syst. 2013, 29, 182–192. [Google Scholar] [CrossRef] [Green Version]
- Anthony, I.O.; Mokryani, G.; Zubo, R.H.; Ezechukwu, O.A.; Ivry, P. Distribution Network Reconfiguration Considering Security-Constraint and Multi-DG Configurations. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Torino, Italy, 1–4 September 2020; pp. 1–6. [Google Scholar]
- Hughes, J. The Integrated Energy and Communication Systems Architecture; Electric Power Research Institute (EPRI) and and Electricity Innovation Institute: Palo Alto, CA, USA, 2004. [Google Scholar]
- Karbalaei, F.; Shahbazi, H.; Mahdavi, M. A new method for solving preventive security-constrained optimal power flow based on linear network compression. Int. J. Electr. Power Energy Syst. 2018, 96, 23–29. [Google Scholar] [CrossRef]
- Dvorkin, Y.; Henneaux, P.; Kirschen, D.S.; Pandžić, H. Optimizing primary response in preventive security-constrained optimal power flow. IEEE Syst. J. 2016, 12, 414–423. [Google Scholar] [CrossRef]
- Capitanescu, F.; Glavic, M.; Ernst, D.; Wehenkel, L. Contingency filtering techniques for preventive security-constrained optimal power flow. IEEE Trans. Power Syst. 2007, 22, 1690–1697. [Google Scholar] [CrossRef]
- Gupta, M.; Abhyankar, A. Impact of Active Distribution Network on Contingency Analysis of Transmission System. In Proceedings of the 2019 North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar]
- Marcelino, C.G.; Almeida, P.E.; Wanner, E.F.; Baumann, M.; Weil, M.; Carvalho, L.M.; Miranda, V. Solving security constrained optimal power flow problems: A hybrid evolutionary approach. Appl. Intell. 2018, 48, 3672–3690. [Google Scholar] [CrossRef] [Green Version]
- Roald, L.; Oldewurtel, F.; Van Parys, B.; Andersson, G. Security constrained optimal power flow with distributionally robust chance constraints. arXiv 2015, arXiv:1508.06061. [Google Scholar]
- Papaefthymiou, G.; Verboomen, J.; Schavemaker, P.H.; van der Sluis, L. Impact of stochastic generation in power systems contingency analysis. In Proceedings of the 2006 International Conference on Probabilistic Methods Applied to Power Systems, Stockholm, Sweden, 11–15 June 2006; pp. 1–6. [Google Scholar]
- Liu, J.; Cheng, H.; Xu, Q.; Lan, Z.; Zeng, P.; Yao, L. Optimal distributed generation placement and size under uncertainties and contingencies in active distribution networks. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 1245–1249. [Google Scholar]
- Ding, T.; Li, C.; Liu, X.; Xie, H.; Tang, Y.; Huang, C. Optimally Allocating Energy Storage for Active Distribution Networks to Reduce the Risk Under N-1 Contingencies. IEEE Syst. J. 2021. [Google Scholar] [CrossRef]
- Mendes, A.; Boland, N.; Guiney, P.; Riveros, C. (N-1) contingency planning in radial distribution networks using genetic algorithms. In Proceedings of the 2010 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America (T&D-LA), Sao Paulo, Brazil, 8–10 November 2010; pp. 290–297. [Google Scholar]
- Brooke, A.; Kendrick, D.; Meeraus, A.; Raman, R.; America, U. The general algebraic modeling system. GAMS Dev. Corp. 1998. Available online: https://camo.ici.ro/language/ml05.htm (accessed on 30 May 2020).
- Smeers, Y. Generalized reduced gradient method as an extension of feasible direction methods. J. Optim. Theory Appl. 1977, 22, 209–226. [Google Scholar] [CrossRef]
- Drud, A. CONOPT. Available online: https://www.gams.com/latest/docs/S_CONOPT.html (accessed on 30 May 2020).
- Abadie, J.; Carpentier, J. Generalization of the Wolfe Reduced Gradient Method to the Case of Nonlinear Constraints; Academic Press: New York, NY, USA, 1969; pp. 37–48. [Google Scholar]
- Lai, C.S.; McCulloch, M.D. Levelized cost of electricity for solar photovoltaic and electrical energy storage. Appl. Energy 2017, 190, 191–203. [Google Scholar] [CrossRef]
- Centre for Sustainable Electricity and Distributed Generation (SEDG), United Kingdom Generic Distribution System (UK GDS). 2011. Available online: https://github.com/sedg/ukgds (accessed on 19 September 2019).

| Characteristics | Meshed | Radial |
|---|---|---|
| Structure | Quite complex network structure | Clear and simple network structure |
| Protection system and load flow | Complicated to design protection system and control the power flow of the system | Easy to design protection system and control the power flow of the system |
| Load density and reliability | High load densities and reliability requirements | Usually has low load density where reliability is not so important |
| Operation | Easy operation under normal operating conditions, but an outage of LV lines will be hard to recognize | Simple operation under normal operating conditions |
| Lines loading | Loading of the lines for normal operating condition up to 70% | Loading of lines during normal operation up to 100% |
| System losses | System losses minimal | System losses comparatively high |
| Overall network cost | Much higher network cost than other topologies, and set-up and maintenance are very difficult | Low overall cost, relatively simple to coordinate and design and maintain |
| Maintenance cost | High maintenance cost | Maintenance cost rather small |
| Voltage Profile | Voltage profile flat | Voltage profile not very good; distinct voltage drops between the feeding and the receiving ends of lines |
| Changed load flexibility | Flexibility for changed load conditions high | Flexibility for changed load conditions is comparatively small |
| Reserve (in case of outage) | Reserve path is available in case of outage of the feeder | Reserve for loss of the feeder is usually missing |
| Standardization | Standardization of cross-sections of lines possible | Standardization of cross-sections of lines possible, but not advisable |
| Ref No. | Type of Problem | Network Topology/Type | Contingency Type | Number of Contingencies | ANM Scheme | Multi DG Configuration | Computational Time (minutes) |
|---|---|---|---|---|---|---|---|
| [29] | Operation | Radial DN 1 | Selected lines and generators | 10 | No | No | 10 |
| [30] | Operation | Meshed TN 2 | Selected generators | 22 | No | No | 4 |
| [32] | Operation | Radial DN | Selected lines | 6 | No | No | - |
| [33] | Operation | Meshed TN | Selected lines | 9 | No | No | - |
| [36] | Operation | Radial DN | Selected feeder and transformer | 9 | Yes | No | - |
| [37] | Operation | Radial DN | Selected lines | 3 | No | No | 1 |
| [38] | Planning | Radial DN | Selected buses | 34 | No | No | - |
| Proposed | Planning | Meshed DN | All lines | 20 | Yes | Yes | 2 |
| Scenarios | DG5 | DG11 | DG16 |
|---|---|---|---|
| S1 | 1 | 0 | 0 |
| S2 | 0 | 1 | 0 |
| S3 | 0 | 0 | 1 |
| S4 | 1 | 1 | 0 |
| S5 | 0 | 1 | 1 |
| S6 | 1 | 0 | 1 |
| S7 | 1 | 1 | 1 |
| Scenario | Line in Contingency | Disconnected Buses as Result of Contingency | Total Number of Disconnected Buses | ||
|---|---|---|---|---|---|
| Radial | Meshed | Radial | Meshed | ||
| S1 | L4 | - | - | 0 | 0 |
| L5 | 6, 7 | - | 2 | 0 | |
| L7 | 8, 9, 10, 11, 12 | - | 5 | 0 | |
| S3 | L4 | 5 | - | 1 | 0 |
| L5 | 6, 7 | - | 2 | 0 | |
| L7 | 8, 9, 10, 11, 12 | - | 5 | 0 | |
| S5 | L4 | 5 | - | 1 | 0 |
| L5 | 6, 7 | - | 2 | 0 | |
| L7 | - | - | 0 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amjad, B.; Al-Ja’afreh, M.A.A.; Mokryani, G. Active Distribution Networks Planning Considering Multi-DG Configurations and Contingency Analysis. Energies 2021, 14, 4361. https://doi.org/10.3390/en14144361
Amjad B, Al-Ja’afreh MAA, Mokryani G. Active Distribution Networks Planning Considering Multi-DG Configurations and Contingency Analysis. Energies. 2021; 14(14):4361. https://doi.org/10.3390/en14144361
Chicago/Turabian StyleAmjad, Bilal, Mohammad Ahmad A. Al-Ja’afreh, and Geev Mokryani. 2021. "Active Distribution Networks Planning Considering Multi-DG Configurations and Contingency Analysis" Energies 14, no. 14: 4361. https://doi.org/10.3390/en14144361
APA StyleAmjad, B., Al-Ja’afreh, M. A. A., & Mokryani, G. (2021). Active Distribution Networks Planning Considering Multi-DG Configurations and Contingency Analysis. Energies, 14(14), 4361. https://doi.org/10.3390/en14144361