Flyback Photovoltaic Micro-Inverter with a Low Cost and Simple Digital-Analog Control Scheme
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Review and Research Gap
1.3. Aims and Contributions
2. Flyback Micro-Inverter and Its Analysis
- ✓
- Input voltage from PV module is 25–33 V;
- ✓
- RMS grid voltage is 220 V;
- ✓
- Grid frequency is 50 Hz, and;
- ✓
- Maximum transferred power to the grid is 120 W.
2.1. Analysis of Duty Cycle and Turns-Ratio
2.2. Analysis of Magnetizing Inductance
3. Design of Transformer and System Parameters
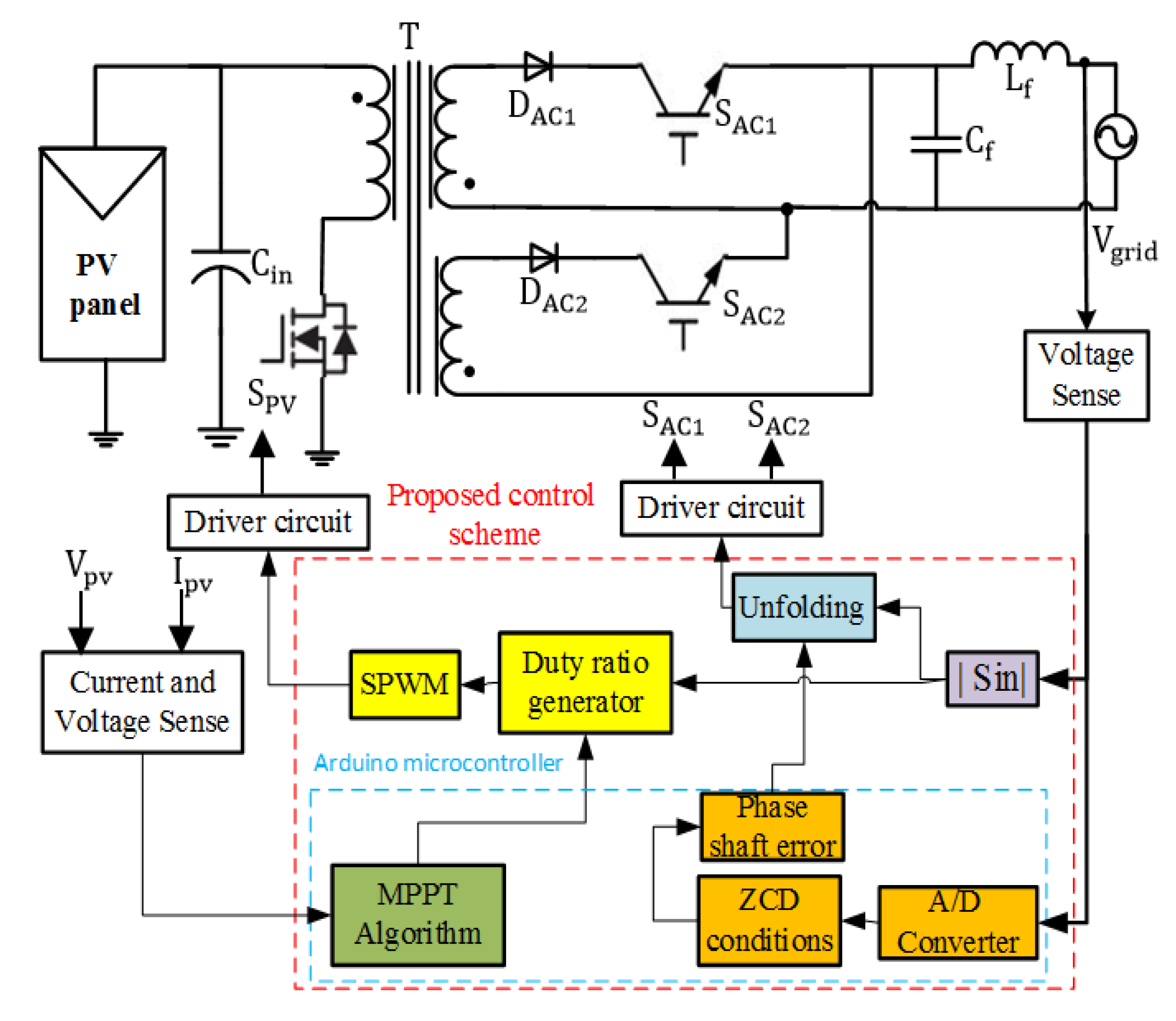
4. Proposed Digital-Analog Control Scheme
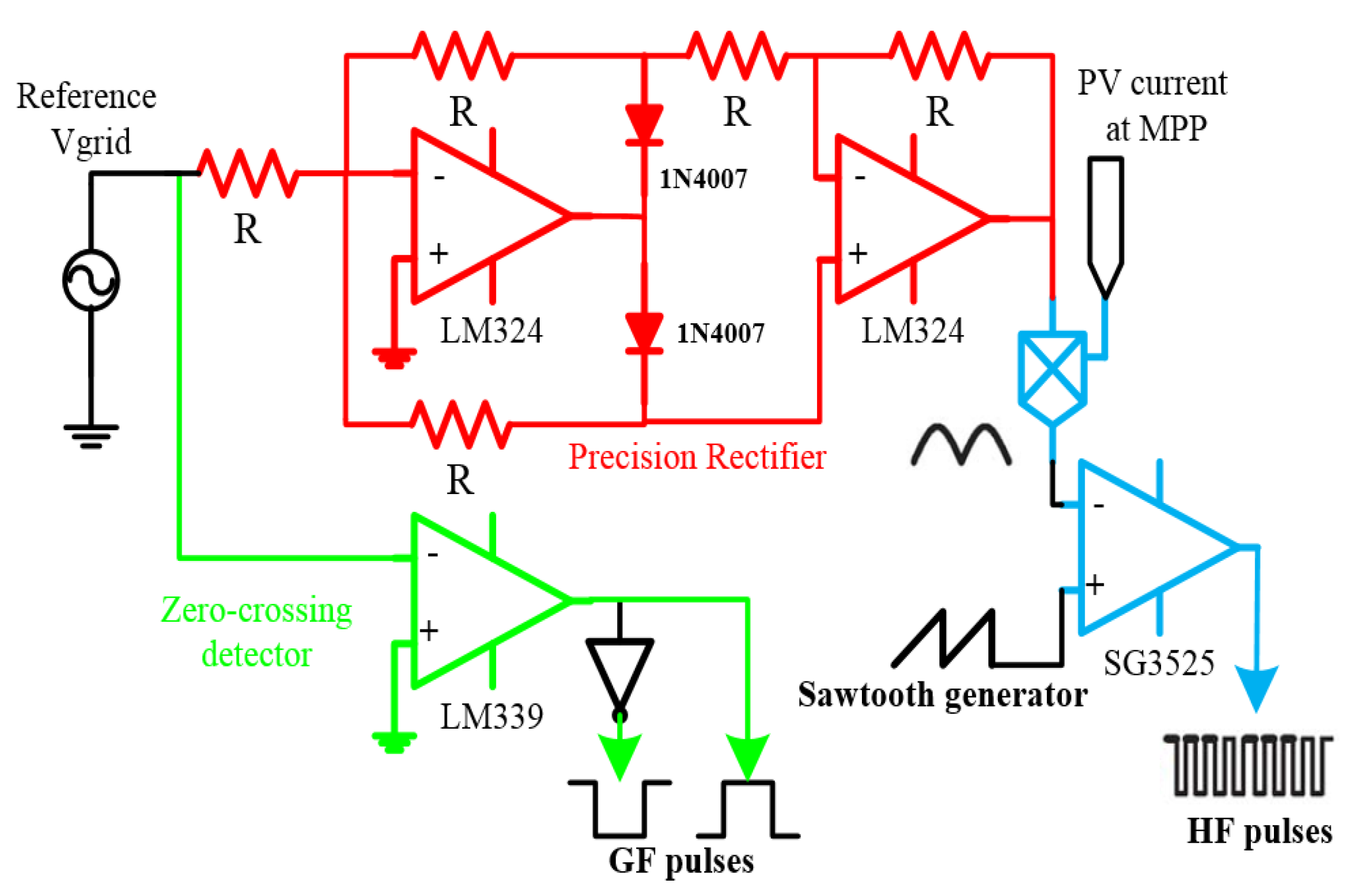
4.1. Simple Analog Control Circuit
4.2. Digital Control Circuit
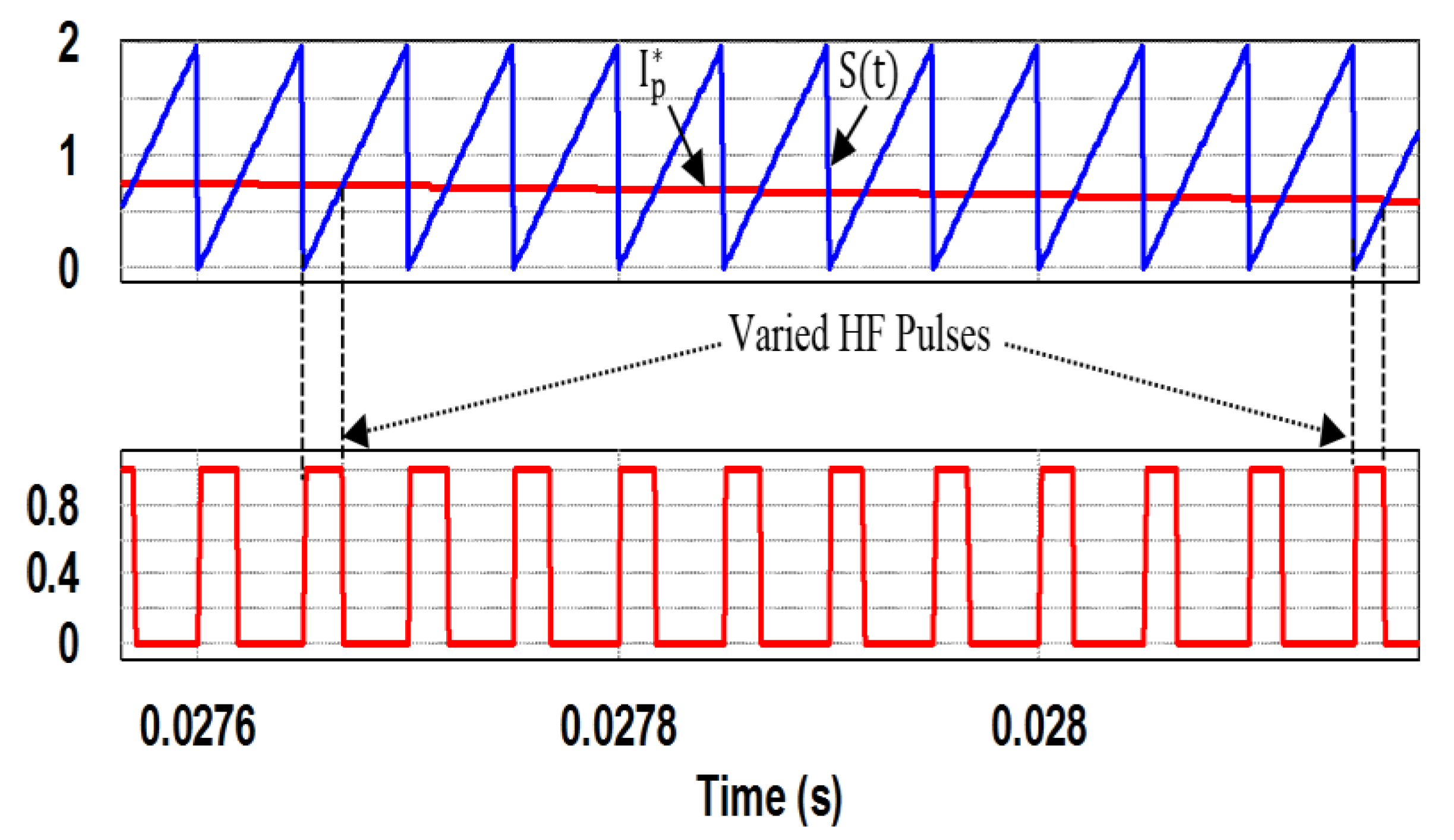
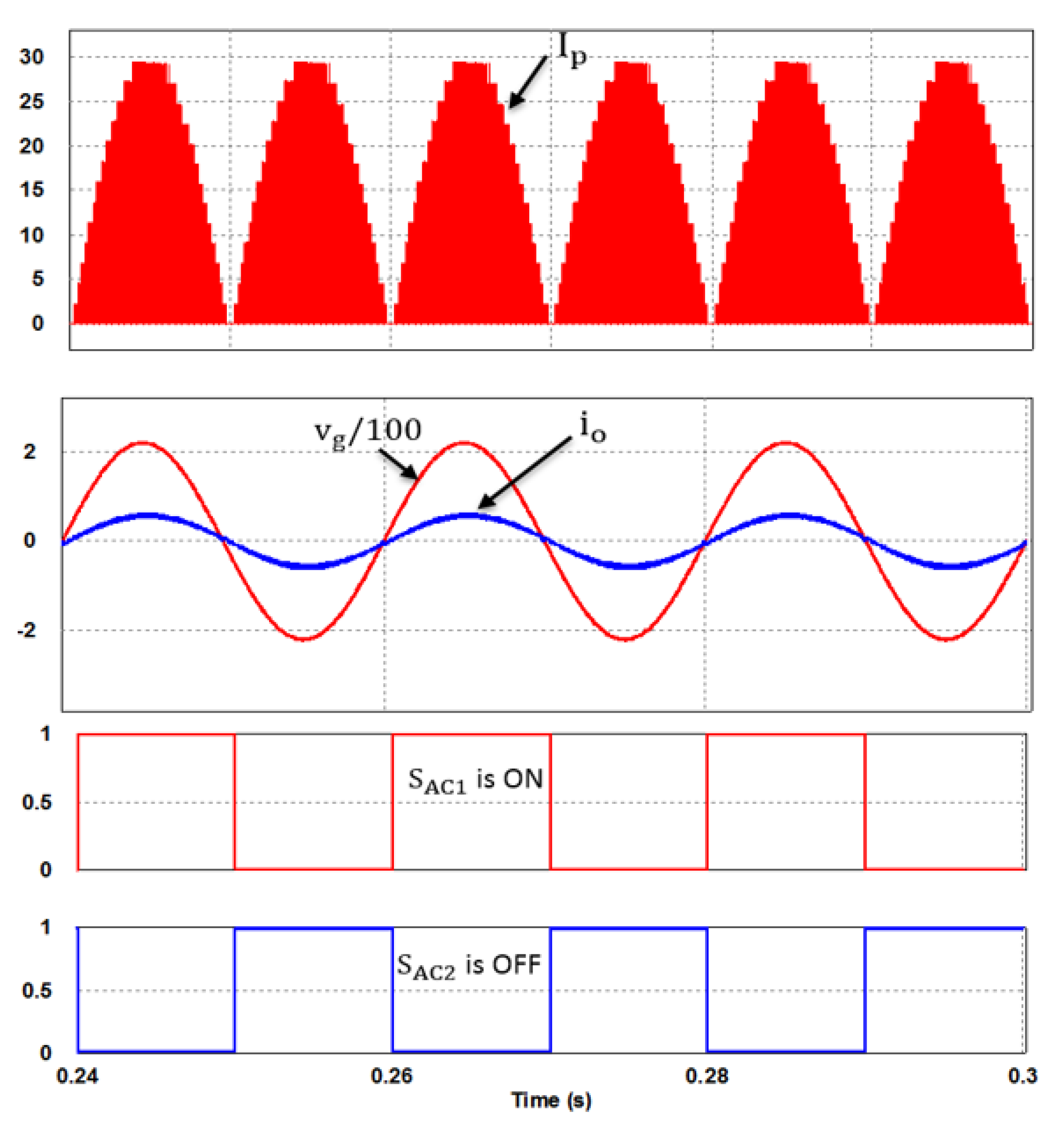
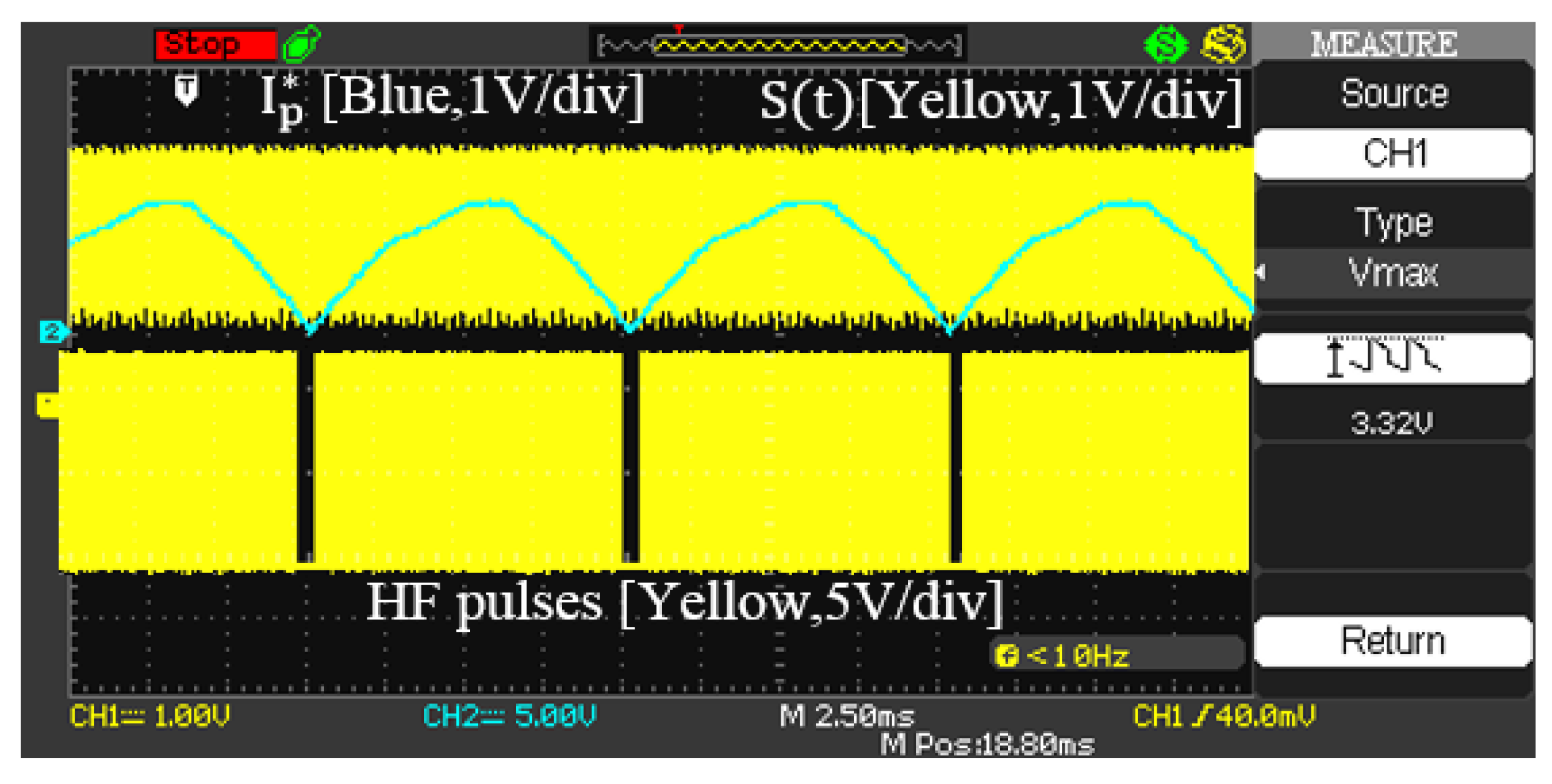
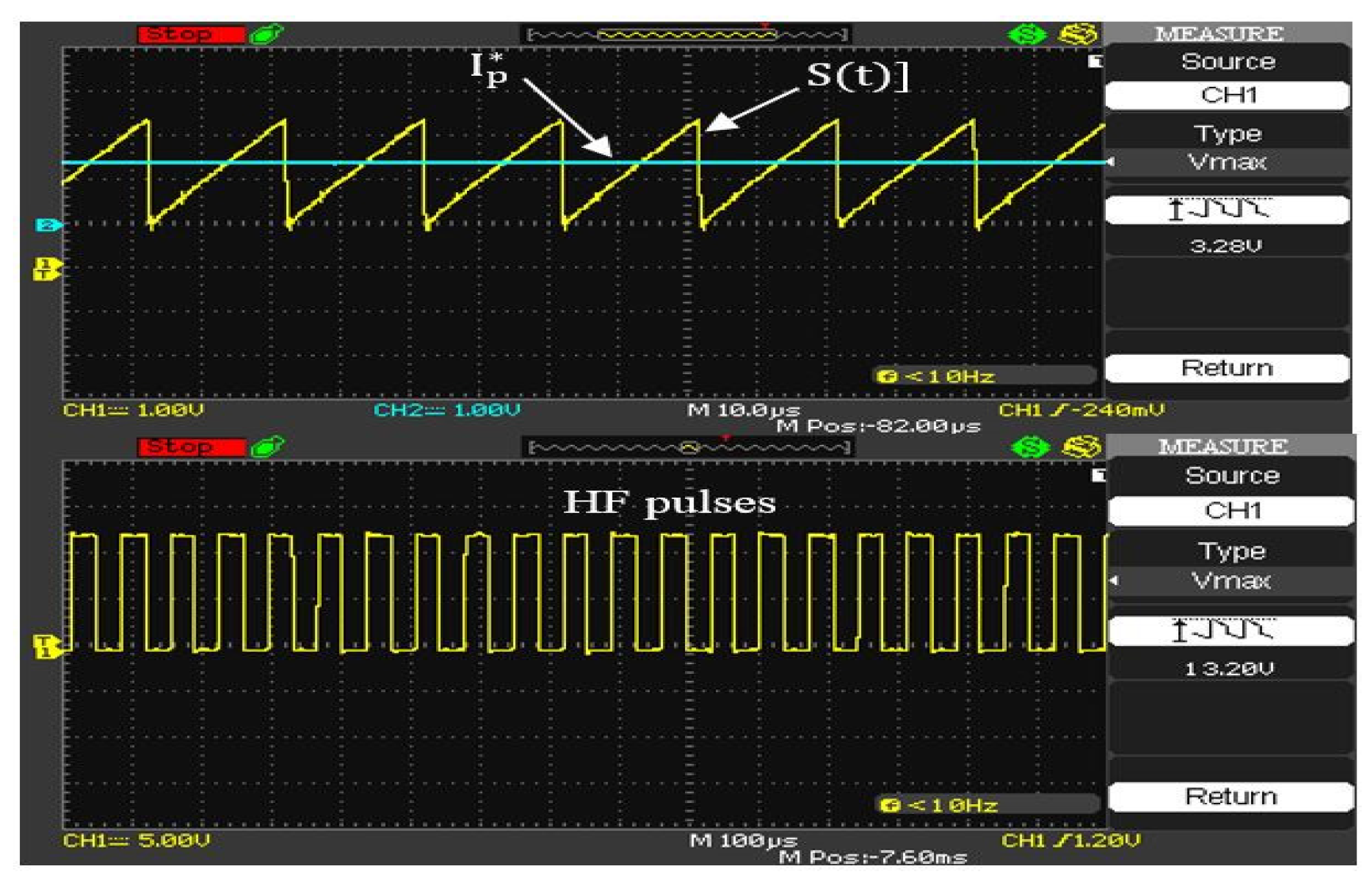
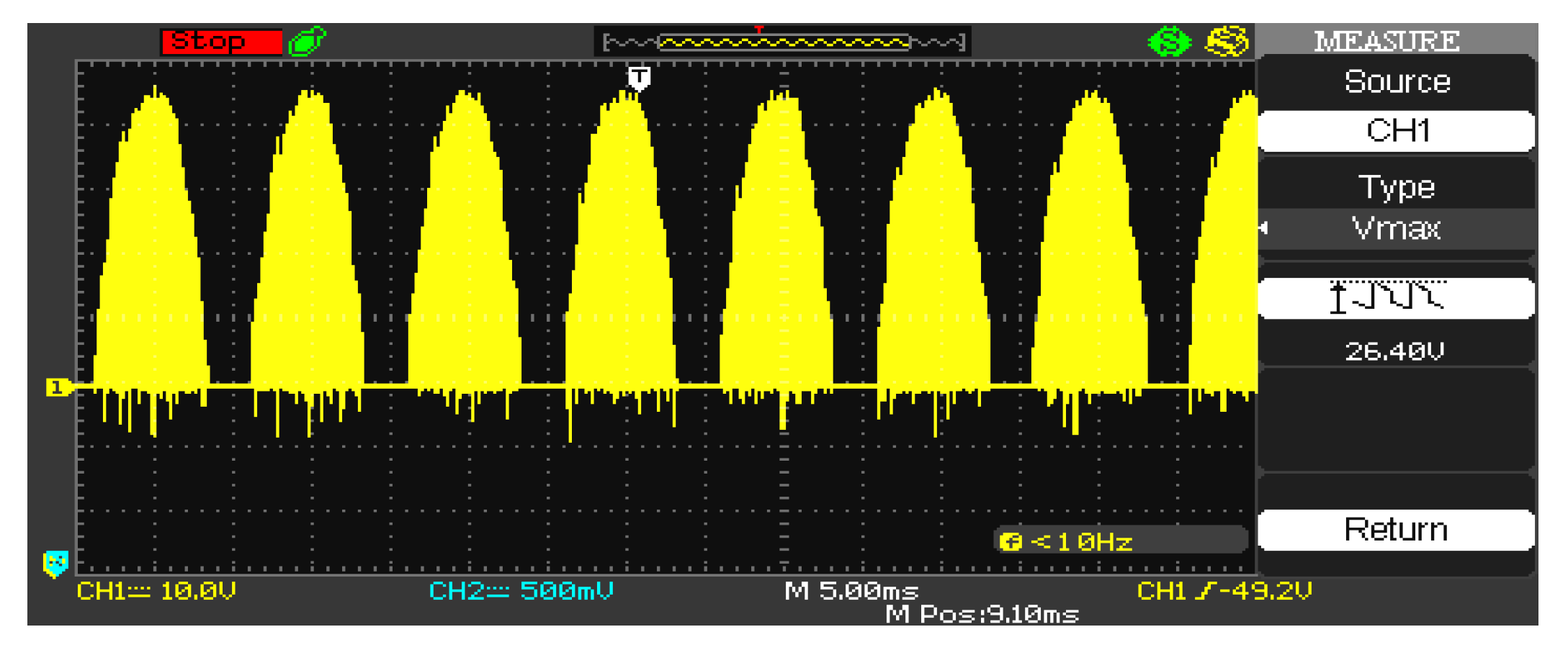
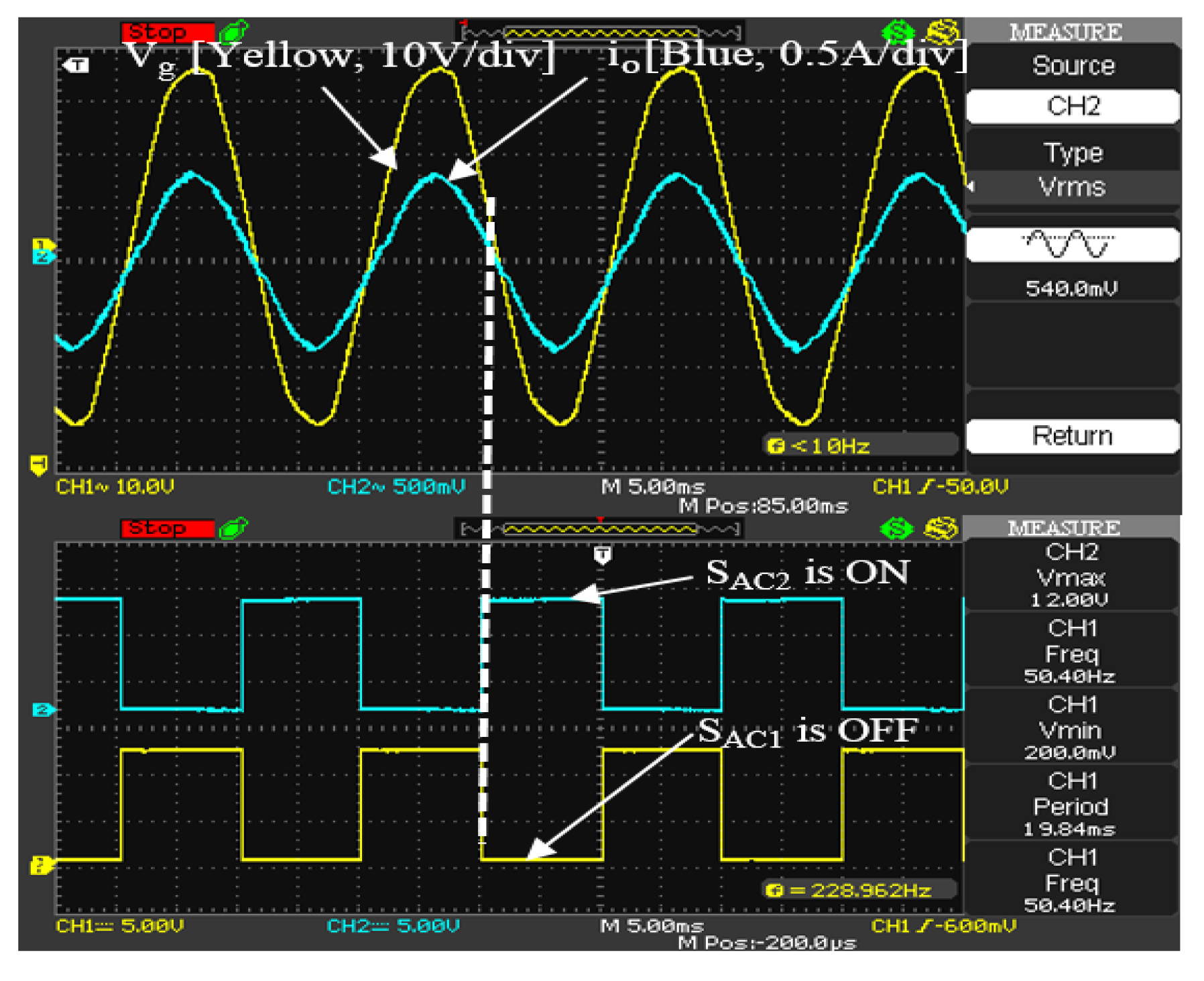
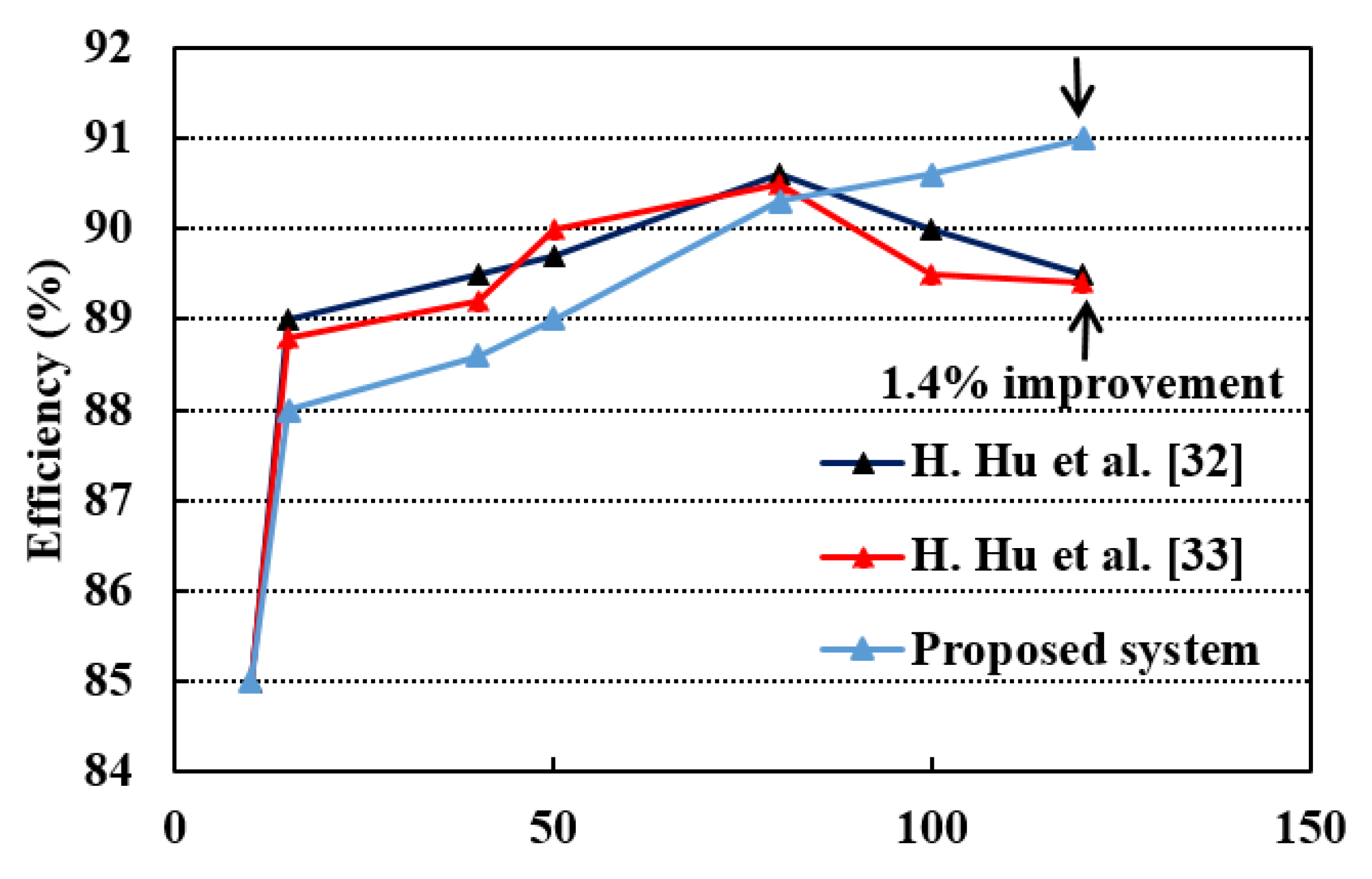
5. Simulation and Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bialasiewicz, J.T. Renewable Energy Systems with Photovoltaic Power Generators: Operation and Modeling. IEEE Trans. Ind. Electron. 2008, 55, 2752–2758. [Google Scholar] [CrossRef]
- Bull, S.R. Renewable energy today and tomorrow. Proc. IEEE 2001, 89, 1216–1226. [Google Scholar] [CrossRef]
- Caracciolo, F.; Dallago, E.; Finarelli, D.G.; Liberale, A.; Merhej, P. Single-Variable Optimization Method for Evaluating Solar Cell and Solar Module Parameters. IEEE J. Photovolt. 2012, 2, 173–180. [Google Scholar] [CrossRef]
- Sera, D.; Mathe, L.; Kerekes, T.; Spataru, S.V.; Teodorescu, R. On the Perturb-and-Observe and Incremental Conductance MPPT Methods for PV Systems. IEEE J. Photovolt. 2013, 3, 1070–1078. [Google Scholar] [CrossRef]
- Lian, K.L.; Jhang, J.H.; Tian, I.S. A Maximum Power Point Tracking Method Based on Perturb-and-Observe Combined with Particle Swarm Optimization. IEEE J. Photovolt. 2014, 4, 626–633. [Google Scholar] [CrossRef]
- Harb, S.; Balog, R. Reliability of Candidate Photovoltaic Module-Integrated-Inverter (PV-MII) Topologies—A Usage Model Approach. IEEE Trans. Power Electron. 2013, 28, 3019–3027. [Google Scholar] [CrossRef]
- Cha, W.J.; Cho, Y.W.; Kwon, J.-M.; Kwon, B.-H. High Efficient Micro-inverter with Soft-switching Step-up Converter and Single-switch-modulation Inverter. IEEE Trans. Ind. Electron. 2014, 62, 1. [Google Scholar] [CrossRef]
- Selvaraj, J.; Rahim, N.A. Multilevel Inverter For Grid-Connected PV System Employing Digital PI Controller. IEEE Trans. Ind. Electron. 2008, 56, 149–158. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Yang, Y.; Yang, D.; Wang, X. Distributed Power-Generation Systems and Protection. Proc. IEEE 2017, 105, 1311–1331. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Wolfs, P. A Review of the Single Phase Photovoltaic Module Integrated Converter Topologies With Three Different DC Link Configurations. IEEE Trans. Power Electron. 2008, 23, 1320–1333. [Google Scholar] [CrossRef] [Green Version]
- Harb, S.; Mirjafari, M.; Balog, R.S. Ripple-Port Module-Integrated Inverter for Grid-Connected PV Applications. IEEE Trans. Ind. Appl. 2013, 49, 2692–2698. [Google Scholar] [CrossRef]
- Liao, C.-Y.; Lin, W.-S.; Chen, Y.-M.; Chou, C.-Y. A PV Micro-inverter With PV Current Decoupling Strategy. IEEE Trans. Power Electron. 2016, 32, 6544–6557. [Google Scholar] [CrossRef]
- Surapaneni, R.K.; Rathore, A.K. A Single-stage CCM Zeta Micro-inverter for Solar Photovoltaic AC Module. IEEE J. Eme. Sel. Top. Power Electron 2015, 3, 892–900. [Google Scholar] [CrossRef]
- Meneses, D.; Garcia, O.; Alou, P.; Oliver, J.A.; Cobos, J.A. Grid-Connected Forward Microinverter With Primary-Parallel Secondary-Series Transformer. IEEE Trans. Power Electron. 2014, 30, 4819–4830. [Google Scholar] [CrossRef] [Green Version]
- Surapaneni, R.K.; Das, P. A Z-Source-Derived Coupled-Inductor-Based High Voltage Gain Microinverter. IEEE Trans. Ind. Electron. 2017, 65, 5114–5124. [Google Scholar] [CrossRef]
- Kasa, N.; Iida, T.; Chen, L. Flyback Inverter Controlled By Sensor Less Current MPPT for Photovoltaic Power System. IEEE Trans. Ind. Elec. 2005, 52, 1145–1152. [Google Scholar] [CrossRef]
- Nanakos, A.C.; Christidis, G.C.; Tatakis, E.C. Weighted Efficiency Optimization of Flyback Microinverter Under Improved Boundary Conduction Mode (i-BCM). IEEE Trans. Power Electron. 2014, 30, 5548–5564. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Ji, Y.-H.; Kim, J.-G.; Jung, Y.-C.; Won, C.-Y. A New Control Strategy for Improving Weighted Efficiency in Photovoltaic AC Module-Type Interleaved Flyback Inverters. IEEE Trans. Power Electron. 2012, 28, 2688–2699. [Google Scholar] [CrossRef]
- Rezaei, M.A.; Lee, K.-J.; Huang, A.Q. A High-Efficiency Flyback Micro-inverter With a New Adaptive Snubber for Photovoltaic Applications. IEEE Trans. Power Electron. 2016, 31, 318–327. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, M.; Chen, W.; Jiang, C.; Qian, Z. Analysis and Implementation of Phase Synchronization Control Strategies for BCM Interleaved Flyback Microinverters. IEEE Trans. Power Electron. 2014, 29, 5921–5932. [Google Scholar] [CrossRef]
- Sukesh, N.; Pahlevaninezhad, M.; Jain, P.K. Analysis and Implementation of a Single-Stage Flyback PV Microinverter with Soft Switching. IEEE Trans. Ind. Electron. 2013, 61, 1819–1833. [Google Scholar] [CrossRef]
- Shimizu, T.; Wada, K.; Nakamura, N. Flyback-Type Single-Phase Utility Interactive Inverter With Power Pulsation Decoupling on the DC Input for an AC Photovoltaic Module System. IEEE Trans. Power Electron. 2006, 21, 1264–1272. [Google Scholar] [CrossRef]
- Edwin, F.F.; Xiao, W.; Khadkikar, V. Dynamic Modeling and Control of Interleaved Flyback Module-Integrated Converter for PV Power Applications. IEEE Trans. Ind. Electron. 2013, 61, 1377–1388. [Google Scholar] [CrossRef]
- Li, Y.; Oruganti, R. A Low Cost Flyback CCM Inverter for AC Module Application. IEEE Trans. Power Electron. 2011, 27, 1295–1303. [Google Scholar] [CrossRef]
- Lee, S.-H.; Cha, W.-J.; Kwon, B.-H.; Kim, M. Discrete-Time Repetitive Control of Flyback CCM Inverter for PV Power Applications. IEEE Trans. Ind. Electron. 2015, 63, 976–984. [Google Scholar] [CrossRef]
- Hadi, M.; Mohamadian, M.; Beiranvand, R. A Single-Phase Grid-connected Photovoltaic Inverter Based on a Three-switch Three-port flyback with Series Power Decoupling Circuit. IEEE, Trans. Ind. Electron. 2017, 64, 2062–2071. [Google Scholar] [CrossRef]
- Lee, S.-H.; Cha, W.-J.; Kwon, J.-M.; Kwon, B.-H. Control Strategy of Flyback Micro-inverter with Hybrid Mode for PV AC Modules. IEEE Trans. Ind. Electron. 2016, 63, 995–1002. [Google Scholar] [CrossRef]
- Radin, Z.; Jamaludin, J.; Rahim, N.A. Photovoltaic Flyback Micro-inverter with Tertiary Winding Current Sensing. IEEE Trans. Power Electron. 2018, 34, 7588–7602. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.S.; Kim, M. Down Sampled Iterative Learning Controller for Flyback CCM Inverter. IEEE Trans. Ind. Electron. 2018, 65, 510–520. [Google Scholar] [CrossRef]
- Shitole, A.B.; Sathyan, S.; Suryawanshi, H.M.; Talapur, G.G.; Chaturvedi, P. Soft Switched High Voltage Gain Boost Integrated Flyback Converter Interfaced Single-Phase Grid Tied Inverter for SPV Integration. IEEE Trans. Ind. Appl. 2018, 54, 482–493. [Google Scholar] [CrossRef]
- Gao, M.; Chen, M.; Zhang, C.; Qian, Z. Analysis and Implementation of an Improved Flyback Inverter for Photovoltaic AC Module Applications. IEEE Trans. Power Electron. 2013, 29, 3428–3444. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X.-F.; Liu, Y.-F. An Optimal Control Method for Photovoltaic Grid-Tied-Interleaved Flyback Microinverters to Achieve High Efficiency in Wide Load Range. IEEE Trans. Power Electron. 2013, 28, 5074–5087. [Google Scholar] [CrossRef]
- Hu, H.; Harb, S.; Kutkut, N.H.; Shen, Z.J.; Batarseh, I. A Single-Stage Microinverter Without Using Eletrolytic Capacitors. IEEE Trans. Power Electron. 2013, 28, 2677–2687. [Google Scholar] [CrossRef]
- Hu, H.; Harb, S.; Fang, X.; Zhang, D.; Zhang, Q.; Shen, Z.J.; Batarseh, I. A Three-port Flyback for PV Micro-inverter Applications with Power Pulsation Decoupling Capability. IEEE Trans. Power Electron. 2012, 27, 3953–3964. [Google Scholar] [CrossRef]
- Kyristis, A.C.; Tatakis, E.C.; Papanikolaou, N.P. Optimum Design of the Current-Source Flyback Inverter for Decentralized Grid-connected Photovoltaic Systems. IEEE Trans. Energy Conv. 2008, 23, 281–293. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K. High-Frequency Magnetic Components, 2nd ed.; Wiley: Hoboken, NJ, USA, 2013; ISBN 978-1-118-71778-3. [Google Scholar]
- Mclyman, C.W.T. Transformer and Inductor Design Handbook, 3rd ed.; Revised and Expanded; CRC Press: Boca Raton, FL, USA, 2004; ISBN 0-8247-5393-3. [Google Scholar] [CrossRef]
- Alldatasheet.com. Ferroxcube International Holding B.V. 2008. Available online: https://www.alldatasheet.com/datasheet-pdf/pdf/341302/FERROXCUBE/3C90.html (accessed on 1 September 2008).




| Component | Quantity | Price (USD) |
|---|---|---|
| Arduino Uno | 1 | 4.2 |
| Quad op. amps LM324N | 2 | 1.24 |
| Quad comparator LM339 | 1 | 0.95 |
| Signal transformer (220/6 V) | 1 | 2.8 |
| 10 k (1/4 w) resistor | 8 | 0.5 |
| Diode 1N4007 | 2 | 0.1 |
| Hall current sensor (20 A) | 1 | 1.68 |
| Total cost | 11.47 |
| Parameter | Symbol | Value |
|---|---|---|
| Rated output power | 120W | |
| PV module voltage | 33V-38V | |
| Grid voltage | 220V, 50Hz | |
| Switching frequency | 30kHz | |
| Total input capacitance | ||
| Main MOSFET | FDH50N50 | |
| IGBTs | , | FGL40N120 |
| Power diode | , | RHRG75120 |
| Flyback transformer | ||
| Core type | - | E55/28/2-3C90 |
| Effective length | ||
| Turn’s ratio | 10 | |
| Magnetizing inductance | ||
| Maximum flux density | Bm | 0.2 T |
| Output power | 12 W | 50 W | 100 W | 120 W |
| Proposed THD | 6% | 4.6% | 3.5% | 3% |
| Zhang Z.et al. [20] | 7.8% | 6.6% | 5.4% | 4.2% |
| Paper | Type of Micro-Inverter | Controller Used | Maximum Efficiency | Cost |
|---|---|---|---|---|
| Z. Zhang et al. [20] | Interleaved flyback, 200 W | FPGA EP3C10E | 94% | 29$ |
| H. Hu et al. [33] | Single-stage flyback, 120 W | Microprocessor STM32F103 | 89.7% | 7.77$ |
| Y.H. Kim et al. [18] | Interleaved flyback, 100 W | TMS320F28035 | 94.5% | 17$ |
| H. Hu et al. [32] | Single-stage flyback,100 W | Microprocessor STM32F103 | 90% | 7.77$ |
| Proposed | Single-stage flyback, 120 W | Arduino Uno microcontroller | 91% | 4.2$ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaqoob, S.J.; Obed, A.; Zubo, R.; Al-Yasir, Y.I.A.; Fadhel, H.; Mokryani, G.; Abd-Alhameed, R.A. Flyback Photovoltaic Micro-Inverter with a Low Cost and Simple Digital-Analog Control Scheme. Energies 2021, 14, 4239. https://doi.org/10.3390/en14144239
Yaqoob SJ, Obed A, Zubo R, Al-Yasir YIA, Fadhel H, Mokryani G, Abd-Alhameed RA. Flyback Photovoltaic Micro-Inverter with a Low Cost and Simple Digital-Analog Control Scheme. Energies. 2021; 14(14):4239. https://doi.org/10.3390/en14144239
Chicago/Turabian StyleYaqoob, Salam J., Adel Obed, Rana Zubo, Yasir I. A. Al-Yasir, Hussein Fadhel, Geev Mokryani, and Raed A. Abd-Alhameed. 2021. "Flyback Photovoltaic Micro-Inverter with a Low Cost and Simple Digital-Analog Control Scheme" Energies 14, no. 14: 4239. https://doi.org/10.3390/en14144239
APA StyleYaqoob, S. J., Obed, A., Zubo, R., Al-Yasir, Y. I. A., Fadhel, H., Mokryani, G., & Abd-Alhameed, R. A. (2021). Flyback Photovoltaic Micro-Inverter with a Low Cost and Simple Digital-Analog Control Scheme. Energies, 14(14), 4239. https://doi.org/10.3390/en14144239










