Appropriate Volt–Var Curve Settings for PV Inverters Based on Distribution Network Characteristics Using Match Rate of Operating Point
Abstract
:1. Introduction
1.1. Background and Related Works
1.2. Motivation and Contribution
1.3. Outline
2. Specifications in Volt–Var Curve for PV Inverter
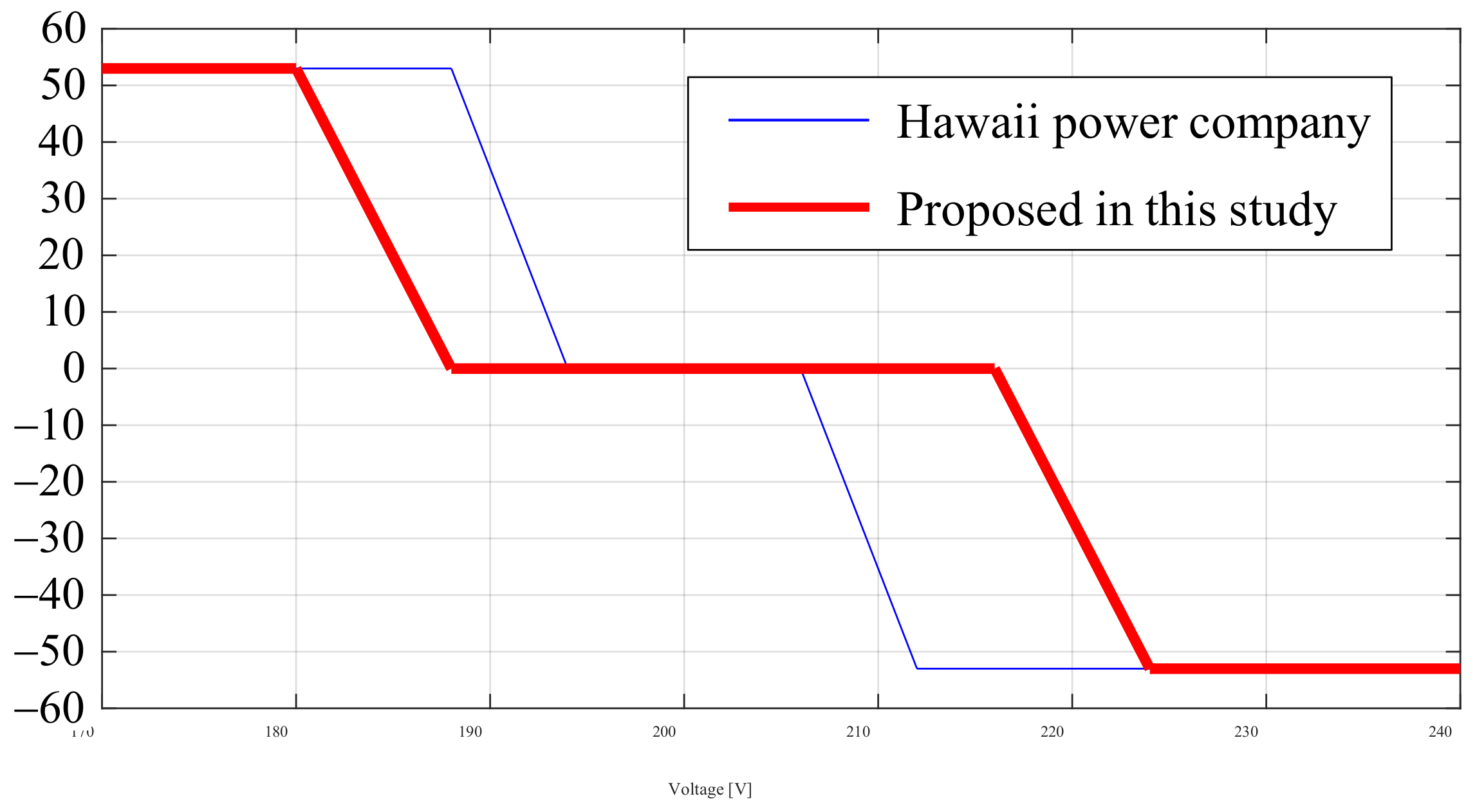
2.1. Volt–Var Characterictic
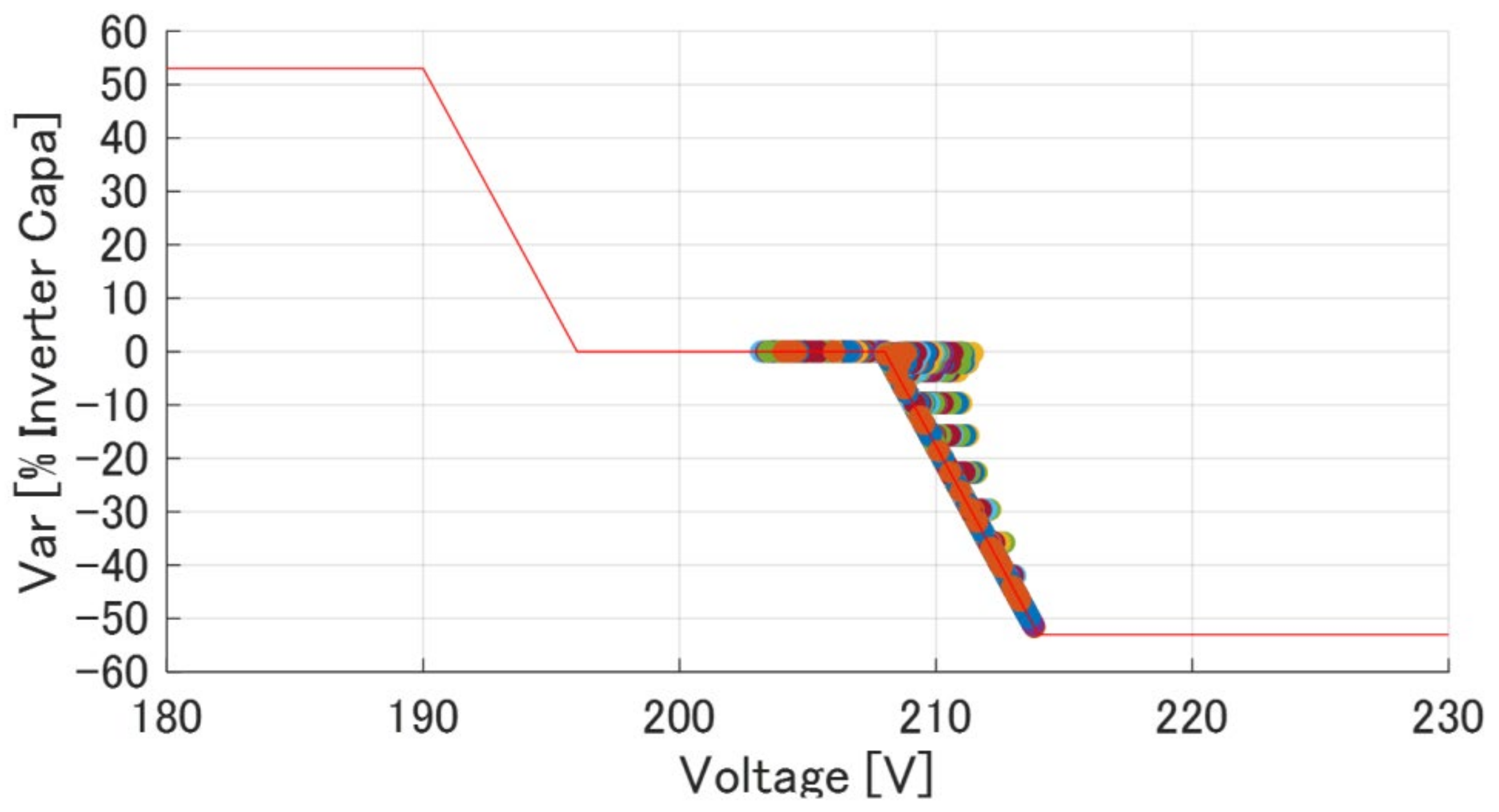
2.2. Capacity Restriction of Inverter
2.3. Calculation of Operating Point on Volt–Var Curve
3. Dependence of Effect of Volt–Var Curve on Distribution System Configuration
3.1. Residential Area 1
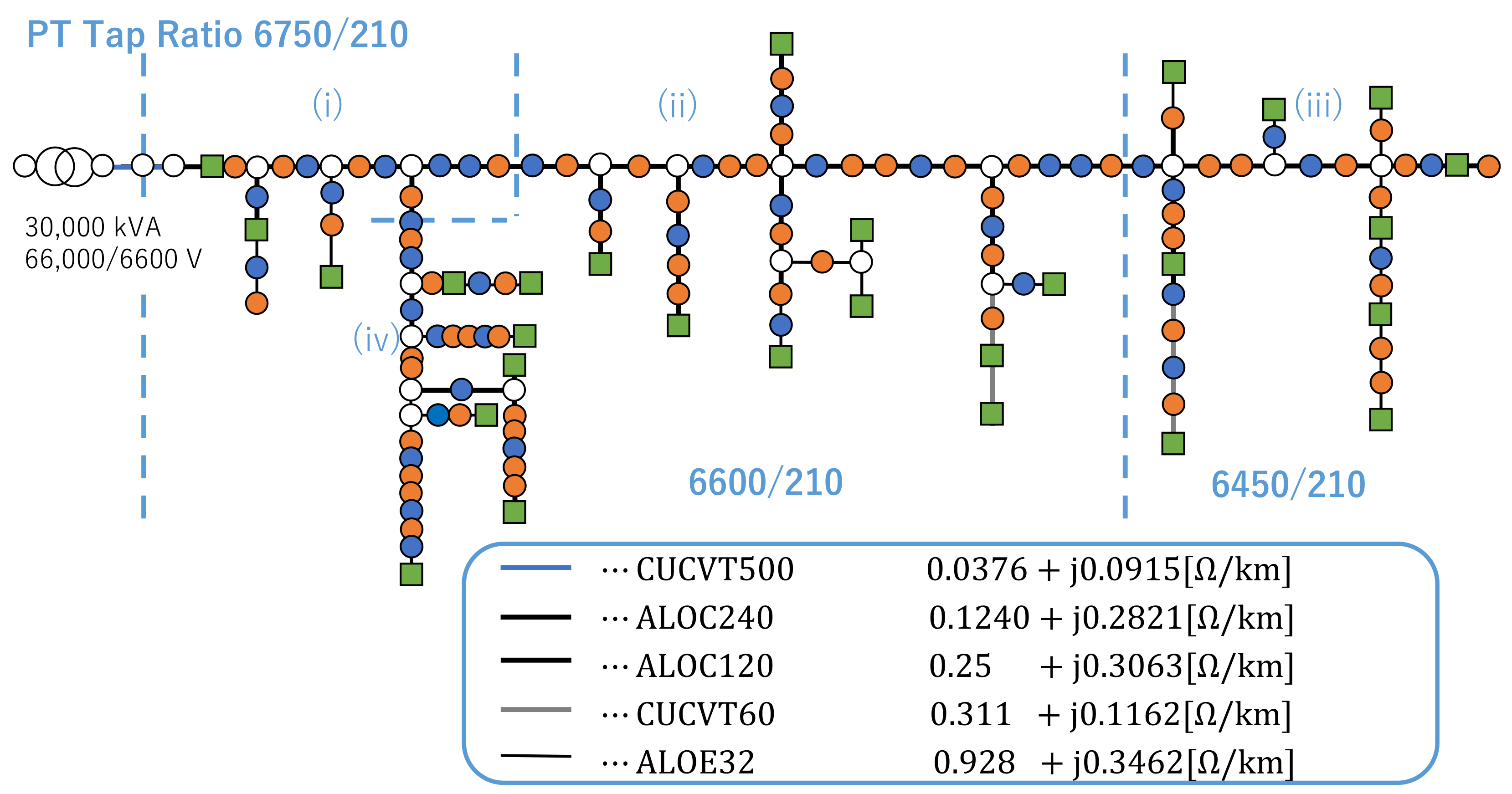
3.1.1. Simulation Model
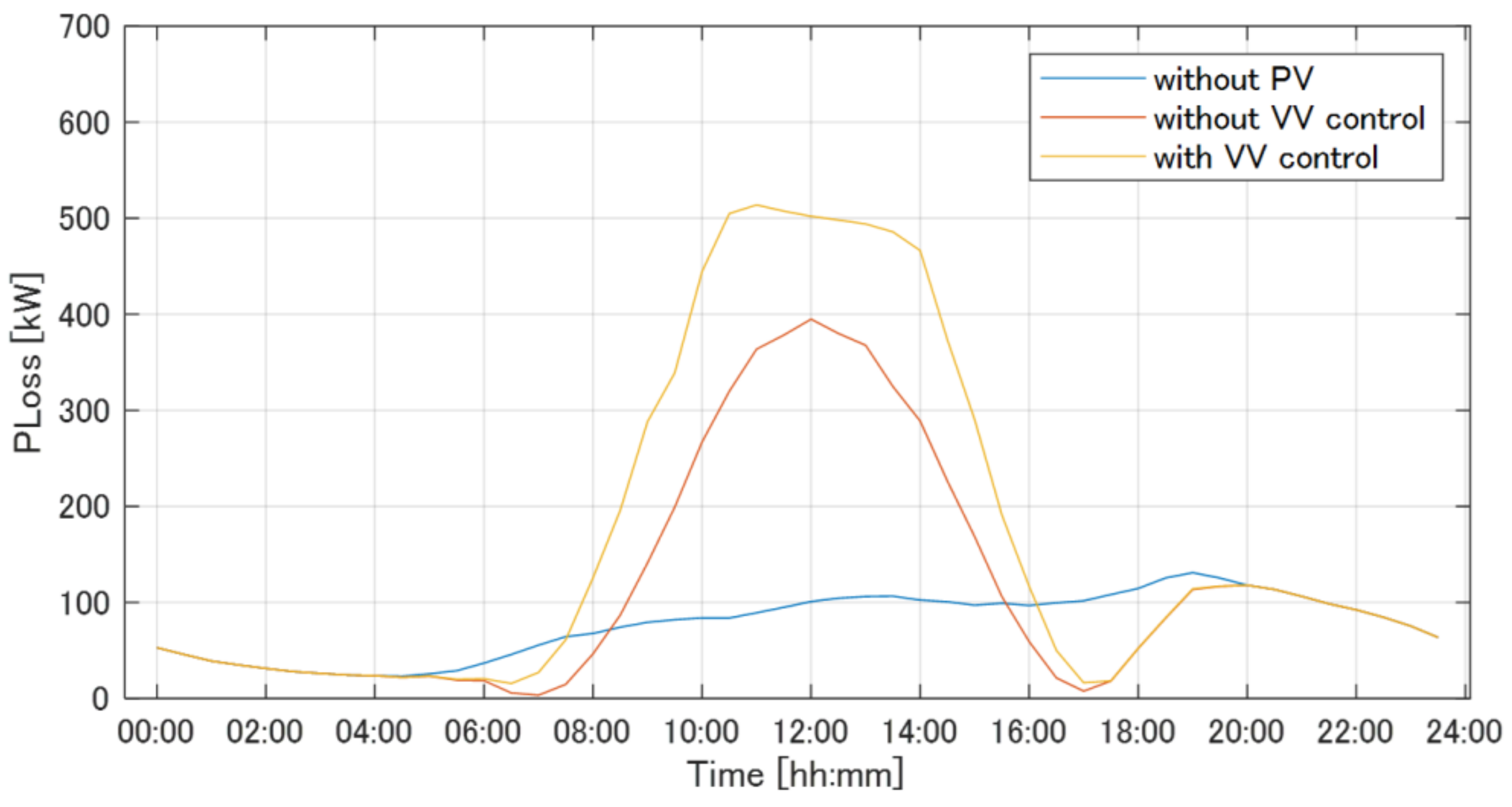
3.1.2. Simulation Results
3.1.3. Control Characteristics
3.2. Rural Area 1
3.2.1. Simulation Model
3.2.2. Control Characteristics
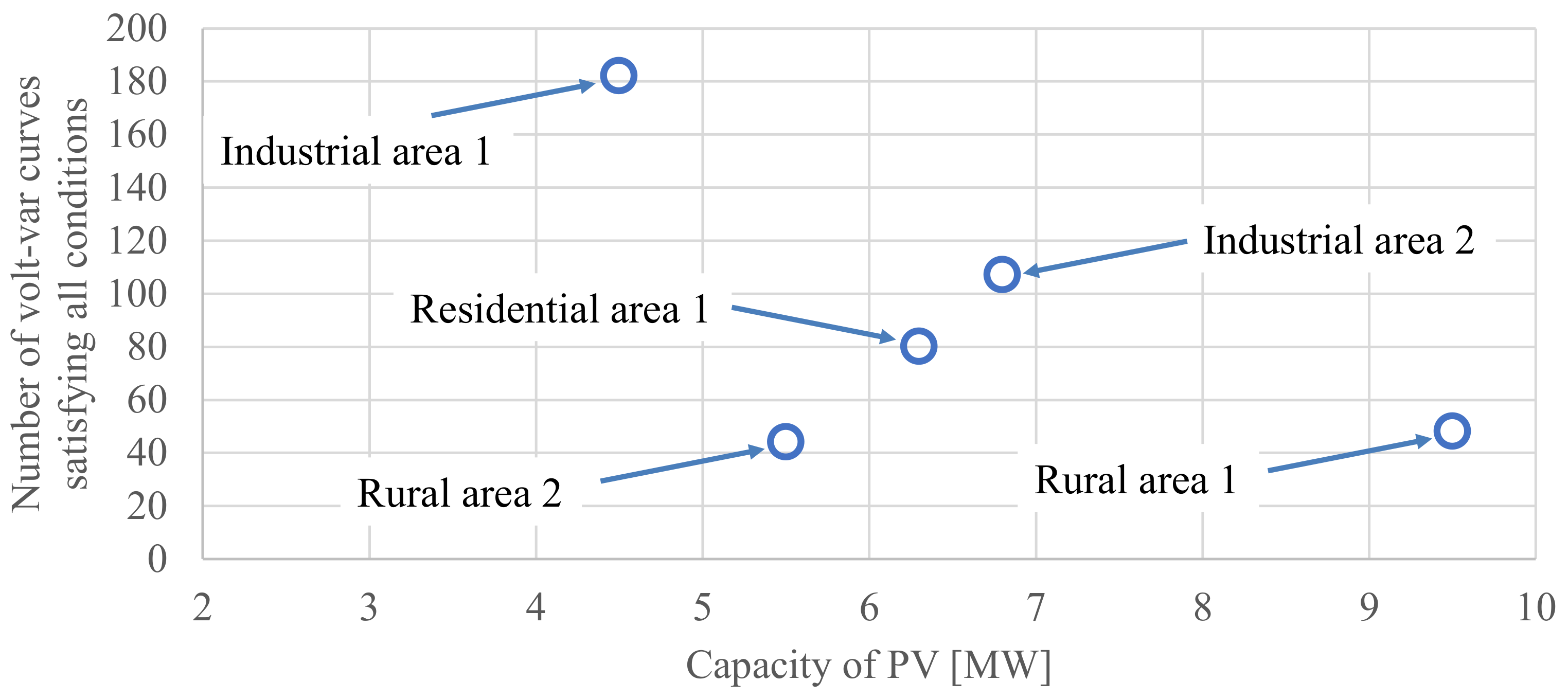
3.3. Dependence on PV Capacity and Line Length
4. Selection of Volt–Var Curve
5. Discussion
6. Conclusions
- From the simulation results for the 360 patterns of the volt–var curve, the reactive-power-output accumulation of the PV inverters, distribution loss, and the number of tap operations of LRT are plotted in a three-dimensional graph, and the response of the volt–var curve can be characterized visually.
- The three-dimensional graph indicates that as the lagged reactive power accumulation increases, the distribution line loss also increases; however, the increase or decrease in the number of tap operations depends on the characteristics of the distribution line.
- Owing to the power factor constraint of the inverter, it is not possible to output the commanded reactive power according to the volt–var curve. By calculating the match rate to evaluate this, we can narrow down the volt–var curve that can effectively utilize the reactive power of the PV inverter for voltage control.
- Furthermore, by selecting the volt–var curve that can control the voltage within the appropriate range, we were able to narrow down the 360 patterns of volt–var curves to 23 patterns. When the volt–var curve that minimizes the reactive power output is selected and compared with the standard volt–var curve of the Hawaii Power Company, it was found that the volt–var curve selected using the proposed method is superior to that of the Hawaii Power Company from the viewpoint of distribution loss, voltage violation, and match rate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Green, M.A. Photovoltaic technology and visions for the future. Prog. Energy 2019, 1, 013001. [Google Scholar] [CrossRef]
- Wang, R.; Mujahid, M.; Duan, Y.; Wang, Z.-K.; Xue, J.; Yang, Y. A Review of Perovskites Solar Cell Stability. Adv. Funct. Mater. 2019, 29, 1808843. [Google Scholar] [CrossRef]
- Xiao, L.; Kolaczkowski, M.A.; Min, Y.; Liu, Y. Substitution Effect on Thiobarbituric Acid End Groups for High Open-Circuit Voltage Non-Fullerene Organic Solar Cells. ACS Appl. Mater. Interfaces 2020, 12, 41852–41860. [Google Scholar] [CrossRef]
- Gandhi, O.; Kumar, D.S.; Rodríguez-Gallegos, C.D.; Srinivasan, D. Review of power system impacts at high PV penetration Part I: Factors limiting PV penetration. Sol. Energy 2002, 210, 181–201. [Google Scholar] [CrossRef]
- Noone, B.; Bruce, A.; MacGill, I.; Bletterie, B.; Bründlinger, R.; Mayr, C.; De Brabandere, K.; Dierckxsens, C.; Yibo, W.; Stetz, T.; et al. High Penetration of PV in Local Distribution Grids; Report IEA PVPS T14-02; International Energy Agency (IEA): Paris, France, 2014. [Google Scholar]
- Iioka, D.; Fujii, T.; Orihara, D.; Tanaka, T.; Harimoto, T.; Shimada, A.; Goto, T.; Kubuki, M. Voltage reduction due to reverse power flow in distribution feeder with photovoltaic system. Int. J. Electr. Power Energy Syst. 2019, 113, 411–418. [Google Scholar] [CrossRef]
- Hossain, M.I.; Yan, R.; Saha, T.K. Investigation of the interaction between step voltage regulators and large-scale photovoltaic systems regarding voltage regulation and unbalance. IET Renew. Power Gener. 2016, 10, 299–309. [Google Scholar] [CrossRef] [Green Version]
- Iioka, D.; Sakakibara, K.; Yokomizu, Y.; Matsumura, T.; Izuhara, N. Distribution voltage rise at dense photovoltaic generation area and its suppression by SVC. Electr. Eng. Jpn. 2009, 166, 47–53. [Google Scholar] [CrossRef]
- Zeraati, M.; Hamedani Golshan, M.E.; Guerrero, J.M. Distributed Control of Battery Energy Storage Systems for Voltage Regulation in Distribution Networks with High PV Penetration. IEEE Trans. Smart Grid 2018, 9, 3582–3593. [Google Scholar] [CrossRef] [Green Version]
- Iioka, D.; Miura, K.; Machida, M.; Kikuchi, S.; Imanaka, M.; Baba, J.; Takagi, M.; Asano, H. Hosting capacity of large scale PV power station in future distribution networks. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Kikuchi, S.; Machida, M.; Tamura, J.; Imanaka, M.; Baba, J.; Iioka, D.; Miura, K.; Takagi, M.; Asano, H. Hosting capacity analysis of many distributed photovoltaic systems in future distribution networks. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, X.; Aichhorn, A.; Liu, L.; Li, H. Coordinated Control of Distributed Energy Storage System with Tap Changer Transformers for Voltage Rise Mitigation Under High Photovoltaic Penetration. IEEE Trans. Smart Grid 2012, 3, 897–906. [Google Scholar] [CrossRef]
- Agalgaonkar, Y.P.; Pal, B.C.; Jabr, R.A. Distribution Voltage Control Considering the Impact of PV Generation on Tap Changers and Autonomous Regulators. IEEE Trans. Power Syst. 2014, 29, 182–192. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Bai, F.; Yan, R.; Saha, T.K. Real-Time Coordinated Voltage Control of PV Inverters and Energy Storage for Weak Networks with High PV Penetration. IEEE Trans. Power Syst. 2018, 33, 3383–3395. [Google Scholar] [CrossRef] [Green Version]
- Iioka, D.; Fujii, T.; Tanaka, T.; Harimoto, T.; Motoyama, J. Voltage Reduction in Medium Voltage Distribution Systems Using Constant Power Factor Control of PV PCS. Energies 2020, 13, 5430. [Google Scholar] [CrossRef]
- Edge, R.; York, B.; Enber, N. Rolling Out Smart Inverters—Assessing Utility Strategies and Approaches. Solar Electric Power Association (SEPA) and Electric Power Research Institute (EPRI)s’ Technical Report; EPRI: Washington, DC, USA, 2015. [Google Scholar]
- International Electrotechnical Commission (IEC). IEC TR 61850-90-7. IEC’s Technical Report; Edition 1.0 2013-02; International Electrotechnical Commission (IEC): London, UK, 2013. [Google Scholar]
- Seal, B.; Ealey, B. Common Function for Smart Inverters, 4th ed.; Electric Power Research Institute (EPRI)’s Technical Report; EPRI: Washington, DC, USA, 2016. [Google Scholar]
- Ding, F.; Nagarajian, A.; Chakrabotory, C.; Baggu, M.; Nguyen, A.; Walinga, S.; McCarty, M.; Bell, F. Photovoltaic Impact Assessment of Smart Inverter Volt-Var Control on Distribution System Conservation Voltage Reduction and Power Quality; NREL Technical Report; NREL: Golden, CO, USA, 2016. [Google Scholar]
- Parajeles, M.J.; Quirós-Tortós, J.; Valverde, G. Assessing the performance of smart inverters in large-scale distribution networks with PV systems. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Quito, Ecuador, 20–22 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Horowitz, K.A.; Peterson, Z.; Coddington, M.H.; Ding, F.; Sigrin, B.O.; Saleem, D.; Baldwin, S.E.; Lydic, B.; Stanfield, S.C.; Enbar, N.; et al. An Overview of Distributed Energy Resource (DER) Interconnection: Current Practices and Emerging Solutions; NREL Technical Report, TP-6A20-72102; NREL: Golden, CO, USA, 2019. [Google Scholar]
- Bello, M.; Montenegro-Martinez, D.; York, B.; Smith, J. Optimal Settings for Multiple Groups of Smart Inverters on Secondary Systems Using Autonomous Control. IEEE Trans. Ind. Appl. 2018, 54, 1218–1223. [Google Scholar] [CrossRef]
- Rylander, M.; Reno, M.J.; Quiroz, J.E.; Ding, F.; Li, H.; Broderick, R.J.; Mather, B.; Smith, J. Methods to determine recommended feeder-wide advanced inverter settings for improving distribution system performance. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 1393–1398. [Google Scholar] [CrossRef]
- Dao, V.T.; Ishii, H.; Hayashi, Y. Optimal smart functions of large-scale PV inverters in distribution systems. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Jafari, M.; Olowu, T.O.; Sarwat, A.I. Optimal Smart Inverters Volt-VAR Curve Selection with a Multi-Objective Volt-VAR Optimization using Evolutionary Algorithm Approach. In Proceedings of the 2018 North American Power Symposium (NAPS), Fargo, ND, USA, 9–11 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Lee, H.; Kim, J.C.; Cho, S.M. Optimal Volt–Var Curve Setting of a Smart Inverter for Improving Its Performance in a Distribution System. IEEE Access 2020, 8, 157931–157945. [Google Scholar] [CrossRef]
- Yamane, K.; Orihara, D.; Iioka, D.; Aoto, Y.; Hashimoto, J.; Goda, T. Determination method of Volt-Var and Volt-Watt curve for smart inverters applying optimization of active/reactive power allocation for each inverter. Electr. Eng. Jpn. 2019, 209, 10–19. [Google Scholar] [CrossRef]
- Yoshizawa, S.; Yanagiya, Y.; Ishii, H.; Hayashi, Y.; Matsuura, T.; Hamada, H.; Mori, K. Voltage-Sensitivity-Based Volt-VAR-Watt Settings of Smart Inverters for Mitigating Voltage Rise in Distribution Systems. IEEE Open Access J. Power Energy 2021, 8, 584–595. [Google Scholar] [CrossRef]
- Kraiczy, M.; York, B.; Bello, M.; Montenegro, D.; Akagi, S.; Braun, M. Coordinating Smart Inverters with Advanced Distribution Voltage Control Strategies. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Rylander, M.; Li, H.; Smith, J.; Sunderman, W. Default Volt-Var inverter settings to improve distribution system performance. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
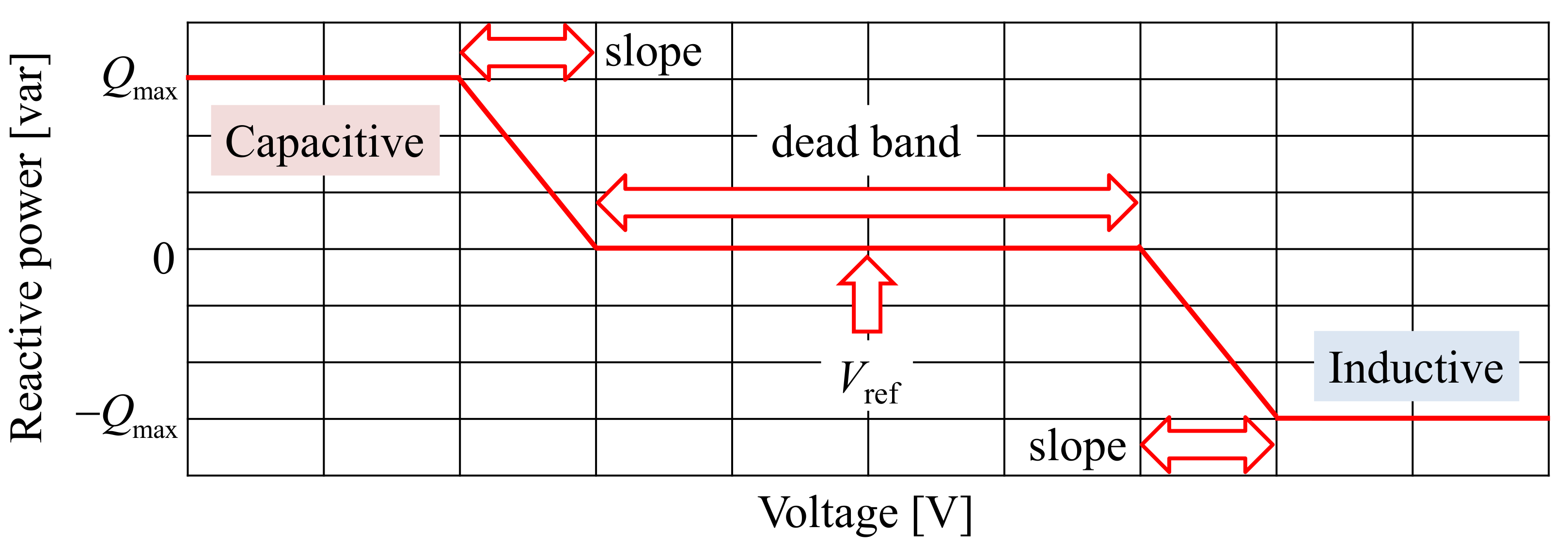
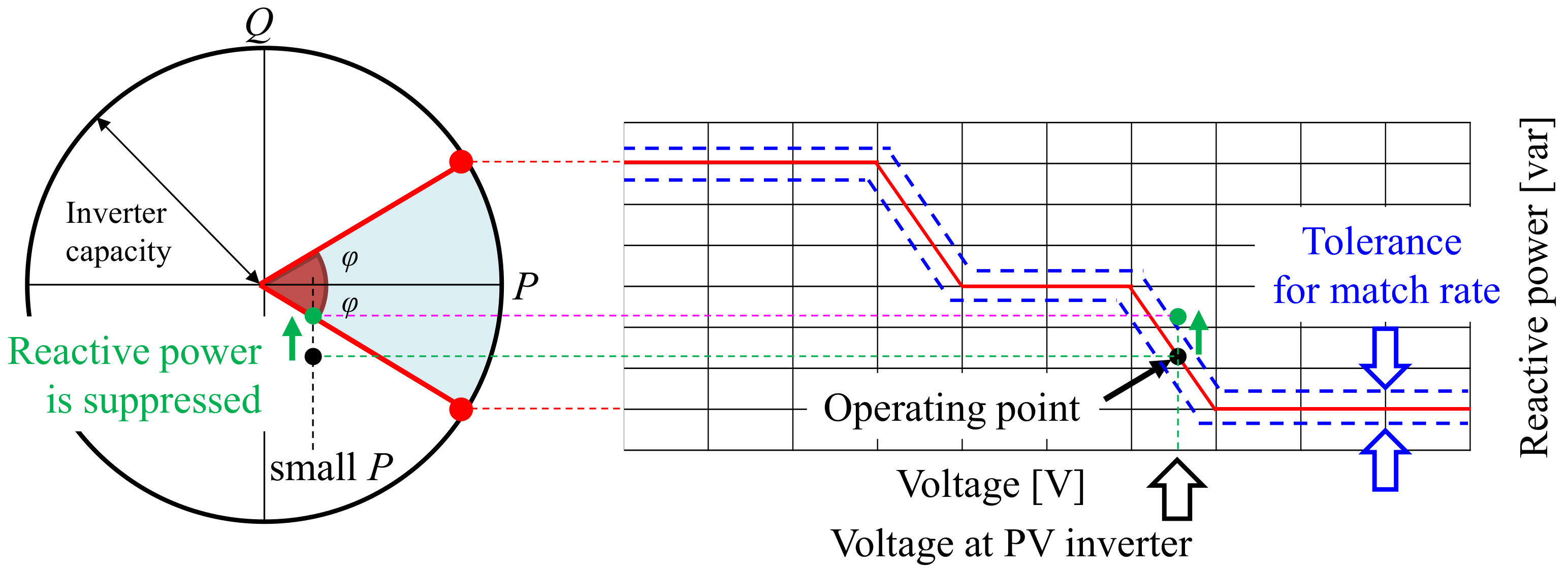




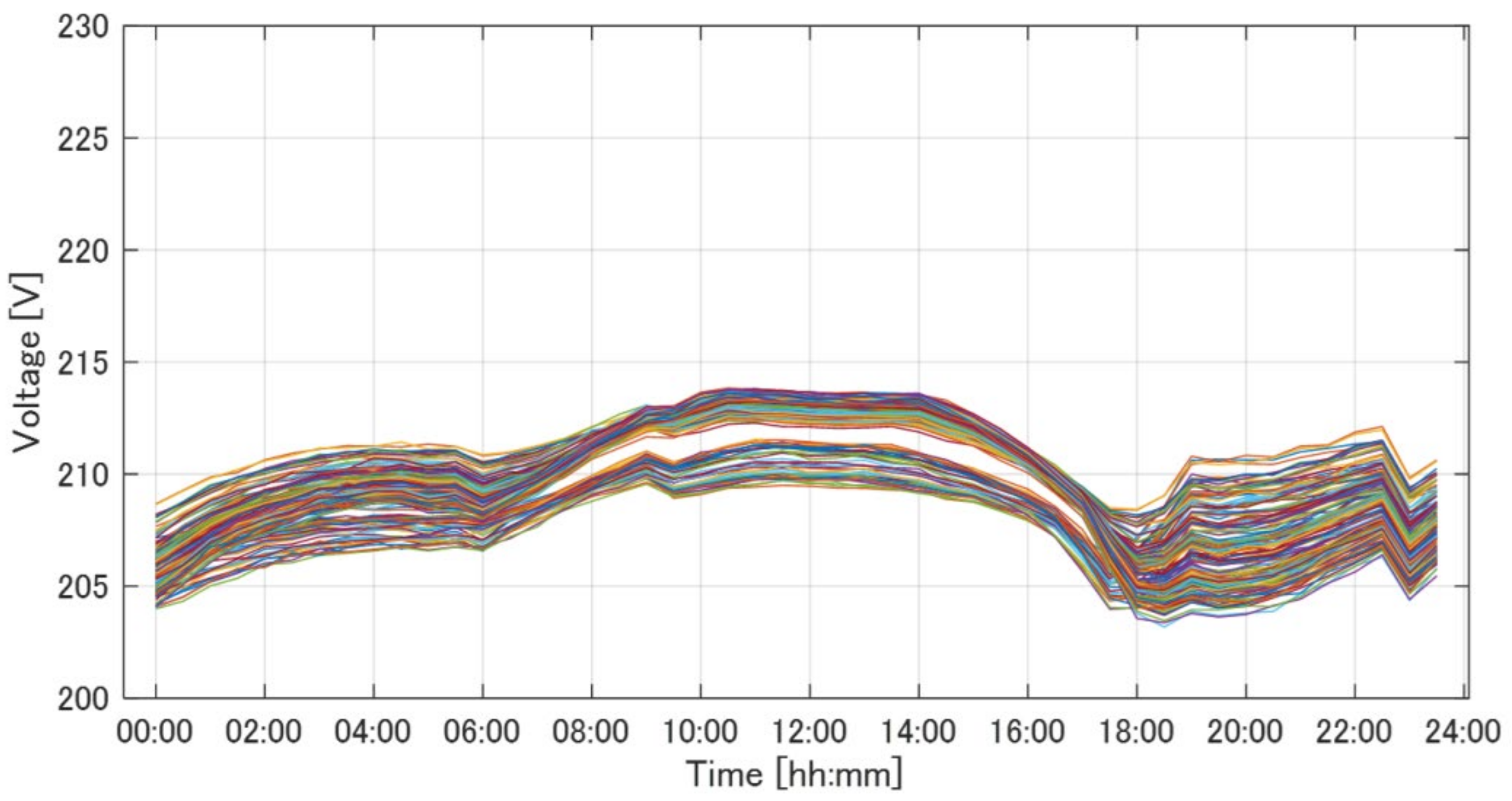

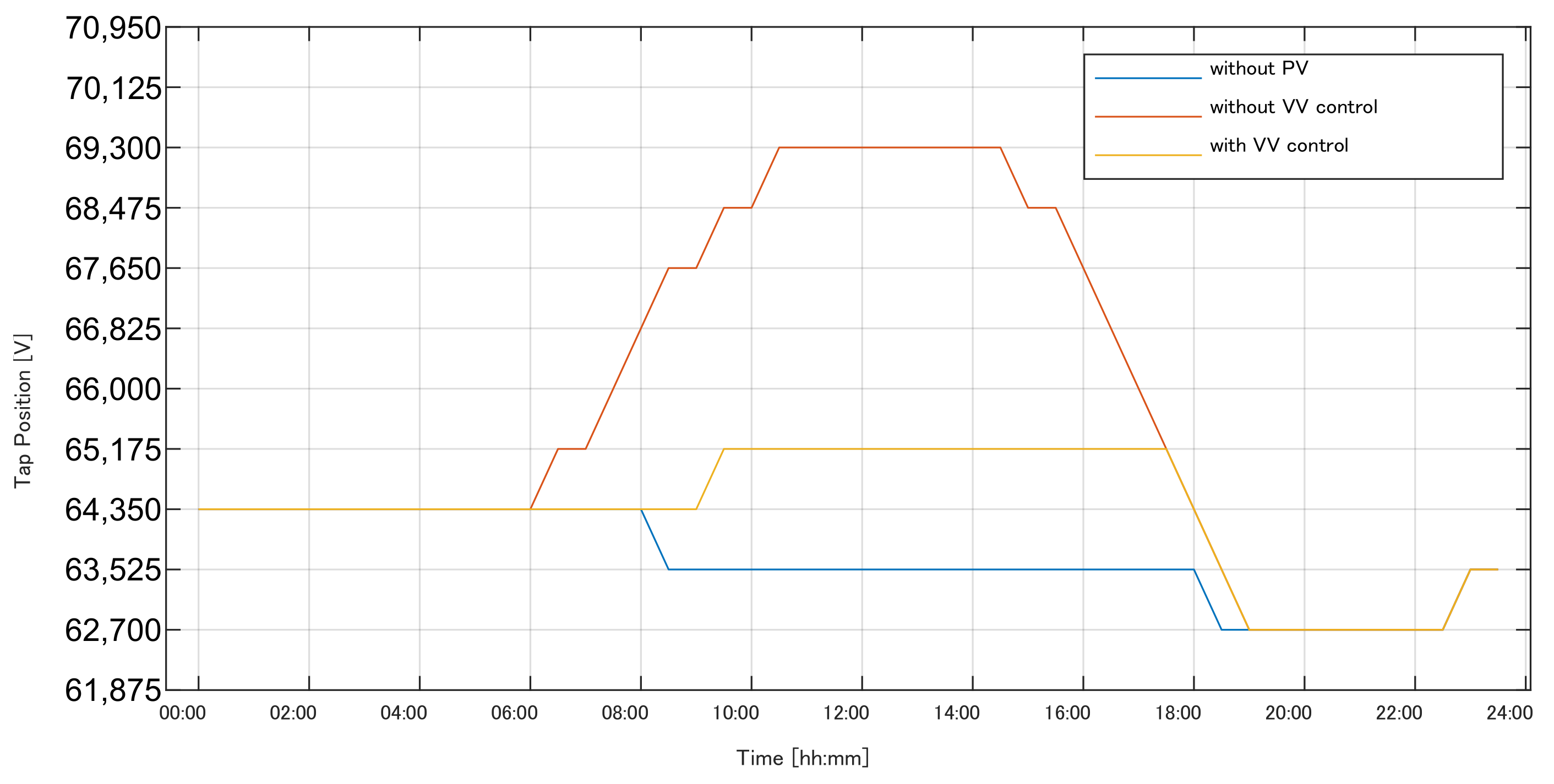



| Parameter | List of Values |
|---|---|
| Center voltage Vref [V] | 202, 204, 206, 208, 210, 212, 214, 216, 218 |
| deadband [V] | 0, 4, 8, 12, 16, 20, 24, 28 |
| slope [V] | 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 |
| Maximum reactive power Qmax [%] | 53 (Value dependent on power factor constraint) |
| Vref (V) | Slope (V) | Dead Band (V) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | ||
| 202 | 2 | 26.0 | 27.7 | 43.4 | 59.2 | 71.2 | 82.9 | 88.6 | 100.0 |
| 4 | 26.1 | 33.7 | 50.2 | 70.5 | 96.3 | 100.0 | 100.0 | 100.0 | |
| 6 | 29.1 | 40.1 | 61.2 | 83.8 | 97.2 | 100.0 | 100.0 | 100.0 | |
| 8 | 33.5 | 51.7 | 73.1 | 87.3 | 97.5 | 100.0 | 100.0 | 100.0 | |
| 10 | 43.3 | 64.2 | 77.5 | 88.5 | 97.7 | 100.0 | 100.0 | 100.0 | |
| 204 | 2 | 27.0 | 43.4 | 59.2 | 71.2 | 82.9 | 88.6 | 100.0 | 100.0 |
| 4 | 33.0 | 50.2 | 70.5 | 96.3 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 6 | 39.8 | 61.2 | 83.8 | 97.2 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 8 | 51.4 | 73.1 | 87.3 | 97.5 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 10 | 63.9 | 77.5 | 88.5 | 97.7 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 206 | 2 | 38.4 | 58.7 | 70.9 | 82.9 | 88.6 | 100.0 | 100.0 | 100.0 |
| 4 | 46.0 | 70.1 | 96.1 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 6 | 57.7 | 83.4 | 97.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 8 | 70.0 | 86.8 | 97.3 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 10 | 74.8 | 88.1 | 97.6 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 208 | 2 | 47.4 | 66.2 | 81.5 | 88.2 | 100.0 | 100.0 | 100.0 | 100.0 |
| 4 | 59.6 | 91.8 | 98.7 | 99.7 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 6 | 73.6 | 93.1 | 98.7 | 99.7 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 8 | 77.0 | 93.7 | 98.7 | 99.8 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 10 | 79.9 | 94.1 | 98.8 | 99.8 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 210 | 2 | 47.4 | 67.6 | 83.4 | 98.6 | 99.6 | 100.0 | 100.0 | 100.0 |
| 4 | 73.3 | 86.4 | 95.5 | 98.7 | 99.7 | 100.0 | 100.0 | 100.0 | |
| 6 | 75.1 | 88.1 | 95.8 | 98.7 | 99.7 | 100.0 | 100.0 | 100.0 | |
| 8 | 76.5 | 88.9 | 96.2 | 98.7 | 99.8 | 100.0 | 100.0 | 100.0 | |
| 10 | 77.3 | 90.3 | 96.3 | 98.8 | 99.8 | 100.0 | 100.0 | 100.0 | |
| 212 | 2 | 39.5 | 57.0 | 83.5 | 94.9 | 98.6 | 99.6 | 100.0 | 100.0 |
| 4 | 63.3 | 74.9 | 85.4 | 95.5 | 98.7 | 99.7 | 100.0 | 100.0 | |
| 6 | 65.7 | 76.6 | 88.1 | 95.8 | 98.7 | 99.7 | 100.0 | 100.0 | |
| 8 | 67.7 | 77.9 | 88.9 | 96.2 | 98.7 | 99.8 | 100.0 | 100.0 | |
| 10 | 68.8 | 79.4 | 90.3 | 96.3 | 98.8 | 99.8 | 100.0 | 100.0 | |
| 214 | 2 | 42.5 | 57.9 | 68.5 | 82.8 | 94.9 | 98.6 | 99.6 | 100.0 |
| 4 | 52.3 | 60.9 | 73.5 | 85.1 | 95.5 | 98.7 | 99.7 | 100.0 | |
| 6 | 57.5 | 63.4 | 76.2 | 88.1 | 95.8 | 98.7 | 99.7 | 100.0 | |
| 8 | 59.4 | 65.8 | 77.9 | 88.9 | 96.2 | 98.7 | 99.8 | 100.0 | |
| 10 | 61.4 | 67.8 | 79.4 | 90.3 | 96.3 | 98.8 | 99.8 | 100.0 | |
| 216 | 2 | 44.7 | 48.9 | 57.4 | 68.0 | 82.4 | 94.9 | 98.6 | 99.6 |
| 4 | 47.6 | 51.2 | 60.2 | 72.9 | 84.8 | 95.5 | 98.7 | 99.7 | |
| 6 | 49.7 | 56.4 | 62.7 | 76.0 | 88.1 | 95.8 | 98.7 | 99.7 | |
| 8 | 52.3 | 58.8 | 65.5 | 77.9 | 88.9 | 96.2 | 98.7 | 99.8 | |
| 10 | 55.6 | 60.8 | 67.8 | 79.4 | 90.3 | 96.3 | 98.8 | 99.8 | |
| 218 | 2 | 38.9 | 44.3 | 48.3 | 57.4 | 68.0 | 82.4 | 94.9 | 98.6 |
| 4 | 43.3 | 47.2 | 51.0 | 60.2 | 72.9 | 84.8 | 95.5 | 98.7 | |
| 6 | 46.4 | 49.3 | 56.2 | 62.7 | 76.0 | 88.1 | 95.8 | 98.7 | |
| 8 | 48.5 | 52.2 | 58.8 | 65.5 | 77.9 | 88.9 | 96.2 | 98.7 | |
| 10 | 50.6 | 55.6 | 60.8 | 67.8 | 79.4 | 90.3 | 96.3 | 98.8 | |
| Model | PV Capacity (MW) | Main Line Length (km) |
|---|---|---|
| Residential area 1 | 6.3 | 4.2 |
| Rural area 1 | 9.5 | 4.4 |
| Rural area 2 | 5.5 | 7.5 |
| Industrial area 1 | 4.5 | 3.6 |
| Industrial area 2 | 6.8 | 4.7 |
| Parameter | Evaluation Condition |
|---|---|
| Voltage of low-voltage customer V (pu) | 0.9 ≤ V≤ 1.1 |
| Match rate PM (%) | 99 ≤ PM |
| LRT tap operation N per day | N ≤ 15 |
| Vref (V) | Deadband (V) | Slope (V) | Line Loss (kWh) | Curtailment (kWh) | Match Rate(%) | Voltage Violation (kV2s) | LRT Tap Operation |
|---|---|---|---|---|---|---|---|
| 202 | 28 | 4 | 2620 | 122 | 99.9 | 0 | 5.2 |
| 202 | 28 | 6 | 2582 | 58 | 99.9 | 0 | 5.6 |
| 202 | 28 | 8 | 2570 | 39 | 99.9 | 0 | 5.6 |
| 204 | 24 | 4 | 2620 | 122 | 99.9 | 0 | 5.2 |
| 204 | 24 | 6 | 2582 | 58 | 99.9 | 0 | 5.6 |
| 204 | 24 | 8 | 2570 | 39 | 99.9 | 0 | 5.6 |
| 204 | 28 | 2 | 2546 | 74 | 100.0 | 0 | 6.4 |
| 204 | 28 | 4 | 2537 | 40 | 100.0 | 0 | 6.4 |
| 206 | 20 | 4 | 2620 | 122 | 99.9 | 0 | 5.2 |
| 206 | 20 | 6 | 2582 | 58 | 99.9 | 0 | 5.6 |
| 206 | 20 | 8 | 2570 | 39 | 99.9 | 0 | 5.6 |
| 206 | 24 | 2 | 2546 | 74 | 100.0 | 0 | 6.4 |
| 206 | 24 | 4 | 2537 | 40 | 100.0 | 0 | 6.4 |
| 206 | 28 | 2 | 2521 | 25 | 100.0 | 0 | 7.6 |
| 208 | 16 | 4 | 2620 | 122 | 99.9 | 0 | 5.2 |
| 208 | 16 | 6 | 2582 | 58 | 99.9 | 0 | 5.6 |
| 208 | 16 | 8 | 2570 | 39 | 99.9 | 0 | 5.6 |
| 208 | 20 | 2 | 2546 | 74 | 100.0 | 0 | 6.4 |
| 208 | 20 | 4 | 2537 | 40 | 100.0 | 0 | 6.4 |
| 208 | 24 | 2 | 2521 | 25 | 100.0 | 0 | 7.6 |
| 210 | 16 | 2 | 2546 | 74 | 99.9 | 0 | 6.4 |
| 210 | 16 | 4 | 2537 | 40 | 99.9 | 0 | 6.4 |
| 210 | 20 | 2 | 2521 | 25 | 100.0 | 0 | 7.6 |
| Volt-Var Curve | Model | Line Loss (kWh) | Curtailment (kWh) | Match Rate (%) | Voltage Violation (kV2s) | LRT Tap Operation |
|---|---|---|---|---|---|---|
| (a) | Residential area 1 | 4482 | 1801 | 61.2 | 0 | 3 |
| Rural area 1 | 5505 | 3867 | 26.0 | 0 | 9 | |
| Rural area 2 | 3038 | 1560 | 50.9 | 0 | 6 | |
| Industrial area 1 | 1998 | 1722 | 34.3 | 5.9 | 8 | |
| Industrial area 2 | 3448 | 2321 | 45.1 | 0 | 10 | |
| (b) | Residential area 1 | 2906 | 12 | 100 | 0 | 13 |
| Rural area 1 | 3875 | 113 | 99.7 | 0 | 5 | |
| Rural area 2 | 2400 | 59 | 100 | 0 | 4 | |
| Industrial area 1 | 1278 | 0 | 100 | 0 | 4 | |
| Industrial area 2 | 2392 | 11 | 100 | 0 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iioka, D.; Kusano, K.; Matsuura, T.; Hamada, H.; Miyazaki, T. Appropriate Volt–Var Curve Settings for PV Inverters Based on Distribution Network Characteristics Using Match Rate of Operating Point. Energies 2022, 15, 1375. https://doi.org/10.3390/en15041375
Iioka D, Kusano K, Matsuura T, Hamada H, Miyazaki T. Appropriate Volt–Var Curve Settings for PV Inverters Based on Distribution Network Characteristics Using Match Rate of Operating Point. Energies. 2022; 15(4):1375. https://doi.org/10.3390/en15041375
Chicago/Turabian StyleIioka, Daisuke, Kenichi Kusano, Takahiro Matsuura, Hiromu Hamada, and Teru Miyazaki. 2022. "Appropriate Volt–Var Curve Settings for PV Inverters Based on Distribution Network Characteristics Using Match Rate of Operating Point" Energies 15, no. 4: 1375. https://doi.org/10.3390/en15041375
APA StyleIioka, D., Kusano, K., Matsuura, T., Hamada, H., & Miyazaki, T. (2022). Appropriate Volt–Var Curve Settings for PV Inverters Based on Distribution Network Characteristics Using Match Rate of Operating Point. Energies, 15(4), 1375. https://doi.org/10.3390/en15041375





