A Dual Rising Edge Shift Algorithm for Eliminating the Transient DC-Bias Current in Transformer for a Dual Active Bridge Converter
Abstract
:1. Introduction
- No need for any measurements or parameter values: Solutions presented in [20,21,22,23,24,26,28] incorporate relatively complex formulas, including input and output voltage measurement values and/or equivalent inductance values. This raises the computational burden of the algorithm and makes it possibly vulnerable to measurement noises and parameter identification errors (as described in [21]). Solutions presented in [25,27] do not posses this drawback, which also leads to relatively simple calculation formulas;
- Power flow reversal functionality: One of the most important advantages of the DAB topology is the bi-directional power flow capability. Hence, it is very important that the DC-bias current cancellation algorithm supports this functionality; otherwise, the full potential of the converter features cannot be utilized. Among the analyzed solutions, only [21,23,24] present experimental proofs of such a functionality. The authors of [27] also claim it, but it was not supported with experimental results;
- Settling within the first half of the switching cycle during transients: From the closed loop voltage control point of view, it is advantageous that the current waveforms (and hence, also the power flow level) settle to their steady-state as fast as possible. The algorithm presented in [20] needs several switching cycles to settle. The authors of [21,22,23,24,27] claim a settling time of one switching cycle. Only solutions provided in [25,26] provide a settling of the current waveforms within the first half of the switching cycle;
- Update and calculation once per switching cycle: Some of the algorithms, i.e., [20,21,25], require an update of pulse width modulation (PWM) control values and/or algorithm calculations twice per switching cycle. This is disadvantageous, especially when the algorithm is implemented on a microcontroller. The reason is that it requires two invocations of the interrupt service routine per switching cycle. With all the other solutions, i.e., [22,23,24,26,27,28], it is sufficient to perform the modulation-algorithm-related calculations only once per switching cycle. Thanks to this, these algorithms can be executed in the same interrupt service routine as the overlaying voltage control algorithm. Hence, these interrupts do not need to be nested, which is obviously a convenient feature for implementation;
- No asynchronous operation: This point relates to only two solutions. The algorithm presented in [24] requires an injection of an additional half switching cycle with zero voltage during power flow reversal. The solution proposed in [27] incorporates an injection of such a zero voltage period (which also has a variable duration based on the requested amount of power flow value) between each consecutive switching cycle. It introduces an asynchronous operation of the converter. With solution [24], it occurs only occasionally during power flow reversal, so its impact is not severe. On the other hand, the impact on the operation of a converter controlled with an algorithm presented in [27] is significant. Such an asynchronous operation introduces either asynchronous sampling (if it is bounded with a switching cycle) or de-synchronization of sampling in relation to switching cycle. In both situations, it makes it very hard to analyze the dynamics of such an asynchronous system. Hence, a closed loop control system synthesis can become a relatively tedious task;
- Dead-time compensation: All the analyzed solutions are derived based on the so-called simplified lossless converter model. As described in [23], this model neglects an influence of the converter blanking times (often referred to as dead times) on the converter operation. For this reason, every algorithm which does not take this effect into account is unable to perfectly compensate the DC-bias current. On the other hand, the remaining compensation error was quantified in [23], and it appears to be reasonably small enough to simply accept it. Nevertheless, the authors of [21,23] decided to introduce an additional module to their base algorithms, which compensates the dead-time related effects. These solutions are based on an analytical model of the dead-time influence on current waveforms.
2. Materials and Methods
2.1. Steady-State Operation—Double-Sided Single Phase Shift (DSSPS) Modulation
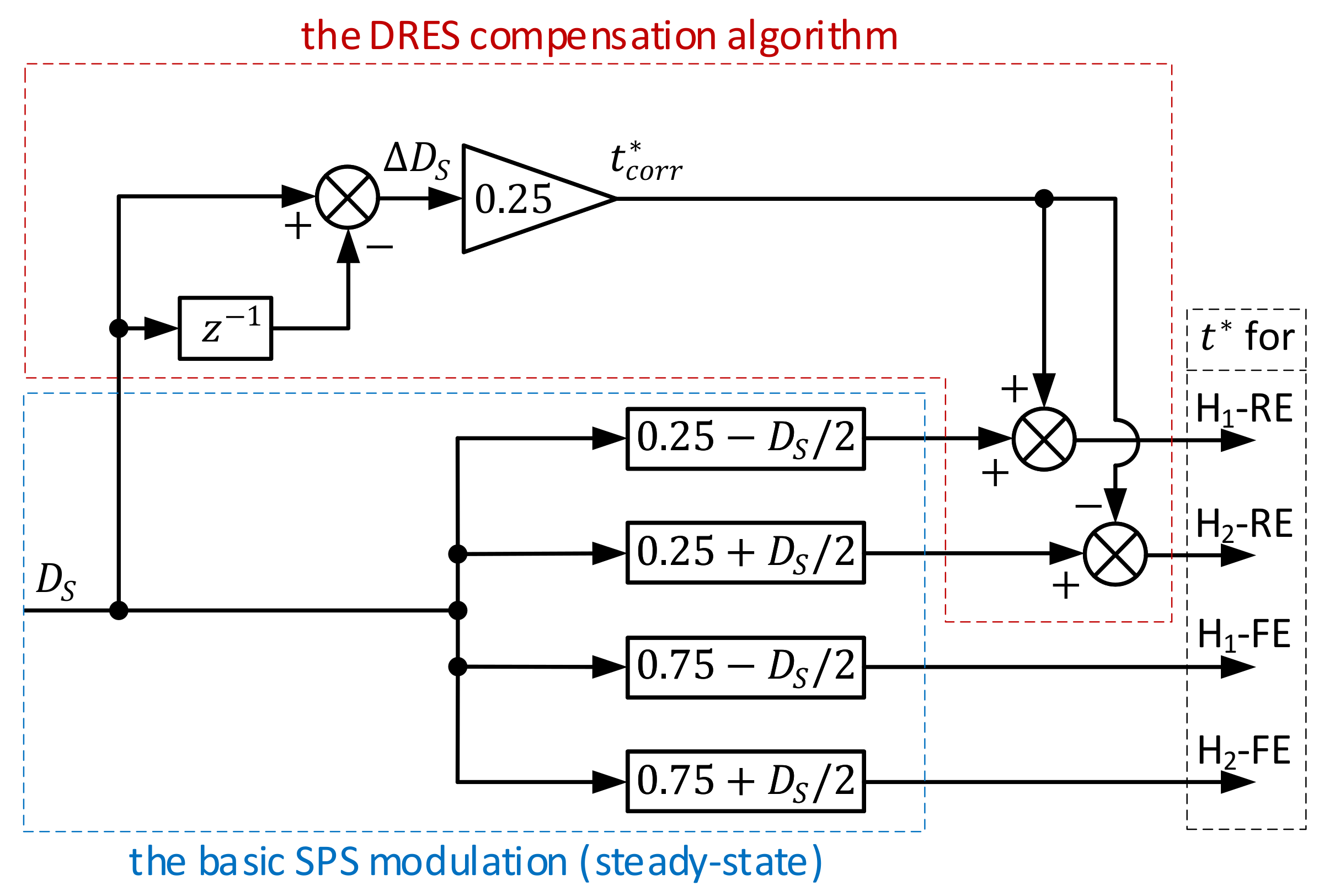
2.2. Dynamic Operation—Dual Rising Edge Shift (DRES) Algorithm
- reduced, if and ,
- extended, if and ,
- extended, if and ,
- reduced, if and .
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| DAB | Dual Active Bridge |
| DC | Direct Current |
| DRES | Dual Rising Edge Shift (algorithm) |
| DSSPS | Double-Sided Single Phase Shift (modulation) |
| ePWM | Enhanced Pulse Width Modulator (microcontroller peripheral) |
| FE | Falling Edge |
| FPGA | Field Programmable Gate Array |
| PWM | Pulse Width Modulation |
| RE | Rising Edge |
| SST | Solid State Transformer |
| SPS | Single Phase Shift (modulation) |
| TPS | Triple Phase Shift (modulation) |
Appendix A. Details of the Software Implementation


| Event | ePWM1 | ePWM2 | ePWM3 | ePWM4 |
|---|---|---|---|---|
| counter = CMPA (at count-up) | SET | CLEAR | SET | CLEAR |
| counter = CMPB (at count-down) | CLEAR | SET | CLEAR | SET |




References
- Hou, N.; Li, Y.W. Overview and Comparison of Modulation and Control Strategies for a Nonresonant Single-Phase Dual-Active-Bridge DC–DC Converter. IEEE Trans. Power Electron. 2020, 35, 3148–3172. [Google Scholar] [CrossRef]
- De Doncker, R.W.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high power density DC/DC converter for high power applications. In Proceedings of the Conference Record of the 1988 IEEE Industry Applications Society Annual Meeting, Pittsburgh, PA, USA, 2–7 October 1988; pp. 796–805. [Google Scholar] [CrossRef]
- De Doncker, R.W.A.A.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high-power-density DC/DC converter for high-power applications. IEEE Trans. Ind. Appl. 1991, 27, 63–73. [Google Scholar] [CrossRef]
- Kheraluwala, M.N.; Gascoigne, R.W.; Divan, D.M.; Baumann, E.D. Performance characterization of a high-power dual active bridge DC-to-DC converter. IEEE Trans. Ind. Appl. 1992, 28, 1294–1301. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of Dual-Active-Bridge Isolated Bidirectional DC–DC Converter for High-Frequency-Link Power-Conversion System. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Segaran, D.S. Dynamic Modelling and Control of Dual Active Bridge Bi-Directional DC-DC Converters for Smart Grid Applications. Ph.D. Thesis, School of Electrical and Computer Engineering (SECE), RMIT University, Melbourne, VIC, Australia, 2006. Available online: https://core.ac.uk/download/pdf/15628024.pdf (accessed on 19 April 2021).
- Inoue, S.; Akagi, H. A Bidirectional Isolated DC–DC Converter as a Core Circuit of the Next-Generation Medium-Voltage Power Conversion System. IEEE Trans. Power Electron. 2007, 22, 535–542. [Google Scholar] [CrossRef]
- Mi, C.; Bai, H.; Wang, C.; Gargies, S. Operation, design and control of dual H-bridge-based isolated bidirectional DC-DC converter. IET Power Electron. 2008, 1, 507–517. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Sun, J.; Freudenberg, J.S. Power Flow Characterization of a Bidirectional Galvanically Isolated High-Power DC/DC Converter Over a Wide Operating Range. IEEE Trans. Power Electron. 2010, 25, 54–66. [Google Scholar] [CrossRef]
- Krismer, F. Modelling and Optimization of Bidirectional Dual Active Bridge DC-DC Converter Topologies. Ph.D. Thesis, Department of Information Technology and Electrical Engineering, ETH Zuerich, Zuerich, Switzerland, 2010. Available online: https://www.pes-publications.ee.ethz.ch/uploads/tx_ethpublications/Krismer_2011_03_17_Modeling_and_Optimization_of_Bidirectional_Dual_Active_Bridge_DC-DC_Converter_Topologies.pdf (accessed on 19 April 2021).
- Tan, N.M.L.; Abe, T.; Akagi, H. Design and Performance of a Bidirectional Isolated DC–DC Converter for a Battery Energy Storage System. IEEE Trans. Power Electron. 2012, 27, 1237–1248. [Google Scholar] [CrossRef]
- Everts, J. Modelling and Optimization of Bidirectional Dual Active Bridge AC-DC Converter Topologies. Ph.D. Thesis, Faculty of Engineering Science, KU Leuven, Leuven, Belgium, 2014. Available online: https://limo.libis.be/primo-explore/fulldisplay?docid=LIRIAS1731206&context=L&vid=Lirias&search_scope=Lirias&tab=default_tab&lang=en_US&fromSitemap=1 (accessed on 19 April 2021).
- Costinett, D.; Maksimovic, D.; Zane, R. Design and Control for High Efficiency in High Step-Down Dual Active Bridge Converters Operating at High Switching Frequency. IEEE Trans. Power Electron. 2013, 28, 3931–3940. [Google Scholar] [CrossRef]
- Han, S.; Munuswamy, I.; Divan, D. Preventing transformer saturation in bi-directional dual active bridge buck-boost DC/DC converters. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 1450–1457. [Google Scholar] [CrossRef]
- Ortiz, G.; Mühlethaler, J.; Kolar, J.W. “Magnetic Ear”-based balancing of magnetic flux in high power medium frequency dual active bridge converter transformer cores. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 1307–1314. [Google Scholar] [CrossRef]
- Peña-Alzola, R.; Mathe, L.; Liserre, M.; Blaabjerg, F.; Kerekes, T. DC-bias cancellation for phase shift controlled dual active bridge. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–14 November 2013; pp. 596–600. [Google Scholar] [CrossRef]
- Baddipadiga, B.P.; Ferdowsi, M. Dual loop control for eliminating DC-bias in a DC-DC dual active bridge converter. In Proceedings of the 2014 International Conference on Renewable Energy Research and Application (ICRERA), Milwaukee, WI, USA, 19–22 October 2014; pp. 490–495. [Google Scholar] [CrossRef]
- Dutta, S.; Bhattacharya, S. A method to measure the DC bias in high frequency isolation transformer of the dual active bridge DC to DC converter and its removal using current injection and PWM switching. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 1134–1139. [Google Scholar] [CrossRef]
- Zhang, B.; Shao, S.; Chen, L.; Wu, X.; Zhang, J. Steady-State and Transient DC Magnetic Flux Bias Suppression Methods for a Dual Active Bridge Converter. IEEE Trans. Emerg. Sel. Top. Power Electron. 2021, 9, 744–753. [Google Scholar] [CrossRef]
- Dutta, S.; Bhattacharya, S.; Chandorkar, M. A novel predictive phase shift controller for bidirectional isolated dc to dc converter for high power applications. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 418–423. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.; Zhao, Z.; Li, K.; Yuan, L.; Wen, W. Deadbeat Current Controller for Bidirectional Dual-Active-Bridge Converter Using an Enhanced SPS Modulation Method. IEEE Trans. Power Electron. 2021, 36, 1274–1279. [Google Scholar] [CrossRef]
- Li, X.; Li, Y. An Optimized Phase-Shift Modulation For Fast Transient Response in a Dual-Active-Bridge Converter. IEEE Trans. Power Electron. 2014, 29, 2661–2665. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Zhao, Y. Transient DC Bias and Current Impact Effects of High-Frequency-Isolated Bidirectional DC–DC Converter in Practice. IEEE Trans. Power Electron. 2016, 31, 3203–3216. [Google Scholar] [CrossRef]
- Chattopadhyay, R.; Raheja, U.; Gohil, G.; Nair, V.; Bhattacharya, S. Sensorless phase shift control for phase shifted DC-DC converters for eliminating DC transients from transformer winding currents. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1882–1889. [Google Scholar] [CrossRef]
- Takagi, K.; Fujita, H. Dynamic control and performance of an isolated dual-active-bridge DC–DC converter. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015; pp. 1521–1527. [Google Scholar] [CrossRef]
- Li, K.; Wang, Y.; Xu, J.; Wang, J.; Li, R.; Lv, C. A Novel Control Method for Eliminating DC Bias in Dual-Active-Bridge DC-DC Converters. In Proceedings of the 2018 IEEE International Power Electronics and Applications Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wattenberg, M.; Schwalbe, U.; Pfost, M. Impact of DC-Bias on Dual Active Bridge Control and How to Avoid it. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 2–6 September 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Sun, C.; Li, X. Instantaneous Current Balance Modulation for Fast Transient Response in a Dual-Active-Bridge Converter. In Proceedings of the 2018 IEEE International Power Electronics and Applications Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Bu, Q.; Wen, H.; Wen, J. Optimized Transient Modulation Control of Bidirectional Full-Bridge DC-DC Converter. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Korea, 27–30 May 2019; pp. 3102–3107. [Google Scholar] [CrossRef]
- Bu, Q.; Wen, H.; Wen, J.; Hu, Y.; Du, Y. Transient DC Bias Elimination of Dual-Active-Bridge DC–DC Converter with Improved Triple-Phase-Shift Control. IEEE Trans. Ind. Electron. 2020, 67, 8587–8598. [Google Scholar] [CrossRef]
- Texas Instruments Incorporated. Enhanced Pulse Width Modulator (ePWM). In TMS320F2837xD Dual-Core Microcontrollers Technical Reference Manual (Rev. I); Texas Instruments Incorporated: Dallas, TX, USA, 2019; pp. 1861–2125. Available online: https://www.ti.com/product/TMS320F28379D#tech-docs (accessed on 7 June 2021).
- CCSSTUDIO-C2000 IDE. Available online: https://www.ti.com/tool/CCSTUDIO-C2000 (accessed on 7 June 2021).










| Solution | Meas. & Parameter Free | No Conditional Branches | Power Flow Reversal | Settl. in Half Cycle | Update and Calc. Once per Cycle | No Asynch. Operation | Dead-Time Compensation |
|---|---|---|---|---|---|---|---|
| [20] | − | + | − | − | − | + | − |
| [21] | − | + | + | − | − | + | + |
| [22] | − | + | − | − | + | + | − |
| [23] | − | − | + | − | + | + | + |
| [24] | − | − | + | − | + | − | − |
| [25] | + | + | − | + | − | + | − |
| [26] | − | + | − | + | + | + | − |
| [27] | + | − | + * | − | + | − | − |
| [28] | − | ** | − | − | + | + | − |
| This paper/Dual Rising Edge Shift Algorithm | + | + | + | + | + | + | − |
| Name | Symbol | Value | Unit |
|---|---|---|---|
| Switching frequency | 40 | kHz | |
| Commutation blanking time | |||
| Drain-Source on-state resistance of MOSFETs | 25 | ||
| Inductance of the equivalent circuit | |||
| Inductance of the auxiliary inductor | |||
| Input and output capacitance | 200 | ||
| Transformer turns ratio | − | ||
| Transformer magnetizing inductance | mH | ||
| Primary-side transformer leakage inductance | |||
| Secondary-side transformer leakage inductance | |||
| Primary-side transformer resistance | |||
| Primary-side transformer resistance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gierczynski, M.; Grzesiak, L.M.; Kaszewski, A. A Dual Rising Edge Shift Algorithm for Eliminating the Transient DC-Bias Current in Transformer for a Dual Active Bridge Converter. Energies 2021, 14, 4264. https://doi.org/10.3390/en14144264
Gierczynski M, Grzesiak LM, Kaszewski A. A Dual Rising Edge Shift Algorithm for Eliminating the Transient DC-Bias Current in Transformer for a Dual Active Bridge Converter. Energies. 2021; 14(14):4264. https://doi.org/10.3390/en14144264
Chicago/Turabian StyleGierczynski, Michal, Lech M. Grzesiak, and Arkadiusz Kaszewski. 2021. "A Dual Rising Edge Shift Algorithm for Eliminating the Transient DC-Bias Current in Transformer for a Dual Active Bridge Converter" Energies 14, no. 14: 4264. https://doi.org/10.3390/en14144264






