Analysis of the Influence of Silicone Rubber Aging on the Transmission Parameters of Terahertz Waves
Abstract
:1. Introduction
2. Theoretical and Computational Methods
3. First Principle Calculations
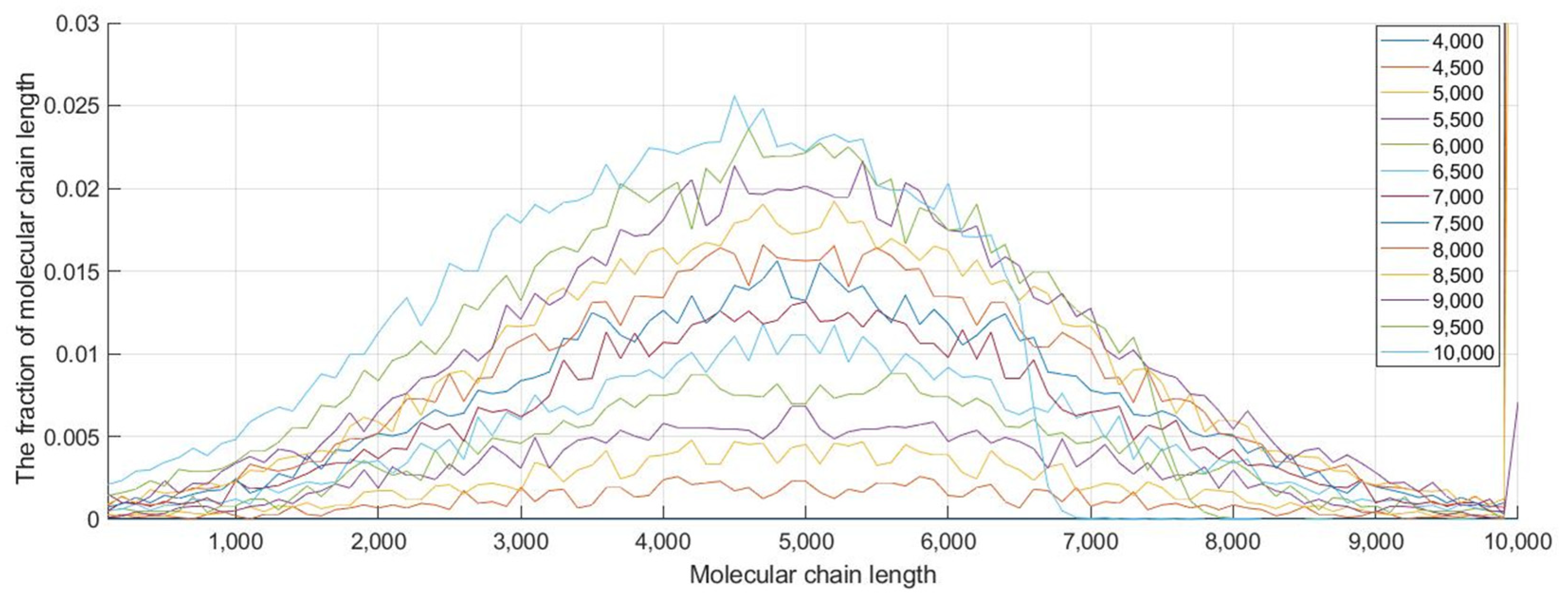
3.1. Molecular Simulation Method PMVS Aging Analysis
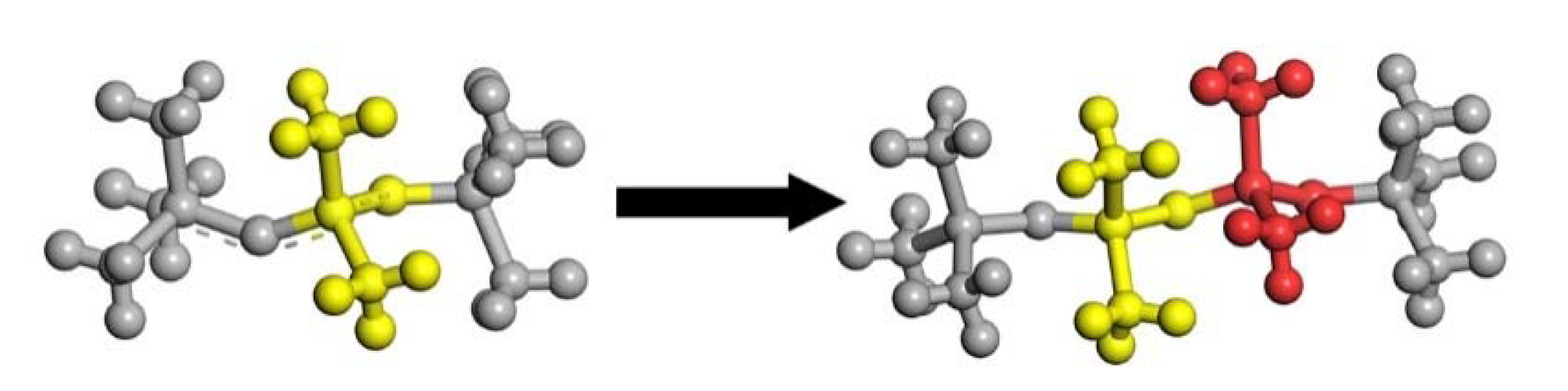
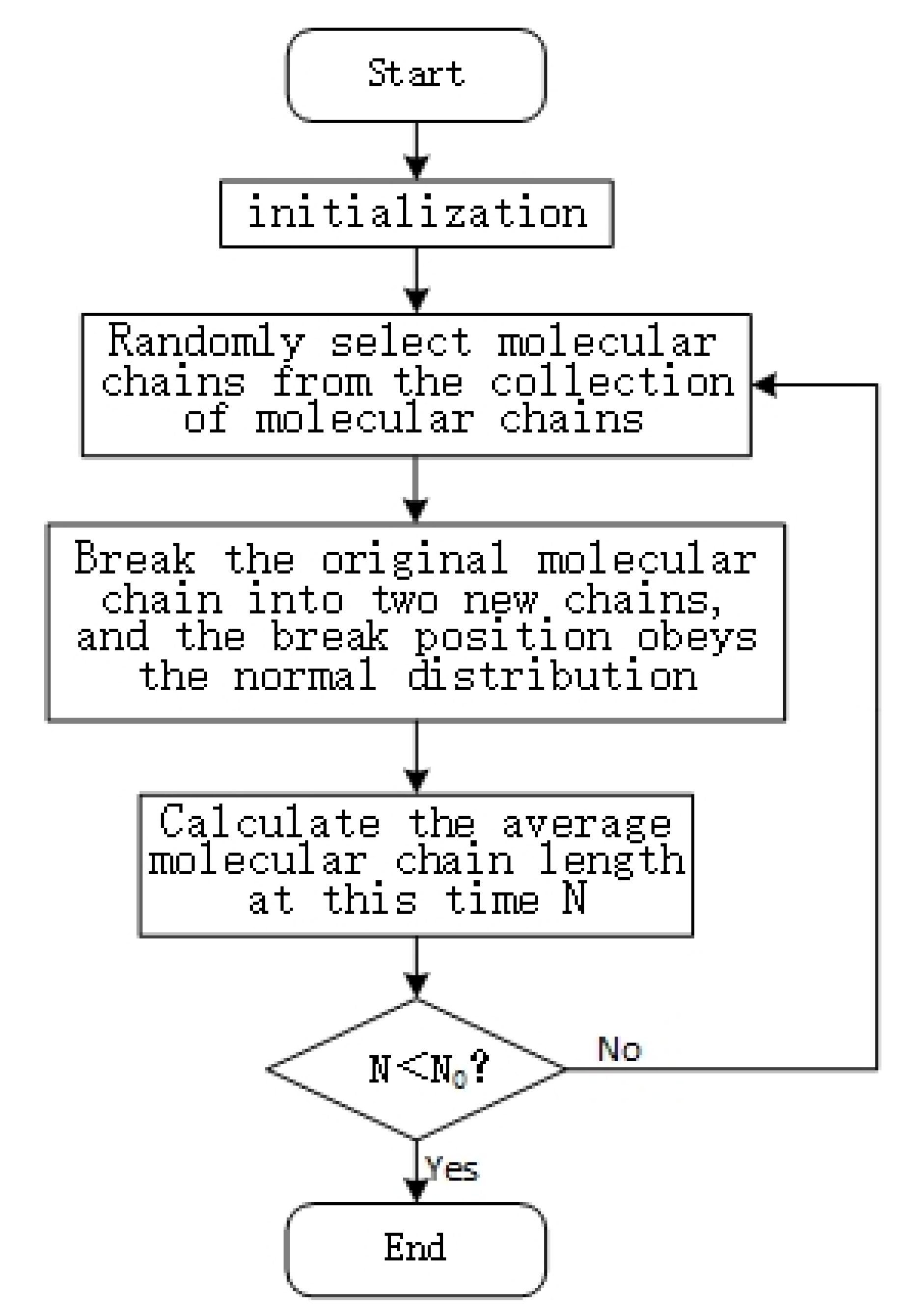
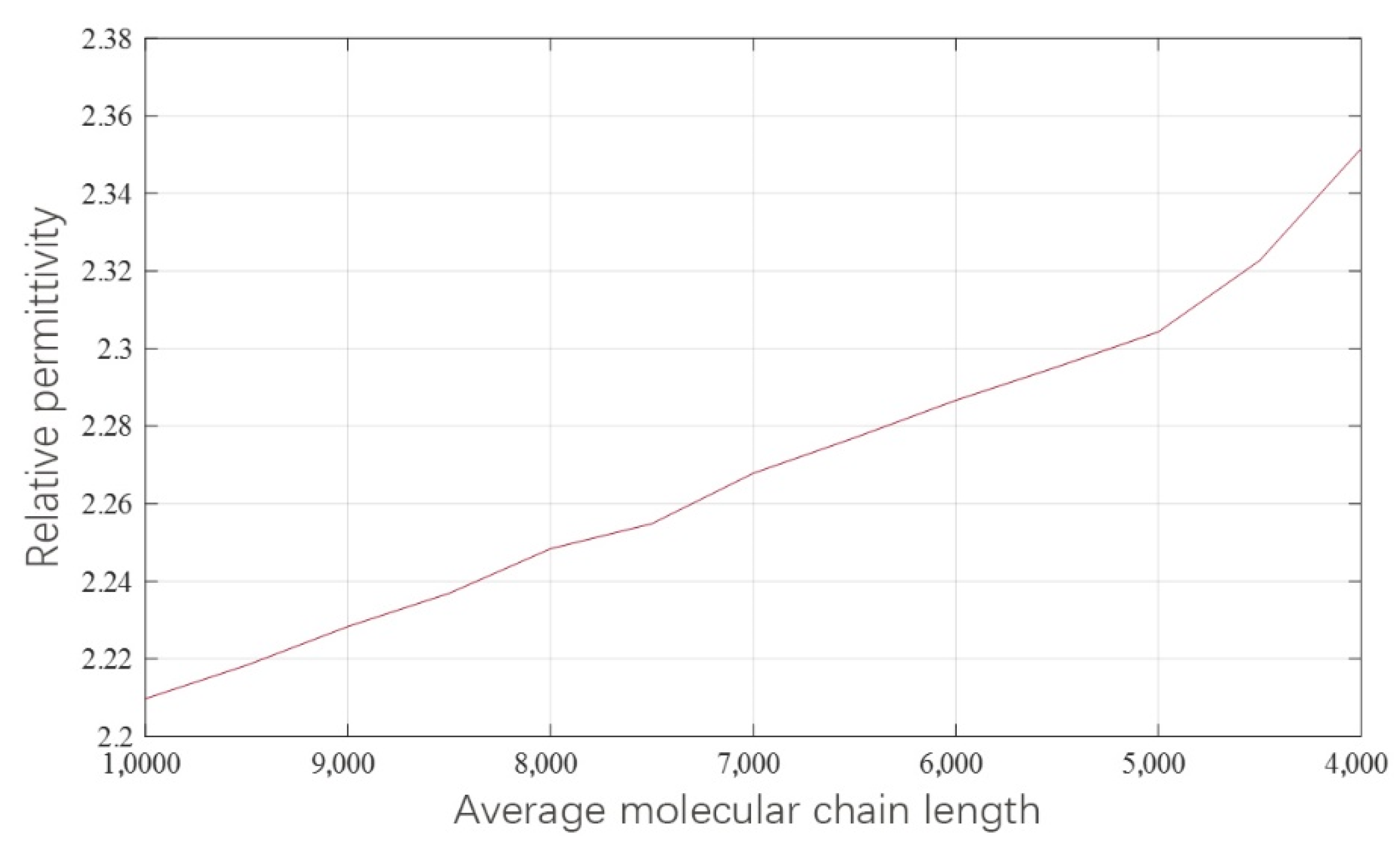
3.2. Molecular Chain Break Model Based on Normal Distribution
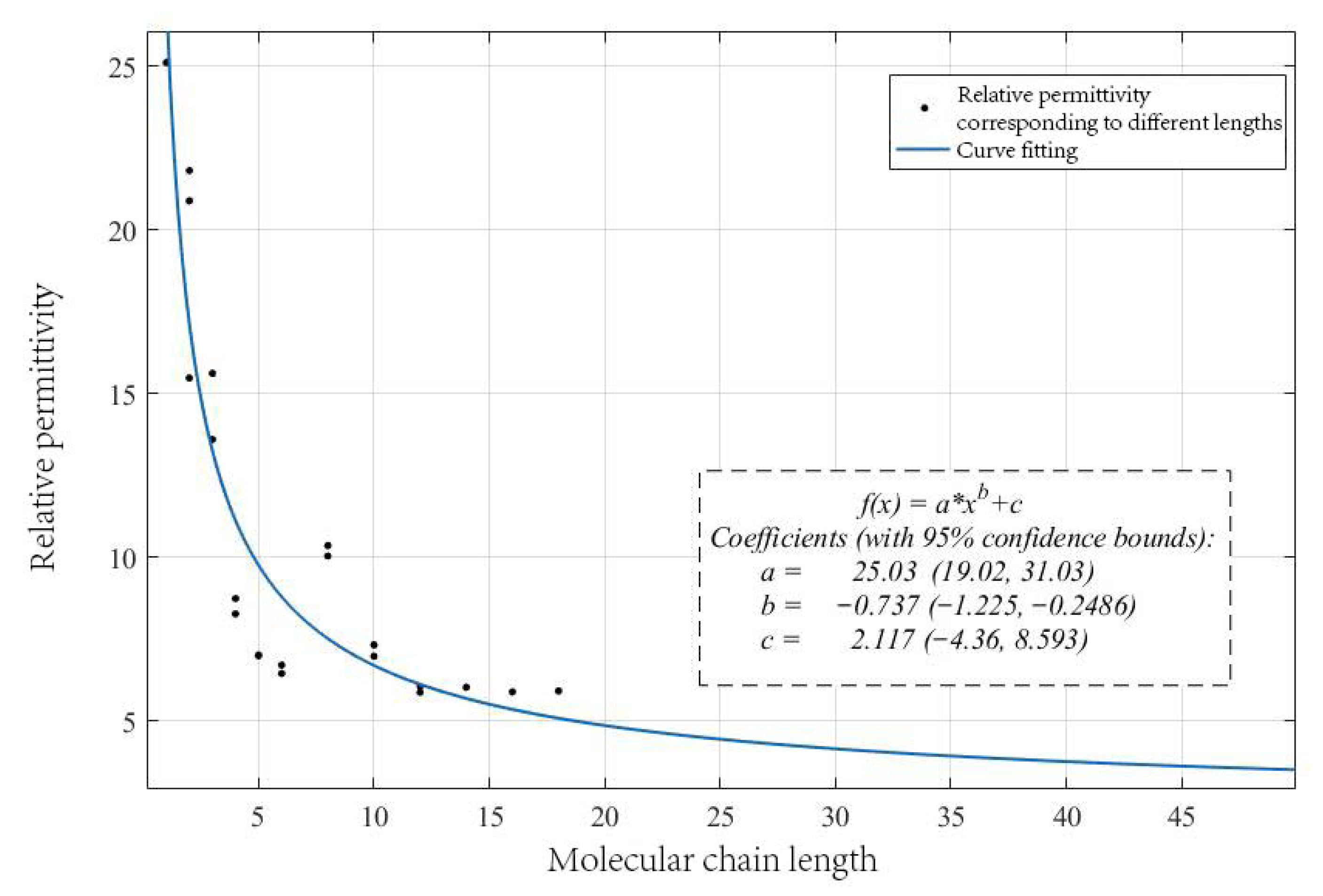
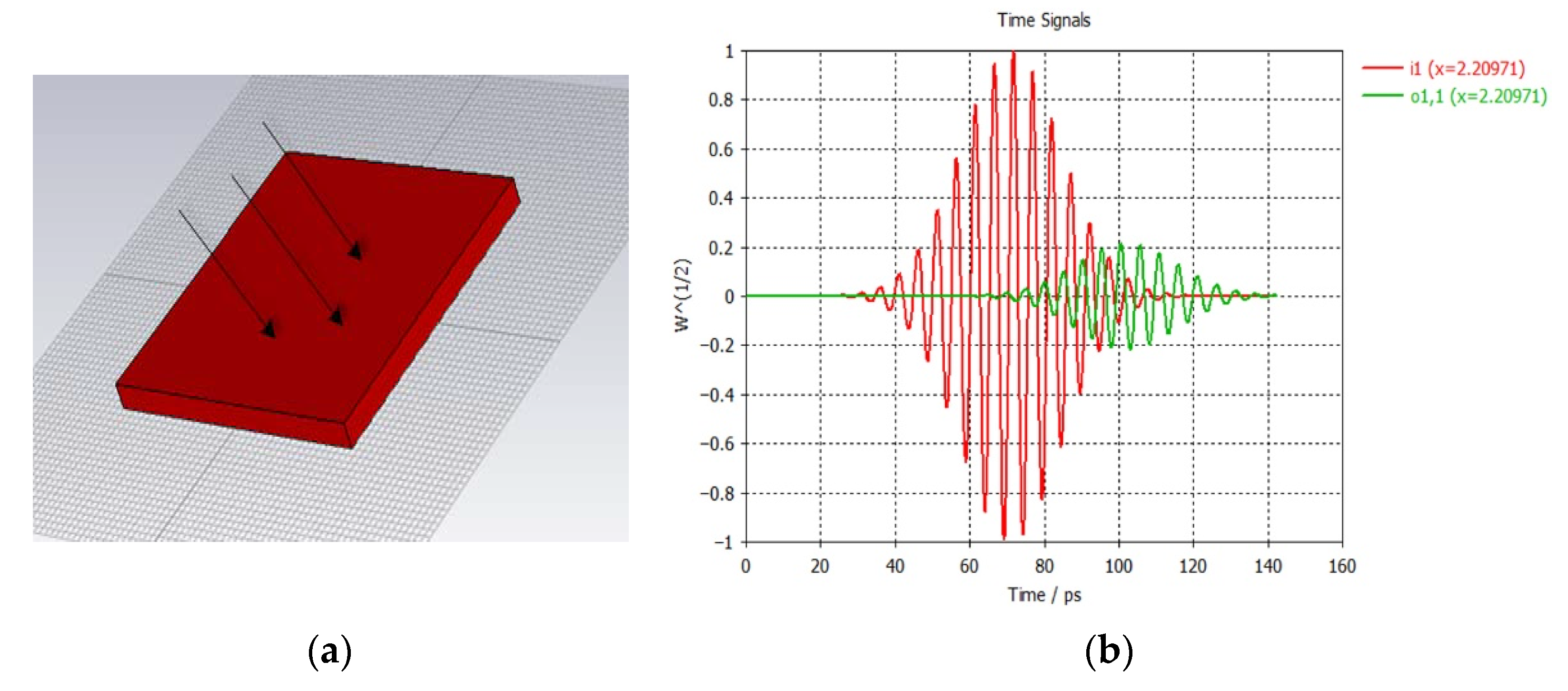
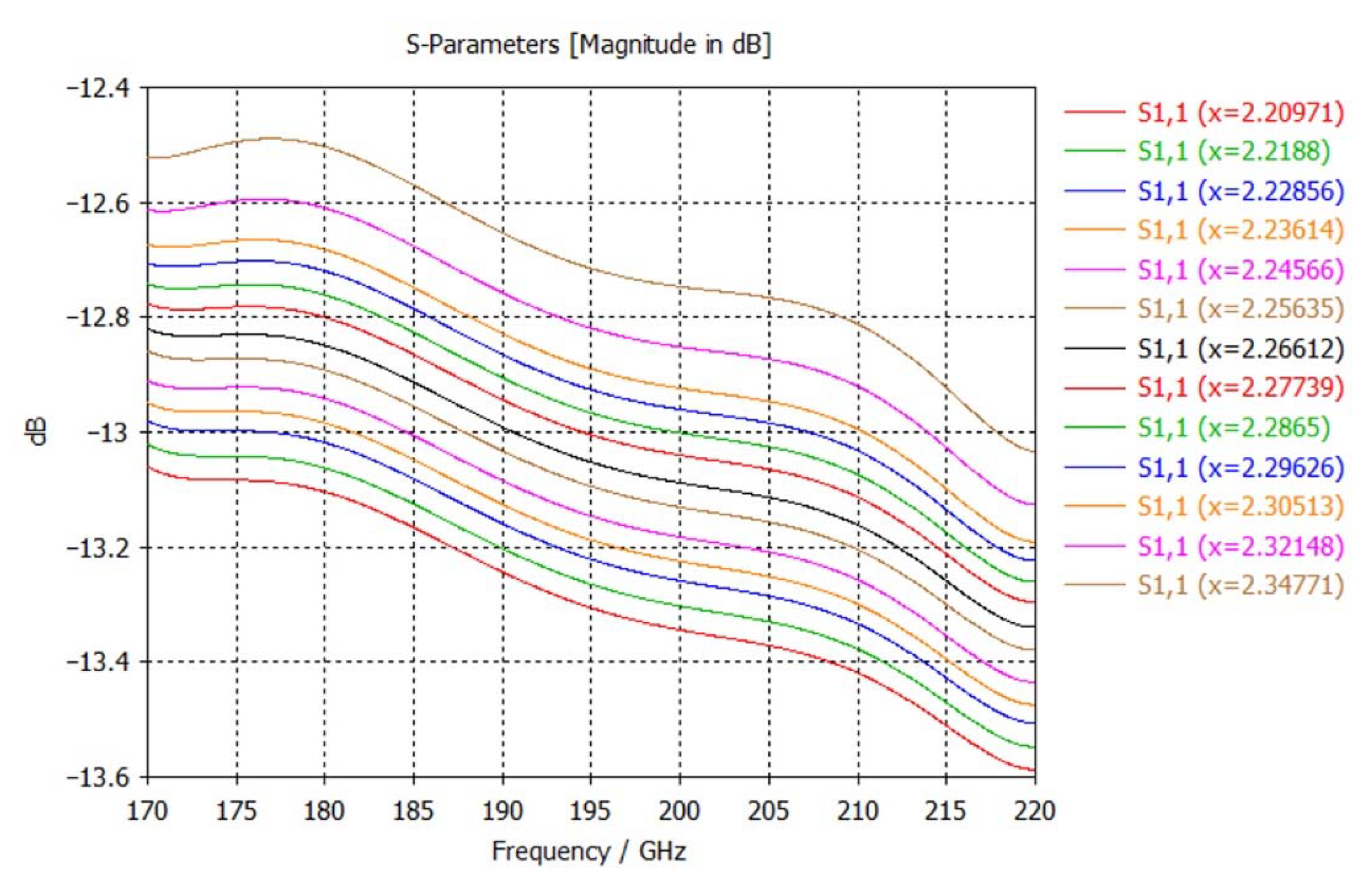
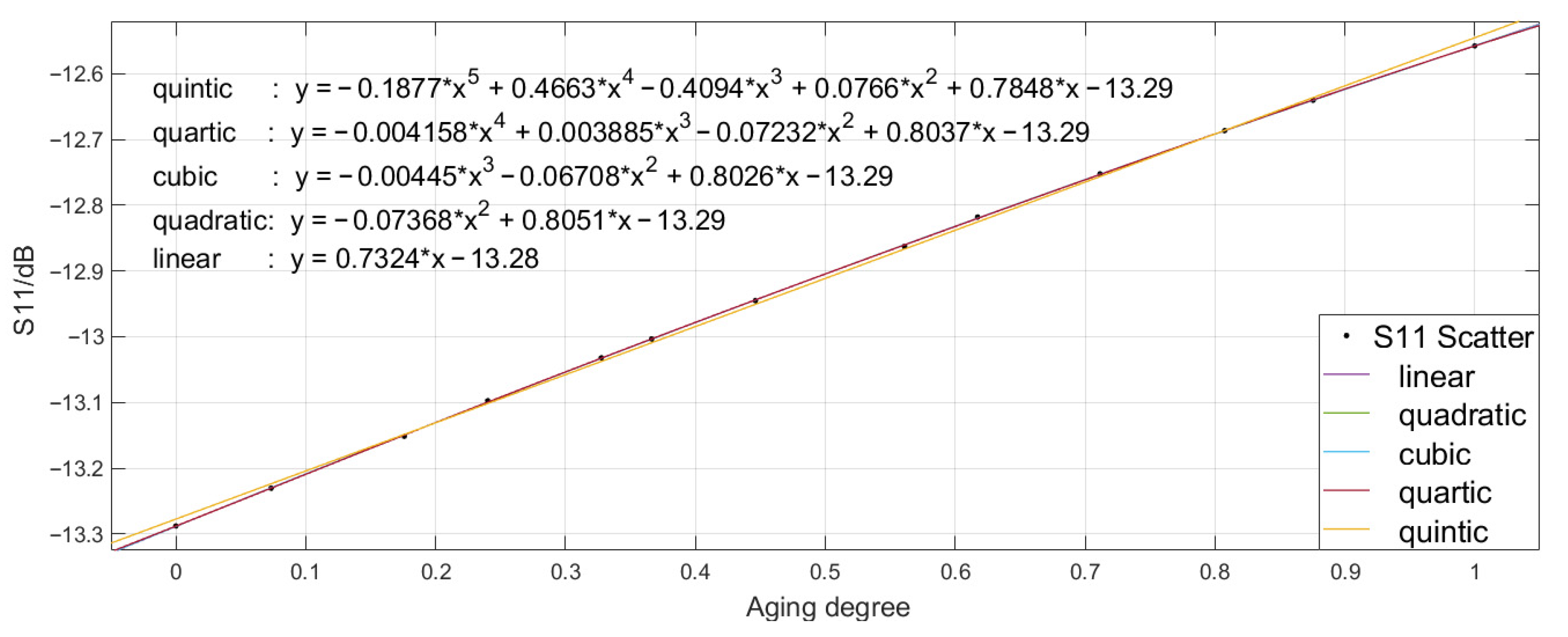
3.3. Simulation Analysis of Terahertz Signal PMVS Medium Transmission
4. Experiment and Discussion
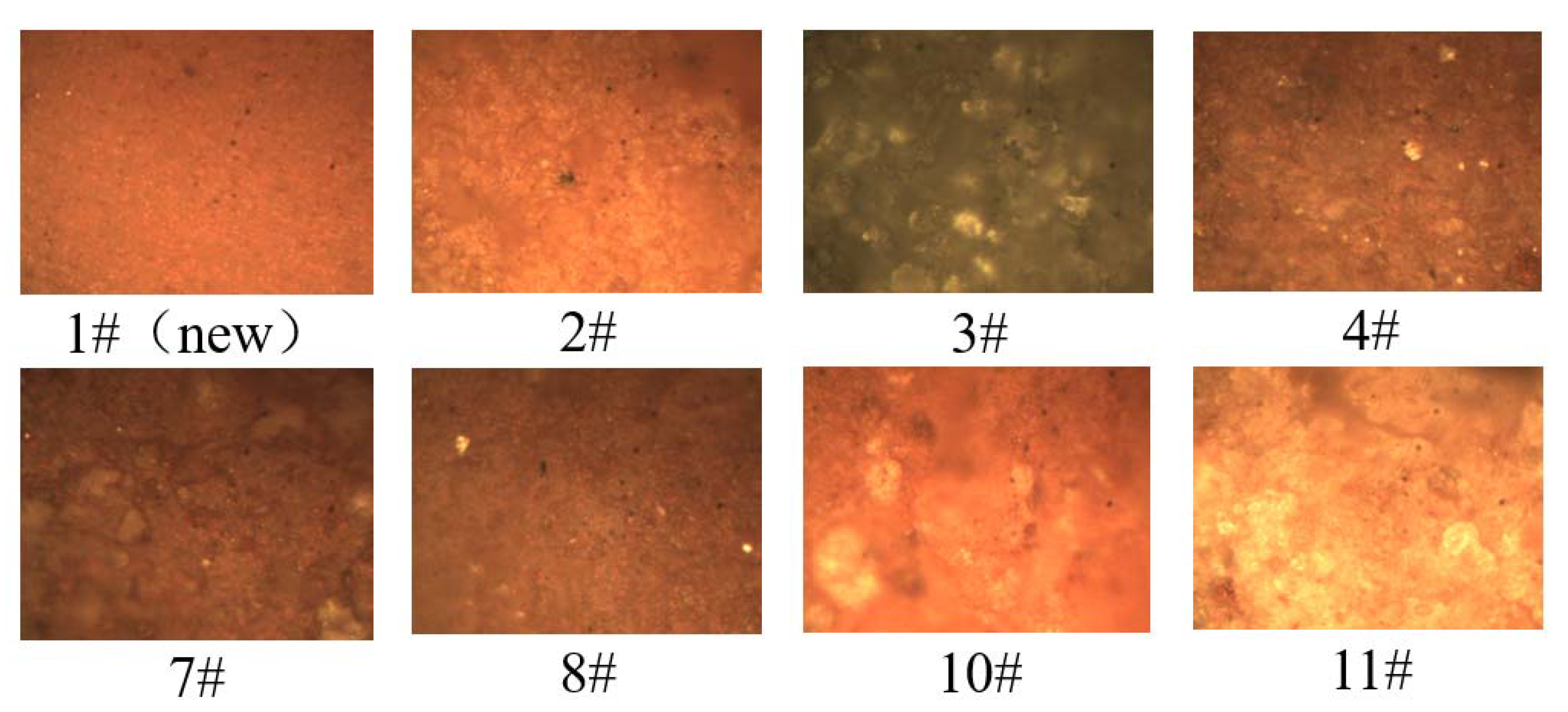
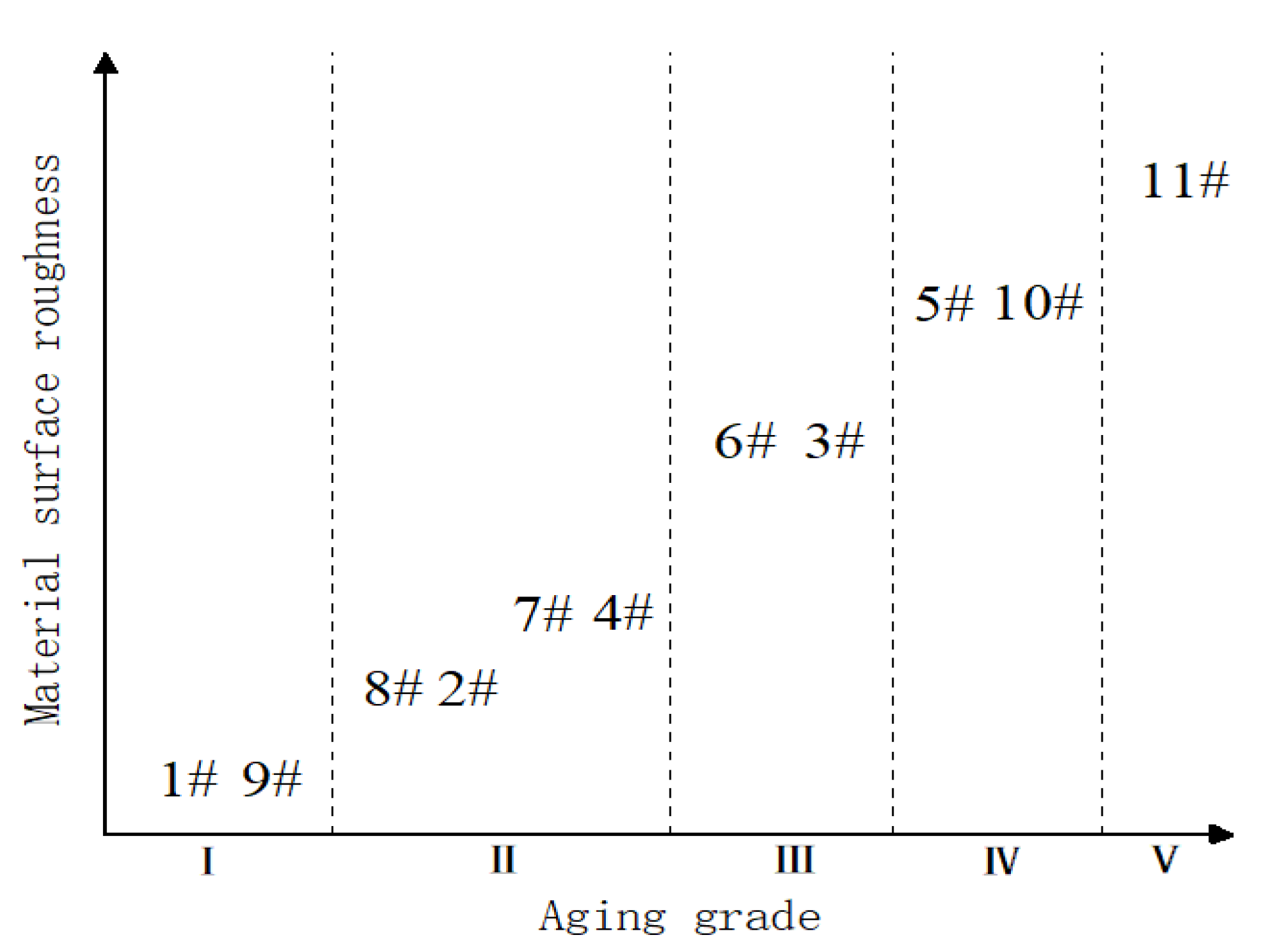
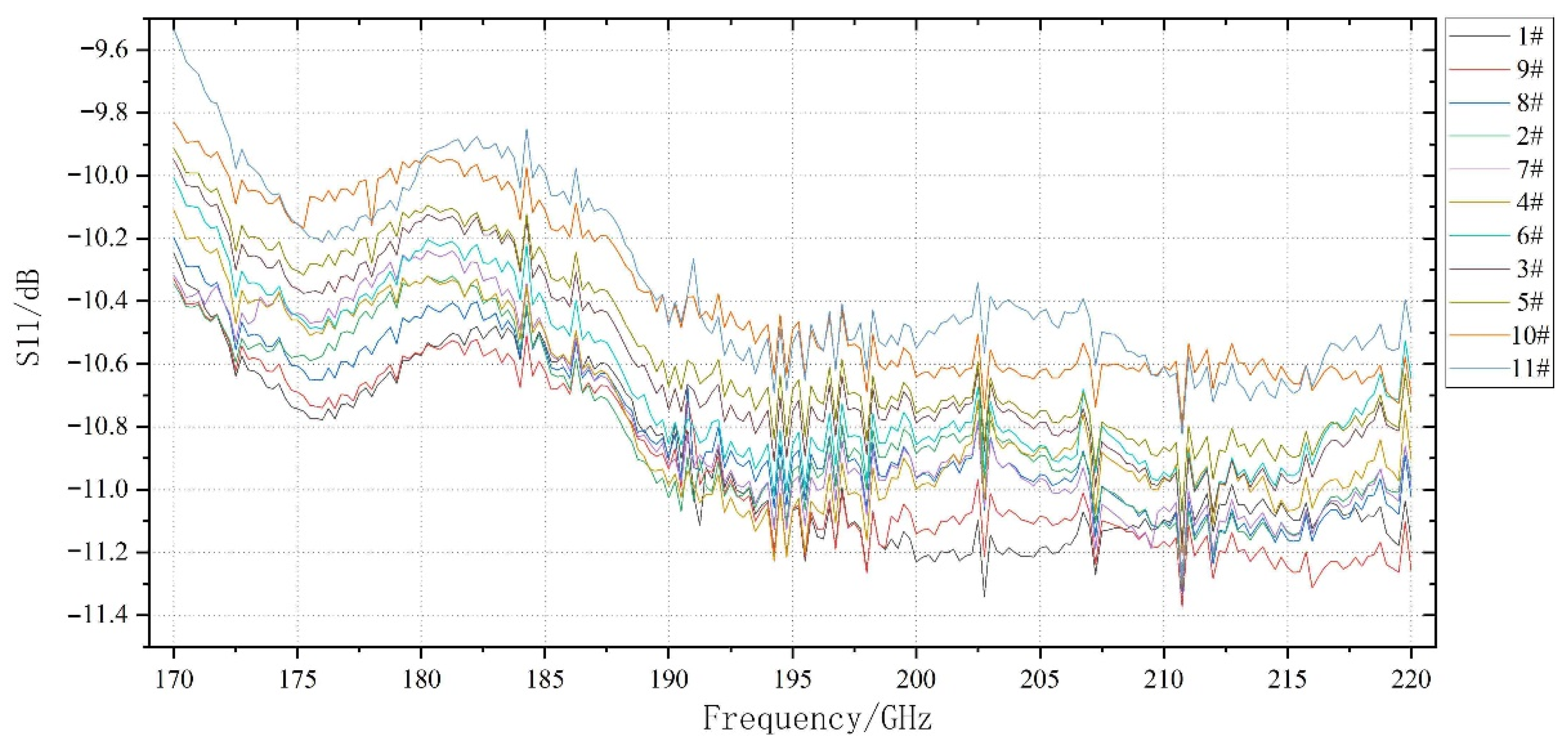
4.1. Sample Aging Degree Calibration
- Samples 1# and 9#, no aging or very low aging;
- Samples 8#, 2#, 7#, and 4#, the insulators have detectable aging, the surface hydrophobicity gradually decreases, and there are holes, etc.;
- Samples 6# and 3#, the water repellency further decreased, some defects appeared, the area of pores increased, and the aging was gradually serious;
- Samples 5# and 10#, the surface defects of the material increased and deepened, and the insulation performance was affected;
- Samples 11#, The surface of the material is severely powdered, and the aging extends to the inside of the material.
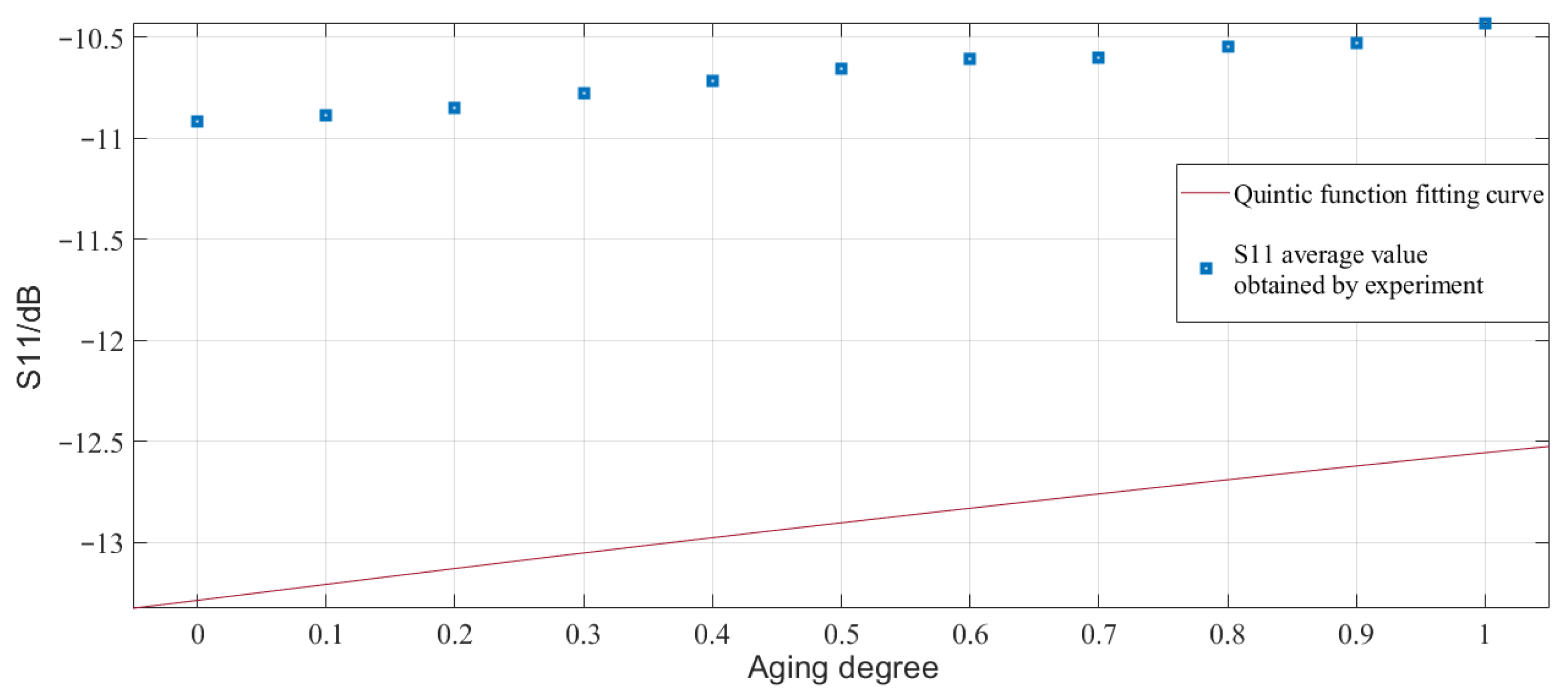
4.2. Terahertz Reflection Experiment and Result Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hackam, R. Outdoor HV Composite Polymeric Insulators. IEEE Trns. Dielectr. Electr. Insul. 1999, 6, 557–585. [Google Scholar] [CrossRef]
- Yoshimura, N.; Kumagai, S.; Nishimura, S. Electrical and Environmental Aging of Silicone Rubber Used in Outdoor Insulation. IEEE Trns. Dielectr. Electr. Insul. 1999, 6, 632–650. [Google Scholar] [CrossRef]
- Hussain, M.M.; Chaudhary, M.A.; Razaq, A. Mechanism of Saline Deposition and Surface Flashover on High-Voltage Insulators near Shoreline: Mathematical Models and Experimental Validations. Energies 2019, 12, 3685. [Google Scholar] [CrossRef] [Green Version]
- Shaik, M.G.; Karuppaiyan, V. Investigation of Surface Degradation of Aged High Temperature Vulcanized (HTV) Silicone Rubber Insulators. Energies 2019, 12, 3769. [Google Scholar] [CrossRef] [Green Version]
- Song, W.; Shen, W.W.; Zhang, G.J.; Song, B.P.; Lang, Y.; Su, G.Q.; Mu, H.B.; Deng, J.B. Aging Characterization of High Temperature Vulcanized Silicone Rubber Housing Material Used for Outdoor Insulation. IEEE Trns. Dielectr. Electr. Insul. 2015, 22, 961–969. [Google Scholar] [CrossRef]
- Gao, R.M.; Zhang, X.Q.; Guo, Y.J.; Fan, C.; Qiu, Y.; Li, Y.S.; Wu, G.N.; IEEE. Study on Detection Method of Composite Insulator Ageing Based on Hyperspectral Technology. In Proceedings of the 2019 2nd International Conference on Electrical Materials and Power Equipment (Icempe 2019), Guangzhou, China, 7–10 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 461–466. [Google Scholar]
- Gonchar, N.R.; Treskina, M.N.; Ivanov, G.F. Study of Chemical Changes in Rubber Due to Ionization Aging by Means of Ir-Spectroscopy. Izv. Vyss. Uchebnykh Zaved. Fiz. 1972, 1, 138. [Google Scholar]
- Li, J.J.; Zhang, H.H.; Li, G.F.; Zhang, S.G.; Liu, Y.; Dong, K.; Zu, E.D.; Yu, L. Aging Mechanism Analysis of High Temperature Vulcanization Silicone Rubber Irradiated by Ultraviolet Radiation Based on Infrared Spectra. Spectrosc. Spectr. Anal. 2020, 40, 1063–1070. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, C.Y.; Chen, Z.Y.; Wang, L.M.; IEEE. Effect of Surface Aging on UV Intensity Characteristics for Long-Term Energized Conductors of HVDC Transmission Lines. In Proceedings of the IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 19–22 September 2016. [Google Scholar]
- Deng, H.L.; He, Z.F.; Chen, L. Ultrasonic Guided Wave-based Detection of Composite Insulator Debonding. IEEE Trns. Dielectr. Electr. Insul. 2017, 24, 3586–3593. [Google Scholar] [CrossRef]
- Yuan, C.; Xie, C.Z.; Li, L.C.; Zhang, F.Z.; Gubanski, S.M. Ultrasonic Phased Array Detection of Internal Defects in Composite Insulators. IEEE Trns. Dielectr. Electr. Insul. 2016, 23, 525–531. [Google Scholar] [CrossRef]
- Liang, H.; Rodrigue, D.; Brisson, J. Characterization of Recycled Styrene Butadiene Rubber Ground Tire Rubber: Combining X-Ray Fluorescence, Differential Scanning Calorimetry, and Dynamical Thermal Analysis for Quality Control. J. Appl. Polym. Sci. 2015, 132, 14. [Google Scholar] [CrossRef]
- Xu, F.; Mu, Q.D.D.; Li, L.J.; Yang, D.; Xia, B.L. Nondestructive Evaluation of Rubber Composites Using Terahertz Time Domain Spectroscopy. Fibres Text. East. Eur. 2018, 26, 67–72. [Google Scholar] [CrossRef]
- Wieczorek, K.; Ranachowski, P.; Ranachowski, Z.; Paplinski, P. Ageing Tests of Samples of Glass-Epoxy Core Rods in Composite Insulators Subjected to High Direct Current (DC) Voltage in a Thermal Chamber. Energies 2020, 13, 6724. [Google Scholar] [CrossRef]
- Liang, Y.; Gao, T.; Wang, X.; Sun, M.; Gao, L. Electric Field Intensity Effects on the Microstructural Characteristics Evolution of Methyl Vinyl Silicone Rubber via Molecular Simulation. Molecules 2018, 23, 1861. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singh, R.; Kumar, A.; Harbola, M.K.; Samal, P. Semianalytical Wavefunctions and Kohn-Sham Exchange-Correlation Potentials for Two-Electron Atomic Systems in Two-Dimensions. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 3. [Google Scholar] [CrossRef]
- Alam, S.; Serdyuk, Y.V.; Gubanski, S.M. Temperature and Field Induced Variations of Electric Conductivities of HTV Silicone Rubbers Derived from Measured Currents and Surface Potential Decay Characteristics. Energies 2020, 13, 2982. [Google Scholar] [CrossRef]
- Nayak, P.K.; Periasamy, N. Calculation of Ionization Potential of Amorphous Organic Thin-Films Using Solvation Model and DFT. Org. Electron. 2009, 10, 532–535. [Google Scholar] [CrossRef]
- Ruuska, H.; Arola, E.; Kortelainen, T.; Rantala, T.T.; Kannus, K.; Valkealahti, S. A Density Functional Study on Dielectric Properties of Acrylic Acid Grafted Polypropylene. J. Chem Phys. 2011, 134, 134904. [Google Scholar] [CrossRef] [PubMed]
- Popovic, Z.; Grossman, E.N. THz Metrology and Instrumentation. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 133–144. [Google Scholar] [CrossRef]
Short Biography of Authors
 | Haitao Yang is a PhD student in Beijing Jiaotong University. From September 2013 to July 2020, he studied for bachelor and master degrees in the School of Electrical Engineering of the University of Jinan; From September -now, September 2020-present, PhD in Beijing Jiaotong University; His current research direction is power system and its automation, Insulation detection technology, Sensor Technology... |
 | Zhensheng Wu is an associate professor and doctoral supervisor at Beijing Jiaotong University. From September 1993 to July 2003, he studied for bachelor, master and doctorate degrees in the Department of Electrical Engineering and Applied Electronic Technology of Tsinghua University, and finally obtained a doctorate degree in engineering. Since July 2003, he works in the School of Electrical Engineering, Beijing Jiaotong University, undertaking teaching and research work; 2011.02-2011.09, a visiting scholar at the University of California, IRVINE.; His current research direction is power system and its automation, high voltage and insulation technology, electrical engineering. And He is now the Deputy Secretary-General of the IEEE Smart Village China Committee... |
 | Dong Weinan is a master of Beijing Jiaotong University. From September 2015 to July 2019, he studied for bachelor’s degree in school of electrical engineering, North China University of technology; From September 2019 to now, I have studied for a master’s degree in Beijing Jiaotong University. His current research direction is intelligent monitoring and diagnosis of electrical equipment... |
 | Junpeng Dang, currently working for the Science and Technology Center of Yuxi Power Supply Bureau of Yunnan Power Grid Co., Ltd., graduated from Xi’an Electric Power College in June 2011, graduated from Jilin University in July 2020, and joined Yunnan Power Grid Corporation in July 2011 Work in Yuxi Power Supply Bureau. In 2018, he engaged in voltage management of the Production Technology Department of Yuxi Power Supply Bureau, and carried out professional management of power transformation, distribution voltage quality, line loss, and reactive power. Since 2020, he has been engaged in scientific and technological management of Yuxi Yuxi Power Supply Bureau. He has won the Yunnan Power Grid Corporation Scientific and Technological Progress Award for many times, and won the first prize of CEC Staff Technological Innovation and many other honorary awards... |
 | Hao Ren is an associate professor at China University of Petroleum (East China). He received his B.S. degree in Chemistry in 2003 at Shandong University, a Ph.D. degree in Physical Chemistry at University of Science and Technology of China, and a Ph.D degree in Biotechnology at Royal Institute of Technology, Sweden. From 2010 to 2013, he worked as a post-doc at University of California, Irvine. His current research mainly focuses on the development of ab-initio and machine learning methods for molecular spectroscopy... |
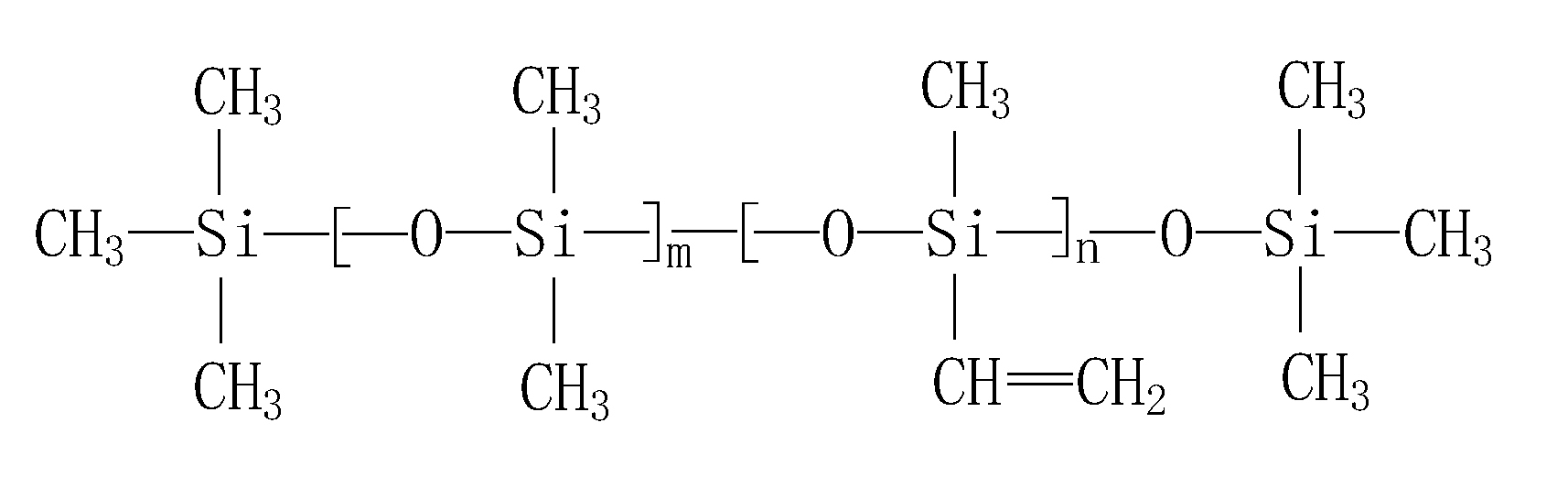



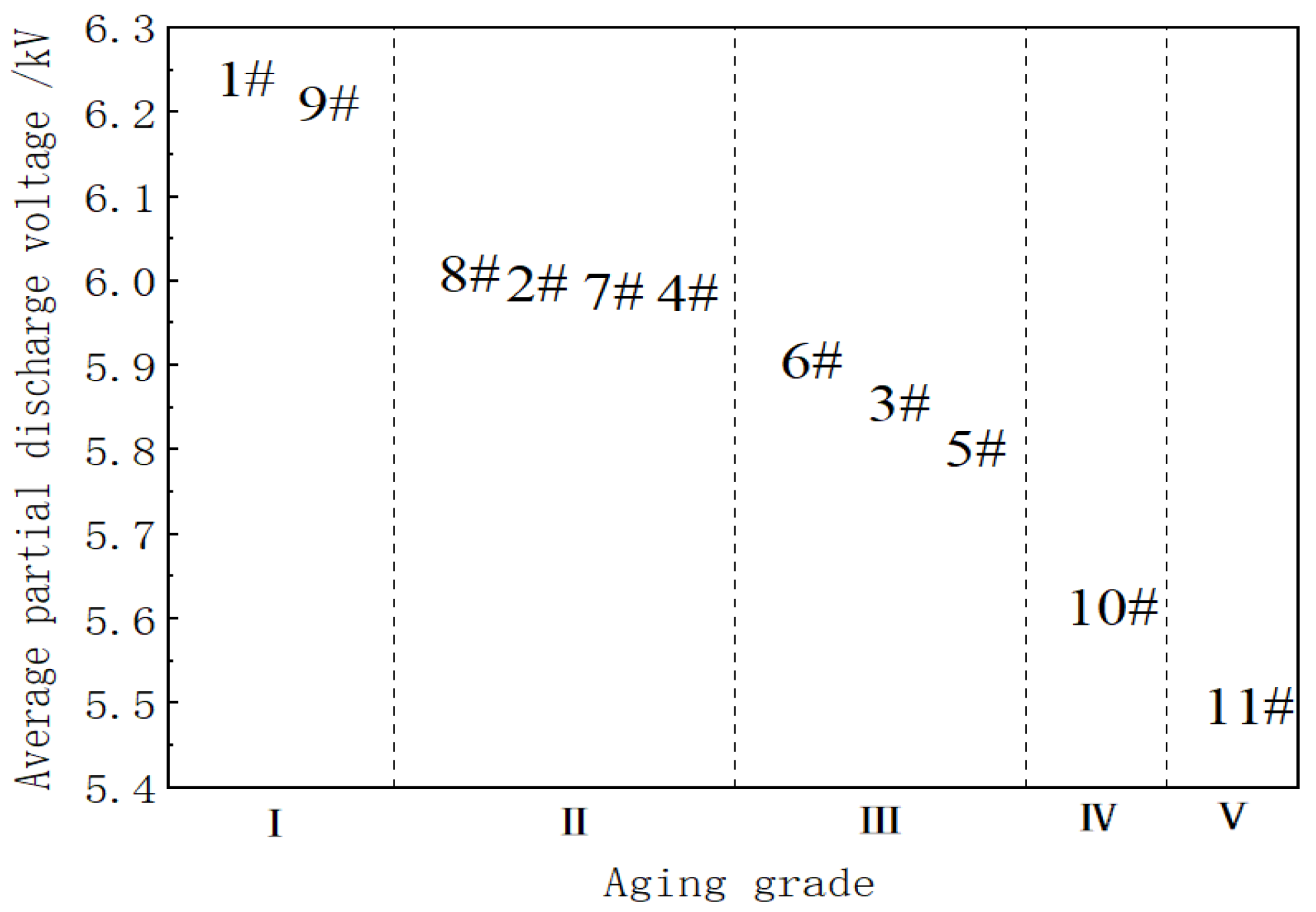

| Sample Number | Start Discharge Voltage/kV | Current Sound Voltage/kV | Impending Breakdown Voltage/kV | Average Discharge Voltage/kV |
|---|---|---|---|---|
| 1# | 4.75 | 5 | 9 | 6.25 |
| 2# | 4.625 | 4.875 | 8.75 | 6.083 |
| 3# | 4.5 | 4.75 | 8.375 | 5.875 |
| 4# | 4.625 | 4.875 | 8 | 6.000 |
| 5# | 4.5 | 4.875 | 8.125 | 5.833 |
| 6# | 4.75 | 5 | 8 | 5.917 |
| 7# | 4.75 | 4.875 | 8.5 | 6.042 |
| 8# | 4.625 | 5 | 8.75 | 6.125 |
| 9# | 4.75 | 4.875 | 9 | 6.208 |
| 10# | 4.375 | 4.5 | 8 | 5.625 |
| 11# | 4.125 | 4.625 | 7.75 | 5.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Wu, Z.; Dong, W.; Dang, J.; Ren, H. Analysis of the Influence of Silicone Rubber Aging on the Transmission Parameters of Terahertz Waves. Energies 2021, 14, 4238. https://doi.org/10.3390/en14144238
Yang H, Wu Z, Dong W, Dang J, Ren H. Analysis of the Influence of Silicone Rubber Aging on the Transmission Parameters of Terahertz Waves. Energies. 2021; 14(14):4238. https://doi.org/10.3390/en14144238
Chicago/Turabian StyleYang, Haitao, Zhensheng Wu, Weinan Dong, Junpeng Dang, and Hao Ren. 2021. "Analysis of the Influence of Silicone Rubber Aging on the Transmission Parameters of Terahertz Waves" Energies 14, no. 14: 4238. https://doi.org/10.3390/en14144238
APA StyleYang, H., Wu, Z., Dong, W., Dang, J., & Ren, H. (2021). Analysis of the Influence of Silicone Rubber Aging on the Transmission Parameters of Terahertz Waves. Energies, 14(14), 4238. https://doi.org/10.3390/en14144238





