Digital Twin Concepts with Uncertainty for Nuclear Power Applications
Abstract
:1. Introduction
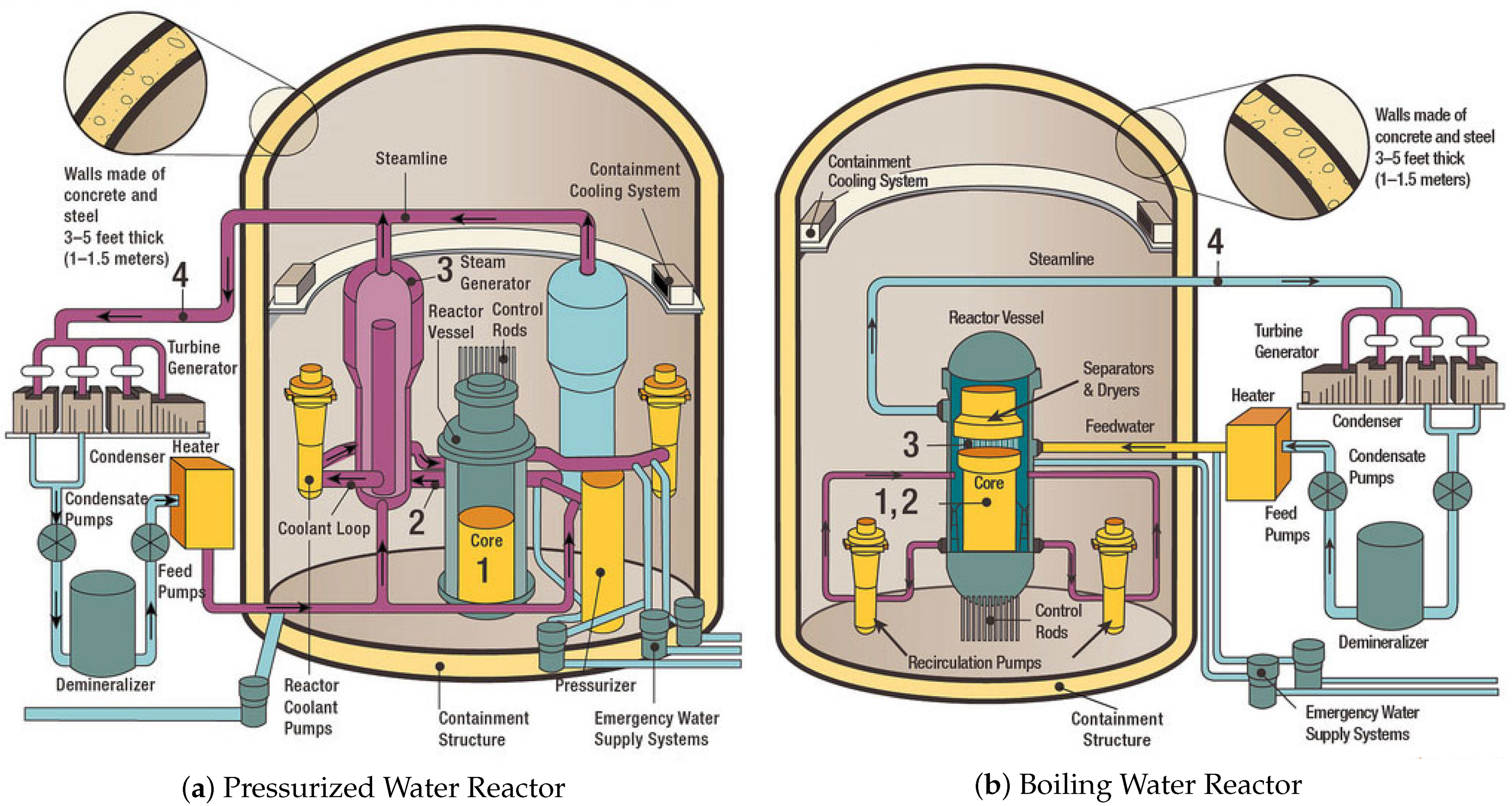
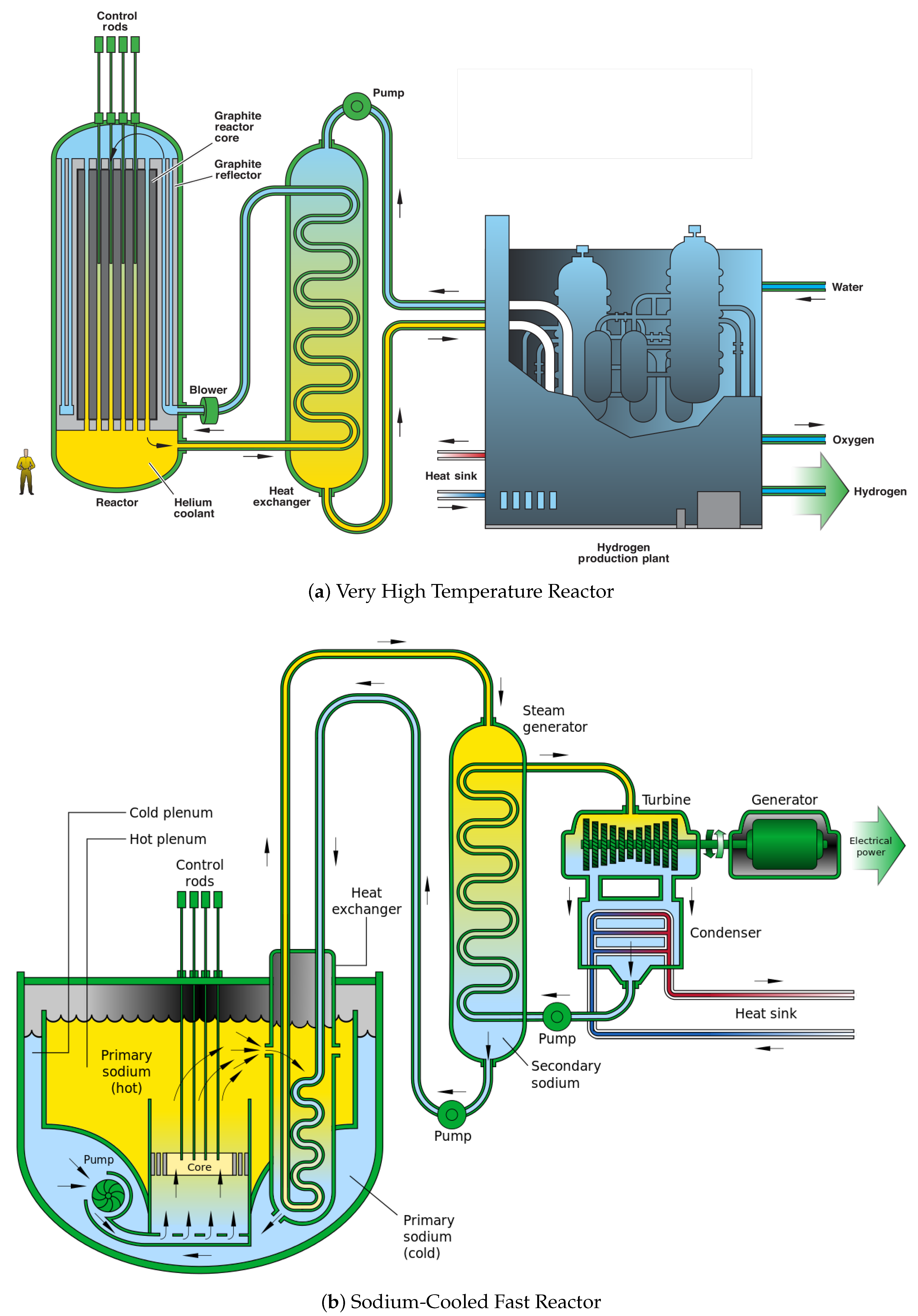
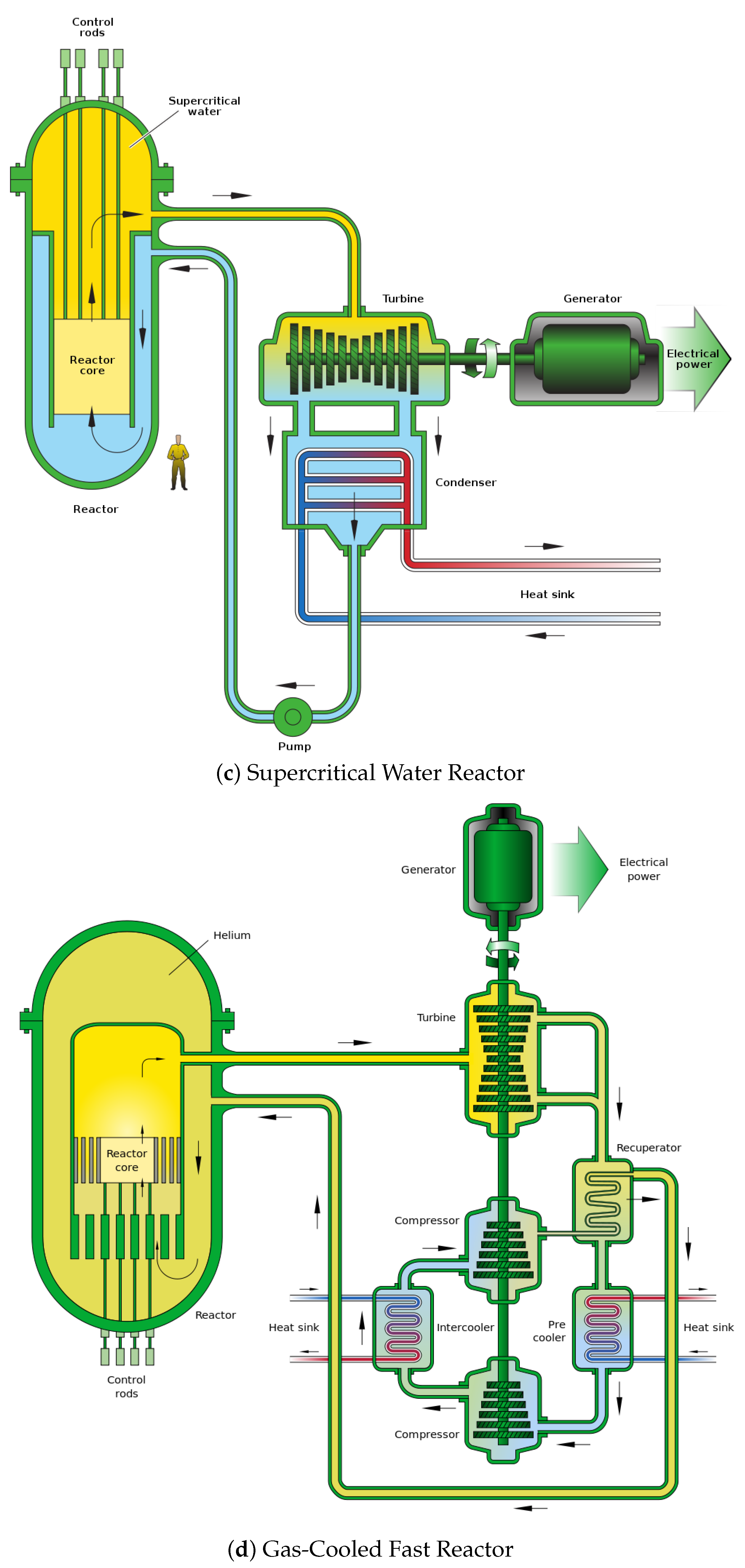
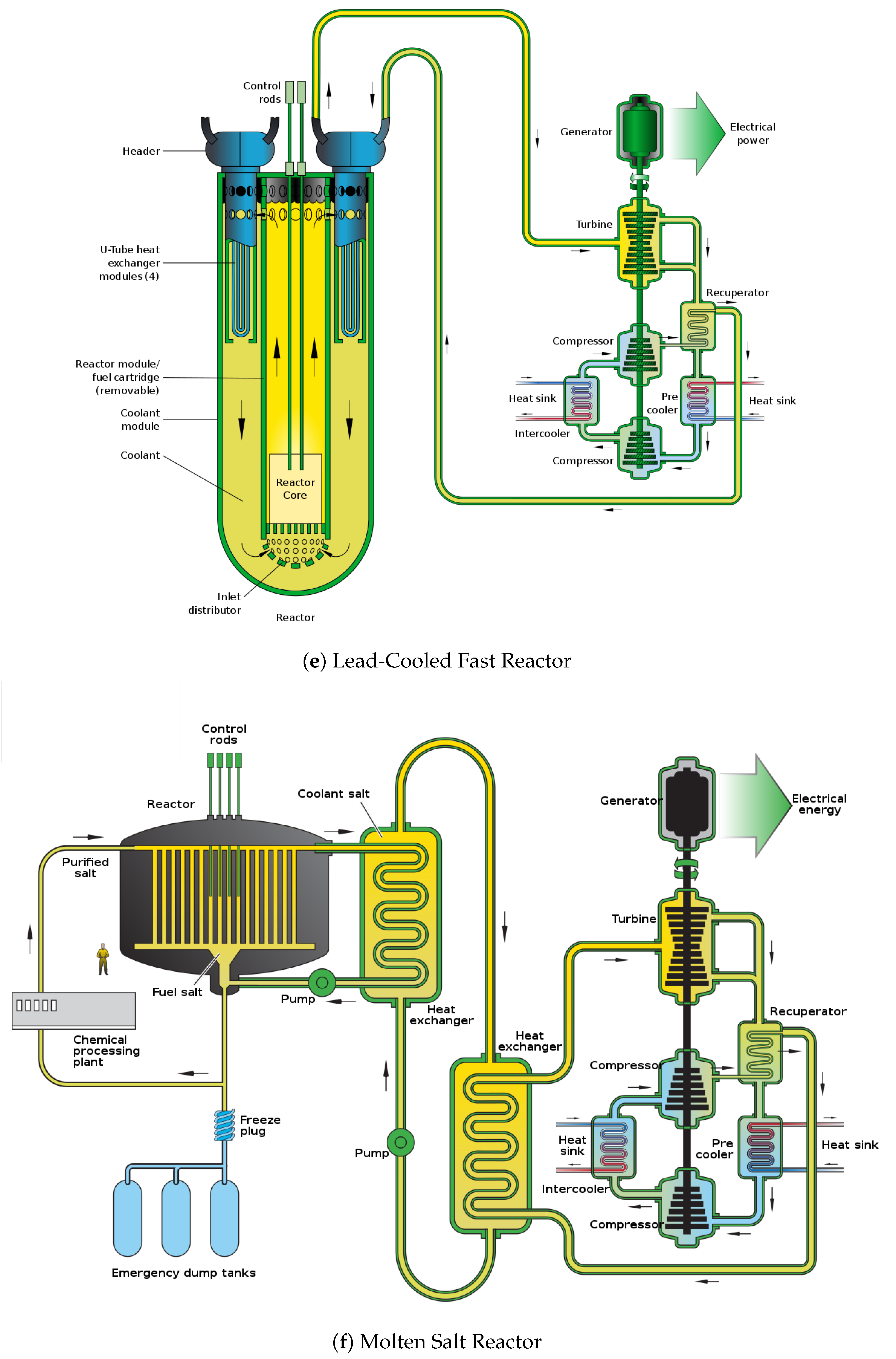
2. Brief Overview of Nuclear Power Systems
3. Defining Digital Twins for Nuclear Power Systems
3.1. Review of Digital Twin Definitions
- Tuegel et al. [5] define the DT as being “ultrarealistic in geometric detail, including manufacturing anomalies, and in material detail, including the statistical microstructure level, specific to this aircraft tail number”. Here, the DT concept is focused on high-fidelity simulation by the finite element method (FEM) and computational fluid dynamics (CFD) for the prediction and management of the structural life of aircraft. The authors note that another key feature of their concept is the ability to “translate uncertainties in inputs into probabilities of obtaining various structural outcomes”.
- Glaessgen and Stargel [6] have a similar definition centering on ultra-high-fidelity simulation being integrated with a vehicle’s health management system. In this paper, the authors focus more on certification of the vehicles and a reliance on the assumed similitude of data used for certification. They identify this as a shortcoming to be addressed by DTs. Their definition for a DT is “an integrated multiphysics, multiscale, probabilistic simulation of an as-built vehicle or system that uses the best available physical models, sensor updates, fleet history, etc., to mirror the life of its corresponding flying twin”.
- Boschert and Rosen [7] provide a very general definition with “the Digital Twin itself refers to a comprehensive physical and functional description of a component, product or system, which includes more or less all information which could be useful in all—the current and subsequent—life cycle phases”. Here, the authors acknowledge that the DT concept is variable in terms of where it is applied in the product life cycle and the overall fidelity of data and models encompassed.
- Chen [8] similarly broadens the usage of DT and defines it as “a computerized model of a physical device or system that represents all functional features and links with the working elements”.
- Schluse et al. [10] take a slightly different perspective on DTs focusing on the value as an asset for experimentation. Nevertheless, many of the same fundamental requirements arise from their definition of experimental DTs as “a one-to-one replica of a real system incorporating all components and aspects relevant to use simulations for engineering purposes but also inside the real system during real-world operations”.
- Tao et al. [21] describe the DT in a few ways. First, it is a concept “associated with cyber-physical integration.“ Further, DTs create “high-fidelity virtual models of physical objects in virtual space in order to simulate their behaviors in the real world and provide feedback”, and “reflects a bi-directional dynamic mapping process”.
- Rasheed et al. [3] state that a “Digital twin can be defined as a virtual representation of a physical asset enabled through data and simulators for real-time prediction, optimization, monitoring, controlling, and improved decision making”.
- Lin et al. [19] also offer a good definition with: “A DT is a digital representation of a physical asset or system that relies on real-time and history data for inferring complete reactor states, finding available control actions, predicting future transients, and identifying the most preferred actions”.
3.2. Analysis of Key Characteristics
3.3. Proposed Definition
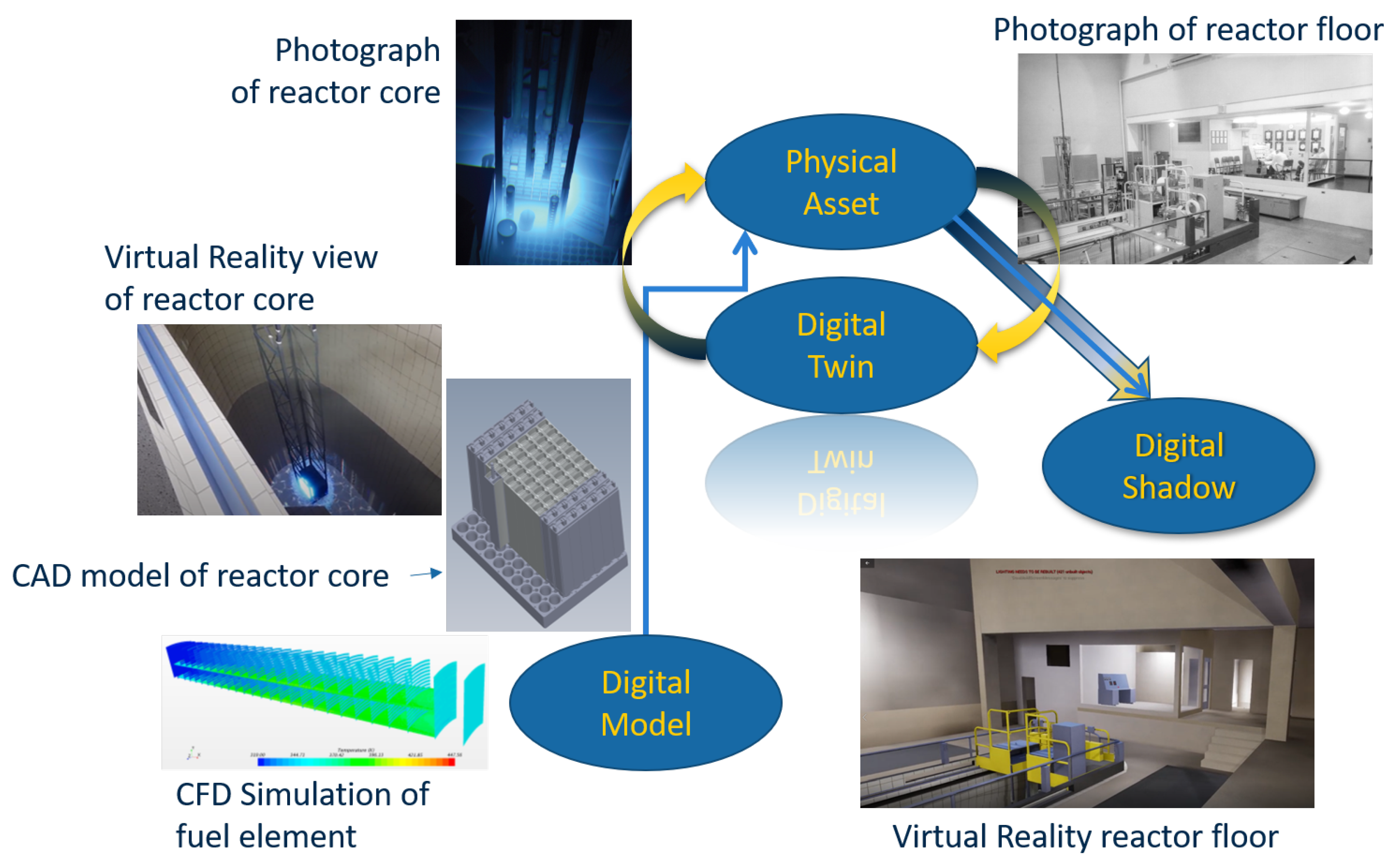
- The digital model may or may not be associated with a physical asset. Thus, it need not integrate with physically measured or sensed quantities. This is how we might think of most of the existing M&S efforts in nuclear engineering. Full simulation models of planned or existing reactors, and their systems and components, capable of simulating the system physics and dynamics comprise the digital model. What distinguishes the digital model from the digital twin is that information generated by the digital model is not automatically integrated with the physical asset.
- The digital shadow extends the digital model by incorporating information from an existing physical asset to update the digital model, but does not utilize any information generated by the digital representation in the physical asset. We note that digital representations of historic facilities that no longer exist can qualify as digital shadows. The inverse of the digital shadow, where information only flows from a digital model to a physical asset, is not a coherent paradigm for useful engineering analysis as there is a physical system operating with essentially no connection to reality. Therefore, this situation is not explicitly defined or discussed further (For the curious reader, this paradigm essentially aligns with Plato’s Allegory of the Cave [22] or Putnam’s more contemporary “Brain in a vat” [23]).
- The digital twin is therefore the “closed loop” model of the physical asset and the digital representation(s). The digital twin exchanges information in real-time with the physical system to update its state and perform predictive calculations that are then used to inform decisions and control actions on the physical asset.
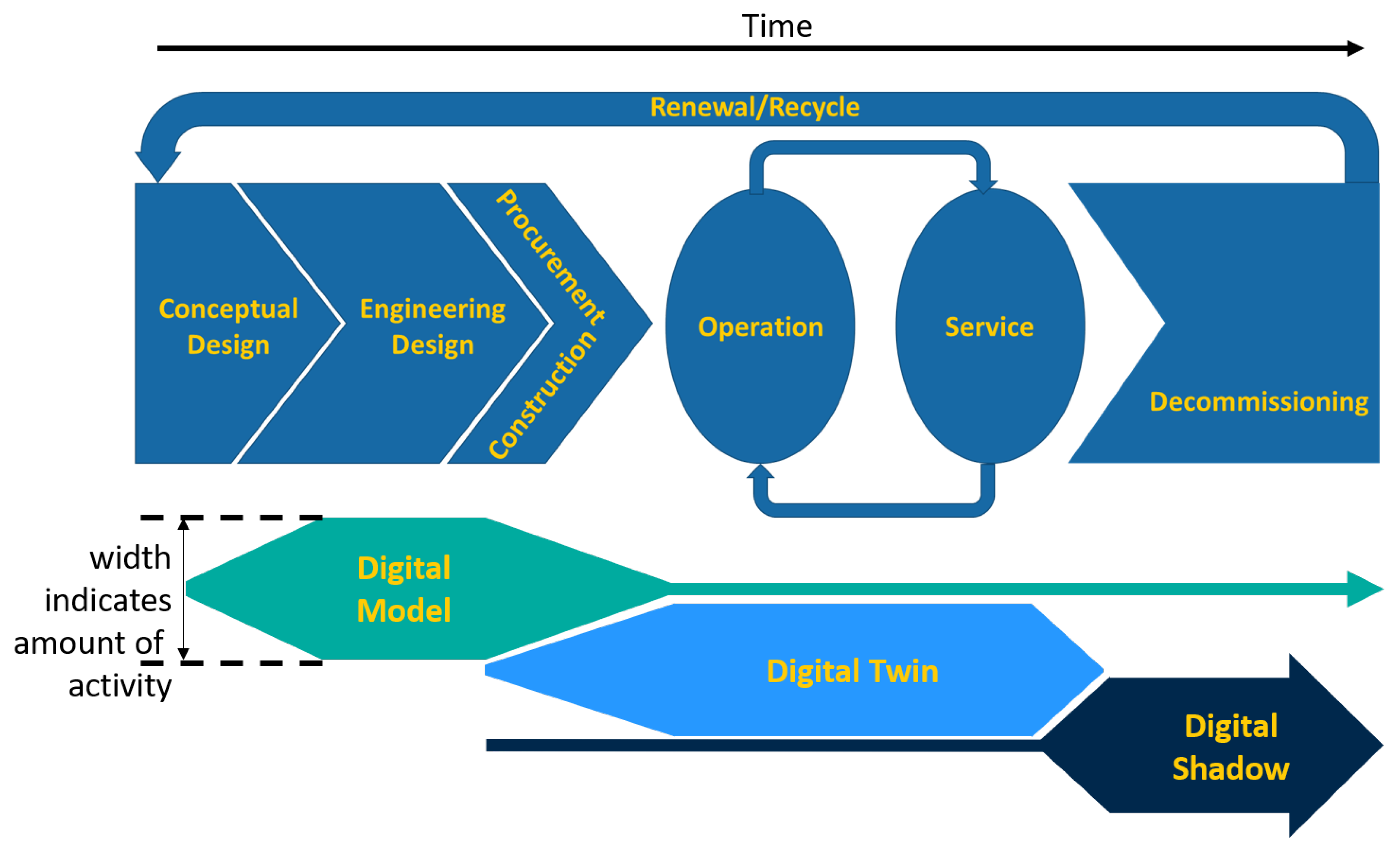
- the initial conceptual design,
- the engineering design,
- procurement and construction,
- the operational phase that undergoes intermediate service, and
- and finally the decommissioning phase.
- Prior to the existence of any information exchange between the digital and physical assets, the digital object is described as a digital model. This often encompasses the conceptual and engineering design phases.
- The digital model may exist alongside the physical twin and indefinitely, if there is no information exchange with the physical asset.
- Following the creation of a physical asset, a digital shadow may be created that incorporates information from the physical asset in either an automated or manual sense, but it does not provide information back to the physical asset.
- The digital shadow may also persist indefinitely.
- The digital twin exists only as long as there is a physical asset.
- The digital twin has real-time, automated, two-way information exchange between the digital representation and physical asset.
- The digital twin may involve a set of models of varying fidelity and complexity.
- A digital twin has a corresponding digital model and digital shadow. The digital model and digital shadow are specific aspects of the twin.
4. Historical and Contemporary Digital Representations of Nuclear Power Systems
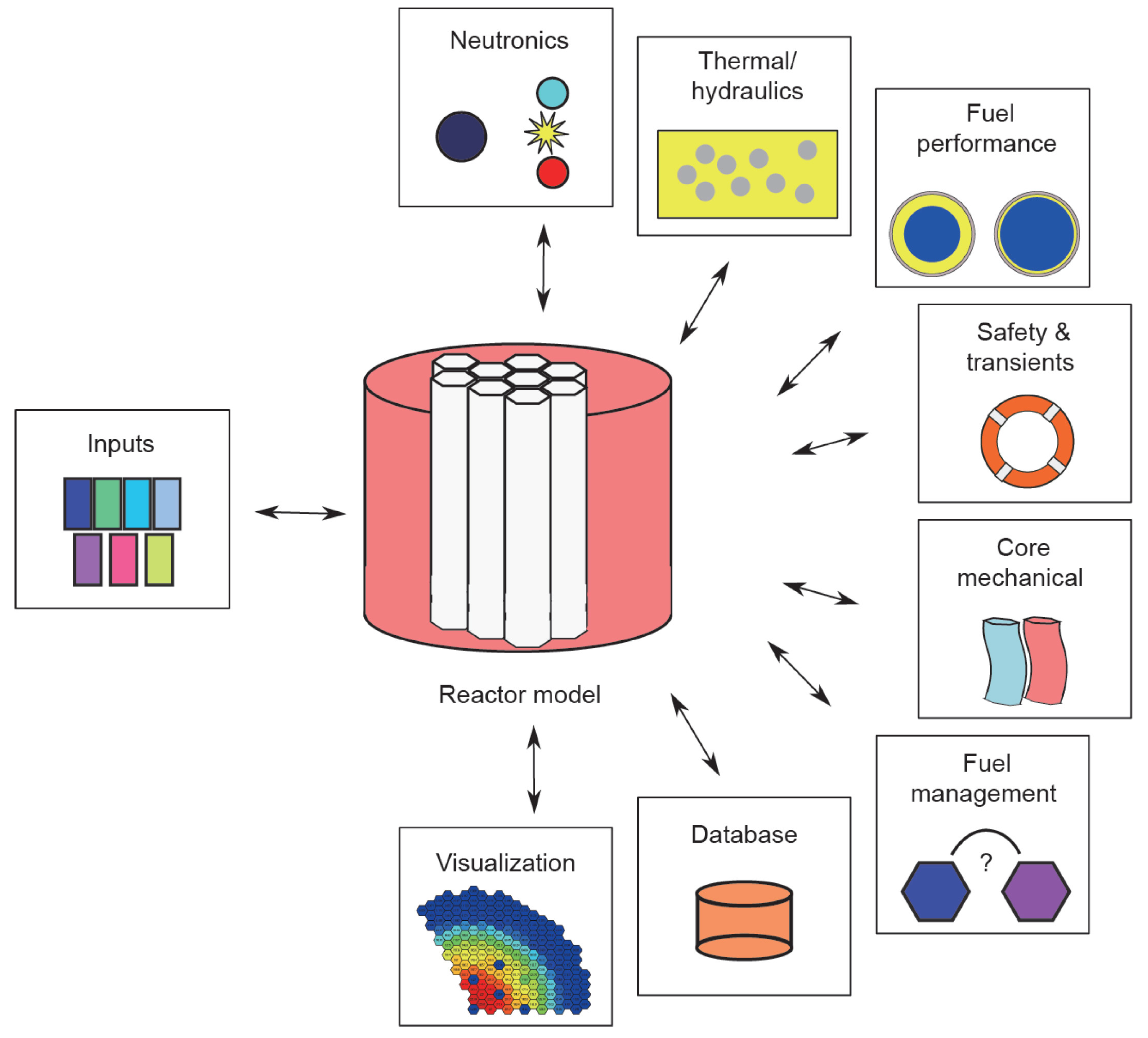
4.1. Common Nuclear Engineering Simulation Tools
4.2. Relevant Non-Nuclear Commercial Simulation Tools
4.3. Emerging Tools and Capabilities
5. Enabling Technologies and Challenges for Digital Twins of Nuclear Power Systems
5.1. Enabling Technologies
5.1.1. System Dynamics Modeling
5.1.2. Model Based Controllers
5.1.3. Automated ROM Construction
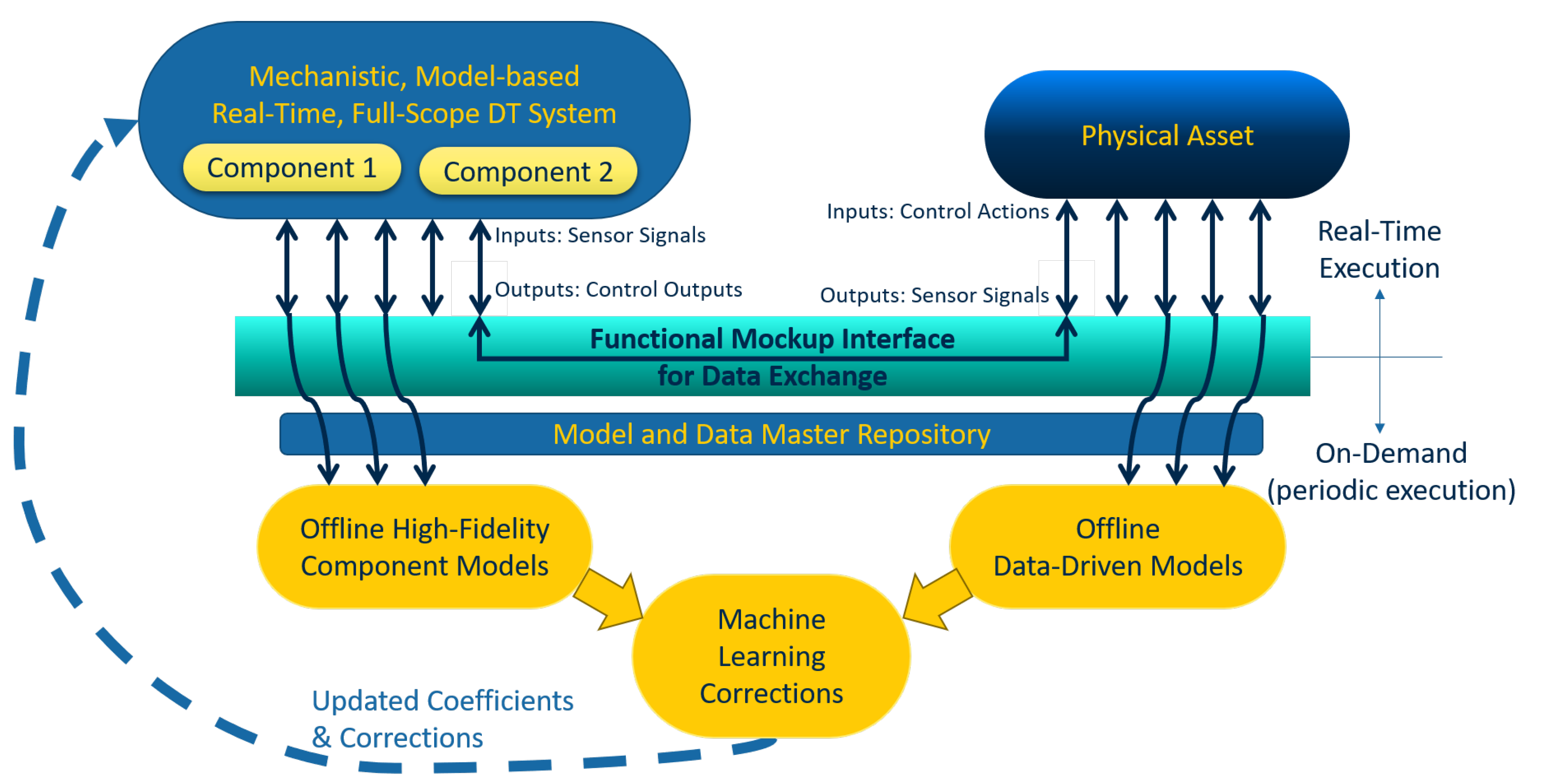
5.1.4. Functional Mockup Interfaces
5.2. A Digital Twin Paradigm
5.3. Challenges to Realizing Digital Twins
5.3.1. Security
5.3.2. Integration with Prognostics and Health Management
5.3.3. Data Collection, Curation, Transmission, and Integration
5.3.4. Integration with Risk Assessments
5.4. Computing Infrastructure and Reliability
5.4.1. Standardization
5.4.2. Leverage the Progress in High-Fidelity Advanced Modeling Simulation
5.4.3. Uncertainty Quantification
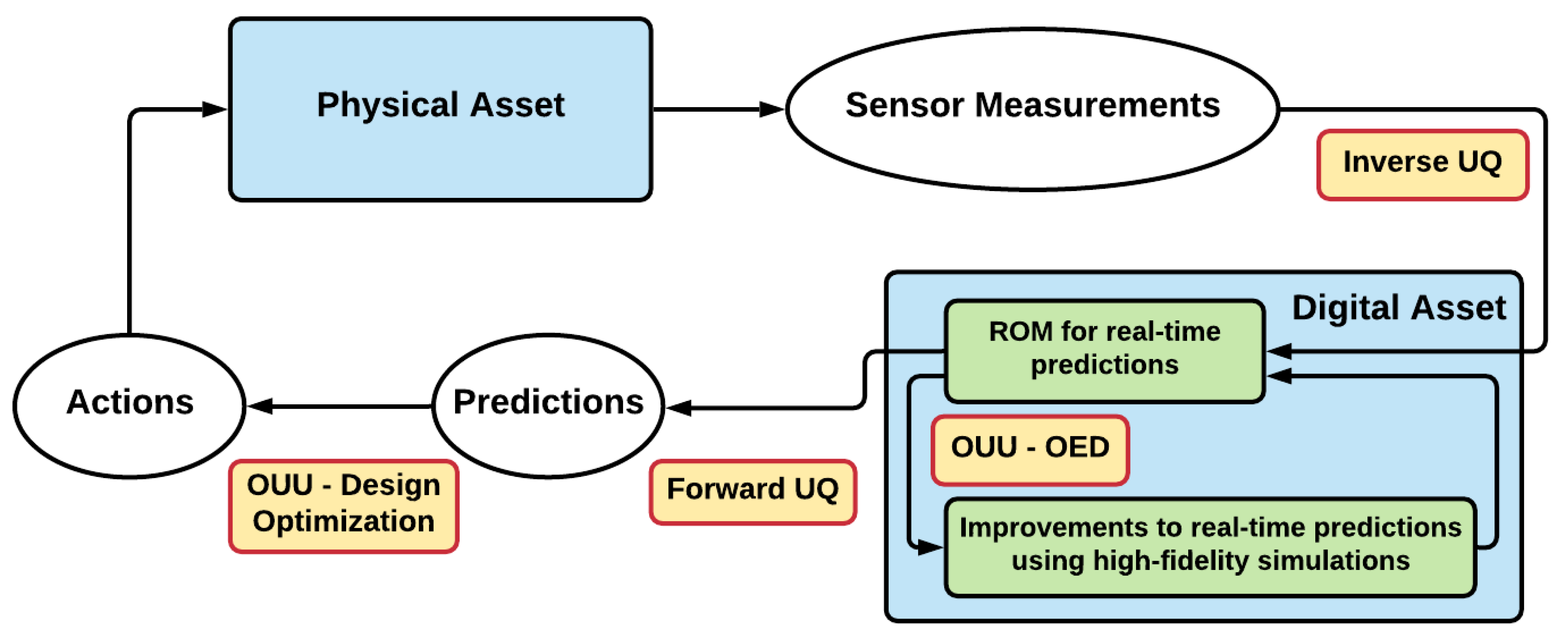
6. Uncertainty Quantification for Digital Twins
6.1. Forward UQ
6.2. Inverse UQ
6.3. Optimization under Uncertainty
6.4. Challenges in UQ for Digital Twins
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schwab, K. The Fourth Industrial Revolution, 1st ed.; Crown Business: New York, NY, USA, 2016. [Google Scholar]
- Fuller, A.; Fan, Z.; Day, C.; Barlow, C. Digital Twin: Enabling Technologies, Challenges and Open Research. IEEE Access 2020, 8, 108952–108971. [Google Scholar] [CrossRef]
- Rasheed, A.; San, O.; Kvamsdal, T. Digital twin: Values, challenges and enablers from a modeling perspective. IEEE Access 2020, 8, 21980–22012. [Google Scholar] [CrossRef]
- Grieves, M. Digital Twin: Manufacturing Excellence through Virtual Factory Replication. 2015. Available online: https://www.researchgate.net/publication/275211047_Digital_Twin_Manufacturing_Excellence_through_Virtual_Factory_Replication (accessed on 4 May 2021).
- Tuegel, E.J.; Ingraffea, A.R.; Eason, T.G.; Spottswood, S.M. Reengineering aircraft structural life prediction using a digital twin. Int. J. Aerosp. Eng. 2011. [Google Scholar] [CrossRef] [Green Version]
- Glaessgen, E.H.; Stargel, D.S. The Digital Twin Paradigm for Future NASA and U.S. Air Force Vehicles. In Proceedings of the 53rd AIAA Structures, Structural Dynamics, and Materials, Honolulu, HI, USA, 23–26 April 2012; American Institute of Aeronautics and Astronautics: Honolulu, HI, USA, 2012. [Google Scholar]
- Boschert, S.; Rosen, R. Digital Twin—The Simulation Aspect. In Mechatronic Futures; Springer: Berlin/Heidelberg, Germany, 2016; pp. 59–74. [Google Scholar] [CrossRef]
- Chen, Y. Integrated and Intelligent Manufacturing: Perspectives and Enablers. Engineering 2017, 3, 588–595. [Google Scholar] [CrossRef]
- Liu, Z.; Meyendorf, N.; Mrad, N. The role of data fusion in predictive maintenance using digital twin. In AIP Conference Proceedings; American Institute of Physics Inc.: College Park, MD, USA, 2018; Volume 1949, p. 50007. [Google Scholar] [CrossRef]
- Schluse, M.; Priggemeyer, M.; Atorf, L.; Rossmann, J. Experimentable Digital Twins-Streamlining Simulation-Based Systems Engineering for Industry 4.0. IEEE Trans. Ind. Inform. 2018, 14, 1722–1731. [Google Scholar] [CrossRef]
- Consortium, I.I. Digital Twins for Industrial Applications. White Paper, Object Management Group. 2020. Available online: https://www.iiconsortium.org/pdf/IIC_Digital_Twins_Industrial_Apps_White_Paper_2020-02-18.pdf (accessed on 15 July 2020).
- Jones, D.; Snider, C.; Nassehi, A.; Yon, J.; Hicks, B. Characterising the Digital Twin: A systematic literature review. CIRP J. Manuf. Sci. Technol. 2020, 29, 36–52. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, Y.; Pessôa, M.V.P.; Peng, Q.; Tan, R. Conceptual digital twin modeling based on an integrated five-dimensional framework and TRIZ function model. J. Manuf. Syst. 2021, 58, 79–93. [Google Scholar] [CrossRef]
- Qi, Q.; Tao, F.; Hu, T.; Anwer, N.; Liu, A.; Wei, Y.; Wang, L.; Nee, A.Y. Enabling technologies and tools for digital twin. J. Manuf. Syst. 2021, 58, 3–21. [Google Scholar] [CrossRef]
- Liu, M.; Fang, S.; Dong, H.; Xu, C. Review of digital twin about concepts, technologies, and industrial applications. J. Manuf. Syst. 2021, 58, 346–361. [Google Scholar] [CrossRef]
- Garcia, H.E.; Aumeier, S.E.; Al-Rashdan, A.Y.; Rolston, B.L. Secure embedded intelligence in nuclear systems: Framework and methods. Ann. Nucl. Energy 2020, 140, 107261. [Google Scholar] [CrossRef]
- Garcia, H.E.; Aumeier, S.E.; Al-Rashdan, A.Y. Integrated State Awareness through Secure Embedded Intelligence in Nuclear Systems: Opportunities and Implications. Nucl. Sci. Eng. 2020, 194, 249–269. [Google Scholar] [CrossRef]
- Lu, C.; Lyu, J.; Zhang, L.; Gong, A.; Fan, Y.; Yan, J.; Li, X. Nuclear power plants with artificial intelligence in industry 4.0 era: Top-level design and current applications—A systemic review. IEEE Access 2020, 8, 194315–194332. [Google Scholar] [CrossRef]
- Lin, L.; Bao, H.; Dinh, N. Uncertainty Quantification and Software Risk Analysis for Digital Twins in the Nearly Autonomous Management and Control Systems: A Review. Ann. Nucl. Energy 2021, 160, 108362. [Google Scholar] [CrossRef]
- GIF Portal—Portal Site Public Home. Web. Available online: https://www.gen-4.org/ (accessed on 4 May 2021).
- Tao, F.; Qi, Q.; Wang, L.; Nee, A.Y. Digital Twins and Cyber–Physical Systems toward Smart Manufacturing and Industry 4.0: Correlation and Comparison. Engineering 2019, 5, 653–661. [Google Scholar] [CrossRef]
- Richards, I.A. Plato’s Republic; Cambridge U.P.: Cambridge, UK, 1966. [Google Scholar]
- Putnam, H. Representation and Reality; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- RELAP5-3D Code Development Team. RELAP5-3D Code Manual; Technical Report INEEL-EXT-98-00834; Idaho National Engineering and Environmental Laboratory: Idaho Falls, ID, USA, 2012. [Google Scholar]
- Chung, B.D.; Kim, K.D.; Bae, S.W.; Jeong, J.J.; Lee, S.W.; Hwang, M.K.; Yoon, C. MARS Code Manual Volume I: Code Structure, System Models, and Solution Methods; Korea Atomic Energy Research Institute: Daejeon, Korea, 2010. [Google Scholar]
- Turinsky, P.J.; Al-Chalabi, R.M.; Engrand, P.; Sarsour, H.N.; Faure, F.X.; Guo, W. NESTLE: Few-Group Neutron Diffusion Equation Solver Utilizing the Nodal Expansion Method for Eigenvalue, Adjoint, Fixed-Source Steady-State and Transient Problems; U.S. Department of Energy, Office of Scientific and Technical Information: Washington, DC, USA, 1994. [CrossRef] [Green Version]
- Wiltshire, J. Developments in Full-Scope, Real-Time Nuclear Plant Simulators. In Advances in Nuclear Science and Technology: Simulators for Nuclear Power; Lewins, J., Becker, M., Eds.; Springer US: Boston, MA, USA, 1986; pp. 191–218. [Google Scholar] [CrossRef]
- TRACE V5.0 Theory Manual. Technical Report ADAMS Accession No. ML120060218. 2012. Available online: http://www.nrc.gov/docs/ML1200/ML120060218.pdf (accessed on 23 February 2021).
- Studsvik Scandpower, Inc. SIMULATE-3: Advanced Three-Dimensional Two-Group Reactor Analysis Code; Technical Report SSP-09/447-U Rev 0; Studsvik Scandpower, Inc.: Newton, MA, USA, 2009. [Google Scholar]
- Derstine, K. DIF3D: A Code to Solve One-, Two-, and Three-Dimensional Finite-Difference Diffusion Theory Problems; Number ANL-82-64; Argonne National Laboratory: Lemont, IL, USA, 1984; pp. 1–175. [Google Scholar]
- Multer, E.; Teuchert, E. VSOP-A, Input Manual: A Multi-Scale, Multi-Physics Simulation Package for High-Temperature Gas Cooled Reactors; Technical Report; Nuclear Technical Consultants: Rockville, MD, USA, 2006. [Google Scholar]
- Seker, V.; Drzewiecki, T.; Downar, T.; Kelly, J.M. Modeling Prismatic HTGRs with U.S. N.R.C Advanced Gas Reactor Evaluator (Agree). In PHYSOR 2012—Advances in Reactor Physics; American Nuclear Society: Knoxville, TN, USA, 2012. [Google Scholar]
- CASL|The Consortium for Advance Simulation of Light Water Reactors. Available online: www.casl.gov (accessed on 1 September 2016).
- NEAMS—INL. Web. Available online: https://inl.gov/neams/ (accessed on 4 May 2021).
- Turner, J.A.; Clarno, K.; Sieger, M.; Bartlett, R.; Collins, B.; Pawlowski, R.; Schmidt, R.; Summers, R. The Virtual Environment for Reactor Applications (VERA): Design and architecture. J. Comput. Phys. 2016, 326, 544–568. [Google Scholar] [CrossRef] [Green Version]
- Kochunas, B.; Collins, B.; Stimpson, S.; Salko, R.; Jabaay, D.; Graham, A.; Liu, Y.; Seog Kim, K.; Wieselquist, W.; Godfrey, A.; et al. VERA Core Simulator Methodology for Pressurized Water Reactor Cycle Depletion. Nucl. Sci. Eng. 2017, 185, 217–231. [Google Scholar] [CrossRef]
- Permann, C.J.; Gaston, D.R.; Andrš, D.; Carlsen, R.W.; Kong, F.; Lindsay, A.D.; Miller, J.M.; Peterson, J.W.; Slaughter, A.E.; Stogner, R.H.; et al. MOOSE: Enabling massively parallel multiphysics simulation. SoftwareX 2020, 11, 100430. [Google Scholar] [CrossRef]
- Hu, R.; Zou, L.; Hu, G.; Nunez, D.; Mui, T.; Fei, T. SAM Theory Manual; Technical Report ANL/NSE-17/4 Rev. 1; Argonne National Laboratory: Lemont, IL, USA, 2021. [Google Scholar] [CrossRef]
- Alfonsi, A.; Rabiti, C.; Mandelli, D.; Cogliati, J.; Wang, C.; Talbot, P.W.; Maljovec, D.P.; Smith, C. RAVEN Theory Manual; Technical Report; Idaho National Laboratory (INL): Idaho Falls, ID, USA, 2020. [Google Scholar]
- Modelica Language Specification Version 3.4. Modelica Association. 2017. Available online: https://modelica.org/documents/ModelicaSpec34.pdf (accessed on 10 October 2020).
- Greenwood, M. TRANSFORM—TRANsient Simulation Framework of Reconfigurable Models; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2017. [Google Scholar] [CrossRef]
- Frick, K.; Bragg-Sitton, S. Development of the NuScale Power Module in the INL Modelica Ecosystem. Nucl. Technol. 2020, 1–22. [Google Scholar] [CrossRef]
- Guillen, D.; Wendt, D. Integration of a Microturbine Power Conversion Unit in MAGNETl; Technical Report INL/EXT-20-57712; Idaho National Laboratory: Idaho Falls, ID, USA, 2020. [Google Scholar]
- De wet, D.; Peterson, P.F.; Greenwood, M.S. A Frequency Response Approach to Model Validation for the Compact Integral Effects Test Facility in Transform; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2019. [Google Scholar]
- Zou, L.; Hu, G.; O’Grady, D.; Hu, R. Code validation of SAM using natural-circulation experimental data from the compact integral effects test (CIET) facility. Nucl. Eng. Des. 2021, 377, 111144. [Google Scholar] [CrossRef]
- PROJECT“SAFARI”—Secure Automation For Advanced Reactor Innovation. Available online: https://arpa-e.energy.gov/technologies/projects/project-safari-secure-automation-advanced-reactor-innovation (accessed on 7 April 2021).
- Digital Twin-Based Asset Performance and Reliability Diagnosis for the HTGR Reactor Cavity Cooling System Using Metroscope. Available online: https://arpa-e.energy.gov/technologies/projects/digital-twin-based-asset-performance-and-reliability-diagnosis-htgr-reactor (accessed on 7 April 2021).
- High-Fidelity Digital Twins for BWRX-300 Critical Systems. Available online: https://arpa-e.energy.gov/technologies/projects/high-fidelity-digital-twins-bwrx-300-critical-systems (accessed on 7 April 2021).
- Advanced Operation & Maintenance Techniques Implemented in the Xe-100 Plant Digital Twin to Reduce Fixed O&M Cost. Available online: https://arpa-e.energy.gov/technologies/projects/advanced-operation-maintenance-techniques-implemented-xe-100-plant-digital (accessed on 7 April 2021).
- AI-Enabled Predictive Maintenance Digital Twins for Advanced Nuclear Reactors. Available online: https://arpa-e.energy.gov/technologies/projects/ai-enabled-predictive-maintenance-digital-twins-advanced-nuclear-reactors (accessed on 7 April 2021).
- McClure, P.R.; Poston, D.I.; Gibson, M.A.; Mason, L.S.; Robinson, R.C. Kilopower Project: The KRUSTY Fission Power Experiment and Potential Missions. Nucl. Technol. 2020, 206, S1–S12. [Google Scholar] [CrossRef]
- Suzuki, K.; Shimazaki, J.; Shinohara, Y. Application of H∞ control theory to power control of a nonlinear reactor model. Nucl. Sci. Eng. 1993, 115, 142–151. [Google Scholar] [CrossRef]
- Wang, G.; Wu, J.; Zeng, B.; Xu, Z.; Wu, W.; Ma, X. State-Space Model Predictive Control Method for Core Power Control in Pressurized Water Reactor Nuclear Power Stations. Nucl. Eng. Technol. 2017, 49, 134–140. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Wu, J.; Zeng, B.; Xu, Z.; Ma, X. A nonlinear model predictive tracking control strategy for modular high-temperature gas-cooled reactors. Ann. Nucl. Energy 2018, 122, 229–240. [Google Scholar] [CrossRef]
- Choi, S.; Kinast, S.; Seker, V.; Filippone, C.; Kochunas, B. Preliminary Study of Model Predictive Control for Load Follow Operation of Holos Reactor. Trans. Am. Nucl. Soc. 2020, 122, 660–663. [Google Scholar] [CrossRef]
- Mowrey, J.A.; Boylan, P.R.; Abdel-Khalik, S.I. Modeling of boiling water reactor feedwater control algorithms. Nucl. Technol. 1998, 124, 223–242. [Google Scholar] [CrossRef]
- Li, G. Modeling and LQG/LTR control for power and axial power difference of load-follow PWR core. Ann. Nucl. Energy 2014, 68, 193–203. [Google Scholar] [CrossRef]
- García, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M. Robust model predictive control: A survey. In Robustness in Identification and Control; Springer: London, UK, 2007; pp. 207–226. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control. In Communications and Control Engineering; Springer: Berlin/Heidelberg, Germany, 2011; pp. 43–66. ISBN 9780857295002. [Google Scholar] [CrossRef]
- Kabzan, J.; Hewing, L.; Liniger, A.; Zeilinger, M.N. Learning-Based Model Predictive Control for Autonomous Racing. IEEE Robot. Autom. Lett. 2019, 4, 3363–3370. [Google Scholar] [CrossRef] [Green Version]
- Mandelli, D.; Alfonsi, A.; Rabiti, C. Generation and Use of Reduced Order Models for Safety Applications Using RAVEN. Trans. Am. Nucl. Soc. 2015, 113, 779–782. [Google Scholar]
- Modelica Association. Functional Mock-Up Interface for Model Exchange and Co-Simulation Version 2.0.2; Modelica Association: Linköping, Sweden, 2020. [Google Scholar]
- Diachin, L.; Bauer, A.; Fix, B.; Kraftcheck, J.; Jansen, K.; Luo, X.; Miller, M.; Ollivier-Gooch, C.; Shephard, M.S.; Tautges, T.; et al. Interoperable mesh and geometry tools for advanced petascale simulations. J. Phys. Conf. Ser. 2007, 78, 012015. [Google Scholar] [CrossRef]
- Schmidt, R.; Belcourt, N.; Hooper, R.; Pawlowski, R. An Introduction to LIME 1.0 and its Use in Coupling Codes for Multiphysics Simulations; Technical Report SAND2011-8524; Sandia National Laboratories: Albuquerque, NM, USA, 2011. [Google Scholar]
- Gaston, D.R.; Permann, C.J.; Peterson, J.W.; Slaughter, A.E.; Andrš, D.; Wang, Y.; Short, M.P.; Perez, D.M.; Tonks, M.R.; Ortensi, J.; et al. Physics-based multiscale coupling for full core nuclear reactor simulation. Ann. Nucl. Energy 2015, 84, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Slattery, S.R. Mesh-free data transfer algorithms for partitioned multiphysics problems: Conservation, accuracy, and parallelism. J. Comput. Phys. 2016, 307, 164–188. [Google Scholar] [CrossRef] [Green Version]
- Touran, N.W.; Gilleland, J.; Malmgren, G.T.; Whitmer, C.; Gates, W.H. Computational Tools for the Integrated Design of Advanced Nuclear Reactors. Engineering 2017, 3, 518–526. [Google Scholar] [CrossRef]
- ISO Central Secretary. Cybersecurity—IoT Security and Privacy—Guidelines; Standard ISO/IEC DIS 27400; International Organization for Standardization: Geneva, Switzerland, 2021. [Google Scholar]
- Kawatsu, K. PHM by Using Multi-Physics System-Level Modeling and Simulation for EMAs of Liquid Rocket Engine. In IEEE Aerospace Conference Proceedings; IEEE Computer Society: Washington, DC, USA, 2019. [Google Scholar] [CrossRef]
- Pascale, F.; Adinolfi, E.A.; Avagliano, M.; Giannella, V.; Salas, A. A Low Energy IoT Application Using Beacon for Indoor Localization. Appl. Sci. 2021, 11, 4902. [Google Scholar] [CrossRef]
- U.S. Nuclear Regulatory Commission. Systems Analysis Programs for Hands-on Integrated Reliability Evaluations (SAPHIRE) Version 8: Overview and Summary; Technical Report NUREG/CR-7039; U.S. Nuclear Regulatory Commission: Rockland, MD, USA, 2011.
- Bao, H.; Zhang, H.; Thomas, K. An Integrated Risk Assessment Process for Digital Instrumentation and Control Upgrades of Nuclear Power Plants; Technical Report; Idaho National Laboratory: Idaho Falls, ID, USA, 2019. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Min, D.; Choi, E.; Lee, J.W. Dependability and Security Quantification of an Internet of Medical Things Infrastructure based on Cloud-Fog-Edge Continuum for Healthcare Monitoring using Hierarchical Models. IEEE Internet Things J. 2021, 1. [Google Scholar] [CrossRef]
- Lee, J.C.; McCormick, N.J. Risk and Safety Analysis of Nuclear Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Industrial-Process Measurement, Control and Automation—Digital Factory Framework—Part 1: General Principles; Standard IEC 62832-1:2020; International Electrotechnical Commission: Geneva, Switzerland, 2020. [Google Scholar]
- ISO Central Secretary. Digital Twin—Use Cases; Standard ISO/IEC AWI 30172; International Organization for Standardization: Geneva, Switzerland, 2021. [Google Scholar]
- ISO Central Secretary. Automation Systems and Integration—Digital Twin Framework for Manufacturing—Part 1: Overview and General Principles; Standard ISO/FDIS 23247-1; International Organization for Standardization: Geneva, Switzerland, 2020. [Google Scholar]
- ISO Central Secretary. Automation Systems and Integration—Digital Twin Framework for Manufacturing—Part 2: Reference Architecture; Standard ISO/FDIS 23247-2; International Organization for Standardization: Geneva, Switzerland, 2020. [Google Scholar]
- ISO Central Secretary. Automation Systems and Integration—Digital Twin Framework for Manufacturing—Part 3: Digital Representation of Manufacturing Elements; Standard ISO/FDIS 23247-3; International Organization for Standardization: Geneva, Switzerland, 2020. [Google Scholar]
- ISO Central Secretary. Automation Systems and Integration—Digital Twin Framework for Manufacturing—Part 4: Information Exchange; Standard ISO/FDIS 23247-4; International Organization for Standardization: Geneva, Switzerland, 2020. [Google Scholar]
- ISO Central Secretary. Automation Systems and Integration—Industrial Data—Visualization Elements of Digital Twins; Standard ISO/TR 24464:2020; International Organization for Standardization: Geneva, Switzerland, 2020. [Google Scholar]
- Oberkampf, W.L.; Trucano, T.G.; Hirsch, C. Verification, validation, and predictive capability in computational engineering and physics. Appl. Mech. Rev. 2004, 57, 345–384. [Google Scholar] [CrossRef] [Green Version]
- Berger, J.O. Statistical Decision Theory and Bayesian Analysis; Springer: New York, NY, USA, 1985. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability, 3rd ed.; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Bernardo, J.M.; Smith, A.F.M. Bayesian Theory; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Jaynes, E.T.; Bretthorst, G.L. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Cox, R.T. Probability, Frequency and Reasonable Expectation. Am. J. Phys. 1946, 14, 1–13. [Google Scholar] [CrossRef]
- Barron, A.; Schervish, M.J.; Wasserman, L. The consistency of posterior distributions in nonparametric problems. Ann. Stat. 1999, 27, 536–561. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Sivia, D.S.; Skilling, J. Data Analysis: A Bayesian Tutorial, 2nd ed.; Oxford University Press: New York, NY, USA, 2006; p. 246. [Google Scholar]
- Von Toussaint, U. Bayesian inference in physics. Rev. Mod. Phys. 2011, 83, 943–999. [Google Scholar] [CrossRef] [Green Version]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods; Springer: New York, NY, USA, 2004. [Google Scholar] [CrossRef] [Green Version]
- Huang, D.; Abdel-Khalik, H.S. Nuclear data uncertainty propagation and modeling uncertainty impact evaluation in neutronics core simulation. Prog. Nucl. Energy 2020, 128, 103443. [Google Scholar] [CrossRef]
- Trivedi, I.; Hou, J.; Grasso, G.; Ivanov, K.; Franceschini, F. Nuclear Data Uncertainty Quantification and Propagation for Safety Analysis of Lead-Cooled Fast Reactors. Sci. Technol. Nucl. Install. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Andrieu, C.; de Freitas, N.; Doucet, A.; Jordan, M.I. An Introduction to MCMC for Machine Learning. Mach. Learn. 2003, 50, 5–43. [Google Scholar] [CrossRef] [Green Version]
- Brooks, S.; Gelman, A.; Jones, G.; Meng, X.L. (Eds.) Handbook of Markov Chain Monte Carlo; Chapman & Hall/CRC: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Neal, R.M. MCMC Using Hamiltonian Dynamics. In Handbook of Markov Chain Monte Carlo; Chapman and Hall/CRC: New York, NY, USA, 2011; pp. 113–162. [Google Scholar] [CrossRef] [Green Version]
- Betancourt, M. A Conceptual Introduction to Hamiltonian Monte Carlo. arXiv 2017, arXiv:1701.02434. [Google Scholar]
- Wu, X.; Xie, Z.; Alsafadi, F.; Kozlowski, T. A Comprehensive Survey of Inverse Uncertainty Quantification of Physical Model Parameters in Nuclear System Thermal-Hydraulics Codes. arXiv 2021, arXiv:2104.12919. [Google Scholar]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Law, K.; Stuart, A.; Zygalakis, K. Data Assimilation. In Texts in Applied Mathematics; Springer International Publishing: Cham, Switzerland, 2015; Volume 62. [Google Scholar] [CrossRef] [Green Version]
- Lindley, D.V. On a Measure of the Information Provided by an Experiment. Ann. Math. Stat. 1956, 27, 986–1005. [Google Scholar] [CrossRef]
- Fedorov, V.V. Theory of Optimal Experiments; Academic Press: New York, NY, USA, 1972; p. 291. [Google Scholar]
- Chaloner, K.; Verdinelli, I. Bayesian Experimental Design: A Review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Müller, P. Simulation Based Optimal Design. Handb. Stat. 2005, 25, 509–518. [Google Scholar] [CrossRef]
- Cox, D.R.; Reid, N. The Theory of the Design of Experiments; Chapman & Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Santner, T.J.; Williams, B.J.; Notz, W.I. The Design and Analysis of Computer Experiments, 2nd ed.; Springer: New York, NY, USA, 2018. [Google Scholar]
- Wang, G.G.; Shan, S. Review of Metamodeling Techniques in Support of Engineering Design Optimization. J. Mech. Des. 2007, 129, 370–380. [Google Scholar] [CrossRef]
- Ryan, K.J. Estimating Expected Information Gains for Experimental Designs With Application to the Random Fatigue-Limit Model. J. Comput. Graph. Stat. 2003, 12, 585–603. [Google Scholar] [CrossRef]
- Ryan, E.G.; Drovandi, C.C.; Mcgree, J.M.; Pettitt, A.N. A Review of Modern Computational Algorithms for Bayesian Optimal Design. Int. Stat. Rev. 2016, 84, 128–154. [Google Scholar] [CrossRef] [Green Version]
- Adams, B.; Bohnhoff, W.; Dalbey, K.; Ebeida, M.; Eddy, J.; Eldred, M.; Hooper, R.; Hough, P.; Hu, K.; Jakeman, J.; et al. Dakota, A Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis: Version 6.12 User’s Manual; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2020. [Google Scholar]
- Debusschere, B.J.; Najm, H.N.; Pébay, P.P.; Knio, O.M.; Ghanem, R.G.; Le Maître, O.P. Numerical Challenges in the Use of Polynomial Chaos Representations for Stochastic Processes. SIAM J. Sci. Comput. 2004, 26, 698–719. [Google Scholar] [CrossRef]
- Prudencio, E.E.; Schulz, K.W. The Parallel C++ Statistical Library ‘QUESO’: Quantification of Uncertainty for Estimation, Simulation and Optimization. In Euro-Par 2011: Parallel Processing Workshops. Euro-Par 2011. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 398–407. [Google Scholar] [CrossRef]
- Niederreiter, H. Random Number Generation and Quasi-Monte Carlo Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Haario, H.; Laine, M.; Mira, A.; Saksman, E. DRAM: Efficient adaptive MCMC. Stat. Comput. 2006, 16, 339–354. [Google Scholar] [CrossRef]
- Roberts, G.O.; Tweedie, R.L. Exponential convergence of Langevin distributions and their discrete approximations. Bernoulli 1996, 2, 341–363. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Butepage, J.; Kjellstrom, H.; Mandt, S. Advances in Variational Inference. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2008–2026. [Google Scholar] [CrossRef] [Green Version]
- Huan, X.; Marzouk, Y.M. Simulation-based optimal Bayesian experimental design for nonlinear systems. J. Comput. Phys. 2013, 232, 288–317. [Google Scholar] [CrossRef] [Green Version]
- Huan, X.; Marzouk, Y.M. Gradient-Based Stochastic Optimization Methods in Bayesian Experimental Design. Int. J. Uncertain. Quantif. 2014, 4, 479–510. [Google Scholar] [CrossRef]
- Long, Q.; Scavino, M.; Tempone, R.; Wang, S. Fast estimation of expected information gains for Bayesian experimental designs based on Laplace approximations. Comput. Methods Appl. Mech. Eng. 2013, 259, 24–39. [Google Scholar] [CrossRef]
- Alexanderian, A.; Petra, N.; Stadler, G.; Ghattas, O. A Fast and Scalable Method for A-Optimal Design of Experiments for Infinite-dimensional Bayesian Nonlinear Inverse Problems. SIAM J. Sci. Comput. 2016, 38, A243–A272. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Chen, P.; Ghattas, O. A fast and scalable computational framework for large-scale and high-dimensional Bayesian optimal experimental design. arXiv 2020, arXiv:2010.15196. [Google Scholar]
- Van Der Maaten, L.J.P.; Postma, E.O.; Van Den Herik, H.J. Dimensionality Reduction: A Comparative Review. J. Mach. Learn. Res. 2009, 10, 1–41. [Google Scholar] [CrossRef]
- Cunningham, J.P.; Ghahramani, Z. Linear dimensionality reduction: Survey, insights, and generalizations. J. Mach. Learn. Res. 2015, 16, 2859–2900. [Google Scholar]
- Mahoney, M.W. Randomized Algorithms for Matrices and Data. Found. Trends® Mach. Learn. 2010, 3, 123–224. [Google Scholar] [CrossRef]
- Agarwal, P.K.; Har-Peled, S.; Varadarajan, K.R. Geometric Approximation via Coresets. Comb. Comput. Geom. 2005, 52, 1–30. [Google Scholar]
- Feldman, D.; Langberg, M. A unified framework for approximating and clustering data. In Proceedings of the 43rd Annual ACM Symposium on Theory of Computing—STOC’11, San Jose, CA, USA, 4–11 June 2011; ACM Press: New York, NY, USA, 2011; p. 569. [Google Scholar] [CrossRef] [Green Version]
- Huan, X.; Marzouk, Y.M. Sequential Bayesian optimal experimental design via approximate dynamic programming. arXiv 2016, arXiv:1604.08320. [Google Scholar]
- Kapteyn, M.G.; Pretorius, J.V.; Willcox, K.E. A probabilistic graphical model foundation for enabling predictive digital twins at scale. arXiv 2020, arXiv:2012.05841. [Google Scholar]
- Singh, V.; Willcox, K.E. Decision-Making Under Uncertainty for a Digital Thread-Enabled Design Process. J. Mech. Des. 2021, 143, 1–12. [Google Scholar] [CrossRef]
- Mcknight, D.H.; Carter, M.; Thatcher, J.B.; Clay, P.F. Trust in a specific technology. ACM Trans. Manag. Inf. Syst. 2011, 2, 1–25. [Google Scholar] [CrossRef]
- Thiebes, S.; Lins, S.; Sunyaev, A. Trustworthy artificial intelligence. Electron. Mark. 2020, 1–18. [Google Scholar] [CrossRef]

| Component | Differential Eqn. | Algebraic Eqn. | Boolean Eqn. |
|---|---|---|---|
| Reactor (x,y) | – | ||
| Reactor Axial | – | ||
| Steam Generator | – | ||
| Turbine | – | ||
| Feed Pumps | – | ||
| Control Systems | – | ||
| Electrical System | – | ||
| Protection System | – | – | |
| Total |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kochunas, B.; Huan, X. Digital Twin Concepts with Uncertainty for Nuclear Power Applications. Energies 2021, 14, 4235. https://doi.org/10.3390/en14144235
Kochunas B, Huan X. Digital Twin Concepts with Uncertainty for Nuclear Power Applications. Energies. 2021; 14(14):4235. https://doi.org/10.3390/en14144235
Chicago/Turabian StyleKochunas, Brendan, and Xun Huan. 2021. "Digital Twin Concepts with Uncertainty for Nuclear Power Applications" Energies 14, no. 14: 4235. https://doi.org/10.3390/en14144235
APA StyleKochunas, B., & Huan, X. (2021). Digital Twin Concepts with Uncertainty for Nuclear Power Applications. Energies, 14(14), 4235. https://doi.org/10.3390/en14144235






